এই আর্টিকেলে আমরা মাধ্যমিক ভৌতবিজ্ঞানের একটি গুরুত্বপূর্ণ প্রশ্ন “কোনো প্রিজমের মধ্য দিয়ে আলোর প্রতিসরণের ক্ষেত্রে দেখাও যে চ্যুতিকোণ, \(\delta=i_1+i_2-A\), যেখানে \(i_1\) = প্রথম প্রতিসারক তলে আপতন কোণ, \(i_2\) = দ্বিতীয় প্রতিসারক তলের প্রতিসরণ কোণ এবং \(A\) = প্রিজমের প্রতিসারক কোণ।” নিয়ে আলোচনা করব। এই প্রশ্নটি মাধ্যমিক ভৌতবিজ্ঞান পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ। এই “কোনো প্রিজমের মধ্য দিয়ে আলোর প্রতিসরণের ক্ষেত্রে দেখাও যে চ্যুতিকোণ, \(\delta=i_1+i_2-A\), যেখানে \(i_1\) = প্রথম প্রতিসারক তলে আপতন কোণ, \(i_2\) = দ্বিতীয় প্রতিসারক তলের প্রতিসরণ কোণ এবং \(A\) = প্রিজমের প্রতিসারক কোণ।” প্রশ্নটি মাধ্যমিক ভৌতবিজ্ঞানের পঞ্চম অধ্যায় “আলো“ -এর একটি গুরুত্বপূর্ণ প্রশ্ন। এই প্রশ্নটি মাধ্যমিক পরীক্ষায় এবং চাকরির পরীক্ষায় প্রায়ই দেখা যায়।

কোনো প্রিজমের মধ্য দিয়ে আলোর প্রতিসরণের ক্ষেত্রে দেখাও যে চ্যুতিকোণ, \(\delta=i_1+i_2-A\), যেখানে \(i_1\) = প্রথম প্রতিসারক তলে আপতন কোণ, \(i_2\) = দ্বিতীয় প্রতিসারক তলের প্রতিসরণ কোণ এবং \(A\) = প্রিজমের প্রতিসারক কোণ।
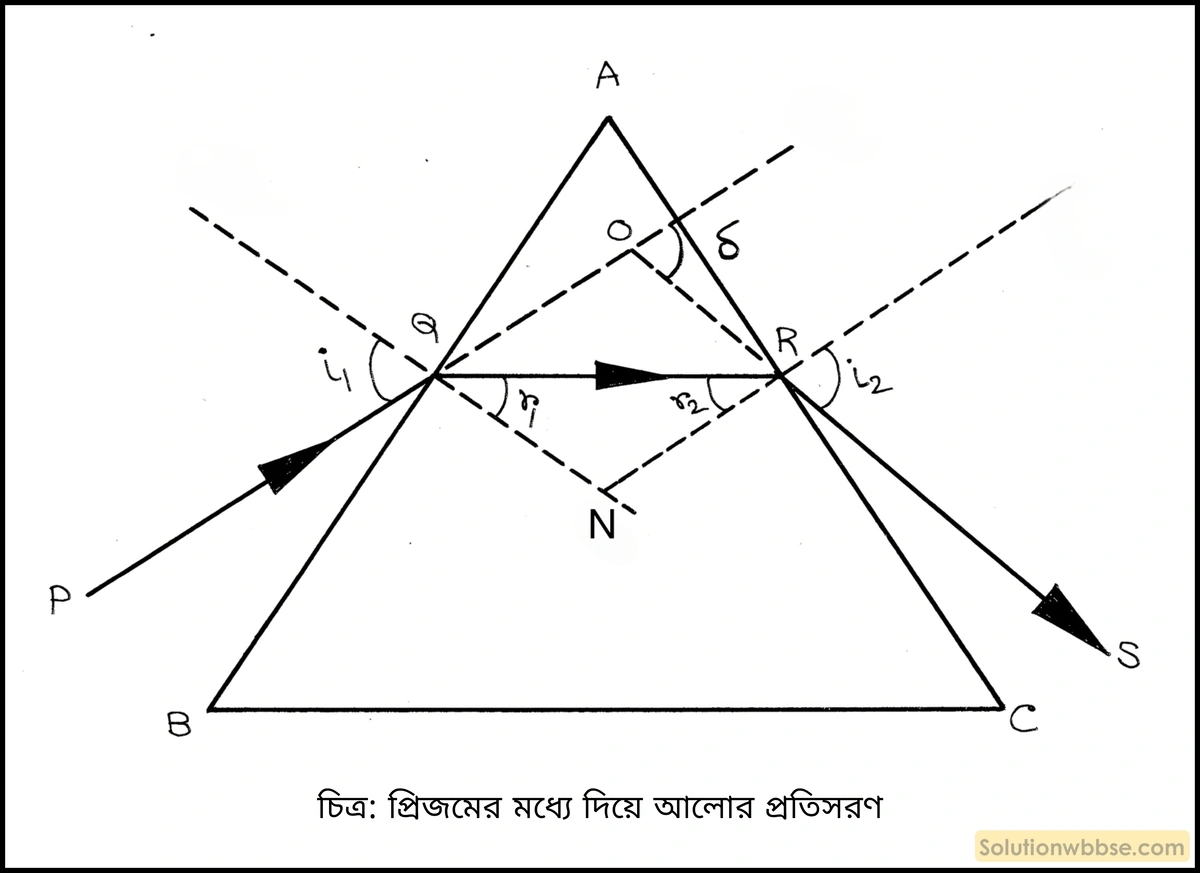
\(A\) প্রতিসারক কোণবিশিষ্ট একটি প্রিজমের প্রধান ছেদ \(ABC\) চিত্রে প্রদর্শিত হয়েছে। প্রিজমটি বায়ুতে অবস্থিত এবং এর উপাদানের প্রতিসরাঙ্ক \(\mu\)।
একটি আলোকরশ্মি \(PQ\) প্রিজমটির প্রধান ছেদের প্রতিসারক তল \(AB\) -এর ওপর \(Q\) বিন্দুতে আপতিত হয়ে প্রতিসরণের নিয়মানুযায়ী প্রিজমের মধ্য দিয়ে \(QR\) পথে প্রতিসৃত হয় এবং প্রিজমের অপর প্রতিসারক তল \(AC\) -এর ওপর \(R\) বিন্দুতে দ্বিতীয়বার প্রতিসৃত হয়ে \(RS\) পথে প্রিজম থেকে বায়ুতে নির্গত হয়। আপতিত রশ্মি \(PQ\) -কে সামনের দিকে ও নির্গত রশ্মি \(RS\) -কে পিছনের দিকে বর্ধিত করা হলে এরা \(O\) বিন্দুতে মিলিত হয়। আপতিত রশ্মির অভিমুখ ও নির্গত রশ্মির অভিমুখের অন্তর্বর্তী কোণ আলোকরশ্মির চ্যুতিকোণ \(\left(\delta\right)\) -কে সূচিত করে।
প্রিজমের দুই প্রতিসারক তল \(AB\) ও \(AC\) -এর উপর যথাক্রমে \(Q\) ও \(R\) বিন্দুতে অঙ্কিত অভিলম্বদ্বয় প্রিজমের ভিতর \(N\) বিন্দুতে মিলিত হয়। প্রদত্ত চিত্রানুযায়ী প্রিজমের \(AB\) প্রতিসারক তলের \(Q\) বিন্দুতে আপতন ও প্রতিসরণ কোণ যথাক্রমে \(i_1\) ও \(r_1\) এবং অপর প্রতিসারক তল \(AC\) -এর \(R\) বিন্দুতে আপতন ও প্রতিসরণ কোণ যথাক্রমে \(r_2\) ও \(i_2\)।
প্রদত্ত চিত্রে, \(\bigtriangleup QOR\) -এর ক্ষেত্রে \(\angle OQR=\left(i_1-r_1\right)\)
এবং \(\angle ORQ=\left(i_2-r_2\right)\)।
∴ চ্যুতি কোণ, \(\delta=\angle OQR+\angle ORQ\) [∵ ত্রিভুজের বহিস্থ কোণ অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান]
\(=\left(i_1-r_1\right)+\left(i_2-r_2\right)\\\)\(=\left(i_1+i_2\right)-\left(r_1+r_2\right)\) —\(\left(1\right)\)
আবার, \(AQNR\) চতুর্ভুজের ক্ষেত্রে
\(\angle QAR+\angle ARN+\angle AQN+\angle QNR=360^\circ\\\)বা, \(A+90^\circ+90^\circ+\angle QNR=360^\circ\) [এখানে \(\angle QAR=A=\) প্রিজমের প্রতিসারক কোণ]
বা, \(A+\angle QNR=180^\circ\) —\(\left(2\right)\)
এখন \(\bigtriangleup NQR\) -এর ক্ষেত্রে,
\(r_1+r_2+\angle QNR=180^\circ\) —\(\left(3\right)\)
∴ \(\left(2\right)\) ও \(\left(3\right)\) নং সমীকরণদ্বয়কে তুলনা করে পাই,
\(A=r_1+r_2\) —\(\left(4\right)\)
∴ \(\left(1\right)\) নং ও \(\left(4\right)\) নং সমীকরণ থেকে পাই,
\(\delta=i_1+i_2-A\\\)এটিই হল প্রিজমে প্রতিসরণের ক্ষেত্রে আপতিত ও নির্গত রশ্মির মধ্যে চ্যুতিকোণের রাশিমালা।
কিছু গুরুত্বপূর্ণ প্রশ্নোত্তর
প্রিজমের মাধ্যমে আলোর প্রতিসরণে চ্যুতিকোণ (δ) কী?
চ্যুতিকোণ হলো আপতিত রশ্মির অভিমুখ ও নির্গত রশ্মির অভিমুখের মধ্যবর্তী কোণ। এটি প্রিজমের মাধ্যমে আলোকরশ্মির বেঁকে যাওয়ার পরিমাণ নির্দেশ করে।
প্রিজমের প্রতিসারক কোণ (A) কী?
প্রিজমের প্রতিসারক কোণ (A) হল প্রিজমের দুটি প্রতিসারক তলের মধ্যবর্তী কোণ। চিত্রে ∠BAC কে A দ্বারা সূচিত করা হয়েছে।
প্রিজমের মাধ্যমে সাদা আলোর বিচ্ছুরণ কেন হয়?
বিভিন্ন রঙের আলোর জন্য প্রিজমের উপাদানের প্রতিসরাঙ্ক ভিন্ন হওয়ায় (μ রঙের উপর নির্ভরশীল), ফলে চ্যুতিকোণও ভিন্ন হয়। এভাবে আলো বর্ণালীতে বিভক্ত হয়।
প্রিজমের বাইরে আলোর গতি কীভাবে পরিবর্তিত হয়?
প্রিজমের ভিতরে আলোর গতি \(\frac c\mu\) (যেখানে c শূন্যস্থানে আলোর গতি), কিন্তু বাইরে গতি আবার c -তে ফিরে আসে।
চ্যুতিকোণ ঋণাত্মক হতে পারে কি?
চ্যুতিকোণ ঋণাত্মক হতে পারে না, চ্যুতিকোণ সর্বদা ধনাত্মক, কারণ এটি আপতিত ও নির্গত রশ্মির মধ্যবর্তী সূক্ষ্মতম কোণ।
প্রিজমের কার্যকরী ব্যবহার কী?
প্রিজমের কার্যকরী ব্যবহার হল –
1. বর্ণালী বিশ্লেষণ,
2. আলোকীয় যন্ত্রে (যেমন – বাইনোকুলার, ক্যামেরা লেন্স),
3. লেজার রশ্মি নিয়ন্ত্রণে।
আপতন কোণ (i₁) ও প্রতিসরণ কোণ (r₁)-এর মধ্যে সম্পর্ক কী?
স্নেলের সূত্র অনুযায়ী – \(\mu=\frac{\sin\;i_1}{\sin\;r_1}\), যেখানে μ প্রিজমের উপাদানের প্রতিসরাঙ্ক।
চ্যুতিকোণ ন্যূনতম হয় কখন?
যখন i1 = i2 এবং r1 = r2 (সাম্যমিতিক পথ), তখন চ্যুতিকোণ ন্যূনতম মান δmin ধারণ করে।
এই আর্টিকেলে আমরা মাধ্যমিক ভৌতবিজ্ঞানের একটি গুরুত্বপূর্ণ প্রশ্ন “কোনো প্রিজমের মধ্য দিয়ে আলোর প্রতিসরণের ক্ষেত্রে দেখাও যে চ্যুতিকোণ, \(\delta=i_1+i_2-A\), যেখানে \(i_1\) = প্রথম প্রতিসারক তলে আপতন কোণ, \(i_2\) = দ্বিতীয় প্রতিসারক তলের প্রতিসরণ কোণ এবং A = প্রিজমের প্রতিসারক কোণ।” নিয়ে আলোচনা করব। এই প্রশ্নটি মাধ্যমিক ভৌতবিজ্ঞান পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ। এই “কোনো প্রিজমের মধ্য দিয়ে আলোর প্রতিসরণের ক্ষেত্রে দেখাও যে চ্যুতিকোণ, \(\delta=i_1+i_2-A\), যেখানে \(i_1\) = প্রথম প্রতিসারক তলে আপতন কোণ, \(i_2\) = দ্বিতীয় প্রতিসারক তলের প্রতিসরণ কোণ এবং A = প্রিজমের প্রতিসারক কোণ।” প্রশ্নটি মাধ্যমিক ভৌতবিজ্ঞানের পঞ্চম অধ্যায় “আলো“ -এর একটি গুরুত্বপূর্ণ প্রশ্ন। এই প্রশ্নটি মাধ্যমিক পরীক্ষায় এবং চাকরির পরীক্ষায় প্রায়ই দেখা যায়। আশা করি এই আর্টিকেলটি আপনাদের জন্য উপকারী হয়েছে। আপনাদের কোনো প্রশ্ন বা অসুবিধা থাকলে, আমাদের সাথে টেলিগ্রামে যোগাযোগ করতে পারেন, আমরা উত্তর দেওয়ার চেষ্টা করব। তাছাড়া, নিচে আমাদের এই পোস্টটি আপনার প্রিয়জনের সাথে শেয়ার করুন, যাদের এটি প্রয়োজন হতে পারে। ধন্যবাদ।






মন্তব্য করুন