এই আর্টিকেলে আমরা WBBSE বোর্ডের 2026 সালের মাধ্যমিক গণিত (Mathematics) বিষয়ের সাজেশন নিয়ে আলোচনা করবো। এখানে দেওয়া MCQ প্রশ্নগুলো আসন্ন মাধ্যমিক পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ।

পাটিগণিত
1. সরল সুদ ও চক্রবৃদ্ধি সুদের হার বার্ষিক \(10\%\) হলে, দ্বিতীয় বছরে কোনো মূলধনের সরল সুদ ও চক্রবৃদ্ধি সুদের অনুপাত—
(a) \(20:21\)
(b) \(10:11\) [M.P. 2024]
(c) \(5:6\)
(d) \(1:1\)
উত্তর – (b) \(10:11\)
2. A, B, C তিন বন্ধু যথাক্রমে \(x\), \(2x\), \(y\) টাকা মূলধন নিয়ে ব্যবসা শুরু করল, মেয়াদান্তে \(z\) টাকা লাভ হলে, A-এর লভ্যাংশ হবে— [M.P. 2023]
(a) \(\frac{xz}{3x + y}\) টাকা
(b) \(\frac{2xz}{3x + y}\) টাকা
(c) \(\frac{z}{2x + y}\) টাকা
(d) \(\frac{xyz}{3x + y}\) টাকা
উত্তর – (a) \(\frac{xz}{3x + y}\) টাকা
সমাধান – A, B, C এর মূলধনের অনুপাত = \(x : 2x : y\)
লাভ = \(z\) টাকা
∴ A-এর লভ্যাংশ = \(\frac{z}{x + 2x + y} \times x\) টাকা
= \(\frac{xz}{3x + y}\) টাকা
3. একটি গ্রামের বর্তমান জনসংখ্যা \(P\) এবং প্রতি বছর জনসংখ্যা বৃদ্ধির হার \(2r\%\) হলে, \(n\) বছর পর জনসংখ্যা হবে : [M.P. ’22]
(a) \(P(1 + \frac{r}{100})^n\)
(b) \(P(1 + \frac{r}{50})^n\)
(c) \(P(1 + \frac{r^2}{100})^n\)
(d) \(P(1 – \frac{r}{100})^n\)
উত্তর – (b) \(P(1 + \frac{r}{50})^n\)
সমাধান – \(n\) বছর পর জনসংখ্যা হবে
= \(P(1 + \frac{2r}{100})^n \)
= \(P(1 + \frac{r}{50})^n\)
4. ফতিমা, শ্রেয়া এবং স্মিতা তিনজনে মোট \(6,000\) টাকা দিয়ে একটি ব্যবসা শুরু করে। এক বছর পরে ফতিমা, শ্রেয়া এবং স্মিতা যথাক্রমে লভ্যাংশের \(50\) টাকা, \(100\) টাকা এবং \(150\) টাকা পায়। স্মিতা ঐ ব্যবসায় নিয়োজিত করে : [M.P. 2022]
(a) \(1,000\) টাকা
(b) \(2,000\) টাকা
(c) \(3,000\) টাকা
(d) \(4,000\) টাকা
উত্তর – (c) \(3,000\) টাকা
সমাধান – ফতিমা, শ্রেয়া এবং স্মিতার মূলধনের অনুপাত
= তাদের লভ্যাংশের অনুপাত = \(50 : 100 : 150 = 1:2:3\)
∴ স্মিতার মূলধন = \(\frac{6000}{1+2+3} \times 3\) টাকা
= \(\frac{6000}{6} \times 3\) টাকা
= \(3000\) টাকা
5. \(10\) বছরে কোনো আসল দ্বিগুণ হলে, বার্ষিক সরল সুদের হার হল – [M.P. 2020]
(a) \(5\%\)
(b) \(10\%\)
(c) \(15\%\)
(d) \(20\%\)
উত্তর – (b) \(10\%\)
সমাধান – ধরি, আসল = \(₹ 100\)
∴ সুদ-আসল = \(₹ 2 \times 100 = ₹ 200\)
সুদ = \(₹ (200 – 100) = ₹ 100\)
সময় = \(10\) বছর
∴ বার্ষিক সুদের হার = \(\frac{100 \times 100}{100 \times 10} \% = 10\%\)
6. কোনো অংশীদারী ব্যবসাতে দুই বন্ধুর লাভের অনুপাত \(\frac{1}{2} : \frac{1}{3}\) হলে, তাদের মূলধনের অনুপাত হল–[M.P. 2019]
(a) \(2:3\)
(b) \(3:2\)
(c) \(1:1\)
(d) \(5:3\)
উত্তর – (b) \(3:2\)
সমাধান – মূলধনের অনুপাত = লাভের অনুপাত = \(\frac{1}{2} : \frac{1}{3}\)
= \(\frac{1}{2} \times 6 : \frac{1}{3} \times 6\)
= 3 : 2
7. বার্ষিক \(10\%\) সরল সুদে \(b\) মাসের \(a\) টাকার সুদ হল— [M.P. 2018]
(a) \(₹ \frac{ab}{100}\)
(b) \(₹ \frac{ab}{120}\)
(c) \(₹ \frac{ab}{1200}\)
(d) \(₹ \frac{ab}{10}\)
উত্তর – (b) \(₹ \frac{ab}{120}\)
সমাধান – সুদ = \(₹ \frac{a \times b \times 10}{12 \times 100} = ₹ \frac{ab}{120}\)
8. যদি কোনো আসল এবং এক বছরের সুদাসলের অনুপাত \(25:28\) হয়, তাহলে বার্ষিক সুদের হার হল – [M.P. 2017]
(a) \(3\%\)
(b) \(12\%\)
(c) \(10\frac{5}{7}\%\)
(d) \(8\%\)
উত্তর – (b) \(12\%\)
সমাধান – ধরি, আসল = \(₹ 25x\)
∴ সুদাসল = \(₹ 28x\)
∴ সুদ = \(₹ (28x – 25x) = ₹ 3x\)
বার্ষিক সুদের হার = \(\frac{3x \times 100}{25x \times 1} \% = 12\%\)
9. চক্রবৃদ্ধি সুদের ক্ষেত্রে প্রতি-বছর বার্ষিক চক্রবৃদ্ধি সুদের হার—
(a) সমান
(b) অসমান
(c) সমান অথবা অসমান
(d) কোনোটিই নয়
উত্তর – (c) সমান অথবা অসমান
10. \(x\%\) বার্ষিক সরল সুদের হারে কোনো মূলধনের \(x\) বছরের সুদ \(x\) টাকা হলে, মূলধনের পরিমাণ
(a) \(x\) টাকা
(b) \(100x\) টাকা
(c) \(\frac{100}{x}\) টাকা
(d) \(\frac{100}{x^2}\) টাকা
উত্তর – (c) \(\frac{100}{x}\) টাকা
সমাধান – \(I = \frac{prt}{100}\) (সূত্র থেকে পাই)
\(x = \frac{p \times x \times x}{100}\)বা, \(100 = px\)
∴ \(p = \frac{100}{x}\)
11. বার্ষিক \(r\%\) সরল সুদের হারে কোনো মূলধনের \(n\) বছরে মোট সুদ \(\frac{pnr}{25}\) টাকা হলে, মূলধনের পরিমাণ –
(a) \(2p\) টাকা
(b) \(4p\) টাকা
(c) \(\frac{p}{2}\) টাকা
(d) \(\frac{p}{4}\) টাকা
উত্তর – (b) \(4p\) টাকা
সমাধান – মনে করি, মূলধনের পরিমাণ = \(x\) টাকা
\(I = \frac{prt}{100}\) (সূত্র থেকে পাই)
∴ \(\frac{pnr}{25} = \frac{x \times r \times n}{100}\)
বা, \(p = \frac{x}{4}\)
∴ \(x = 4p\)
12. বার্ষিক \(8\%\) হারে সুদে যে টাকার মাসিক সুদ \(10\) টাকা তা হল–
(a) \(1200\) টাকা
(b) \(1500\) টাকা
(c) \(1600\) টাকা
(d) \(1650\) টাকা
উত্তর – (b) \(1500\) টাকা
সমাধান – \(\frac{Prt}{100} = I\), [এখানে \(t = \frac{1}{12}\) বছর]
বা, \(\frac{P \times 8 \times 1}{100 \times 12} = 10\) বা, \(P = \frac{12000}{8} = 1500\)
13. বার্ষিক \(r\%\) হার সরল সুদে \(p\) টাকার \(t\) বছরের সুদ \(I\) হলে,
(a) \(I = prt\)
(b) \(prt I = 100\)
(c) \(prt = 100 \times I\)
(d) কোনোটিই নয়
উত্তর – (c) \(prt = 100 \times I\)
সমাধান – \(I = \frac{prt}{100}\), বা, \(prt = 100 \times I\)
14. একটি ব্যবসায় A \(6000\) টাকা \(4\) মাস এবং B \(12000\) টাকা কিছুমাস খাটায়। ব্যবসার মোট লাভ \(2:3\) অনুপাতে বণ্টিত হলে, B এর টাকা খেটেছিল—
(a) \(3\) মাস
(b) \(4\) মাস
(c) \(6\) মাস
(d) \(8\) মাস
উত্তর – (a) \(3\) মাস
সমাধান – মনে করি, B এর মূলধন \(x\) মাস খাটে
1 মাস সাপেক্ষে A এর মূলধন = \(6000 \times 4\) টাকা = \(24000\) টাকা এবং B এর মূলধন = \(12000x\) টাকা
∴ \(24000 : 12000x = 2:3\)
বা, \(2 : x = 2:3\)
∴ \(x = 3\)
15. বার্ষিক চক্রবৃদ্ধি সুদের হার কত হলে \(2\) বছরে \(2304\) টাকার সমূল চক্রবৃদ্ধি \(2500\) টাকা হবে?
(a) \(4\frac{1}{2}\%\)
(b) \(4\frac{1}{5}\%\)
(c) \(4\frac{1}{6}\%\)
(d) \(4\frac{1}{3}\%\)
উত্তর – (c) \(4\frac{1}{6}\%\)
সমাধান – \(A = P(1 + \frac{r}{100})^n\), (\(A=2500\), \(P=2304\), \(n=2\) বছর)
বা, \(2500 = 2304 (1 + \frac{r}{100})^2\)
বা, \(1 + \frac{r}{100} = \sqrt{\frac{2500}{2304}} = \frac{50}{48}\)
বা, \(\frac{r}{100} = \frac{2}{48} = \frac{1}{24}\),
বা, \(r = \frac{100}{24} = \frac{25}{6} = 4\frac{1}{6}\)
16. কোনো মূলধন \(10\) বছরে দ্বিগুণ হলে, বার্ষিক সরল সুদের হার
(a) \(5\%\)
(b) \(10\%\)
(c) \(15\%\)
(d) \(20\%\)
উত্তর – (b) \(10\%\)
সমাধান – মনে করি মূলধন = \(P\) টাকা
\(10\) বছরে মূলধন দ্বিগুণ হলে সুদের পরিমাণ = \(P\) টাকা
∴ \(I = \frac{prt}{100}\) (সূত্র থেকে পাই)
\(P = \frac{P \times r \times 10}{100}\), বা, \(r = 10\)
∴ সুদের হার = \(10\%\)
17. বার্ষিক \(8\%\) হার সরল সুদে, আসল ও সুদের পরিমাণ এক হলে সময়কাল হবে —
(a) \(6\frac{1}{4}\) বছর
(b) \(8\frac{1}{3}\) বছর
(c) \(12\frac{1}{2}\) বছর
(d) কোনোটিই নয়
উত্তর – (c) \(12\frac{1}{2}\) বছর
সমাধান – ধরি, আসল \( P= x\) টাকা
সুদ \( I= x\) টাকা
∴ \(\frac{Prt}{100} = I\)
বা, \(\frac{x \times 8 \times t}{100} = x\)
বা, \(t = \frac{100}{8} = \frac{25}{2} = 12\frac{1}{2}\)
18. কোনো মূলধন একটি নির্দিষ্ট সরল সুদের হারে \(20\) বছরে দ্বিগুণ হয়। একই সরল সুদের হারে ওই মূলধন তিনগুণ হবে –
(a) \(30\) বছরে
(b) \(35\) বছরে
(c) \(40\) বছরে
(d) \(45\) বছরে
উত্তর – (c) \(40\) বছরে
19. কোন যৌথ ব্যবসায় তিন বন্ধুর মূলধন যথাক্রমে \(200\) টাকা, \(150\) টাকা ও \(250\) টাকা। একই সময় পরে তাদের লভ্যাংশের অনুপাত হবে —
(a) \(5:3:4\)
(b) \(4:3:5\)
(c) \(3:5:4\)
(d) \(5:4:3\)
উত্তর – (b) \(4:3:5\)
সমাধান – তিন বন্ধুর মূলধনের অনুপাত = \(200:150:250 = 4:3:5\)
∴ মূলধনের অনুপাত = লভ্যাংশের অনুপাত
∴ তিন বন্ধুর লভ্যাংশের অনুপাত = \(4:3:5\)
20. এক ব্যক্তি একটি ব্যাঙ্কে \(100\) টাকা জমা রেখে, \(2\) বছর পরে সমূল চক্রবৃদ্ধি পেলেন \(121\) টাকা। বার্ষিক চক্রবৃদ্ধি সুদের হার—
(a) \(10\%\)
(b) \(20\%\)
(c) \(5\%\)
(d) \(10\frac{1}{2}\%\)
উত্তর – (a) \(10\%\)
সমাধান – \(P(1 + \frac{r}{100})^n = A\) (\(A = 121\) টাকা, \(P = 100\) টাকা, \(n = 2\) বছর)
বা, \(100(1 + \frac{r}{100})^2 = 121\)
বা, \(1 + \frac{r}{100} = \sqrt{\frac{121}{100}}\)
বা, \(\frac{r}{100} = \frac{1}{10}\)
বা, \(r = 10\)
21. A, B, C তিনজনে মোট \(12000\) টাকা দিয়ে একটি ব্যবসা শুরু করে। এক বছর পরে তাদের লভ্যাংশ হয় যথাক্রমে \(300\) টাকা, \(200\) টাকা ও \(100\) টাকা। A এর মূলধনের পরিমাণ হল—
(a) \(2000\) টাকা
(b) \(4000\) টাকা
(c) \(5000\) টাকা
(d) \(6000\) টাকা
উত্তর – (d) \(6000\) টাকা
সমাধান – A, B ও C এর মূলধনের অনুপাত
= A, B ও C এর লভ্যাংশের অনুপাত
= \(300:200:100\)
= \(3:2:1\)
অনুপাতের সমষ্টি = \(3+2+1=6\)
∴ A এর মূলধন = \(\frac{12000}{6} \times 3\) টাকা
= \(6000\) টাকা
22. অমল এবং বিমল একটি ব্যবসা শুরু করে। অমল \(500\) টাকা \(9\) মাসের জন্য এবং বিমল কিছু টাকা \(6\) মাসের জন্য ব্যবসায় নিয়োজিত করে। ব্যবসায় মোট লাভ হয় \(69\) টাকা এবং বিমল লাভের \(46\) টাকা পায়। ব্যবসায় বিমলের মূলধন –
(a) \(1500\) টাকা
(b) \(3000\) টাকা
(c) \(4500\) টাকা
(d) \(6000\) টাকা
উত্তর – (a) \(1500\) টাকা
সমাধান – মনে করি, বিমলের মূলধন \(x\) টাকা
∴ 1 মাস সাপেক্ষে অমলের মূলধন = \(500 \times 9\) টাকা = \(4500\) টাকা
এবং বিমলের মূলধন = \(6x\) টাকা
∴ তাদের মূলধনের অনুপাত = \(4500 : 6x = 750 : x\)
প্রশ্নানুসারে,
\(\frac{x}{750 + x} \times 69 = 46\)বা, \(\frac{3x}{750 + x} = 2\)
বা, \(3x = 1500 + 2x\)
বা, \(x = 1500\)
23. শুভেন্দু ও নৌসাদ যথাক্রমে \(1500\) টাকা এবং \(1000\) টাকা দিয়ে একটি ব্যবসা শুরু করে। এক বছর পরে ব্যবসায় \(75\) টাকা ক্ষতি হলে, শুভেন্দুর ক্ষতি হয়
(a) \(45\) টাকা
(b) \(30\) টাকা
(c) \(25\) টাকা
(d) \(40\) টাকা
উত্তর – (a) \(45\) টাকা
সমাধান – শুভেন্দু ও নৌসাদের মূলধনের অনুপাত = \(1500 : 1000\) = \(15 : 10 = 3 : 2\)
মূলধনের অনুপাতের সমষ্টি = \(3+2=5\)
∴ শুভেন্দুর ক্ষতি = \(75 \times \frac{3}{5}\) টাকা = \(45\) টাকা
24. চক্রবৃদ্ধি সুদের ক্ষেত্রে
(a) প্রতিবছর আসল একই থাকে
(b) প্রতিবছর আসল পরিবর্তিত হয়
(c) প্রতিবছর আসল একই থাকতে পারে বা পরিবর্তিত হয়
(d) কোনোটিই নয়
উত্তর – (b) প্রতিবছর আসল পরিবর্তিত হয়
25. পল্লবী \(500\) টাকা \(9\) মাসের জন্য এবং রাজিয়া \(600\) টাকা \(5\) মাসের জন্য একটি ব্যবসায় নিয়োজিত করে। লভ্যাংশ তাদের মধ্যে বণ্টিত হবে যে অনুপাতে তা হলো —
(a) \(3:2\)
(b) \(5:6\)
(c) \(6:5\)
(d) \(9:5\)
উত্তর – (a) \(3:2\)
সমাধান – পল্লবী ও রাজিয়ার মূলধনের অনুপাত = \(9 \times 500 : 5 \times 600\) = \(4500 : 3000 = 3:2\)
∴ লভ্যাংশের অনুপাত = মূলধনের অনুপাত
∴ লভ্যাংশের অনুপাত = \(3:2\)
26. একটি মোটর গাড়ির মূল্য \(3\) লক্ষ টাকা। গাড়িটির বাৎসরিক অপচয়ের হার \(30\%\) হলে, \(3\) বছর পরে গাড়িটির কী দাম হবে?
(a) \(120990\) টাকা
(b) \(109920\) টাকা
(c) \(190920\) টাকা
(d) \(102900\) টাকা
উত্তর – (d) \(102900\) টাকা
সমাধান – গাড়িটির বর্তমান মূল্য \( P = 300000\) টাকা
অপচয়ের বার্ষিক হার \( r = 30\%\)
∴ \(3\) বছর পর গাড়িটির দাম = \(P(1 – \frac{r}{100})^n\)
= \(300000 (1 – \frac{30}{100})^3\) টাকা
= \(300000 \times (\frac{7}{10})^3\) টাকা
= \(102900\) টাকা
বীজগণিত
27. যদি \( ax^2 + abcx + bc = 0 \) (\( a \neq 0 \)) দ্বিঘাত সমীকরণের একটি বীজ অপর বীজের অন্যোন্যক হয়, তাহলে —
(a) \( abc = 1 \)
(b) \( b = ac \)
(c) \( bc = 1 \)
(d) \( a = bc \)
উত্তর – (d) \( a = bc \)
28. \( x^2 = x \) এই সমীকরণটির সমাধান সংখ্যা [M.P. 2023]
(a) 1 টি
(b) 2 টি
(c) 0 টি
(d) 3 টি
উত্তর – (b) 2 টি
29. \( A:B = 2:3 \), \( B:C = 5:8 \), \( C:D = 6:7 \), হলে, \( A:D = \) কত? [M.P. 2022]
(a) \( 2 : 7 \)
(b) \( 7 : 2 \)
(c) \( 5 : 8 \)
(d) \( 5 : 14 \)
সমাধান – \( A : B = 2 : 3 \) বা, \( \frac{A}{B} = \frac{2}{3} \)
\( B : C = 5 : 8 \) বা, \( \frac{B}{C} = \frac{5}{8} \)
\( C : D = 6 : 7 \) বা, \( \frac{C}{D} = \frac{6}{7} \)
∴ \( \frac{A}{D} = \frac{A}{B} \cdot \frac{B}{C} \cdot \frac{C}{D} = \frac{2}{3} \cdot \frac{5}{8} \cdot \frac{6}{7} = \frac{5}{14} \)
∴ \( A : D = 5 : 14 \)
30. \( x^2 – 7x + 3 = 0 \) সমীকরণের বীজদ্বয়ের গুণফল [M.P. 2020]
(a) 7
(b) -7
(c) 3
(d) -3
উত্তর – (c) 3
সমাধান – বীজদ্বয়ের গুণফল = ধ্রুবক পদ / \( x^2 \) এর সহগ = \( \frac{3}{1} = 3 \)
31. যদি \( p + q = \sqrt{13} \) এবং \( p – q = \sqrt{5} \) হয়, তবে \( pq \) এর মান —
(a) 2
(b) 18
(c) 9
(d) 8
উত্তর – (a) 2
সমাধান – ∴ \( pq = \left( \frac{p+q}{2} \right)^2 – \left( \frac{p-q}{2} \right)^2 \)
= \(\left( \frac{\sqrt{13}}{2} \right)^2 – \left( \frac{\sqrt{5}}{2} \right)^2 \)
= \(\frac{13}{4} – \frac{5}{4} = \frac{8}{4} = 2 \)
32. যদি \( x \propto y \) হয় তাহলে
(a) \( x^2 \propto y^3 \)
(b) \( x^3 \propto y^2 \)
(c) \( x \propto y^3 \)
(d) \( x^2 \propto y^2 \)
উত্তর – (d) \( x^2 \propto y^2 \)
সমাধান - \( x \propto y \)
বা, \( x = ky \), [\( k \) = অশূন্য ভেদ ধ্রুবক]
বা, \( x^2 = k^2 y^2 \)
বা, \( x^2 = m y^2 \) [যেখানে \( k^2 = m \), ধ্রুবক]
বা, \( x^2 \propto y^2 \)
33. কী শর্তে \( ax^2 + bx + c = 0 \) দ্বিঘাত সমীকরণের একটি বীজ শূন্য হবে? [M.P. 2017]
(a) \( a = 0 \)
(b) \( b = 0 \)
(c) \( c = 0 \)
(d) কোনটিই নয়
উত্তর – (c) \( c = 0 \)
সমাধান – \( ax^2 + bx + c = 0 \) দ্বিঘাত সমীকরণটির একটি বীজ সর্বদা শূন্য হবে যদি \( c = 0 \) হয়।
34. \( x^2 + 4x + k = 0 \) সমীকরণের বীজদুটি সমান হলে, k এর মান
(a) 1
(b) 2
(c) 3
(d) 4
উত্তর – (d) 4
সমাধান – যেহেতু সমীকরণটির বীজদুটি সমান
∴ \( b^2 – 4ac = 0 \)
বা, \( (4)^2 – 4 \cdot 1 \cdot k = 0 \)
বা, \( -4k = -16 \)
বা, \( k = 4 \)
35. \( 2x^2 – 3x – K + 2 = 0 \) সমীকরণের একটি বীজ শূন্য হলে K এর মান —
(a) 2
(b) \( -2 \)
(c) \( \frac{1}{2} \)
(d) \( -\frac{1}{2} \)
উত্তর – (a) 2
সমাধান – যেহেতু একটি বীজ শূন্য
∴ \( -K + 2 = 0 \)
বা, \( -K = -2 \)
∴ \( K = 2 \)
36. \( \frac{a}{3} = \frac{b}{4} = \frac{c}{7} \) হলে \( \frac{a+b+c}{c} \) এর মান হবে
(a) 1
(b) 2
(c) 3
(d) 4
উত্তর – (b) 2
সমাধান – ধরি, \( \frac{a}{3} = \frac{b}{4} = \frac{c}{7} = k \), [যেখানে k হল একটি অশূন্য বাস্তব সংখ্যা]
∴ \( a = 3k \), \( b = 4k \), \( c = 7k \)
∴ \( \frac{a+b+c}{c} = \frac{3k + 4k + 7k}{7k} = \frac{14k}{7k} = 2 \)
37. যদি \( a + b = \sqrt{5} \) এবং \( a – b = \sqrt{3} \) হয়, তাহলে \( a^2 + b^2 \) এর মান হবে —
(a) 8
(b) 4
(c) 2
(d) 1
উত্তর – (b) 4
সমাধান –
∴ \( 2(a^2 + b^2) = (a + b)^2 + (a – b)^2 \)
\( = (\sqrt{5})^2 + (\sqrt{3})^2 = 5 + 3 = 8 \)∴ \( a^2 + b^2 = \frac{8}{2} = 4 \)
38. \( x^2 – 6x + k = 0 \) সমীকরণের বীজদুটি বাস্তব এবং অসমান হলে k এর মান হবে —
(a) 6 এর থেকে বৃহত্তর
(b) 6 এর থেকে ক্ষুদ্রতর
(c) 9 এর থেকে বৃহত্তর
(d) 9 এর থেকে ক্ষুদ্রতর
উত্তর – (d) 9 এর থেকে ক্ষুদ্রতর
সমাধান – যেহেতু বীজদুটি বাস্তব এবং অসমান
∴ \( b^2 – 4ac > 0 \)
বা, \( (-6)^2 – 4 \cdot 1 \cdot k > 0 \)
বা, \( 36 – 4k > 0 \)
বা, \( k < 9 \)
39. \( x^2 – 22x + 105 = 0 \) সমীকরণের বীজদ্বয় \( \alpha \) এবং \( \beta \) হলে, \( (\alpha – \beta) \) এর মান হবে —
(a) \( \pm 8 \)
(b) \( \pm 6 \)
(c) \( \pm 9 \)
(d) কোনটিই নয়
উত্তর – (a) \( \pm 8 \)
সমাধান – \( x^2 – 22x + 105 = 0 \) সমীকরণের বীজদ্বয় \( \alpha \) ও \( \beta \)
∴ \( \alpha + \beta = -(-22) = 22 \) এবং \( \alpha\beta = 105 \)
∴ \( (\alpha – \beta)^2 = (\alpha + \beta)^2 – 4\alpha\beta \)
\( = (22)^2 – 4 \times 105 \)\( = 484 – 420 = 64 \)∴ \( \alpha – \beta = \pm 8 \)
40. 9 এবং 49 এর মধ্যসমানুপাতিটি হল—
(a) 20
(b) 21
(c) 41
(d) 441
উত্তর – (b) 21
সমাধান – ধরি, 9 এবং 49 এর মধ্য সমানুপাতিটি = \( x \)
∴ \( \frac{9}{x} = \frac{x}{49} \)
বা, \( x^2 = 441 \)
বা, \( x = 21 \)
41. \( x^2 – 3x + k = 10 \) সমীকরণের বীজদ্বয়ের গুণফল \( -2 \) হলে, \( k \) এর মান —
(a) \( -2 \)
(b) \( -8 \)
(c) 8
(d) 12
উত্তর – (c) 8
সমাধান – \( x^2 – 3x + k = 10 \)
বা, \( x^2 – 3x + (k – 10) = 0 \)
বীজদ্বয়ের গুণফল = \( k – 10 \)
∴ শর্তানুসারে, \( k – 10 = -2 \)
বা, \( k = -2 + 10 = 8 \)
42. \( 3x^2 + 8x + 2 = 0 \) সমীকরণের বীজদ্বয় \( \alpha \) এবং \( \beta \) হলে \( \frac{1}{\alpha} + \frac{1}{\beta} \) এর মান —
(a) \( -\frac{3}{8} \)
(b) \( \frac{2}{3} \)
(c) \( -4 \)
(d) 4
উত্তর – (c) \( -4 \)
সমাধান – যেহেতু, \( 3x^2 + 8x + 2 = 0 \) সমীকরণের বীজদ্বয় \( \alpha \) ও \( \beta \)
∴ \( \alpha + \beta = -\frac{8}{3} \) এবং \( \alpha\beta = \frac{2}{3} \)
∴ \( \frac{1}{\alpha} + \frac{1}{\beta} = \frac{\alpha + \beta}{\alpha\beta} = \frac{-\frac{8}{3}}{\frac{2}{3}} = -4 \)
43. \( (k+1)x^2+2kx+(k+2)=0 \) দ্বিঘাত সমীকরণটির বীজদ্বয় সমান এবং বিপরীত চিহ্নবিশিষ্ট হলে, k এর মান হবে —
(a) 1
(b) –1
(c) 0
(d) – 2
উত্তর – (c) 0
সমাধান – ধরি, বীজদুটি হল \( \alpha \) ও \( -\alpha \)
∴ \( \alpha + (-\alpha) = -\frac{2k}{k+1} \)
বা, \( -\frac{2k}{k+1} = 0 \)
বা, \( -2k = 0 \)
বা, \( k = 0 \)
44. \( ax^2 + bx + c = 0, (a \neq 0) \) সমীকরণের বীজদ্বয় সমান হলে
(a) \( c = -\frac{b}{2a} \)
(b) \( c = \frac{b}{2a} \)
(c) \( c = -\frac{b^2}{4a} \)
(d) \( c = \frac{b^2}{4a} \)
উত্তর – (d) \( c = \frac{b^2}{4a} \)
সমাধান – যেহেতু, \( ax^2 + bx + c = 0 \) সমীকরণের বীজদ্বয় সমান
∴ \( b^2 – 4ac = 0 \)
∴ \( c = \frac{b^2}{4a} \)
45. যদি \( x \propto y \) এবং \( y \propto z \) হয় তাহলে —
(a) \( x \propto z \)
(b) \( x \propto yz \)
(c) \( x \propto \frac{y}{z} \)
(d) \( z \propto xy \)
উত্তর – (a) \( x \propto z \)
সমাধান – \( x \propto y \)
বা, \( x = k_1 y \), [যেখানে \( k_1 \) হল একটি অশূন্য ধ্রুবক]
আবার \( y \propto z \)
বা, \( y = k_2 z \), [যেখানে \( k_2 \) হল একটি অশূন্য ধ্রুবক]
∴ \( x = k_1 y = k_1 k_2 z \)
\( x = m z \) [\( m = k_1 k_2 \) = ধ্রুবক]
\( x \propto z \)বা, \( x \propto z \)
46. \( ab \) ও \( bc \) এর তৃতীয় সমানুপাতী হল —
(a) \( \frac{ab^2}{c} \)
(b) \( \frac{bc^2}{a} \)
(c) \( \frac{ca^2}{b} \)
(d) কোনোটিই নয়
উত্তর – (b) \( \frac{bc^2}{a} \)
সমাধান – মনে করি, \(ab\) ও \(bc\) এর তৃতীয় সমানুপাতী \(x\)
∴ \(\frac{ab}{bc} = \frac{bc}{x}\)
বা, \(abx = b^2c^2\)
বা, \(x = \frac{b^2c^2}{ab} = \frac{bc^2}{a}\)
47. \( \frac{2a}{3b} = \frac{3c}{4d} = \frac{1}{2} \) হলে, \( \frac{4a+9c}{6b+12d} \) এর মান হবে —
(a) \( \frac{2}{3} \)
(b) \( \frac{3}{4} \)
(c) \( \frac{1}{2} \)
(d) কোনোটিই নয়
উত্তর – (c) \( \frac{1}{2} \)
সমাধান – যেহেতু \( \frac{2a}{3b} = \frac{3c}{4d} = \frac{1}{2} \)
∴ \( \frac{2a}{3b} = \frac{1}{2} \) এবং \( \frac{3c}{4d} = \frac{1}{2} \)
বা, \( \frac{2 \times 2a}{2 \times 3b} = \frac{1}{2} \)
বা, \( \frac{3 \times 3c}{3 \times 4d} = \frac{1}{2} \)
বা, \( \frac{4a}{6b} = \frac{1}{2} \)
বা, \( \frac{9c}{12d} = \frac{1}{2} \)
বা, \( 4a = \frac{1}{2} \times 6b \)
বা, \( 9c = \frac{1}{2} \times 12d \)
এখন \( \frac{4a+9c}{6b+12d} = \frac{ \frac{1}{2} \times 6b + \frac{1}{2} \times 12d }{6b+12d} = \frac{ \frac{1}{2}(6b+12d) }{6b+12d} = \frac{1}{2} \)
48. \( x \propto y^2 \) এবং \( y = 4 \) যখন \( x = 8 \); \( x = 32 \) হলে, \( y \)-এর ধনাত্মক মান —
(a) 4
(b) 8
(c) 16
(d) 32
উত্তর – (b) 8
সমাধান – \( x \propto y^2 \)
বা, \( x = k y^2 \) [\( k \) হল অশূন্য ভেদ ধ্রুবক]
\( y = 4 \) যখন \( x = 8 \)
∴ \( 8 = k \cdot (4)^2 \)
বা, \( k = \frac{1}{2} \)
∴ \( x = \frac{1}{2} y^2 \)
এখন \( x = 32 \) হলে \( 32 = \frac{1}{2} y^2 \)
বা, \( y^2 = 64 \)
বা, \( y = 8 \)
49. \( kx^2 + 4x + 1 = 0 \) দ্বিঘাত সমীকরণটির বীজদ্বয় সমান হলে, k এর মান হবে —
(a) \( -4 \)
(b) 6
(c) \( -6 \)
(d) 4
উত্তর – (d) 4
সমাধান – যেহেতু সমীকরণটির বীজদ্বয় সমান
∴ নিরূপক = 0
বা, \( (4)^2 – 4 \cdot k \cdot 1 = 0 \)
বা, \( 4k = 16 \)
বা, \( k = 4 \)
50. \( x^2 – 6x + 2 = 0 \) সমীকরণের বীজদ্বয়ের সমষ্টি
(a) 2
(b) \( -2 \)
(c) 6
(d) \( -6 \)
উত্তর – (c) 6
সমাধান – \( x^2 – 6x + 2 = 0 \) সমীকরণের বীজদ্বয়ের সমষ্টি = \( \frac{-(-6)}{1} = 6 \)
51. 16 এবং 25 এর মধ্য সমানুপাতী —
(a) 400
(b) 100
(c) 20
(d) 40
উত্তর – (c) 20
সমাধান – মনে করি, 16 এবং 25 এর মধ্য সমানুপাতী হল \( x \)
∴ \( \frac{16}{x} = \frac{x}{25} \)
বা, \( x^2 = 400 \)
`বা, \( x = 20 \)
52. \( \sqrt{125} \) থেকে \( \sqrt{5} \) বিয়োগ করলে বিয়োগফল হবে —
(a) \( \sqrt{80} \)
(b) \( \sqrt{120} \)
(c) \( \sqrt{100} \)
(d) কোনোটিই নয়
উত্তর – (a) \( \sqrt{80} \)
সমাধান –
\( \sqrt{125} – \sqrt{5} \)= \( \sqrt{5 \times 5 \times 5} – \sqrt{5} \)
= \( 5\sqrt{5} – \sqrt{5} \)
= \( 4\sqrt{5} \)
= \( \sqrt{4 \times 4 \times 5} \)
= \( \sqrt{80} \)
53. \( x = 2 + \sqrt{3} \) হলে, \( x + \frac{1}{x} \) এর মান —
(a) 2
(b) \( 2\sqrt{3} \)
(c) 4
(d) \( 2 – \sqrt{3} \)
উত্তর – (c) 4
সমাধান – \( x = 2 + \sqrt{3} \)
∴ \( \frac{1}{x} = \frac{1}{2 + \sqrt{3}} = \frac{2 – \sqrt{3}}{(2 + \sqrt{3})(2 – \sqrt{3})} = \frac{2 – \sqrt{3}}{4 – 3} = 2 – \sqrt{3} \)
∴ \( x + \frac{1}{x} = 2 + \sqrt{3} + 2 – \sqrt{3} = 4 \)
54. \( a \propto b^2 \) এবং \( b \propto c^3 \) হলে \( a \) ও \( c \) এর ভেদ সম্পর্কটি হবে
(a) \( a \propto c^6 \)
(b) \( a \propto c^4 \)
(c) \( a \propto c^3 \)
(d) \( a \propto \sqrt{c} \)
উত্তর – (a) \( a \propto c^6 \)
সমাধান – \( a \propto b^2 \)
বা, \( a = k_1 b^2 \) [যেখানে \( k_1 \) হল একটি অশূন্য ভেদ ধ্রুবক]
\( b \propto c^3 \)
বা, \( b = k_2 c^3 \) [যেখানে \( k_2 \) হল একটি অশূন্য ভেদ ধ্রুবক]
∴ \( a = k_1 b^2 = k_1 (k_2 c^3)^2 = k_1 k_2^2 c^6 \)
∴ \( a = m c^6 \), [যেখানে \( m = k_1 k_2^2 \) = ধ্রুবক]
∴ \( a \propto c^6 \)
58. দুটি সংখ্যার অনুপাত 3 : 7 এবং তাদের গ.সা.গু 5 হলে সংখ্যা দুটির সমষ্টি হবে—
(a) 100
(b) 50
(c) 105
(d) কোনোটিই নয়
উত্তর – (b) 50
সমাধান – ধরি, সংখ্যা দুইটি \( 3k \) এবং \( 7k \), [যেখানে \( k \) হল অশূন্য বাস্তব সংখ্যা]
∴ \( 3k \) ও \( 7k \) এর গ.সা.গু = \( k \)
শর্তানুসারে, \( k = 5 \)
∴ সংখ্যা দুইটি \( 3 \times 5 = 15 \) এবং \( 7 \times 5 = 35 \)
সংখ্যা দুইটির সমষ্টি = \( 15 + 35 = 50 \)
59. \( x \propto \frac{1}{y} \) হলে —
(a) \( x = \frac{1}{y} \)
(b) \( y = \frac{1}{x} \)
(c) \( xy = \frac{1}{y} \)
(d) \( xy \) = অশূন্য ধ্রুবক
উত্তর – (d) \( xy \) = অশূন্য ধ্রুবক
সমাধান – \( x \propto \frac{1}{y} \)
বা, \( x = \frac{k}{y} \), [\( k \) হল অশূন্য ভেদ ধ্রুবক]
বা, \( xy = k \)
60. যদি \( y – z \propto \frac{1}{x} \), \( z – x \propto \frac{1}{y} \) এবং \( x – y \propto \frac{1}{z} \) হয়, তাহলে তিনটি ভেদ ধ্রুবকের সমষ্টি —
(a) 0
(b) 1
(c) \( -1 \)
(d) 2
উত্তর – (a) 0
সমাধান – \( y – z \propto \frac{1}{x} \), \( z – x \propto \frac{1}{y} \) এবং \( x – y \propto \frac{1}{z} \)
বা, \( y – z = \frac{k_1}{x} \), \( z – x = \frac{k_2}{y} \) এবং \( x – y = \frac{k_3}{z} \)
[\( k_1, k_2, k_3 \) হল তিনটি ভেদ ধ্রুবক]
বা, \( k_1 = xy – xz \), \( k_2 = yz – xy \) এবং \( k_3 = xz – yz \)
∴ \( k_1 + k_2 + k_3 = xy – xz + yz – xy + xz – yz = 0 \)
61. \( (5 – \sqrt{3})(\sqrt{3} – 1)(5 + \sqrt{3})(\sqrt{3} + 1) \)-এর গুণফল —
(a) 22
(b) 44
(c) 2
(d) 11
উত্তর – (b) 44
সমাধান – \( (5 – \sqrt{3})(\sqrt{3} – 1)(5 + \sqrt{3})(\sqrt{3} + 1) \)
\( = (5 – \sqrt{3})(5 + \sqrt{3})(\sqrt{3} – 1)(\sqrt{3} + 1) \)\( = \{(5)^2 – (\sqrt{3})^2\} \{(\sqrt{3})^2 – (1)^2\} \)\( = (25 – 3)(3 – 1) = 22 \times 2 = 44 \)62. \( q \propto p^{3/2} \) এবং \( p = 4 \) হলে \( q = 8 \) হয়। \( p \) ও \( q \) এর মধ্যে সম্বন্ধ হল—
(a) \( p^2 = q \)
(b) \( p^3 = q^2 \)
(c) \( p^2 = q^3 \)
(d) \( p = q^2 \)
উত্তর – (b) \( p^3 = q^2 \)
সমাধান – \( q \propto p^{3/2} \)
বা, \( q = k p^{3/2} \) [যেখানে \( k \) হল একটি অশূন্য ভেদ ধ্রুবক]
যেহেতু \( p = 4 \) হলে \( q = 8 \) হয়
\( 8 = k (4)^{3/2} \)বা, \( (2)^3 k = 8 \)
বা, \( k = \frac{8}{8} = 1 \)
∴ \( q = p^{3/2} \)
বা, \( q^2 = p^3 \)
বা, \( p^3 = q^2 \)
63. কোনো দ্বিঘাত সমীকরণের বীজদ্বয় বাস্তব এবং অসমান হলে, নিরূপকের মান হবে —
(a) 0
(b) \( > 0 \)
(c) \( < 0 \)
(d) কোনটিই নয়
উত্তর – (b) \( > 0 \)
জ্যামিতি
64. 5 সেমি ও 7 সেমি ব্যাস বিশিষ্ট দুটি বৃত্ত পরস্পরকে অন্তঃস্থভাবে স্পর্শ করলে তাদের কেন্দ্রদ্বয়ের দূরত্ব —
(a) 1 cm
(b) 2 cm
(c) 3 cm
(d) 4 cm
উত্তর – (a) 1 cm
65. দুটি বৃত্ত পরস্পরকে অন্তঃস্পর্শ করলে বৃত্তদুটির সাধারণ স্পর্শকের সংখ্যা হবে —
(a) 1 টি
(b) 2 টি
(c) 3 টি
(d) 4 টি
উত্তর – (a) 1 টি
66. দুটি বৃত্ত পরস্পরকে স্পর্শ বা ছেদ না করলে বৃত্ত দুটির সাধারণ স্পর্শক সংখ্যা —
(a) 2 টি
(b) 1 টি
(c) 3 টি
(d) 4 টি
উত্তর – (d) 4 টি
67. O কেন্দ্রীয় বৃত্তে PQ একটি ব্যাস এবং R বিন্দুটি বৃত্তের ওপর এমনভাবে অবস্থিত যাতে PR = RQ হয়। \( \angle RPQ \) – এর মান —
(a) \( 30^\circ \)
(b) \( 90^\circ \)
(c) \( 60^\circ \)
(d) \( 45^\circ \)
উত্তর – (d) \( 45^\circ \)
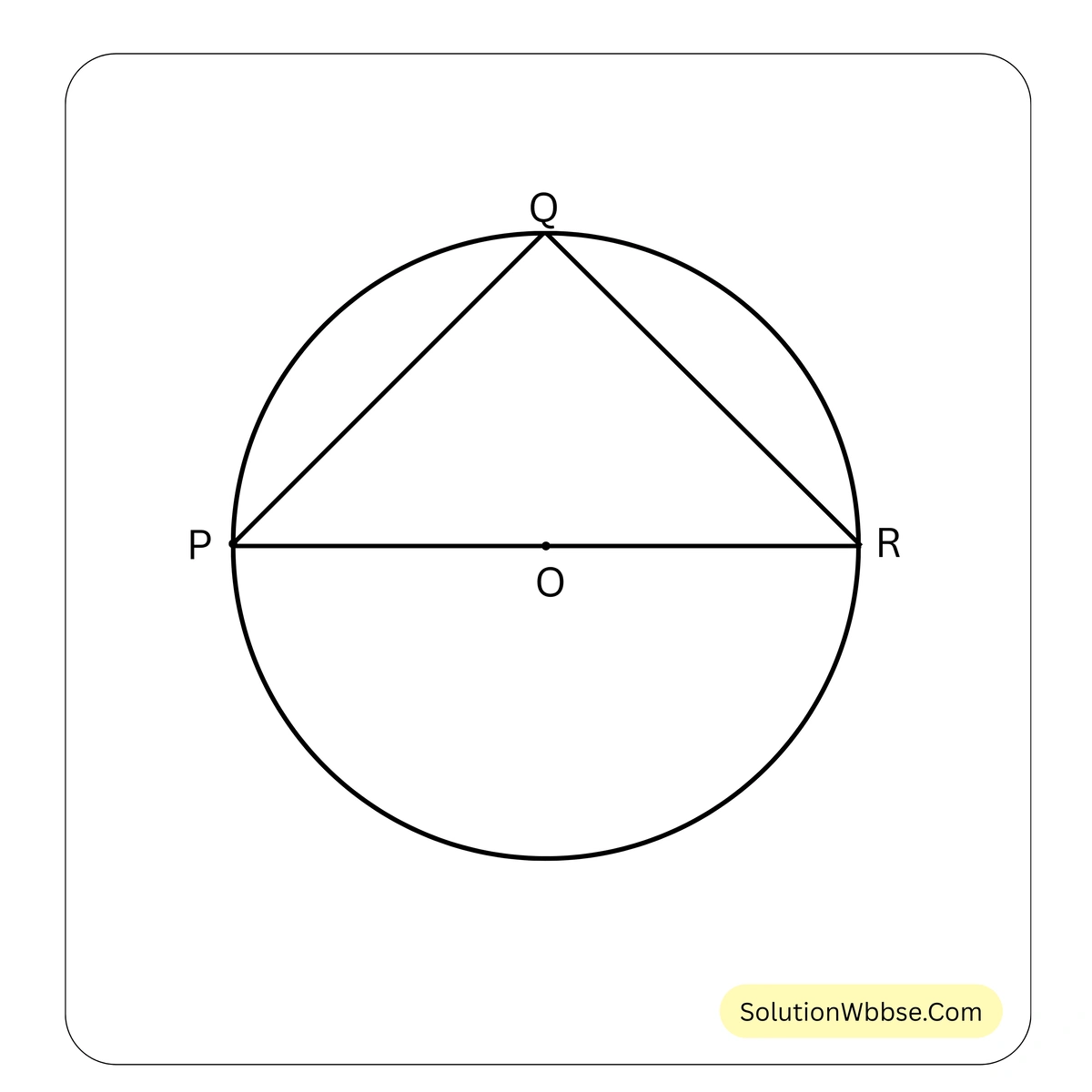
সমাধান – যেহেতু PQ বৃত্তের ব্যাস
∴ \( \angle PRQ = 90^\circ \)
আবার \( \triangle PQR \) এর \( PR = RQ \)
∴ \( \angle RPQ = \angle RQP \)
∴ সমকোণী ত্রিভুজ PQR এর
\( \angle RPQ + \angle RQP = 90^\circ \)বা, \( \angle RPQ + \angle RPQ = 90^\circ \), [∵ \( \angle RPQ = \angle RQP \)]
বা, \( 2\angle RPQ = 90^\circ \)
বা, \( \angle RPQ = 45^\circ \)
68. O কেন্দ্রীয় বৃত্তের AB ও CD জ্যা দুটির দৈর্ঘ্য সমান। \( \angle AOB = 60^\circ \) হলে \( \angle COD \) এর মান —
(a) \( 40^\circ \)
(b) \( 30^\circ \)
(c) \( 60^\circ \)
(d) \( 90^\circ \)
উত্তর – (c) \( 60^\circ \)
সমাধান –
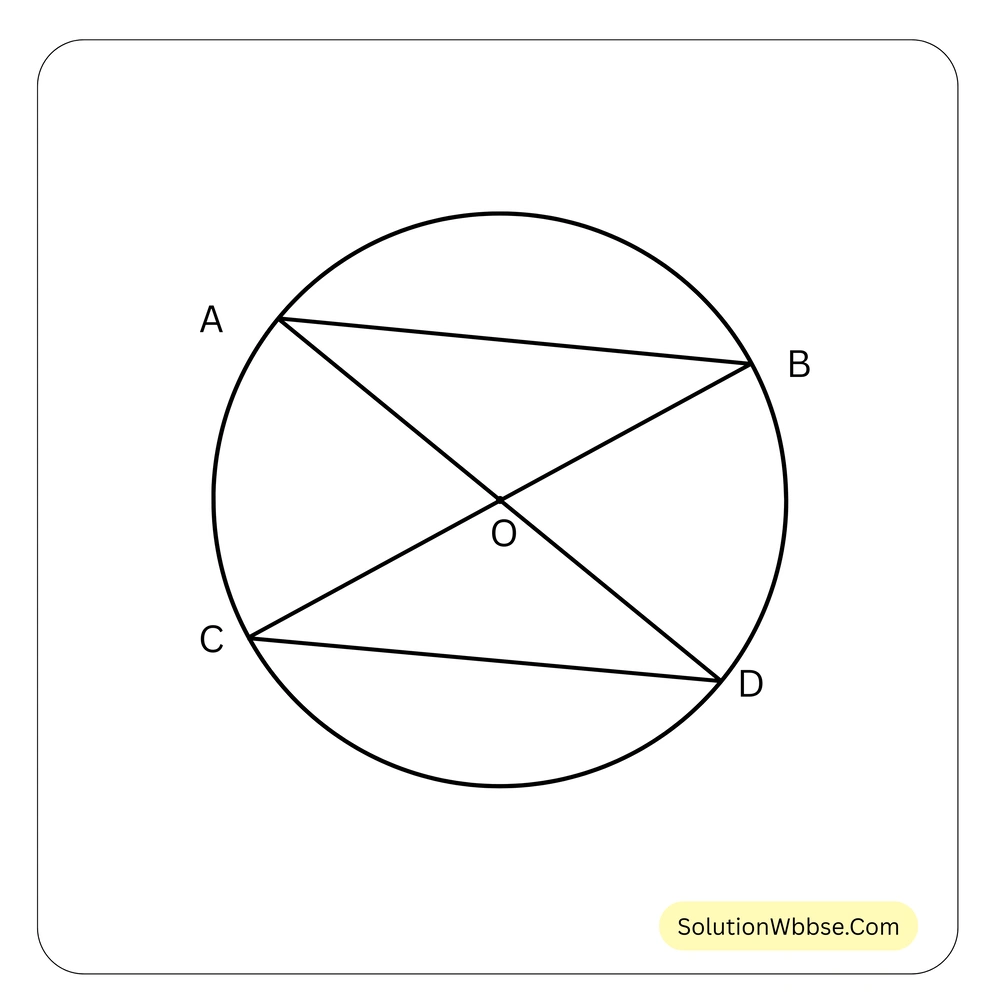
∴ \( AB = CD \)
এবং \( OA = OB = OC = OD \) [একই বৃত্তের ব্যাসার্ধ]
∴ \( \triangle AOB \cong \triangle COD \), [S-S-S শর্তে]
∴ \( \angle AOB = \angle COD = 60^\circ \)
69. O কেন্দ্রীয় বৃত্তের AB ব্যাস। ABCD বৃত্তস্থ চতুর্ভুজ। \( \angle ABC = 65^\circ \), \( \angle DAC = 40^\circ \) হলে \( \angle BCD \) -এর মান –
(a) \( 75^\circ \)
(b) \( 105^\circ \)
(c) \( 115^\circ \)
(d) \( 80^\circ \)
উত্তর – (c) \( 115^\circ \)
সমাধান –
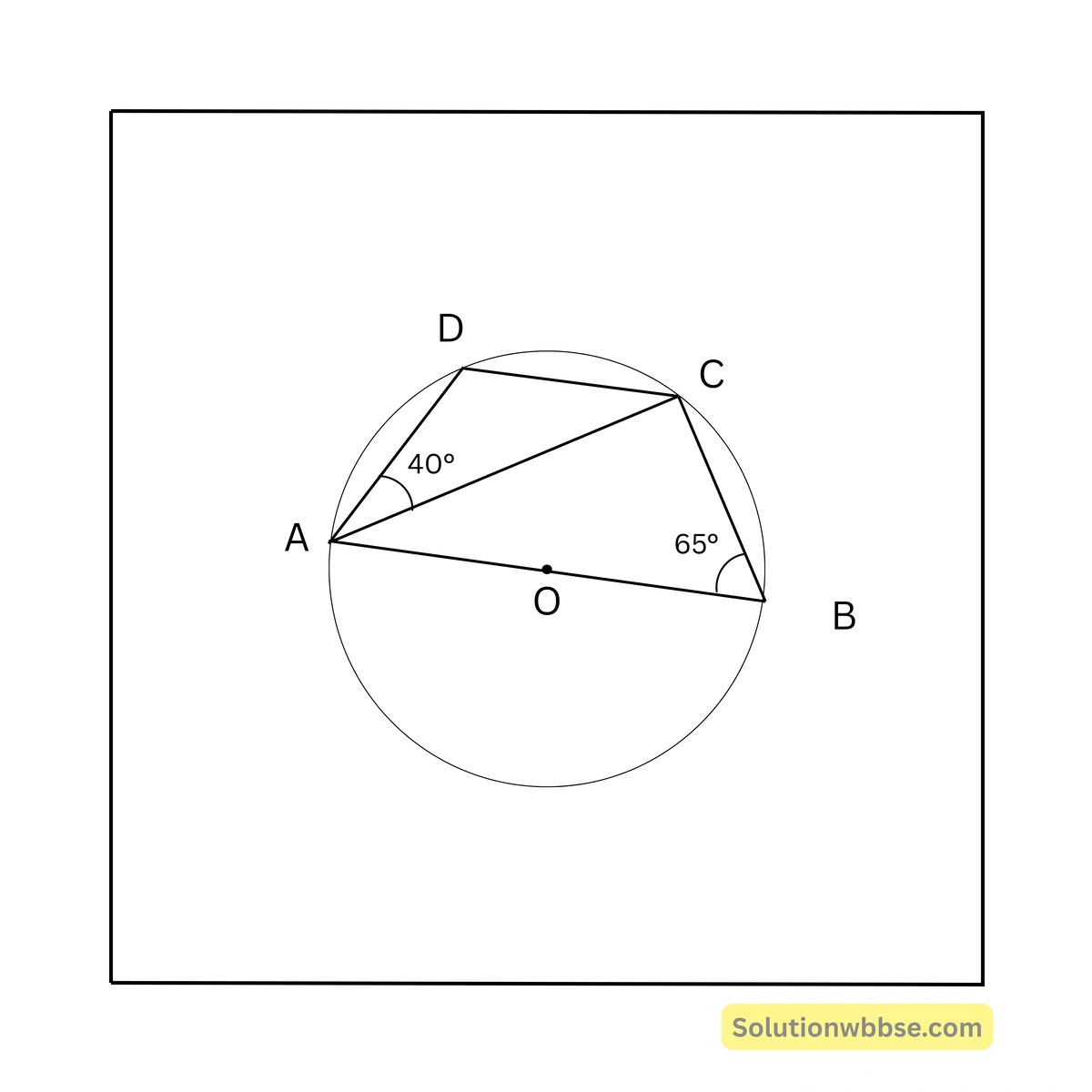
\( \angle ACB = 90^\circ \) [অর্ধবৃত্তস্থ কোণ]
∴ \( \angle BAC = 180^\circ – (90^\circ + 65^\circ) = 25^\circ \)
∴ \( \angle BAD = \angle BAC + \angle DAC = 25^\circ + 40^\circ = 65^\circ \)
\( \angle BCD = 180^\circ – \angle BAD = 180^\circ – 65^\circ = 115^\circ \)70. বৃত্তস্থ চতুর্ভুজ ABCD এর \( \angle A = 100^\circ \) হলে \( \angle C \) -এর মান
(a) \( 50^\circ \)
(b) \( 80^\circ \)
(c) \( 180^\circ \)
(d) \( 200^\circ \)
উত্তর – (b) \( 80^\circ \)
সমাধান – যেহেতু ABCD একটি বৃত্তস্থ চতুর্ভুজ
∴ \( \angle A + \angle C = 180^\circ \)
বা, \( 100^\circ + \angle C = 180^\circ \)
বা, \( \angle C = 180^\circ – 100^\circ = 80^\circ \)
71. দুটি বৃত্ত পরস্পরকে ছেদ বা স্পর্শ না করলে বৃত্ত দুটির সাধারণ স্পর্শকের সংখ্যা — [M.P. 2017]
(a) 2
(b) 1
(c) 3
(d) 4
উত্তর – (d) 4
72. পাশের চিত্রে O বৃত্তের কেন্দ্র এবং PQ ব্যাস হলে, x এর মান
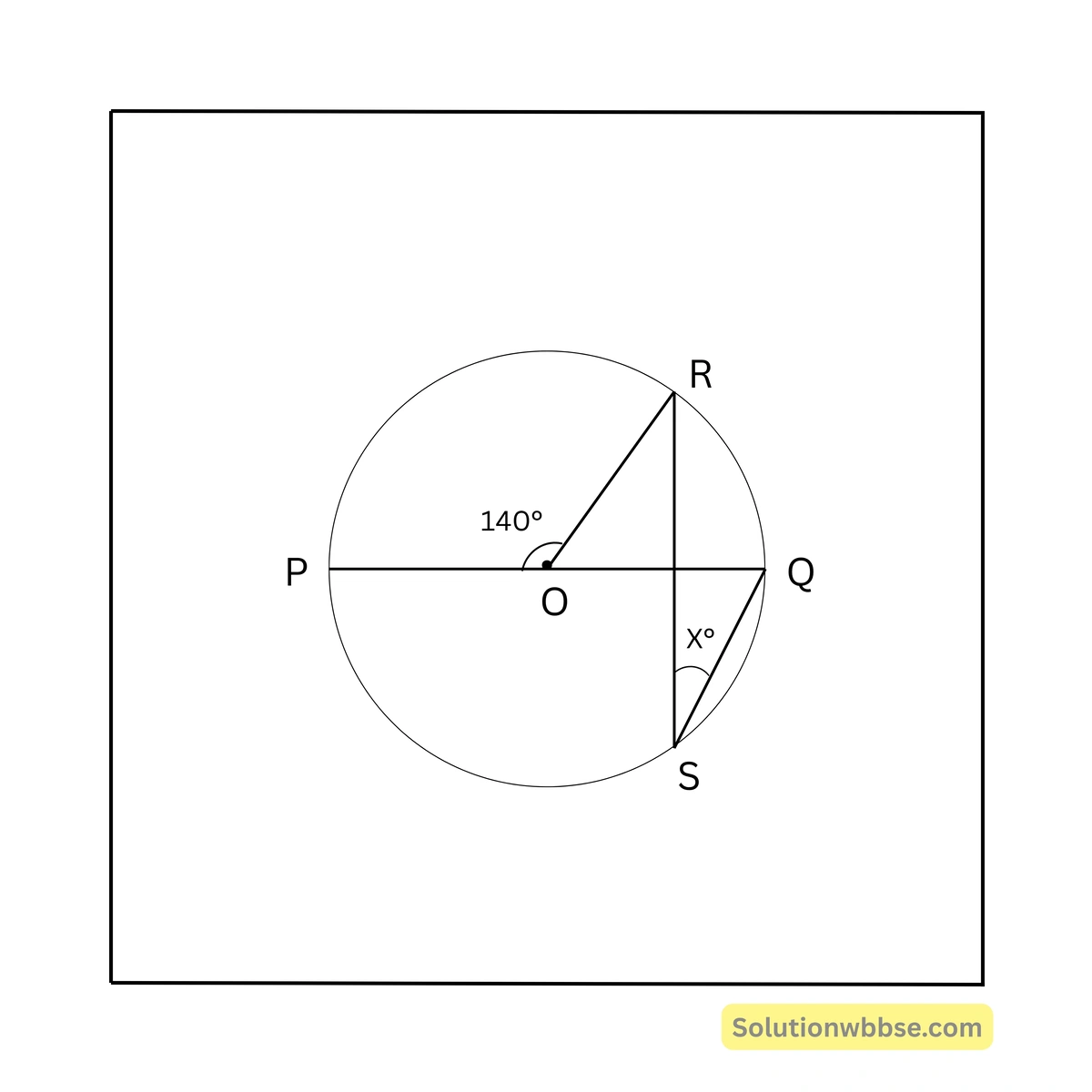
(a) \( 140^\circ \)
(b) \( 40^\circ \)
(c) \( 80^\circ \)
(d) \( 20^\circ \)
উত্তর – (d) \( 20^\circ \)
সমাধান – \( \angle ROQ = 180^\circ – 140^\circ = 40^\circ \)
∴ পরিধিস্থ \( \angle RSQ = \frac{1}{2} \) কেন্দ্রস্থ \( \angle ROQ = \frac{1}{2} \times 40^\circ = 20^\circ \)
73. r ব্যাসার্ধবিশিষ্ট O কেন্দ্রীয় একটি বৃত্তের বাইরে P যে কোন একটি বিন্দু হলে—
(a) \( OP = r \)
(b) \( OP < r \)
(c) \( OP > r \)
(d) কোনটিই নয়
উত্তর – (c) \( OP > r \)
74. পাশের চিত্রে O বৃত্তের কেন্দ্র, \( \angle ACB = 30^\circ \), \( \angle ABC = 60^\circ \), \( \angle DAB = 35^\circ \) এবং \( \angle DBC = x^\circ \) হলে, x এর মান
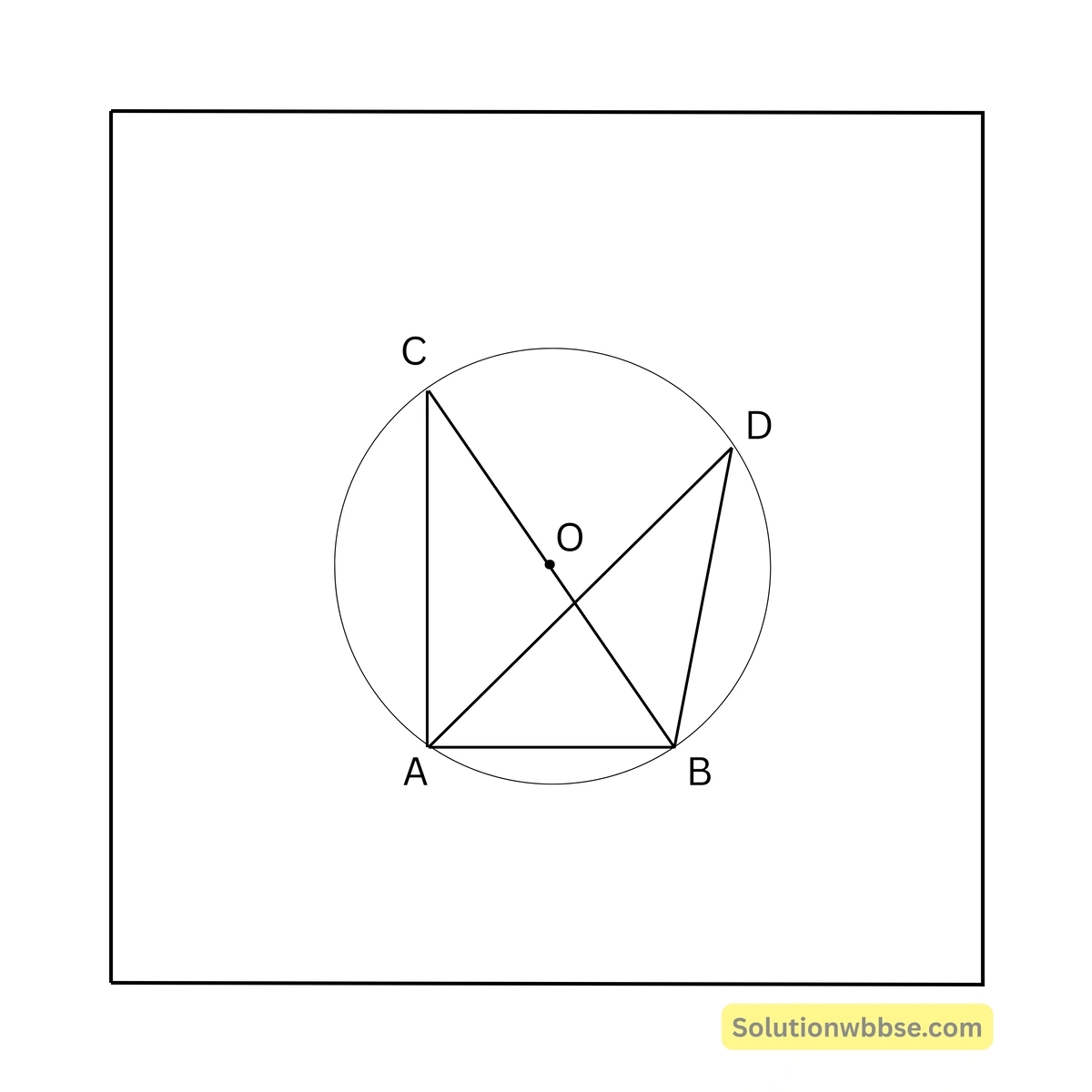
(a) \( 35^\circ \)
(b) \( 70^\circ \)
(c) \( 65^\circ \)
(d) \( 55^\circ \)
উত্তর – (d) \( 55^\circ \)
সমাধান – \( \angle ACB = 30^\circ \) ∴ \( \angle ADB = 30^\circ \) [একই বৃত্তাংশস্থ কোণ]
\( \angle DAB + \angle ADB + \angle ABD = 180^\circ \)বা, \( 35^\circ + 30^\circ + (60^\circ + x^\circ) = 180^\circ \)
∴ \( x^\circ = 55^\circ \)
75. একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 13 সেমি এবং বৃত্তের একটি জ্যা-এর দৈর্ঘ্য 10 সেমি। বৃত্তের কেন্দ্র থেকে জ্যা-এর দূরত্ব —
(a) 12.5 সেমি
(b) 12 সেমি
(c) \( \sqrt{69} \) সেমি
(d) 24 সেমি
উত্তর – (b) 12 সেমি
সমাধান –
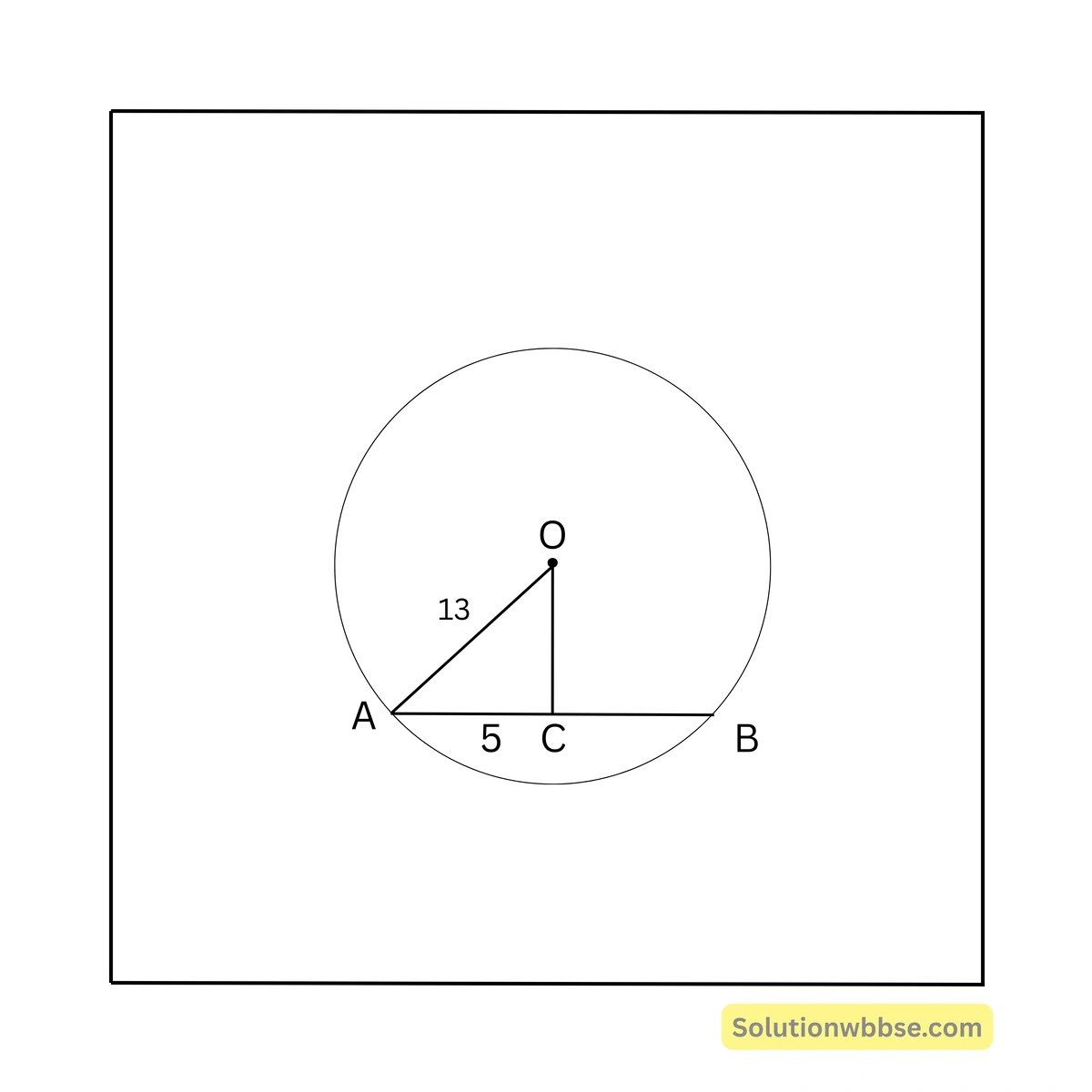
\( OA = 13 \) সেমি
\( AC = \frac{1}{2} AB = 5 \) সেমি
∴ \( OC = \sqrt{OA^2 – AC^2} \)
\( = \sqrt{169 – 25} = \sqrt{144} = 12 \) সেমি
76. পাশের চিত্রে, AB হল বৃত্তটির ব্যাস এবং \( \angle ACD = 50^\circ \) হলে x এর মান হবে —
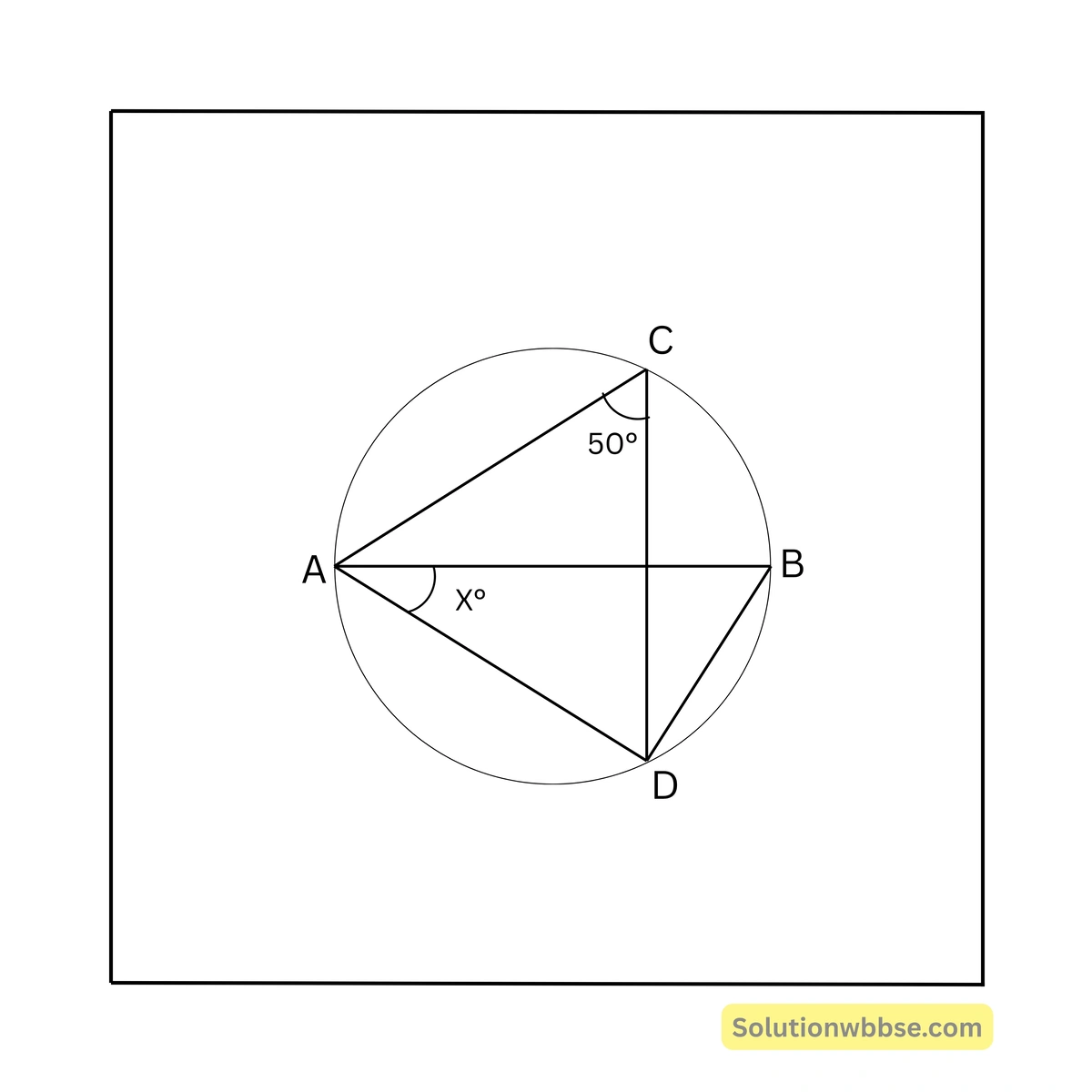
(a) 50
(b) 40
(c) 30
(d) কোনোটিই নয়
উত্তর – (b) 40
সমাধান – \( \angle ABD = \angle ACD = 50^\circ \) [একই বৃত্তাংশস্থ কোণ]
\( \angle ADB = 90^\circ \), [অর্ধবৃত্তস্থ কোণ]
∴ \( \angle BAD + \angle ABD + \angle ADB = 180^\circ \)
বা, \( x^\circ + 50^\circ + 90^\circ = 180^\circ \)
বা, \( x^\circ = 40^\circ \)
77. পাশের চিত্রে O বৃত্তের কেন্দ্র হলে, \( \angle POR \) এর মান
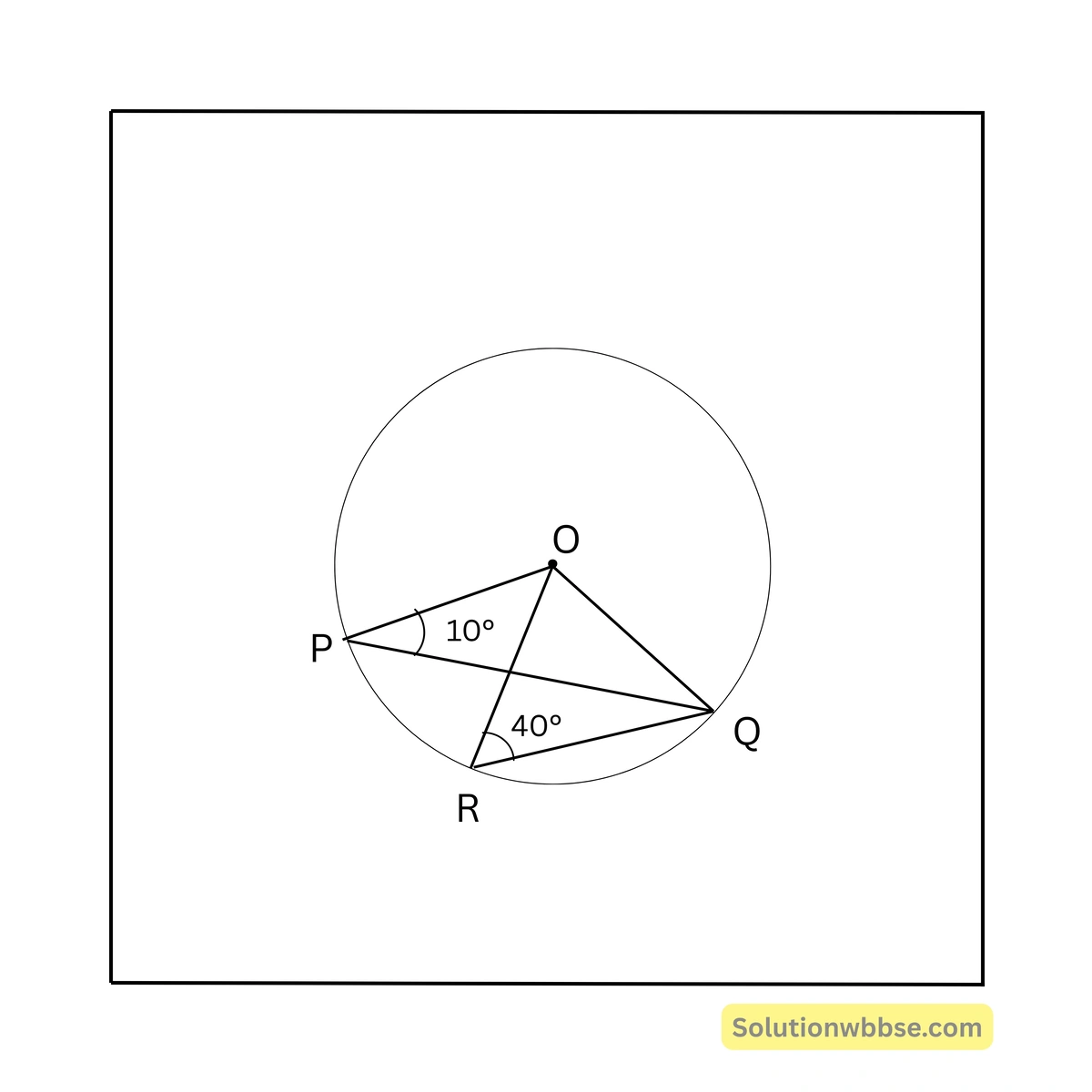
(a) \( 20^\circ \)
(b) \( 40^\circ \)
(c) \( 60^\circ \)
(d) \( 80^\circ \)
উত্তর – (c) \( 60^\circ \)
সমাধান – \( \angle OQR = \angle ORQ = 40^\circ \) [∵ OQ = OR]
\( \angle OPQ = \angle OQP = 10^\circ \) [∵ OQ = OP]
∴ \( \angle PQR = \angle OQR – \angle OQP \)
\( = 40^\circ – 10^\circ = 30^\circ \)∴ কেন্দ্রস্থ \( \angle POR = 2 \times \) বৃত্তস্থ \( \angle PQR \)
\( = 2 \times 30^\circ = 60^\circ \)78. দুটি বৃত্ত পরস্পরকে C বিন্দুতে বহিস্পর্শ করে। AB বৃত্ত দুটির একটি সাধারণ স্পর্শক বৃত্ত দুটিকে A ও B বিন্দুতে স্পর্শ করে। \( \angle ACB \) এর পরিমাপ —
(a) \( 60^\circ \)
(b) \( 45^\circ \)
(c) \( 30^\circ \)
(d) \( 90^\circ \)
উত্তর – (d) \( 90^\circ \)
সমাধান –
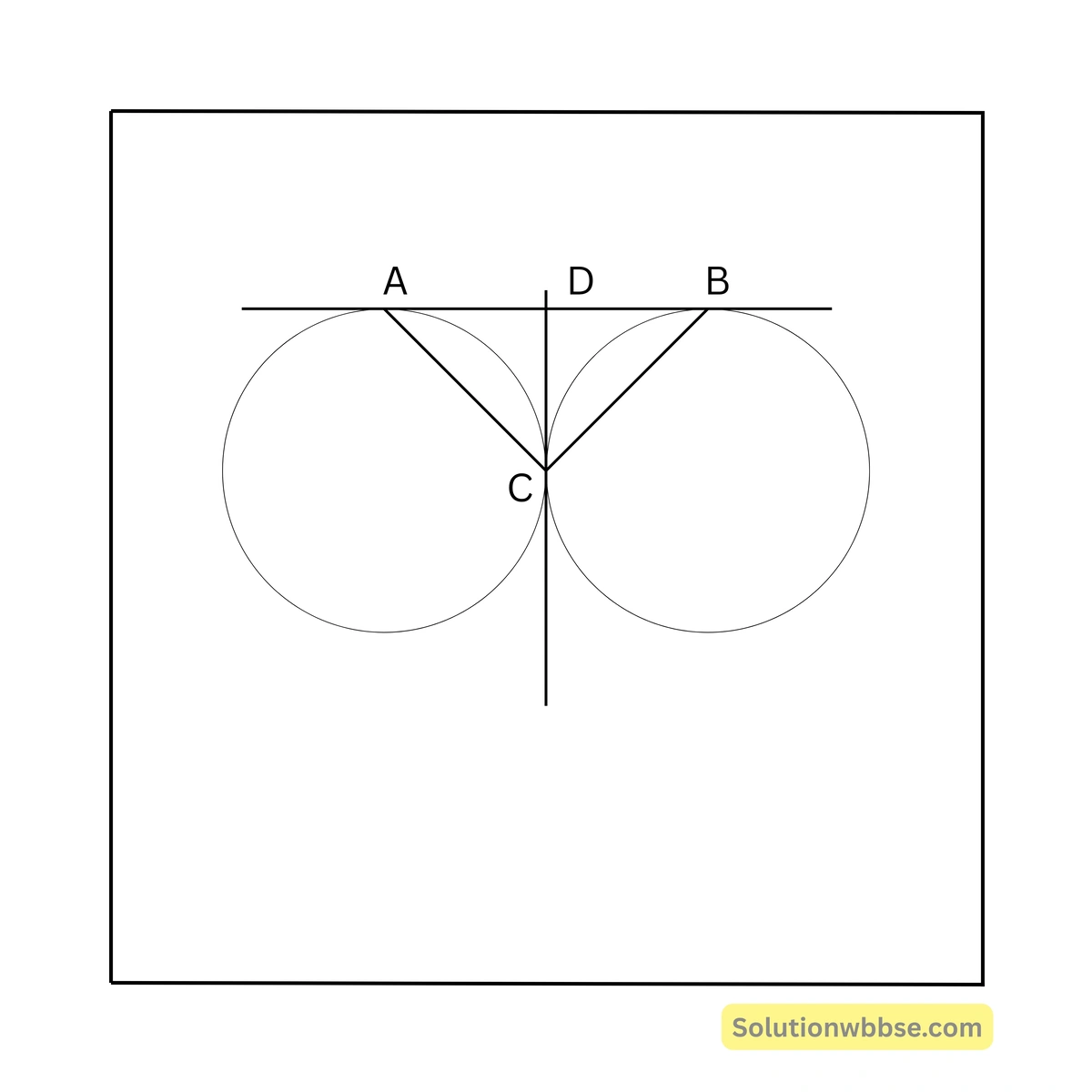
C বিন্দুতে বৃত্ত দুটির একটি সাধারণ স্পর্শক অঙ্কন করা হল যেটি AB কে D বিন্দুতে ছেদ করে।
এখন DA = DC এবং DB = DC
∴ \( \angle DAC = \angle DCA \) এবং
\( \angle DBC = \angle DCB \)এখন \( \triangle ABC \) থেকে পাই
\( \angle BAC + \angle ABC + \angle ACB = 180^\circ \)বা, \( \angle DAC + \angle DBC + \angle ACB = 180^\circ \)
বা, \( \angle DCA + \angle DCB + \angle ACB = 180^\circ \)
বা, \( \angle ACB + \angle ACB = 180^\circ \)
∴ \( \angle ACB = 90^\circ \)
79. দুটি সমকেন্দ্রীয় বৃত্তের কেন্দ্র O, একটি সরলরেখা একটি বৃত্তকে A ও B বিন্দুতে এবং অপর বৃত্তকে C ও D বিন্দুতে ছেদ করে। AC = 5 সেমি হলে BD এর দৈর্ঘ্য —
(a) 2.5 সেমি
(b) 5 সেমি
(c) 10 সেমি
(d) কোনোটিই নয়
উত্তর – (b) 5 সেমি
সমাধান –
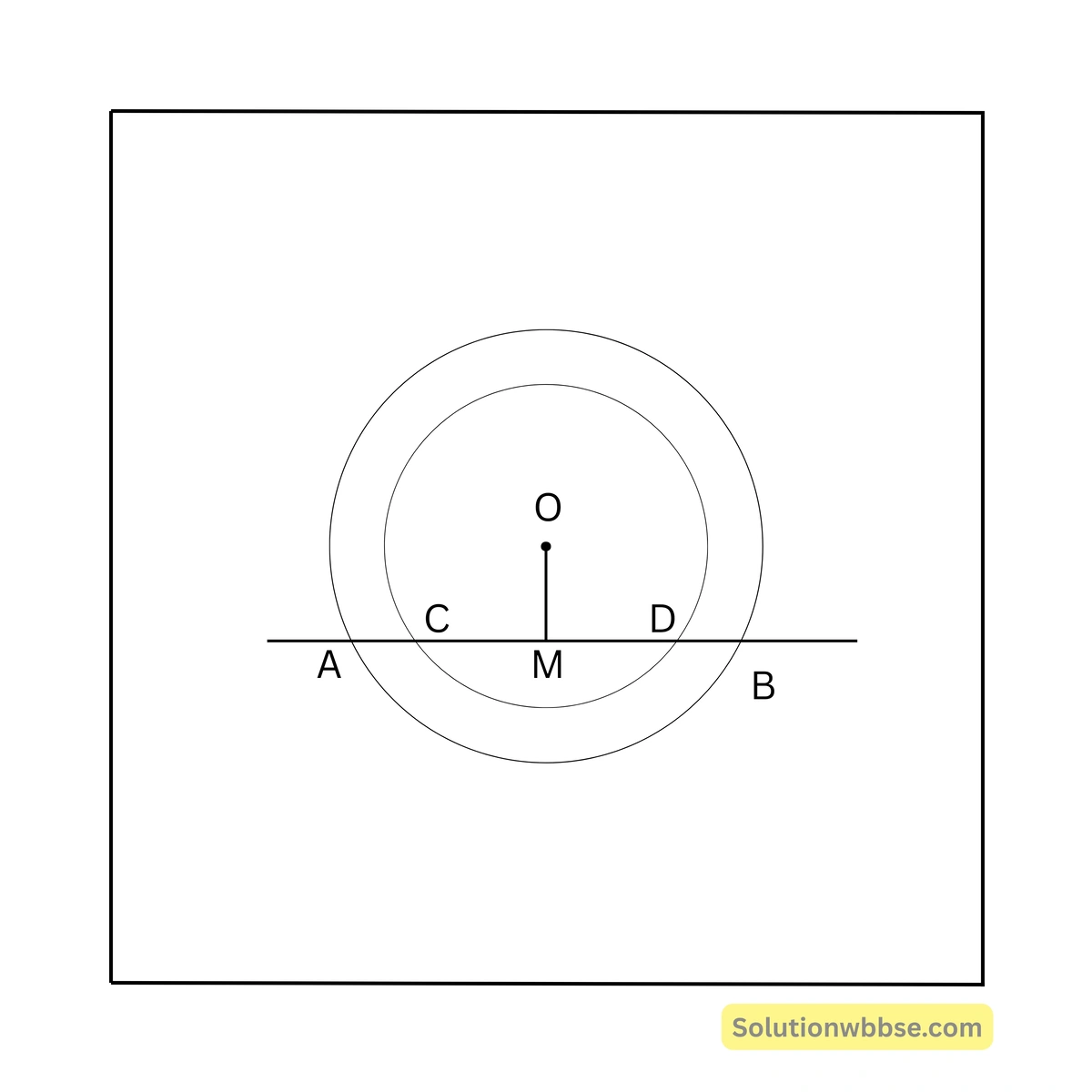
O থেকে সরলরেখাটির ওপর OM লম্ব অঙ্কন করা হল,
∴ AM = BM এবং CM = DM
∴ AM – CM = BM – DM
বা, AC = BD
∴ BD = 5 সেমি
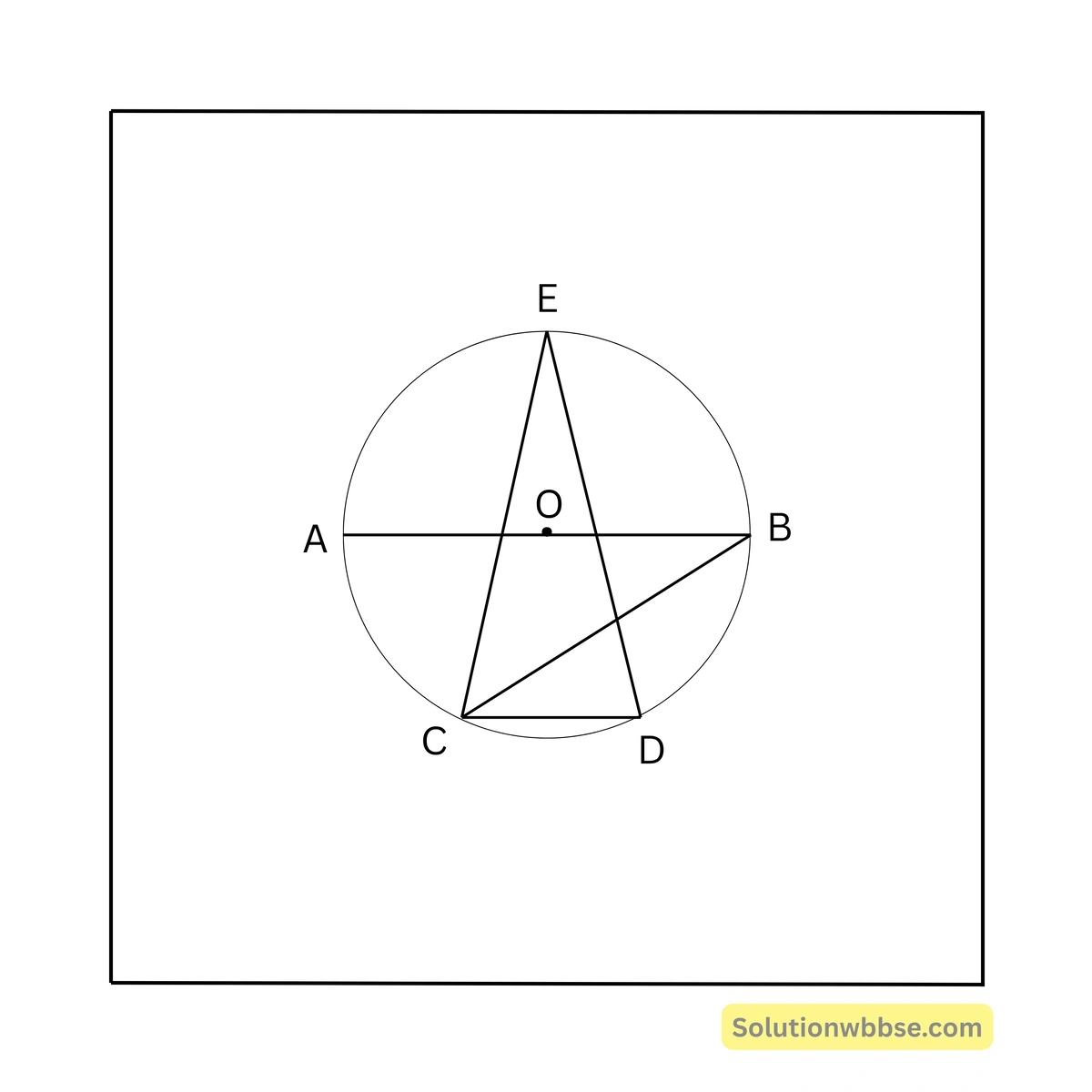
80. পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস। \( AB \parallel CD \)। \( \angle ABC = 25^\circ \) হলে, \( \angle CED \) এর মান –
(a) \( 80^\circ \)
(b) \( 50^\circ \)
(c) \( 25^\circ \)
(d) \( 40^\circ \)
উত্তর – (d) \( 40^\circ \)
সমাধান –
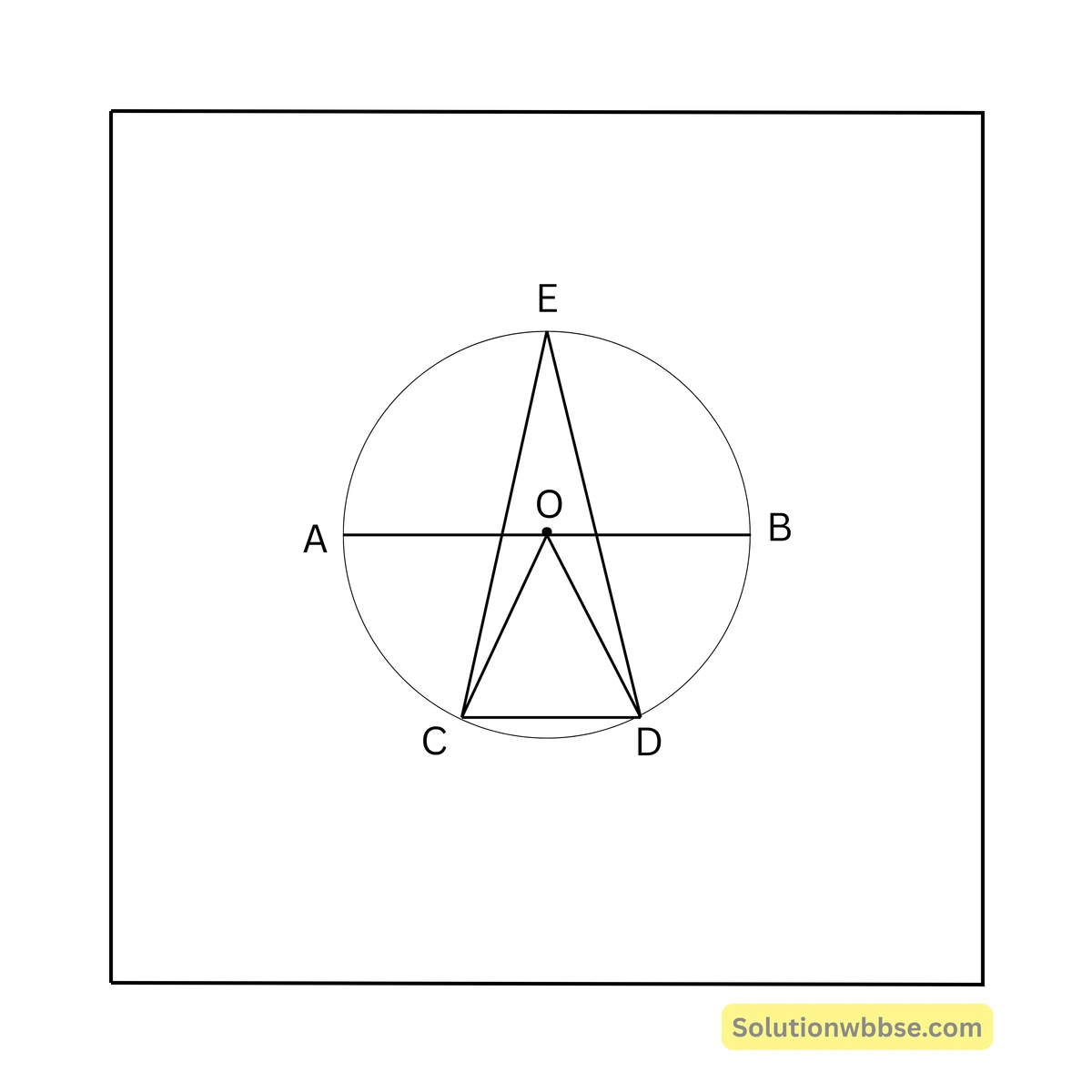
O, C এবং O, D যুক্ত করা হল
∴ \( \angle AOC = 2 \angle ABC = 2 \times 25^\circ = 50^\circ \)
\( \angle OCD = \angle AOC = 50^\circ \) [∵ \( AB \parallel CD \) এবং OC ভেদক]
\( \angle ODC = \angle OCD = 50^\circ \) [∵ OC = OD]
∴ \( \angle COD = 180^\circ – \angle OCD – \angle ODC \)
\( = 180^\circ – 50^\circ – 50^\circ = 80^\circ \)∴ \( \angle CED = \frac{1}{2} \angle COD = \frac{1}{2} \times 80^\circ = 40^\circ \)
81. একটি বৃত্তে AB ও BC দুটি জ্যা পরস্পর লম্ব। বৃত্তটির ব্যাসার্ধ 5 সেমি এবং AB = 6 সেমি হলে BC =
(a) 8 সেমি
(b) 12 সেমি
(c) 16 সেমি
(d) কোনোটিই নয়
উত্তর – (a) 8 সেমি
সমাধান –
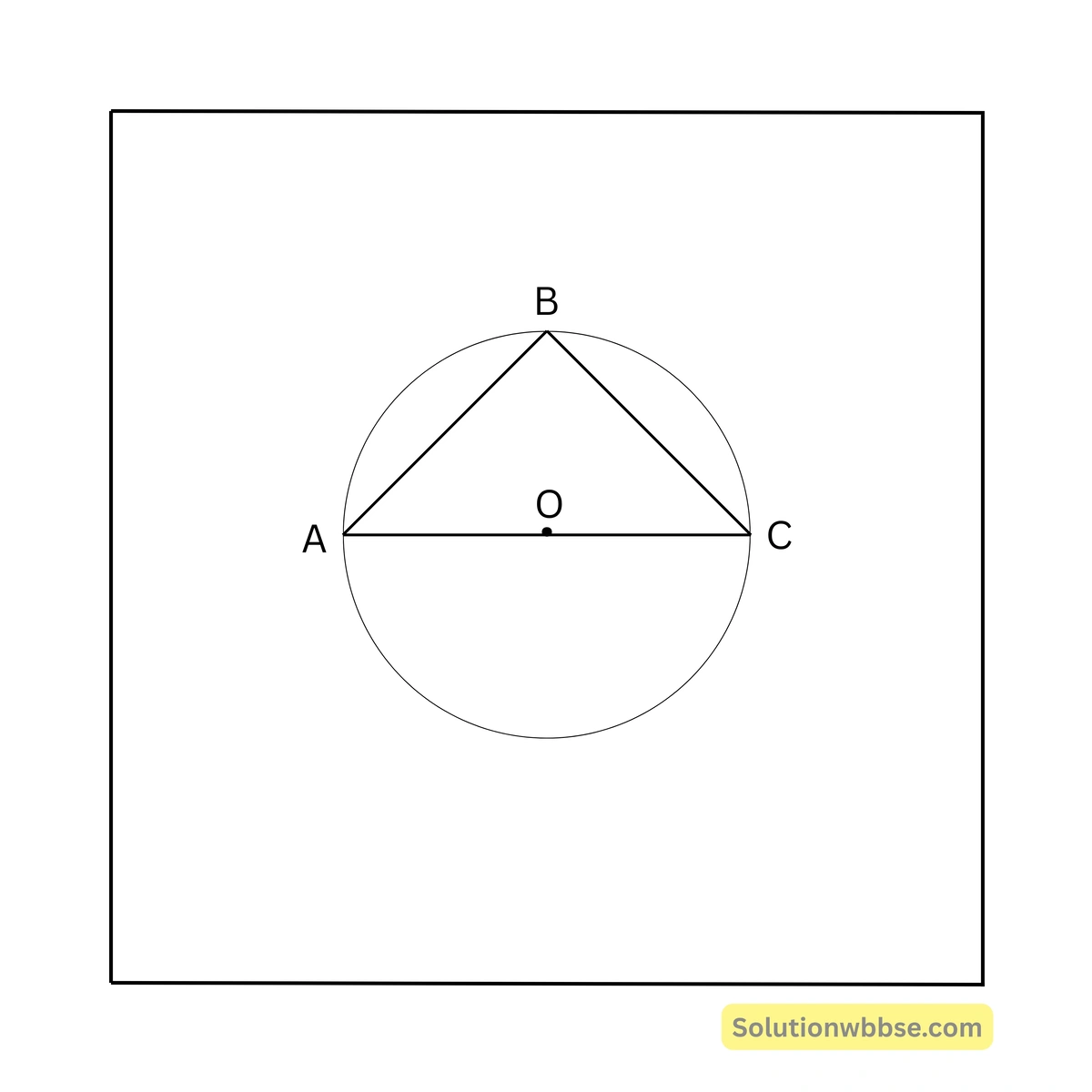
যেহেতু জ্যা AB ও BC পরস্পর লম্ব
∴ \( \angle ABC = 90^\circ \)
∴ অবশ্যই A, O, C সমরেখ এবং
এবং \( \triangle ABC \) একটি সমকোণী ত্রিভুজ
∴ AC = 6 সেমি
OA = 5 সেমি (বৃত্তের ব্যাসার্ধ)
∴ AC = 2 × OA = 2 × 5 = 10 সেমি.
∴ \( BC = \sqrt{AC^2 – AB^2} = \sqrt{(10)^2 – (6)^2} \)
\( = \sqrt{100 – 36} = \sqrt{64} = 8 \) সেমি.
82. পাশের চিত্রে ABC ত্রিভুজটি একটি বৃত্তে পরিবৃত এবং বৃত্তকে P, Q, R বিন্দুতে স্পর্শ করে। যদি AP = 4 সেমি, BP = 6 সেমি, AC = 12 সেমি এবং BC = x সেমি হয়, তাহলে x এর মান

(a) 12
(b) 14
(c) 10
(d) 16
উত্তর – (b) 14
সমাধান – BQ = BP = 6 সেমি,
AR = AP = 4 সেমি
CR = AC – AR = (12 – 4) সেমি = 8 সেমি
CQ = CR = 8 সেমি
BC = BQ + CQ = (6 + 8) সেমি = 14 সেমি
83. পাশের চিত্রে O বৃত্তের কেন্দ্র হলে, x এর মান
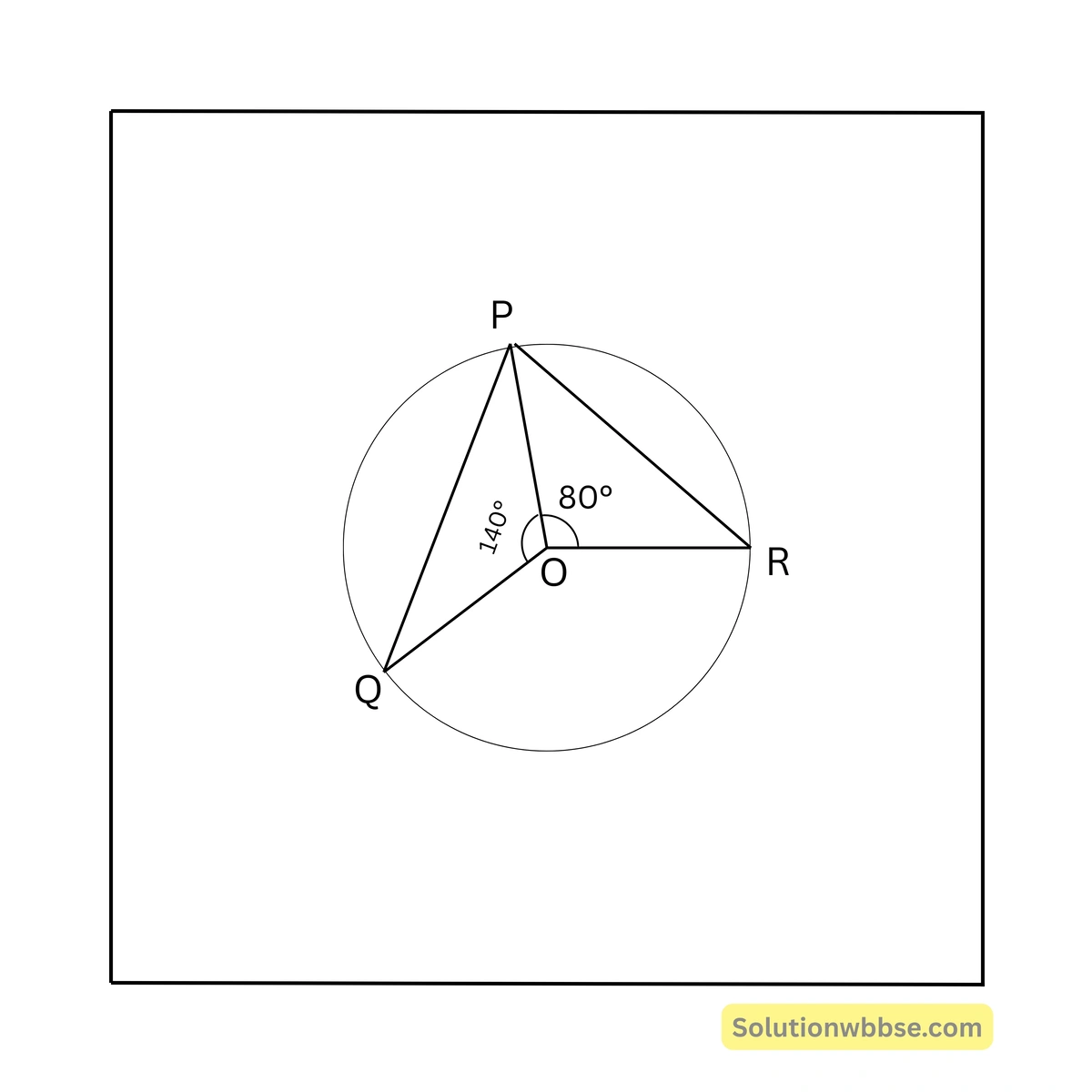
(a) \( 70^\circ \)
(b) \( 60^\circ \)
(c) \( 40^\circ \)
(d) \( 200^\circ \)
উত্তর – (a) \( 70^\circ \)
সমাধান – \( \angle QOR = 360^\circ – 140^\circ – 80^\circ = 140^\circ \)
∴ পরিধিস্থ \( \angle QPR = \frac{1}{2} \) কেন্দ্রস্থ \( \angle QOR = \frac{1}{2} \times 140^\circ = 70^\circ \)
84. চিত্রে, AOB বৃত্তের ব্যাস। AC = 3 সেমি. ও BC = 4 সেমি. হলে AB এর দৈর্ঘ্য —
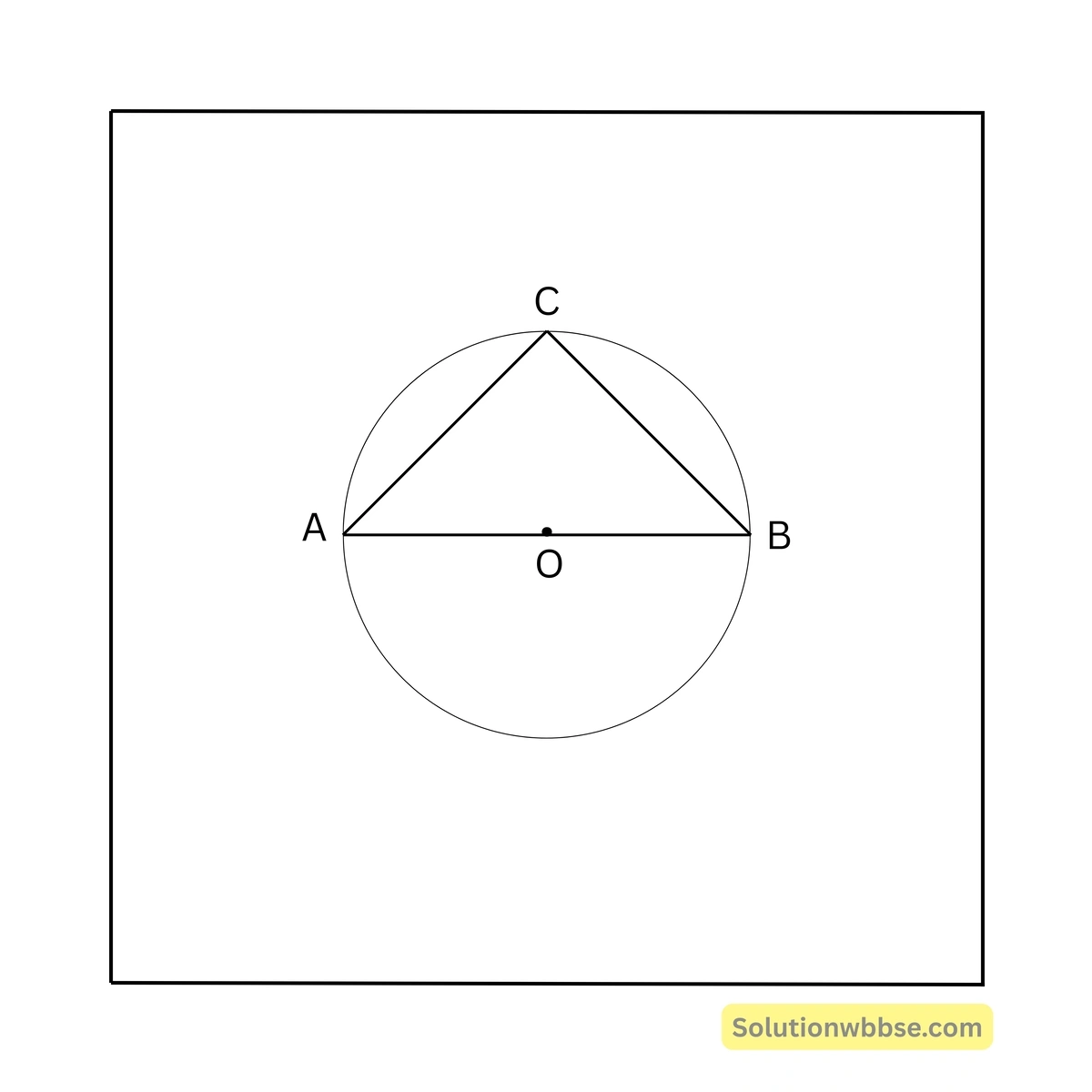
(a) 3 সেমি.
(b) 4 সেমি.
(c) 5 সেমি.
(d) 8 সেমি.
উত্তর – (c) 5 সেমি.
সমাধান – AOB বৃত্তের ব্যাস হওয়ায় \( \angle ACB = 90^\circ \)
∴ \( AB = \sqrt{AC^2 + BC^2} = \sqrt{3^2 + 4^2} = 5 \) সেমি.
85. AB ও CD দুটি সমান্তরাল জ্যা-এর প্রত্যেকটির দৈর্ঘ্য 16 সেমি। বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 10 সেমি হলে, জ্যা দুটির মধ্যে দূরত্ব —
(a) 12 সেমি
(b) 16 সেমি
(c) 20 সেমি
(d) 5 সেমি
উত্তর – (a) 12 সেমি
সমাধান –
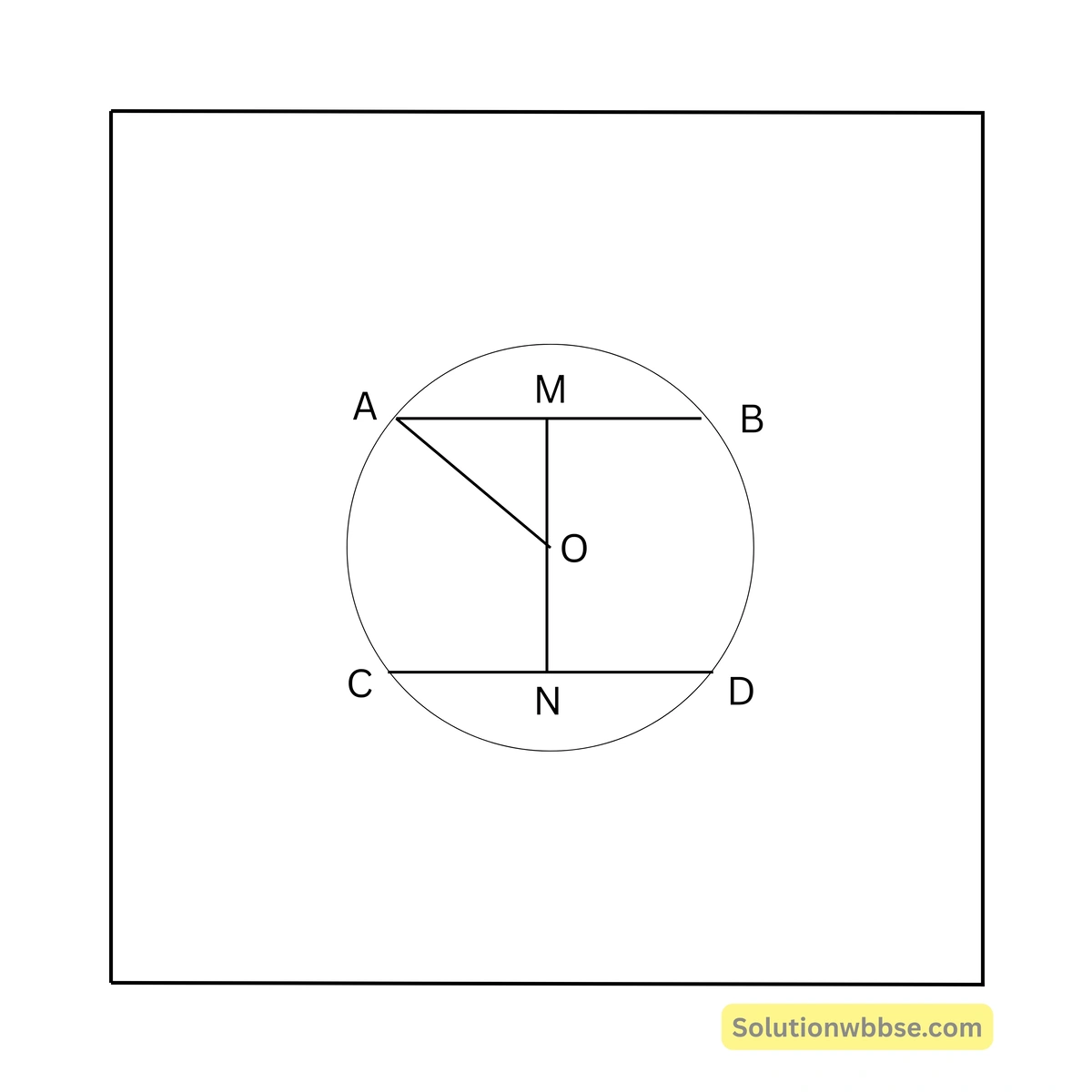
\( OA = 10 \) সেমি, \( AM = \frac{1}{2} AB = 8 \) সেমি
∴ \( OM = \sqrt{OA^2 – AM^2} \)
\( = \sqrt{100 – 64} \)\( = 6 \) সেমি
একইভাবে \( ON = 6 \) সেমি
∴ \( MN = (6 + 6) \) সেমি = 12 সেমি
86. পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস। ABCD বৃত্তস্থ চতুর্ভুজ। \( \angle ADC = 120^\circ \) হলে, \( \angle BAC \)-এর মান —
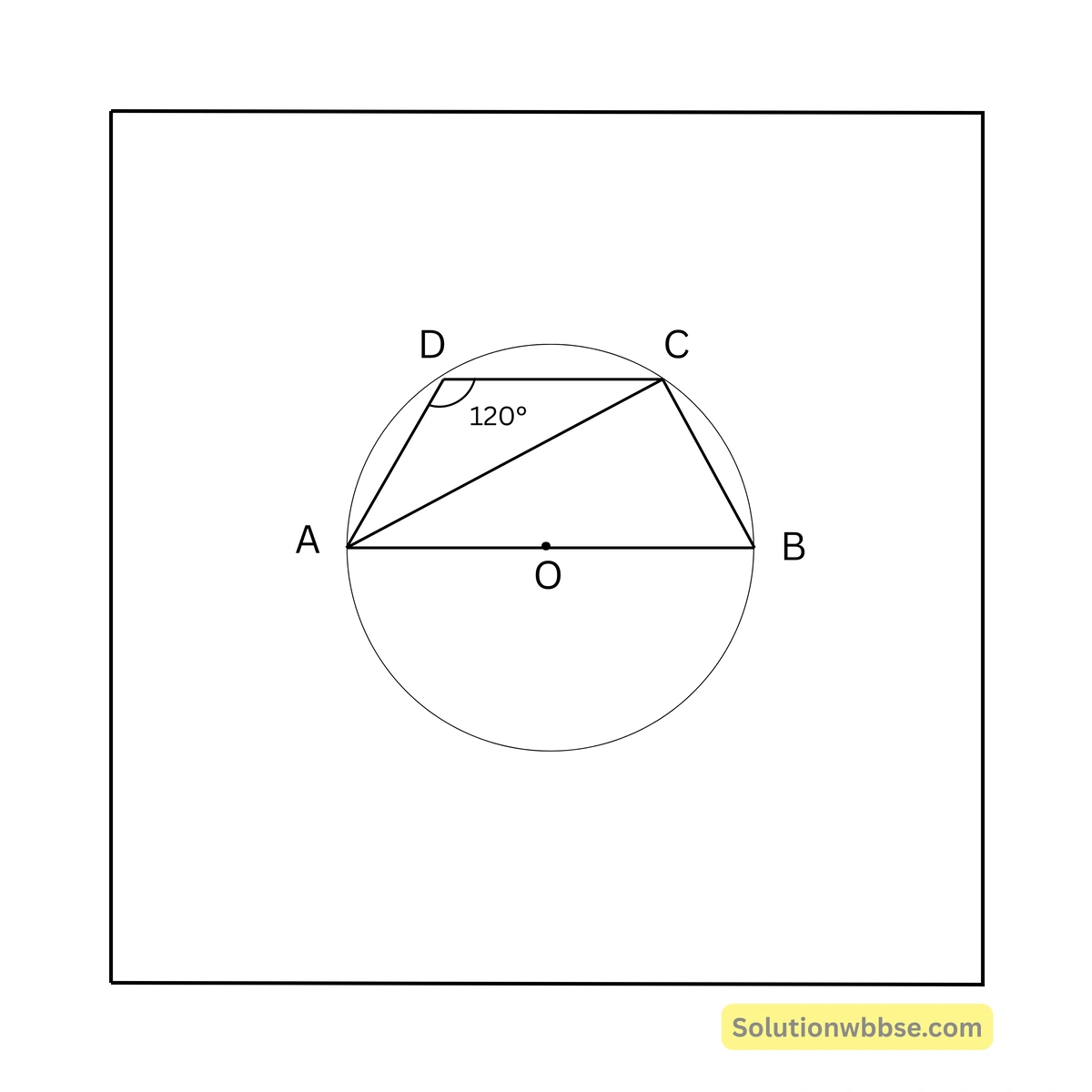
(a) \( 50^\circ \)
(b) \( 60^\circ \)
(c) \( 30^\circ \)
(d) \( 40^\circ \)
উত্তর – (c) \( 30^\circ \)
সমাধান – \( \angle ABC = 180^\circ – 120^\circ = 60^\circ \)
\( \angle ACB = 90^\circ \) [অর্ধবৃত্তস্থ কোণ]
∴ \( \angle BAC = 180^\circ – 60^\circ – 90^\circ \)
\( = 30^\circ \)87. পাশের চিত্রে দুটি বৃত্ত পরস্পরকে C ও D বিন্দুতে ছেদ করে, D ও C বিন্দুগামী দুটি সরলরেখা একটি বৃত্তকে যথাক্রমে A ও B বিন্দুতে এবং অপর বৃত্তকে E ও F বিন্দুতে ছেদ করে। \( \angle DAB = 75^\circ \) হলে, \( \angle DEF \) এর মান –
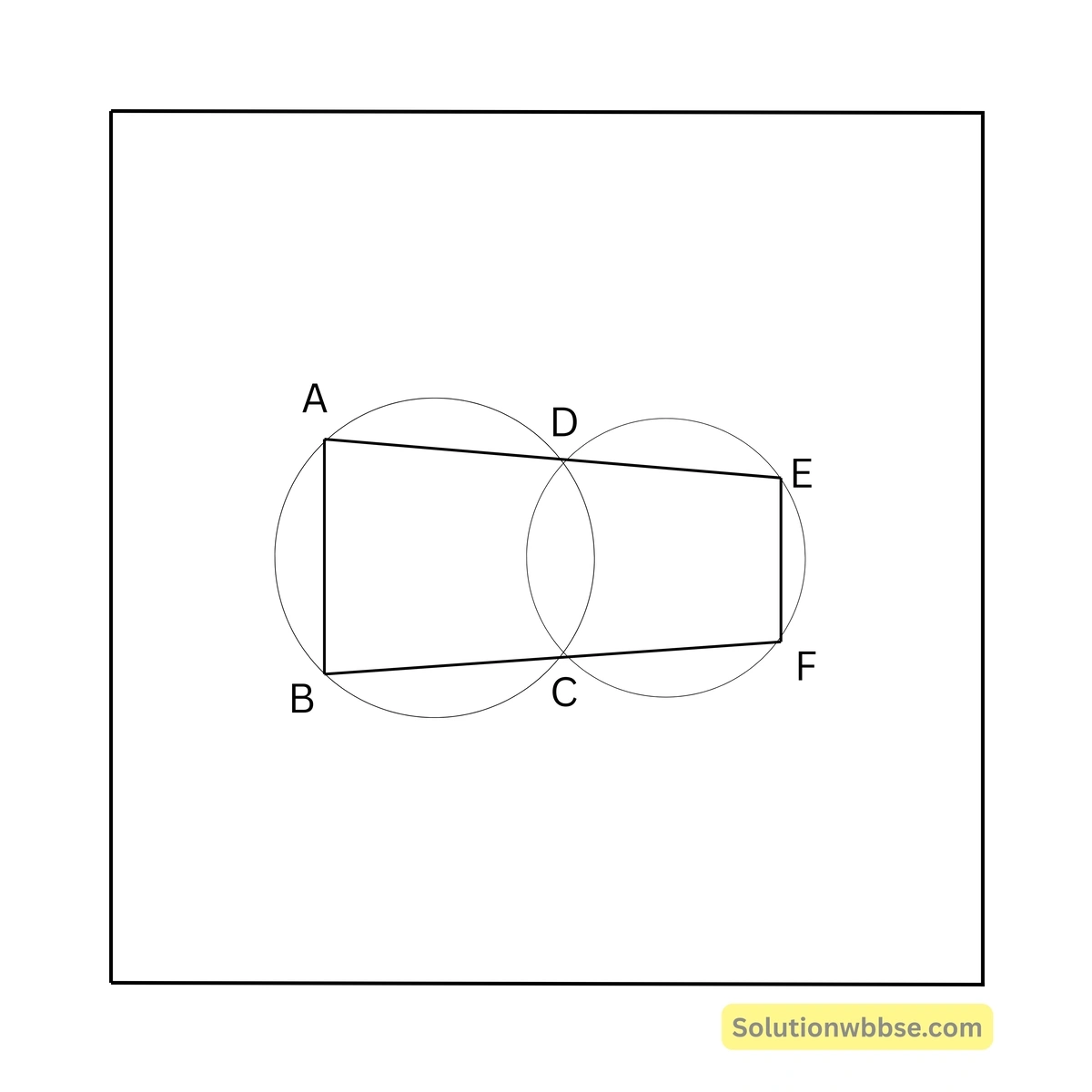
(a) \( 75^\circ \)
(b) \( 70^\circ \)
(c) \( 60^\circ \)
(d) \( 105^\circ \)
উত্তর – (d) \( 105^\circ \)
সমাধান – C, D যুক্ত করা হল, ABCD বৃত্তস্থ চতুর্ভুজের
\( \angle BCD = 180^\circ – \angle DAB = 180^\circ – 75^\circ = 105^\circ \)আবার, DCFE বৃত্তস্থ চতুর্ভুজ হওয়ায় \( \angle DEF = \angle BCD = 105^\circ \)
88. পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB বৃত্তের ব্যাস। ABCD বৃত্তস্থ চতুর্ভুজ যার \( AB \parallel DC \) এবং \( \angle BAC = 25^\circ \) হলে \( \angle DAC \) এর মান —
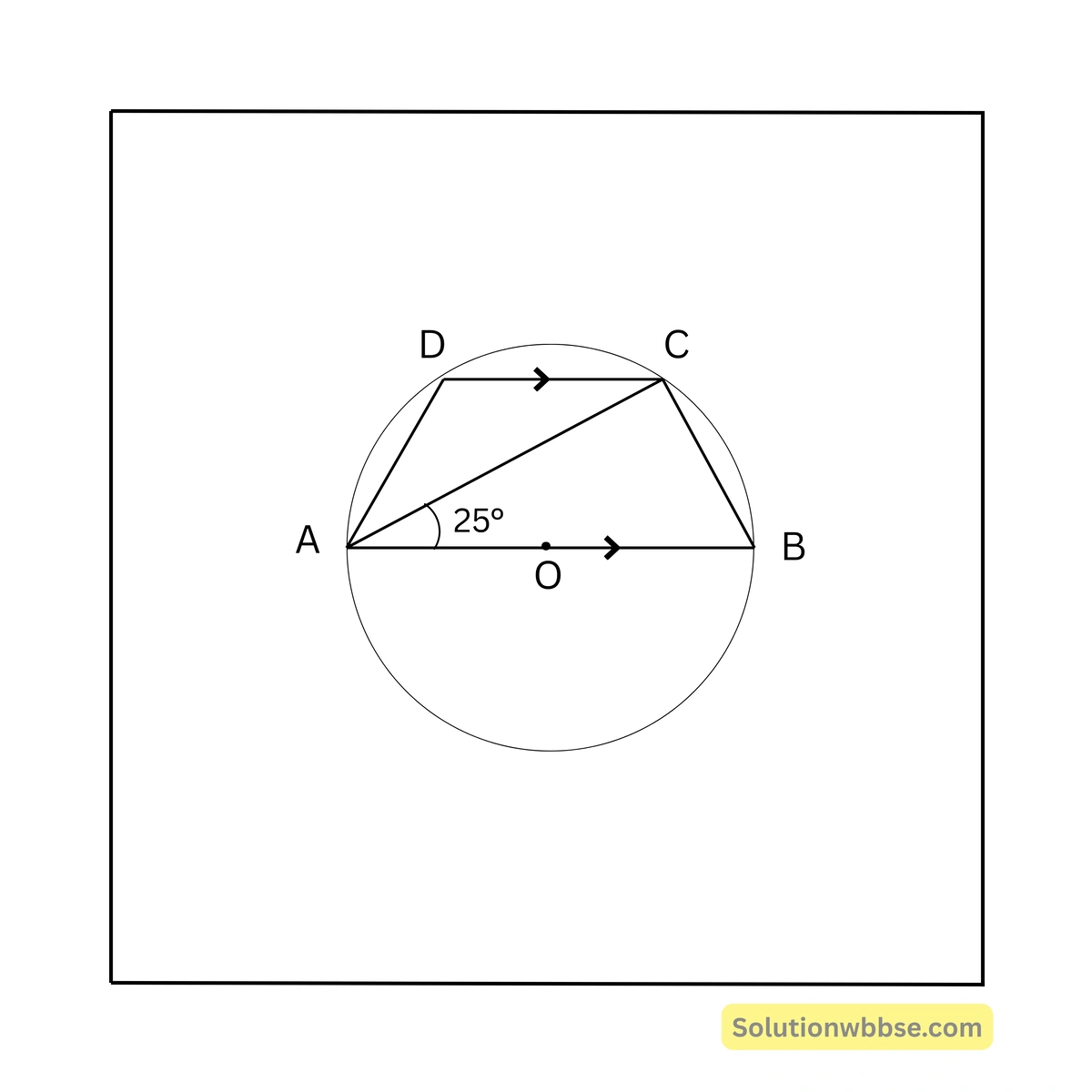
(a) \( 50^\circ \)
(b) \( 25^\circ \)
(c) \( 130^\circ \)
(d) \( 40^\circ \)
উত্তর – (d) \( 40^\circ \)
সমাধান – \( \angle ACB = 90^\circ \), [অর্ধবৃত্তস্থ কোণ]
\( \angle ACD = \angle BAC = 25^\circ \) [∵ \( AB \parallel DC \) এবং AC ভেদক]
∴ \( \angle BCD = \angle ACB + \angle ACD \)
\( = 90^\circ + 25^\circ = 115^\circ \)∴ \( \angle BAD = 180^\circ – 115^\circ = 65^\circ \)
∴ \( \angle DAC = \angle BAD – \angle BAC = 65^\circ – 25^\circ = 40^\circ \)
89. পাশের চিত্রে ABCD বৃত্তস্থ চতুর্ভুজ, BA কে F বিন্দু পর্যন্ত বর্ধিত করা হল। \( AE \parallel CD \), \( \angle ABC = 92^\circ \) এবং \( \angle FAE = 20^\circ \) হলে, \( \angle BCD \)-এর মান
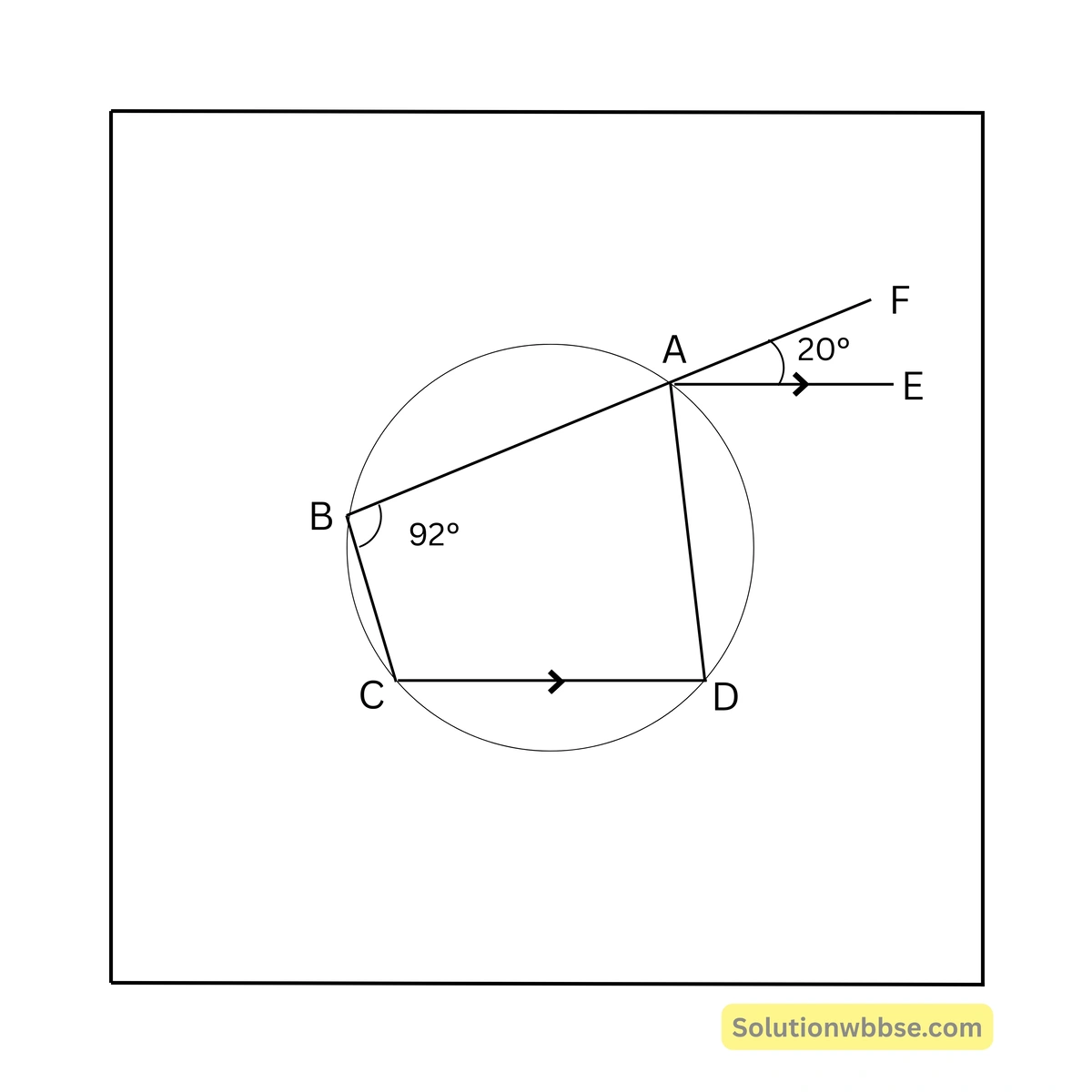
(a) \( 20^\circ \)
(b) \( 88^\circ \)
(c) \( 108^\circ \)
(d) \( 72^\circ \)
উত্তর – (c) \( 108^\circ \)
সমাধান – \( \angle ADC = 180^\circ – \angle ABC = 180^\circ – 92^\circ = 88^\circ \)
∴ \( \angle DAE = \angle ADC = 88^\circ \) [∵ \( AE \parallel CD \) এবং AD ভেদক]
∴ \( \angle DAF = \angle DAE + \angle FAE = 88^\circ + 20^\circ = 108^\circ \)
∴ \( \angle BCD = \angle DAF = 108^\circ \)
90. পাশের চিত্রে \( \angle BAD = 65^\circ \), \( \angle ABD = 70^\circ \) এবং \( \angle BDC = 45^\circ \) হলে \( \angle CBD = \)
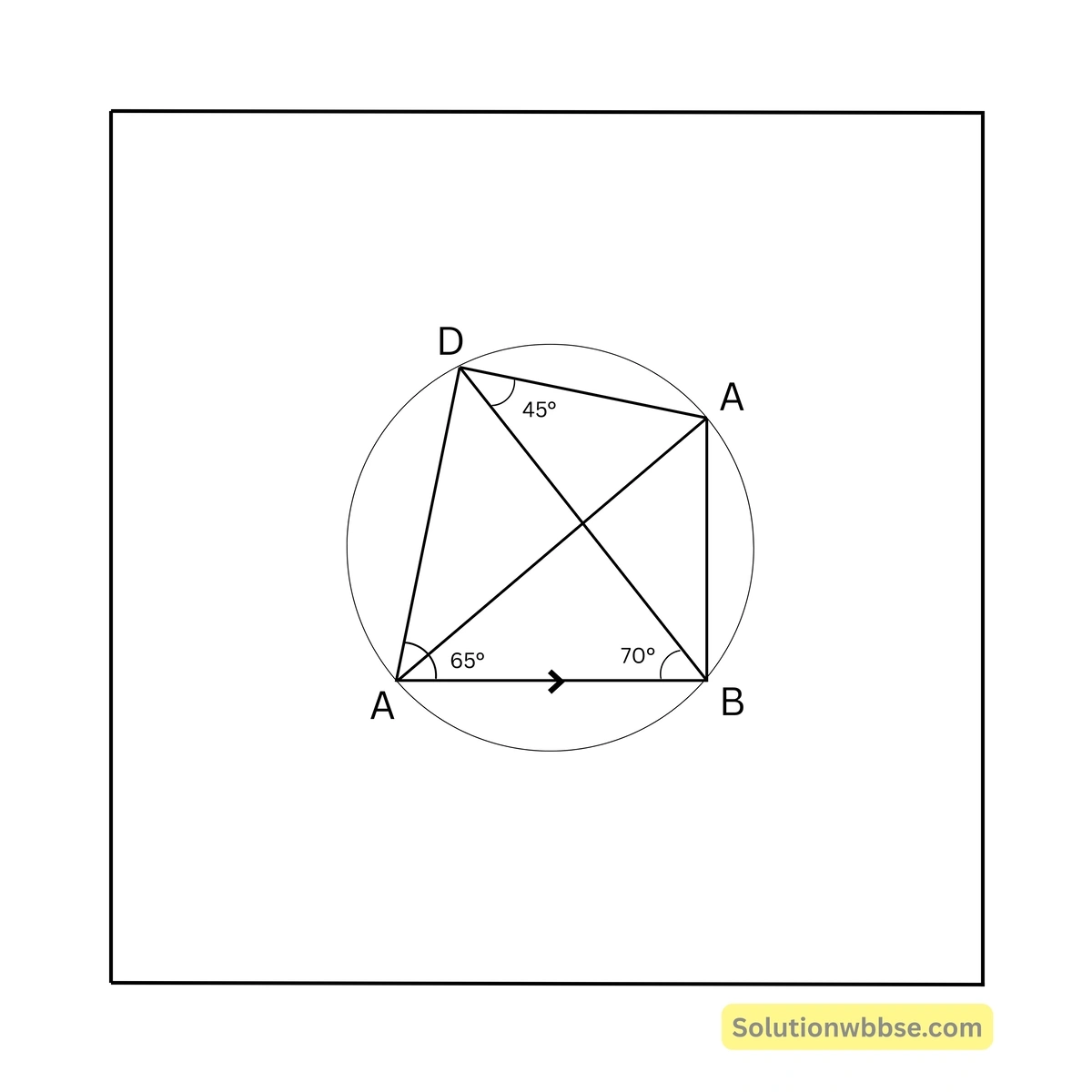
(a) \( 45^\circ \)
(b) \( 30^\circ \)
(c) \( 25^\circ \)
(d) \( 20^\circ \)
উত্তর – (d) \( 20^\circ \)
সমাধান – \( \angle BCD = 180^\circ – \angle DAB \)
\( = 180^\circ – 65^\circ \)\( = 115^\circ \) [∵ ABCD বৃত্তস্থ চতুর্ভুজ]
\( \triangle BCD \) এর \( \angle CBD + \angle BDC + \angle DCB = 180^\circ \)
বা, \( \angle CBD + 45^\circ + 115^\circ = 180^\circ \)
বা, \( \angle CBD = 180^\circ – 160^\circ = 20^\circ \)
91. O কেন্দ্রীয় একটি বৃত্তের ব্যাসার্ধ 8 সেমি, বৃত্তের বহিঃস্থ একটি বিন্দু C থেকে ওই বৃত্তে একটি স্পর্শক CD অঙ্কন করা হল। CD = 6 সেমি হলে, OC =
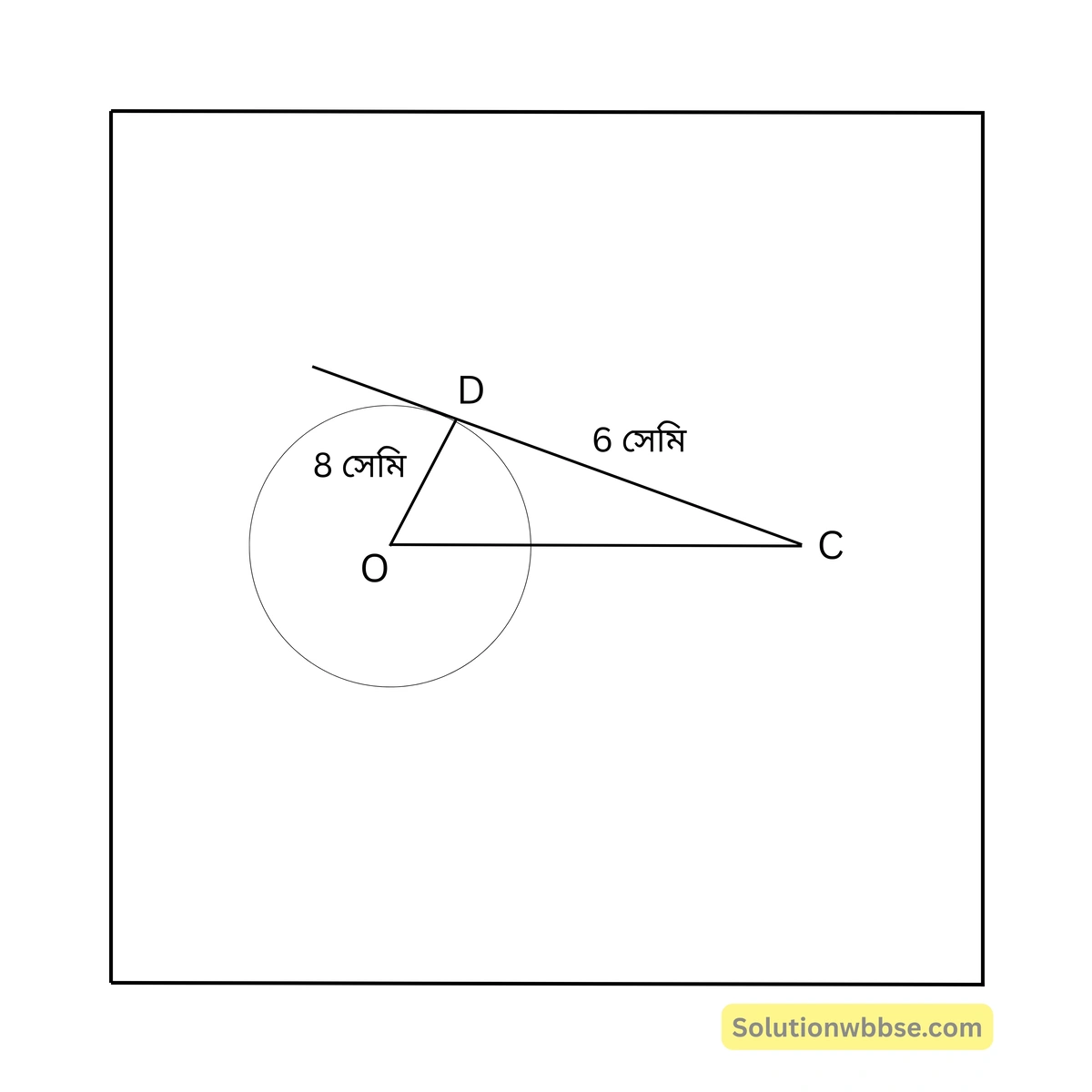
(a) 14 সেমি
(b) 13 সেমি
(c) 12 সেমি
(d) 10 সেমি
উত্তর – (d) 10 সেমি
সমাধান – চিত্রে, \( OD = 8 \) সেমি, \( CD = 6 \) সেমি
∴ \( OC = \sqrt{CD^2 + OD^2} \)
\( = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = 10 \) সেমি
92. একটি রম্বসের দুটি কর্ণের দৈর্ঘ্য 24 সেমি এবং 10 সেমি হলে রম্বসটির পরিসীমা —
(a) 13 সেমি
(b) 26 সেমি
(c) 52 সেমি
(d) 25 সেমি
উত্তর – (c) 52 সেমি
সমাধান – ABCD রম্বসটির কর্ণদ্বয় P বিন্দুতে ছেদ করে।
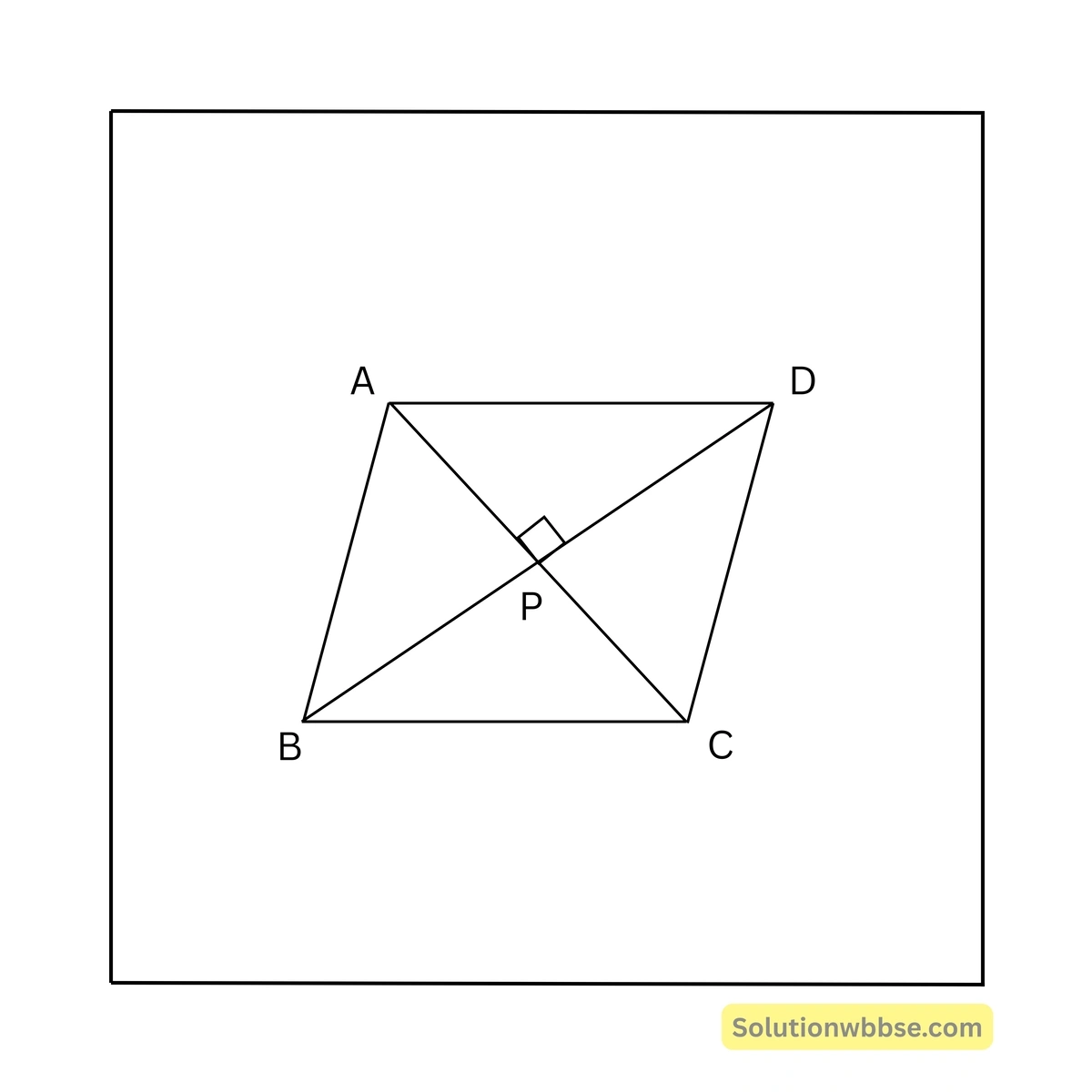
ধরি BD = 24 সেমি ও AC = 10 সেমি
∴ \( PD = \frac{1}{2} BD = 12 \) সেমি ও \( PA = \frac{1}{2} AC = 5 \) সেমি
এখন \( AC \perp BD \)
∴ \( AD^2 = PD^2 + PA^2 = 12^2 + 5^2 = 169 \)∴
AD = 13 সেমি
∴ রম্বসটির পরিসীমা = 4 × 13 = 52 সেমি
93. দুটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি ও 3 সেমি, বৃত্ত দুটি পরস্পরকে বহিস্পর্শ করে। বৃত্ত দুটির কেন্দ্রদ্বয়ের মধ্যে দূরত্ব হবে?
(a) 2 সেমি
(b) 2.5 সেমি
(c) 1.5 সেমি
(d) 8 সেমি
উত্তর – (d) 8 সেমি
সমাধান – (5 + 3) সেমি = 8 সেমি
94. \( \triangle DEF \) ও \( \triangle PQR \) এ \( \angle D = \angle Q \) এবং \( \angle R = \angle E \) হলে, নীচের কোনটি সঠিক নয়
(a) \( \frac{EF}{PR} = \frac{DF}{PQ} \)
(b) \( \frac{QR}{PQ} = \frac{EF}{DF} \)
(c) \( \frac{DE}{QR} = \frac{DF}{PQ} \)
(d) \( \frac{EF}{RP} = \frac{DF}{QR} \)
উত্তর – (b) \( \frac{QR}{PQ} = \frac{EF}{DF} \)
সমাধান – \( \triangle DEF \) ও \( \triangle PQR \) এর \( \angle D = \angle Q \), \( \angle E = \angle R \)
এবং \( \angle F = \angle P \) ∴ \( \triangle DFE \sim \triangle PQR \)
অনুরূপ বাহুগুলি হল EF, PR; DF, PQ ও DE, QR
∴ \( \frac{EF}{PR} = \frac{DF}{PQ} = \frac{DE}{QR} \)
95. দুটি সদৃশ ত্রিভুজের পরিসীমার অনুপাত 4:9 হলে তাদের ক্ষেত্রফলের অনুপাত হবে –
(a) 16 : 81
(b) 81 : 16
(c) 4 : 9
(d) 2 : 3
উত্তর – (a) 16 : 81
সমাধান – দুটি সদৃশ ত্রিভুজের ক্ষেত্রফলের অনুপাত = ত্রিভুজ দুইটির পরিসীমার বর্গের অনুপাত
= 16 : 81
96. এক ব্যক্তি একটি স্থান থেকে 24 মিটার পশ্চিমদিকে যান এবং তারপর 10 মিটার উত্তর দিকে যান। যাত্রাস্থান থেকে ব্যক্তির দূরত্ব —
(a) 34 মিটার
(b) 17 মিটার
(c) 26 মিটার
(d) 25 মিটার
উত্তর – (c) 26 মিটার
সমাধান –
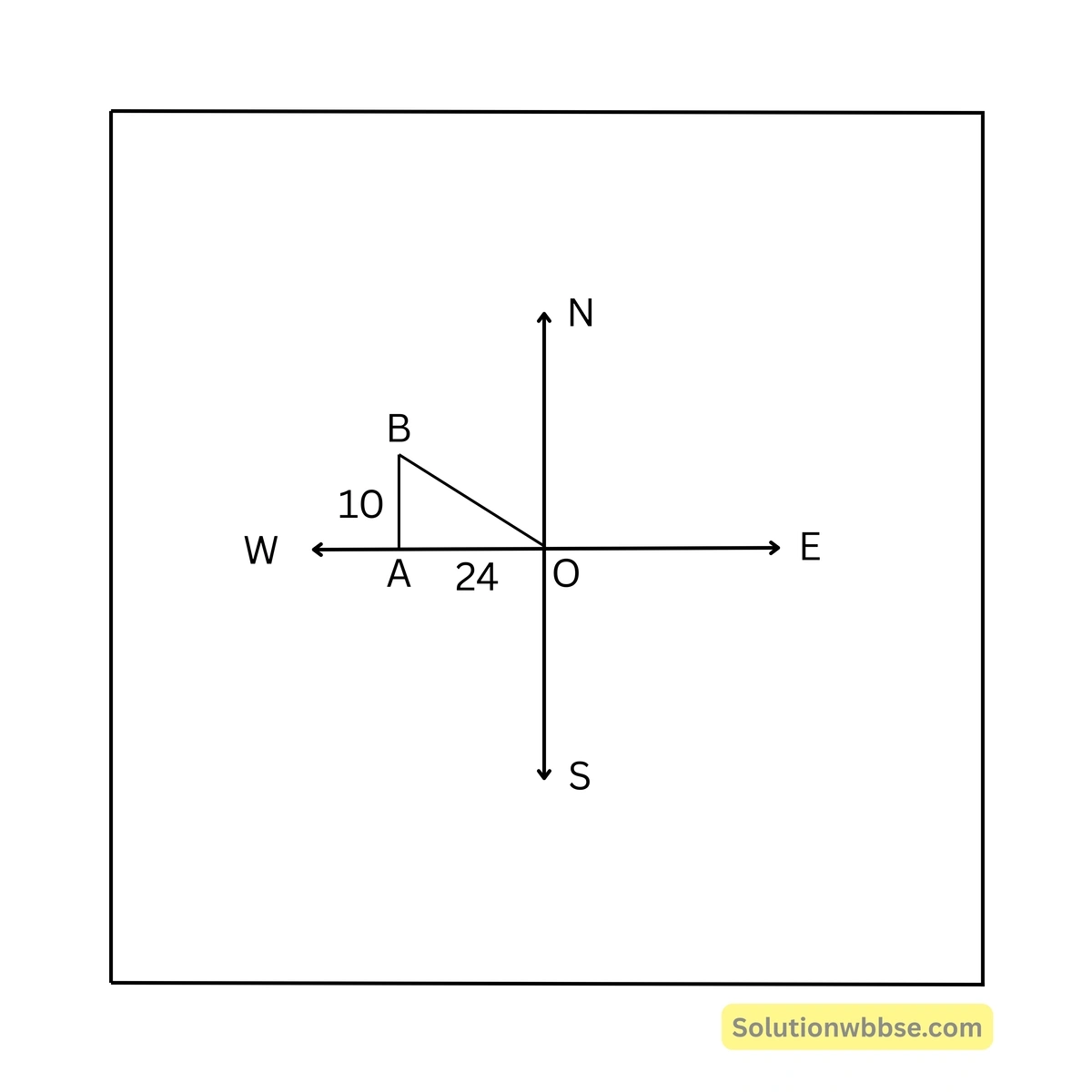
যাত্রাস্থান থেকে ব্যক্তির দূরত্ব = OB
∴ \( OB = \sqrt{(24)^2 + (10)^2} = \sqrt{676} = 26 \) মিটার
97. পাশের চিত্রে ABCD চতুর্ভুজের একটি অন্তর্লিখিত বৃত্ত অঙ্কন করা হয়েছে। AB = 6 সেমি এবং CD = 5 সেমি হলে (BC + AD) এর মান হবে —
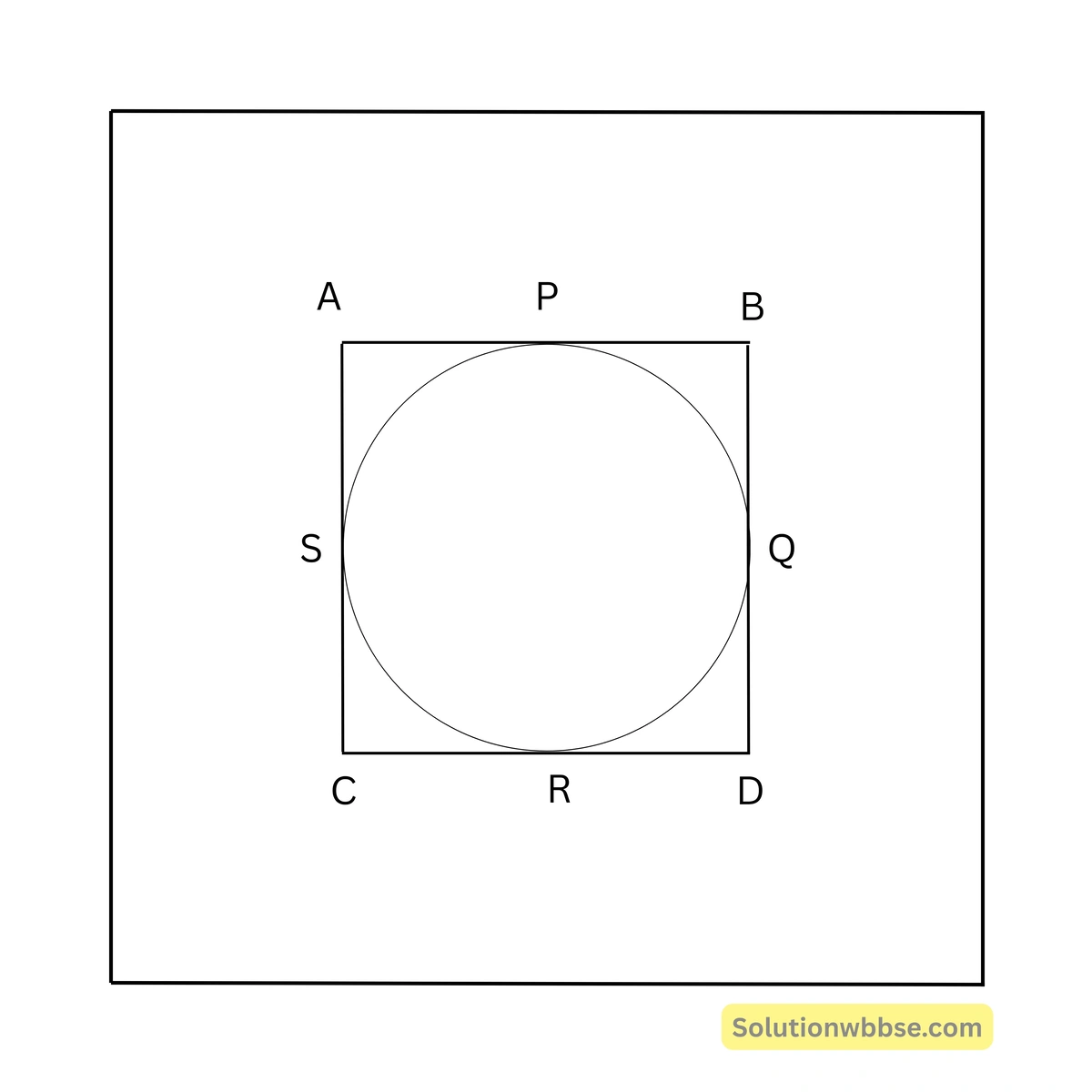
(a) 9 সেমি
(b) 10 সেমি
(c) 11 সেমি
(d) 12 সেমি
উত্তর – (c) 11 সেমি
সমাধান – যেহেতু ABCD চতুর্ভুজের চারটি বাহু AB, BC, CD ও DA বৃত্তটিকে P, Q, R ও S বিন্দুতে স্পর্শ করে,
∴ AP = AS, BP = BQ, CR = CQ, DS = DR
∴ BC + AD = BQ + CQ + AS + DS
= BP + CR + AP + DR
= (AP + BP) + (CR + DR)
= AB + CD
= 6 + 5 = 11 সেমি.
98. \( \triangle ABC \) এবং \( \triangle PQR \) এ \( \frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ} \) হলে
(a) \( \angle A = \angle Q \)
(b) \( \angle A = \angle P \)
(c) \( \angle A = \angle R \)
(d) \( \angle B = \angle Q \)
উত্তর – (a) \( \angle A = \angle Q \)
সমাধান – \( \triangle ABC \) ও \( \triangle PQR \) এ \( \frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ} \)
∴ \( \triangle ABC \sim \triangle QRP \)
অনুরূপ কোণগুলি হল \( \angle A = \angle Q \); \( \angle B = \angle R \); \( \angle C = \angle P \)
∴ \( \angle A = \angle Q \), \( \angle B = \angle R \), \( \angle C = \angle P \)
99. \( \tan\theta + \cot\theta \)-এর সর্বনিম্ন মান— [M.P. 2024]
(a) 0
(b) 2
(c) -2
(d) 1
উত্তর – (b) 2
100. \( \theta \)-এর যে কোন মানের জন্য \( 5 + 4 \sin\theta \)-র বৃহত্তম মান হবে : [M.P. 2023]
(a) 9
(b) 1
(c) 0
(d) 5
উত্তর – (a) 9
সমাধান – \( \theta = 90^\circ \) হলে \( \sin\theta \)-এর মান সর্বাধিক অর্থাৎ = 1
∴ \( \theta = 90^\circ \) হলে \( 5 + 4 \sin\theta \) এর মান বৃহত্তম হবে
∴ বৃহত্তম মান = 5 + 4 × 1 = 9
101. যদি \( \sin\theta – \cos\theta = 0 \) (\( 0^\circ \le \theta \le 90^\circ \)) এবং \( \sec\theta + \text{cosec}\,\theta = x \) হয়, তাহলে x-এর মান— [M.P. 2020]
(a) 1
(b) 2
(c) \( \sqrt{2} \)
(d) \( 2\sqrt{2} \)
উত্তর – (d) \( 2\sqrt{2} \)
সমাধান –
∵ \( \sin\theta – \cos\theta = 0 \)
বা, \( \sin\theta = \cos\theta \)
বা, \( \frac{\sin\theta}{\cos\theta} = 1 \)
বা, \( \tan\theta = 1 \)
বা, \( \tan\theta = \tan 45^\circ \) [∵ \( 0^\circ \le \theta \le 90^\circ \)]
∴ \( \theta = 45^\circ \)
\( x = \sec\theta + \text{cosec}\,\theta = \sec 45^\circ + \text{cosec}\,45^\circ \)\( = \sqrt{2} + \sqrt{2} = 2\sqrt{2} \)102. যদি \( \tan\alpha + \cot\alpha = 2 \) হয়, তাহলে \( (\tan^{13}\alpha + \cot^{13}\alpha) \)-এর মান— [M.P. 2019]
(a) 1
(b) 0
(c) 2
(d) কোনটিই নয়
উত্তর – (c) 2
সমাধান – \( \tan\alpha + \cot\alpha = 2 \)
বা, \( \tan\alpha + \frac{1}{\tan\alpha} = 2 \)
বা, \( \frac{\tan^2\alpha + 1}{\tan\alpha} = 2 \)
বা, \( \tan^2\alpha + 1 = 2\tan\alpha \)
বা, \( \tan^2\alpha – 2\tan\alpha + 1 = 0 \)
বা, \( (\tan\alpha – 1)^2 = 0 \)
∴ \( \tan\alpha = 1 \) ∴ \( \cot\alpha = 1 \)
\( \tan^{13}\alpha + \cot^{13}\alpha = (\tan\alpha)^{13} + (\cot\alpha)^{13} = (1)^{13} + (1)^{13} = 2 \)103. \( A+B=120^\circ \) এবং \( A = \frac{5\pi}{12} \) হলে B কোণের বৃত্তীয় মান হবে
(a) \( \frac{\pi}{3} \)
(b) \( \frac{7\pi}{12} \)
(c) \( \frac{2\pi}{15} \)
(d) \( \frac{\pi}{4} \)
উত্তর – (d) \( \frac{\pi}{4} \)
সমাধান –
∴ \( A+B=120^\circ \) বা, \( A+B = 120^\circ \times \frac{\pi}{180} \)
বা, \( A+B = \frac{2\pi}{3} \)
বা, \( B = \frac{2\pi}{3} – A = \frac{2\pi}{3} – \frac{5\pi}{12} = \frac{\pi}{4} \)
104. একটি ঘড়ির মিনিটের কাঁটার প্রান্তবিন্দু 1 ঘন্টায় আবর্তন করে
(a) \( \frac{\pi}{4} \) রেডিয়ান
(b) \( \frac{\pi}{2} \) রেডিয়ান
(c) \( \pi \) রেডিয়ান
(d) \( 2\pi \) রেডিয়ান
উত্তর – (d) \( 2\pi \) রেডিয়ান
সমাধান – ঘড়ির মিনিটের কাঁটার প্রান্তবিন্দু 1 ঘন্টায় আবর্তন করে = \( 360^\circ \)
বা, \( 2\pi \) রেডিয়ান
105. r একক দৈর্ঘ্যবিশিষ্ট কোন বৃত্তের একটি চাপ কেন্দ্রে \( \theta^\circ \) কোণ উৎপন্ন করলে, চাপটির দৈর্ঘ্য হবে —
(a) \( r\theta \) একক
(b) \( \frac{\pi r\theta}{180} \) একক
(c) \( \frac{180 r\theta}{\pi} \) একক
(d) কোনটিই নয়
উত্তর – (b) \( \frac{\pi r\theta}{180} \) একক
106. \( \theta \) কোণটি \( 75^\circ \) কোণের সম্পূরক হলে \( \theta \)-এর বৃত্তীয় মান হবে
(a) \( \frac{7\pi}{12} \)
(b) \( \frac{7\pi}{15} \)
(c) \( \frac{8\pi}{15} \)
(d) কোনটিই নয়
উত্তর – (a) \( \frac{7\pi}{12} \)
সমাধান –
∴ \( \theta \) ও \( 75^\circ \) পরস্পর সম্পূরক
∴ \( \theta = 180^\circ – 75^\circ = 105^\circ \)
∴ \( \theta = 105 \times \frac{\pi}{180} \) রেডিয়ান = \( \frac{7\pi}{12} \) রেডিয়ান
107. একটি ত্রিভুজের তিনটি কোণের পরিমাপ \( x^\circ, 2x^\circ \) এবং \( \frac{\pi x}{240} \) রেডিয়ান হলে \( x \) এর মান হবে—
(a) 12
(b) 24
(c) 36
(d) 48
উত্তর – (d) 48
সমাধান – \( \frac{\pi x}{240} \) রেডিয়ান = \( \frac{3x^\circ}{4} \)
∴ \( x^\circ + 2x^\circ + \frac{3x^\circ}{4} = 180^\circ \)
বা, \( \frac{4x^\circ + 8x^\circ + 3x^\circ}{4} = 180^\circ \)
বা, \( 15x^\circ = 720^\circ \)
বা, \( x^\circ = \frac{720^\circ}{15^\circ} = 48^\circ \)
108. \( s = r\theta \) সম্পর্কে \( \theta \)-এর পরিমাপ করা হয়—
(a) ষষ্ঠিক পদ্ধতিতে
(b) বৃত্তীয় পদ্ধতিতে
(c) ওই দুই পদ্ধতিতে
(d) ওই দুই পদ্ধতির কোনোটিতেই নয়
উত্তর: (b) বৃত্তীয় পদ্ধতিতে
109. \( \sin(\theta – 15^\circ) = \frac{1}{2} \) এবং \( \theta \) ধনাত্মক সূক্ষ্মকোণ। \( \cos(\theta + 15^\circ) \)-এর মান হবে –
(a) \( \frac{1}{2} \)
(b) \( \frac{\sqrt{3}}{2} \)
(c) \( \frac{1}{\sqrt{2}} \)
(d) 1
উত্তর – (a) \( \frac{1}{2} \)
সমাধান –
∴ \( \theta \) ধনাত্মক সূক্ষ্মকোণ
∴ \( \sin(\theta – 15^\circ) = \frac{1}{2} = \sin 30^\circ \)
∴ \( \theta – 15^\circ = 30^\circ \) বা, \( \theta = 45^\circ \)
∴ \( \cos(\theta + 15^\circ) = \cos(45^\circ + 15^\circ) = \cos 60^\circ = \frac{1}{2} \)
110. \( x\tan 30^\circ = \cos 60^\circ \) হলে, \( x \)-এর মান হবে —
(a) \( 2\sqrt{3} \)
(b) \( \frac{2}{\sqrt{3}} \)
(c) \( \frac{\sqrt{3}}{2} \)
(d) কোনটিই নয়
উত্তর – (c) \( \frac{\sqrt{3}}{2} \)
সমাধান – \( x\tan 30^\circ = \cos 60^\circ \)
বা, \( x \times \frac{1}{\sqrt{3}} = \frac{1}{2} \)
বা, \( x = \frac{\sqrt{3}}{2} \)
111. যদি \( 2x = \sec A \) এবং \( \frac{2}{x} = \tan A \) হয়, তাহলে \( 2(x^2 – \frac{1}{x^2}) \)-এর মান –
(a) \( \frac{1}{2} \)
(b) \( \frac{1}{4} \)
(c) \( \frac{1}{8} \)
(d) \( \frac{1}{16} \)
উত্তর – (a) \( \frac{1}{2} \)
সমাধান –
\( 2(x^2 – \frac{1}{x^2}) = 2(\frac{\sec^2 A}{4} – \frac{\tan^2 A}{4}) = \frac{1}{2}(\sec^2 A – \tan^2 A) \)\( = \frac{1}{2} \times 1 = \frac{1}{2} \)112. \( \alpha \) একটি ধনাত্মক সূক্ষ্মকোণ হলে —
(a) \( \sin\alpha \le 0 \)
(b) \( 0 < \sin\alpha < 1 \)
(c) \( 0 \le \sin\alpha \le 1 \)
(d) \( \sin\alpha \ge 1 \)
উত্তর – (b) \( 0 < \sin\alpha < 1 \)
113. \( \sec^2\theta + \tan^2\theta = \frac{5}{4} \) হলে, \( (\sec^4\theta – \tan^4\theta) \)-এর মান হবে –
(a) 0
(b) \( \frac{9}{4} \)
(c) \( \frac{5}{4} \)
(d) \( \frac{25}{16} \)
উত্তর – (c) \( \frac{5}{4} \)
সমাধান –
\( \sec^4\theta – \tan^4\theta = (\sec^2\theta)^2 – (\tan^2\theta)^2 \)\( = (\sec^2\theta + \tan^2\theta)(\sec^2\theta – \tan^2\theta) \)\( = \frac{5}{4} \times 1 = \frac{5}{4} \)[∵ \( \sec^2\theta = 1 + \tan^2\theta \) ∴ \( \sec^2\theta – \tan^2\theta = 1 \)]
114. \( (\sin 43^\circ \cos 47^\circ + \cos 43^\circ \sin 47^\circ) \)-এর মান —
(a) 0
(b) 1
(c) \( \sin^4 \)
(d) \( \cos^4 \)
উত্তর – (b) 1
সমাধান – \( \sin 43^\circ \cos 47^\circ + \cos 43^\circ \sin 47^\circ \)
\( = \sin(90^\circ – 47^\circ) \cos 47^\circ + \cos(90^\circ – 47^\circ) \sin 47^\circ \)\( = \cos 47^\circ \cos 47^\circ + \sin 47^\circ \sin 47^\circ \)= \(\cos^2 47^\circ + \sin^2 47^\circ = 1 \)
115. ABC একটি ত্রিভুজ। \( \sin\left(\frac{B+C}{2}\right) = \)
(a) \( \sin\frac{A}{2} \)
(b) \( \cos\frac{A}{2} \)
(c) \( \sin A \)
(d) \( \cos A \)
উত্তর – (b) \( \cos\frac{A}{2} \)
সমাধান –
∵ ABC একটি ত্রিভুজ
∴ \( A + B + C = 180^\circ \)
বা, \( B + C = 180^\circ – A \)
∴ \( \sin\left(\frac{B+C}{2}\right) = \sin\left(\frac{180^\circ-A}{2}\right) = \sin\left(90^\circ-\frac{A}{2}\right) = \cos\frac{A}{2} \)
116. \( \tan A \cdot \tan(90^\circ – A) = \tan\theta \) হলে \( (\sin\theta + \cos\theta) \) এর মান-
(a) 0
(b) \( \sqrt{2} \)
(c) \( 2\sqrt{2} \)
(d) 1
উত্তর – (b) \( \sqrt{2} \)
সমাধান – \( \tan A \cdot \tan (90^\circ – A) = \tan\theta \)
বা, \( \tan\theta = \tan A \cdot \cot A = 1 \)
বা, \( \tan\theta = \tan 45^\circ \)
বা, \( \theta = 45^\circ \)
\( \sin\theta + \cos\theta = \sin 45^\circ + \cos 45^\circ \)\( = \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} \)\( = \frac{2}{\sqrt{2}} = \sqrt{2} \)117. \( \cos^2\alpha + \cos^2\beta = 1 \) হলে \( \alpha + \beta = \)
(a) 0
(b) \( \frac{\pi}{4} \)
(c) \( \frac{\pi}{2} \)
(d) \( \pi \)
উত্তর – (c) \( \frac{\pi}{2} \)
সমাধান –
\( \cos^2\alpha + \cos^2\beta = 1 \)বা, \( \cos^2\alpha = 1 – \cos^2\beta = \sin^2\beta \)
বা, \( \cos\alpha = \sin\beta = \cos\left(\frac{\pi}{2} – \beta\right) \)
∴ \( \alpha = \frac{\pi}{2} – \beta \)
বা, \( \alpha + \beta = \frac{\pi}{2} \)
118. মাঠের উপর একটি বিন্দু থেকে মোবাইল টাওয়ারের চুড়ায় উন্নতি কোণ \( 60^\circ \) এবং টাওয়ারের গোড়া থেকে ওই বিন্দুর দূরত্ব 10 মিটার। টাওয়ারের উচ্চতা —
(a) 10 মিটার
(b) \( 10\sqrt{3} \) মিটার
(c) \( \frac{10}{\sqrt{3}} \) মিটার
(d) 100 মিটার
উত্তর – (b) \( 10\sqrt{3} \) মিটার
সমাধান – \( \tan 60^\circ = \frac{AB}{BC} \)
বা, \( \sqrt{3} = \frac{AB}{10} \)
বা, \( AB = 10\sqrt{3} \)
119. একটি টাওয়ারের উচ্চতা \( 100\sqrt{3} \) মিটার। টাওয়ারের পাদবিন্দু থেকে 100 মিটার দূরে একটি বিন্দু থেকে টাওয়ারের চূড়ার উন্নতি কোণ—
(a) \( 30^\circ \)
(b) \( 45^\circ \)
(c) \( 60^\circ \)
(d) কোনটিই নয়
উত্তর – (c) \( 60^\circ \)
সমাধান – \( \tan\theta = \frac{AB}{BC} = \frac{100\sqrt{3}}{100} \)
বা, \( \tan\theta = \sqrt{3} = \tan 60^\circ \)
∴ \( \theta = 60^\circ \)
120. \( 2\cos 3\theta = 1 \) হলে, \( \theta \)-এর মান —
(a) \( 10^\circ \)
(b) \( 15^\circ \)
(c) \( 20^\circ \)
(d) \( 30^\circ \)
উত্তর – (c) \( 20^\circ \)
সমাধান – \( 2\cos 3\theta = 1 \)
বা, \( \cos 3\theta = \frac{1}{2} = \cos 60^\circ \)
∴ \( 3\theta = 60^\circ \)
বা, \( \theta = 20^\circ \)
121. সমান ভূমি বিশিষ্ট একটি নিরেট অর্ধগোলক ও একটি নিরেট চোঙের উচ্চতা সমান হলে তাদের ঘনফলের অনুপাত — [M.P. 2024]
(a) 1 : 3
(b) 1 : 2
(c) 2 : 3
(d) 3 : 4
উত্তর – (c) 2 : 3
122. দুটি নিরেট গোলকের আয়তনের অনুপাত 27 : 8 হলে তাদের বক্রতলের ক্ষেত্রফলের অনুপাত হবে — [M.P. 2023]
(a) 1 : 2
(b) 9 : 4
(c) 1 : 8
(d) 1 : 16
সমাধান – ধরি গোলক দুইটির ব্যাসার্ধ যথাক্রমে \( r_1 \) ও \( r_2 \) একক
∴ আয়তন যথাক্রমে \( \frac{4}{3}\pi r_1^3 \) ঘনএকক এবং \( \frac{4}{3}\pi r_2^3 \) ঘনএকক
∴ \( \frac{4}{3}\pi r_1^3 : \frac{4}{3}\pi r_2^3 = 27 : 8 \)
বা, \( \frac{r_1^3}{r_2^3} = \frac{27}{8} = \left(\frac{3}{2}\right)^3 \) ∴ \( r_1 : r_2 = 3 : 2 \)
বা, \( r_1^2 : r_2^2 = 9 : 4 \)
বা, \( 4\pi r_1^2 : 4\pi r_2^2 = 9 : 4 \)
উত্তর – (b) 9 : 4
123. 2r একক দৈর্ঘ্যের ব্যাসার্ধবিশিষ্ট নিরেট গোলকের আয়তন – [M.P. 2022]
(a) \( \frac{32\pi r^3}{3} \) ঘন একক
(b) \( \frac{16\pi r^3}{3} \) ঘন একক
(c) \( \frac{8\pi r^3}{3} \) ঘন একক
(d) \( \frac{64\pi r^3}{3} \) ঘন একক
উত্তর – (a) \( \frac{32\pi r^3}{3} \) ঘন একক
সমাধান –
আয়তন = \( \frac{4}{3}\pi (2r)^3 \) ঘন একক = \( \frac{32\pi r^3}{3} \) ঘন একক
124. দুটি লম্ববৃত্তাকার শঙ্কুর আয়তনের অনুপাত 1 : 4 এবং তাদের ভূমিতলের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত 4 : 5 হলে, তাদের উচ্চতার অনুপাত — [M.P. 2020]
(a) 1 : 5
(b) 5 : 4
(c) 25 : 16
(d) 25 : 64
উত্তর – (d) 25 : 64
সমাধান – ধরি শঙ্কু দুটির ব্যাসার্ধ \( r_1, r_2 \) এবং উচ্চতা \( h_1, h_2 \)
শঙ্কুর আয়তন = \( \frac{1}{3}\pi r^2 h \)
∴ \( \frac{\frac{1}{3}\pi r_1^2 h_1}{\frac{1}{3}\pi r_2^2 h_2} = \frac{1}{4} \)
বা, \( \frac{r_1^2 h_1}{r_2^2 h_2} = \frac{1}{4} \)
বা, \( \left(\frac{r_1}{r_2}\right)^2 \cdot \frac{h_1}{h_2} = \frac{1}{4} \)
বা, \( \left(\frac{4}{5}\right)^2 \cdot \frac{h_1}{h_2} = \frac{1}{4} \)
বা, \( \frac{16}{25} \cdot \frac{h_1}{h_2} = \frac{1}{4} \)
বা, \( \frac{h_1}{h_2} = \frac{1}{4} \times \frac{25}{16} = \frac{25}{64} \)
125. 2r একক দৈর্ঘ্যের ব্যাসার্ধ বিশিষ্ট নিরেট গোলকের আয়তন — [M.P. 2022]
(a) \( \frac{32\pi r^3}{3} \) ঘনএকক
(b) \( \frac{16\pi r^3}{3} \) ঘনএকক
(c) \( \frac{8\pi r^3}{3} \) ঘনএকক
(d) \( \frac{64\pi r^3}{3} \) ঘনএকক
উত্তর – (a) \( \frac{32\pi r^3}{3} \) ঘনএকক
সমাধান – কোন গোলকের ব্যাসার্ধ 2r একক হলে, তার আয়তন
= \( \frac{4}{3}\pi (2r)^3 \) ঘনএকক
= \( \frac{32\pi r^3}{3} \) ঘনএকক
126. \( 2\sqrt{6} \) সেমি বাহুবিশিষ্ট দুটি ঘনক পাশাপাশি রাখলে উৎপন্ন আয়তঘনকটির কর্ণের দৈর্ঘ্য হবে [M.P. 2019]
(a) 10 সেমি
(b) 6 সেমি
(c) 2 সেমি
(d) 12 সেমি
উত্তর – (d) 12 সেমি
সমাধান – দুটি ঘনক পাশাপাশি রাখলে উৎপন্ন আয়তঘনকটির দৈর্ঘ্য, প্রস্থ ও উচ্চতা হবে যথাক্রমে \( 4\sqrt{6} \) সেমি, \( 2\sqrt{6} \) সেমি ও \( 2\sqrt{6} \) সেমি।
∴ কর্ণের দৈর্ঘ্য = \( \sqrt{(4\sqrt{6})^2 + (2\sqrt{6})^2 + (2\sqrt{6})^2} \) সেমি
= \( \sqrt{96 + 24 + 24} \) সেমি
= \( \sqrt{144} \) সেমি = 12 সেমি
127. একটি ঘনকের একটি বাহুর দৈর্ঘ্য a একক এবং কর্ণের দৈর্ঘ্য d একক হলে a এবং d এর মধ্যে সম্পর্ক হবে [M.P. 2018]
(a) \( \sqrt{2}a = d \)
(b) \( \sqrt{3}a = d \)
(c) \( a = \sqrt{3}d \)
(d) \( a = \sqrt{2}d \)
উত্তর – (b) \( \sqrt{3}a = d \)
সমাধান – ঘনকের কর্ণের দৈর্ঘ্য \( d = a\sqrt{3} \)
∴ \( \sqrt{3}a = d \)
128. একটি শঙ্কুর ভূমির ব্যাসার্ধের দৈর্ঘ্য এবং উচ্চতা প্রত্যেকটি দ্বিগুণ হলে, শঙ্কুটির আয়তন হয় পূর্বের শঙ্কুর আয়তনের [M.P. 2017]
(a) 3 গুণ
(b) 4 গুণ
(c) 6 গুণ
(d) 8 গুণ
উত্তর – (d) 8 গুণ
সমাধান – মনে করি, শঙ্কুর ভূমিতলের ব্যাসার্ধ \( r \) একক এবং উচ্চতা \( h \) একক
আয়তন (\( V_1 \)) = \( \frac{1}{3} \pi r^2 h \) ঘন একক
শঙ্কুর ভূমিতলের ব্যাসার্ধ এবং উচ্চতাকে দ্বিগুণ করলে আয়তন হয় (\( V_2 \))
= \( \frac{1}{3} \pi (2r)^2 \cdot 2h \) ঘনএকক = \( 8 \cdot \frac{1}{3} \pi r^2 h \) ঘনএকক
∴ \( \frac{V_1}{V_2} = \frac{\frac{1}{3} \pi r^2 h}{8 \cdot \frac{1}{3} \pi r^2 h} = \frac{1}{8} \)
∴ \( V_2 = 8V_1 \)
129. একটি ঘনকের প্রতিটি বাহুকে 25% কমানো হল। মূল ঘনক ও পরিবর্তিত ঘনক দুটির আয়তনের অনুপাত হবে
(a) 64 : 1
(b) 4 : 3
(c) 64 : 27
(d) 32 : 9
উত্তর – (c) 64 : 27
সমাধান – মনে করি, ঘনকটির প্রতিটি বাহুর দৈর্ঘ্য = \( a \) একক
∴ আয়তন (\( v_1 \)) = \( a^3 \) ঘনএকক
পরিবর্তিত ঘনকের প্রতিটি বাহুর দৈর্ঘ্য = \( (a – \frac{a \times 25}{100}) \) একক
= \( (a – \frac{a}{4}) \) একক = \( \frac{3a}{4} \) একক
∴ পরিবর্তিত ঘনকের আয়তন (\( v_2 \)) = \( \frac{27a^3}{64} \) ঘনএকক
∴ \( v_1 : v_2 = a^3 : \frac{27a^3}{64} = 64 : 27 \)
130. দুটি লম্ববৃত্তাকার নিরেট চোঙের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত 2 : 3 এবং উচ্চতার অনুপাত 5 : 3 হলে, তাদের আয়তনের অনুপাত
(a) 27 : 20
(b) 20 : 27
(c) 4 : 9
(d) 9 : 4
উত্তর – (b) 20 : 27
সমাধান – মনে করি, চোঙ দুটির ব্যাসার্ধ যথাক্রমে \( 2x \) একক এবং \( 3x \) একক এবং উচ্চতা যথাক্রমে \( 5y \) একক এবং \( 3y \) একক।
∴ চোঙ দুইটির আয়তনের অনুপাত = \( \frac{\pi (2x)^2 (5y)}{\pi (3x)^2 3y} = \frac{20}{27} = 20 : 27 \)
131. দুটি লম্ববৃত্তাকার নিরেট চোঙের আয়তন সমান এবং তাদের উচ্চতার অনুপাত 1 : 2 হলে, তাদের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত
(a) 1 : \( \sqrt{2} \)
(b) \( \sqrt{2} \) : 1
(c) 1 : 2
(d) 2 : 1
উত্তর – (b) \( \sqrt{2} \) : 1
সমাধান – মনে করি, চোঙ দুটির উচ্চতা যথাক্রমে x একক এবং 2x একক এবং ব্যাসার্ধ যথাক্রমে \( r_1 \) একক এবং \( r_2 \) একক
∴ \( \pi r_1^2 x = \pi r_2^2 (2x) \)
বা, \( r_1^2 = 2r_2^2 \)
বা, \( r_1 = \sqrt{2} r_2 \)
বা, \( \frac{r_1}{r_2} = \frac{\sqrt{2}}{1} \)
∴ \( r_1 : r_2 = \sqrt{2} : 1 \)
132. দুটি ঘনকের আয়তনের অনুপাত 1 : 27 হলে, ঘনক দুটির সমগ্রতলের ক্ষেত্রফলের অনুপাত
(a) 1 : 3
(b) 1 : 8
(c) 1 : 9
(d) 1 : 18
উত্তর – (c) 1 : 9
সমাধান – মনে করি, ঘনক দুইটির বাহুর দৈর্ঘ্য যথাক্রমে a একক এবং b একক
\( \frac{a^3}{b^3} = \frac{1}{27} \)বা, \( \left(\frac{a}{b}\right)^3 = \left(\frac{1}{3}\right)^3 \)
∴ \( \frac{a}{b} = \frac{1}{3} \)
∴ সমগ্র ক্ষেত্রফলের অনুপাত = \( 6a^2 : 6b^2 = a^2 : b^2 = 1 : 9 \)
133. একটি ঘনকের সমগ্রতলের ক্ষেত্রফল s বর্গএকক এবং কর্ণের দৈর্ঘ্য d একক হলে s এবং d এর মধ্যে সম্পর্ক
(a) \( s = 6d^2 \)
(b) \( 3s = 7d \)
(c) \( s^3 = d^2 \)
(d) \( d^2 = \frac{s}{2} \)
উত্তর – (d) \( d^2 = \frac{s}{2} \)
সমাধান – ঘনকটির প্রতি ধারের দৈর্ঘ্য a একক হলে \( s = 6a^2 \) ………(i)
এবং \( d = \sqrt{3}a \)
বা, \( a = \frac{d}{\sqrt{3}} \)
(i) থেকে \( s = 6\left(\frac{d}{\sqrt{3}}\right)^2 = 2d^2 \)
বা, \( d^2 = \frac{s}{2} \)
134. 14 সেমি উচ্চতা বিশিষ্ট একটি লম্ববৃত্তাকার চোঙের আয়তন 6336 ঘনসেমি হলে তার ভূমির ব্যাস হবে
(a) 12 সেমি
(b) 14 সেমি
(c) 21 সেমি
(d) 24 সেমি
উত্তর – (d) 24 সেমি
সমাধান – মনে করি, লম্ববৃত্তাকার চোঙের ব্যাসার্ধ = \( r \) সেমি
∴ প্রশ্নানুসারে, \( \pi r^2 \cdot 14 = 6336 \)
বা, \( r^2 = 6336 \times \frac{7}{22} \times \frac{1}{14} = 144 \)
বা, \( r = 12 \)
∴ \( 2r = 24 \)
135. দুটি নিরেট গোলকের আয়তনের অনুপাত 1 : 8 হলে, তাদের বক্রতলের ক্ষেত্রফলের অনুপাত
(a) 1 : 2
(b) 1 : 4
(c) 1 : 8
(d) 1 : 16
উত্তর – (b) 1 : 4
সমাধান – ধরি, গোলক দুইটির ব্যাসার্ধ যথাক্রমে \( r_1 \) একক এবং \( r_2 \) একক
প্রদত্ত, \( \frac{\frac{4}{3}\pi r_1^3}{\frac{4}{3}\pi r_2^3} = \frac{1}{8} \)
বা, \( \frac{r_1^3}{r_2^3} = \frac{1}{8} \)
বা, \( \left(\frac{r_1}{r_2}\right)^3 = \left(\frac{1}{2}\right)^3 \)
∴ \( \frac{r_1}{r_2} = \frac{1}{2} \)
∴ গোলকদুইটির ক্ষেত্রফলের অনুপাত = \( \frac{4\pi r_1^2}{4\pi r_2^2} = \left(\frac{r_1}{r_2}\right)^2 = \left(\frac{1}{2}\right)^2 = \frac{1}{4} = 1:4 \)
136. একটি লম্ববৃত্তাকার শঙ্কুর ব্যাসার্ধের দৈর্ঘ্য একই রেখে উচ্চতা দ্বিগুণ করলে শঙ্কুর আয়তন বৃদ্ধি পায়
(a) 100%
(b) 200%
(c) 300%
(d) 400%
উত্তর – (a) 100%
সমাধান – মনে করি, লম্ব বৃত্তাকার শঙ্কুর ভূমির ব্যাসার্ধ = \( r \) একক এবং উচ্চতা = \( h \) একক
∴ আয়তন (\( v \)) = \( \frac{1}{3}\pi r^2 h \) ঘনএকক
এখন শঙ্কুর উচ্চতা \( 2h \) একক হলে,
আয়তন = \( \frac{1}{3}\pi r^2 (2h) \) ঘনএকক
= \( 2 \times \frac{1}{3}\pi r^2 h \) ঘনএকক = \( 2v \)
∴ শতকরা আয়তন বৃদ্ধি = \( \frac{2v – v}{v} \times 100\% = 100\% \)
137. একটি লম্ববৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য অর্ধেক এবং উচ্চতা দ্বিগুণ করা হলে, চোঙটির আয়তন হবে পূর্বের চোঙের আয়তনের
(a) সমান
(b) দ্বিগুণ
(c) অর্ধেক
(d) 4 গুণ
উত্তর – (c) অর্ধেক
সমাধান – মনে করি, চোঙটির ব্যাসার্ধ \( r \) একক এবং উচ্চতা \( h \) একক
∴ চোঙটির আয়তন (\( v_1 \)) = \( \pi r^2 h \) ঘনএকক
পরিবর্তিত চোঙটির ব্যাসার্ধ \( \left(\frac{r}{2}\right) \) একক এবং উচ্চতা \( 2h \) একক
∴ পরিবর্তিত চোঙটির আয়তন (\( v_2 \)) = \( \pi \left(\frac{r}{2}\right)^2 \cdot 2h \) ঘনএকক
∴ \( \frac{v_2}{v_1} = \frac{\pi \cdot \frac{r^2}{4} \cdot 2h}{\pi r^2 h} = \frac{1}{2} \) ∴ \( v_2 = \frac{1}{2}v_1 \)
138. 7 সেমি দৈর্ঘ্যের ব্যাসার্ধ বিশিষ্ট একটি নিরেট অর্ধগোলকের সমগ্রতলের ক্ষেত্রফল
(a) \( 588\pi \) বর্গসেমি
(b) \( 392\pi \) বর্গসেমি
(c) \( 147\pi \) বর্গসেমি
(d) \( 98\pi \) বর্গসেমি
উত্তর – (c) \( 147\pi \) বর্গসেমি
সমাধান – 7 সেমি ব্যাসার্ধ বিশিষ্ট নিরেট অর্ধগোলকের সমগ্রতলের ক্ষেত্রফল = \( 3\pi (7)^2 \) বর্গসেমি = \( 147\pi \) বর্গসেমি
139. দুটি নিরেট গোলকের বক্রতলের ক্ষেত্রফলের অনুপাত 16 : 9 হলে তাদের আয়তনের অনুপাত
(a) 64 : 27
(b) 4 : 3
(c) 27 : 64
(d) 3 : 4
উত্তর – (a) 64 : 27
সমাধান – মনে করি, গোলক দুটির ব্যাসার্ধ যথাক্রমে \( r_1 \) একক এবং \( r_2 \) একক
∴ \( \frac{4\pi r_1^2}{4\pi r_2^2} = \frac{16}{9} \)
বা, \( \frac{r_1^2}{r_2^2} = \frac{16}{9} \)
বা, \( \left(\frac{r_1}{r_2}\right)^2 = \left(\frac{4}{3}\right)^2 \)
বা, \( \frac{r_1}{r_2} = \frac{4}{3} \)
∴ গোলক দুটির আয়তনের অনুপাত = \( \frac{\frac{4}{3}\pi r_1^3}{\frac{4}{3}\pi r_2^3} = \left(\frac{r_1}{r_2}\right)^3 = \left(\frac{4}{3}\right)^3 = \frac{64}{27} \)
= 64 : 27
140. d একক ব্যাসবিশিষ্ট একটি অর্ধগোলকের আয়তন হল
(a) \( \frac{2}{3}\pi d^3 \) ঘনএকক
(b) \( \frac{1}{6}\pi d^3 \) ঘনএকক
(c) \( \frac{1}{12}\pi d^3 \) ঘনএকক
(d) \( \frac{1}{18}\pi d^3 \) ঘনএকক
উত্তর – (c) \( \frac{1}{12}\pi d^3 \) ঘনএকক
সমাধান –
∴ অর্ধগোলকের ব্যাসার্ধ = \( \frac{d}{2} \) একক
অর্ধগোলকের আয়তন = \( \frac{2}{3}\pi \left(\frac{d}{2}\right)^3 = \frac{1}{12}\pi d^3 \) ঘনএকক
141. একটি নিরেট গোলকের বক্রতলের ক্ষেত্রফল ও 3 গুণ আয়তনের সাংখ্যমান সমান হলে, গোলকটির ব্যাসার্ধের দৈর্ঘ্য
(a) 1 একক
(b) 2 একক
(c) 3 একক
(d) 4 একক
উত্তর – (a) 1 একক
সমাধান – মনে করি, গোলকটির ব্যাসার্ধ = \( r \) একক
∴ \( 4\pi r^2 = 3 \times \frac{4}{3}\pi r^3 \)
∴ \( r = 1 \)
142. r একক দৈর্ঘ্যের ব্যাসার্ধ বিশিষ্ট একটি নিরেট গোলককে গলিয়ে r একক উচ্চতার একটি নিরেট লম্ব বৃত্তাকার শঙ্কু তৈরী করা হলো শঙ্কুটির ভূমির ব্যাসার্ধের দৈর্ঘ্য
(a) 2r একক
(b) 3r একক
(c) r একক
(d) 4r একক
উত্তর – (a) 2r একক
সমাধান – মনে করি, শঙ্কুটির ভূমির ব্যাসার্ধ \( R \) একক
∴ \( \frac{1}{3}\pi R^2 r = \frac{4}{3}\pi r^3 \)
বা, \( R^2 = 4r^2 \)
বা, \( R = 2r \)
143. একটি লম্ববৃত্তাকার শঙ্কুর ব্যাসার্ধের দৈর্ঘ্য \( \frac{r}{2} \) একক এবং তির্যক উচ্চতা \( 2l \) একক হলে সমগ্রতলের ক্ষেত্রফল
(a) \( 2\pi r(l+r) \) বর্গএকক
(b) \( \pi r \left(l+\frac{r}{4}\right) \) বর্গএকক
(c) \( \pi r(l+r) \) বর্গএকক
(d) \( 2\pi r l \) বর্গএকক
উত্তর – (b) \( \pi r \left(l+\frac{r}{4}\right) \) বর্গএকক
সমাধান – শঙ্কুটির ব্যাসার্ধ (\( R \)) = \( \frac{r}{2} \) একক এবং তির্যক উচ্চতা (\( L \)) = \( 2l \) একক
∴ সমগ্রতলের ক্ষেত্রফল = \( \pi R(R+L) = \pi \frac{r}{2} \left(\frac{r}{2} + 2l\right) \)
= \( \pi r \left(\frac{r}{4} + l\right) \) বর্গএকক
144. r একক দৈর্ঘ্যের ব্যাসার্ধ বিশিষ্ট একটি নিরেট অর্ধগোলক থেকে সর্ববৃহৎ যে নিরেট শঙ্কু কেটে নেওয়া যাবে তার আয়তন
(a) \( 4\pi r^3 \) ঘনএকক
(b) \( 3\pi r^3 \) ঘনএকক
(c) \( \frac{\pi r^3}{4} \) ঘনএকক
(d) \( \frac{\pi r^3}{3} \) ঘনএকক
উত্তর – (d) \( \frac{\pi r^3}{3} \) ঘনএকক
সমাধান – সর্ববৃহৎ শঙ্কুটির ব্যাসার্ধ = অর্ধগোলকটির ব্যাসার্ধ = \( r \) একক
শঙ্কুটির উচ্চতা = অর্ধগোলকটির ব্যাসার্ধ = \( r \) একক
∴ শঙ্কুটির আয়তন = \( \frac{1}{3}\pi r^2 r \) ঘনএকক = \( \frac{1}{3}\pi r^3 \) ঘনএকক
145. দুইটি শঙ্কুর উচ্চতা সমান এবং ভূমির ব্যাসার্ধের অনুপাত 2 : 3। তাদের আয়তনের অনুপাত
(a) 2 : 3
(b) 3 : 2
(c) 4 : 9
(d) 9 : 4
উত্তর – (c) 4 : 9
সমাধান – মনে করি, শঙ্কু দুটির ভূমির ব্যাসার্ধ \( 2r \) একক এবং \( 3r \) একক এবং তাদের প্রত্যেকের উচ্চতা \( h \) একক
∴ শঙ্কু দুটির আয়তনের অনুপাত = \( \frac{1}{3}\pi (2r)^2 h : \frac{1}{3}\pi (3r)^2 h \)
= \( 4 : 9 \)
146. h সেমি উচ্চতাবিশিষ্ট একটি লম্ববৃত্তাকার শঙ্কুর আয়তন v ঘনসেমি হলে তার ভূমির ব্যাস হবে
(a) \( 2\sqrt{\frac{\pi h}{3v}} \) সেমি
(b) \( \sqrt{\frac{3v}{\pi h}} \) সেমি
(c) \( \sqrt{\frac{\pi h}{3v}} \) সেমি
(d) \( 2\sqrt{\frac{3v}{\pi h}} \) সেমি
উত্তর – (d) \( 2\sqrt{\frac{3v}{\pi h}} \) সেমি
সমাধান – মনে করি, লম্ব বৃত্তাকার শঙ্কুর ভূমির ব্যাসার্ধ = \( r \) সেমি
∴ শর্তানুসারে \( v = \frac{1}{3}\pi r^2 h \)
বা, \( r^2 = \frac{3v}{\pi h} \)
বা, \( r = \sqrt{\frac{3v}{\pi h}} \)
বা, \( 2r = 2\sqrt{\frac{3v}{\pi h}} \)
147. একটি লম্ববৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য r একক এবং উচ্চতা 2r একক। চোঙটির মধ্যে সর্ববৃহৎ যে গোলকটি রাখা যাবে তার ব্যাসের দৈর্ঘ্য
(a) r একক
(b) 2r একক
(c) \( \frac{r}{2} \) একক
(d) 4r একক
উত্তর – (b) 2r একক
সমাধান – সর্ববৃহৎ গোলকটির ব্যাস = চোঙের ব্যাস = \( 2r \) একক
রাশিবিজ্ঞান
148. প্রথম দশটি স্বাভাবিক সংখ্যার গড় A এবং মধ্যমা M হলে সম্পর্কটি —
(a) \(A > M\)
(b) \(A < M\)
(c) \(A = \frac{1}{M}\)
(d) \(A = M\)
উত্তর – (d) \(A = M\)
149. একটি চলকের তিনটি মান 4, 5 এবং 7, তাদের পরিসংখ্যা যথাক্রমে \((p – 2)\), \((p + 1)\) ও \((p – 1)\)। চলকটির যৌগিক গড় 5.4 হলে p-এর মান হবে: [M.P. 2023]
(a) 1
(b) 2
(c) 3
(d) 4
উত্তর – (d) 4
সমাধান –
যৌগিক গড় \(= \frac{4(p-2)+5(p+1)+7(p-1)}{(p-2)+(p+1)+(p-1)} = \frac{16p-10}{3p-2}\)
\(\therefore\) শর্তানুসারে \(\frac{16p-10}{3p-2} = 5.4\)
বা, \(\frac{16p-10}{3p-2} = \frac{54}{10}\)
বা, \(162p – 108 = 160p – 100\)
বা, \(2p = 8\)
বা, \(p = 4\)
150. 1, 3, 2, 8, 10, 8, 3, 2, 8, 8-এর সংখ্যাগুরু মান –
(a) 2
(b) 3
(c) 8
(d) 10
উত্তর – (c) 8
সমাধান – 8 সবচেয়ে বেশি 4 বার আছে, তাই সংখ্যাগুরু মান 8।
151. \(x_1, x_2, x_3, \ldots, x_{10}\) রাশিগুলির গড় 20 হলে \(x_1+ 4, x_2 + 4, x_3 + 4, \ldots, x_{10} + 4\) রাশিগুলির গড় হবে —
(a) 20
(b) 24
(c) 40
(d) 10
উত্তর – (b) 24
সমাধান – এখানে রাশিগুলি 4 করে বৃদ্ধি পাচ্ছে, তাই রাশিগুলির গড় হবে \((20 + 4) = 24\)
152. 6, 7, x, 8, y, 16 সংখ্যাগুলির গড় 9 হলে —
(a) \(x + y = 21\)
(b) \(x + y = 17\)
(c) \(x – y = 21\)
(d) \(x – y = 19\)
উত্তর – (b) \(x + y = 17\)
সমাধান – সংখ্যাগুলির গড়
\(\frac{6+7+x+8+y+16}{6} = \frac{37+x+y}{6}\)শর্তানুসারে, \(\frac{37+x+y}{6} = 9\)
বা, \(37+x+y = 54\)
বা, \(x+y = 17\)
153. 7, \((x – 3)\), 10, \((x + 3)\) এবং \((x – 5)\) সংখ্যাগুলির যৌগিক গড় 15 হলে x-এর মান –
(a) 20
(b) 21
(c) 22
(d) 23
উত্তর – (b) 21
সমাধান – গড় (\(\bar{x}\)) = \(\frac{7+x-3+10+x+3+x-5}{5} = \frac{3x+12}{5}\)
প্রশ্নানুসারে, \(\frac{3x+12}{5} = 15\)
বা, \(3x + 12 = 75\)
বা, \(3x = 75 – 12\)
বা, \(3x = 63\)
বা, \(x = 21\)
154. 11, 29, 17, 21, 13, 31, 39, 19 তথ্যের মধ্যমা
(a) \(\frac{19+21}{2}\)
(b) 19
(c) 21
(d) কোনোটিই নয়
উত্তর – (a) \(\frac{19+21}{2}\)
সমাধান – মানের ঊর্ধ্বক্রমে সাজিয়ে পাই, 11, 13, 17, 19, 21, 29, 31, 39। এখানে, \(n = 8\)
155. 1, 2, 3, 4, 5, 6, 7 তথ্যের সংখ্যাগুরুমান
(a) 4
(b) 6
(c) 7
(d) কোনোটিই নয়
উত্তর – (d) কোনোটিই নয়
সমাধান – যেহেতু সমস্ত তথ্য একবার করে আছে, তাই প্রদত্ত তথ্যের কোনো সংখ্যাগুরুমান নেই।
156. 16, 15, 17, 16, 15, x, 19, 17, 14 তথ্যের সংখ্যাগুরুমান 15 হলে, x-এর মান
(a) 15
(b) 16
(c) 17
(d) 19
উত্তর – (a) 15
সমাধান – যেহেতু সংখ্যাগুরুমান 15।
\(\therefore\) 15 সংখ্যাটিকে সর্বাধিকবার থাকতে হবে।
\(\therefore x = 15\)2026 সালের মাধ্যমিক পরীক্ষার্থীদের জন্য আমাদের গণিত বিষয়ের MCQ প্রশ্নের সাজেশন এখানেই শেষ হলো। এই প্রশ্নগুলি তোমাদের কতটা সাহায্য করলো বা অন্য কোনো বিষয়ের সাজেশন প্রয়োজন কিনা, তা অবশ্যই আমাদের কমেন্ট করে জানিও। আর্টিকেলটি ভালো লাগলে বন্ধুদের সাথে শেয়ার করতে ভুলো না!
এছাড়াও, টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন