এই আর্টিকেলে আমরা WBBSE বোর্ডের 2026 সালের মাধ্যমিক গণিত বিষয়ের সাজেশন নিয়ে আলোচনা করবো। এখানে দেওয়া সত্য মিথ্যাগুলো আসন্ন মাধ্যমিক পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ।

Madhyamik Mathematics Suggestion 2026 – সত্য মিথ্যা
পাটিগণিত
1. অংশীদারি কারবারে তিনজন সদস্যের মূলধনের অনুপাতে \(a : b : c\) এবং নিয়োজিত সময়ের অনুপাত \(x : y : z\) হলে তাদের লাভের অনুপাত হবে \(ax : by : cz\)। [M.P. 2024]
উত্তর – সত্য
2. চক্রবৃদ্ধি সুদের ক্ষেত্রে যদি প্রথম, দ্বিতীয় ও তৃতীয় বছরের সুদের হার যথাক্রমে \(r_1\%, r_2\%, 2r_3\%\) হয়, তবে P টাকার 3 বছরের শেষে সবৃদ্ধিমূল \(P\left(1+\frac{r_1}{100}\right)\left(1+\frac{r_2}{100}\right)\left(1+\frac{r_3}{100}\right)\) টাকা। [M.P. 2023]
উত্তর – মিথ্যা
3. অংশীদারী ব্যবসায় কমপক্ষে 3 জন লোকের দরকার। [M.P. 2022]
উত্তর – মিথ্যা
4. আসল ও সবৃদ্ধিমূলের মধ্যে সম্পর্কটি হল আসল সবৃদ্ধিমূল। [M.P. 2022]
উত্তর – মিথ্যা
5. বার্ষিক \(\frac{r}{2}\%\) সরল সুদের হারে 2p টাকার t বছরের সুদ-আসল হলো \(\left(2p + \frac{prt}{100}\right)\) টাকা। [M.P. 2020]
উত্তর – সত্য
6. বার্ষিক 10% হারে 100 টাকার 1 বছরের সরল সুদ ও চক্রবৃদ্ধি সুদের পার্থক্য 1 টাকা। [M.P. 2019]
উত্তর – মিথ্যা
7. নির্দিষ্ট আসলের ওপর সমান হারে সুদ হলে 2 বছরের সরল সুদ চক্রবৃদ্ধি সুদের তুলনায় বেশি। [M.P. 2018]
উত্তর – মিথ্যা
8. একটি দ্রব্যের বর্তমান মূল্য 100 টাকা। দ্রব্যটির মূল্য প্রতি বছর 10% হ্রাস হয়। 2 বছর পর দ্রব্যটির মূল্য হয় 81 টাকা।
উত্তর – সত্য
সমাধান –
= \(100\left(\frac{9}{10}\right)^2\)
= \(100 \times \frac{81}{100}\)
= \(81\) টাকা
9. A, 10000 টাকা দিয়ে ব্যবসা শুরু করার 6 মাস পরে B, 20000 টাকা দিল। বৎসরান্তে তাদের লভ্যাংশের পরিমাণ সমান হবে। [M.P. 2017]
উত্তর – সত্য
সমাধান – লভ্যাংশের অনুপাত = 1 মাসের সাপেক্ষে A ও B-এর মূলধনের অনুপাত = \(10000 \times 12 : 20000 \times 6 = 1 : 1\)
10. যে ব্যক্তি টাকা ধার করেন তাকে অধমর্ণ বলে।
উত্তর – সত্য
11. আসল ও শতকরা বার্ষিক সরল সুদের হার একই থাকলে মোট সুদ সময়ের সঙ্গে ব্যস্ত সমানুপাতে থাকে।
উত্তর – সত্য
12. নির্দিষ্ট পরিমাণ টাকার বার্ষিক নির্দিষ্ট শতকরা হার সুদে নির্দিষ্ট সময়ের জন্য চক্রবৃদ্ধি সুদ সরল সুদের থেকে কম হবে।
উত্তর – মিথ্যা
13. চক্রবৃদ্ধি সুদের ক্ষেত্রে নির্দিষ্ট সময় অন্তর সুদ আসলের সঙ্গে যোগ হয়। সেই কারণে আসলের পরিমাণ ক্রমাগত বাড়তে থাকে।
উত্তর – সত্য
14. সুদ পর্ব 6 মাসের পরিবর্তে 1 বছর হলে চক্রবৃদ্ধি সুদের পরিমাণ বৃদ্ধি পায়।
উত্তর – মিথ্যা
15. একটি দ্রব্যের বর্তমান মূল্য x টাকা। দ্রব্যটির মূল্য প্রতি বছর y% বৃদ্ধি পায়। z বছর পর দ্রব্যটির মূল্য হয় \(x \left( 1 + \frac{y}{100} \right)^z\) টাকা।
উত্তর – সত্য
16. অংশীদারি ব্যবসায় কমপক্ষে লোকের দরকার হয় 3 জন।
উত্তর – মিথ্যা
17. একটি ব্যবসায় রাজু ও আসিফের মূলধনের অনুপাত 5 : 4 এবং রাজু মোট লাভের 80 টাকা পেলে আসিফ পায় 100 টাকা।
উত্তর – মিথ্যা
সমাধান – \(80 : 100 = 4 : 5\)
18. একটি অংশীদারী ব্যবসায় A ও B-এর মূলধনের অনুপাত 2 : 3 এবং B ও C-এর মূলধনের অনুপাত 4 : 5 হলে, A, B ও C-এর মূলধনের অনুপাত হয় 8 : 12 : 15
উত্তর – সত্য
সমাধান – A : B = 2 : 3 = \(2 \times 4 : 3 \times 4 = 8 : 12\)
B : C = 4 : 5 = \(4 \times 3 : 5 \times 3 = 12 : 15\)
∴ A : B : C = \(8 : 12 : 15\)
19. যদি দুই বন্ধু 450 টাকা ও 750 টাকা দিয়ে একটি অংশীদারী ব্যবসা শুরু করে তাহলে তাদের লভ্যাংশের অনুপাত হয় 3 : 5
উত্তর – সত্য
20. যে অংশীদারী কারবারে অংশীদারদের মূলধন বিভিন্ন সময়ের জন্য নিয়োজিত হয়, তাকে মিশ্র অংশীদারী কারবার বলে।
উত্তর – সত্য
বীজগণিত
21. যদি a ∝ b, b ∝ 1/c এবং c ∝ d হয় তবে a ∝ 1/d হবে। [M.P. 2024]
উত্তর – সত্য
22. 2ab : c², bc : a² এবং ca : 2b² এর যৌগিক অনুপাত 1 : 1. [M.P. 2023]
উত্তর – সত্য
23. x² = 100 সমীকরণের দুটি বীজ হল ± 10 [M.P. 2022]
উত্তর – সত্য
24. a ও b ব্যস্ত ভেদে থাকলে, a/b = ধ্রুবক হবে। [M.P. 2022]
উত্তর – মিথ্যা
25. 2a = 3b = 4c হলে a : b : c = 2 : 3 : 4 হবে। [M.P. 2020]
উত্তর – মিথ্যা
26. ab : c², bc : a² হলে ca : b² -এর যৌগিক অনুপাত 1 : 1 [M.P. 2019]
উত্তর – সত্য
সমাধান – ab : c², bc : a² এবং ca : b² -এর যৌগিক অনুপাত
= ab . bc . ca : c² . a² . b²
= a²b²c² : a²b²c² = 1 : 1
27. x³y, x²y² এবং xy³ ক্রমিক সমানুপাতী। [M.P. 2018]
উত্তর – সত্য
সমাধান – (x²y²) / (x³y) = y/x এবং (xy³) / (x²y²) = y/x
যেহেতু, (x²y²) / (x³y) = (xy³) / (x²y²)
অতএব x³y, x²y², xy³ ক্রমিক সমানুপাতী
28. x = 2 + √3 হলে x + 1/x এর মান হবে 2√3
উত্তর – মিথ্যা
29. যদি \(x \propto y\) হয়, তাহলে \(x^n \propto y^n\) হবে।
উত্তর – সত্য
30. \(x^2+x+1 = 0\) সমীকরণের বীজদ্বয় বাস্তব
উত্তর – মিথ্যা
সমাধান – \(b^2-4ac = (1)^2 – 4 . 1 . 1 = 1 – 4 = -3 < 0\)
যেহেতু \(b^2 – 4ac < 0\) অতএব \(x^2 + x + 1 = 0\) সমীকরণের বীজদ্বয় বাস্তব নয়।
31. \(x^2-x+2 = 0\) সমীকরণের বীজদ্বয় বাস্তব নয়
উত্তর – সত্য
সমাধান – \(b^2 – 4ac = (-1)^2 – 4 . 1 . 2 = 1 – 8 = -7 < 0\)
যেহেতু \(b^2 – 4ac < 0\) অতএব \(x^2 – x + 2 = 0\) সমীকরণের বীজদ্বয় বাস্তব নয়।
32. \(2x^2-3x-5=0\) সমীকরণের একটি বীজ \(-1\)।
উত্তর – সত্য
সমাধান – সমীকরণটির বামপক্ষে \(x = -1\) বসিয়ে পাই
বামপক্ষ \(= 2(-1)^2 – 3(-1) – 5 = 2 + 3 – 5 = 0 =\) ডানপক্ষ
অর্থাৎ \(x = -1\) সমীকরণটিকে সিদ্ধ করে
অতএব \(x = -1\) সমীকরণটির একটি বীজ
33. \(\frac{a}{b} = \frac{c}{d} = \frac{e}{f}\) হলে, প্রতিটি অনুপাত \(= \frac{a+c+e}{b+d+f}\)
উত্তর – সত্য
34. \(4 : 7\) হল একটি গুরু অনুপাত
উত্তর – মিথ্যা
35. \(\sqrt{75}\) এবং \(\sqrt{147}\) সদৃশ করণী।
উত্তর – সত্য
সমাধান – \(\sqrt{75} = \sqrt{5\times5\times3} = 5\sqrt{3}\)
\(\sqrt{147} = \sqrt{7\times7\times3} = 7\sqrt{3}\)\(\therefore \sqrt{75}\) এবং \(\sqrt{147}\) সদৃশ করণী।
36. \(\sqrt{\pi}\) একটি দ্বিঘাত করণী
উত্তর – মিথ্যা
37. \(y \propto \frac{1}{x}\) হলে, \(\frac{y}{x} =\) অশূন্য ধ্রুবক
উত্তর – মিথ্যা
38. \(x \propto z\) এবং \(y \propto z\) হলে \(xy \propto z\)
উত্তর – সত্য
39. \(a^2+b^2 \propto ab\) হলে, \(a+b \propto a-b\) হয়।
উত্তর – সত্য
সমাধান – \(a^2+b^2 \propto ab\) \(\therefore a^2+b^2=2kab\) [2k = অশূন্য ভেদ ধ্রুবক]
বা, \(\frac{a^2 + b^2}{2ab} = k\)
বা, \(\frac{a^2 + b^2 + 2ab}{a^2 + b^2 – 2ab} = \frac{k+1}{k-1}\) [যোগ ভাগ প্রক্রিয়া]
বা, \(\left(\frac{a+b}{a-b}\right)^2 = \left(\sqrt{\frac{k+1}{k-1}}\right)^2\) \(\therefore \frac{a+b}{a-b} = \sqrt{\frac{k+1}{k-1}} = m\) [ধরি, \(m = \sqrt{\frac{k+1}{k-1}} =\) ধ্রুবক ]
বা, \((a + b) = m (a – b)\)
বা, \(a + b \propto a – b\)
40. \(x^2 = 25\) সমীকরণটির একটি মাত্র বীজ 5
উত্তর – মিথ্যা
সমাধান – \(x^2 = 25\) বা, \(x = \pm \sqrt{25}\) বা, \(x = \pm 5\)
41. \(3x^2 – 2\sqrt{6}x + 2 = 0\) সমীকরণের বীজদ্বয় বাস্তব এবং সমান।
উত্তর – সত্য
সমাধান – \(b^2 – 4ac = (-2\sqrt{6})^2 – 4.3.2 = 24 – 24 = 0\)
\(\therefore\) সমীকরণটির বীজদ্বয় বাস্তব এবং সমান
জ্যামিতি
42. কোনো বৃত্তের দুটি জ্যা কেন্দ্র থেকে সমদূরবর্তী হলে তারা অবশ্যই সমান্তরাল হবে। [M.P. 2024]
উত্তর – মিথ্যা
43. কোনো বহিঃস্থ বিন্দু থেকে বৃত্তের ওপর কেবলমাত্র একটি স্পর্শক টানা যায়। [M.P. 2023]
উত্তর – মিথ্যা
44. দুটি এককেন্দ্রীয় বৃত্তের একটি মাত্র সাধারণ স্পর্শক থাকবে। [M.P. 2022]
উত্তর – মিথ্যা
45. একটি ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যের অনুপাত 3 : 4 : 5 হলে, ত্রিভুজটি সর্বদা সমকোণী ত্রিভুজ হবে। [M.P. 2020]
উত্তর – সত্য
সমাধান – ধরি ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য 3x একক, 4x একক এবং 5x একক
\(\therefore\) ত্রিভুজটি সর্বদা সমকোণী
46. তিনটি অসমরেখ বিন্দু দিয়ে একটি মাত্র বৃত্ত আঁকা যায়। [M.P. 2019]
উত্তর – সত্য
47. অর্ধবৃত্তাংশস্থ অপেক্ষা ক্ষুদ্রতর বৃত্তাংশস্থ কোণ স্থূলকোণ। [M.P. 2018]
উত্তর – সত্য
48. 7 সেমি ও 3 সেমি ব্যাসার্ধ বিশিষ্ট দুটি বৃত্ত বহিস্পর্শ করলে তাদের কেন্দ্রদ্বয়ের মধ্যে দূরত্ব 4 সেমি হবে। [M.P. 2017]
উত্তর – মিথ্যা
49. ABCDA ও ABEA বৃত্ত দুটি একই বৃত্ত।
উত্তর – সত্য
50. O কেন্দ্রীয় বৃত্তের AB এবং AC জ্যা দুটি OA ব্যাসার্ধের বিপরীত পার্শ্বে অবস্থিত হলে, \(\angle OAB = \angle OAC\)
উত্তর – মিথ্যা
সমাধান – \(\angle OAB = \angle OAC\) হবে যদি AB = AC হয়, অতএব বিবৃতিটি মিথ্যা
51. পাশের চিত্রে O বৃত্তের কেন্দ্র হলে \(\angle AOB = 2\angle ACD\)
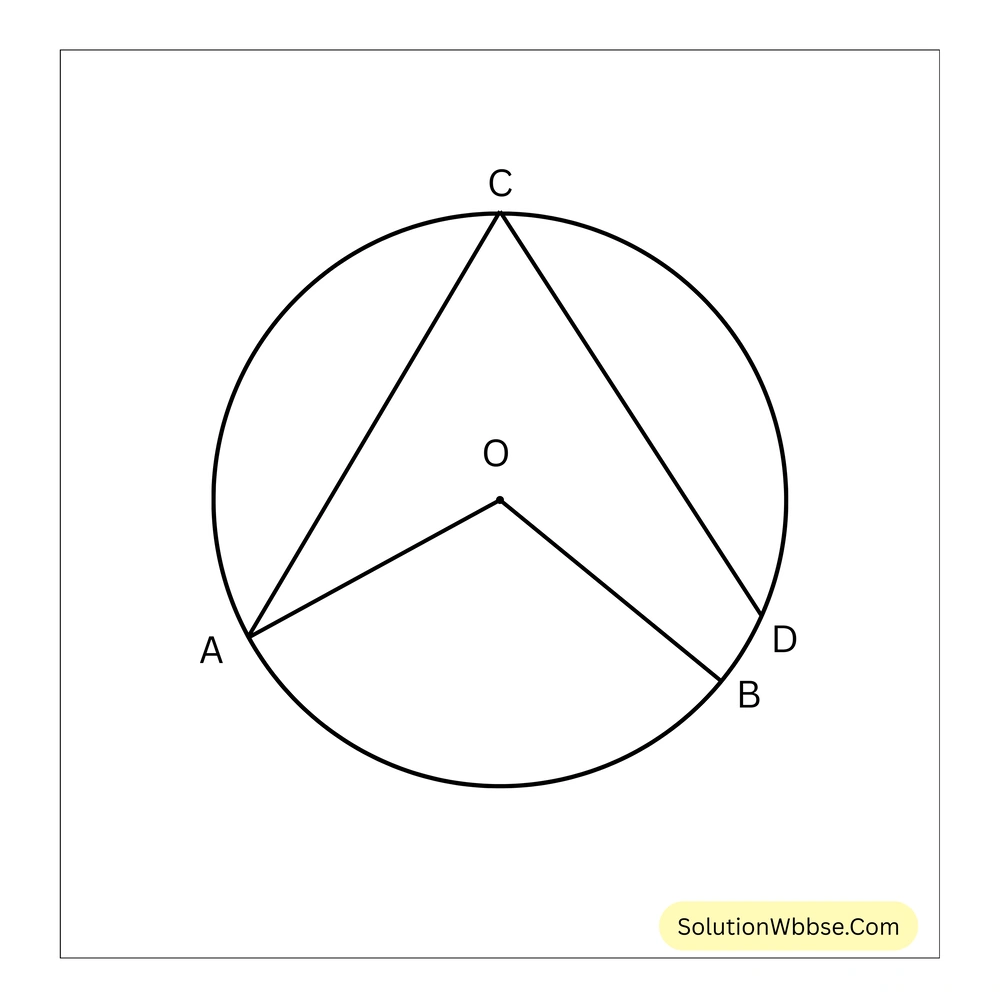
উত্তর – মিথ্যা
52. ABC ত্রিভুজাকার ক্ষেত্রের ভিতর O বিন্দু এমনভাবে অবস্থিত যে OA = OB এবং \(\angle AOB = 2\angle ACB\)। O বিন্দুকে কেন্দ্র করে OA দৈর্ঘ্যের ব্যাসার্ধ নিয়ে বৃত্ত অঙ্কন করলে C বিন্দু বৃত্তের ওপর অবস্থিত হবে।
উত্তর – সত্য
সমাধান – যেহেতু কেন্দ্রস্থ \(\angle AOB = 2\) বৃত্তস্থ \(\angle ACB\)
অতএব C বিন্দুটি বৃত্তের উপর অবস্থিত হবে
53. ABC ত্রিভুজের AB বাহুর মধ্যবিন্দু O এবং OA = OB = OC, AB বাহুকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি C বিন্দু দিয়ে যাবে।
উত্তর – সত্য
সমাধান – যেহেতু AB বাহুর মধ্যবিন্দু O \(\therefore\) OA = OB
আবার OA = OB = OC
অতএব OA কে ব্যাসার্ধ ধরে বৃত্ত অঙ্কন করলে বৃত্তটি B ও C বিন্দু দিয়ে যাবে
অর্থাৎ বৃত্তটি C বিন্দু দিয়ে যাবে
54. ABC ত্রিভুজের AB = AC; BE ও CF যথাক্রমে \(\angle ABC\) ও \(\angle ACB\) এর সমদ্বিখণ্ডক এবং AC ও AB বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করে। B, C, E, F বিন্দু চারটি সমবৃত্তস্থ নয়।
উত্তর – মিথ্যা
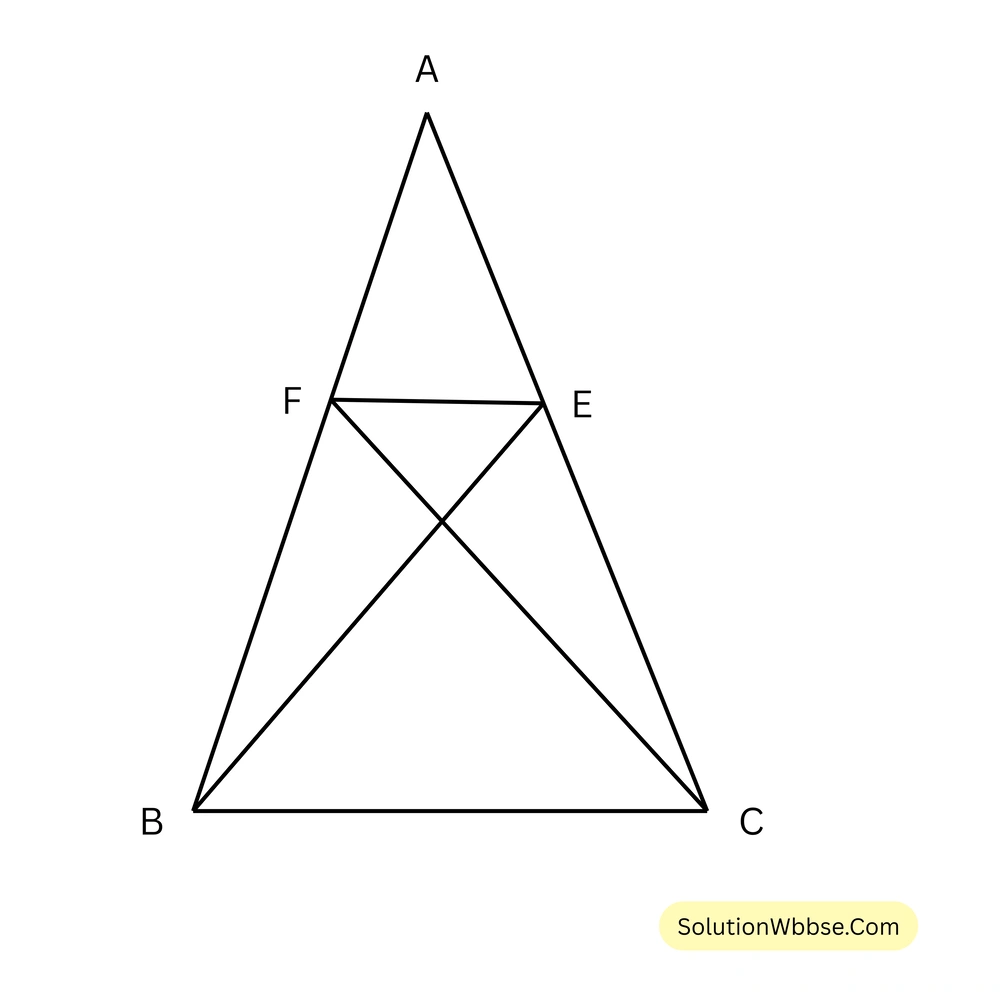
সমাধান – E, F যুক্ত করা হল
\(\Delta ABC\) এর AB = AC
\(\therefore \angle B = \angle C\)\(\therefore \angle EBF = \frac{1}{2} \angle B\)এবং \(\angle ECF = \frac{1}{2} \angle C\)
\(\therefore \angle EBF = \angle ECF\)\(\therefore\) B, C, E, F বিন্দু চারটি সমবৃত্তস্থ
\(\therefore\) প্রদত্ত বিবৃতিটি মিথ্যা
55. একটি বৃত্তস্থ চতুর্ভুজের বিপরীত কোণ পরস্পর পূরক।
উত্তর – মিথ্যা
56. একটি বৃত্তস্থ চতুর্ভুজের একটি বাহুকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণ বিপরীত অন্তঃস্থ কোণের সমান হয়।
উত্তর – সত্য
57. একটি বৃত্তের অন্তঃস্থ একটি বিন্দু P; বৃত্তে অঙ্কিত কোনো স্পর্শক P বিন্দুগামী নয়।
উত্তর – সত্য
58. একটি বৃত্তে একটি নির্দিষ্ট সরলরেখার সমান্তরাল দুইয়ের অধিক স্পর্শক অঙ্কন করা যায়।
উত্তর – মিথ্যা
59. দুটি সদৃশ ত্রিভুজ সর্বদা সর্বসম।
উত্তর – মিথ্যা
60. পাশের চিত্রে DE || BC হলে, \(\frac{AB}{BD} = \frac{AC}{CE}\) হবে।
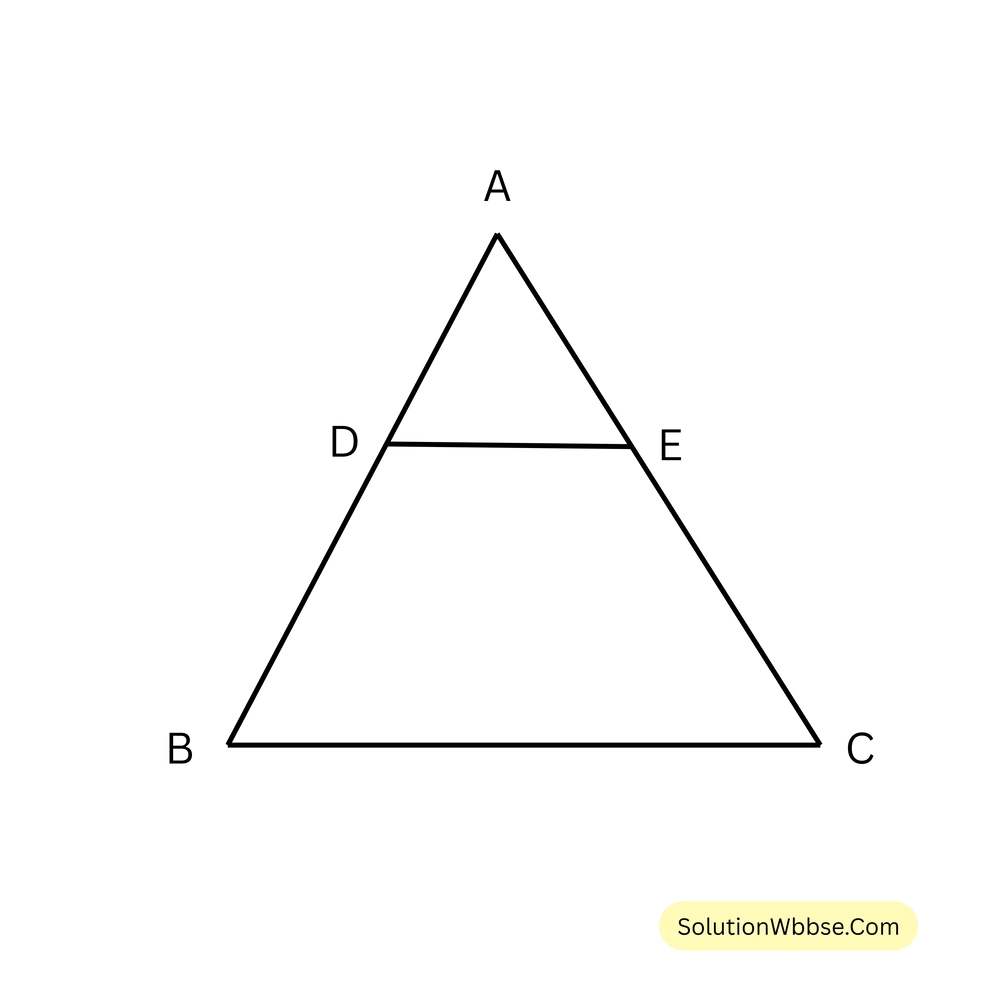
উত্তর – সত্য
সমাধান – DE || BC হলে, \(\frac{AD}{BD} = \frac{AE}{CE}\)
বা, \(\frac{AD}{BD} + 1 = \frac{AE}{CE} + 1\)
বা, \(\frac{AD+BD}{BD} = \frac{AE+CE}{CE}\)
বা, \(\frac{AB}{BD} = \frac{AC}{CE}\)
61. দুটি চতুর্ভুজের অনুরূপ কোণগুলি সমান হলে চতুর্ভুজ দুটি সদৃশ।
উত্তর – মিথ্যা
62. পাশের চিত্রে \(\angle ADE = \angle ACB\) হলে, \(\Delta ADE \sim \Delta ACB\)
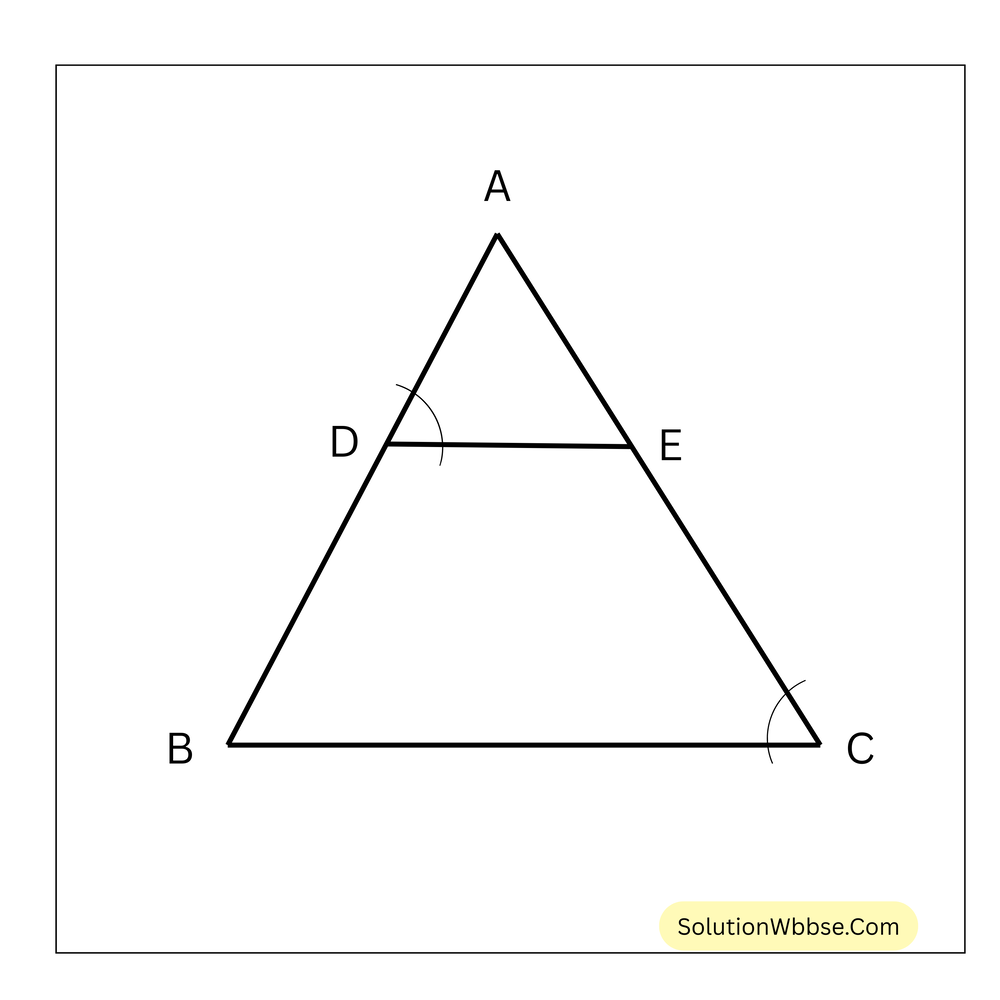
উত্তর – সত্য
সমাধান – \(\Delta ABC\) ও \(\Delta ADE\) এর
\(\angle A\) সাধারণ কোণ
\(\angle ACB = \angle ADE\)\(\therefore \Delta ABC \sim \Delta ADE\)63. \(\Delta PQR\) এর QR বাহুর উপর D এমন একটি বিন্দু যে \(PD \perp QR\) সুতরাং \(\Delta PQD \sim \Delta RPD\)
উত্তর – মিথ্যা
64. 10 সেমি দৈর্ঘ্যের ব্যাসার্ধ বিশিষ্ট একটি বৃত্তে কোনো জ্যা কেন্দ্রে সমকোণ উৎপন্ন করলে জ্যাটির দৈর্ঘ্য 5 সেমি হবে।
উত্তর – মিথ্যা
সমাধান – 10 সেমি ব্যাসার্ধ বিশিষ্ট একটি বৃত্তে কোনো জ্যা কেন্দ্রে সমকোণ উৎপন্ন করলে, জ্যাটির দৈর্ঘ্য হবে = \(\sqrt{(10)^2 + (10)^2}\) সেমি
\(= 10\sqrt{2}\) সেমি
65. ABC একটি সমবাহু ত্রিভুজ যার \(AD \perp BC\) হলে \(4AD^2 = 3 AB^2\) হবে।
উত্তর – সত্য
পরিমিতি
66. একই ব্যাসার্ধ বিশিষ্ট নিরেট গোলক ও নিরেট অর্ধগোলকের সমগ্রতলের অনুপাত 2 : 1। [M.P. 2024]
উত্তর – মিথ্যা
67. কোনো গোলকের বক্রতলের ক্ষেত্রফল এবং আয়তনের সাংখ্য মান সমান হলে ব্যাসার্ধ 3 একক হবে। [M.P. 2023]
উত্তর – সত্য
68. একটি লম্ব বৃত্তাকার শঙ্কুর উচ্চতা, ব্যাসার্ধ এবং তির্যক উচ্চতা সর্বদা একটি সমকোণী ত্রিভুজের বাহুত্রয়। [M.P. 2022]
উত্তর – সত্য
69. একটি লম্ববৃত্তাকার শঙ্কুর ভূমিতলের ব্যাসার্ধের দৈর্ঘ্য অর্ধেক এবং উচ্চতা দ্বিগুণ করা হলে শঙ্কুটির আয়তন একই থাকে। [M.P. 2020]
উত্তর – মিথ্যা
সমাধান – ধরি, শঙ্কুর ব্যাসার্ধ = r একক, উচ্চতা = h একক
∴ আয়তন (\(v_1\)) = \(\frac{1}{3}\pi r^2h\) ঘন একক
পরিবর্তিত শঙ্কুর ব্যাসার্ধ = \(\frac{r}{2}\) একক, উচ্চতা = 2h একক
∴ আয়তন (\(v_2\)) = \(\frac{1}{3}\pi \left(\frac{r}{2}\right)^2 \cdot 2h\) ঘনএকক = \(\frac{1 }{6}\pi r^2h\) ঘন একক
\(\therefore v_2 \ne v_1\)70. একই ভূমি ও একই উচ্চতা বিশিষ্ট একটি লম্ব বৃত্তাকার শঙ্কু ও একটি লম্ব বৃত্তাকার চোঙের আয়তনের অনুপাত 1 : 3 হবে। [M.P. 2019]
উত্তর – সত্য
সমাধান – ধরি, লম্ববৃত্তাকার শঙ্কু ও লম্ববৃত্তাকার চোঙ উভয়ের ব্যাসার্ধ r একক এবং উচ্চতা h একক
\(\therefore\) তাদের আয়তনের অনুপাত = \(\frac{1}{3}\pi r^2h : \pi r^2h = 1 : 3\)
71. একটি গোলকের ব্যাসার্ধ দ্বিগুণ হলে গোলকটির আয়তন প্রথম গোলকের আয়তনের দ্বিগুণ হবে। [M.P. 2018]
উত্তর – মিথ্যা
সমাধান – ধরি, গোলকটির ব্যাসার্ধ = r একক
\(\therefore\) আয়তন (\(v_1\)) = \(\frac{4}{3}\pi r^3\) ঘনএকক
গোলকটির ব্যাসার্ধ দ্বিগুণ হলে পরিবর্তিত গোলকের ব্যাসার্ধ = 2r একক
\(\therefore\) আয়তন (\(v_2\)) = \(\frac{4}{3}\pi (2r)^3\) ঘনএকক
\(\therefore \frac{v_1}{v_2} = \frac{\frac{4}{3}\pi r^3}{\frac{4}{3}\pi (2r)^3} = \frac{1}{8}\)\(\therefore v_2 = 8v_1\)72. একটি অর্ধগোলকের সমগ্রতলের ক্ষেত্রফল \(36\pi\) বর্গসেমি হলে উহার ব্যাসার্ধ 3 সেমি হবে।
উত্তর – মিথ্যা
সমাধান – ধরি, অর্ধগোলকের ভূমির ব্যাসার্ধ = r সেমি
\(\therefore 3\pi r^2 = 36\pi\)বা, \(r^2 = 12\)
বা, \(r = 2\sqrt{3}\)
73. একটি ঘনকের প্রতিটি ধারের দৈর্ঘ্য দ্বিগুণ হলে, ঘনকটির আয়তন প্রথম ঘনকের 4 গুণ হবে।
উত্তর – মিথ্যা
সমাধান – ধরি, ঘনকের প্রতিটি ধারের দৈর্ঘ্য = a একক
\(\therefore\) আয়তন (\(v_1\)) = \(a^3\) ঘনএকক
ঘনকের প্রতিটি ধারের দৈর্ঘ্য দ্বিগুণ করলে, পরিবর্তিত ঘনকের প্রতিটি ধারের দৈর্ঘ্য = 2a একক
আয়তন (\(v_2\)) = \( 2a^3\) ঘনএকক = \(8a^3\) ঘনএকক
\(\therefore \frac{v_2}{v_1} = \frac{8a^3}{a^3}\) বা, \(v_2 = 8v_1\)
74. বর্ষার সময় 2 হেক্টর জমিতে বৃষ্টিপাত 5 সেমি উচ্চতার হলে, বৃষ্টির জলের আয়তন 1000 ঘন মিটার।
উত্তর – সত্য
সমাধান – 2 হেক্টর = 2 × 100 × 100 বর্গমি = 20000 বর্গমি
5 সেমি = 0.05 মিটার
∴ বৃষ্টির জলের আয়তন = 20000 × 0.05 ঘনমিটার = 1000 ঘনমিটার
75. দুটি ঘনকের আয়তনের অনুপাত 1 : 8 হলে, তাদের সমগ্রতলের ক্ষেত্রফলের অনুপাত 1 : 2 হবে।
উত্তর – মিথ্যা
সমাধান – দুটি ঘনকের আয়তনের অনুপাত = 1 : 8 = \(1^3 : (2)^3\)
∴ ঘনকদুইটির বাহুর অনুপাত = 1 : 2
ঘনক দুইটির সমগ্রতলের ক্ষেত্রফলের অনুপাত = \(6(1)^2 : 6(2)^2 = 1 : 4\)
76. একটি লম্ব চোঙাকৃতি ড্রামের ব্যাসার্ধের দৈর্ঘ্য r সেমি এবং উচ্চতা h সেমি। ড্রামের অর্ধেক জলপূর্ণ থাকলে, জলের আয়তন হবে \(\pi r^2h\) ঘন সেমি।
উত্তর – মিথ্যা
সমাধান – ড্রামের আয়তন = \(\pi r^2h\) ঘনসেমি
অর্ধেক জলপূর্ণ থাকলে, জলের আয়তন = \(\frac{1}{2}\pi r^2h\) ঘনসেমি
77. একটি লম্ব বৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য 2 একক হলে, চোঙটির যে-কোনো উচ্চতার জন্য চোঙটির আয়তন এবং বক্রতলের ক্ষেত্রফলের সাংখ্যমান সমান হবে।
উত্তর – সত্য
সমাধান – ধরি, লম্ব বৃত্তাকার চোঙের উচ্চতা = h একক
∴ আয়তন = \(\pi(2)^2 \cdot h\) ঘনএকক = \(4\pi h\) ঘনএকক
বক্রতলের ক্ষেত্রফল = \(2\pi(2) \cdot h\) বর্গএকক = \(4\pi h\) বর্গএকক
∴ চোঙটির আয়তনের সাংখ্যমান = চোঙটির বক্রতলের ক্ষেত্রফল
78. দুটি অর্ধগোলকের বক্রতলের ক্ষেত্রফলের অনুপাত 4 : 9 হলে, তাদের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত হবে 2 : 3।
উত্তর – সত্য
সমাধান – ধরি, অর্ধগোলক দুইটির ব্যাসার্ধ যথাক্রমে \(r_1\) একক ও \(r_2\) একক
\(\therefore 2\pi r_1^2 : 2\pi r_2^2 = 4 : 9\)বা, \( r_1^2 : (r_2)^2 = (2)^2 : (3)^2\)
\(\therefore r_1 : r_2 = 2 : 3\)79. একটি লম্ববৃত্তাকার শঙ্কুর ভূমিতলের ব্যাসার্ধের দৈর্ঘ্য অর্ধেক এবং উচ্চতা দ্বিগুণ করা হলে শঙ্কুটির আয়তন একই থাকে।
উত্তর – মিথ্যা
সমাধান – r একক ভূমিতলের ব্যাসার্ধ ও h উচ্চতা বিশিষ্ট শঙ্কুর আয়তন = \(\frac{1}{3}\pi r^2h\) ঘনএকক
\(\frac{r}{2}\) একক ভূমিতলের ব্যাসার্ধ এবং 2h একক উচ্চতা বিশিষ্ট শঙ্কুর আয়তন = \(\frac{1} {3}\pi\left(\frac{r}{2}\right)^2 2h\) ঘনএকক
= \(\frac{1}{6}\pi r^2h\) ঘনএকক
80. একটি লম্ববৃত্তাকার শঙ্কুর উচ্চতা, ব্যাসার্ধ এবং তির্যক উচ্চতা সর্বদা একটি সমকোণী ত্রিভুজের বাহুত্রয়।
উত্তর – সত্য
81. দুটি একই ধরনের নিরেট অর্ধগোলক যাদের ভূমিতলের প্রত্যেকের ব্যাসার্ধের দৈর্ঘ্য r একক এবং তা ভূমি বরাবর জোড়া হলে, মিলিত ঘনবস্তুর সমগ্রতলের ক্ষেত্রফল হবে \(6\pi r^2\) বর্গ একক।
উত্তর – মিথ্যা
সমাধান – অর্ধগোলকদুটি ভূমি বরাবর জোড়া হলে একটি পূর্ণগোলক পাওয়া যায়।
\(\therefore\) পূর্ণগোলকের সমগ্রতলের ক্ষেত্রফল \(4\pi r^2\) বর্গএকক
82. একটি নিরেট লম্ববৃত্তাকার শঙ্কুর ভূমিতলের ব্যাসার্ধের দৈর্ঘ্য r একক উচ্চতা h একক এবং তির্যক উচ্চতা l একক। শঙ্কুটির ভূমিতলকে একটি নিরেট লম্ব বৃত্তাকার চোঙের ভূমিতল বরাবর জুড়ে দেওয়া হল যদি চোঙের ও শঙ্কুর ভূমিতলের ব্যাসার্ধের দৈর্ঘ্য এবং উচ্চতা একই হয়, তবে মিলিত ঘনবস্তুর সমগ্রতলের ক্ষেত্রফল \((\pi rl + 2\pi rh + 2\pi r^2)\) বর্গএকক।
উত্তর – মিথ্যা
সমাধান – মিলিত ঘনবস্তুর সমগ্রতলের ক্ষেত্রফল = শঙ্কুটির পার্শ্বতলের ক্ষেত্রফল + চোঙটির বক্রতলের ক্ষেত্রফল + চোঙটির একটি সমতলের ক্ষেত্রফল = \((\pi rl + 2\pi rh + \pi r^2)\) বর্গএকক
83. একই ভূমিতলের ব্যাসার্ধ এবং একই উচ্চতা বিশিষ্ট একটি চোঙ এবং একটি শঙ্কুর আয়তনের অনুপাত 1 : 3।
উত্তর – মিথ্যা
সমাধান – ধরি চোঙ এবং শঙ্কুর উভয়ের ব্যাসার্ধ = r একক এবং উচ্চতা = h একক
\(\therefore\) চোঙের আয়তন = \(\pi r^2h\) ঘনএকক
শঙ্কুর আয়তন = \(\frac{1}{3}\pi r^2h\) ঘনএকক
\(\therefore\) চোঙ ও শঙ্কুর আয়তনের অনুপাত = \(\pi r^2h : \frac{1}{3}\pi r^2h = 3 : 1\)
84. a একক বাহুবিশিষ্ট একটি কাঠের ঘনক থেকে সর্ববৃহৎ যে গোলকটি তৈরি করা যায়, তার ব্যাস হল \(\sqrt{3}a\) একক।
উত্তর – মিথ্যা
সমাধান – গোলকটির ব্যাস = ঘনকের বাহু = a একক
ত্রিকোণমিতি
85. একটি ঘড়ির ঘন্টার কাঁটা 2 ঘন্টায় \(\frac{\pi}{6}\) রেডিয়ান কোণ আবর্তন করে। [M.P. 2024]
উত্তর – মিথ্যা
86. \(\cos 36^\circ\) এবং \(\sin 54^\circ\) এর মান সমান। [M.P. 2023]
উত্তর – সত্য
87. \(\sin30^\circ + \sin60^\circ > \sin90^\circ\) [M.P. 2019]
উত্তর – সত্য
88. \(\sec^2 27^\circ – \cot^2 63^\circ\)-এর সরলতম মান 1। [M.P. 2018]
উত্তর – সত্য
সমাধান – \(\sec^2 27^\circ – \cot^2 63^\circ = \sec^2 27^\circ – \cot^2(90^\circ – 27^\circ)\)
\(= \sec^2 27^\circ – \tan^2 27^\circ = 1\)89. \(0^\circ < \theta < 90^\circ\) হলে, \(\sin\theta > \sin 2\theta\) হবে। [M.P. 2017]
উত্তর – মিথ্যা
90. একটি রশ্মির প্রান্তবিন্দুকে কেন্দ্র করে রশ্মিটির ঘড়ির কাঁটার বিপরীত দিকে ঘোরার জন্য উৎপন্ন কোণটি ধনাত্মক।
উত্তর – সত্য
91. একটি রশ্মির প্রান্তবিন্দুকে কেন্দ্র করে রশ্মিটির ঘড়ির কাঁটার দিকে দু-বার পূর্ণ আবর্তনের জন্য \(720^\circ\) কোণ উৎপন্ন হয়।
উত্তর – মিথ্যা
92. 1 রেডিয়ান = \(\frac{2}{\pi}\) সমকোণ
উত্তর – সত্য
93. \(\tan A\) এর মান সর্বদা 1 অপেক্ষা বড়ো।
উত্তর – মিথ্যা
94. \(\cos0^\circ \times \cos1^\circ \times \cos2^\circ \times \cos3^\circ \times … \times \cos90^\circ\) এর মান 1
উত্তর – মিথ্যা
95. একটি কোণ \(\theta\) এর জন্য \(\sin\theta = \frac{4}{3}\)
উত্তর – মিথ্যা
96. যদি \(0^\circ \le \alpha \le 90^\circ\) হয়, তাহলে \(\sec^2\alpha + \cos^2\alpha\)-এর সর্বনিম্ন মান 2
উত্তর – সত্য
97. \(\cos54^\circ\) এবং \(\sin36^\circ\)-এর মান সমান
উত্তর – সত্য
98. \((\sin12^\circ – \cos78^\circ)\)-এর সরলতম মান 1
উত্তর – মিথ্যা
99. \(\sin^2 72^\circ + \sin^2 18^\circ = 0\)
উত্তর – মিথ্যা
100. \(\Delta ABC\) এর \(AB = BC\), \(\angle B = 90^\circ\) হলে \(\angle C = 60^\circ\)
উত্তর – মিথ্যা
101. PQ একটি বাড়ির উচ্চতা, QR ভূমি। P বিন্দু থেকে R বিন্দুর অবনতি কোণ \(\angle SPR\); সুতরাং \(\angle SPR = \angle PRQ\)
উত্তর – সত্য
রাশিবিজ্ঞান
102. একটি শ্রেণীতে \(n\) সংখ্যক সংখ্যার গড় \(\bar{x}\)। যদি প্রথম \((n-1)\) সংখ্যার সমষ্টি K হয়, তাহলে \(n\)-তম সংখ্যাটি হবে \((n-1) \bar{x} + K\)। [M.P. 2024]
উত্তর – মিথ্যা
103. 5, 2, 4, 3, 5, 2, 5, 2, 5, 2 তথ্যের সংখ্যাগুরু মান হবে 2। [M.P. 2023]
উত্তর – মিথ্যা
104. 2, 3, 9, 10, 9, 3, 9 তথ্যের মধ্যমার মান 10। [M.P. 2019]
উত্তর – মিথ্যা
105.
| স্কোর | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| বিদ্যার্থীর সংখ্যা | 3 | 6 | 4 | 7 | 5 |
বিভাজনটির সংখ্যাগুরু মান হল 3। [M.P. 2019]
উত্তর – মিথ্যা
106. 2, 3, 9, 10, 9, 3, 9 তথ্যের সংখ্যাগুরু মান 10।
উত্তর – মিথ্যা
107. 3, 14, 18, 20, 5 তথ্যের মধ্যমা 18।
উত্তর – মিথ্যা
108. কোনো রাশি তথ্যের বৃহত্তম মানটি হল সর্বদা তার সংখ্যাগুরু মান।
উত্তর – মিথ্যা
109. কোনো পরিসংখ্যা বিভাজনের একাধিক মধ্যমা থাকতে পারে।
উত্তর – মিথ্যা
110. 1 থেকে 10 পর্যন্ত পূর্ণসংখ্যার গড় 5.5
উত্তর – সত্য
111. 8, 10, 7, 6, 10, 11, 6, 11, 10 তথ্যের সংখ্যাগুরু মান 11
উত্তর – মিথ্যা
112. 112, 12, 98, 62, 75, 30, 48, 94 তথ্যের মধ্যমা 86.5
উত্তর – মিথ্যা
2026 সালের মাধ্যমিক পরীক্ষার্থীদের জন্য আমাদের গণিত বিষয়ের সত্য/মিথ্যা সাজেশন এখানেই শেষ হলো। এই প্রশ্নগুলি তোমাদের কতটা সাহায্য করলো বা অন্য কোনো অধ্যায়ের সাজেশন প্রয়োজন কিনা, তা অবশ্যই আমাদের কমেন্ট করে জানিও। আর্টিকেলটি ভালো লাগলে বন্ধুদের সাথে শেয়ার করতে ভুলো না!
এছাড়াও, টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন