Madhyamik Mathematics Suggestion 2026 – সংক্ষিপ্ত প্রশ্ন

এই আর্টিকেলে আমরা WBBSE বোর্ডের 2026 সালের মাধ্যমিক গণিত বিষয়ের সাজেশন নিয়ে আলোচনা করবো। এখানে দেওয়া সংক্ষিপ্ত প্রশ্নগুলো আসন্ন মাধ্যমিক পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ।

পাটিগণিত

1. শতকরা বার্ষিক সরল সুদের হার কত হলে কোনো টাকার 5 বছরের সুদ আসলের \( \frac{2}{5} \) অংশ হবে তা নির্ণয় করো। [M.P. 2023]

2. কোন ব্যবসায় A ও B এর মূলধনের অনুপাত \( \frac{1}{7} : \frac{1}{4} \), বছরের শেষে 11,000 টাকা লাভ হলে তাদের লভ্যাংশের পরিমাণ নির্ণয় কর। [M.P. 2023]

3. বার্ষিক সুদ আসলের \( \frac{1}{16} \) অংশ হলে, ৪ মাসে 690 টাকার সুদ কত হবে? [M.P. 2022]

4. কোনো স্থানে লোকসংখ্যা 13,310 জন ছিল। কি হারে বৃদ্ধি পেলে 3 বছরে 17,280 জন হবে। [M.P. 2022]

5. কোনো ব্যবসায় A, B, C এর মূলধনের অনুপাত \( \frac{1}{x} : \frac{1}{y} : \frac{1}{z} \) বছরের শেষে ব্যবসায় z টাকা ক্ষতি হয়েছে। C এর ক্ষতির পরিমাণ নির্ণয় কর। [M.P. 2022]

6. কোনো আসল ও তার 5 বছরের সবৃদ্ধি মূলের অনুপাত \( 5 : 6 \) হলে, বার্ষিক সরল সুদের হার নির্ণয় কর। [M.P. 2020]

7. A ও B কোনো ব্যবসায় 1,050 টাকা লাভ করে। A এর মূলধন 900 টাকা এবং লভ্যাংশ 630 টাকা হলে Bএর মূলধন কত? [M.P. 2020]

8. বার্ষিক \( 5\% \) সরল সুদের হারে কত টাকার মাসিক সুদ 1 টাকা হবে তা নির্ণয় কর। [M.P. 2019]

9. এক অংশীদারী ব্যবসায় তিনজনের মূলধনের অনুপাত \( 3 : 5 : 8 \) প্রথম ব্যক্তির লাভ তৃতীয় ব্যক্তির লাভের থেকে 60 টাকা কম হলে ব্যবসায় মোট কত লাভ হয়েছিল? [M.P. 2019]

10. বার্ষিক সরল সুদের হার \( 4\% \) থেকে \( 3\frac{3}{4}\% \) হওয়ায় এক ব্যক্তির বার্ষিক আয় 60 টাকা কম হয়। ওই ব্যক্তির মূলধন নির্ণয় কর। [M.P. 2018]

11. A ও B যথাক্রমে 15,000 টাকা ও 45,000 টাকা দিয়ে একটি ব্যবসা শুরু করল। 6 মাস পরে B লভ্যাংশ হিসাবে 3030 টাকা পেল। A এর লভ্যাংশ কত? [M.P. 2018]

12. \( r\% \) হার চক্রবৃদ্ধি সুদে কোন মূলধন 8 বছরে দ্বিগুণ হলে চারগুণ হবে কত বছরে? [M.P. 2017]

13. কোন এক ব্যবসায় Aএর মূলধন Bএর মূলধনের দেড়গুণ। ওই ব্যবসায় বৎসরান্তে B 1500 টাকা লভ্যাংশ পেলে, A কত টাকা লভ্যাংশ পাবে? [M.P. 2017]

14. বার্ষিক নির্দিষ্ট শতকরা চক্রবৃদ্ধি হার সুদে কিছু টাকা \( n \) বছরে দ্বিগুণ হলে, কত বছরে 4 গুণ হবে?

15. শতকরা বার্ষিক সরল সুদের হার কত হলে কোনো টাকার 4 বছরের সুদ আসলের \( \frac{8}{25} \) অংশ হবে?

16. বার্ষিক সরল সুদের হার কত হলে 4 বছরের সুদ ও আসলের অনুপাত \( 3 : 25 \) হবে।

17. কোনো মূলধন বার্ষিক \( 6\frac{1}{4}\% \) সরল সুদের হারে কত বছরে দ্বিগুণ হবে?

18. জয়ন্ত, অজিত এবং কুনাল মোট 15000 টাকা দিয়ে একটি অংশীদারী ব্যবসা শুরু করে। বছরের শেষে জয়ন্ত, অজিত এবং কুনালের যথাক্রমে লাভ হয় 800 টাকা, 1000 টাকা এবং 1200 টাকা। জয়ন্ত ব্যবসায় কত টাকা নিয়োজিত করেছিল?

19. প্রতিবছর জনসংখ্যা \( r\% \) বৃদ্ধি হলে \( n \) বছর পর জনসংখ্যা হয় \( p \) ; \( n \) বছর পূর্বে জনসংখ্যা কত ছিল?

20. দুইজনের একটি অংশীদারী ব্যবসায় মোট লাভ হয় 1500 টাকা। রাজীবের মূলধন 6000 টাকা এবং লাভ 900 টাকা হলে আফতারের মূলধন কত?

21. একটি অংশীদারি ব্যবসায় সমীর, ইদ্রিশ এবং অ্যান্টনির মূলধনের অনুপাত \( \frac{1}{6} : \frac{1}{5} : \frac{1}{4} \) বছরের শেষে ব্যবসায় মোট লাভ 3700 টাকা হলে, অ্যান্টনির লাভ কত?

22. প্রতিবছর \( r\% \) হ্রাসপ্রাপ্ত হলে, \( n \) বছর পর একটি মেশিনের মূল্য হয় \( v \) টাকা。 \( n \) বছর পূর্বে মেশিনটির মূল্য কত ছিল?

23. একটি অংশীদারি ব্যবসায় পৃথা ও রাবেয়ার মূলধনের অনুপাত \( 2 : 3 \) এবং রাবেয়া ও জেসমিনের মূলধনের অনুপাত \( 4 : 5 \) হলে পৃথা, রাবেয়া ও জেসমিনের মূলধনের অনুপাত নির্ণয় কর।

24. 400 টাকার 2 বছরে সমূল চক্রবৃদ্ধি 441 টাকা হলে, বার্ষিক শতকরা চক্রবৃদ্ধি সুদের হার কত?

বীজগণিত

25. \( x^2 – x = K (2x – 1) \) সমীকরণের বীজদ্বয়ের সমষ্টি 2 হলে, K-এর মান নির্ণয় করো। [M.P. 2023]

26. যদি \( b \propto a^2 \) হয় এবং a-এর বৃদ্ধি হয় 2 : 3 অনুপাতে, তাহলে b-এর বৃদ্ধি কী অনুপাতে হয় তা নির্ণয় করো। [M.P. 2023]

27. \( 7x^2 – 66x + 27 = 0 \) সমীকরণটির বীজদ্বয়ের যোগফল ও গুণফলের অনুপাত কত? [M.P. 2022]

28. হরের করণী নিরসন করো: \( \frac{12}{\sqrt{15} – 3} \) [M.P. 2022]

29. \( x \propto y, y \propto z \) এবং \( z \propto x \) হলে ভেদ ধ্রুবক তিনটির গুণফল নির্ণয় করো। [M.P. 2020]

30. \( 5x^2 – 2x + 3 = 0 \) দ্বিঘাত সমীকরণের বীজদুটি \( \alpha \) ও \( \beta \) হলে \( \frac{1}{\alpha} + \frac{1}{\beta} \)-এর মান নির্ণয় করো। [M.P. 2020]

31. \( \frac{a}{2} = \frac{b}{3} = \frac{c}{4} = \frac{2a – 3b + 4c}{p} \) হলে, p-এর মান কত? [M.P. 2019]

32. \( x \propto y^2 \) এবং \( y = 2a \), \( x = a \) হলে দেখাও যে, \( y^2 = 4ax \) [M.P. 2019]

33. \( 2x + \frac{1}{x} = 2 \) হলে, \( \frac{x}{2x^2 + x + 1} \)-এর মান কত? [M.P. 2018]

34. কোন দ্বিঘাত সমীকরণের বীজদ্বয় 2, -3 হলে সমীকরণটি লেখো। [M.P. 2018]

35. সমাধান না করে ‘p’-এর যে সকল মানের জন্য \( x^2 + (p – 3)x + p = 0 \) সমীকরণের বাস্তব ও সমান বীজ আছে তা নির্ণয় করো। [M.P. 2017]

36. \( x \propto yz \) এবং \( y \propto zx \) হলে, দেখাও যে, \( z (\neq 0) \) একটি ধ্রুবক। [M.P. 2017]

37. x, 12, y, 27 ক্রমিক সমানুপাতী হলে x ও y-এর ধনাত্মক মান নির্ণয় কর।

38. \( a : b = 3 : 2 \) এবং \( b : c = 3 : 2 \) হলে \( a + b : b + c \) কত হবে?

39. \( Kx^2 + 2x + 3K = 0, (K \neq 0) \) সমীকরণের বীজদ্বয়ের সমষ্টি এবং গুণফল সমান হলে, K-এর মান নির্ণয় কর।

40. \( x^2 + ax + 3 = 0 \) সমীকরণের একটি বীজ 1 হলে, a-এর মান নির্ণয় কর।

41. \( (\sqrt{15} + \sqrt{3}) \) এবং \( (\sqrt{10} + \sqrt{8}) \)-এর মধ্যে কোনটি বড়?

42. \( x^2 – 22x + 105 = 0 \) সমীকরণের বীজদ্বয় \( \alpha \) ও \( \beta \) হলে, \( (\alpha – \beta) \)-এর মান নির্ণয় কর।

43. \( a : b = 3 : 4 \) এবং \( x : y = 5 : 7 \) হলে, \( (3ax – by) : (4by – 7ax) \) কত?

44. \( x \propto \frac{1}{y} \) এবং \( y \propto \frac{1}{z} \) হলে, x, z-এর সঙ্গে কোন ভেদে আছে তা নির্ণয় কর।

45. \( (ax + by) \propto (ax – by) \) হলে প্রমাণ কর যে, \( x \propto y \)

46. \( \sqrt{72} \) থেকে কত বিয়োগ করলে \( \sqrt{32} \) হবে?

47. \( x = 3 + 2\sqrt{2} \) হলে, \( x + \frac{1}{x} \)-এর মান কত?

48. \( \frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} \)-এর সরলতম মান কত?

জ্যামিতি

49. একটি বৃত্তের \( AB \) ও \( CD \) দুটি জ্যা। \( BA \) এবং \( DC \) কে বর্ধিত করলে পরস্পর \( P \) বিন্দুতে ছেদ করে। প্রমাণ কর যে, \( \angle PCB = \angle PAD \). [M.P. 2023]

50. \( \triangle ABC \) এর \( AC \) এবং \( BC \) বাহু দুটির উপর যথাক্রমে \( L \) এবং \( M \) দুটি বিন্দু এমন ভাবে অবস্থান করে যাতে \( LM \parallel AB \) এবং \( AL = (x-2) \) একক, \( AC = (2x+3) \) একক, \( BM = (x-3) \) একক এবং \( BC = 2x \) একক, তবে \( x \) এর মান নির্ণয় করো। [M.P. 2023]

51. দুটি বৃত্ত পরস্পরকে \( C \) বিন্দুতে বহিঃস্পর্শ করে। বৃত্ত দুটির একটি সাধারণ স্পর্শক \( AB \) বৃত্ত দুটিকে \( A \) ও \( B \) বিন্দুতে স্পর্শ করে। \( \angle ACB \) এর মান নির্ণয় করো। [M.P. 2023]

52. \( AOB \) বৃত্তের একটি ব্যাস যার কেন্দ্র \( O \), \( C \) বৃত্তের উপর একটি বিন্দু \( \angle OBC = 60^\circ \) হলে \( \angle OCA \) এর মান নির্ণয় করো। [M.P. 2022]

53. \( O \) কেন্দ্রীয় একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 13 সেমি এবং \( AB \) একটি জ্যা এর দৈর্ঘ্য 10 সেমি, \( O \) বিন্দু থেকে \( AB \) জ্যা এর দূরত্ব কতো? [M.P. 2022]

54. একটি \( O \) কেন্দ্রীয় বৃত্ত যার কেন্দ্র থেকে 26 সেমি দূরে অবস্থিত \( P \) বিন্দু থেকে অঙ্কিত বৃত্তের স্পর্শকের দৈর্ঘ্য 10 সেমি হলে, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য কত? [M.P. 2022]

55. \( \triangle ABC \) এর \( DE \parallel BC \), যেখানে \( D \) ও \( E \) যথাক্রমে \( AB \) ও \( AC \) বাহুর ওপর অবস্থিত। যদি \( AD = 5 \) সেমি, \( DB = 6 \) সেমি এবং \( AE = 7.5 \) সেমি হয় তবে \( AC \) এর দৈর্ঘ্য নির্ণয় কর। [M.P. 2022]

56. \( ABCD \) আয়তকার চিত্রের অভ্যন্তরে \( O \) বিন্দু এমনভাবে অবস্থিত যে \( OB = 6 \) সেমি, \( OD = 8 \) সেমি এবং \( OA = 5 \) সেমি। \( OC \) এর দৈর্ঘ্য নির্ণয় কর। [M.P. 2020]

57. \( \triangle ABC \) সমকোণী ত্রিভুজের \( \angle ABC = 90^\circ \), \( AB = 3 \) সেমি, \( BC = 4 \) সেমি এবং \( B \) বিন্দু থেকে \( AC \) বাহুর উপর লম্ব \( BD \) যা \( AC \) বাহুর সঙ্গে \( D \) বিন্দুতে মিলিত হয়। \( BD \) এর দৈর্ঘ্য নির্ণয় করো। [M.P. 2020]

58. দুটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 8 সেমি এবং 3 সেমি। তাদের কেন্দ্রদ্বয়ের দূরত্ব 13 সেমি। বৃত্ত দুটির সরল সাধারণ স্পর্শকের দৈর্ঘ্য কত? [M.P. 2020]

59. \( ABCD \) ট্রাপিজিয়ামের \( BC \parallel AD \) এবং \( AD = 4 \) সেমি। \( AC \) ও \( BD \) কর্ণদ্বয় এমনভাবে \( O \) বিন্দুতে ছেদ করে যে \( \frac{AO}{OC} = \frac{DO}{OB} = \frac{1}{2} \) হয়। \( BC \) এর দৈর্ঘ্য কত? [M.P. 2019]

60. \( \triangle ABC \) এর \( \angle ABC = 90^\circ \) এবং \( BD \perp AC \), যদি \( AB = 5 \) সেমি এবং \( BC = 12 \) সেমি হয়, তার \( BD \) এর দৈর্ঘ্য কত? [M.P. 2019]

61. একটি বৃত্তে দুটি জ্যা \( AB \) এবং \( AC \) পরস্পর লম্ব, \( AB = 4 \) সেমি এবং \( AC = 3 \) সেমি হলে বৃত্তটির ব্যাসার্ধের দৈর্ঘ্য নির্ণয় কর। [M.P. 2019]

62. \( O \) কেন্দ্রীয় বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি। \( O \) বিন্দু থেকে 13 সেমি দূরত্ব \( P \) একটি বিন্দু \( PQ \) এবং \( PR \) বৃত্তের দুইটি স্পর্শক হলে \( PQOR \) চতুর্ভুজের ক্ষেত্রফল কত? [M.P. 2018]

63. \( \triangle ABC \) এর \( BC \) বাহুর সমান্তরাল সরলরেখা \( AB \) ও \( AC \) কে যথাক্রমে \( P \) ও \( Q \) বিন্দুতে ছেদ করে যদি \( AP = 4 \) সেমি, \( QC = 9 \) সেমি এবং \( PB = AQ \) হয় তাহলে \( PB \) এর দৈর্ঘ্য নির্ণয় করো। [M.P. 2018]

64. \( O \) কেন্দ্রীয় বৃত্তে \( AB \) ও \( CD \) জ্যা দুটি কেন্দ্র থেকে সমদূরবর্তী \( \angle AOB = 60^\circ \) এবং \( CD = 6 \) সেমি হলে বৃত্তটির ব্যাসার্ধের দৈর্ঘ্য কত? [M.P. 2018]

65. \( \triangle ABC \) এর \( \angle ABC = 90^\circ \), \( AB = 5 \) সেমি \( BC = 12 \) সেমি হলে ওই ত্রিভুজটির পরিব্যাসার্ধের দৈর্ঘ্য কত? [M.P. 2017]

66. দুটি সদৃশ ত্রিভুজের পরিসীমা যথাক্রমে 20 সেমি ও 16 সেমি, প্রথম ত্রিভুজের একটি বাহুর দৈর্ঘ্য 9 সেমি হলে দ্বিতীয় ত্রিভুজের অনুরূপ বাহুর দৈর্ঘ্য কত? [M.P. 2017]

67. \( \triangle ABC \) এর \( AB = (2a – 1) \) সেমি, \( AC = 2\sqrt{2}a \) সেমি এবং \( BC = (2a + 1) \) সেমি হলে \( \angle BAC \) এর মান লেখ। [M.P. 2017]

68. \( P \) ও \( Q \) কেন্দ্র বিশিষ্ট দুটি বৃত্ত \( A \) ও \( B \) বিন্দুতে ছেদ করে। \( A \) বিন্দু দিয়ে \( PQ \)-এর সমান্তরাল সরলরেখা বৃত্ত দুটিকে \( C \) ও \( D \) বিন্দুতে ছেদ করে। \( PQ = 5 \) সেমি হলে, \( CD \) এর দৈর্ঘ্য নির্ণয় করো।

69. 10 সেমি দৈর্ঘ্যের ব্যাসার্ধের দুটি সমান বৃত্ত পরস্পরকে ছেদ করে এবং তাদের সাধারণ জ্যা এর দৈর্ঘ্য 12 সেমি। বৃত্ত দুটির কেন্দ্রদ্বয়ের মধ্য দূরত্ব নির্ণয় করো।

70. \( O \) কেন্দ্রীয় বৃত্তের ওপর \( A, B, C \) তিনটি বিন্দু এমনভাবে অবস্থিত যে \( AOCB \) একটি সমান্তরিক, \( \angle AOC \) এর মান নির্ণয় করো।

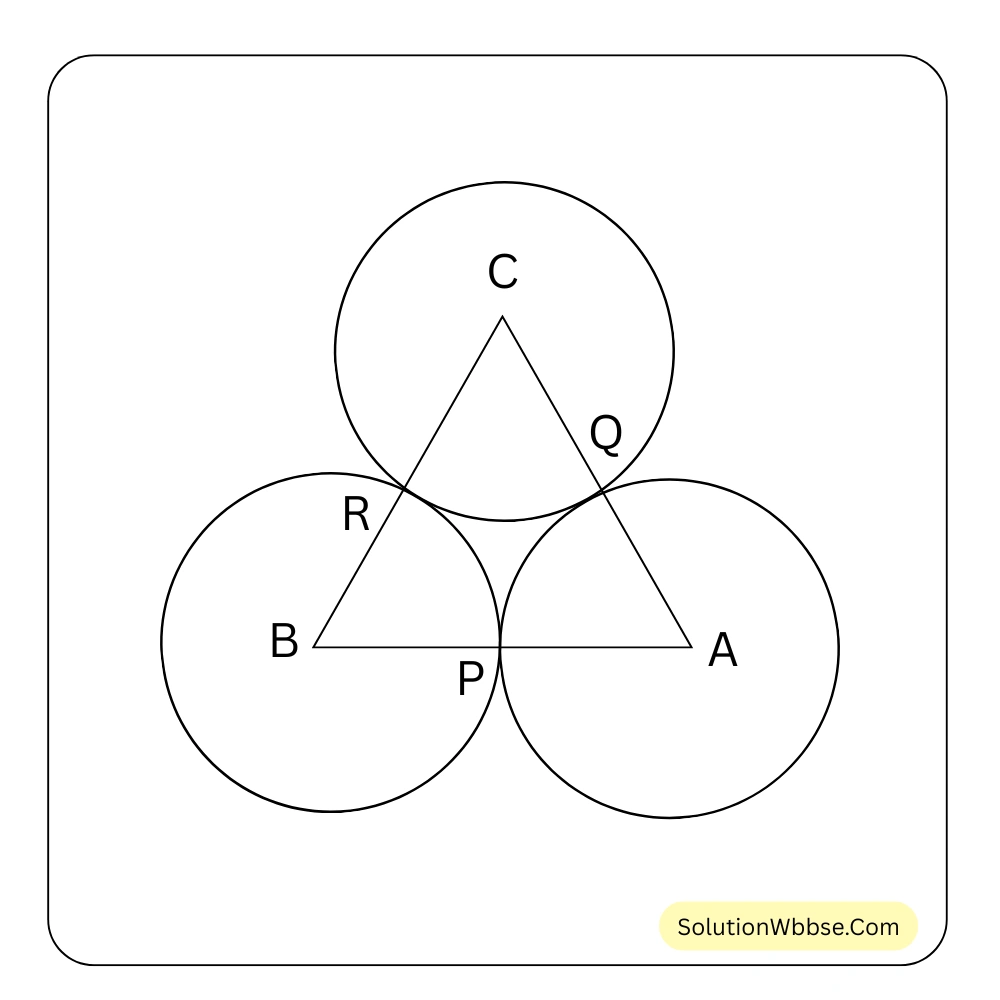
71. পাশের চিত্রে \( A, B, C \) কেন্দ্র বিশিষ্ট তিনটি বৃত্ত পরস্পরকে বহিঃস্পর্শ করে। যদি \( AB = 5 \) সেমি, \( BC = 7 \) সেমি, এবং \( CA = 6 \) সেমি হয় তাহলে \( A \) কেন্দ্র বিশিষ্ট বৃত্তের ব্যাসার্ধের দৈর্ঘ্য নির্ণয় করো।

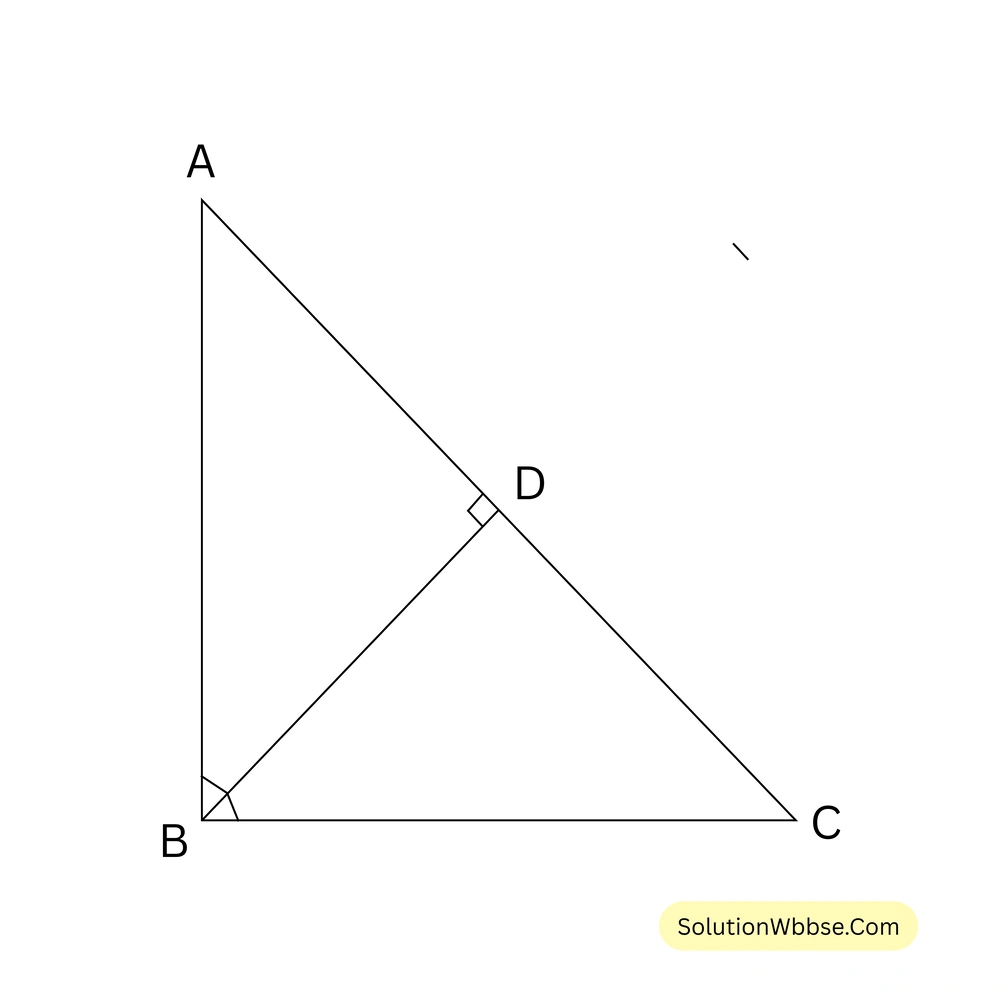
72. পাশের চিত্রে, \( \angle ABC = 90^\circ \) এবং \( BD \perp AC \); যদি \( BD = 8 \) সেমি এবং \( AD = 4 \) সেমি হয় তাহলে \( CD \) এর দৈর্ঘ্য নির্ণয় করো।

73. একটি বৃত্তে দুটি জ্যা \( PQ \) এবং \( PR \) পরস্পর লম্ব। বৃত্তের ব্যাসার্ধের দৈর্ঘ্য \( r \) সেমি হলে, জ্যা \( PQ \) এর দৈর্ঘ্য নির্ণয় করো।

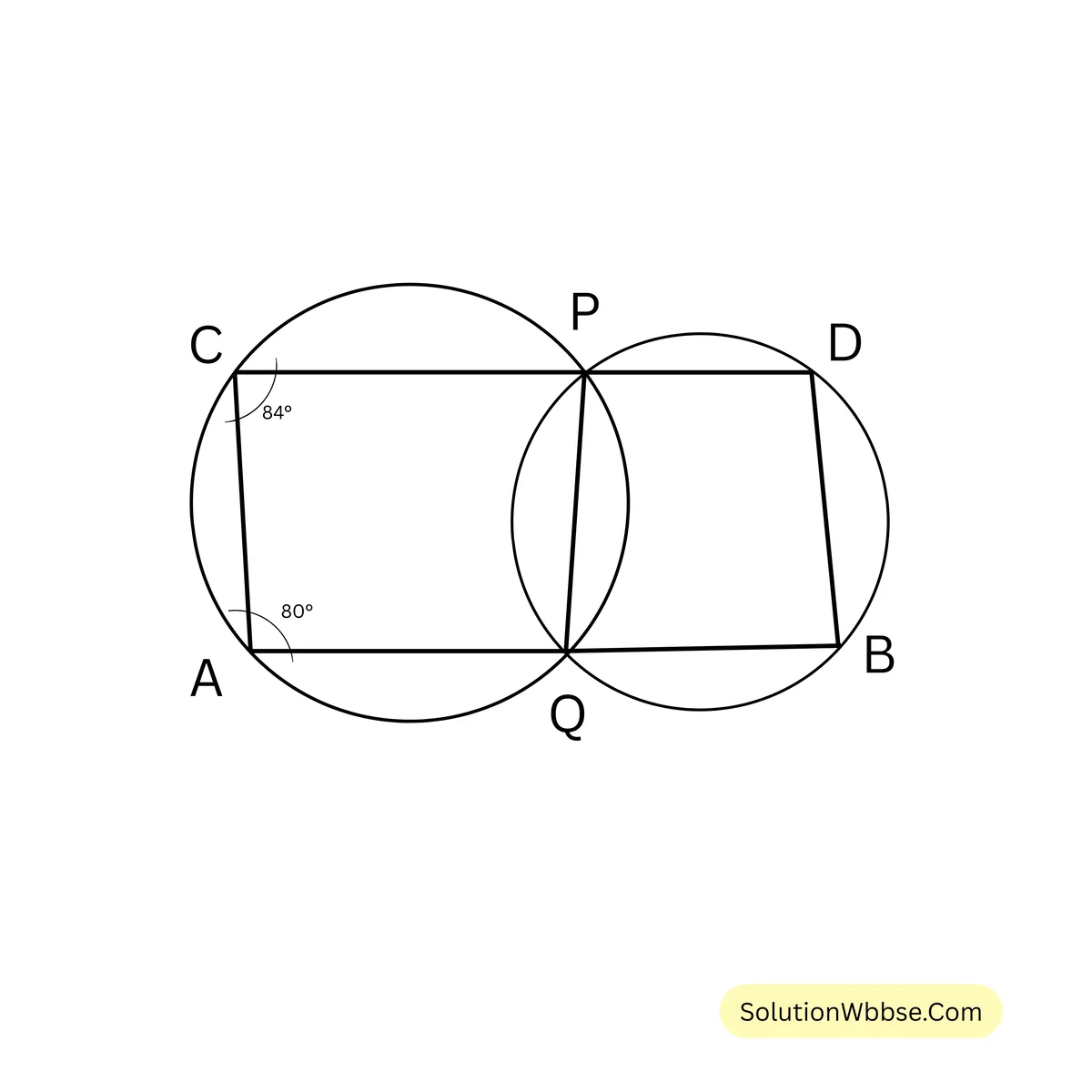
74. পাশের চিত্রে দুটি বৃত্ত পরস্পর \( P \) ও \( Q \) বিন্দুতে ছেদ করে। \( \angle QAD = 80^\circ \) এবং \( \angle PDA = 84^\circ \) হলে \( \angle QBC \) ও \( \angle BCP \) এর মান নির্ণয় করো।

75. \( O \) কেন্দ্রীয় বৃত্তের ভিতর \( P \) যে কোনো একটি বিন্দু। বৃত্তের ব্যাসার্ধের দৈর্ঘ্য \( 5 \) সেমি এবং \( OP = 3 \) সেমি হলে \( P \) বিন্দুগামী যে জ্যাটির দৈর্ঘ্য ন্যূনতম তা নির্ণয় করো।

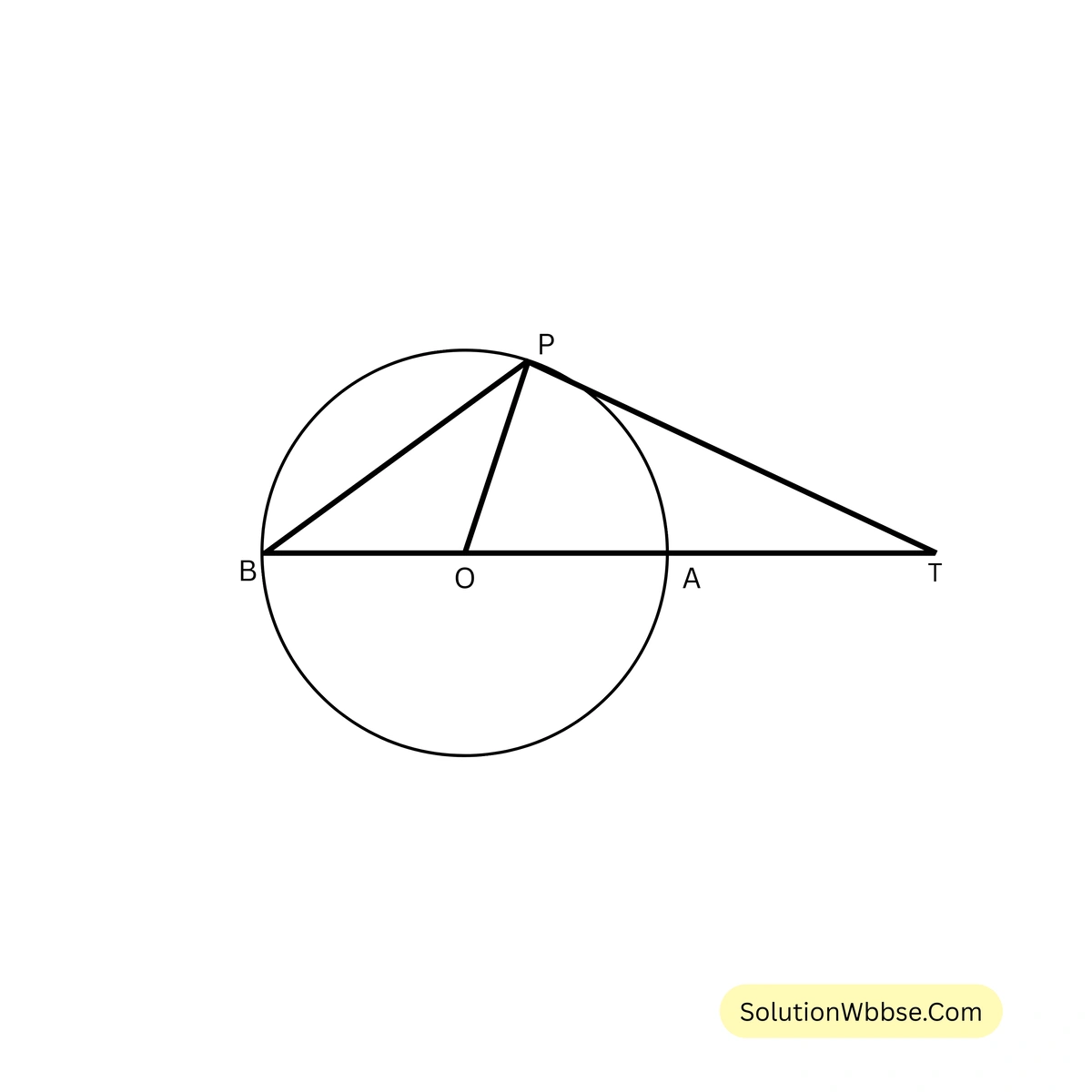
76. পাশের চিত্রে বৃত্তের কেন্দ্র \( O \) এবং \( BOA \) বৃত্তের ব্যাস। বৃত্তের \( P \) বিন্দুতে অঙ্কিত স্পর্শক বর্ধিত \( BA \) কে \( T \) বিন্দুতে ছেদ করে। \( \angle PBO = 30^\circ \) হলে, \( \angle PTA \) এর মান নির্ণয় করো।

77. পাশের চিত্রে, \( \triangle ABC \) ত্রিভুজে \( DE \parallel PQ \parallel BC \) এবং \( AD = 3 \) সেমি, \( DP = x \) সেমি, \( PB = 4 \) সেমি, \( AE = 4 \) সেমি, \( EQ = 5 \) সেমি, \( QC = y \) সেমি হলে \( x \) এবং \( y \) এর মান নির্ণয় করো।

78. পাশের চিত্রে \( \frac{AD}{DB} = \frac{AE}{EC} \) এবং \( \angle ADE = \angle ACB \) হলে, বাহুভেদে \( \triangle ABC \) ত্রিভুজটি কী ধরনের?

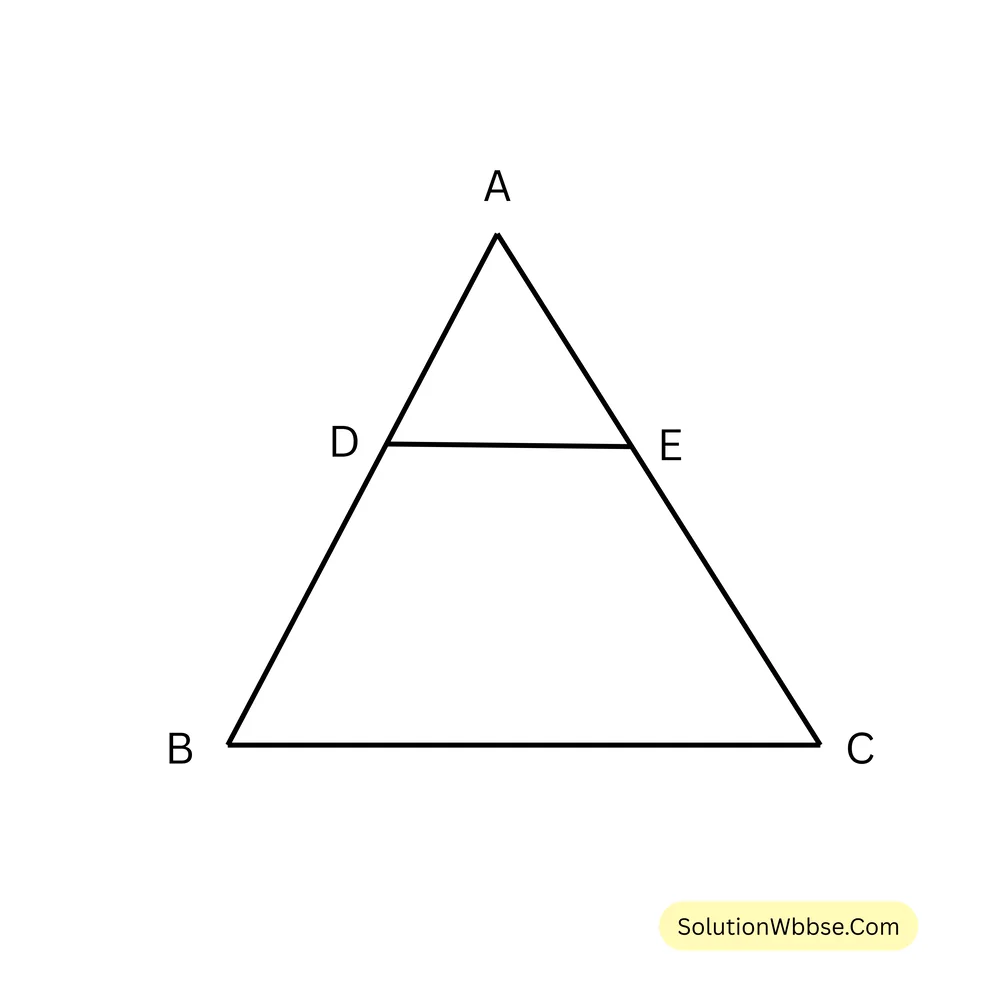
79. \( \triangle ABC \) সমদ্বিবাহু ত্রিভুজের \( AB = AC \); \( AB \) বাহুকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি \( BC \) বাহুকে \( D \) বিন্দুতে ছেদ করে, \( BD = 4 \) সেমি হলে \( CD \) এর দৈর্ঘ্য নির্ণয় কর।

80. পাশের চিত্রে \( \angle ACB = \angle BAD \), \( AC = 8 \) সেমি, \( AB = 16 \) সেমি এবং \( AD = 3 \) সেমি হলে, \( BD \) এর দৈর্ঘ্য কত?

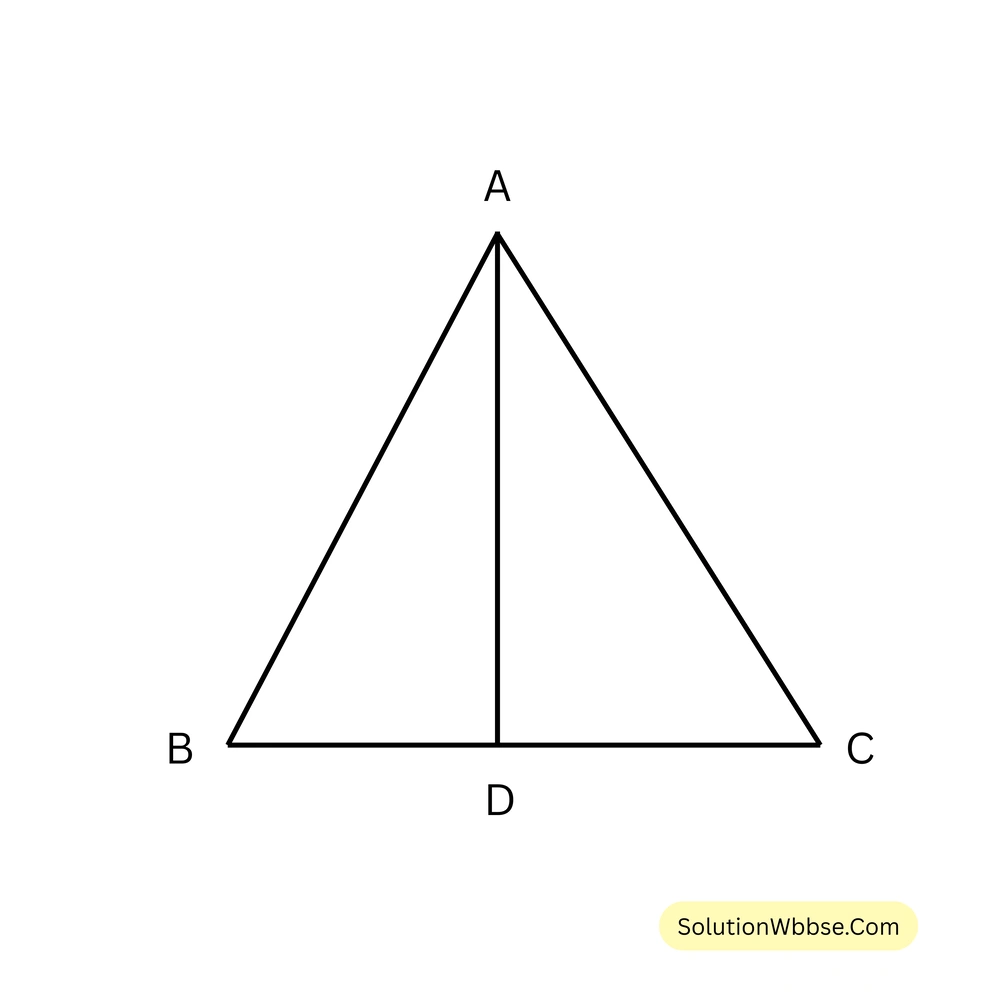
81. পাশের চিত্রে \( O \) বৃত্তের কেন্দ্র এবং \( AB \) বৃত্তের ব্যাস। \( \angle AOD = 140^\circ \), এবং \( \angle CAB = 50^\circ \), হলে, \( \angle BED \) এর মান নির্ণয় করো।

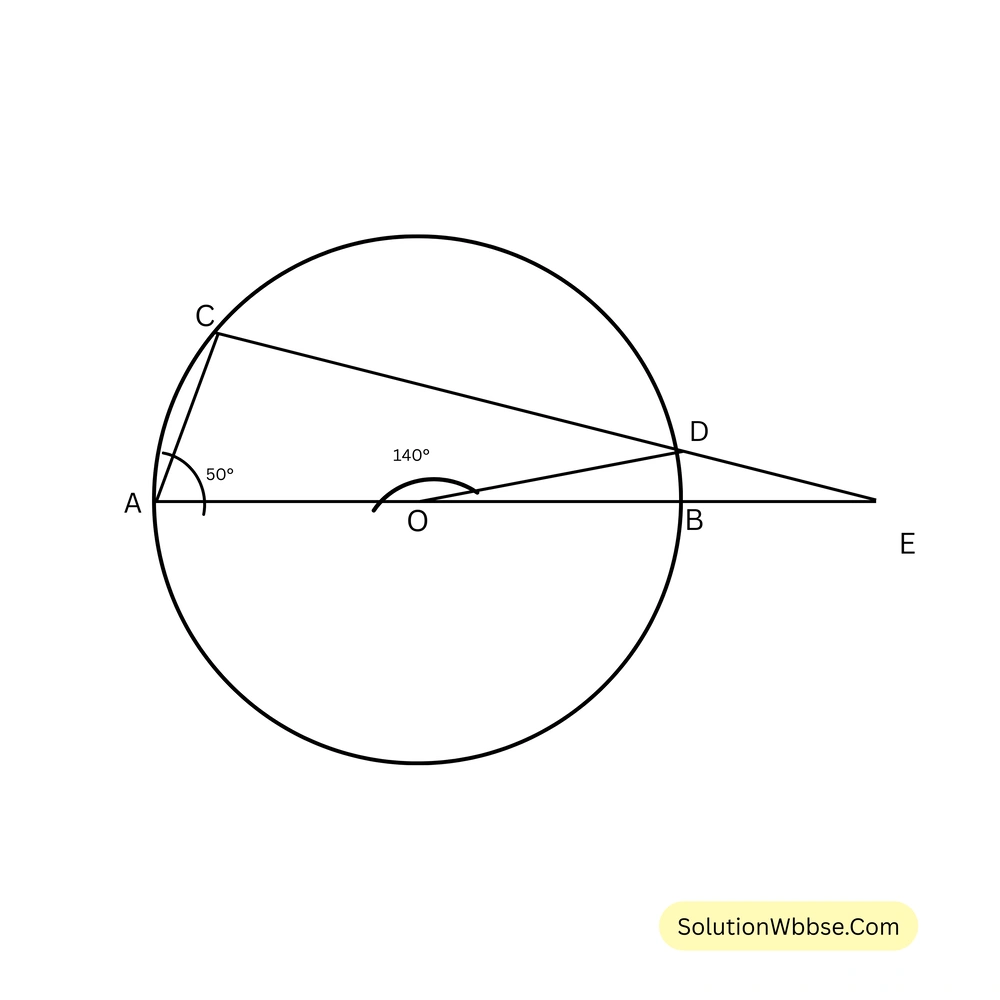
82. পাশের চিত্রে \( \triangle ABC \) ত্রিভুজটি একটি বৃত্তে পরিলিখিত এবং বৃত্তকে \( P, Q, R \) বিন্দুতে স্পর্শ করে। যদি \( AP = 4 \) সেমি, \( BP = 6 \) সেমি, \( AC = 12 \) সেমি, এবং \( BC = x \) সেমি হয়। তাহলে \( x \) এর মান নির্ণয় করো।

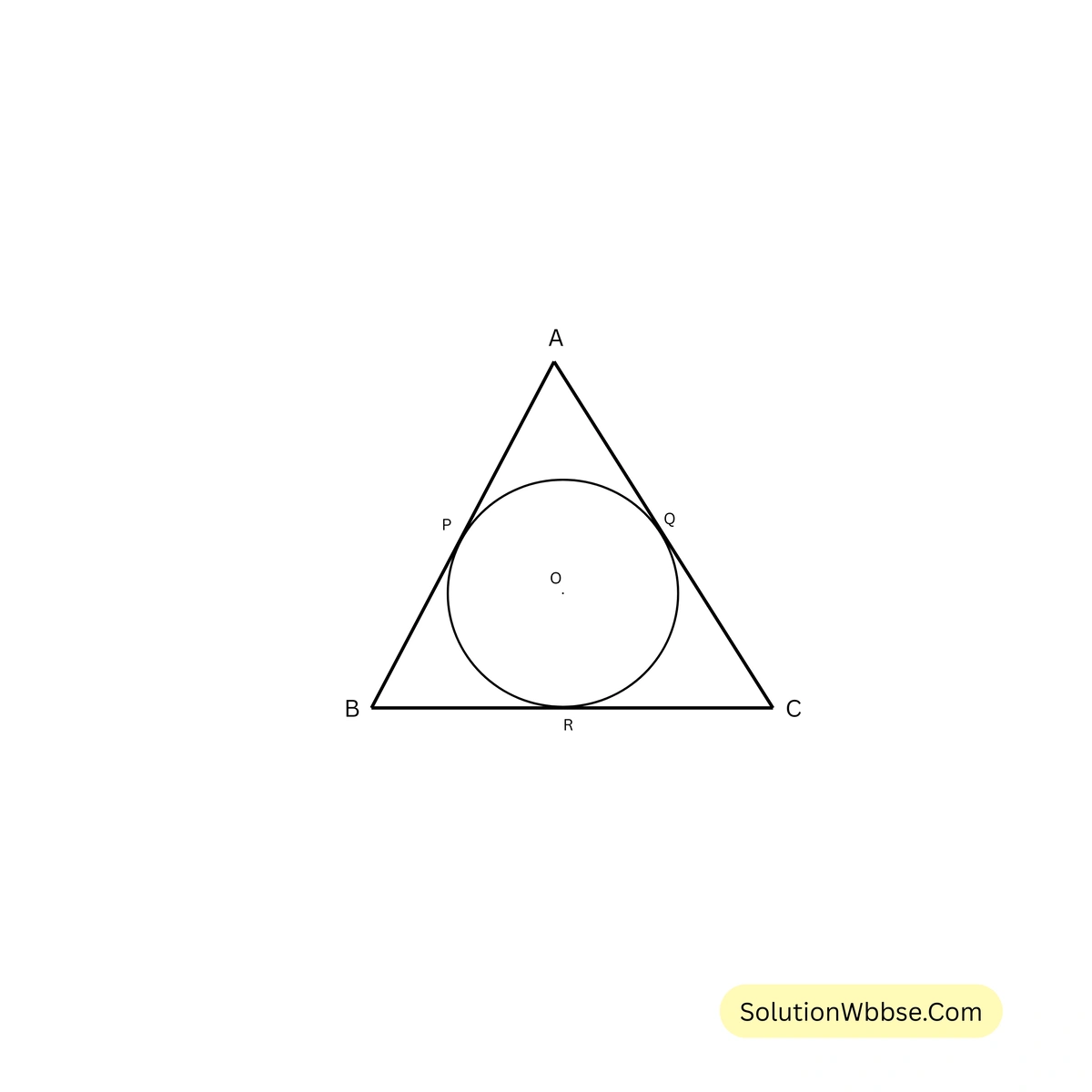
83. \( O \) কেন্দ্রীয় বৃত্তের ওপর \( A, B, C \) তিনটি বিন্দু এমনভাবে অবস্থিত যে \( AOCB \) একটি সমান্তরিক, \( \angle AOC \) এর মান নির্ণয় করো।

পরিমিতি

84. একটি লম্ব বৃত্তাকার শঙ্কুর আয়তন \( V \) ঘন একক, ভূমিতলের ক্ষেত্রফল \( A \) বর্গএকক এবং উচ্চতা \( H \) একক হলে \( \frac{AH}{3V} \) এর মান নির্ণয় করো। [M.P. 2023]

85. সমান দৈর্ঘ্যের ব্যাসার্ধ এবং সমান উচ্চতা বিশিষ্ট নিরেট লম্ববৃত্তাকার চোঙ এবং নিরেট লম্ববৃত্তাকার শঙ্কুর আয়তনের অনুপাত নির্ণয় করো। [M.P. 2023]

86. দুটি লম্ববৃত্তাকার চোঙের উচ্চতার অনুপাত \( 1 : 2 \), ভূমির পরিধির অনুপাত \( 3 : 4 \) হলে, তাদের আয়তনের অনুপাত নির্ণয় করো। [M.P. 2022]

87. একটি গোলকের ব্যাসার্ধের দৈর্ঘ্য \( 50\% \) বৃদ্ধি করলে, বক্রতলের ক্ষেত্রফল শতকরা কত বৃদ্ধি পায় তা নির্ণয় করো। [M.P. 2022]

88. একটি ঘনকের কর্ণের দৈর্ঘ্য \( 4\sqrt{3} \) সেমি। ঘনকটির সমগ্রতলের ক্ষেত্রফল নির্ণয় করো। [M.P. 2022]

89. একটি লম্ব বৃত্তাকার শঙ্কুর উচ্চতা \( 12 \) সেমি এবং আয়তন \( 100\pi \) ঘন সেমি। শঙ্কুটির তির্যক উচ্চতা নির্ণয় করো। [M.P. 2020]

90. দুটি গোলকের বক্রতলের ক্ষেত্রফলের অনুপাত \( 1 : 4 \) হলে, তাদের আয়তনের অনুপাত নির্ণয় করো। [M.P. 2020]

91. একটি আয়তঘনাকৃতি ঘরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে \( a \), \( b \) এবং \( c \) একক এবং \( a + b + c = 25 \), \( ab + bc + ca = 240.5 \) হলে ঘরটির মধ্যে যে বৃহত্তম দণ্ডটি রাখা যাবে তার দৈর্ঘ্য কত হবে? [M.P. 2019]

92. একটি লম্ব বৃত্তাকার শঙ্কুর পার্শ্বতলের ক্ষেত্রফল ভূমির ক্ষেত্রফলের \( \sqrt{5} \) গুণ। শঙ্কুটির উচ্চতা ও ভূমির ব্যাসার্ধের অনুপাত কত? [M.P. 2019]

93. দুটি লম্ব বৃত্তাকার চোঙের আয়তন সমান ও তাদের উচ্চতার অনুপাত \( 1 : 2 \) হলে, চোঙ দুটির ব্যাসার্ধের দৈর্ঘ্যের অনুপাত কত? [M.P. 2018]

94. একটি নিরেট অর্ধগোলকের আয়তন \( 144\pi \) ঘনসেমি হলে, গোলকটির ব্যাসের দৈর্ঘ্য কত? [M.P. 2018]

95. একটি গোলকের ব্যাস অপর একটি গোলকের ব্যাসের দ্বিগুণ যদি গোলকটির সমগ্রতলের ক্ষেত্রফলের সংখ্যামান ছোটো গোলকটির আয়তনের সংখ্যামানের সমান হয়, তবে ছোটো গোলকটির ব্যাসার্ধ কত? [M.P. 2017]

96. একটি আয়তঘনকের তলসংখ্যা \( x \), ধার সংখ্যা \( y \), শীর্ষবিন্দুর সংখ্যা \( z \), এবং কর্ণের সংখ্যা \( p \) হলে \( x – y + z + p \) এর মান কত? [M.P. 2017]

97. তিনটি নিরেট ঘনক যাদের প্রত্যেকটি ধারের দৈর্ঘ্য যথাক্রমে \( 3 \) সেমি, \( 4 \) সেমি এবং \( 5 \) সেমি। ঘনক তিনটিকে গলিয়ে একটি নতুন নিরেট ঘনক তৈরী করা হয়। নতুন ঘনকটির একটি ধারের দৈর্ঘ্য কত হবে?

98. একটি নিরেট লম্ববৃত্তাকার শঙ্কু এবং একটি নিরেট গোলকের ব্যাসার্ধের দৈর্ঘ্য সমান এবং আয়তন সমান। গোলকটির ব্যাসের দৈর্ঘ্য এবং শঙ্কুর উচ্চতার অনুপাত নির্ণয় করো।

99. একটি ঘনকের সমগ্রতলের ক্ষেত্রফলের সাংখ্যমান তার ঘনফলের সাংখ্যমানের সমান হলে, ঘনকটির বাহুর দৈর্ঘ্য কত?

100. একটি লম্ব বৃত্তাকার চোঙের বক্রতলের ক্ষেত্রফল \( c \) বর্গএকক, ভূমির ব্যাসার্ধের দৈর্ঘ্য \( r \) একক এবং আয়তন \( v \) ঘনএকক হলে, \( \frac{cr}{v} \) এর মান নির্ণয় করো।

101. দুটি আয়তঘনের মাত্রাগুলির দৈর্ঘ্য যথাক্রমে \( 4, 6, 4 \) একক এবং \( 8, (2h-1), 2 \) একক। যদি আয়তঘন দুটির ঘনফল সমান হয়, তাহলে \( h \) এর মান নির্ণয় করো।

102. একটি লম্ববৃত্তাকার শঙ্কুর আয়তন এবং পার্শ্বতলের ক্ষেত্রফলের সাংখ্যমান সমান। শঙ্কুটির উচ্চতা এবং ব্যাসার্ধের দৈর্ঘ্য যথাক্রমে \( h \) একক এবং \( r \) একক হলে, \( \frac{1}{h^2} + \frac{1}{r^2} \) এর মান নির্ণয় করো।

103. একটি নিরেট অর্ধগোলকের আয়তন এবং সমগ্রতলের ক্ষেত্রফলের সাংখ্যমান সমান। অর্ধগোলকটির ব্যাসার্ধের দৈর্ঘ্য কত?

104. একটি নিরেট লম্ববৃত্তাকার শঙ্কুকে গলিয়ে একটি নিরেট লম্ববৃত্তাকার চোঙ তৈরী করা হলো। উভয়ের ব্যাসার্ধের দৈর্ঘ্য সমান। যদি শঙ্কুর উচ্চতা \( 15 \) সেমি হয়, তাহলে নিরেট চোঙের উচ্চতা কত?

105. একটি লম্ববৃত্তাকার চোঙ এবং লম্ববৃত্তাকার শঙ্কুর ভূমিতলের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত এবং তাদের উচ্চতার অনুপাত \( 2 : 3 \), \( 3 : 4 \)। চোঙ এবং শঙ্কুর আয়তনের অনুপাত কত?

106. একটি নিরেট গোলকের বক্রতলের ক্ষেত্রফল \( S \) এবং আয়তন \( V \) হলে \( \frac{S^3}{V^2} \) এর মান নির্ণয় করো। (\( \pi \) এর মান না বসিয়ে)

107. একটি লম্ববৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য \( 50\% \) হ্রাস করা হলো এবং উচ্চতা \( 50\% \) বৃদ্ধি করা হলো, চোঙটির আয়তনের শতকরা কত পরিবর্তন হবে?

108. একটি লম্ব বৃত্তাকার চোঙাকৃতি স্তম্ভের বক্রতলের ক্ষেত্রফল \( 264 \) বর্গমিটার এবং আয়তন \( 924 \) ঘনমিটার হলে, স্তম্ভের ভূমির ব্যাসার্ধের দৈর্ঘ্য নির্ণয় করো।

ত্রিকোণমিতি

109. \( \tan 2A = \cot(A – 30^\circ) \) হলে, \( \sec(A + 20^\circ) \) এর মান নির্ণয় করো। [M.P. 2023]

110. \( \tan\theta = \frac{8}{15} \) হলে, \( \sin\theta \)-এর মান নির্ণয় করো। [M.P. 2023]

111. \( \tan 4\theta \tan 6\theta = 1 \) এবং \( 6\theta \) ধনাত্মক সূক্ষ্মকোণ হলে, \( \theta \)-এর মান নির্ণয় করো। [M.P. 2020]

112. একটি ঘড়ির ঘন্টার কাঁটা 1 ঘন্টায় যে কোণ আবর্তন করে তার বৃত্তীয় মান কত? [M.P. 2020]

113. \( \theta \) (\( 0^\circ \leq \theta \leq 90^\circ \))-এর কোন মান/মানগুলির জন্য \( 2\sin\theta\cos\theta = \cos\theta \) হবে? [M.P. 2019]

114. \( \sin 10\theta = \cos 8\theta \) এবং \( 10\theta \) ধনাত্মক সূক্ষ্মকোণ হলে \( \tan 9\theta \) এর মান নির্ণয় করো। [M.P. 2019]

115. একটি স্তম্ভের ছায়ার দৈর্ঘ্য এবং স্তম্ভের উচ্চতার অনুপাত \( \sqrt{3} : 1 \) হলে, সূর্যের উন্নতি কোণ নির্ণয় করো। [M.P. 2018]

116. \( \tan\theta + \cot\theta = 2 \) হলে, \( \tan^7\theta + \cot^7\theta \)-এর মান কত? [M.P. 2018]

117. \( x = a \sec\theta \), \( y = b \tan\theta \) হলে \( x \) এবং \( y \)-এর \( \theta \) বর্জিত সম্পর্ক নির্ণয় করো। [M.P. 2017]

118. \( \tan(\theta + 15^\circ) = \sqrt{3} \) হলে \( \sin\theta + \cos\theta \) এর মান নির্ণয় করো। [M.P. 2017]

119. \( 63^\circ 35′ 15” \) পরিমাপের কোণটির পূরক কোণের মান নির্ণয় করো।

120. \( \sin A + \sin B = 2 \) হলে, যেখানে \( 0^\circ \leq A \leq 90^\circ \) এবং \( 0^\circ \leq B \leq 90^\circ \), \( \cos A + \cos B \) এর মান নির্ণয় করো।

121. যদি \( 0^\circ < \theta < 90^\circ \) হয়, তাহলে \( (9\tan^2\theta + 4\cot^2\theta) \)-এর সর্বনিম্ন মান নির্ণয় করো।

122. \( (\sin^6\alpha + \cos^6\alpha + 3\sin^2\alpha\cos^2\alpha) \)-এর মান নির্ণয় করো।

123. একটি কোণের ডিগ্রিতে মান \( D \) এবং ওই কোণের রেডিয়ানে মান \( R \) হলে, \( \frac{R}{D} \)-এর মান নির্ণয় করো।

124. \( \frac{2\sin^2 63^\circ + 1 + 2\sin^2 27^\circ}{3\cos^2 17^\circ – 2 + 3\cos^2 73^\circ} \)-এর মান নির্ণয় করো।

125. \( (\tan 1^\circ \times \tan 2^\circ \times \tan 3^\circ \times \cdots \times \tan 89^\circ) \)-এর মান কত?

126. \( \triangle ABC \) সমকোণী ত্রিভুজে \( \angle B = 90^\circ \), \( AB \)-এর উপর \( D \) এমন একটি বিন্দু যে \( AB : BC : BD = \sqrt{3} : 1 : 1 \), \( \angle ACD \) এর মান নির্ণয় করো।

127. একটি ঘুড়ির উন্নতি কোণ \( 60^\circ \) এবং সুতোর দৈর্ঘ্য \( 20\sqrt{3} \) মিটার হলে, ঘুড়িটি মাটি থেকে কত উচ্চতায় আছে?

রাশিবিজ্ঞান

128. ঊর্ধ্বক্রমে সাজানো \( 6, 8, 10, 12, 13, x \) তথ্যের গড় ও মধ্যমা সমান হলে \( x \) এর মান নির্ণয় করো। [M.P. 2023]

129. যদি \( u_i = \frac{x_i – 35}{10} \), \( \sum f_i u_i = 30 \) এবং \( \sum f_i = 60 \) হয়, তাহলে \( \bar{x} \) এর মান নির্ণয় করো। [M.P. 2020]

130. প্রথম \( (2n+1) \) সংখ্যক ক্রমিক স্বাভাবিক সংখ্যার মধ্যবর্তী সংখ্যা \( \frac{n+103}{2} \) হলে, \( n \) এর মান নির্ণয় করো। [M.P. 2019]

131. একটি পরিসংখ্যা বিভাজনের গড় 8.1, \( \sum f_i x_i = 132 + 5k \) এবং \( \sum f_i = 20 \) হলে, \( k \) এর মান কত? [M.P. 2018]

132. \( 11, 12, 14, x-2, x+4, x+9, 32, 38, 47 \) রাশিগুলি উর্ধ্বক্রমানুসারে সাজানো এবং তাদের মধ্যমা 24 হলে, \( x \)-এর মান নির্ণয় করো। [M.P. 2017]

133. \( 7, x-3, 10, x+3, x-5 \) সংখ্যাগুলির যৌগিক গড় 15 হলে তাদের মধ্যমা কত?

134. \( 11, 27, 18, 26, 13, 12, 9, 15, 4, 9 \) তথ্যগুলির সংখ্যাগুরু মান নির্ণয় করো।

135. \( u_i = \frac{x_i – 25}{10} \), \( \sum f_i u_i = 20 \) এবং \( \sum f_i = 100 \) হলে \( \bar{x} \) এর মান নির্ণয় করো।

136.

(i) উপরের পরিসংখ্যা বিভাজন ছকের মধ্যমা শ্রেণীর উর্ধ্ব শ্রেণী-সীমানা এবং সংখ্যাগুরুমান শ্রেণীর নিম্ন শ্রেণীসীমানার অন্তরফল নির্ণয় করো।

2026 সালের মাধ্যমিক পরীক্ষার্থীদের জন্য আমাদের গণিত বিষয়ের সংক্ষিপ্ত প্রশ্নের সাজেশন এখানেই শেষ হলো। এই প্রশ্নগুলি তোমাদের কতটা সাহায্য করলো বা অন্য কোনো বিষয়ের সাজেশন প্রয়োজন কিনা, তা অবশ্যই আমাদের কমেন্ট করে জানিও। আর্টিকেলটি ভালো লাগলে বন্ধুদের সাথে শেয়ার করতে ভুলো না!

এছাড়াও, টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।