এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের সপ্তম অধ্যায়, ‘বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য’ -এর ‘কষে দেখি – 7.1’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

1. ABC সমদ্বিবাহু ত্রিভুজের AB = AC সমদ্বিবাহু ত্রিভুজটির পরিকেন্দ্র O এবং BC বাহুর যেদিকে A বিন্দু অবস্থিত তার বিপরীত পার্শ্বে কেন্দ্র অবস্থিত। ∠BOC = 100° হলে ∠ABC ও ∠ABO -এর মান হিসাব করে লিখি।
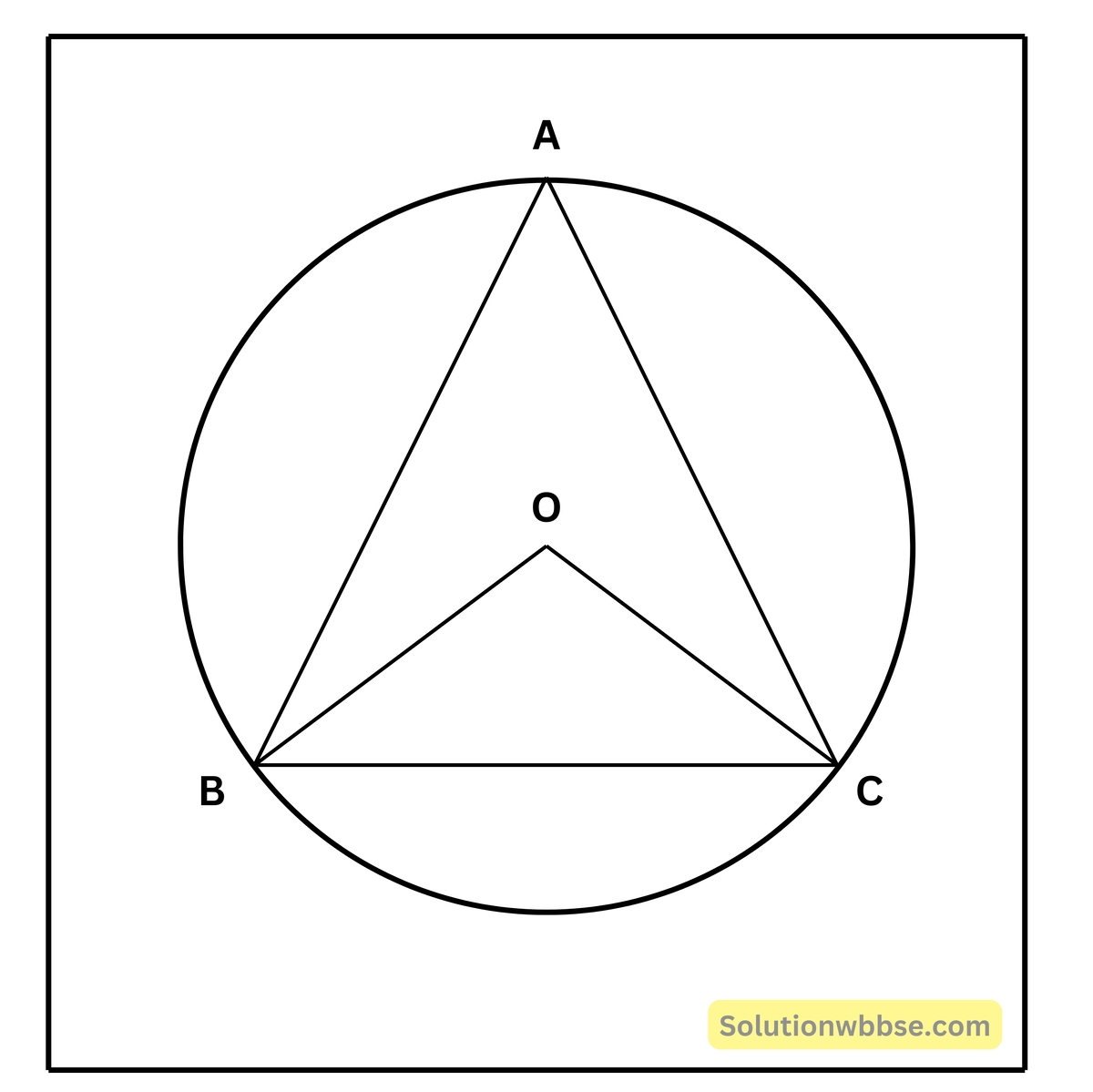
দেওয়া আছে, ABC সমদ্বিবাহু ত্রিভুজের AB = AC এবং O পরিকেন্দ্র। O কেন্দ্রের যে পার্শ্বে A বিন্দু, BC বাহু তার বিপরীত পার্শ্বে। OB, OC যোগ করা হয়েছে।
কোণের পরিমাপ নির্ণয় – O কেন্দ্রীয় বৃত্তের BC চাপের উপর অবস্থিত ∠BAC পরিধিস্থ কোণ এবং ∠BOC কেন্দ্রস্থ কোণ।
∴ ∠BAC = \(\frac12\)∠BOC = \(\left(\frac12\times100\right)\)° = 50°
আবার ABC সমদ্বিবাহু ত্রিভুজে AB = AC,
সেজন্য ∠ABC = ∠ACB
আবার ABC ত্রিভুজে, ∠BAC + ∠ABC + ∠ACB = 180°
বা, 50° + ∠ABC + ∠ABC = 180°
বা, 2∠ABC = 180° – 50° = 130°
∴ ∠ABC = \(\frac12\times130\)° = 65°
আবার OBC ত্রিভুজে, OB = OC [একই বৃত্তের ব্যাসার্ধ।
∴ ∠OBC = ∠OCB, OBC ত্রিভুজে, ∠BOC + ∠OBC + ∠OCB = 180°
বা, 100° + 2∠OBC = 180°
বা, 2∠OBC = 180° – 100° = 80°
∴ ∠OBC = \(\frac12\times80\)° = 40°
এখন, ∠ABO = ∠ABC – ∠OBC = 65° – 40° = 25°
তাহলে, ∠ABC = 65° এবং ∠ABO = 25°
2. পাশের চিত্রে ত্রিভুজ ΔABC -এর পরিবৃত্তের কেন্দ্র O, ∠AOC = 110°, ∠ABC -এর মান হিসাব করে লিখি।
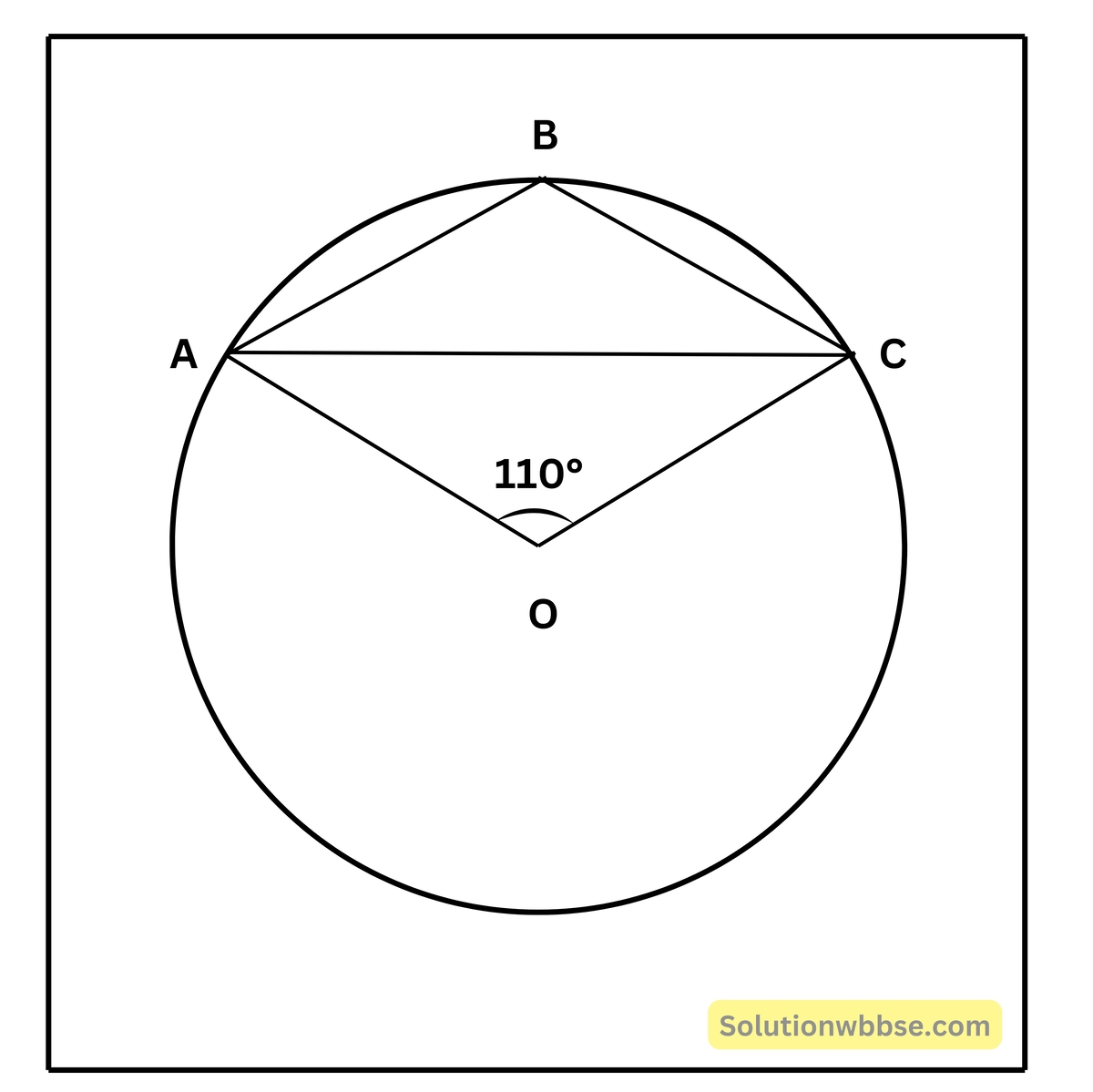
প্রদত্ত ছবিতে ∠AOC = 110°,
∴ প্রদত্ত ∠AOC = 360° – 110° = 250°
এখন AC চাপের উপর অবস্থিত পরিধিস্থ ∠ABC = \(\frac12\) × কেন্দ্রস্থ প্রবৃদ্ধ
∠ABC = \(\frac12\) × 250° = 125°
3. O কেন্দ্রীয় বৃত্তের ABCD একটি বৃত্তস্থ চতুর্ভুজ; DC বাহুকে P পর্যন্ত বর্ধিত করা হলো। ∠BCP = 108° হলে, ∠BOD -এর মান হিসাব করে লিখি।
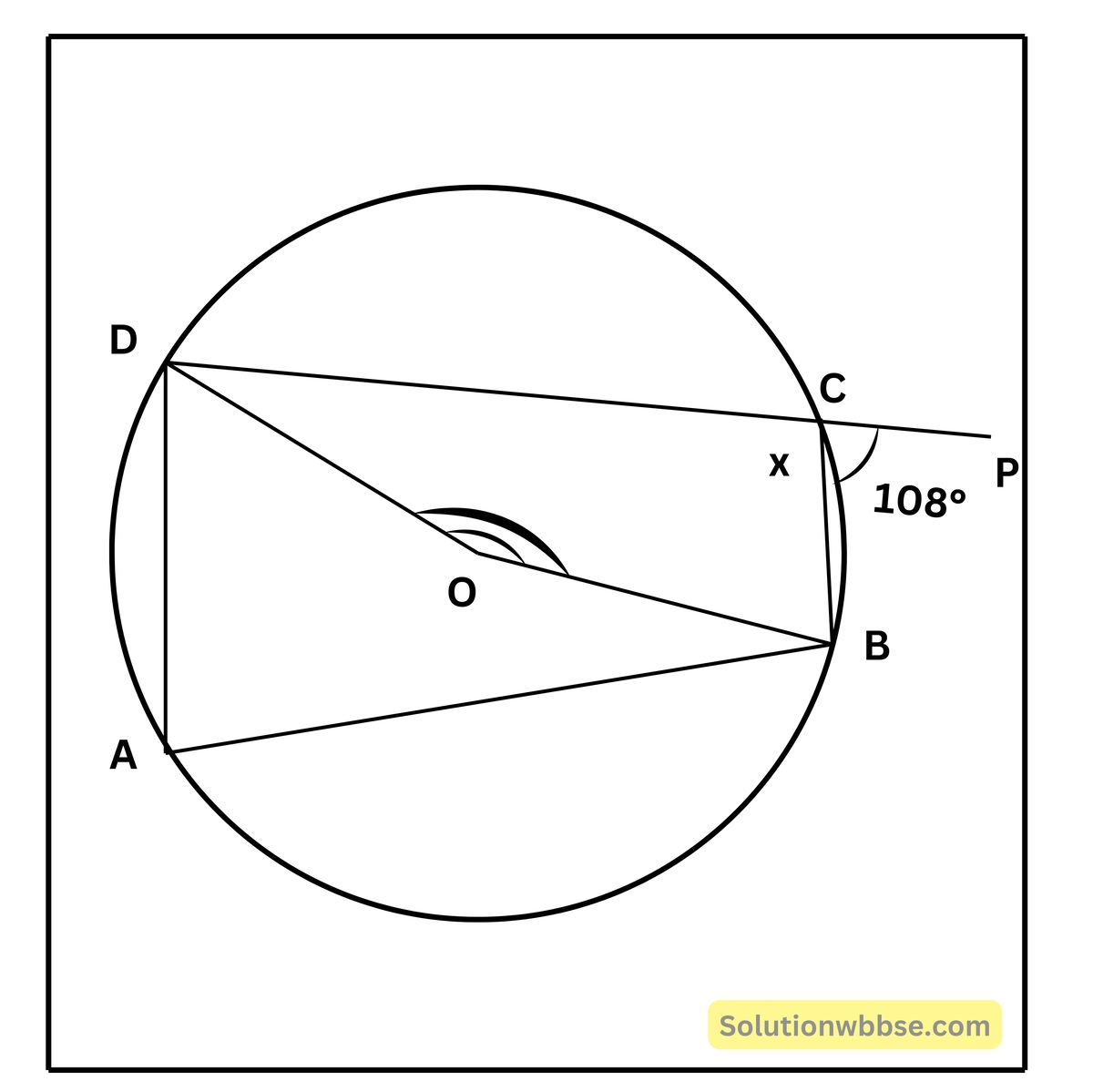
দেওয়া আছে, O কেন্দ্রস্থ বৃত্তের ABCD একটি বৃত্তস্থ চতুর্ভুজ। DC বাহুকে P পর্যন্ত বর্ধিত করায় ∠BCP = 108° হয়েছে।
∠BOD -এর মান নির্ণয় করতে হবে।
কোণের মান নির্ণয় – যেহেতু ∠BCD + ∠BCP = 180°
∠BCD = 180° – ∠BCP = 180° – 72°
আবার, BD চাপের উপর অবস্থিত ∠BOD কেন্দ্রস্থ কোণ এবং ∠BCD পরিধিস্থ কোণ।
∴ ∠BOD = 2 × ∠BCD = 2 × 72° = 144°
আবার প্রবৃদ্ধ ∠BOD = (360° – 144°) = 216°
4. O কেন্দ্রীয় বৃত্তের ∠AOD = 40° এবং ∠ACB = 35° হলে ∠BCO ও ∠BOD এর মান হিসাব করে লিখি ও উত্তরের সপক্ষে যুক্তি দাও।
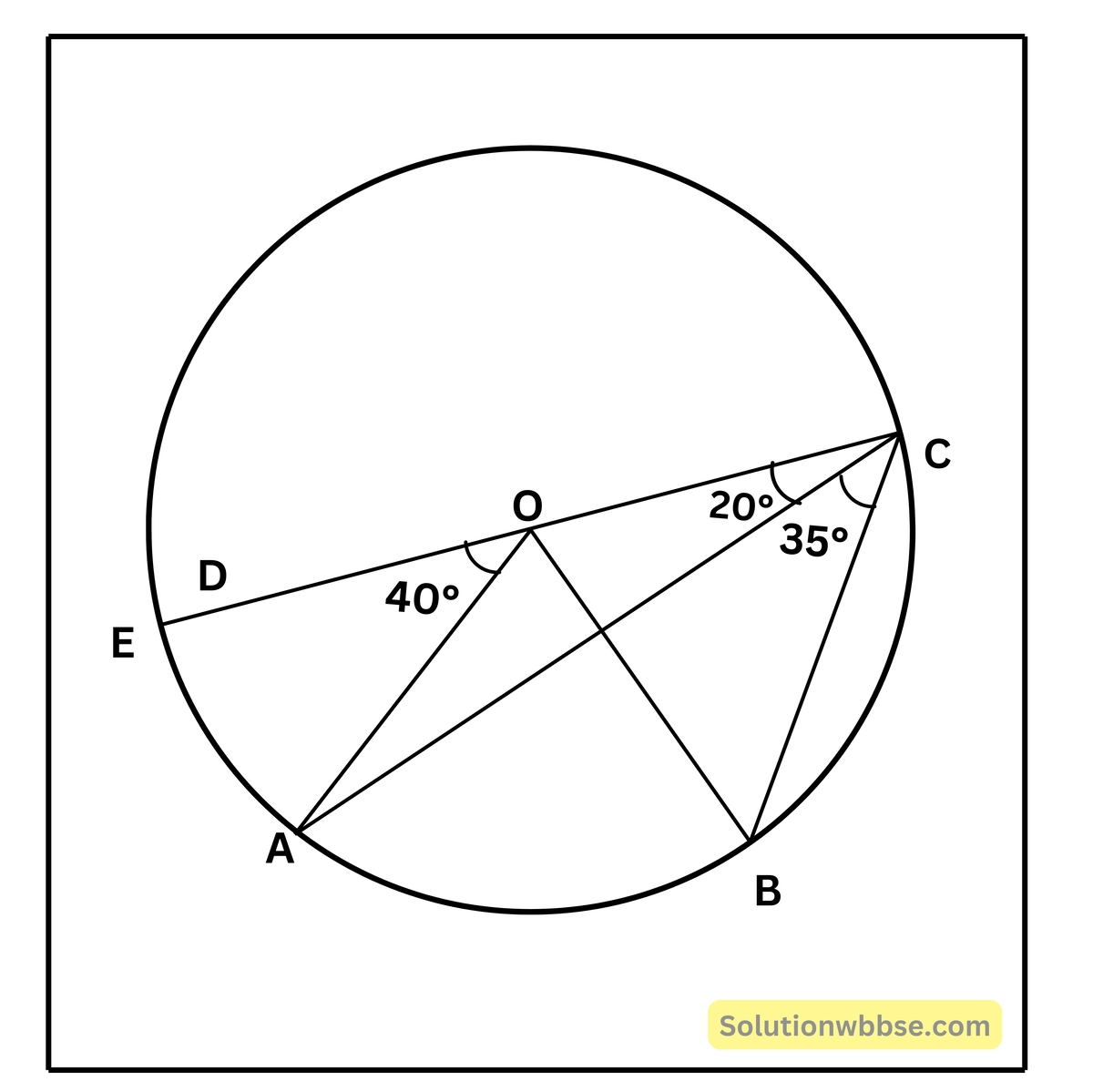
প্রদত্ত ছবিতে দেওয়া আছে; বৃত্তের কেন্দ্র O, ∠AOD = 40° এবং ∠ACB = 35°
নির্ণয় করতে হবে – ∠BCO এবং ∠BOD -এর মান।
অঙ্কন – CD -কে বর্ধিত করা হল; বর্ধিত CD বৃত্তের পরিধিকে E বিন্দুতে ছেদ করল।
কোণের পরিমাপ নির্ণয় – AE চাপের উপর অবস্থিত ∠AOE কেন্দ্রস্থ কোণ এবং ∠ACE পরিধিস্থ কোণ।
∠ACE = \(\frac12\)∠AOE = \(\frac12\) × 40° = 20°
এখন, ∠BCO = ∠BCA + ∠ACO = ∠ACB + ∠ACE = 35° + 20° = 55°
আবার, AB চাপের উপর অবস্থিত ∠AOB কেন্দ্রস্থ কোণ এবং ∠ACB পরিধিস্থ কোণ।
∴ ∠AOB = 2 × ∠ACB = 2 × 35° = 70°
এখন ∠BOD = ∠AOB + ∠AOD = 70° + 40° = 110°
সুতরাং দেখা গেল যে, ∠BCO = 55°, ∠BOD = 110°
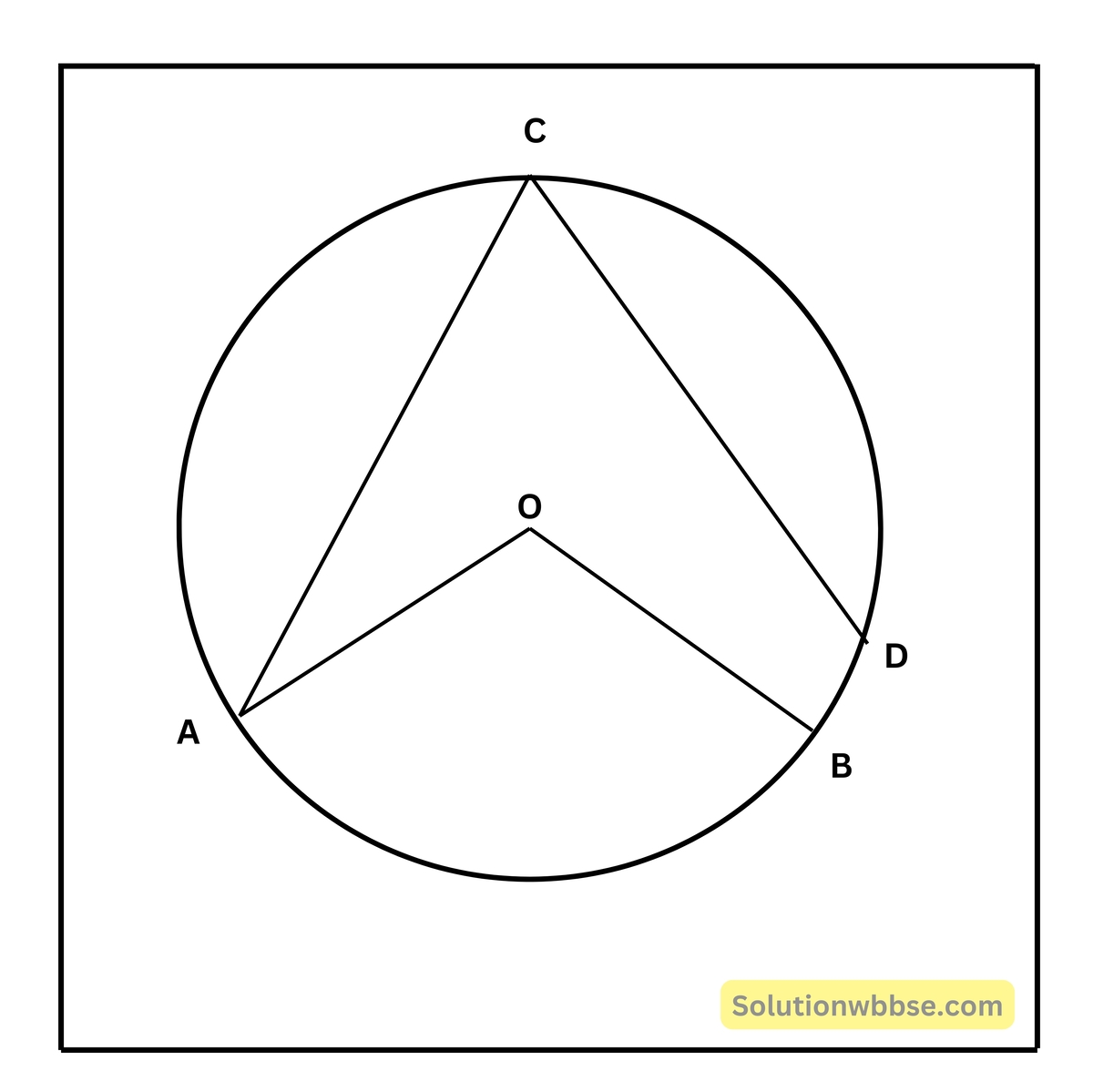
5. চিত্রের O কেন্দ্রীয় বৃত্তের ∠APB = 80° হলে, ∠AOB ও ∠COD -এর মানের সমষ্টি নির্ণয় করি ও উত্তরের সপক্ষে যুক্তি দিই।
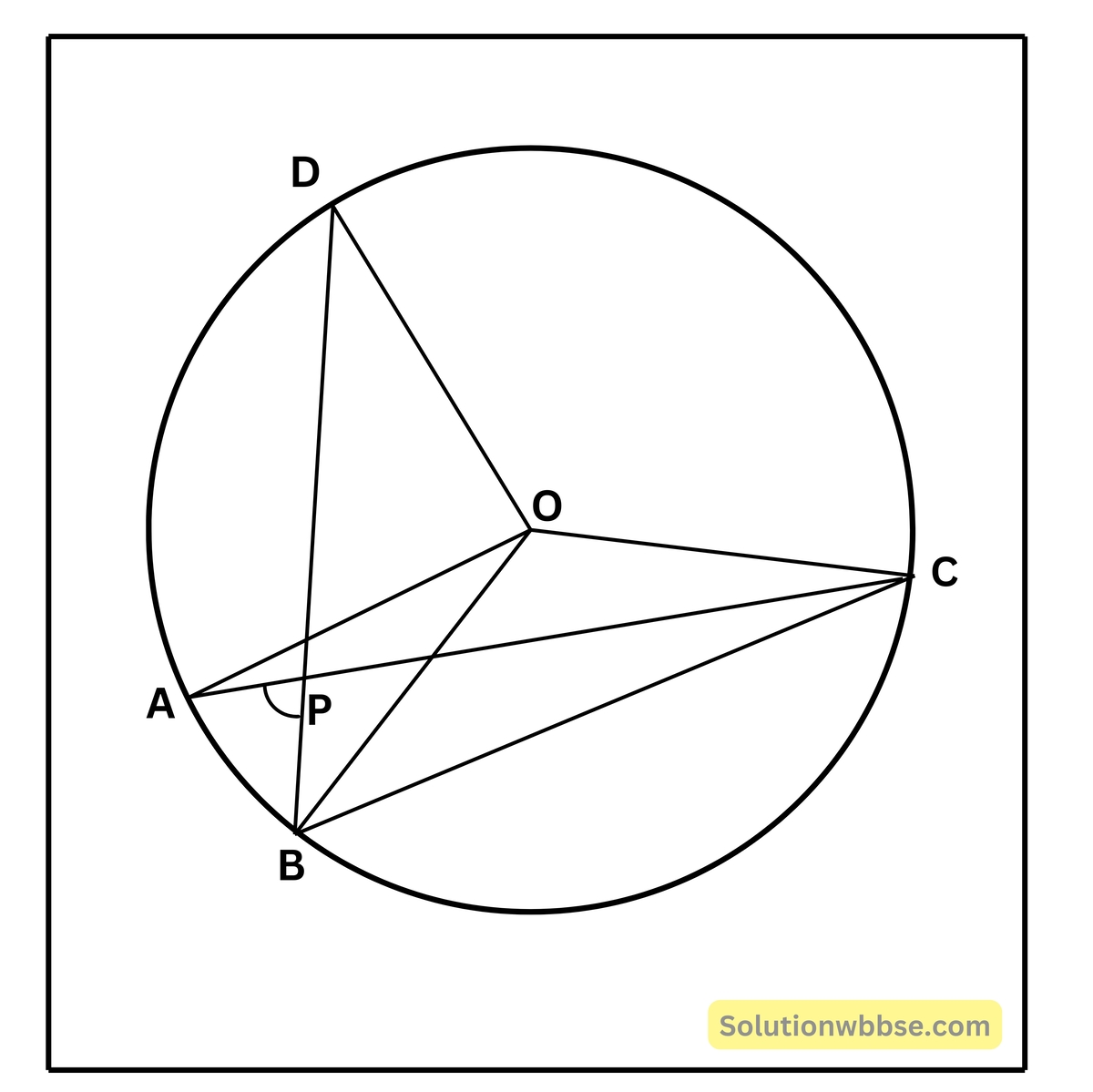
দেওয়া আছে, প্রদত্ত চিত্রে বৃত্তটির কেন্দ্র এবং ∠ADB = 80°
নির্ণয় করতে হবে – ∠AOB এবং ∠COD -এর সমষ্টি।
অঙ্কন – B, C যুক্ত করা হল।
কোণদ্বয়ের সমষ্টির মান নির্ণয় – AB চাপের উপর অবস্থিত কেন্দ্রস্থ কোণ ∠AOB এবং পরিধিস্থ কোণ ∠ACB
∴ ∠AOB = 2 × ∠ACB
আবার, CD চাপের উপর অবস্থিত কেন্দ্রস্থ কোণ ∠COD এবং পরিধিস্থ কোণ ∠DBC
∴ ∠COD = 2 × ∠DBC
∴ ∠AOB × ∠COD = 2 × (∠ACB × ∠DBC) —(i)
এখন, ΔBCP-এর CP বাহু A পর্যন্ত বর্ধিত হয়েছে
সেজন্য বহিস্থ ∠BPA = ∠PCB + ∠PBC
অর্থাৎ, ∠APB = ∠ACB + ∠DBC
বা, ∠ACB + ∠DBC = ∠APB = 80° —(ii)
এবার (i) এবং (ii) থেকে ∠AOB + ∠COD = 2 × (∠ACB + ∠DBC) = 2 × 80° = 160°
6. পাশের ছবির মতো C ও D কেন্দ্রবিশিষ্ট দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে A ও B বিন্দুতে ছেদ করেছে। A বিন্দুগামী একটি সরলরেখা অঙ্কন করেছি যা C কেন্দ্রীয় বৃত্তকে P বিন্দুতে এবং D কেন্দ্রীয় বৃত্তকে Q বিন্দুতে ছেদ করেছে।
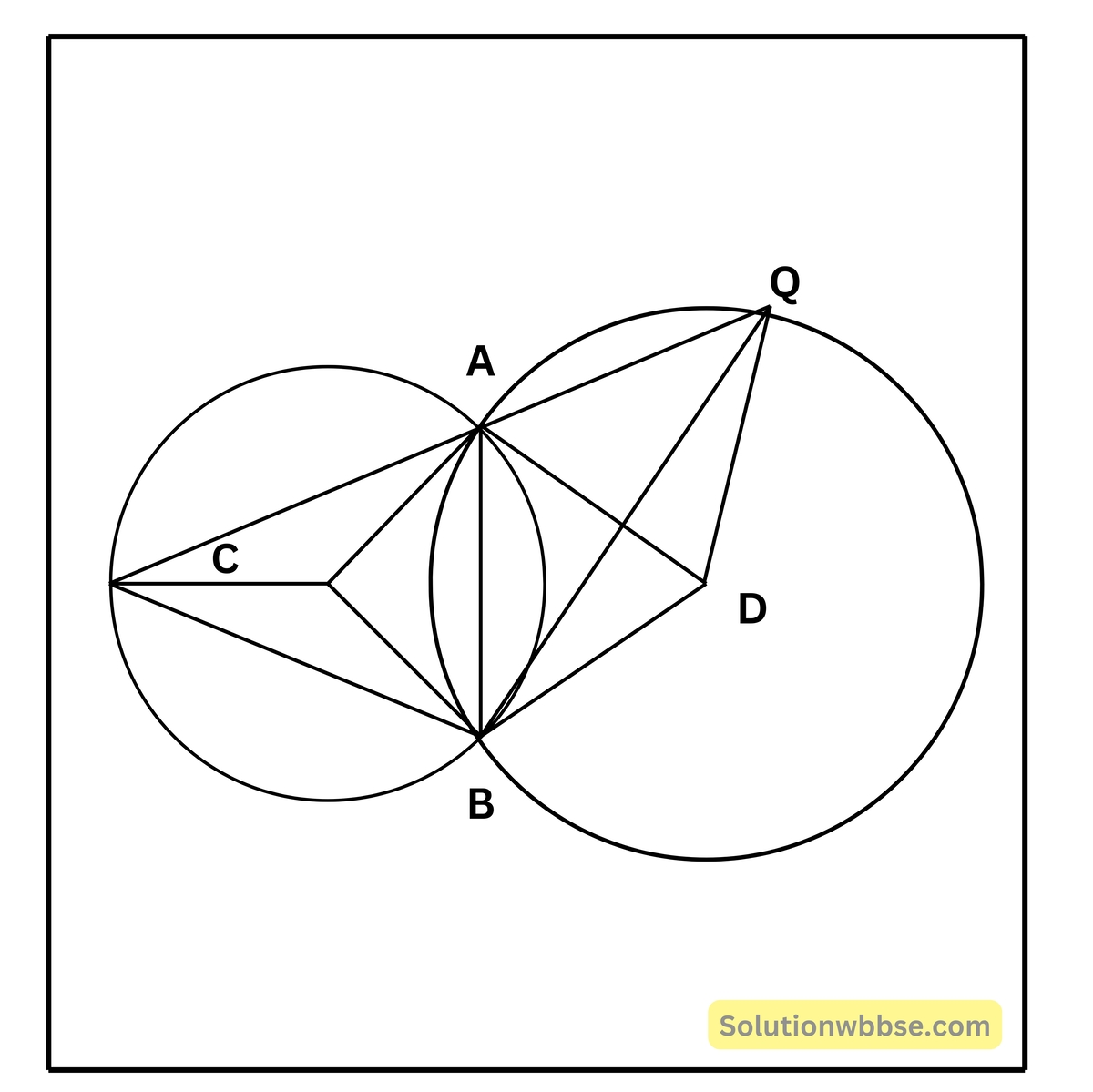
দেওয়া আছে, C এবং D কেন্দ্র বিশিষ্ট দুটি বৃত্ত পরস্পরকে A এবং B বিন্দুতে ছেদ করেছে। A বিন্দুগামী একটি সরলরেখা C-কেন্দ্রীয় বৃত্তকে P বিন্দুতে এবং D কেন্দ্রীয় বৃত্তকে Q বিন্দুতে ছেদ করেছে।
প্রমাণ করি যে, (i) ∠PBQ = ∠CAD এবং (ii) ∠BPC = ∠BQD
অঙ্কন – A, B; P, C; A, C; A, D; D, Q; B, P; B, Q; B, C এবং B এবং B, D যুক্ত করা হল।
প্রমাণ – C কেন্দ্রীয় বৃত্তের একই বৃত্তচাপ AP -এর উপর অবস্থিত ∠ACP কেন্দ্রস্থ কোণ এবং ∠ABP পরিধিস্থ কোণ।
∴ ∠ABP = \(\frac12\)∠ACP
আবার ΔCAP -এর CA = CP [একই বৃত্তের ব্যাসার্ধ]
∴ ∠CAP = ∠CPA
এবার ΔCAP -এর ∠CAP + ∠CPA + ∠ACP = 180°
বা, 2∠CAP + ∠ACP = 180°
বা, 2∠CAP = 180° – ∠ACP
∴ ∠CAP = 90° – \(\frac12\)∠ACP = 90° – ∠ABP [পূর্বে প্রমাণিত]
সুতরাং ∠CAP = 90° – ∠ABP —(i)
আবার, D কেন্দ্রীয় বৃত্তের একই AQ বৃত্তচাপের উপর অবস্থিত ∠ADQ কেন্দ্রস্থ কোণ এবং ∠ABQ পরিধিস্থ কোণ।
∴ ∠ABQ = \(\frac12\)∠ADQ, ADQ ত্রিভুজের DA = DQ [একই বৃত্তের ব্যাসার্ধ)
সেজন্য ∠DAQ = ∠DQA
∴ ∠DAQ + ∠DQA = 2∠DAQ
ADQ ত্রিভুজে, ∠ADQ + ∠DAQ + ∠DQA = 180°
বা, ∠AOQ + 2∠DAQ = 180°
বা, 2∠DAQ =180° – ∠ADQ
∴ ∠DAQ = 90° – \(\frac12\)∠ADQ = 90° – ∠ABQ [পূর্বে প্রমাণিত]
∠DAQ = 90° – ∠ABQ —(ii)
(i) এবং (ii)-এর দুদিক যোগ করলে
∠CAP + ∠DAQ = 90° – ∠ABP + 90° – ∠ABQ = 180° – (∠ABP + ∠ABQ) = 180° – ∠PBQ
বা, ∠PBQ = 180°(∠CAP + ∠DAQ) = ∠CAD [প্রথম অংশ প্রমাণিত হল]
আবার, ABC ত্রিভুজে CA = CB [একই বৃত্তের ব্যাসার্ধ]
∴ ∠CAB = ∠CBA এবং DAB ত্রিভুজে DA = DB [একই বৃত্তের ব্যাসার্ধ]
∴ ∠DAB = ∠DBA সেজন্য ∠CAB + ∠DAB = ∠CBA + ∠DBA
অর্থাৎ, ∠CAD = ∠CBD কিন্তু ∠CAD = ∠PBQ [পূর্বে প্রমাণিত]
∴ ∠CBD = ∠CAD = ∠PBQ
দুদিকে ∠PBD যোগ করলে ∠CBD + ∠PBD = ∠PAD + ∠PBQ
বা, ∠CBP = ∠DBQ যেহেতু BC = PC, [একই বৃত্তের ব্যাসার্ধ]
এবং BD = DQ [একই বৃত্তের ব্যাসার্ধ]
সেজন্য ∠BPC = ∠CBP এবং ∠DBQ = ∠BQD
∴ ∠BPC = ∠CBP = ∠DBQ = ∠BQD
সুতরাং প্রমাণিত হল যে, ∠BPC = ∠BQD [দ্বিতীয় অংশ প্রমাণিত]
7. ABC ত্রিভুজের পরিকেন্দ্র O; প্রমাণ করি যে, ∠OBC + ∠BAC = 90°

∠BOC = 2∠BAC
∴ ∠BAC = \(\frac12\)∠BOC
∴ ΔOBC -এর ∠OBC = ∠OCB
আবার ∠OBC + ∠OCB + ∠BOC = 180°
বা, 2∠OBC + ∠BOC = 180°
বা, 2∠OBC = 180° – ∠BOC
বা, ∠OBC = 90° – ∠BOC
সুতরাং ∠OBC + ∠BAC = 90° – \(\frac12\)∠BOC + \(\frac12\)∠BOC = 90° (প্রমাণিত)।
8. দুটি সমান বৃত্ত একটি অপরটির কেন্দ্রগামী। বৃত্ত দুটি পরস্পরকে A ও B বিন্দুতে ছেদ করে। A বিন্দুগামী একটি সরলরেখা বৃত্ত দুটিকে C ও D বিন্দুতে ছেদ করে। প্রমাণ করো যে, ABCD সমবাহু ত্রিভুজ।
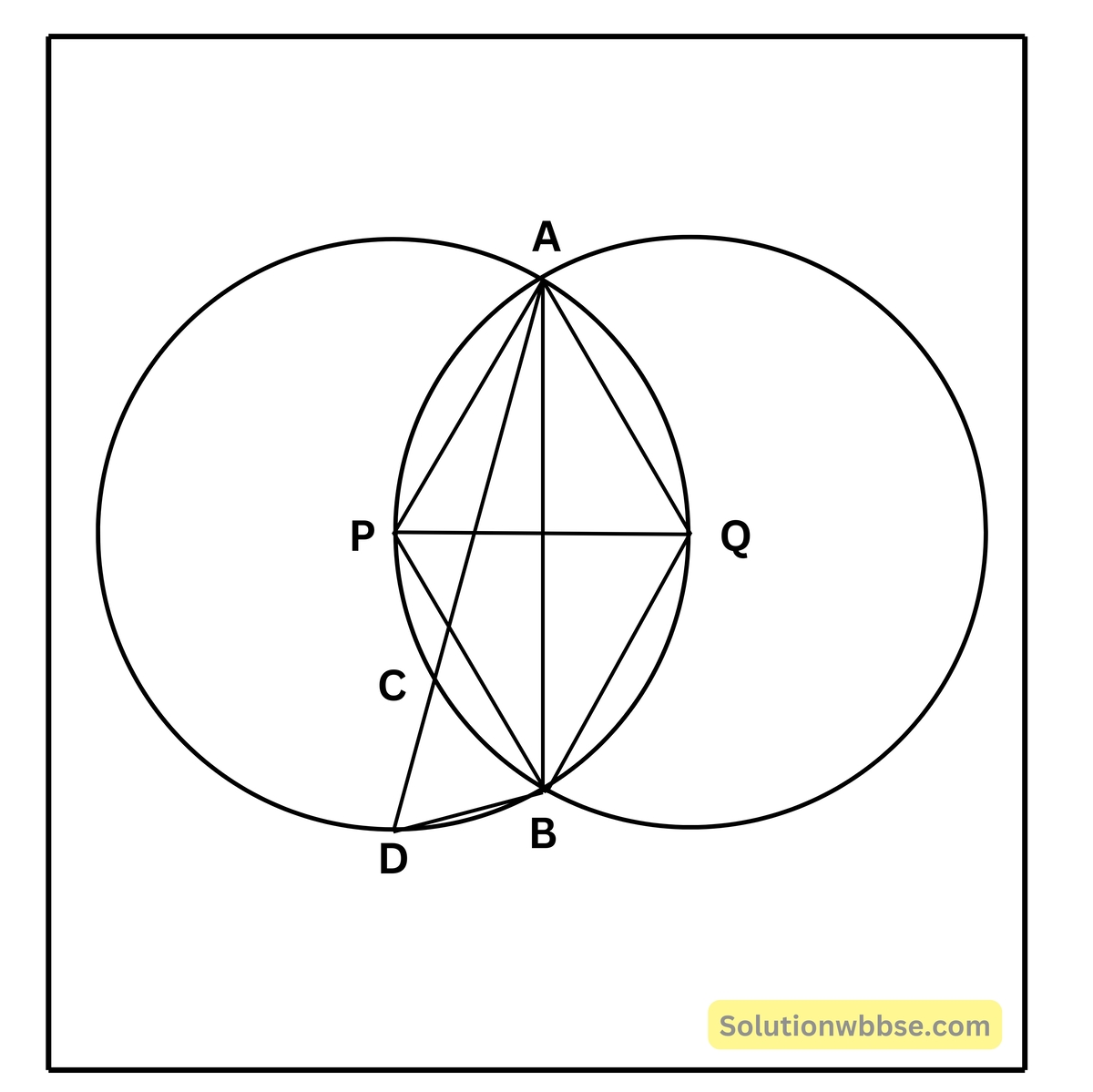
দেওয়া আছে, সমান ব্যাসার্ধের দুটি বৃত্তের কেন্দ্র P এবং Q; বৃত্ত দুটি পরস্পরের কেন্দ্রগামী এবং পরস্পরকে A ও B বিন্দুতে ছেদ করেছে।
A বিন্দুগামী CD সরলরেখা P কেন্দ্রীয় বৃত্তকে C এবং Q কেন্দ্রীয় বৃত্তকে D বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে যে, ΔBCD ত্রিভুজটি সমবাহু।
অঙ্কন – A, P; A, Q; B, P; B, Q; A, B এবং P, Q যুক্ত করা হল।
প্রমাণ – সমান সমান বৃত্তের ব্যাসার্ধ হওয়ার জন্য AP = BP = BQ = AQ = PQ
সেজন্য ΔAPQ, ΔBPQ সমবাহু।
∴ ∠PAQ = ∠APQ = ∠AQP = ∠PBQ = ∠BPQ = ∠PQB = 60°
কারণ, সমবাহু ত্রিভুজের তিনটি কোণ সমান এবং তাদের সমষ্টি 180°
এখন, ∠APB = ∠APQ + ∠BPQ = 60° + 60° = 120°
এবং ∠AQB = ∠AQP + ∠PQB = 60° + 60° = 120°
অর্থাৎ, ∠APB = ∠AQB = 120°
P কেন্দ্রীয় বৃত্তের AQB বৃত্তচাপের উপর অবস্থিত DAPB কেন্দ্রস্থ কোণ এবং ∠ADB পরিধিস্থ কোণ।
∴ ∠ADB = \(\frac12\)∠APB = \(\frac12\) ×120° = 60° অর্থাৎ, ∠CDB = 60°
আবার, ∠APB এবং ∠ACB কোণ দুটি Q কেন্দ্রীয় বৃত্তের একই APB বৃত্তাংশস্থ কোণ
∴ ∠ACB = ∠APB = 120°
∴ ∠BCD = 180° – ∠ACB =180° – 120° = 60°
তাহলে, ΔBCD -এর ∠CDB = ∠BCD = 60°
∴ পরিশিষ্ট ∠DBC = 180° (∠CDB + ∠BCD) = 180° – (60° + 60°) = 60°
প্রমাণিত হল যে, ΔBCD -এর তিনটি কোণ সমান।
∴ ΔBCD সমবাহু। (প্রমাণিত)।
9. ∆ABC -এর পরিবৃত্তের কেন্দ্র S; AD ⊥ BC হলে, প্রমাণ করি যে ∠BAD = ∠SAC।
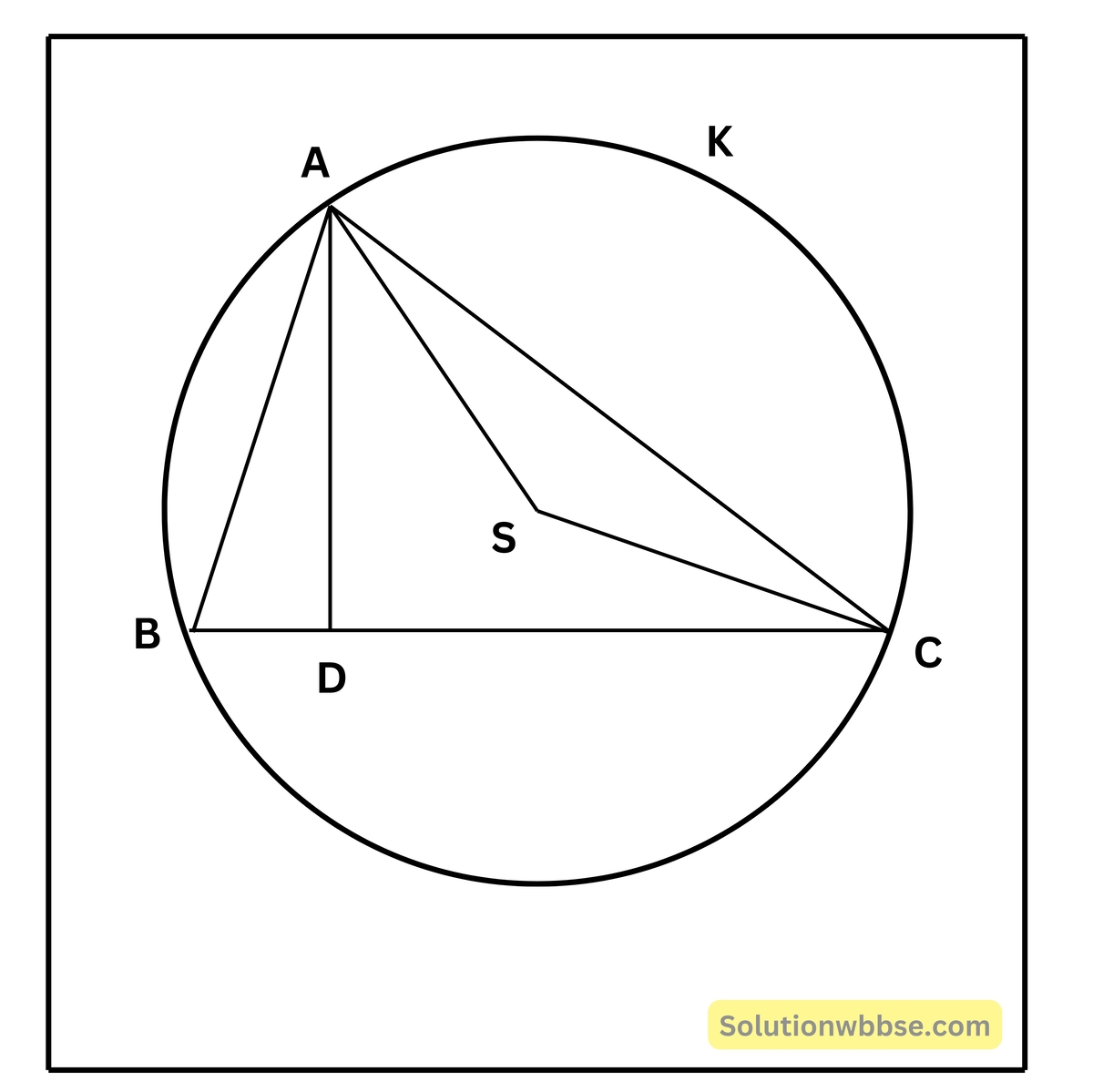
দেওয়া আছে, ∆ABC -এর পরিবৃত্তের কেন্দ্র S; AD সরলরেখা ∆ABC -এর BC বাহুর উপর লম্ব।
প্রমাণ করতে হবে, যে ∠BAD = ∠SAC
অঙ্কন – S, A এবং S, C যুক্ত করা হল।
প্রমাণ – SA = SC [একই বৃত্তের ব্যাসার্ধ]
অর্থাৎ ΔSAC -এর দুটি বাহু সমান সেজন্য ∠SAC = ∠SCA
আবার ΔSAC -এর ∠ASC + ∠SAC + ∠SCA = 180°
বা, ∠ASC + 2∠SAC = 180°, [∴ ∠SAC = ∠SCA]
অর্থাৎ, 2∠SAC = 180° – ∠ASC
বা, ∠SAC = 90° – \(\frac12\)∠ASC —(i)
আবার, S কেন্দ্রীয় বৃত্তের AKC বৃত্তচাপের উপর অবস্থিত ∠ASC কেন্দ্রস্থ কোণ এবং ∠ABC পরিধিস্থ কোণ।
∴ ∠ABC = \(\frac12\)∠ASC —(ii)
∴ ∠SAC = 90° – ∠ABC —(iii) [(i) -এর সাহায্যে]
আবার ΔABD -এর ∠ADB = ∠ADC = 90°
∴ ∠ADB + ∠BAD = 90°
বা, ∠BAD = 90° – ∠ADB = 90° – ∠ABC —(ii)
(iii) এবং (iv) থেকে ∠SAC = ∠BAD (প্রমাণিত)।
10. O কেন্দ্রীয় একটি বৃত্তের দুটি জ্যা AB ও CD পরস্পরকে P বিন্দুতে ছেদ করে। প্রমাণ করি যে, ∠AOD + ∠BOC = 2∠BPC।
যদি ∠AOD ও ∠BOC পরস্পর সম্পূরক হয়, তাহলে প্রমাণ করি যে জ্যা দুটি পরস্পর লম্ব।
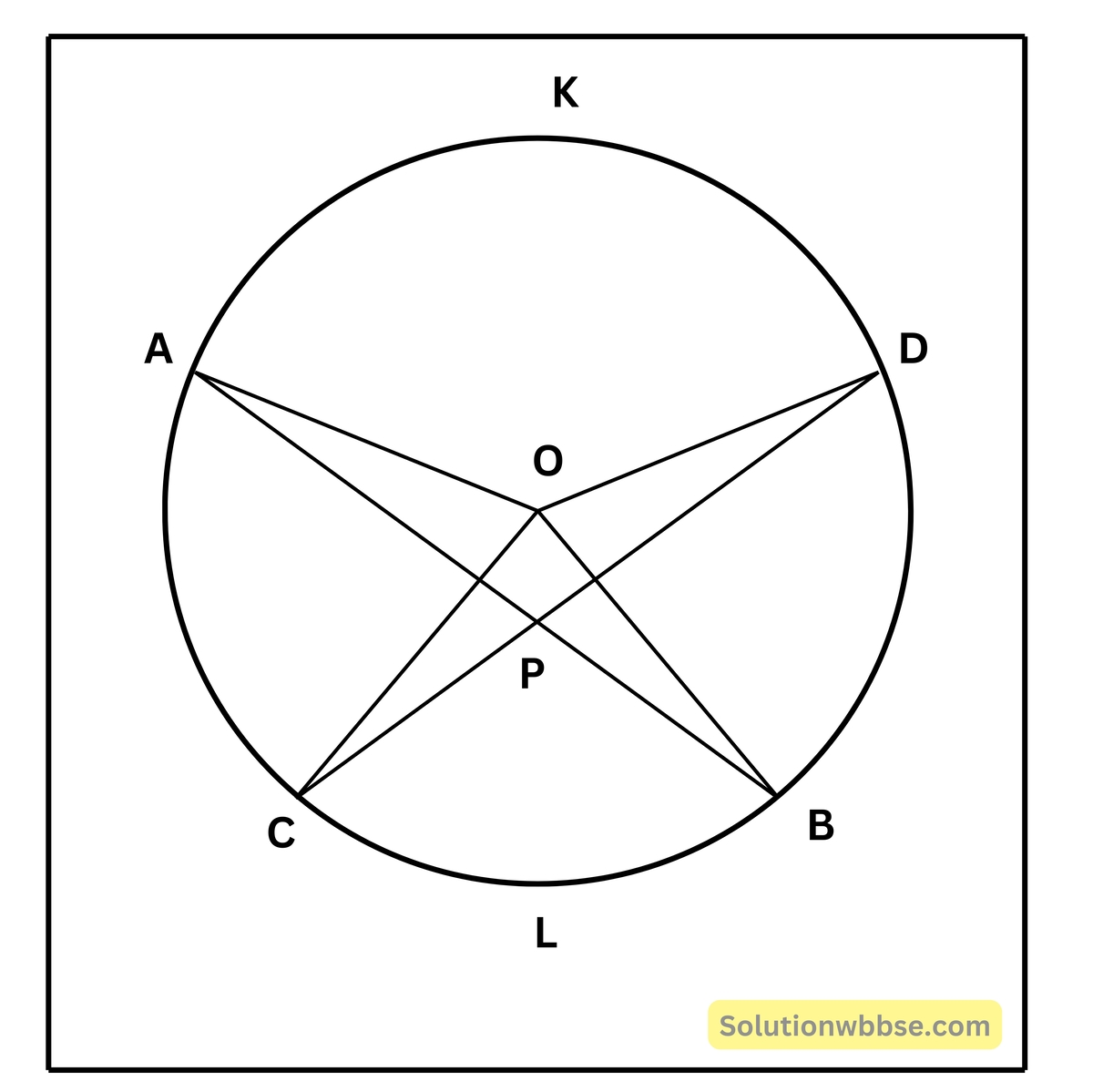
দেওয়া আছে, O কেন্দ্রীয় বৃত্তের দুটি জ্যা AB এবং CD পরস্পর P বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে – ∠AOD + ∠BOC = 2∠BPC
আরও প্রমাণ করতে হবে যে, যদি ∠AOD এবং ∠BOC পরস্পর সম্পূরক হয়, তাহলে AB এবং CD পরস্পর লম্ব।
অঙ্কন – O, A; O, B; O, C; O, D এবং B, D যুক্ত করা হল।
প্রমাণ – O কেন্দ্রীয় বৃত্তের AKD বৃত্তচাপের উপর কেন্দ্রস্থ কোণ ∠AOB এবং ∠ABD পরিধিস্থ কোণ।
∴ ∠ABD = \(\frac12\)∠AOD
বা, ∠AOD = 2∠ABO
আবার, O কেন্দ্রীয় বৃত্তের BLC বৃত্তচাপের উপর অবস্থিত ∠BOC কেন্দ্রস্থ কোণ ∠BDC পরিধিস্থ কোণ।
∴ ∠BOC = 2 × ∠BDC
সুতরাং ∠AOD + ∠BOC = 2(∠ABD + ∠BDC) = 2(∠PBD + ∠BDP) —(i)
আবার, ΔPBD -এর বহিঃকোণ ∠BPC = অন্তস্থ বিপরীত ∠PBD + ∠BDP
∴ (i) থেকে ∠AOD + ∠BOC = 2∠BPC [প্রথম অংশ প্রমাণিত।
এবার যদি, ∠AOD + ∠BOC = 2 সমকোণ হয়,
তাহলে, 2∠BPC = ∠AOD + ∠BOC = 2 সমকোণ বা, ∠BPC = 90°
∴ BP ⊥ PC অর্থাৎ, AB ও CD জ্যাদ্বয় পরস্পর লম্ব। [দ্বিতীয় অংশ প্রমাণিত]
11. O কেন্দ্রীয় একটি বৃত্তের AB ও CD দুটি জ্যা-কে বর্ধিত করলে তারা পরস্পরকে P বিন্দুতে ছেদ করলে। প্রমাণ করি যে, ∠AOC – ∠BOD = 2∠BPC
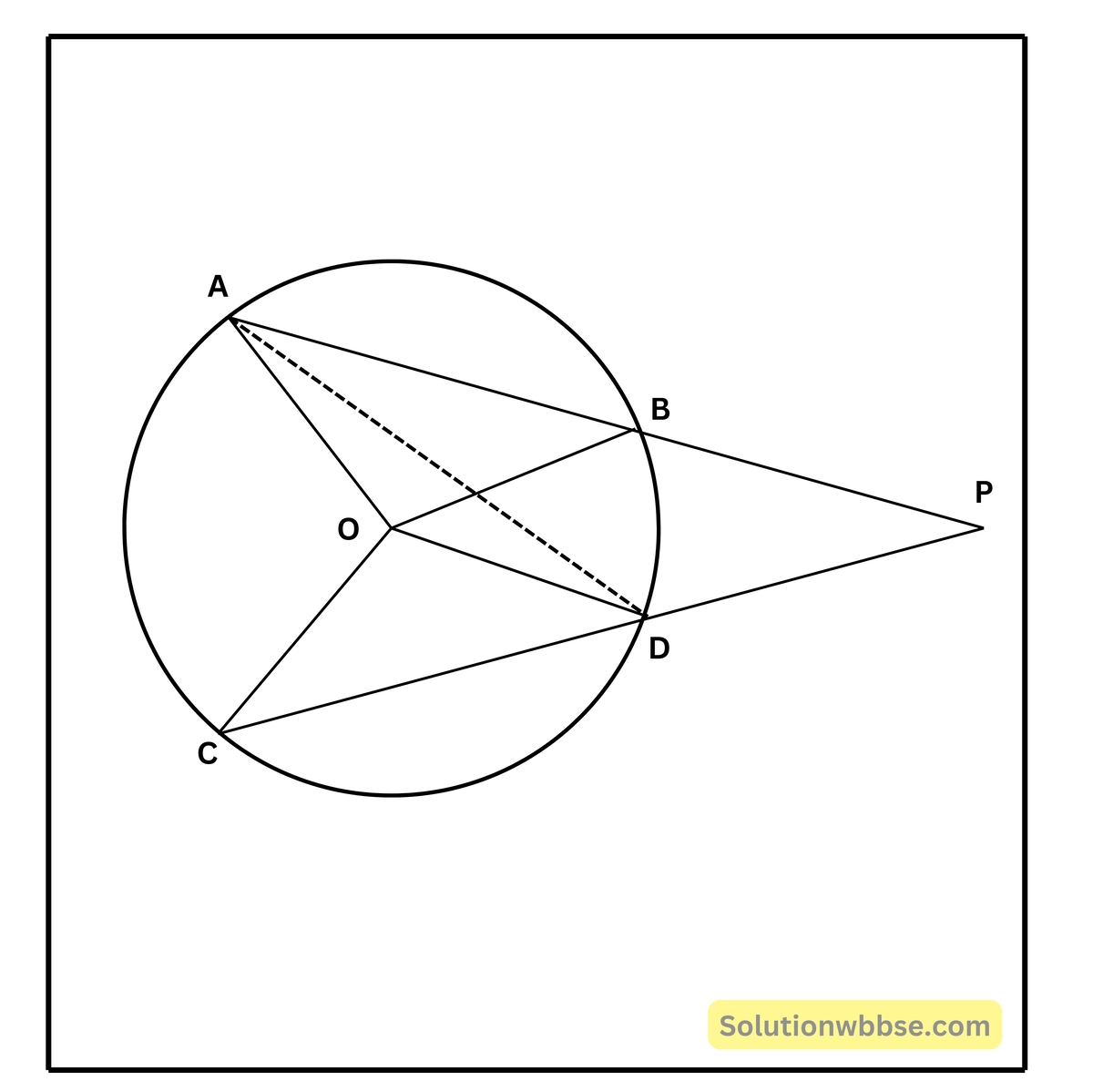
O কেন্দ্রীয় একটি বৃত্তের AB ও CD দুটি জ্যা কে বর্ধিত করলে তারা পরস্পরকে P বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে, ∠AOC – ∠BOD = 2∠BPC
অঙ্কন – A, D যুক্ত করা হল।
প্রমান – AC বৃত্তচাপের ওপর ∠AOC কেন্দ্রস্থ কোণ এবং ∠ADC পরিধিস্থ কোণ
∴ ∠AOC = 2∠ADC —(i)
আবার, BD বৃত্তচাপের ওপর ∠BOD কেন্দ্রস্থ কোণ এবং ∠BAD পরিধিস্থ কোণ
∴ ∠BOD = 2∠BAD —(ii)
আবার ত্রিভুজ ΔAPD এর ক্ষেত্রে,
∠ADC = ∠APD + ∠PAD [∵ ত্রিভুজের বহিঃস্থ কোণ, অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান।
∴ ∠ADC – ∠PAD = ∠APD —(iii)
(i) থেকে (ii) বিয়োগ করে পাই,
∠AOC – ∠BOD
= 2(∠ADC – ∠BAD)
= 2(∠ADC – ∠PAD) [∵ ∠BAD = ∠PAD]
= 2∠APD
= 2∠BPC [∵ ∠APD = ∠BPC]
∴ ∠AOC – ∠BOD = 2∠BPC [প্রমাণিত]
12. ABCD চতুর্ভুজের A বিন্দুকে কেন্দ্র করে একটি বৃত্ত অঙ্কন করা হলো যেটি B, C ও D বিন্দু দিয়ে যায়, প্রমাণ করি যে ∠CBD + ∠CDB = \(\frac12\)∠BAD
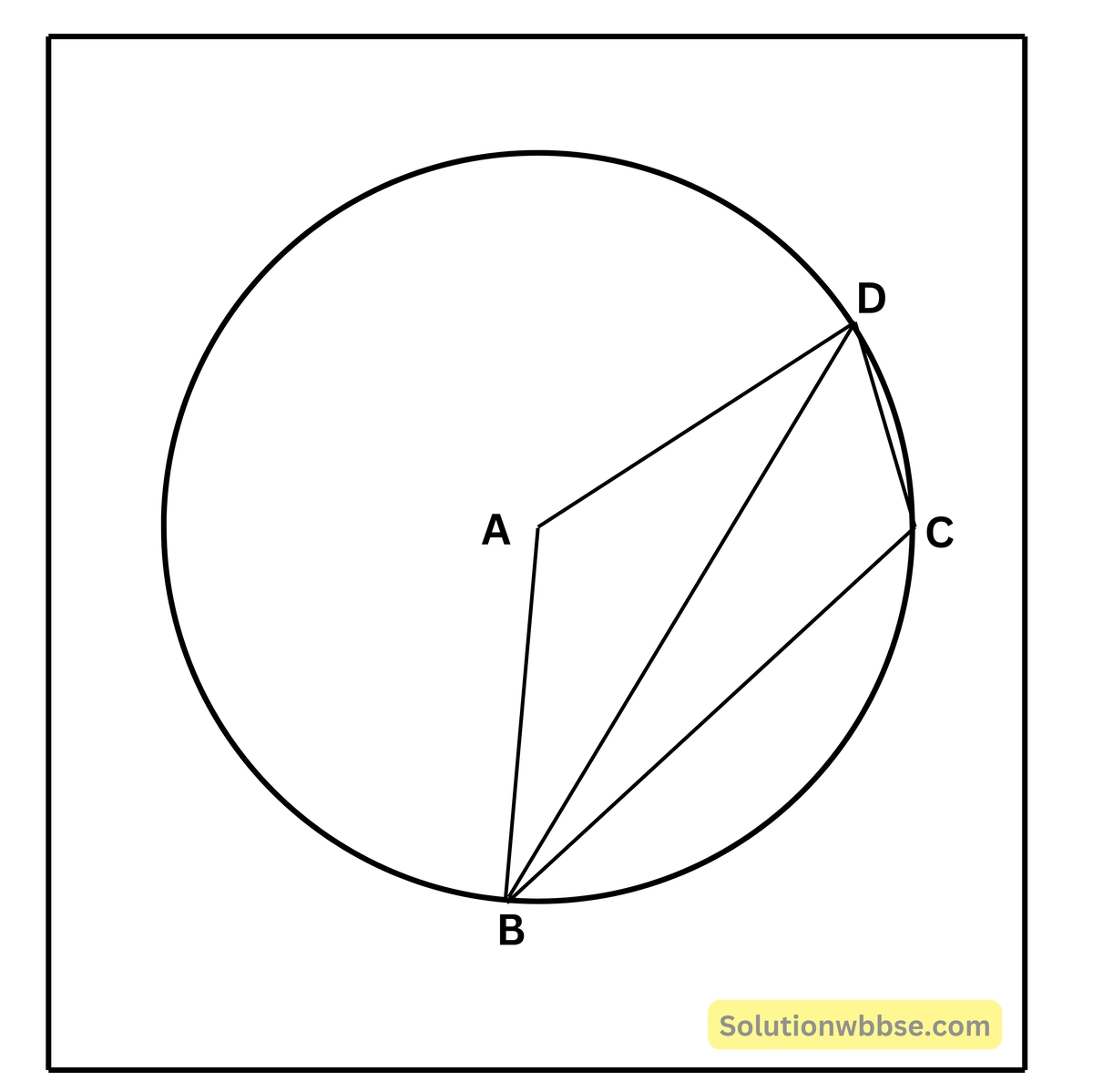
মনে করি, ABCD চতুর্ভুজের A বিন্দুকে কেন্দ্র করে বৃত্ত অঙ্কন করলে তা B, C, D বিন্দু দিয়ে যায়।
প্রমাণ করতে হবে যে – ∠CBD + ∠CDB = \(\frac12\)∠BAD
প্রমাণ – 2∠BCD = 360° – ∠BAD
∠BCD = 180° – \(\frac12\)∠BAD —(i)
আবার, ΔBCD থেকে পাই ∠BDC + ∠CBD = 180° – ∠BCD
বা, ∠CBD + ∠CDB = 180° – (180° – \(\frac12\)∠BAD) = \(\frac12\)∠BAD [(i) এ থেকে] প্রমাণিত।
13. ΔABC এর পরিকেন্দ্র O এবং OD, BC বাহুর উপর লম্ব। প্রমাণ করি যে ∠BOD = ∠BAC
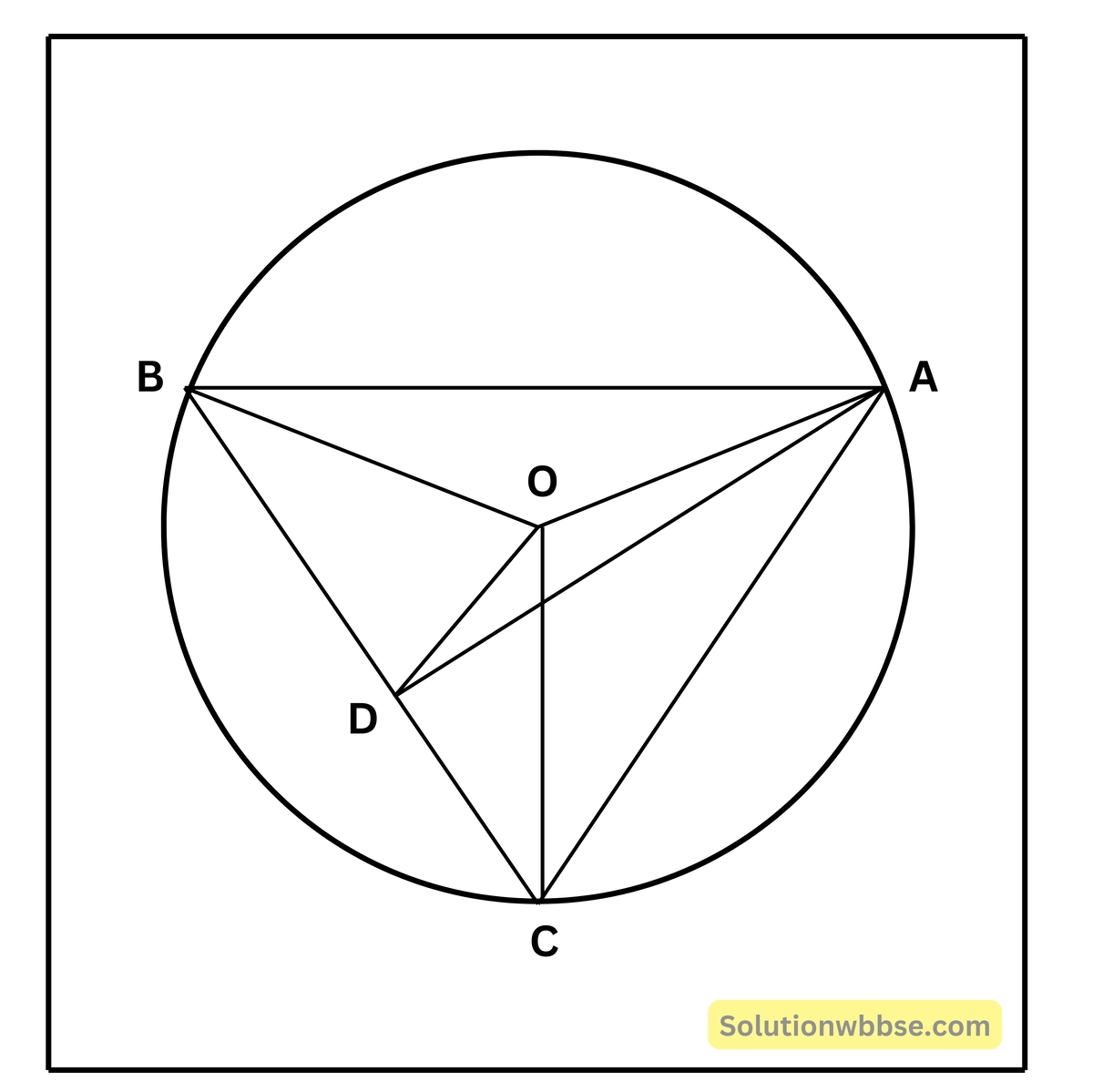
ΔABC -এর পরিকেন্দ্র O এবং OD ⊥ BC
প্রমাণ করতে হবে যে, ∠BOD = ∠BAC
অঙ্কন – O, A ও O, এবং A, D যোগ করা হল।
প্রমাণ – ΔAOC থেকে পাই ∠AOC + ∠OAC + ∠OCA = 180°
∴ 2∠OAC – 180° – ∠AOC [∵ OA = OC]
∴ ∠OAC = 90° – \(\frac12\)∠AOC = 90° – ∠ABC
∴ ∠BAD = 90° – ∠ABC = ∠OAC
∴ ∠BAC = ∠OAC + ∠OAB = ∠BOD (প্রমাণিত।)
14. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহু বিকল্পীয় প্রশ্ন (M.C.Q.) –
(i) পাশের চিত্রে বৃত্তের কেন্দ্র এবং PQ ব্যাস হলে, x -এর মান
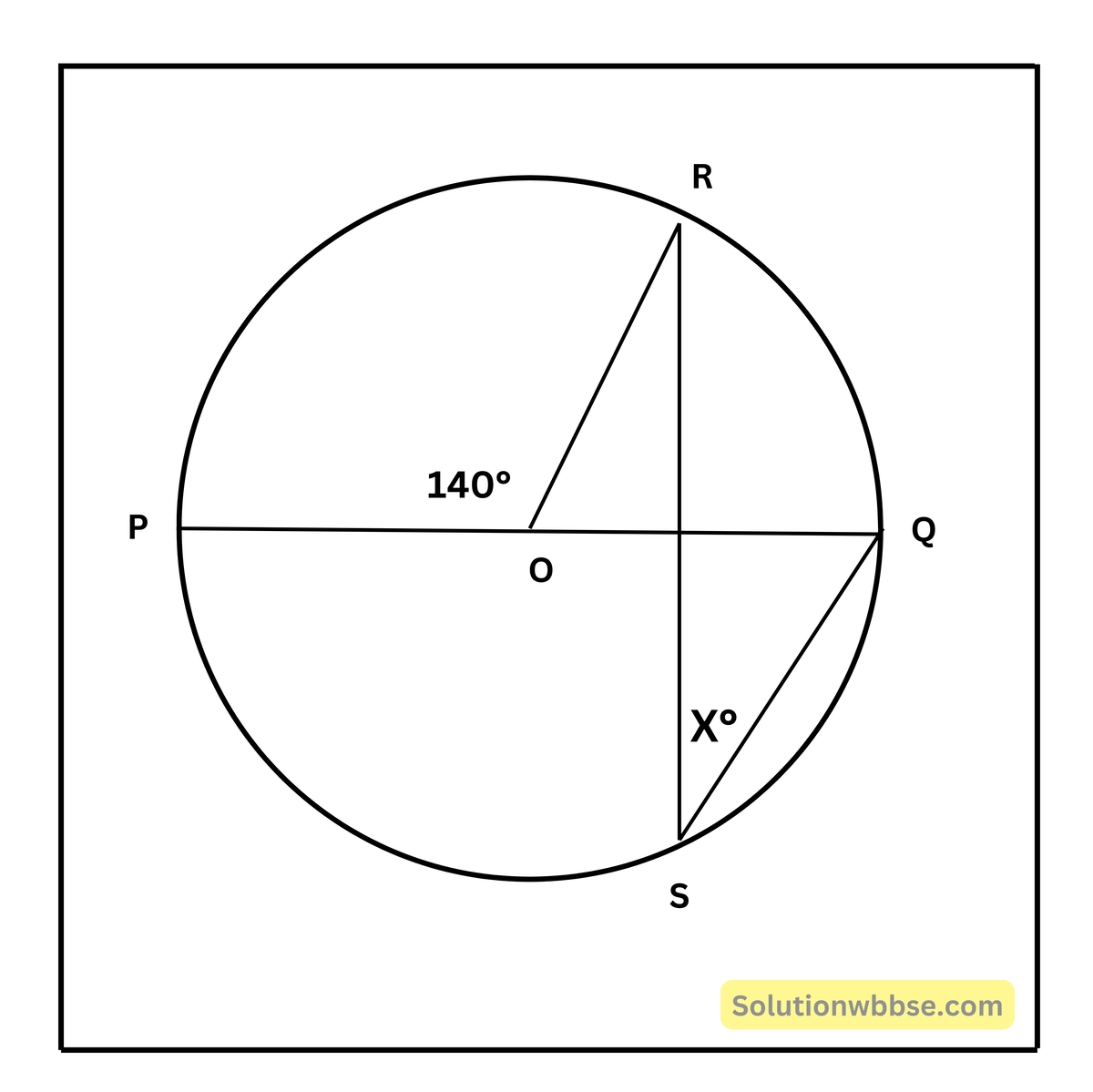
(a) 140
(b) 40
(c) 80
(d) 20
উত্তর – (d) 20
সমাধান
∠ROQ = 180° – 140° = 40°
∴ x = ∠ RSQ = \(\frac12\) × 40 = 20
(d) উত্তরটি সঠিক।
(ii) পাশের চিত্রে O বৃত্তের কেন্দ্র হলে, x -এর মান
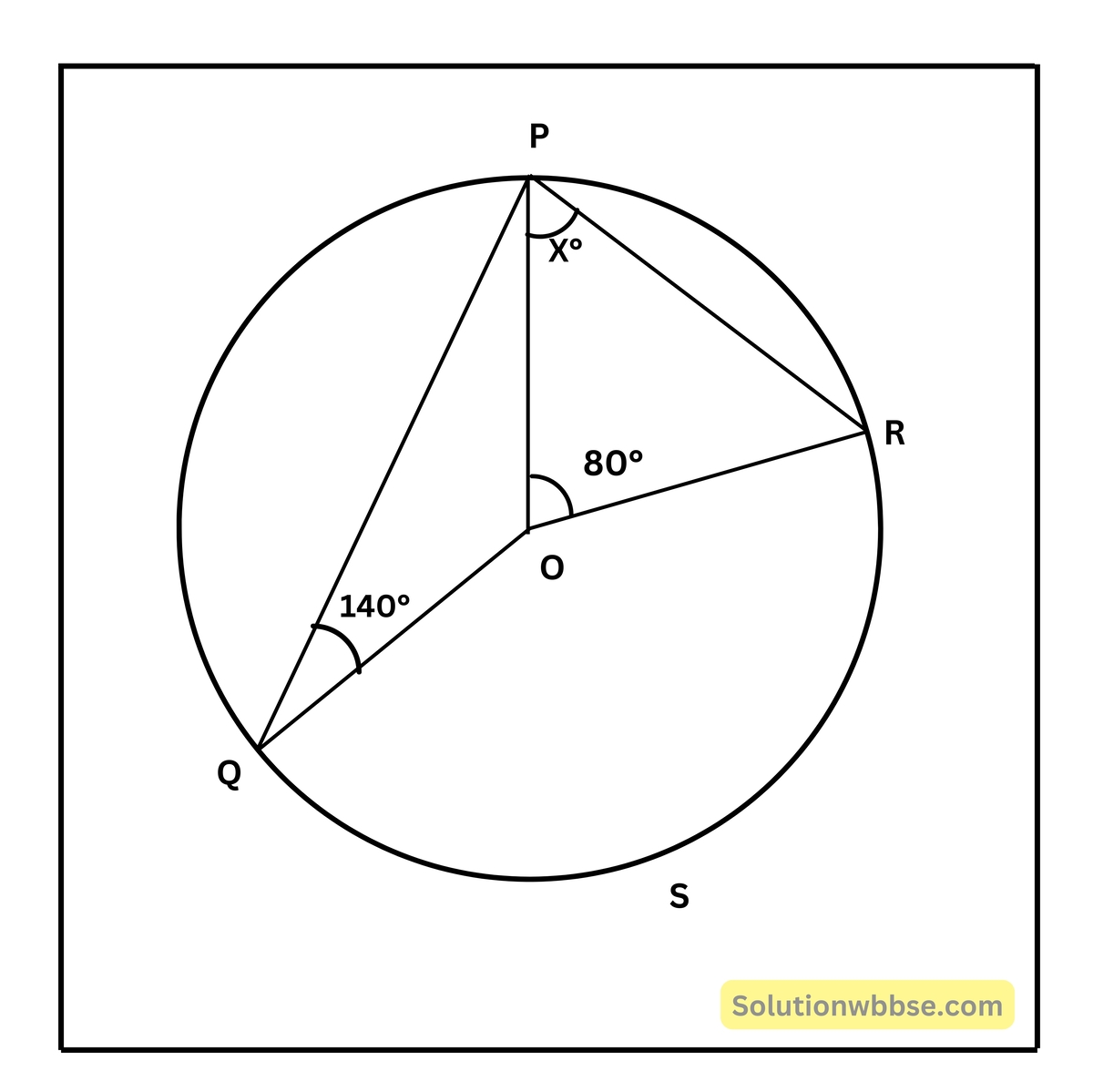
(a) 70
(b) 60
(c) 40
(d) 200
উত্তর – (a) 70
সমাধান
∠BOR = 360° – (140° + 80°) = 360° – 220° = 140°
∴ ∠QPR = \(\frac12\)∠QOR = \(\frac12\) × 140° = 70°
∴ (a) উত্তরটি সঠিক।
(iii) পাশের চিত্রে বৃত্তের কেন্দ্র এবং BC ব্যাস হলে, x -এর মান
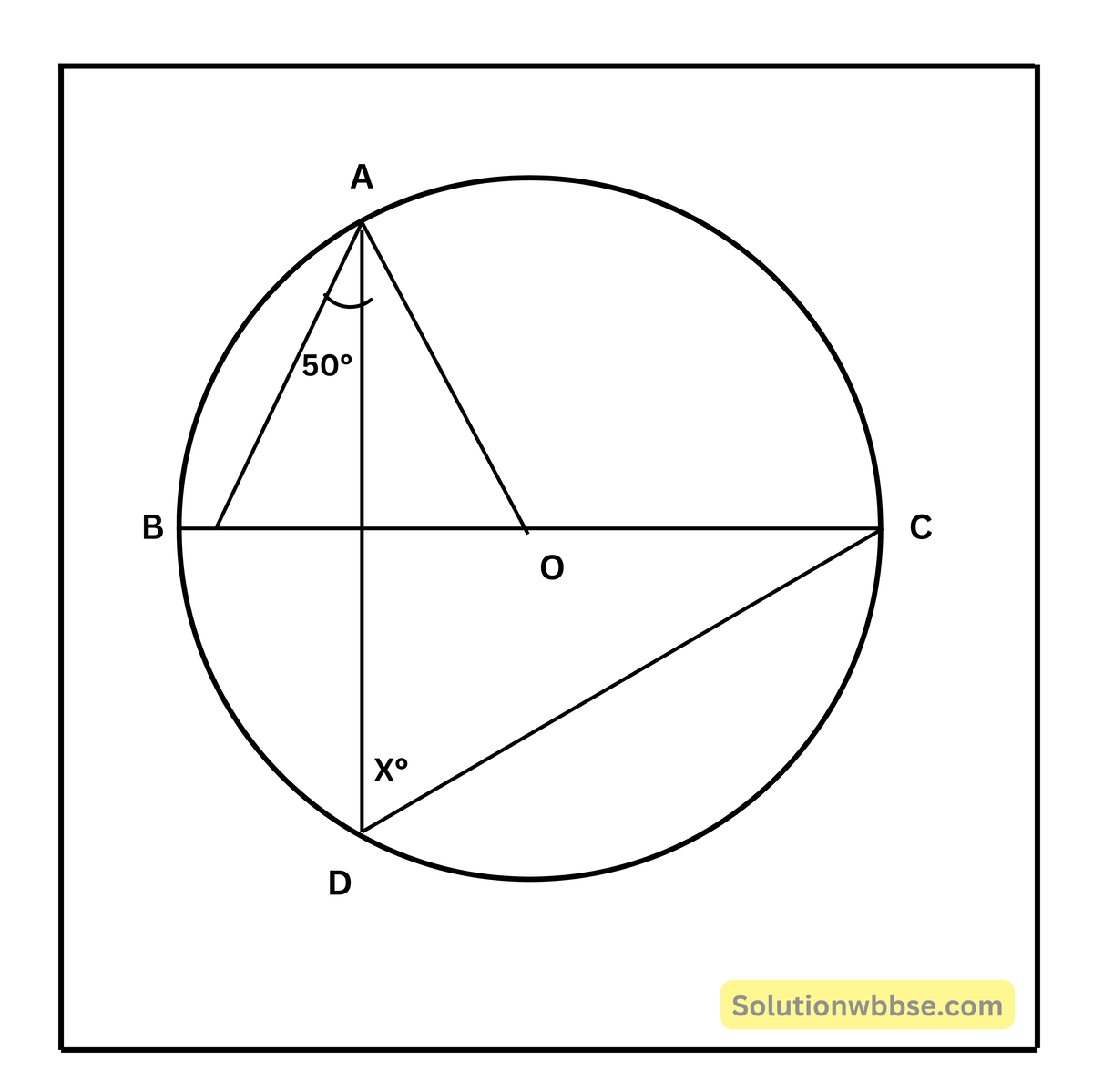
(a) 60
(b) 50
(c) 100
(d) 80
উত্তর – (b) 50
সমাধান
∠AOC = 180° – 80° = 100°
∴ ∠ADC = x° = \(\frac{100^\circ}2\) = 50°
∴ (b) উত্তরটি সঠিক।
(iv) ABC ত্রিভুজের O পরিকেন্দ্র। ∠OAB = 50° হলে, ∠ACB -এর মান
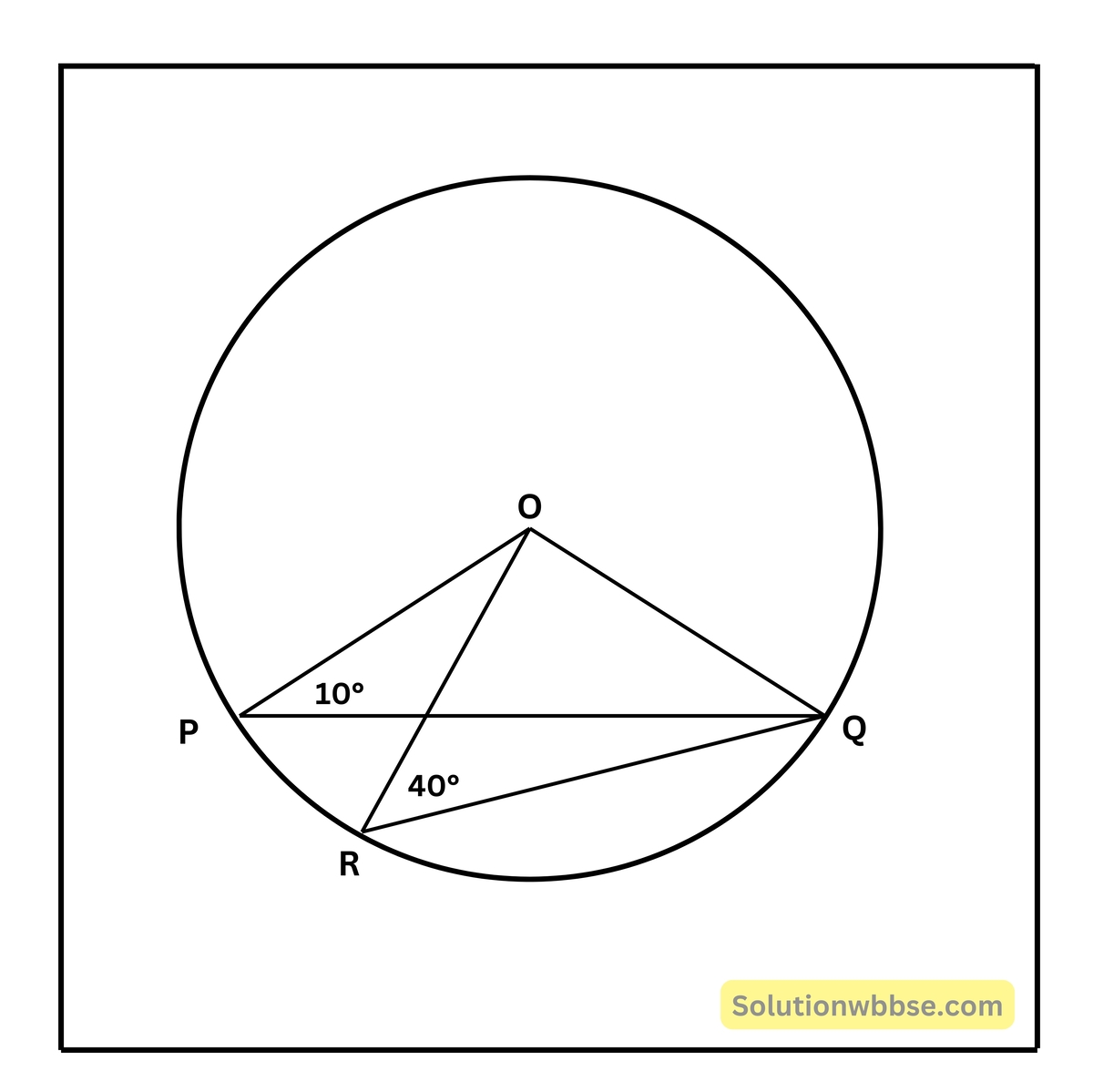
(a) 50°
(b) 100°
(c) 40°
(d) 80°
উত্তর – (c) 40°
সমাধান
∠AOB = 180° – (50° + 50°) = 180° – 100° = 80°
∴ ∠ACB = \(\frac12\) × 80° = 40°
∴ (c) উত্তরটি সঠিক।
(v) পাশের চিত্রে বৃত্তের কেন্দ্র হলে, ∠POR-এর মান
(a) 20º
(b) 40°
(c) 60°
(d) 80°
উত্তর – (c) 60°
সমাধান
∠POQ = 180° – 20 = 160°
∠QOR = 180° – 80° = 100°
∠POR = 160° – 100° = 60°
∴ (c) উত্তরটি সঠিক।
(B) সত্য বা মিথ্যা লিখি –
(i) পাশের চিত্রে O বৃত্তের কেন্দ্র হলে, ∠AOB = 2∠ACD
উত্তর – মিথ্যা।
(ii) ABC ত্রিভুজাকার ক্ষেত্রের ভিতর O বিন্দু এমনভাবে অবস্থিত যে OA = OB এবং ∠AOB = 2∠ACB. O বিন্দুকে কেন্দ্র করে OA দৈর্ঘ্যের ব্যাসার্ধ নিয়ে বৃত্ত অঙ্কন করলে C বিন্দু বৃত্তের উপর অবস্থিত হবে।
উত্তর – সত্য।
(C) শূন্যস্থান পূরণ করি –
(i) একই চাপের দ্বারা গঠিত সম্মুখ বৃত্তস্থ কোণ কেন্দ্রস্থ কোণের ___।
উত্তর – একই চাপের দ্বারা গঠিত সম্মুখ বৃত্তস্থ কোণ কেন্দ্রস্থ কোণের সমান।
(ii) O কেন্দ্রীয় বৃত্তে AB ও AC জ্যা দুটির দৈর্ঘ্য সমান। ∠APB ও ∠DQC বৃত্তস্থ কোণ হলে, কোণ দুটির মান ___।
উত্তর – O কেন্দ্রীয় বৃত্তে AB ও AC জ্যা দুটির দৈর্ঘ্য সমান। ∠APB ও ∠DQC বৃত্তস্থ কোণ হলে, কোণ দুটির মান সমান।
(iii) একটি সমবাহু ত্রিভুজের পরিবৃত্তের কেন্দ্র O হলে, যে-কোনো একটি বাহু দ্বারা উৎপন্ন সম্মুখ কেন্দ্রস্থ কোণের মান ___।
উত্তর – একটি সমবাহু ত্রিভুজের পরিবৃত্তের কেন্দ্র O হলে, যে-কোনো একটি বাহু দ্বারা উৎপন্ন সম্মুখ কেন্দ্রস্থ কোণের মান 120°।
15. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
(i) পাশের চিত্রে O বৃত্তের কেন্দ্র। ∠OAB = 40°, ∠ABC = 120°, ∠BCO = y° এবং ∠COA = x° হলে, x ও y -এর মান নির্ণয় করি।
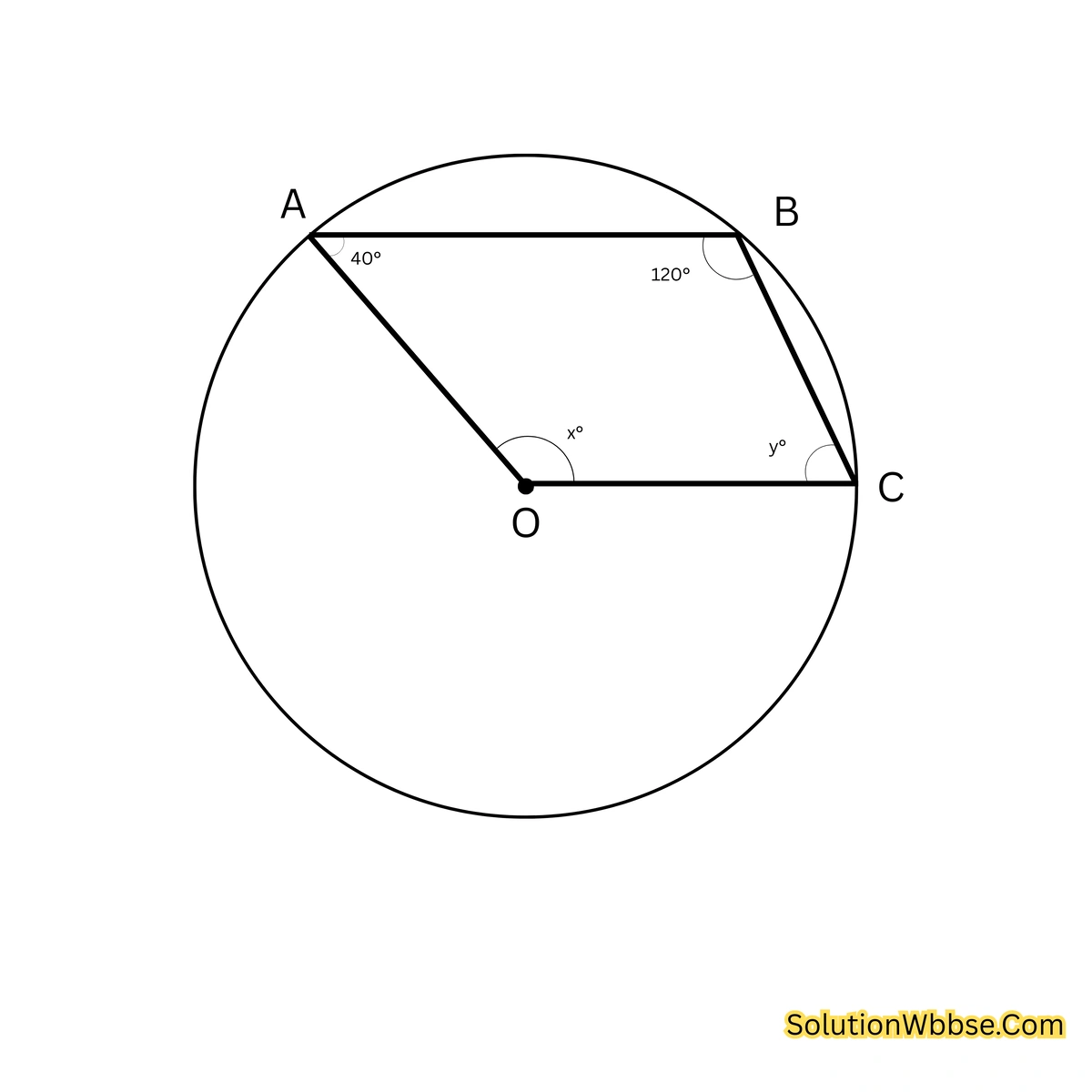
সমাধান –
AC বৃত্তচাপের ওপর কেন্দ্রস্থ কোণ ,প্রবিদ্ধ ∠AOC এবং পরিধিস্থ কোণ ∠ABC।
∴ ∠ABC = ½ প্রবিদ্ধ ∠AOC [∵একই বৃত্তচাপের ওপর অবস্থিত পরিধিস্থ কোণ কেন্দ্রস্থ কোণের অর্ধেক ]
∴ 120° = ½(360°-x)
বা, 240° = 360°-x
বা, x = 360°-240°
বা, x = 120°
∴ y = 360° – (40°+120°+120°)
= 360°-280°
= 80° [∵ চতুর্ভুজের চারটি কোণের সমষ্টি 360°]
∴x = 120°, y = 80° [উত্তর]
(ii) ABC ত্রিভুজের পরিকেন্দ্র O এবং D বিন্দু BC বাহুর মধ্যবিন্দু। ∠BAC = 40° হলে, ∠BOD -এর মান নির্ণয় করি।
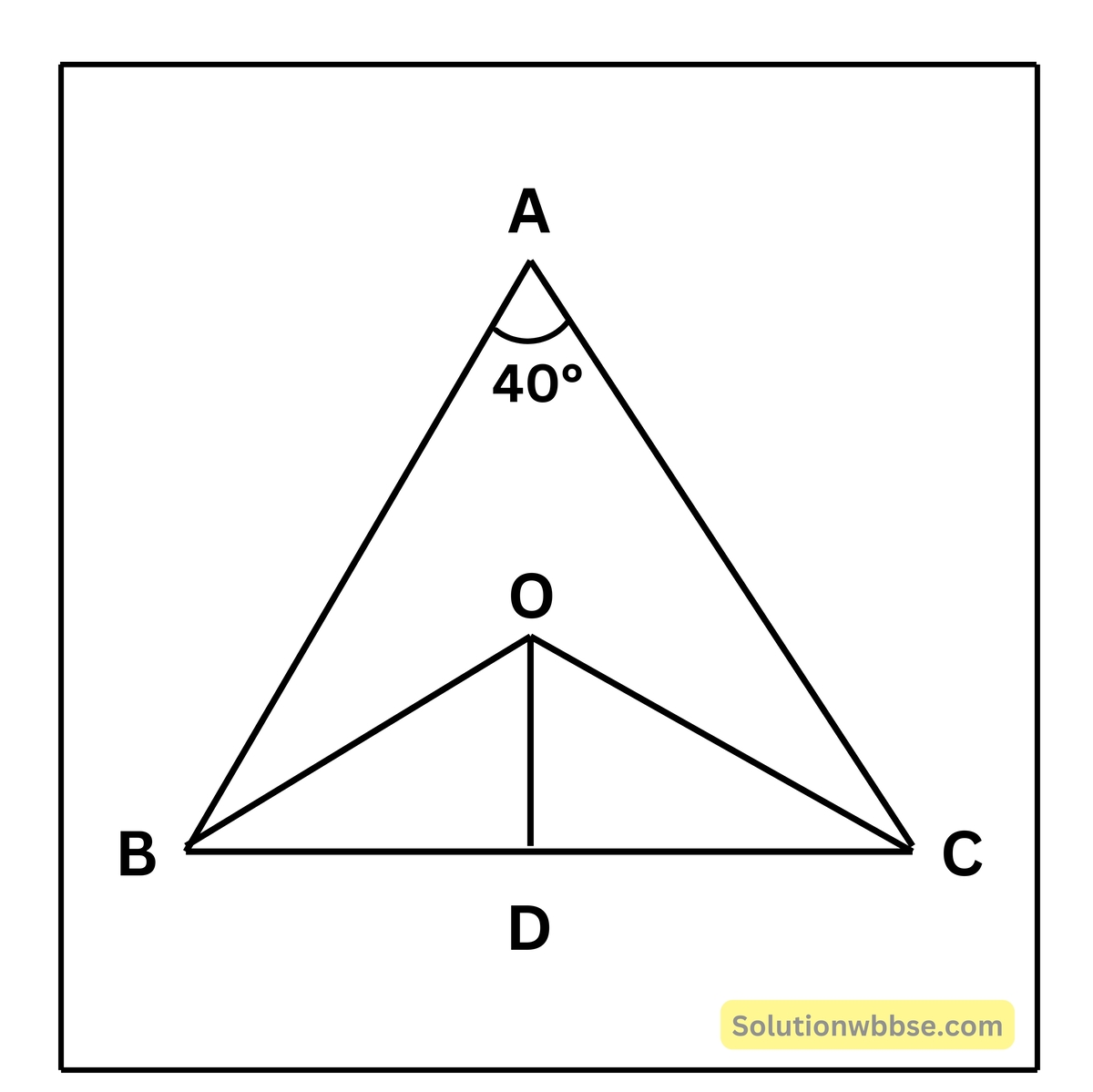
অঙ্কন – OC অঙ্কন করা হল।
প্রমান – OBAC বৃত্তচাপের ওপর ∠BAC পরিধিস্থ কোণ এবং ∠BOC কেন্দ্রস্থ কোণ।
∠BOC = 2∠BAC = 2 ✕40° = 80°
∆BOD ও ∆ COD এর ক্ষেত্রে,
BD = DC [∵ D,BC এর মধ্যবিন্দু ]
OB = OC [ একই বৃত্তের ব্যাসার্ধ ]
OD সাধারণ বাহু
∴ BOD ≅ COD [বাহু-বাহু-বাহু শর্তানুসারে ]
∴ ∠BOD = ∠COD
আবার ∠BOC = 80°
∴ ∠BOD = ∠COD =40°
(iii) O কেন্দ্রীয় বৃত্তের উপর A, B, C তিনটি বিন্দু এমনভাবে অবস্থিত যে AOCB একটি সামান্তরিক। ∠AOC -এর মান নির্ণয় করি।
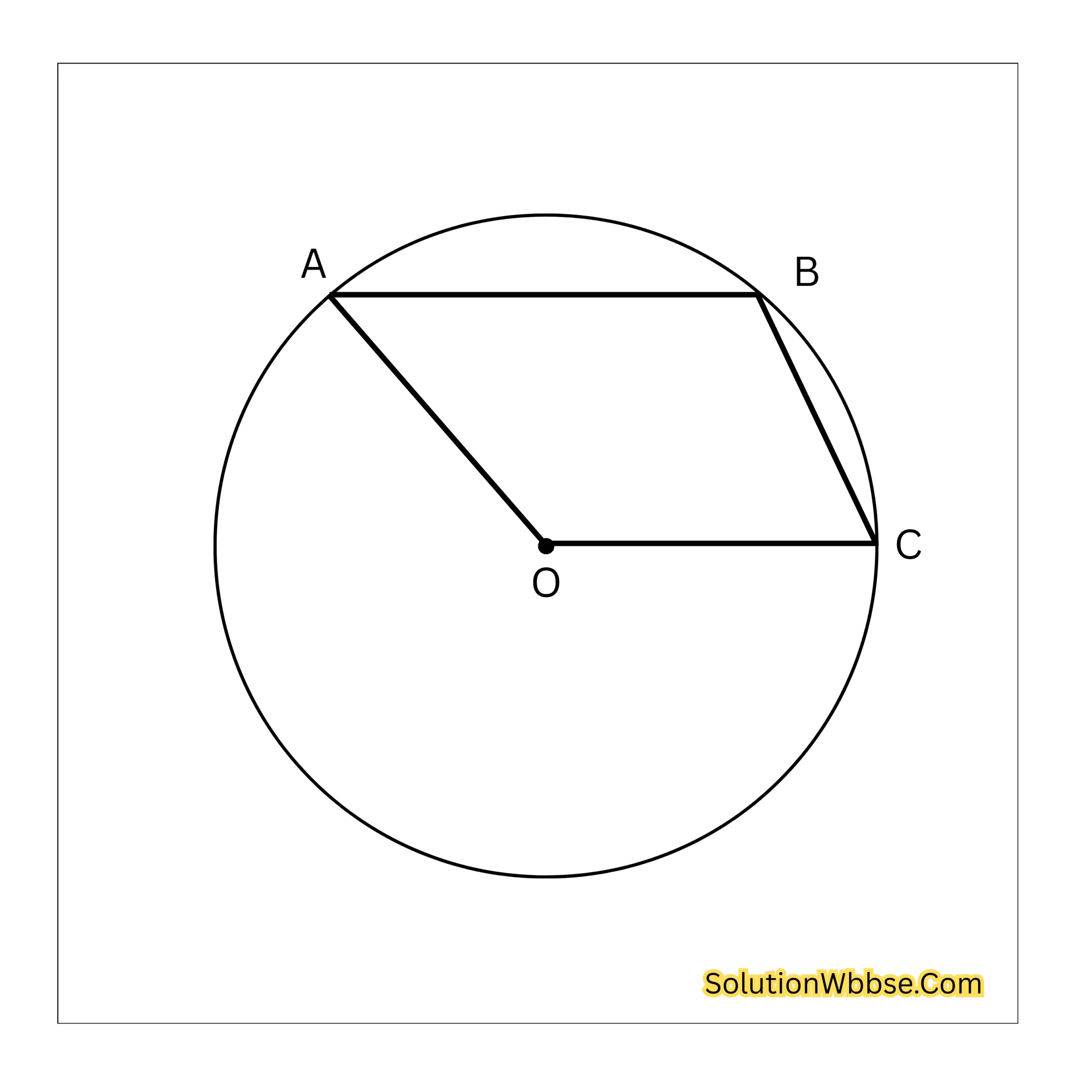
AOCB একটি সমান্তরিক।
∴∠AOC = ∠ABC [∵ সামান্তরিকের বিপরীত কোণগুলি পরস্পর সমান]—(i)
আবার , ∠ABC = ½ প্রবিদ্ধ ∠AOC [∵একই বৃত্তচাপের ওপর কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন =]—(ii)
(i) ও (ii) থেকে পাই ,
∴∠AOC = ½ প্রবিদ্ধ ∠AOC —(iii)
আবার, ∠AOC + প্রবিদ্ধ ∠AOC = 360°
বা, ½ প্রবিদ্ধ ∠AOC + প্রবিদ্ধ ∠AOC = 360° [(iii) থেকে পাই]
বা, 3/2 × (প্রবৃদ্ধ ∠AOC) = 360°
বা, 360° – ∠AOC = 360° × 2/3
বা, ∠AOC = 360°– 240°
বা, ∠AOC = 120°
(iv) ABC সমদ্বিবাহু ত্রিভুজের পরিবৃত্তের কেন্দ্র O এবং ∠ABC = 120°; বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি. হলে, AB বাহুর দৈর্ঘ্য নির্ণয় করি।
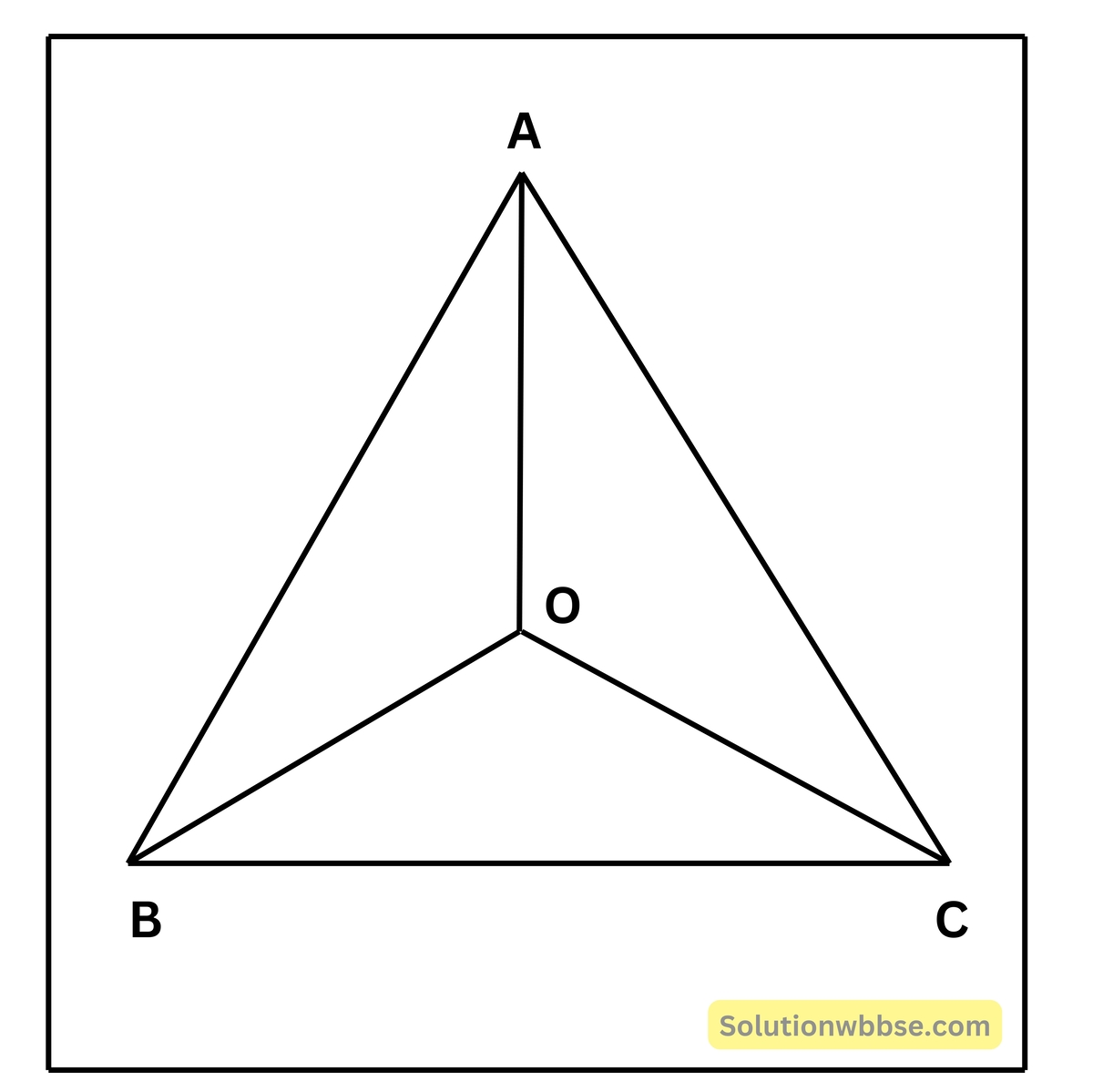
O,A ; O,B ; O,C যুক্ত করা হল।
∆OAB এবং ∆OCB এর মধ্যে,
OA=OC [একই বৃত্তের ব্যাসার্ধ]
OB সাধারণ বাহু
AB = BC [∆ABC সমদ্বিবাহু ত্রিভুজ]
∴∆OAB ≅ ∆OCB [বাহু-বাহু-বাহু শর্তানুসারে]
∴ ∠OBA = ∠OBC = 60° [∵∠ABC =120°]
আবার, ∠OAB = ∠OBA = 60° [∵OA=OB একই বৃত্তের ব্যাসার্ধ]
∴ ∠AOB = 60° [∵ ত্রিভুজের তিনটি কোণের সমষ্টি 180° ]
∴ ত্রিভুজ AOB -এর ∠OAB = ∠OBA = ∠AOB = 60°
∴ AOB সমবাহু ত্রিভুজ।
∴ OA = OB = AB = 5 সেমি.
∴ AB = 5 সেমি. [উত্তর]
(v) A ও B কেন্দ্রীয় বৃত্তদ্বয় C এবং D বিন্দুতে ছেদ করে। A কেন্দ্রীয় বৃত্তের উপর অপর বৃত্তের কেন্দ্র B অবস্থিত। ∠CQD = 70° হলে, ∠CPD -এর মান নির্ণয় করি।
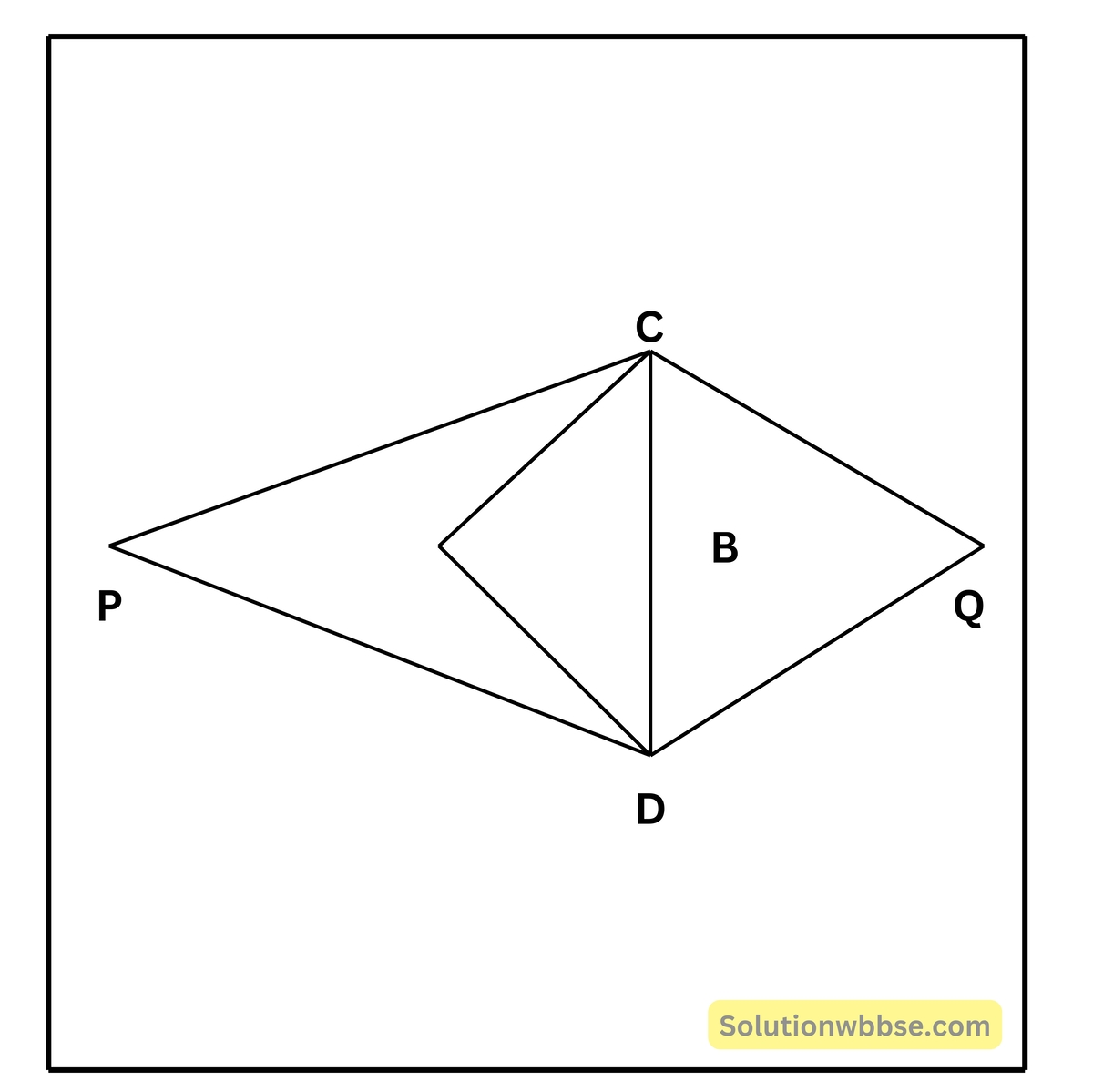
B,C ; B,D যুক্ত করা হল।
CD বৃত্তচাপের ওপর ∠CBD কেন্দ্রস্থ কোণ এবং ∠CQD পরিধিস্থ কোণ
∴ ∠CBD = 2✕∠CQD = 2✕70° = 140°
আবার, ∠CBD+∠CPD = 180° [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ]
বা, ∠CPD = 180°–∠CBD
বা, ∠CPD = 180°-140°
বা, ∠CPD = 40° [উত্তর]
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের সপ্তম অধ্যায়, ‘বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য’ -এর ‘কষে দেখি – 7.1’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment