মাধ্যমিক গণিত – বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য – কষে দেখি – 7.3

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের সপ্তম অধ্যায়, ‘বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য’ -এর ‘কষে দেখি – 7.3’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

1. ABC ত্রিভুজের B কোণটি সমকোণ। যদি AC কে ব্যাস করে একটি বৃত্ত অঙ্কন করি যা AB -কে D বিন্দুতে ছেদ করে, তবে নীচের তথ্যগুলির মধ্যে কোনটি ঠিক লিখি -(i) AB > AD (ii) AB = AD (iii) AB < AD

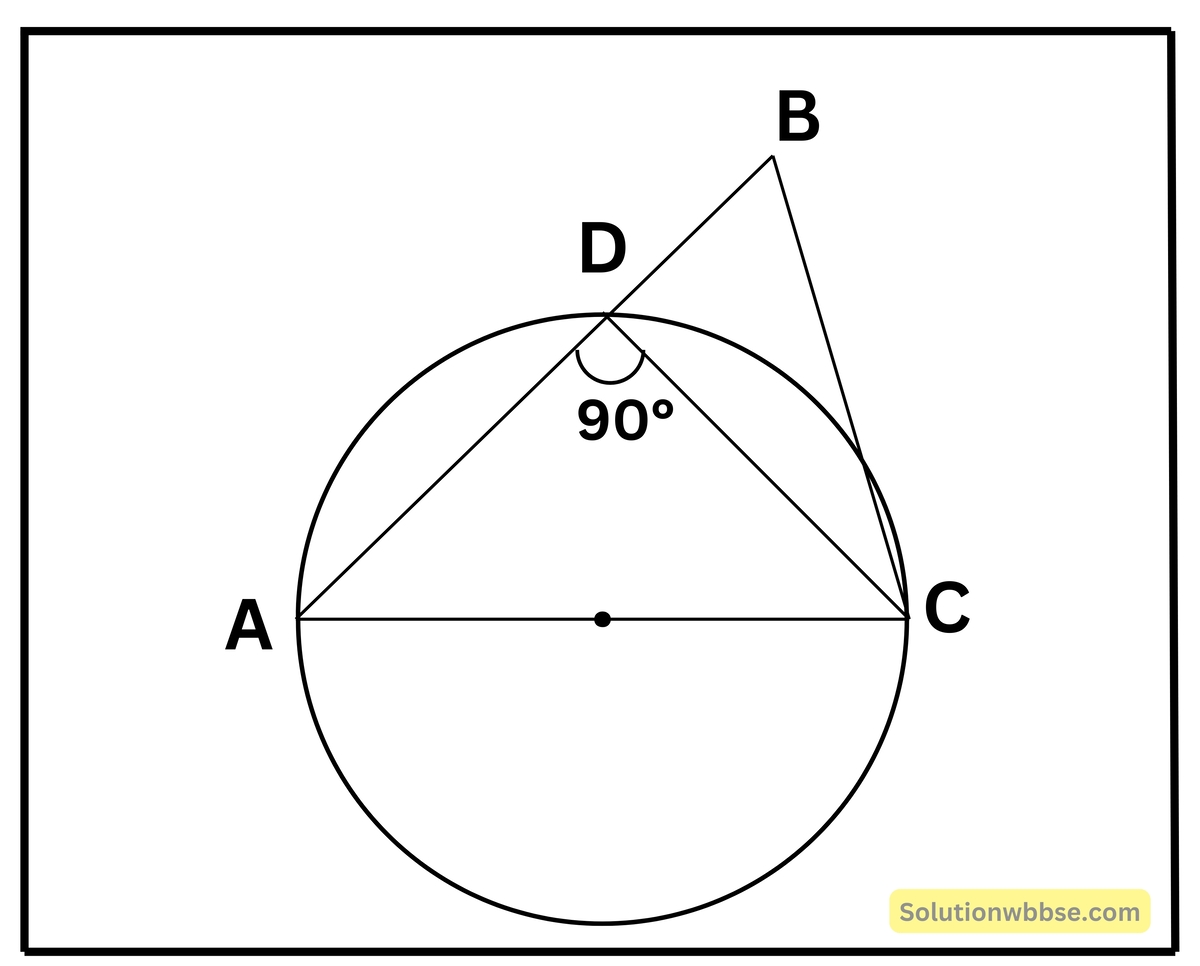
আমরা জানি অর্ধবৃত্তস্থ কোণ = 90°

∴ ∠ADC = 90°

আবার প্রদত্ত ∠ABC = 90°

ইহার একমাত্র সম্ভব যদি B ও D একই বিন্দু হয়।

সুতরাং AB = AD

2. প্রমাণ করি যে একটি সমদ্বিবাহু ত্রিভুজের সমান বাহু দুটির যে-কোনোটিকে ব্যাস করে অঙ্কিত বৃত্ত অসমান বাহুটিকে সমদ্বিখণ্ডিত করে।

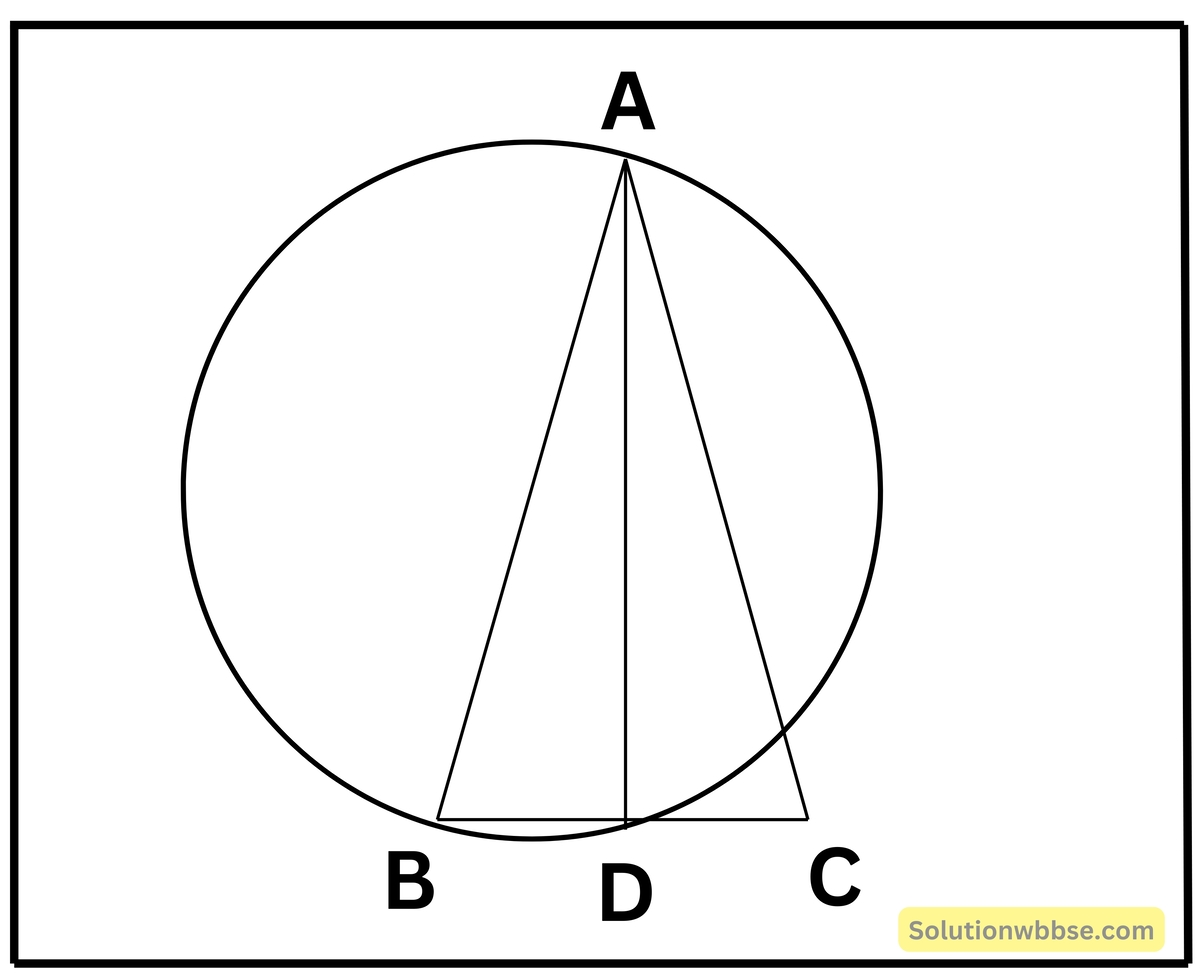
ধরি, ΔABC একটি সমদ্বিবাহু ত্রিভুজ যার AB = AC, AB বাহুকে ব্যাস করে একটি বৃত্ত অঙ্কন করলে বৃত্তটি BC কে D বিন্দুতে ছেদ করেছে।

প্রমাণ করতে হবে যে, বৃত্তটি ΔABC ত্রিভুজের অসমান বাহু অর্থাৎ BC কে সমদ্বিখণ্ডিত করে।

অঙ্কন – AD যুক্ত করা হল।

প্রমাণ – AB বৃত্তের ব্যাস

∴ ∠ADB অর্ধবৃত্তস্থ কোণ

∴ ∠ADB = 90°

∴ ∠AD ⊥ BC

এখন, ΔABD ও ΔACD এর মধ্যে,

AB = AC [প্রদত্ত।

∠ADB = ∠ADC [উভয়ই 90°]

AD সাধারণ বাহু

∴ ΔΑΒΟ ≅ ΔACD

∴ BD=DC

∴ D, BC এর মধ্যবিন্দু

∴ বৃত্তটি সমদ্বিবাহু ত্রিভুজটির অসমান বাহুটিকে সমদ্বিখণ্ডিত করে।

3. সাহানা দুটি বৃত্ত এঁকেছে যারা পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে। PA ও PB যথাক্রমে দুটি বৃত্তের ব্যাস হলে, প্রমাণ করি যে A, Q ও B বিন্দুত্রয় সমরেখ।

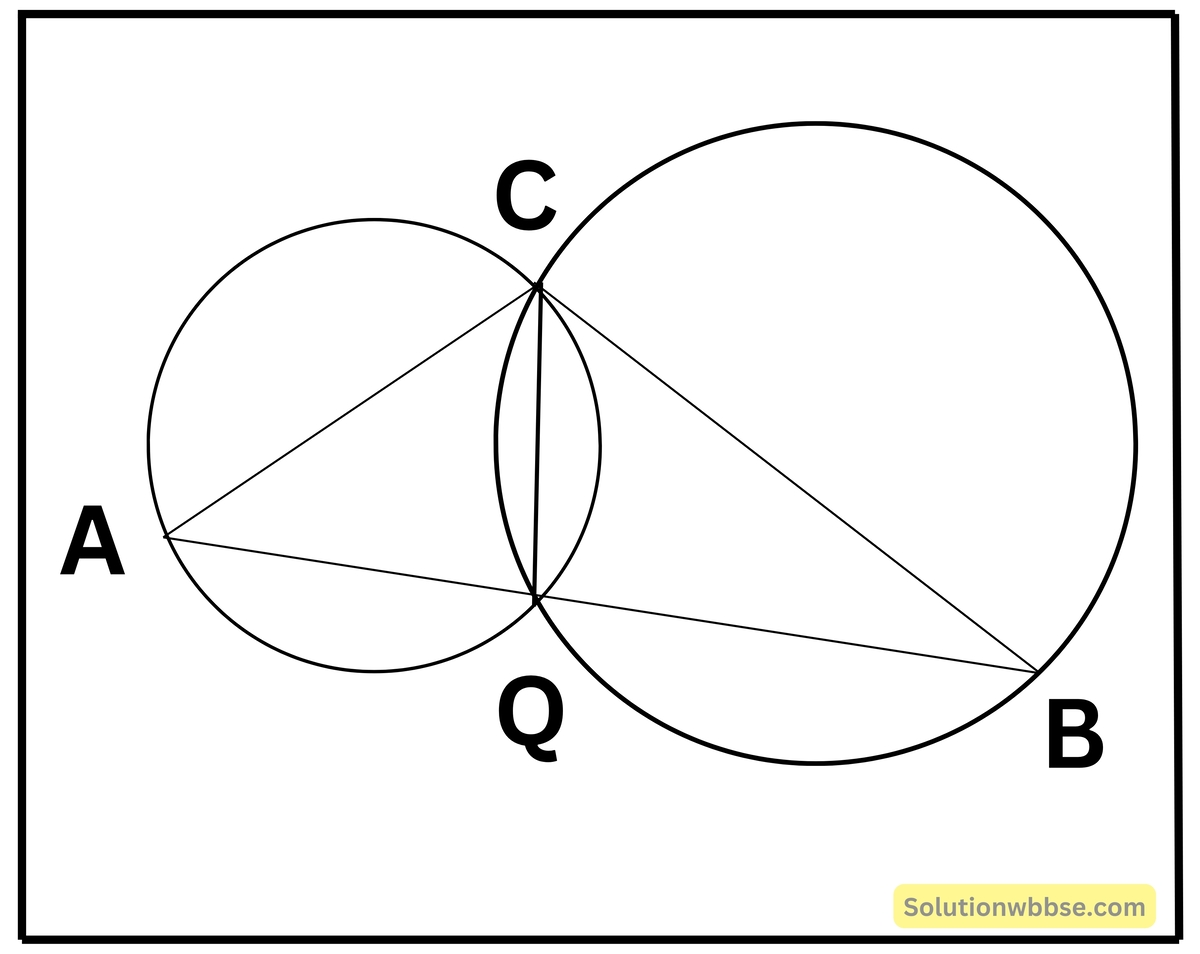
দুটি বৃত্ত পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে, PA ও PB যথাক্রমে দুটি বৃত্তের ব্যাস প্রমাণ করেতে হবে যে A, Q ও B বিন্দুত্রয় সমরেখ।

অঙ্কন – P, Q যুক্ত করা হল।

প্রমাণ – ΔAPQ ত্রিভুজে, AP ব্যাস।

∴ ∠AQP = 90° [ যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ]

আবার, ΔBQP ত্রিভুজে, PB ব্যাস

∴ PQB = 90° [ যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ]

এখন, ∠AQB

= ∠AQP + ∠PQB

= 90° + 90°

= 180°

∴ A, Q ও B একই সরলরেখায় অবস্থিত।

∴ A, Q ও B সমরেখ (প্রমাণিত)।

4. রজত একটি সরলরেখাংশ PQ অঙ্কন করেছে যার মধ্যবিন্দু R এবং সে PR ও PQ -কে ব্যাস করে দুটি বৃত্ত অঙ্কন করেছে। আমি P বিন্দুগামী একটি সরলরেখা অঙ্কন করেছি যা প্রথম বৃত্তকে S বিন্দুতে এবং দ্বিতীয় বৃত্তকে T বিন্দুতে ছেদ করেছে। যুক্তি দিয়ে প্রমাণ করি যে PS = ST

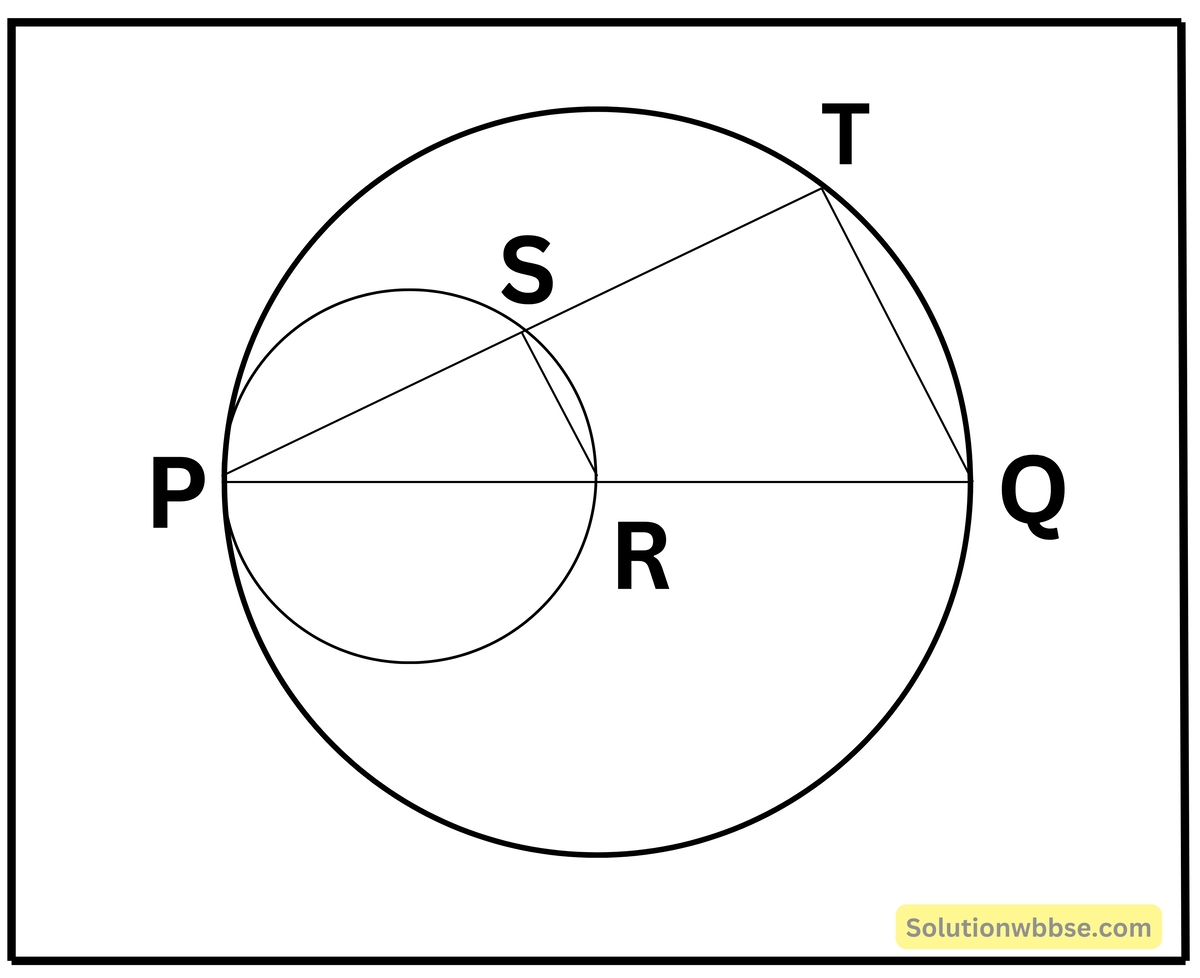
PQ একটি সরলরেখা অঙ্কন করা হল যার মধ্যবিন্দু। PR ও PQ কে ব্যাস করে দুটি বৃত্ত অঙ্কন করা হয়েছে। P বিন্দুগামী একটি সরলরেখা অঙ্কন করা হয়েছে যা প্রথম বৃত্তকে S বিন্দুতে এবং দ্বিতীয় বৃত্তকে T বিন্দুতে ছেদ করেছে।

প্রমাণ করতে হবে যে, PS = ST

অঙ্কন – S, R এবং T, Q যোগ করা হল।

প্রমাণ – PR ব্যাস

∴ ∠PSR = 90° [যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ]

আবার, PQ ব্যাস

∴ ∠PTQ = 90° [ যেহেতু অর্ধবৃত্তস্থ কোণ সমকোণ]

এখন, ΔPSR এবং ΔPTQ ত্রিভুজে,

∠PSR = ∠PTQ [উভয়ই 90°]

∴ SR ∥ TQ

আবার, R, PQ -এর মধ্যবিন্দু

একটি ত্রিভুজের কোনো বাহুর মধ্যবিন্দু দিয়ে অঙ্কিত দ্বিতীয় বাহুর সমান্তরাল সরলরেখা তৃতীয় বাহুকে সমদ্বিখণ্ডিত করে

∴ S, PT এর মধ্যবিন্দু

∴ PS = ST [ প্রমাণিত]

5. একটি বৃত্তের উপর তিনটি বিন্দু P, Q ও R অবস্থিত। PQ ও PR -এর উপর P বিন্দুতে অঙ্কিত লম্ব দুটি বৃত্তকে যথাক্রমে S ও T বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, RQ = ST

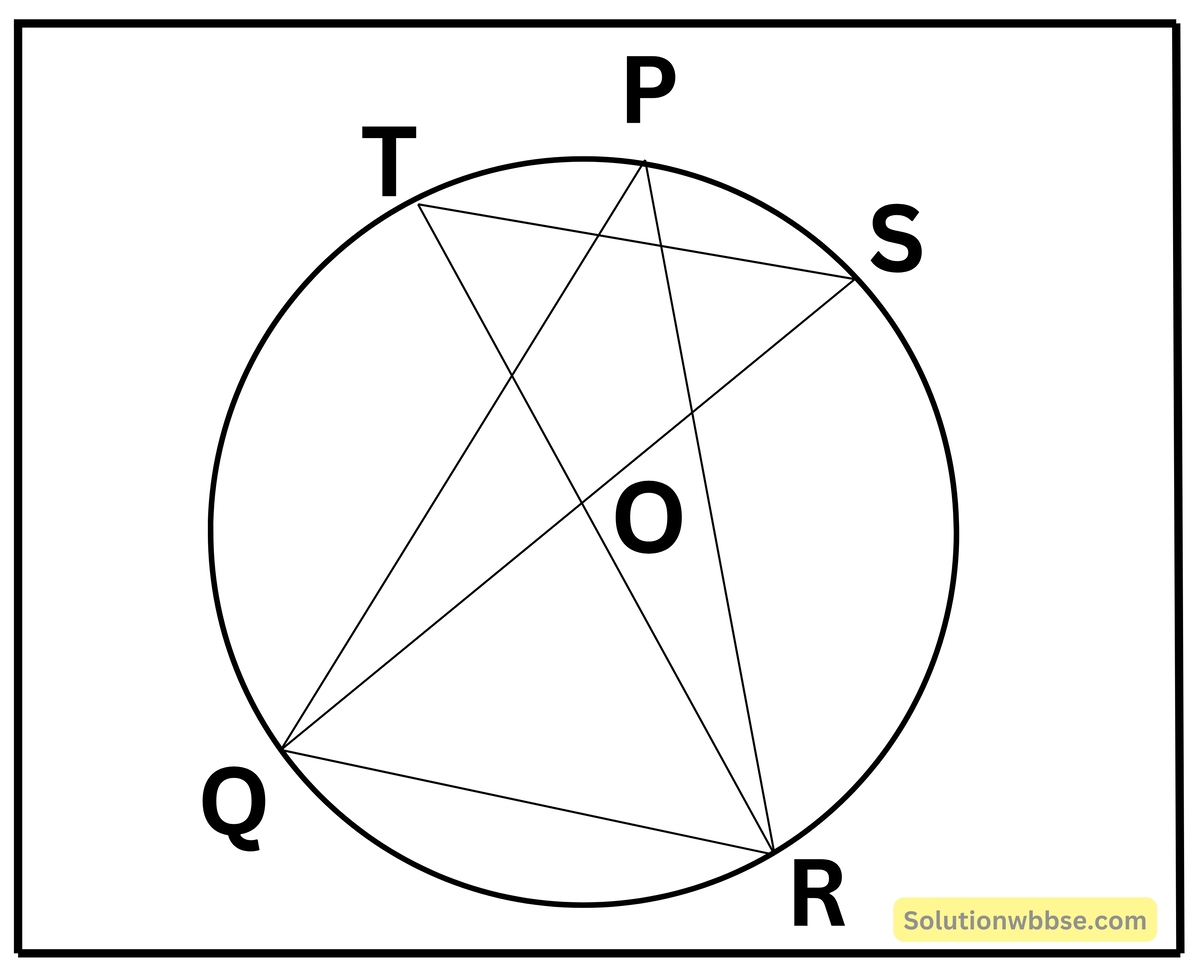
ধরা যাক, O কেন্দ্রীয় বৃত্তের ওপর P, Q এবং R তিনটি বিন্দু। PQ ও PR এর ওপর P বিন্দুতে অঙ্কিত লম্বদুটি বৃত্তকে যথাক্রমে S ও T বিন্দুতে ছেদ করেছে।

প্রমাণ করতে হবে যে, RQ = ST

অঙ্কন – S, Q; T, R যুক্ত করা হল।

প্রমাণ – যেহেতু, PQ ও PR এর ওপর P বিন্দুতে অঙ্কিত লম্ব দুটি বৃত্তকে যথাক্রমে S ও T বিন্দুতে ছেদ করেছে।

∴ ∠TPR = 90° এবং ∠SPQ = 90°

যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ

∴ TR এবং SQ উভয়ই বৃত্তের ব্যাস।

এখন, ত্রিভুজ ΔOST এবং ΔORQ এর মধ্যে,

OT = OS [একই বৃত্তের ব্যাসার্ধ]

OQ = OR [একই বৃত্তের ব্যাসার্ধ।]

∠SOT = ∠QOR [বিপ্রতীপ কোণ]

ΔSOT ≅ ΔPQR

∴ ST = QR [প্রমাণিত]

6. ABC একটি সূক্ষ্মকোণী ত্রিভুজ। ABC ত্রিভুজের পরিবৃত্তের ব্যাস AP; BE ও CF যথাক্রমে AC ও AB বাহুর উপর লম্ব এবং তারা পরস্পরকে Q বিন্দুতে ছেদ করে। প্রমাণ করি যে, BPCQ একটি সামান্তরিক।

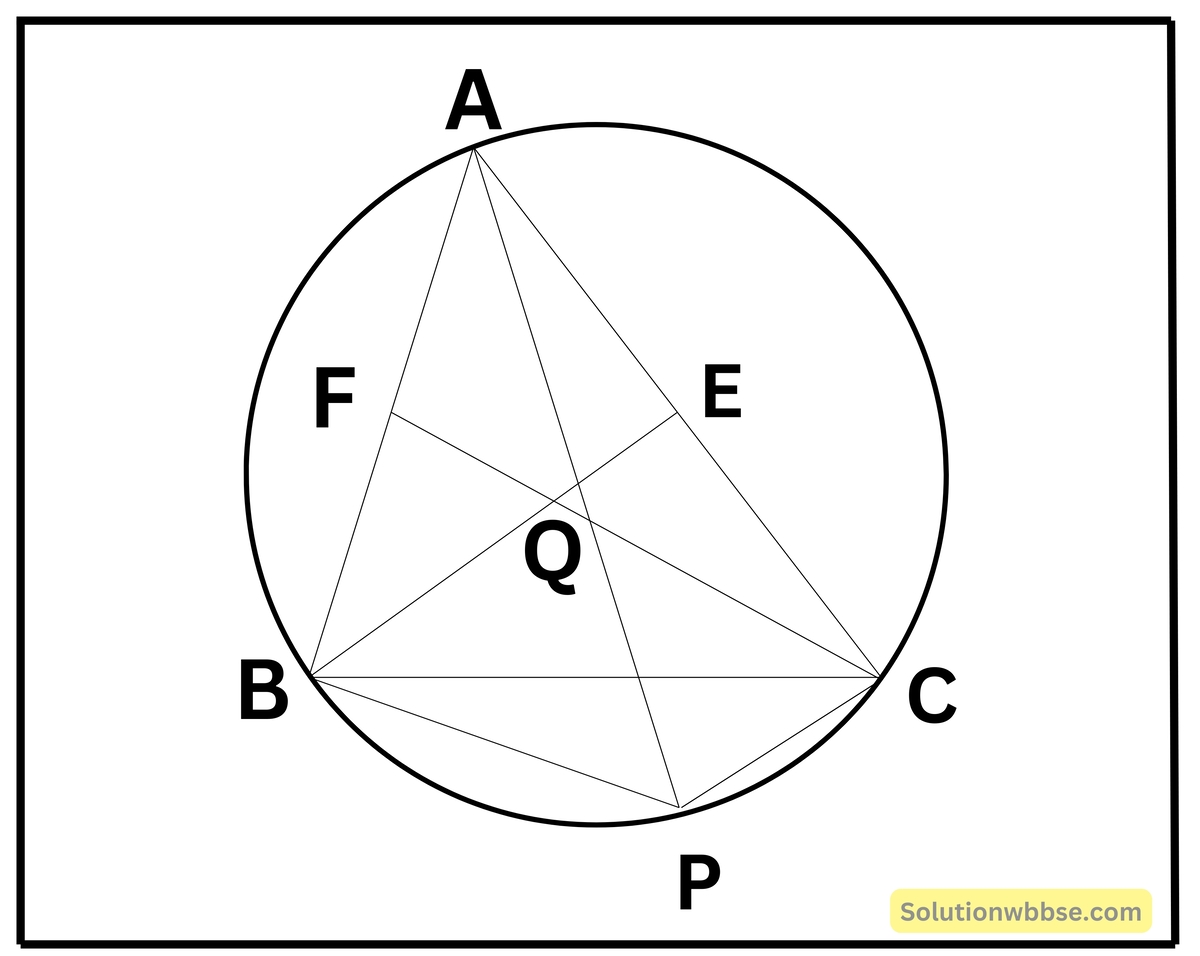
ΔABC একটি সূক্ষ্মকোণী ত্রিভুজ। ΔABC এর পরিবৃত্তের ব্যাস AP; BE ও CF যথাক্রমে AC ও AB বাহুর ওপর লম্ব এবং তারা পরস্পরকে Q বিন্দুতে ছেদ করে।

প্রমাণ করতে হবে – BPCQ একটি সামান্তরিক।

অঙ্কন – B, P এবং C, P যুক্ত করা হল।

প্রমাণ – যেহেতু, AP বৃত্তের ব্যাস

∴ ∠ABP = 90°

আবার, ∠CFB = 90° [যেহেতু, CF, AB এর ওপর লম্ব]

∴ FC ∥ BP অর্থাৎ,

QC || BP —(i)

আবার, যেহেতু AP বৃত্তের ব্যাস

∠ACP = 90°

আবার, ∠BEC = 90° [যেহেতু, BE, AC এর ওপর লম্ব]

∴ BE ∥ PC

অর্থাৎ BQ ∥ PC —(ii)

(i) ও (ii) থেকে পাই,

∴ BPCQ একটি সামান্তরিক [প্রমাণিত]।

7. একটি ত্রিভুজের শীর্ষকোণের অন্তসমদ্বিখণ্ডক ও বহিসমদ্বিখণ্ডক ত্রিভুজটির পরিবৃত্তকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে। প্রমাণ করি যে, PQ বৃত্তের একটি ব্যাস।

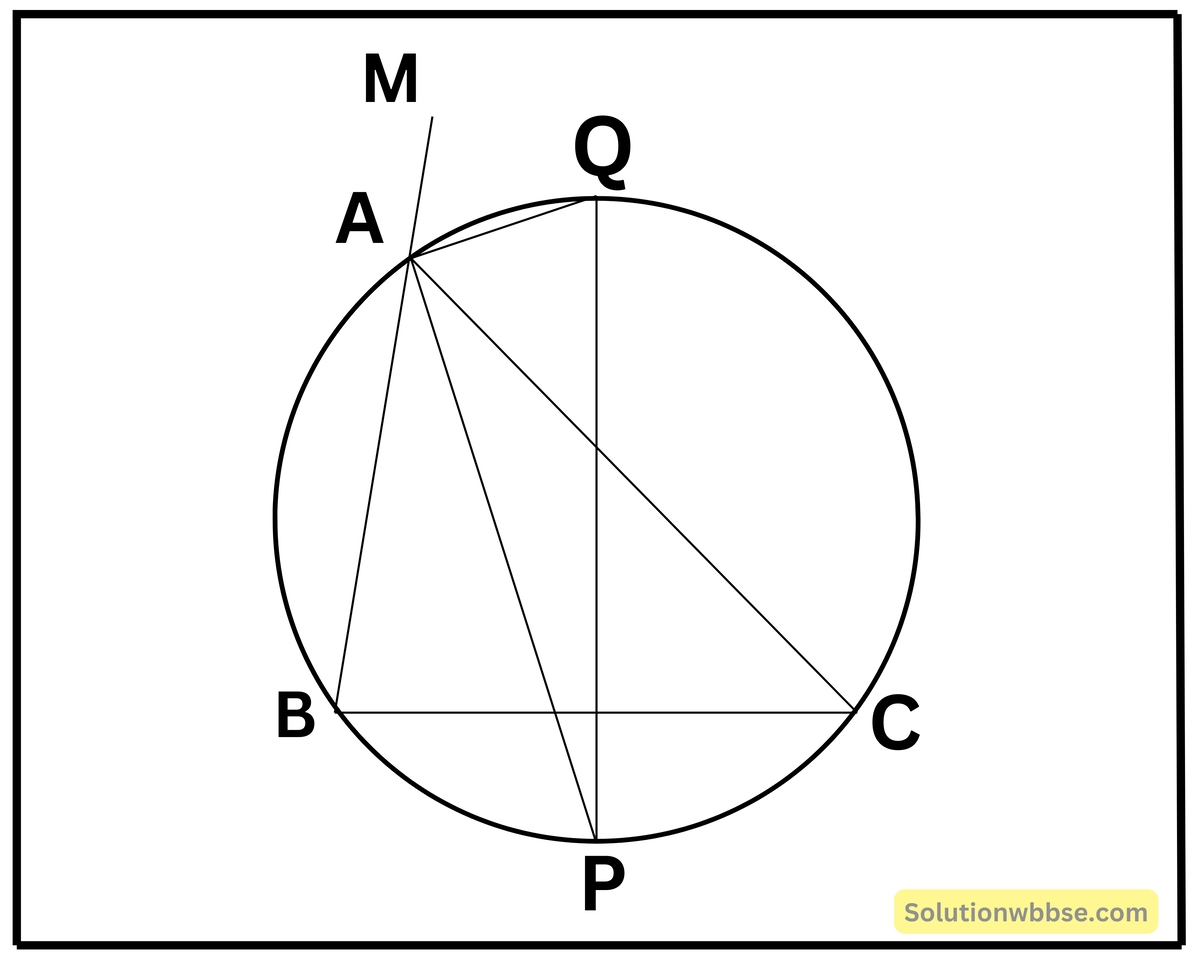
ধরি, ΔABC এর ∠BAC এর অন্তর্দ্বিখণ্ডক ও বহির্দ্বিখণ্ডক ত্রিভুজটির পরিবৃত্তকে P ও Q বিন্দুতে ছেদ করে।

প্রমাণ করতে হবে – PQ বৃত্তের একটি ব্যাস।

প্রমাণ – যেহেতু, AP ও AQ উভয়ই যথাক্রমে ∠BAC এর অন্তর্দ্বিখণ্ডক এবং বহির্দ্বিখণ্ডক;

সুতরাং, ∠PAQ = 1 সমকোণ [যেহেতু, কোনো কোণের অন্তর্দ্বিখণ্ডক এবং বহির্দ্বিখণ্ডক-এর মধ্যবর্তী কোণ 1 সমকোণ।]

∴ ∠PAQ অর্ধবৃত্তস্থ কোণ।

∴ PQ বৃত্তের ব্যাস [প্রমাণিত]

8. AB এবং CD একটি বৃত্তের দুটি ব্যাস। প্রমাণ করি যে, ACBD একটি আয়তাকার চিত্র।

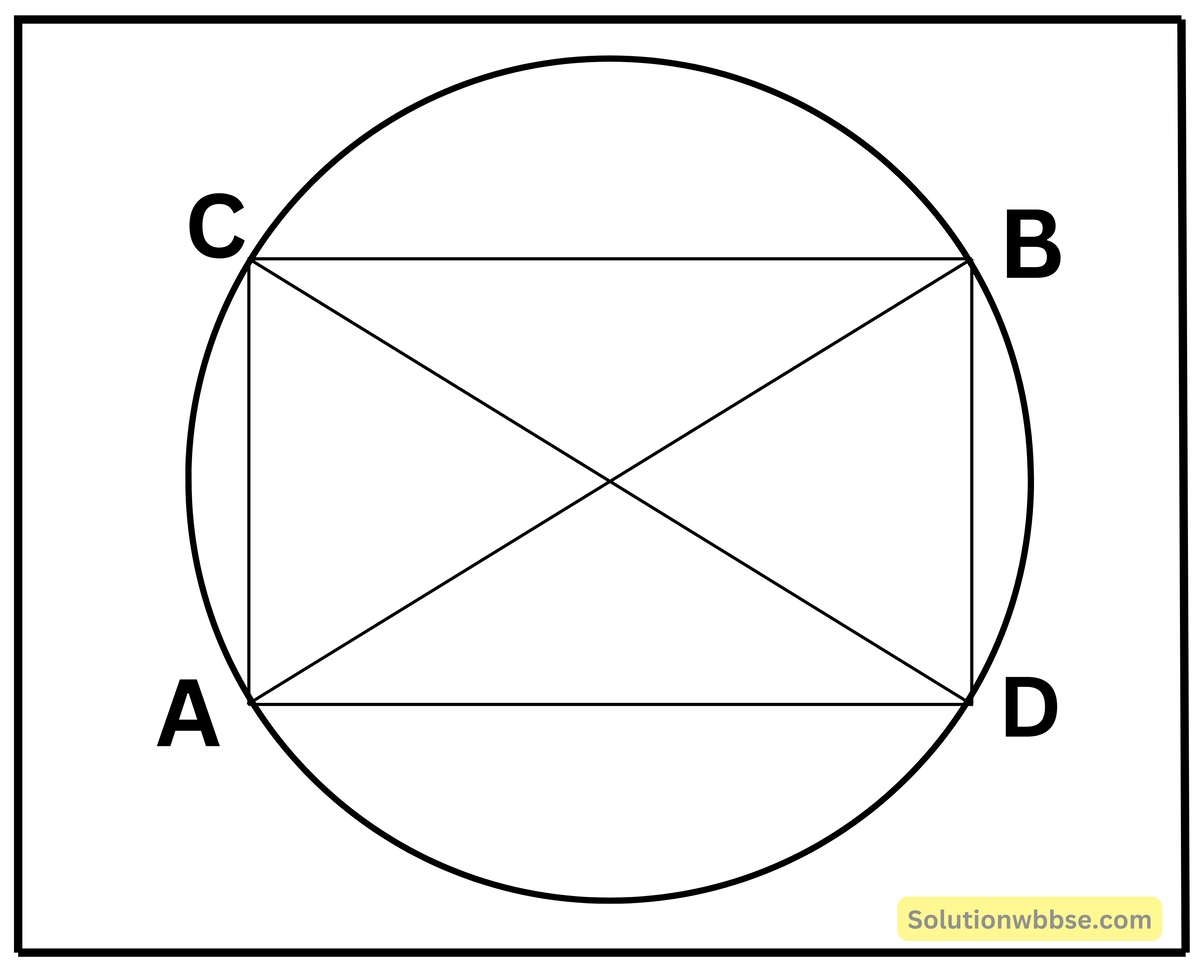
AB এবং CD বৃত্তের দুটি ব্যাস।

প্রমাণ করতে হবে যে, ACBD একটি আয়তকার চিত্র।

অঙ্কন – A, D; A, C এবং B, C যুক্ত করা হল।

প্রমাণ – যেহেতু AB বৃত্তের ব্যাস

∴ ∠ACB = ∠ADB = 1 সমকোণ [ যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ]

আবার, যেহেতু CD বৃত্তের ব্যাস,

∴ ∠CAD = ∠DBC = 1 সমকোণ [ যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ]

∴ ACBD চতুর্ভুজের চারটি কোণ প্রত্যেকে সমকোণ।

∴ ACBD একটি আয়তকার চিত্র। [প্রমাণিত]

ABCD একটি রম্বস।

প্রমাণ করি, একটি রম্বসের বাহুগুলিকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তগুলি একটি নির্দিষ্ট বিন্দু দিয়ে যায়।

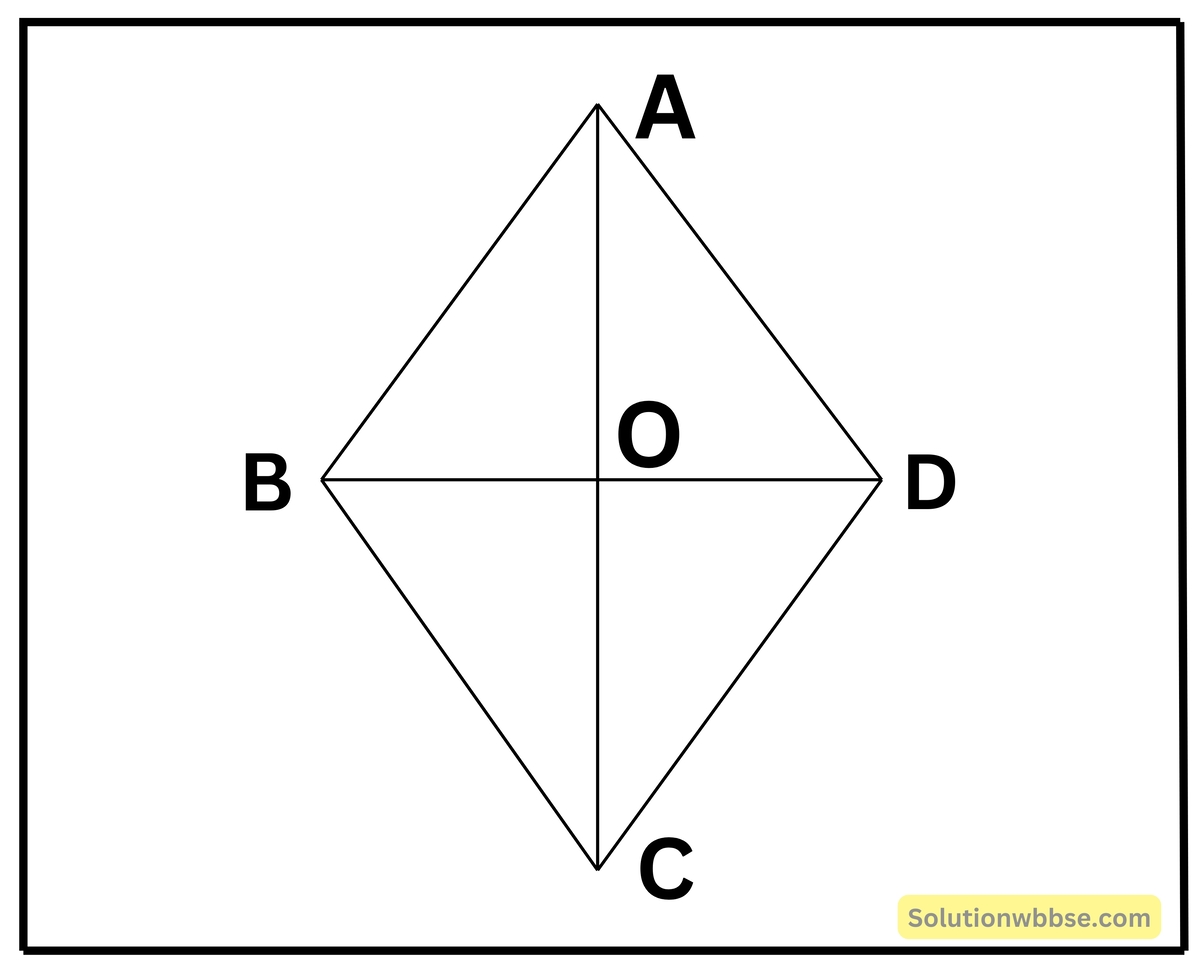
ABCD একটি রম্বস।

প্রমাণ করতে হবে যে, রম্বসের বাহুগুলিকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তগুলি একটি নির্দিষ্ট বিন্দু দিয়ে যাবে।

অঙ্কন – A, C এবং B, D যুক্ত করা হল যারা পরস্পরকে বিন্দুতে ছেদ করল।

প্রমাণ – যেহেতু রম্বসের কর্ণগুলি পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে

সুতরাং, ∠AOB = ∠BOC = COD = ∠DOA = 90°

আবার যেহেতু অর্ধবৃত্তস্থ কোণ। সমকোণ, তাই AB বা BC বা CD বা DA যেকোনো বাহুকে ব্যাস ধরে বৃত্ত অঙ্কন করলে তা বিন্দু দিয়ে যাবে।

∴ রম্বসের বাহুগুলিকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তগুলি একটি নির্দিষ্ট বিন্দু দিয়ে যাবে [প্রমাণিত]

অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V. S. A.)

(A) বহু বিকল্পীয় প্রশ্ন (M.C.Q.)

(i) O কেন্দ্রীয় বৃত্তে PQ একটি ব্যাস এবং PR = RQ; ∠RPQ -এর মান –

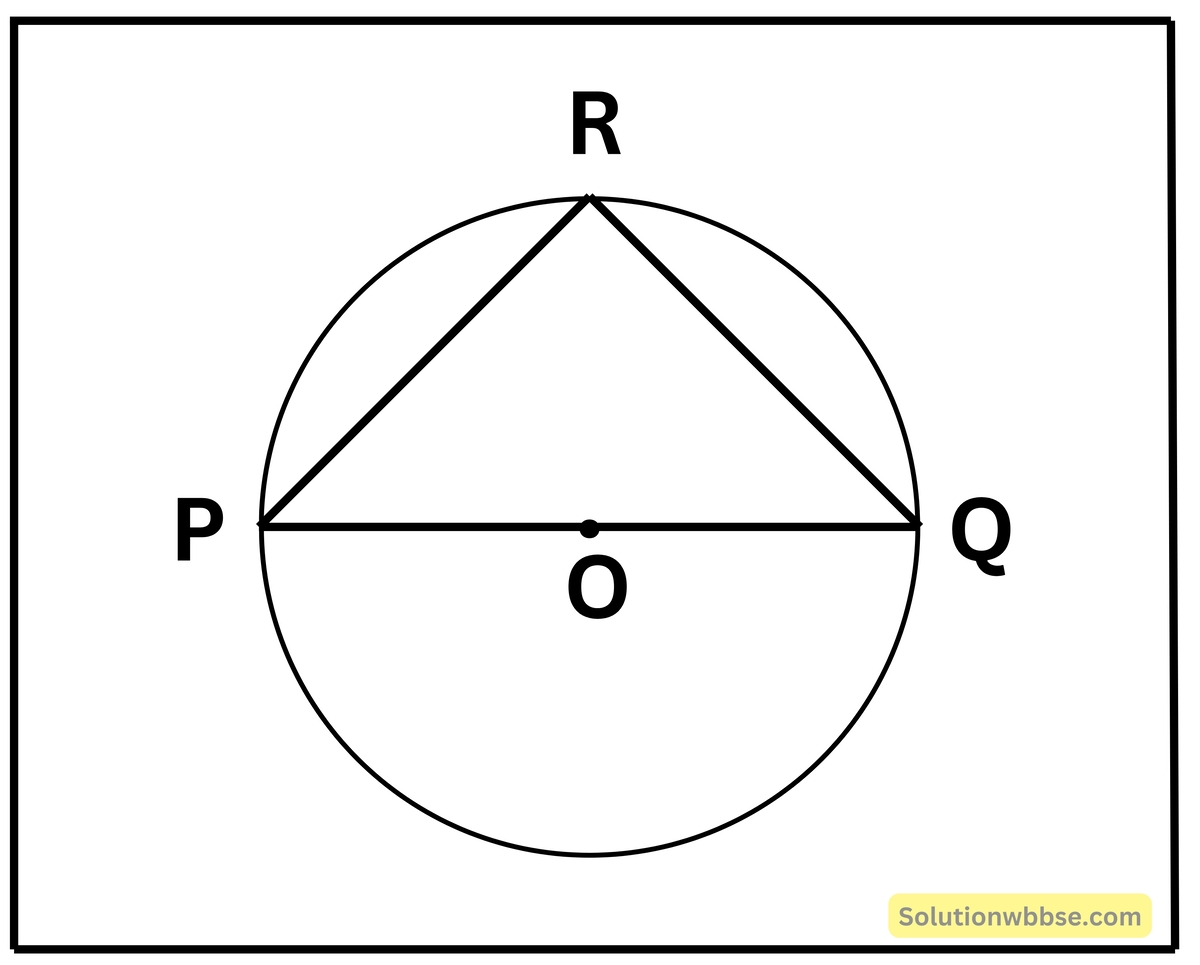
(a) 30°
(b) 90°
(c) 60°
(d) 45°

উত্তর – (d) 45°

(ii) QR বৃত্তের একটি জ্যা এবং POR বৃত্তের একটি ব্যাস। OD, QR বাহুর উপর লম্ব। OD = 4 সেমি. হলে, PQ -এর দৈর্ঘ্য

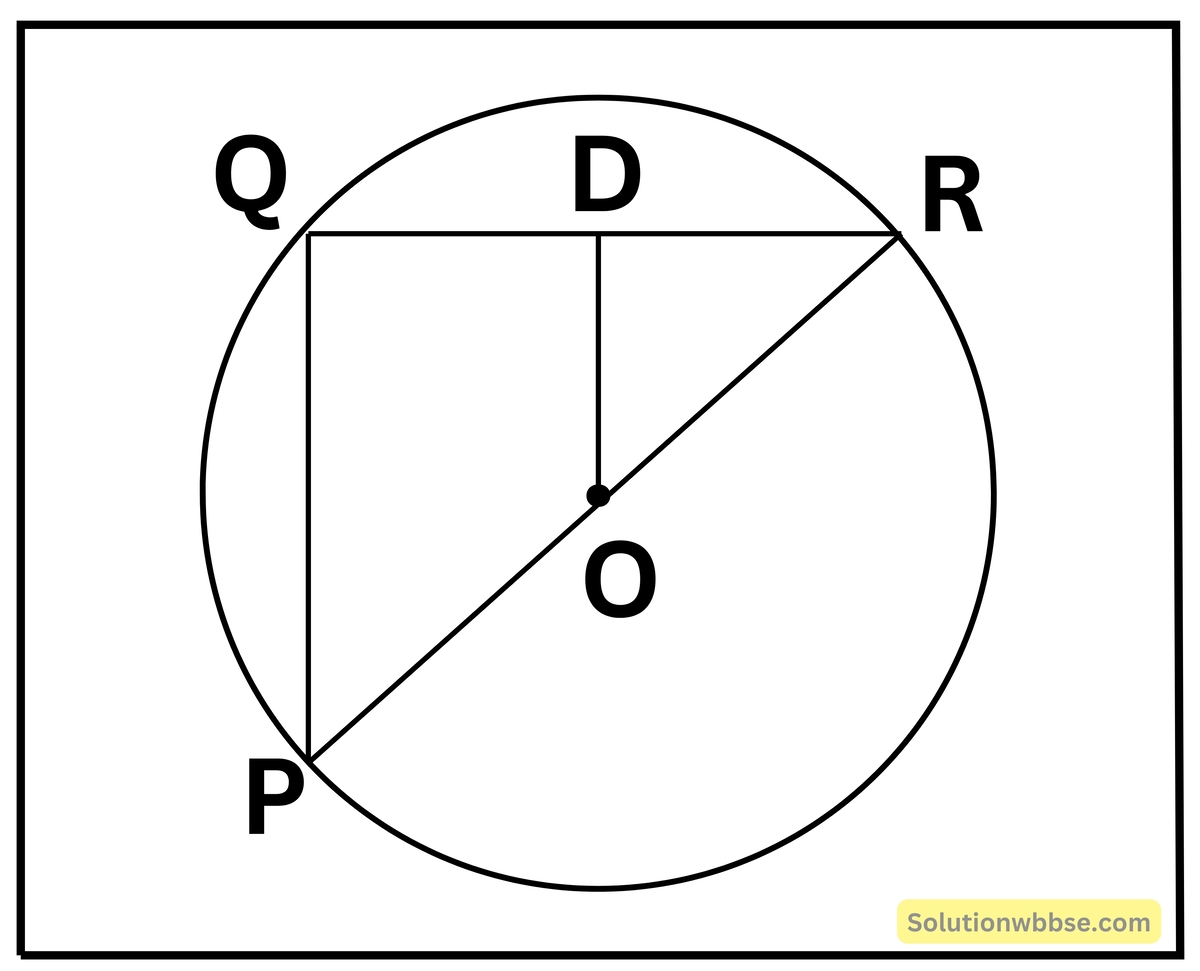
(a) 4 সেমি.
(b) 2 সেমি.
(c) 8 সেমি.
(d) কোনটিই নয়

উত্তর – (c) 8 সেমি.

(iii) AOB বৃত্তের ব্যাস। AC এবং BD জ্যা দুটি বর্ধিত করলে E বিন্দুতে মিলিত হয়। ∠COD = 40° হলে ∠CED -এর মান

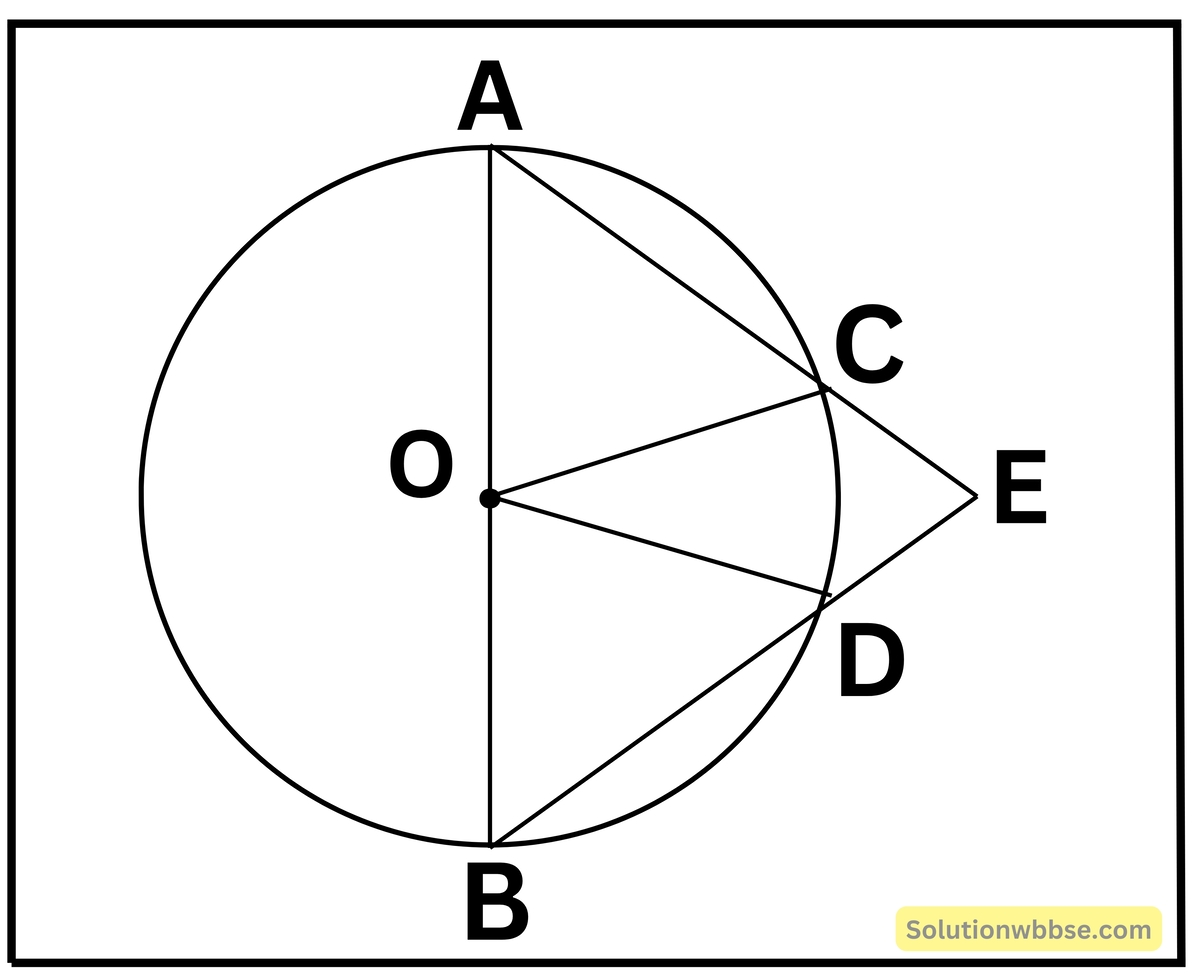
(a) 40°
(b) 80°
(c) 20°
(d) 70°

উত্তর – (d) 70°

সমাধান

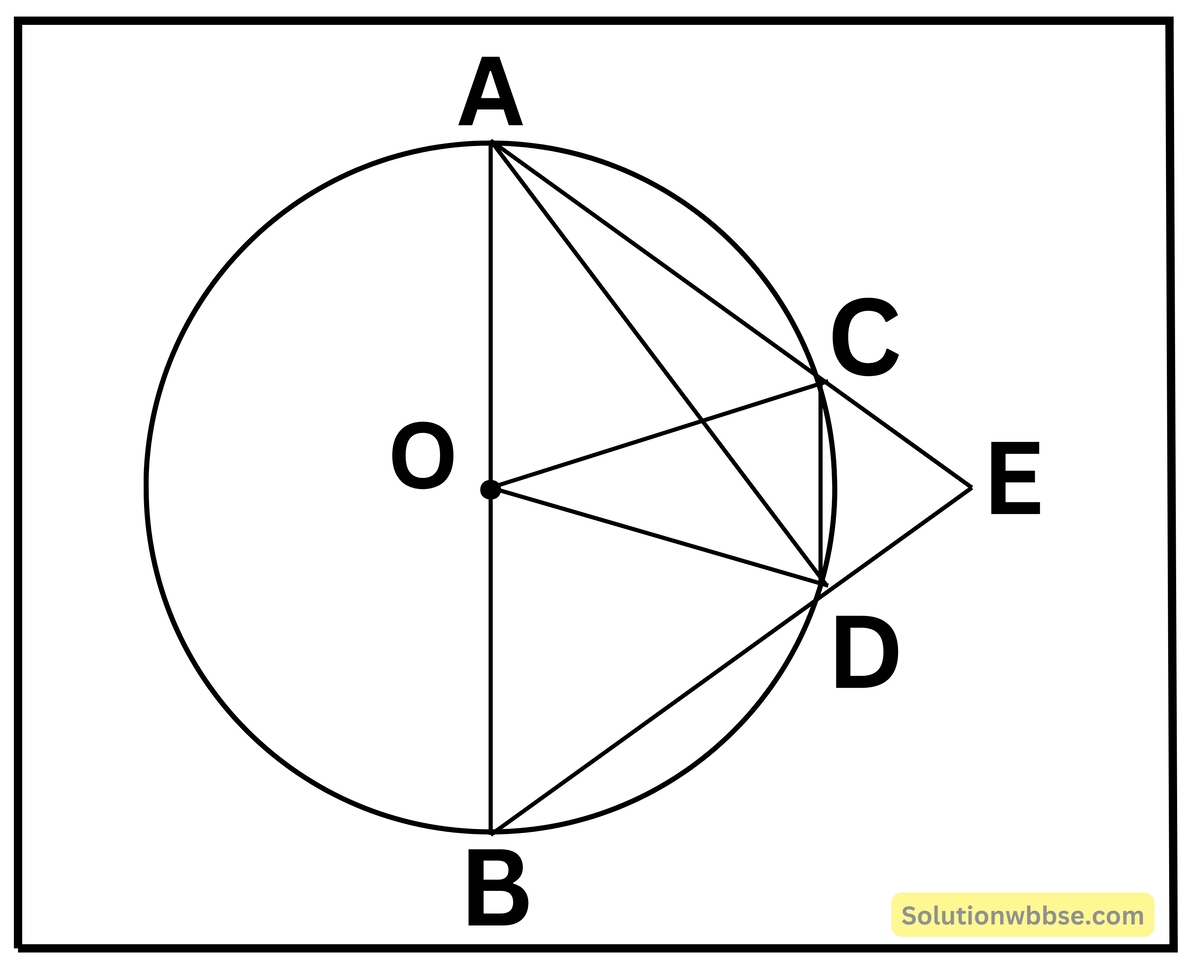
A, D এবং C, D যুক্ত করা হল।

∠ADB = 90° [ যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ]

∴ ∠ADE = 90°

CD, বৃত্তচাপের ওপর CAD বৃত্তস্থ কোণ এবং COD পরিধিস্থ কোণ।

সুতরাং, ∠CAD = \(\frac12\) × ∠COD

বা, ∠CAD = \(\frac12\) × 40°

বা, ∠CAD = 20°

ΔAED তে, ∠ADE + ∠DAE + ∠AED = 180°

বা, 90° + 20° + ∠AED = 180°

বা, ∠AED = 70°

(iv) AOB বৃত্তের ব্যাস। AC = 3 সেমি. ও BC = 4 সেমি. হলে AB -এর দৈর্ঘ্য

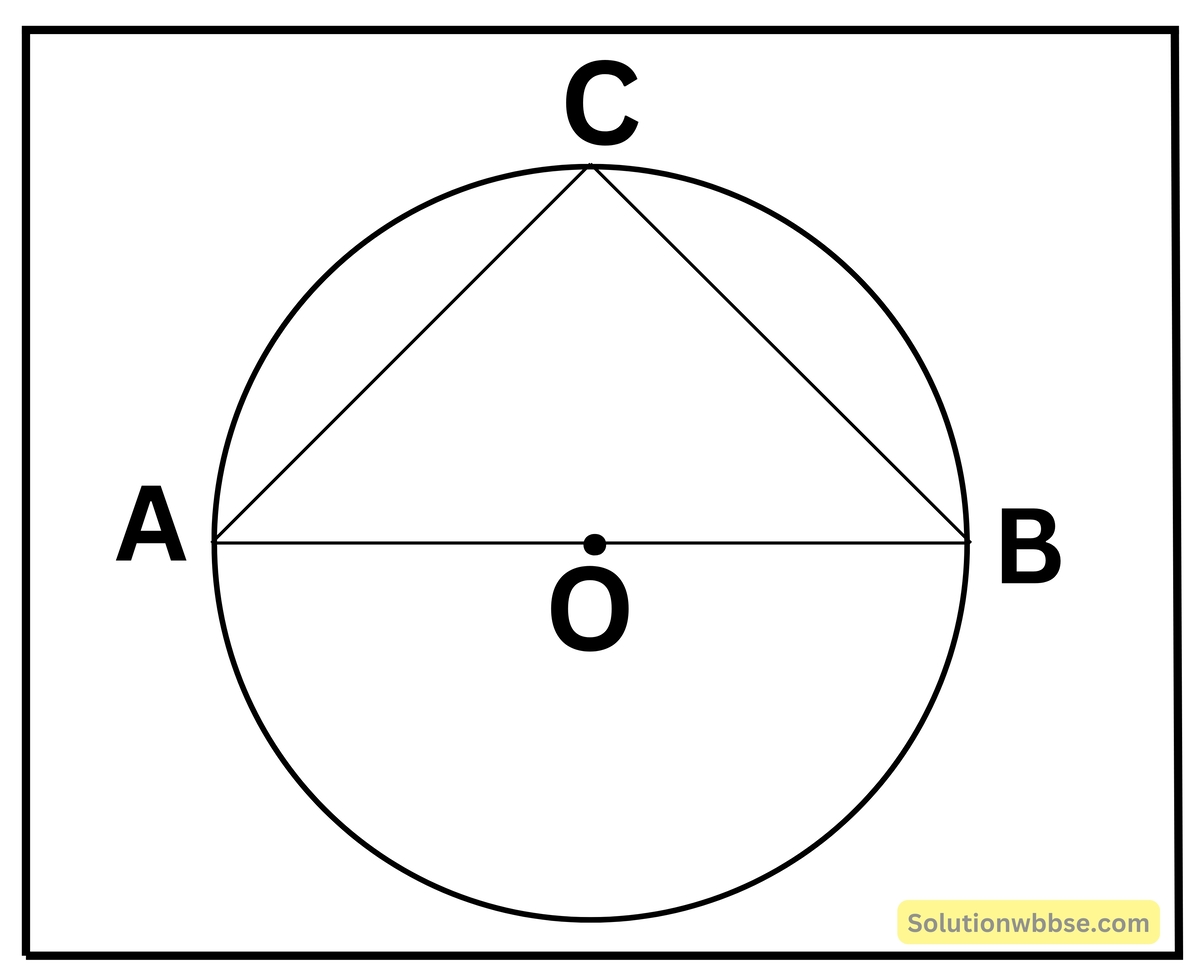
(a) 3 সেমি.
(b) 4 সেমি.
(c) 5 সেমি.
(d) 8 সেমি.

উত্তর – (c) 5 সেমি.

(v) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস। ∠BCE = 20°, ∠CAE = 25° হলে ∠ABC -এর মান নির্ণয় করি।

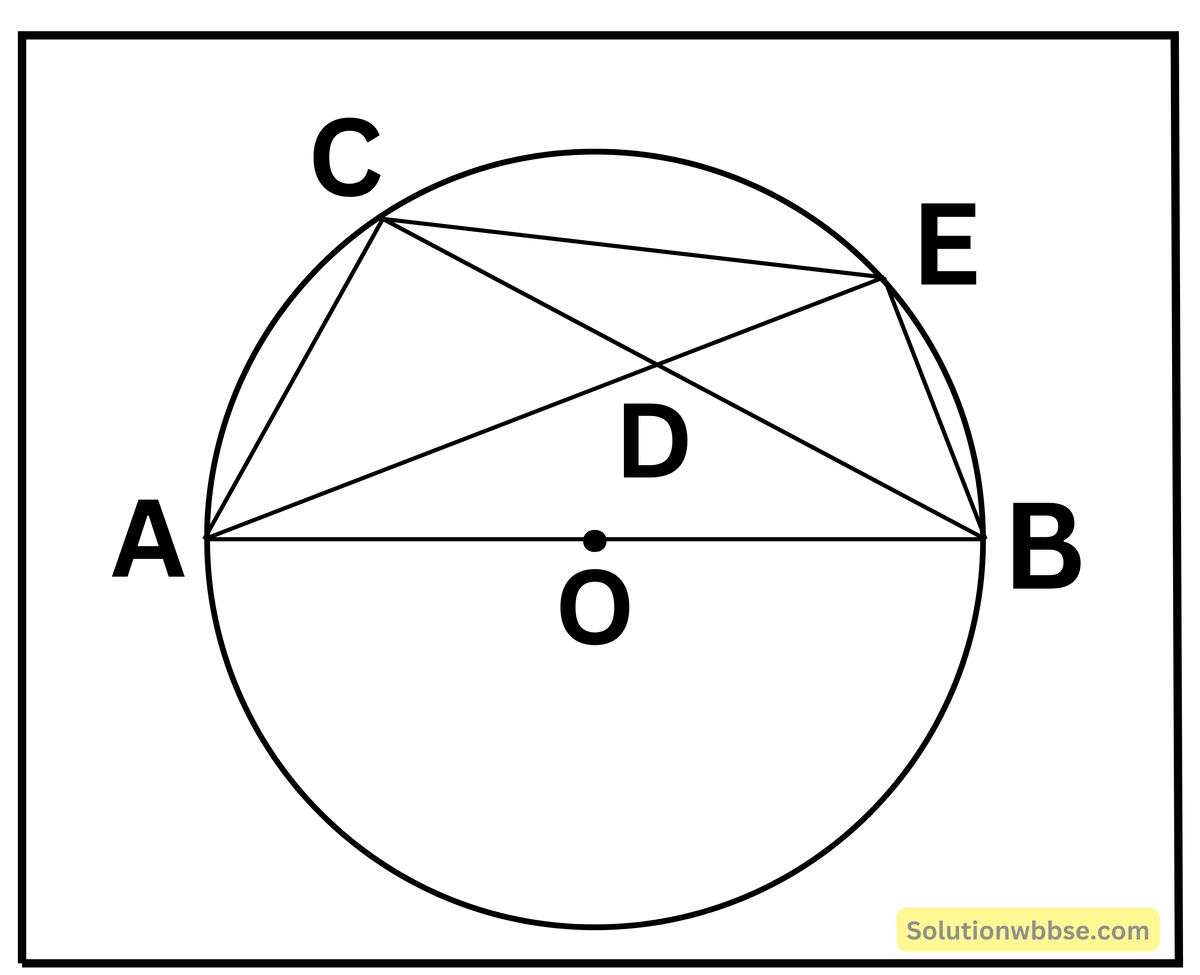
(a) 50°
(b) 90°
(c) 45°
(d) 20°

উত্তর – (c) 45°

(B) সত্য বা মিথ্যা লিখি –

(i) অর্ধবৃত্ত অপেক্ষা বৃহত্তর বৃত্তাংশস্থ কোণ স্থূলকোণ।

উত্তর – মিথ্যা।

(ii) ABC ত্রিভুজের AB বাহুর মধ্যবিন্দু O এবং OA = OB = OC; AB বাহুকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি C বিন্দু দিয়ে যাবে।

উত্তর – সত্য।

(C) শূন্যস্থান পূরণ করি –

(i) অর্ধবৃত্তস্থ কোণ ___।

উত্তর – সমকোণ।

(ii) অর্ধবৃত্ত অপেক্ষা ক্ষুদ্রতর বৃত্তাংশস্য কোণ ___।

উত্তর – স্থূলকোণ।

(iii) সমকোণী ত্রিভুজের অতিভুজকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি ___ বিন্দু দিয়ে যাবে।

উত্তর – সমকৌণিক।

11. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S. A.)

(i) ABC সমদ্বিবাহু ত্রিভুজের AB = AC; AB বাহুকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি BC বাহুকে D বিন্দুতে ছেদ করে, BD = 4 সেমি. হলে CD -এর দৈর্ঘ্য নির্ণয় করি।

ΔABC সমদ্বিবাহু ত্রিভুজের AB = AC

AB বাহুকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি BC বাহুকে D বিন্দুতে ছেদ করে।

∴ ∠ADB = 90° [∵ অর্ধবৃত্তস্থ কোণ 1 সমকোণ]

∴ AD ⊥ BC

∴ D, BC এর মধ্যবিন্দু [∵ বৃত্তের কেন্দ্রগামী কোনো সরলরেখা, ব্যাস নয় এরূপ কোনো জ্যা এর ওপর লম্ব হলে ওই সরলরেখাটি ওই জ্যা কে সমদ্বিখণ্ডিত করে।

∴ BD = CD

∴ CD = 4 সেমি.

(ii) একটি বৃত্তে দুটি জ্যা AB এবং AC পরস্পর লম্ব। AB = 4 সেমি. ও AC = 3 সেমি. হলে, বৃত্তটির ব্যাসার্ধের দৈর্ঘ্য নির্ণয় করি।

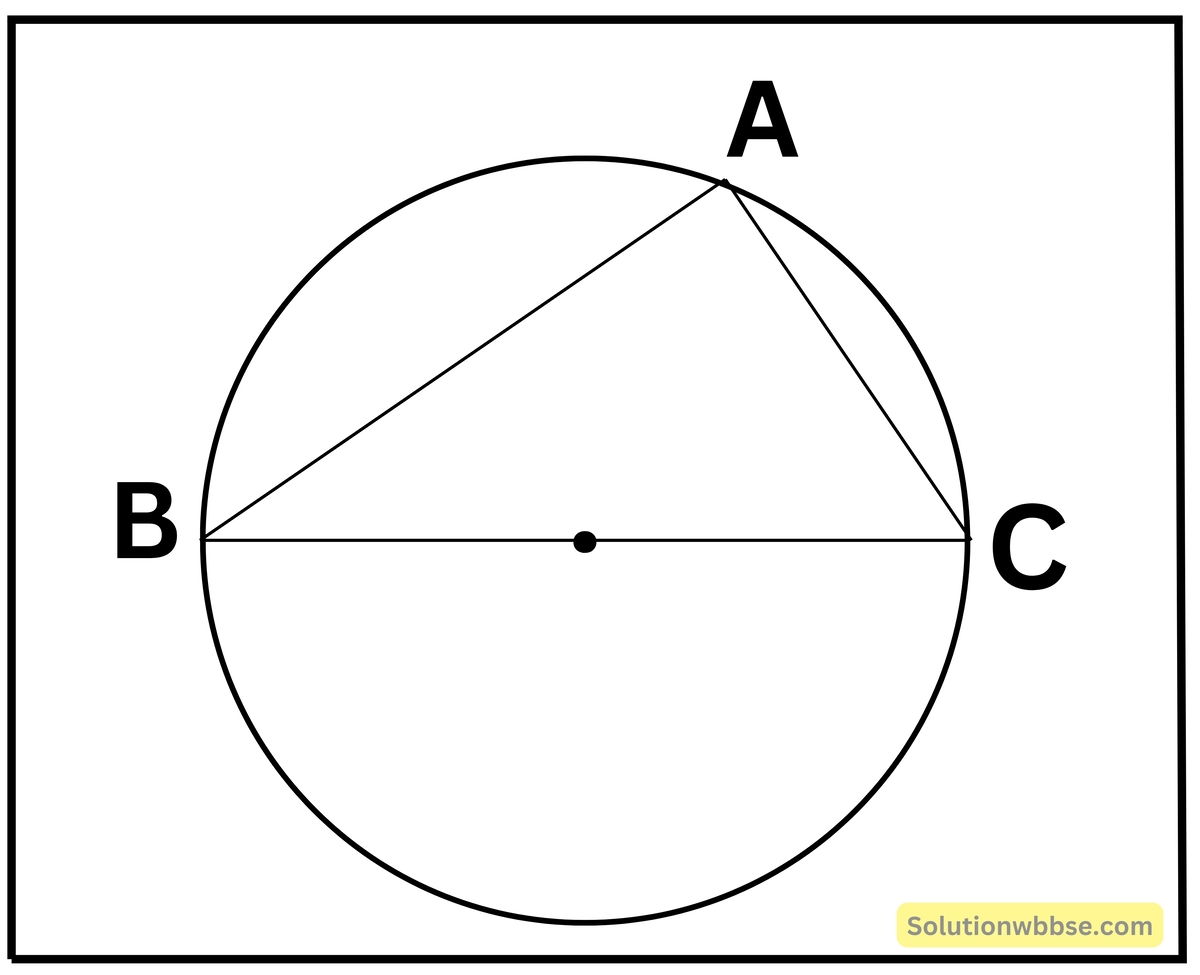
যেহেতু, AB ও AC জ্যা দুটি পরস্পর লম্ব।

∠BAC = 90° [অর্ধবৃত্তস্থ কোণ]

∴ BC বৃত্তের ব্যাস

এখন, ΔABC সমকোণী ত্রিভুজ থেকে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই,

BC² = AB² + AC²

বা, BC² = (4)² + (3)²

বা, BC² = 16 + 9

বা, BC² = 25

বা, BC = 5

∴ বৃত্তের ব্যাসার্ধ = \(\frac{BC}2\) = \(\frac{BC}2\) = 2.5 সেমি.

(iii) একটি বৃত্তে দুটি জ্যা PQ এবং PR পরস্পর লম্ব। বৃত্তের ব্যাসার্ধের দৈর্ঘ্য r সেমি. হলে, জ্যা QR -এর দৈর্ঘ্য নির্ণয় করি।

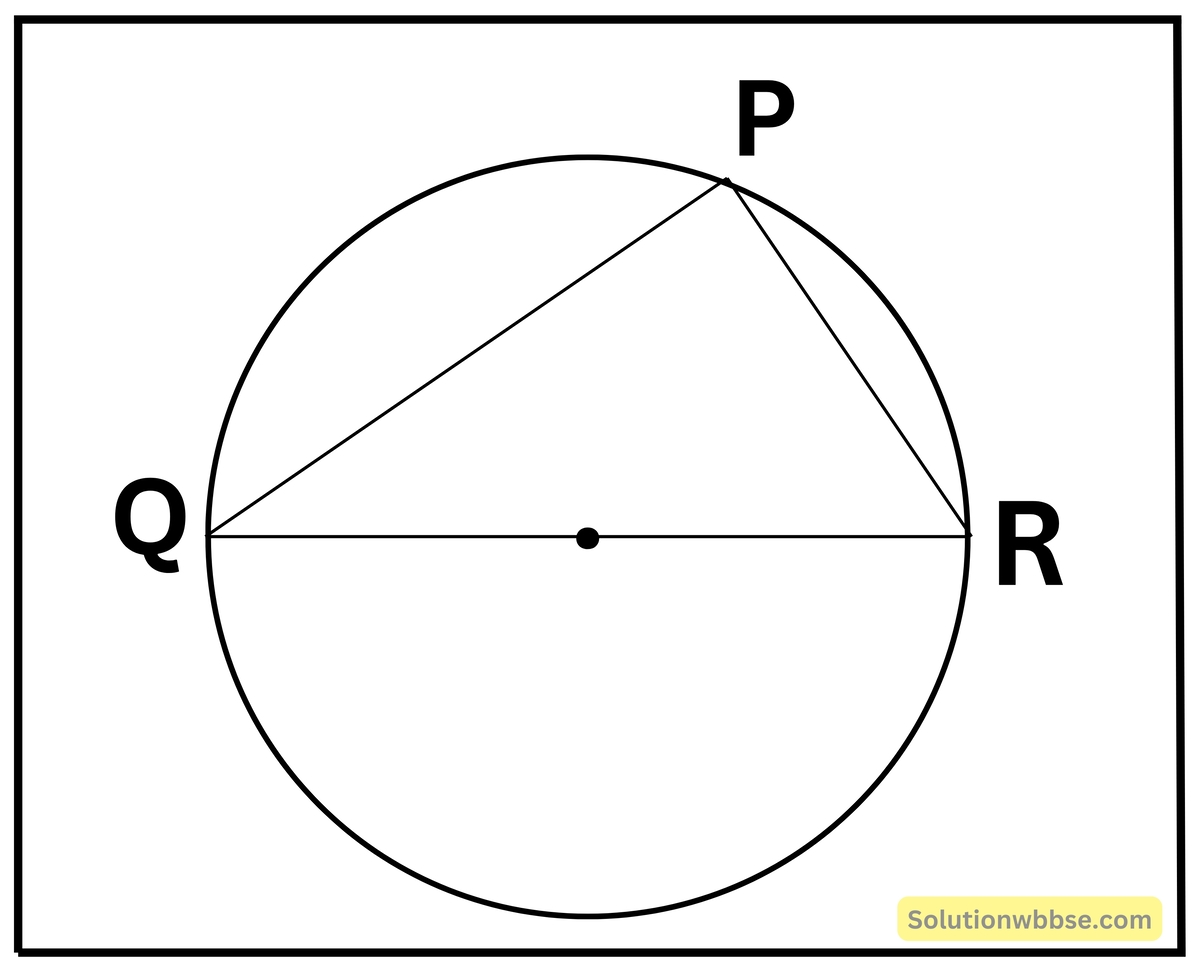
যেহেতু, PQ ও PR জ্যা দুটি পরস্পর লম্ব।

∠QPR = 90° [অর্ধবৃত্তস্থ কোণ]

∴ QR বৃত্তের ব্যাস।

∴ OR ব্যাসের দৈর্ঘ্য = 2 × ব্যাসার্ধ = 2r সেমি.

(iv) AOB বৃত্তের একটি ব্যাস। C বৃত্তের উপর একটি বিন্দু। ∠OBC = 60° হলে ∠OCA -এর মান নির্ণয় করি।

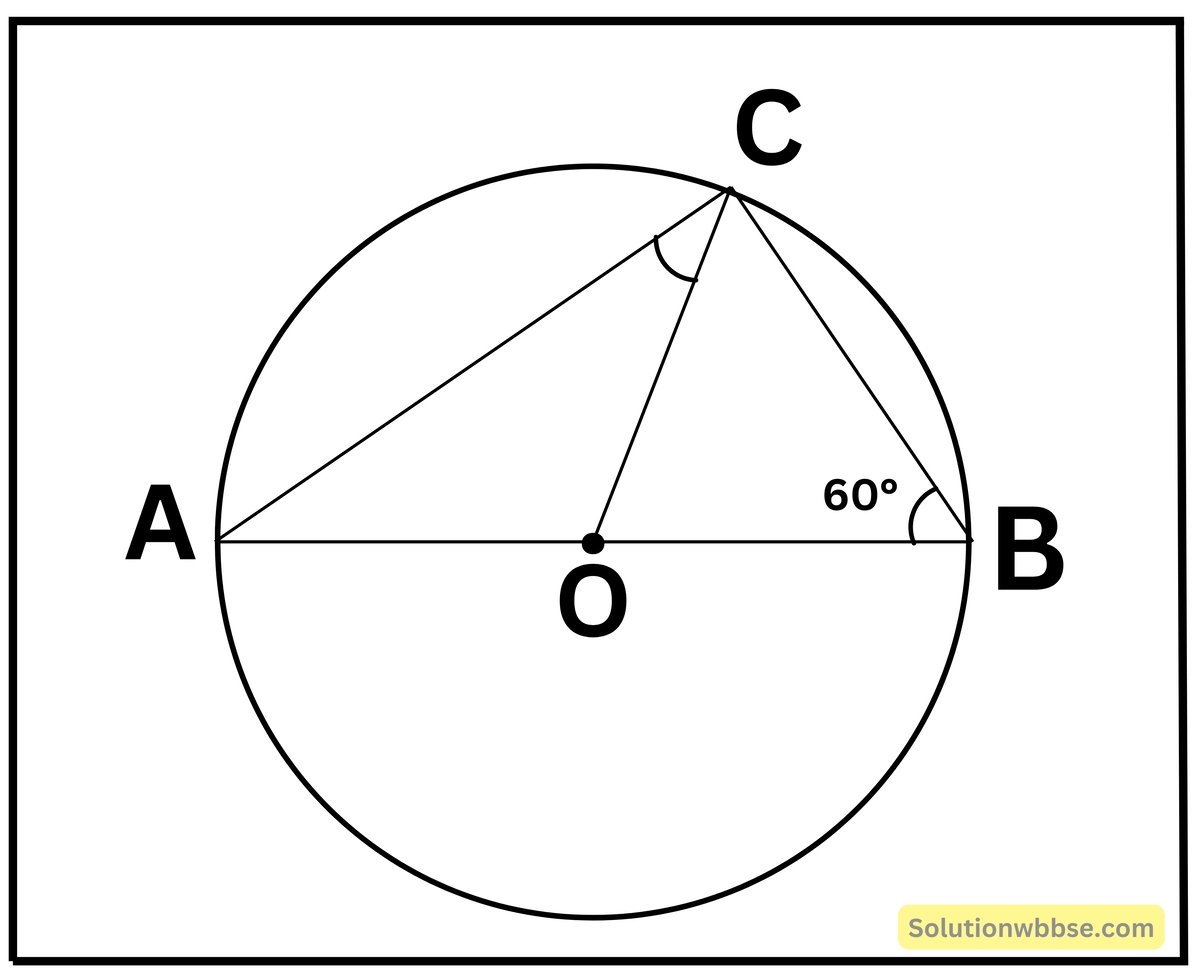
AOB বৃত্তটির একটি ব্যাস।

C বৃত্তের ওপর একটি বিন্দু।

∴ ∠ACB = 1 সমকোণ [∵ অর্ধবৃত্তস্থ কোণ 1 সমকোণ]

আবার, ∠OBC = 60°

∠ABC = 60°

∠BAC = 180° – (90° + 60°)

= 180° – 150°

= 30°

∴ ∠OAC = 30°

∴ ∠OCA = 30° [∵ OA = OC, একই বৃত্তের ব্যাসার্ধ]

(v) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস। জ্যা CD -এর দৈর্ঘ্য বৃত্তের ব্যাসার্ধের দৈর্ঘ্যের সমান। AC ও BD -কে বর্ধিত করায় P বিন্দুতে ছেদ করে। ∠APB -এর মান নির্ণয় করি।

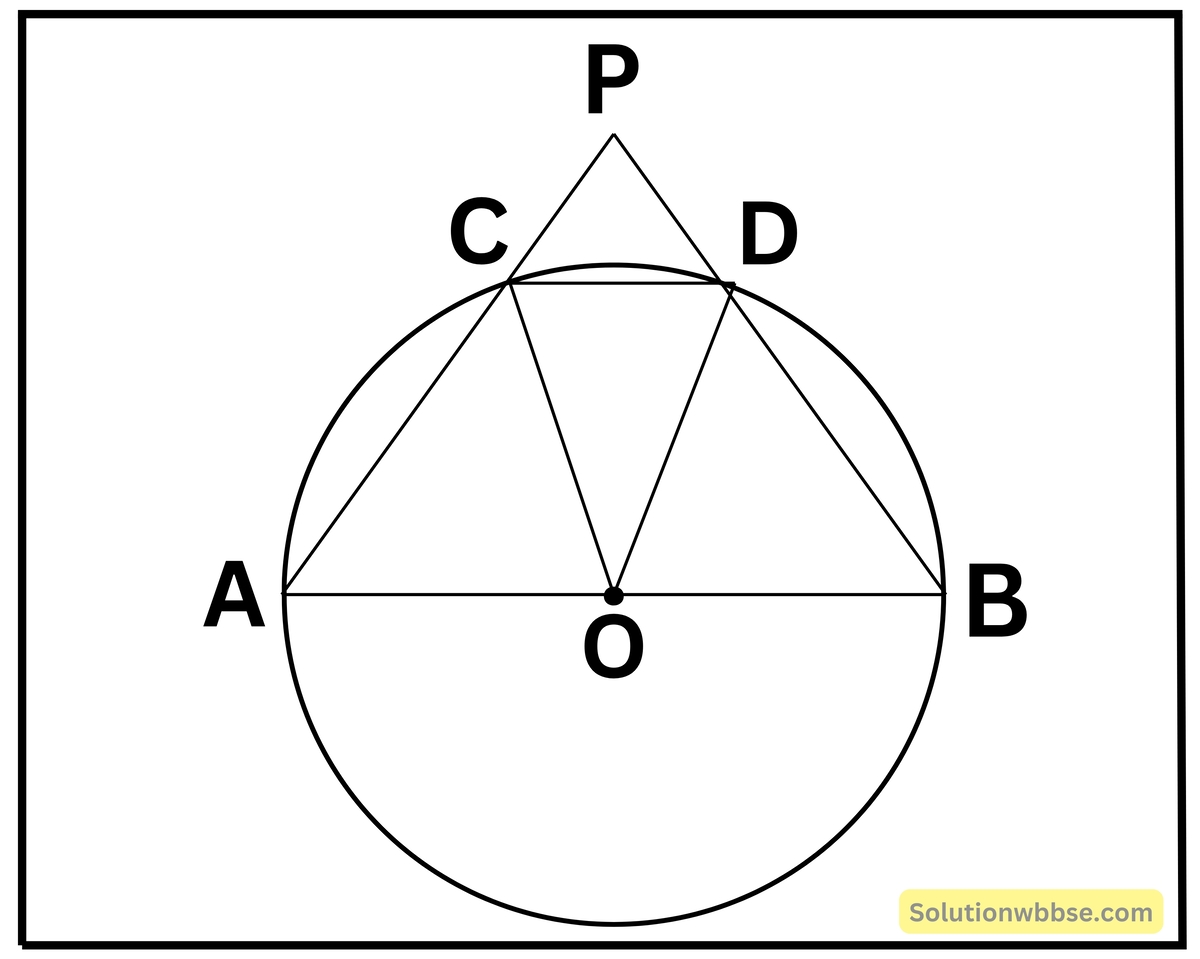
A, D যুক্ত করা হল।

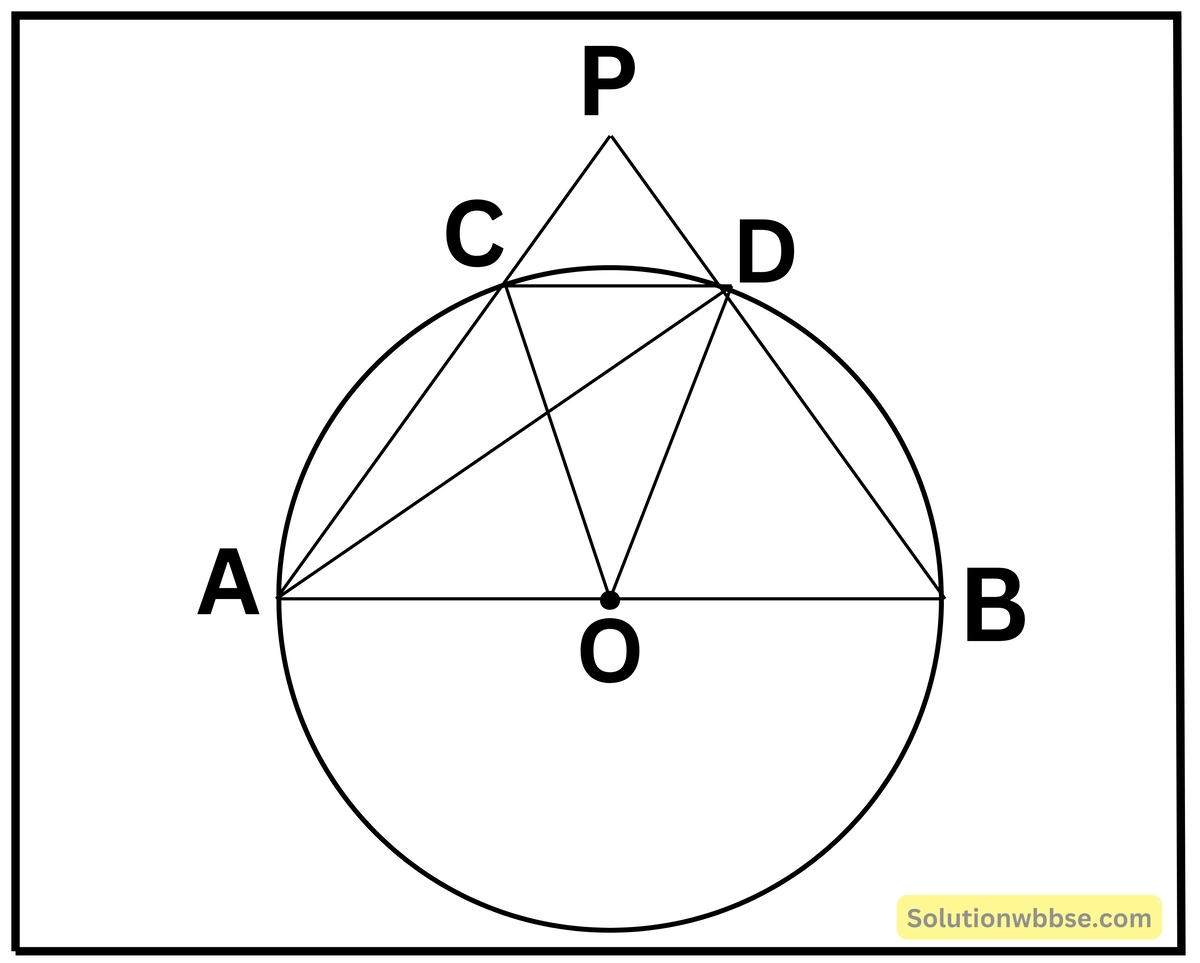
O বৃত্তের কেন্দ্র এবং AB ব্যাস।

জ্যা CD এর দৈর্ঘ্য বৃত্তের ব্যাসার্ধের দৈর্ঘ্য এর সমান

OC = OD = CD

∴ ΔOCD সমবাহু ত্রিভুজ

∴ ∠COD = 60° [যেহেতু, সমবাহু ত্রিভুজের প্রতিটি কোণের মাণ 60°]

∴ ∠CAD = 30°[যেহেতু, একই বৃত্তচাপের ওপর ∠COD কেন্দ্রস্থ কোণ এবং ∠CAD পরিধিস্থ কোণ এবং একই বৃত্তচাপের ওপর কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুণ।

আবার, ∠ADB অর্ধবৃত্তস্থ কোণ

∴ ∠ADB = 90°

∴ ∠ADP = 90°

∠APD = 180° – (∠ADP + ∠PAD)

= 180° – (90° + 30°)

= 180° – 120°

= 60°

∴ ∠APB = 60°

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের সপ্তম অধ্যায়, ‘বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য’ -এর ‘কষে দেখি – 7.3’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।

আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।