এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের একাদশ অধ্যায়, ‘সম্পাদ্য: ত্রিভুজের পরিবৃত্ত ও অন্তবৃত্ত অঙ্কন’ -এর ‘কষে দেখি – 11.1’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

1. নিম্নলিখিত ত্রিভুজগুলি অঙ্কন করি। প্রতিটি ত্রিভুজের পরিবৃত্ত অঙ্কন করে প্রতিক্ষেত্রে পরিকেন্দ্রের অবস্থান লিখি ও পরিব্যাসার্ধের [অর্থাৎ পরিবৃত্তের ব্যাসার্ধের দৈর্ঘ্য] দৈর্ঘ্য মেপে লিখি। [প্রতিক্ষেত্রে কেবলমাত্র অঙ্কন চিহ্ন দিই]
(i) একটি সমবাহু ত্রিভুজ যার প্রতিটি বাহুর দৈর্ঘ্য 6 সেমি.।
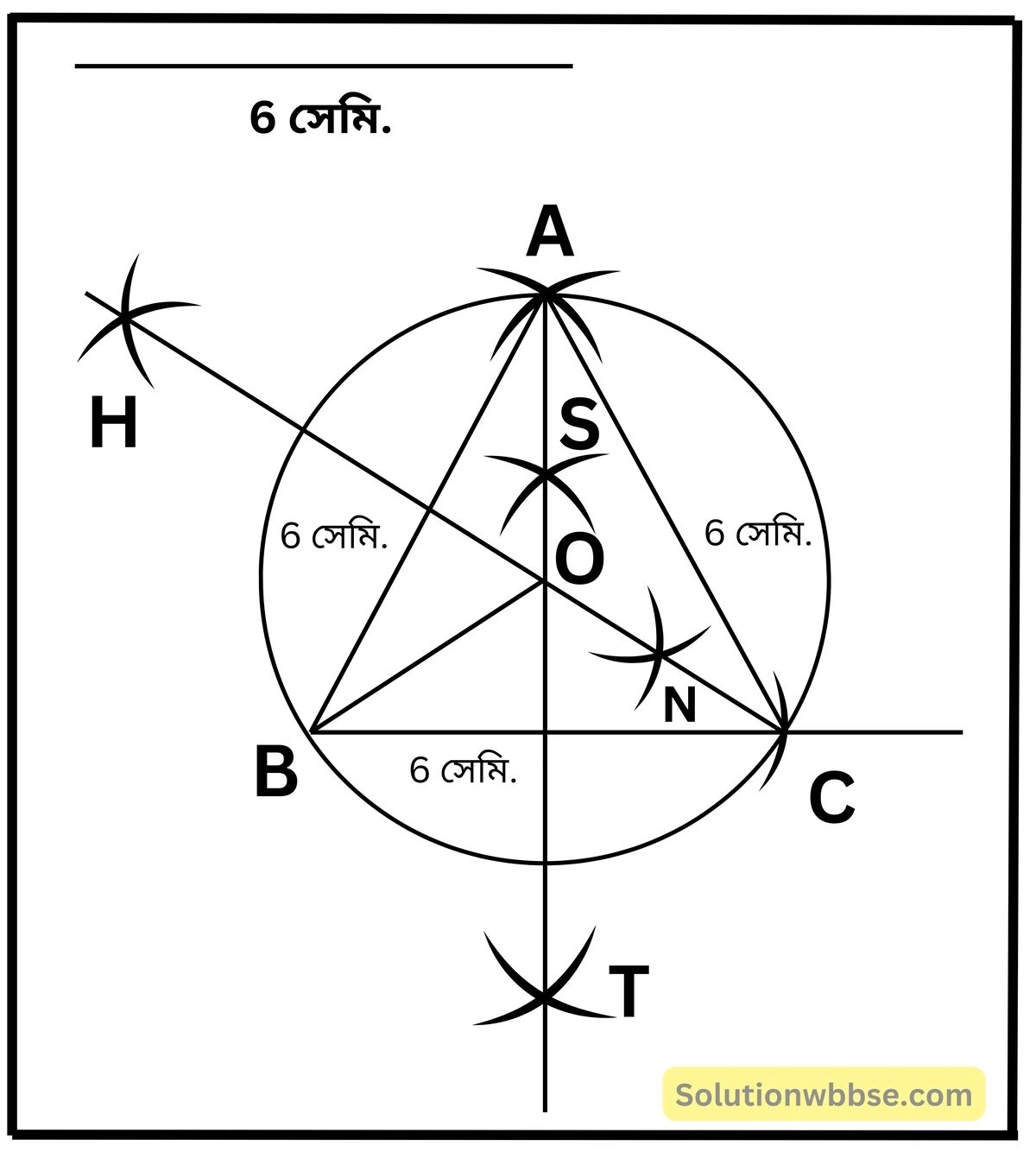
চিত্রে ABC হল 6 সেমি. বাহু বিশিষ্ট একটি সমবাহু ত্রিভুজ। যার পরিবৃত্ত অঙ্কন করলাম এবং ত্রিভুজটির পরিকেন্দ্র O ত্রিভুজাকার ক্ষেত্রটির ভিতরে অবস্থিত পরিব্যাসার্ধের দৈর্ঘ্য 3.5 সেমি. (প্রায়)।
(ii) একটি সমদ্বিবাহু ত্রিভুজ যার ভূমির দৈর্ঘ্য 5.2 সেমি. এবং সমান বাহুর প্রত্যেকটির দৈর্ঘ্য 7 সেমি.।
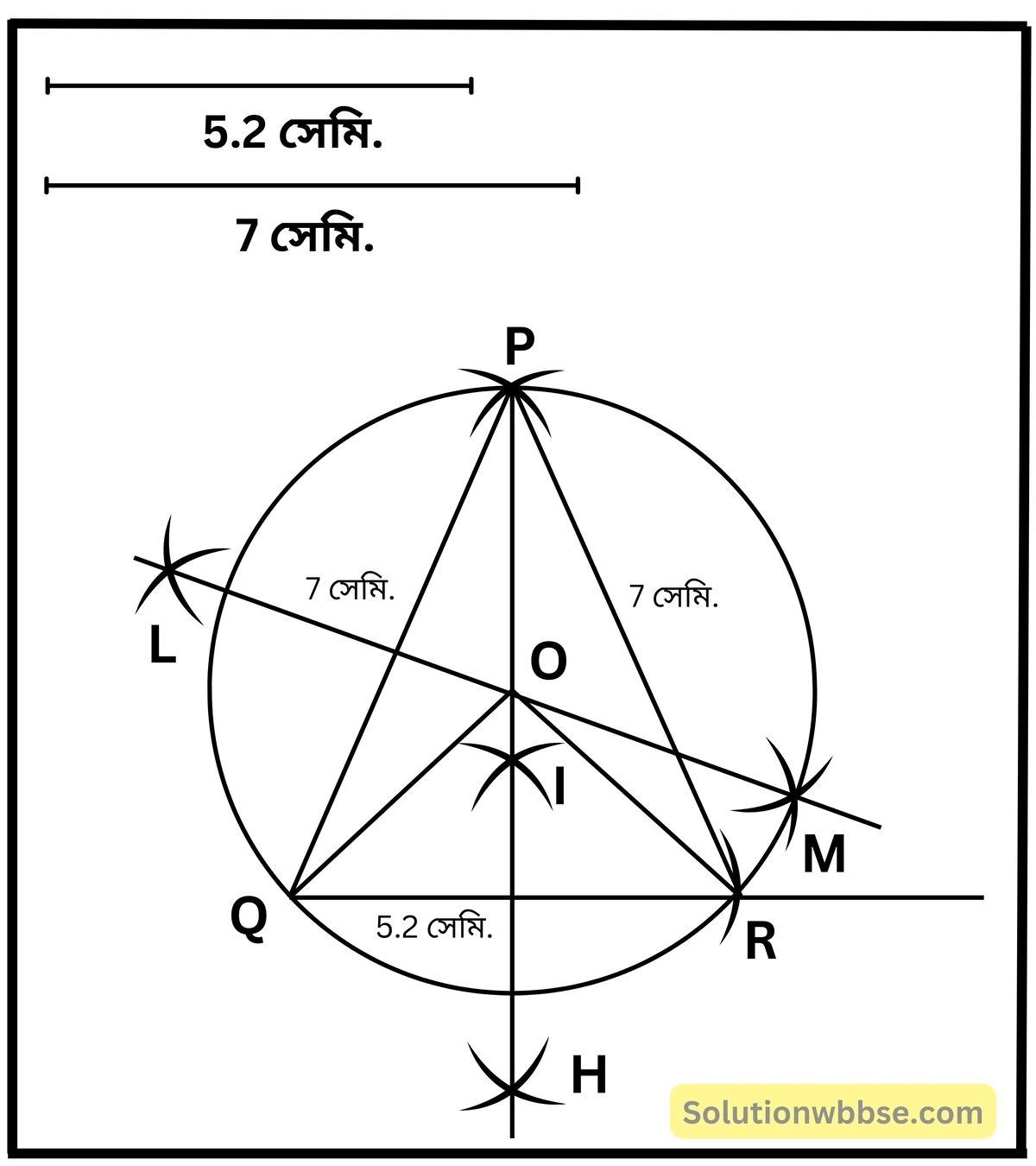
ত্রিভুজ PQR -এর পরিবৃত্ত অঙ্কন করা হল। যার পরিকেন্দ্র O ত্রিভুজাকার ক্ষেত্রটির ভিতরে অবস্থিত। যার পরি ব্যাসার্ধের দৈর্ঘ্য 4 সেমি. (প্রায়)।
(iii) একটি সমকোণী ত্রিভুজ যার সমকোণ সংলগ্ন বাহুদুটির দৈর্ঘ্য 4 সেমি. ও 8 সেমি.।
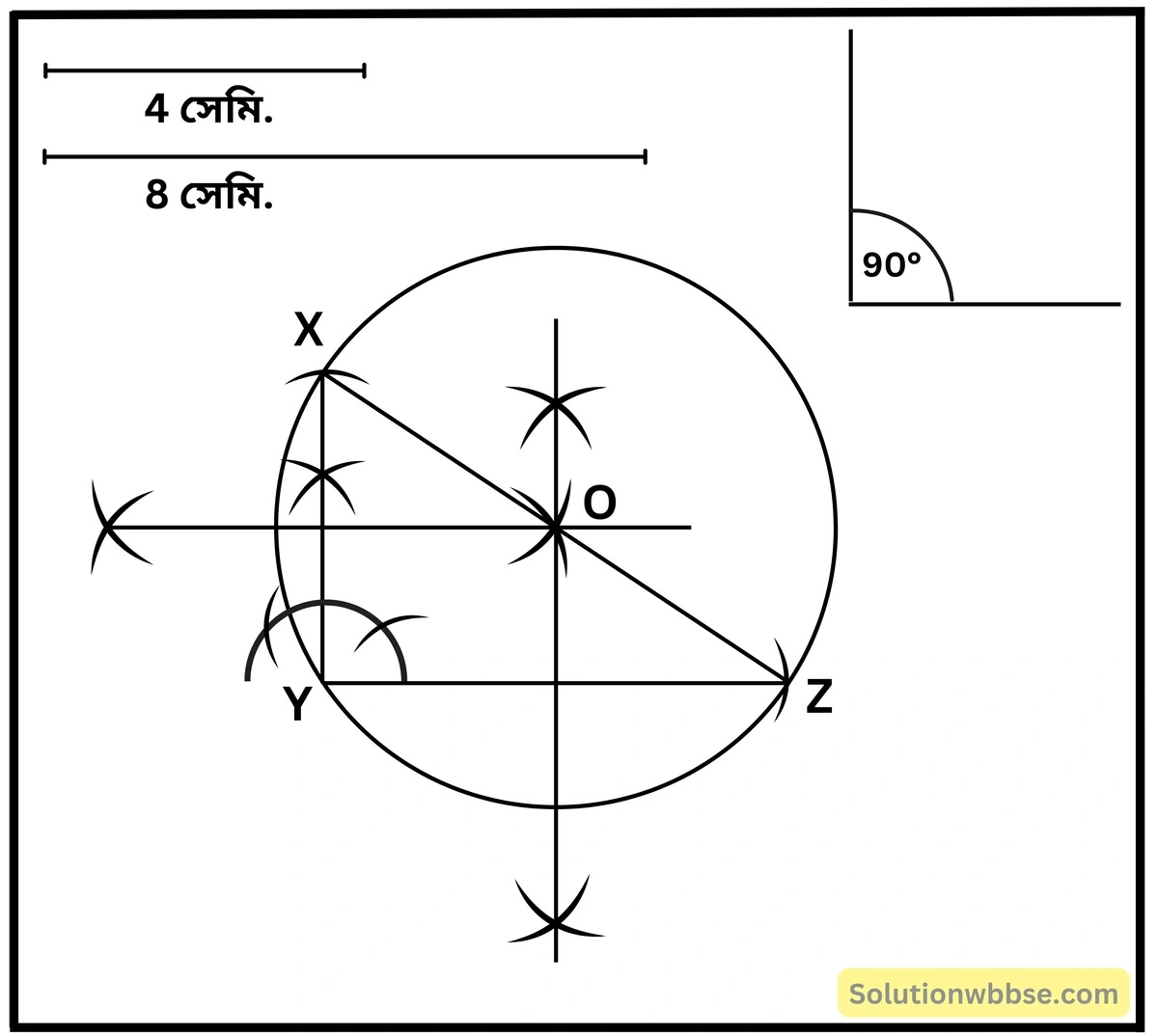
XYZ সমকোণী ত্রিভুজের পরিবৃত্ত আঁকলাম। যার পরিকেন্দ্র O অতিভুজের উপরে আছে এবং অতিভুজের মধ্যবিন্দুতে আছে পরিব্যাসার্ধের দৈর্ঘ্য 4.6 সেমি. (প্রায়)।
(iv) একটি সমকোণী ত্রিভুজ যার অতিভুজের দৈর্ঘ্য 12 সেমি. এবং অপর একটি বাহুর দৈর্ঘ্য 5 সেমি.।
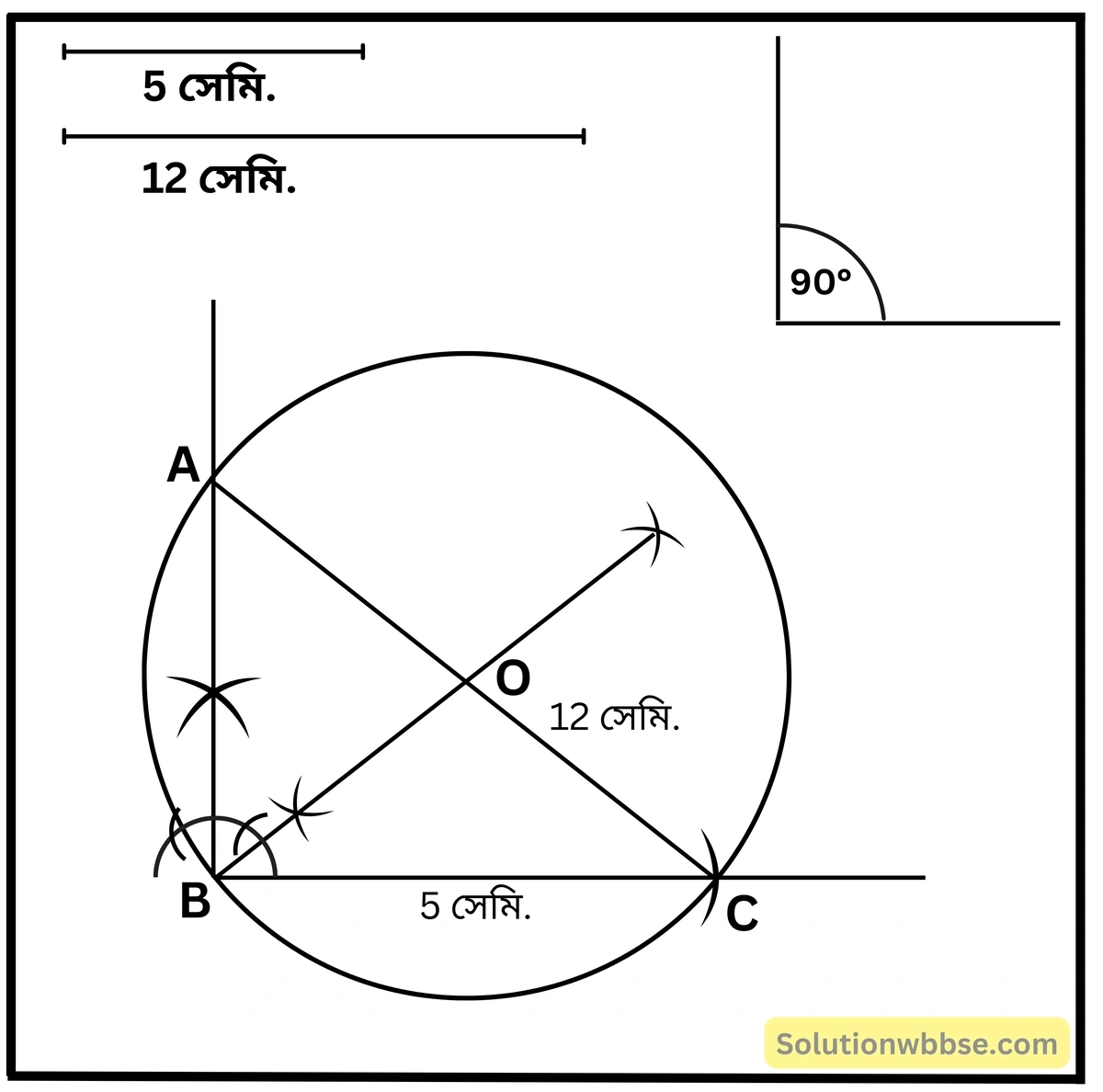
ABC সমকোণী ত্রিভুজের পরিবৃত্ত অঙ্কন – করলাম। যার পরিকেন্দ্র O এবং পরিকেন্দ্র অতিভুজ AC-এর মধ্যবিন্দু। পরিব্যাসার্ধের দৈর্ঘ্য 6 সেমি. (প্রায়)।
(v) একটি ত্রিভুজ আঁকি যার একটি বাহুর দৈর্ঘ্য 6.7 সেমি. এবং বাহুসংলগ্ন কোণ দুটির পরিমাণ 75° ও 55°.
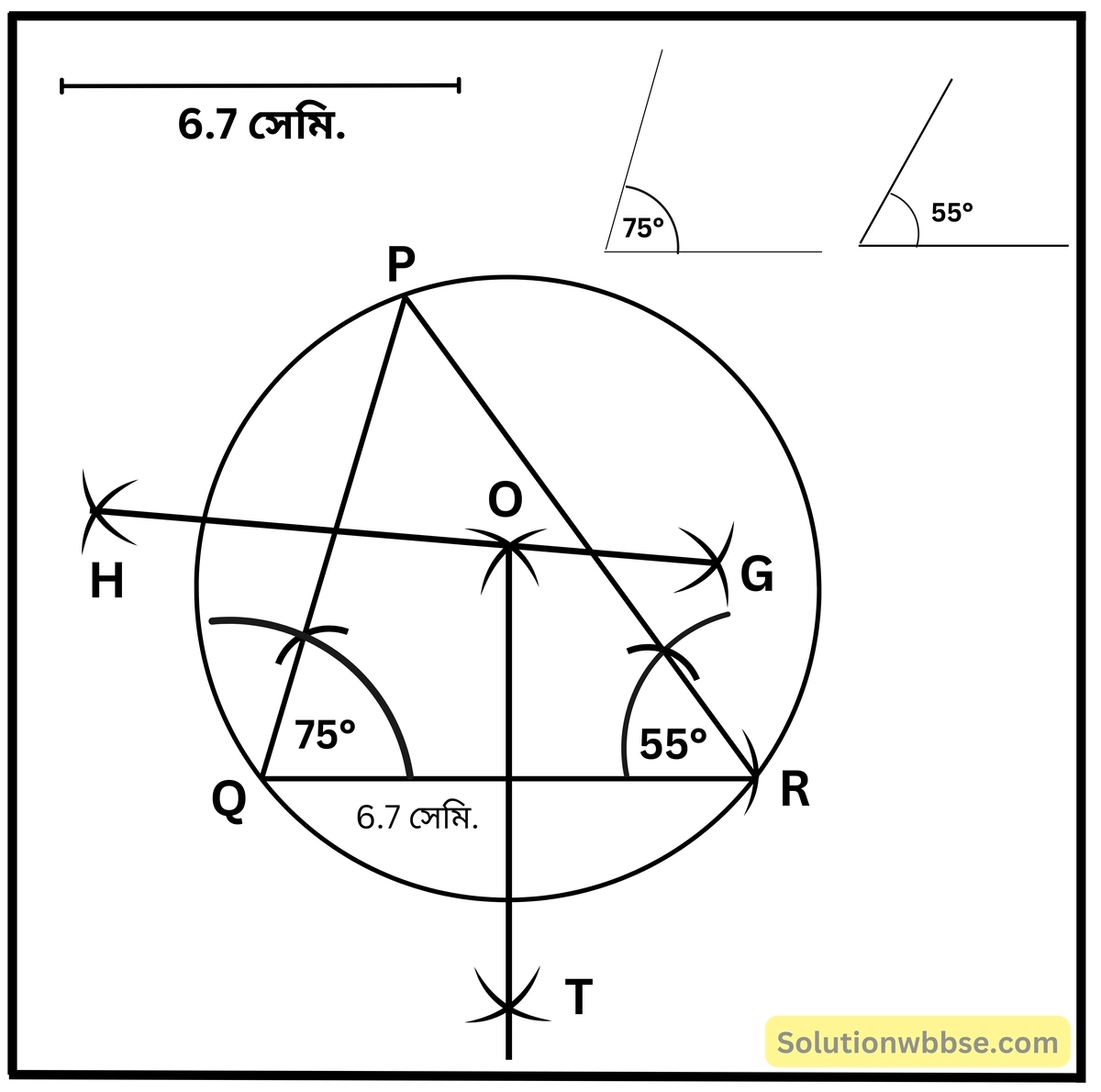
ত্রিভুজ PQR-এর পরিবৃত্ত অঙ্কন করলাম। যার পরিকেন্দ্র O ত্রিভুজাকার ক্ষেত্রের ভিতরে অবস্থিত এবং পরিবৃত্তের ব্যাসার্ধের দৈর্ঘ্য 4.6 সেমি.।
(vi) ABC একটি ত্রিভুজ যার ভূমি BC = 5 সেমি., ∠ABC = 100° এবং AB = 4 সেমি.
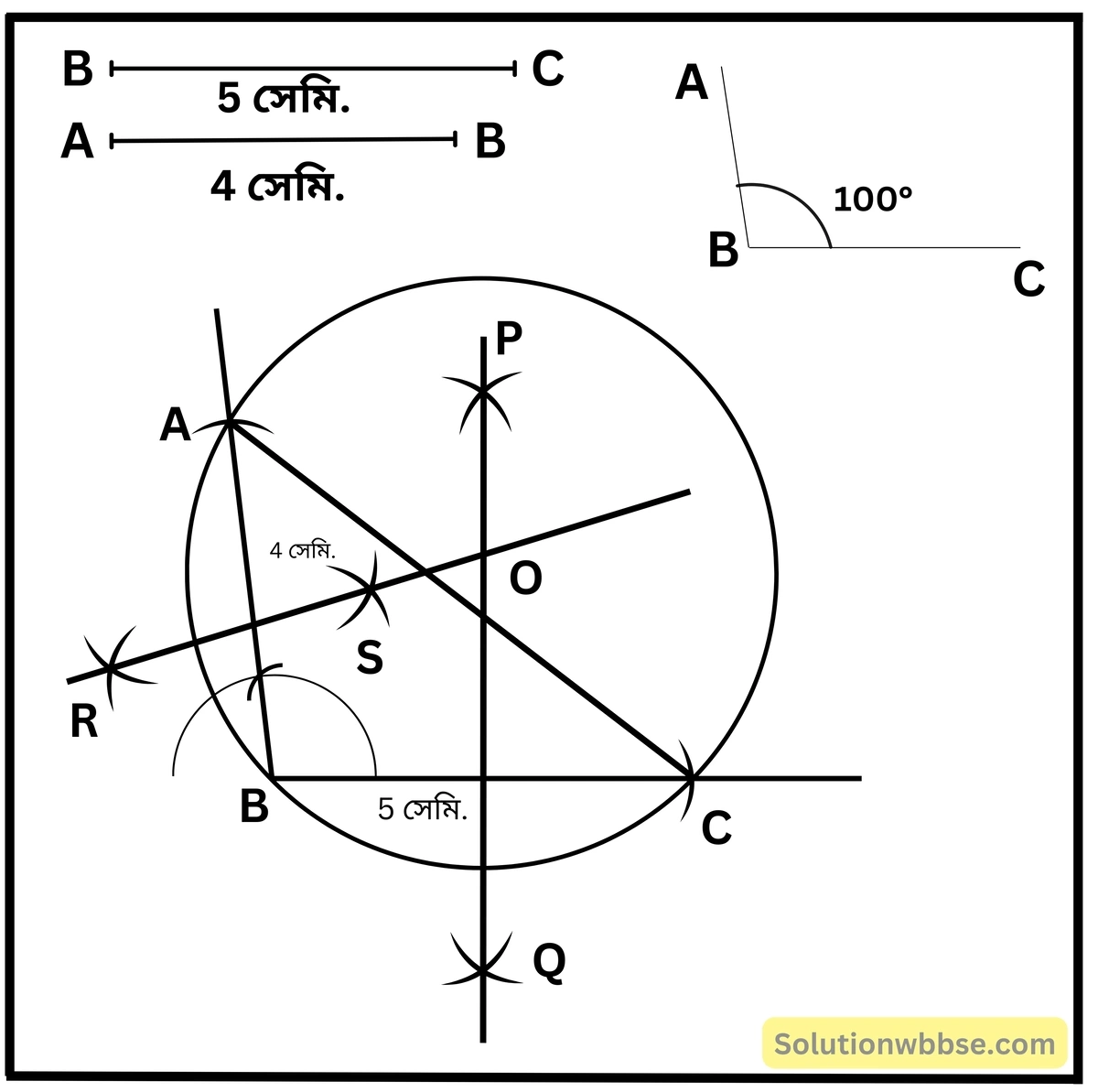
চিত্রে ABC ত্রিভুজের পরিবৃত্ত অঙ্কন করলাম। যার পরিবৃত্ত ত্রিভুজাকার ক্ষেত্রের বাহিরে অবস্থিত এবং পরিব্যাসার্ধের দৈর্ঘ্য 3.7 সেমি.।
2. PQ = 7.5 সেমি. ∠QPR = 45°, ∠PQR = 75°;
PQ = 7.5 সেমি. ∠QPS = 60°, ∠PQS = 60°;
∆PQR ও ∆PQS এমনভাবে অঙ্কন করি যে R ও S বিন্দু যেন PQ -এর একই দিকে অবস্থিত হয়। ∆PQR -এর পরিবৃত্ত অঙ্কন করি এবং এই পরিবৃত্তের সাপেক্ষে S বিন্দুর অবস্থান তার ভিতরে, উপরে, না বাহিরে তা লক্ষ করে লিখি ও তার ব্যাখ্যা খুঁজি।
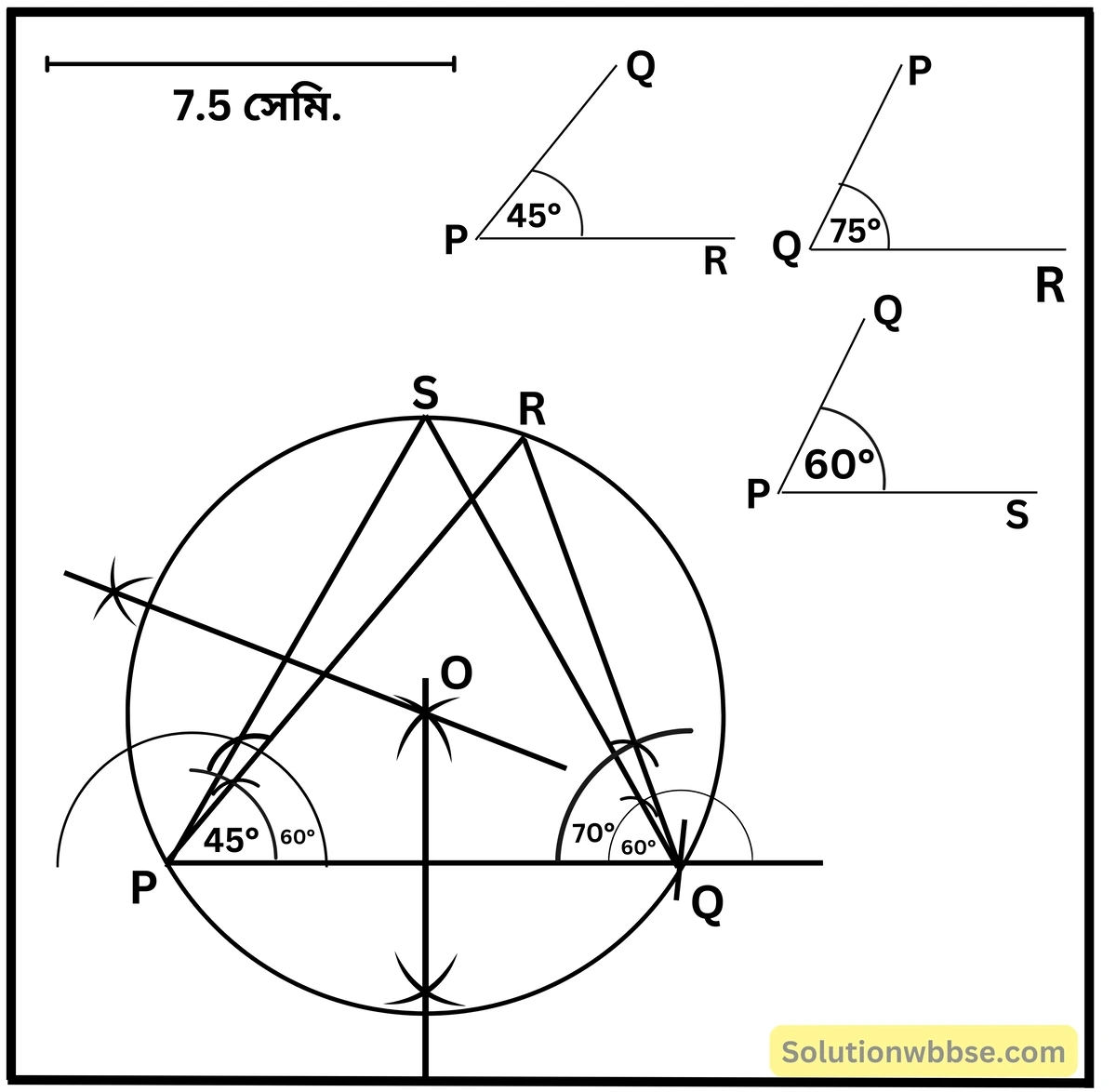
ত্রিভুজ PQR -এর পরিবৃত্ত অঙ্কন করলাম এবং S বিন্দু PQR ত্রিভুজের পরিবৃত্তের উপর অবস্থিত।
3. AB = 5 সেমি. ∠BAC = 30°, ∠ABC = 60°;
AB = 5 সেমি. ∠BAD = 45°, ∠ABD = 45°;
∆ABC ও ∆ABD এমনভাবে অঙ্কন করি যে, C ও D বিন্দু যেন AB -এর বিপরীত পার্শ্বে অবস্থিত হয়। ∆ABC -এর পরিবৃত্ত অঙ্কন করি এবং ওই পরিবৃত্তের সাপেক্ষে D বিন্দুর অবস্থান লিখি। এছাড়াও অন্য কী কী বৈশিষ্ট্য লক্ষ করছি বুঝে লিখি।
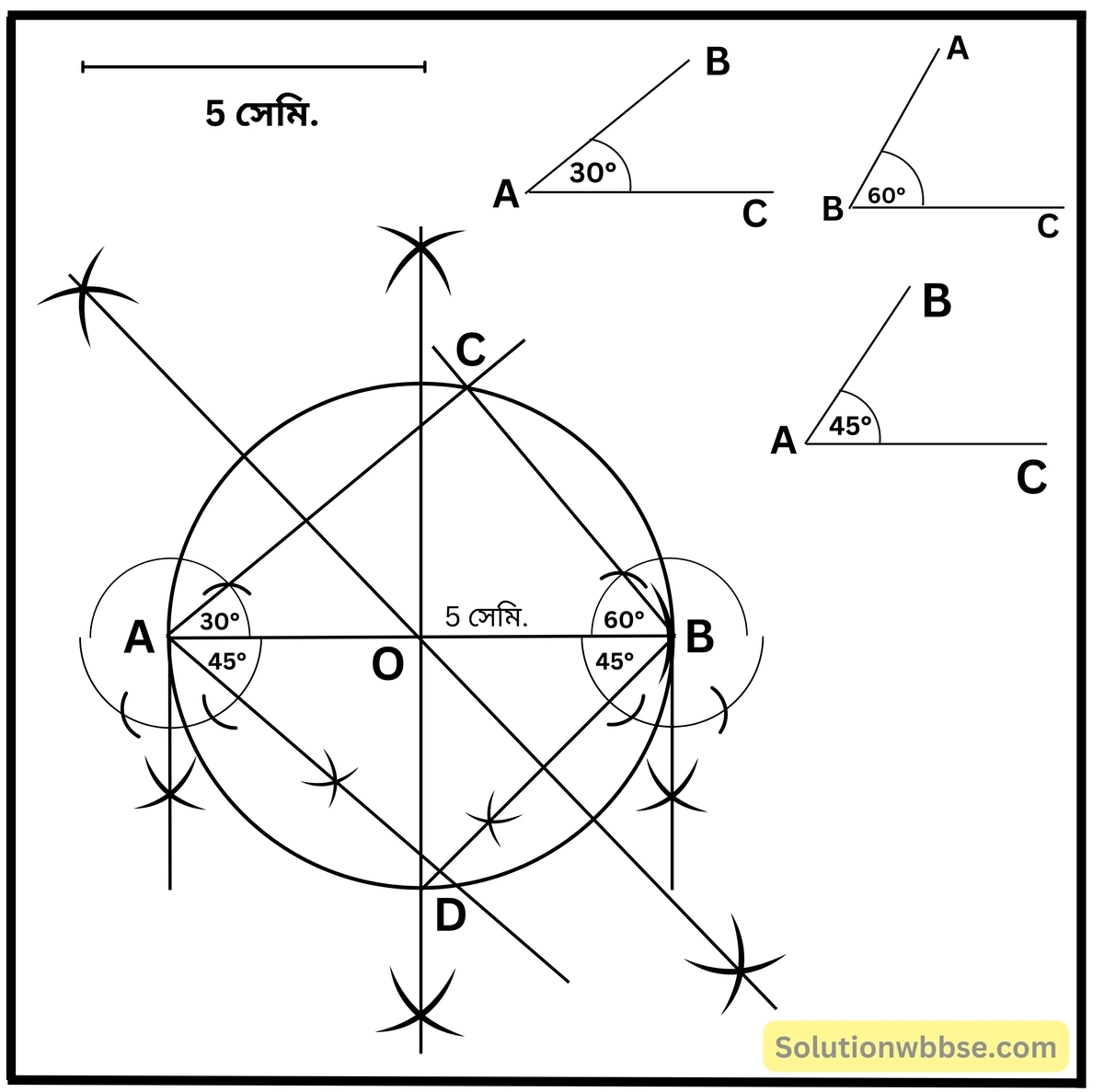
চিত্রে ∆ABC -এর পরিবৃত্ত অঙ্কন করা হল, এবং D বিন্দু ত্রিভুজ ABC -এর পরিবৃত্তের উপরে অবস্থিত এবং পরিকেন্দ্র AB -এর মধ্যবিন্দুর উপর অবস্থিত।
4. ABCD একটি চতুর্ভুজ অঙ্কন করি যার AB = 4 সেমি., BC = 7 সেমি., CD = 4সেমি., ∠ABC = 60°, ∠BCD = 60°; ΔΑΒC -এর পরিবৃত্ত অঙ্কন করি এবং এর কী কী বৈশিষ্ট্য লক্ষ করছি বুঝে লিখি।
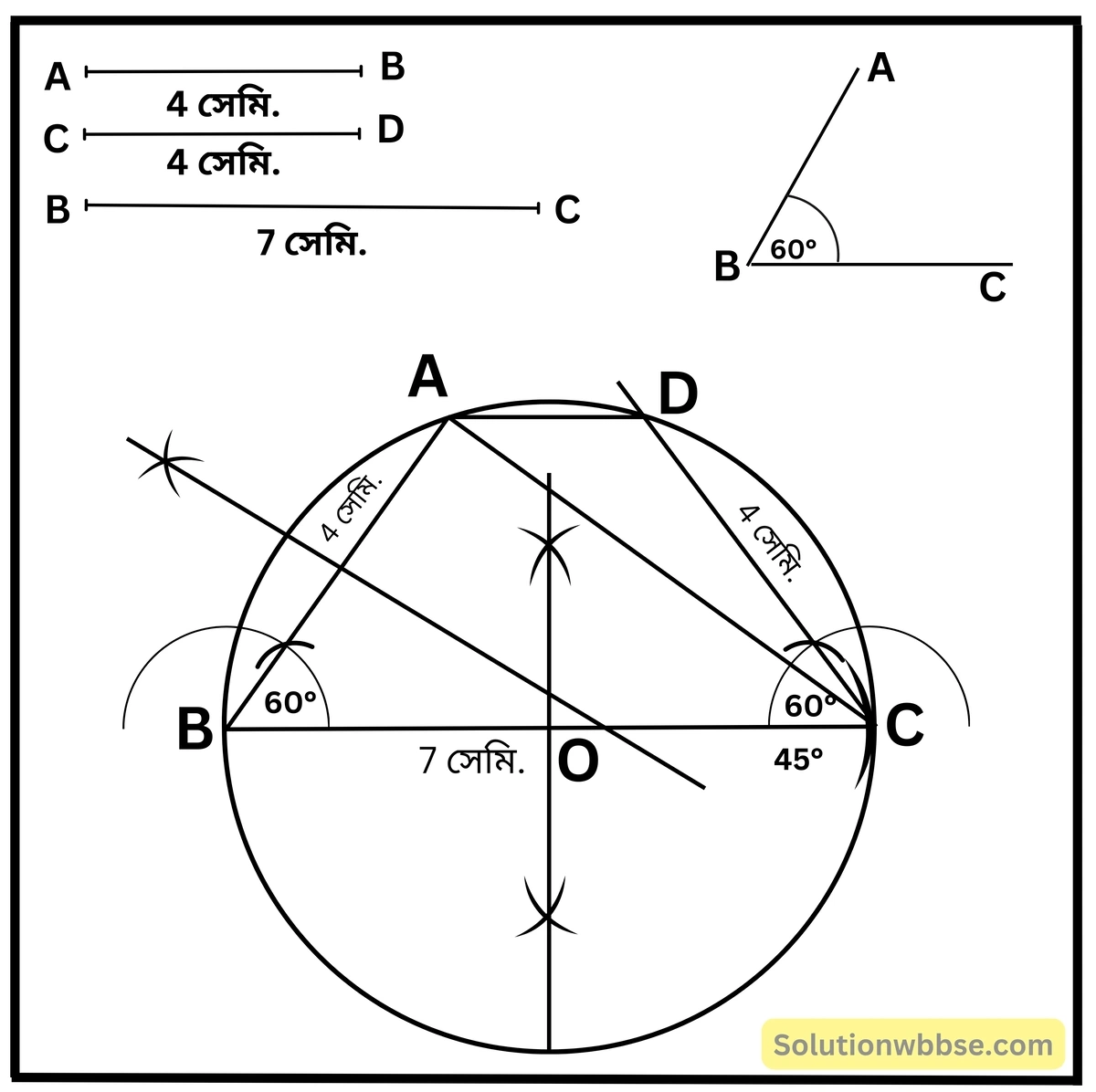
∆ABC -এর পরিবৃত্ত অঙ্কন করলাম। যার পরিকেন্দ্র O এবং এই পরিকেন্দ্রটি ত্রিভুজ ABC ও চতুর্ভুজ ABCD -এর ভিতরে অবস্থিত।
5. একটি আয়তক্ষেত্র PQRS অঙ্কন করি যার PQ = 4 সেমি. এবং QR = 6 সেমি.। আয়তক্ষেত্রের কর্ণদুটি অঙ্কন করি এবং অঙ্কন না করে ∆PQR -এর পরিকেন্দ্র কোথায় হবে এবং পরিব্যাসার্ধের দৈর্ঘ্য কত হবে হিসাব করে লিখি।
∆PQR -এর পরিবৃত্ত অঙ্কন করে যাচাই করি।
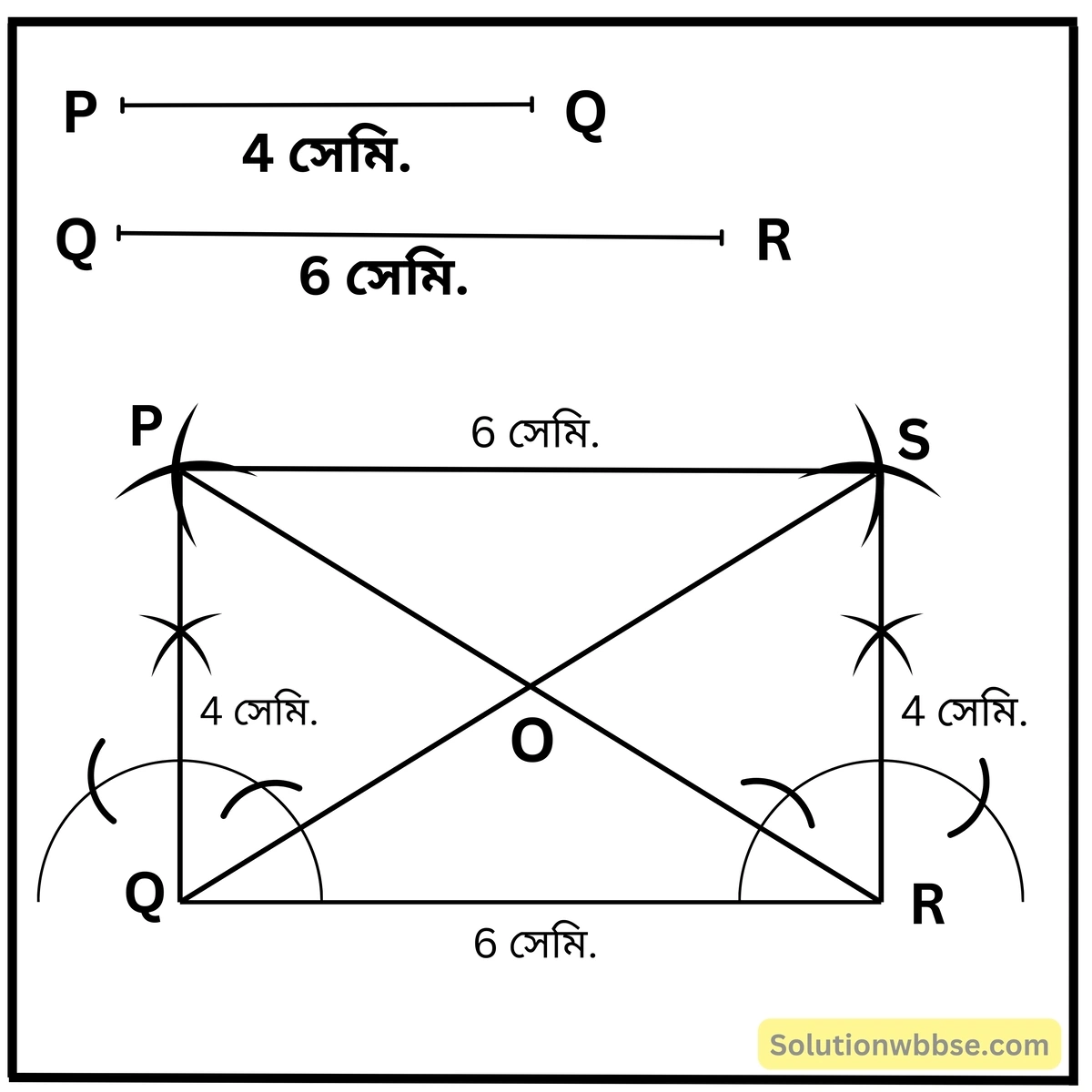
PQRS আয়তক্ষেত্রের কর্ণদুটি PQ এবং RS অঙ্কন করা হল। ∆PQR -এর পরিকেন্দ্র PQRS আয়তক্ষেত্রের কর্ণদ্বয়ের ছেদ বিন্দু O -তে অবস্থিত হবে এবং পরিব্যাসার্ধের দৈর্ঘ্য 3.8 সেমি হবে।
∆PQR -এর পরিবৃত্ত অঙ্কন করা হল। যার পরিকেন্দ্র O এবং পরিব্যাসার্ধের দৈর্ঘ্য 3.8 সেমি. হবে।
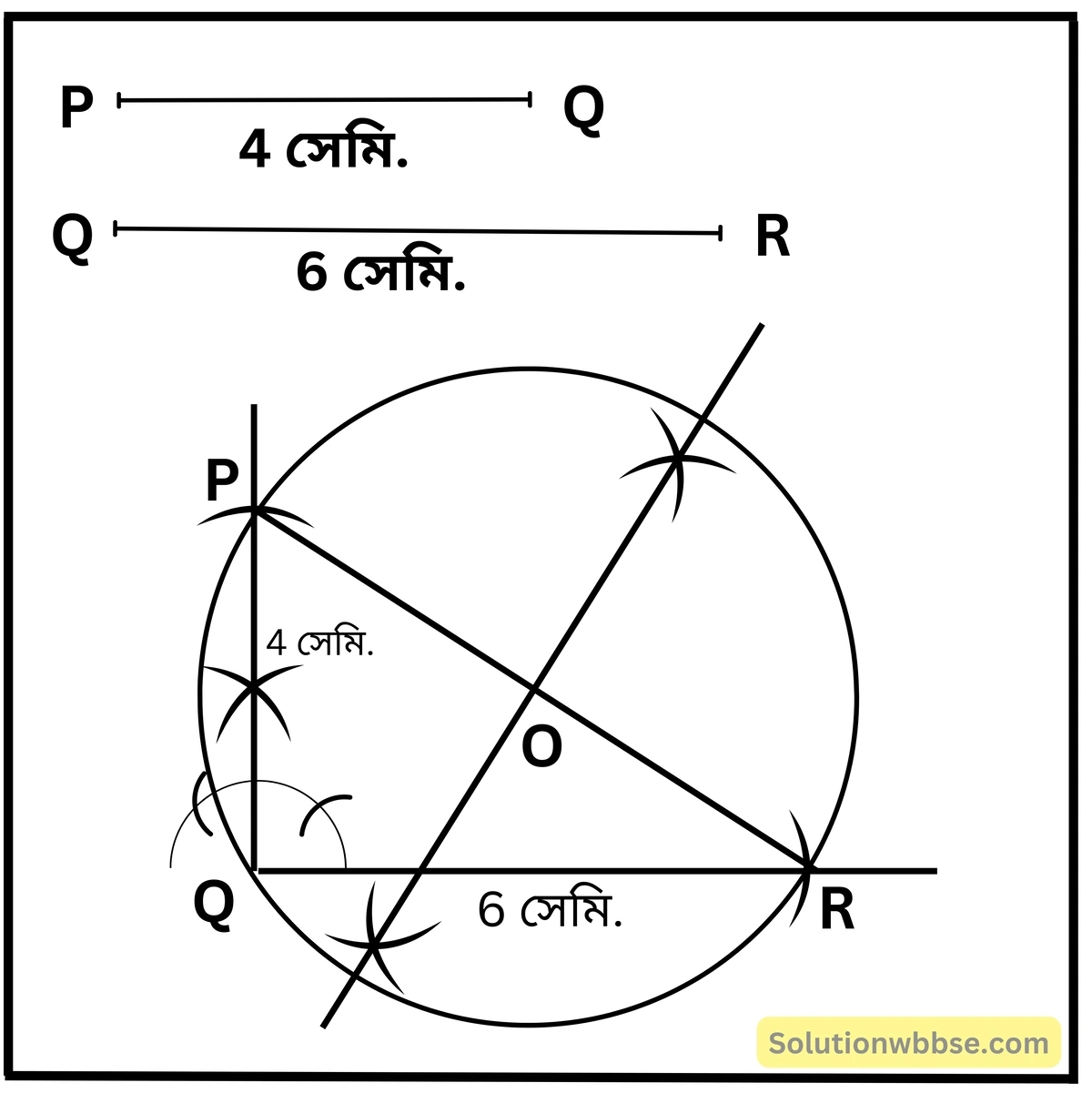
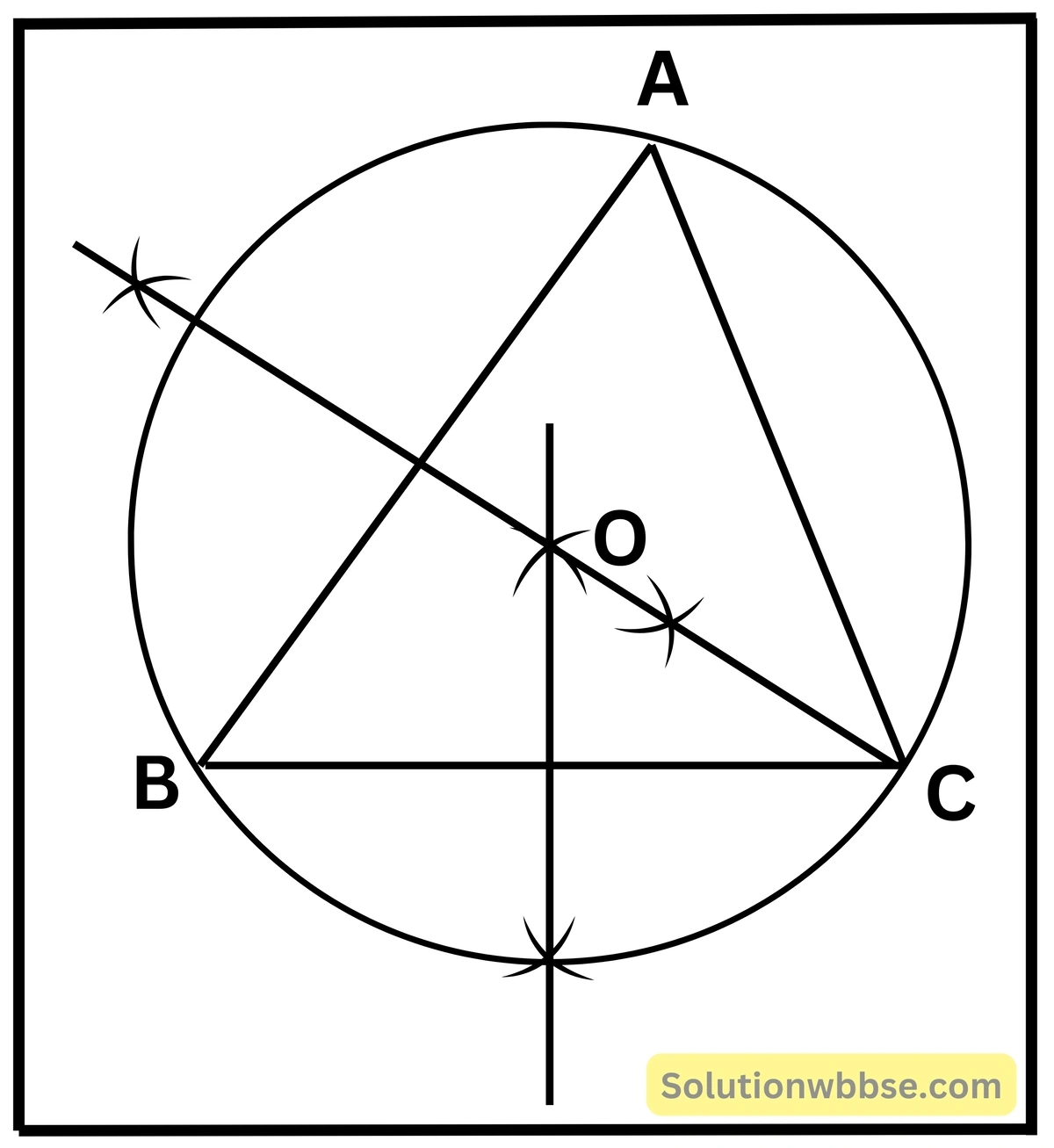
6. যে-কোনো বৃত্তাকার চিত্র প্রদত্ত হলে তার কেন্দ্র কীরূপে নির্ণয় করব? পাশের বৃত্তাকার চিত্রের কেন্দ্র নির্ণয় করি।
যে কোনো বৃত্তাকার চিত্র প্রদত্ত হলে তার ভিতরে যে-কোনো একটি ত্রিভুজ অঙ্কন করিতে হইবে। তারপর ত্রিভুজটির যে-কোনো দুটি বাহুর লম্ব সমদ্বিখণ্ডক অঙ্কন করিতে হইবে এবং এই লম্ব সমদ্বিখণ্ডকদ্বয়ের ছেদ বিন্দু হল প্রদত্ত বৃত্তাকার চিত্রের কেন্দ্র।
এই বৃত্তাকার চিত্রটির কেন্দ্র O।
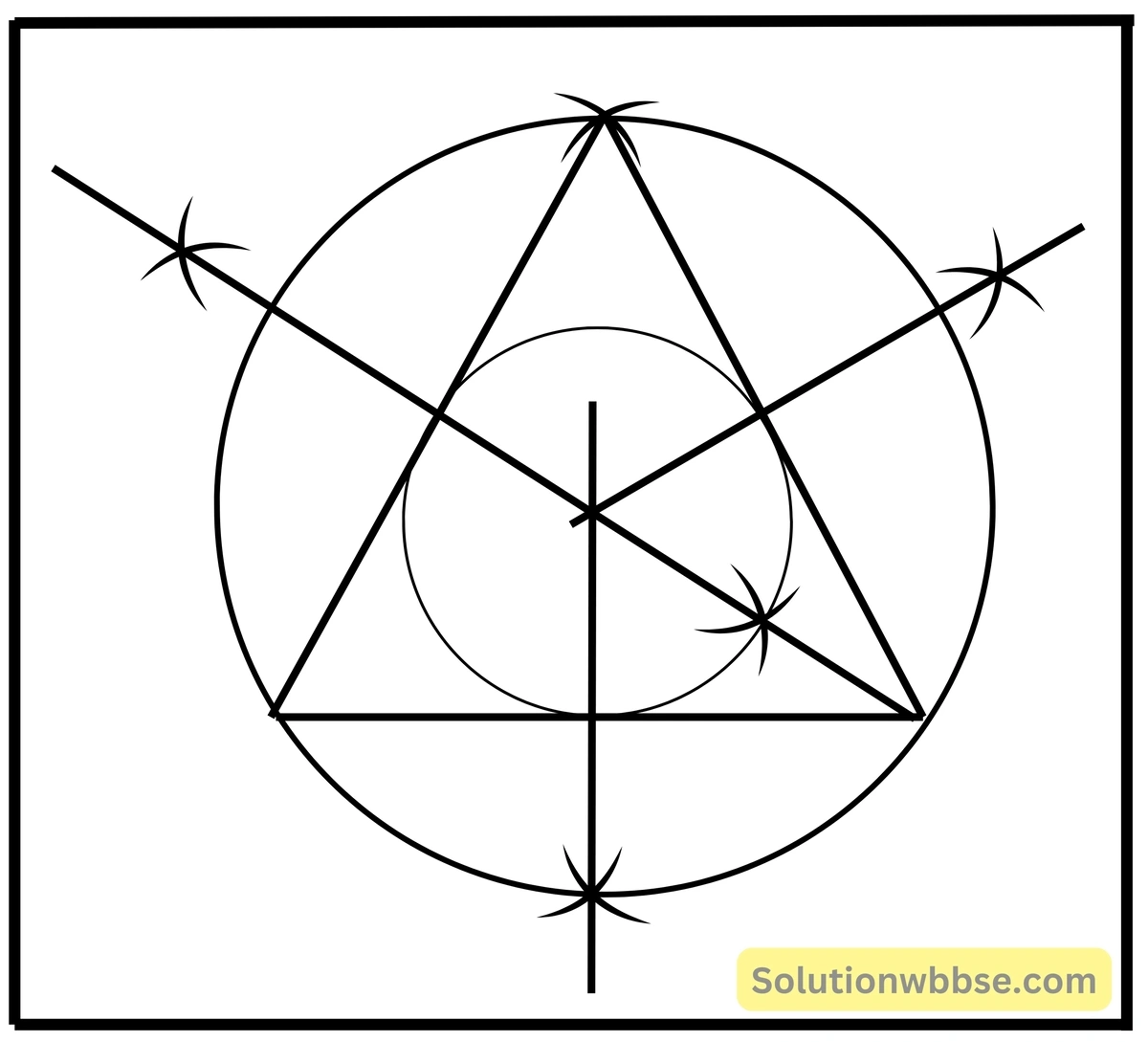
সমবাহু ত্রিভুজের পরিকেন্দ্র ও অন্তঃকেন্দ্র কোথায় অবস্থিত হবে অঙ্কন করে যাচাই করি –
সমবাহু ত্রিভুজে পরিকেন্দ্র ও অন্তঃকেন্দ্র অঙ্কন করে দেখেছি, সমবাহু ত্রিভুজের পরিকেন্দ্র ও অন্তঃকেন্দ্র একই বিন্দু।
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের একাদশ অধ্যায়, ‘সম্পাদ্য: ত্রিভুজের পরিবৃত্ত ও অন্তবৃত্ত অঙ্কন’ -এর ‘কষে দেখি – 11.1’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment