এই আর্টিকেলে আমরা WBBSE বোর্ডের 2026 সালের মাধ্যমিক গণিত বিষয়ের সাজেশন নিয়ে আলোচনা করবো। এখানে দেওয়া শূন্যস্থান পূরণগুলো আসন্ন মাধ্যমিক পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ।

Madhyamik Mathematics Suggestion 2026 – শূন্যস্থান পূরণ
পাটিগণিত
1. আসল বা মূলধন এবং কোনো নির্দিষ্ট সময়ের চক্রবৃদ্ধি সুদের সমষ্টিকে ______ বলে। [M.P. 2024]
উত্তর – সবৃদ্ধিমূল
2. 180 টাকার বছরের সুদ-আসল 198 টাকা হলে বার্ষিক সরল সুদের হার ______ । [M.P. 2023]
উত্তর – 10%
সমাধান – সুদের হার = \(\frac{18}{180} \times 100\% = 10\%\)
3. বার্ষিক চক্রবৃদ্ধি সুদের হার r% এবং প্রথম বছরের মূলধন P টাকা হলে, দ্বিতীয় বছরের মূলধন ______ । [M.P. 2022]
উত্তর – \(P(1 + \frac{r}{100})\) টাকা
4. 7√11 একটি ______ সংখ্যা। [M.P. 2022]
উত্তর – অমূলদ
5. আনিসুর 500 টাকা 9 মাসের জন্য এবং ডেভিড 600 টাকা 5 মাসের জন্য একটি যৌথ ব্যবসায় নিয়োজিত করে। তাদের লভ্যাংশের অনুপাত হবে ______ । [M.P. 2020]
উত্তর – 3 : 2
সমাধান –
এক মাসের সাপেক্ষে আনিসুর ও ডেভিডের মূলধনের অনুপাত
= \(9 \times 500 : 5 \times 600 = 3 : 2\)
∴ লভ্যাংশের অনুপাত = মূলধনের অনুপাত = 3 : 2
6. এক ব্যক্তি ব্যাঙ্কে 100 টাকা জমা রেখে 2 বছর পর সমূল চক্রবৃদ্ধি পেলেন 121 টাকা। বার্ষিক সুদের হার ছিল ______ । [M.P. 2019]
উত্তর – 10%
সমাধান –
∵ \(P(1 + \frac{r}{100})^n = A\) ∴ \(100(1 + \frac{r}{100})^2 = 121\)
বা, \((1 + \frac{r}{100})^2 = (\frac{11}{10})^2\)
বা, \(1 + \frac{r}{100} = \frac{11}{10}\)
বা, \(\frac{r}{100} = \frac{1}{10}\)
বা, \(r = 10\)
7. বার্ষিক r% সরল সুদের হারে কোনো মূলধনের n বছরের সুদ \(\frac{pnr}{25}\) টাকা হলে মূলধনের পরিমাণ ______ টাকা হবে।
উত্তর – \(4p\) টাকা
সমাধান – আসল = \(\frac{pnr \times 100}{25 \times n \times r}\) টাকা = \(4p\) টাকা [M.P. 2018]
8. কোনো মূলধন বার্ষিক শতকরা একই সুদের হারে ______ বছরের সরলসুদ ও চক্রবৃদ্ধি সুদের পরিমাণ সমান।
উত্তর – এক [M.P. 2017]
9. যে ব্যক্তি টাকা ধার দেন তাঁকে ______ বলে।
উত্তর – উত্তমর্ণ বা পাওনাদার
10. নির্দিষ্ট পরিমাণ টাকার বার্ষিক নির্দিষ্ট শতকরা হার সুদে এক বছরের চক্রবৃদ্ধি সুদের পরিমাণ এবং সরল সুদের পরিমাণ ______ ।
উত্তর – সমান
11. দুই ব্যক্তি কোনো ব্যবসাতে a টাকা ও b টাকা যথাক্রমে \(n_1\) একক সময় ও \(n_2\) একক সময়ের জন্য বিনিয়োগ করলে তাদের লভ্যাংশের অনুপাত হবে ______ ।
উত্তর – \(an_1 : bn_2\)
সমাধান – লভ্যাংশের অনুপাত = মূলধনের অনুপাত = \(an_1 : bn_2\)
12. অন্য কোনো শর্ত ছাড়া অংশীদারি ব্যবসায় অংশীদারগণ ভিন্ন ভিন্ন সময়ের জন্য মূলধন নিয়োজিত করলে তাকে ______ অংশীদারি কারবার বলে।
উত্তর – মিশ্র
13. সময়ের সঙ্গে কোন নির্দিষ্ট হারে হ্রাস হলে সেটি সমহার ______ ।
উত্তর – হ্রাস
14. যে ব্যক্তি টাকা ধার নেন তাঁকে ______ বলে。
উত্তর – অধমর্ণ বা দেনাদার
15. বার্ষিক \(\frac{r}{2}\%\) সরল সুদের হারে 2p টাকার t বছরের সুদ-আসল (2p + ______) টাকা।
উত্তর – \(\frac{prt}{100}\)
সমাধান –
সুদ (I) = \(\frac{2p \times \frac{r}{2} \times t}{100} = \frac{prt}{100}\) টাকা
\(\therefore\) সুদাসল = \(\left(2p + \frac{prt}{100}\right)\) টাকা
16. অন্য কোনো শর্ত ছাড়া অংশীদারি ব্যবসায় অংশীদারগণ সমান সময়ের জন্য মূলধন নিয়োজিত করলে তাকে ________ অংশীদারি কারবার বলে।
উত্তর – সরল
17. 1 বছরে আসল ও সুদ-আসলের অনুপাত 8 : 9 হলে বার্ষিক সরল সুদের হার ________ ।
উত্তর – 12.5%
সমাধান – ধরি, আসল (p) = 8x টাকা
∴ সুদ-আসল (A) = 9x টাকা
∴ সুদ (I) = (9x – 8x) = x টাকা
∴ \(I = \frac{prt}{100}\) বা, \(x = \frac{8x \cdot r \cdot 1}{100}\)
বা, \(r = \frac{25}{2} = 12.5\)
18. অংশীদারি কারবার ________ ধরনের।
উত্তর – দুই
বীজগণিত
19. P-এর মান কত হলে (P – 3)x² + 5x + 10 = 0 সমীকরণটি দ্বিঘাত সমীকরণ হবে না। P = ______ [M.P. 2024]
উত্তর – 3
20. a²bc এবং 4bc-এর মধ্য সমানুপাতী x হলে, x-এর মান ______ । [M.P. 2023]
উত্তর – \(2abc\)
সমাধান – \(a^2bc : x :: x : 4bc\)
বা, \(\frac{a^2bc}{x} = \frac{x}{4bc}\)
বা, \(x^2 = 4a^2b^2c^2\) ∴ \(x = 2abc\)
21. 5√11 একটি ______ সংখ্যা [M.P. 2022]
উত্তর – অমূলদ
22. ax² + 2bx + c = 0 (a ≠ 0), দ্বিঘাত সমীকরণের বীজদ্বয় বাস্তব ও সমান হলে b² = ______ হবে। [M.P. 2020]
উত্তর – \(ac\)
সমাধান – যেহেতু বীজদ্বয় বাস্তব এবং সমান
∴ \(4b^2 – 4ac = 0\) বা, \(b^2 = ac\)
23. দুটি দ্বিঘাত করণীর যোগফল ও গুণফল একটি মূলদ সংখ্যা হলে করণীদ্বয় ______ করণী। [M.P. 2019]
উত্তর – অনুবন্ধী
24. \((a-2)x^2 + 3x + 5 = 0\) সমীকরণটি a-এর মান ______ এর জন্য দ্বিঘাত সমীকরণ হবে না। [M.P. 2018]
উত্তর – 2
সমাধান – \(\therefore (a-2)x^2 + 3x + 5 = 0\) সমীকরণটি দ্বিঘাত সমীকরণ হবে না, যদি \((a-2)x^2 = 0\)
\(a-2 = 0\) \(\because x \ne 0\)
\(a = 2\)25. \(ax^2 + bx + c = 0, (a \ne 0)\) দ্বিঘাত সমীকরণের \(b^2 = 4ac\) হলে বীজদ্বয় বাস্তব ও ______ হবে। [M.P. 2017]
উত্তর – সমান
26. \(kx^2 + 4x + 1 = 0\) দ্বিঘাত সমীকরণটির বীজদ্বয় সমান হলে, k-এর মান হবে ______ ।
উত্তর – 4
সমাধান – \(\because kx^2 + 4x + 1 = 0\) সমীকরণের বীজদ্বয় সমান
\(\therefore\) নিরূপক \(= b^2 – 4ac = 0\)
বা, \(4^2 – 4 \cdot k \cdot 1 = 0\)
বা, \(4k = 16\)
বা, \(k = 4\)
27. \(3x^2 – 4x + 1 = 0\) সমীকরণটির নিরূপক হল ______ ।
উত্তর – 4
সমাধান – নিরূপক \(= (-4)^2 – 4 \cdot 3 \cdot 1 = 16 – 12 = 4\)
28. \(x : y = 3 : 2\) হলে \(\frac{x+y}{x-y}\)-এর মান হবে ______ ।
উত্তর – 5
সমাধান – \(\because x : y = 3 : 2\) বা, \(\frac{x}{y} = \frac{3}{2}\) বা, \(\frac{x}{3} = \frac{y}{2} = k\) [যেখানে k হল অশূন্য বাস্তব সংখ্যা]
\(\therefore x = 3k, y = 2k\)এখন \(\frac{x+y}{x-y} = \frac{3k+2k}{3k-2k} = \frac{5k}{k} = 5\)
29. \((x-2)\) এবং \((x-3)\)-এর মধ্যসমানুপাতী x হলে x-এর মান ______ ।
উত্তর – \(\frac{6}{5}\)
সমাধান – \(x-2, x, x-3\) ক্রমিক সমানুপাতী
\(\therefore \frac{x-2}{x} = \frac{x}{x-3}\)বা, \(x^2 = x^2 – 5x + 6\) বা, \(5x = 6\) বা, \(x = \frac{6}{5}\)
30. \(ax^2 + bx + c = 0 \ (a \ne 0)\) সমীকরণের বীজদ্বয় পরস্পর অন্যোন্যক এবং বিপরীত (ঋণাত্মক) হলে, a + c = ______ ।
উত্তর – 0
সমাধান – মনে করি, \(ax^2 + bx + c = 0\) সমীকরণের বীজদ্বয় \(\alpha\) ও \(−1α-\frac{1}{\alpha}\)
\(\alpha \cdot (-\frac{1}{\alpha}) = \frac{c}{a}\)বা, \(\frac{c}{a} = -1\)
বা, \(c = -a\)
বা, \(a + c = 0\)
31. \(7x^2 – 12x + 18 = 0\) সমীকরণের বীজদ্বয়ের সমষ্টি ও গুণফলের অনুপাত ______ ।
উত্তর – 2 : 3
সমাধান – মনে করি, \(7x^2 – 12x + 18 = 0\) সমীকরণের বীজদ্বয় \(\alpha\) ও \(\beta\)
\(\therefore \alpha + \beta = -\frac{(-12)}{7} = \frac{12}{7}\) এবং \(\alpha\beta = \frac{18}{7}\)
\(\therefore (\alpha + \beta) : \alpha\beta = \frac{12}{7} : \frac{18}{7} = 2 : 3\)32. দুটি দ্বিঘাত করণীর যোগফল এবং গুণফল একটি মূলদ সংখ্যা হলে করণীদ্বয় ______ ।
উত্তর – অনুবন্ধী
33. \(ax^2 + bx + c = 0 \ (a \ne 0)\) সমীকরণের বীজদ্বয় পরস্পর অন্যোন্যক হলে c = ______ ।
উত্তর – a
সমাধান – \(\because ax^2 + bx + c = 0\) সমীকরণের বীজদ্বয় পরস্পর অন্যোন্যক
\(\therefore\) বীজদ্বয়ের গুণফল = 1
বা, \(\frac{c}{a} = 1\) বা, \(c = a\)
34. \(\sqrt{3} – 5\)-এর অনুবন্ধী করণী ______ ।
উত্তর – \(-\sqrt{3} – 5\)
35. তিনটি ক্রমিক সমানুপাতী ধনাত্মক সংখ্যার গুণফল 64 হলে, তাদের মধ্যসমানুপাতী ______ ।
উত্তর – 4
সমাধান – মনে করি, তিনটি ক্রমিক ধনাত্মক সংখ্যা হল a, b, c
বা, \(b \cdot b^2 = 64\) বা, \(b^3 = (4)^3\) \(\therefore b = 4\)
36. a : 2 = b : 5 = c : 8 হলে a-এর 50% = b-এর 20% = c-এর ______ % ।
উত্তর – 12.5%
সমাধান – \(\because a : 2 = b : 5 = c : 8\)
বা, \(\frac{a}{2} = \frac{b}{5} = \frac{c}{8}\)
বা, \(\frac{a}{2} \times 100\% = \frac{b}{5} \times 100\% = \frac{c}{8} \times 100\%\)
বা, a-এর 50% = b-এর 20% = c-এর 12.5%
জ্যামিতি
37. দুটি সদৃশ ত্রিভুজের অনুরূপ বাহুগুলি ______ [M.P. 2024]
উত্তর – সমানুপাতী
38. দুটি ত্রিভুজ সদৃশ হবে, যদি তাদের অনুরূপ বাহুগুলি ______ হয়। [M.P. 2022]
উত্তর – সমানুপাতী
39. একটি চতুর্ভুজের বিপরীত কোণদ্বয় পরস্পর সম্পূরক হলে, চতুর্ভুজের শীর্ষবিন্দুগুলি ______ । [M.P. 2022]
উত্তর – বৃত্তস্থ
40. দুটি কোণের সমষ্টি ______ হলে তাদেরকে পরস্পরের সম্পূরক বলা হয়। [M.P. 2020]
উত্তর – \(180^{\circ}\)
41. দুটি ত্রিভুজের ভূমি একই সরলরেখায় অবস্থিত এবং ত্রিভুজ দুটির অপর শীর্ষবিন্দুটি সাধারণ হলে, ত্রিভুজ দুটির ক্ষেত্রফলের অনুপাত ভূমির দৈর্ঘ্যের অনুপাতের ______ । [M.P. 2019]
উত্তর – সমান
42. ABCD একটি বৃত্তস্থ সামান্তরিক হলে \(\angle A\)-এর মান হবে ______ । [M.P. 2018]
উত্তর – \(90^{\circ}\)
43. দুটি ত্রিভুজের বাহুগুলির দৈর্ঘ্যের পরিমাপ সমানুপাতে থাকলে ত্রিভুজ দুটি ______ হবে। [M.P. 2017]
উত্তর – সদৃশ
44. O কেন্দ্রীয় বৃত্তে AB ও AC জ্যা দুটির দৈর্ঘ্য সমান। \(\angle APB\) ও \(\angle AQC\) বৃত্তস্থ কোণ হলে, কোণ দুটির মান ______ ।
উত্তর – সমান
সমাধান – পরিধিস্থ \(\angle APB = \frac{1}{2}\) কেন্দ্রস্থ \(\angle AOB\)
আবার পরিধিস্থ \(\angle AQC = \frac{1}{2}\) কেন্দ্রস্থ \(\angle AOC\)
\(\because AB = AC\) ∴ \(\angle AOB = \angle AOC\)
∴ \(\angle APB = \angle AQC\)
45. একটি সমবাহু ত্রিভুজের পরিবৃত্তের কেন্দ্র O হলে যে-কোনো একটি বাহু দ্বারা উৎপন্ন সম্মুখ কেন্দ্রস্থ কোণের মান ______ ।
উত্তর – \(120^{\circ}\)
46. O কেন্দ্রীয় বৃত্তে PQ ও RS জ্যা দুটি দৈর্ঘ্যের অনুপাত 1 : 1 হলে, \(\angle POQ : \angle ROS\) = ______ ।
উত্তর – 1 : 1
47. একই চাপের উপর অবস্থিত বৃত্তস্থ কোণ কেন্দ্রস্থ কোণের ______ ।
উত্তর – অর্ধেক
48. অর্ধবৃত্ত অপেক্ষা ক্ষুদ্রতর বৃত্তাংশস্থ কোণ ______ ।
উত্তর – স্থূলকোণ
49. সমকোণী ত্রিভুজের অতিভুজকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি ______ বিন্দু দিয়ে যাবে।
উত্তর – সমকৌণিক
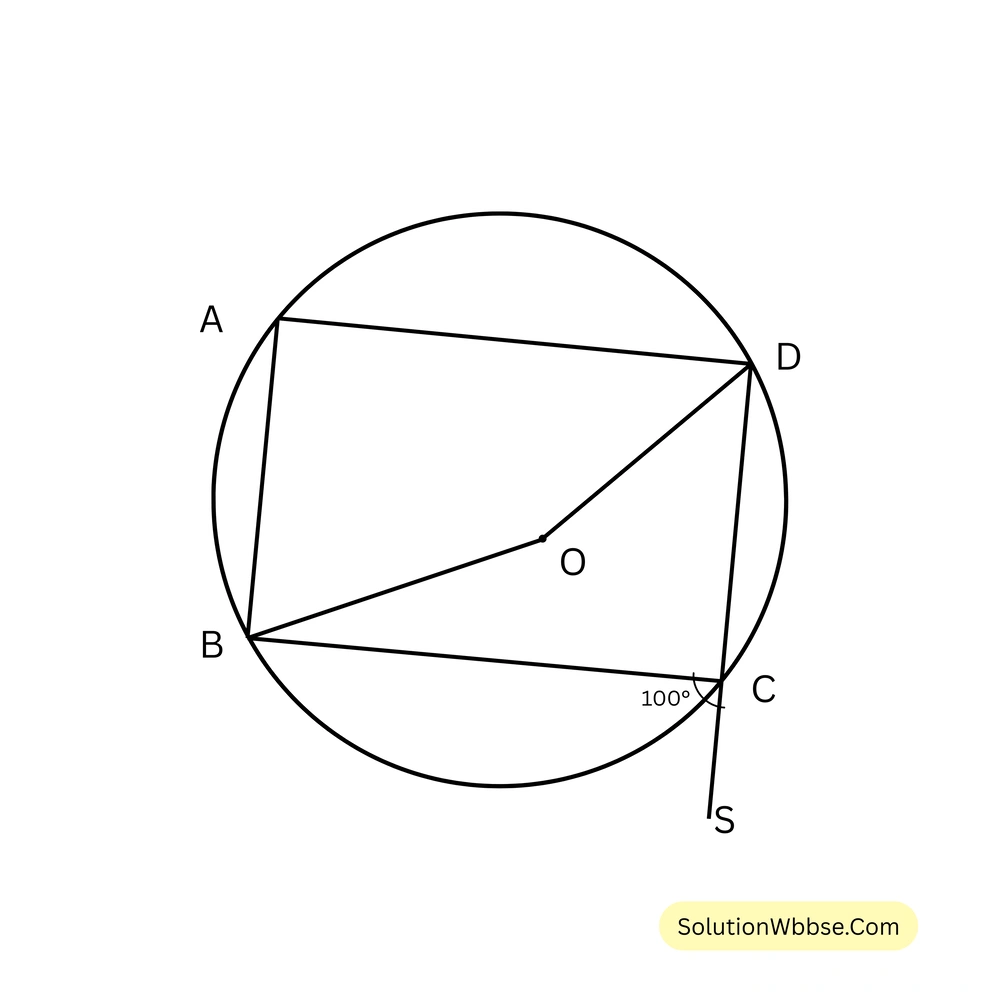
50. O কেন্দ্রীয় বৃত্তের ABCD একটি বৃত্তস্থ চতুর্ভুজ, DC বাহুকে P বিন্দু পর্যন্ত বর্ধিত করা হল। \(\angle BCP = 108^{\circ}\) হলে \(\angle BOD\)-এর মান ______ ।
উত্তর – \(144^{\circ}\)
সমাধান –
51. একই বৃত্তাংশস্থ সকল কোণের মান ______ ।
উত্তর – সমান
52. বৃত্তস্থ সামান্তরিক একটি ______ চিত্র।
উত্তর – আয়তক্ষেত্র
53. একটি বর্গাকার চিত্রের শীর্ষবিন্দুগুলি ______ ।
উত্তর – সমবৃত্তস্থ
54. কোন চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক হলে, চতুর্ভুজটি ______ হবে।
উত্তর – বৃত্তস্থ
55. একটি সরলরেখা বৃত্তকে দুটি বিন্দুতে ছেদ করলে সরলরেখাটিকে বৃত্তের ______ বলে।
উত্তর – ছেদক
56. দুটি বৃত্ত পরস্পরকে ছেদ বা স্পর্শ না করলে বৃত্ত দুটির সর্বাধিক সংখ্যায় ______ টি সাধারণ স্পর্শক অঙ্কন করা যায়।
উত্তর – 4
57. সকল বর্গক্ষেত্র ______ ।
উত্তর – সদৃশ
58. একটি ত্রিভুজের যে-কোনো বাহুর সমান্তরাল সরলরেখা অপর দুটি বাহুকে বা তাদের বর্ধিতাংশকে ______ বিভক্ত করে।
উত্তর – সমানুপাতে
59. একটি ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের সমান্তরাল সরলরেখা অপর বাহুদ্বয়কে ______ বিভক্ত করে।
উত্তর – সমানুপাতে
60. দুইটি সদৃশ বহুভুজের অনুরূপ বাহুগুলি ______ ।
উত্তর – সমানুপাতী
61. একটি সমকোণী সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য \(4\sqrt{2}\) সেমি হলে, অতিভুজের দৈর্ঘ্য ______ সেমি।
উত্তর – 8 সেমি
সমাধান – \(\text{অতিভুজ} = \sqrt{(4\sqrt{2})^2 + (4\sqrt{2})^2} = \sqrt{32 + 32} = \sqrt{64} = 8\)
62. দুটি বিন্দুর সংযোজক সরলরেখাংশ তার একই পার্শ্বে অপর দুটি বিন্দুতে সমান সম্মুখ কোণ উৎপন্ন করলে বিন্দু চারটি ______ হবে।
উত্তর – সমবৃত্তস্থ
63. দুটি বৃত্ত পরস্পর ______ করলে তাদের কেন্দ্র দুটির মধ্যে দূরত্ব তাদের ব্যাসার্ধের যোগফলের সমান হয়।
উত্তর – বহিঃস্পর্শ
ত্রিকোণমিতি
64. \(\sin (\theta – 30^\circ) = \frac{1}{2}\) হলে \(\cos \theta\)-এর মান হবে ______ [M.P. 2024]
উত্তর – \(\frac{1}{2}\)
65. \(\tan \theta \cos 60^\circ = \frac{\sqrt{3}}{2}\) হলে, \(\sin(\theta – 15^\circ)\)-এর মান হবে ______ । [M.P. 2023]
উত্তর – \(60^\circ\)
সমাধান – \(\tan\theta \cos60^\circ = \frac{\sqrt{3}}{2}\)
বা, \(\tan\theta \cdot \frac{1}{2} = \frac{\sqrt{3}}{2}\)
বা, \(\tan\theta = \sqrt{3} = \tan60^\circ\)
\(\therefore \theta = 60^\circ\)66. \(\angle A\) এবং \(\angle B\) দ্বয় পূরক কোণ হলে \(\angle A + \angle B =\) ______ । [M.P. 2023]
উত্তর – \(90^\circ\)
67. \(\frac{\cos53^\circ}{\sin37^\circ}\) এর সরলতম মান ______ । [M.P. 2019]
উত্তর – 1
68. \(\tan35^\circ\tan55^\circ = \sin\theta\) হলে, \(\theta\)-এর সর্বনিম্ন ধনাত্মক মান ______ হবে। [M.P. 2018]
উত্তর – \(90^\circ\)
সমাধান – \(\tan35^\circ\tan55^\circ = \sin\theta\)
বা, \(\sin\theta = \tan35^\circ\tan(90^\circ-35^\circ)\)
\(= \tan35^\circ\cot35^\circ = 1 = \sin90^\circ \therefore \theta = 90^\circ\)69. \(\cos^2\theta – \sin^2\theta = \frac{1}{x}, (x > 1)\), হলে \(\cos^4\theta – \sin^4\theta =\) ______ । [M.P. 2017]
উত্তর – \(\frac{1}{x}\)
সমাধান – \(\cos^4\theta – \sin^4\theta = (\cos^2\theta)^2 – (\sin^2\theta)^2\)
\(= (\cos^2\theta + \sin^2\theta) (\cos^2\theta – \sin^2\theta)\)\(= 1 \times \frac{1}{x} = \frac{1}{x}\)70. \(\sin\theta = \frac{1}{2}\) হলে \(\cos2\theta =\) ______ ।
উত্তর – \(\frac{1}{2}\)
সমাধান – \(\sin\theta = \frac{1}{2} = \sin30^\circ \therefore \theta = 30^\circ\)
\(\cos2\theta = \cos (2 \times 30^\circ) = \cos 60^\circ = \frac{1}{2}\)71. \((\sin12^\circ \times \cos18^\circ \times \sec78^\circ \times \text{cosec}72^\circ)\) এর মান ______ ।
উত্তর – 1
সমাধান – \(\sin12^\circ \times \cos18^\circ \times \sec78^\circ \times \text{cosec}72^\circ\)
\(= \sin12^\circ \times \cos18^\circ \times \frac{1}{\cos 78^\circ} \times \frac{1}{\sin 72^\circ}\)\(= \sin12^\circ \times \cos18^\circ \times \frac{1}{\cos (90^\circ – 12^\circ)} \times \frac{1}{\sin (90^\circ – 18^\circ)}\)\(= \sin12^\circ \times \cos18^\circ \times \frac{1}{\sin 12^\circ} \times \frac{1}{\cos 18^\circ} = 1\)72. A এবং B পরস্পর পূরক কোণ হলে, \(\sin A =\) ______ ।
উত্তর – \(\cos B\)
সমাধান – যেহেতু A এবং B পরস্পর পূরক
\(\therefore A + B = 90^\circ\) বা, \(A = 90^\circ – B\)
73. \((\tan15^\circ \times \tan45^\circ \times \tan60^\circ \times \tan75^\circ)\) এর মান ______ ।
উত্তর – \(\sqrt{3}\)
সমাধান – \(\tan15^\circ \times \tan45^\circ \times \tan60^\circ \times \tan75^\circ\)
\(= \tan15^\circ \times 1 \times \sqrt{3} \times \tan (90^\circ – 15^\circ)\)\(= \sqrt{3} \tan15^\circ \times \cot15^\circ = \sqrt{3} . 1 = \sqrt{3}\)74. \(\frac{\pi}{8}\) রেডিয়ান = ______ ডিগ্রি
উত্তর – \(22\frac{1}{2}^\circ\)
সমাধান – \(\frac{\pi}{8}\) রেডিয়ান \(= \frac{\pi}{8} \times \frac{180^\circ}{\pi} = \frac{45^\circ}{2} = 22\frac{1}{2}^\circ\)
75. সূর্যের উন্নতি কোণ \(45^\circ\) হলে, একটি পোস্টের দৈর্ঘ্য ও তার ছায়ার দৈর্ঘ্য ______ হবে।
উত্তর – সমান
76. সূর্যের উন্নতি কোণ \(30^\circ\) থেকে বৃদ্ধি পেয়ে \(60^\circ\) হলে একটি পোস্টের ছায়ার দৈর্ঘ্য ______ পায়। (হ্রাস / বৃদ্ধি)
উত্তর – হ্রাস
77. \(\frac{3\pi}{8}\) পরিমাপের কোণটির সম্পূরক কোণের বৃত্তীয় মান ______ ।
উত্তর – \(\frac{5\pi}{8}\)
সমাধান – \(\frac{3\pi}{8}\) পরিমাপের কোণটির সম্পূরক কোণের বৃত্তীয় মান
\(= \pi – \frac{3\pi}{8} = \frac{5\pi}{8}\)78. \(\tan\theta = \frac{4}{5}\), হলে \(\sin\theta =\) ______ ।
উত্তর – \(\frac{4}{\sqrt{41}}\)
সমাধান – \(\tan\theta = \frac{4}{5}\)
\(\therefore \sec\theta = \sqrt{1+\tan^2\theta} = \sqrt{1+\left(\frac{4}{5}\right)^2} = \frac{\sqrt{41}}{5}\)\(\therefore \cos\theta = \frac{5}{\sqrt{41}}\)\(\therefore \sin\theta = \sqrt{1-\cos^2\theta} = \sqrt{1-\left(\frac{5}{\sqrt{41}}\right)^2} = \frac{4}{\sqrt{41}}\)79. \(\sin\theta – \cos\theta = \frac{1}{5}\) হলে, \(\sin\theta + \cos\theta\)-এর মান হবে—
উত্তর – \(\frac{7}{5}\)
সমাধান –
\((\sin\theta – \cos\theta)^2 = \left(\frac{1}{5}\right)^2\)বা, \(\sin^2\theta + \cos^2\theta – 2\sin\theta\cos\theta = \frac{1}{25}\)
বা, \(1 – 2\sin\theta\cos\theta = \frac{1}{25}\)
বা, \(-2\sin\theta\cos\theta = \frac{1}{25} – 1\)
বা, \(2\sin\theta\cos\theta = \frac{24}{25}\) বা, \(\sin\theta\cos\theta = \frac{12}{25}\)
\(\therefore \sin\theta + \cos\theta = \sqrt{(\sin\theta – \cos\theta)^2 + 4\sin\theta \cos\theta}\)\(= \sqrt{\left(\frac{1}{5}\right)^2 + 4 \cdot \frac{12}{25}} = \sqrt{\frac{1}{25} + \frac{48}{25}} = \sqrt{\frac{49}{25}} = \frac{7}{5}\)80. \(\sec\theta + \tan\theta = 2 + \sqrt{5}\) হলে, \((\sin\theta + \cos\theta)\) – এর মান হবে ______ ।
উত্তর – \(\frac{3}{\sqrt{5}}\)
সমাধান – যেহেতু \(\sec^2\theta – \tan^2\theta = 1\)
বা, \((\sec\theta + \tan\theta) (\sec\theta – \tan\theta) = 1\)
বা, \(\sec\theta – \tan\theta = \frac{1}{2+\sqrt{5}} = \sqrt{5}-2\)
\(\therefore 2\sec\theta = (\sec\theta + \tan\theta) + (\sec\theta – \tan\theta)\)\(= 2 + \sqrt{5} + \sqrt{5} – 2 = 2\sqrt{5}\)\(\therefore \sec\theta = \sqrt{5}\)\(\therefore \cos\theta = \frac{1}{\sqrt{5}}\)\(\therefore \sin\theta = \sqrt{1 – \cos^2\theta} = \sqrt{1 – \frac{1}{5}} = \frac{2}{\sqrt{5}}\)\(\therefore \sin\theta + \cos\theta = \frac{2}{\sqrt{5}} + \frac{1}{\sqrt{5}} = \frac{3}{\sqrt{5}}\)81. \(\Pi\) রেডিয়ান একটি ______ কোণ।
উত্তর – ধ্রুবক
82. ষষ্ঠিক পদ্ধতিতে 1 রেডিয়ান সমান ______ (প্রায়)
উত্তর – \(57^{\circ}16’22”\)
83. \(\frac{4}{\sec^2\theta} + \frac{1}{1+\cot^2\theta} + 3\sin^2\theta\) এর মান ______ ।
উত্তর – 4
সমাধান – \(\frac{4}{\sec^2\theta} + \frac{1}{1+\cot^2\theta} + 3\sin^2\theta\)
\(= 4\cos^2\theta + \frac{1}{\text{cosec}^2\theta} + 3\sin^2\theta\)\(= 4\cos^2\theta + \sin^2\theta + 3\sin^2\theta\)\(= 4\cos^2\theta + 4\sin^2\theta\)\(= 4(\cos^2\theta + \sin^2\theta) = 4 \times 1 = 4\)84. যদি হয় \(\sqrt{3} \sin\theta = \cos\theta\) তবে \(\theta\) এর মান হবে ______ ।
উত্তর – \(30^{\circ}\)
সমাধান – \(\sqrt{3} \sin\theta = \cos\theta\)
বা, \(\frac{\sin\theta}{\cos\theta} = \frac{1}{\sqrt{3}}\)
বা, \(\tan\theta = \tan30^{\circ}\)
\(\therefore \theta = 30^{\circ}\)পরিমিতি
85. লম্ববৃত্তাকার শঙ্কুর আয়তন V, ভূমির ব্যাসার্ধ R এবং উচ্চতা H হলে, H = ______ [M.P. 2024]
উত্তর – \(\frac{3V}{\pi R^2}\)
86. একমুখ কাটা একটি পেনসিলের আকার ______ ও ______ র সমন্বয়। [M.P. 2023]
উত্তর – শঙ্কু, চোঙ
87. সমকোণী চৌপলের দৈর্ঘ্য, প্রস্থ ও উচ্চতা সমান হলে সেই ঘনবস্তুর বিশেষ নাম ______ ।
উত্তর – ঘনক
88. কোনো গোলকের ব্যাসার্ধ r এবং আয়তন V হলে, V \(\propto\) ______ ।
উত্তর – \(r^3\)
89. একটি নিরেট গোলক গলিয়ে একটি নিরেট লম্ব বৃত্তাকার চোঙ তৈরি করা হলে গোলক ও চোঙের ______ সমান হবে।
উত্তর – আয়তন
90. একটি নিরেট লম্ব বৃত্তাকার চোঙের তলসংখ্যা ______ ।
উত্তর – 3
91. একমুখ কাটা একটি পেন্সিলের আকার চোঙ ও ______ র সমন্বয়। [M.P. 2018]
উত্তর – শঙ্কু
92. একটি নিরেট অর্ধগোলকের সমতল সংখ্যা ______ । [M.P. 2017]
উত্তর – 1
93. একটি সমকোণী চৌপলের কর্ণের সংখ্যা ______ টি।
উত্তর – 4
94. একতল বিশিষ্ট ঘনবস্তুর নাম ______ ।
উত্তর – গোলক
95. একটি নিরেট লম্ববৃত্তাকার চোঙ ও দুইটি অর্ধগোলকের ভূমিতলের ব্যাসার্ধের দৈর্ঘ্য সমান। দুই অর্ধগোলককে চোঙটির দুটি সমতলে আটকে দেওয়া হল নতুন ঘনবস্তুটির সমগ্রতলের ক্ষেত্রফল = একটি অর্ধগোলকের বক্রতলের ক্ষেত্রফল + ______ বক্রতলের ক্ষেত্রফল + অপর অর্ধগোলকটির বক্রতলের ক্ষেত্রফল।
উত্তর – চোঙের
96. একটি আয়তক্ষেত্রাকার কাগজের দৈর্ঘ্য \(l\) একক এবং প্রস্থ \(b\) একক। আয়তক্ষেত্রাকার কাগজটিকে মুড়ে একটি লম্ববৃত্তাকার চোঙ তৈরি করা হল যার পরিধি কাগজটির দৈর্ঘ্যের সমান চোঙটির বক্রতলের ক্ষেত্রফল ______ বর্গ একক।
উত্তর – \(lb\) বর্গএকক
সমাধান – চোঙটির বক্রতলের ক্ষেত্রফল = চোঙটির পরিধি \(\times\) উচ্চতা = আয়তক্ষেত্রের দৈর্ঘ্য \(\times\) আয়তক্ষেত্রের প্রস্থ = \(l \times b\) = \(lb\) বর্গএকক
97. একটি লম্ববৃত্তাকার শঙ্কুর আয়তন v ঘনএকক এবং ভূমির ক্ষেত্রফল A বর্গএকক হলে উচ্চতা ______ ।
উত্তর – \(\frac{3v}{A}\)
সমাধান – মনে করি, শঙ্কুর উচ্চতা = h
শঙ্কুর আয়তন = \(\frac{1}{3} \times\) ভূমির ক্ষেত্রফল \(\times\) উচ্চতা
বা, \(v = \frac{1}{3} \times A \times h\)
\(\therefore h = \frac{3v}{A}\)98. একটি লম্ববৃত্তাকার চোঙ এবং লম্ববৃত্তাকার শঙ্কুর ভূমিতলের ব্যাসার্ধের দৈর্ঘ্য সমান এবং তাদের উচ্চতা সমান। তাদের আয়তনের অনুপাত ______ ।
উত্তর – \(3 : 1\)
সমাধান – মনে করি, চোঙ এবং শঙ্কু উভয়ের ভূমিতলের ব্যাসার্ধ r একক এবং উচ্চতা h একক
\(\therefore\) আয়তনের অনুপাত = \(3 : 1\)
99. একটি লম্ববৃত্তাকার চোঙের আয়তন এবং বক্রতলের সাংখ্যমান সমান হলে, চোঙটির ব্যাসের দৈর্ঘ্য ______ একক।
উত্তর – 4 একক
সমাধান – চোঙটির ভূমির ব্যাসার্ধ = r একক এবং উচ্চতা = h একক
চোঙটির আয়তন = চোঙটির বক্রতলের ক্ষেত্রফল
\(\pi r^2 h = 2 \pi r h\)\(\therefore r = 2\)\(\therefore 2r = 4\)\(\therefore\) ব্যাস = 4 একক
100. একটি ঘনকের একটি তলের কর্ণের দৈর্ঘ্য = ______ \(\times\) একটি ধারের দৈর্ঘ্য।
উত্তর – \(\sqrt{2}\)
101. একটি নিরেট গোলককে গলিয়ে একটি নিরেট লম্ববৃত্তাকার চোঙ তৈরি করা হলো। গোলক ও চোঙের আয়তন ______ ।
উত্তর – সমান
102. একটি নিরেট অর্ধগোলকের ব্যাসার্ধের দৈর্ঘ্য 2r একক হলে সমগ্রতলের ক্ষেত্রফল ______ \(\pi r^2\) বর্গএকক।
উত্তর – 12
সমাধান – 2r একক ব্যাসার্ধবিশিষ্ট অর্ধগোলকের সমগ্রতলের ক্ষেত্রফল
\(= 3\pi(2r)^2\) বর্গএকক \(= 12\pi r^2\) বর্গএকক
103. সমকোণী চৌপলের দৈর্ঘ্য, প্রস্থ ও উচ্চতা সমান হলে সেই ঘনবস্তুর বিশেষ নাম ______ ।
উত্তর – ঘনক
রাশিবিজ্ঞান
104. ঊর্ধ্বক্রমে সাজানো 8, 9, 12, 17, x + 2, x + 4, 30, 34, 39 তথ্যের মধ্যমা 24 হলে x-এর মান ______ [M.P. 2024]
উত্তর – 22
105. 8, 15, 10, 11, 7, 9, 12, 13 এবং 16 সংখ্যাগুলির মধ্যমা হবে ______ । [M.P. 2023]
উত্তর – 11
সমাধান – পর্যবেক্ষণগুলিকে মানের ঊর্ধ্বক্রমে সাজিয়ে পাই 7, 8, 9, 10, 11, 12, 13, 15, 16
\(\therefore\) মধ্যমা = \(\left(\frac{9+1}{2}\right)\) তম পদ = 5ম পদ = 11
106. \(x_1, x_2, ……, x_{100}\) তথ্যগুলি ঊর্ধ্বক্রমে থাকলে এদের মধ্যমা ______ । [M.P. 2019]
উত্তর – \(\frac{1}{2}(x_{50} + x_{51})\)
107. মধ্যগামিতার মাপকগুলি হল গড়, মধ্যমা ও ______ । [M.P. 2018]
উত্তর – সংখ্যাগুরুমান
108. \(x_1, x_2, x_3, ……, x_n\) এই n সংখ্যক সংখ্যার গড় \(\bar{x}\) হলে \(kx_1, kx_2, kx_3, …, kx_n\) এর গড় ______ \(k \ne 0\)। [M.P. 2017]
উত্তর – \(k\bar{x}\)
109. যদি দশটি ছাত্রছাত্রীর পদার্থবিজ্ঞানের পরীক্ষার নম্বর 65, 52, 71, 47, 49, 51, 37, 29, 77, 62 হয়, তবে তাদের গড় নম্বর ______ ।
উত্তর – 54
সমাধান – গড় = \(\frac{65+52+71+47+49+51+37+29+77+62}{10}\)
110. x এবং y এর মধ্যে সম্পর্কটি হল \(2x + 3y = 7\)। যদি y এর মধ্যমা 2 হয় তবে x এর মধ্যমা ______ ।
উত্তর – \(\frac{1}{2}\)
সমাধান – \(2x + 3y = 7\)
\(\therefore 2x_{me} + 3y_{me} = 7\)বা, \(2x_{me} = 7 – 3 \times 2 = 1\)
\(\therefore x_{me} = \frac{1}{2}\)111. 8, 9, 6, 7, 5, 6, 7, 8, 9, 10 পর্যবেক্ষণগুলির মধ্যমা হল ______ ।
উত্তর – 7
সমাধান – পর্যবেক্ষণগুলিকে মানের ঊর্ধ্বক্রমে সাজিয়ে পাই: 5, 6, 6, 7, 7, 8, 8, 9, 9, 10
\(\therefore\) মধ্যমা = \(\left(\frac{10+1}{2}\right)\) তম পদ = 5.5তম পদ = \(\frac{7+8}{2} = 7.5\)
112. 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 5, 6, 7 তথ্যের সংখ্যাগুরু মান ______ ।
উত্তর – 2, 3
113. 2, 3, 4, 3, 6, 7, 8 তথ্যের সংখ্যাগুরু মান ______ ।
উত্তর – 3
114. 2, 3, 5, 6, 2, 4, 2, 8, 6, 9 তথ্যের সংখ্যাগুরু মান ______ ।
উত্তর – 2
115. 21, 33, 27, 23, 24, 32, 28, 24, 27, 22, 28, 30 রাশিগুলির মধ্যমা ______ ।
উত্তর – 27
সমাধান – পর্যবেক্ষণগুলিকে মানের ঊর্ধ্বক্রমে সাজিয়ে পাই: 21, 22, 23, 24, 24, 27, 27, 28, 28, 30, 32, 33
\(\therefore\) মধ্যমা = \(\frac{6\text{তম পদ} + 7\text{তম পদ}}{2} = \frac{27 + 27}{2} = 27\)
2026 সালের মাধ্যমিক পরীক্ষার্থীদের জন্য আমাদের গণিত বিষয়ের শূন্যস্থান পূরণ সাজেশন এখানেই শেষ হলো। এই প্রশ্নগুলি তোমাদের কতটা সাহায্য করলো বা অন্য কোনো বিষয়ের সাজেশন প্রয়োজন কিনা, তা অবশ্যই আমাদের কমেন্ট করে জানিও। আর্টিকেলটি ভালো লাগলে বন্ধুদের সাথে শেয়ার করতে ভুলো না!
এছাড়াও, টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন