এই আর্টিকেলে আমরা মাধ্যমিক ভৌতবিজ্ঞানের একটি গুরুত্বপূর্ণ অংশ “আলোর প্রতিফলন ও দর্পণ” নিয়ে আলোচনা করব। এই অংশটি মাধ্যমিক ভৌতবিজ্ঞান পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ। এই “আলোর প্রতিফলন ও দর্পণ” অংশটি মাধ্যমিক ভৌতবিজ্ঞানের পঞ্চম অধ্যায় “আলো -এর একটি গুরুত্বপূর্ণ অংশ। এই “আলোর প্রতিফলন ও দর্পণ” থেকে গুরুত্বপূর্ণ প্রশ্ন মাধ্যমিক পরীক্ষায় এবং চাকরির পরীক্ষায় প্রায়ই দেখা যায়।

মাধ্যমিক ভৌতবিজ্ঞান – আলো – আলোর প্রতিফলন ও দর্পণ
আলোর প্রতিফলন –
আলোকরশ্মি একটি মাধ্যমের মধ্যে দিয়ে যাওয়ার সময় অন্য মাধ্যমে আপতিত হয়ে আবার প্রথম মাধ্যমে ফিরে এলে তাকে আলোর প্রতিফলন বলে।
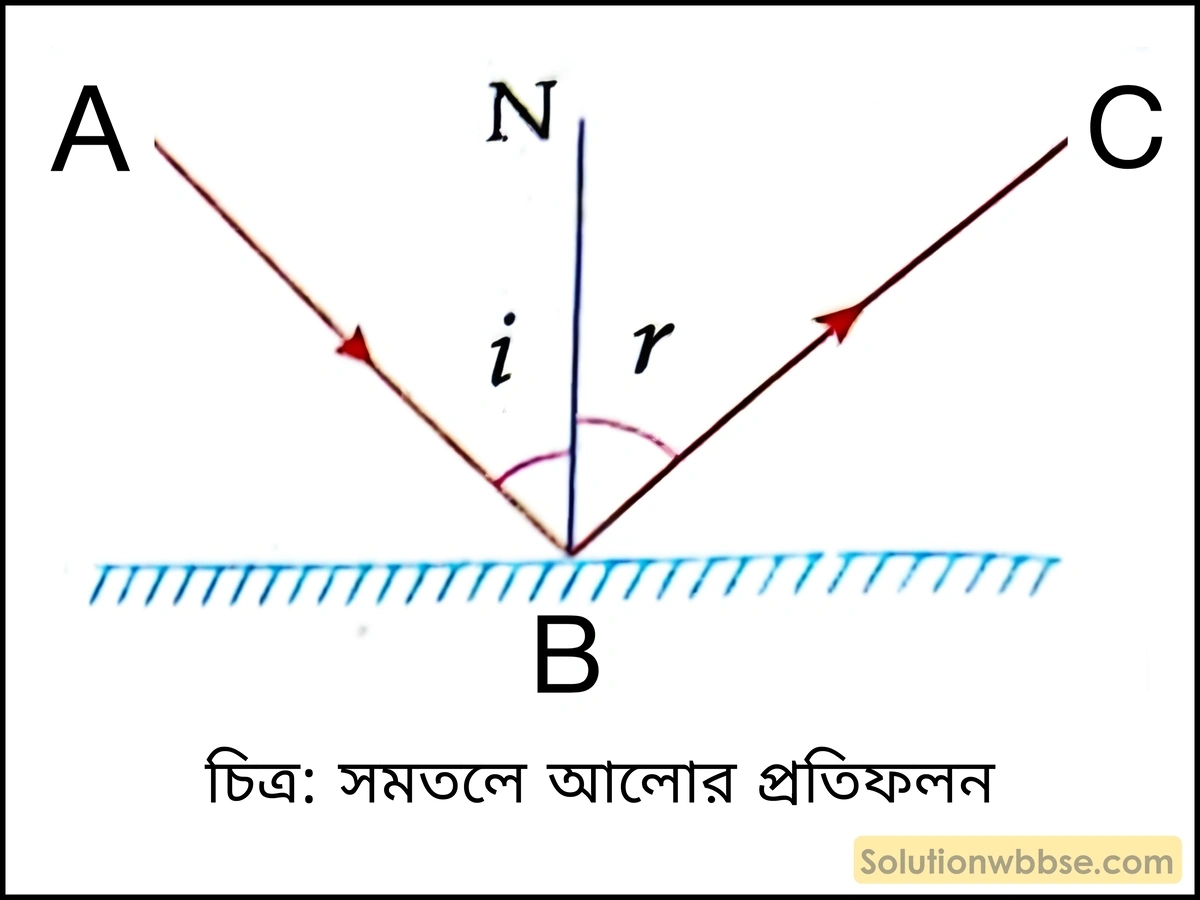
প্রতিফলনের সূত্র –
আপতিত রশ্মি, প্রতিফলিত রশ্মি ও আপতন বিন্দুতে অঙ্কিত অভিলম্ব একই সমতলে থাকে।
আপতন কোণ ও প্রতিফলন কোণ সমান অর্থাৎ, i = r
প্রতিফলন সংক্রান্ত তথ্য –
- অমসৃণ তলে অনিয়মিত প্রতিফলন হয় এবং প্রতিবিম্ব গঠিত হয় না, কিন্তু মসৃণ তলে নিয়মিত প্রতিফলন ঘটে ও প্রতিবিম্ব গঠিত হয়।
- প্রতিফলিত ও প্রতিসৃত রশ্মি কোনো বিন্দুতে মিলিত হলে সেখানে যে প্রতিবিম্ব হয় সেটি সদবিম্ব কিন্তু কোনো বিন্দু থেকে নির্গত হচ্ছে বলে মনে হলে সেটি অসদবিম্ব।
- সমতল দর্পণ সাধারণত অসদবিম্ব গঠন করে কিন্তু অভিসারী রশ্মি আপতিত হলে তখন সদবিম্ব গঠিত হয়।
গোলীয় দর্পণ –
যে দর্পণ কোনো গোলকের অংশ তাকে গোলীয় দর্পণ বলে।
অবতল দর্পণ –
যে গোলীয় দর্পণের বক্রতা কেন্দ্রের দিক মসৃণ ও আলোর প্রতিফলন ঘটায় তাকে অবতল দর্পণ বলে।
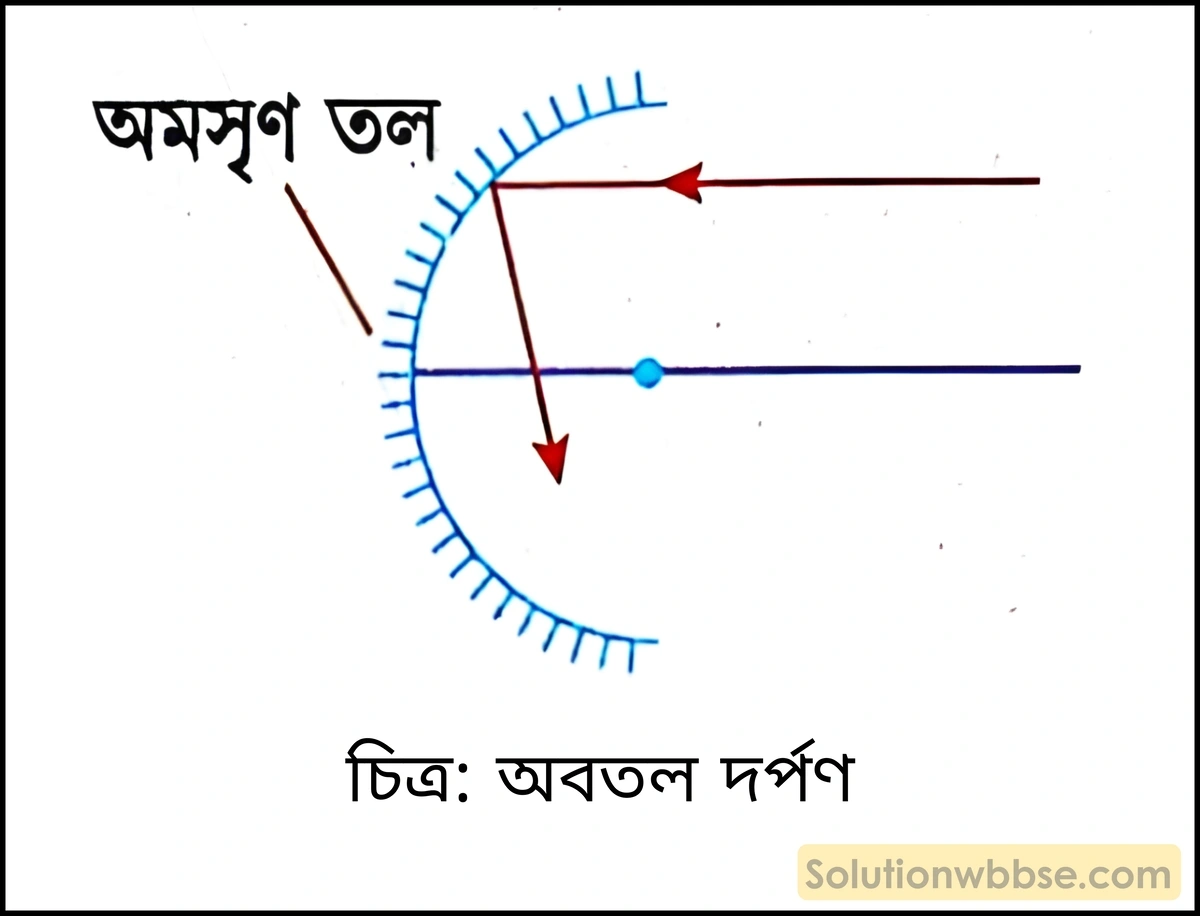
উত্তল দর্পণ –
যে গোলীয় দর্পণের বক্রতা কেন্দ্রের দিকটি অমসৃণ ও বিপরীত তল থেকে আলোর প্রতিফলন হয় তাকে উত্তল দর্পণ বলে।
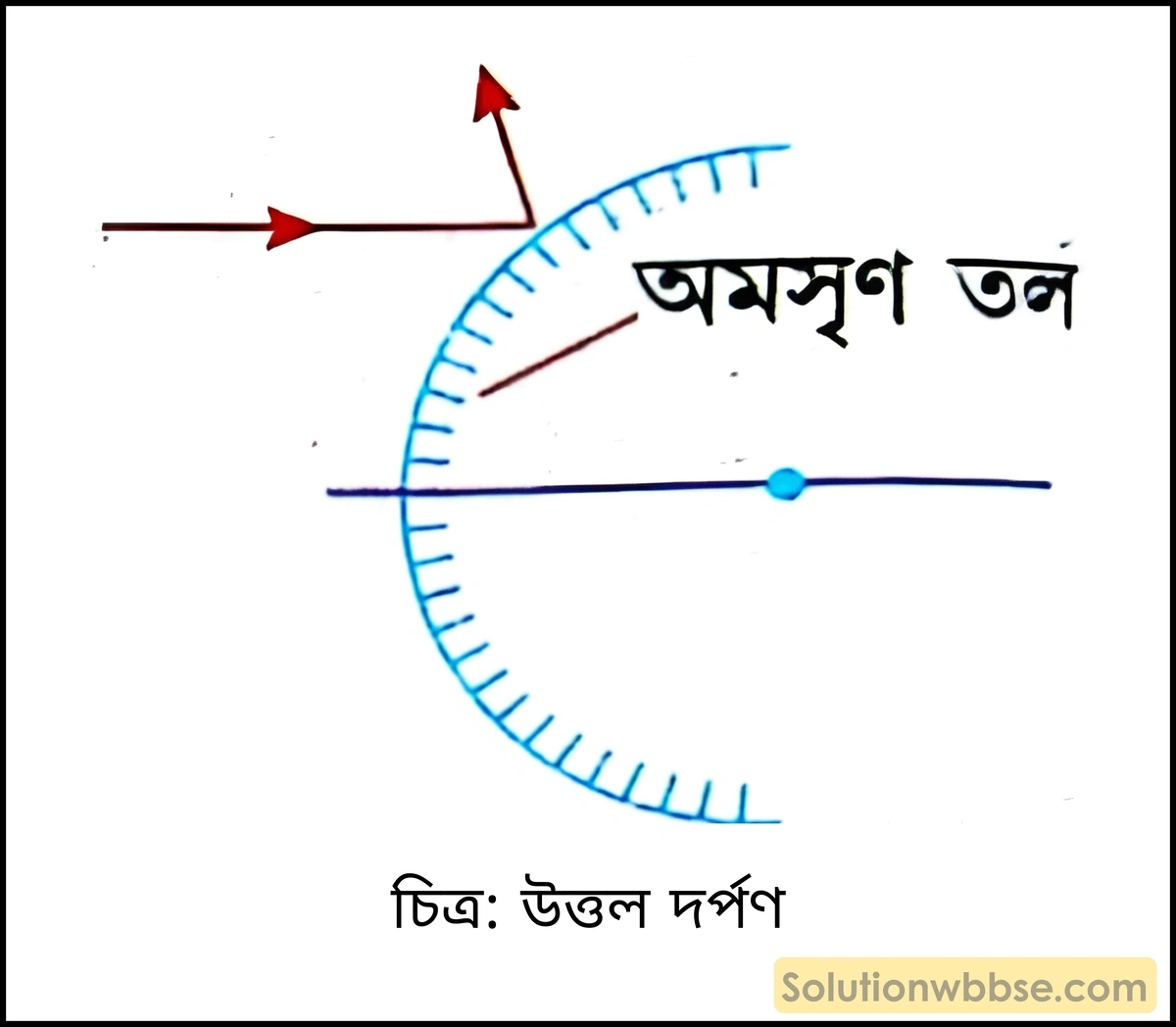
গোলীয় দর্পণ সংক্রান্ত বিভিন্ন রাশি –
বক্রতা কেন্দ্র – কোনো অবতল বা উত্তল দর্পণ যে গোলকের অংশ তার কেন্দ্রকে বলে ওই দর্পণের বক্রতা কেন্দ্র। চিত্রে হল দর্পণের বক্রতা কেন্দ্র এবং OC হল বক্রতা ব্যাসার্ধ।
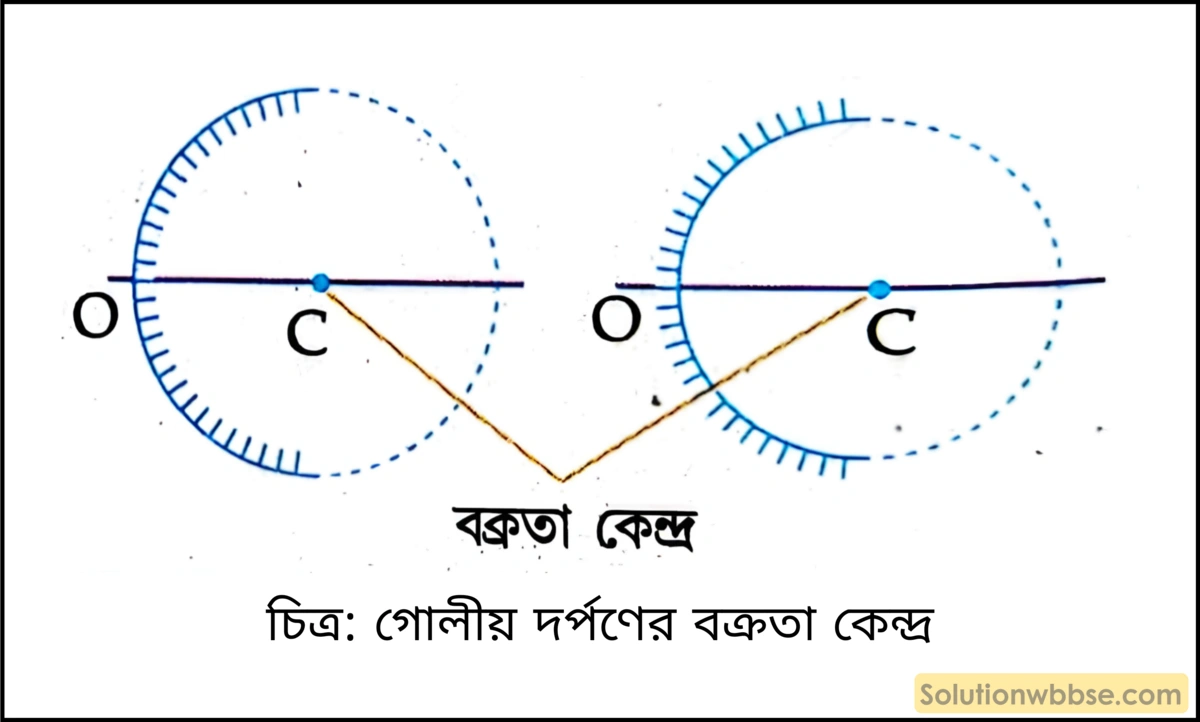
মেরু – কোনো গোলীয় দর্পণের প্রতিফলক তলের মধ্যবিন্দুকে ওর মেরু বলে।
প্রধান অক্ষ – গোলীয় দর্পণের মেরু ও বক্রতাকেন্দ্র সংযোজী সরলরেখাকে প্রধান অক্ষ বলে।
মুখ্য ফোকাস – কোনো গোলীয় দর্পণের প্রধান অক্ষের সমান্তরাল রশ্মি প্রতিফলনের পর প্রধান অক্ষের উপর কোনো বিন্দুতে মিলিত হলে বা প্রধান অক্ষের উপর কোনো বিন্দু থেকে নির্গত হচ্ছে বলে মনে হলে সেই বিন্দুকে মুখ্য ফোকাস বলে।
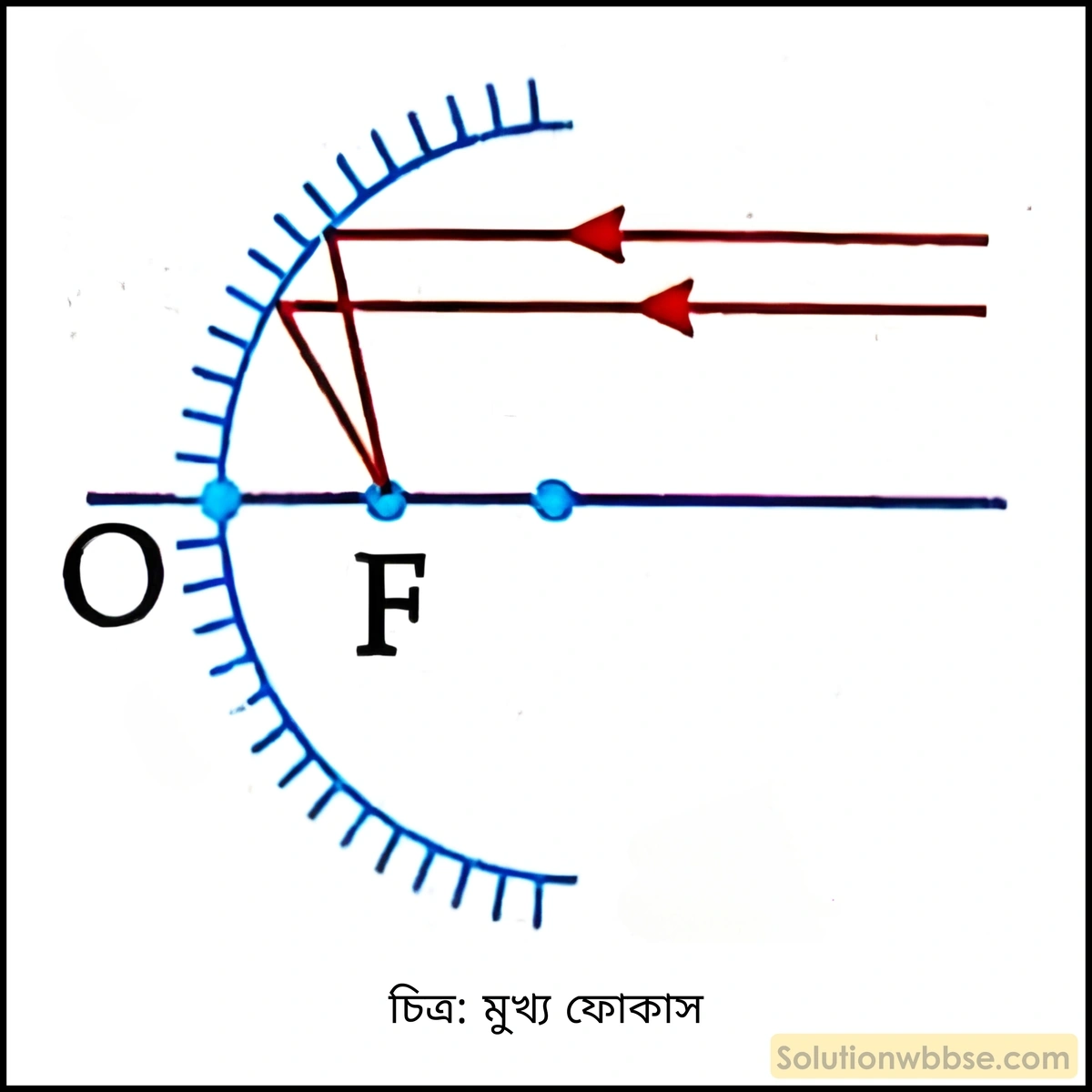
ফোকাস দূরত্ব – মেরু ও মুখ্য ফোকাসের মধ্যে দূরত্বকে ফোকাস দূরত্ব বলে। OF = ফোকাস দূরত্ব।
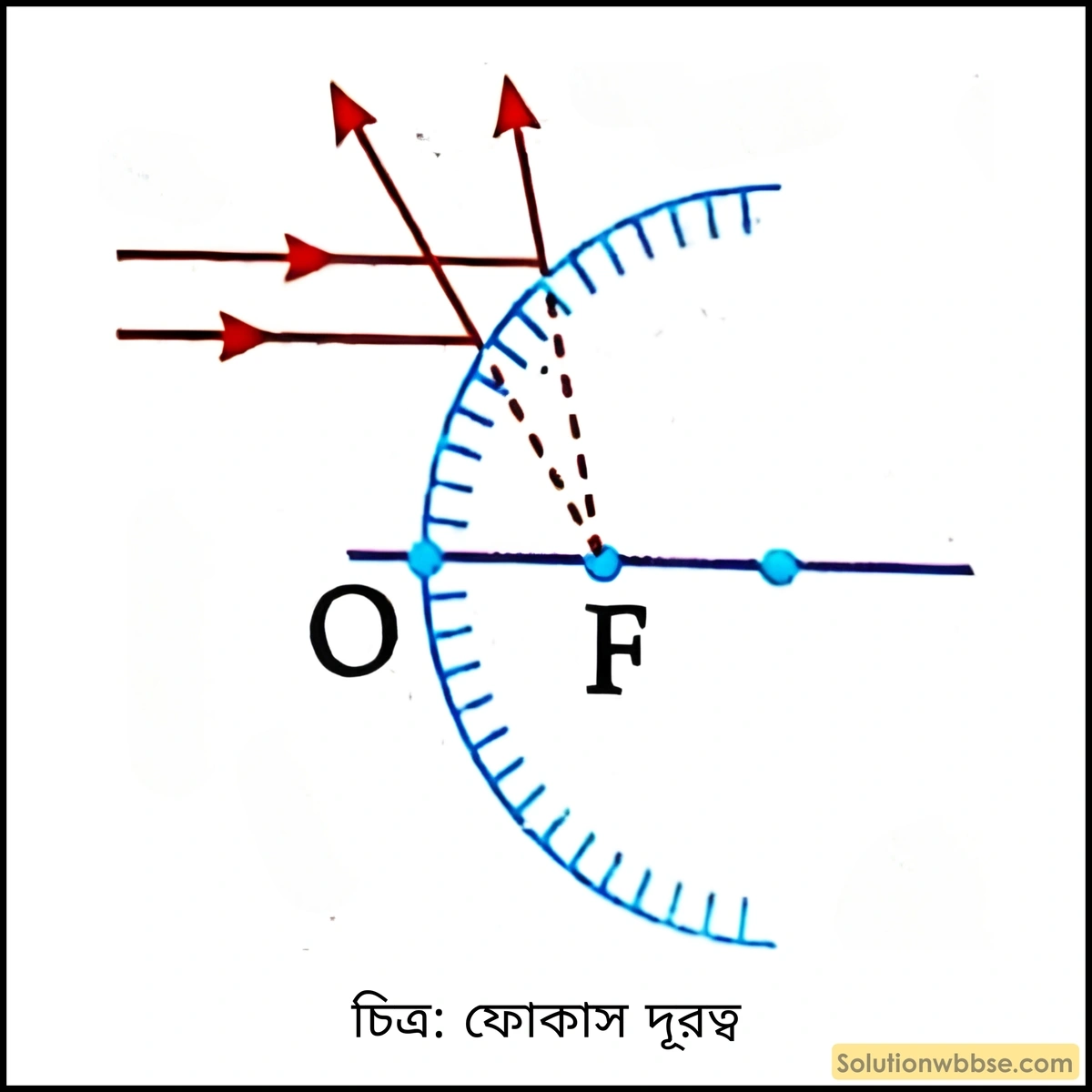
গৌণ ফোকাস – সমান্তরাল রশ্মিগুচ্ছ যারা প্রধান অক্ষের সমান্তরাল নয় প্রতিফলনের পর যে বিন্দুতে মিলিত হয় বা যে বিন্দু থেকে নির্গত হচ্ছে বলে মনে হয় তাকে গৌণ ফোকাস বলে।
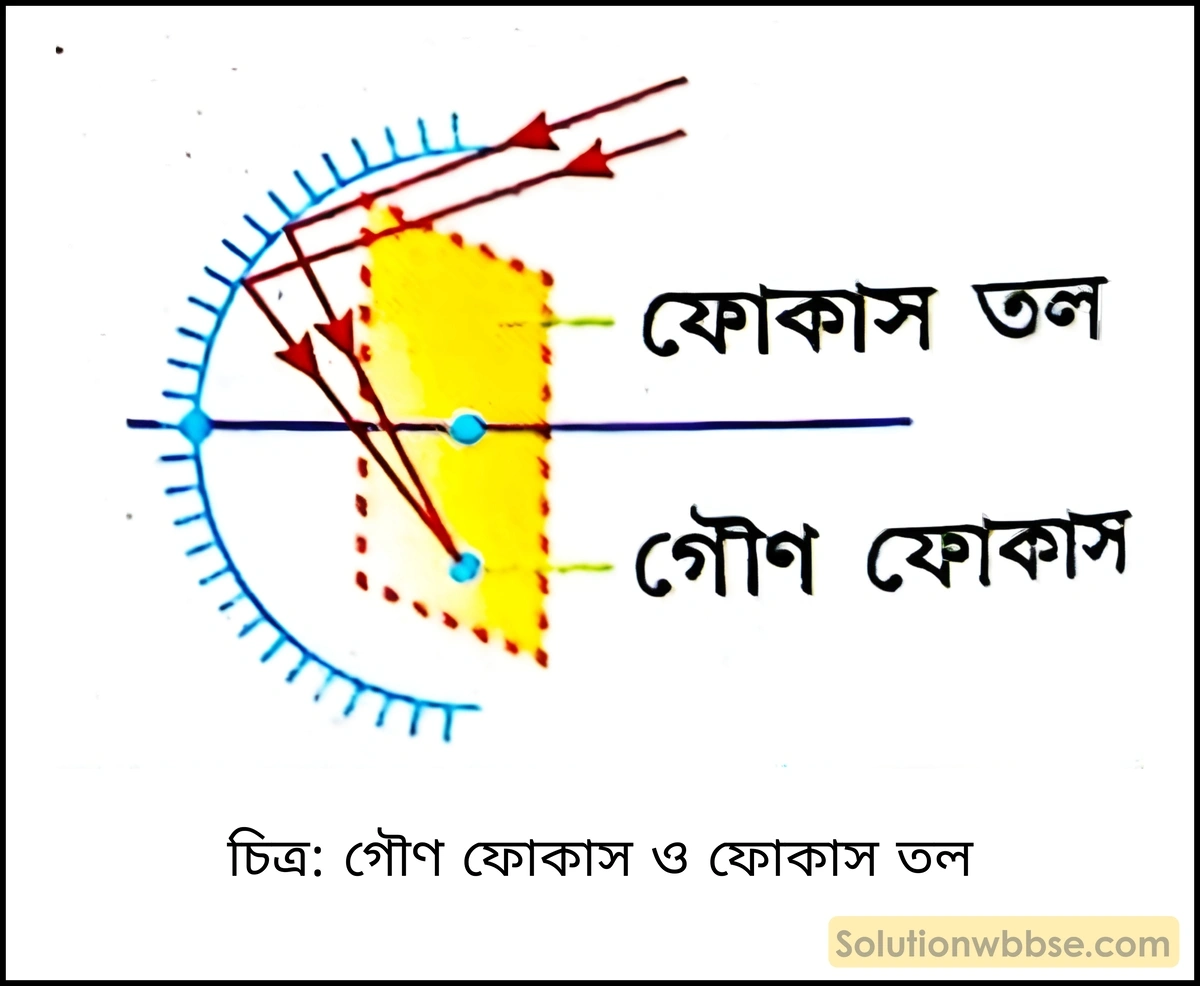
ফোকাস তল – মুখ্য ফোকাস বিন্দুগামী যে সমতল প্রধান অক্ষের সঙ্গে লম্বভাবে থাকে তাকে ফোকাস তল বলে।
দর্পণের ফোকাস দূরত্ব ও বক্রতা ব্যাসার্ধের সম্পর্ক –
অবতল দর্পণ –
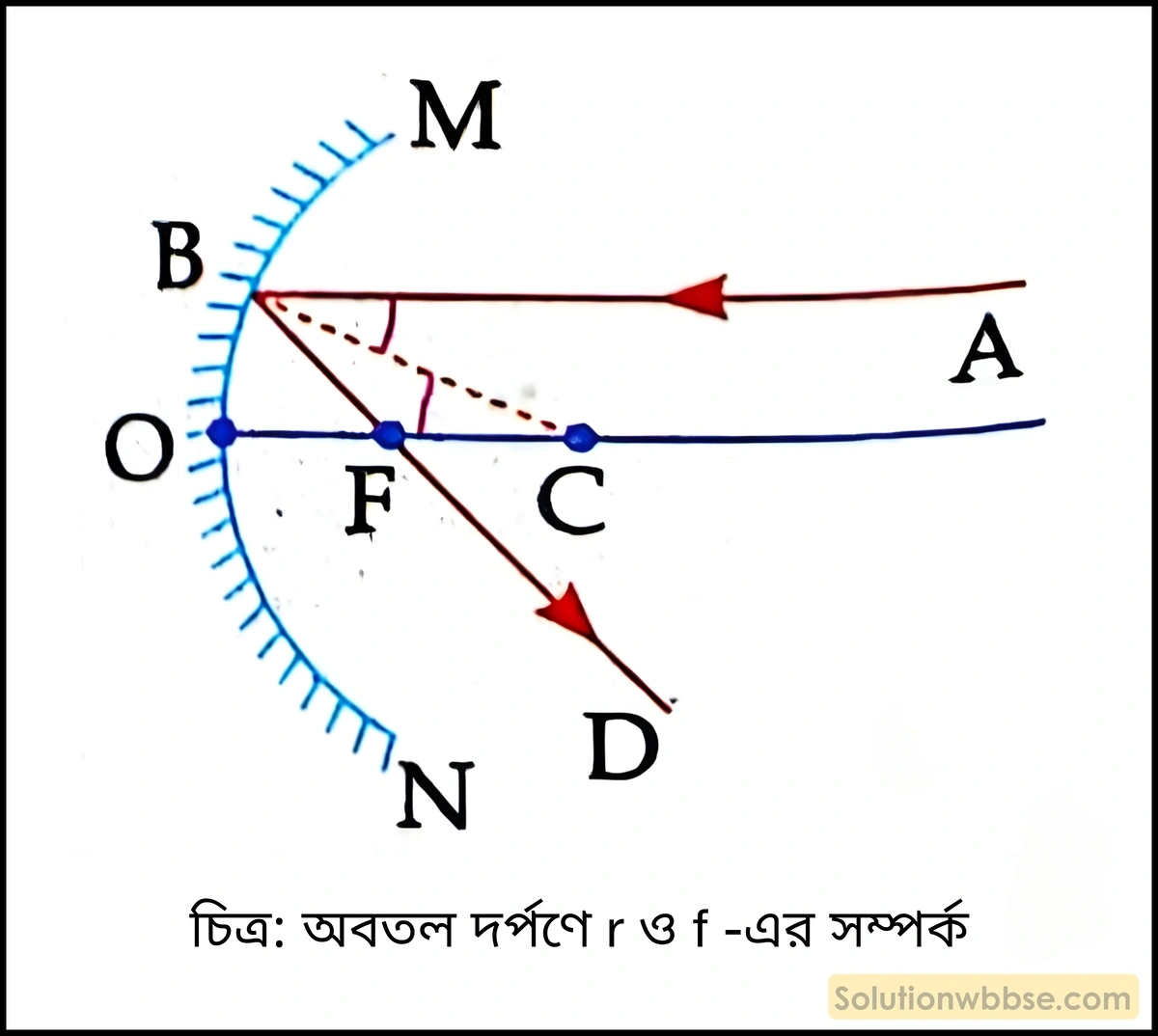
MON অবতল দর্পণের প্রধান অক্ষের সমান্তরাল রশ্মি AB দর্পণে আপতিত হল ও প্রতিফলনের পর BFD পথে চলে গেল। B বিন্দু ও বক্রতা কেন্দ্র C -এর সংযোজক রেখা B বিন্দুতে অভিলম্ব।
∴ ∠ABC = ∠CBF [প্রতিফলনের নিয়মানুসারে]
আবার, ∠ABC = ∠BCF [∵ একান্তর কোণ]
∴ ∠CBF = ∠BCF বা, FB = FC
কিন্তু FB ≃ FO তাই FO = FC
বা, FO = \(\frac{OC}2\)
বা, f = \(\frac r2\)
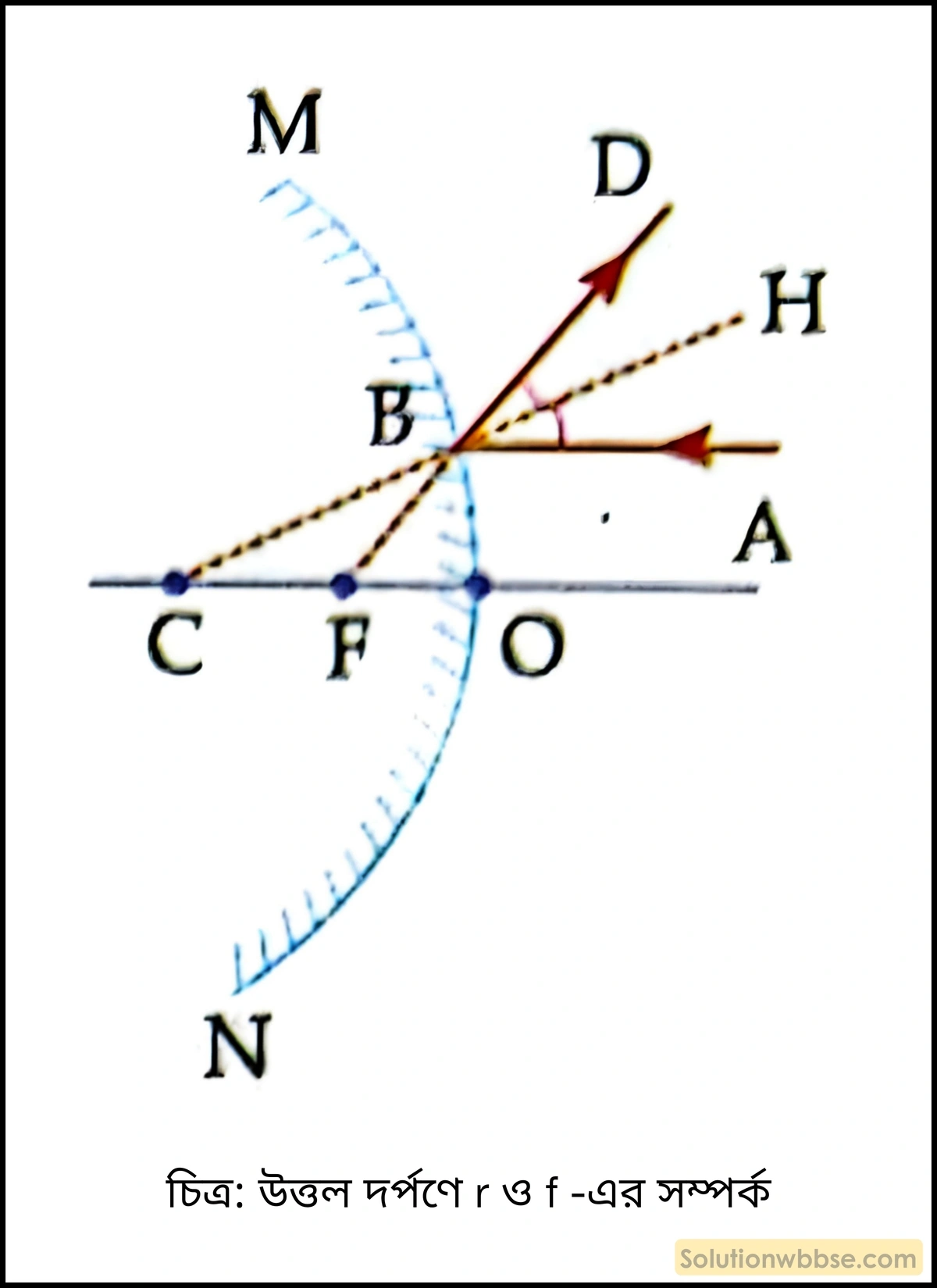
উত্তল দর্পণ –
উত্তল দর্পণে প্রধান অক্ষ OC -এর সমান্তরাল রেখা AB এমনভাবে প্রতিফলিত হল যেন সেটি F বিন্দু থেকে আসছে। এক্ষেত্রে CB হল অভিলম্ব।
∴ ∠ABH = ∠HBD [প্রতিফলনের সূত্রানুযায়ী]
আবার, ∠ABH = ∠FCB [অনুরূপ কোণ]
এবং ∠HBD = ∠CBF [বিপ্রতীপ কোণ]
∴ ∠FCB = ∠CBF বা, FB = FC
আবার, FB ≃ FO
∴ FO = FC
বা, FO = \(\frac{OC}2\)
বা, f = \(\frac r2\)
প্রতিবিম্ব গঠন –
উত্তল দর্পণ দ্বারা প্রতিবিম্ব গঠন –
1.
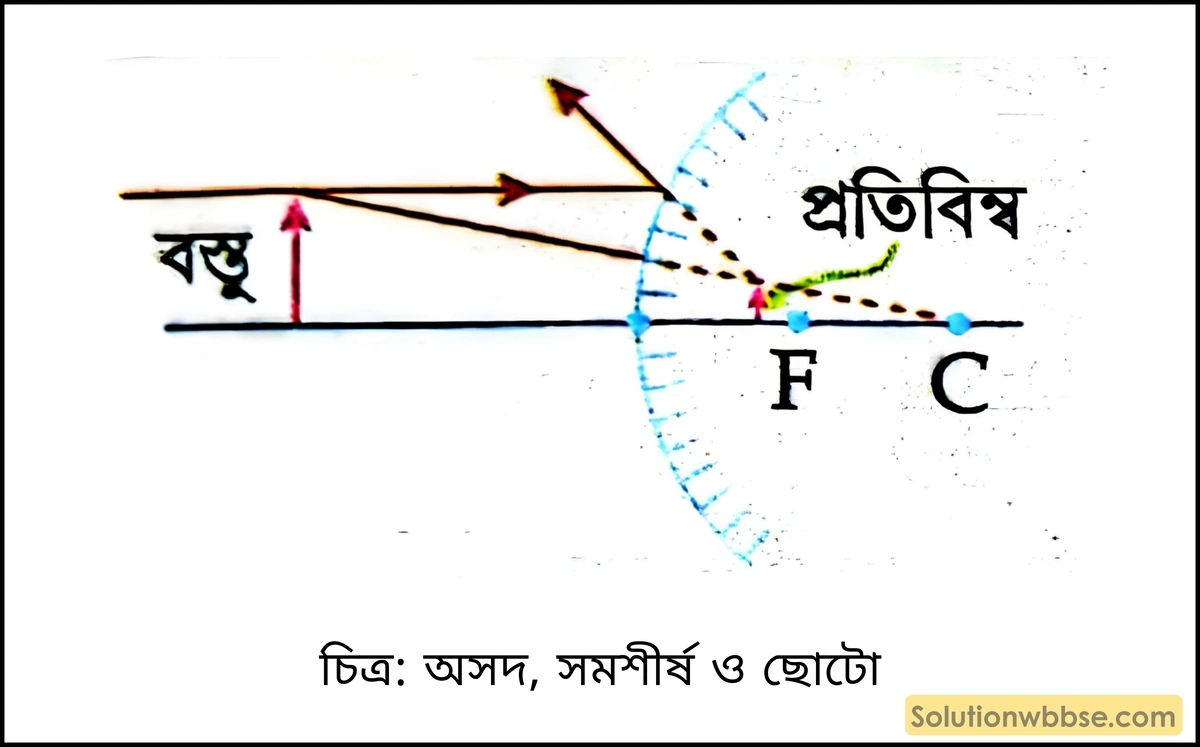
প্রতিবিম্বের প্রকৃতি – অসদ্, সমশীর্ষ ও ছোটো।
2.
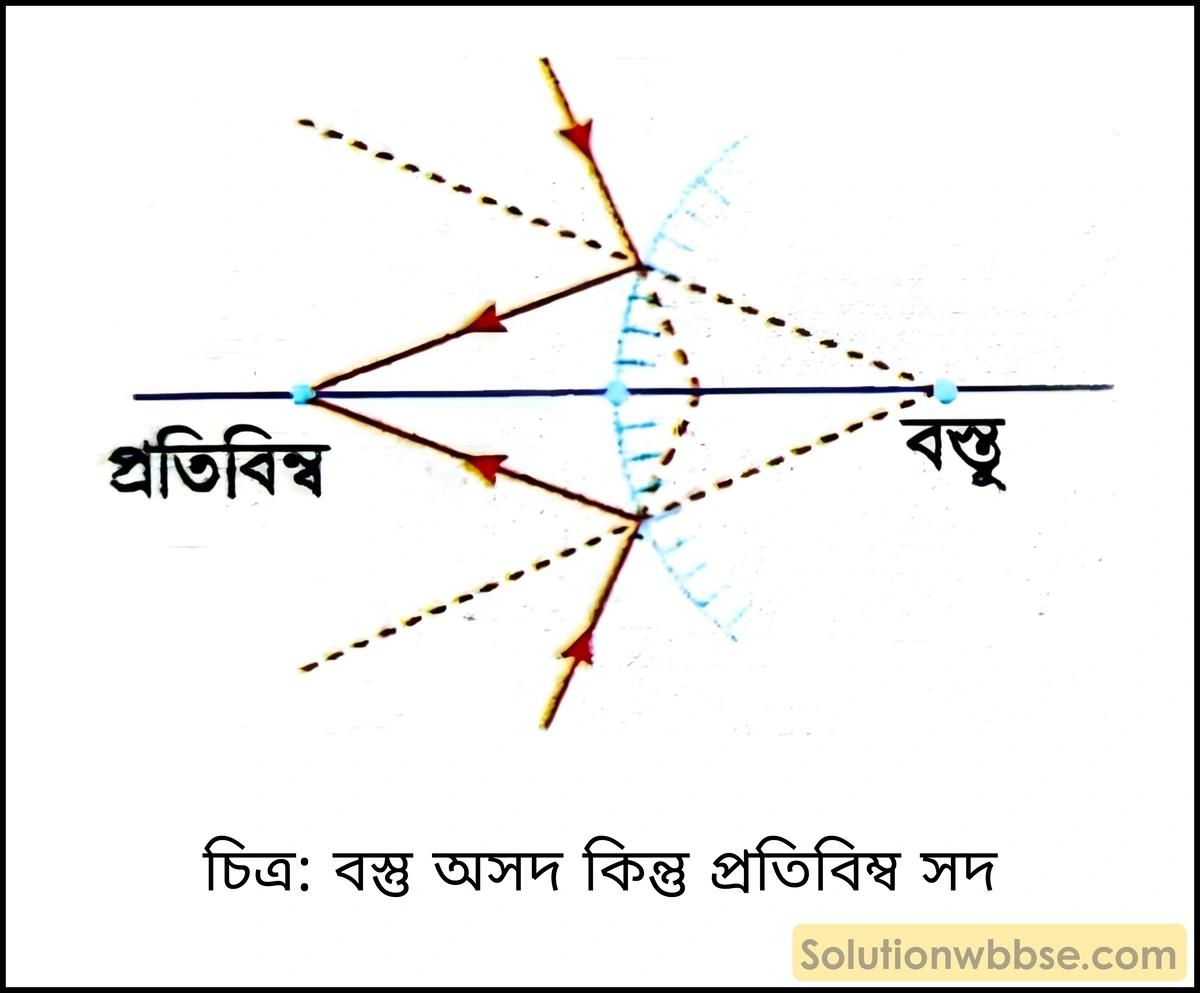
প্রতিবিম্বের প্রকৃতি – যেখানে অসদ্ কিন্তু প্রতিবিম্ব সদ্
3.
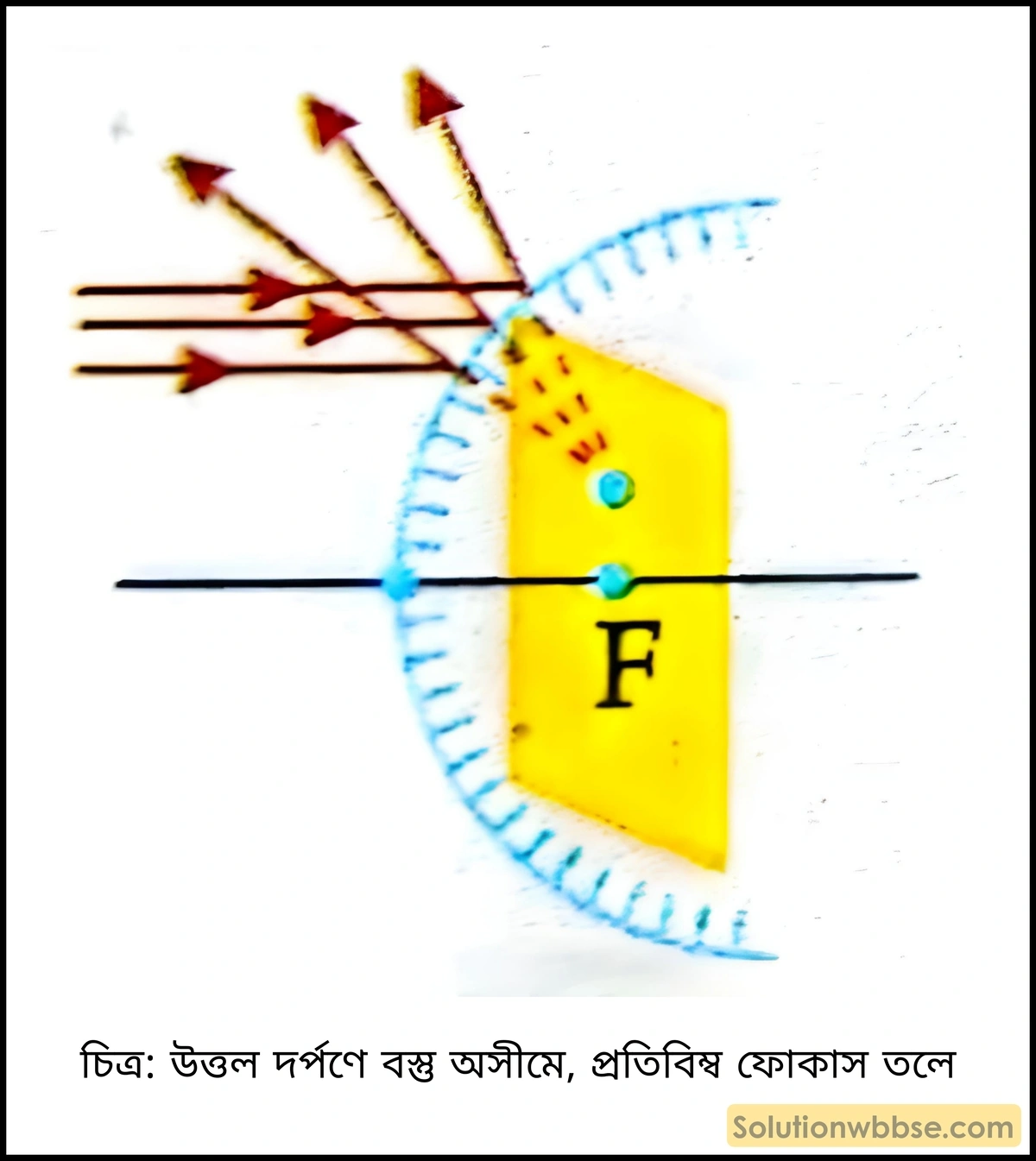
প্রতিবিম্বের প্রকৃতি – বস্তু অসীমে, প্রতিবিম্ব ফোকাস তলে
অবতল দর্পণ দ্বারা প্রতিবিম্ব গঠন –
1.
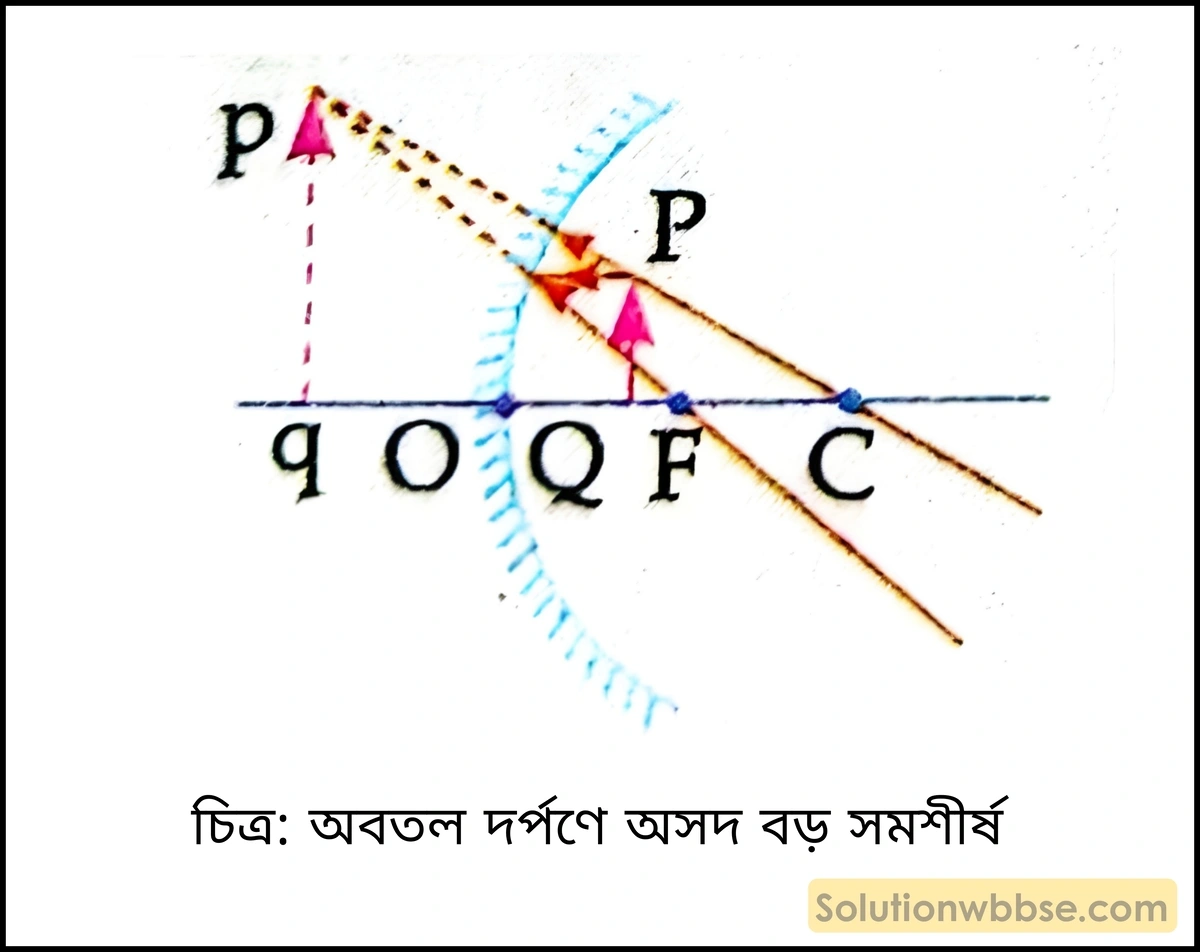
- বস্তুর অবস্থান – Ο এবং F -র মধ্যে
- প্রতিবিম্বের প্রকৃতি – অসদ, বড়ো, সমশীর্ষ
2.
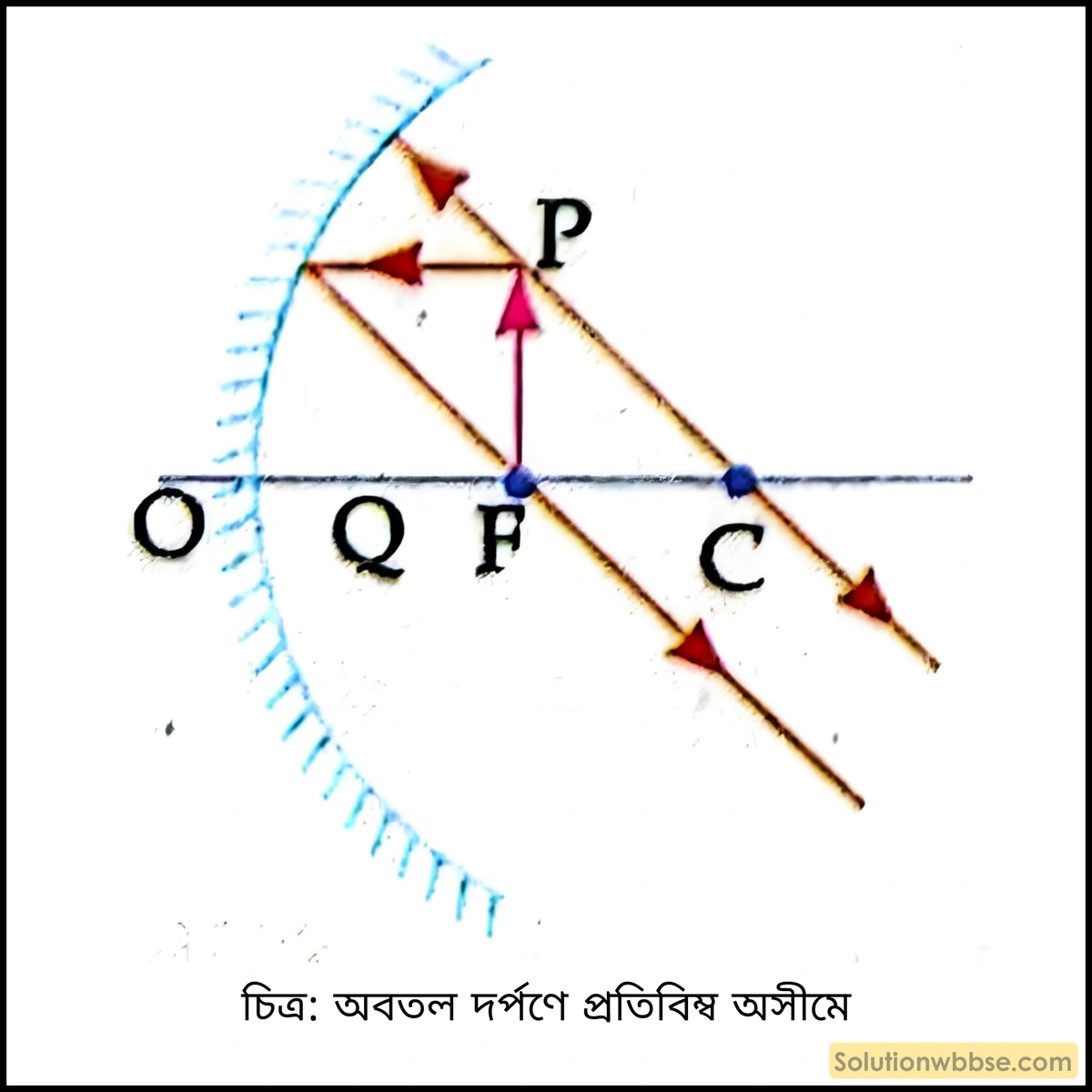
- বস্তুর অবস্থান – বস্তু ফোকাসে
- প্রতিবিম্বের প্রকৃতি – প্রতিবিম্ব অসীমে
3.
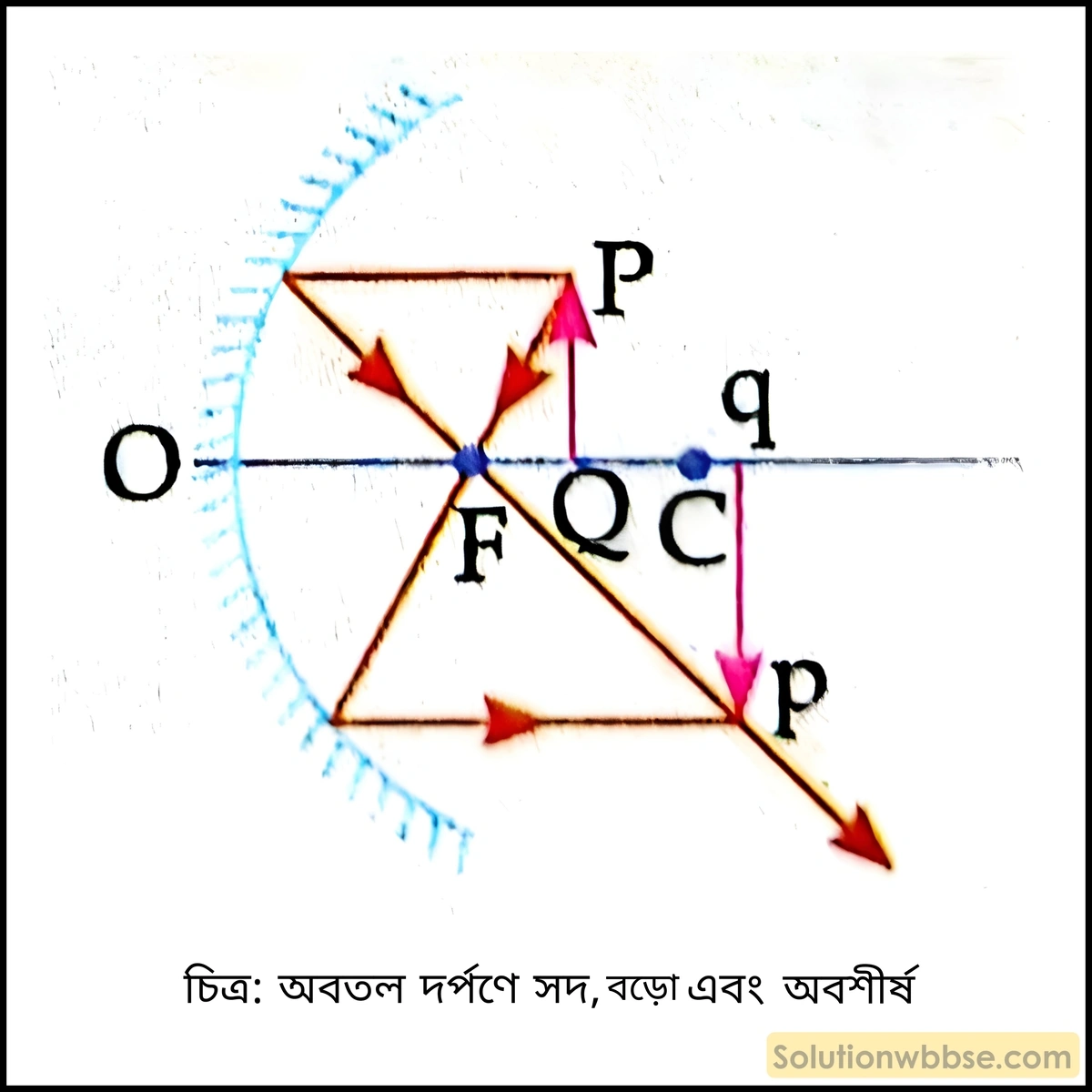
- বস্তুর অবস্থান – F এবং C -এর মধ্যে।
- প্রতিবিম্বের প্রকৃতি – সদ, বড়ো, অবশীর্ষ
4.
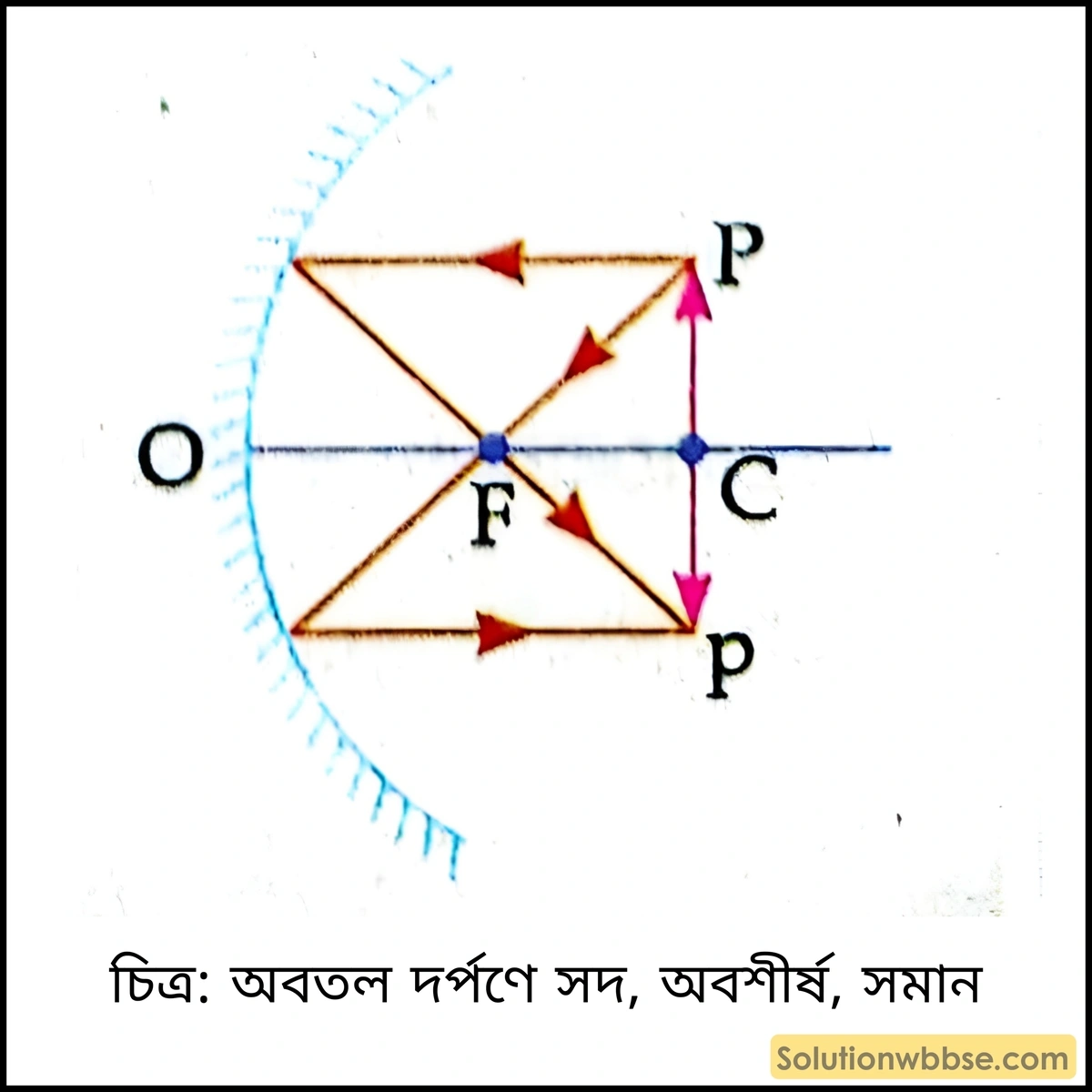
- বস্তুর অবস্থান – C বিন্দুতে
- প্রতিবিম্বের প্রকৃতি – সদ, অবশীর্ষ, সমান
5.
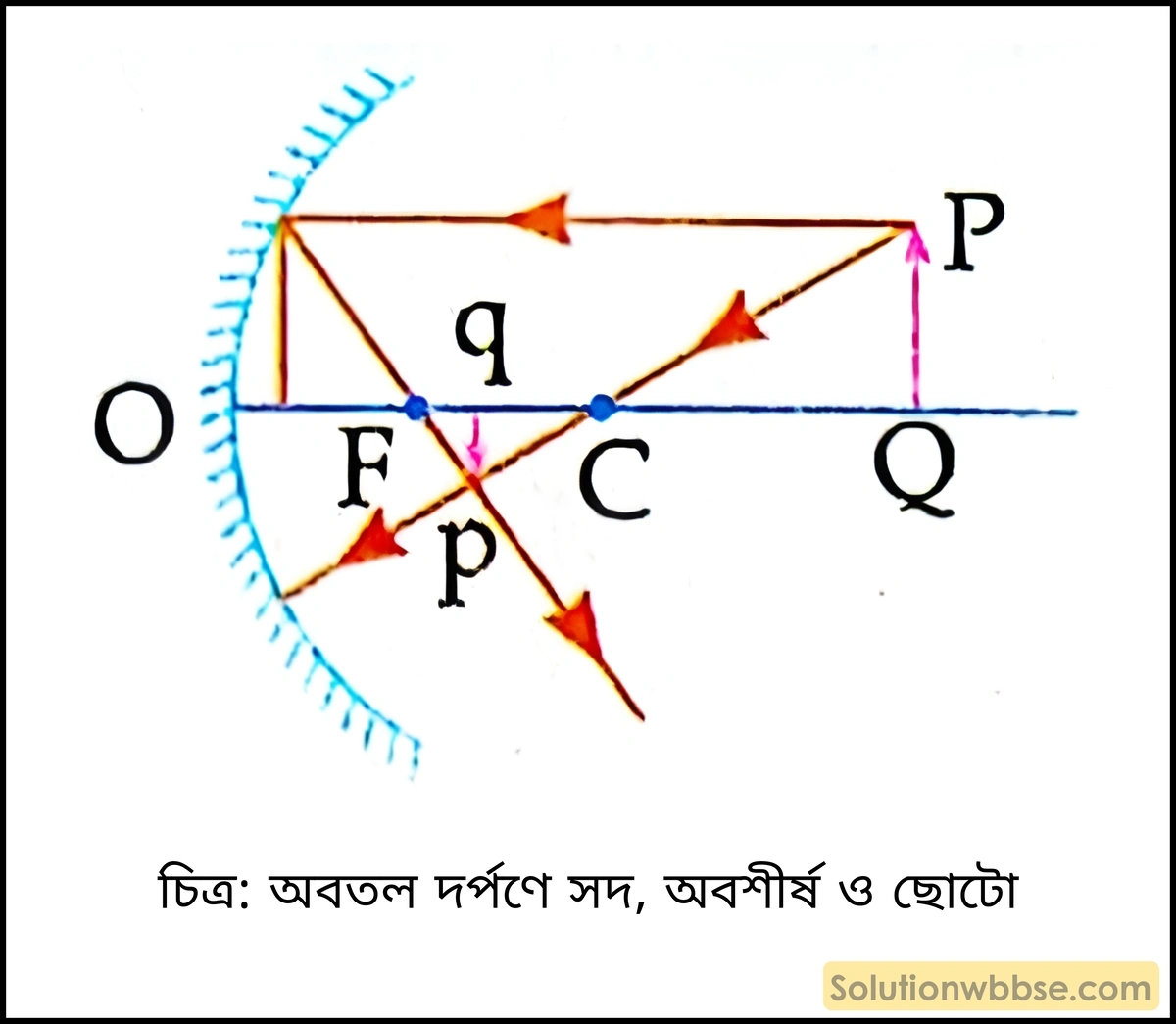
- বস্তুর অবস্থান – বক্রতা কেন্দ্রের পিছনে
- প্রতিবিম্বের প্রকৃতি – সদ, অবশীর্ষ ও ছোটো
6.
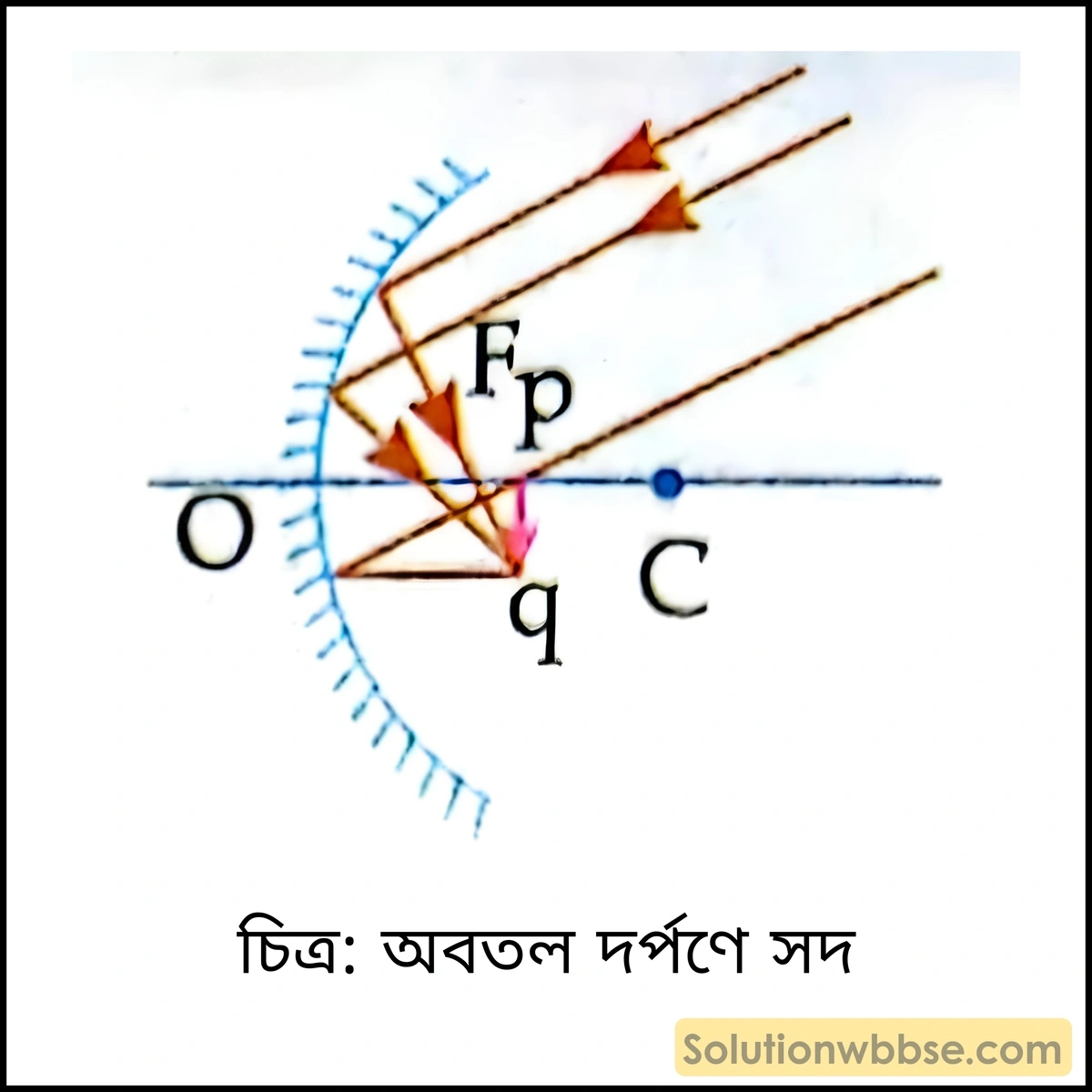
- বস্তুর অবস্থান – অসীমে
- প্রতিবিম্বের প্রকৃতি – সদ
রৈখিক বিবর্ধন –
প্রতিবিম্বের উচ্চতা ও বস্তুর উচ্চতার অনুপাতকে রৈখিক বিবর্ধন বলে। এটি প্রতিবিম্ব দূরত্ব ও বস্তু দূরত্বের অনুপাত।
1.
2. এটি এককহীন সংখ্যা।
3. m > 1 হলে প্রতিবিম্ব বড়ো হয়, m < 1 হলে প্রতিবিম্ব ছোটো হয়।
4. m = 1 হলে প্রতিবিম্বের আকার বস্তুর আকারের সমান হয়।
গোলীয় দর্পণের ব্যবহার –
- দন্ত চিকিৎসায় ব্যবহৃত ডেনটিস্ট মিরর – অবতল দর্পণ।
- মোটরগাড়ির ভিউফাইন্ডার – উত্তল দর্পণ।
- দাড়ি, কামানোর জন্য সেভিং মিরর – অবতল দর্পণ।
- মোটরগাড়ির হেডলাইট বা জ্যোতির্বিদ্যার গবেষণায় ব্যবহৃত দূরবীক্ষণ বা সার্চ লাইটে ব্যবহৃত অধিবৃত্তীয় দর্পণ।
এই আর্টিকেলে আমরা মাধ্যমিক ভৌতবিজ্ঞানের একটি গুরুত্বপূর্ণ অংশ “আলোর প্রতিফলন ও দর্পণ” নিয়ে আলোচনা করেছি। এই অংশটি মাধ্যমিক ভৌতবিজ্ঞান পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ। এই “আলোর প্রতিফলন ও দর্পণ” অংশটি মাধ্যমিক ভৌতবিজ্ঞানের পঞ্চম অধ্যায় “আলো“ -এর একটি গুরুত্বপূর্ণ অংশ। এই “আলোর প্রতিফলন ও দর্পণ” অংশটি মাধ্যমিক পরীক্ষায় এবং চাকরির পরীক্ষায় প্রায়ই দেখা যায়। আশা করি এই আর্টিকেলটি আপনাদের জন্য উপকারী হয়েছে। আপনাদের কোনো প্রশ্ন বা অসুবিধা থাকলে, আমাদের সাথে টেলিগ্রামে যোগাযোগ করতে পারেন, আমরা উত্তর দেওয়ার চেষ্টা করব। তাছাড়া, নিচে আমাদের এই পোস্টটি আপনার প্রিয়জনের সাথে শেয়ার করুন, যাদের এটি প্রয়োজন হতে পারে। ধন্যবাদ।






মন্তব্য করুন