এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের তৃতীয় অধ্যায়, ‘বৃত্ত সম্পর্কিত উপপাদ্য’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

প্রয়োগ 1. একটি বৃত্তে PQ, QR, RS এবং ST জ্যা। যদি PQ = QR = RS = ST হয়, তাহলে প্রমাণ করি যে, PR = QS = RT
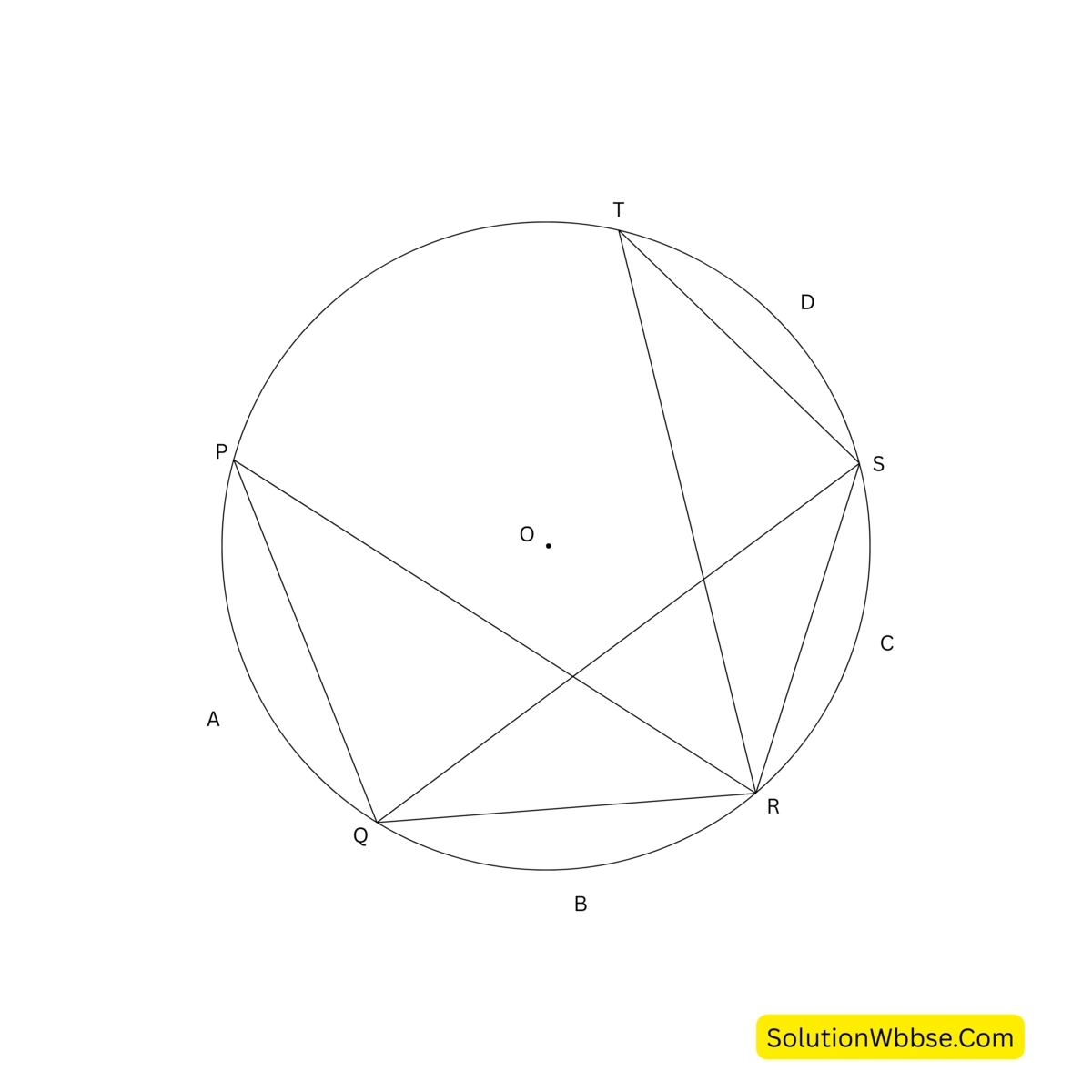
প্রদত্ত – O কেন্দ্রীয় বৃত্তে PQ, QR, RS এবং ST জ্যা এবং PQ = QR = RS = ST
প্রমাণ করতে হবে – PR = QS = RT
প্রমাণ – PQ = QR সুতরাং, \(\stackrel{\frown}{PAQ} = \stackrel{\frown}{QBR}\) …. (i) (যেহেতু, একই বৃত্তে সমান দৈর্ঘ্যের জ্যা সমান দৈর্ঘ্যের চাপ ছিন্ন করে)
আবার, QR = RS সুতরাং, \(\stackrel{\frown}{QBR} = \stackrel{\frown}{RCS}\) …. (ii)
(i) ও (ii) যোগ করে পাই, \(\stackrel{\frown}{PAQ} + \stackrel{\frown}{QBR} = \stackrel{\frown}{QBR} + \stackrel{\frown}{RCS}\)
সুতরাং,
\(\stackrel{\frown}{PQR} = \stackrel{\frown}{QRS}\)\(∴\) PR = QS (যেহেতু একই বৃত্তের চাপ দুটি দৈর্ঘ্যে সমান সুতরাং জ্যা দুটির দৈর্ঘ্য সমান)
আবার, RS = ST সুতরাং, \(\stackrel{\frown}{RCS} = \stackrel{\frown}{SDT}\) …. (iii)
(ii) ও (iii) যোগ করে পাই,
\(\stackrel{\frown}{QBR} + \stackrel{\frown}{RCS} = \stackrel{\frown}{RCS} + \stackrel{\frown}{SDT}\)সুতরাং,
\(\stackrel{\frown}{QRS} = \stackrel{\frown}{RST}\)\(∴\) QS = RT
\(∴\) PR = QS = RT (প্রমাণিত)
প্রয়োগ 2. যুক্তি দিয়ে প্রমাণ করি যে, একটি সমদ্বিবাহু ট্রাপিজিয়ামের শীর্ষবিন্দুগুলি সমবৃত্তস্থ।
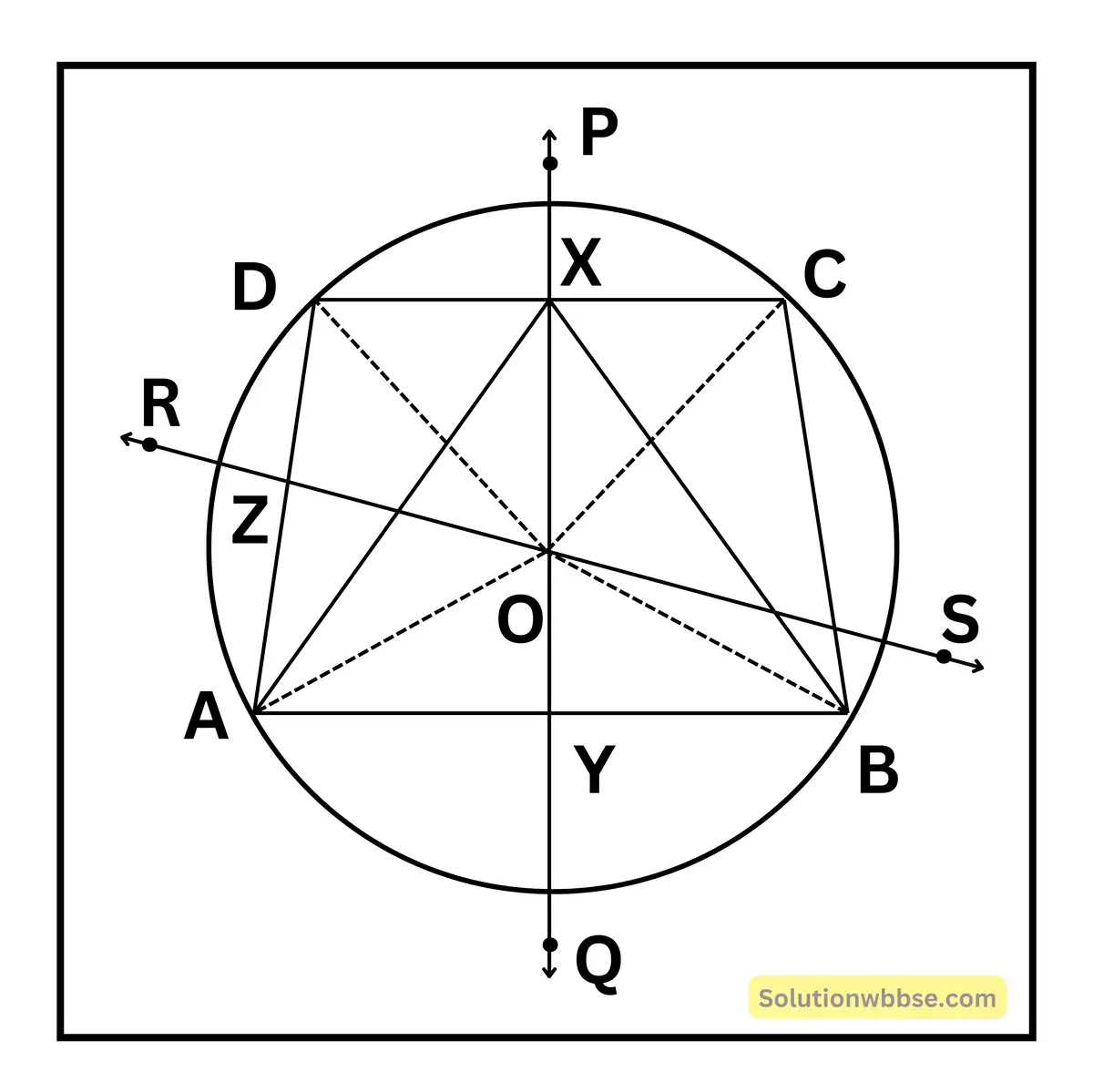
প্রদত্ত – ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম। AB || DC এবং AD = BC
প্রমাণ করতে হবে – ABCD ট্রাপিজিয়ামের শীর্ষবিন্দুগুলি সমবৃত্তস্থ।
অঙ্কন – DC বাহুর লম্বসমদ্বিখণ্ডক PQ এবং AD বাহুর লম্বসমদ্বিখণ্ডক অঙ্কন করলাম যারা যথাক্রমে DC কে X এবং AD কে Z বিন্দুতে ছেদ করল। PQ, AB কে Y বিন্দুতে ছেদ করল। A, X এবং B, X যুক্ত করলাম। PQ, RS কে O বিন্দুতে ছেদ করে। O বিন্দুর সঙ্গে A, B, C ও D যোগ করলাম।
প্রমাণ – ΔADX এবং ΔBCX-এ DX = CX [∵ CD-এর লম্বসমদ্বিখণ্ডক PQ]
∠ADX = ∠BCX [∵ সমদ্বিবাহু ট্রাপিজিয়ামের সমান্তরাল বাহুদুটির যে-কোনো একটি বাহু সংলগ্ন কোণগুলি সমান]
AD = BC [প্রদত্ত]
∴ ΔADX ≅ ΔBCX [S-A-S সর্বসমতার শর্তানুসারে]
∴ AX = BX [সর্বসম ত্রিভুজের অনুরূপ অংশ]
সমকোণী ΔAXY এবং সমকোণী ΔBXY-এ ∠AYX = ∠BYX [∵ AB || CD এবং CD ⊥ PQ, ∴ AB ⊥ PQ]
অতিভুজ AX = অতিভুজ BX [আগে প্রমাণ করা হয়েছে] এবং XY উভয় ত্রিভুজের সাধারণ বাহু।
∴ ΔΑΧΥ ≅ ΔBXY [R-H-S সর্বসমতার শর্তানুসারে]
∴ AY = BY [সর্বসম ত্রিভুজের অনুরূপ অংশ]
∴ PQ, AB-এর লম্বসমদ্বিখণ্ডক হবে।
∴ DC-এর লম্বসমদ্বিখণ্ডক PQ-এর উপর O বিন্দু অবস্থিত,
∴ DO = CO; একইভাবে, DO = AO এবং AO = BO
∴ CO = DO = AO = BO
∴ O বিন্দুকে কেন্দ্র করে OC বা OD বা OA বা OB-এর সমান দৈর্ঘ্যের ব্যাসার্ধ নিয়ে বৃত্ত আঁকলে বৃত্তটি A, B, C ও D বিন্দু দিয়ে যাবে। অর্থাৎ সমদ্বিবাহু ট্রাপিজিয়ামের শীর্ষবিন্দুগুলি সমবৃত্তস্থ। (প্রমাণিত)
প্রয়োগ 3. A কেন্দ্রীয় বৃত্তের ব্যাস নয় এরূপ একটি জ্যা PQ আঁকো। A থেকে PQ-এর উপর AM লম্ব আঁকো। যুক্তি দিয়ে প্রমাণ করো যে PM = MQ
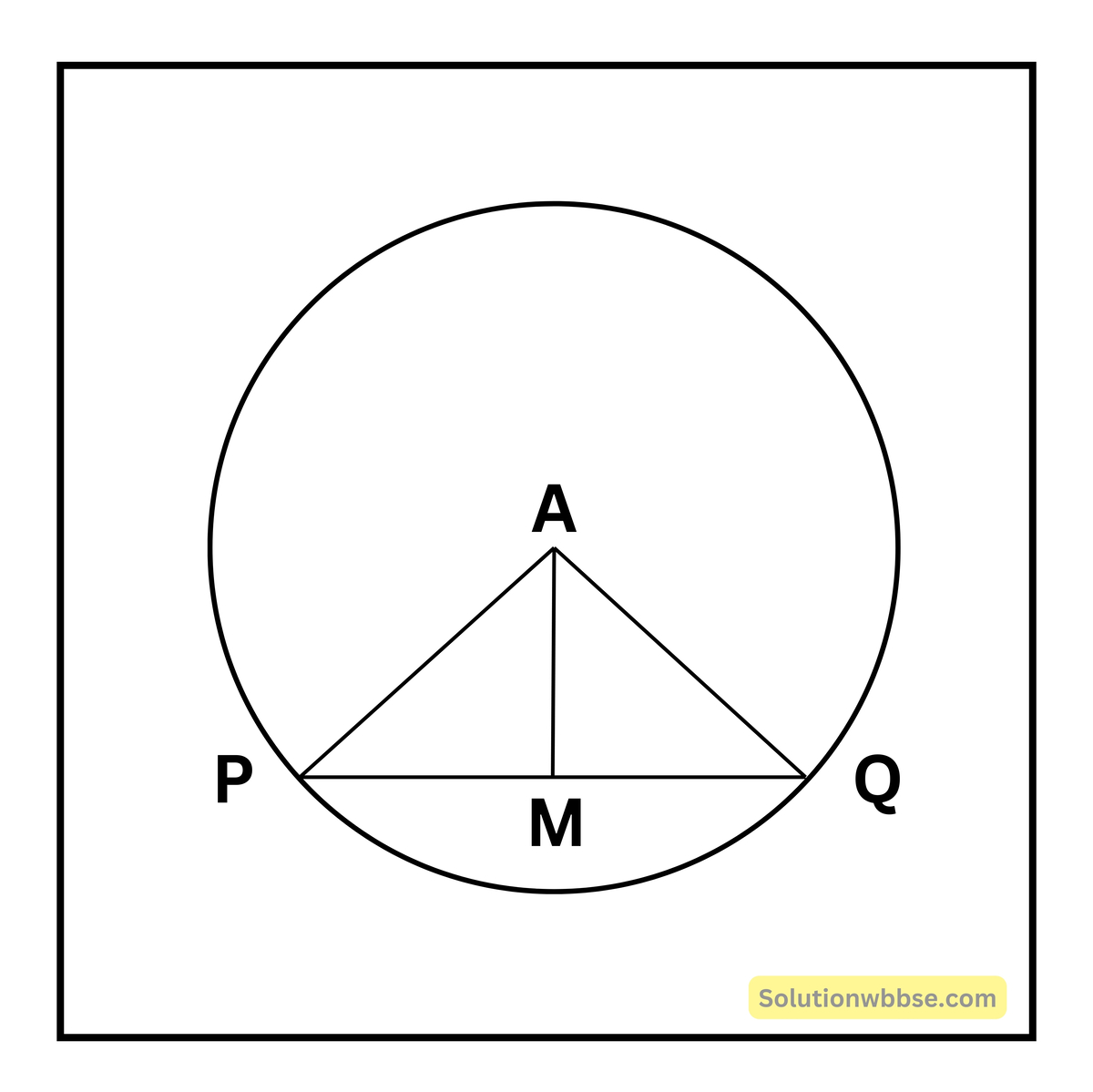
A কেন্দ্রিয় বৃত্তের PQ জ্যার উপর AM লম্ব।
প্রমাণ করতে হবে যে, PM = MQ
অঙ্কন – A, P ও A, Q যোগ করা হল।
প্রমাণ – AM ⊥ PQ
∴ ΔAPM ও ΔAMQ সমকোণী ত্রিভুজ।
সমকোণী ΔAPM ও ΔAMQ-এর
অতিভুজ AP = অতিভুজ AQ (একই বৃত্তের ব্যাসার্ধ)
AM সাধারণ বাহু
∴ ΔAPM ≅ ΔAMQ (R-H-S শর্তানুসারে)
∴ PM = MQ (সর্বসম ত্রিভুজের অনুরূপ বাহু) (প্রমাণিত)
প্রয়োগ 4. সর্বসমতার বাহু-কোণ-বাহু শর্তানুসারে ΔOAD ও ΔOBD সর্বসম প্রমাণ করে প্রমাণ করি যে ব্যাস নয় এরূপ কোনো জ্যা-কে যদি বৃত্তের কেন্দ্রবিন্দুগামী কোনো সরলরেখা সমদ্বিখণ্ডিত করে, তাহলে ওই সরলরেখা ওই জ্যা-এর উপর লম্ব হবে।
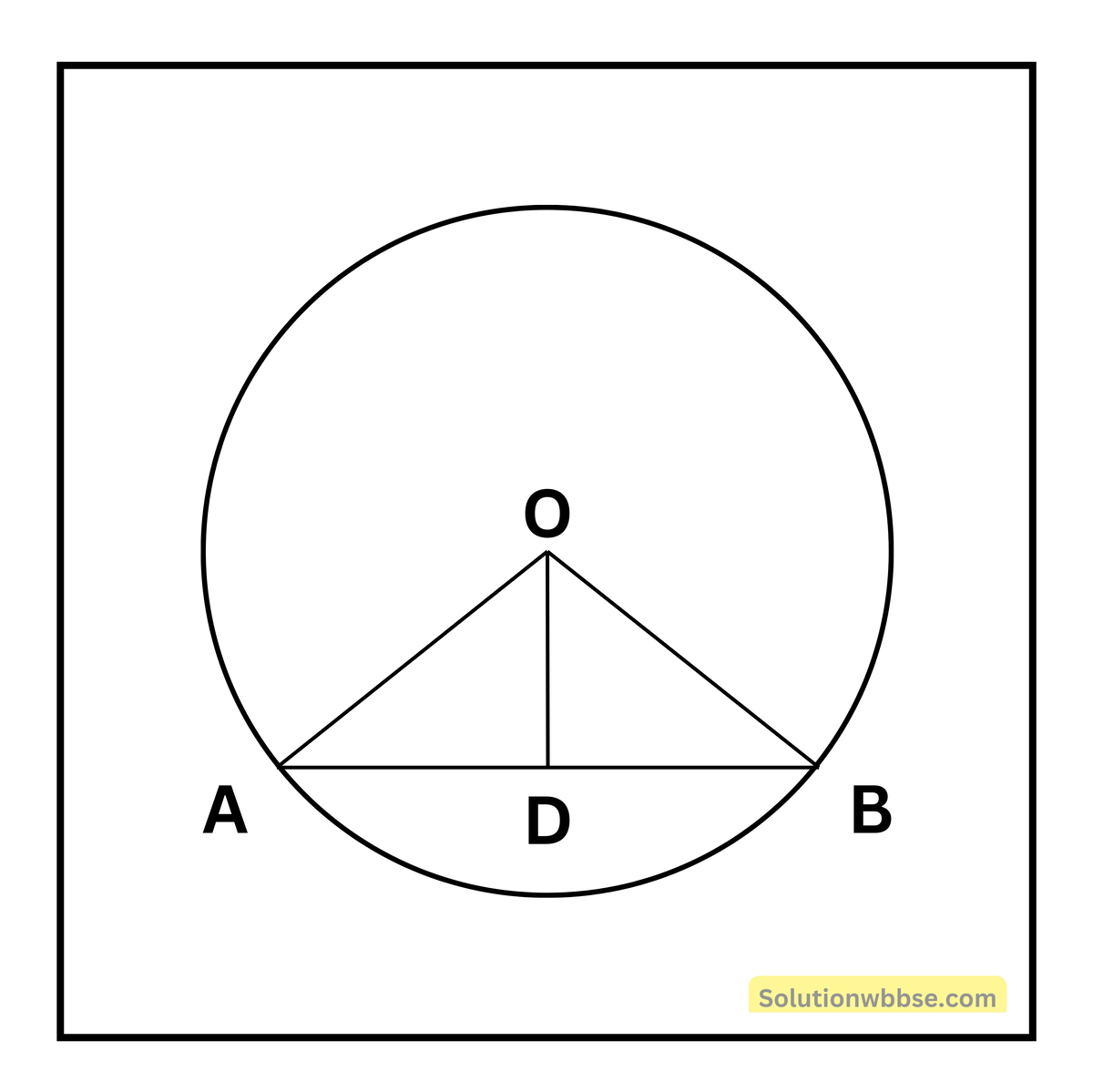
প্রদত্ত – ধরি, O কেন্দ্রীয় বৃত্তের ব্যাস নয় এরূপ একটি জ্যা AB এবং D, AB-এর মধ্যবিন্দু অর্থাৎ AD=DB
প্রমাণ করতে হবে – OD ⊥ AB অর্থাৎ OD, AB জ্যা-এর উপর লম্ব।
অঙ্কন – O, A এবং O, B যুক্ত করি।
প্রমাণ – ΔOAD ও ΔOBD-এর
OA = OB (একই বৃত্তের ব্যাসার্ধ)
∠OAD = ∠OBD (অনুরূপ কোণ)
AD = BD [∵ D, AB-এর মধ্যবিন্দু]
∴ ΔOAD ≅ ΔOBD (S-A-S শর্তানুসারে)
∴ ∠ODA = ∠ODB (সর্বসম ত্রিভুজের অনুরূপ কোণ)
∵ OD, AB জ্যার উপর দণ্ডায়মান হয়ে সমান কোণ উৎপন্ন করেছে।
∴ ∠ODA = ∠ODB = 1 সমকোণ
∴ OD ⊥ AB (প্রমাণিত)
প্রয়োগ 5. নিয়ামত একটি বৃত্ত এঁকেছে যার ব্যাসার্ধের দৈর্ঘ্য 13 সেমি.। তোমরা এই বৃত্তে একটি 10 সেমি. দৈর্ঘ্যের জ্যা AB আঁকো। বৃত্তের কেন্দ্র থেকে এই AB জ্যা-এর দূরত্ব হিসাব করে লেখো।
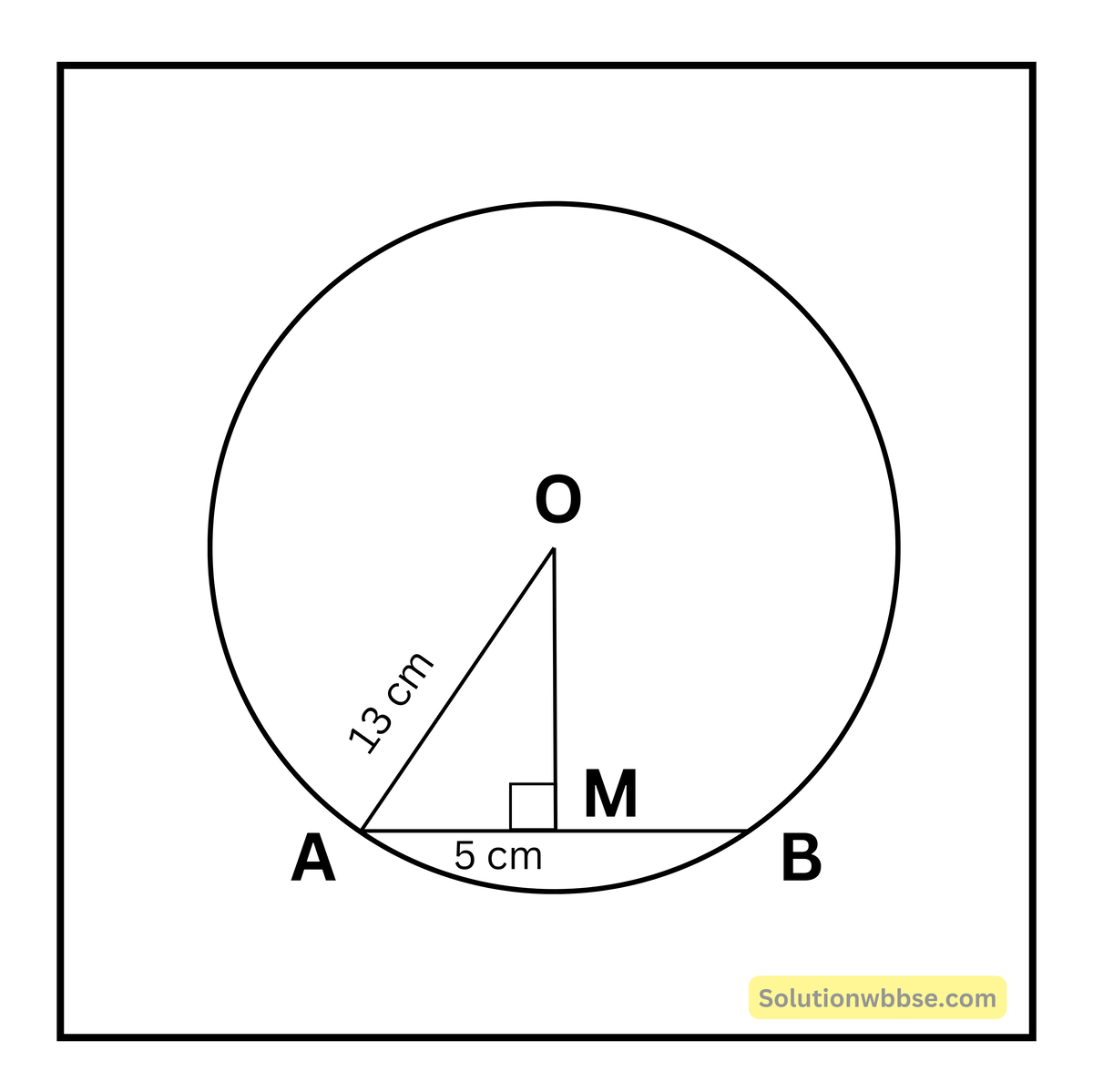
ধরি, বৃত্তের কেন্দ্র O; AB জ্যা-এর উপর O থেকে লম্ব OM অঙ্কন করলাম যা AB-কে M বিন্দুতে ছেদ করল।
∴ AM = \(\frac12\)AB = 5 সেমি. [∵ ব্যাস নয় এরকম কোনো জ্যা-এর উপর বৃত্তের কেন্দ্র থেকে লম্ব অঙ্কন করলে তা ওই জ্যা-কে সমদ্বিখণ্ডিত করে]
সমকোণী ত্রিভুজ AMO-তে
OA2 = AM2 + OM2 (পিথাগোরাসের উপপাদ্য অনুসারে)
OM2 = OA2 – AM2 = (132 – 52) বর্গ সেমি. = 144 বর্গ সেমি.
∴ OM = 12 সেমি.
∴ 13 সেমি. দৈর্ঘ্যের ব্যাসার্ধ বিশিষ্ট বৃত্তের কেন্দ্র থেকে 10 সেমি. জ্যা-এর লম্ব দূরত্ব 12 সেমি.
প্রয়োগ 6. 17 সেমি. দৈর্ঘ্যের ব্যাসার্ধবিশিষ্ট বৃত্তের যে জ্যা-এর কেন্দ্র থেকে দূরত্ব 8 সেমি., তার দৈর্ঘ্য হিসাব করে লিখি।
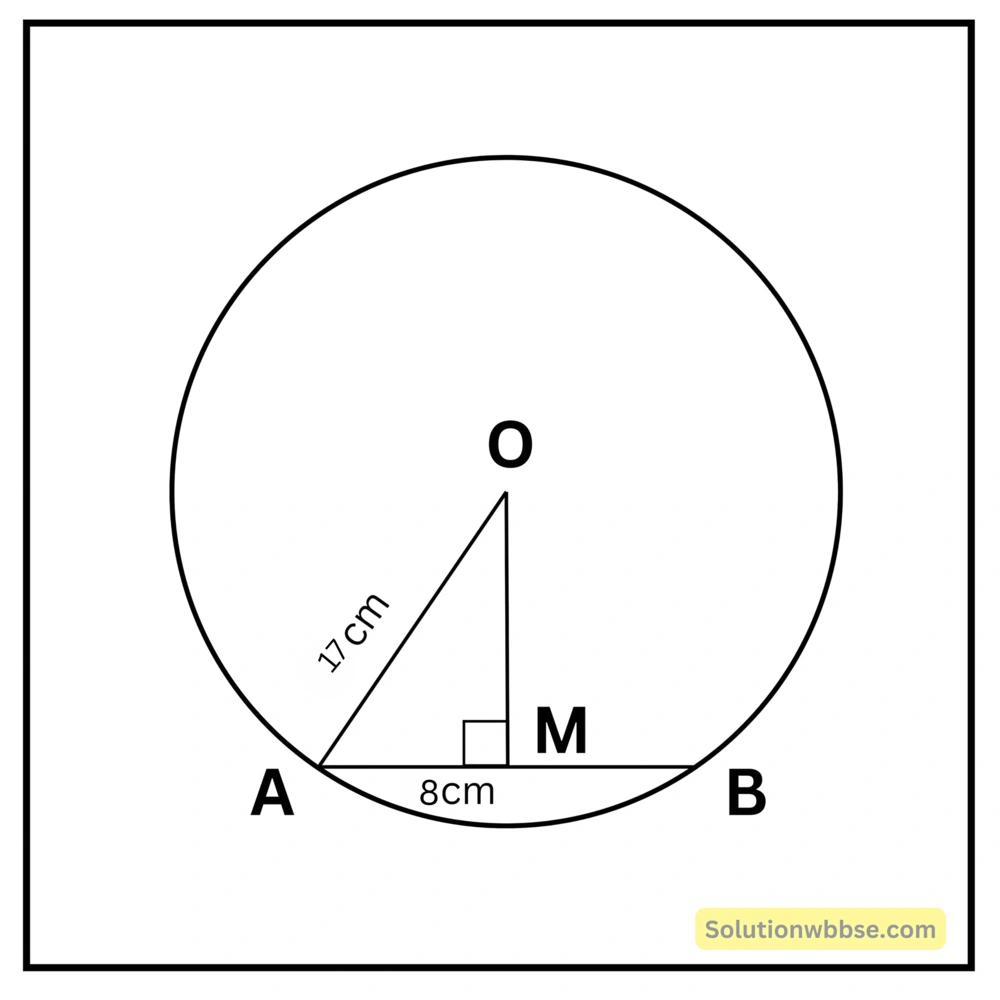
ধরি, বৃত্তের কেন্দ্র O; জ্যা AB-এর উপর O থেকে লম্ব OM অঙ্কন করলাম যা AB-কে M বিন্দুতে ছেদ করল।
\( ∴ OM = 8 \) সেমি. [ধরা]
সমকোণী ত্রিভুজ AMO-তে
\( OA^2 = AM^2 + OM^2 \) (পিথাগোরাসের উপপাদ্য অনুসারে)
\( AM^2 = OA^2 – OM^2 = (17^2 – 8^2) \) বর্গ সেমি. = 225 বর্গ সেমি.
\( ∴ AM = 15 \) সেমি.
\( ∴ AB = 2 \times AM = 30 \) সেমি.
\( ∴ \) 17 সেমি. দৈর্ঘ্যের ব্যাসার্ধ বিশিষ্ট বৃত্তের কেন্দ্র থেকে 8 সেমি. দূরের জ্যা-এর দৈর্ঘ্য 30 সেমি.
প্রয়োগ 7. 10 সেমি. দৈর্ঘ্যের ব্যাসার্ধবিশিষ্ট একটি বৃত্তের দুটি সমান্তরাল জ্যা-এর দৈর্ঘ্য 16 সেমি. এবং 12 সেমি.। হিসাব করে দেখি, ওই দুটি জ্যা-এর মধ্যে দূরত্ব কত যদি তারা কেন্দ্রের (i) একই পার্শ্বে থাকে, (ii) বিপরীত পার্শ্বে থাকে।
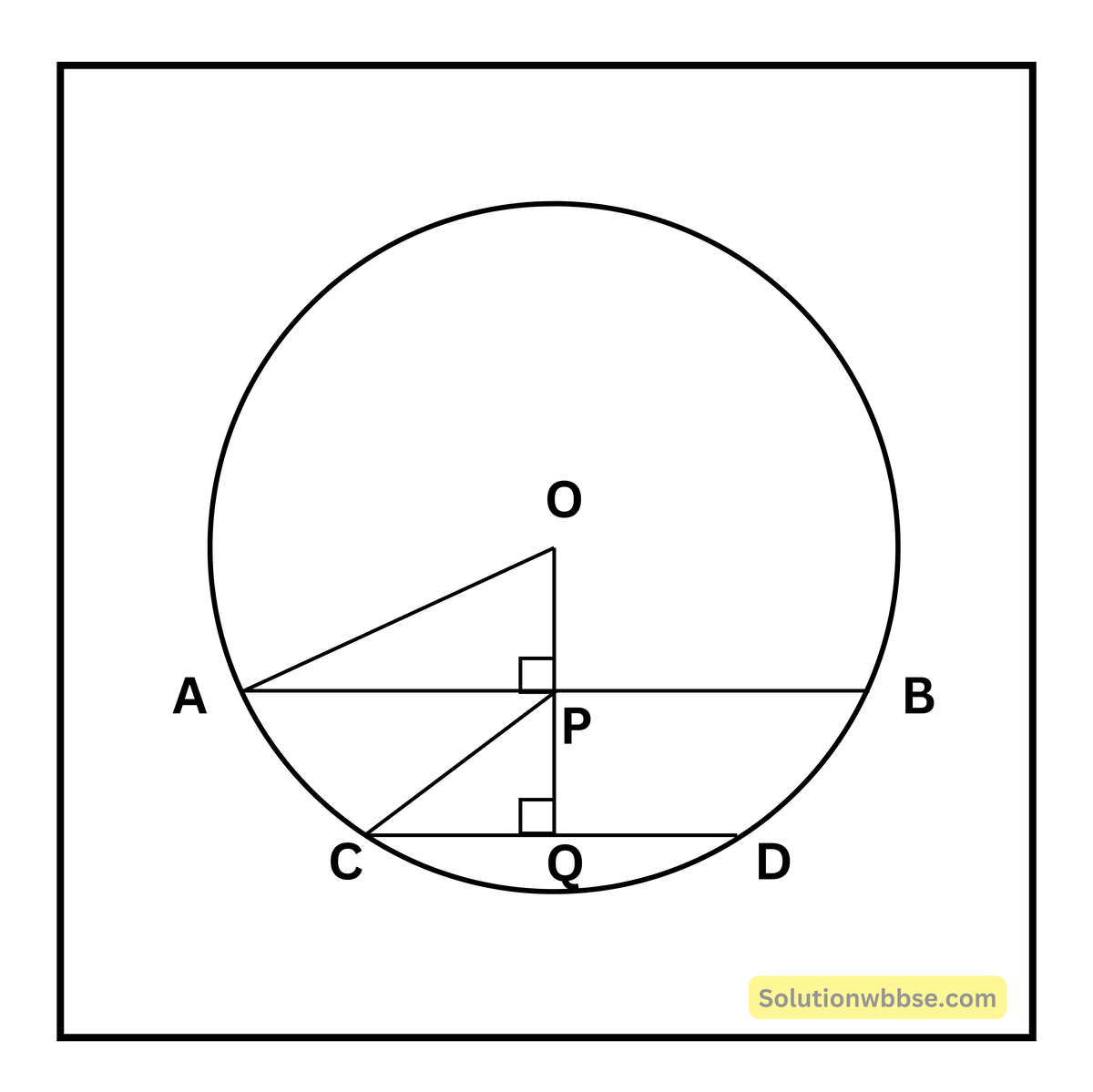
(i) ধরি, O কেন্দ্রীয় বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 10 সেমি. এবং AB ও CD জ্যা দুটি কেন্দ্রের একই পার্শ্বে অবস্থিত। AB ও CD-এর দৈর্ঘ্য যথাক্রমে 16 সেমি. ও 12 সেমি.। AB || CD
O বিন্দু থেকে CD জ্যা-এর উপর OQ লম্ব অঙ্কন করলাম যা AB জ্যা-কে P বিন্দুতে ছেদ করে।
যেহেতু AB || CD এবং OQ ⊥ CD, সুতরাং OP ⊥ AB.
∠OPB = অনুরূপ ∠OQD ∵ ∠OQD = 90°, ∴ ∠OPB = 90°
∴ AP = \(\frac12\)AB = \(\frac12\) × 16 সেমি. = 8 সেমি.
আবার OA = 10 সেমি.
∴ সমকোণী ΔΑΡO-তে,
OP2 = OA2 – AP2 = (102 – 82) বর্গ সেমি. = 36 বর্গ সেমি.
∴ OP = 6 সেমি.
∵ OQ ⊥ CD ∴ CQ = 6
∴ সমকোণী ΔOCQ থেকে পেলাম, OQ = 8
∴ জ্যা AB ও CD-এর মধ্যে দূরত্ব PQ = OQ – OP বর্গ সেমি.
= (8 – 6) সেমি.
= 2 সেমি.
(ii) কিন্তু AB ও CD জ্যা দুটি যদি বৃত্তের কেন্দ্রের বিপরীত পার্শ্বে থাকত,
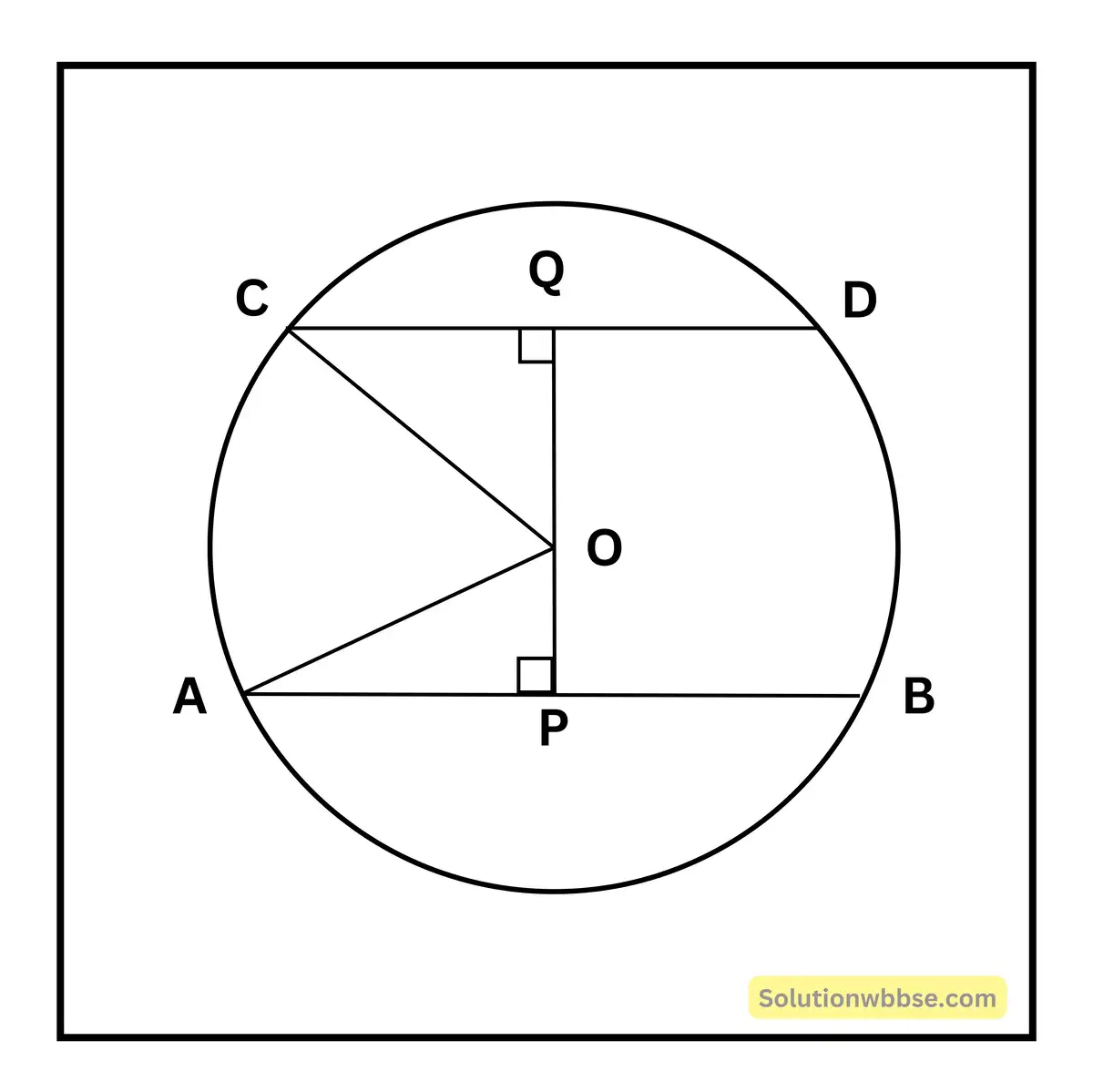
সেক্ষেত্রে AB ও CD জ্যা দুটির দূরত্ব = PQ
= OP + OQ
= (6 + 8) সেমি.
= 14 সেমি.
প্রয়োগ 8. 5 সেমি. দৈর্ঘ্যের ব্যাসার্ধবিশিষ্ট বৃত্তে 8 সেমি. ও 6 সেমি. দৈর্ঘ্যের দুটি সমান্তরাল জ্যা বৃত্তের কেন্দ্রের বিপরীত পার্শ্বে অবস্থিত। জ্যা দুটির মধ্যের দূরত্ব হিসাব করে লিখি।
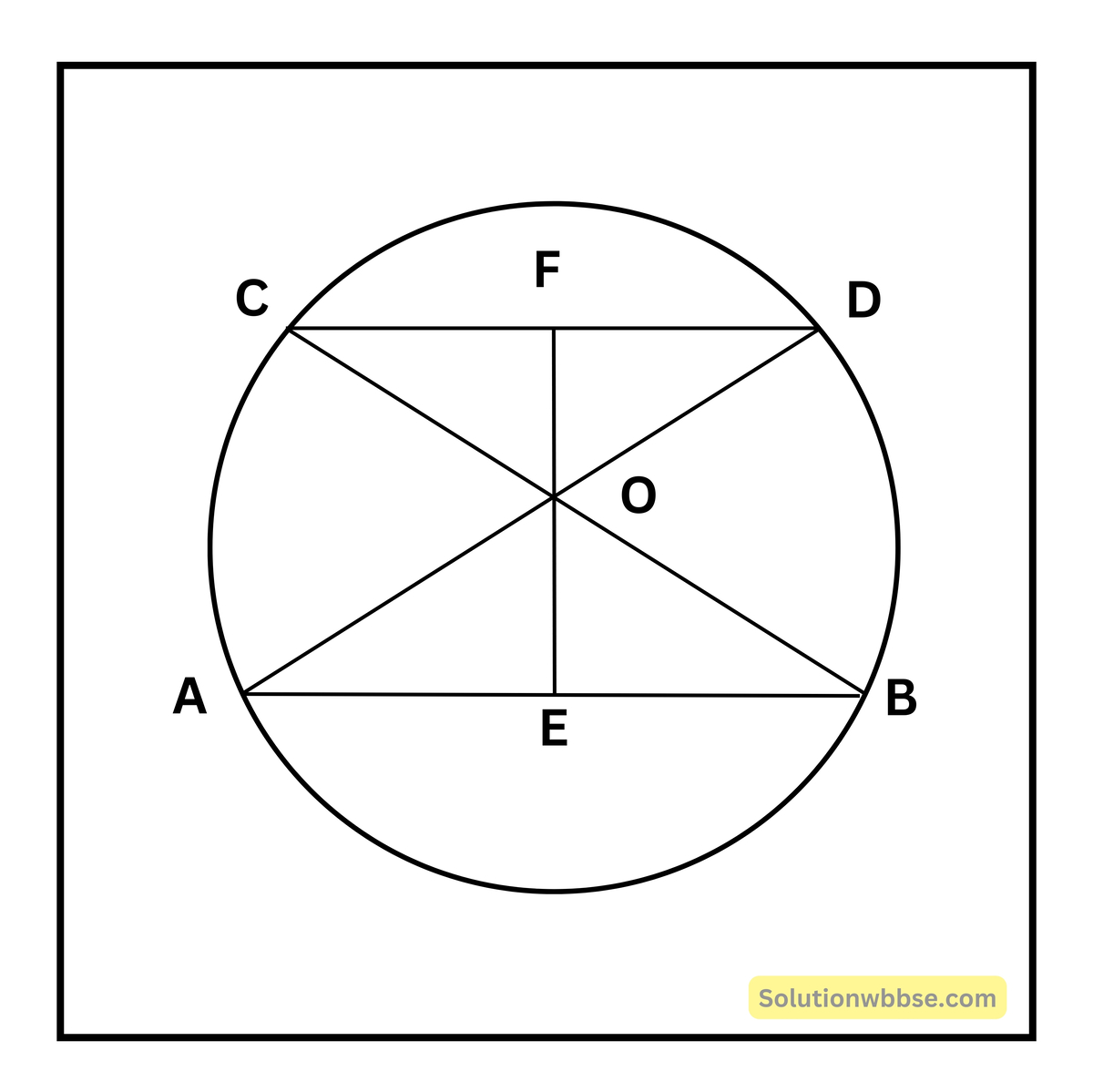
OE = \(\sqrt{5^2-\left(\frac82\right)^2}\) = \(\sqrt{25-16}\) = \(\sqrt9\) সেমি
OF = \(\sqrt{5^2-\left(\frac62\right)^2}\) = \(\sqrt{25-9}\) = \(\sqrt{16}\) সেমি
∴ EF = (3 + 4) = 7 সেমি
∴ কেন্দ্রদ্বয়ের দূরত্ব EF = (3 + 4) = 7 সেমি
প্রয়োগ 9. প্রমাণ করি, ব্যাসই বৃত্তের বৃহত্তম জ্যা।
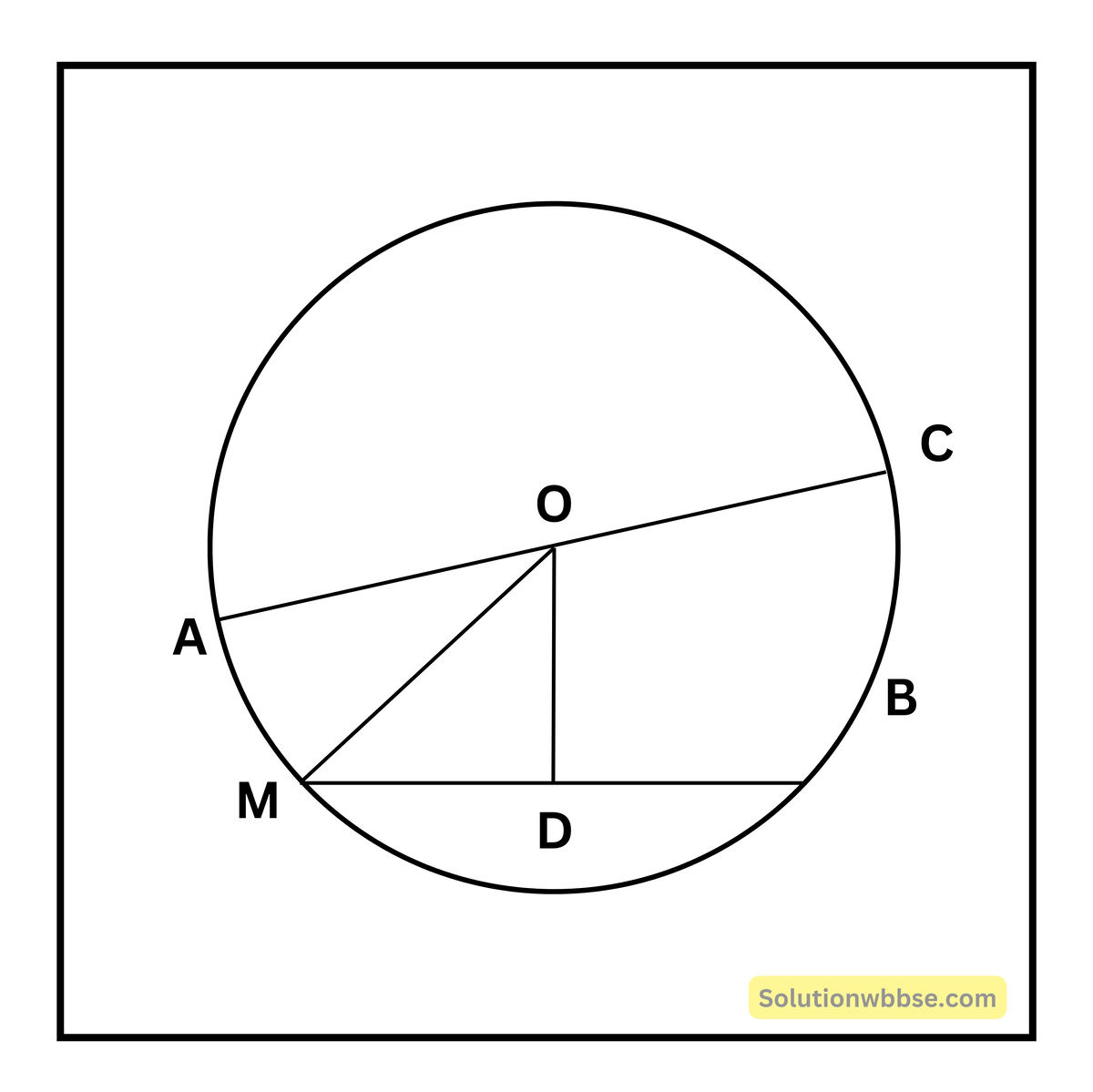
প্রদত্ত – O কেন্দ্রীয় বৃত্তে MN ব্যাস নয় এমন যে-কোনো একটি জ্যা এবং AC একটি ব্যাস।
প্রমাণ করতে হবে – AC > MN অর্থাৎ ব্যাসই বৃত্তের বৃহত্তম জ্যা।
অঙ্কন – কেন্দ্র O থেকে জ্যা MN-এর উপর OD লম্ব অঙ্কন করি। O, M যুক্ত করি।
প্রমাণ – OM > MD ∵ OMD একটি সমকোণী ত্রিভুজ এবং OM অতিভুজ]
বা, OA > MD [∵ OA = OM একই বৃত্তের ব্যাসার্ধ]
বা, \(\frac12\)AC > \(\frac12\)MN
বা, AC > MN
∴ ব্যাসই বৃত্তের বৃহত্তম জ্যা। (প্রমাণিত)
প্রয়োগ 10. যুক্তি দিয়ে প্রমাণ করি যে, কোনো বৃত্তের দুটি সমান জ্যা কেন্দ্র থেকে সমদূরবর্তী।
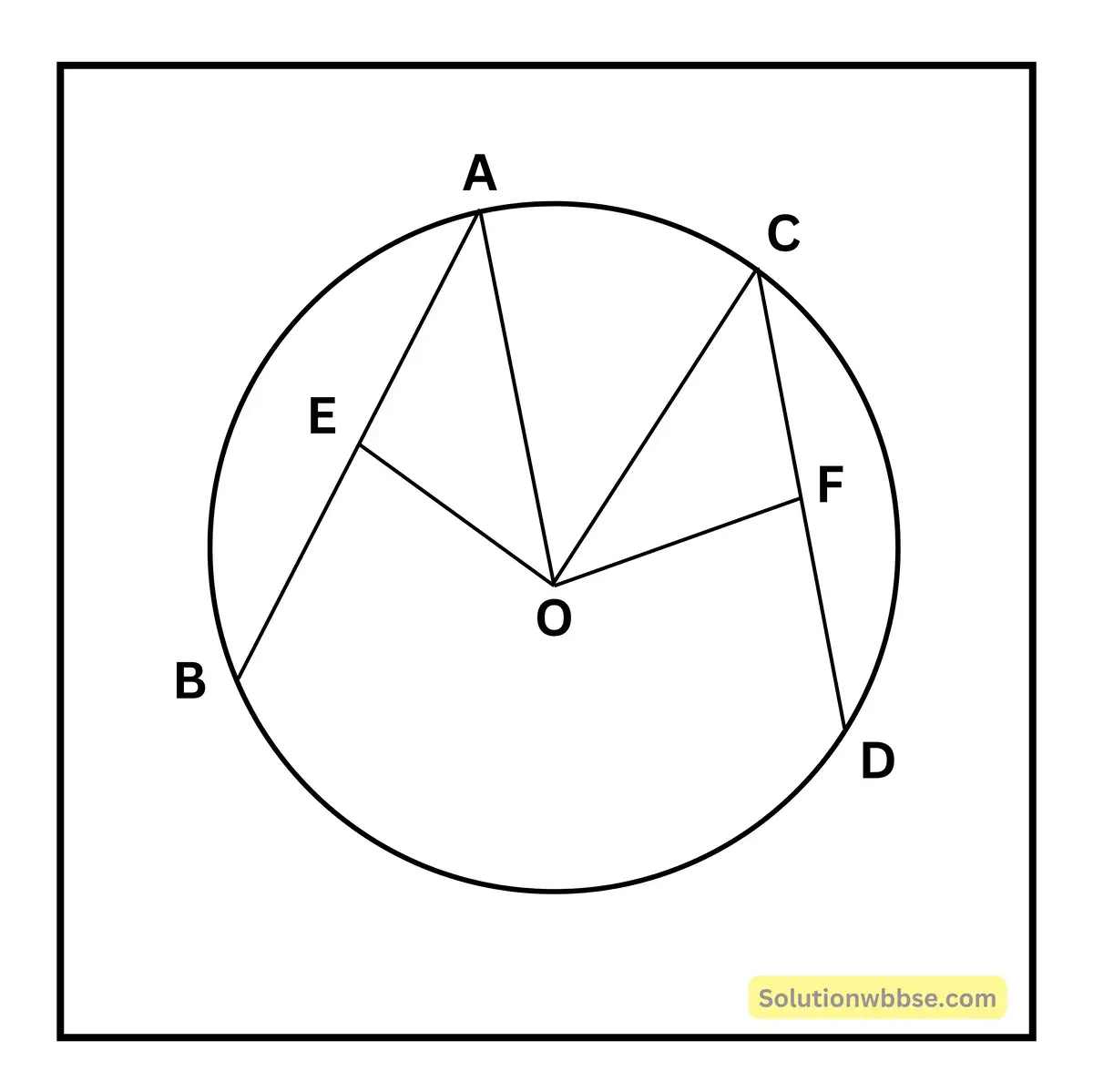
প্রদত্ত – O কেন্দ্রীয় বৃত্তের AB ও CD দুটি সমান দৈর্ঘ্যের জ্যা। কেন্দ্র O থেকে AB ও CD-এর দূরত্ব যথাক্রমে OE ও OF অর্থাৎ OE ⊥ AB এবং OF ⊥ CD
প্রমাণ করতে হবে – OE = OF
অঙ্কন – O, A ও O, C যুক্ত করলাম।
প্রমাণ – OE ⊥ AB এবং OF ⊥ CD [প্রদত্ত]
∴ AE = \(\frac12\)AB এবং CF = \(\frac12\)CD [যেহেতু, বৃত্তের কেন্দ্র থেকে ব্যাস নয় এরূপ কোনো জ্যা-এর উপর লম্ব জ্যাটিকে সমদ্বিখণ্ডিত করে।]
আবার, AB = CD [প্রদত্ত]
∴ AE = CF —-(i)
∴ সমকোণী ΔΑΕΟ ও সমকোণী ΔOFC-তে ∠OEA = ∠OFC (প্রত্যেকটি সমকোণ)
অতিভুজ OA = অতিভুজ OC [একই বৃত্তের ব্যাসার্ধ]
AE = CF [(i) থেকে পাই]
ΔΑΕΟ ≅ ΔCFO [R-H-S সর্বসমতার শর্তানুসারে]
∴ OE = OF [প্রমাণিত]
প্রয়োগ 11. প্রমাণ করি যে বৃত্তের কোনো জ্যা-এর লম্বসমদ্বিখণ্ডক ওই বৃত্তের কেন্দ্রগামী।
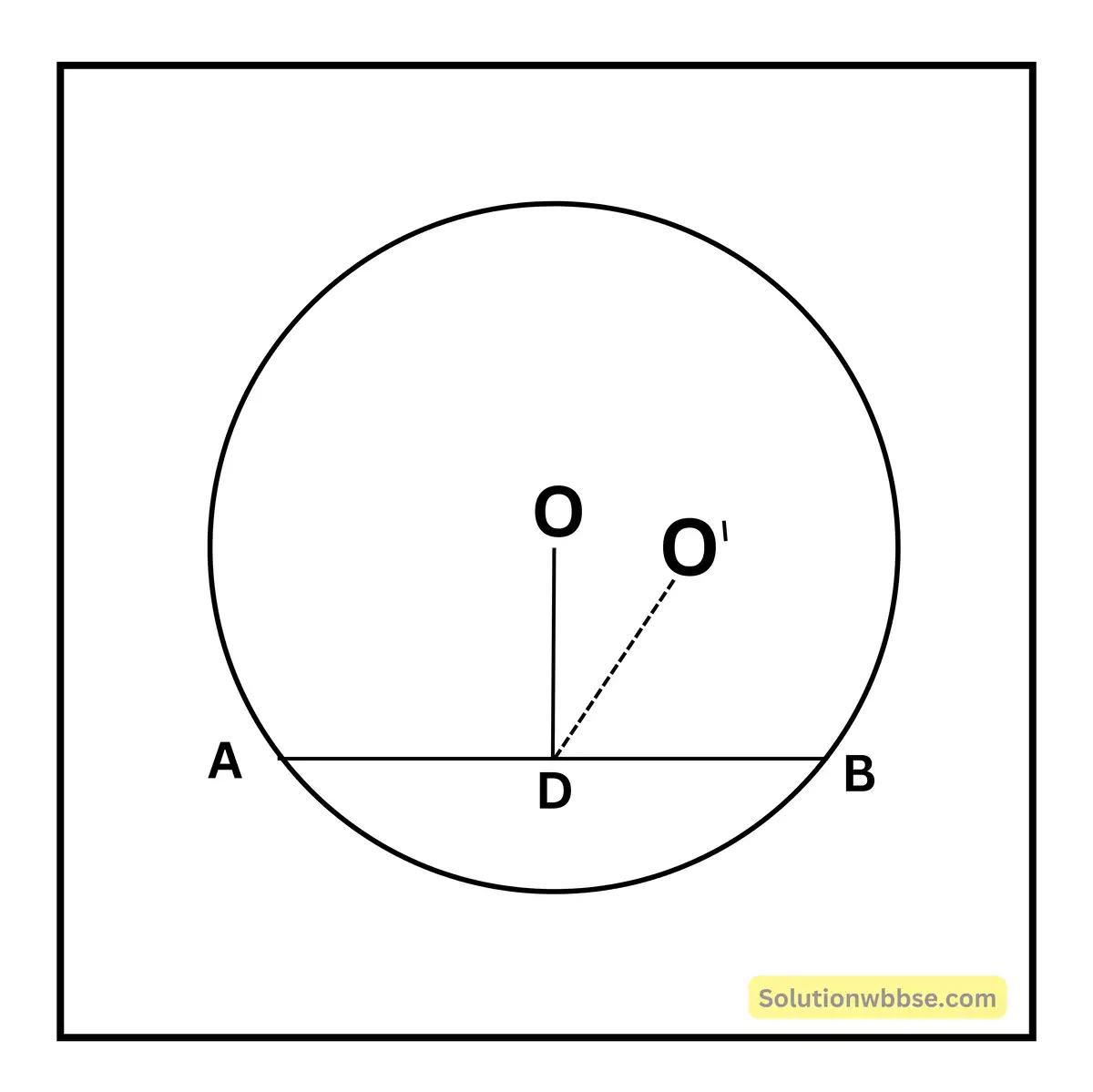
মনেকরি, O কেন্দ্র বিশিষ্ট বৃত্তে AB একটি জ্যা।
প্রমাণ করতে হবে যে, AB জ্যার লম্বসমদ্বিখণ্ডক O বিন্দুগামী।
প্রমাণ – OD ⊥ AB, যদি সম্ভব হয় মনেকরি লম্বসমদ্বিখণ্ডকটি O’ বিন্দুতে মিলিত হয়।
∴ OD ⊥ AB এবং O’D ⊥ AB
সুতরাং OD এবং O’D উভয়েই AB-এর লম্ব।
এটি সম্ভব হবে কেবলমাত্র যদি OD এবং O’D সমাপতিত হয়।
∴ বৃত্তের কোনো জ্যা-র লম্বসমদ্বিখণ্ডক ঐ বৃত্তের কেন্দ্রগামী।
প্রয়োগ 12. প্রমাণ করি, একটি সরলরেখা একটি বৃত্তকে দুই-এর অধিক বিন্দুতে ছেদ করতে পারে না।
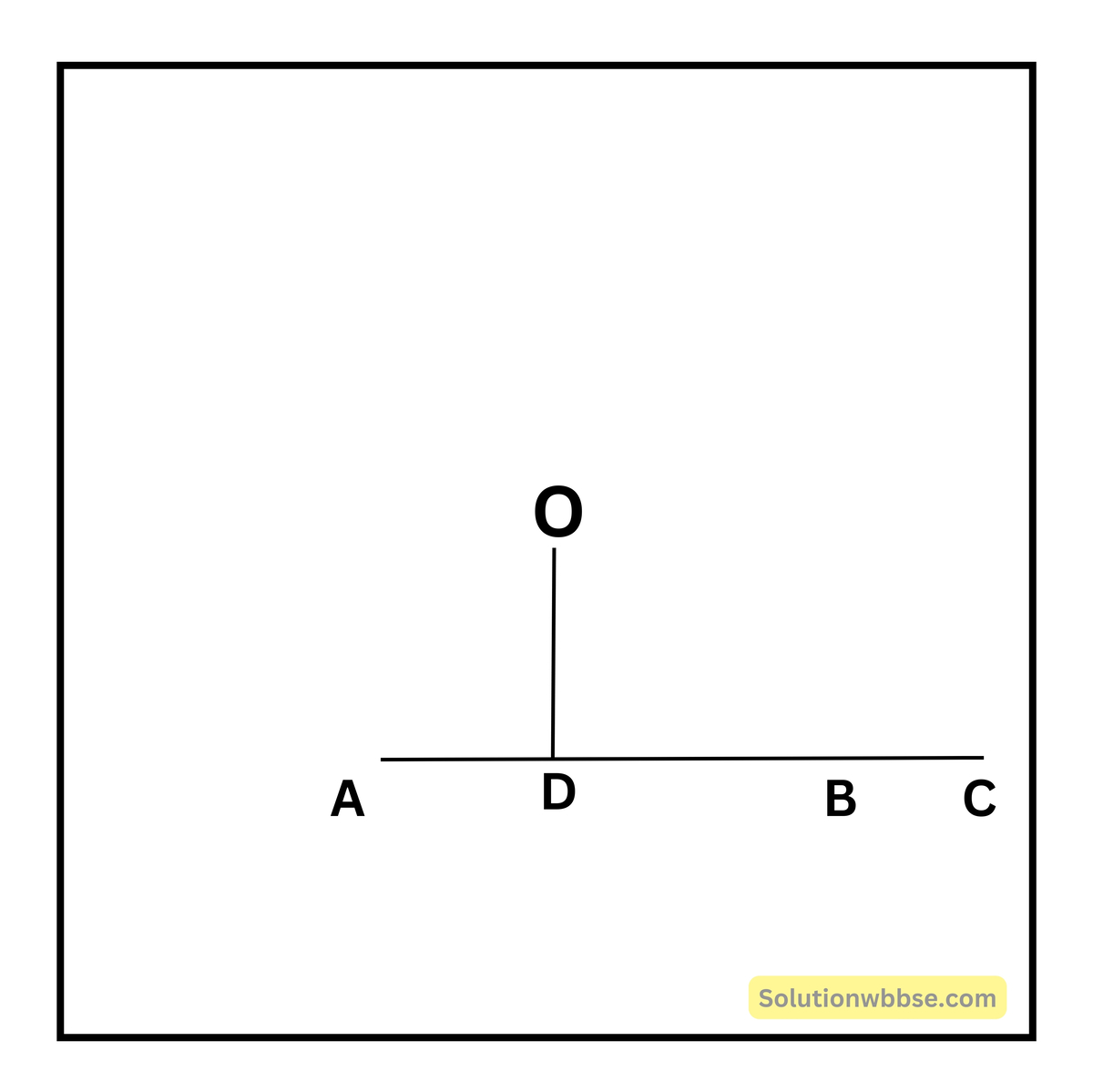
যদি সম্ভব হয় তাহলে মনেকরি O কেন্দ্রিয় বৃত্তে সরলরেখাটি A, B ও C বিন্দুতে ছেদ করে।
O বিন্দু থেকে সরলরেখাটির উপর OD লম্ব অঙ্কন করা হল।
∴ AD = DB এবং AD = DC
অর্থাৎ DB = DC যা অসম্ভব। যদি না B ও C বিন্দু সমাপতিত হয়।
∴ একটি সরলরেখা কোন বৃত্তকে দুটির অধিক বিন্দুতে ছেদ করতে পারে না। (প্রমাণিত)
প্রয়োগ 13. যদি দুটি বৃত্ত পরস্পরকে দুটি বিন্দুতে ছেদ করে, তবে প্রমাণ করি যে, তাদের কেন্দ্রদুটি তাদের সাধারণ জ্যা-এর লম্বসমদ্বিখণ্ডকের উপর আছে।
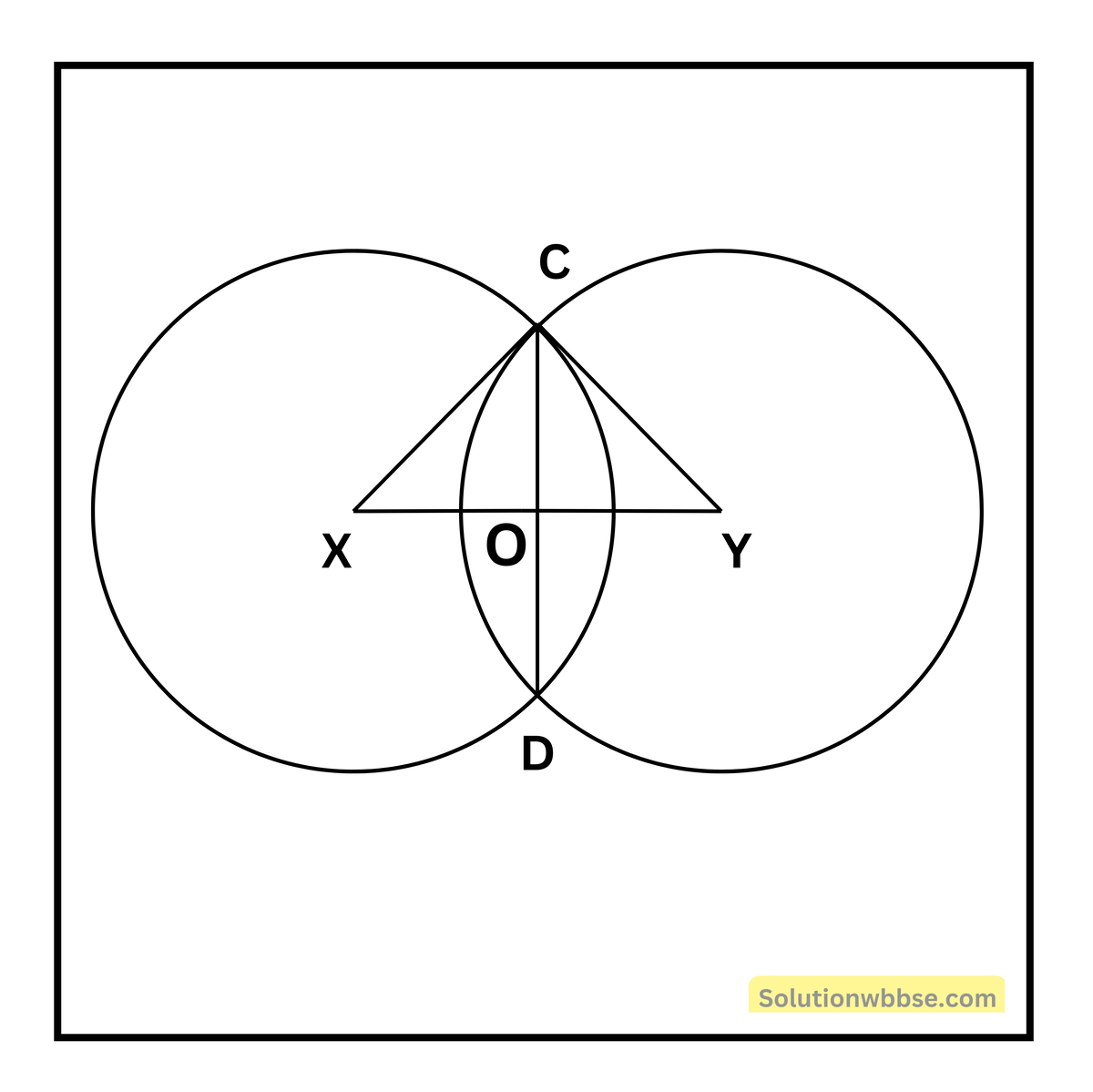
প্রদত্ত – X ও Y কেন্দ্রবিশিষ্ট বৃত্তদুটি পরস্পরকে C ও D বিন্দুতে ছেদ করেছে। সুতরাং CD উহাদের সাধারণ জ্যা।
প্রমাণ করতে হবে – X ও Y বিন্দু দুটি সাধারণ জ্যা CD-এর লম্বসমদ্বিখণ্ডকের উপর আছে।
অঙ্কন – X বিন্দু থেকে CD -এর উপর XO লম্ব অঙ্কন করলাম। O এবং Y বিন্দু দুটি যোগ করলাম।
প্রমাণ – X কেন্দ্রীয় বৃত্তের CD জ্যা এবং XO⊥CD
∴ O, CD-এর মধ্যবিন্দু।
আবার, Y কেন্দ্রীয় বৃত্তের CD জ্যা এবং O, CD -এর মধ্যবিন্দু।
∴ ΟΥ ⊥ CD
যেহেতু কোনো সরলরেখার উপর অবস্থিত একটি বিন্দুতে একটিমাত্র লম্ব অঙ্কন সম্ভব,
সুতরাং, XO ও OY একই সরলরেখায় অবস্থিত।
সূতরাং, XY সাধারণ জ্যা CD-এর লম্বসমদ্বিখণ্ডক।
∴ বৃত্ত দুটির কেন্দ্রদ্বয় X ও Y তাদের সাধারণ জ্যা CD-এর লম্বসমদ্বিখণ্ডকের উপর আছে। [প্রমাণি
প্রয়োগ 14. যুক্তি দিয়ে প্রমাণ করি যে, কোনো বৃত্তের দুটি সমান্তরাল জ্যা-এর মধ্যবিন্দু দুটির সংযোজক সরলরেখা কেন্দ্রবিন্দুগামী।
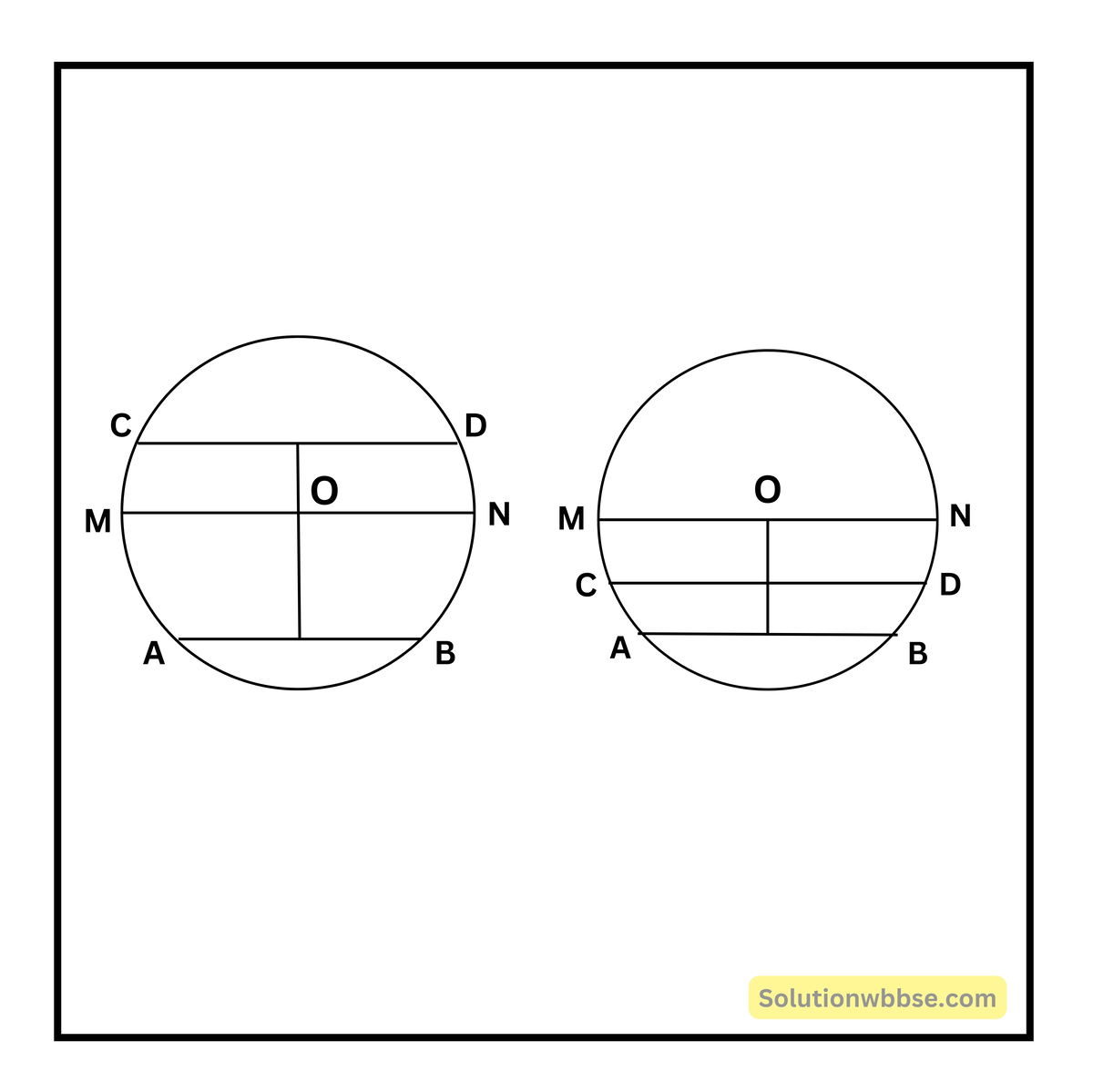
প্রদত্ত – ধরি, O কেন্দ্রীয় বৃত্তের দুটি জ্যা AB ও CD পরস্পর সমান্তরাল এবং AB ও CD-এর মধ্যবিন্দু যথাক্রমে P ও Q
প্রমাণ করতে হবে – PQ, O বিন্দুগামী
অঙ্কন – O, P এবং O, Q যুক্ত করলাম এবং O বিন্দু দিয়ে AB ও CD-এর সমান্তরাল সরলরেখাংশ MN অঙ্কন করলাম।
প্রমাণ – P, AB জ্যা-এর মধ্যবিন্দু। ∴ OP ⊥ AB
আবার AB || MN, ∴ OP ⊥ MN
অনুরূপে, OQ ⊥ CD [∵ Q, CD -এর মধ্যবিন্দু]
∴ OQ ⊥ MN [∵ MN || CD]
∴ OP ও OQ উভয়েই O বিন্দুতে MN -এর উপর লম্ব।
যেহেতু একটি সরলরেখার উপর অবস্থিত একটি বিন্দুতে একটিমাত্র লম্ব অঙ্কন করা যায়, সুতরাং, P, O ও Q সমরেখ।
∴ PQ, বৃত্তের কেন্দ্র O বিন্দুগামী। [প্রমাণিত]
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের তৃতীয় অধ্যায়, ‘বৃত্ত সম্পর্কিত উপপাদ্য’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment