এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের অষ্টদশ অধ্যায়, ‘সদৃশতা’ -এর উপপাদ্যমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

উপপাদ্য 43. কোনো ত্রিভুজের কোনো বাহুর সমান্তরাল সরলরেখা অপর দুটি বাহুকে বা তাদের বর্ধিত বাহুকে সমানুপাতে বিভক্ত করে।
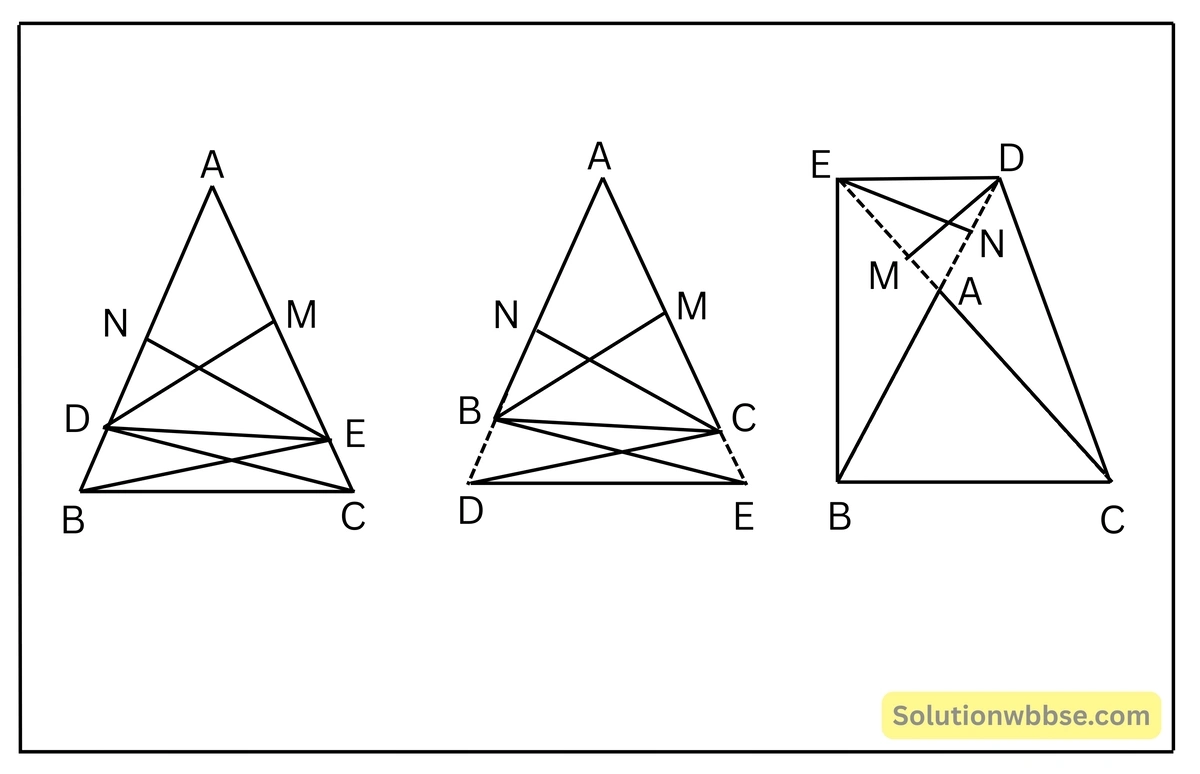
প্রদত্ত – \(\Delta ABC\)-এর \(BC\) বাহুর সমান্তরাল সরলরেখা \(AB\) ও \(AC\) বাহুকে বা \(AB\) ও \(AC\) বাহুর বর্ধিতাংশকে (\(BA\) ও \(CA\) বাহুর বর্ধিতাংশকে) যথাক্রমে \(D\) ও \(E\) বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে – \(\frac{AD}{DB} = \frac{AE}{EC}\)
অঙ্কন – \(B, E\) এবং \(C, D\) যোগ করলাম এবং \(DM \perp AC\) (বা \(CA\) বাহুর বর্ধিতাংশে) ও \(EN \perp AB\) (বা \(BA\) বাহুর বর্ধিতাংশে) অঙ্কন করলাম।
প্রমাণ – \(\triangle ADE \) -এর ক্ষেত্রফল = \(\frac{1}{2} \) \( \times\) ভূমি \( \times \) উচ্চতা
অনুরূপে, \(\triangle BDE\) = \(\frac{1}{2} \) \( \times\) ভূমি \( \times \) উচ্চতা
\(= \frac{1}{2} \times DB \times EN\)∴ \(\frac{\triangle ADE}{\triangle BDE} = \frac{\frac{1}{2} \times AD \times EN}{\frac{1}{2} \times DB \times EN} = \frac{AD}{DB}\) ______ (I)
আবার, \(\triangle ADE = \frac{1}{2} \times AE \times DM\) এবং \(\triangle DEC = \frac{1}{2} \times EC \times DM\)
∴ \(\frac{\triangle ADE}{\triangle DEC} = \frac{\frac{1}{2} \times AE \times DM}{\frac{1}{2} \times EC \times DM} = \frac{AE}{EC}\) ______ (II)
আবার, \(\triangle BDE\) ও \(\triangle DEC\) একই ভূমি \(DE\)-এর উপর এবং একই সমান্তরালযুগল \(DE\) ও \(BC\)-এর মধ্যে অবস্থিত।
∴ \(\triangle BDE = \triangle DEC\)।
∴ (I) ও (II) থেকে পাই, \(\frac{AD}{DB} = \frac{AE}{EC}\) [প্রমাণিত]
অনুসিদ্ধান্ত 1. \(\triangle ABC\)-এর \(BC\) বাহুর সমান্তরাল একটি সরলরেখা \(AB\) ও \(AC\) বাহুকে যথাক্রমে \(D\) ও \(E\) বিন্দুতে ছেদ করলে, প্রমাণ করতে হবে যে,
(i) \(\frac{AB}{DB} = \frac{AC}{EC}\)
(ii) \(\frac{AD}{AB} = \frac{AE}{AC}\)
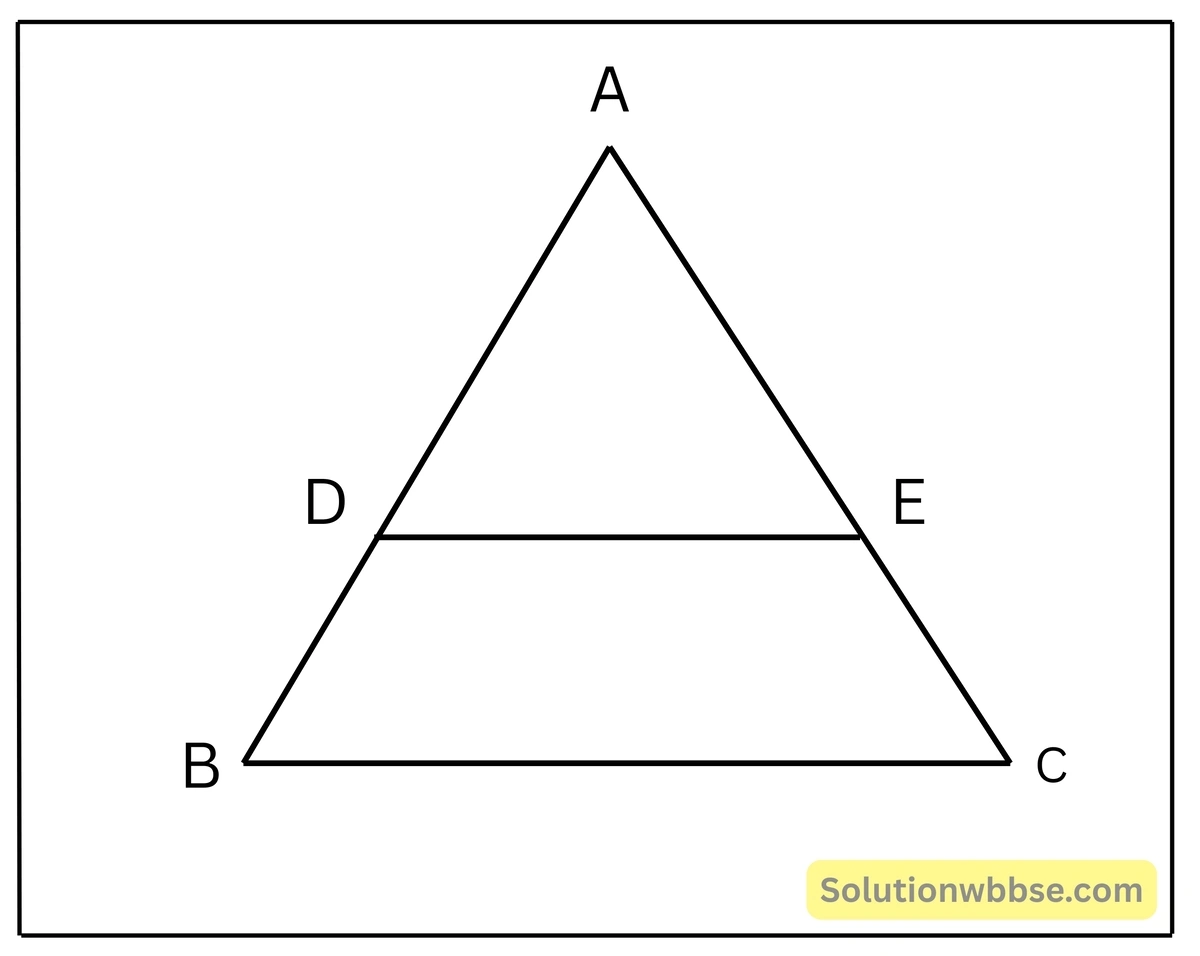
(i) \(\frac{AB}{DB} = \frac{AC}{EC}\)
থ্যালেসের উপপাদ্য থেকে আমরা পাই,
\(\frac{AD}{DB} = \frac{AE}{EC}\)বা, \(\frac{AD}{DB} + 1 = \frac{AE}{EC} + 1\) (উভয় পক্ষে 1 যোগ করে)
বা, \(\frac{AD+DB}{DB} = \frac{AE+EC}{EC}\)
যেহেতু \(AD+DB = AB\) এবং \(AE+EC = AC\),
∴ \(\frac{AB}{DB} = \frac{AC}{EC}\) [প্রমাণিত]
(ii) \(\frac{AD}{AB} = \frac{AE}{AC}\)
আবার, থ্যালেসের উপপাদ্য থেকে পাই,
\(\frac{AD}{DB} = \frac{AE}{EC}\)বা, \(\frac{DB}{AD} = \frac{EC}{AE}\) (ব্যস্ত প্রক্রিয়া করে)
বা, \(1 + \frac{DB}{AD} = 1 + \frac{EC}{AE}\) (উভয় পক্ষে 1 যোগ করে)
বা, \(\frac{AD+DB}{AD} = \frac{AE+EC}{AE}\)
বা, \(\frac{AB}{AD} = \frac{AC}{AE}\)
∴ \(\frac{AD}{AB} = \frac{AE}{AC}\) (পুনরায় ব্যস্ত প্রক্রিয়া করে) [প্রমাণিত]
উপপাদ্য 44. যুক্তি দিয়ে প্রমাণ করি যে কোনো সরলরেখা যে-কোনো ত্রিভুজের দুটি বাহুকে বা তাদের বর্ধিতবাহুকে সমানুপাতে বিভক্ত করলে, তা তৃতীয় বাহুর সমান্তরাল হবে।
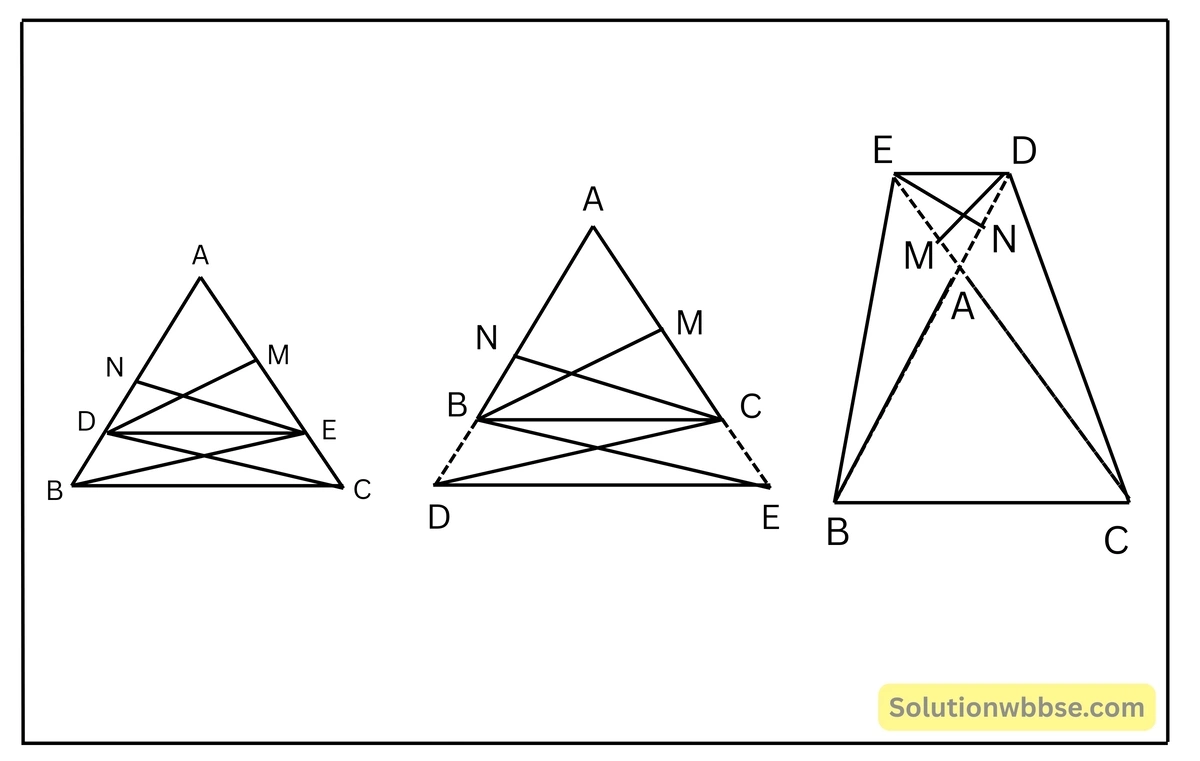
প্রদত্ত – একটি ত্রিভুজ। একটি সরলরেখা এবং বাহুদ্বয়কে বা তাদের বর্ধিতাংশকে (বা এবং -এর বর্ধিতাংশ) যথাক্রমে ও বিন্দুতে এমনভাবে ছেদ করেছে যে,
প্রমাণ করতে হবে –
অঙ্কন – এবং যোগ করলাম। (বা -এর বর্ধিতাংশ) ও (বা -এর বর্ধিতাংশ) অঙ্কন করলাম।
প্রমাণ – -এর ক্ষেত্রফল = ভূমি উচ্চতা =
-এর ক্ষেত্রফল = ভূমি উচ্চতা =
আবার, -এর ক্ষেত্রফল =
-এর ক্ষেত্রফল =
যেহেতু, (প্রদত্ত)
সুতরাং,
-এর ক্ষেত্রফল = -এর ক্ষেত্রফল
ও একই ভূমি -এর উপর অবস্থিত, -এর একই পার্শ্বে অবস্থিত এবং তাদের ক্ষেত্রফল সমান। সুতরাং, তারা একই সমান্তরাল যুগলের মধ্যে অবস্থিত।
[প্রমাণিত]
উপপাদ্য 45. দুটি ত্রিভুজ সদৃশকোণী হলে তাদের অনুরূপ বাহুগুলির অনুপাত সমান হবে অর্থাৎ তাদের অনুরূপ বাহুগুলি সমানুপাতী হবে
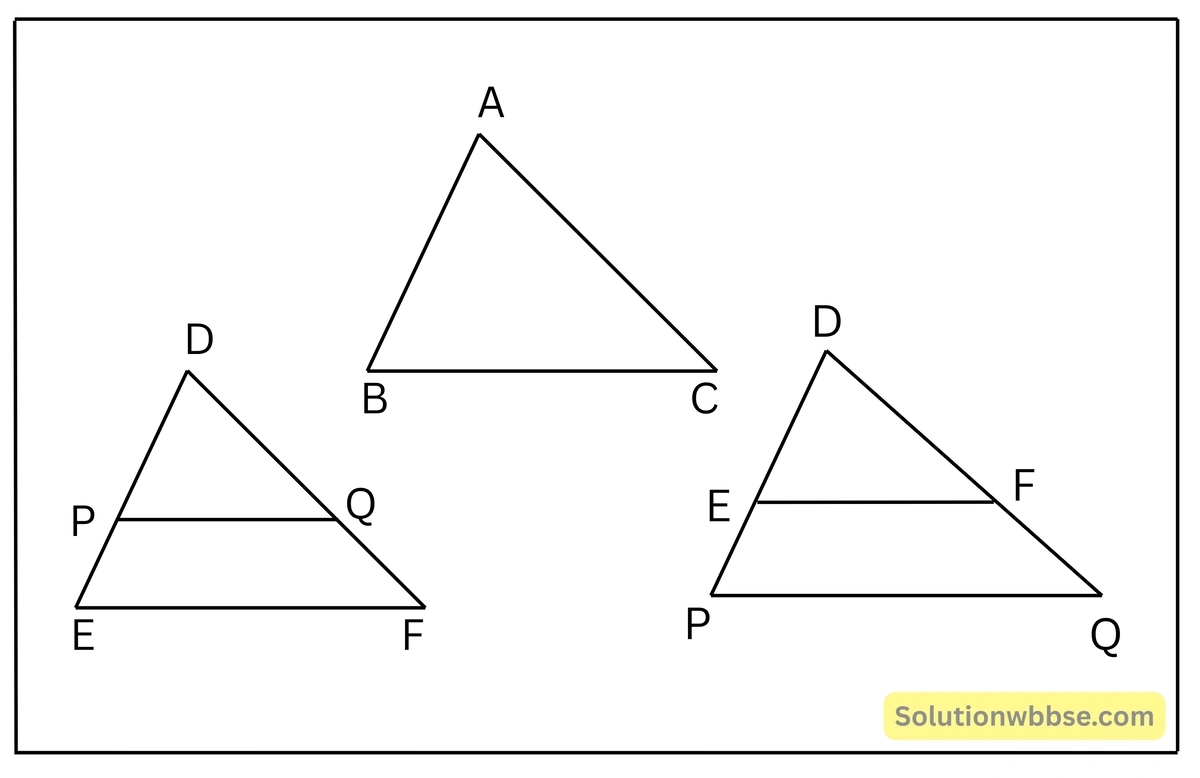
প্রদত্ত – \(\Delta ABC\) ও \(\Delta DEF\) দুটি সদৃশকোণী ত্রিভুজ। অর্থাৎ \(\angle{A} = \angle{D}\), \(\angle{B} = \angle{E}\) এবং \(\angle{C} = \angle{F}\)
প্রমাণ করতে হবে – \(\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}\)
অঙ্কন – \(\Delta DEF\) থেকে \(AB\) ও \(AC\)-এর সমান করে \(DE\) বা বর্ধিত \(DE\) থেকে এবং \(DF\) বা বর্ধিত \(DF\) থেকে যথাক্রমে \(DP\) ও \(DQ\) অংশ কেটে নিলাম। \(P\) ও \(Q\) বিন্দুদ্বয় যোগ করলাম।
প্রমাণ – \(\Delta ABC\) ও \(\Delta DPQ\)-এর মধ্যে,
\(AB = DP\), \(\angle{A} = \angle{D}\) এবং \(AC = DQ\)
∴ \(\Delta ABC \cong \Delta DPQ\) (\(S-A-S\) সর্বসমতার শর্ত অনুসারে)
∴ \(\angle{B} = \angle{P}\)
আবার, \(\angle{B} = \angle{E}\) [প্রদত্ত]
∴ \(\angle{P} = \angle{E}\)
সুতরাং, \(PQ \parallel EF\) [∵ অনুরূপ কোণ সমান]
∴ \(\frac{DP}{DE} = \frac{DQ}{DF}\) (থ্যালেসের উপপাদ্য থেকে পাই)
∴ \(\frac{AB}{DE} = \frac{AC}{DF}\) —- (I) [∵ \(DP = AB\) এবং \(DQ = AC\)]
অনুরূপে, \(ED\) বা বর্ধিত \(ED\) থেকে \(BA\) এবং \(EF\) বা বর্ধিত \(EF\) থেকে \(BC\)-এর সমান করে কেটে নিয়ে প্রমাণ করতে পারি, \(\frac{AB}{DE} = \frac{BC}{EF}\) —– (II)
∴ (I) ও (II) থেকে পেলাম, \(\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}\) [প্রমাণিত]
উপপাদ্য 46. দুটি ত্রিভুজের বাহুগুলি সমানুপাতে থাকলে তাদের অনুরূপ কোণগুলি সমান হবে। অর্থাৎ, ত্রিভুজদ্বয় সদৃশকোণী হবে।
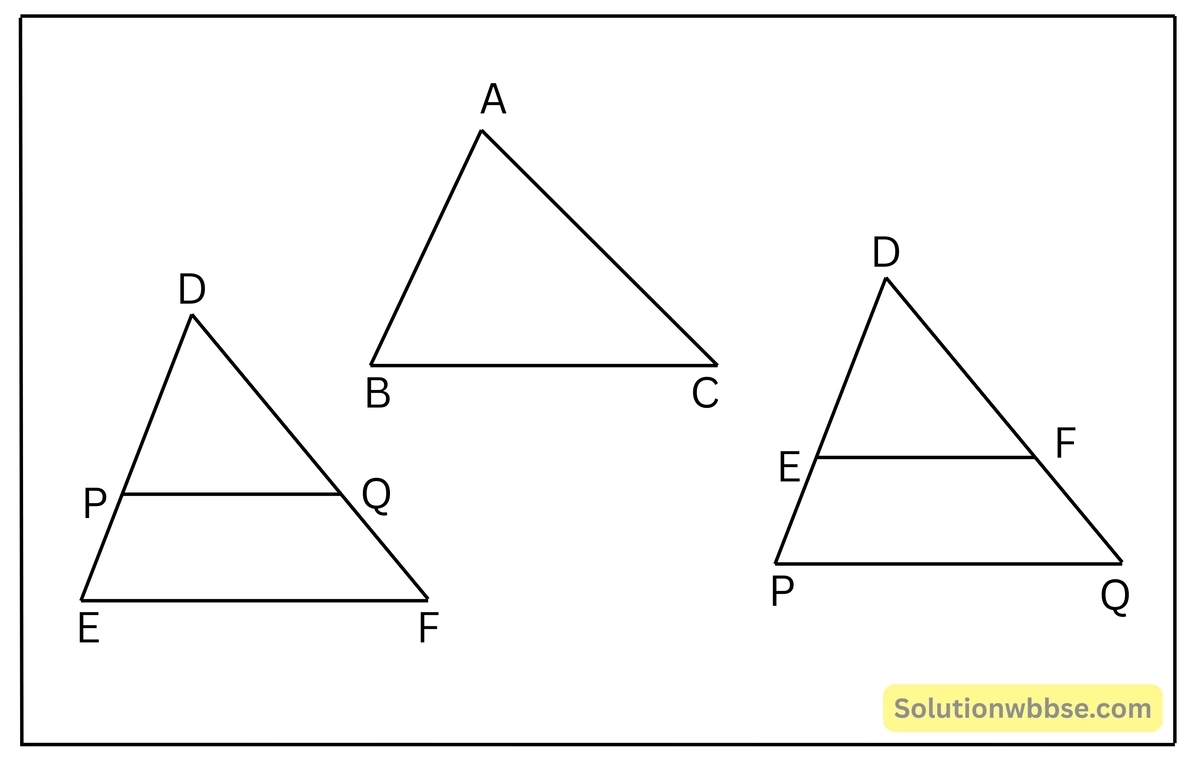
প্রদত্ত – \(\triangle ABC\) ও \(\triangle DEF\)-এর \(\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}\)
প্রমাণ করতে হবে – \(\triangle ABC\) ও \(\triangle DEF\) সদৃশকোণী অর্থাৎ \(\angle A = \angle D, \angle B = \angle E\) এবং \(\angle C = \angle F\)
অঙ্কন – DE বা বর্ধিত DE থেকে AB-এর সমান করে DP এবং DF বা বর্ধিত DF থেকে AC-এর সমান করে DQ কেটে নিলাম। P ও Q বিন্দুদ্বয় যোগ করলাম।
প্রমাণ – \(\frac{AB}{DE} = \frac{AC}{DF}\),
সুতরাং, \(\frac{DP}{DE} = \frac{DQ}{DF}\) [অঙ্কনানুসারে, \(AB = DP\) এবং \(AC = DQ\)]
\(\therefore\) থ্যালেসের বিপরীত উপপাদ্যের সাহায্যে পাই, \(PQ \parallel EF\) \(PQ \parallel EF\) এবং DE ভেদক
\(\therefore \angle P = \angle E\)\(PQ \parallel EF\) এবং DF ভেদক,
\(\therefore \angle Q = \angle F\)\(\therefore \triangle DPQ\) ও \(\triangle DEF\) সদৃশকোণী
\(\therefore \frac{DP}{DE} = \frac{PQ}{EF}\)বা, \(\frac{AB}{DE} = \frac{PQ}{EF}\) [\(\because\) অঙ্কনানুসারে \(DP=AB\)] ________ (i)
কিন্তু \(\frac{AB}{DE} = \frac{BC}{EF}\) [প্রদত্ত] _________ (ii)
\(\therefore\) (i) ও (ii) থেকে পাই, \(\frac{PQ}{EF} = \frac{BC}{EF}\)
\(\therefore PQ = BC.\)\(\therefore \triangle ABC\) ও \(\triangle DPQ\)-এর মধ্যে \(AB=DP, BC=PQ\) এবং \(AC=DQ\)
\(\therefore \triangle ABC \cong \triangle DPQ\) (S-S-S সর্বসমতার শর্ত অনুসারে)
\(\therefore \angle A = \angle D, \angle B = \angle P = \angle E\) এবং \(\angle C = \angle Q = \angle F\)
\(\therefore \angle A = \angle D, \angle B = \angle E\) এবং \(\angle C = \angle F\)
\(\therefore \triangle ABC\) ও \(\triangle DEF\) সদৃশকোণী।
উপপাদ্য 47. দুটি ত্রিভুজের একটির একটি কোণ অপরটির একটি কোণের সমান এবং কোণগুলির ধারক বাহুগুলি সমানুপাতী হলে ত্রিভুজদ্বয় সদৃশ হবে।
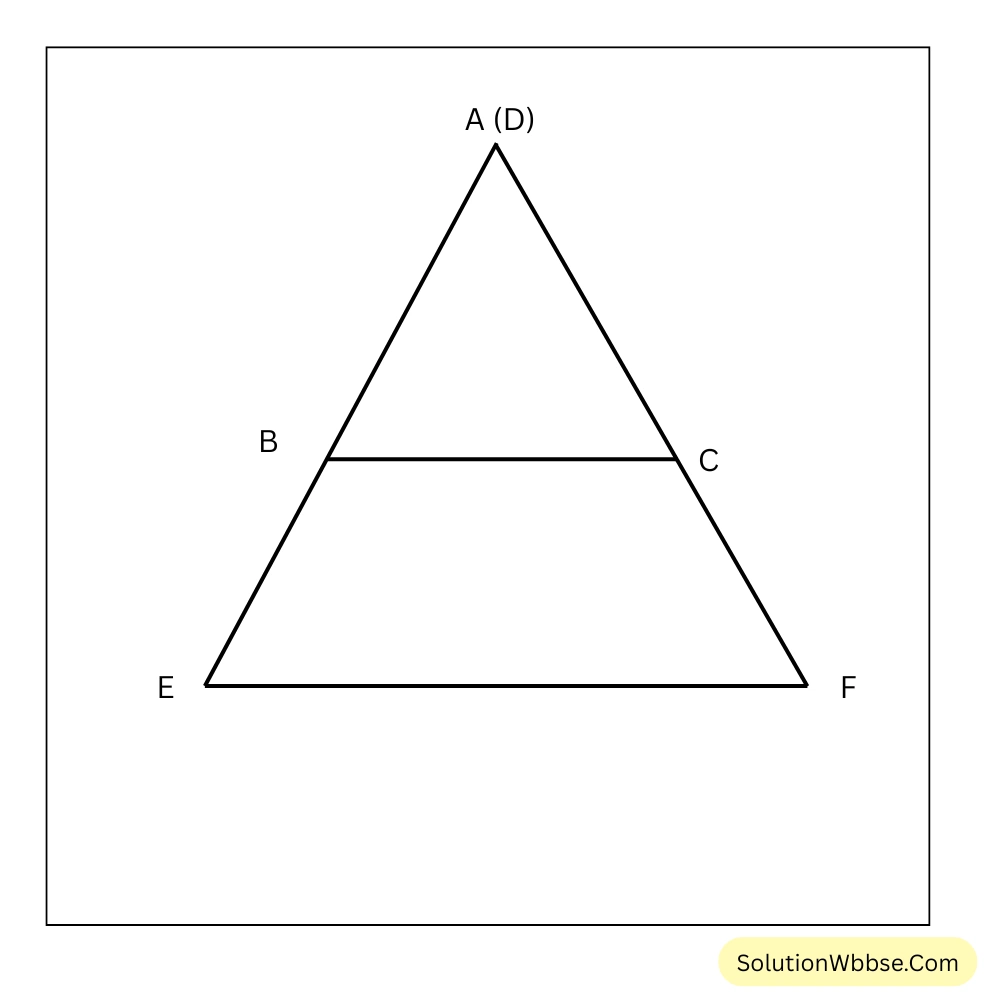
প্রদত্ত – \(\triangle ABC\) ও \(\triangle DEF\) এর \(\angle A = \angle D\) এবং \(\frac{AB}{DE} = \frac{AC}{DF}\)
প্রমাণ করতে হবে – \(\triangle ABC\) ও \(\triangle DEF\) সদৃশ।
প্রমাণ – \(\frac{AB}{DE} = \frac{AC}{DF}\)
বা, \(\frac{DB}{DE} = \frac{DC}{DF}\)
বা, \(\frac{DB}{BE} = \frac{DC}{CF}\)
\(\therefore BC \parallel EF\) [থ্যালেসের বিপরীত উপপাদ্য থেকে পাই]
সুতরাং, \(\angle B =\) অনুরূপ \(\angle E\) এবং \(\angle C =\) অনুরূপ \(\angle F\)
অর্থাৎ \(\triangle ABC\) ও \(\triangle DEF\) সদৃশকোণী।
\(\therefore \triangle ABC\) ও \(\triangle DEF\) সদৃশ।
উপপাদ্য 48. যে-কোনো সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে, এই লম্বের উভয় পার্শ্বস্থিত ত্রিভুজদ্বয় সদৃশ এবং ওই ত্রিভুজগুলির প্রত্যেকে মূল ত্রিভুজের সঙ্গে সদৃশ।
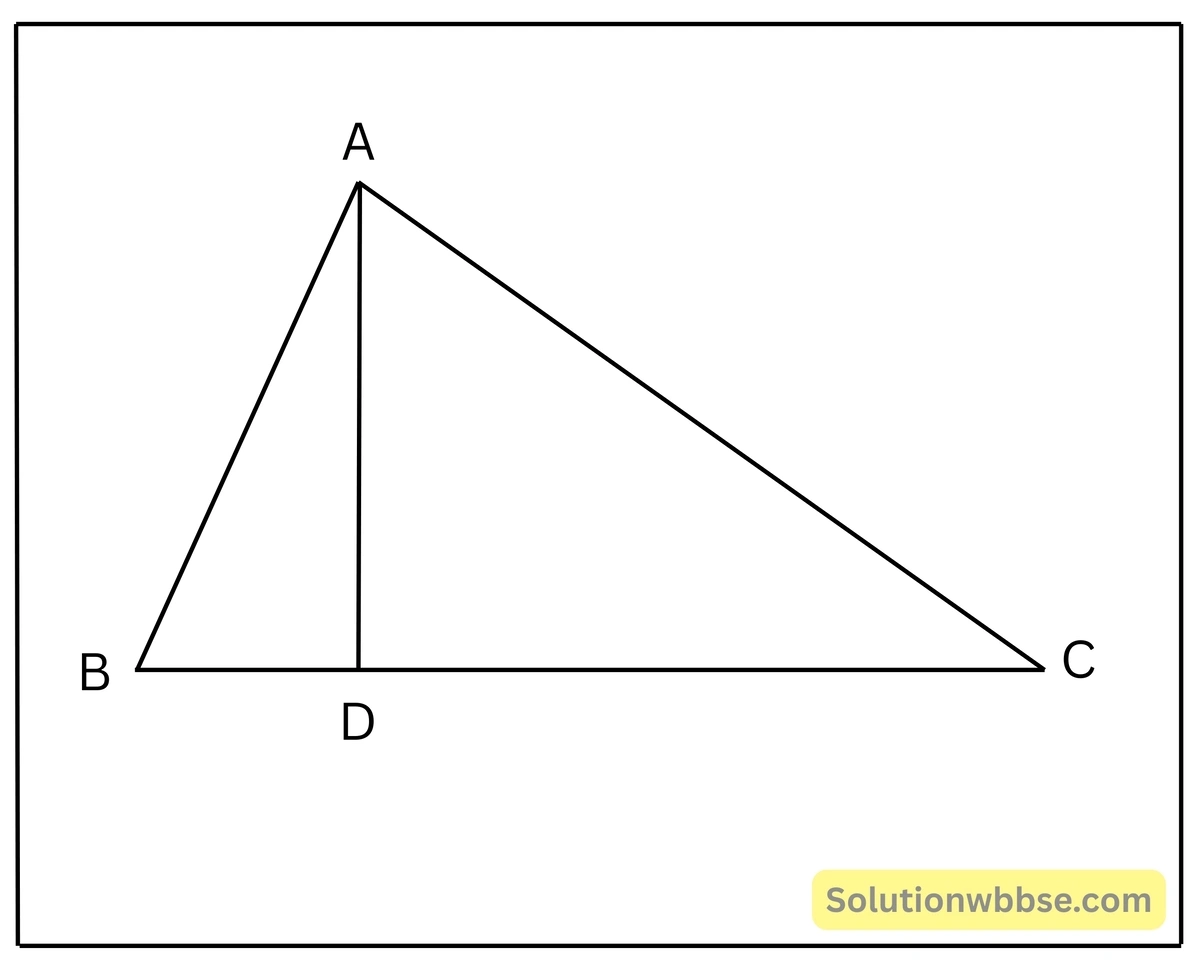
প্রদত্ত – ABC একটি সমকোণী ত্রিভুজ যার ∠A সমকোণ এবং সমকৌণিক বিন্দু A থেকে অতিভুজ BC-এর উপর AD লম্ব।
প্রমাণ করতে হবে – (i) ΔDBA ও ΔABC পরস্পর সদৃশ। (ii) ΔDAC ও ΔABC পরস্পর সদৃশ। (iii) ΔDBA ও ΔDAC পরস্পর সদৃশ।
প্রমাণ – ΔDBA ও ΔABC -এর মধ্যে, ∠BDA = ∠BAC = 90° এবং ∠ABD = ∠CBA.
সুতরাং অবশিষ্ট ∠BAD = ∠BCA ∴ ΔDBA ও ΔABC সদৃশকোণী।
∴ ΔDBA ও ΔABC পরস্পর সদৃশ। [(i) প্রমাণিত]
আবার, ΔDAC ও ΔABC-এর মধ্যে, ∠ADC = ∠BAC = 90°
∠ACD = ∠BCA.
সুতরাং অবশিষ্ট ∠CAD = ∠CBA
∴ ΔDAC ও ΔABC সদৃশকোণী।
∴ ΔDAC ও ΔABC সদৃশ। [(ii) প্রমাণিত]
ΔDBA ও ΔABC পরস্পর সদৃশ। আবার, ΔDAC ও ΔABC পরস্পর সদৃশ। সুতরাং ΔDBA ও ΔDAC পরস্পর সদৃশ। [(iii) প্রমাণিত]
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের অষ্টদশ অধ্যায়, ‘সদৃশতা’ -এর উপপাদ্যমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment