এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের বিংশ অধ্যায়, ‘ত্রিকোণমিতি: কোণ পরিমাপের ধারণা’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

প্রয়োগ 1. একটি ত্রিভুজের দুটি কোণের ষষ্টিক মান যথাক্রমে 75° ও 45°, তৃতীয় কোণের বৃত্তীয় মান নির্ণয় করি।
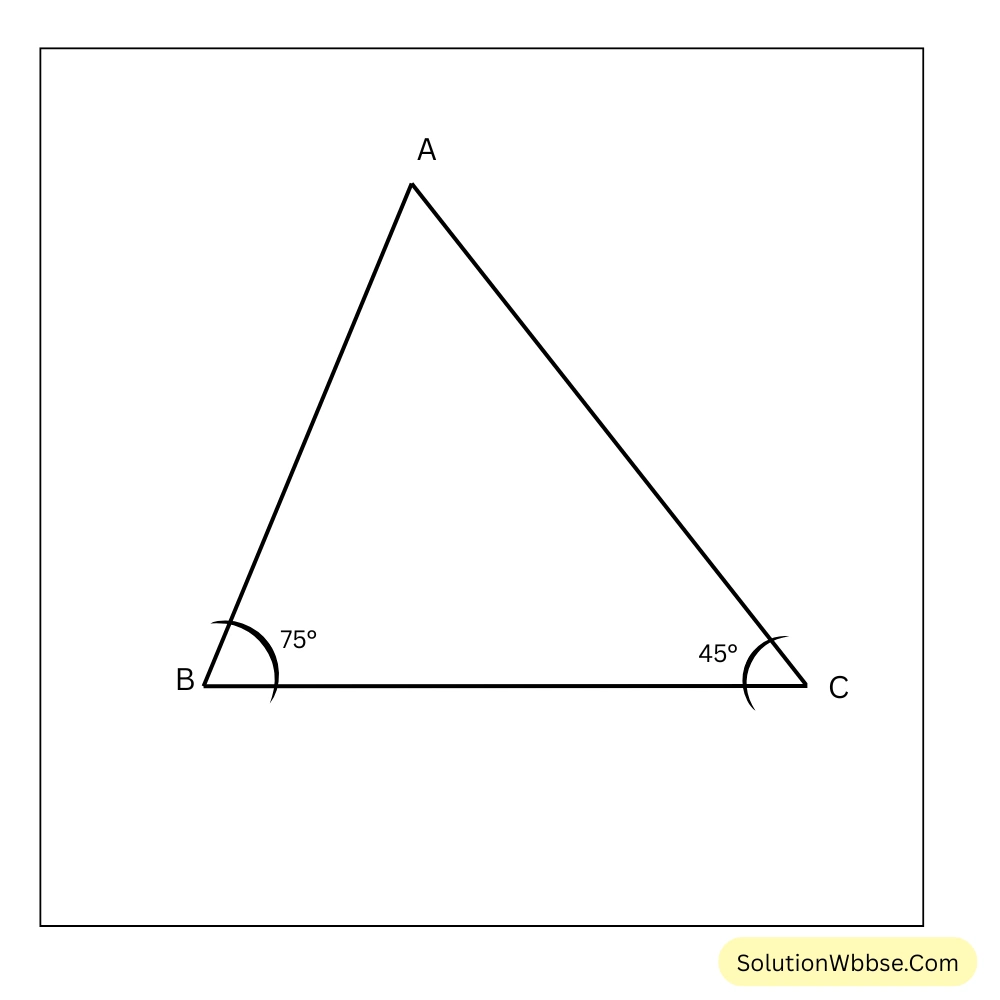
ধরি, ΔABC -এর ∠ABC = 75° এবং ∠ACB = 45°
∴ ∠BAC = 180° – (75°+45°) = 60°
আবার, 180° = π
∴ 60° = π/3
∴ নির্ণেয় তৃতীয় কোণের বৃত্তীয় মান π/3
প্রয়োগ 2. একটি ত্রিভুজের দুটি কোণের ষষ্টিক মান যথাক্রমে 65° ও 85° হলে, তৃতীয় কোণের বৃত্তীয় মান নির্ণয় কর।
সমাধান –
ধরি, ΔABC এর, ∠ABC = 65° এবং ∠BAC = 85°
∴ ∠ACB = 180° – (65° + 85°)
= 180° – 150°
= 30°
∴ তৃতীয় কোণটি হল 30°।
তৃতীয় কোণটির বৃত্তীয় মান = \(\frac{30\pi}{180} = \frac{\pi}{6}\)
প্রয়োগ 3. একটি ঘূর্ণায়মান রশ্মি কোনো একটি অবস্থান থেকে ঘড়ির কাঁটার বিপরীত দিকে দু-বার পূর্ণ আবর্তনের পরেও আরও 30° কোণ আবর্তন করে। ত্রিকোণমিতিক পরিমাপে কোণটির ষষ্টিক ও বৃত্তীয় মান কত হবে হিসাব করে লিখি।
সমাধান –
যেহেতু রশ্মিটি ঘড়ির কাঁটার বিপরীত দিকে ঘুরছে, ∴ কোণটি ধনাত্মক হবে।
ঘূর্ণায়মান রশ্মির একবার পূর্ণ আবর্তনের জন্য 360° ডিগ্রি কোণ উৎপন্ন হয়।
∴ 2 বার পূর্ণ আবর্তনের জন্য কোণ উৎপন্ন করবে 2×360° = 720°
যেহেতু 2 বার পূর্ণ আবর্তনের পরেও 30° কোণ আবর্তন করেছে, সুতরাং, ষষ্টিক পদ্ধতিতে কোণের মান 720°+30° = 750°
আবার, 180° = π
∴ \( 750^\circ = \frac{750}{180}\pi = 4\frac{1}{6}\pi \)
প্রয়োগ 4. আমি 3750”কে ডিগ্রি, মিনিট ও সেকেন্ডে প্রকাশ করি।
সমাধান –
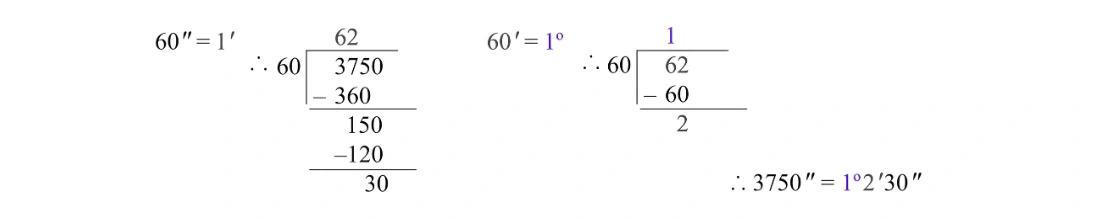
প্রয়োগ 5. আমি 85.12° কে ডিগ্রি, মিনিট ও সেকেন্ডে প্রকাশ করি।
সমাধান –
85.12° = 85°+(0.12)°
= 85°+(0.12×60′) [∵ 1° = 60′]
= 85° + 7.2′
= 85°+7’+0.2′ = 85°+7’+(0.2×60”) [∵ 1′ = 60”]
= 85°+7’+12” = 85°7’12”
প্রয়োগ 6. \(40^\circ 16′ 24”\) -কে রেডিয়ানে প্রকাশ করি।
সমাধান –
\(40^\circ 16′ 24” = 40^\circ + 16′ + 24”\)\(= 40^\circ+16’+\left(\frac{24}{60}\right)’\) [∵ \(60” = 1′\)]
\(= 40^\circ+16’+\frac{2}{5}’ = 40^\circ+\left(16+\frac{2}{5}\right)’\)\(= 40^\circ+\frac{82}{5}’ = 40^\circ+\left(\frac{82}{5 \times 60}\right)^\circ\) [∵ \(60′ = 1^\circ\)]
যেহেতু, \(180^\circ = \pi\)
∴ \(\left(\frac{6041}{150}\right)^\circ = \frac{\pi}{180} \times \frac{6041}{150} = \frac{6041}{27000} \pi\)
প্রয়োগ 7. 22°30′ কে রেডিয়ানে প্রকাশ করি।
সমাধান –
\(22^\circ 30′\)\(= 22^\circ + (\frac{30}{60})^\circ\) [∵\(60′ = 1^\circ\)]
\(= 22^\circ + (\frac{1}{2})^\circ\)\(= (22\frac{1}{2})^\circ\)\(= (\frac{45}{2})^\circ\)\(= \frac{\pi}{180} \times \frac{45}{2}\)\(= \frac{5\pi}{40} = \frac{\pi}{8}\)প্রয়োগ ৪. একটি সমকোণী ত্রিভুজের সূক্ষ্মকোণ দুটির অন্তর \(\frac{2\pi}{5}\) রেডিয়ান। কোণ দুটির মান রেডিয়ান ও ডিগ্রিতে প্রকাশ করি।
সমাধান –
মনে করি, সূক্ষ্মকোণ দুটির মান xᶜ ও yᶜ এবং x > y
শর্তানুসারে, x + y = \(\frac{\pi}{2}\) এবং x – y = \(\frac{2\pi}{5}\)
x + y = \(\frac{\pi}{2}\)
x – y = \(\frac{2\pi}{5}\)
2x = \(\frac{\pi}{2}\) + \(\frac{2\pi}{5}\) = \(\frac{9\pi}{10}\)
∴ x = \(\frac{9\pi}{20}\)
∴ y = \(\frac{\pi}{2}\) – \(\frac{9\pi}{20}\) = \(\frac{\pi}{20}\)
আবার, π = 180°
∴ x = \(\frac{9\pi}{20}\) = \(\frac{9 \times 180°}{20}\) = 81°
এবং y = \(\frac{\pi}{20}\) = \(\frac{180°}{20}\) = 9°
উত্তর – কোণ দুটির মান \(\frac{9\pi}{20}\) বা 81° এবং \(\frac{\pi}{20}\) বা 9°
প্রয়োগ 9. একটি ত্রিভুজের কোণগুলির অনুপাত 2:5:3; ত্রিভুজটির ক্ষুদ্রতম কোণটির বৃত্তীয় মান হিসাব করে লিখি।
সমাধান –
মনে করি, কোণগুলির মান 2x, 5x ও 3x রেডিয়ান। যেখানে x সাধারণ গুণিতক এবং x>0
∴ 2x + 5x + 3x = π
বা, 10x = π
∴ x = \(\frac{\pi}{10}\)
উত্তর – ক্ষুদ্রতম কোণটির বৃত্তীয়মান হবে 2x = \(\frac{2\pi}{10}\) = \(\frac{\pi}{5}\)
প্রয়োগ 10. ABC একটি সমবাহু ত্রিভুজ অঙ্কন করেছি। A শীর্ষবিন্দু থেকে BC বাহুর মধ্যবিন্দু- D এর সংযোগক সরলরেখাংশ AD; ∠BAD এর বৃত্তীয় মান নির্ণয় করে লিখি।
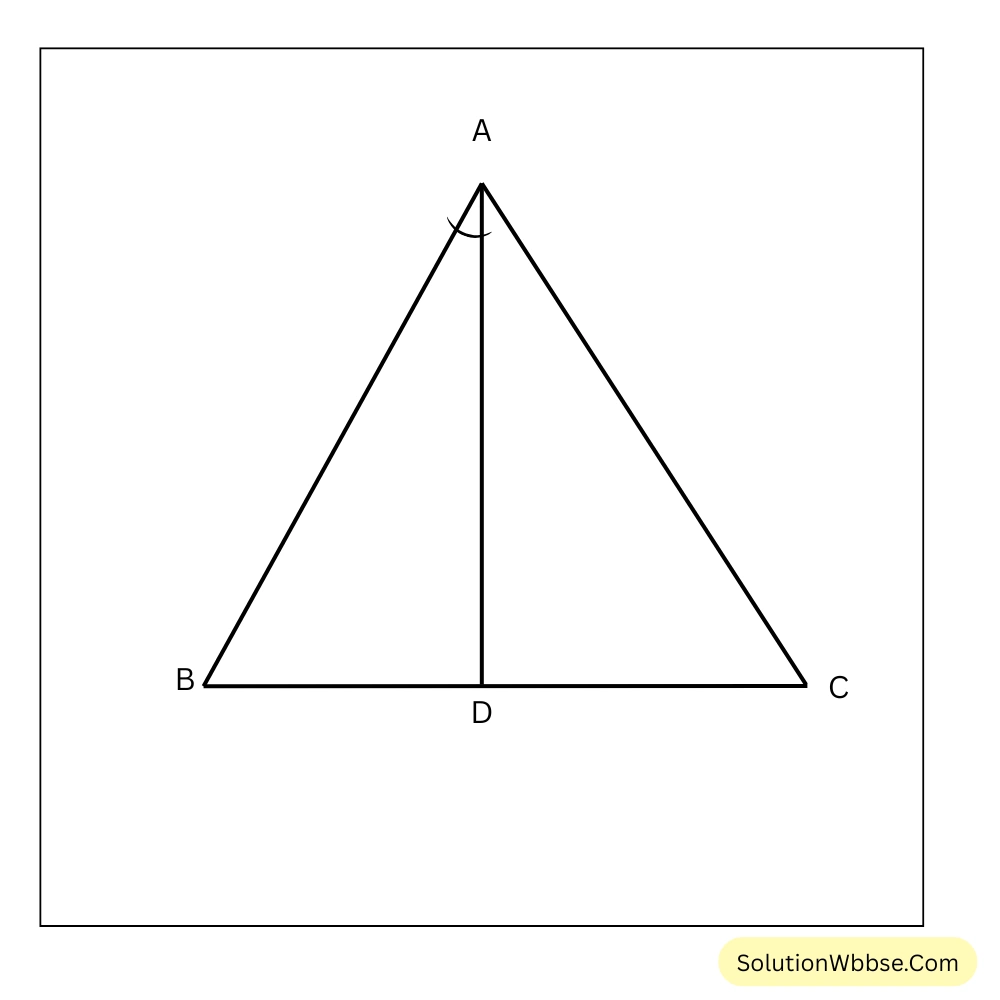
সমাধান –
ABC সমবাহু ত্রিভুজ এবং ∠A = ∠B = ∠C = 60°।
AD হল সমবাহু ত্রিভুজের মধ্যমা অর্থাৎ AD হল ∠BAC এর সমদ্বিখন্ডক।
উত্তর – ∠BAD = 30° = \(\frac{30\pi}{180} = \frac{\pi}{6}\)
প্রয়োগ 11. যদি শুভ-র আঁকা বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 7 সেমি. হয়, তবে ওই বৃত্তে 5.5 সেমি. দৈর্ঘ্যের বৃত্তচাপ দ্বারা কেন্দ্রস্থ কোণটির বৃত্তীয় মান কত হবে হিসাব করে লিখি।
সমাধান –
এখানে, \(r = 7\) সেমি. এবং \(s = 5.5\) সেমি.
ধরি, 5.5 সেমি. বৃত্তচাপ দ্বারা ধৃত কেন্দ্রস্থ কোণের বৃত্তীয় মান = \(θ\)
\(s = rθ\)\(∴ 5.5 = 7×θ\)বা, \(θ = \frac{5.5}{7} = \frac{55}{70} = \frac{11}{14}\)
উত্তর – নির্ণেয় কোণের বৃত্তীয় মান \(\frac{11}{14}\) রেডিয়ান বা, \(\frac{11^c}{14} \)
প্রয়োগ 12. একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 6 সেমি. হলে ওই বৃত্তে 15 সেমি. দৈর্ঘ্যের বৃত্তচাপ কেন্দ্রে যে কেন্দ্রস্থ কোণ তৈরি করে তার বৃত্তীয় মান কত হবে তা হিসাব করে লিখি।
সমাধান –
এখানে \(r = 6\) সেমি. এবং \(s = 15\) সেমি.
ধরি, 15 সেমি. বৃত্তচাপ দ্বারা ধৃত কেন্দ্রস্থ কোণের বৃত্তীয়-মান \(θ\).
\(s = rθ\)\(∴ 15 = 6θ\)বা, \( θ = \frac{15}{6} = \frac{5}{2}\)
উত্তর – কেন্দ্রস্থ কোণের বৃত্তীয় মান \(\frac{5}{2}\) রেডিয়ান।
প্রয়োগ 13. একটি বৃত্তের অসমান দৈর্ঘ্যের দুটি চাপ কেন্দ্রে যে দুটি কোণ ধারণ করে আছে তাদের অনুপাত \(5:3\) এবং দ্বিতীয় কোণটির ষষ্ঠিক মান \(45°\); প্রথম কোণটির ষষ্ঠিক মান এবং বৃত্তীয় মান নির্ণয় করি।
সমাধান –
মনে করি, প্রথম কোণটির ষষ্ঠিক মান \(θ°\)
শর্তানুসারে, \(\frac{θ°}{45°} = \frac{5}{3}\)
বা, \(θ° = \frac{5×45°}{3} = 75°\)
যেহেতু, \(180° = π^c\)
সুতরাং, \(75° = \frac{75}{180} × π^c = \frac{5}{12}π^c\)
উত্তর – প্রথম কোণের ষষ্ঠিক মান \(75°\) এবং বৃত্তীয় মান = \(\frac{5}{12}π^c\)
প্রয়োগ 14. একটি ত্রিভুজের দুটি কোণের পরিমাপ 35°57’4” এবং 39°2’56” হলে, তৃতীয় কোণটির বৃত্তীয় মান নির্ণয় করি।
সমাধান –
ত্রিভুজের দুটি কোণের সমষ্টি = 35°57’4” + 39°2’56”
= 74°59’60”
= 74°60′
= 75°
∴ তৃতীয় কোণের পরিমাপ = \(180° – 75° \)
\(= 105° \)\(= 105×\frac{π^c}{180} \)\(= \frac{7}{12}π^c\)সুতরাং, তৃতীয় কোণটির বৃত্তীয় মান \(\frac{7}{12}π\)
প্রয়োগ 15. 65°35′25′′ কোণটির পূরক কোণের মান ষষ্ঠিক পদ্ধতিতে লিখি।
সমাধান –
90° = 89°60′ = 89°59′60′′
(89°59′60′′ − 65°35′25′′) = 24°24′35′′
উত্তর – 65°35′25′′ কোণটির পূরক কোণের মান 24°24′35′′
প্রয়োগ 16. 27°27′27′′ কোণটির পূরক কোণের মান ষষ্ঠিক পদ্ধতিতে লিখি।
সমাধান –
90° = 89°60′ = 89°59′60′′
(89°59′60′′ −27°27′27′′) = 62°32′33′′
উত্তর – 27°27′27′′ কোণটির পূরক কোণের মান 62°32′33′′।
প্রয়োগ 17. 75°36′24′′ কোণটির সম্পূরক কোণের মান ষষ্ঠিক পদ্ধতিতে লিখি।
সমাধান –
180° = 179°60′ = 179°59′60′′
(179°59′60′′ − 75°36′24′′) = 104°23′36′′
উত্তর – 75°36′24′′ কোণটির সম্পূরক কোণের মান 104°23′36′′
প্রয়োগ 18. 85°32′36′′ কোণটির সম্পূরক কোণের মান ষষ্ঠিক পদ্ধতিতে লিখি।
সমাধান –
180° = 179°60′ = 179°59′60′′
(179°59′60′′ − 85°32′36′′) = 94°27′24′′
উত্তর – 85°32′36′′ কোণটির সম্পূরক কোণের মান ষষ্ঠিক পদ্ধতিতে হবে 94°27′24′′।
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের বিংশ অধ্যায়, ‘ত্রিকোণমিতি: কোণ পরিমাপের ধারণা’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment