এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের বিংশ অধ্যায়, ‘ত্রিকোণমিতি: কোণ পরিমাপের ধারণা’ -এর ‘কষে দেখি – 20’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

1. নিম্নলিখিতগুলিকে ডিগ্রি, মিনিট ও সেকেন্ডে প্রকাশ করি
(i) 832′
(ii) 6312”
(iii) 375”
(iv) \(27 \frac{1}{12}^\circ\)
(v) 72.04°
(i) 832′
সমাধান –
∵ 1° = 60´

∴ 832´ = 13°52´ (উত্তর)
(ii) 6312”
সমাধান –
∵ 60´ = 1° এবং 60″ = 1


∴ 6312″ = 1°45´12″ (উত্তর)
(iii) 375”
সমাধান –
∵ 60″ = 1´

∴ 375″ = 6´15″ (উত্তর)
(iv) \(27 \frac{1}{12}^\circ\)
সমাধান –
\(27 \frac{1}{12}^\circ\)= \( 27^\circ + \left(\frac{1}{12}\right)^\circ\)
= \( 27^\circ + \left(\frac{1}{12} \times 60\right)’\) [∵ 1° = 60′]
= \( 27^\circ 5′\)
(v) 72.04°
সমাধান –
72.04°
= 72° + 0.4°
= 72° + (.04×60)´ [যেহেতু 1° =60´]
= 72° + 2.4´
= 72° + 2´ + 0.4´
= 72°2´(0.4×60)″ [যেহেতু 1´=60″]
= 72°2´24″
2. নিম্নলিখিতগুলির বৃত্তীয় মান নির্ণয়
(i) 60°
(ii) 135°
(iii) –150°
(iv) 72°
(v) 22°30´
(vi) –62°30´
(vii) 52° 52´ 30″
(viii) 40° 16´ 24″
(i) 60°
সমাধান –
\(180^\circ = \pi^c\)\(∴ 60^\circ = \frac{\pi}{180} \times 60 = \frac{\pi}{3}\)(ii) 135°
সমাধান –
\(180^\circ = \pi^c\)(iii) \(-150^\circ\)
সমাধান –
\(180^\circ = \pi^c\)\(-150^\circ = \frac{\pi^c}{180} \times (-150) = -\frac{5\pi^c}{6}\)(iv) 72°
সমাধান –
\(180^\circ = \pi^c\)\(∴ 72^\circ = \frac{\pi^c}{180} \times 72 = \frac{2\pi^c}{5}\)(v) 22°30´
সমাধান –
\(22^\circ30′\)= \( 22^\circ + \left(\frac{30}{60}\right)^\circ\)
= \( 22^\circ + \left(\frac{1}{2}\right)^\circ\)
= \( \left(\frac{44+1}{2}\right)^\circ\)
= \( \frac{45}{2}^\circ\)
\(∴ 180^\circ = \pi^c\)(vi) -62°30′
সমাধান –
\(– 62^\circ30′\)= \( -[62 + (\frac{30}{60})]^\circ\)
= \( -[62 + (\frac{1}{2})]^\circ\)
= \( -[\frac{124+1}{2}]^\circ\)
= \( -\frac{125}{2}^\circ\)
\(∵ 180^\circ = \pi^c\)\(∴ -\frac{125}{2}^\circ = -\frac{\pi^c}{180} \times \frac{125}{2} = -\frac{25\pi^c}{72}\)\(∴ -62^\circ30′ = -\frac{25\pi^c}{72}\)(vii) \(52^\circ52’30”\)
সমাধান –
\(52^\circ52’30”\)= \( 52^\circ + 52’+ (\frac{30}{60})’\)
= \( 52^\circ + (52 + \frac{1}{2})’\)
= \( 52^\circ + (\frac{104+1}{2})’\)
= \( 52^\circ + (\frac{105}{2})’\)
= \( 52^\circ + (\frac{105}{2 \times 60})^\circ\)
= \( 52^\circ + (\frac{21}{24})^\circ\)
= \( (\frac{1248+21}{24})^\circ\)
= \( (\frac{1269}{24})^\circ\)
যেহেতু, \(180^\circ = \pi^c\)
\(∴ (\frac{1269}{24})^\circ\)= \( \frac{\pi^c}{180} \times \frac{1269}{24}\)
= \( \frac{47\pi^c}{160}\)
\(∴ 52^\circ52’30” = \frac{47\pi^c}{160}\)(viii) \(40^\circ16’24”\)
সমাধান –
\(40^\circ16’24”\)= \( 40^\circ + 16′ + \left(\frac{24}{60}\right)’\)
= \( 40^\circ + 16′ + \left(\frac{2}{5}\right)’\)
= \( 40^\circ + \left(16 + \frac{2}{5}\right)’\)
= \( 40^\circ + \left(\frac{80+2}{5}\right)’\)
= \( 40^\circ + \left(\frac{82}{5}\right)’\)
= \( 40^\circ + \left(\frac{82}{5 \times 60}\right)^\circ\)
= \( 40^\circ + \frac{41}{150}^\circ\)
= \( \left(\frac{6000+41}{150}\right)^\circ\)
= \( \frac{6041}{150}^\circ\)
যেহেতু, \(180^\circ = \pi^c\)
\(∴ \frac{6041}{150}^\circ\)= \( \frac{\pi^c}{180} \times \frac{6041}{150}\)
= \( \frac{6041\pi^c}{27000}\)
∴ \( 40^\circ16’24”\) = \( \frac{6041\pi^c}{27000}\) (উত্তর)
3. ABC –এর AC = BC এবং BC বাহুকে D পর্যন্ত বর্ধিত করলাম। যদি ∠ACD = 144° হয়, তবে ABC ত্রিভুজের প্রতিটি কোণের বৃত্তীয় মান নির্ণয় করি।
সমাধান –

ABC ত্রিভুজের \(AC =BC\)
\(\therefore \angle ABC = \angle CAB\)এবং BC বাহুকে D পর্যন্ত বর্ধিত করা হলে,
\(\angle ACD = 144^\circ\)\(\therefore \angle ACB = 180^\circ-144^\circ = 36^\circ\)\(\therefore \angle ABC = \angle CAB = \frac{180^\circ-36^\circ}{2} = 72^\circ\)\(\angle ACB\)-এর বৃত্তীয় মান
= \( \frac{36\pi^c}{180}\)
= \( \frac{\pi^c}{5}\)
\(\angle ABC\)-এর বৃত্তীয় মান
= \( \frac{72\pi^c}{180}\)
= \( \frac{2\pi^c}{5}\)
এবং \(\angle CAB\)-এর বৃত্তীয় মান
= \( \frac{72\pi^c}{180}\)
= \( \frac{2\pi^c}{5}\)
4. একটি সমকোণী ত্রিভুজের সূক্ষ্মকোণ দুটির অন্তর \(\frac{2\pi}{3}\) হলে, ষষ্ঠিক পদ্ধতিতে কোণ দুটির মান লেখ।
সমাধান –
ধরি, ABC একটি সমকোণী ত্রিভুজ যার সূক্ষ্মকোণ দুটি হল A এবং C।
\(\therefore A+C = 90^\circ\) —(i) [যেহেতু সমকোণী ত্রিভুজের সূক্ষ্মকোণ দুটির সমষ্টি \(90^\circ\) ]
আবার, \(A-C = \frac{2\pi}{3}\) [যেহেতু \(\pi\) রেডিয়ান =\(180^\circ\)]
বা, \(A-C = 72^\circ\) —(ii)
(i) ও (ii) নং সমীকরণদ্বয় যোগ করে পাই,
\(A+C+A-C = 90^\circ+72^\circ\)বা, \(2A = 162^\circ\)
বা, \(A = \frac{162}{2}\)
বা, \(A = 81^\circ\)
A এর প্রাপ্ত মান (ii) নং সমীকরণে বসিয়ে পাই,
\(81^\circ-C = 72^\circ\)বা, \(81^\circ-72^\circ =C\)
বা, \(C = 9^\circ\)
\(\therefore\) ষষ্ঠিক পদ্ধতিতে কোণ দুটির মান \(81^\circ\) এবং \(9^\circ\)।
5. একটি ত্রিভুজের একটি কোণের পরিমাপ 65° এবং দ্বিতীয়টির পরিমাপ π/12; তৃতীয় কোণটির ষষ্ঠিক ও বৃত্তীয় মান হিসাব করে লিখি।
সমাধান –
ত্রিভুজের একটি কোণের পরিমাপ 65° এবং দ্বিতীয় কোণের পরিমাপ \(\frac{\pi^c}{12} = \frac{180^\circ}{12} = 15^\circ\)
∴ তৃতীয় কোণটির ষষ্ঠিক মান = 180° – (65° + 15°) = 180° – 80° = 100°
∴ তৃতীয় কোণটির বৃত্তীয় মান = \(\frac{\pi}{180} \times 100 = \frac{5\pi^c}{9}\)
6. দুটি কোণের সমষ্টি \(135^\circ\) এবং তাদের অন্তরফল \(\frac{\pi}{12}\) হলে, কোণদুটির ষষ্টিক ও বৃত্তীয় মান নির্ণয় কর।
সমাধান –
ধরি, কোণ দুটি হল \(x\) এবং \(y\)
∴ \(x+y = 135^\circ\) —(i)
এবং \(x-y = \pi/12 = 15^\circ\)[যেহেতু \(\pi\) রেডিয়ান = \(180^\circ\)]
∴ \(x-y = 15^\circ\) —(ii)
(i) ও (ii) নং সমীকরণ যোগ করে পাই,
\(x+y+x-y = 135^\circ+15^\circ\)বা, \(2x = 150^\circ\)
বা, \(x = 150/2\)
বা, \(x = 75^\circ\)
\(x\) এর মান (ii) নং সমীকরণে বসিয়ে পাই,
\(75^\circ – y = 15^\circ\)বা, \(y = 75^\circ-15^\circ\)
বা, \(y = 60^\circ\)
∴ \(x\) ও \(y\) এর ষষ্টিক পদ্ধতিতে মান গুলি হল যথাক্রমে \(75^\circ\) এবং \(60^\circ\)।
∴ \(x = 75\pi^c/180 = 5\pi^c/12\)
এবং \(y = 60\pi^c/180 = \pi^c/3\)
∴ \(x\) ও \(y\) এর বৃত্তীয় মান যথাক্রমে \(5\pi^c/12\) এবং \(\pi^c/3\)
7. একটি ত্রিভুজের তিনটি কোণের অনুপাত \(2:3:4\) হলে, ত্রিভুজটির বৃহত্তম কোণটির বৃত্তীয় মান নির্ণয় কর।
সমাধান –
ধরি, ত্রিভুজের তিনটি কোণ যথাক্রমে \(2x\), \(3x\) এবং \(4x\)।
∴ \(2x+3x+4x=180^\circ\) [যেহেতু ত্রিভুজের তিনটি কোণের সমষ্টি \(180^\circ\)]
বা, \(9x = 180^\circ\)
বা, \(x = 180^\circ/9\)
বা, \(x = 20^\circ\)
∴ বৃহত্তম কোণটি হল \(4x = 4 \times 20^\circ = 80^\circ\)
বৃহত্তম কোণটির বৃত্তীয় মান = \(\frac{80\pi^c}{180} = \frac{4\pi^c}{9}\)
8. একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 28 সেমি.। এই বৃত্তে 5.5 সেমি. দৈর্ঘ্যের বৃত্তচাপ দ্বারা ধৃত কেন্দ্রীয় কোণটির বৃত্তীয় মান হিসাব করে লিখি।
সমাধান –
আমরা জানি r দৈর্ঘ্যের ব্যাসার্ধের বৃত্তে, s দৈর্ঘ্যের বৃত্তচাপ বৃত্তের কেন্দ্রে যে কোণ উৎপন্ন করে তার মান θ হলে, \(s = r\theta\) হয়।
∴ \(5.5 = 28\theta\)
বা, \(\theta = \frac{5.5}{28}\)
বা, \(\theta = \frac{55}{280}\)
বা, \(\theta = \frac{11}{56}\)
বা, \(\theta = \frac{22}{7 \times 16}\)
বা, \(\theta = \frac{\pi^c}{16}\)
∴ কোণটির বৃত্তীয় মান \(\frac{\pi^c}{16}\)
9. একটি বৃত্তের অসমান দৈর্ঘ্যের দুটি চাপ কেন্দ্রে যে কোণ ধারণ করে আছে তার অনুপাত 5:2 এবং দ্বিতীয় কোণটির ষষ্টিক মান 30° হলে, প্রথম কোণটির ষষ্টিক মান ও বৃত্তীয় মান হিসাব করে লেখ।
সমাধান –
ধরি, প্রথম কোণের ষষ্টিক মান θ।
∴ \(\frac{\theta}{30} = \frac{5}{2}\)
বা, \(\theta = \frac{5 \times 30}{2}\)
বা, \(\theta = 75\)
∴ θ-এর বৃত্তীয় মান = \(\frac{75\pi^c}{180} = \frac{5\pi^c}{12}\)
10. একটি ঘূর্ণায়মান রশ্মি \(-5\frac{1}{12}\pi\) কোণ উৎপন্ন করেছে। রশ্মিটি কতবার পূর্ণ আবর্তন করেছে এবং তারপর আরও কত ডিগ্রী কোণ উৎপন্ন করেছে তা হিসাব করে লিখি।
সমাধান –
\(5\frac{1}{12}\pi\)= \( -\frac{61}{12} \times 180^{\circ}\)
= \( -915^{\circ}\)
যেহেতু কোণটি ঋণাত্মক তাই রশ্মিটি ঘড়ির কাঁটার দিকে ঘুরছে। ঘূর্ণায়মান রশ্মি 1 বার পূর্ণ আবর্তনে \(360^{\circ}\) কোণ উৎপন্ন করে।
এখন, \(\frac{915}{360} =\)

∴ রশ্মিটি ঘড়ির কাঁটার দিকে 2 বার পূর্ণ আবর্তন করেছে এবং তারপর 195° কোণ উৎপন্ন করেছে।
11. একটি সমদ্বিবাহু ত্রিভুজ অঙ্কন করেছি যার সমান বাহুদ্বয়ের অন্তর্ভুক্ত কোণ ∠ABC=45°; ∠ABC –এর সমদ্বিখণ্ডক AC বাহুকে D বিন্দুতে ছেদ করেছে। ∠ABD, ∠BAD, ∠CBD এবং ∠BCD –এর বৃত্তীয় মান নির্ণয় করি।
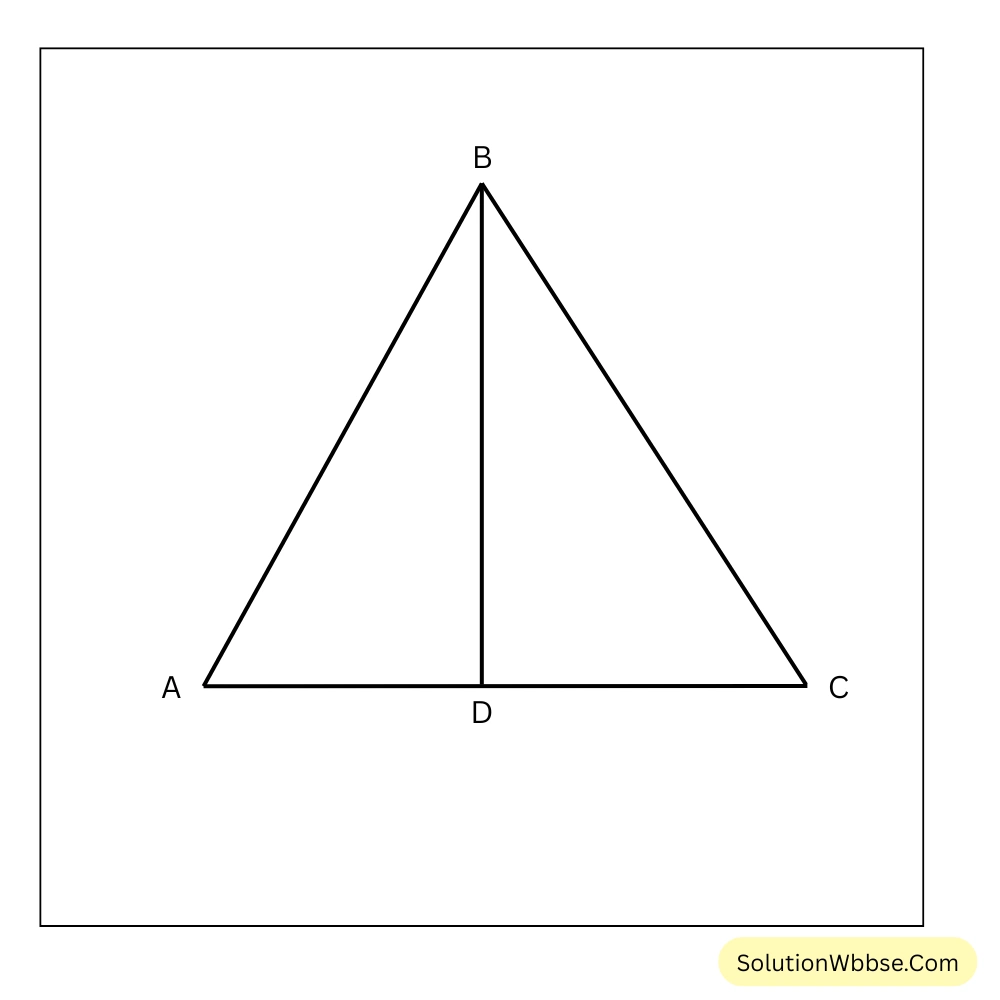
সমাধান –
ABC একটি সমদ্বিবাহু ত্রিভুজ অঙ্কন করেছি যার সমান বাহুদ্বয়ের অন্তর্ভুক্ত কোণ \(∠ABC = 45°\); \(∠ABC\) –এর সমদ্বিখণ্ডক AC বাহুকে D বিন্দুতে ছেদ করেছে। যেহেতু সমদ্বিবাহু ত্রিভুজের সমান বাহু দ্বয়ের অন্তর্ভুক্ত কোণের সমদ্বিখণ্ডক, বিপরীত বাহুকে সমকোণে সমদ্বিখণ্ডিত করে।
∴ \(∠ABD\)
= \(\frac{∠ABC}{2}\)
= \(\frac{45°}{2}\)
= \(\frac{45}{2} \times \frac{\pi^c}{180}\)
= \(\frac{\pi^c}{8}\)
আবার,
∴ \(∠BAD\)
= \(\frac{180° – ∠ABC}{2}\)
= \(\frac{180° – 45°}{2}\)
= \(\frac{135°}{2}\)
= \(\frac{135}{2} \times \frac{\pi^c}{180}\)
= \(\frac{3\pi^c}{8}\)
যেহেতু BD কোণ ABC –এর সমদ্বিখণ্ডক
∴ \(∠ABD = ∠CBD\)
∴ \(∠CBD = \frac{\pi^c}{8}\)
আবার, ABC ত্রিভুজের AB =BC
∴ \(∠BCD = ∠BAD\)
∴ \(∠BCD = \frac{3\pi^c}{8}\)
12. ABC সমবাহু ত্রিভুজের BC ভূমিকে E বিন্দু পর্যন্ত এমনভাবে বর্ধিত করলাম যেন \(CE = BC\) হয়। A, E যুক্ত করে \(ACE\) ত্রিভুজের কোণ গুলির বৃত্তীয়মান নির্ণয় করি।
সমাধান –

\(\Delta ABC\) একটি সমবাহু ত্রিভুজ।
∴ \(AB = BC = CA\)
আবার, \(BC = CE\)
∴ \(AC = CE\)
এখন \(\Delta ACE\) –এর
\(\angle ACE\)= \(180^{\circ} – \angle ACB\)
= \(180^{\circ}-60^{\circ}\)
= \(120^{\circ}\)
= \(\frac{\pi^c}{180} \times 120\)
= \(\frac{2\pi^c}{3}\)
যেহেতু, \(AC = CE\)
∴ \(\angle CAE\)
= \( \angle CEA\)
= \(\frac{180^{\circ} – \angle ACE}{2}\)
= \(\frac{180^{\circ} – 120^{\circ}}{2}\)
= \(\frac{60^{\circ}}{2}\)
= \(30^{\circ}\)
= \(\frac{\pi^c}{180} \times 30\)
= \(\frac{\pi^c}{6}\)
13. কোনো চতুর্ভুজের তিনটি কোণের পরিমাণ যথাক্রমে \(\frac{\pi}{3}\), \(\frac{5\pi}{6}\) ও \(90^\circ\) হলে, চতুর্থ কোণটির ষষ্ঠিক ও বৃত্তীয় মান হিসেব করে লিখি।
সমাধান –
চতুর্ভুজটির তিনটি কোণের পরিমাণ যথাক্রমে \(\frac{\pi}{3}\), \(\frac{5\pi}{6}\) ও \(90^\circ\)
এখন, \(90^\circ = \frac{\pi}{180^\circ} \times 90^\circ = \frac{\pi}{2}\)
চতুর্থ কোণটির বৃত্তীয় মান
= \( 2\pi – (\frac{\pi}{3} + \frac{5\pi}{6} + \frac{\pi}{2})\) [যেহেতু চতুর্ভুজের চারটি কোণের সমষ্টি \(360^\circ = 2\pi\)]
= \( 2\pi – (\frac{2\pi+5\pi+3\pi}{6})\)
= \( 2\pi – \frac{10\pi}{6}\)
= \( \frac{12\pi-10\pi}{6}\)
= \( \frac{2\pi}{6}\)
= \( \frac{\pi}{3}\)
চতুর্থ কোণটির বৃত্তীয় মান = \(\frac{\pi}{3}\)
চতুর্থ কোণটির ষষ্ঠিক মান = \(\frac{\pi}{3} = \frac{180^\circ}{3} = 60^\circ\)
14. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A)
(A) বহু বিকল্পীয় প্রশ্ন (M.C.Q)
(i) একটি ঘড়ির মিনিটের কাঁটার প্রান্তবিন্দু 1 ঘন্টায় আবর্তন করে
(a) \(\frac{\pi}{4}\) রেডিয়ান
(b) \(\frac{\pi}{2}\) রেডিয়ান
(c) \(\pi\)রেডিয়ান
(d) \(2\pi\) রেডিয়ান
Ans – (d) 2π রেডিয়ান
সমাধান – 1 ঘন্টায় ঘড়ির মিনিটের কাঁটার প্রান্তবিন্দু অতিক্রম করে 360° = 2π রেডিয়ান।
(ii) \(\frac{\pi}{6}\)রেডিয়ান সমান
(a) 60°
(b) 45°
(c) 90°
(d) 30°
Ans – (d) 30°
সমাধান – \(\frac{\pi}{6}\) রেডিয়ান= \(\frac{180^\circ}{6}\) = 30°
(iii) একটি সুষম ষড়ভুজের প্রতিটি অন্তঃকোণের বৃত্তীয় মান
(a) \(\frac{\pi}{3}\)
(b) \(\frac{2\pi}{3}\)
(c) \(\frac{\pi}{6}\)
(d) \(\frac{\pi}{4}\)
Ans – (b) \(\frac{2\pi}{3}\)
সমাধান –
একটি সুষম ষড়ভুজের প্রতিটি অন্তঃকোণ
= \( \frac{(2n-4) \times 90^\circ}{n}\)
= \( \frac{{2(6)-4} \times 90}{6}\)
= \( \frac{720^\circ}{6}\)
= \(120^\circ\)
(iv) s = rϴ সম্পর্কে ϴ -এর পরিমাপ করা হয়
(a) ষষ্টিক পদ্ধতিতে
(b) বৃত্তীয় পদ্ধতিতে
(c ) ওই দুই পদ্ধতিতে
(d) ওই দুই পদ্ধতির কোনোটিতে নয়
Ans – (b) বৃত্তীয় পদ্ধতিতে
(v) ABCD বৃত্তস্থ চতুর্ভুজের ∠A = 120° হলে, ∠C এর বৃত্তীয় মান
(a) π/3
(b) π/6
(c) π/2
(d) 2π/3
Ans –
সমাধান – যেহেতু বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক,
∴∠A+∠C =180°
∴ ∠C = 180°- ∠A
বা, ∠C = 180° -120°
বা, ∠C = 60°
∴ ∠C -এর বৃত্তীয় মান = (π/180°) × 60° = π/3
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি
(i) একটি রশ্মির প্রান্তবিন্দুকে কেন্দ্র করে রশ্মিটির ঘড়ির কাঁটার বিপরীত দিকে ঘোরার জন্য উৎপন্ন কোণটি ধনাত্মক।
উত্তর – বিবৃতিটি সত্য।
(ii) একটি রশ্মির প্রান্তবিন্দুকে কেন্দ্র করে রশ্মিটির ঘড়ির কাঁটার দিকে দুবার পূর্ণ আবর্তনের জন্য 720° কোণ উৎপন্ন হয়।
উত্তর – বিবৃতিটি মিথ্যা।
সমাধান – একটি রশ্মির প্রান্তবিন্দুকে কেন্দ্র করে রশ্মিটির ঘড়ির কাঁটার দিকে দুবার পূর্ণ আবর্তনের জন্য -720° কোণ উৎপন্ন হয়।
(C) শূন্যস্থান পূরণ করি
(i) π রেডিয়ান একটি _________ কোণ।
উত্তর – ধ্রুবক কোণ।
(ii) ষষ্টিক পদ্ধতিতে 1 রেডিয়ান সমান _______ কোণ (প্রায়)।
উত্তর – 1 রেডিয়ান = \(\frac{180°}{\pi} = \frac{180°}{\frac{22}{7}} = \frac{180° \times 7}{22} = \frac{630°}{11} = 57° 16′ 22”\)
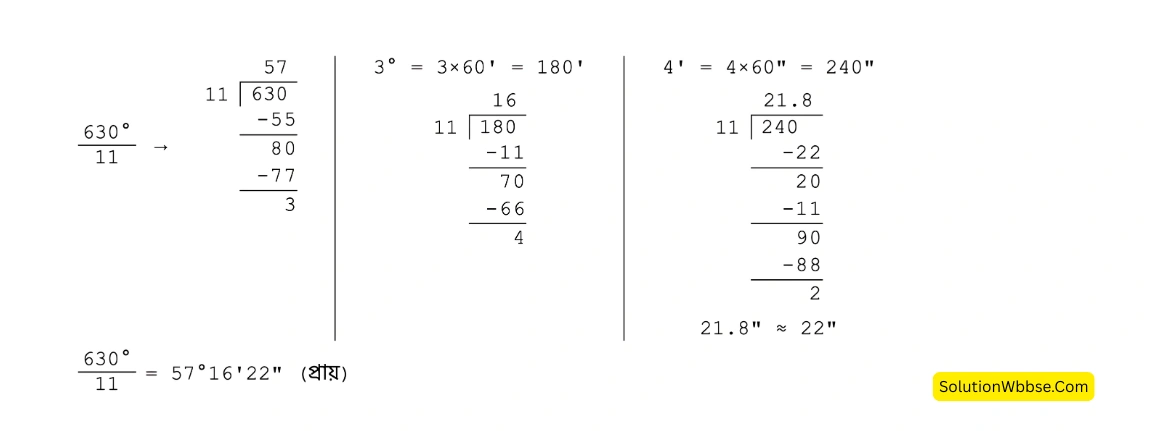
(iii) \(\frac{3\pi}{8}\) পরিমাপের কোণটির সম্পূরক কোণের বৃত্তীয় মান _______।
উত্তর – \(\frac{3\pi}{8}\) পরিমাপের কোণটির সম্পূরক কোণের বৃত্তীয় মান = \(\pi – \frac{3\pi}{8}\) = \(\frac{8\pi-3\pi}{8}\) = \(\frac{5\pi}{8}\)
15. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A)
(i) একটি কোণের ডিগ্রিতে মান \(D\) এবং ওই কোণের রেডিয়ানে মান \(R\) হলে, [ latex]R/D[/latex] এর মান নির্ণয় করি।
সমাধান –
\(\pi^c = 180^\circ\)\(\therefore 1^c = \frac{180}{\pi}\)বা, \(R^c = \frac{180R}{\pi}\)
শর্তানুসারে,
\(D = \frac{180R}{\pi}\)বা, \(\frac{\pi}{180} = \frac{R}{D}\)
\(\therefore \frac{R}{D} = \frac{\pi}{180}\)(ii) 63°35’15” পরিমাপের কোণটির পূরক কোণের মান লিখি।
সমাধান –
90° = 89°60′ = 89°59’60”
∴ 63°35’15” পরিমাপের কোণটির পূরক কোণের মান = 89°59’60” – 63°35’15” = 26°24’45”
(iii) একটি ত্রিভুজের দুটি কোণের পরিমাপ 65°56’55” এবং 64°3’5″ হলে, তৃতীয় কোণটির বৃত্তীয় মান নির্ণয় করি।
সমাধান –
তৃতীয় কোণটির ষষ্ঠিক মান
= \( 180^\circ – (65^\circ 56′ 55” + 64^\circ 3′ 5”)\)
= \( 180^\circ – 130^\circ\)
= \( 50^\circ\)
তৃতীয় কোণটির বৃত্তীয় মান = \(50 \times \frac{\pi^c}{100} = \frac{\pi^c}{2}\)
(iv) একটি বৃত্তে 220 সেমি. দৈর্ঘ্যের বৃত্তচাপ কেন্দ্রে 63°পরিমাপের কোণ উৎপন্ন করলে, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য নির্ণয় করি।
সমাধান –
\(63 = 63^\circ \times \frac{\pi^c}{180} = \frac{21\pi^c}{60}\)আমরা জানি, s= rθ [ s= বৃত্তচাপের দৈর্ঘ্য , r = বৃত্তের ব্যাসার্ধ , θ =কেন্দ্রে উৎপন্ন কোণের বৃত্তীয় মান]
\(\therefore 220 = r \times \frac{21\pi}{60}\)বা, \(r = \frac{220 \times 60}{21\pi}\)
বা, \(r = \frac{220 \times 60}{21 \times \frac{22}{7}}\)
বা, \(r = \frac{220 \times 60}{3 \times 22}\)
বা, r = 200
\(\therefore\) বৃত্তের ব্যাসার্ধ 200 সেমি.।
(v) একটি ঘড়ির ঘণ্টার কাঁটার প্রান্তবিন্দু 1 ঘণ্টা আবর্তনে যে পরিমাণ কোণ উৎপন্ন করে তার বৃত্তীয় মান লিখি।
সমাধান –
একটি ঘড়ির ঘণ্টার কাঁটা 12 ঘন্টায় কেন্দ্রে 360° বা 2π রেডিয়ান কোণ উৎপন্ন করে।
\(\therefore\) 1 ঘন্টায় কেন্দ্রে উৎপন্ন করা কোণের পরিমাপ = \(\frac{2\pi}{12} = \frac{\pi}{6}\)
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের বিংশ অধ্যায়, ‘ত্রিকোণমিতি: কোণ পরিমাপের ধারণা’ -এর ‘কষে দেখি – 20’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment