পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) অষ্টম শ্রেণির গণিত পাঠ্যবইয়ের ষোড়শ অধ্যায় হলো ‘কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই’। এই পোস্টে আমরা ‘কষে দেখি – 16.2’-এর সমস্ত প্রশ্নের সহজ ও নির্ভুল সমাধান নিয়ে আলোচনা করেছি। আশা করি, এই নোটসগুলো তোমাদের গণিত শিখতে এবং পরীক্ষার প্রস্তুতিতে দারুণভাবে সহায়তা করবে।

1. চিত্রে \(\angle QPR > \angle PQR\) PR এবং QR বাহুর সম্পর্ক লিখি।
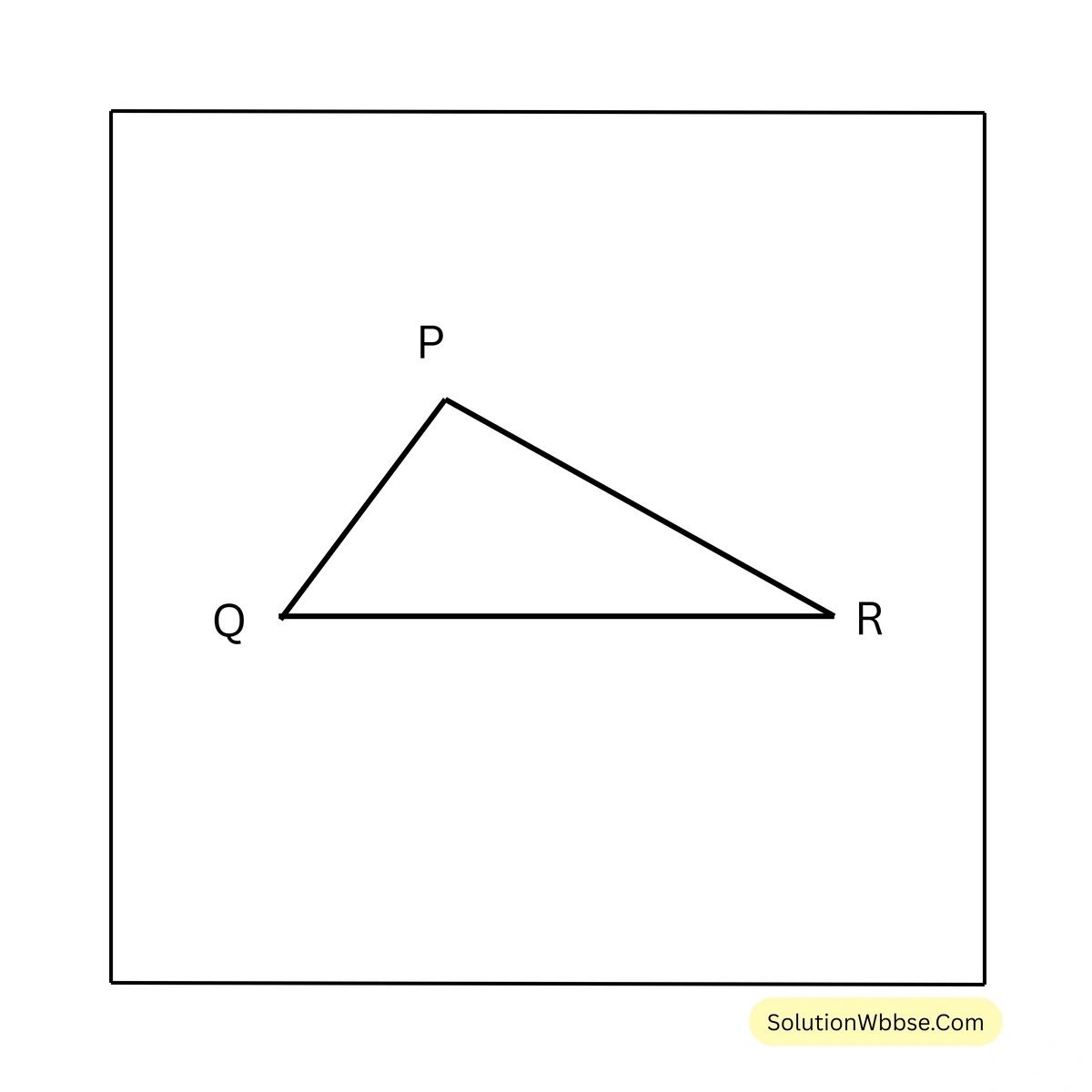
সমাধান – \(\triangle PQR\) এর \(\angle QPR > \angle PQR\)
যেহেতু, একটি ত্রিভুজের বৃহত্তম কোণের বিপরীত বাহুর দৈর্ঘ্য ক্ষুদ্রতর কোণটির বিপরীত বাহুর দৈর্ঘ্য অপেক্ষা বৃহত্তর।
\(\therefore QR > PR\)2. \(\triangle ABC\) তে, \(AC > AB\)। AC বাহুর উপর D এমন একটি বিন্দু যে \(\angle ADB = \angle ABD\); প্রমাণ করি যে, \(\angle ABC > \angle ACB\)।
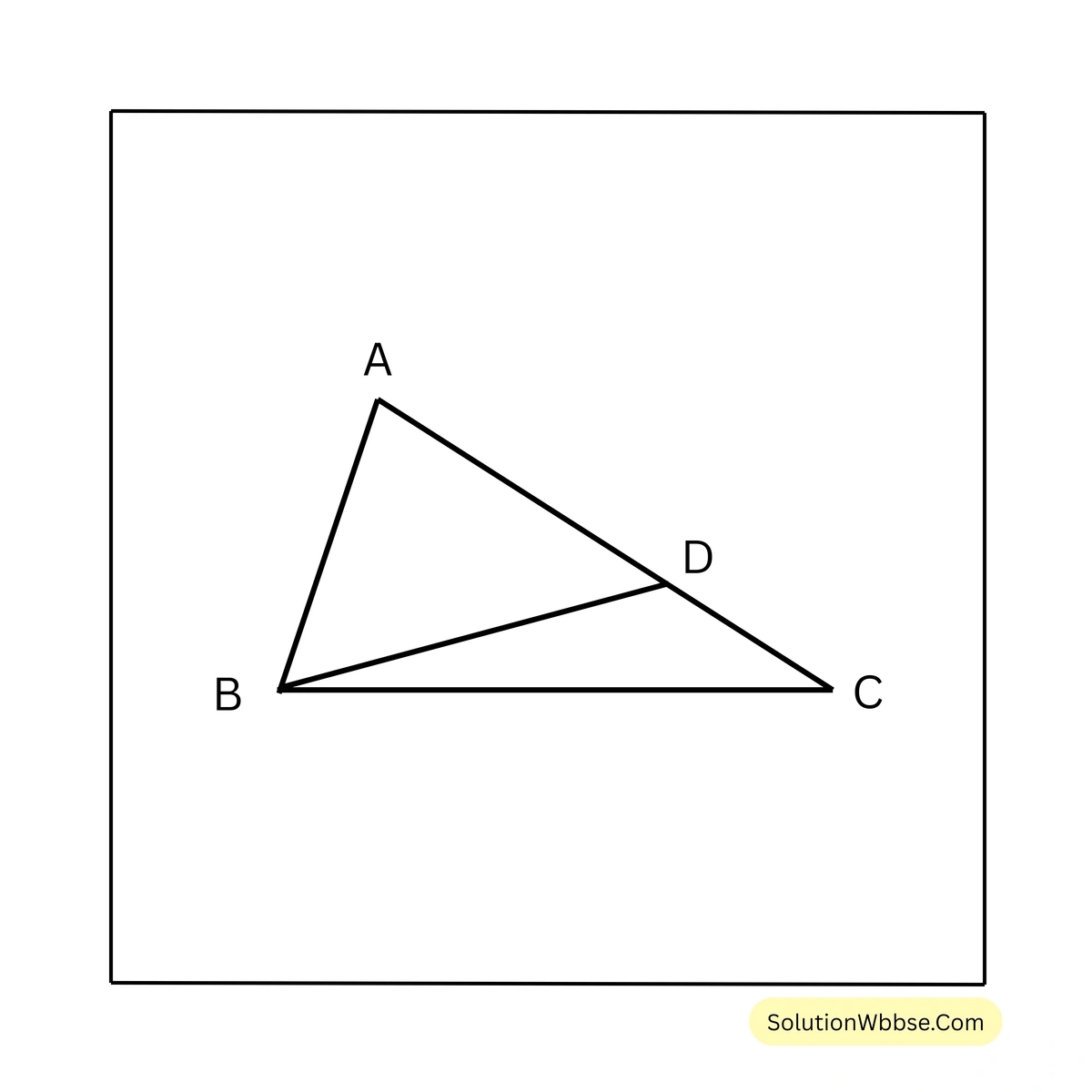
প্রদত্ত – \(\triangle ABC\) এর \(AC > AB\), AC বাহুর উপর D এমন একটি বিন্দু যে \(\angle ADB = \angle ABD\)
প্রামাণ্য – \(\angle ABC > \angle ACB\)
প্রমাণ – \(\triangle BCD\) এর বহিঃস্থ কোণ \(\angle ADB = \angle CBD + \angle BCD\)
\(\therefore \angle ADB > \angle BCD\)যেহেতু, \(\angle ADB = \angle ABD\) \(\therefore \angle ABD > \angle BCD\) —-(i)
আবার, \(\angle ABC = \angle ABD + \angle CBD\)
বা, \(\angle ABC > \angle ABD\) —-(ii)
(i) নং ও (ii) নং থেকে পাই,
\(\angle ABC > \angle BCD\)\(\therefore \angle ABC > \angle ACB\) [প্রমাণিত]
3. ABC ত্রিভুজের \(AB > AC\); \(\angle BAC\) এর সমদ্বিখণ্ডক BC বাহুকে D বিন্দুতে ছেদ করে। প্রমাণ করি যে, \(BD > CD\)।
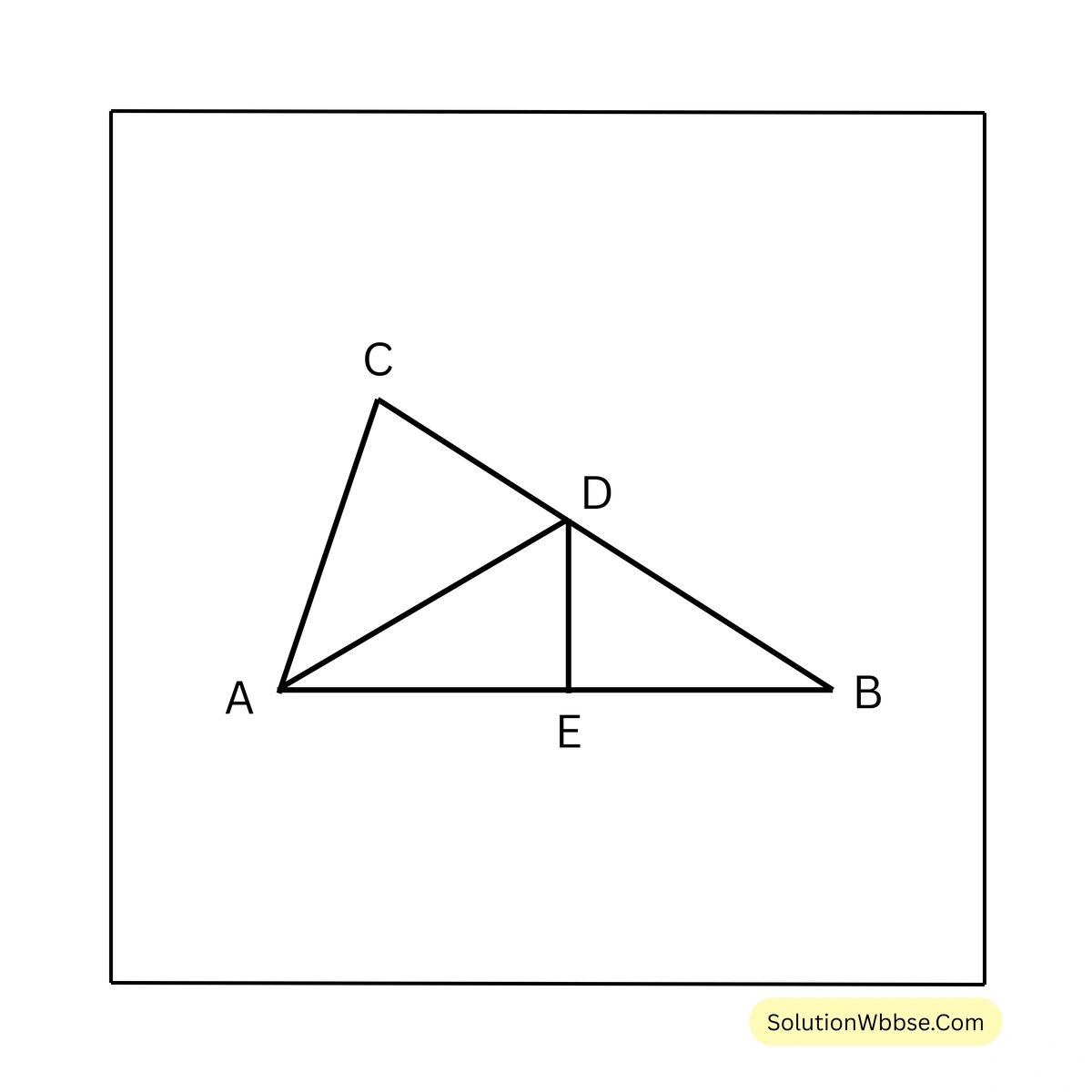
প্রদত্ত – ABC ত্রিভুজে \(AB > AC\); \(\angle BAC\) এর সমদ্বিখণ্ডক BC বাহুকে D বিন্দুতে ছেদ করে। অর্থাৎ \(\angle BAD = \angle CAD\)
প্রামাণ্য – \(BD > CD\)
অঙ্কন – AC এর সমান করে AB বাহু থেকে AE অংশ কেটে নিলাম।
প্রমাণ – \(\triangle ACD\) এবং \(\triangle AED\) এর মধ্যে,
\(AC = AE\) [অঙ্কনানুসারে]
\(\angle EAD = \angle CAD\) [যেহেতু, \(\angle BAD = \angle CAD\)]
\(AD\) সাধারণ বাহু
\(\therefore \triangle ACD \cong \triangle AED\) [সর্বসমতার S-A-S শর্তানুসারে]
\(\therefore \angle ADC = \angle ADE\) [সর্বসম ত্রিভুজের অনুরূপ কোণ]
এবং \(DE = CD\) [সর্বসম ত্রিভুজের অনুরূপ বাহু] —-(i)
\(\triangle ABD\) এর বহিঃস্থ কোণ \(\angle ADC > \angle ABD\)
\(\therefore \angle ADE > \angle ABD\) —-(ii)
\(\triangle AED\) এর বহিঃস্থ কোণ \(\angle BED = \angle ADE\) —–(iii)
(ii) নং ও (iii) নং থেকে পাই,
\(\angle BED > \angle ABD\)\(\therefore \angle BED > \angle EBD\)যেহেতু, একটি ত্রিভুজের বৃহত্তম কোণের বিপরীত বাহুর দৈর্ঘ্য ক্ষুদ্রতর কোণটির বিপরীত বাহুর দৈর্ঘ্য অপেক্ষা বৃহত্তর।
\(\therefore BD > CD\) [(i) নং থেকে পাই] [প্রমাণিত]
4. ABC ত্রিভুজের \(AD\), BC বাহুর উপর লম্ব এবং \(AC > AB\); প্রমাণ করি যে, (i) \(\angle CAD > \angle BAD\) (ii) \(DC > BD\)
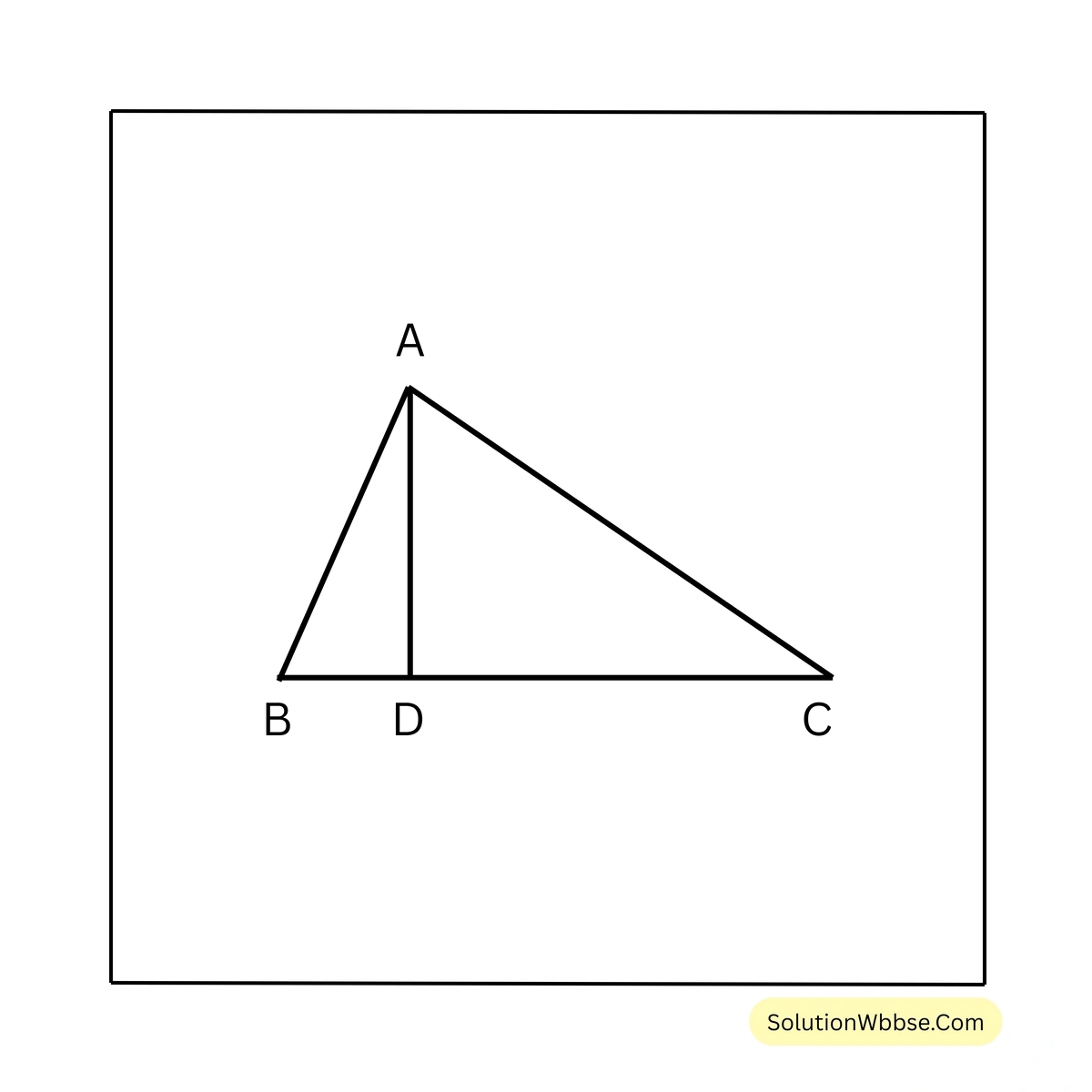
প্রদত্ত – ABC ত্রিভুজের \(AD\), BC বাহুর উপর লম্ব এবং \(AC > AB\)
প্রামাণ্য – (i) \(\angle CAD > \angle BAD\) (ii) \(DC > BD\)
প্রমাণ – যেহেতু, \(AD \perp BC\)
\(\therefore \triangle ACD\) এবং \(\triangle ADB\) উভয়েই সমকোণী ত্রিভুজ।
\(\triangle ADC\) সমকোণী ত্রিভুজ থেকে পাই,
\(\angle ACD + \angle CAD = 90^\circ\) ——(1)
\(\triangle ADB\) সমকোণী ত্রিভুজ থেকে পাই,
\(\angle ABD + \angle BAD = 90^\circ\) ——(2)
ABC ত্রিভুজের \(AC > AB\)
\(\therefore \angle ABC > \angle ACB\)বা, \(\angle ABD > \angle ACD\)
(1) নং ও (2) নং থেকে পাই,
\(\angle ACD + \angle CAD = \angle ABD + \angle BAD\)যেহেতু, \(\angle ABD > \angle ACD\)
\(\therefore \angle CAD > \angle BAD\) [(i) নং প্রমাণিত]
যেহেতু, বৃহত্তর কোণের বিপরীত বাহু > ক্ষুদ্রতর কোণের বিপরীত বাহু,
\(\therefore DC > BD\) [(ii) নং প্রমাণিত]
5. একটি চতুর্ভুজের বৃহত্তম ও ক্ষুদ্রতম বাহু দুটির বিপরীত। প্রমাণ করি যে, বৃহত্তম বাহুর সন্নিহিত একটি কোণ তার বিপরীত কোণের চেয়ে ছোটো।
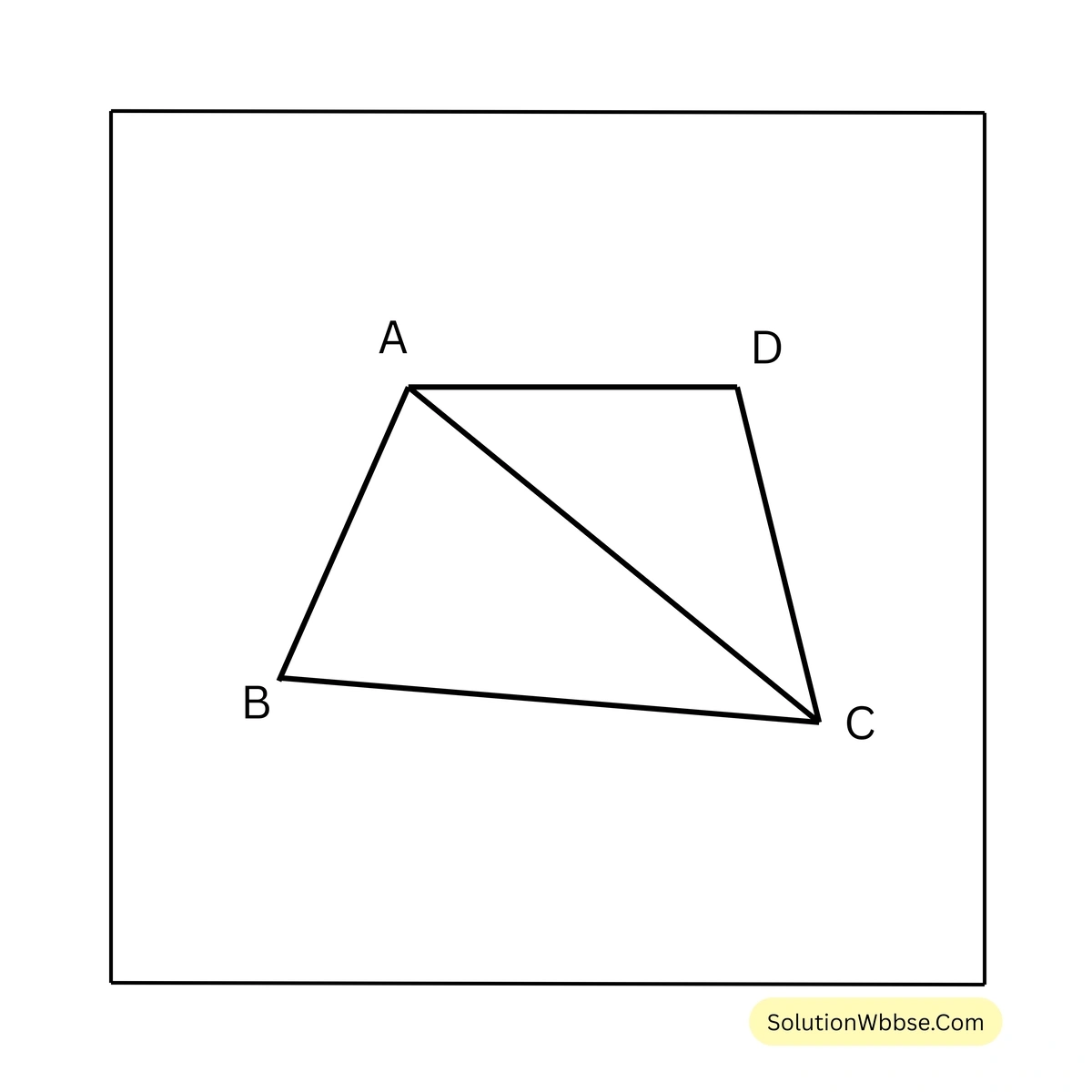
প্রদত্ত – ABCD চতুর্ভুজের বৃহত্তম বাহু BC এবং ক্ষুদ্রতম বাহু AD পরস্পর বিপরীত বাহু।
প্রামাণ্য – \(\angle BCD < \angle BAD\)
অঙ্কন – AC কর্ণ অঙ্কন করা হল।
প্রমাণ – ABCD চতুর্ভুজের বৃহত্তম বাহু BC \(\therefore AB < BC\)
\(\triangle ABC\) এর \(AB < BC\), \(\therefore \angle ACB < \angle BAC\) —– (1)
ABCD চতুর্ভুজের ক্ষুদ্রতম বাহু AD
\(\therefore AD < DC\)\(\triangle ADC\) এর \(AD < DC\), \(\therefore \angle ACD < \angle CAD\) —–(2)
(1) নং ও (2) নং যোগ করে পাই,
\(\angle ACB + \angle ACD < \angle BAC + \angle CAD\)\(\therefore \angle BCD < \angle BAD\) [প্রমাণিত]
6. চিত্রে, \(AB < OB\) এবং \(CD > OD\); প্রমাণ করি যে, \(\angle BAO > \angle OCD\)
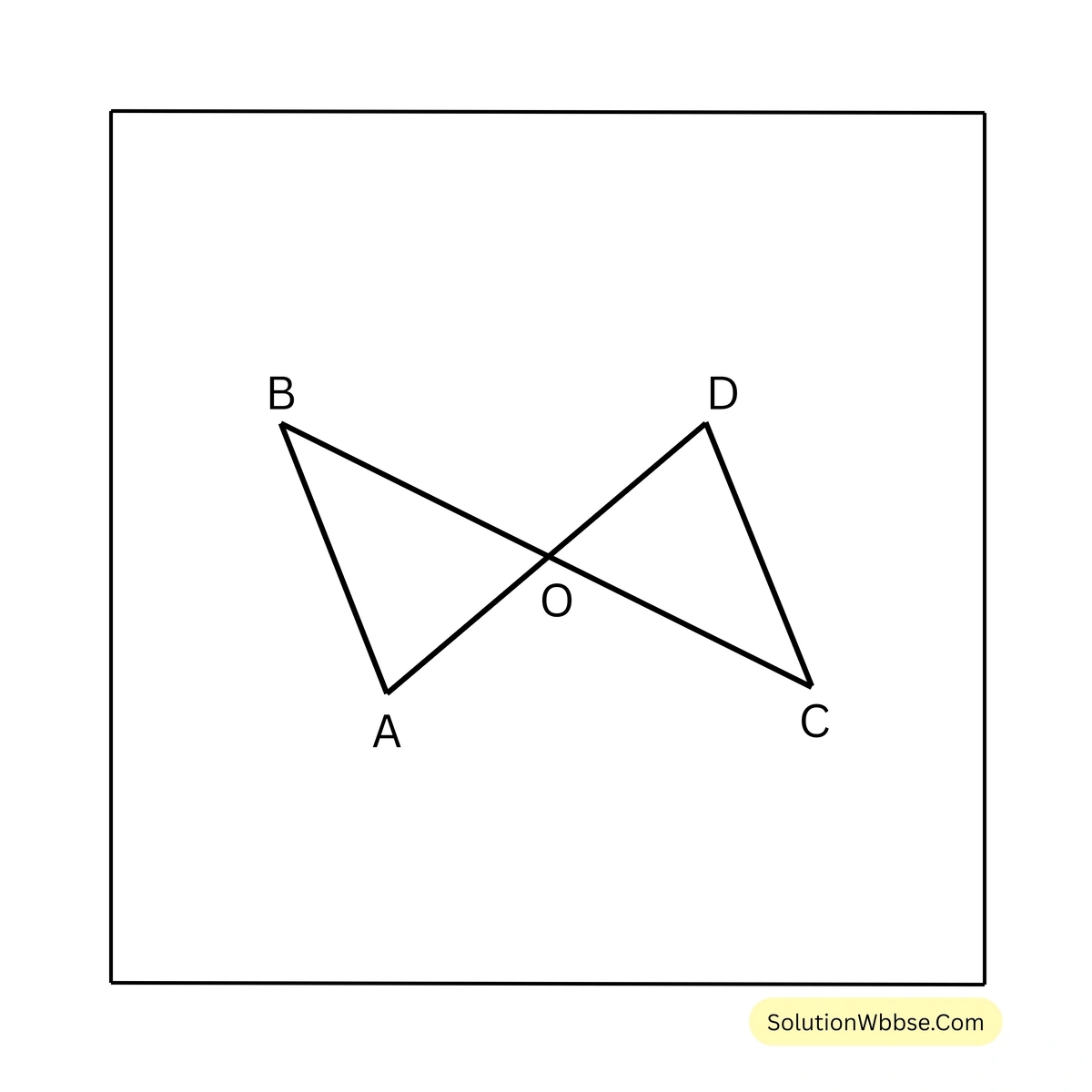
প্রমাণ – \(\triangle AOB\) এর \(AB < OB\) \(\therefore \angle AOB < \angle BAO\) —-(i)
\(\triangle COD\) এর \(CD > OD\) \(\therefore \angle COD > \angle OCD\) —–(ii)
আবার, \(\angle AOB =\) বিপ্রতীপ \(\angle COD\)
(i) নং থেকে পাই, \(\angle COD < \angle BAO\) —-(iii)
(ii) নং ও (iii) নং থেকে পাই,
\(\angle BAO > \angle COD > \angle OCD\)\(\therefore \angle BAO > \angle OCD\) [প্রমাণিত]
7. \(\triangle PQR\) এর \(PQ > PR\); PQ বাহু থেকে PR বাহুর দৈর্ঘ্যর সমান করে PS সরলরেখাংশ কেটে নিলাম। R এবং S বিন্দু দুটি যুক্ত করলাম। প্রমাণ করি যে,
(i) \(\angle PSR = \frac{1}{2} (\angle PQR + \angle PRQ)\)
(ii) \(\angle QRS = \frac{1}{2} (\angle PRQ – \angle PQR)\)
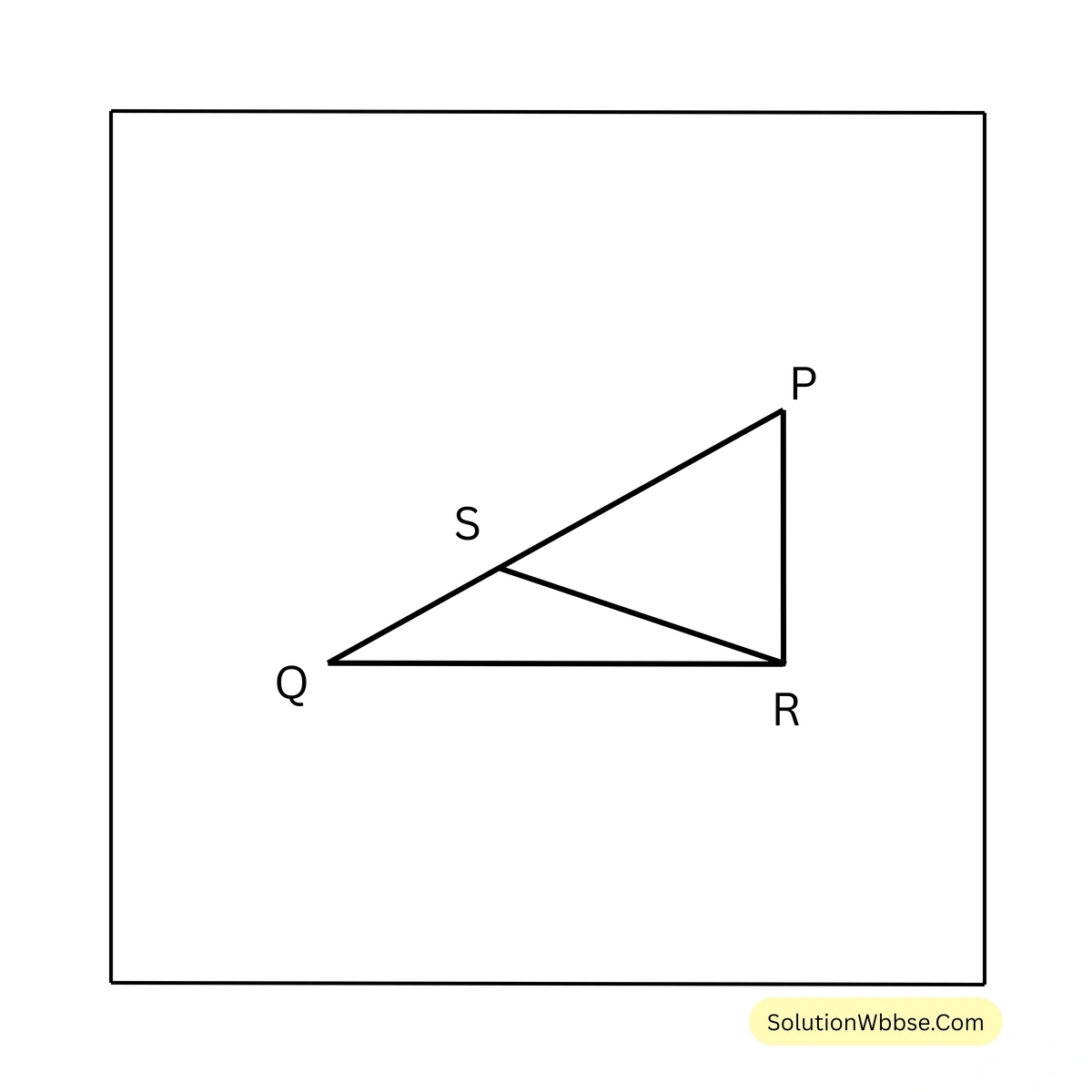
প্রদত্ত – \(\triangle PQR\) এর \(PQ > PR\); PQ বাহু থেকে PR বাহুর দৈর্ঘ্যর সমান করে PS সরলরেখাংশ কেটে নিলাম। R এবং S বিন্দু দুটি যুক্ত করলাম।
প্রামাণ্য – (i) \(\angle PSR = \frac{1}{2} (\angle PQR + \angle PRQ)\)
(ii) \(\angle QRS = \frac{1}{2} (\angle PRQ – \angle PQR)\)
প্রমাণ – \(\triangle PQR\) এর \(PR = PS\) \(\therefore \angle PSR = \angle PRS\)
(i) \(\triangle QSR\) ত্রিভুজের বহিঃস্থ কোণ \(\angle PSR = \angle SQR + \angle SRQ\)
বা, \(\angle PSR = \angle PQR + \angle PRQ – \angle PRS\)
বা, \(\angle PSR = \angle PQR + \angle PRQ – \angle PSR\) [∵ \(\angle PSR = \angle PRS\)]
বা, \(\angle PSR + \angle PSR = \angle PQR + \angle PRQ\)
বা, \(2 \angle PSR = \angle PQR + \angle PRQ\)
\(\therefore \angle PSR = \frac{1}{2} (\angle PQR + \angle PRQ)\) [প্রমাণিত]
(ii) \(\triangle QSR\) ত্রিভুজের বহিঃস্থ কোণ \(\angle PSR = \angle SQR + \angle QRS\)
বা, \(\angle QRS = \angle PSR – \angle SQR\)
বা, \(\angle QRS = \angle PRS – \angle PQR\)
বা, \(\angle QRS = \angle PRQ – \angle QRS – \angle PQR\)
বা, \(\angle QRS + \angle QRS = \angle PRQ – \angle PQR\)
বা, \(2 \angle QRS = \angle PRQ – \angle PQR\)
\(\therefore \angle QRS = \frac{1}{2} (\angle PRQ – \angle PQR)\) [প্রমাণিত]
8. ABC ত্রিভুজে, \(AB > AC\); \(\angle BAC\) এর সমদ্বিখণ্ডক BC বাহুকে D বিন্দুতে ছেদ করে। AB বাহু থেকে AC এর দৈর্ঘ্যর সমান করে AE সরলরেখাংশ কেটে নিলাম। D, E যুক্ত করলাম। প্রমাণ করি যে, (i) \(\triangle ACD \cong \triangle AED\) (ii) \(\angle ACB > \angle ABC\)
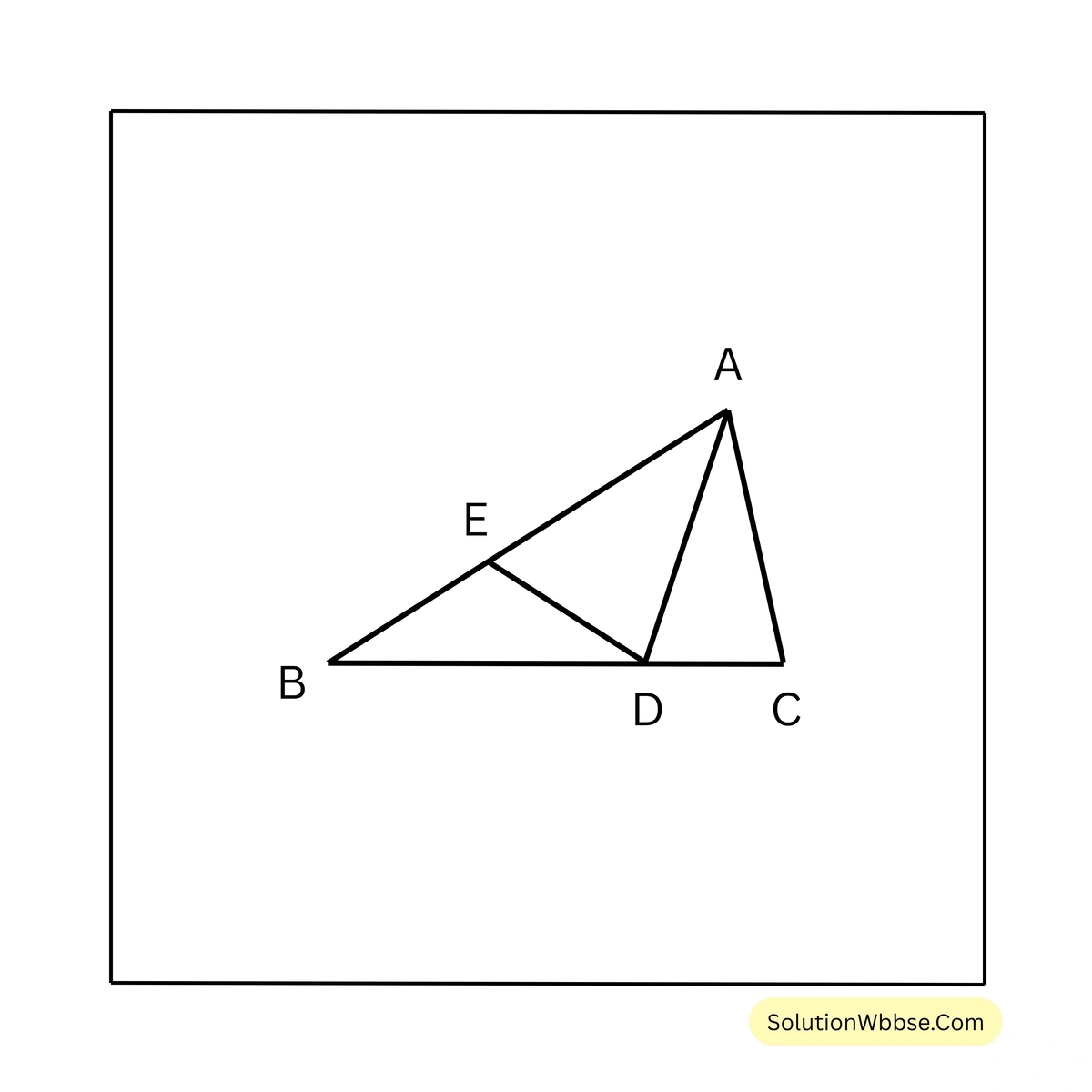
প্রদত্ত – ABC ত্রিভুজে, \(AB > AC\); \(\angle BAC\) এর সমদ্বিখণ্ডক BC বাহুকে D বিন্দুতে ছেদ করে। \(AE = AC\)
প্রামাণ্য – (i) \(\triangle ACD \cong \triangle AED\) (ii) \(\angle ACB > \angle ABC\)
প্রমাণ – \(\triangle ACD\) এবং \(\triangle AED\) এর মধ্যে
\(AE = AC\) [প্রদত্ত]
\(\angle DAE = \angle DAC\) [AD, \(\angle BAC\) এর সমদ্বিখণ্ডক]
\(AD\) সাধারণ বাহু
\(\therefore \triangle ACD \cong \triangle AED\) [সর্বসমতার S-A-S শর্তানুসারে] [(i) নং প্রমাণিত]
\(\therefore \angle AED = \angle ACD\) [সর্বসম ত্রিভুজের অনুরূপ কোণ]
\(\triangle BED\) এর বহিঃস্থ কোণ \(\angle AED = \angle EBD + \angle BDE\)
\(\therefore \angle ACD = \angle EBD + \angle BDE\)বা, \(\angle ACB = \angle ABC + \angle BDE\) [∵ \(\angle ABC = \angle EBD\) এবং \(\angle ACB = \angle ACD\)]
\(\therefore \angle ACB > \angle ABC\) [(ii) নং প্রমাণিত]
9. চিত্রে, \(AB = CD\), \(\angle OCD > \angle COD\) এবং \(\angle OAB < \angle AOB\) প্রমাণ করি যে, \(OB < OD\)
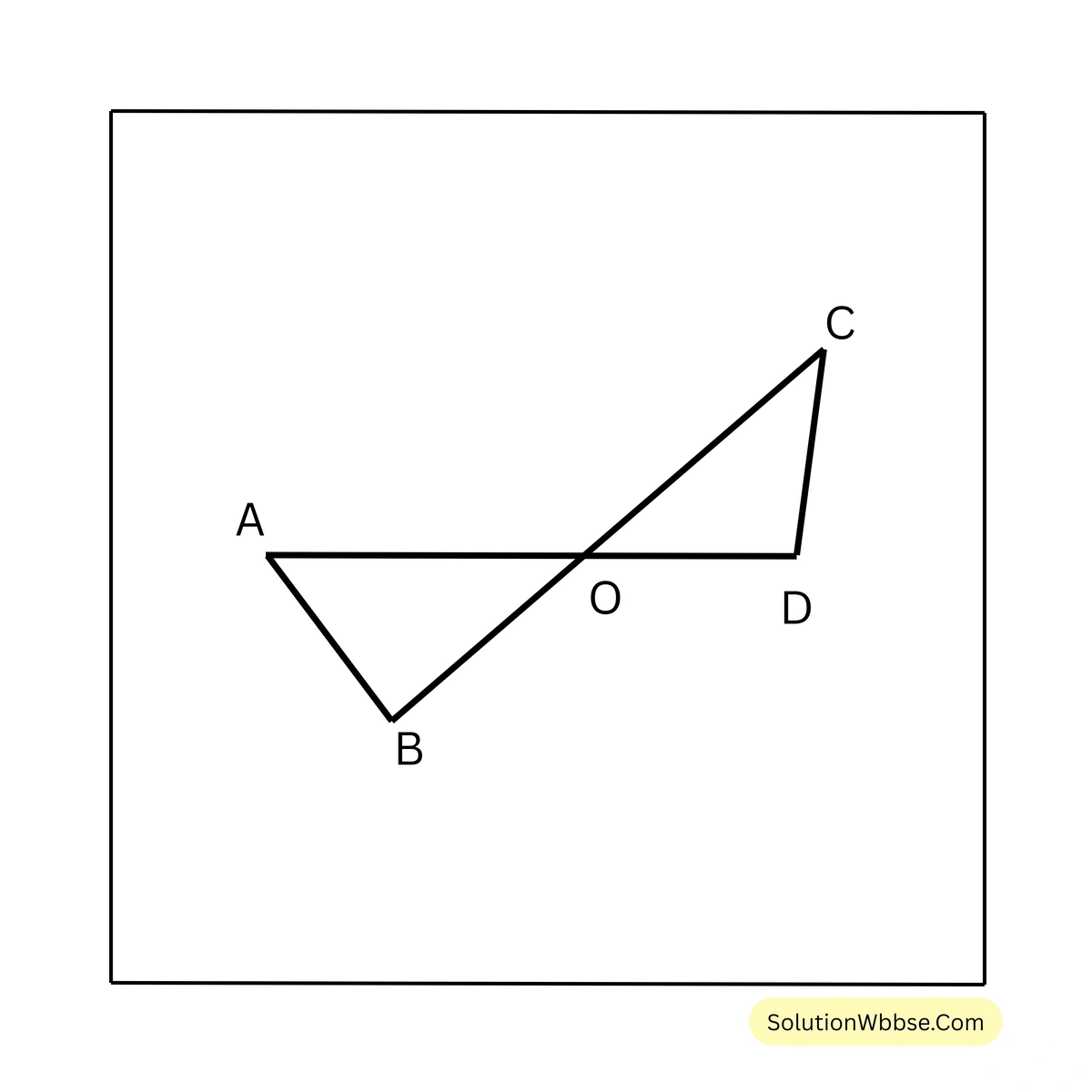
প্রমাণ – \(\triangle OCD\) এর \(\angle OCD > \angle COD\), \(\therefore OD > CD\) —-(1)
\(\triangle AOB\) এর \(\angle OAB < \angle AOB\), \(\therefore OB < AB\)
∵ \(AB = CD\), \(\therefore OB < CD\) ——- (2)
(1) নং ও (2) নং থেকে পাই,
\(OB < CD < OD\)\(\therefore OB < OD\) [প্রমাণিত]
10. প্রমাণ করি যে, সমকোণী ত্রিভুজের অতিভুজ বৃহত্তম বাহু।
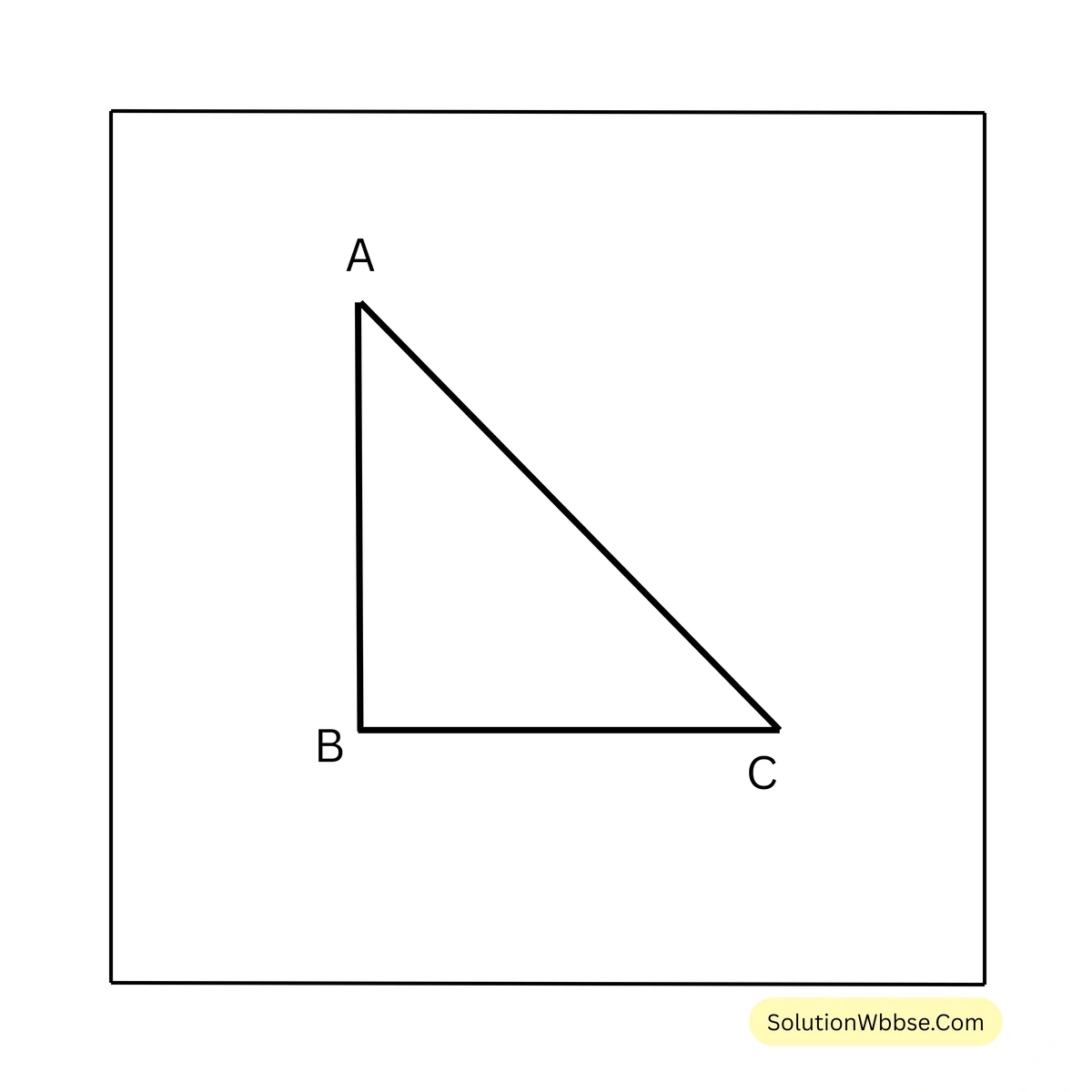
প্রদত্ত – ABC সমকোণী ত্রিভুজের \(\angle B\) সমকোণ এবং অতিভুজ \(AC\)।
প্রামাণ্য – অতিভুজ \(AC\) হল বৃহত্তম বাহু। অর্থাৎ \(AC > AB\) এবং \(AC > BC\)
প্রমাণ – ABC সমকোণী ত্রিভুজের
\(\angle B > \angle A\) [∵ সমকোণ > সুক্ষকোণ]
\(\therefore AC > BC\)আবার, \(\angle B > \angle C\) [∵ সমকোণ > সুক্ষকোণ]
\(\therefore AC > AB\)\(\therefore AC > AB\) এবং \(AC > BC\)
সুতরাং, অতিভুজ \(AC\) হল বৃহত্তম বাহু।
11. প্রমাণ করি যে, স্থূলকোণী ত্রিভুজের স্থূলকোণের বিপরীত বাহু বৃহত্তম।
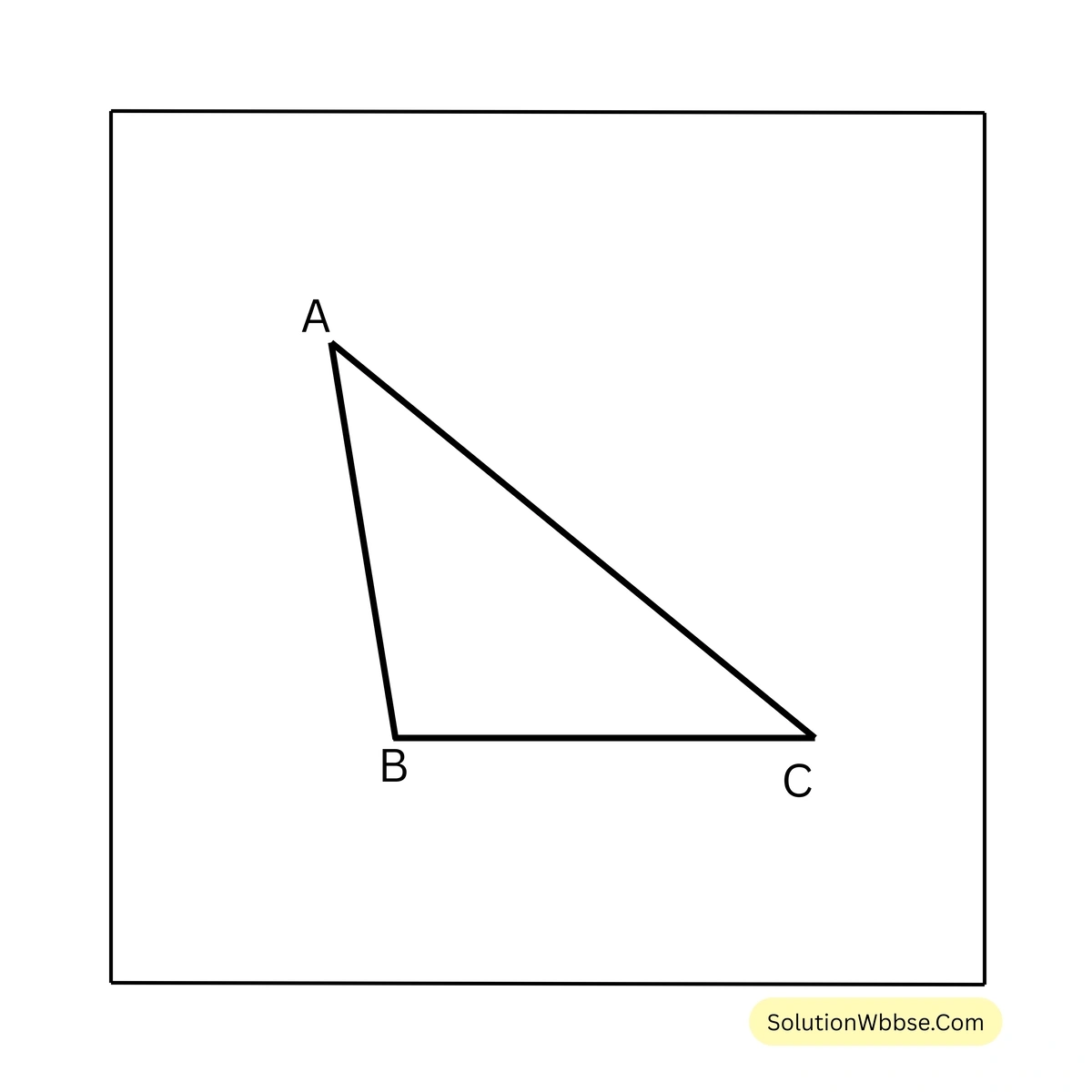
প্রদত্ত – ABC স্থূলকোণী ত্রিভুজের \(\angle B\) স্থূলকোণ। স্থূলকোণের বিপরীত বাহু \(AC\)।
প্রামাণ্য – \(AC\) হল বৃহত্তম বাহু। অর্থাৎ, \(AC > AB\) এবং \(AC > BC\)
প্রমাণ – ABC স্থূলকোণী ত্রিভুজের
\(\angle B > \angle A\) [∵ স্থূলকোণ > সুক্ষকোণ]
\(\therefore AC > AB\)আবার, \(\angle B > \angle C\) [∵ স্থূলকোণ > সুক্ষকোণ]
\(\therefore AC > BC\)\(\therefore AC > AB\) এবং \(AC > BC\)
সুতরাং, \(AC\) হল বৃহত্তম বাহু। [প্রমাণিত]
12. ABC ত্রিভুজের \(\angle ABC\) ও \(\angle ACB\) এর সমদ্বিখণ্ডকদ্বয় I বিন্দুতে মিলিত হয়। যদি \(AB > AC\) হয়, তবে প্রমাণ করি যে, \(IB > IC\)
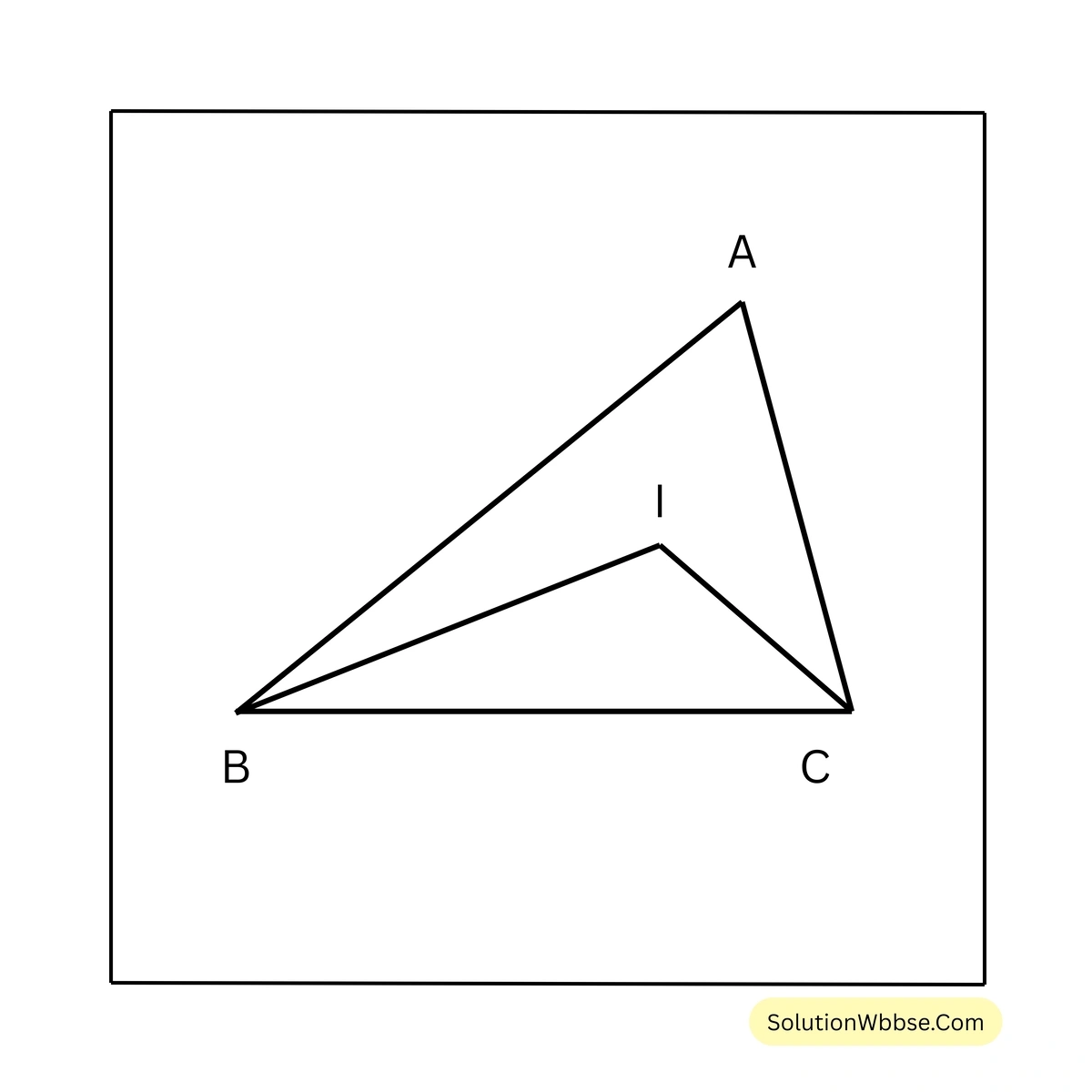
প্রদত্ত – ABC ত্রিভুজের \(\angle ABC\) ও \(\angle ACB\)-এর সমদ্বিখণ্ডকদ্বয় I বিন্দুতে মিলিত হয় এবং \(AB > AC\)
প্রামাণ্য – \(IB > IC\)
প্রমাণ – ABC ত্রিভুজের \(AB > AC\)
\(\therefore \angle ACB > \angle ABC\) —— (1)
\(BI\), \(\angle ABC\) এর সমদ্বিখণ্ডক, \(\therefore \angle ABC = 2 \angle IBC\)
\(CI\), \(\angle ACB\) এর সমদ্বিখণ্ডক, \(\therefore \angle ACB = 2 \angle ICB\)
(1) নং থেকে পাই,
\(2 \angle ICB > 2 \angle IBC\)বা, \(\angle ICB > \angle IBC\)
\(\therefore IB > IC\) [প্রমাণিত]
এই আর্টিকেলে অষ্টম শ্রেণির গণিতের ‘কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই’ অধ্যায়ের ‘কষে দেখি – 16.2’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরেছি। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে। কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করতে পারেন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন