পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) অষ্টম শ্রেণির গণিত পাঠ্যবইয়ের ষোড়শ অধ্যায় হলো ‘কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই’। এই পোস্টে আমরা ‘কষে দেখি – 16.1’-এর সমস্ত প্রশ্নের সহজ ও নির্ভুল সমাধান নিয়ে আলোচনা করেছি। আশা করি, এই নোটসগুলো তোমাদের গণিত শিখতে এবং পরীক্ষার প্রস্তুতিতে দারুণভাবে সহায়তা করবে।

1. নীচের প্রতিটি ক্ষেত্রে (x) এর মান লিখি
(i)
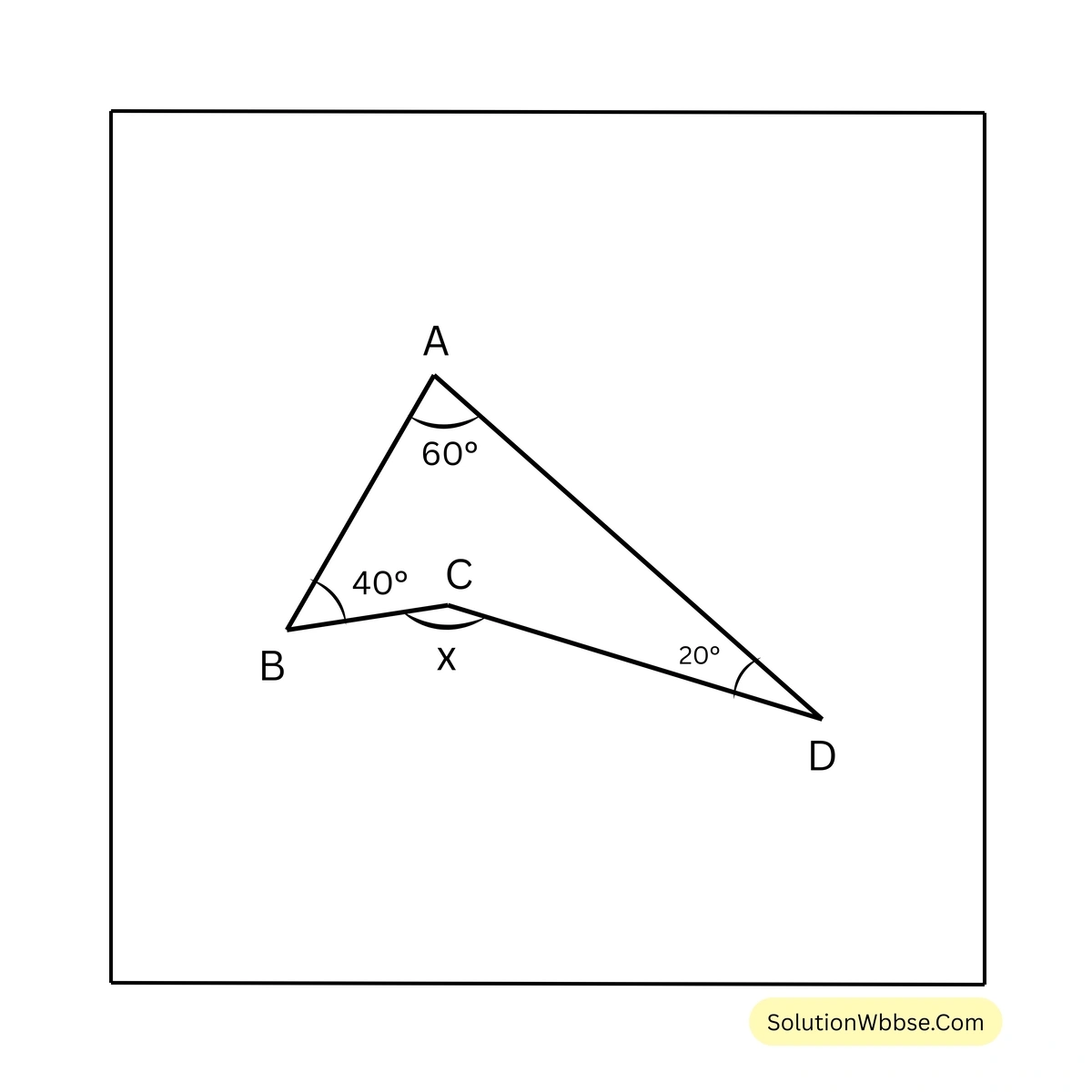
সমাধান –
DC বাহুকে বর্ধিত করা হল যা AB বাহুকে E বিন্দুতে ছেদ করেছে।
\(\triangle ADE\) এর বহিঃস্থ কোণ \(\angle BED\)
\(\therefore \angle BED = \angle DAE + \angle ADE = 60^\circ + 20^\circ = 80^\circ\)আবার, \(\triangle BCE\) এর বহিঃস্থ কোণ \(\angle BCD\)
\(\therefore \angle BCD = \angle CBE + \angle BEC\)\(= 40^\circ + 80^\circ\) [∵ \(\angle BED = 80^\circ\) ∴ \(\angle BEC = 80^\circ\)]
\(= 120^\circ\)\(\therefore x = 120^\circ\)(ii)
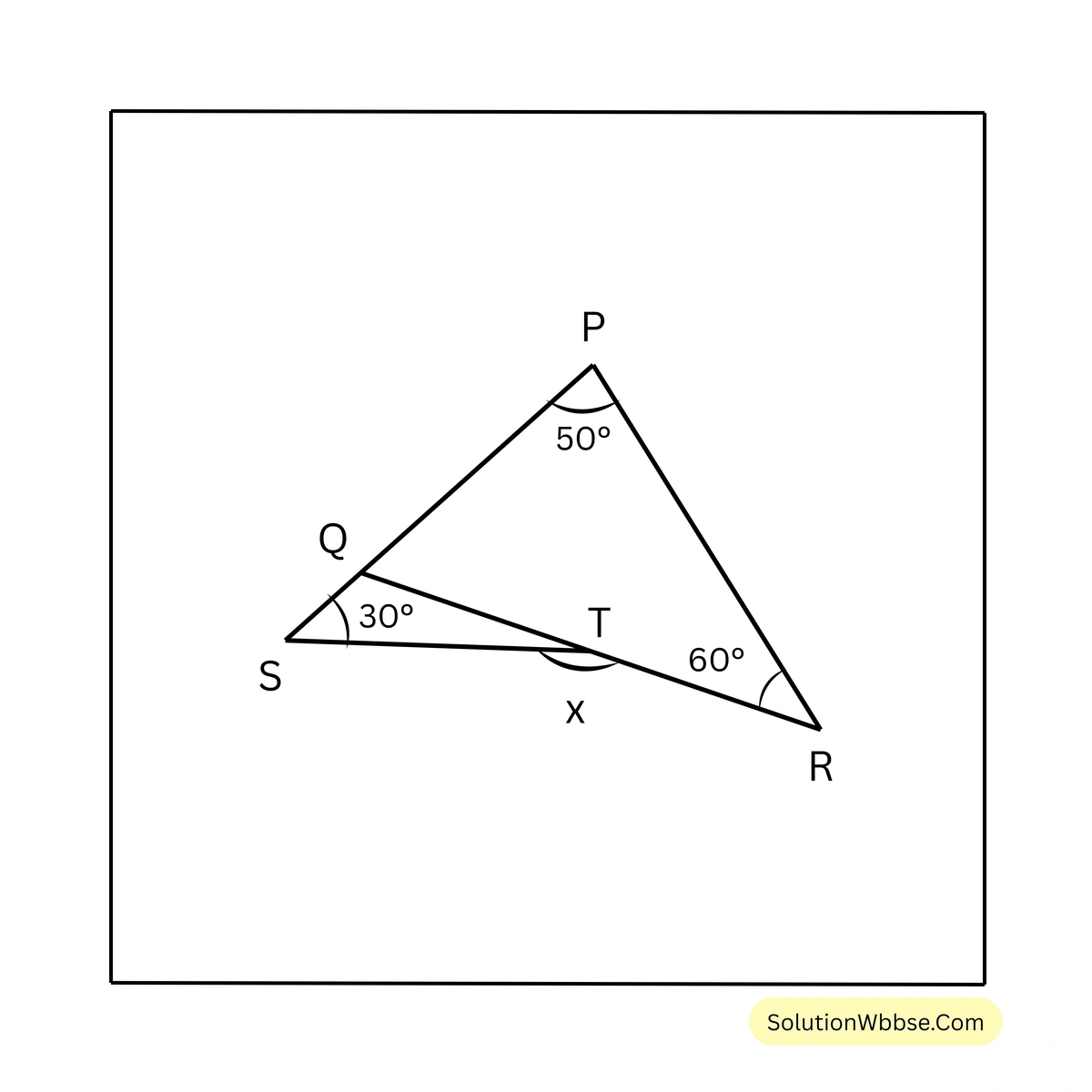
সমাধান –
\(\triangle PRQ\) এর বহিঃস্থ কোণ \(\angle RQS\)
আবার, \(\triangle SQT\) এর বহিঃস্থ কোণ \(\angle STR\)
\(\therefore \angle STR = \angle TSQ + \angle TQS\)\(= 30^\circ + 110^\circ\) [∵ \(\angle RQS = 110^\circ\) ∴ \(\angle TQS = 110^\circ\)]
\(= 140^\circ\)\(\therefore x = 140^\circ\)(iii)
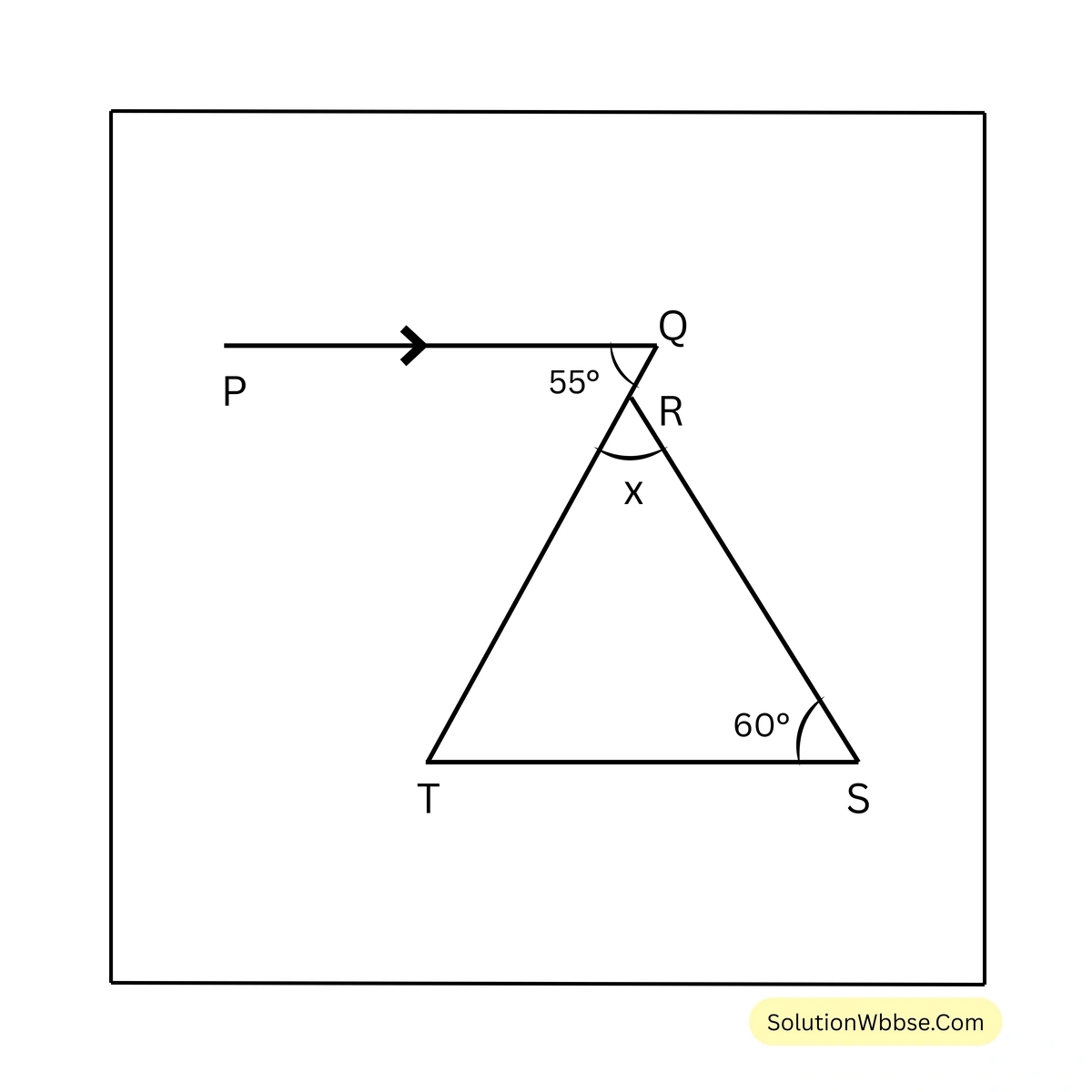
সমাধান –
এখানে \(PQ \parallel TS\) এবং \(TQ\) ছেদক।
\(\therefore \angle STQ =\) একান্তর \(\angle PQT = 55^\circ\)
\(\triangle SRT\) এর \(\angle STR = 55^\circ\) এবং \(\angle RST = 60^\circ\)
\(\therefore \angle SRT = 180^\circ – \angle STR – \angle RST = 180^\circ – 55^\circ – 60^\circ = 65^\circ\)2. পাশের চিত্রে \(\triangle EHG\) এর কোণগুলির পরিমাপ লিখি।
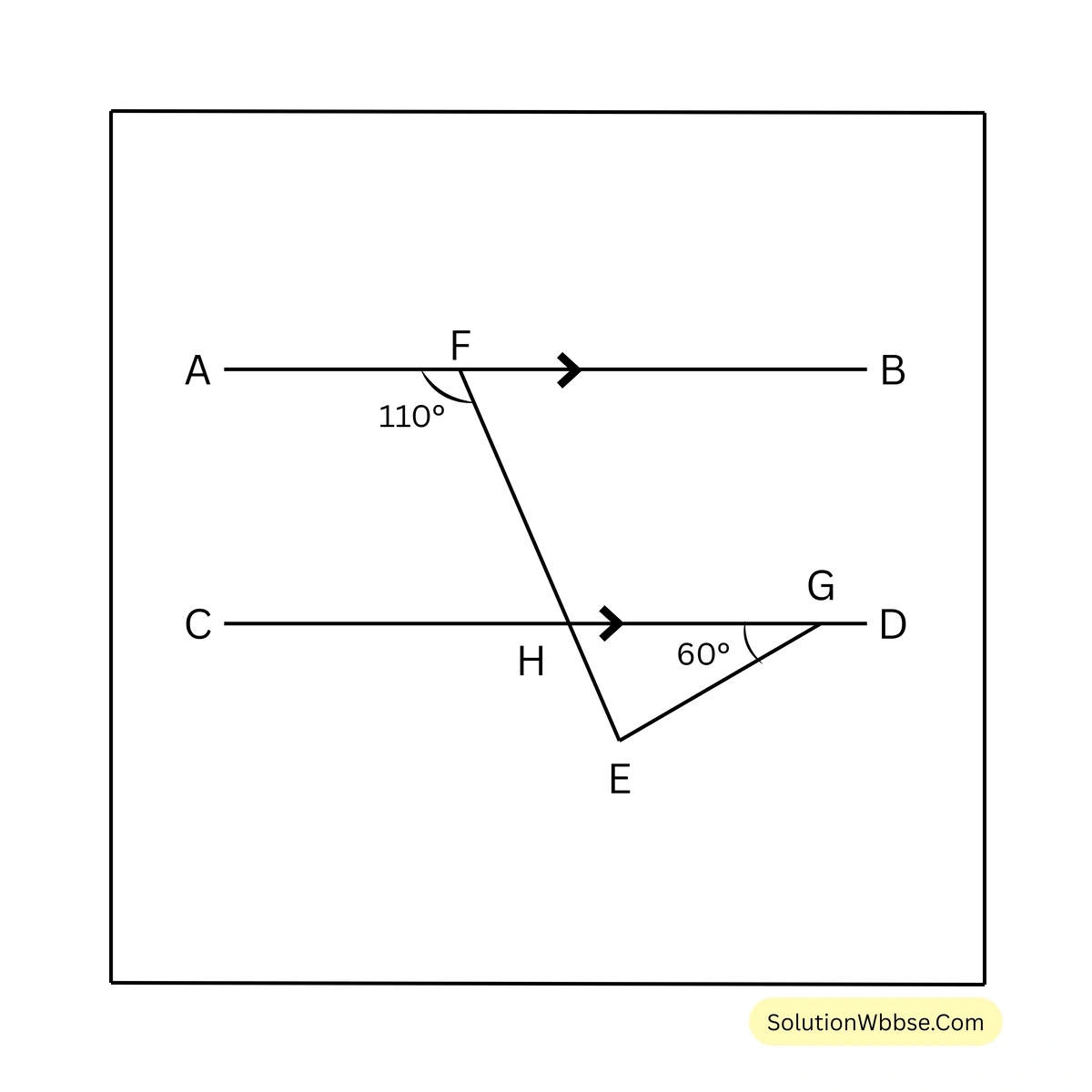
সমাধান –
\(AB \parallel CD\) এবং \(FE\) ছেদক।
\(\therefore \angle CHE =\) অনুরূপ \(\angle AFH = 110^\circ\)
\(\angle EHG = 180^\circ – \angle CHE = 180^\circ – 110^\circ = 70^\circ\)\(\triangle EHG\) এর \(\angle EHG = 70^\circ\) এবং \(\angle EGH = 60^\circ\)
\(\therefore \triangle EHG\) এর \(\angle EHG = 70^\circ\), \(\angle EGH = 60^\circ\) ও \(\angle GEH = 50^\circ\)
3. পাশের চিত্রে \(\angle A + \angle B + \angle C + \angle D + \angle E + \angle F\) এর পরিমাপ লিখি।
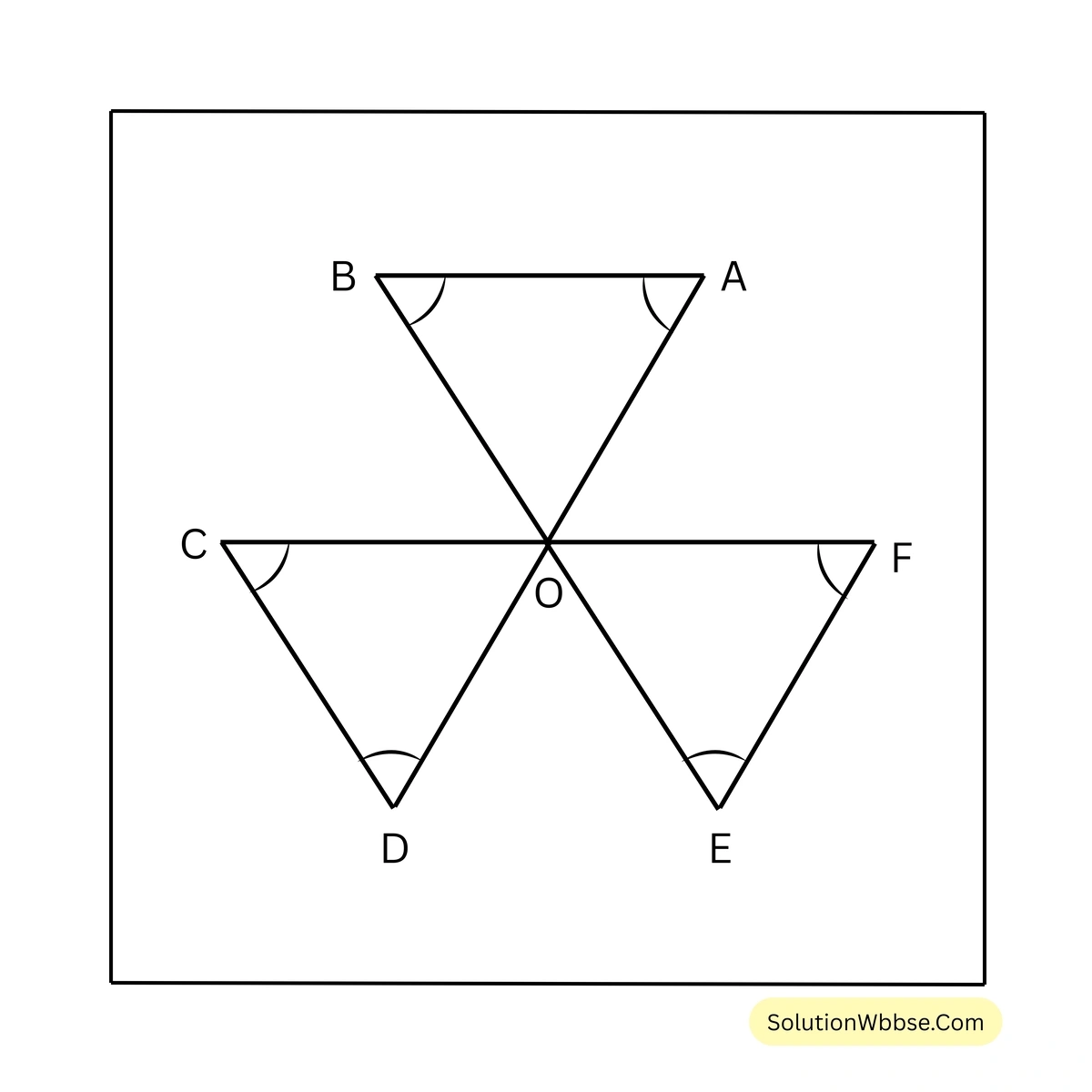
সমাধান –
\(\triangle AOB\) থেকে পাই, \(\angle A + \angle B + \angle AOB = 180^\circ\) —-(i)
\(\triangle COD\) থেকে পাই, \(\angle C + \angle D + \angle COD = 180^\circ\) —–(ii)
\(\triangle EOF\) থেকে পাই, \(\angle E + \angle F + \angle EOF = 180^\circ\) —–(iii)
\(\angle DOE =\) বিপ্রতীপ \(\angle AOB\)
\(\angle AOF =\) বিপ্রতীপ \(\angle COD\)
\(\angle BOC =\) বিপ্রতীপ \(\angle EOF\)
O বিন্দুতে অবস্থিত সব কোণগুলির সমষ্টি \(360^\circ\)
\(\therefore \angle AOB + \angle BOC + \angle COD + \angle DOE + \angle EOF + \angle AOF = 360^\circ\)বা, \(\angle AOB + \angle EOF + \angle COD + \angle AOB + \angle EOF + \angle COD = 360^\circ\)
বা, \(2(\angle AOB + \angle COD + \angle EOF) = 360^\circ\)
বা, \(\angle AOB + \angle COD + \angle EOF = 180^\circ\)
বা, \(180^\circ – \angle A – \angle B + 180^\circ – \angle C – \angle D + 180^\circ – \angle E – \angle F = 180^\circ\) [(i) নং, (ii) নং ও (iii) নং থেকে পাই]
বা, \(540^\circ – \angle A – \angle B – \angle C – \angle D – \angle E – \angle F = 180^\circ\)
বা, \(-\angle A – \angle B – \angle C – \angle D – \angle E – \angle F = 180^\circ – 540^\circ\)
বা, \(-(\angle A + \angle B + \angle C + \angle D + \angle E + \angle F) = -360^\circ\)
\(\therefore \angle A + \angle B + \angle C + \angle D + \angle E + \angle F = 360^\circ\)4. \(AB = AC\) হলে \(\angle ABC\), \(\angle ACB\) ও \(\angle BAC\) এর পরিমাপ লিখি।
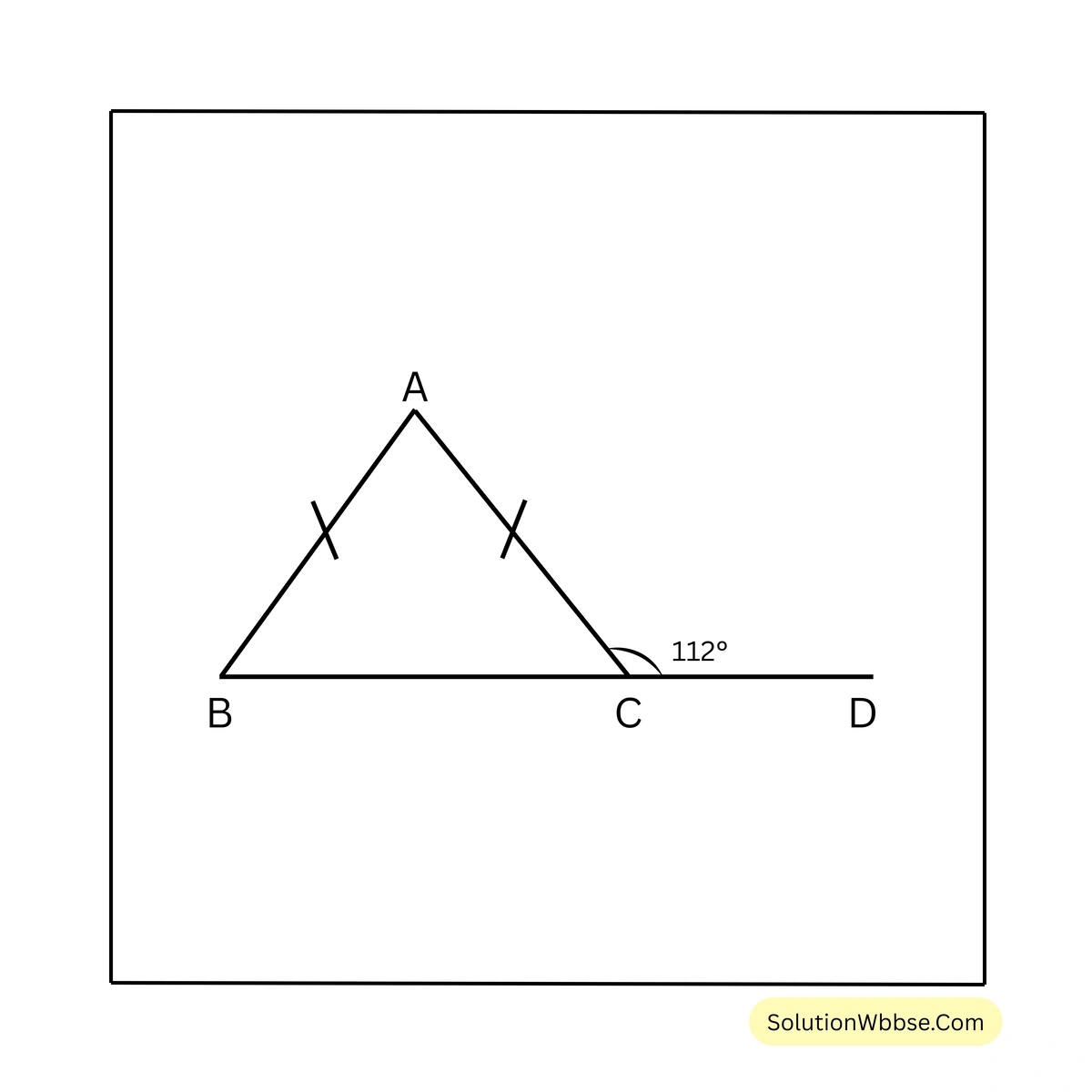
সমাধান –
\(\angle ACD = 112^\circ\)BD সরলরেখার উপর CA দণ্ডায়মান।
\(\therefore \angle ACB = 180^\circ – \angle ACD = 180^\circ – 112^\circ = 68^\circ\)\(\triangle ABC\) এর \(AB = AC\) ∴ \(\angle ABC = \angle ACB = 68^\circ\)
\(\triangle ABC\) এর বহিঃস্থ কোণ \(\angle ACD = \angle ABC + \angle BAC\)
\(\therefore \angle BAC = \angle ACD – \angle ABC = 112^\circ – 68^\circ = 44^\circ\)\(\therefore \angle ABC = \angle ACB = 68^\circ\) এবং \(\angle BAC = 44^\circ\)
5. \(AB = AC\) হলে \(\angle ABC\) ও \(\angle ACB\) এর পরিমাপ লিখি।
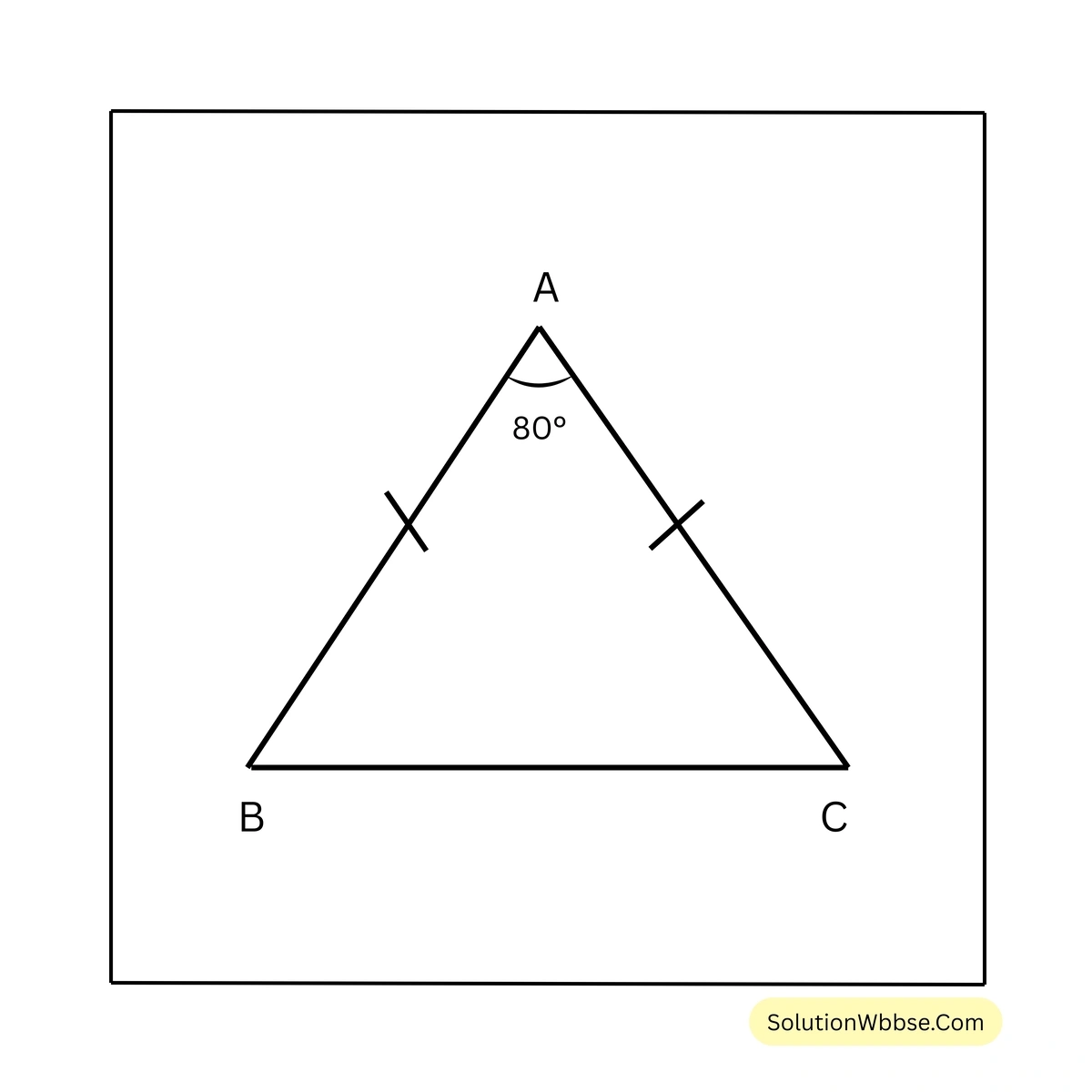
সমাধান –
\(\triangle ABC\) এর \(AB = AC\), ∴ \(\angle ABC = \angle ACB\)
\(\triangle ABC\) থেকে পাই,
\(\angle ABC + \angle ACB + \angle BAC = 180^\circ\)বা, \(\angle ABC + \angle ABC + 80^\circ = 180^\circ\)
বা, \(2\angle ABC = 180^\circ – 80^\circ\)
বা, \(2\angle ABC = 100^\circ\)
বা, \(\angle ABC = \frac{100^\circ}{2}\)
\(\therefore \angle ABC = 50^\circ\)\(\therefore \angle ABC = \angle ACB = 50^\circ\)6. \(AB = AC\) হলে \(\angle ACB\) ও \(\angle BAC\) এর পরিমাপ লিখি।
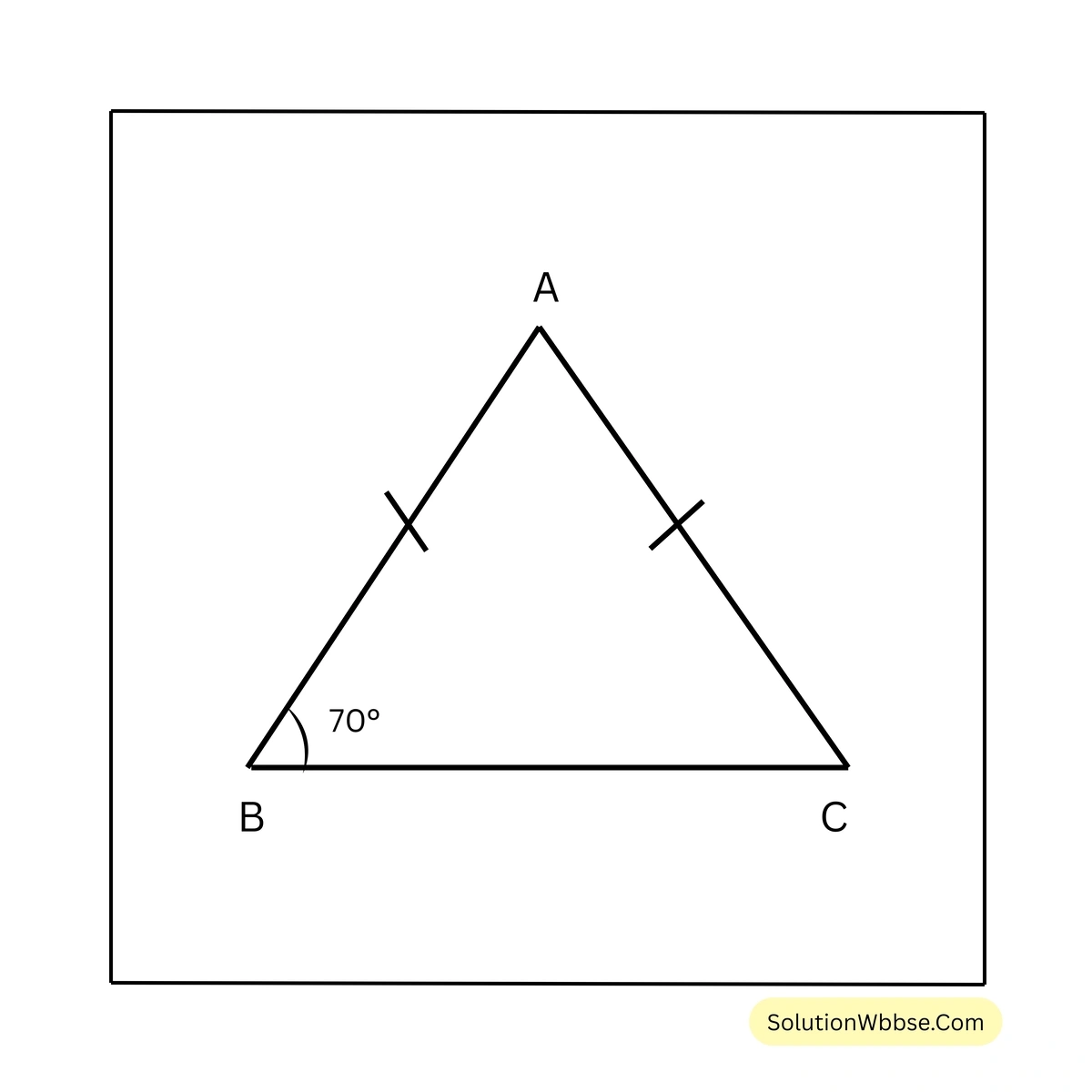
সমাধান –
\(\angle ABC = 70^\circ\)\(\triangle ABC\) এর \(AB = AC\)
∴ \(\angle ABC = \angle ACB = 70^\circ\)
\(\triangle ABC\) থেকে পাই,
\(\angle ABC + \angle ACB + \angle BAC = 180^\circ\)বা, \(70^\circ + 70^\circ + \angle BAC = 180^\circ\)
বা, \(\angle BAC = 180^\circ – 70^\circ – 70^\circ\)
\(\therefore \angle BAC = 40^\circ\)\(\therefore \angle ACB = 70^\circ\) এবং \(\angle BAC = 40^\circ\)
7. \(AB = BC\) এবং \(\angle BAC + \angle ACB = 50^\circ\); \(\triangle ABC\) এর কোণগুলির পরিমাপ লিখি।
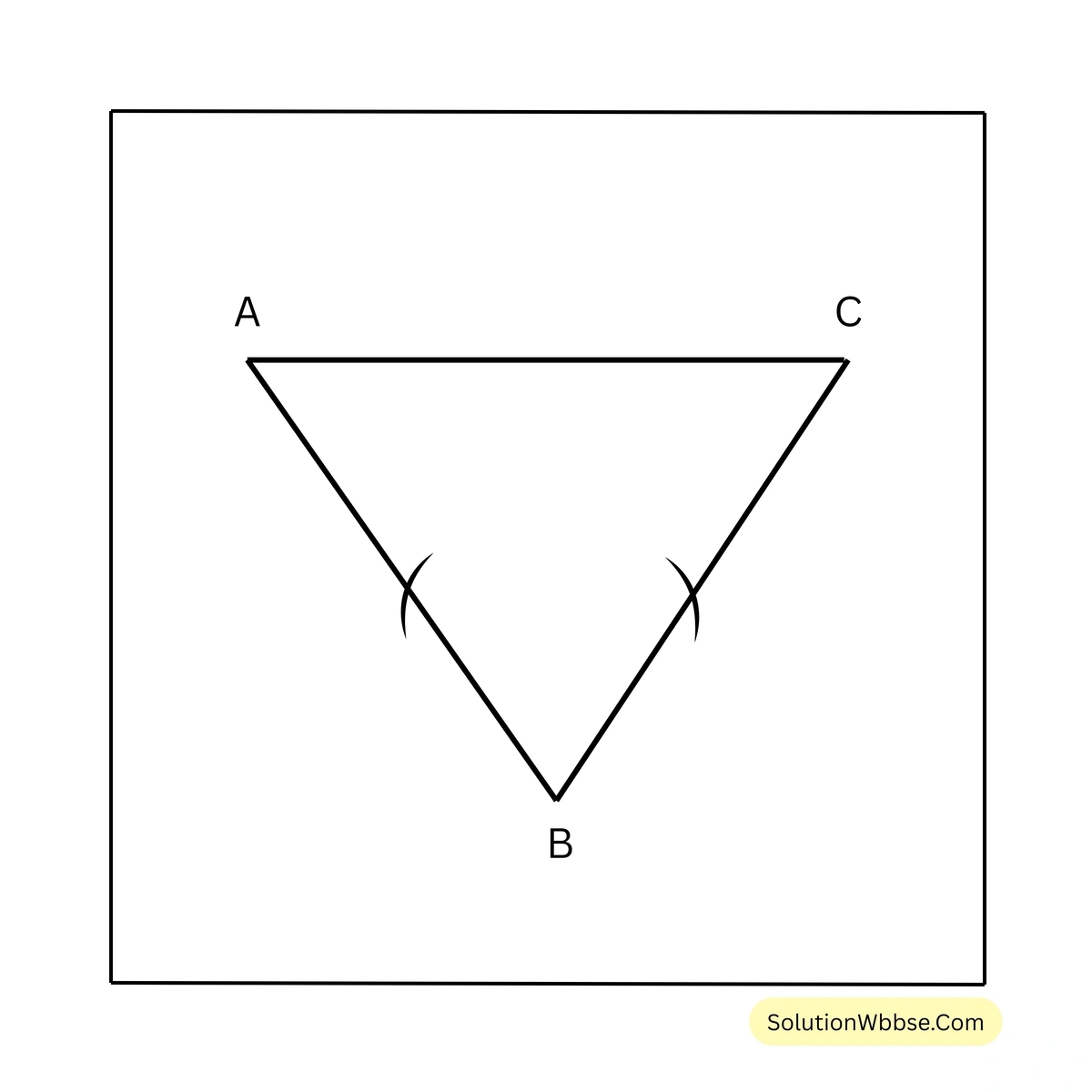
সমাধান –
\(\triangle ABC\) এর \(AB = BC\)
∴ \(\angle BAC = \angle ACB\)
\(\angle BAC + \angle ACB = 50^\circ\) [প্রদত্ত]
বা, \(\angle BAC + \angle BAC = 50^\circ\)
বা, \(2\angle BAC = 50^\circ\)
\(\triangle ABC\) থেকে পাই,
\(\angle ABC + \angle ACB + \angle BAC = 180^\circ\)বা, \(\angle ABC + 50^\circ = 180^\circ\) [∵ \(\angle BAC + \angle ACB = 50^\circ\)]
বা, \(\angle ABC = 180^\circ – 50^\circ\)
\(\therefore \angle ABC = 130^\circ\)সুতরাং, \(\angle BAC = \angle ACB = 25^\circ\) এবং \(\angle ABC = 130^\circ\)
8. \(\triangle ABC\) এর অন্তঃস্থ একটি বিন্দু O; প্রমাণ করি যে \(\angle BOC > \angle BAC\)
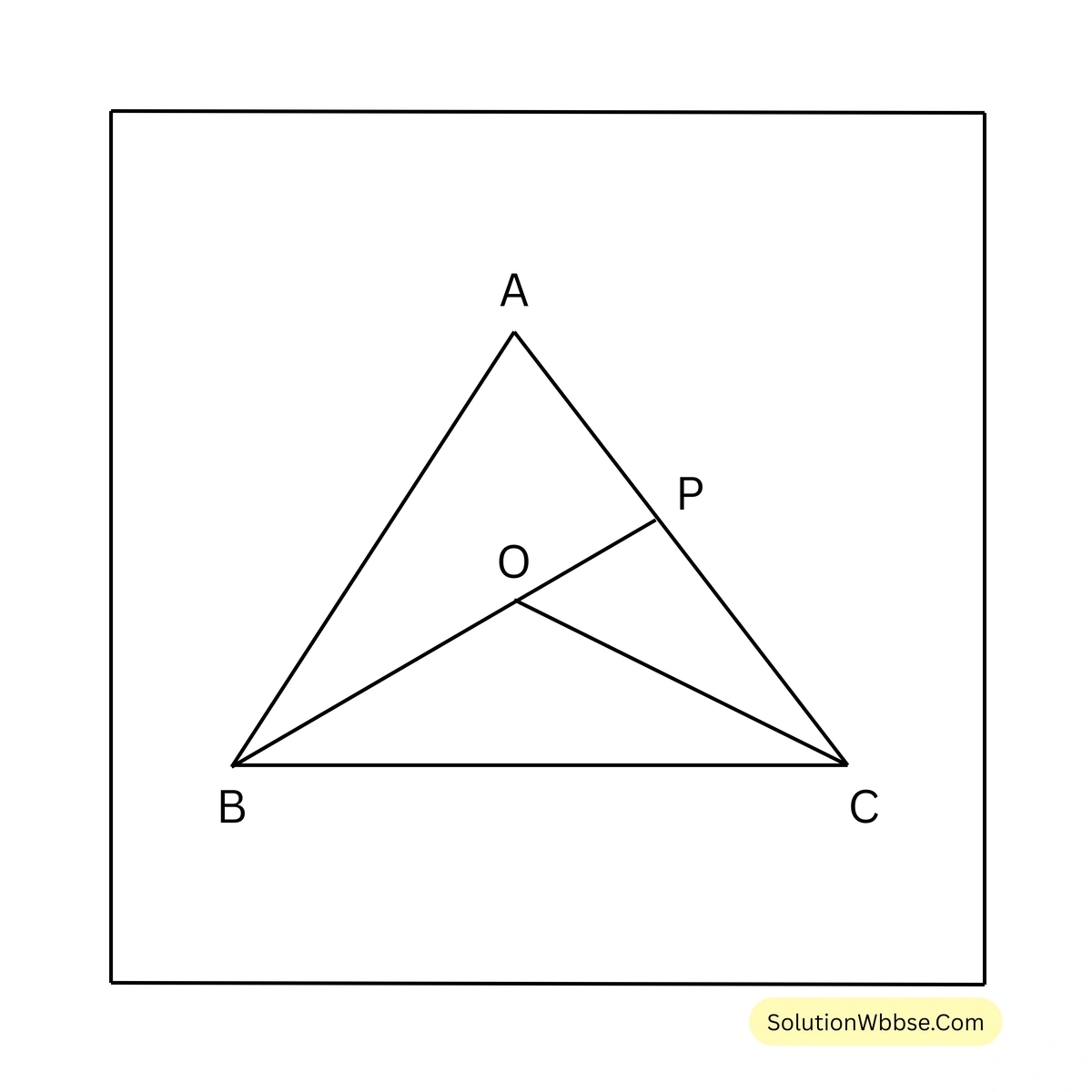
প্রদত্ত – \(\triangle ABC\) এর অন্তঃস্থ একটি বিন্দু O
প্রামাণ্য – \(\angle BOC > \angle BAC\)
অঙ্কন – BO কে বর্ধিত করা হল যা AC বাহুকে P বিন্দুতে ছেদ করেছে।
প্রমাণ – \(\triangle POC\) এর বহিঃস্থ কোণ \(\angle BOC = \angle OPC + \angle OCP\)
\(\therefore \angle BOC > \angle OPC\) —-(i)
আবার, \(\triangle ABP\) এর বহিঃস্থ কোণ \(\angle BPC = \angle ABP + \angle BAP\)
\(\therefore \angle BPC > \angle BAP\)বা, \(\angle OPC > \angle BAC\) —-(ii)
(i) নং ও (ii) নং থেকে পাই,
\(\angle BOC > \angle BAC\) [প্রমাণিত]
9. প্রমাণ করি যে, \(\triangle ABC\) এর BC বাহুকে উভয়দিকে বাড়ালে যে দুটি বহিঃকোণ উৎপন্ন হয় তাদের সমষ্টি 2 সমকোণের বেশি।
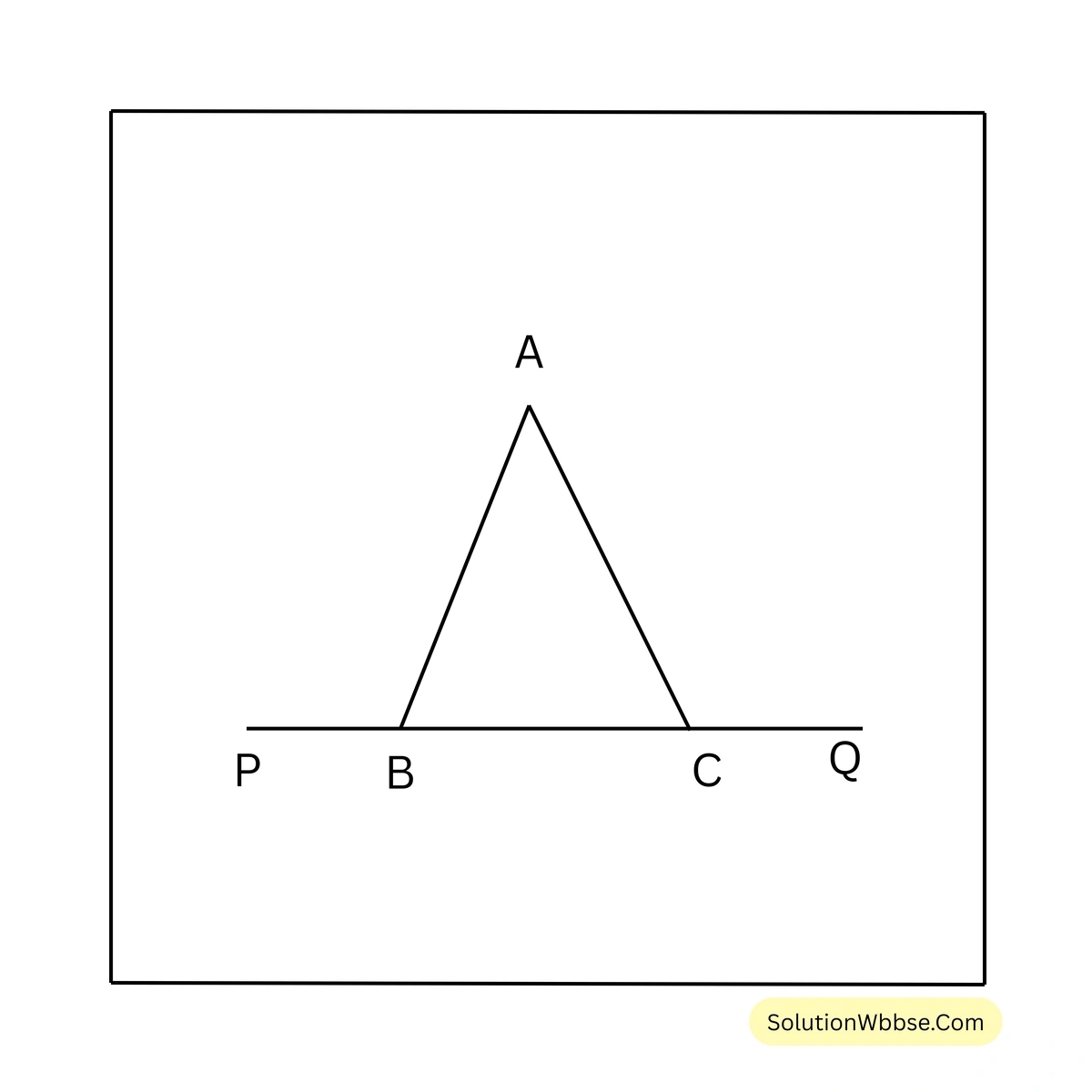
\(\triangle ABC\) এর BC বাহুকে উভয়দিকে বাড়ানোর ফলে দুটি বহিঃকোণ \(\angle ABP\) এবং \(\angle ACQ\) উৎপন্ন হল।
প্রামাণ্য – \(\angle ABP + \angle ACQ > 180^\circ\)
প্রমাণ – \(\triangle ABC\) এর বহিঃস্থ কোণ \(\angle ABP = \angle ACB + \angle BAC\) —– (1)
\(\triangle ABC\) এর বহিঃস্থ কোণ \(\angle ACQ = \angle ABC + \angle BAC\) —— (2)
(1)+(2) করে পাই,
\(\angle ABP + \angle ACQ = \angle ACB + \angle BAC + \angle ABC + \angle BAC\)বা, \(\angle ABP + \angle ACQ = 180^\circ + \angle BAC\)
[∵ ত্রিভুজের তিনটি কোণের সমষ্টি \(180^\circ\), ∴ \(\angle ACB + \angle BAC + \angle ABC = 180^\circ\)]
\(\therefore \angle ABP + \angle ACQ > 180^\circ\) [প্রমাণিত]
10. \(\triangle ABC\) এর কৌণিক বিন্দু A ও C দিয়ে যথাক্রমে BC ও BA বাহুর সমান্তরাল সরলরেখাংশ D বিন্দুতে মিলিত হয়। প্রমাণ করি যে, \(\angle ABC = \angle ADC\)
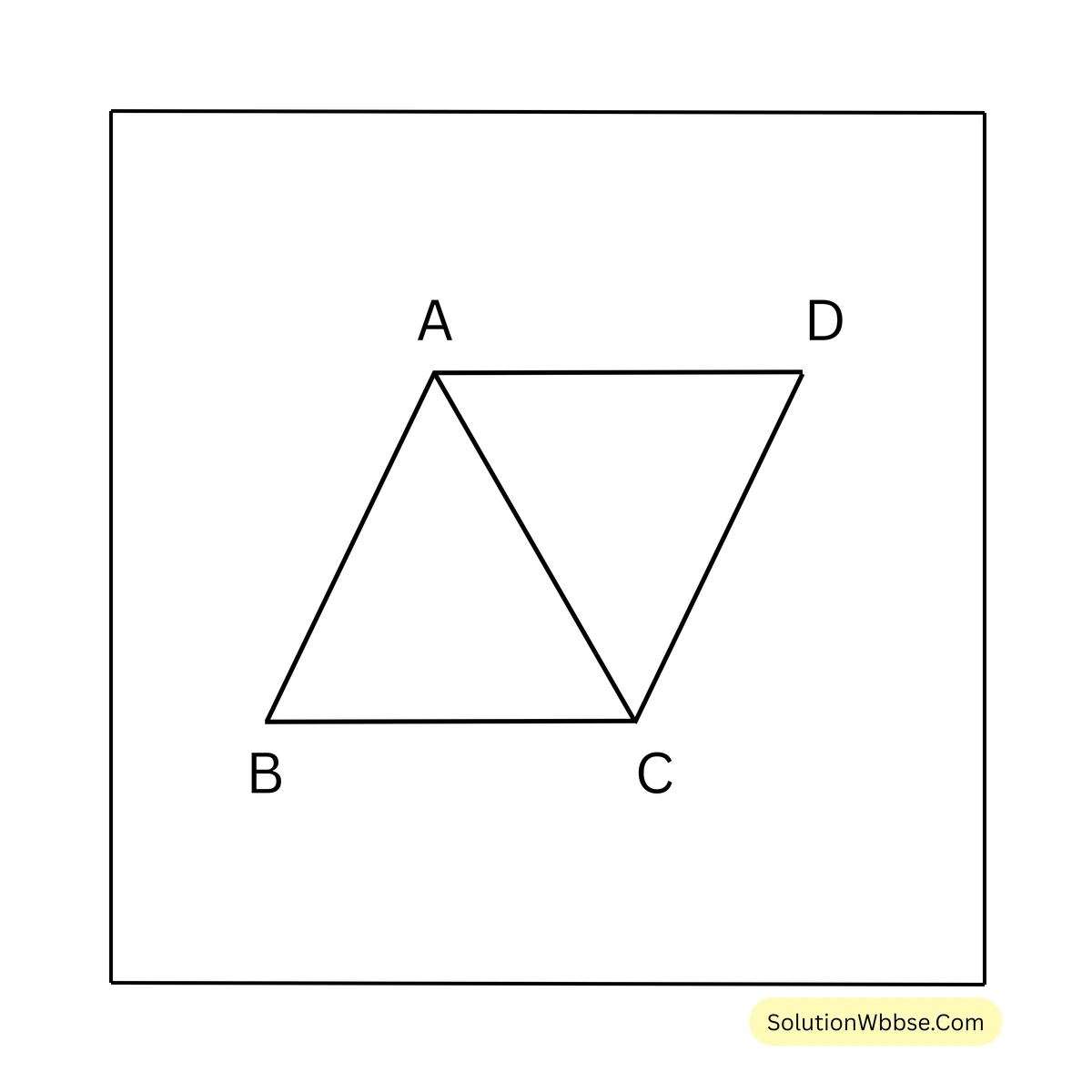
প্রদত্ত – \(\triangle ABC\) এর কৌণিক বিন্দু A ও C দিয়ে যথাক্রমে BC ও BA বাহুর সমান্তরাল সরলরেখাংশ D বিন্দুতে মিলিত হয়। অর্থাৎ, \(AD \parallel BC\) এবং \(CD \parallel BA\)
প্রামাণ্য – \(\angle ABC = \angle ADC\)
প্রমাণ – \(\triangle ABC\) থেকে পাই,
\(\angle ABC + \angle ACB + \angle BAC = 180^\circ\) —- (1)
\(\triangle ADC\) থেকে পাই,
\(\angle ADC + \angle ACD + \angle CAD = 180^\circ\) ——-(2)
\(AD \parallel BC\) এবং \(AC\) ছেদক
\(\therefore \angle BCA = \angle CAD\) [একান্তর কোণ]—–(3)
\(DC \parallel BA\) এবং \(AC\) ছেদক
\(\therefore \angle BAC = \angle ACD\) [একান্তর কোণ]—– (4)
(3) নং ও (4) নং যোগ করে পাই,
\(\angle BCA + \angle BAC = \angle ACD + \angle CAD\)বা, \(180^\circ – \angle ABC = 180^\circ – \angle ADC\) [(1) নং ও (2) নং থেকে পাই]
\(\therefore \angle ABC = \angle ACD\) [প্রমানিত]
11. \(\triangle ABC\) এর \(\angle ABC\) ও \(\angle ACB\) এর অন্তঃসমদ্বিখণ্ডকদ্বয় O বিন্দুতে মিলিত হয়। প্রমাণ করি যে, \(\angle BOC = 90^\circ + \frac{1}{2} \angle BAC\)
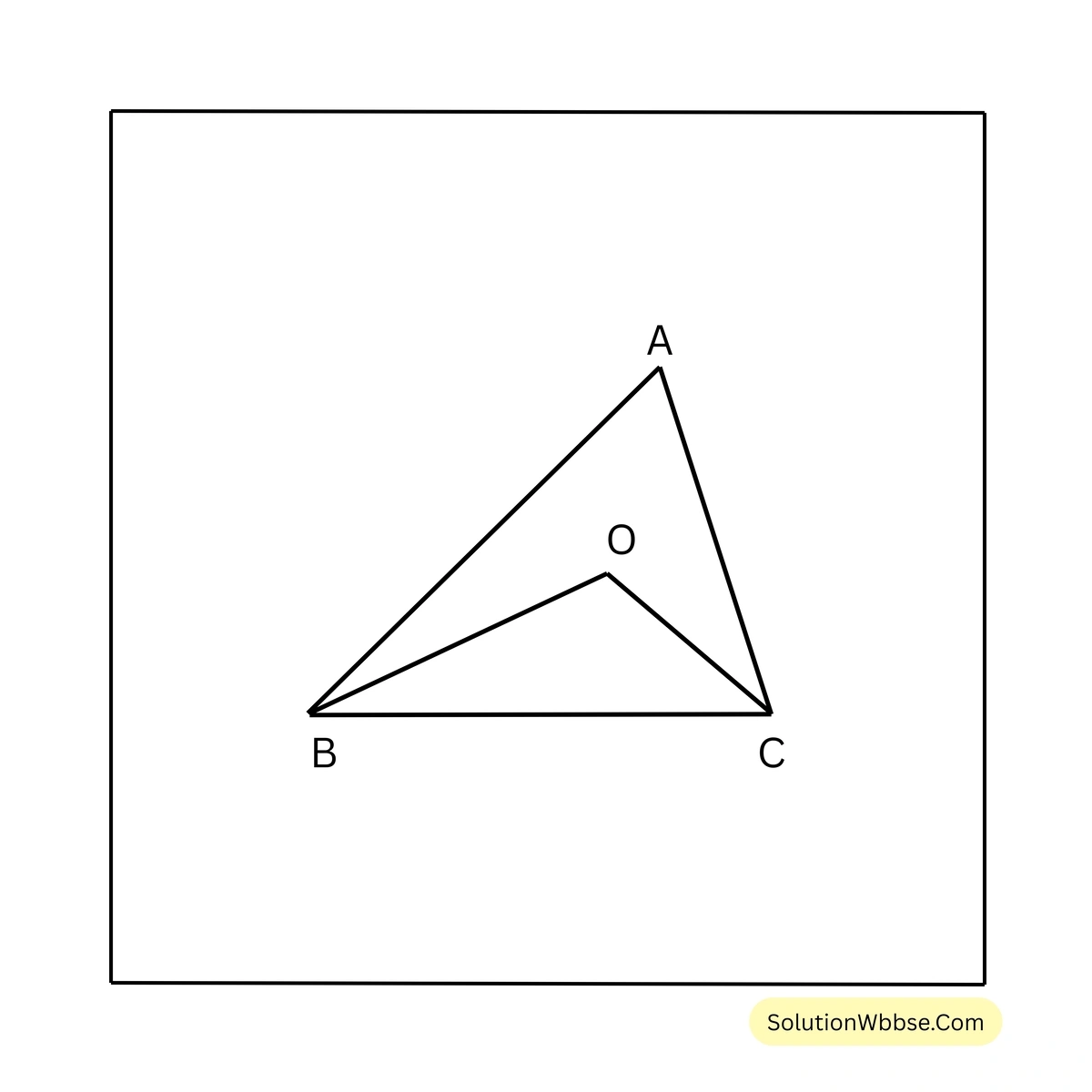
প্রদত্ত – \(\triangle ABC\) এর \(\angle ABC\) ও \(\angle ACB\) এর অন্তঃসমদ্বিখণ্ডকদ্বয় O বিন্দুতে মিলিত হয়।
প্রামাণ্য – \(\angle BOC = 90^\circ + \frac{1}{2} \angle BAC\)
প্রমাণ – \(\triangle ABC\) এর অন্তঃসমদ্বিখণ্ডক \(BO\)
\(\therefore \angle OBC = \frac{1}{2} \angle ABC\) ——- (1)
\(\triangle ACB\) এর অন্তঃসমদ্বিখণ্ডক \(CO\)
\(\therefore \angle OCB = \frac{1}{2} \angle ACB\) —–(2)
\(\triangle ABC\) থেকে পাই,
\(\angle ABC + \angle ACB + \angle BAC = 180^\circ\) ——-(3)
\(\triangle OBC\) থেকে পাই,
\(\angle OBC + \angle OCB + \angle BOC = 180^\circ\) ——(4)
বা, \(\frac{1}{2} \angle ABC + \frac{1}{2} \angle ACB + \angle BOC = 180^\circ\)
বা, \(\frac{1}{2} (\angle ABC + \angle ACB) + \angle BOC = 180^\circ\)
বা, \(\frac{1}{2} (180^\circ – \angle BAC) + \angle BOC = 180^\circ\)
বা, \(90^\circ – \frac{1}{2} \angle BAC + \angle BOC = 180^\circ\)
বা, \(\angle BOC = 180^\circ – 90^\circ + \frac{1}{2} \angle BAC\)
\(\therefore \angle BOC = 90^\circ + \frac{1}{2} \angle BAC\) [প্রমানিত]
12. \(\triangle ABC\) এর \(\angle ABC\) ও \(\angle ACB\) বহিঃসমদ্বিখণ্ডকদ্বয় O বিন্দুতে মিলিত হয়। প্রমাণ করি যে, \(\angle BOC = 90^\circ – \frac{1}{2} \angle BAC\)
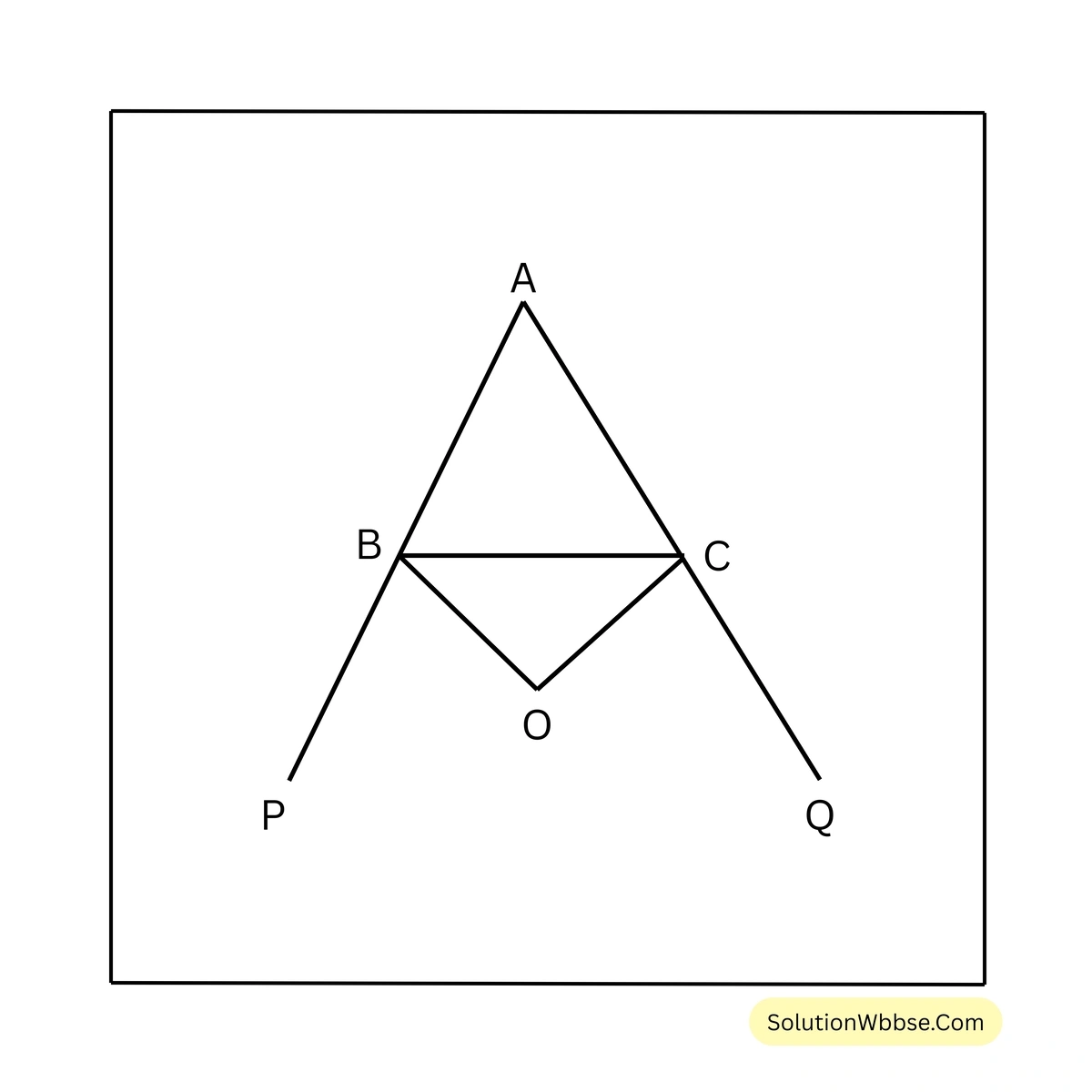
প্রদত্ত – \(\triangle ABC\) এর \(\angle ABC\) ও \(\angle ACB\) বহিঃসমদ্বিখণ্ডকদ্বয় O বিন্দুতে মিলিত হয়।
প্রামাণ্য – \(\angle BOC = 90^\circ – \frac{1}{2} \angle BAC\)
প্রমাণ – \(\triangle ABC\) থেকে পাই,
\(\angle ABC + \angle BCA + \angle BAC = 180^\circ\)——(1)
\(\angle ABC\) এর বহিঃসমদ্বিখণ্ডক \(BO\)
\(\therefore \angle OBC = \frac{1}{2} \angle CBP\) ——-(2)
\(\angle ACB\) এর বহিঃসমদ্বিখণ্ডক \(CO\)
\(\therefore \angle OCB = \frac{1}{2} \angle BCQ\) ——-(3)
\(\triangle ABC\) এর বহিঃকোণ \(\angle CBP = \angle BAC + \angle BCA\) ——(4)
\(\triangle ABC\) এর বহিঃকোণ \(\angle BCQ = \angle ABC + \angle BAC\) —–(5)
\(\triangle OBC\) থেকে পাই,
\(\angle OBC + \angle OCB + \angle BOC = 180^\circ\)বা, \(\frac{1}{2} \angle CBP + \frac{1}{2} \angle BCQ + \angle BOC = 180^\circ\) [(2) নং ও (3) নং থেকে পাই]
বা, \(\frac{1}{2} (\angle CBP + \angle BCQ) + \angle BOC = 180^\circ\)
বা, \(\frac{1}{2} (\angle BAC + \angle BCA + \angle ABC + \angle BAC) + \angle BOC = 180^\circ\) [(4) নং ও (5) নং থেকে পাই]
বা, \(\frac{1}{2} (180^\circ + \angle BAC) + \angle BOC = 180^\circ\) [∵ত্রিভুজের তিনটি কোণের সমষ্টি \(180^\circ\)]
বা, \(90^\circ + \frac{1}{2} \angle BAC + \angle BOC = 180^\circ\)
\(\therefore \angle BOC = 90^\circ – \frac{1}{2} \angle BAC\) [প্রমানিত]
13. \(\triangle ABC\) এর \(\angle ACB\) এর বহিঃসমদ্বিখণ্ডক A বিন্দু দিয়ে BC বাহুর সমান্তরাল সরলরেখাকে D বিন্দুতে ছেদ করে। প্রমান করি যে, \(\angle ADC = 90^\circ – \frac{1}{2} \angle ACB\)
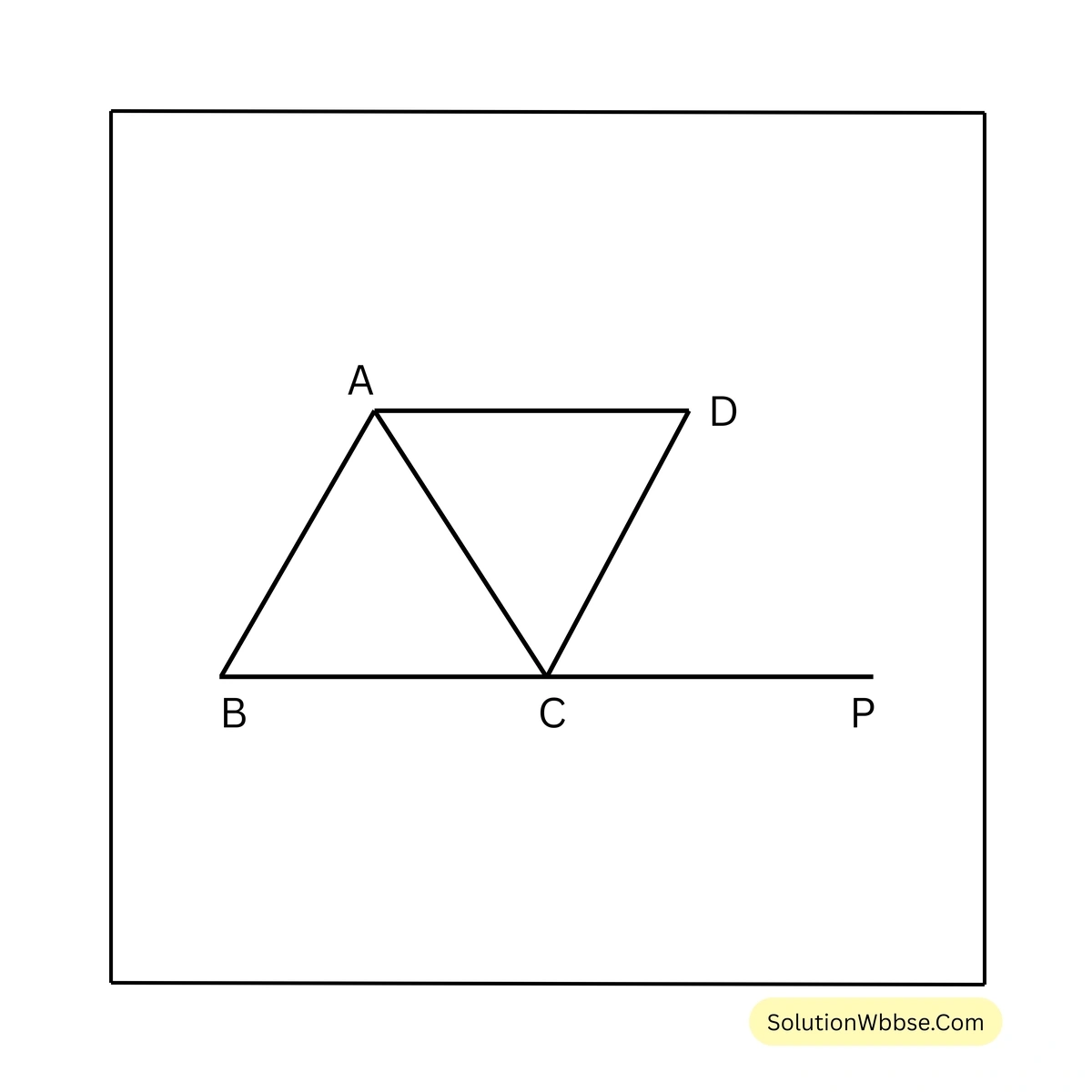
প্রদত্ত – \(\triangle ABC\) এর \(\angle ACB\) এর বহিঃকোণ \(\angle ACP\), \(\angle ACP\) এর সমদ্বিখণ্ডক \(CD\) এবং \(AD \parallel BC\)
প্রামাণ্য – \(\angle ADC = 90^\circ – \frac{1}{2} \angle ACB\)
প্রমাণ – BP সরলরেখার উপর \(CA\) লম্ব
\(\therefore \angle ACP + \angle ACB = 180^\circ\)বা, \(\angle ACP = 180^\circ – \angle ACB\) ——(1)
\(\angle ACP\) এর সমদ্বিখণ্ডক \(CD\) \(\therefore \angle DCP = \frac{1}{2} \angle ACP\) —-(2)
\(AD \parallel BC\) এবং \(CD\) ছেদক
\(\therefore \angle DCP =\) একান্তর \(\angle ADC\) —–(3)
(1)নং ও (2) নং থেকে পাই,
\(\angle DCP = \frac{1}{2} (180^\circ – \angle ACB)\) ——(4)
(3)নং ও (4) নং থেকে পাই,
\(\angle ADC = \frac{1}{2} (180^\circ – \angle ACB)\)\(\therefore \angle ADC = 90^\circ – \frac{1}{2} \angle ACB\) [প্রমানিত]
14. প্রমাণ করি যে, একটি ত্রিভুজের শীর্ষকোণের সমদ্বিখণ্ডক এবং শীর্ষকোণ থেকে ভূমির উপর অঙ্কিত লম্বের অন্তর্ভুক্ত কোণ ত্রিভুজের ভুমিস্থ কোণদ্বয়ের অন্তরের অর্ধেক।
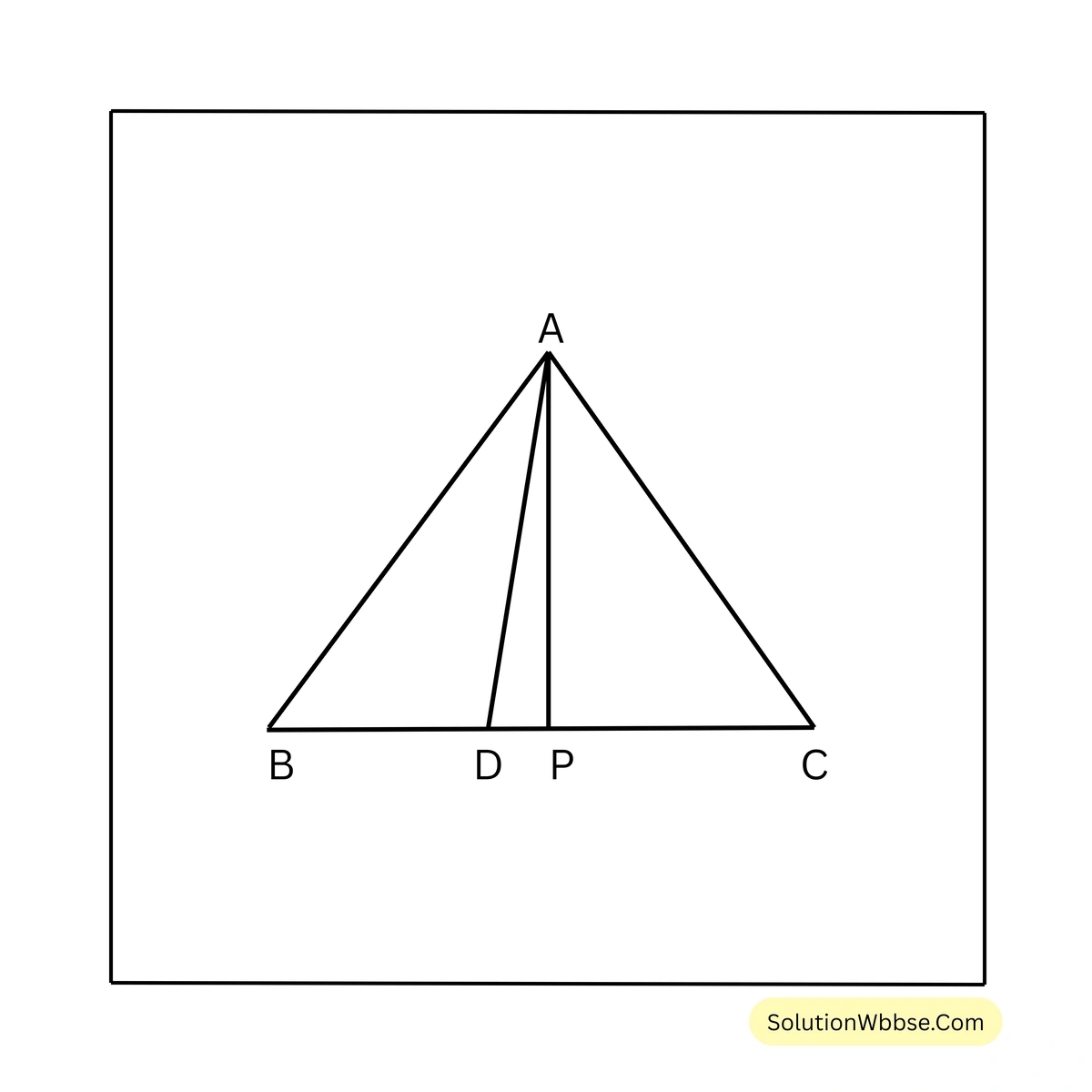
প্রদত্ত – \(\triangle ABC\) এর সমদ্বিখণ্ডক \(AP\), BC বাহুকে \(P\) বিন্দুতে ছেদ করেছে। A বিন্দু থেকে \(AD\) লম্ব যা BC কে \(D\) বিন্দুতে ছেদ করেছে। ধরি, \(\angle ABC > \angle ACB\)
প্রামাণ্য – \(\angle DAP = \frac{1}{2} (\angle ABC – \angle ACB)\)
প্রমাণ – \(\angle BAC\) এর সমদ্বিখণ্ডক \(AP\)
\(\therefore \angle CAP = \angle BAP\)\(\triangle ABC\) সমকোণী ত্রিভুজ থেকে পাই,
\(\angle ABD = 90^\circ – \angle BAD\)—–(1)
\(\triangle ADC\) সমকোণী ত্রিভুজ থেকে পাই,
\(\angle ACD = 90^\circ – \angle CAD\)——(2)
(1)-(2) করে পাই,
\(\angle ABD – \angle ACD = 90^\circ – \angle BAD – 90^\circ + \angle CAD\)বা, \(\angle ABC – \angle ACB = \angle CAD – \angle BAD\)
\(= \angle CAP + \angle DAP – (\angle BAP – \angle DAP)\)\(= \angle BAP + \angle DAP – \angle BAP + \angle DAP\)\(= 2 \angle DAP\)\(\therefore \angle DAP = \frac{1}{2} (\angle ABC – \angle ACB)\) [প্রমানিত]
15. ABC সমদ্বিবাহু ত্রিভুজের ভূমির একটি কোণ শীর্ষ কোণের দ্বিগুন। ত্রিভুজটির কোণগুলির পরিমাপ লিখি।
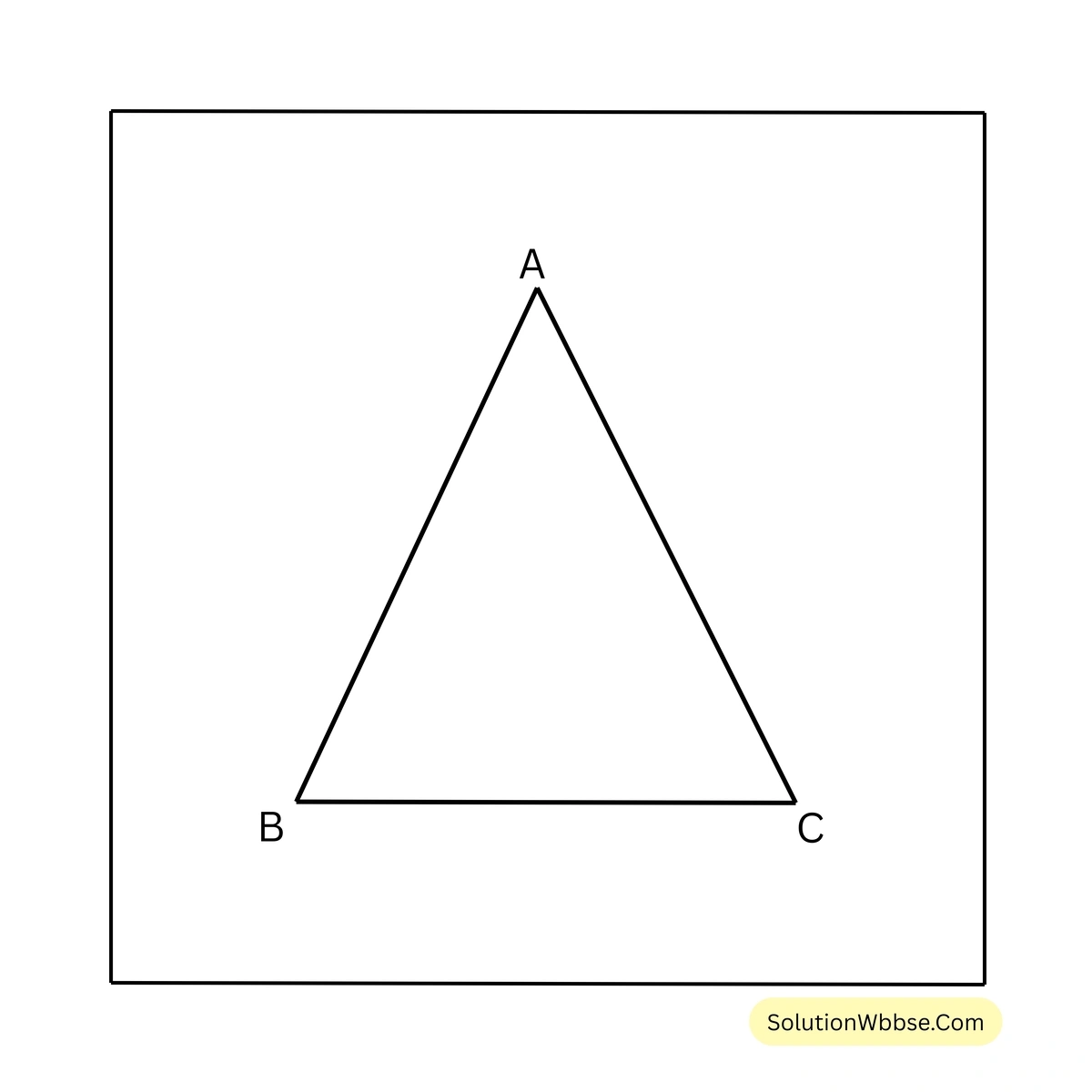
সমাধান –
ধরি, \(\triangle ABC\) এর \(AB = AC\)
\(\therefore \angle ABC = \angle ACB\)মনেকরি, \(\angle BAC = X\)
\(\therefore \angle ABC = \angle ACB = 2X\)\(\triangle ABC\) থেকে পাই
\(\angle ABC + \angle ACB + \angle BAC = 180^\circ\)\(\therefore 2X + 2X + X = 180^\circ\)বা, \(5X = 180^\circ\)
বা, \(X = \frac{180^\circ}{5}\)
\(\therefore X = 36^\circ\)\(\therefore \angle BAC = 36^\circ\) এবং \(\angle ABC = \angle ACB = 2 \times 36^\circ = 72^\circ\)
16. \(\triangle ABC\) এর \(\angle BAC = 90^\circ\) এবং \(\angle BCA = 30^\circ\); প্রমান করি যে, \(AB = \frac{1}{2} BC\)
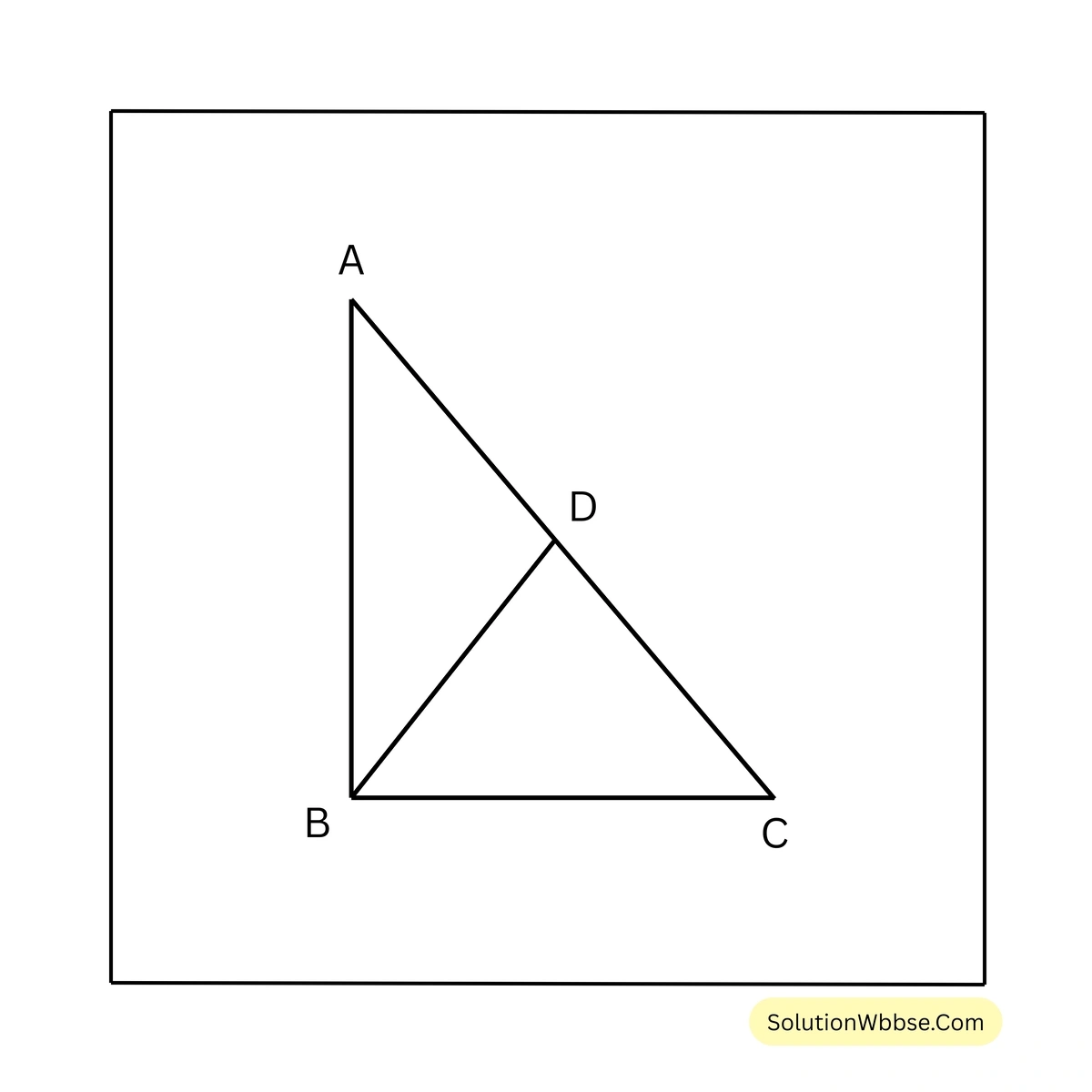
প্রদত্ত – \(\triangle ABC\) এর \(\angle BAC = 90^\circ\) এবং \(\angle BCA = 30^\circ\)
প্রামাণ্য – \(AB = \frac{1}{2} BC\)
অঙ্কন – BC বাহুর উপর AB এর সমান করে BD অংশ কেটে নেওয়া হল। A,D জুক্ত করা হল।
প্রমাণ – \(\triangle ABC\) থেকে পাই,
\(\angle ABC = 180^\circ – \angle BAC – \angle BCA\)\(\therefore \angle ABC = 180^\circ – 90^\circ – 30^\circ = 60^\circ\)\(\triangle ABD\) এর \(AB = BD\) [অঙ্কনানুসারে]
\(\therefore \angle BAD = \angle ADB\)\(\triangle ABD\) থেকে পাই,
\(\angle ABD + \angle ADB + \angle BAD = 180^\circ\)বা, \(60^\circ + \angle BAD + \angle BAD = 180^\circ\) [∵ \(\angle BAD = \angle ADB\)]
বা, \(2 \angle BAD = 180^\circ – 60^\circ\)
বা, \(\angle BAD = \frac{120^\circ}{2}\) \(\therefore \angle BAD = 60^\circ\)
\(\therefore \angle ABD = \angle ADB = \angle BAD = 60^\circ\)সুতরাং, \(\triangle ABD\) একটি সমবাহু ত্রিভুজ
\(\therefore AB = AD = BD\) —–(i)
\(\angle CAD = 90^\circ – \angle BAD = 90^\circ – 60^\circ = 30^\circ\)\(\triangle ACD\) এর \(\angle CAD = 30^\circ = \angle DCA\) \(\therefore AD = CD\) —-(ii)
(1) নং ও (2) নং থেকে পাই, \(AD = BD = CD\)
\(\therefore AD = \frac{1}{2} BC\) [প্রমানিত]
17. \(\triangle XYZ\) এর \(\angle XYZ = 90^\circ\) এবং \(XY = \frac{1}{2} XZ\); প্রমাণ করি যে, \(\angle YXZ = 60^\circ\)
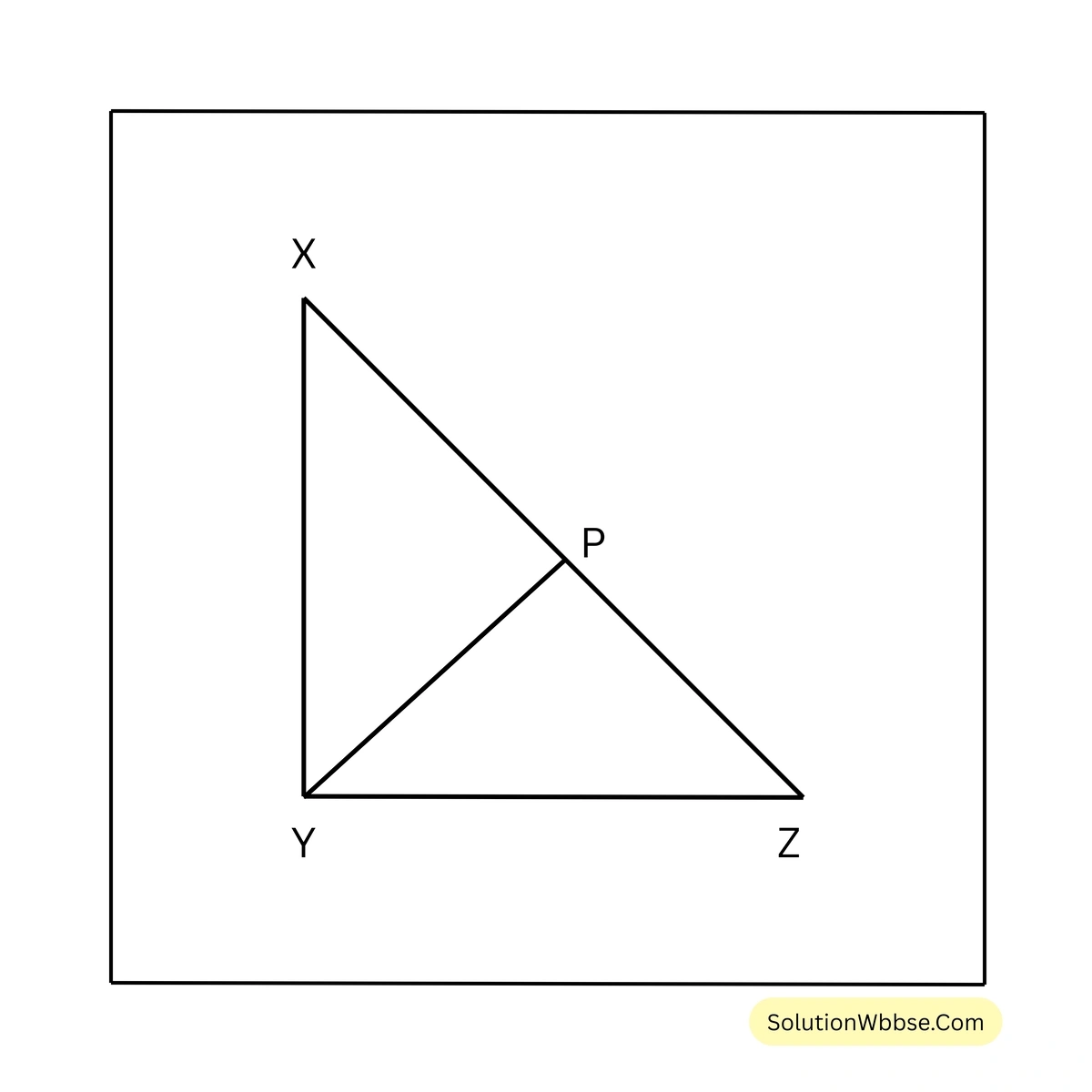
প্রদত্ত – \(\triangle XYZ\) এর \(\angle XYZ = 90^\circ\) এবং \(XY = \frac{1}{2} XZ\)
প্রামাণ্য – \(\angle YXZ = 60^\circ\)
অঙ্কন – Y বিন্দু থেকে \(\angle Z\) এর সমান করে \(\angle PYZ\) অঙ্কন করলাম।
প্রমাণ – \(\triangle PYZ\) এর \(\angle PYZ = \angle PZY\) [অঙ্কনানুসারে]
\(\therefore PY = PZ\) —-(1)
ধরি, \(\angle PYZ = \angle PZY = \theta\)
\(\triangle XYZ\) সমকোণী ত্রিভুজের \(\angle YXZ = 90^\circ – \angle XZY\)
\(\therefore \angle PXY = 90^\circ – \theta\)আবার, \(\angle XYP + \angle PYZ = 90^\circ\)
বা, \(\angle XYP + \theta = 90^\circ\) \(\therefore \angle XYP = 90^\circ – \theta\)
\(\triangle PXY\) ত্রিভুজের \(\angle PXY = \angle XYP = 90^\circ – \theta\) —-(2)
\(\therefore XP = PY\) —-(3)
(1)নং ও (3) নং থেকে পাই, \(XP = PZ\)
\(\therefore PX = \frac{1}{2} XZ\)আবার \(XY = \frac{1}{2} XZ\) \(\therefore PX = XY\)
\(\triangle XPY\) এর \(PX = XY\) \(\therefore \angle XPY = \angle XYP\) —–(4)
(2)নং ও (4) নং থেকে পাই,
\(\angle XPY = \angle XYP = \angle PXY\)\(\triangle XPY\) এর \(\angle XPY + \angle XYP + \angle PXY = 180^\circ\)
বা, \(\angle PXY + \angle PXY + \angle PXY = 180^\circ\)
বা, \(3 \angle PXY = 180^\circ\)
\(\therefore \angle PXY = 60^\circ\)\(\therefore \angle YXZ = 60^\circ\) [প্রমানিত]
18. প্রমাণ করি যে, সমবাহু ত্রিভুজের প্রতিটি কোণের মান \(60^\circ\)
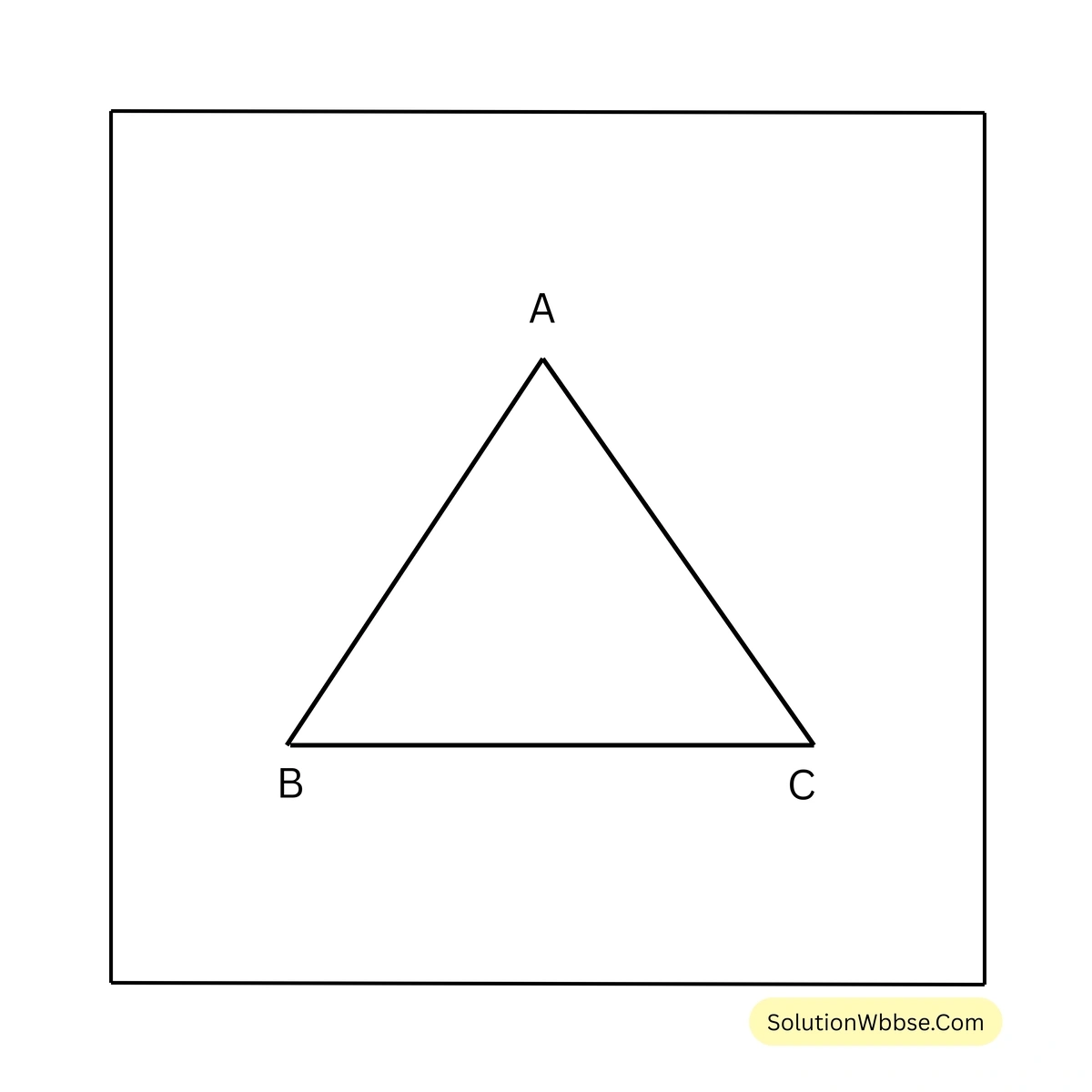
প্রদত্ত – ABC সমবাহু ত্রিভুজের \(AB = BC = CA\)
প্রামাণ্য – \(\angle ABC = \angle ACB = \angle BAC = 60^\circ\)
প্রমাণ – \(\triangle ABC\) এর \(AB = AC\)
\(\therefore \angle ABC = \angle ACB\) —–(1)
আবার, \(\triangle ABC\) এর \(AB = BC\)
\(\therefore \angle BAC = \angle ACB\) —–(2)
(1)নং ও (2) নং থেকে পাই,
\(\angle ABC = \angle ACB = \angle BAC\)\(\triangle ABC\) এর \(\angle ABC + \angle ACB + \angle BAC = 180^\circ\)
বা, \(\angle ABC + \angle ABC + \angle ABC = 180^\circ\)
বা, \(3 \angle ABC = 180^\circ\)
\(\therefore \angle ABC = 60^\circ\)\(\angle ABC = \angle ACB = \angle BAC = 60^\circ\) [প্রমানিত]
19. \(\triangle ABC\) ত্রিভুজের \(\angle BAC\) এর সমদ্বিখণ্ডক এবং AC বাহুর মধ্যবিন্দু D দিয়ে AB বাহুর সমান্তরাল সরলরেখা পরস্পর BC বাহুর বাইরে E বিন্দুতে মিলিত হয়। প্রমাণ করি যে, \(\angle AEC = 1\) সমকোণ।
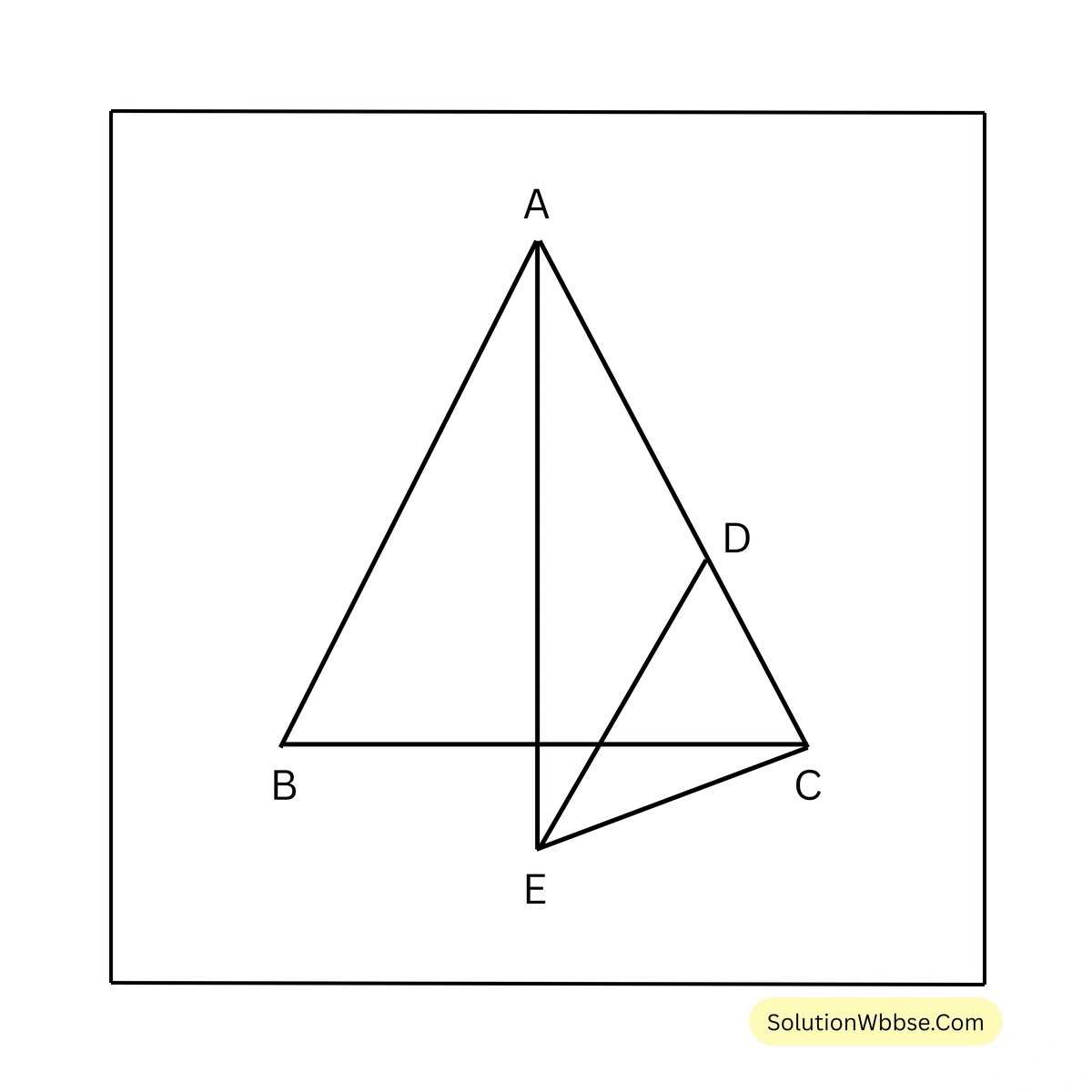
প্রদত্ত – \(\triangle ABC\) ত্রিভুজের \(\angle BAC\) এর সমদ্বিখণ্ডক এবং AC বাহুর মধ্যবিন্দু D দিয়ে AB বাহুর সমান্তরাল সরলরেখা পরস্পর BC বাহুর বাইরে E বিন্দুতে মিলিত হয়।
প্রামাণ্য – \(\angle ACE = 1\) সমকোণ
প্রমাণ – \(AB \parallel DE\) এবং \(AE\) ছেদক
\(\therefore \angle BAE = \angle AED\)\(\angle BAC\) এর সমদ্বিখণ্ডক \(AE\)
\(\therefore \angle BAE = \angle EAC\)\(\therefore \angle AED = \angle EAC = \angle EAD\) [∵ \(\angle BAE = \angle AED\)] —–(1)
\(\triangle ADE\) এর \(\angle AED = \angle EAD\) \(\therefore AD = DE\) —- (2)
D, AC বাহুর মধ্যবিন্দু \(\therefore AD = DC\) —–(3)
(2)নং ও (3) নং থেকে পাই, \(DE = DC\)
\(\triangle CDE\) এর \(DE = DC\) \(\therefore \angle DEC = \angle DCE\) —-(4)
\(\triangle AEC\) এর \(\angle AEC + \angle ACE + \angle EAC = 180^\circ\) —–(5)
(1)+(4) করে পাই,
\(\angle AED + \angle DEC = \angle EAD + \angle DCE\)বা, \(\angle AED + \angle DEC = \angle EAC + \angle ACE\)
বা, \(\angle AEC = 180^\circ – \angle AEC\) [(5) নং থেকে পাই]
বা, \(2 \angle AEC = 180^\circ\)
\(\therefore \angle AEC = 90^\circ\)\(\therefore \angle ACE = 1\) সমকোণ [প্রমানিত]
এই আর্টিকেলে অষ্টম শ্রেণির গণিতের ‘কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই’ অধ্যায়ের ‘কষে দেখি – 16.1’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরেছি। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে। কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করতে পারেন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন