মাধ্যমিক গণিত – বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য – প্রয়োগ

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের দশম অধ্যায়, ‘বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

একটি বৃত্তস্থ চতুর্ভুজের কোনো বাহুকে বর্ধিত করলে যে বহিঃস্থ কোণটি উৎপন্ন হয় তা অন্তঃস্থ বিপরীত কোণের সমান হবে – যুক্তি দিয়ে প্রমাণ করি।

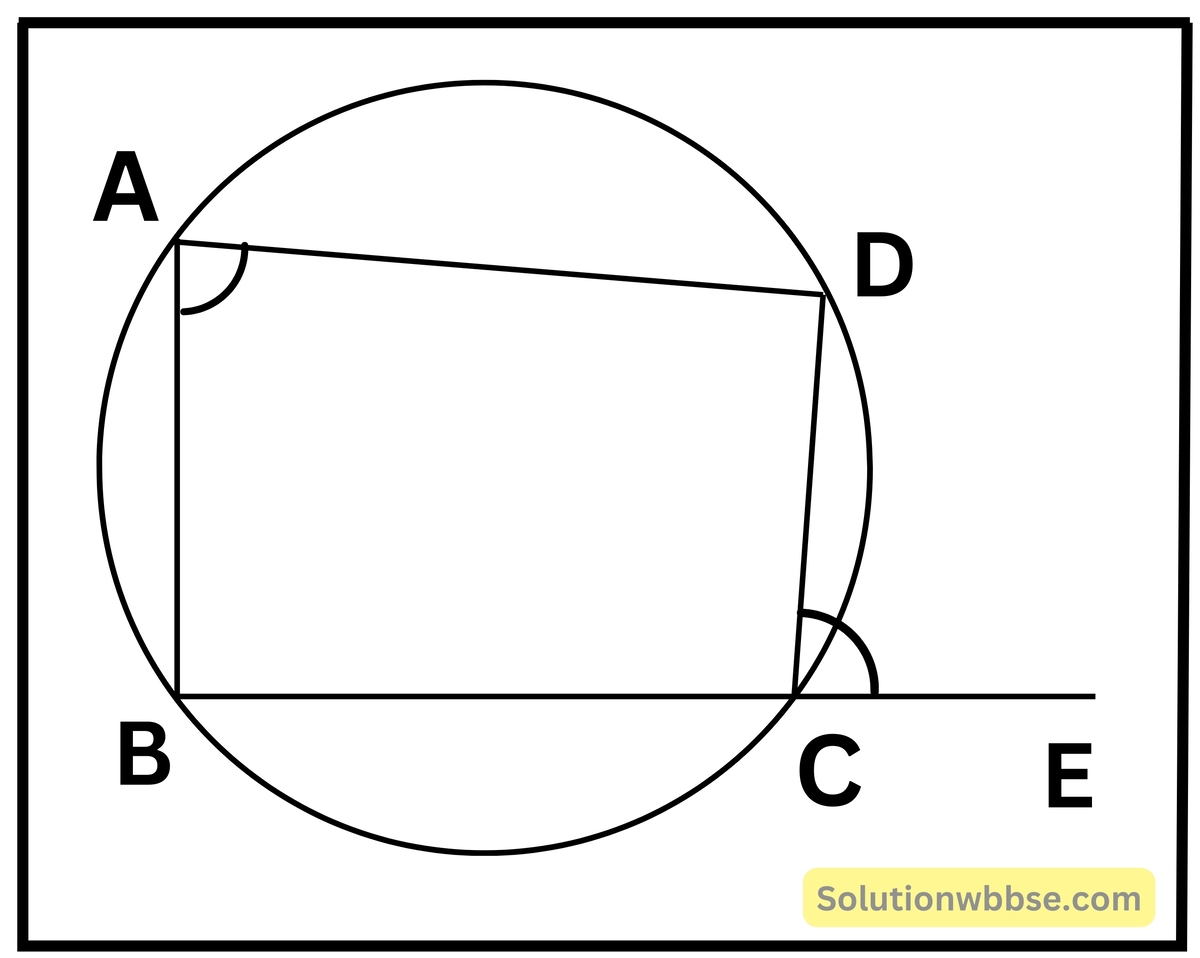
প্রদত্ত – ABCD বৃত্তস্থ চতুর্ভুজের BC বাহুকে E বিন্দু পর্যন্ত বর্ধিত করায় ∠DCE বহিঃস্থ কোণ উৎপন্ন হলো।

প্রমাণ করতে হবে যে – ∠DCE = বিপরীত অন্তঃস্থ ∠BAD

প্রমাণ – ∠BAD + ∠BCD = 180° [∵ ABCD বৃত্তস্থ চতুর্ভুজ]

আবার, ∠BCD + ∠DCE = 180° [∵ BE সরলরেখাংশের উপর DC দণ্ডায়মান]

সুতরাং, ∠BAD + ∠BCD = ∠BCD + ∠DCE

∴ ∠DCE = ∠BAD [প্রমাণিত]

প্রয়োগ 1. নীচের দুটি O কেন্দ্রীয় বৃত্তের ছবি দেখি এবং প্রতিক্ষেত্রে x -এর মান হিসাব করে লিখি।

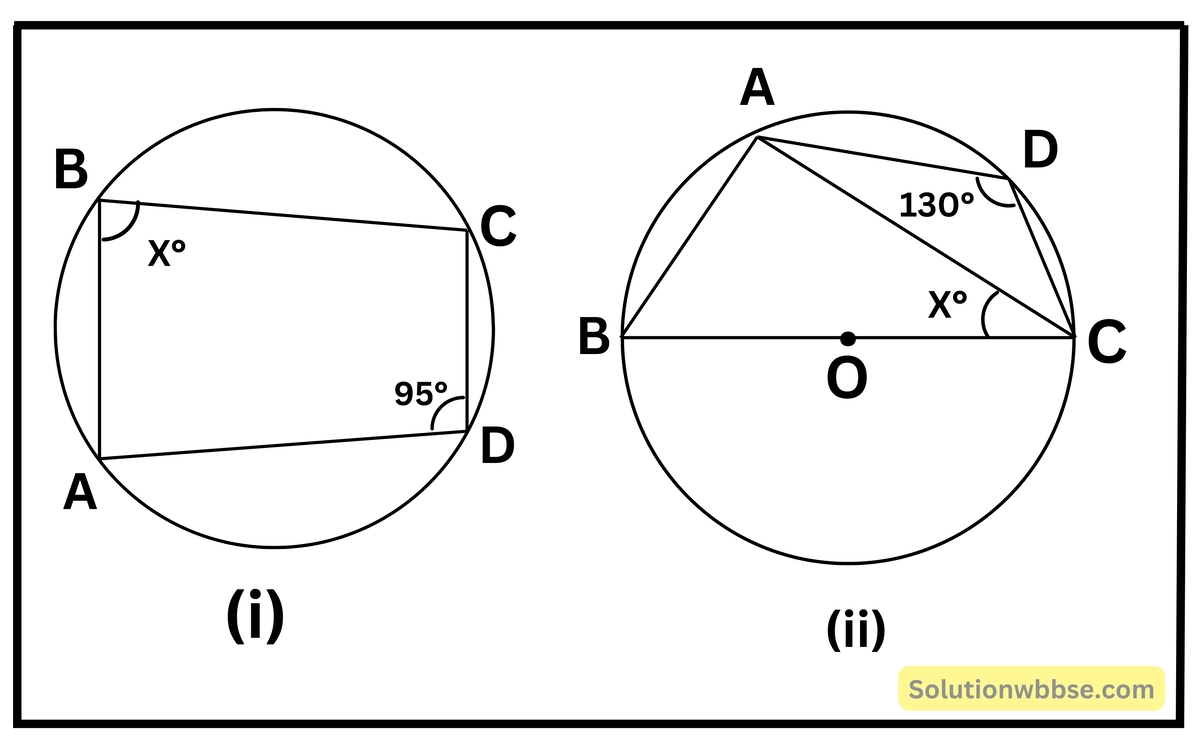
(i) ABCD বৃত্তস্থ চতুর্ভুজ,

∴ ∠ABC + ∠ADC = 180°

∴ x° = ∠ABC = 180° – 95°

∴ x = 85°

(ii) ABCD বৃত্তস্থ চতুর্ভুজ,

∴ ∠ABC + ∠ADC = 180°

∴ ∠ABC = 50°

আবার ∠BAC = 1 সমকোণ,

∴ ∠BAC = 90°

∴ x° + ∠ABC + ∠BAC = 180°;

∴ x° + 50° + 90° = 180°;

∴ x = 180° – 140° = 50°

প্রয়োগ 2. ABCD একটি বৃত্তস্থ চতুর্ভুজ এবং O ওই বৃত্তের কেন্দ্র। যদি ∠COD = 120° এবং ∠BAC = 30° হয়, তবে ∠BOC ও ∠BCD -এর মান কত হবে, হিসাব করে লিখি।

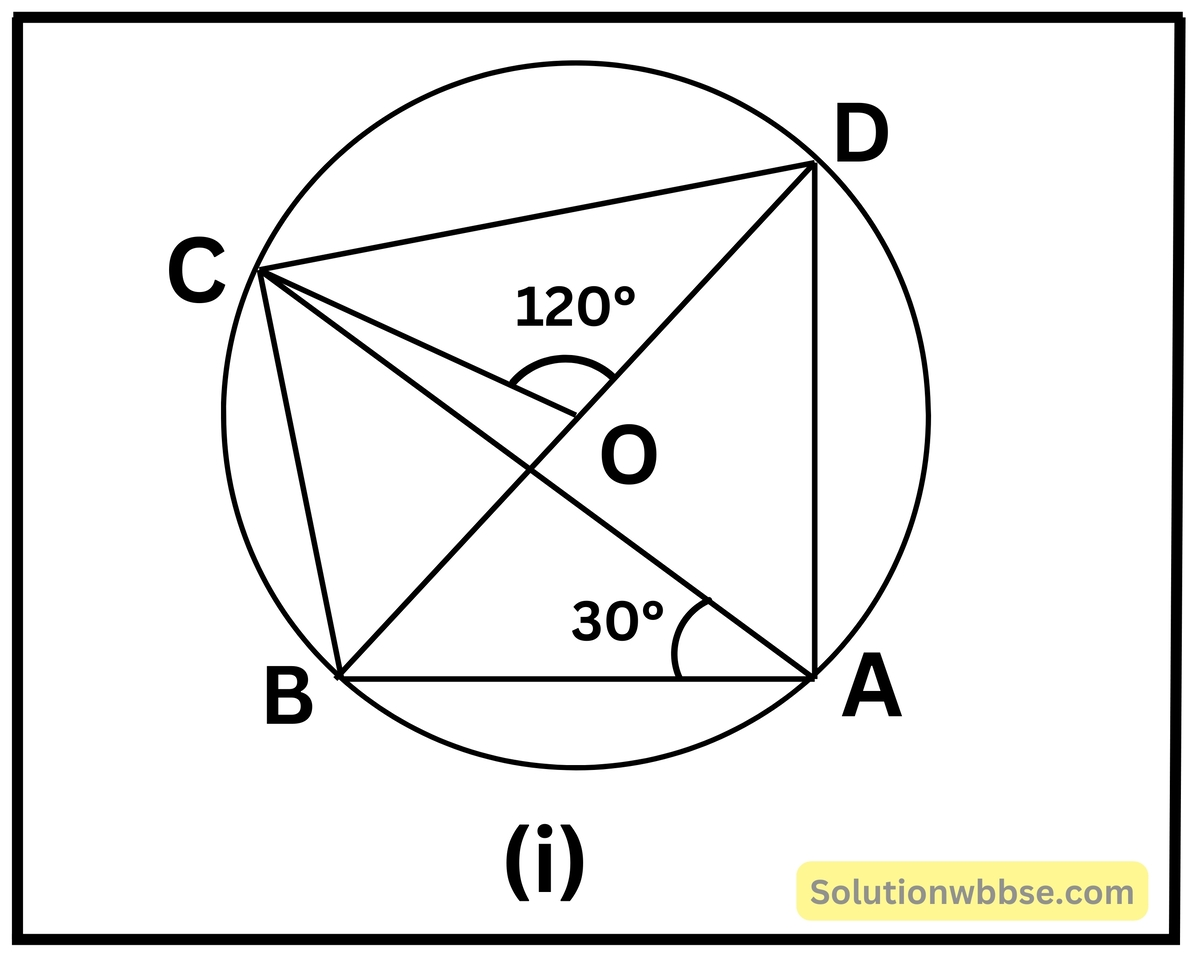
BC উপচাপের দ্বারা গঠিত কেন্দ্রস্থ কোণ ∠BOC এবং বৃত্তস্থ কোণ ∠BAC

∴ ∠BOC = 2∠BAC = 60°

CD উপচাপের উপর কেন্দ্রস্থ কোণ ∠COD এবং বৃত্তস্থ কোণ ∠CAD,

∴ \(\angle COD=\frac12\angle CAD\)

= \(\frac12\times120^\circ\)

= 60°

∴ ∠BAD = 30° + 60° = 90°

∴ ABCD বৃত্তস্থ চতুর্ভুজে ∠BCD + ∠BAD = 180°

∴ ∠BCD = 180° – ∠BAD

∴ ∠BCD = 180° – 90°

∴ ∠BCD = 90°

প্রয়োগ 3. পাশের বৃত্তস্থ চতুর্ভুজ ABCD -এর AD ও AB বাহুকে যথাক্রমে E ও F বিন্দু পর্যন্ত বর্ধিত করলাম। ∠CBF = 120° হলে, ∠CDE -এর মান হিসাব করে লিখি।

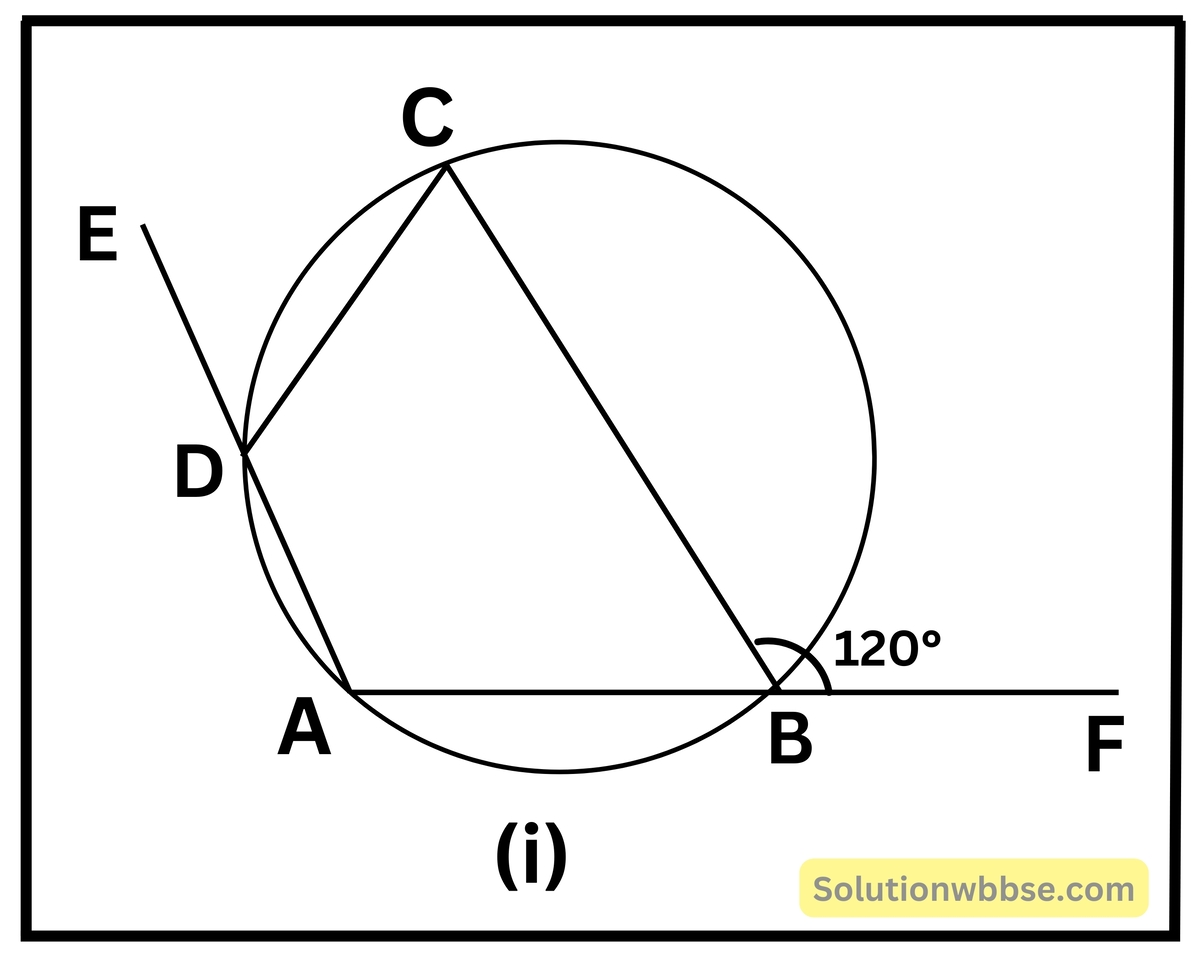
বৃত্তস্থ চতুর্ভুজ ABCD -এর AD ও AB বাহুকে যথাক্রমে E ও F বিন্দু পর্যন্ত বর্ধিত করলাম।

∠CBF = 120°

∴ ∠CBA = 180° – 120° = 60°

আবার, ∠CBA + ∠CDA = 180° [∵ ABCD বৃত্তস্থ চতুর্ভূজ]

∴ ∠CDA = 180° – 60° = 120°

∴ ∠CDA = 180° – ∠CDA

= 180° – 120°

= 60°

প্রয়োগ 4. ABCD বৃত্তস্থ চতুর্ভুজের AB ও DC বাহুকে বর্ধিত করায় P বিন্দুতে এবং AD ও BC বাহুকে বর্ধিত করায় বিন্দুতে মিলিত হয়েছে। ∠ADC = 85° এবং ∠BPC = 40° হলে ∠BAD ও ∠CQD -এর মান হিসাব করে লিখি।

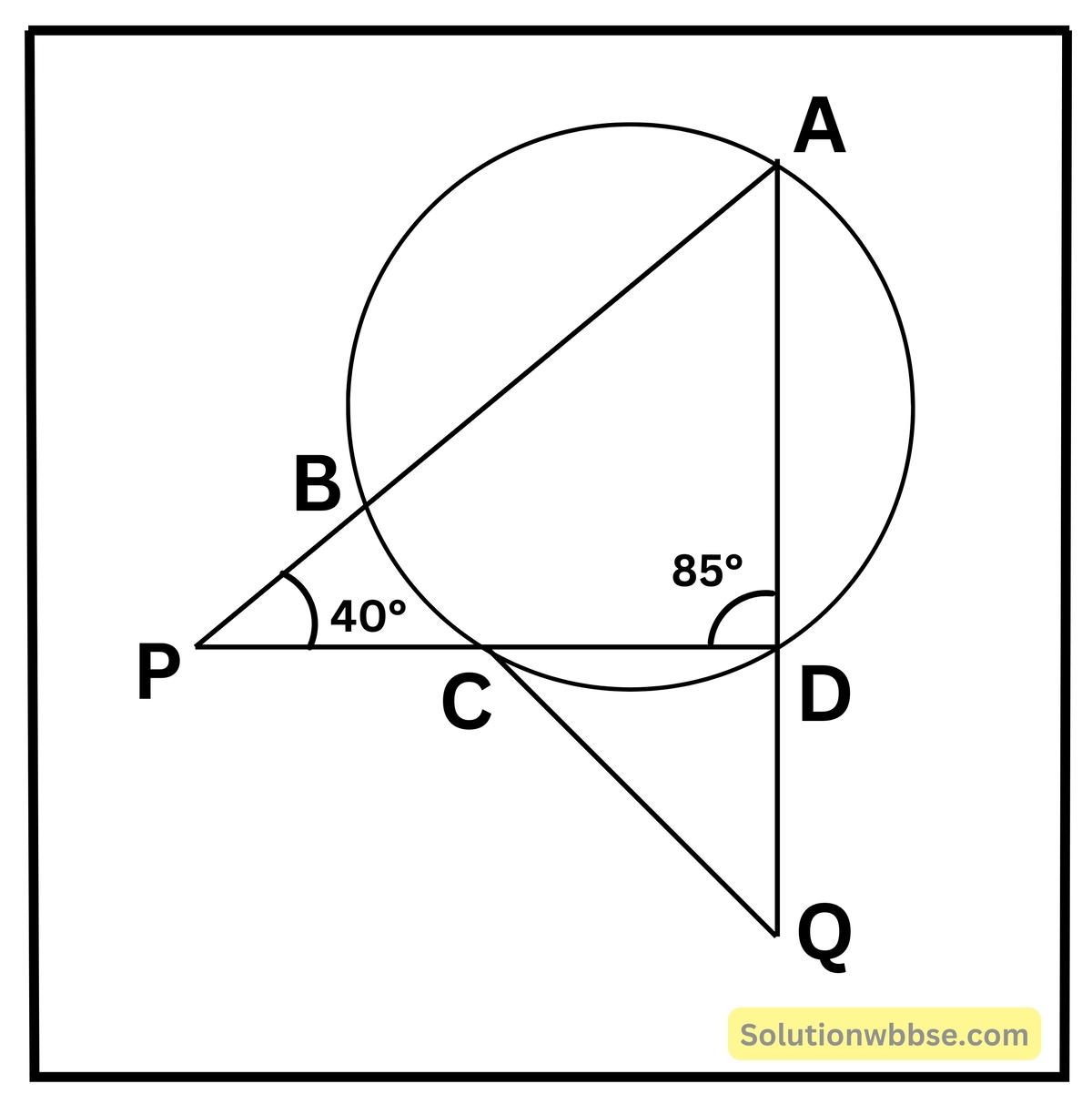
ABCD বৃত্তস্থ চতুর্ভুজের বহিঃস্থ ∠PBC = ∠ADC = 85°

ΔBPC -এর ∠BCP = 180° – (85° + 40°) = 180° – 125° = 55°

আবার, ∠BAD = বহিঃস্থ ∠BCP = 55°

ΔCQD -এর, ∠CQD + ∠DCQ = 85°

∴ ∠CQD = 85° – ∠DCQ = 85° – ∠BCP = 85° – 55° = 30°

∴ ∠BAD = 55° এবং ∠CQD = 30°

প্রয়োগ 5. প্রমাণ করি যে, বৃত্তস্থ সামান্তরিক একটি আয়তাকার চিত্র।

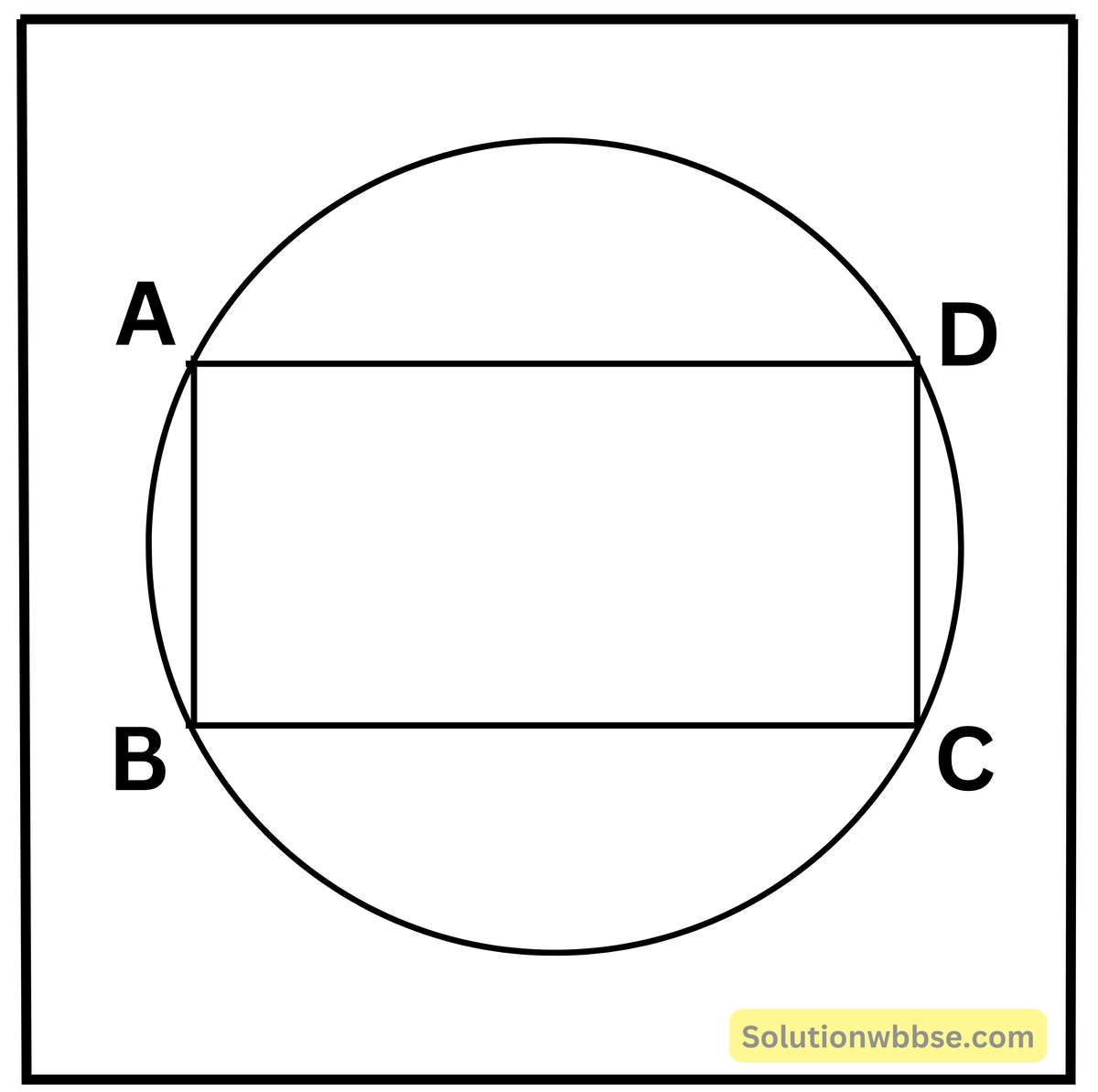
প্রদত্ত – ABCD চতুর্ভুজটি বৃত্তস্থ সামান্তরিক।

প্রমাণ করতে হবে যে – ABCD সামান্তরিক আয়তাকার চিত্র।

প্রামাণ – ABCD একটি সামান্তরিক

∴ ∠ABC = ∠ADC

আবার, ABCD একটি বৃত্তস্থ চতুর্ভুজ

∠ABC + ∠ADC = 180°

সুতরাং, 2∠ABC = 180°

∴ ∠ABC = 90°

যেহেতু, এই সামান্তরিকের একটি কোণ সমকোণ, সুতরাং, ABCD সামান্তরিকটি একটি আয়তাকার চিত্র।

প্রয়োগ 6. ABCD একটি বৃত্তস্থ চতুর্ভুজ। ∠DAB ও ∠BCD -এর সমদ্বিখণ্ডকদ্বয় বৃত্তকে X ও Y বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, XY ওই বৃত্তের ব্যাস।

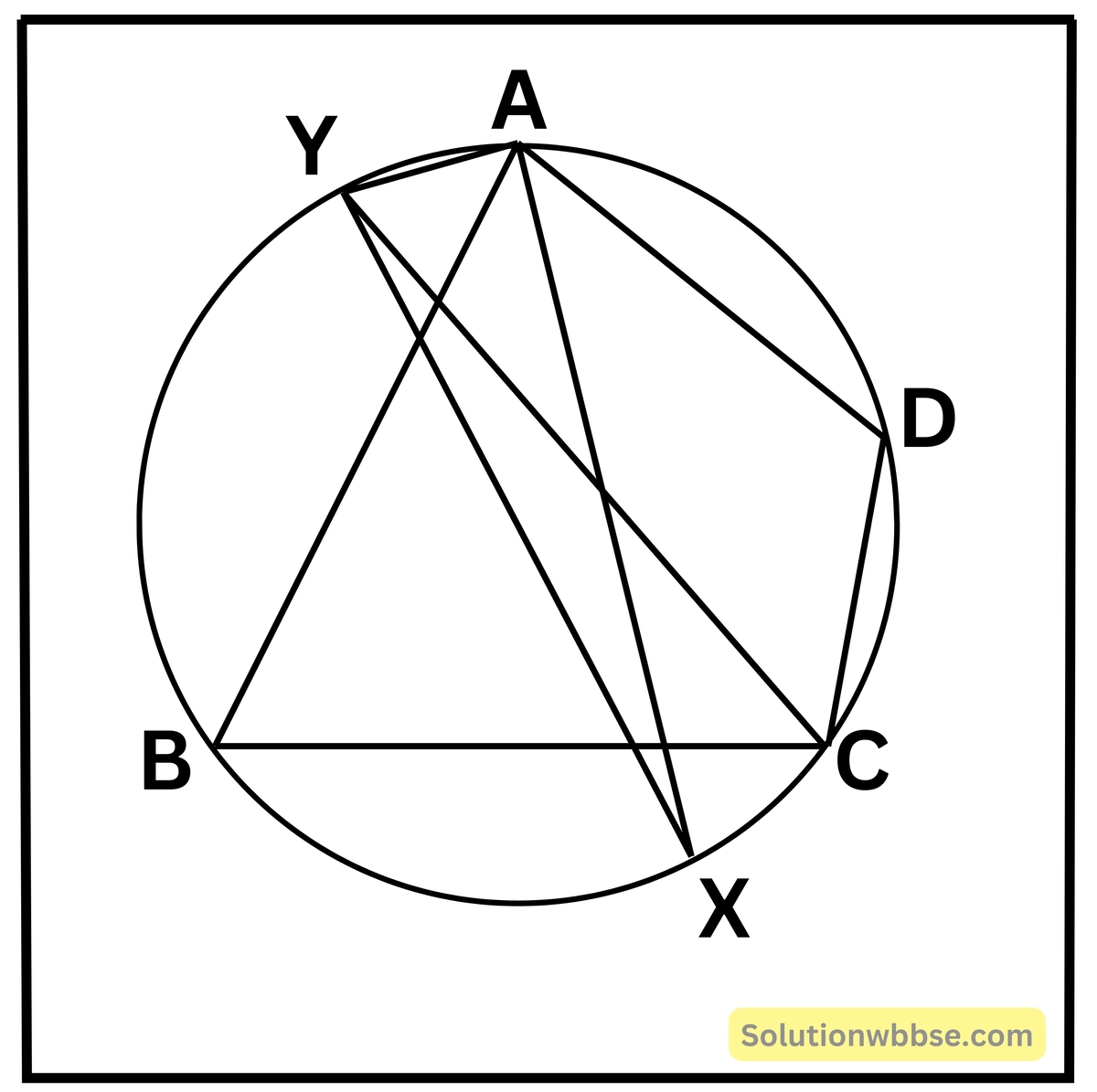
প্রদত্ত – ABCD বৃত্তস্থ চতুর্ভুজের ∠DAB ও ∠BCD-এর সমদ্বিখণ্ডকদ্বয় বৃত্তকে X ও Y বিন্দুতে ছেদ করে।

প্রমাণ করতে হবে যে – XY বৃত্তের একটি ব্যাস।

অঙ্কন – A, Y বিন্দুদ্বয় যোগ করি।

প্রমাণ – ∠YAB ও ∠YCB বৃত্তের উপচাপ YB -এর দ্বারা গঠিত একই বৃত্তাংশস্থ বৃত্তস্থ কোণ।

∠YAB = ∠YCB = ∠BCD —(I) [∵ CY, ∠BCD -এর সমদ্বিখণ্ডক]

আবার, ∠XAY = ∠XAB + ∠YAB

= \(\frac12\angle BAD+\frac12\angle BCD\) [(I) হইতে পেলাম] [∵ AX, ∠DAB -এর সমদ্বিখণ্ডক]

= \(\frac12\left(\angle BAD+\angle BCD\right)\)

= \(\frac12\times180^\circ\) [∵ ABCD বৃত্তঃস্থ চতুর্ভুজ]

= 90° 

∴ ∠XAY একটি অর্ধবৃত্তস্থ কোণ।

∴ XY বৃত্তের ব্যাস।

প্রয়োগ 7. প্রমাণ করি যে, আয়তক্ষেত্র নয় এমন বৃত্তস্থ ট্রাপিজিয়াম সমদ্বিবাহু ট্রাপিজিয়াম এবং কর্ণদ্বয়ের দৈর্ঘ্য সমান।

প্রমাণ করি যে, আয়তক্ষেত্র নয় এমন বৃত্তস্থ ট্রাপিজিয়াম সমদ্বিবাহু ট্রাপিজিয়াম এবং কর্ণদ্বয়ের দৈর্ঘ্য সমান।

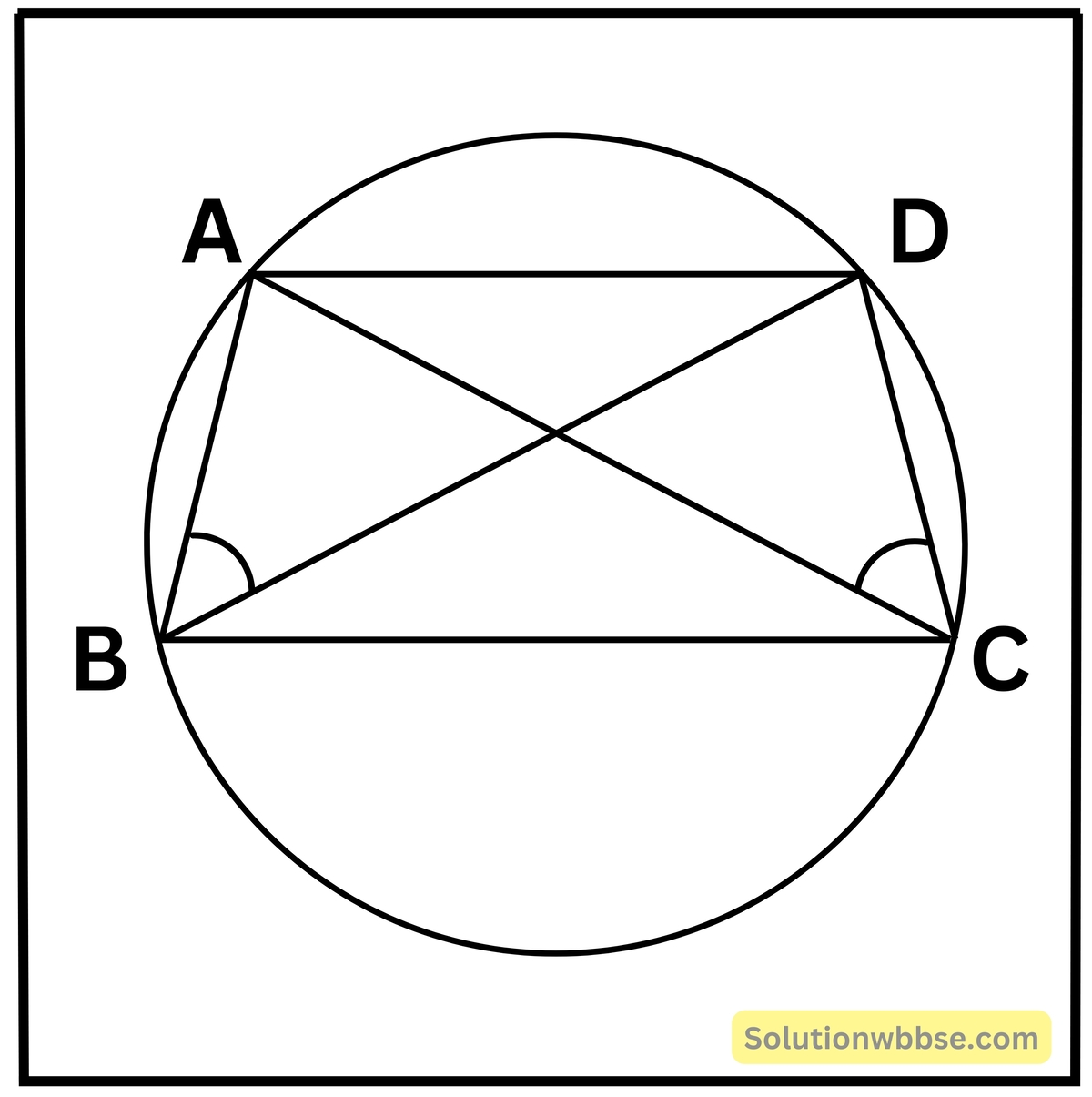
প্রদত্ত – ABCD একটি বৃত্তস্থ ট্রাপিজিয়াম যার AD || BC

প্রমাণ করতে হবে যে – AB = DC এবং AC = BD

প্রমাণ – ∠ADC + ∠DCB = 180° [∵ AD || BC এবং DC ভেদক]

আবার, ∠BAD + ∠DCB = 180° [∵ ABCD বৃত্তঃস্থ চতুর্ভুজ]

∴ ∠ADC + ∠DCB = ∠BAD + ∠DCB

∴ ∠ADC = ∠BAD —(I)

ΔBAD ও ΔADC -এর মধ্যে, ∠BAD = ∠ADC [(I) থেকে পেলাম]

∠ABD = ∠DCA [একই বৃত্তাংশস্থ কোণ]

AD সাধারণ বাহু

∴ ΔBAD ≅ ΔADC [সর্বসমতার A-A-S শর্তানুসারে] 

∴ AB = DC এবং AC = BD (∵ সর্বসম ত্রিভুজের অনুরূপ অংশ) [প্রমাণিত]

প্রয়োগ 8. O কেন্দ্রীয় বৃত্তের AP, AQ দুটি জ্যা-এর মধ্যবিন্দু যথাক্রমে R ও S; প্রমাণ করি যে, O, R, A, S বিন্দু চারটি সমবৃত্তস্থ।

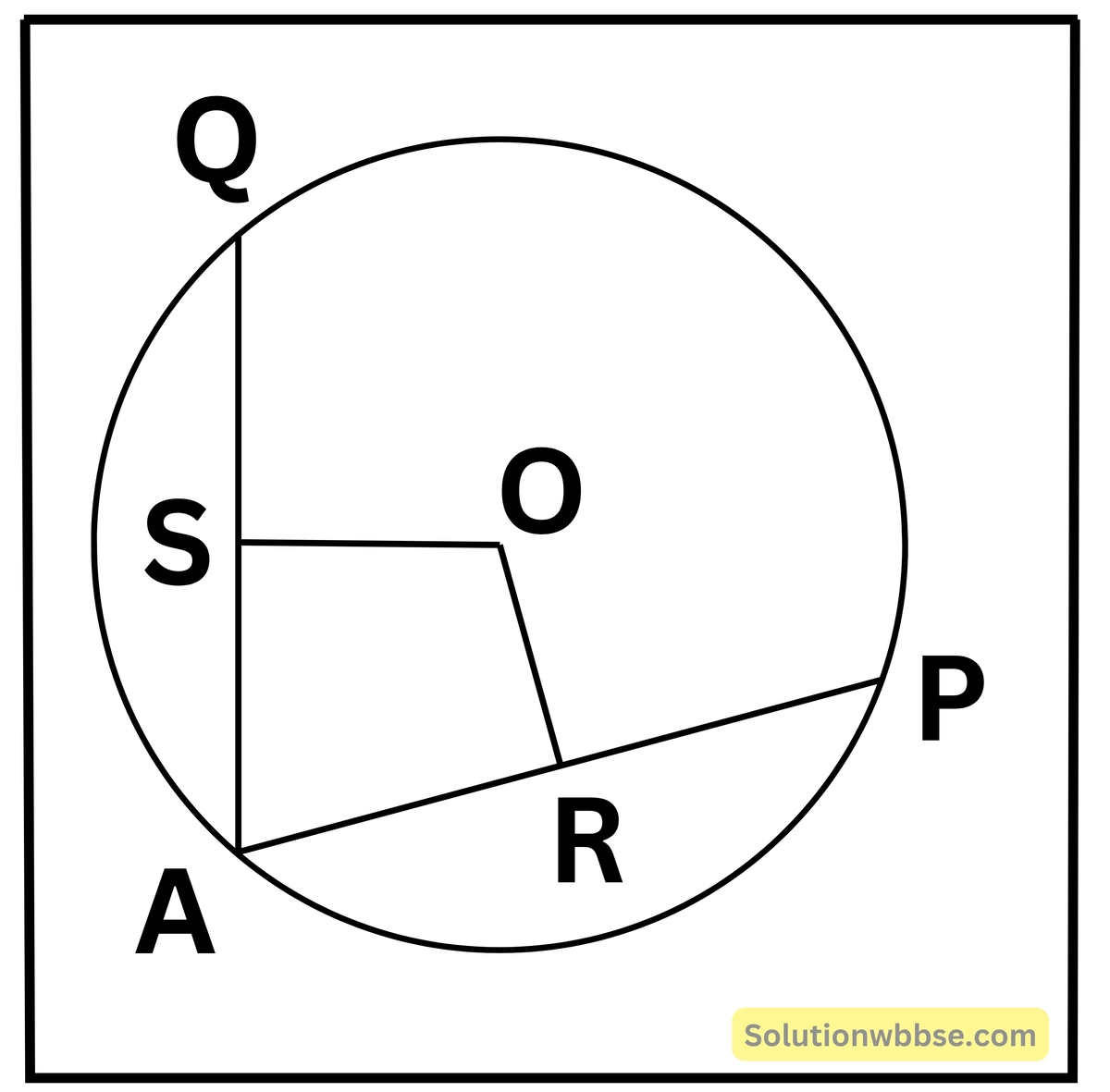
প্রদত্ত – O কেন্দ্রীয় বৃত্তের AP ও AQ দুটি জ্যা-এর মধ্যবিন্দু যথাক্রমে R ও S

প্রমাণ করতে হবে যে – O, R, A, S বিন্দু চারটি সমবৃত্তস্থ।

অঙ্কন – O, R বিন্দুদ্ধদ্বয় এবং O, S বিন্দুদ্বয় যুক্ত করি।

প্রমাণ – OR, AP জ্যাকে সমদ্বিখণ্ডিত করে। ∴ OR ⊥ AP

অর্থাৎ, ∠ARO = 90°

OS, AQ জ্যাকে সমদ্বিখণ্ডিত করে। ∴ OS ⊥ AQ

অর্থাৎ, ∠ASO = 90°

∴ ∠ARO + ∠ASO = 90° + 90° = 180°

যেহেতু AROS চতুর্ভুজের এক জোড়া বিপরীত কোণ পরস্পর সম্পূরক, সুতরাং, O, R, A, S বিন্দু চারটি সমবৃত্তস্থ।

প্রয়োগ 9. প্রমাণ করি যে চতুর্ভুজের চারটি কোণের সমদ্বিখণ্ডকগুলি পরস্পর মিলিত হয়ে যে চতুর্ভুজ গঠন করে সেটি বৃত্তস্থ চতুর্ভুজ।

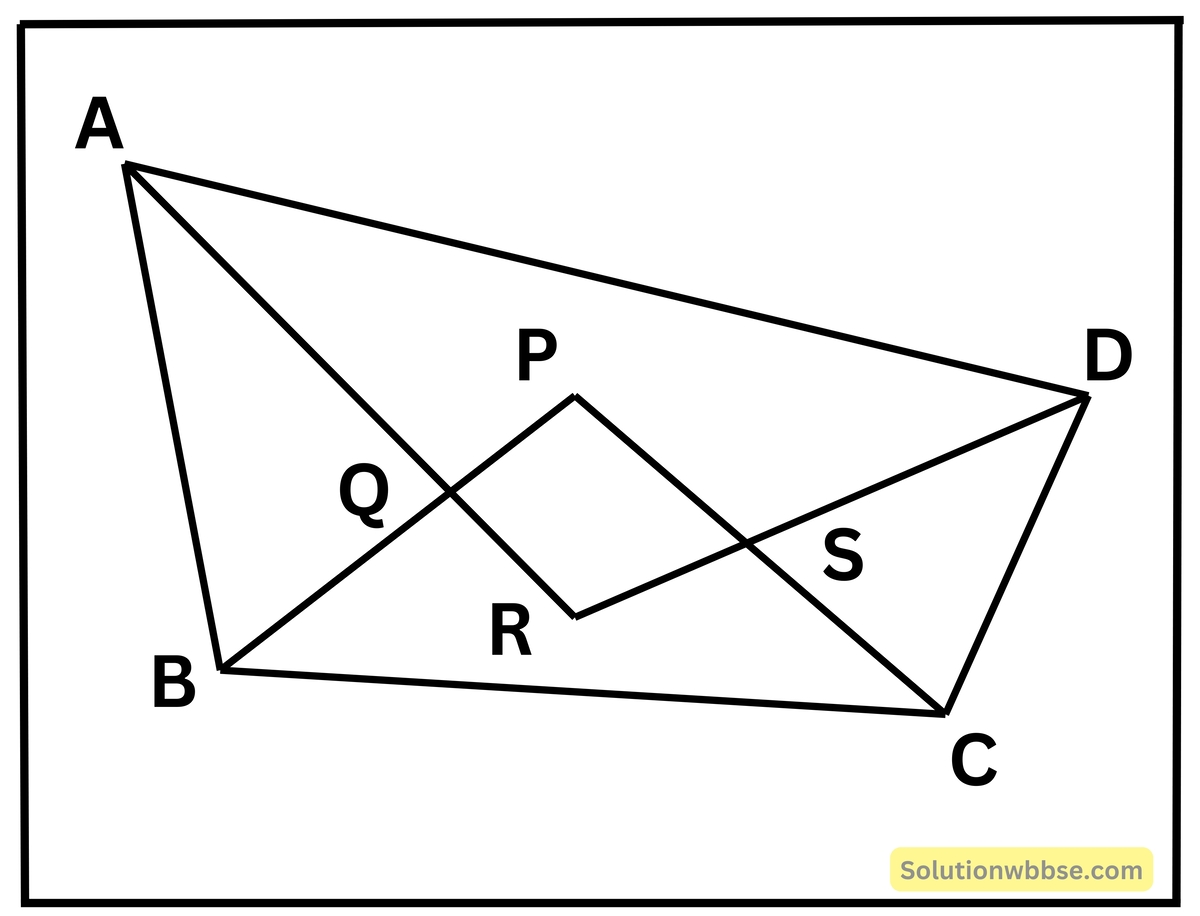
প্রদত্ত – ABCD একটি চতুর্ভুজের AR, BP, CP ও DR যথাক্রমে ∠A, ∠B, ∠Cও ∠D -এর সমদ্বিখণ্ডক পরস্পর মিলিত হয়ে PQRS চতুর্ভুজ উৎপন্ন করেছে।

প্রমাণ করতে হবে যে – PQRS বৃত্তস্থ চতুর্ভুজ।

প্রমাণ – ΔARD -এর, ∠ARD + ∠RDA + ∠DAR = 180°

আবার, ΔBPC -এর, ∠BPC + ∠PCB + ∠CBP = 180°

(I) ও (II) হইতে পাই,

\(\angle ARD+\frac12\angle A+\frac12\angle D+\angle BPC+\frac12\angle C+\frac12\angle B=180^\circ+180^\circ\)

বা, \(\angle ARD+\angle BPC+\frac12\left(\angle A+\angle B+\angle C+\angle D\right)=360^\circ\)

বা, \(\angle ARD+\angle BPC+\frac12\times360^\circ=360^\circ\)

বা, ∠ARD + ∠BPC = 360° – 180° = 180°

∴ ∠QRS + ∠QPS = 180°

PQRS চতুর্ভুজের একজোড়া বিপরীত কোণগুলি পরস্পর সম্পূরক।

∴ PQRS চতুর্ভুজটি বৃত্তস্থ চতুর্ভুজ।

---

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের দশম অধ্যায়, ‘বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।

আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।