এই আর্টিকেলে আমরা মাধ্যমিক ভৌতবিজ্ঞানের একটি গুরুত্বপূর্ণ প্রশ্ন “কুলম্বের সূত্রটি বিবৃত করো ও গাণিতিক রূপসহ ব্যাখ্যা করো।” নিয়ে আলোচনা করব। এই প্রশ্নটি মাধ্যমিক ভৌতবিজ্ঞান পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ। এই “কুলম্বের সূত্রটি বিবৃত করো ও গাণিতিক রূপসহ ব্যাখ্যা করো।” প্রশ্নটি মাধ্যমিক ভৌতবিজ্ঞানের ষষ্ঠ অধ্যায় “চলতড়িৎ“ -এর একটি গুরুত্বপূর্ণ প্রশ্ন। এই প্রশ্নটি মাধ্যমিক পরীক্ষায় এবং চাকরির পরীক্ষায় প্রায়ই দেখা যায়।

কুলম্বের সূত্রটি বিবৃত করো ও গাণিতিক রূপসহ ব্যাখ্যা করো।
কুলম্বের সূত্র – দুটি স্থির বিন্দু আধানের মধ্যে আকর্ষণ বা বিকর্ষণ বল আধান দুটির গুণফলের সমানুপাতিক ও বিন্দু দুটির ভিতর দূরত্বের বর্গের ব্যস্তানুপাতিক।
\(q_1\) ও \(q_1\) দুটি বিন্দু আধান পরস্পরের থেকে r দূরত্বে থাকলে তাদের মধ্যে আকর্ষণ বা বিকর্ষণ বল \(F\propto q_1q_2\) [যখন r ধ্রুবক]
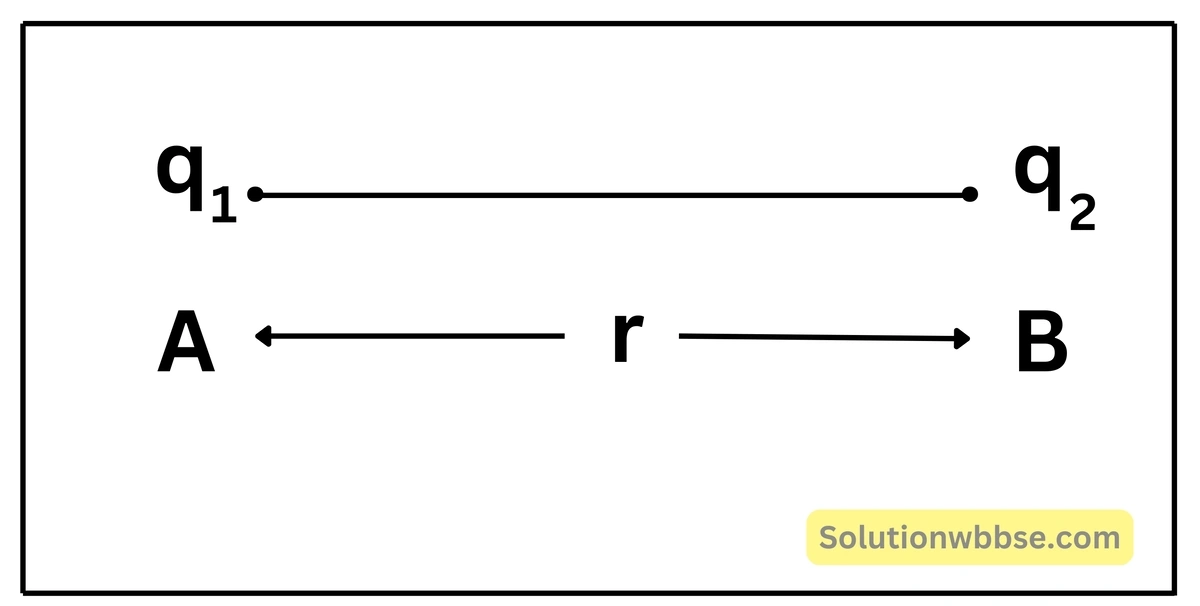
\(F\propto\frac1{r^2}\) [যখন \(q_1q_2\) ধ্রুবক]
∴ \(F\propto\frac{q_1q_2}{r^2}\) [যখন \(q_1,\;q_2\) ও \(r\) পরিবর্তিত]
CGS -এ ধ্রুবক হল \(F=\frac{q_1q_2}{kr^2}\) এবং
SI -এ ধ্রুবক হল \(F=\frac1{4\pi\varepsilon_0}\cdot\frac{q_1q_2}{r^2}\)
কিছু গুরুত্বপূর্ণ প্রশ্নোত্তর
কুলম্বের সূত্রটি কী?
দুটি স্থির বিন্দু আধানের মধ্যকার আকর্ষণ বা বিকর্ষণ বলের মান আধান দুটির গুণফলের সমানুপাতিক এবং তাদের মধ্যবর্তী দূরত্বের বর্গের ব্যস্তানুপাতিক। এই বল আধান দুটির সংযোগকারী সরলরেখা বরাবর ক্রিয়া করে।
CGS ও SI পদ্ধতিতে কুলম্বের ধ্রুবকের মান কত?
SI পদ্ধতিতে ধ্রুবকটির মান 1/(4πε₀) = 9 × 10⁹ N m² C⁻²।
CGS পদ্ধতিতে ধ্রুবকটির মান 1 নির্ধারণ করা হয়। এই পদ্ধতিতে আধানের একক স্টেটকুলম্ব (statC) এবং দূরত্বের একক সেন্টিমিটার (cm) ব্যবহার করা হয়। সূত্রটি হয় F = (q₁q₂) / r²।
কুলম্বের বলটি আকর্ষণধর্মী নাকি বিকর্ষণধর্মী হবে তা কিভাবে বুঝবে?
বলের দিক আধান দুটির প্রকৃতির উপর নির্ভর করে।
1. যদি দুটি আধান সমজাতীয় হয় (উভয়ই ধনাত্মক বা উভয়ই ঋণাত্মক), তাহলে তাদের মধ্যে বিকর্ষণ বল কাজ করে।
2. যদি দুটি আধান বিষমজাতীয় হয় (একটি ধনাত্মক ও অপরটি ঋণাত্মক), তাহলে তাদের মধ্যে আকর্ষণ বল কাজ করে।
3. গাণিতিক সূত্রে q₁ এবং q₂ -এর মান ধনাত্মক বা ঋণাত্মক হিসেবে ব্যবহার করলে F -এর মান ঋণাত্মক হলে তা আকর্ষণ বল (attractive force) এবং ধনাত্মক হলে বিকর্ষণ বল (repulsive force) নির্দেশ করে।
কুলম্বের সূত্র কেবলমাত্র ‘বিন্দু আধানের’ জন্য প্রযোজ্য কেন?
বিন্দু আধান একটি আদর্শীকৃত ধারণা, যেখানে আধানের নিজস্ব কোনো আয়তন বা আকৃতি নেই। এটি একটি বিন্দু হিসাবে বিবেচিত হয় যেখানে সমস্ত আধান কেন্দ্রীভূত থাকে। কুলম্বের সূত্র কেবলমাত্র এই ধরনের বিন্দু আধানের জন্যই সঠিকভাবে প্রযোজ্য। তবে, আধানযুক্ত বস্তুর আকার যদি তাদের মধ্যেকার দূরত্ব r-এর তুলনায় যথেষ্ট ছোট হয়, তাহলে সেগুলোকে বিন্দু আধান হিসেবে প্রায়-সঠিকভাবে বিবেচনা করা যায়।
কুলম্বের সূত্রটি কীসের ক্ষেত্রে প্রযোজ্য?
এটি শুধুমাত্র বিন্দু আধান (point charges) এবং স্থির অবস্থায় থাকা আধানের (electrostatics) জন্য প্রযোজ্য।
বল (F) কীভাবে আধান (q) এর উপর নির্ভর করে?
বল আধানদ্বয়ের গুণফলের সমানুপাতিক (F ∝ q₁q₂)। একটি আধান দ্বিগুণ করলে বলও দ্বিগুণ হবে।
এই আর্টিকেলে আমরা মাধ্যমিক ভৌতবিজ্ঞানের একটি গুরুত্বপূর্ণ প্রশ্ন “কুলম্বের সূত্রটি বিবৃত করো ও গাণিতিক রূপসহ ব্যাখ্যা করো।” নিয়ে আলোচনা করব। এই প্রশ্নটি মাধ্যমিক ভৌতবিজ্ঞান পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ। এই “কুলম্বের সূত্রটি বিবৃত করো ও গাণিতিক রূপসহ ব্যাখ্যা করো।” প্রশ্নটি মাধ্যমিক ভৌতবিজ্ঞানের ষষ্ঠ অধ্যায় “চলতড়িৎ“ -এর একটি গুরুত্বপূর্ণ প্রশ্ন। এই প্রশ্নটি মাধ্যমিক পরীক্ষায় এবং চাকরির পরীক্ষায় প্রায়ই দেখা যায়। আশা করি এই আর্টিকেলটি আপনাদের জন্য উপকারী হয়েছে। আপনাদের কোনো প্রশ্ন বা অসুবিধা থাকলে, আমাদের সাথে টেলিগ্রামে যোগাযোগ করতে পারেন, আমরা উত্তর দেওয়ার চেষ্টা করব। তাছাড়া, নিচে আমাদের এই পোস্টটি আপনার প্রিয়জনের সাথে শেয়ার করুন, যাদের এটি প্রয়োজন হতে পারে। ধন্যবাদ।






মন্তব্য করুন