মাধ্যমিক গণিত – আয়তঘন – কষে দেখি – 4

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের চতুর্থ অধ্যায়, ‘আয়তঘন’ -এর ‘কষে দেখি – 4’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

1. আমরা পরিবেশের 4টি আয়তঘনাকার ও 4টি ঘনক আকার বস্তুর নাম লিখি।

সমাধান –

4টি আয়তঘনাকার বস্তুর নাম – ইট, বাক্স, মুড়ির টিন এবং সুটকেশ।

4টি ঘনকাকার বস্তুর নাম – লুডোর ছক্কা, চৌকো টিনের বাক্স, চৌকো বাড়ি এবং চৌকো কাচের ব্লক।

2. পাশের আয়তঘনাকার চিত্রের তলগুলি, ধারগুলি ও শীর্ষবিন্দুগুলির নাম লিখি।

সমাধান –

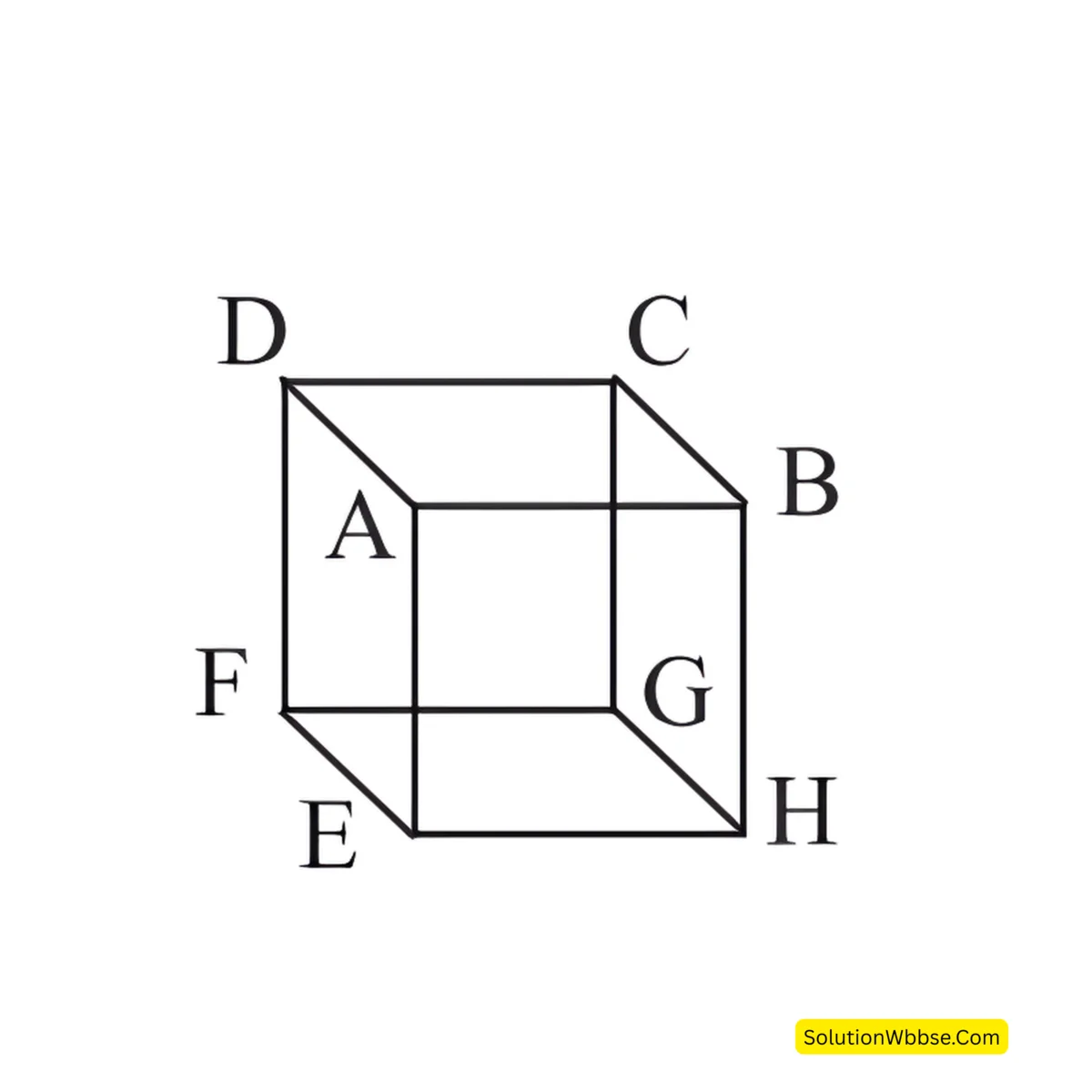
চিত্রে তলগুলি হল ABCD, EFGH, ADEF, BCGH, ABEH ও CDFG চিত্রে ধারগুলি হল AB, BC, CD, DA, EF, FG, EH, GH, AE, BH, CG ও FG চিত্রে শীর্ষবিন্দুগুলি হল A, B, C, D, E, F, G ও H.

3. একটি সমকোণী চৌপলাকার ঘরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 5 মি., 4 মি. ও 3 মি. হলে, ওই ঘরে সবচেয়ে লম্বা যে দণ্ড রাখা যাবে তার দৈর্ঘ্য হিসাব করে লিখি।

সমাধান –

সমকোণী চৌপলাকার ঘরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 5 মি., 4 মি. ও 3 মি.।

ঘরে সবচেয়ে লম্বা যে দণ্ড রাখা যাবে তার দৈর্ঘ্য = \(\sqrt{5^2+4^2+3^2}\) মি

= \(\sqrt{25+16+9}\) মি.

= \(\sqrt{50}\) মি.

= \(5\sqrt2\) মিটার।

4. একটি ঘনকের একটি তলের ক্ষেত্রফল 64 বর্গ মিটার হলে, ঘনকটির আয়তন হিসাব করে লিখি।

সমাধান –

ঘনকের একটি তলের ক্ষেত্রফল= 64 বর্গ মিটার

ঘনকের বাহুর দৈর্ঘ্য = \(\sqrt{64}\) = 8 মি

∴ ঘনকের আয়তন = (8)³ = 512 ঘনমিটার।

5. আমাদের বকুলতলা গ্রামে 2 মিটার চওড়া এবং 8 ডেসিমি. গভীর একটি খাল কাটা হয়েছে। যদি মোট 240 ঘন মিটার মাটি কাটা হয়ে থাকে তবে খালটি কত লম্বা হিসাব করে লিখি। 

সমাধান –

মনে করি, খালটি x মিটার লম্বা। 8 ডেসিমি = 0.8 মি. 

প্রশ্নানুসারে, 2 × x × 0.8 = 240

বা, 2 × x × \(\frac8{10}\) = 240

বা, \(x = \frac{150}{2400}\)

বা, x = 150

∴ খালটি 150 মিটার লম্বা।

6. একটি ঘনকের কর্ণের দৈর্ঘ্য \(4\sqrt3\) সেমি. হলে, ঘনকটির সমগ্রতলের ক্ষেত্রফল হিসাব করে লিখি।

সমাধান –

ঘনকের কর্ণের দৈর্ঘ্য = \(4\sqrt3\) সেমি.

ঘনকের বাহুর দৈর্ঘ্য = \(\frac{4\sqrt3}{\sqrt3}\) = 4 সেমি.

ঘনকের সমগ্রতলের ক্ষেত্রফল = 6 × (4)² বর্গ সেমি = 6 × 16 বর্গ সেমি = 96 বর্গসেমি।

7. একটি ঘনকের ধারগুলির দৈর্ঘ্যের সমষ্টি 60 সেমি. হলে, ঘনকটির ঘনফল হিসাব করে লিখি।

সমাধান –

ঘনকের ধারগুলির দৈর্ঘ্যের সমষ্টি 60 সেমি

ঘনকের একটি ধারের দৈর্ঘ্য = \(\frac{60}{12}\) = 5 সেমি .

∴ ঘনকটির ঘনফল = (5)³ ঘন সেমি = 125 ঘন সেমি

8. যদি একটি ঘনকের ছয়টি পৃষ্ঠতলের ক্ষেত্রফলের সমষ্টি 216 বর্গ সেমি. হয়, তবে ঘনকটির আয়তন কত হবে হিসাব করে লিখি।

সমাধান –

ঘনকের 6টি তলের ক্ষেত্রফল = 216 বর্গ সেমি

ঘনকের 1টি তলের ক্ষেত্রফল = \(\frac{216}6\) = 36 ঘন সেমি

ঘনকের বাহুর দৈর্ঘ্য = \(\sqrt6\) = 6 সেমি

∴ ঘনকের আয়তন = (6)³ ঘন সেমি = 216 ঘন সেমি

9. একটি সমকোণী চৌপলের আয়তন 432 ঘন সেমি। তাকে সমান আয়তন বিশিষ্ট দুটি ঘনকে পরিণত করা হলে, প্রতিটি ঘনকের প্রত্যেক ধারের দৈর্ঘ্য কত হবে হিসাব করে লিখি।

সমাধান –

প্রতিটি ঘনকের আয়তন = \(\frac{432}2\) = 216 ঘন সেমি

ধরি, ঘনকের প্রতিটি ধারের দৈর্ঘ্য = x সেমি

প্রশ্নানুসারে, x³ = 216

বা, x³ = 6³

বা, x = 6

∴ প্রতিটি ধারের দৈর্ঘ্য 6 সেমি। 

10. একটি ঘনকের প্রতিটি বাহুকে 50% কমানো হলো। মূল ঘনক ও পরিবর্তিত ঘনকের ঘনফলের অনুপাত কী হবে হিসাব করে লিখি।

সমাধান –

মনেকরি, ঘনকের বাহুর দৈর্ঘ্য = a সেমি

∴ ঘনকের আয়তন = a³ ঘন সেমি

ঘনকের বাহুর দৈর্ঘ্য 50% কমানো হলে ঘনকের বাহুর দৈর্ঘ্য হবে = \(\left(a-a\times\frac{50}{100}\right)=\left(a-\frac a2\right)=\frac a2\) সেমি

∴ পরিবর্তিত ঘনকের আয়তন = \(\left(\frac a2\right)^3=\frac{a^3}8\) ঘন সেমি

∴ মূল ঘনক ও পরিবর্তিত ঘনকের আয়তনের অনুপাত = \(a^3:\frac{a^3}8=8:1\)

11. একটি সমকোণী চৌপল আকারের বাক্সের দৈর্ঘ্য, প্রস্থ ও উচ্চতার অনুপাত 3 : 2 : 1 এবং উহার আয়তন 384 ঘন সেমি হলে বাক্সটির সমগ্রতলের ক্ষেত্রফল কত হবে হিসাব করে লিখি।

সমাধান –

মনেকরি, বাক্সটির দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে \(3x\) সেমি, \(2x\) সেমি ও \(x\) সেমি। প্রশ্নানুসারে, \(3x \times 2x \times x = 384\)

বা, \(6x^3 = 384\)

বা, \(x^3=\frac{384}{6}\)

বা, \(x^3=64=4^3\)

বা, \(x = 4\)

∴ ঘনকটির সমগ্রতলের ক্ষেত্রফল = \(2(3x \times 2x + 3x \times x + x \times 2x)\) ঘন সেমি

= \(2(6x^2 + 3x^2 + 2x^2)\) বর্গ সেমি

= \(22 \times (4)^2\) বর্গ সেমি

= \(22 \times 16\)

= \(352\) বর্গসেমি।

12. একটি চা-এর বাক্সের ভিতরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 7.5 ডেসিমি, 6 ডেসিমি এবং 5.4 ডেসিমি। চা ভর্তি বাক্সটির ওজন 52 বিগ্রা 350 গ্রাম। কিন্তু খালি অবস্থায় বাক্সটির ওজন 3.75 কিগ্রা হলে। ঘন ডেসিমি চা-এর ওজন কত হবে তা হিসাব করে লিখি।

সমাধান –

চা বাক্সে চা -এর ওজন = (52.350 – 3.75) কিগ্রা = 48.60 কিগ্রা

চা বাক্সের আয়তন = (7.5 × 6 × 5.4) ঘন ডেসিমি = 243 কিগ্রা

∴ প্রতি ঘন ডেসিমি চায়ের ওজন = \(\frac{48.60}{243}\) কিগ্রা = 0.2 কিগ্রা= 200 গ্রাম।

13. একটি বর্গাকার ভূমিবিশিষ্ট পিতলের প্লেটের দৈর্ঘ্য x সেমি, বেধ 1 মিলিমি হয় প্লেটটির ওজন 4725 গ্রাম, যদি 1 ঘন সেমি পিতলের ওজন 8.4 গ্রাম হয়, তাহলে x-এর মান কত হবে তা হিসাব করে লিখি।

সমাধান –

1 মিলিমি. = \(\frac{1}{10}\) সেমি

∴ পিতলের প্লেটের আয়তন = \(\left(x\times x\times\frac{1}{10}\right)=\frac{x^2}{10}\) ঘন সেমি

প্রশ্নানুসারে, \(\frac{x^2}{10}\times 8.4=4725\)

বা, \(\frac{x^2}{10}=\frac{4725}{8.4}\)

বা, \(x^2=\frac{4725\times10}{8.4}\)

বা, \(x^2 = \frac{4725\times100}{84}\)

বা, \(x^2=5625\)

বা, \(x=\sqrt{5625}\) = 75

∴ x-এর মান 75 সেমি।

14. চাঁদমারির রাস্তাটি উঁচু করতে হবে। তাই রাস্তার দুধারে 30 টি সমান গভীর ও সমান মাপের আয়তঘনাকার গর্ত খুঁড়ে সেই মাটি দিয়ে রাস্তাটি উঁচু করা হয়েছে। যদি প্রতিটি গর্তের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 14 মিটার ও 8 মিটার হয় এবং রাস্তাটি তৈরি করতে মোট 2520 ঘনমিটার মাটি লেগে থাকে তবে প্রতিটি গর্তের গভীরতা হিসাব করে লিখি।

সমাধান –

প্রতিটি গর্তের গভীরতা \(x\) মিটার

∴ প্রতিটি আয়তঘনাকার গর্তের আয়তন

= দৈর্ঘ্য ✕ প্রস্থ ✕ উচ্চতা

= \(14 \times 8 \times x\) ঘনমিটার

= \(112x\) ঘনমিটার

∴ \(30\) টি গর্তের আয়তন

= \(30 \times 112x\) ঘনমিটার

= \(3360x\) ঘনমিটার

শর্তানুসারে ,

\(3360x = 2520\)

বা, \(x = \frac{2520}{3360}\)

বা, \(x = 0.75\)

সুতরাং প্রতিটি গর্তের গভীরতা = \(0.75\) মিটার = \(75\) সেমি.।

15. ঘনকাকৃতি একটি সম্পূর্ণ জলপূর্ণ চৌবাচ্চা থেকে সমান মাপের 64 বালতি জল তুলে নিলে চৌবাচ্চাটির 1/3 অংশ জলপূর্ণ থাকে। চৌবাচ্চাটির একটি ধারের দৈর্ঘ্য 1.2 মিটার হলে প্রতিটি বালতিতে কত লিটার জল ধরে হিসাব করে লিখি।

সমাধান –

ঘনকাকৃতি জলপূর্ণ চৌবাচ্চাটির আয়তন

= \(1.2 \times 1.2 \times 1.2\) ঘন মিটার

= \(1.728\) ঘন মিটার

= \(1728\) ঘন ডেসিমি.

= \(1728\) লিটার

সমগ্র চৌবাচ্চাটির \(\frac{1}{3}\) অংশ

= \(\frac{1}{3} \times 1.728\) ঘনমিটার

= \(0.576\) ঘন মিটার

= \(576\) ঘন ডেসিমি

= \(576\) লিটার

চৌবাচ্চাটি থেকে তুলে নেওয়া জলের পরিমান

= \(1728 – 576\)

= \(1152\) লিটার

ধরি প্রতিটি বালতিতে জলধরে = \(x\) লিটার

∴ \(64\) বালতিতে জল ধরে \(64x\) লিটার

শর্তানুসারে ,

\(64x = 1152\)

বা, \(x = 18\)

∴ প্রতিটি বালতিতে \(18\) লিটার জল ধরে।

16. এক গ্রোস দেশলাই বাক্সের একটি প্যাকেটর দৈর্ঘ্য, প্রস্থ, উচ্চতা যথাক্রমে 2.8 ডেসিমি., 1.5 ডেসিমি. এবং 0.9 ডেসিমি. হলে একটি দেশলাই বাক্সের আয়তন কত হিসাব করি। [ 1 গ্রোস = 12 ডজন ] কিন্তু যদি একটি দেশলাই বাক্সের দৈর্ঘ্য 5 সেমি. এবং প্রস্থ 3.5 সেমি. হয়, তবে তার উচ্চতা কত হিসাব করে লিখি।

সমাধান –

ধরি, প্রতিটি দেশলাই বাক্সের উচ্চতা = \(h\) সেমি.

∴ একটি দেশলাই বাক্সের আয়তন = \(5 \times 3.5 \times h\) ঘনসেমি.

এক গ্রোস দেশলাই বাক্সের দৈর্ঘ্য

= \(2.8\) ডেসিমি.

= \(28\) সেমি.

প্রস্থ = \(1.5\) ডেসিমি. = \(15\) সেমি.

উচ্চতা = \(0.9\) ডেসিমি. = \(9\) সেমি.

এখন 1 গ্রোস দেশলাই বাক্সের আয়তন

= \(28 \times 15 \times 9\) ঘনসেমি.

শর্তানুসারে,

\(5 \times 3.5 \times h \times 12 \times 12 = 28 \times 15 \times 9\) [যেহেতু 1 গ্রোস = 12 ডজন আবার 1 ডজন = 12 টি]

বা, \(h = \frac{28 \times 15 \times 9}{5 \times 3.5 \times 12 \times 12}\)

বা, \(h = 1.5\)

∴ প্রতিটি দেশলাই বাক্সের আয়তন

= \(5 \times 3.5 \times 1.5\) ঘনসেমি.

= \(26.25\) ঘনসেমি.

অর্থাৎ প্রতিটি দেশলাই বাক্সের আয়তন = \(26.25\) ঘনসেমি.

প্রতিটি দেশলাই বাক্সের উচ্চতা = \(1.5\) সেমি.।

17. 2.1 মিটার দীর্ঘ, 1.5 মিটার প্রস্থ একটি আয়তঘনাকার চৌবাচ্চার অর্ধেক জলপূর্ণ আছে। ঐ চৌবাচ্চায় আরও 630 লিটার জল ঢাললে জলের গভীরতা কত বৃদ্ধি পাবে হিসাব করে লিখি।

সমাধান –

ধরি, আরও 630 লিটার জল ঢাললে জলতল h ডেসিমিটার বৃদ্ধি পাবে

চৌবাচ্চার দৈর্ঘ্য = 2.1 মিটার = 21 ডেসিমি.

চৌবাচ্চার প্রস্থ = 1.5 মিটার = 15 ডেসিমি.

এখন h ডেসিমিটার উচ্চতা বিশিষ্ট জলস্তম্ভের আয়তন = \(21 \times 15 \times h\) ঘনডেসিমি.

= \(21 \times 15 \times h\) লিটার [ যেহেতু 1 ঘন ডেসিমি. = 1 লিটার ]

শর্তানুসারে,

\(21 \times 15 \times h = 630\)

বা, \(h = \frac{630}{15 \times 21}\)

বা, \(h = 2\)

∴ জলতল 2 ডেসিমি. বৃদ্ধি পাবে।

18. গ্রামের আয়তক্ষেত্রাকার মাঠের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 20 মিটার ও 15 মিটার। ঐ মাঠের ভিতরের চারিদিকে চারটি কোনে পিলার বসানোর জন্য 4 মিটার দৈর্ঘ্য বিশিষ্ট চারটি ঘনকাকৃতি গর্ত কেটে অপসারিত মাটি অবশিষ্ট জমির ওপর ছড়িয়ে দেওয়া হল। মাঠের তলের উচ্চতা কততা বৃদ্ধি পেল হিসাব করে লিখি।

সমাধান –

4টি ঘনকাকৃতি গর্ত থেকে উত্তলিত মাটির পরিমান

= 4টি গর্তের আয়তন

= \(4 \times (4)^3\) ঘনমিটার

= 256 ঘনমিটার

4টি গর্ত বাদে মাঠের অবশিষ্ট অংশের ক্ষেত্রফল

= \({(20 \times 15) – 4 \times (4)^2}\) বর্গ মিটার

= (300 – 64) বর্গ মিটার

= 236 বর্গমিটার

ধরি , মাঠের তলের উচ্চতা বৃদ্ধি পেল h মিটার

শর্তানুসারে ,

\(236 \times h = 256\)

বা, \(h = \frac{256}{236}\)

বা, \(h = \frac{64}{59}\)

বা, \(h = 1 \frac{5}{59}\)

∴ মাঠের উচ্চতা বৃদ্ধি পাবে = \(\left(1 \frac{5}{59}\right)\) মিটার।

19. 48 মিটার লম্বা এবং 31.5 মিটার চওড়া একখণ্ড নীচু জমিকে 6.5 ডেসিমি. উঁচু করার জন্য ঠিক করা হয়েছে পাশের 27 মিটার লম্বা এবং 18.2 মিটার চওড়া একটি জমি গর্ত করে মাটি তোলা হবে। গর্তটি কত মিটার গভীর করতে হবে হিসাব করে লিখি।

সমাধান –

48 মিটার লম্বা এবং 31.5 মিটার চওড়া একখণ্ড নীচু জমিকে 6.5 ডেসিমি = 0.65 মিটার উঁচু করার জন্য প্রয়োজনীয় মাটির পরিমাণ = \(48 \times 31.5 \times 0.65\) ঘনমিটার

ধরি যে গর্ত থেকে মাটি তোলা হল তার গভীরতা = \(h\) মিটার

এখন উত্তলিত মাটির পরিমাণ = \(27 \times 18.2 \times h\) ঘনমিটার

শর্তানুসারে,

\(48 \times 31.5 \times 0.65 = 27 \times 18.2 \times h\)

বা, \(h = \frac{48 \times 31.5 \times 0.65}{27 \times 18.2}\)

বা, \(h = 2\)

সুতরাং গর্তটি 2 মিটার গভীর করতে হবে।

∴ গর্তটির গভীরতা 2 মিটার।

20. বাড়ির 3 টি কেরোসিন তেলের ড্রামে যথাক্রমে 800 লিটার , 725 লিটার এবং 575 লিটার তেল ছিল। ঐ তিনটি ড্রামের তেল একটি আয়তঘনাকার পাত্রে ঢালা হল এবং এতে পাত্রের গভীরতা 7 ডেসিমি. হল। ঐ আয়তঘনাকার পাত্রের দৈর্ঘ্য ও প্রস্থের অনুপাত 4:3 হলে পাত্রের দৈর্ঘ্য ও প্রস্থ হিসাব করে লিখি।

সমাধান –

3 টি ড্রামের মোট তেলের পরিমাণ = (800 + 725 + 575) লিটার

= 2100 লিটার

ধরি , আয়তঘনাকার পাত্রের দৈর্ঘ্য = \(4x\) ডেসিমি. , প্রস্থ = \(3x\) ডেসিমি.

জল ঢালার পর আয়তঘনাকার পাত্রের জলতলের উচ্চতা হয় 7 ডেসিমি.

এখন আয়তঘনাকার পাত্রের জলস্তম্ভের আয়তন

= \(4x \times 3x \times 7\) ঘনডেসিমি.

= \(84x^2\) ঘনডেসিমি.

= \(84x^2\) লিটার [ যেহেতু 1 ঘনডেসিমি. = 1 লিটার ]

শর্তানুসারে ,

\(84x^2 = 2100\)

বা, \(x^2 = \frac{2100}{84}\)

বা, \(x^2 = 25\)

বা, \(x = 5\)

∴ পাত্রটির দৈর্ঘ্য = \(4 \times 5 = 20\) ডেসিমি.

পাত্রটির প্রস্থ = \(3 \times 5 = 15\) ডেসিমি.

এখন আয়তঘনাকার পাত্রের গভীরতা \(5\) ডেসিমি. হলে আয়তন হত

= \(20 \times 15 \times 5\) ঘনডেসিমি.

= \(1500\) ঘনডেসিমি.

= \(1500\) লিটার [যেহেতু 1 ঘনডেসিমি.=1 লিটার]

সুতরাং পাত্রটিতে সর্বাধিক 1500 লিটার জল ধরে

অর্থাৎ পাত্রটিতে 1620 লিটার জল কোনোভাবে রাখা সম্ভব নয়।

21.আমাদের তিনতলা ফ্ল্যাটের তিনটি পরিবারের দৈনিক জলের চাহিদা যথাক্রমে 1200 লিটার, 1050 লিটার এবং 950 লিটার। এই চাহিদা মেটানোর পরও 25 % জল মজুদ থাকে এমন একটি ট্যাঙ্ক বসানোর জন্য মাত্র 2.5 মিটার দীর্ঘ এবং 1.6 মিটার চওড়া একটি জায়গা পাওয়া গেছে। ট্যাঙ্কটি কত মিটার গভীর করতে হবে হিসাব করে লিখি। জায়গাটি যদি প্রস্থের দিকে আরও 4 ডেসিমি বেশি হত তবে ট্যাঙ্কটি কতটা গভীর করতে হত হিসাব করে লিখি।

সমাধান –

তিনটি পরিবারের দৈনিক মোট জলের চাহিদা

= \((1200 + 1050 + 950)\) লিটার

= \(3200\) লিটার

মোট দৈনিক চাহিদার \(25%\)

= \(\frac{25}{100} \times 3200\) লিটার

= \(800\) লিটার

অর্থাৎ যে ট্যাঙ্কটি বানাতে হবে তার আয়তন হবে

= \(3200 + 800\) লিটার

= \(4000\) লিটার

= \(4000\) ঘনডেসিমি

= \(4\) ঘনমিটার

ট্যাঙ্কটির দৈর্ঘ্য = \(2.5\) মিটার

ট্যাঙ্কটির প্রস্থ = \(1.6\) মিটার

ধরি, ট্যাঙ্কটির গভীরতা = \(x\) মিটার

শর্তানুসারে,

\(2.5 \times 1.6 \times x = 4\)

বা, \(x = \frac{4}{1.6 \times 2.5}\)

বা, \(x = 1\)

∴ ট্যাঙ্কটি \(1\) মিটার গভীর করতে হবে।

ট্যাঙ্কটির প্রস্থ আরও \(4\) ডেসিমি. বৃদ্ধি করলে পরিবর্তিত প্রস্থ হবে = \((1.6 \times 10) + 4 = 20\) ডেসিমি.

ধরি ট্যাঙ্কটির গভীরতা হবে = \(d\) ডেসিমি.

শর্তানুসারে,

\(2.5 \times 10 \times 20 \times d = 4000\)

বা, \(25 \times 20 \times d = 4000\)

বা, \(d = \frac{4000}{500} = 8\)

∴ ট্যাঙ্কটির গভীরতা হবে = \(8\) ডেসিমি. = \(0.8\) মিটার।

22. 5 সেমি পুরু কাঠের তক্তায় তৈরি ঢাকনাসহ একটি কাঠের বাক্সের ওজন 115.5 কিগ্রা। কিন্তু চাল ভরতি বাক্সের ওজন 880.5 কিগ্রা। বাক্সটির ভিতরের দিকের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 12 ডেসিমি. ও 8.5 ডেসিমি. এবং 1 ঘন ডেসিমি. চালের ওজন 1.5 কিগ্রা। বাক্সতির ভিতরের উচ্চতা কত হিসাব করে লিখি। প্রতি বর্গডেসিমি. 1.50 টাকা হিসাবে বাক্সটির বাইরের চারপাশ রঙ করতে কত খরচ পরবে হিসাব করে লিখি।

সমাধান –

কাঠের বাক্সের ওজন \(115.5\) কিগ্রা.

চালু কাঠের বাক্সের ওজন \(880.5\) কিগ্রা.

∴ শুধু চালের ওজন = \((880.50 – 115.50)\) কিগ্রা. = \(765\) কিগ্রা.

1 ঘন ডেসিমি চালের ওজন \(1.5\) কিগ্রা.

∴ চালের আয়তন = \(765/1.5\) ঘনডেসিমি. = \(510\) ঘনডেসিমি.

বাক্সটির ভিতরের দিকের দৈর্ঘ্য ও প্রস্থ যথাক্রমে \(12\) ডেসিমি. ও \(8.5\) ডেসিমি.

ধরি বাক্সটির ভিতরের দিকের উচ্চতা \(h\) ডেসিমি.

∴ \( 12 \times 8.5 \times h = 510\)

বা, \(h = \frac{510}{12 \times 8.5}\)

বা, \(h = 5\)

∴ বাক্সটির ভিতরের দিকের উচ্চতা = \(5\) ডেসিমি.

এখন \(5\) সেমি. = \(0.5\) ডেসিমি. পুরু ঢাকনাসহ বাক্সটির বাইরের দিকের দৈর্ঘ্য

= \(12 + 0.5 + 0.5 = 13\) ডেসিমি.

বাইরের দিকের প্রস্থ

= \(8.5 + 0.5 + 0.5 = 9.5\) ডেসিমি.

বাইরের দিকের উচ্চতা

= \(5 + 0.5 + 0.5 = 6\) ডেসিমি.

∴ ঢাকনাসহ বাক্সটির সমগ্রতলের ক্ষেত্রফল

= \(2(13 \times 9.5 + 9.5 \times 6 + 6 \times 13)\) বর্গডেসিমি.

= \(2(123.5 + 57 + 78)\) বর্গডেসিমি.

= \(517\) বর্গডেসিমি.

প্রতি বর্গডেসিমি. \(1.50\) টাকা হিসাবে বাক্সটির বাইরের সমগ্রতল রঙ করতে মোট খরচ হয়

= \(517 \times 1.50 = 775.50\) টাকা.

23. 20 মিটার দীর্ঘ এবং 18.5 মিটার চওড়া একটি আয়তঘনাকার পুকুরে 3.2 মিটার গভীর জল আছে। ঘণ্টায় 160 কিলোলিটার জলসেচ করতে পারে এমন একটি পাম্প দিয়ে কতক্ষনে পুকুরটির সমস্ত জলসেচ করা যাবে হিসাব করে লিখি। ঐ জল যদি 59.2 মিটার দীর্ঘ এবং 40 মিটার চওড়া একটি আল দেওয়া ক্ষেতে ফেলা হয়,তবে সেই জমিতে জলের গভীরতা কত হবে হিসাব করে লিখি। [1 ঘন মিটার = 1 কিলো লিটার]

সমাধান –

পুকুরের মোট জলের পরিমাণ = \(20 \times 18.5 \times 3.2\) ঘন মিটার

= \(1184\) কিলোলিটার [ যেহেতু 1 ঘন মিটার = 1 কিলোলিটার ]

পাম্প দিয়ে পুকুরের সমস্ত জল সেচ করতে সময় লাগবে

= \(1184 / 160\) ঘণ্টা

= \(37/5\) ঘণ্টা

= \(7\) পূর্ণ \(2/5\) ঘণ্টা

= \(7\) ঘণ্টা \((2/5 \times 60)\) মিনিট

= \(7\) ঘণ্টা 24 মিনিট

ধরি , ওই জল \(59.5\) মিটার দীর্ঘ , \(40\) মিটার চওড়া আল দেওয়া ধানক্ষেতে ফেললে সেই জমিতে জলের গভীরতা \(h\) মিটার হবে।

প্রশ্নানুসারে,

\(59.2 \times 40 \times h = 1184\)

বা, \(h = \frac{1184}{59.2 \times 40}\)

বা, \(h = \frac{1}{2}\)

বা, \(h = 0.5\)

সুতরাং ধানক্ষেতে জলের গভীরতা হবে \(0.5\) মিটার।

অতিসংক্ষিপ্তধর্মী প্রশ্ন

(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.):

(i) একটি সমকোণী চৌপলাকৃতি বাক্সের ভিতরের আয়তন 440 ঘন সেমি এবং ভিতরের ভূমিতলের ক্ষেত্রফল 88 বর্গ সেমি। বাক্সটির ভিতরের উচ্চতা-

(a) 4 সেমি
(b) 5 সেমি
(c) 3 সেমি
(d) 6 সেমি

উত্তর – (b) 5 সেমি

(ii) একটি আয়তঘনাকার গর্তের দৈর্ঘ্য 40 মি., প্রস্থ 12 মি. এবং গভীরতা 16 মি.। ঐ গর্তের মধ্যে 5 মি. দৈর্ঘ্য, 4 মি. প্রস্থ ও 2 মি. পুরু তক্তা রাখা যাবে

(a) 190 টি
(b) 192 টি
(c) 184 টি
(d) 180 টি

উত্তর – (b) 192 টি

(iii) একটি ঘনকের পার্শ্বতলের ক্ষেত্রফল 256 বর্গ মিটার। ঘনকটির আয়তন

(a) 64 ঘন মি.
(b) 216 ঘন মি.
(c) 256. ঘন মি.
(d) 512 ঘন মি.

উত্তর – (d) 512 ঘন মি.

(iv) দুটি ঘনকের আয়তনের অনুপাত 1 : 27 হলে, ঘনক দুটির সমগ্রতলের ক্ষেত্রফলের অনুপাত

(a) 1 : 3
(b) 1 : 8
(c) 1 : 9
(d) 1 : 18

উত্তর – (c) 1 : 9

(v) একটি ঘনকের সমগ্রতলের ক্ষেত্রফল s বর্গ একক এবং কর্ণের দৈর্ঘ্য d একক হলে s ও d-এর সম্পর্ক

(a) s = 6d²

(b) 3s = 7d

(c) s³ = d²

(d) \(d^2=\frac s2\)

উত্তর – (d) \(d^2=\frac s2\)

(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখ:

(i) একটি ঘনকের প্রতিটি ধারের দৈর্ঘ্য দ্বিগুন হলে, ঘনকটির আয়তন প্রথম ঘনকের 4 গুন হবে।

উত্তর – উক্তিটি মিথ্যা।

(ii) বর্ষার সময় 2 হেক্টর জমিতে বৃষ্টিপাত 5 সেমি উচ্চতার হলে বৃষ্টি জলের আয়তন 1000 ঘনমিটার।

উত্তর – উক্তিটি সত্য।

(C) শূন্যস্থান পূরণ করি –

(i) একটি ঘনকের একটি তলের কর্ণের দৈর্ঘ্য ___।

উত্তর – একটি সমকোণী চৌপলের কর্ণের সংখ্যা 4 টি।

(ii) একটি ঘনকের একটি তলের কর্ণের দৈর্ঘ্য = __× একটি ধারের দৈর্ঘ্য।

উত্তর – একটি ঘনকের একটি তলের কর্ণের দৈর্ঘ্য = \(\sqrt2\) × একটি ধারের দৈর্ঘ্য।

(iii) সমকোণী চৌপলের দৈর্ঘ্য, প্রস্থ ও উচ্চতা সমান হলে সেই ঘনবস্তুর বিশেষ নাম ___।

উত্তর – সমকোণী চৌপলের দৈর্ঘ্য, প্রস্থ ও উচ্চতা সমান হলে সেই ঘনবস্তুর বিশেষ নাম ঘনক।

সংক্ষিপ্তধর্মী প্রশ্ন (S.A.)

(i) একটি আয়তঘনের তলসংখ্যা = x, ধারসংখ্যা = y, শীর্ষবিন্দুর সংখ্যা = z এবং কর্ণের সংখ্যা = p হলে x – y + z + p এর মান কত তা লিখি।

সমাধান –

আয়তঘনের তল সংখ্যা = x = 6 টি

ধার সংখ্যা = y = 12 টি

শীর্ষবিন্দুর সংখ্যা = z = 8 টি

কর্ণের সংখ্যা = p = 4 টি

∴ x-y+z+p=6-12+8+4 = 6

(ii) দুটি আয়তঘনের মাত্রাগুলির দৈর্ঘ্য যথাক্রমে 4, 6, 4 একক এবং 8, (2h 1), 2 একক। যদি আয়তঘন দুটির ঘনফল সমান হয়, তাহলে h-এর মান কত লিখি।

সমাধান –

যেহেতু আয়তঘন দুটির আয়তন সমান

∴ \(4 \times 6 \times 4 = 8 \times (2h-1) \times 2\)

বা, \(96 = 16 \times (2h-1)\)

বা, \((2h-1) = 96/16\)

বা, \(2h-1 = 6\)

বা, \(h = 7/2\)

বা, \(h = 3.5\)

(iii) একটি ঘনকের প্রত্যেকটি ধারের দৈর্ঘ্য 50% বৃদ্ধি পেলে, ঘনকটির সমগ্রতলের ক্ষেত্রফল শতকরা কত বৃদ্ধি পাবে তা হিসাব করে লিখি।

সমাধান –

ধরি একটি ঘনকের বাহুর দৈর্ঘ্য \(a\) একক

∴ ঘনকটির সমগ্র তলের ক্ষেত্রফল = \(6a^2\) বর্গ একক

এখন বাহুর দৈর্ঘ্য 50% বৃদ্ধি করলে পরিবর্তিত ঘনকের বাহুর দৈর্ঘ্য হবে

= \(a + \frac{50}{100} \times a\) একক = \(a + \frac{a}{2}\) একক = \(\frac{3a}{2}\) একক

∴ পরিবর্তিত ঘনকের সমগ্রতলের ক্ষেত্রফল = \(6 \times \left(\frac{3a}{2}\right)^2\) বর্গ একক

= \(6 \times \frac{9a^2}{4}\) বর্গ একক

= \(\frac{27}{2} a^2\) বর্গ একক

∴ সমগ্রতলের ক্ষেত্রফল বৃদ্ধি পেল = \(\frac{27}{2} a^2 – 6a^2\) বর্গ একক

= \(\frac{27a^2 – 12a^2}{2}\) বর্গ একক

= \(\frac{15a^2}{2}\) বর্গ একক

∴ ক্ষেত্রফল শতকরা বৃদ্ধি পেল = \(\frac{\frac{15a^2}{2}}{6a^2} \times 100\)

= \(\frac{15a^2}{12a^2} \times 100\)

= \(125%\)

∴ একটি ঘনকের বাহুর দৈর্ঘ্য 50% বৃদ্ধি করলে ঘনকটির সমগ্রতলের ক্ষেত্রফলের ক্ষেত্রফল শতকরা বৃদ্ধি পাবে 125%।

(iv) একটি নিরেট ঘনক যাদের প্রত্যেকটি ধারের দৈর্ঘ্য যথাক্রমে 3 cm ,4cm এবং 5 cm। ঘনক তিনটিকে গলিয়ে একটি নতুন ঘনক তৈরি করা হল। নতুন ঘনকটির একটি ধারের দৈর্ঘ্য কত হবে তা লিখি।

সমাধান –

ধরি নতুন ঘনকের প্রতিটি ধারের দৈর্ঘ্য \(a\) cm.

যেহেতু তিনটি ছোটো ঘনক কে গলিয়ে একটি বড় ঘনক তৈরি করা হয়েছে সুতরাং তিনটি ঘনকের মোট আয়তন বড় ঘনকটির আয়তনের সাথে সমান হবে।

∴ \( (3)^3 + (4)^3 + (5)^3 = a^3\)

বা, \(27 + 64 + 125 = a^3\)

বা, \(a^3 = 216\)

বা, \(a^3 = (6)^3\)

বা, \(a = 6\)

∴ নতুন ঘনকটির প্রতিটি ধারের দৈর্ঘ্য হবে \(6\) cm.

(v) একটি ঘরের দুটি সংলগ্ন দেয়ালের দৈর্ঘ্য যথাক্রমে 12 মিটার ও 8 মিটার। ঘরটির উচ্চতা 4 মিটার হলে ঘরটির মেঝের ক্ষেত্রফল কত তা হিসাব করে লিখি।

ঘরটির মেঝের ক্ষেত্রফল = (12 × 8) বর্গ মিটার = 96 বর্গ মিটার।

---

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের চতুর্থ অধ্যায়, ‘আয়তঘন’ -এর ‘কষে দেখি – 4’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।

আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।