মাধ্যমিক গণিত – বৃত্ত সম্পর্কিত উপপাদ্য – কষে দেখি – 3.2

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের তৃতীয় অধ্যায়, ‘বৃত্ত সম্পর্কিত উপপাদ্য’ -এর ‘কষে দেখি – 3.2’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

1. O কেন্দ্রীয় একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি. এবং AB একটি জ্যা -এর দৈর্ঘ্য 8 সেমি.। O বিন্দু থেকে AB জ্যা-এর দূরত্ব হিসাব করে লিখি।

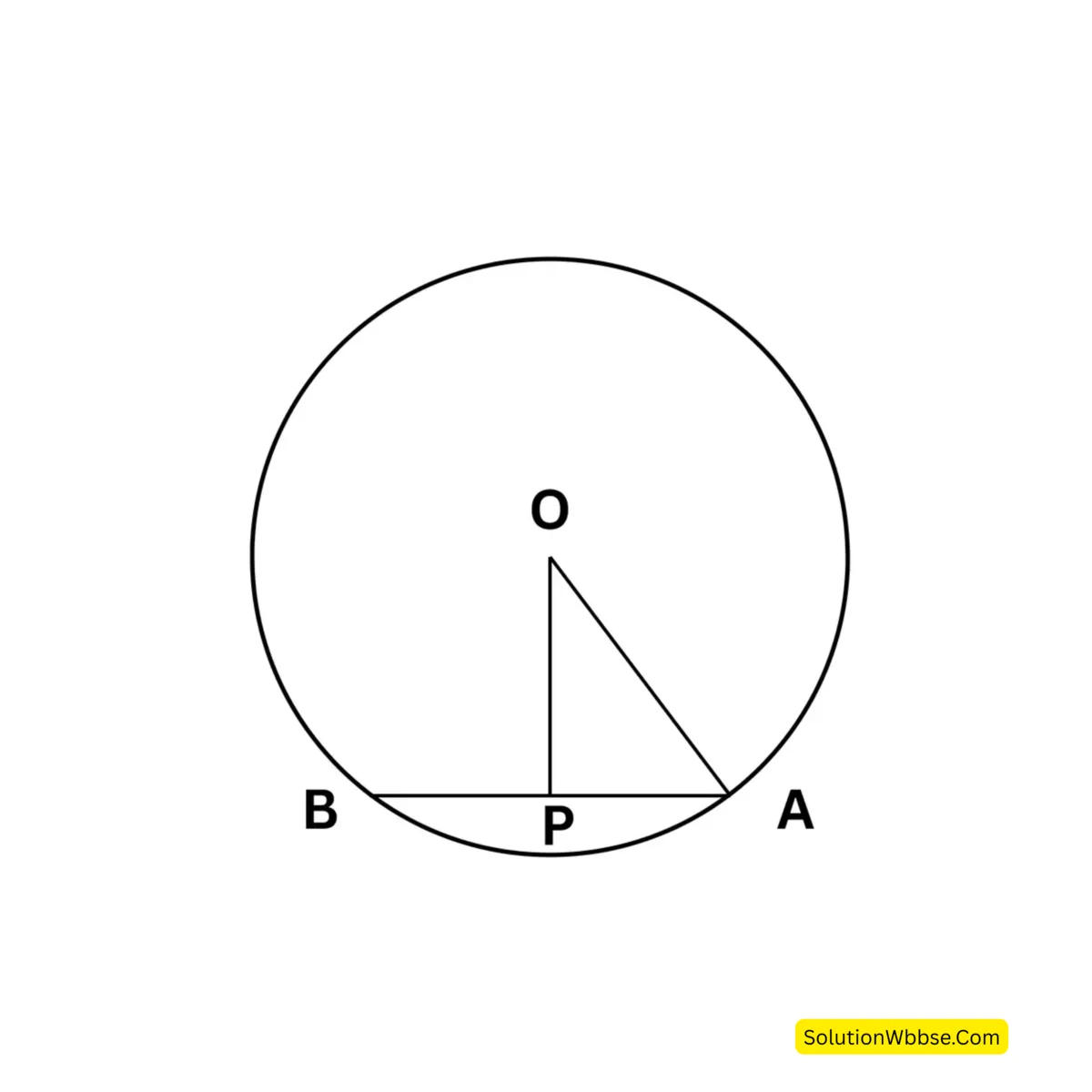
O কেন্দ্রীয় বৃত্তের ব্যাসার্ধ OA = 5 সেমি. ঐ বৃত্তের AB জ্যার দৈর্ঘ্য 8 সৈমি.। O বিন্দু থেকে AB জ্যার উপর OP লম্বপাত করা হয়েছে। OP হল O বিন্দু থেকে AB জ্যার লম্ব দূরত্ব। OP ⊥ AB, সেজন্য AB জ্যা P বিন্দুতে সমদ্বিখণ্ডিত হয়।

অর্থাৎ \(AP=\frac12AB=\frac12\times8\) সেমি = 4 সেমি। এখন OAP সমকোণী ত্রিভুজে OA অতিভুজ; সেজন্য \(OP^2+AP^2=OA^2\)

বা, OP² = OA² – AP² = (5)² – (4)² = 25 – 16 = 9

∴ OP = \(\sqrt9\) = 3

O বিন্দু থেকে AB জ্যার লম্ব দূরত্ব = 3 সেমি।

2. Ο কেন্দ্রীয় একটি বৃত্তের ব্যাসের দৈর্ঘ্য 26 সেমি.। O বিন্দু থেকে PQ জ্যা-এর দূরত্ব 5 সেমি.। PQ জ্যা-এর দৈর্ঘ্য হিসাব করে লিখি।

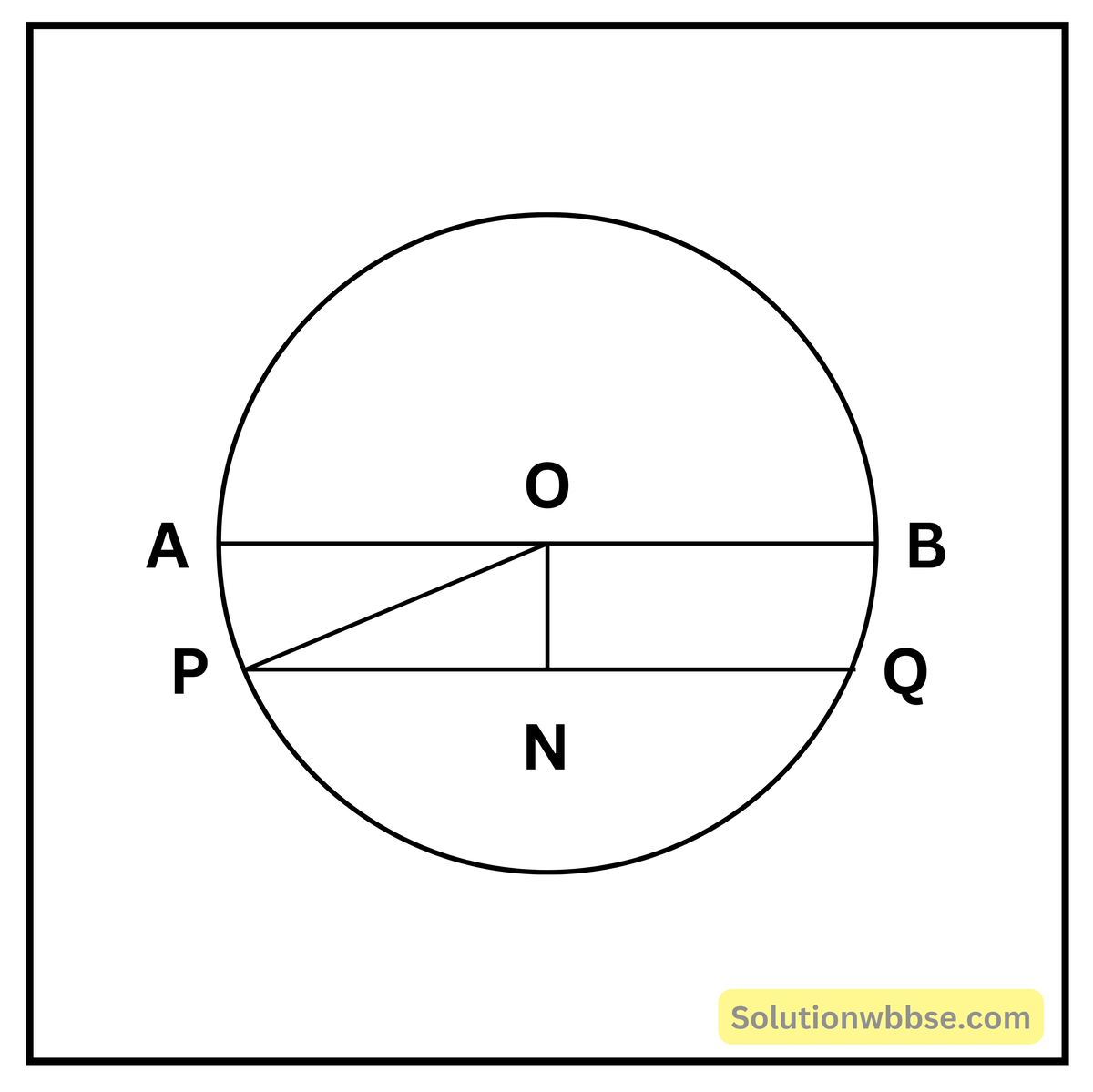
O কেন্দ্রীয় বৃত্তের একটি ব্যাস AB এবং PQ একটি জ্যা। O বিন্দু থেকে PQ-জ্যার উপর ON লম্ব আঁকা হয়েছে। দেওয়া আছে AB = 26 সেমি এবং ON = 5 সেমি।

PQ জ্যাটির দৈর্ঘ্য নির্ণয় করতে হবে। যেহেতু ব্যাস AB = 26 সেমি, OA = ব্যাসার্ধ = OP = 13 সেমি। আবার যেহেতু ON ⊥ PQ, PN = QN, এখন OA সমকোণী ত্রিভুজে OP অতিভুজ সেজন্য PN² + ON² = OP² বা, PN² = OP² – ON² = (13)² – (5)² = 169 – 25 = 144

∴ PN = \(\sqrt{144}\) = 12 সেমি।

যেহেতু PN = QN, PQ = 2PN = 2 × 12 সেমি = 24 সেমি।

∴ PQ জ্যার দৈর্ঘ্য = 24 সেমি।

3. O কেন্দ্রীয় একটি বৃত্তের PQ জ্যা-এর দৈর্ঘ্য 4 সেমি. এবং O বিন্দু থেকে PQ-এর দূরত্ব 2.1 সেমি.। বৃত্তের ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।

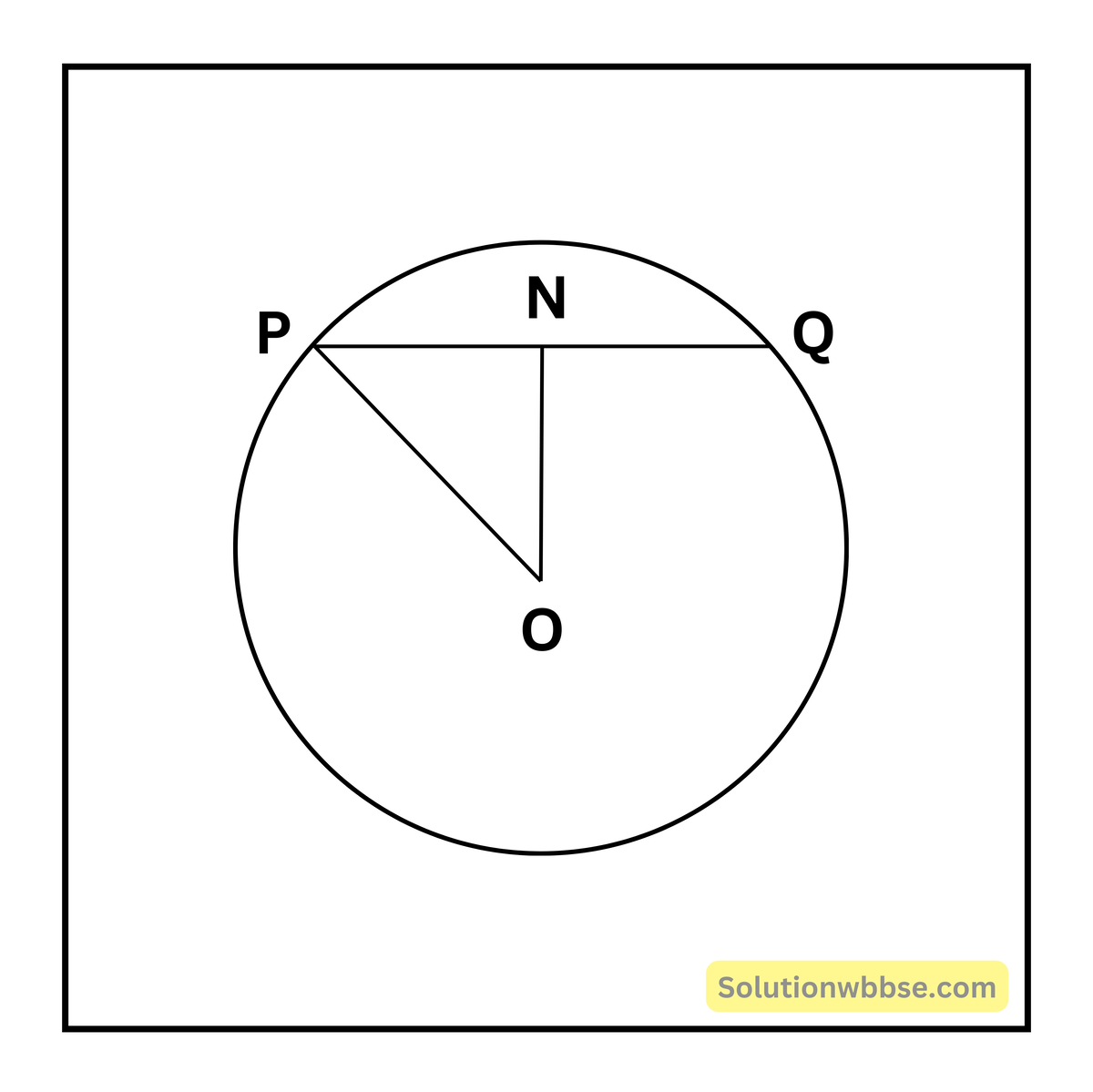
O কেন্দ্রীয় বৃত্তের PQ জ্যা-র দৈর্ঘ্য = 4 সেমি; কেন্দ্র O বিন্দু থেকে PQ জ্যার উপর ON লম্ব আঁকা হয়েছে; দেওয়া আছে যে, ON = 2.1 সেমি।

যেহেতু ON ⊥ PQ; PN = QN = \(\frac12\)PQ = \(\frac12\) × 4 সেমি = 2 সেমি।

OPN সমকোণী ত্রিভুজে OP অতিভুজ সেজন্য OP² = ON² + PN² = (2.1)² + (2)² = 4.41 + 4 = 8.41

∴ OP = \(\sqrt{8.41}\) = 2.9 সেমি

বৃত্তটির ব্যাসার্ধ = 2.9 সেমি

বৃত্তের ব্যাসের দৈর্ঘ্য = 2 × ব্যাসার্ধ = (2 × 2.9) সেমি = 5.8 সেমি।

4. O কেন্দ্রীয় বৃত্তে 6 সেমি. ও 8 সেমি. দৈর্ঘ্যের দুটি জ্যা। যদি ছোটো দৈর্ঘ্যের জ্যা-টির বৃত্তের কেন্দ্র থেকে দূরত্ব 4 সেমি. হয়, তাহলে অপর জ্যাটির কেন্দ্র থেকে দূরত্ব কত তা হিসাব করে লিখি।

ধরি, AB = 6 সেমি, CD = 8 সেমি

AM = BM = \(\frac62\) = 3 সেমি

সমকোণী ΔMOB হইতে পাই OB² = OM² + MB² = 4² + 3² = 16 + 9 = 25

∴ OB = \(\sqrt{25}\) = 5 সেমি অর্থাৎ বৃত্তটির ব্যাসার্ধ 5 সেমি. OC = 5 সেমি

CM = \(\frac12\) × CD = \(\frac12\) × 8 = 4 সেমি

সমকোণী ΔCON হইতে পাই,

ON = \(\sqrt{OC^2-CN^2}\) সেমি = \(\sqrt{5^2-4^2}\) সেমি = \(\sqrt{25-16}\) সেমি = \(\sqrt9\) সেমি = 3 সেমি

∴ অপর জ্যাটির কেন্দ্র থেকে দূরত্ব 3 সেমি।

5. যদি কোনো বৃত্তের একটি জ্যা-এর দৈর্ঘ্য 48 সেমি. এবং কেন্দ্র থেকে ওই জ্যা-এর দূরত্ব 7 সেমি. হয়, তবে ওই বৃত্তের কেন্দ্র থেকে যে জ্যা-এর দূরত্ব 20 সেমি., সেই জ্যা-এর দৈর্ঘ্য কত হবে তা হিসাব করে লিখি।

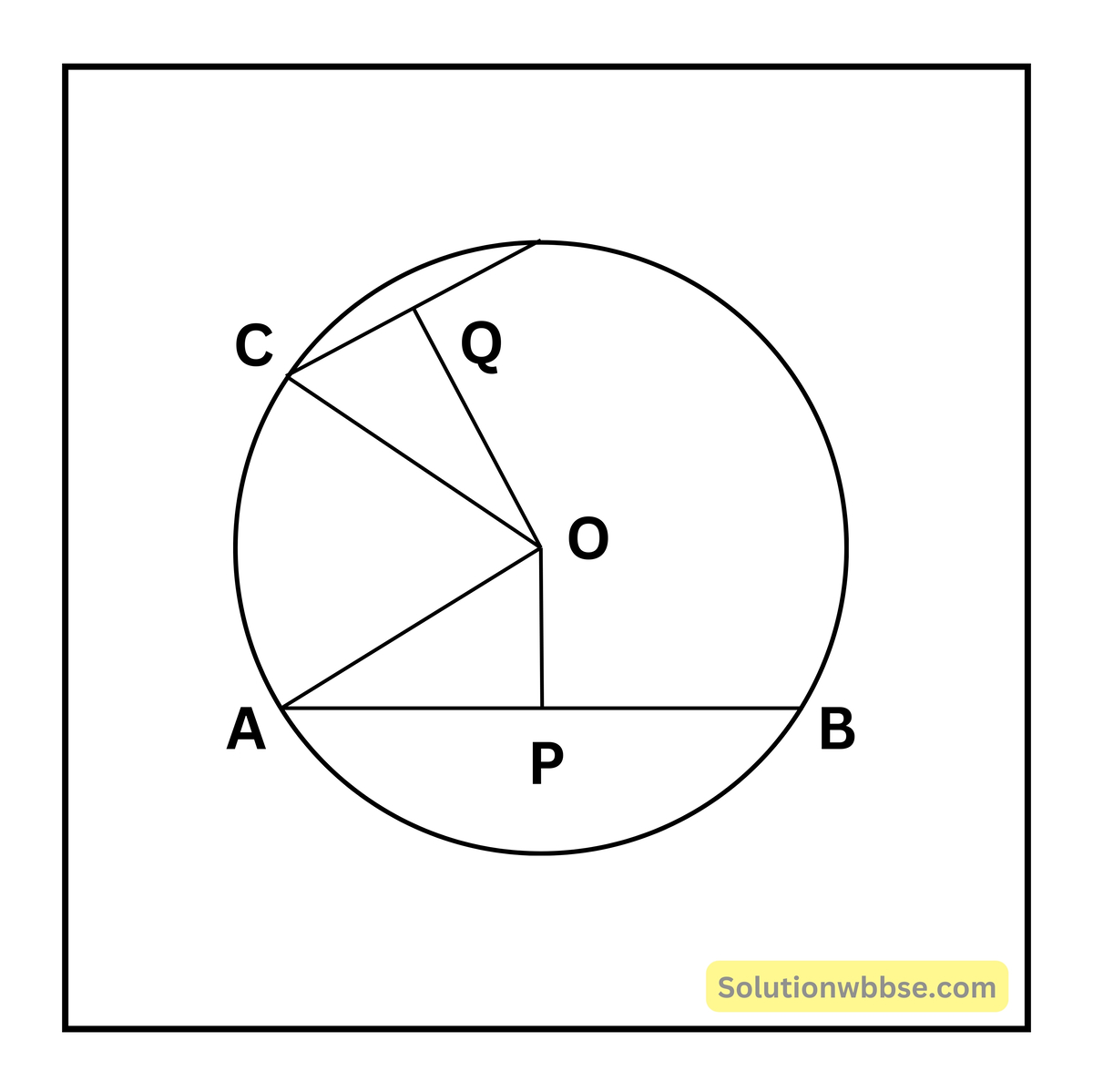
O কেন্দ্রীয় বৃত্তের AB জ্যাটির দৈর্ঘ্য 48 সেমি এবং O কেন্দ্র থেকে AB জ্যার দূরত্ব 7 সেমি। আবার, ঐ বৃত্তের কেন্দ্র থেকে CD জ্যার দূরত্ব 20 সেমি; CD-এর দৈর্ঘ্য নির্ণয় করতে হবে।

OP ⊥ AB এবং OQ ⊥ CD আঁকা হল। O, A এবং O, C যুক্ত করা হল।

∵ OP ⊥ AB, AP = BP = \(\frac12\)AB = \(\frac12\) × 48 সেমি = 24 সেমি।

আরও দেওয়া আছে, OP = 7 সেমি, OQ = 20 সেমি।

OAP সমকোণী ত্রিভুজে OA অতিভুজ সেজন্য OA² = OP² + AP² = (7)² + (24)² = 49 + 576 = 625

∴ OA = \(\sqrt{625}\) = 25 সেমি।

সুতরাং ব্যাসার্ধ OC = ব্যাসার্ধ OA = 25 সেমি। এবার OCQ সমকোণী ত্রিভুজে CQ² + OQ² = OC² বা, CQ² = OC² – OQ² = (25)² – (20)² = 625 – 400 = 225

∴ CQ = \(\sqrt{225}\) = 15 সেমি।

যেহেতু OQ ⊥ CD, CD জ্যা Q বিন্দুতে সমদ্বিখণ্ডিত হয়।

∴ CD = 2CQ = 2 × 15 সেমি = 30 সেমি। কেন্দ্র O থেকে যে জ্যার দূরত্ব 20 সেমি, সেই জ্যার দৈর্ঘ্য= 30 সেমি।

6. পাশের O কেন্দ্রীয় বৃত্তের ছবিতে OP ⊥ AB; AB = 6 সেমি. এবং PC = 2 সেমি. হলে, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য হিসাব করে লিখি।

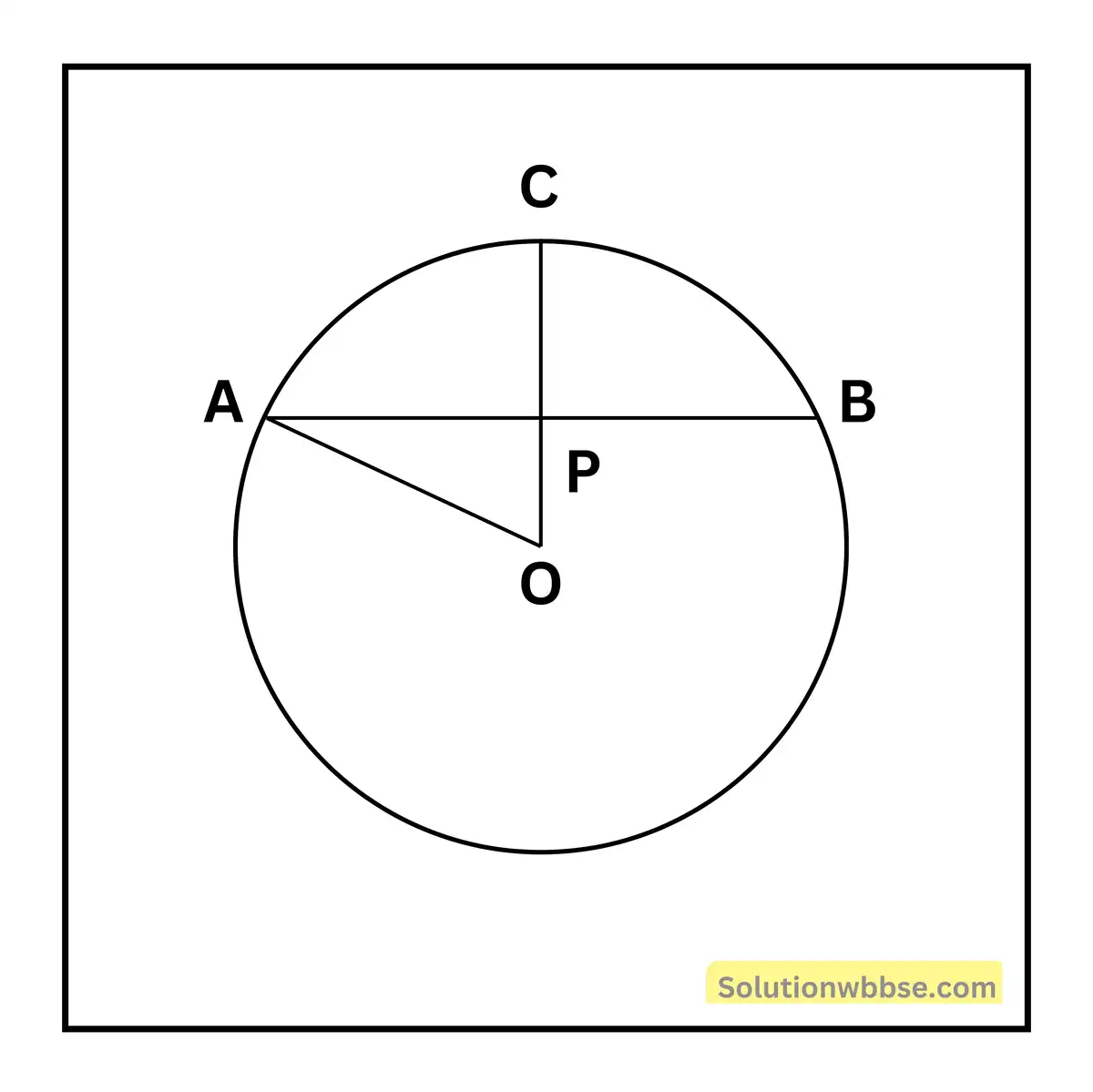
O, A যোগ করা হল। তাহলে ব্যাসার্ধ OA = OC = r সেমি মনে করা যাক। দেওয়া আছে PC = 2 সেমি

∴ OP = OC – PC = (r – 2) সেমি।

যেহেতু OP ⊥ AB, AB জ্যা P বিন্দুতে সমদ্বিখণ্ডিত হয় সেজন্য AP = \(\frac12\)

AB = \(\frac12\) × 6 সেমি = 3 সেমি।

OAP সমকোণী ত্রিভুজে OA² = OP² + AP²

বা, (r)² = (r – 2)² + (3)²

বা, r² = r² – 4r + 4 + 9

বা, 4r = 13

∴ r = \(\frac{13}4\) = 3.25, বৃত্তটির ব্যাসার্ধের দৈর্ঘ্য = 3.25 সেমি।

7. একটি সরলরেখা দুটি এককেন্দ্রীয় বৃত্তের একটিকে A ও B বিন্দুতে এবং অপরটিকে C ও D বিন্দুতে ছেদ করেছে। যুক্তি দিয়ে প্রমাণ করি যে AC = DB

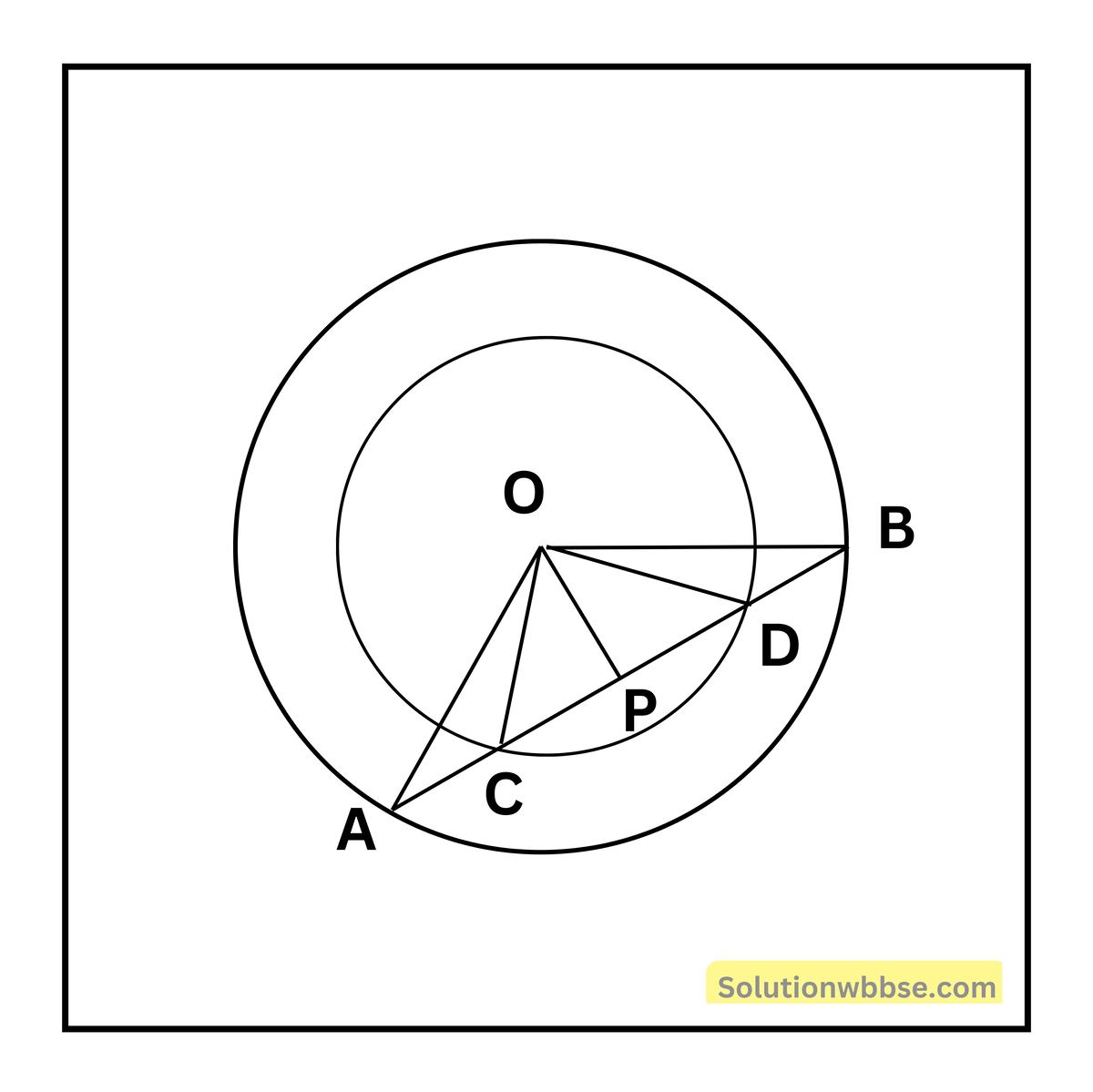
দেওয়া আছে – একটি সরলরেখা O কেন্দ্রীয় দুটি বৃত্তের একটিকে A ও B বিন্দুতে এবং অপরটিকে C ও D বিন্দুতে ছেদ করে। 

প্রমাণ করতে হবে যে, AC = BD

অঙ্কন – O, A; O, C; O, B; O, D যুক্ত করা হল এবং AB-র উপর OP লম্ব আঁকা হল।

প্রমাণ – O কেন্দ্রীয় বৃত্তের কেন্দ্র O থেকে AB জ্যার উপর OP লম্ব। সেজন্য AB জ্যা P বিন্দুতে সমদ্বিখণ্ডিত হয়। 

অর্থাৎ, AP = BP আবার কেন্দ্রীয় বৃত্তের কেন্দ্র O থেকে CD-জ্যার উপর OP লম্ব। সেজন্য CP = DP এখন, AP – CP = BP – DP অর্থাৎ, AC = BD (প্রমাণিত)

8. প্রমাণ করি, কোনো বৃত্তের দুটি পরস্পরচ্ছেদী জ্যা পরস্পরকে সমদ্বিখণ্ডিত করতে পারে না, যদি না উভয়েই বৃত্তের ব্যাস হয়।

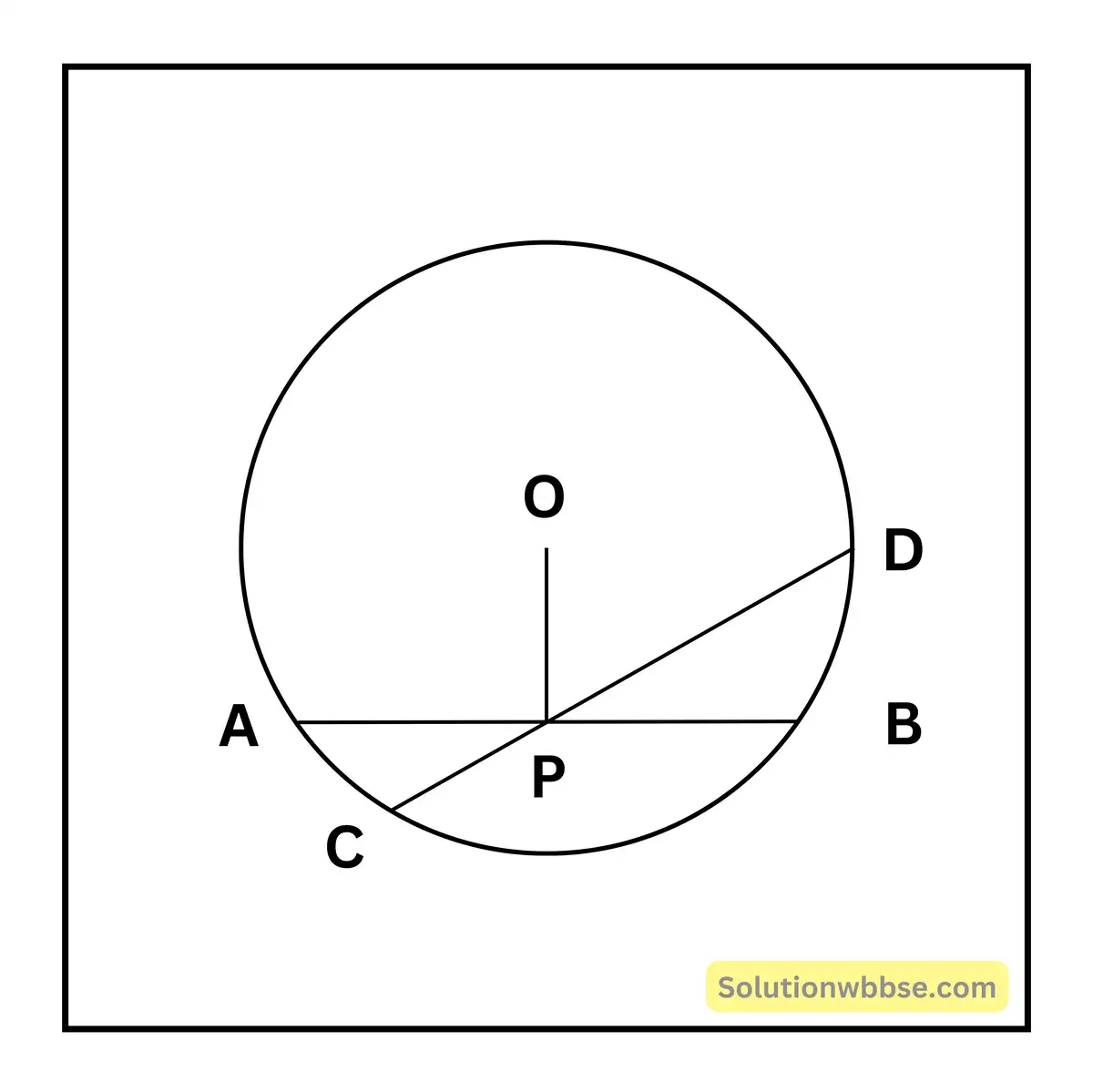
ধরা যাক, কেন্দ্রীয় একটি বৃত্তের AB ও CD দুটি জ্যা পরস্পরকে P বিন্দুতে এমনভাবে ছেদ করেছে যে, P বিন্দু AB-এর মধ্যবিন্দু।

প্রমাণ করতে হবে যে, P, CD-এর মধ্যবিন্দু হবে না।

অঙ্কন – O, P যুক্ত করা হল।

প্রমাণ – P, AB-এর মধ্যবিন্দু।

∴ OP ⊥ AB

∴ AB ও CD উভয়েই P বিন্দুগামী

∴ AB ও CD উভয়েই OP-এর উপর P বিন্দুতে লম্ব হতে পারে না।

∴ AB, OP-এর উপর লম্ব।

∴ CD, OP-এর উপর লম্ব নয়।

আবার যেহেতু কোনো জ্যা-এর মধ্যবিন্দু ও বৃত্তের কেন্দ্র-সংযোজক রেখাংশ জ্যা-এর উপর লম্ব। সুতরাং, P, CD-এর মধ্যবিন্দু নয়। উভয়েই ব্যাস হলে, অবশ্যই সংজ্ঞানুসারে পরস্পরকে সমদ্বিখণ্ডিত করবে।

9. X ও Y কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে A ও B বিন্দুতে ছেদ করেছে। XY-এর মধ্যবিন্দু S-এর সঙ্গে A বিন্দু যুক্ত করলাম এবং A বিন্দু দিয়ে অঙ্কিত SA-এর উপর লম্ব অঙ্কন করলাম যা বৃত্ত দুটিকে P ও Q বিন্দুতে ছেদ করে। প্রমাণ করি যে PA = AQ.

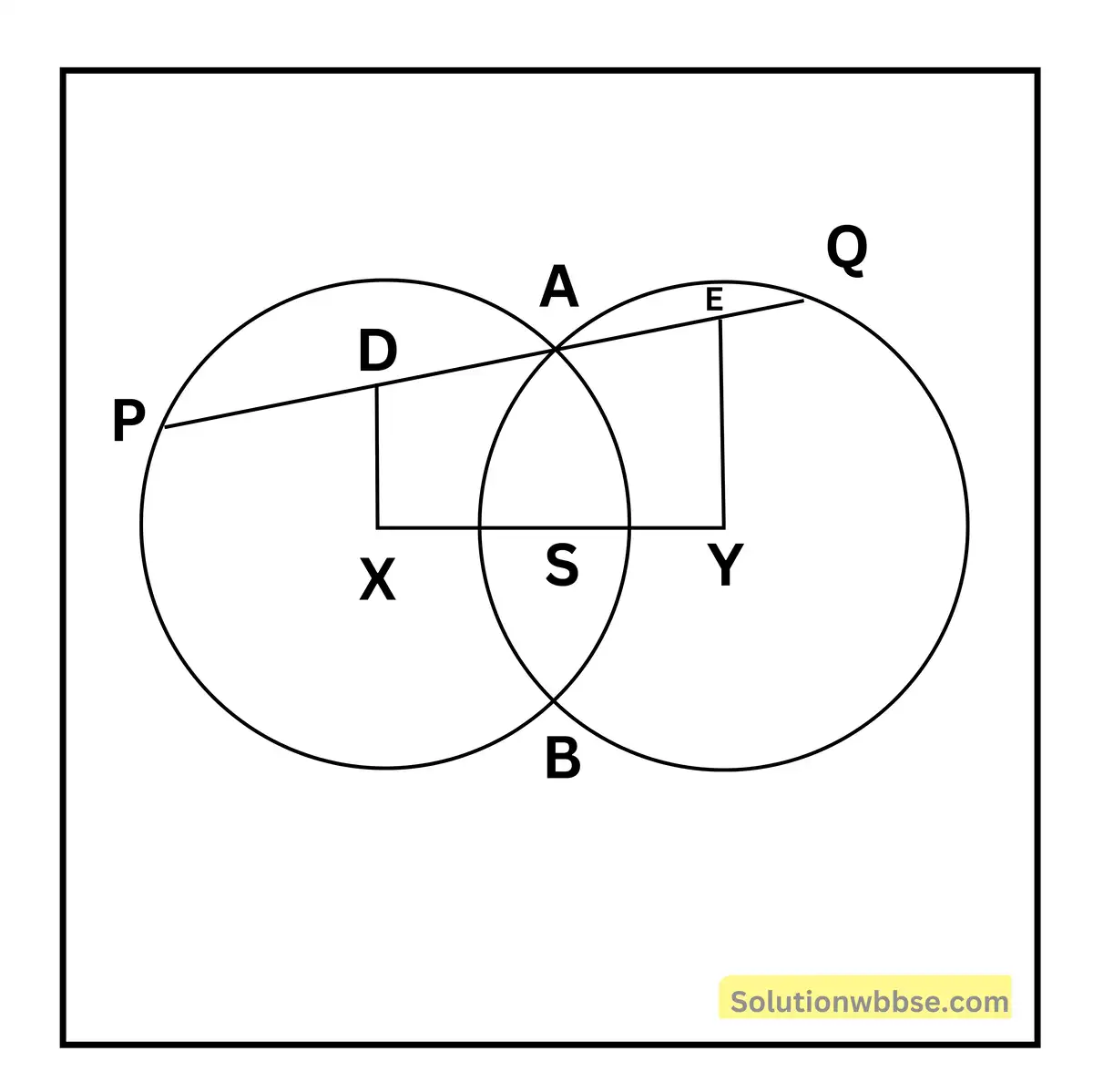
দেওয়া আছে – X এবং Y কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে A এবং B বিন্দুতে ছেদ করেছে। XY-এর মধ্যবিন্দু S-এর সঙ্গে A বিন্দুটি যোগ করা হল। A বিন্দু দিয়ে SA সরলরেখার উপর আঁকা লম্ব বৃত্তকে দুটি P এবং Q বিন্দুতে ছেদ করেছে।

প্রমাণ করতে হবে যে, AP = AQ

অঙ্কন – X এবং Y বিন্দু দুটি থেকে PQ-এর উপর যথাক্রমে XD এবং YE লম্ব অঙ্কন করা হল।

প্রমাণ – অঙ্কন অনুসারে, XD, SA এবং YE সরলরেখা তিনটির প্রতিটি একই সরলরেখা PQ-এর উপর লম্ব।

সেজন্য XD || SA || YE

যেহেতু S বিন্দুটি XY রেখাংশের মধ্যবিন্দু, SX = SY

অর্থাৎ, XD, SA এবং YE সমান্তরাল সরলরেখা তিনটি XY ভেদককে সমান দুটি অংশে ছিন্ন করে। সুতরাং XD, SA এবং YE সমান্তরাল সরলরেখা তিনটি অপর ভেদক PQ থেকেও সমান দুটি অংশ ছিন্ন করবে।

অর্থাৎ, DA = AE যেহেতু X কেন্দ্রীয় বৃত্তের কেন্দ্র X থেকে XD সরলরেখা PA-জ্যার উপর লম্ব, (অঙ্কন অনুসারে)

DA = \(\frac12\)AP অনুরূপভাবে, যেহেতু YE ⊥ AQ, AE = \(\frac12\)AQ

যেহেতু DA = AE (পূর্বে প্রমাণিত) \(\frac12\)AP = \(\frac12\)AQ সুতরাং AP = AQ (প্রমাণিত)

10. Ο কেন্দ্রীয় বৃত্তের 10 সেমি. ও 24 সেমি. দৈর্ঘ্যের দুটি সমান্তরাল জ্যা AB এবং CD কেন্দ্রের বিপরীত পার্শ্বে অবস্থিত। যদি AB ও CD-জ্যা দুটির মধ্যে দূরত্ব 17 সেমি. হয়, তবে হিসাব করে বৃত্তের ব্যাসার্ধের দৈর্ঘ্য লিখি।

উত্তর সংকেত – ধরি, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য r সেমি. এবং বৃত্তের কেন্দ্র থেকে AB জ্যা-এর দূরত্ব x সেমি.। ∴ বৃত্তের কেন্দ্র থেকে CD জ্যা-এর দূরত্ব (17 – x) সেমি.।
∴ r² = x² + 5² এবং r² = (17 – x)² + (12)², সুতরাং, x² + 5² = (17 – x)² + 12² ∴ x = 12

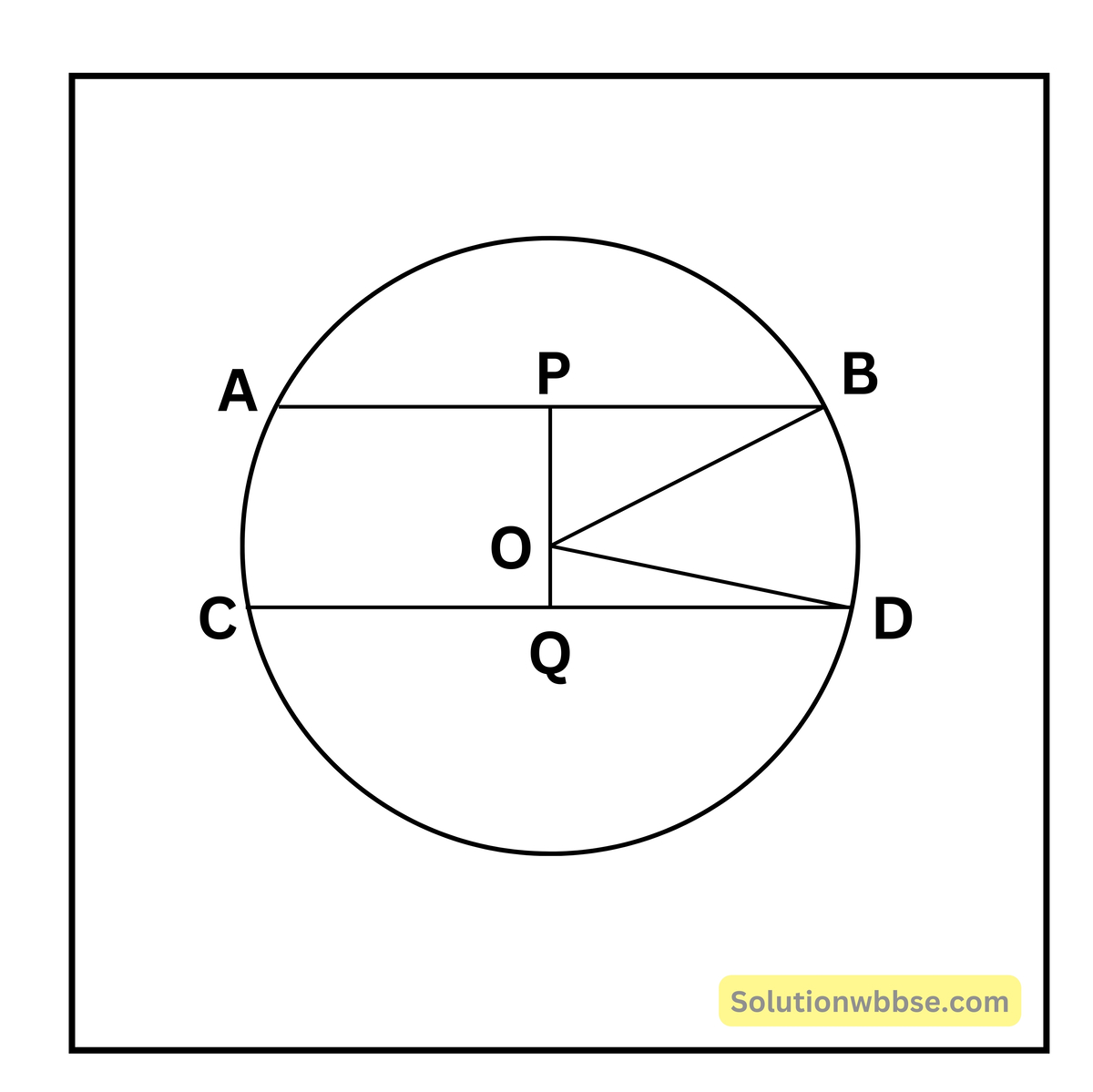
জ্যা দুটির মধ্যে দূরত্ব = PQ = 10 সেমি AB = 10 সেমি

∴ PB = 5 সেমি। CD = 24 সেমি ∴ QD = 12 সেমি

ধরি বৃত্তের ব্যাসার্ধ = x সেমি

ΔΟΡΒ তে; OP² = OB² – PB² = x² – 5² = x² – 25

∴ OP = \(\sqrt{x^2-25}\)

আবার অনুরূপে, ΔOQD তে; OQ² = OD² – QD² = x² – 12² = x² – 144

∴ OQ = \(\sqrt{x^2-144}\)

প্রশ্নানুসারে, OP + OQ = 17

∴ \(\sqrt{x^2-25}+\sqrt{x^2-144}=17\)

বা, \(x^2-25+x^2-144+2\sqrt{\left(x^2-25\right)\left(x^2-144\right)}=289\)

বা, \(2x^2+2\sqrt{\left(x^2-25\right)\left(x^2-144\right)}=289+169\)

বা, \(2x^2+2\sqrt{\left(x^2-25\right)\left(x^2-144\right)}=458\)

বা, \(x^2+\sqrt{\left(x^2-25\right)\left(x^2-144\right)}=229\)

বা, (x² – 229)² = (x² – 25)(x² – 144)

বা, x⁴ – 458x² + (229)² = x⁴ – 169x² + 3600

বা, – 458x² + 169x² + 52441 = 3600

বা, 458x² – 169x² – 48841 = 0

বা, 289x² = 48841

বা, \(x^2=\frac{48841}{289}=169\)

বা, \(x=\sqrt{169}=13\)

∴ বৃত্তের ব্যাসার্ধ = 13 সেমি।

11. দুটি বৃত্তের কেন্দ্র P এবং Q; বৃত্ত দুটি A এবং B বিন্দুতে ছেদ করে। A বিন্দু দিয়ে PQ সরলরেখাংশের সমান্তরাল সরলরেখা বৃত্ত দুটিকে C ও D বিন্দুতে ছেদ করে। প্রমাণ করি যে, CD = 2PQ

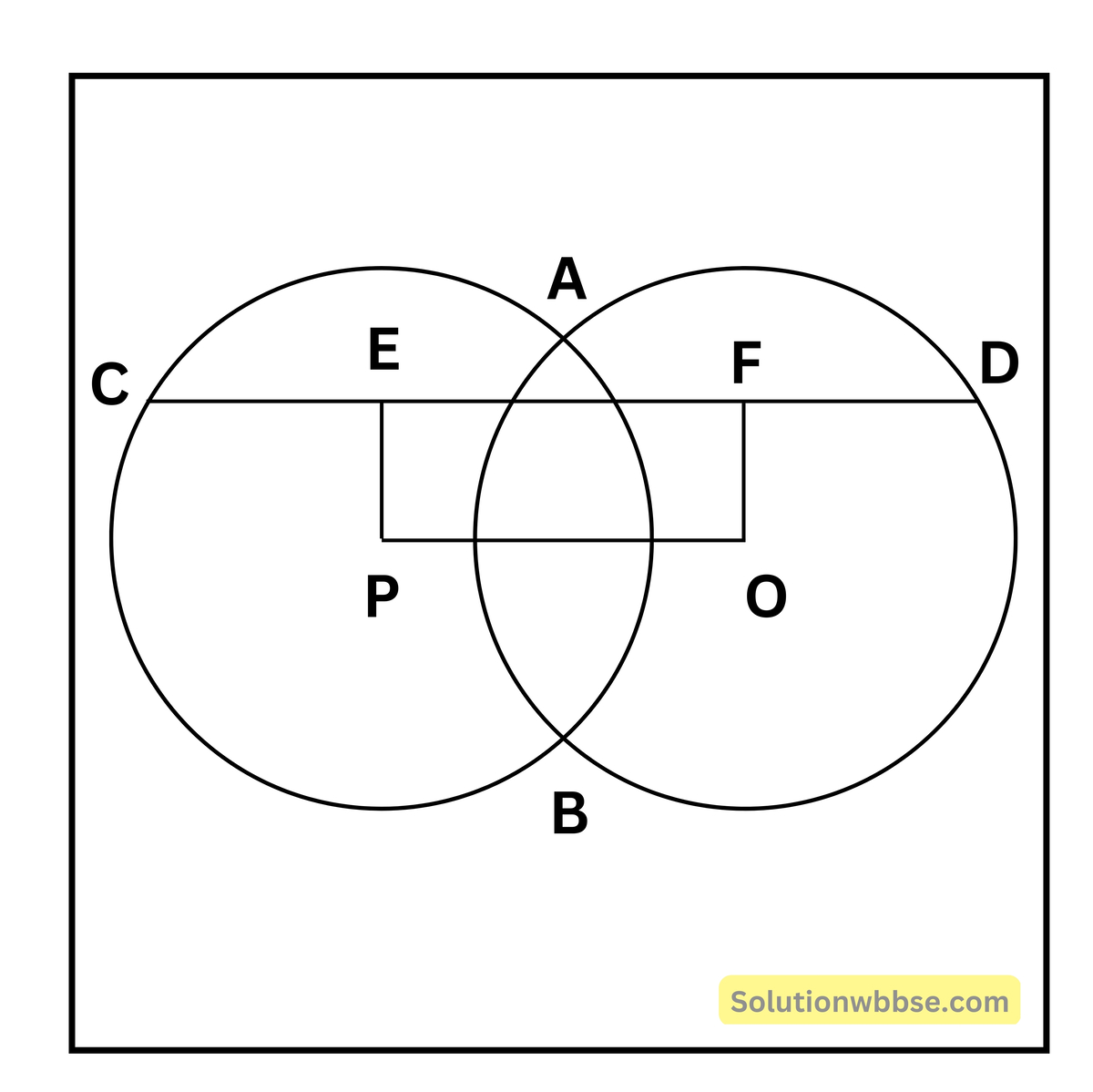
P ও Q বিন্দু থেকে CD সরলরেখার ওপর PE এবং QF লম্ব অঙ্কন করলাম।

QF, AD কে সমদ্বিখণ্ডিত করেছে ∴ AF = \(\frac12\)AD

অনুরূপে PE, AC কে সমদ্বিখণ্ডিত করেছে। ∴ AE = \(\frac12\)AC

EF = AF + AE

= \(\frac12AD+\frac12AC\)

= \(\frac12\left(AD+AC\right)\)

= \(\frac12\)CD

আবার PQ = EF

∴ PQ = \(\frac12\)CD

∴ CD = 2PQ (প্রমাণিত)

12. একটি বৃত্তের AB ও AC জ্যা দুটি সমান। প্রমাণ করি যে, ∠BAC-এর সমদ্বিখণ্ডক কেন্দ্রগামী।

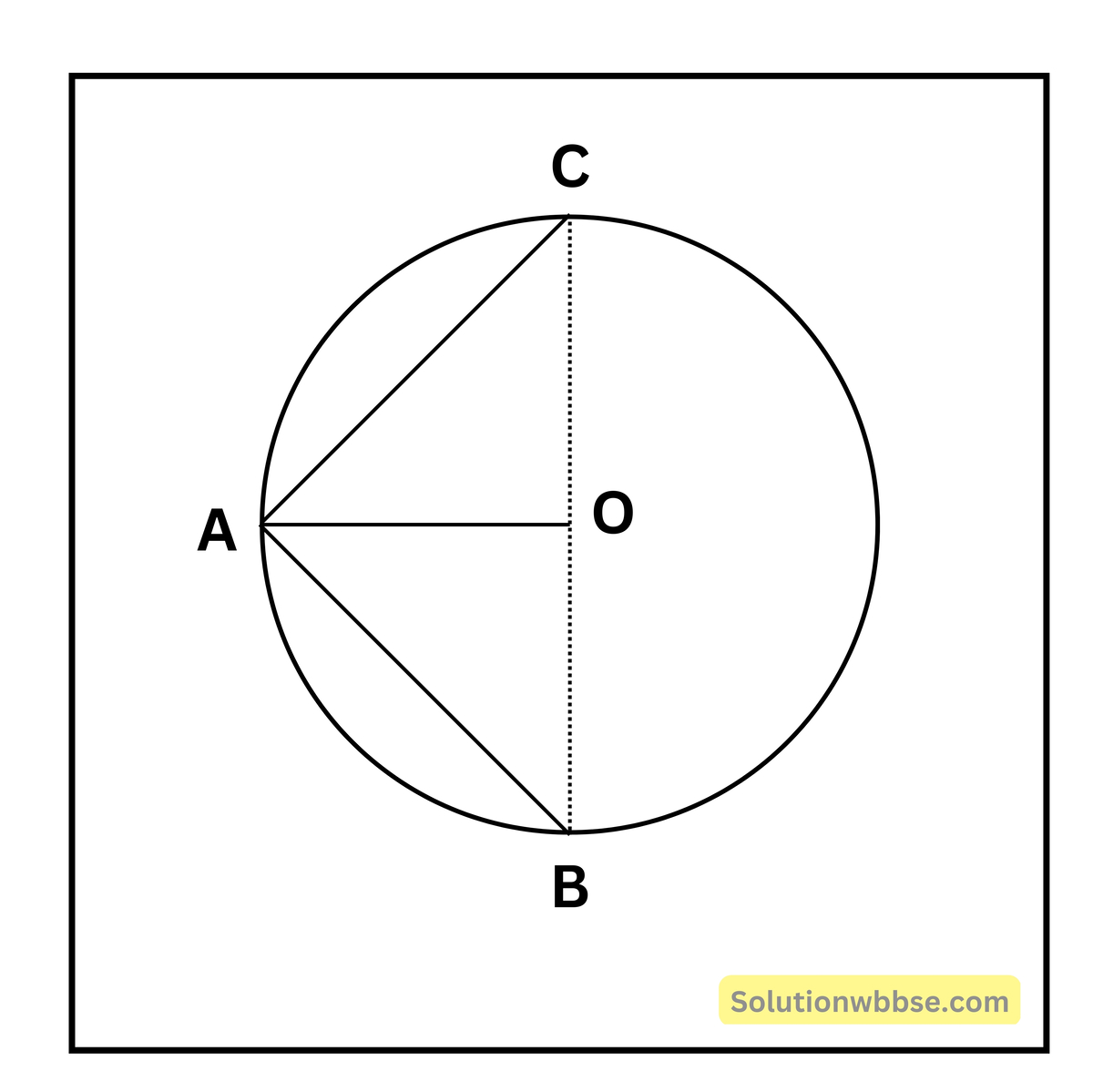
বৃত্তের কেন্দ্রবিন্দু O-এর সাথে A বিন্দু যোগ করলাম। OC এবং OB যোগ করলাম।

ΔΑΟC এবং ΔΑΟΒ-এর মধ্যে,

(i) AO সাধারণ বাহু (ii) OB = OC (একই বৃত্তের ব্যাসার্ধ) এবং (iii) AB = AC (প্রদত্ত)

∴ ΔАОС = ΔАОВ ∴ ∠OAC = ∠OAB

অর্থাৎ, OA, ∠BAC-এর সমদ্বিখণ্ডক।

অন্যথায় বলা যায়, ∠BAC-এর সমদ্বিখণ্ডক কেন্দ্রগামী।

13. একটি বৃত্তের দুটি পরস্পরচ্ছেদী জ্যা-এর অন্তর্ভুত কোণের সমদ্বিখণ্ডক যদি কেন্দ্রগামী হয়, তাহলে প্রমাণ করি যে, জ্যা দুটি সমান।

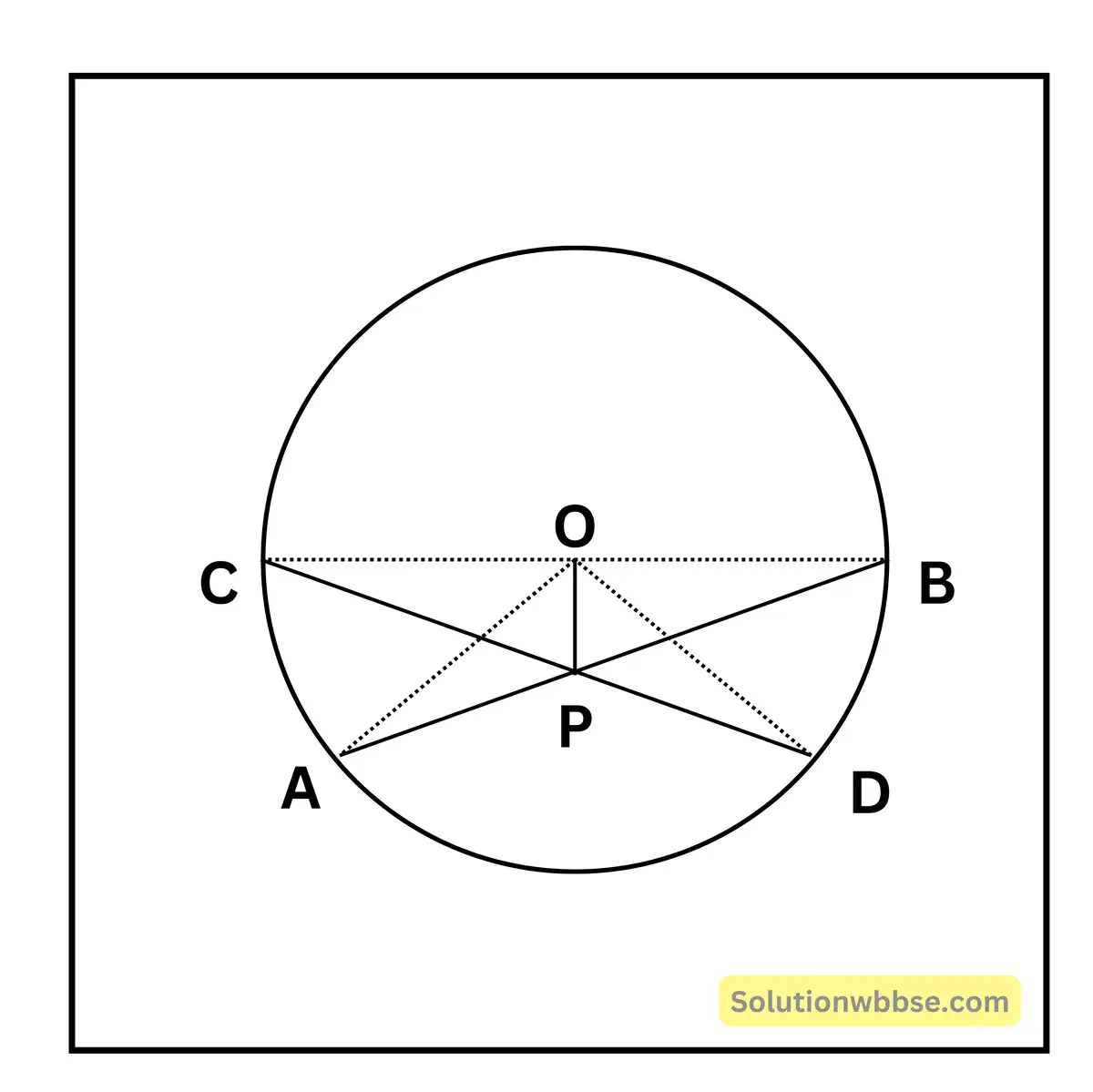
মনেকরি AB ও CD দুটি জ্যা। উহারা O বিন্দুতে ছেদ করেছে।

OA, OB, OC এবং OD যোগ করলাম। জ্যা দুটির ছেদবিন্দু হল P, OP, ∠BOC-এর সমদ্বিখণ্ডক ΔCOP এবং ΔBOD এর

(i) OP সাধারণ বাহু
(ii) OC = OB (একই বৃত্তের ব্যাসার্ধ) এবং
(iii) ∠OPC = ∠OPB (∵ OP, ∠BOC-এর সমদ্বিখণ্ডক)

∴ ΔCOP = ΔBOD ∴ CP = PB

আবার, ∠APO = ∠CPO + ∠APC

∠DPO = ∠DPB + ∠BPD

∵ ∠CPO = ∠BΡΟ

এবং ∠APC = ∠DPB (∵ বিপ্রতীপ) ∴ ∠APO = ∠DPO

এখন ∆AOP এবং ΔDOP-এর মধ্যে

(i) OP সাধারণ বাহু (ii) OA = OB (একই বৃত্তের ব্যাসার্ধ) (iii) ∠APC = ∠DPB

∴ ΔΑΟΡ = ΔDOP

∴ AP = PD

CP + PD = PB + AP

বা, CD = AB (প্রমাণিত)

14. প্রমাণ করি, একটি বৃত্তে দুটি জ্যা-এর মধ্যে যে জ্যাটি কেন্দ্রের নিকটবতী সেটির দৈর্ঘ্য অপর জ্যাটির দৈর্ঘ্য অপেক্ষা বৃহত্তর।

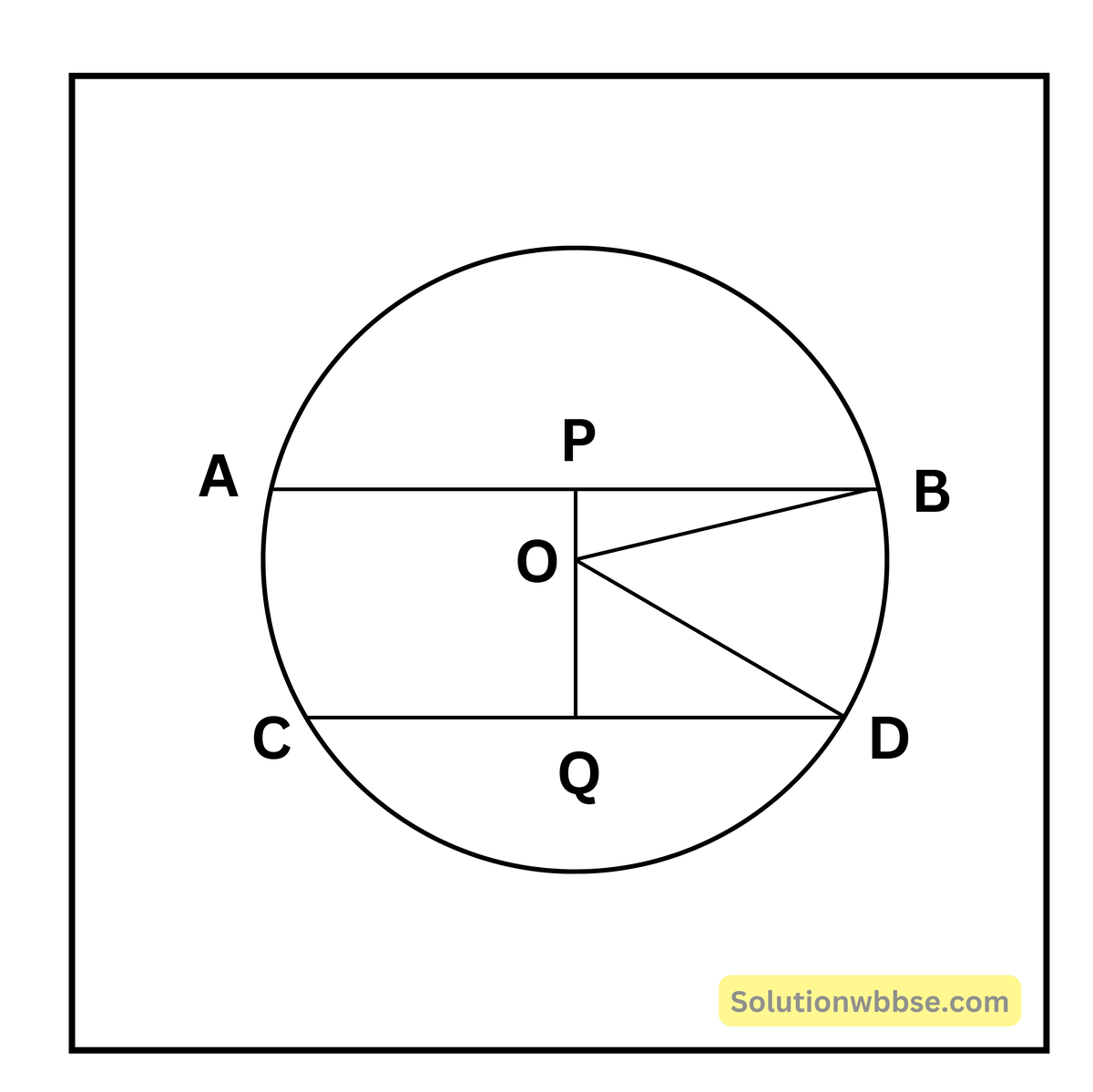
প্রমাণ – AB এবং CD দুটি জ্যা। বৃত্তের কেন্দ্র থেকে উহাদের দূরত্ব যথাক্রমে OP ও OQ, OP < OQ

প্রমাণ করতে হবে যে, AB > CD

OB ও OD যোগ করা হল। এখন P, AB-এর মধ্যবিন্দু

∴ PB = \(\frac12\)AB এবং Q, CD-এর মধ্যবিন্দু

∴ QD = \(\frac12\)CD

ΔΟΡΒ তে; OB = \(\sqrt{PB^2+OP^2}\)

ΔOQD তে; OD = \(\sqrt{OQ^2+QD^2}\) ∵ OB = OD

∴ \(\sqrt{PB^2+OP^2}=\sqrt{OQ^2+QD^2}\)

∵ OP < OQ ∴ PB > QD

বা, AB > CD

বা, AB > CD (প্রমাণিত)

15. একটি বৃত্তের ভিতর যে-কোনো বিন্দু দিয়ে ক্ষুদ্রতম জ্যা কোনটি হবে তা প্রমাণ করে লিখি।

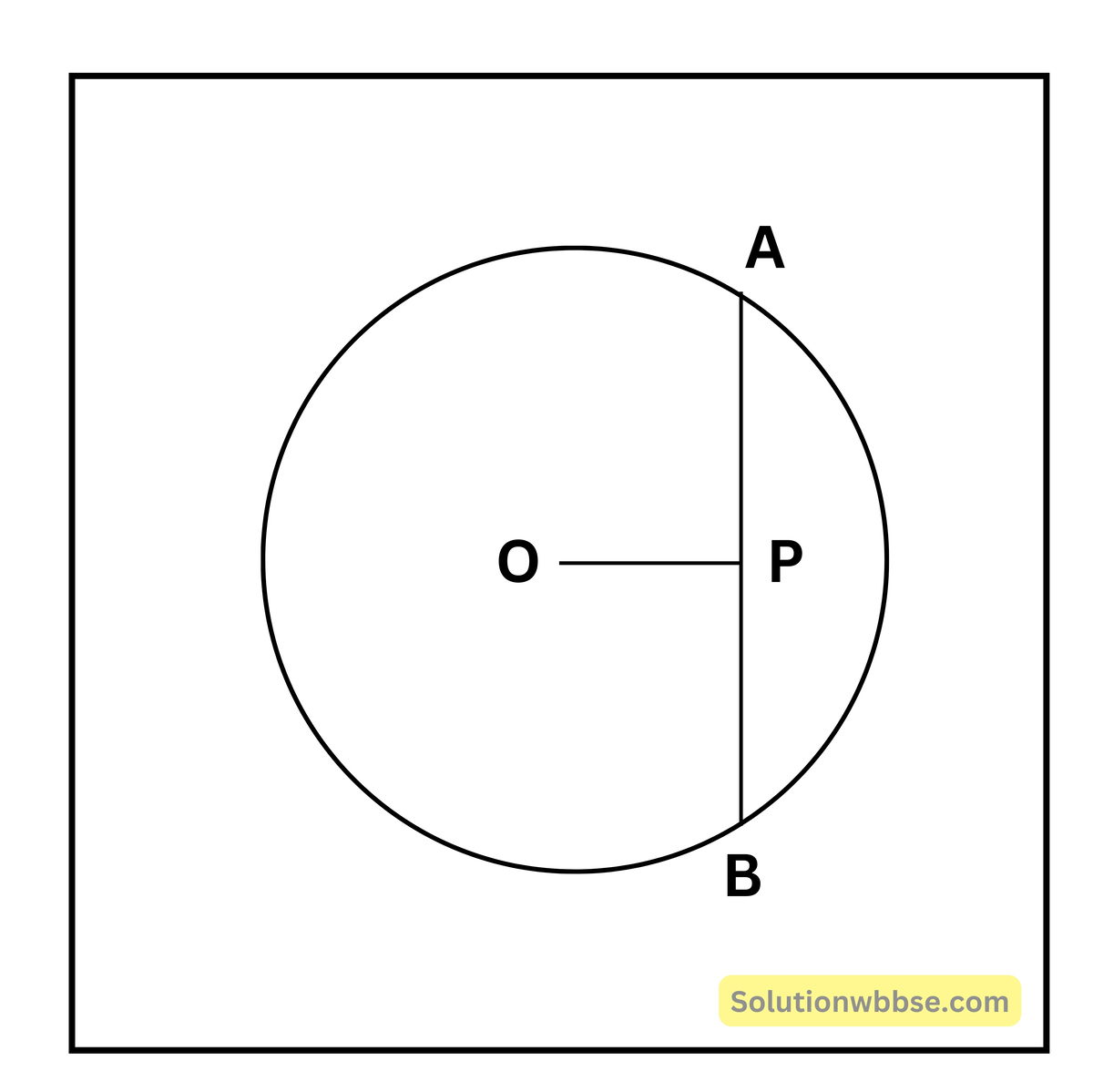
বৃত্তের ভিতর যে কোনো একটি বিন্দু P। P বিন্দু দিয়ে অঙ্কিত AB জ্যা-টি ক্ষুদ্রতম হতে গেলে, P বিন্দুটিকে AB-এর মধ্যবর্তী হতে হবে।

প্রমাণ – যদি P, AB-এর মধ্যবিন্দু হয়, তাহলে; OP ⊥ AB হবে।

আমরা জানি লম্ব সরলরেখা হয় ক্ষুদ্রতম সরলরেখা, সুতরাং, AB ক্ষুদ্রতম। (প্রমাণিত)

16. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.)

(i) O কেন্দ্রীয় বৃত্তের AB ও CD জ্যা দুটির দৈর্ঘ্য সমান। ∠AOB = 60° হলে ∠COD-এর মান

(a) 40°
(b) 30°
(c) 60°
(d) 90°

উত্তর – (c) 60°

(ii) একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 13 সেমি এবং বৃত্তের একটি জ্যা-এর দৈঘ্য 10 সেমি। বৃত্তের কেন্দ্র থেকে জ্যা-এর দূরত্ব

(a) 12.5 সেমি.

(b) 12 সেমি.

(c) \(\sqrt{69}\) সেমি.

(d) 24 সেমি.

উত্তর – (b) 12 সেমি.

সমাধান,

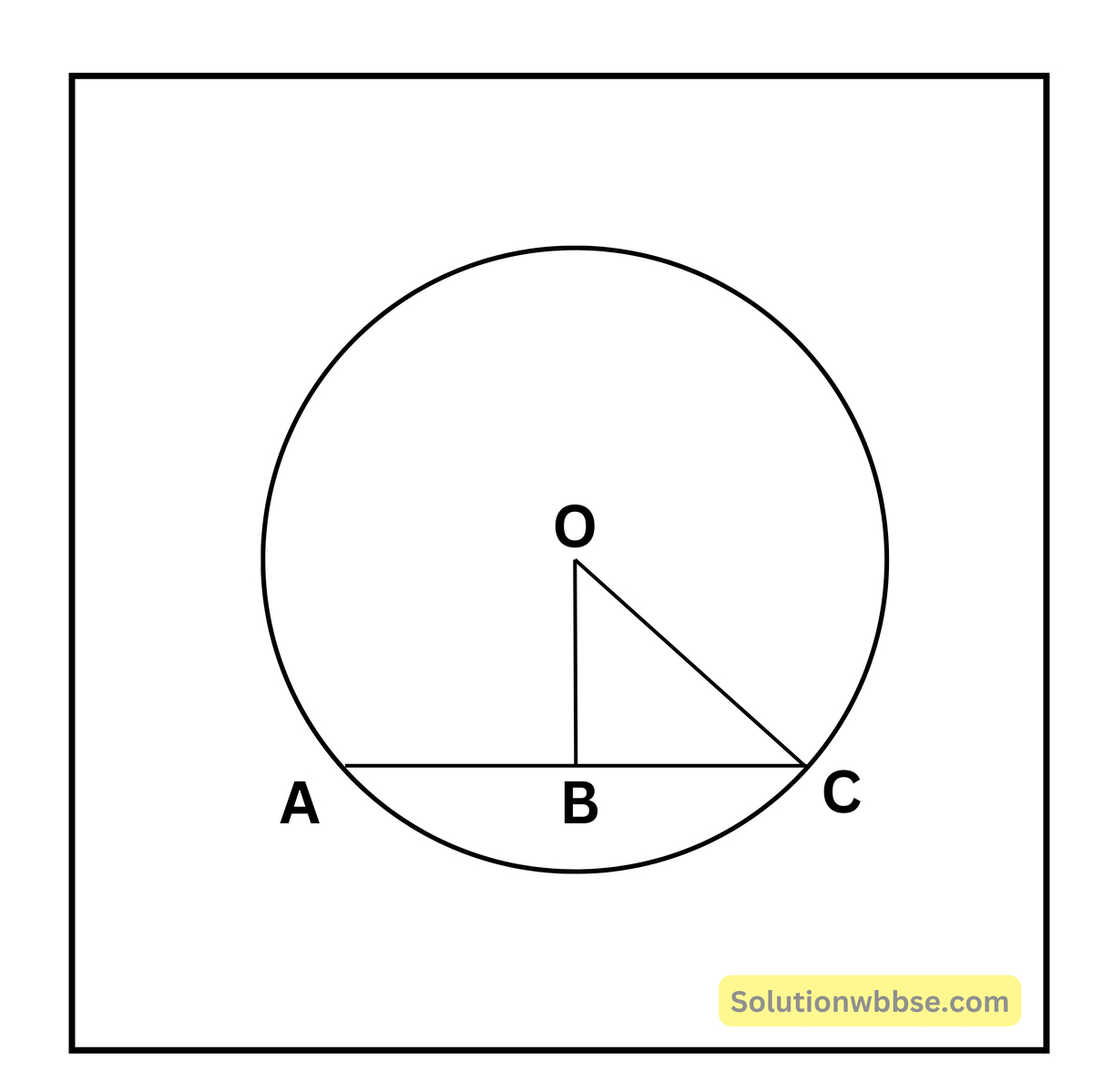
বৃত্তের ব্যাসার্ধ = OA = 13 সেমি। বৃত্তের জ্যা AB = 10 সেমি

∴ BC = \(\frac{10}2\) = 5 সেমি

∴ OC² = OA² – BC² = B² – 5² = 169 – 25 = 144

∴ OC = \(\sqrt{144}\) = 12

উত্তর – (b) 12 সেমি.

(iii) O কেন্দ্রীয় বৃত্তের AB ও CD দুটি সমান দৈর্ঘ্যের জ্যা। O বিন্দু থেকে AB জ্যা-এর দূরত্ব 4 সেমি. হলে, CD জ্যা-এর দূরত্ব

(a) 2 সেমি.
(b) 4 সেমি.
(c) 6 সেমি.
(d) 8 সেমি.

উত্তর – (b) 4 সেমি.

সমাধান,

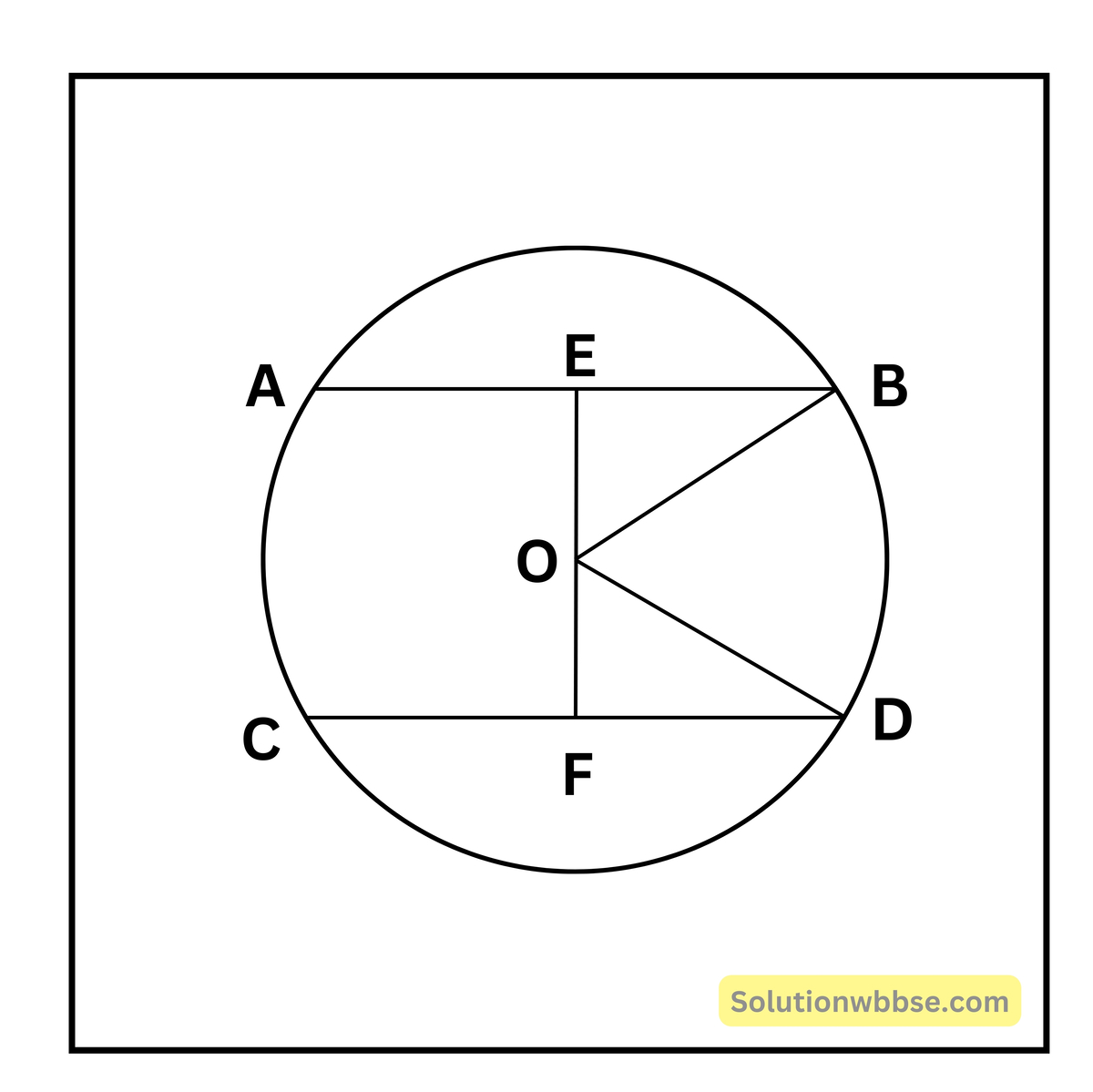
জ্যা AB = জ্যা CD

OE = 4

ΔΒΟΕ ≅ ΔDOF

∴ OE = OF = 4 সেমি

উত্তর – (b) 4 সেমি.।

(iv) AB ও CD দুটি সমান্তরাল জ্যা-এর প্রত্যেকটির দৈর্ঘ্য 16 সেমি.। বৃত্তের ব্যাসার্ঘ্যের দৈর্ঘ্য 10 সেমি. হলে, জ্যা-দুটির মধ্যে দূরত্ব

(a) 12 সেমি.
(b) 16 সেমি.
(c) 20 সেমি.
(d) 5 সেমি.

উত্তর – (a) 12 সেমি.।

সমাধান,

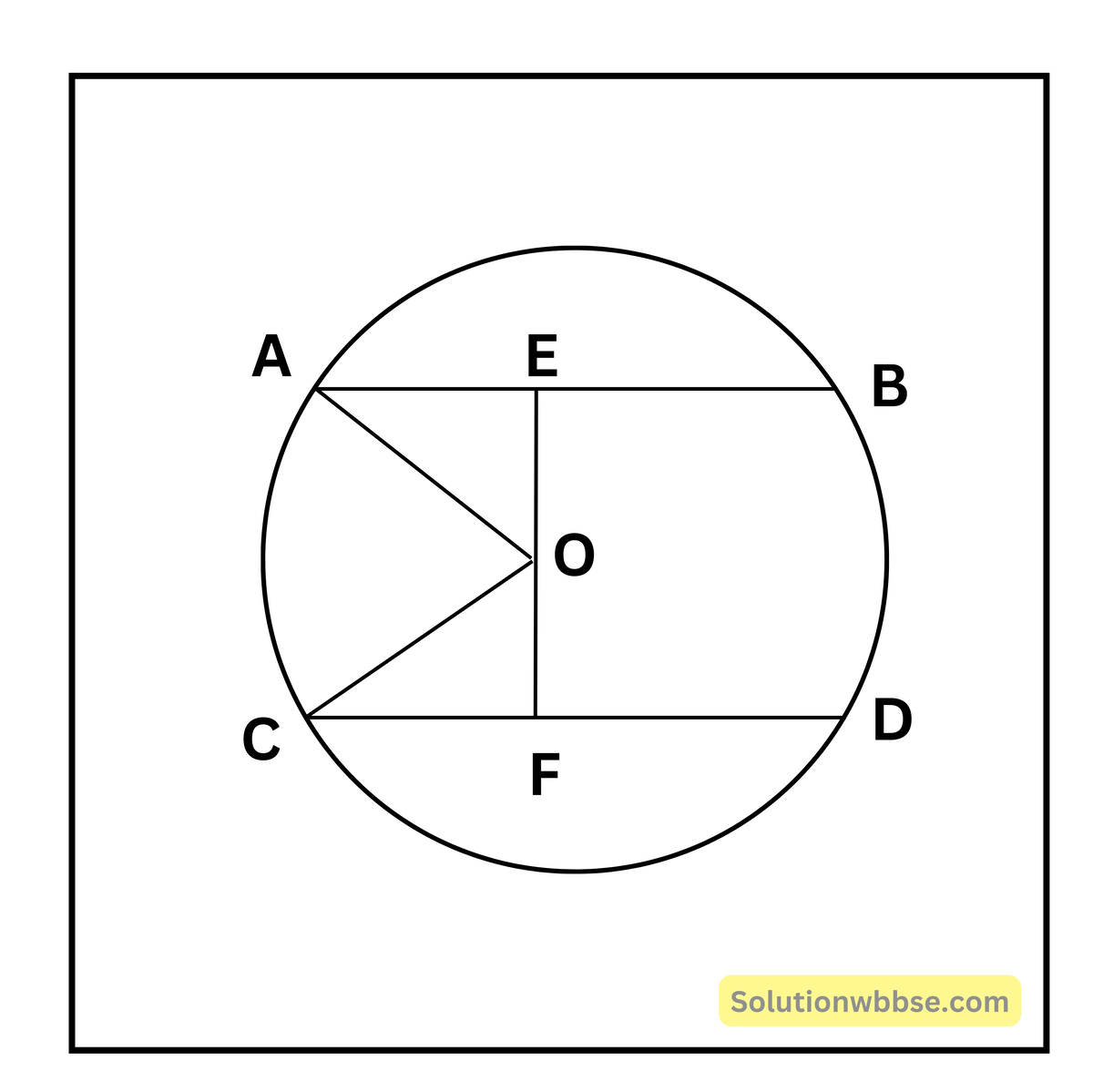
চিত্রে AB = CD = 16 সেমি, OA = OC = 10 সেমি

AE = CF = \(\frac{16}2\) = 8 সেমি

OE² = OA² – AE² = 10² – 8² = 100 – 64 = 36

∴ OE = \(\sqrt{36}\) = 6 সেমি

আবার, OF² = OC² – CF² = 10² – 8² = 100 – 64 = 36 সেমি

∴ OF = \(\sqrt{36}\) = 6 সেমি

EF = OE + OF = 6 + 6 = 12 সেমি.

∴ জ্যা দুটির মধ্যে দূরত্ব 12 সেমি।

উত্তর – (a) 12 সেমি.।

(v) দুটি সমকেন্দ্রীয় বৃত্তের কেন্দ্র O; একটি সরলরেখা একটি বৃত্তকে A ও B বিন্দুতে এবং অপর বৃত্তকে C ও D বিন্দুতে ছেদ করে। AC = 5 সেমি. হলে BD-এর দৈর্ঘ্য

(a) 2.5 সেমি.
(b) 5 সেমি.
(c) 10 সেমি.
(d) কোনোটিই নয়।

উত্তর – (b) 5 সেমি.

সমাধান,

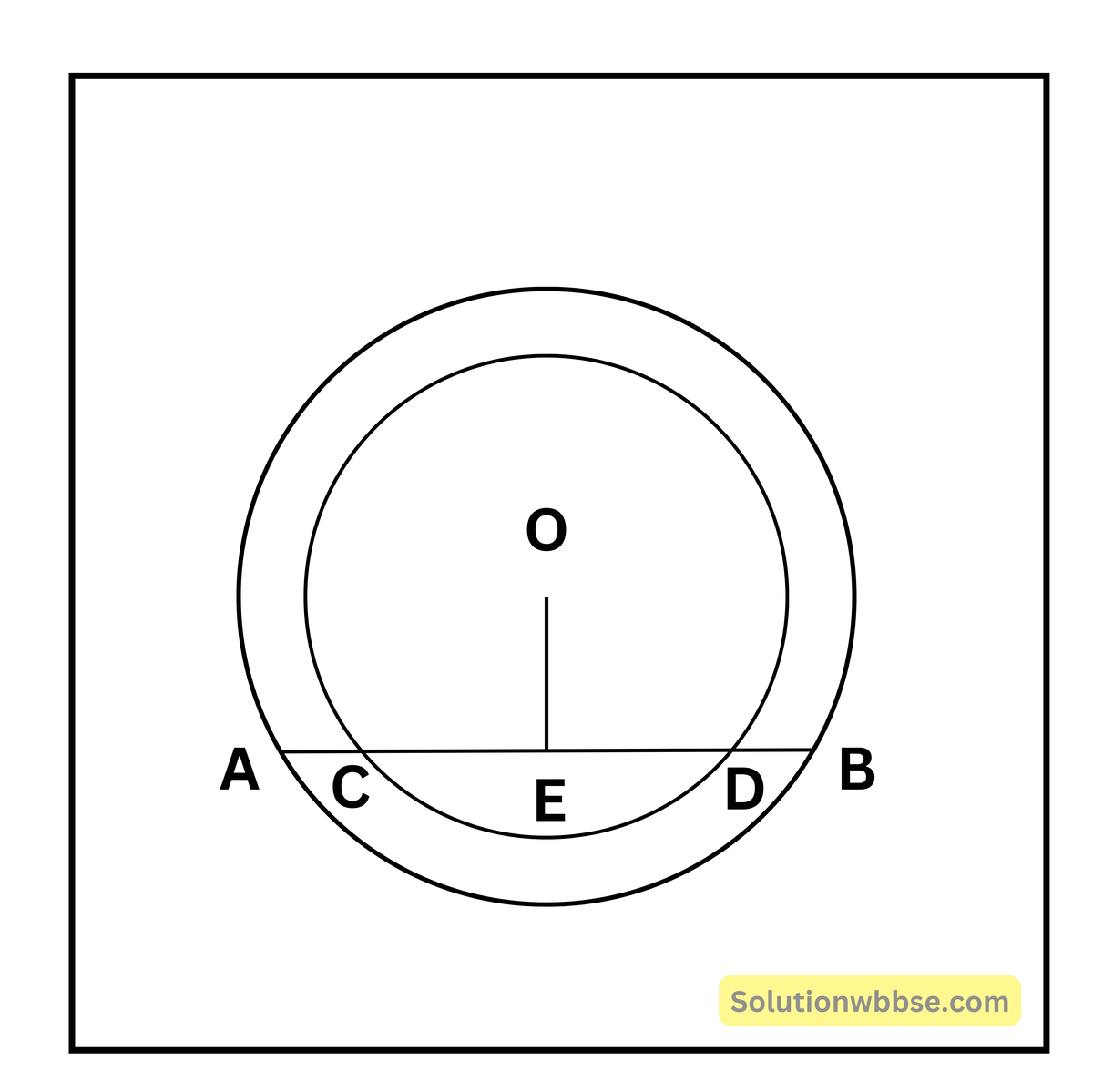
OE ⊥ AB ∴ OE ⊥ CD, CE = ED

∴ AE – CE = EB – ED বা, AC = BD = 5

উত্তর – (b) 5 সেমি.।

(B) সত্য / মিথ্যা লিখি –

(i) তিনটি সমরেখ বিন্দু দিয়ে যায় এরকম একটি বৃত্ত অঙ্কন করা যায়।

উত্তর – মিথ্যা।

(ii) ABCDA ও ABCEA বৃত্ত দুটি একই বৃত্ত।

উত্তর – সত্য।

(iii) কেন্দ্রীয় বৃত্তের AB এবং AC জ্যা দুটি OA ব্যাসার্ধের বিপরীত পার্শ্বে অবস্থিত হলে ∠OAB = ∠OAC

উত্তর – মিথ্যা।

(C) শূন্যস্থান পূরণ করি –

(i) O কেন্দ্রীয় বৃত্তে PQ ও RS জ্যা দুটির দৈর্ঘ্যের অনুপাত 1:1 হলে ∠POQ: ∠ROS = ___।

উত্তর – O কেন্দ্রীয় বৃত্তে PQ ও RS জ্যা দুটির দৈর্ঘ্যের অনুপাত 1 : 1 হলে ∠POQ : ∠ROS 1 : 1।

(ii) বৃত্তের কোনো জ্যা-এর লম্বসমদ্বিখণ্ডক ওই বৃত্তের ___। 

উত্তর – বৃত্তের কোনো জ্যা-এর লম্বসমদ্বিখণ্ডক ওই বৃত্তের কেন্দ্রগামী।

সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন. (S.A.) –

(i) 10 সেমি. দৈর্ঘ্যের ব্যাসার্ধের দুটি সমান বৃত্ত পরস্পরকে ছেদ করে এবং তাদের সাধারণ জ্যা-এর দৈর্ঘ্য 12 সেমি.। বৃত্ত দুটির কেন্দ্রদ্বয়ের মধ্যে দূরত্ব নির্ণয় করি।

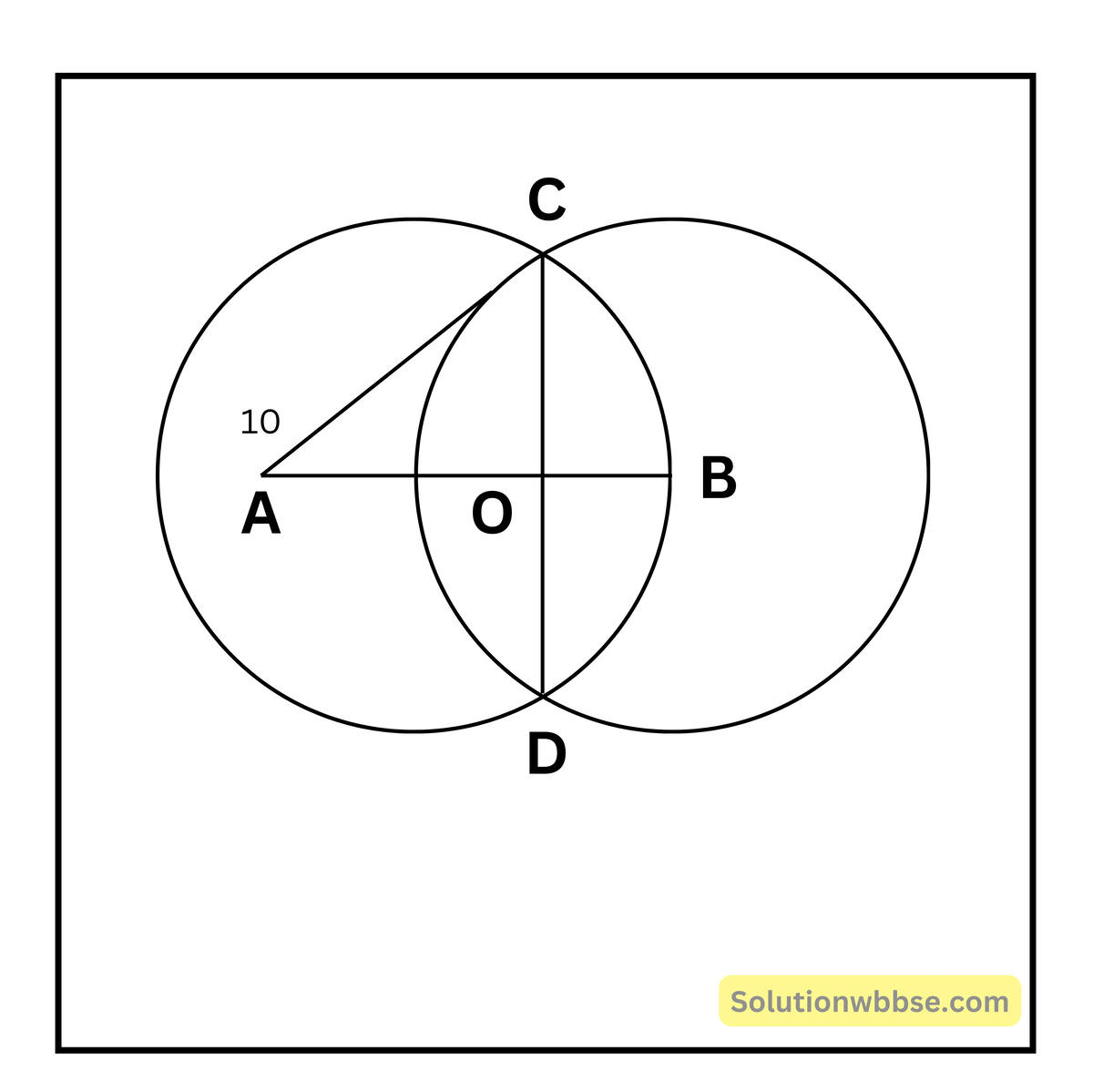
CO = \(\frac{12}2\) = 6 সেমি.

AO = \(\sqrt{10^2-6^2}\) = \(\sqrt{100-36}\) = \(\sqrt{64}\) = 8 সেমি.

AB = (2 × 8) = 16 সেমি.

∴ বৃত্তদুটির কেন্দ্রদ্বয়ের দূরত্ব = 16 সেমি.।

(ii) 5 সেমি. দৈর্ঘ্যের ব্যাসার্ধের একটি বৃত্তে AB এবং AC দুটি সমান দৈর্ঘ্যের জ্যা। বৃত্তের কেন্দ্র ABC ত্রিভুজের বাইরে অবস্থিত। AB = AC = 6 সেমি. হলে, BC জ্যা-এর দৈর্ঘ্য নির্ণয় করি।

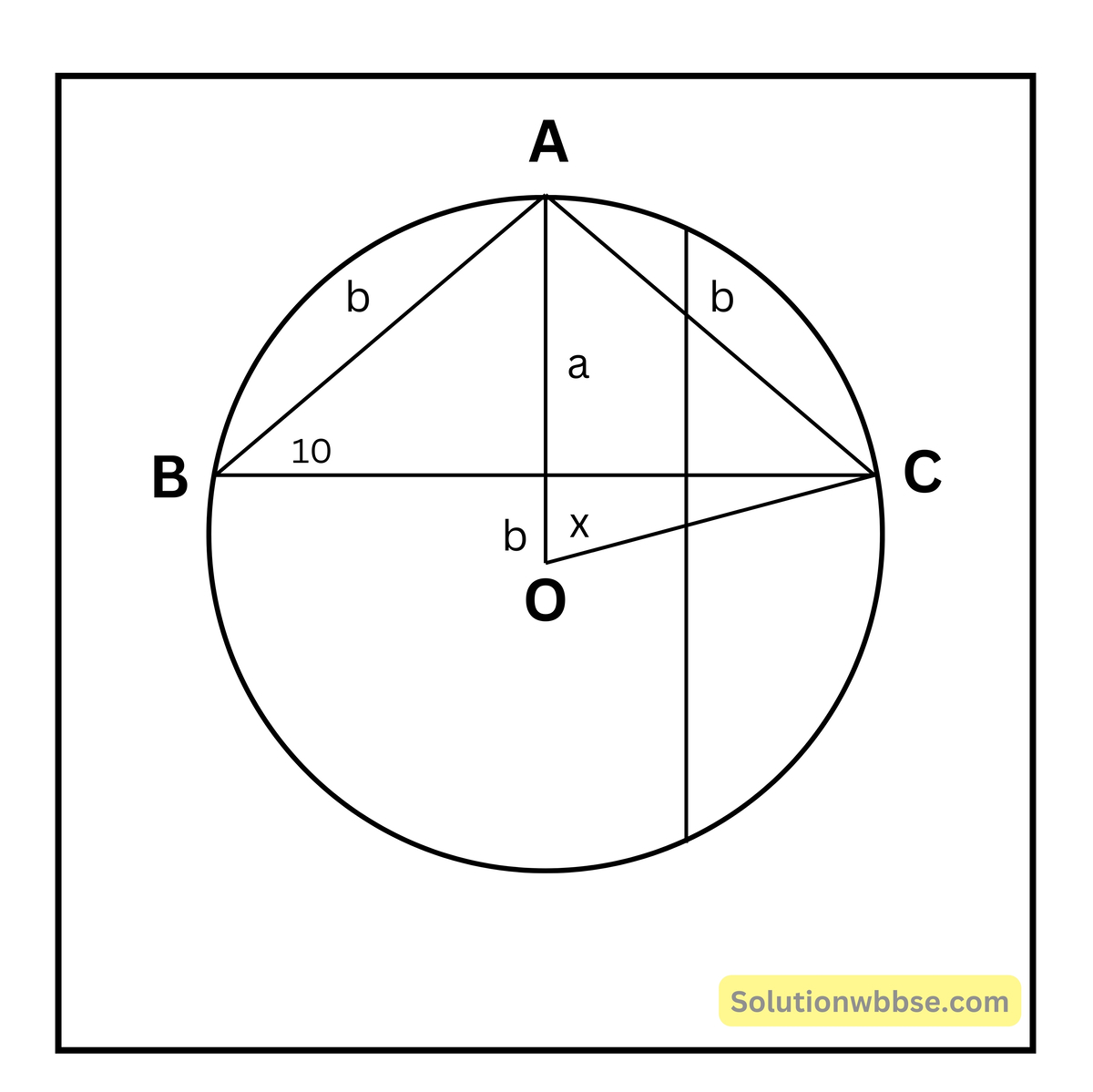
a² + n² = 6² এবং b² + n² = 5²

∴ \(a^2-b^2\) = 11 ∴ a – b = \(\frac{11}5\) [∵ a + b = 5 = OA]

∴ a = \(\frac12\left(\frac{11}5+5\right)=\frac{18}5\) ∴ x = \(\sqrt{36-\frac{324}{25}}=\sqrt{\frac{576}{25}}=\frac{24}5\)

∴ BC = 2x = \(\frac{48}5\) = 9.6 সেমি.।

(iii) O কেন্দ্রীয় বৃত্তে AB ও CD জ্যা দুটির দৈর্ঘ্য সমান। ∠AOB = 60° এবং CD = 6 সেমি. হলে, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য কত তা নির্ণয় করি।

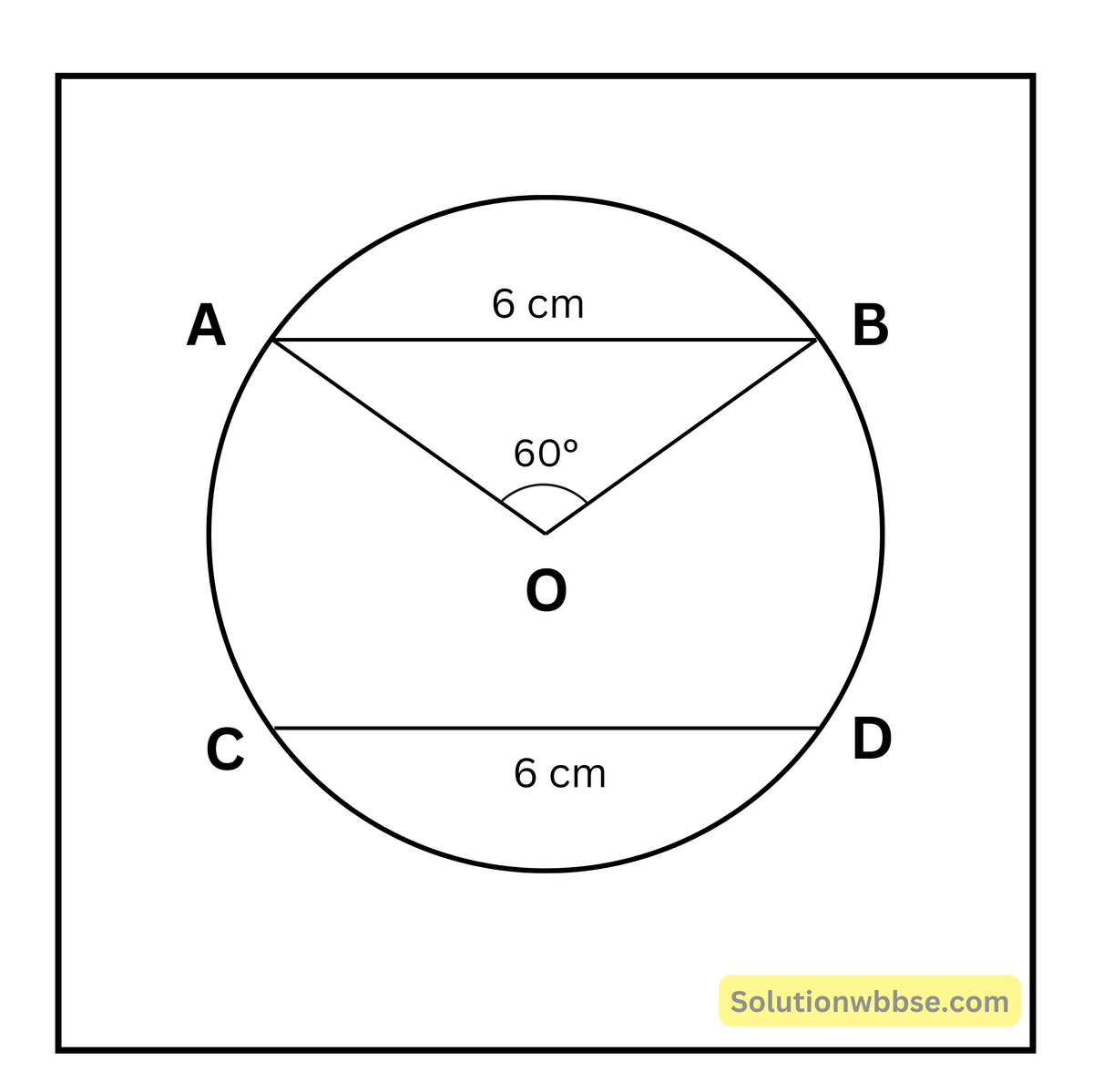
AB = CD = 6 সেমি. ∠AOB = 60°

ΔΑΟΒ সমবাহু ত্রিভুজ OA = OB = 6 সেমি.

∴ ব্যাসার্ধ 6 সেমি.।

(iv) O কেন্দ্রীয় বৃত্তের ভিতর P যে-কোনো একটি বিন্দু। বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি. এবং OP = 3 সেমি. হলে, P বিন্দুগামী যে জ্যাটির দৈর্ঘ্য ন্যূনতম তা নির্ণয় করি।

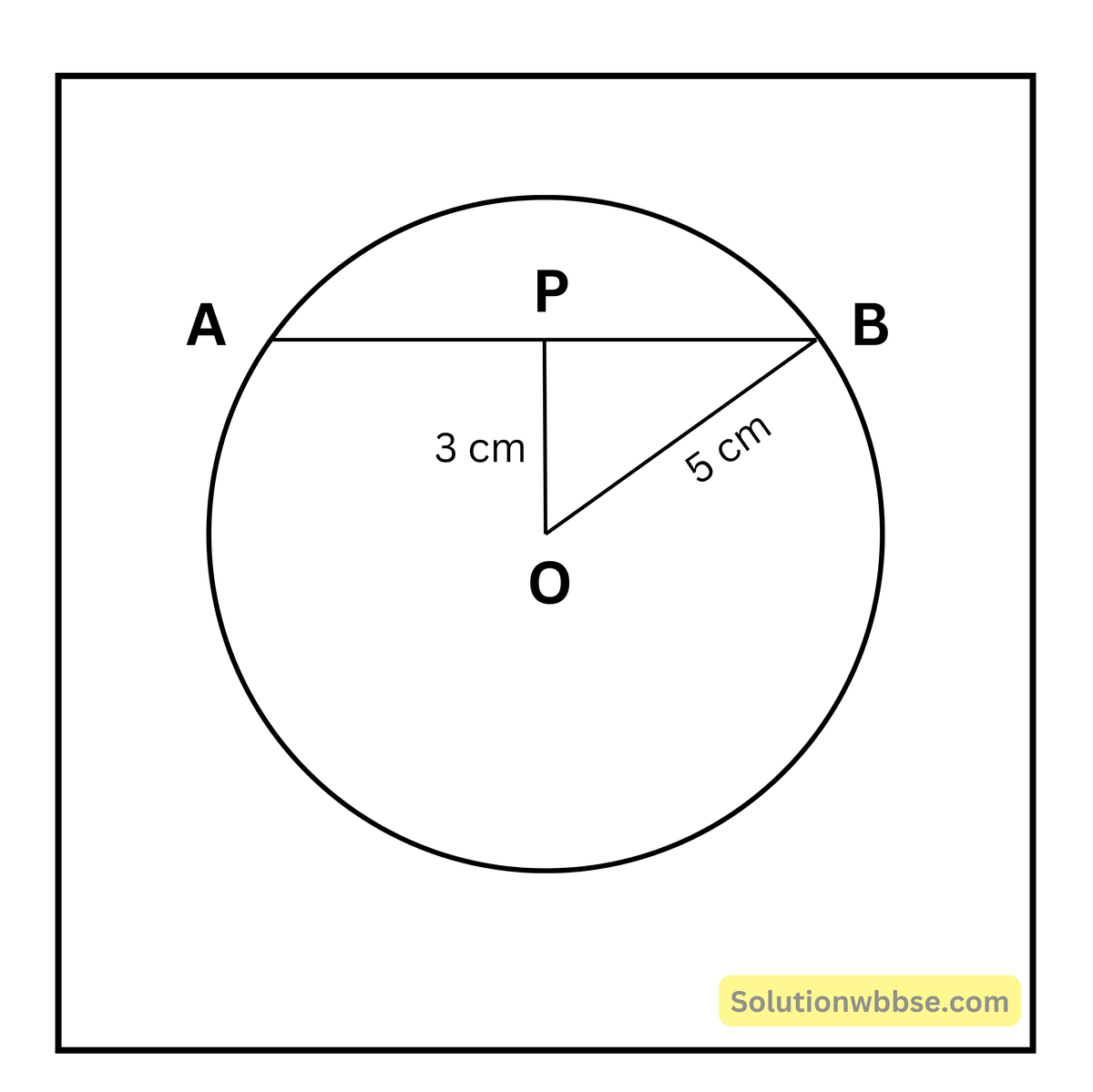
BP = \(\sqrt{5^2-3^3}\) = \(\sqrt{25-9}\) = \(\sqrt{16}\) = 4 সেমি.

∴ জ্যাটির দৈর্ঘ্য = (4 × 2) = 8 সেমি.।

(v) P ও Q কেন্দ্রবিশিষ্ট দুটি বৃত্ত A ও B বিন্দুতে ছেদ করে। A বিন্দু দিয়ে PQ-এর সমান্তরাল সরলরেখা বৃত্তদুটিকে যথাক্রমে C ও D বিন্দুতে ছেদ করে। PQ = 5 সেমি. হলে, CD-এর দৈর্ঘ্য কত তা নির্ণয় করি।

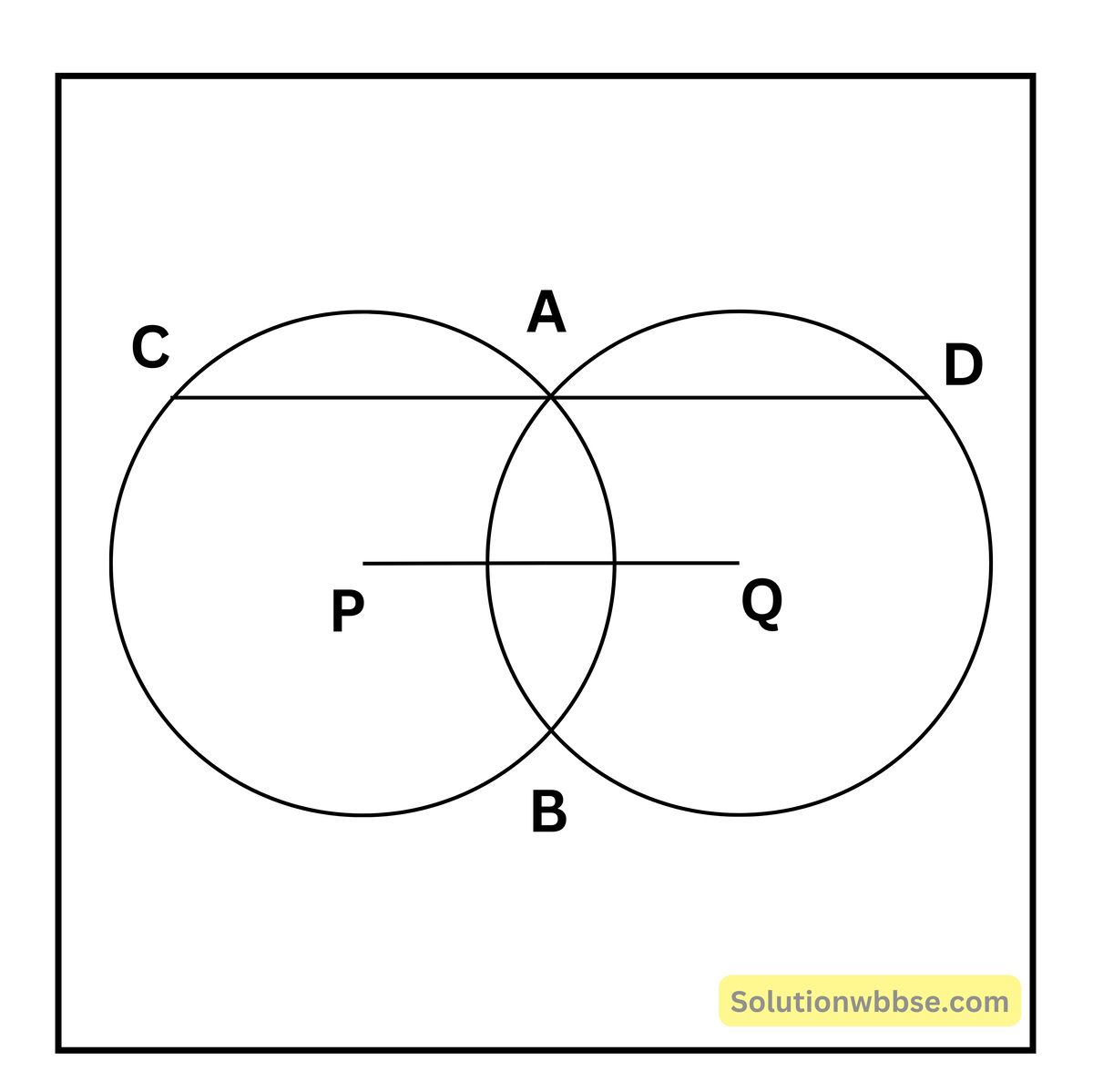
PQ = 5 সেমি., CD = 2PQ = (2 × 5) = 10 সেমি।

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের তৃতীয় অধ্যায়, ‘বৃত্ত সম্পর্কিত উপপাদ্য’ -এর ‘কষে দেখি – 3.2’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।

আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।