এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের সপ্তম অধ্যায়, ‘বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য’ -এর উপপাদ্যমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

উপপাদ্য – 34. কোনো বৃত্তের একটি বৃত্তচাপের দ্বারা গঠিত সম্মুখ কেন্দ্রস্থ কোণ ওই চাপের দ্বারা গঠিত যে-কোনো বৃত্তস্থ কোণের দ্বিগুণ।
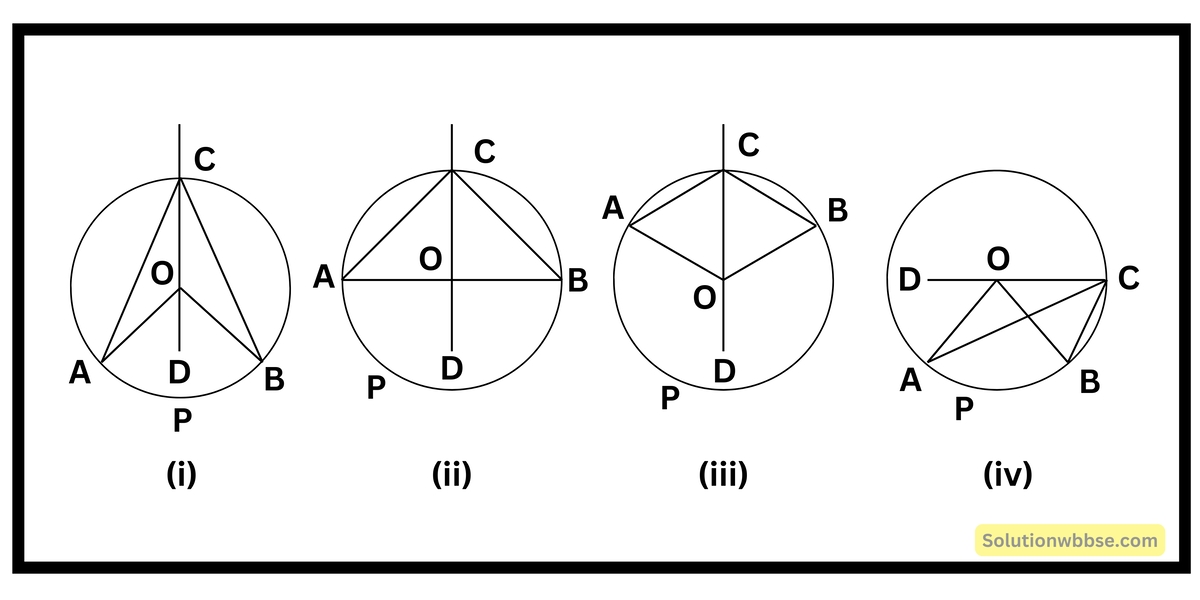
প্রদত্ত – O কেন্দ্রীয় বৃত্তের বৃত্তচাপ APB -এর দ্বারা গঠিত কেন্দ্রস্থ কোণ ∠AOB এবং একটি বৃত্তস্থ কোণ ∠ACB
প্রমাণ করতে হবে – ∠AOB = 2∠ACB
বৃত্তচাপ AB -এর দৈর্ঘ্য অনুযায়ী বিষয়টি তিনরকম হতে পারে। (i) ও (iv) নং চিত্রে APB উপচাপ (ii) নং চিত্রে APB অর্ধবৃত্তচাপ (iii) নং চিত্রে APB অধিচাপ।
অঙ্কন – C, O যুক্ত করে D বিন্দু পর্যন্ত বর্ধিত করলাম।
প্রমাণ – প্রতিক্ষেত্রেই ΔAOC -এর OA = OC [একই বৃত্তের ব্যাসার্ধ]
∴ ∠OCA = ∠OAC
আবার, প্রতিক্ষেত্রেই, ΔAOC -এর CO বাহুকে D বিন্দু পর্যন্ত বর্ধিত করায়
বহিঃস্থ ∠AOD = ∠OAC + ∠OCA
= 2 ∠OCA —-(I) [∵ ∠OAC = ∠OCA]
প্রতিক্ষেত্রেই ΔBOC -এর, OB = OC [একই বৃত্তের ব্যাসার্ধ]
সুতরাং ∠OBC = ∠OCB
আবার প্রতিক্ষেত্রেই ΔBOC -এর বাহুকে CO বাহুকে D বিন্দু পর্যন্ত বর্ধিত করায়
বহিঃস্থ ∠BOD = ∠OCB + ∠OBC
= 2∠OCB —- (II) [∵ ∠OBC = ∠OCB]
(i) ও (ii) নং চিত্রের ক্ষেত্রে, ∠AOD + ∠BOD = 2∠OCA + 2∠OCB [I ও II থেকে পেলাম]
∴ ∠AOB = 2(∠OCA + ZOCB) = 2∠ACB —-(III)
কিন্তু (iii) নং চিত্রের ক্ষেত্রে অর্থাৎ যখন APB অধিচাপ, (III) -কে লিখব,
প্রবৃদ্ধ ∠AOB = 2∠ACB
(iv) নং চিত্রের ক্ষেত্রে, ∠BOD – ∠AOD = 2∠OCB – 2∠OCA
বা, ∠AOB = 2(∠OCB – ∠OCA)
∴ ∠AOB = 2∠ACB (প্রমাণিত)
উপপাদ্য – 35. একই বৃত্তাংশস্থ সকল বৃত্তস্থ কোণের মান সমান।
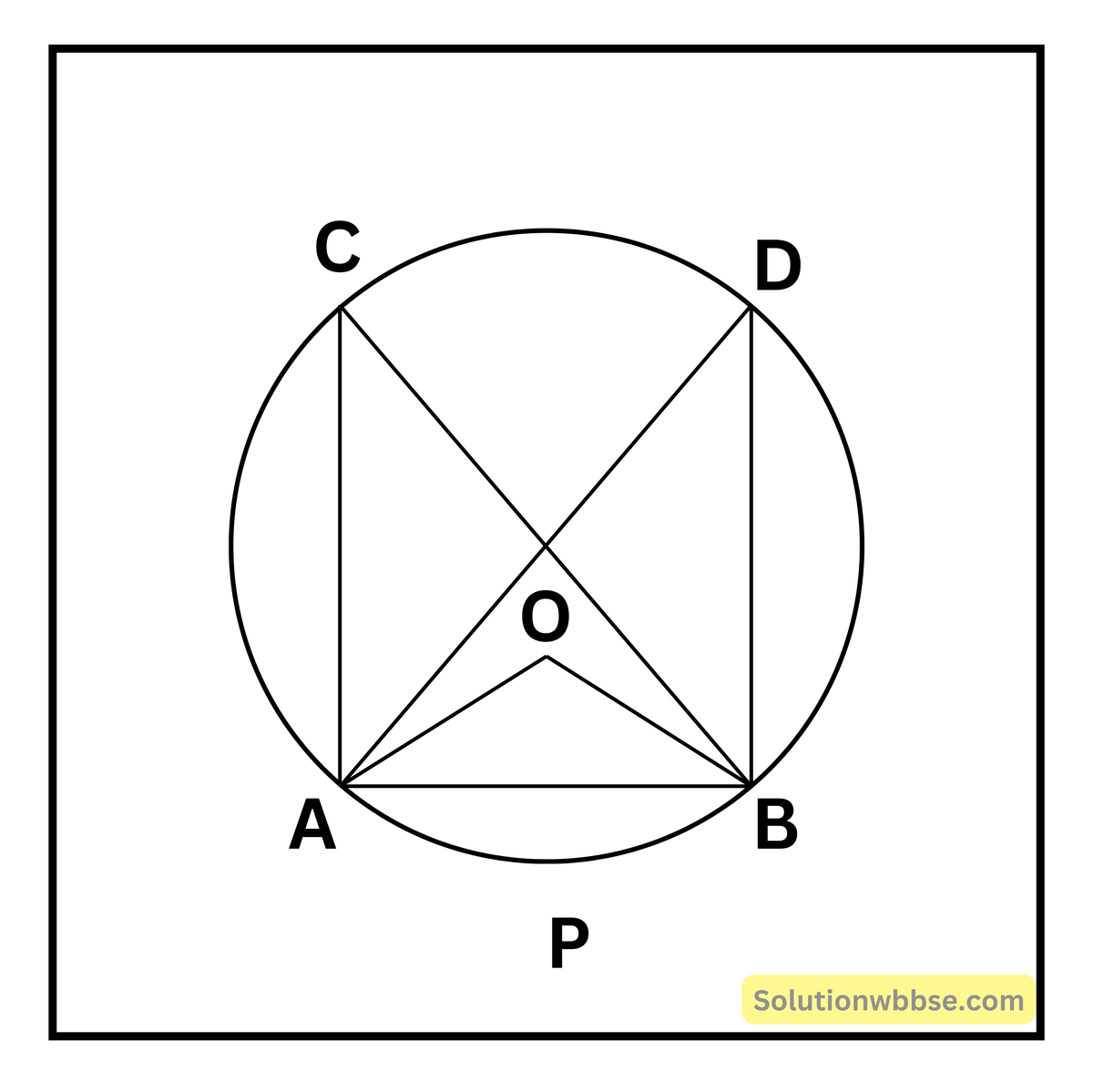
প্রদত্ত – মনে করি O কেন্দ্রীয় বৃত্তের ∠ACB ও ∠ADB যে-কোনো দুটি কোণ ABDC বৃত্তাংশে অবস্থিত।
প্রমাণ করতে হবে – ACDB বৃত্তাংশস্থ সকল বৃত্তস্থ কোণই সমান।
যেহেতু ∠ACB ও ∠ADB ওই বৃত্তাংশস্থ যে-কোনো দুটি বৃত্তস্থ কোণ, সুতরাং ∠ACB ও ∠ADB পরস্পর সমান প্রমাণ করলেই উপপাদ্যটি প্রমাণিত হবে।
অঙ্কন – O, A বিন্দুদ্বয় ও O, B বিন্দুদ্বয় সরলরেখাংশ দ্বারা যুক্ত করলাম।
প্রমাণ – APB বৃত্তচাপের দ্বারা গঠিত ∠AOB কেন্দ্রস্থ কোণ এবং ∠ACB ও ∠ADB বৃত্তস্থ কোণ।
∴ ∠AOB = 2∠ACB
এবং ∠AOB = 2∠ADB
সুতরাং, 2∠ACB = 2∠ADB
∴ ∠ACB = ∠ADB (প্রমাণিত)
উপপাদ্য – 36. দুটি বিন্দুর সংযোজক সরলরেখাংশ তার একই পার্শ্বে অপর দুটি বিন্দুতে দুটি সমান কোণ উৎপন্ন করলে ওই চারটি বিন্দু সমবৃত্তস্থ হবে।
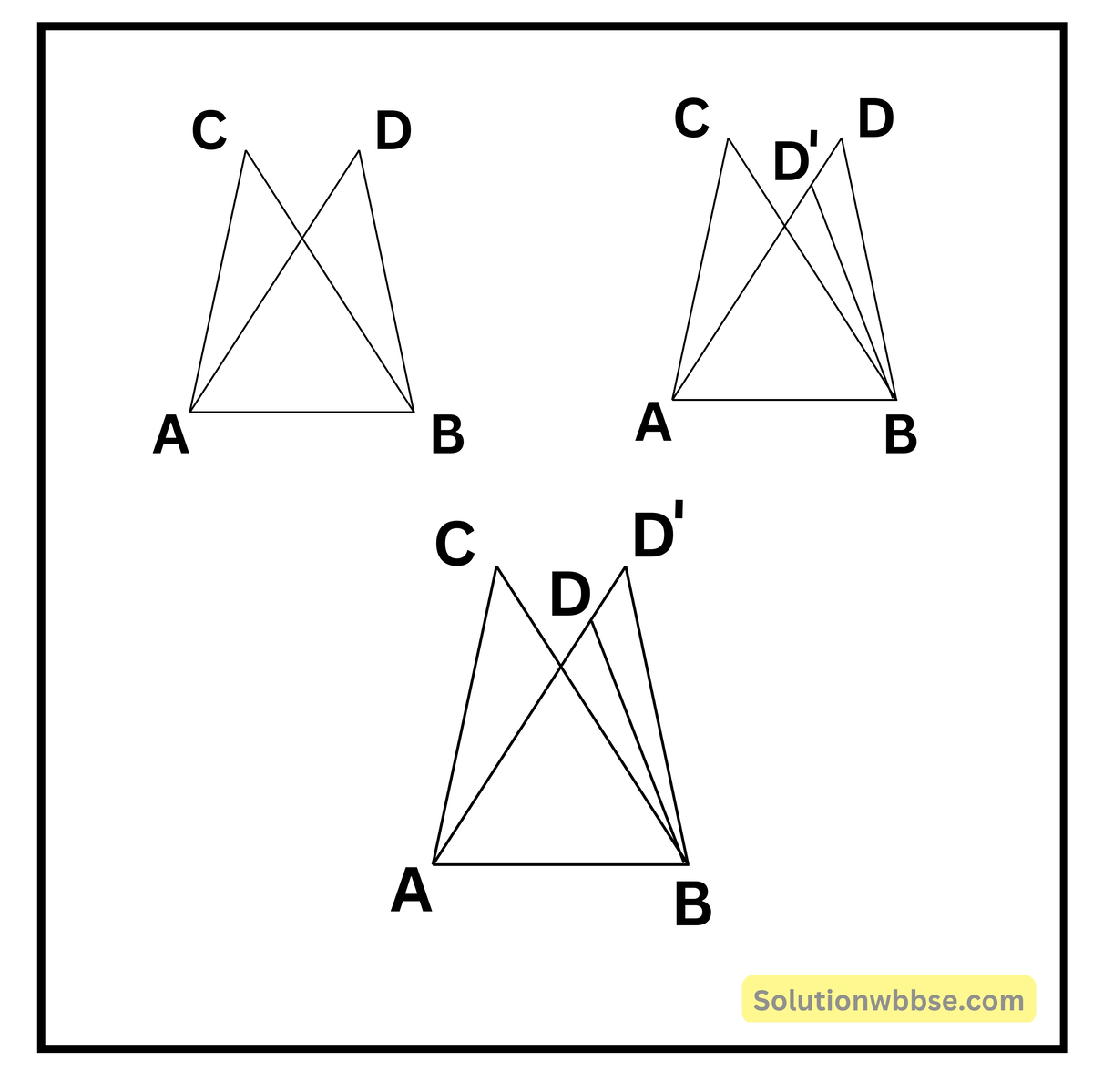
প্রদত্ত – দুটি বিন্দু A ও B -এর সংযোজক সরলরেখাংশ C ও D বিন্দুতে সমান কোণ উৎপন্ন করেছে।
∴ ∠ACB = ∠ADB
প্রমাণ করতে হবে – A, B, D ও C বিন্দুগুলি সমবৃত্তস্থ।
প্রমাণ – A, B ও C তিনটি অসমরেখ বিন্দু দিয়ে নির্দিষ্ট বৃত্ত অঙ্কন করি।
যদি নির্দিষ্ট বৃত্তটি D বিন্দুগামী না হয় তবে বৃত্তটি AD -কে বা বর্ধিত AD -কে একটি বিন্দুতে ছেদ করবে।
ধরি, বৃত্তটি AD -কে বা বর্ধিত AD -কে D’ বিন্দুতে ছেদ করেছে।
∴ A, B, D’ ও C বিন্দুচারটি সমবৃত্তস্থ। D’ ও B বিন্দু দুটি সরলরেখাংশ দ্বারা যুক্ত করি।
∴ ∠ACB = ∠AD’B (একই বৃত্তাংশস্থ বৃত্তস্ত কোণ)
কিন্তু ∠ACB = ∠ADB
∴ ∠AD’B = ∠ADB
কিন্তু ইহা সম্ভব নয়, যদি না D ও D’ বিন্দুদ্বয় সমাপতিত হয়। [কারণ একটি ত্রিভুজের বহিঃস্থ কোণ বিপরীত অন্তঃস্থকোণের সমান হতে পারে না]
∴ A, B, D ও C বিন্দু চারটি সমবৃত্তস্থ। (প্রমাণিত)
উপপাদ্য – 37. অর্ধবৃত্তস্থ কোণ সমকোণ।
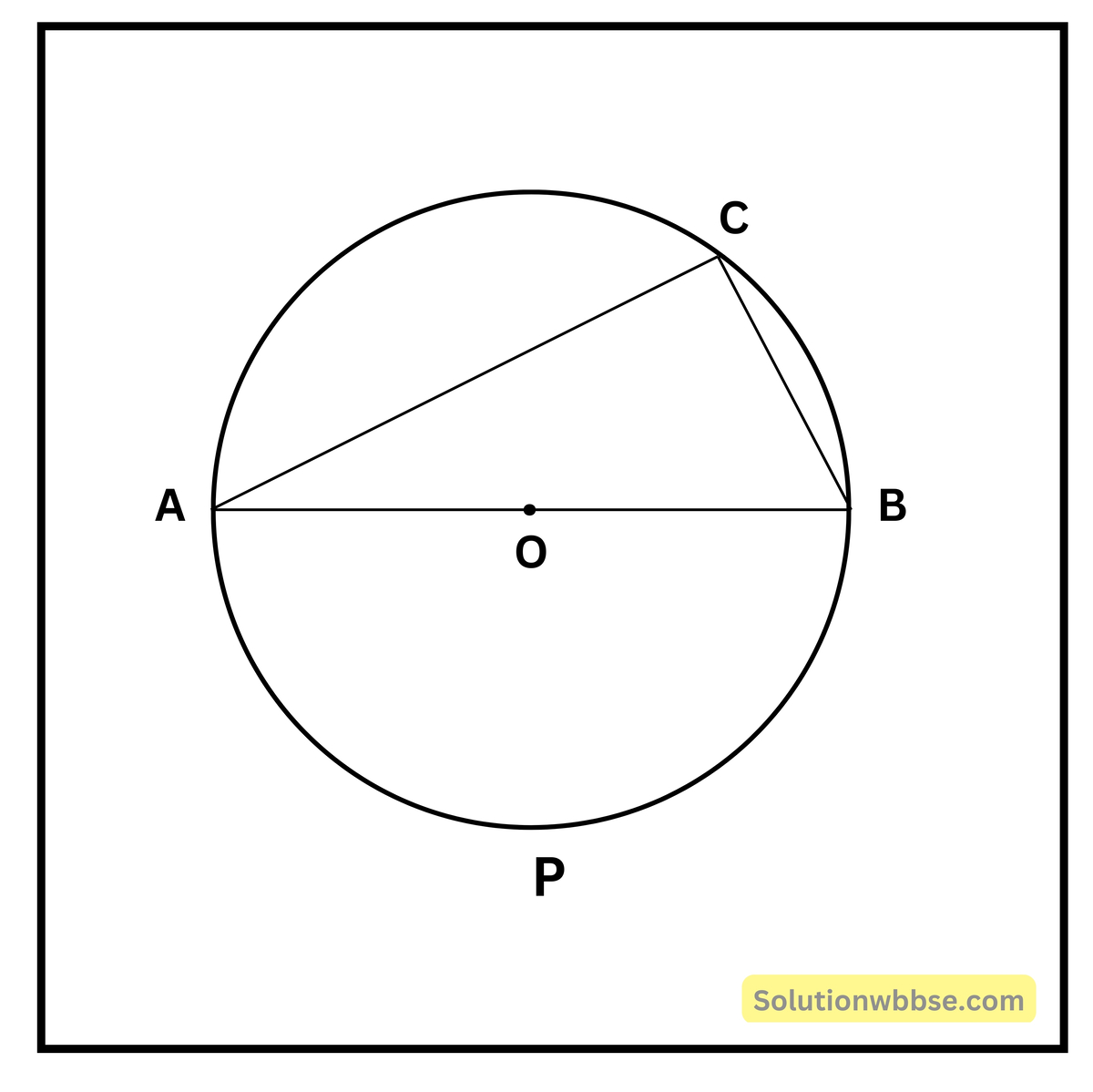
প্রদত্ত – O কেন্দ্রীয় বৃত্তের ∠ACB যে-কোনো একটি অর্ধবৃত্তস্থ কোণ।
প্রমাণ করতে হবে যে – ∠ACB = 1 সমকোণ।
প্রমাণ – O কেন্দ্রীয় বৃত্তের \(\overset\frown{APB}\) বৃত্তচাপের দ্বারা গঠিত সম্মুখ কেন্দ্রস্থ কোণটি ∠AOB এবং ∠ACB ওই \(\overset\frown{APB}\) বৃত্তচাপের দ্বারা গঠিত সম্মুখ বৃত্তস্থ কোণ।
∴ ∠AOB = 2∠ACB —(I)
যেহেতু AB একটি সরলরেখাংশ, সুতরাং ∠AOB একটি সরলকোণ।
∴ ∠AOB = 2 সমকোণ
সুতরাং, 2∠ACB = 2 সমকোণ [I থেকে পেলাম]
∴ ∠ACB = 1 সমকোণ [প্রমাণিত]
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের সপ্তম অধ্যায়, ‘বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য’ -এর উপপাদ্যমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment