এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের সপ্তম অধ্যায়, ‘বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

প্রয়োগ 1 – P কেন্দ্রবিশিষ্ট একটি বৃত্ত অঙ্কন করো এবং ঐ বৃত্তে ACB বৃত্তচাপের দ্বারা গঠিত কেন্দ্রস্থ কোণ ∠APB ও বৃত্তস্থ কোণ ∠AQB অঙ্কন করে প্রমাণ করি ∠APB = 2∠AQB।
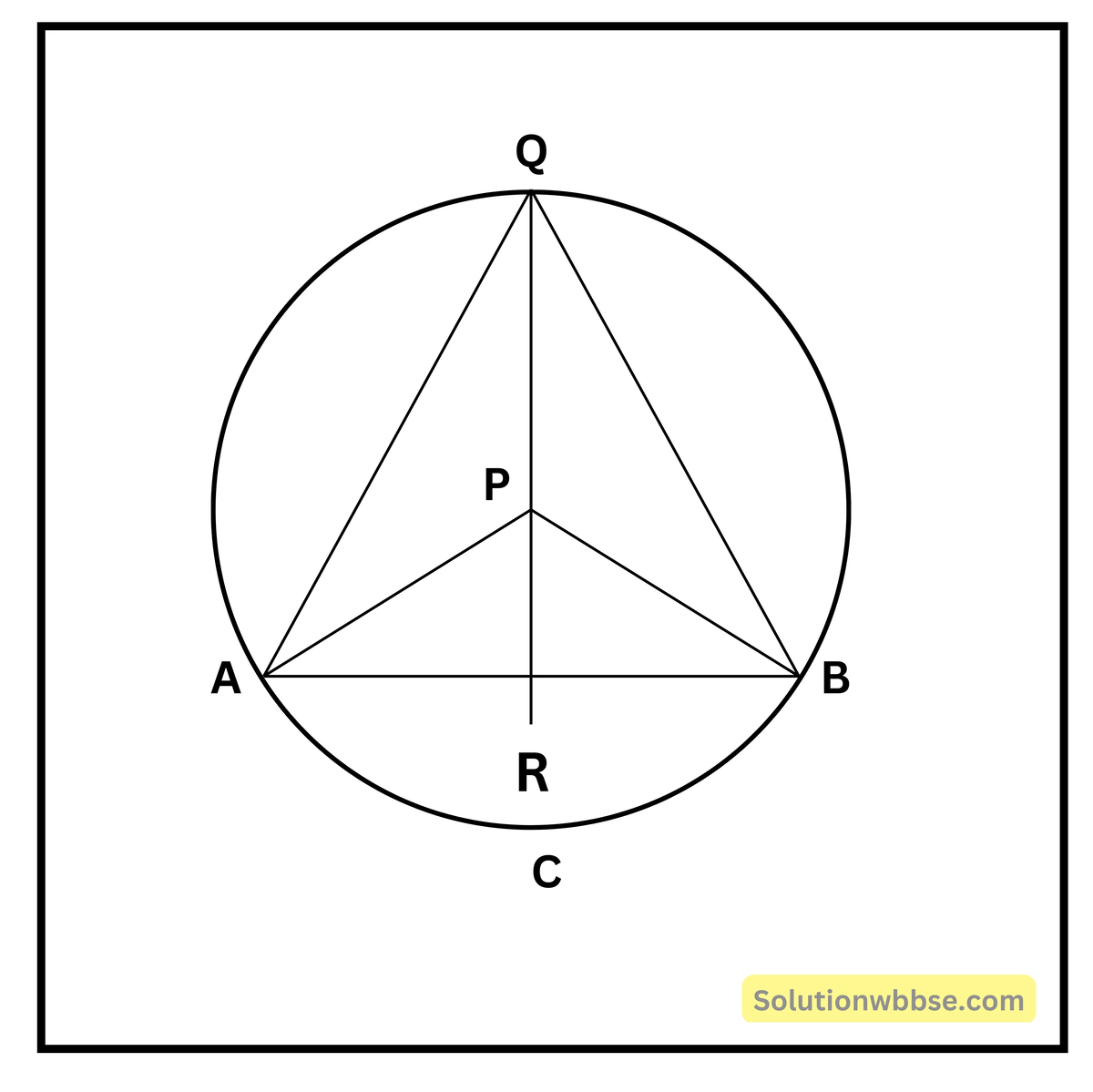
মনে করি, ACB বৃত্তচাপের উপর অবস্থিত P কেন্দ্রীয় বৃত্তে \(\angle APB\) কেন্দ্রস্থ কোণ \(\angle AQB\) বৃত্তস্থ কোণ।
প্রমাণ করতে হবে, \(\angle APB = 2\angle AQB\)
অঙ্কন – Q, P যোগ করে R পর্যন্ত বর্ধিত করা হল।
প্রমাণ – \(\Delta APQ\) এর \(AP = PQ\) (একই বৃত্তের ব্যাসার্ধ)
অতএব \(\angle PAQ = \angle AQP\)।
আবার, \(\Delta AQP\) এর QP বাহুকে R পর্যন্ত বর্ধিত করা হয়েছে
অর্থাৎ বহিঃকোণ \(\angle APR = \angle PAQ + \angle AQP \)
\(= 2\angle AQP\)অনুরূপভাবে \(\Delta BQP\) থেকে পাওয়া যাবে \(\angle BPR = 2\angle BQP\)
∴ \( \angle APB = \angle APR + \angle BPR\)
\( = 2(\angle AQP + \angle BQP) \)\( = 2\angle AQB\) (প্রমাণিত)।
প্রয়োগ 2. ABC ত্রিভুজের পরিবৃত্তের কেন্দ্র O; বিন্দু A এবং BC জ্যা কেন্দ্রের বিপরীত পার্শ্বে অবস্থিত। ∠BOC = 120° হলে ∠BAC -এর মান হিসাব করে লিখি।
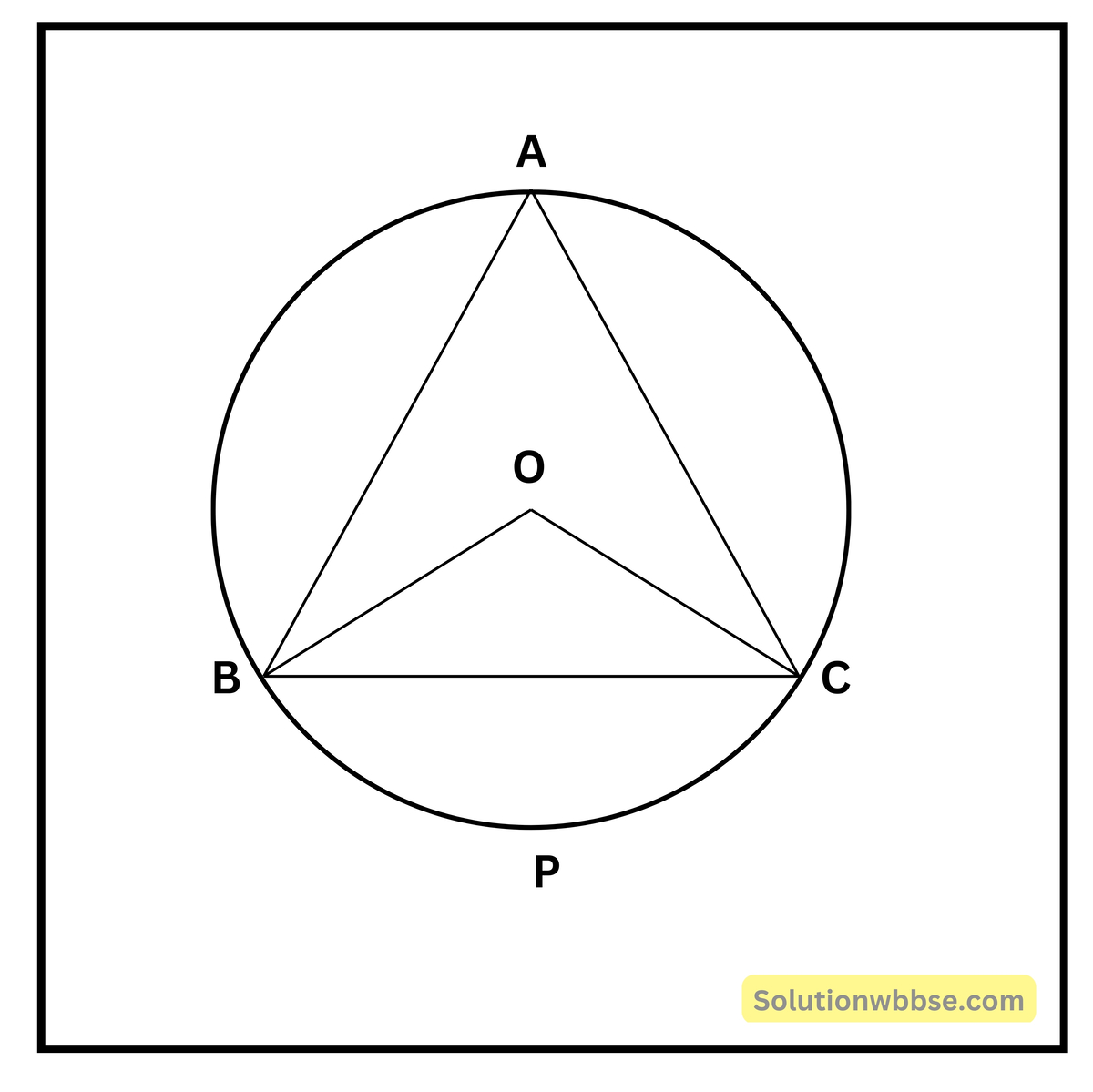
ছবি এঁকে দেখছি, Oকেন্দ্রীয় বৃত্তের একই বৃত্তচাপ BPC -এর দ্বারা গঠিত কেন্দ্রস্থ কোণ ∠BOC ও বৃত্তস্থ কোণ ∠BAC
∴ ∠BAC = ∠BOC = \(\frac12\) × 120° = 60°
প্রয়োগ. 3 পাশের ছবির O কেন্দ্রীয় বৃত্তটি A, B ও C বিন্দুগামী। ∠ABO = 35° এবং ∠ACO = 45° হলে, ∠BOC -এর মান হিসাব করে লিখি।
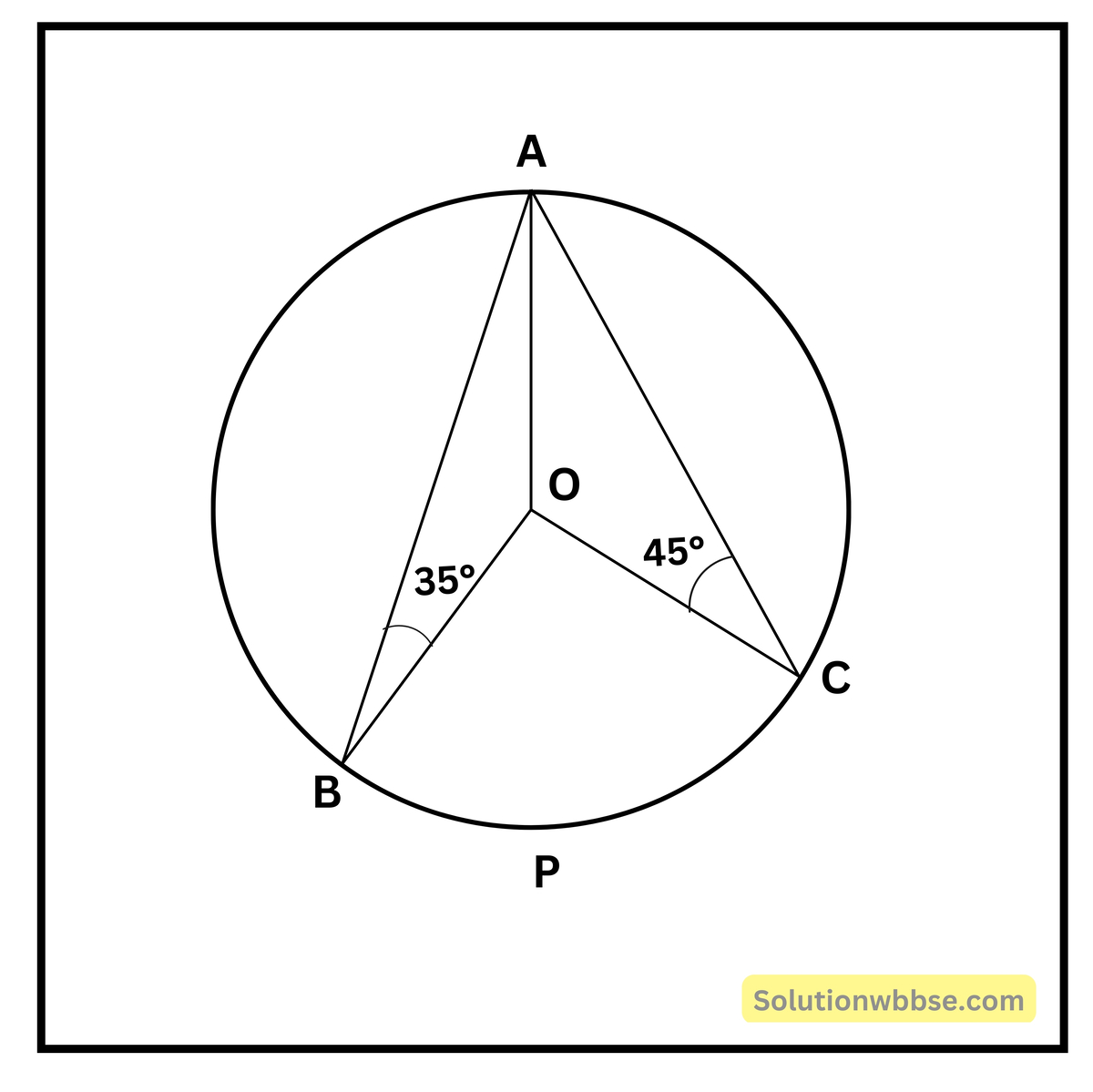
ΔOAB -তে, OA = OB (একই বৃত্তের ব্যাসার্ধ) ∴ ∠OAB = ∠OBA = 35°
ΔOAC -তে, OA = OC (একই বৃত্তের ব্যাসার্ধ) ∴ ∠OAC = ∠OCA = 45°
∴ ∠BAC = 35° + 45° = 80°
যেহেতু, O কেন্দ্রীয় বৃত্তে BPC বৃত্তচাপের দ্বারা গঠিত কেন্দ্রস্থ কোণ ∠BOC এবং বৃত্তস্থ কোণ ∠BAC, সুতরাং ∠BOC = 2∠BAC = 160°
প্রয়োগ 4. পাশের O কেন্দ্রীয় বৃত্তের ছবিটি দেখি এবং ∠OAB -এর মান হিসাব করে লিখি যখন ∠OAP = 25° এবং ∠OBP = 35°।
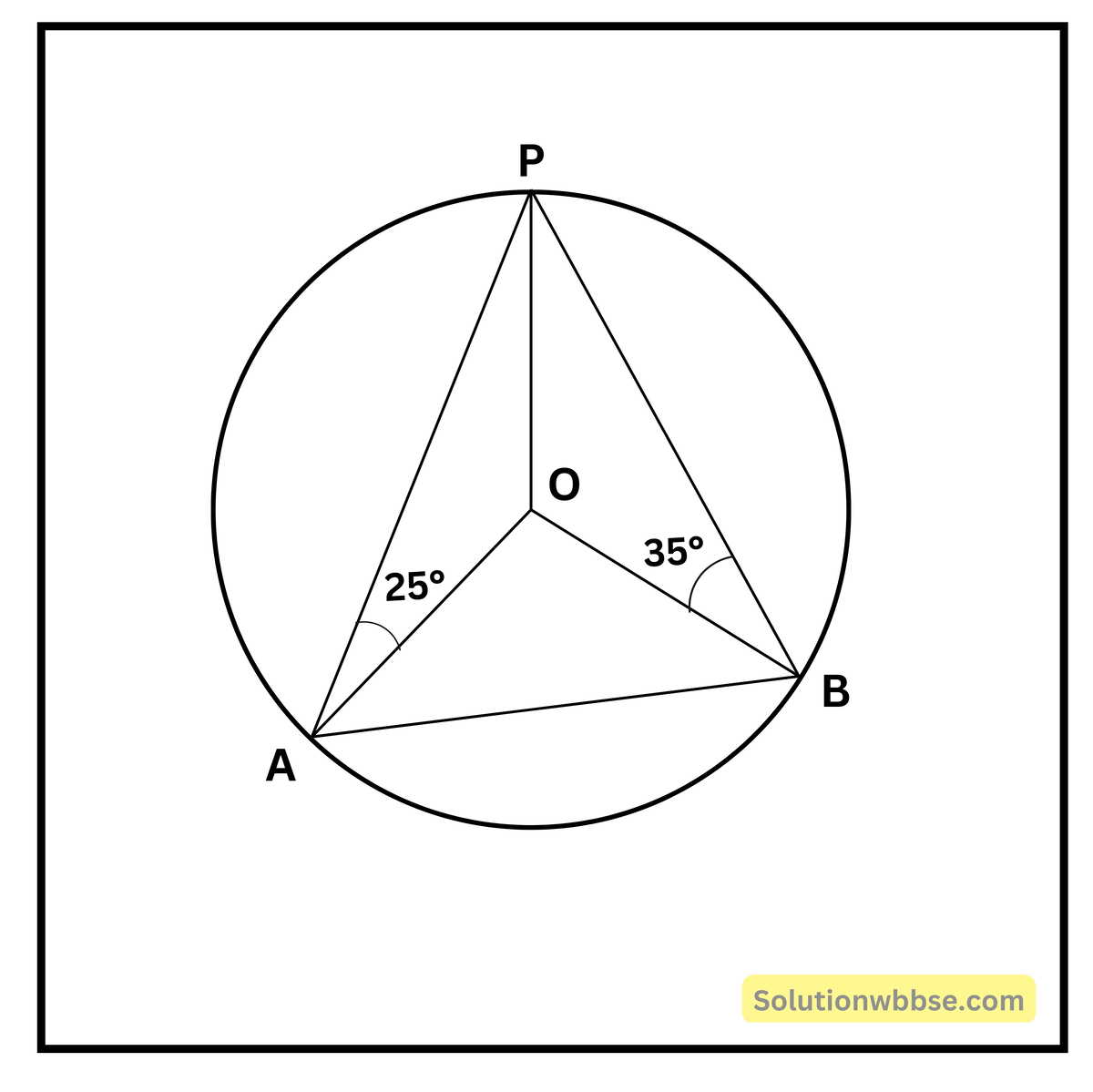
অঙ্কন – OP যোগ করি।
প্রমাণ – OA = OP (একই বৃত্তের ব্যাসার্ধ) ∴ ∠OAP = ∠OΡΑ
∵ ∠OAP = 25°, সুতরাং, ∠OPA = 25°
OB = OP (একই বৃত্তের ব্যাসার্ধ) ∴ ∠OBP = ∠OPB
∵ ∠OBP = 35°, সুতরাং, ∠OPB = 35°
∠APB = ∠OPA + ∠OPB = 25° + 35° = 60°
∠AOB – 2∠APB = 2 × 60° = 120°
ΔΑΟΒ -তে, ∠OAB + ∠OBA = 180° – 120° = 60° [ত্রিভুজের তিনটি কোণের সমষ্টি 180°]
∵ AO = BO [একই বৃত্তের ব্যাসার্ধ)
∴ ∠OAB = ∠OBA = \(\frac12\) × 60° = 30°
প্রয়োগ 5. নীচের চিত্রদুটি দেখে x ও y -এর মান হিসাব করে লিখি।
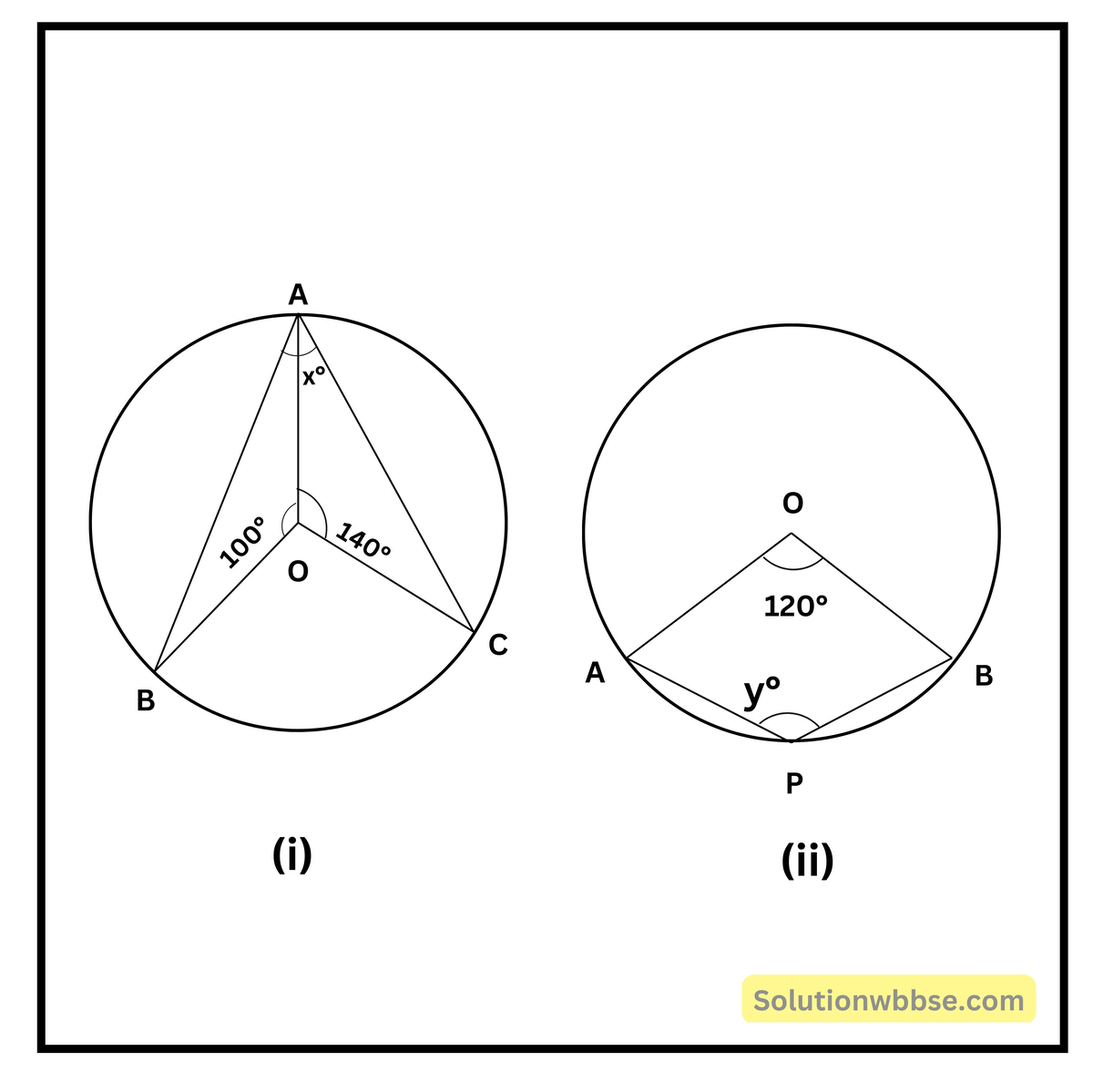
(i) চিত্রে ∠OAC = ∠OCA = \(\frac{180-140}2\) = 20°
∠OBA = ∠OAB = \(\frac{180-100}2\) = 40°
x° = ∠BAC = (20° + 40°) = 60°
(ii) চিত্রে প্রকৃত কোণ ∠AOB = 360° – 120° = 240°
y° = ∠APB = \(\frac12\) × 240° = 120°
প্রয়োগ 6. দুটি সমান দৈর্ঘ্যের ব্যাসার্ধবিশিষ্ট বৃত্ত যারা পরস্পরকে A ও B বিন্দুতে ছেদ করেছে। A বিন্দুগামী একটি সরলরেখা AB -এর বিপরীত পার্শ্বে একটি বৃত্তকে P বিন্দুতে এবং অপর বৃত্তকে বিন্দুতে ছেদ করে। যেখানে, P ও Q বিন্দুদ্বয় AB -এর বিপরীত পার্শ্বে অবস্থিত। প্রমাণ করি যে, BP = BQ
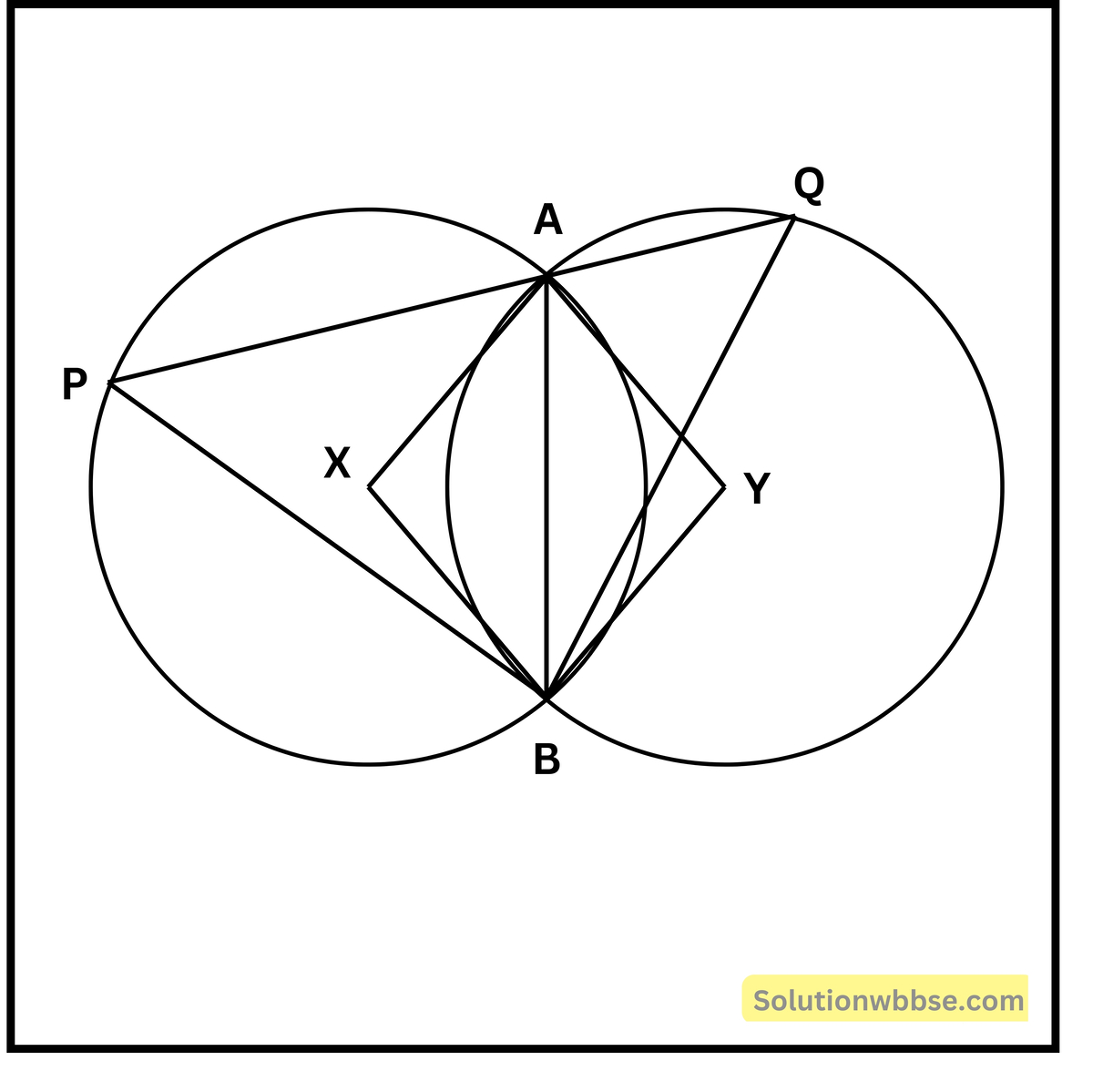
প্রদত্ত – দুটি সমান বৃত্ত পরস্পরকে A ও B বিন্দুতে ছেদ করেছে। A বিন্দুগামী সরলরেখা একটি বৃত্তকে P বিন্দুতে এবং অপর বৃত্তকে বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে – BP=BQ
অঙ্কন – ধরি, X ও Y যথাক্রমে প্রথম বৃত্ত ও দ্বিতীয় বৃত্তের কেন্দ্র। A, B; A, X; B, X; A, Y; B, Y যুক্ত করলাম।
প্রমাণ – ΔΑΧB ও ΔAYB -এর AX = AY [∵ সমান বৃত্তের ব্যাসার্ধ]
BX = BY [∵ দুটি সমান বৃত্তের ব্যাসার্ধ]
AB সাধারণ বাহু।
∴ ΔΑΧΒ ≅ Δ ΑΥB (S-S-S সর্বসমতার শর্তানুসারে)
∴ ∠AXB = ∠AYB [সর্বসম ত্রিভুজের অনুরূপ অংশ]
∴ \(\frac12\)∠AXB = \(\frac12\)∠AYB
আবার, ∠APB = \(\frac12\)∠AXB [∵ প্রথম বৃত্তের AB উপচাপের দ্বারা গঠিত ∠AXB কেন্দ্রস্থ কোণ ও ∠APB বৃত্তস্থ কোণ]
অনুরূপভাবে, ∠AQB = \(\frac12\)∠AYB [∵ দ্বিতীয় বৃত্তের AB উপচাপের দ্বারা গঠিত ∠AYB কেন্দ্রস্থ কোণ ও ∠AQB বৃত্তস্থ কোণ]
∴ ∠APB = ∠AQB অর্থাৎ ∠QPB = ∠PQB
∴ ΔPQB -এর ∠QPB = ∠PQB
∴ BP = BQ [প্রমাণিত]
[যদি AB -এর একই পার্শ্বে সরলরেখাটি P ও Q বিন্দুতে বৃত্তকে ছেদ করে তাহলে নিজে ছবি এঁকে প্রমাণ করি BP = BQ]
প্রয়োগ 7. ABC একটি সমদ্বিবাহু ত্রিভুজ যার AB = AC; BC -এর যে পার্শ্বে ΔABC অবস্থিত, সেই পার্শ্বেই ΔDBC এমনভাবে অঙ্কন করা হলো যাতে ∠BAC = 2∠BDC হয়। প্রমাণ করি যে, A -কে কেন্দ্র করে AB ব্যাসার্ধ নিয়ে যে বৃত্ত অঙ্কন করা হবে তা D বিন্দুগামী হবে অর্থাৎ D বিন্দু ওই বৃত্তের উপর অবস্থিত হবে।
[উত্তর সংকেত – ধরি D বিন্দু ওই বৃত্তের উপর অবস্থিত নয়। ∴ বৃত্তটি BD বা বর্ধিত BD -কে ধরি D’ বিন্দুতে ছেদ করেছে। D’ ও C বিন্দু দুটি যুক্ত করি।
∴ ∠BAC = 2∠BD’C;
কিন্তু ∠BAC = 2∠BDC;
∴ ∠BD’C = ∠BDC, কিন্তু এটা অসম্ভব যদি না D ও D’ বিন্দু সমাপতিত হয়। কারণ ত্রিভুজের বহিঃস্থ কোণ অন্তঃস্থ বিপরীত একটি কোণের সমান হতে পারে না।]
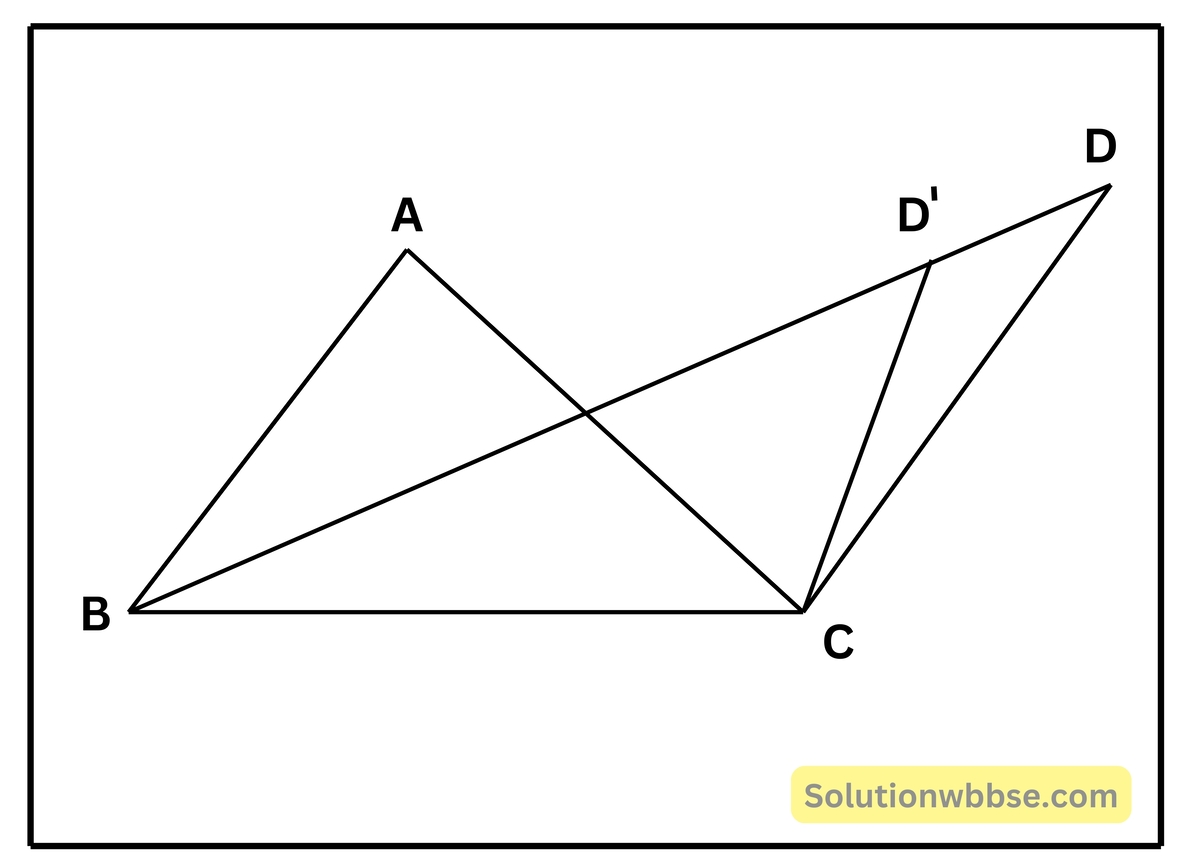
ধরে নেওয়া হল বৃত্তটি D বিন্দু দিয়ে না গিয়ে BD রেখাংশকে D’ বিন্দুতে ছেদ করে। CD’ যোগ করা হল। এখন A কেন্দ্রীয় বৃত্তের একই চাপ BC -এর ওপর ∠BAC কেন্দ্রস্থ কোণ এবং ∠BD’C বৃত্তস্থ কোণ।
∴ ∠BAC = 2∠BD’C
আবার দেওয়া আছে ∠BAC = 2∠BDC এবং ∠BDC = ∠BD’C
কিন্তু ইহা অসম্ভব যদি D’ বিন্দু D বিন্দুতে সমাপতিত না হয়। কারণ ত্রিভুজের বহিঃস্থ কোণ অন্তঃস্থ বিপরীত একটি কোণের সমান হতে পারে না।
অর্থাৎ বৃত্তটি D বিন্দুগামী হবে।
প্রয়োগ 8. নীচের বৃত্তের ছবি দেখি ও x -এর মান নির্ণয় করি। O বৃত্তের কেন্দ্র।
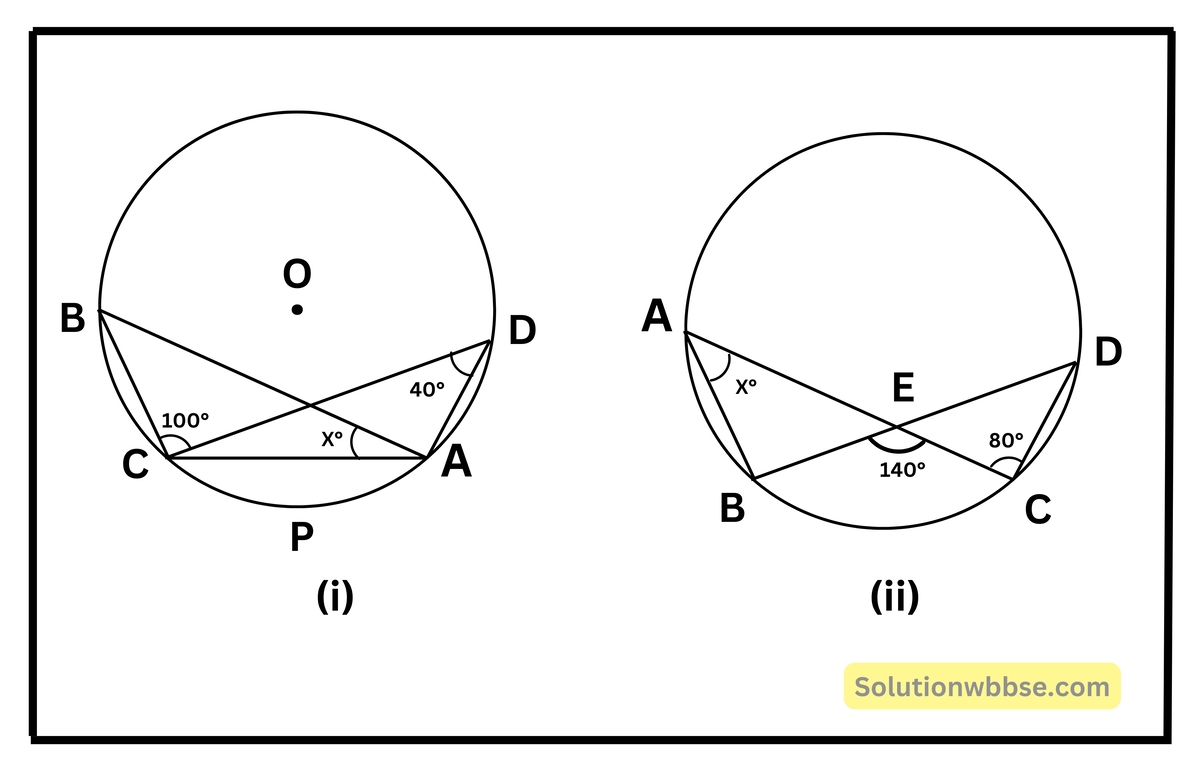
(i) O বৃত্তের কেন্দ্র।
দুটি বৃত্তস্থ কোণ ∠ABC ও ∠ADC উপচাপ CPA -এর দ্বারা গঠিত সম্মুখ কোণ।
∴ ∠ABC = ∠ADC = 40° (∵ দেওয়া আছে ∠ADC = 40°)
এবং ΔABC -এর ∠ABC + ∠ACB + ∠BAC = 180°
∴ 40° + 100° + x° = 180°
বা, x° = 180° – 140° = 40°
∴ x = 40°
(ii) O বৃত্তের কেন্দ্র।
∴ ∠BEC = ∠AED = 140° [বিপ্রতীপ কোণ]
আবার, ∠BEC + ∠BAE = 180° [একই সরলরেখায় অবস্থিত]
বা, 140° + ∠BAE = 180°
বা, ∠BAE = 180° – 140° = 40°
আবার, ∠DCE = ∠EBA = 80° [বৃত্তস্থ কোণ]
বা, ∠BAE + ∠ ABE + ∠AEB = 180°
বা, X° + 80° + 40° = 180°
বা, X° = 180° – 120° = 60°
প্রয়োগ 9. পাশের ছবির ∠BDC = 50°, ∠APB = 65°, ∠CBD = 28°; ∠ADB, ∠ABD, ∠BAC, ∠ACB, ∠CAD এবং ∠ACD -এর মান নির্ণয় করি।
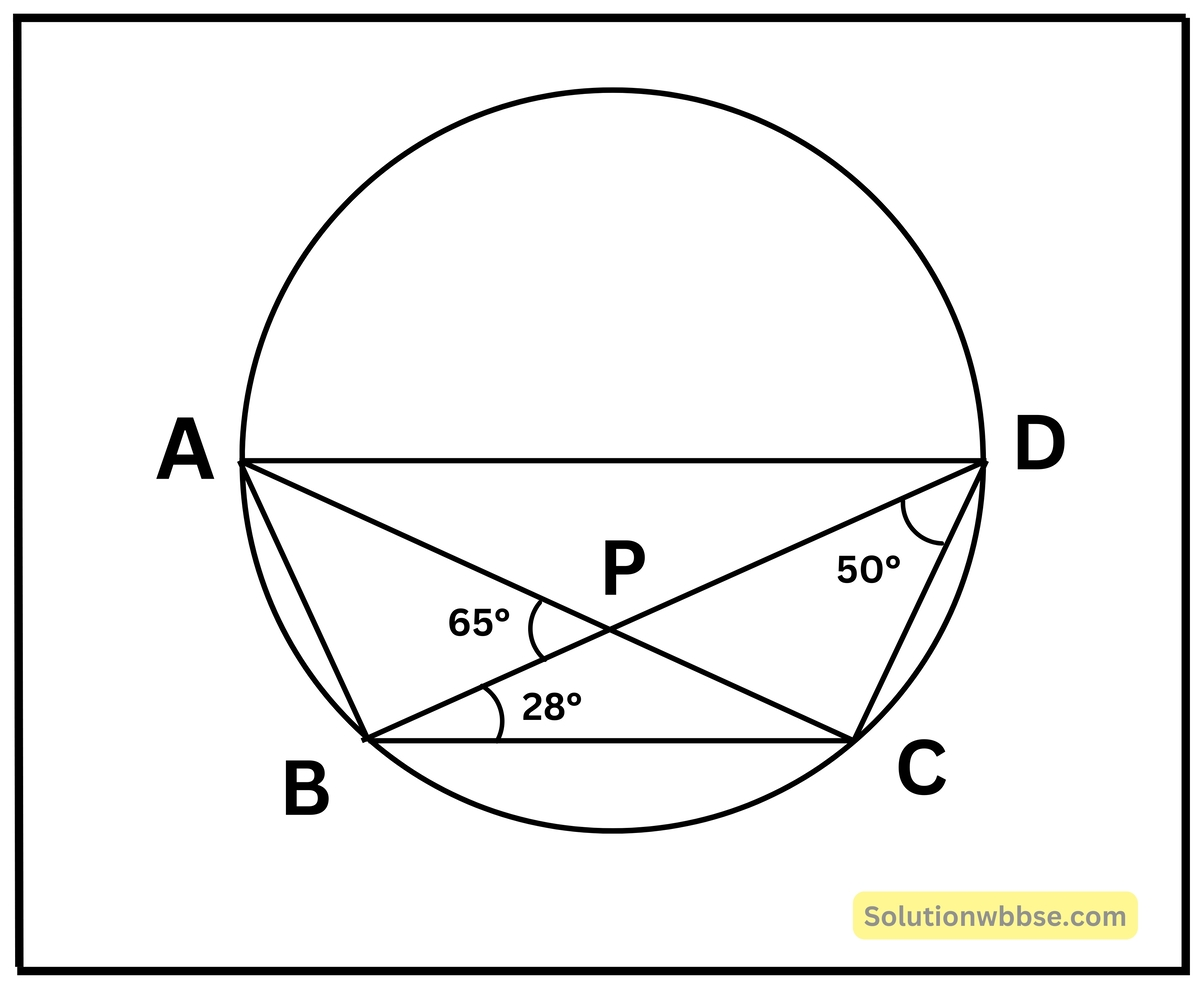
BAC = ∠BDC = 50° [যেহেতু, একই বৃত্তাংশস্থ বৃত্তস্ত কোণ]
আবার, ∠CAD = ∠ABD = 28° [যেহেতু, একই বৃত্তাংশস্থ বৃত্তস্ত কোণ]
ABPC-এর, বহিঃস্থ ∠APB = ∠PBC+∠PCB.
∴ 65° = 28° + ∠ACB; ∴ ∠ACB = 37°
∴ ∠ADB = ∠ACB = 37° [একই বৃত্তাংশস্থ বৃত্তস্ত কোণ]
ΔABP -এর, ∠ABP + ∠BPA + ∠PAB = 180°
∴ ∠ABP = 65°
∴ ∠ABD = 37°
∠ACD = ∠ABD = 65° [∵ একই বৃত্তচাপের দ্বারা গঠিত সম্মুখ বৃত্তস্থ বৃত্তস্ত কোণ]
প্রয়োগ 10. প্রমাণ করি যে-কোনো বৃত্তে একই বৃত্তাংশস্থ সমস্ত কোণের সমদ্বিখণ্ডকগুলি একটি নির্দিষ্ট বিন্দুগামী।
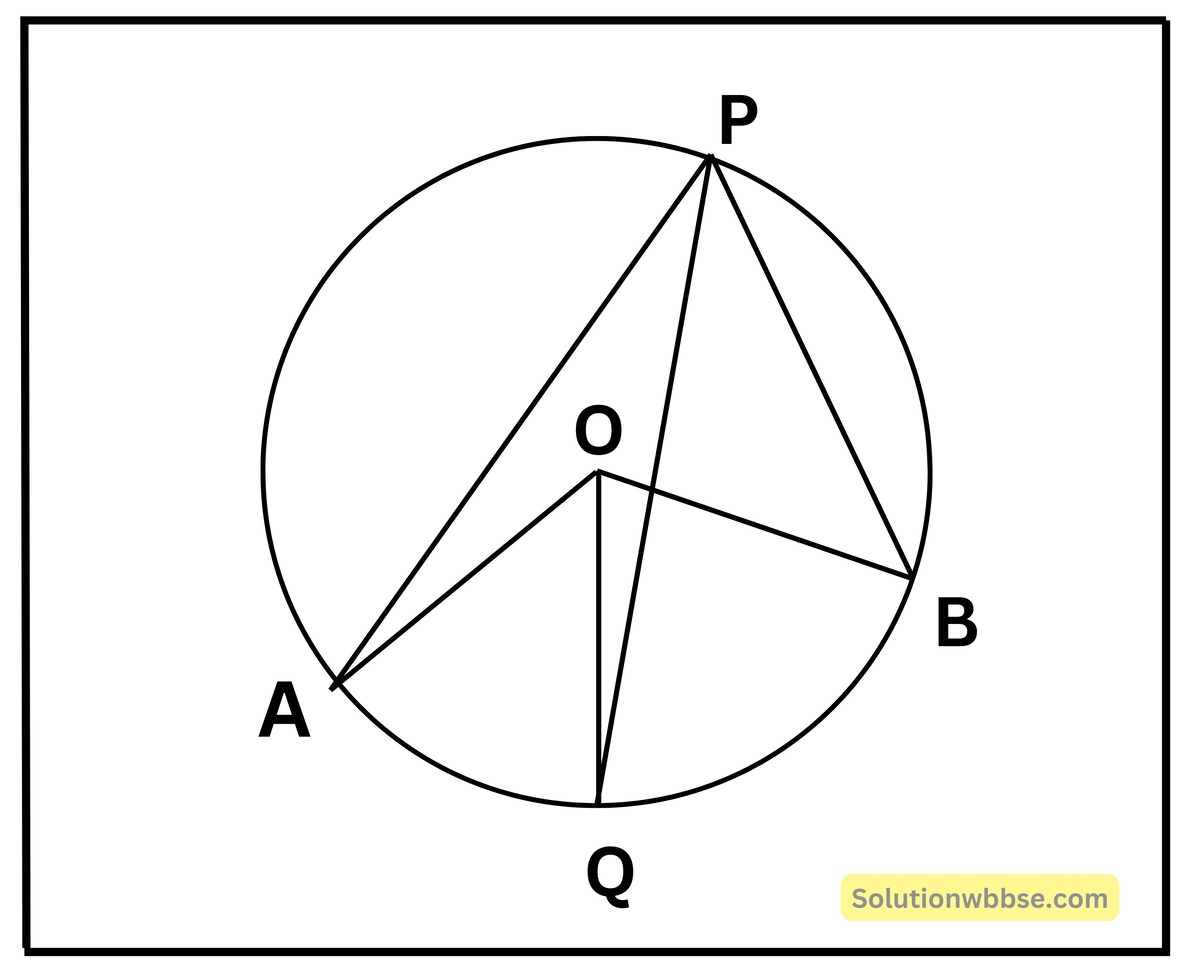
প্রদত্ত – O কেন্দ্রীয় একটি বৃত্তের APB বৃত্তাংশে অবস্থিত একটি কোণ ∠APB. ∠APB -এর সমদ্বিখণ্ডক বৃত্তটিকে Q বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে – PQ একটি নির্দিষ্ট বিন্দুগামী।
প্রমাণ – ∠APQ = ∠BPQ [∵ PQ, ∠APB -এর সমদ্বিখণ্ডক]
∠AOQ = 2∠APQ; আবার ∠BOQ = 2∠BPQ
যেহেতু, ∠APQ = ∠BPQ, সুতরাং ∠AOQ = ∠BOQ
∴ বৃত্তচাপ AQ = বৃত্তচাপ BQ (যেহেতু চাপ AQ ও চাপ BQ কেন্দ্রে সমান সম্মুখ কোণ উৎপন্ন করে)
∴ AQB বৃত্তচাপের মধ্যবিন্দু Q.
AQB নির্দিষ্ট হলে, Q একটি নির্দিষ্ট বিন্দু।
∴ APB বৃত্তচাপের উপর P বিন্দুর যে-কোনো অবস্থানের জন্য ∠APB -এর সমদ্বিখণ্ডক উহার বিপরীত চাপের মধ্যবিন্দুগামী অর্থাৎ নির্দিষ্ট বিন্দুগামী হবে।
প্রয়োগ 11. পাশের চিত্রের একটি বৃত্তের AB ও CD দুটি জ্যা। BA ও DC -কে বর্ধিত করলে পরস্পর P বিন্দুতে ছেদ করে। প্রমাণ করি যে ∠PCB = ∠PAD
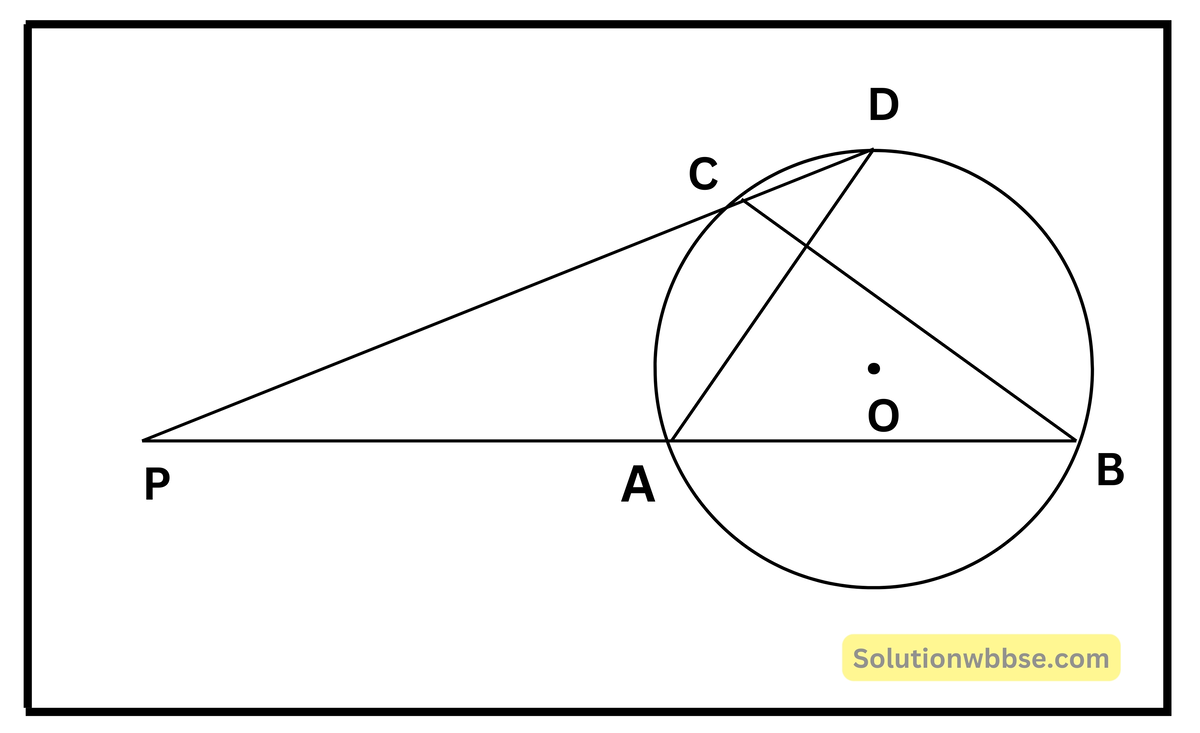
প্রদত্ত – একটি বৃত্তের AB ও CD দুটি জ্যা। BA ও DC -কে বর্ধিত করলে পরস্পরকে P বিন্দুতে ছেদ করে।
প্রমাণ করতে হবে – ∠PCB = ∠PAD
প্রমাণ – ∠BCD = ∠BAD (একই বৃত্তাংশস্থ বৃত্তস্ত কোণ)
আবার ∠PCB = 180° – ∠BCD
এবং PAD = 180°-/BAD
∵ ∠BCD = ∠BAD, সুতরাং 180° – ∠BCD = 180° – ∠BAD
∴ ∠PCB = ∠PAD [প্রমাণিত]
প্রয়োগ 12. ABC সমবাহু ত্রিভুজটি একটি বৃত্তে অন্তলিখিত। BC উপচাপের উপর P যে-কোনো একটি বিন্দু। প্রমাণ করি যে PA = PB + PC
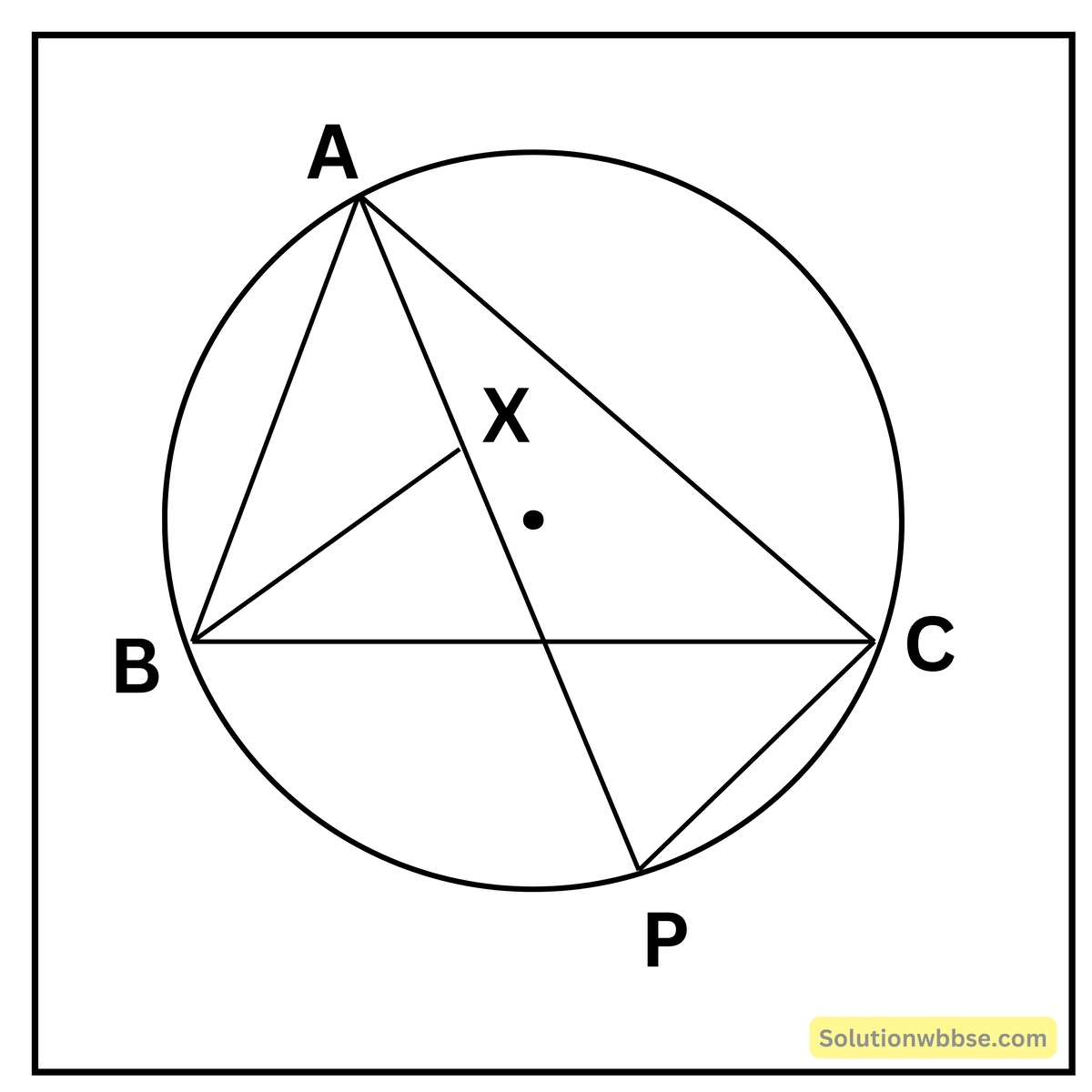
প্রদত্ত – ABC সমবাহু ত্রিভুজটি একটি বৃত্তে অন্তর্লিখিত। BC উপচাপের উপর P যে-কোনো একটি বিন্দু।
প্রমাণ করতে হবে – PA = PB + PC
অঙ্কন – PA -এর থেকে PB -এর সমান করে PX অংশ কেটে নিলাম। B, X বিন্দুদ্বয় যোগ করলাম।
প্রমাণ – PB = PX [অঙ্কনানুসারে]
∴ ∠PBX = ∠PXB —(I)
আবার, ∠ACB = ∠APB [একই বৃত্তাংশস্থ বৃত্তস্ত কোণ]
= 60° [যেহেতু, ABC সমবাহু ত্রিভুজ, সুতরাং ∠ACB = 60°]
∴ ∠PBX + ∠PXB = 180° – 60° = 120°
∴ ∠PBX = ∠PXB = 60° [(I) থেকে পেলাম]
∴ PBX সমবাহু ত্রিভুজ।
∴ ∠PBC = ∠PBX – ∠CBX = ∠CBA – ∠CBX = ∠XBA —(II)
ΔPBC ও ΔΑΒX -এর মধ্যে AB = BC [∵ Δ ABC সমবাহু]
∠ABX = ∠PBC [(II) থেকে পেলাম]
ΒΧ = ΡΒ (∵ ΔBPX সমবাহু)
∴ ΔBPC ≅ ΔΑΒΧ [সর্বসমতার S-A-S শর্তনুসারে]
সুতরাং, AX = PC
∴ PA = PX + XA = PB + PC [প্রমাণিত]
যে-কোনো O কেন্দ্রীয় বৃত্তে ∠PQR একটি অর্ধবৃত্তস্থ কোণ। যুক্তি দিয়ে প্রমাণ করি যে ∠PQR = 90°।
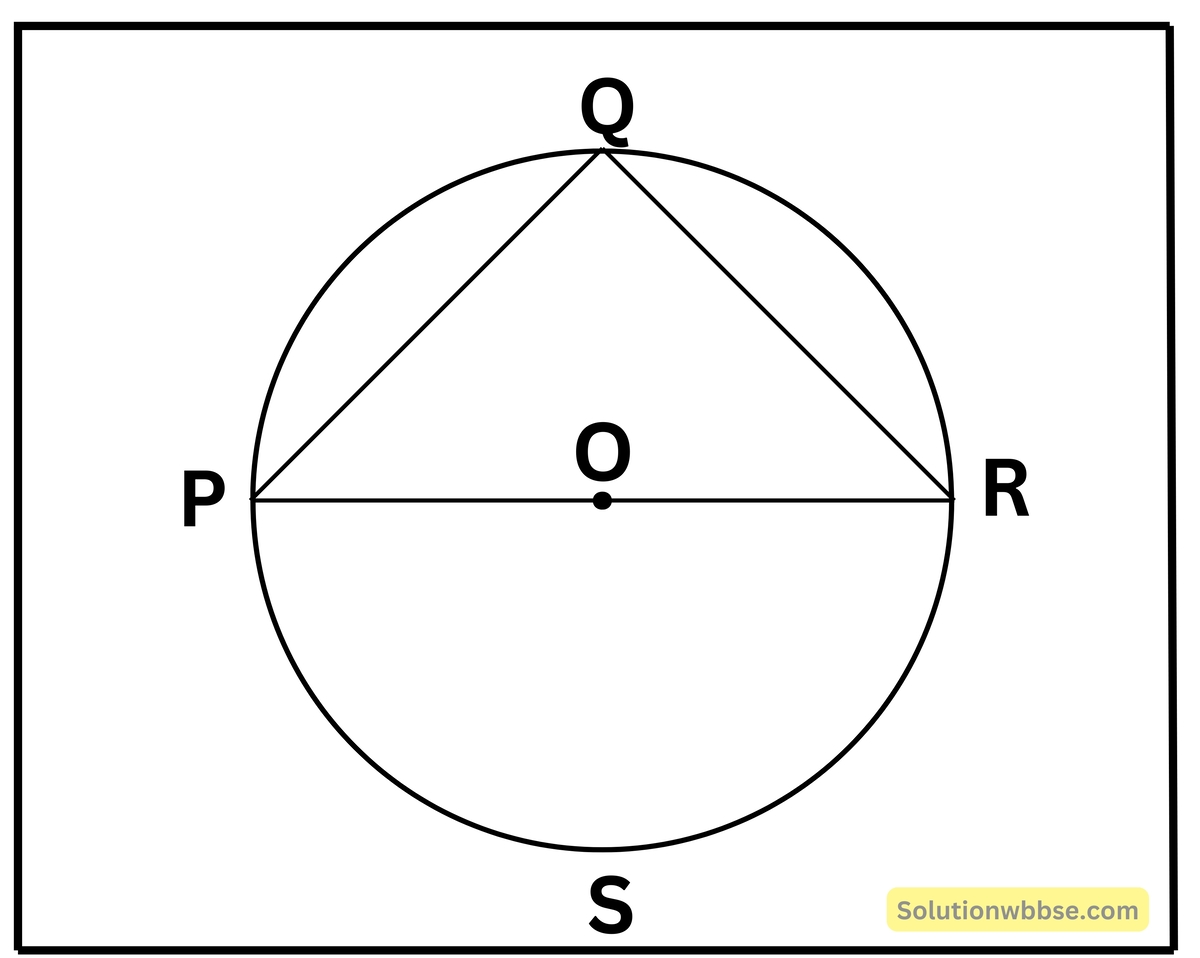
প্রদত্ত – O কেন্দ্রীয় বৃত্তের ∠PQR একটি অর্ধবৃত্তস্থ কোণ।
অঙ্কন – P, Q, R একটি সরলরেখার সাহায্যে যুক্ত করলাম।
প্রমান করতে হবে যে – ∠PQR = 90°
প্রমাণ – O কেন্দ্রীর বৃত্তের \(\overset\frown{PSR}\) বৃত্তচাপের দ্বারা গঠিত সম্মুখ কেন্দ্রস্থ কোণটি ∠POR এবং ∠PQR ওই \(\overset\frown{PSR}\) বৃত্তচাপের দ্বারা গঠিত সম্মুখ কেন্দ্রস্থ কোণ
∴ ∠POR = 2∠PQR —(i)
যেহেতু PR একটি সরলরেখাংশ, সুতরাং ∠POR একটি সরলকোণ
∴ ∠POR = 2 সমকোণ, [1 নং সমীকরণ থেকে পাই]
∴ 2∠PQR = 2 সমকোণ
বা, ∠PQR =1 সমকোণ (180°)
প্রয়োগ 13. একটি বৃত্তের ব্যাস AB এবং P বৃত্তের উপর যে-কোনো একটি বিন্দু। ∠PAB = 30° হলে, PBA -এর মান নির্ণয় করি।
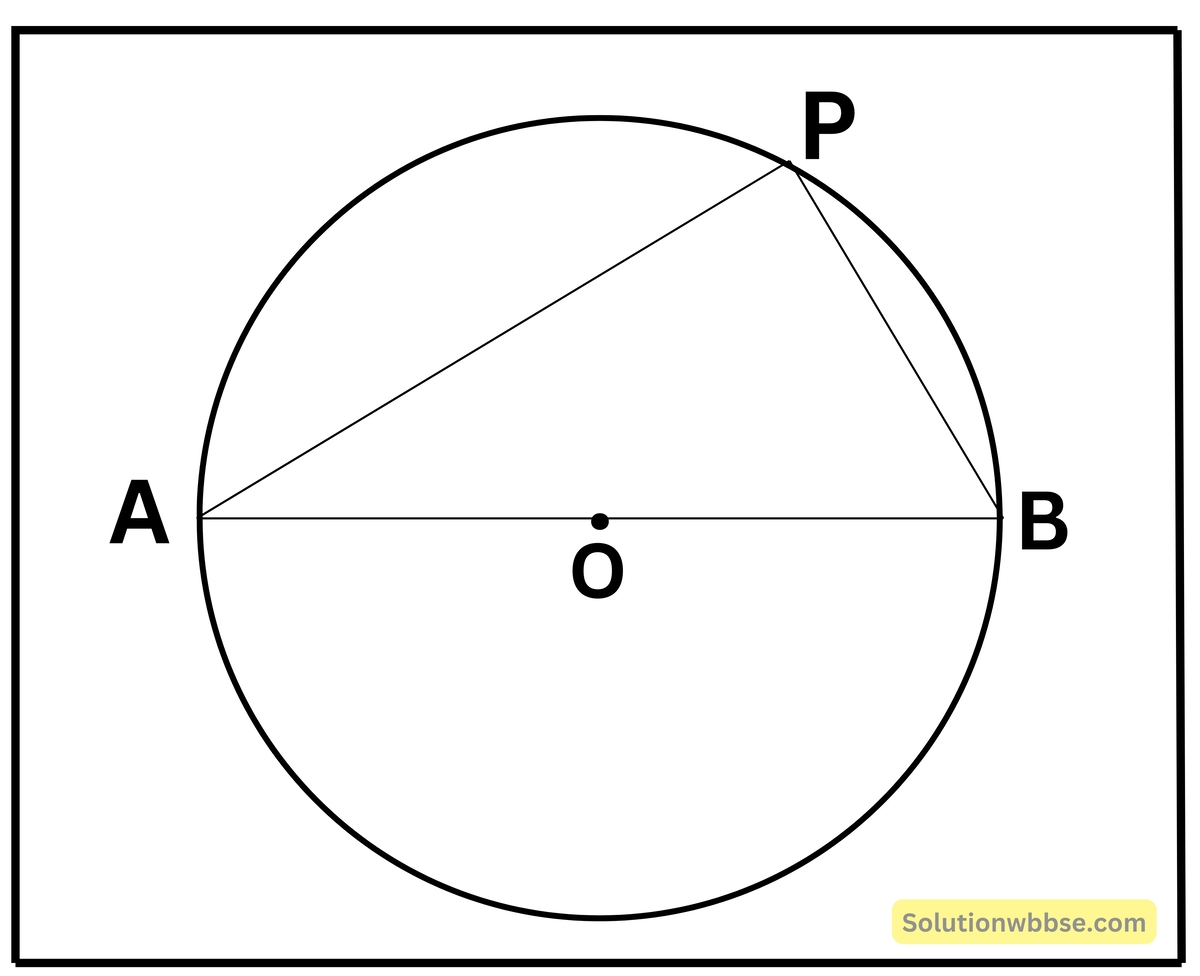
∠APB অর্ধবৃত্তস্থ কোণ।
∠APB = 90°; ∠PAB = 30°
∴ ∠PBA = 90° – 30° = 60°
প্রয়োগ 14. পাশের চিত্রে O কেন্দ্রীয় বৃত্তে AB ব্যাস। C বৃত্তের উপর যে-কোনো একটি বিন্দু। ∠BAC = 50° এবং CD, AB -এর উপর লম্ব হলে, ∠BCD -এর মান নির্ণয় করি।
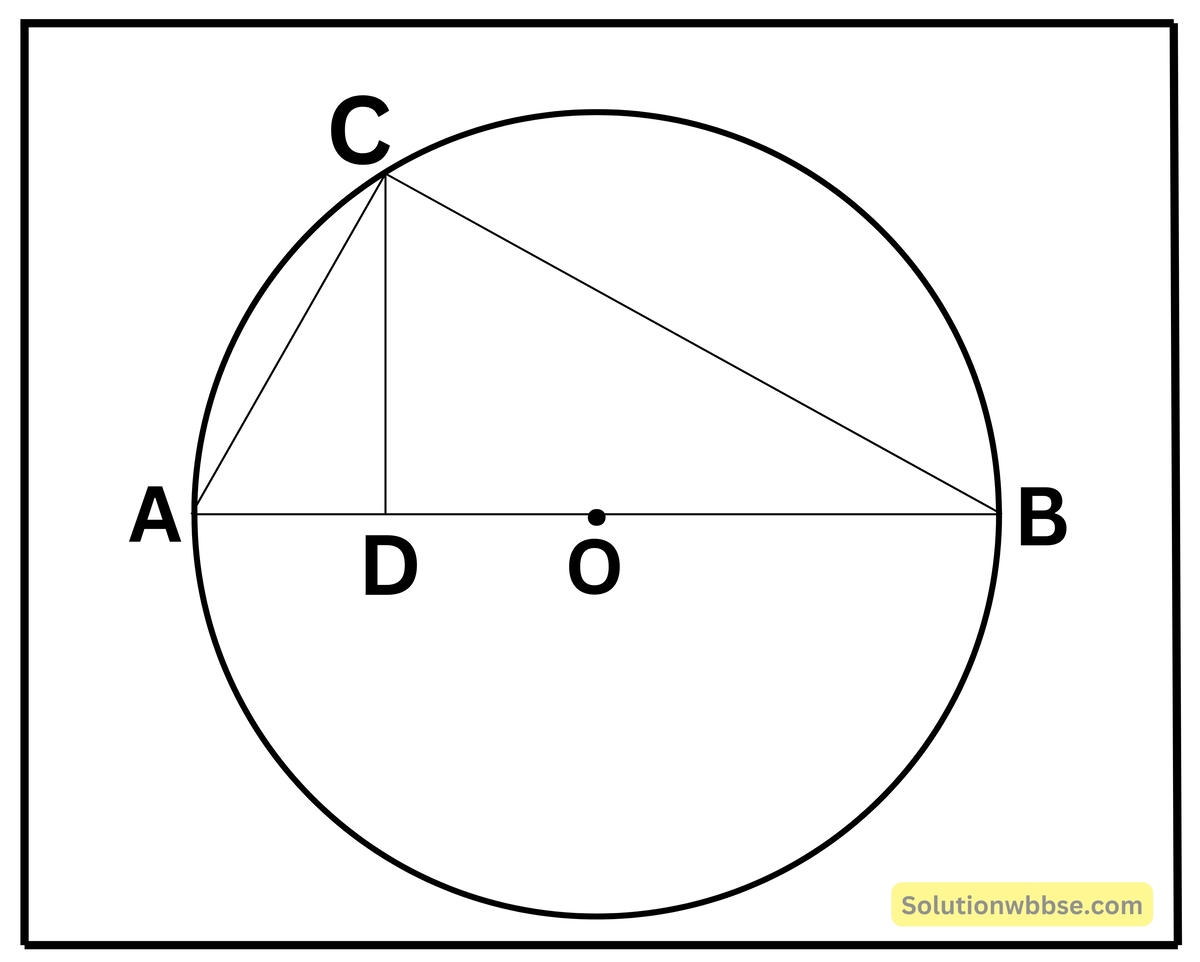
∠ACB অর্ধবৃত্তস্থ কোণ। সুতরাং ∠ACB = 90°
সমকোণী ΔACD -তে, ∠ADC = 90°, ∠DAC = 50°,
সুতরাং ∠ACD = 90° – 50° = 40°
আবার, ∠ACB = 90°;
সুতরাং ∠BCD = 90° – 40° = 50°
প্রয়োগ 15. পাশের চিত্রে AB ও CD সরলরেখাংশ দুটি বৃত্তের কেন্দ্র O -তে ছেদ করেছে। যদি ∠AOC = 80° ও ∠CDE = 40° হয়, তাহলে (i) ∠DCE ও (ii) ∠ABC -এর মান নির্ণয় করি।
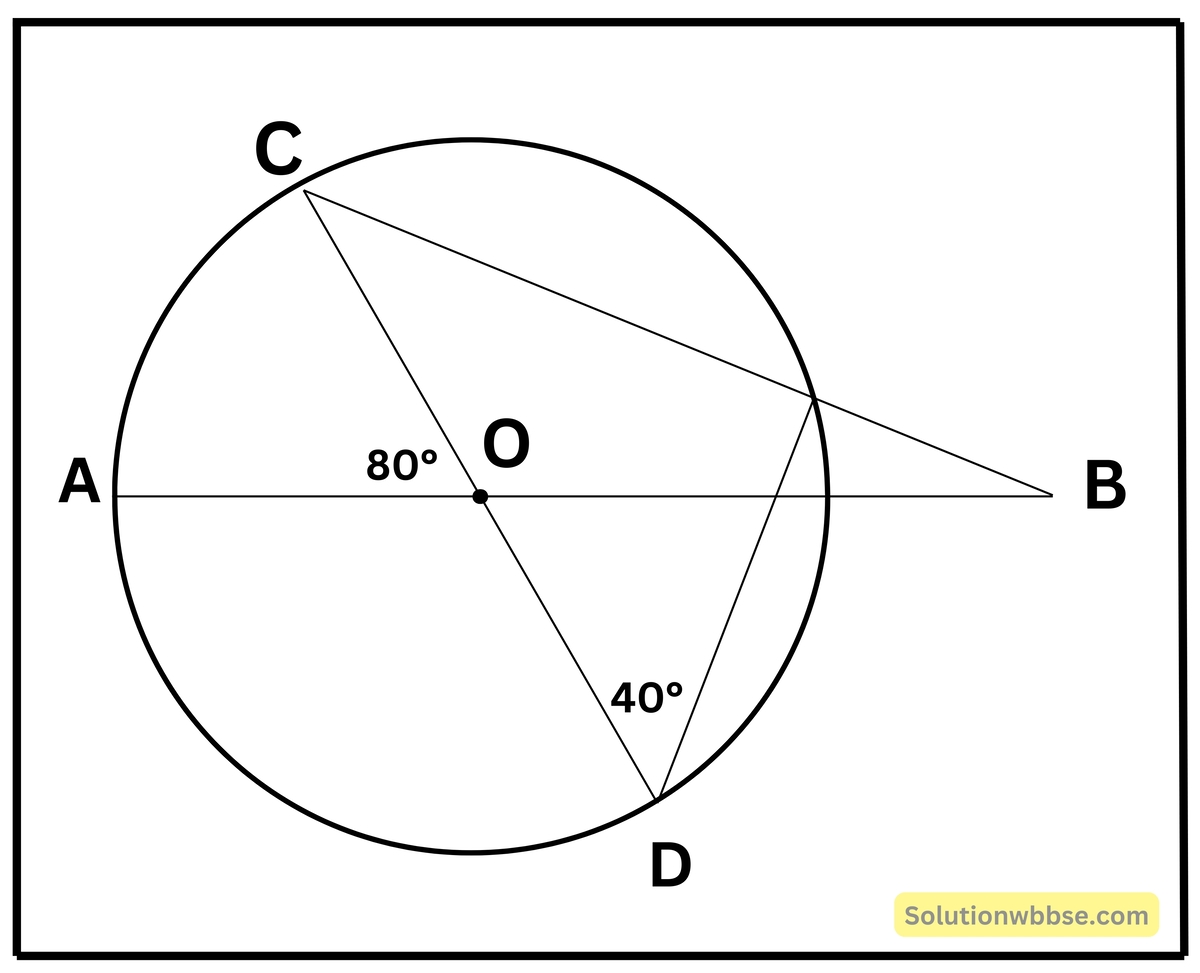
∠CED অর্ধবৃত্তস্থ কোণ। ∴ ∠CED = 90°
সমকোণী ΔCED -তে, ∠CED = 90°, ∠CDE = 40°,
∴ ∠DCE = 90° – 40° = 50° —(i)
ΔBOC -তে, বহিঃস্থ ∠AOC = ∠OBC + ∠OCB
80° = ∠OBC + 50° (∵ ∠DCE = 50°)
∴ ∠OBC = 30°
সুতরাং, ∠ABC = 30° —(ii)
প্রয়োগ 16. যুক্তি দিয়ে প্রমাণ করি যে অর্ধবৃত্তাংশস্থ অপেক্ষা বৃহত্তর বৃত্তাংশস্থ কোণ সূক্ষ্মকোণ।
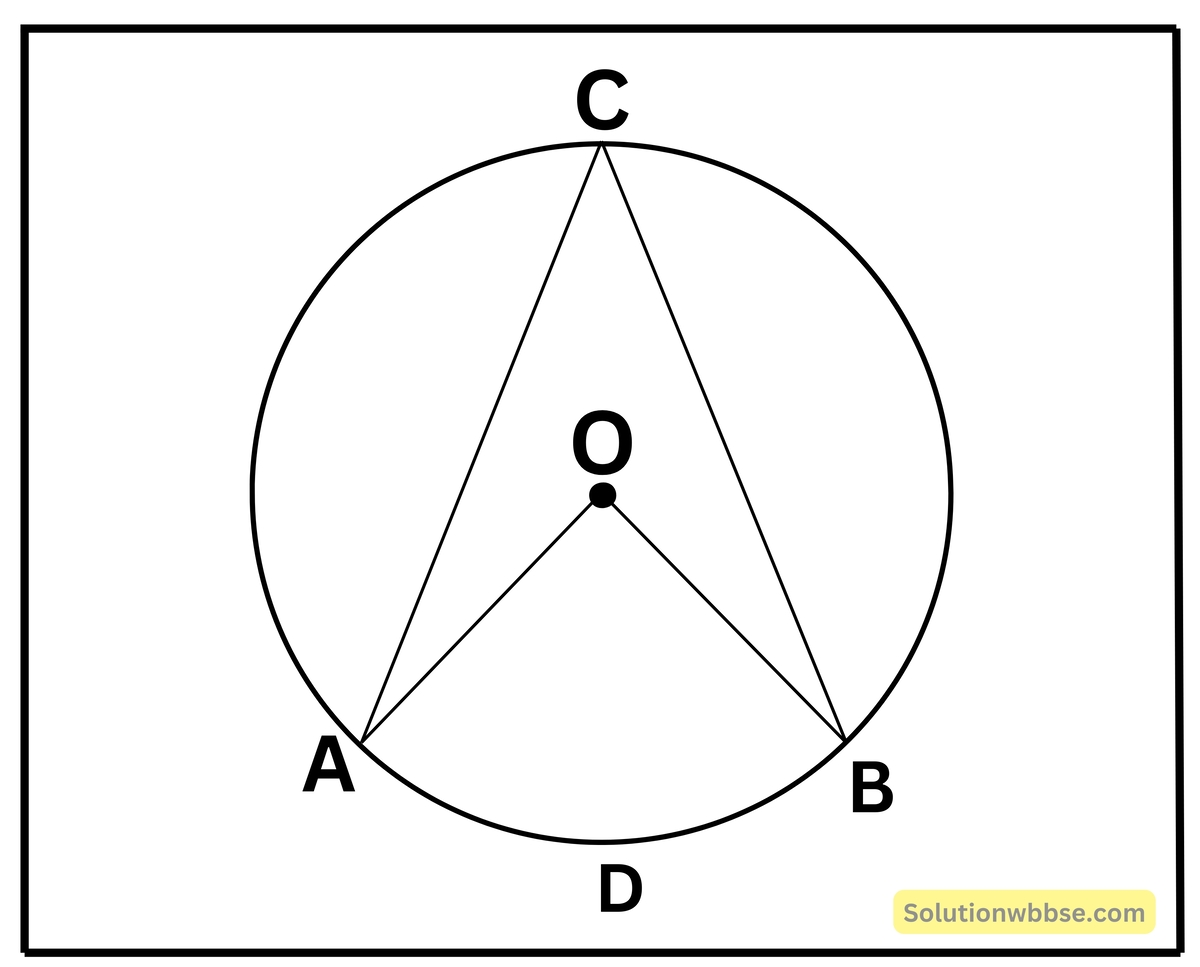
প্রদত্ত – O কেন্দ্রীয় বৃত্তের ACB বৃত্তাংশ অর্ধবৃত্তাংশস্থ অপেক্ষা বৃহত্তর।
প্রমাণ করতে হবে যে – ∠ACB একটি সূক্ষ্মকোণ।
প্রমাণ – যেহেতু, ACB বৃত্তাংশ অর্ধবৃত্তাংশস্থ অপেক্ষা বৃহত্তর বৃত্তাংশস্থ,
∴ \(\overset\frown{ADB}\) একটি উপচাপ।
∴ ADB উপচাপের দ্বারা গঠিত কেন্দ্রস্থ কোণ ∠AOB, 2 সমকোণ অপেক্ষা ক্ষুদ্রতর।
আবার, ADB উপচাপের দ্বারা গঠিত বৃত্তস্থ কোণ ∠ACB; ∠AOB < 180°
অর্থাৎ, 2∠ACB < 180°
∴ ∠ACB < 90°
∴ ∠ACB, 1 সমকোণ অপেক্ষা ক্ষুদ্রতর অর্থাৎ ∠ACB সূক্ষ্মকোণ। [প্রমাণিত]
প্রয়োগ 17. প্রমাণ করি যে অর্ধবৃত্তাংশস্থ অপেক্ষা ক্ষুদ্রতর বৃত্তাংশস্থ কোণ স্থূলকোণ।
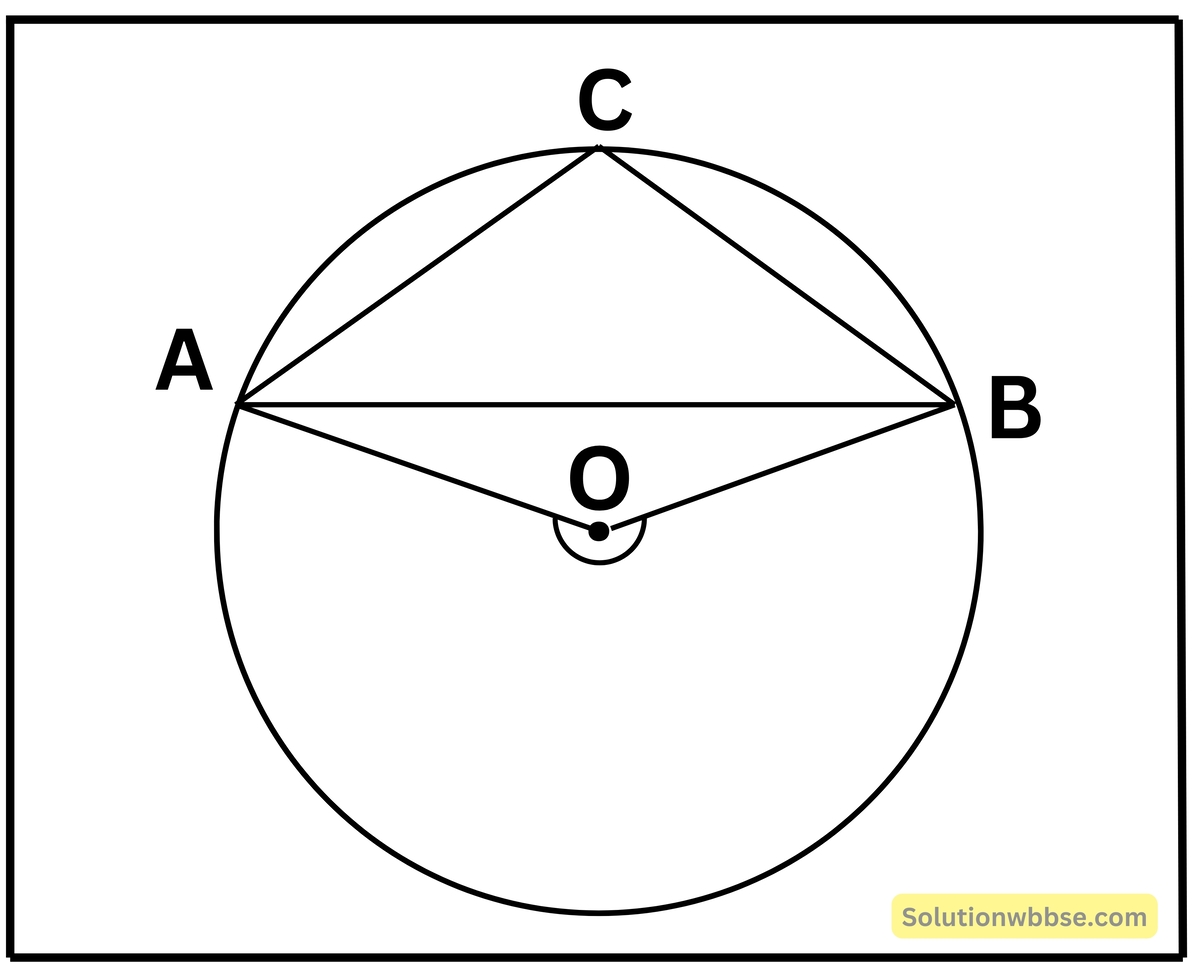
মনে করি O কেন্দ্রীয় বৃত্তে ADB বৃত্তচাপের উপর অবস্থিত ∠ACB একটি বৃত্তাংশস্থ কোণ। ∠ACB বৃত্তাংশটি অর্ধবৃত্ত অপেক্ষা ক্ষুদ্রতর।
প্রমাণ করতে হবে যে, ∠ACB স্থূলকোণ।
প্রমাণ – ADB একটি অধিচাপ। ঐ চাপের উপর অবস্থিত কেন্দ্রস্থ প্রবৃদ্ধ কোণ
∠AOB দুই সমকোণ অপেক্ষা বৃহত্তর।
∵ ∠ACB ঐ একই চাপের উপর অবস্থিত বৃত্তস্থ কোণ।
∴ ∠ACB 1 সমকোণ অপেক্ষা বৃহত্তর।
∴ ∠ACB স্থূলকোণ। (প্রমাণিত)।
প্রয়োগ 18. যুক্তি দিয়ে প্রমাণ করি যে, যে-কোনো সমকোণী ত্রিভুজের অতিভুজের মধ্যবিন্দু ত্রিভুজের তিনটি শীর্ষবিন্দু থেকে সমদূরবর্তী।
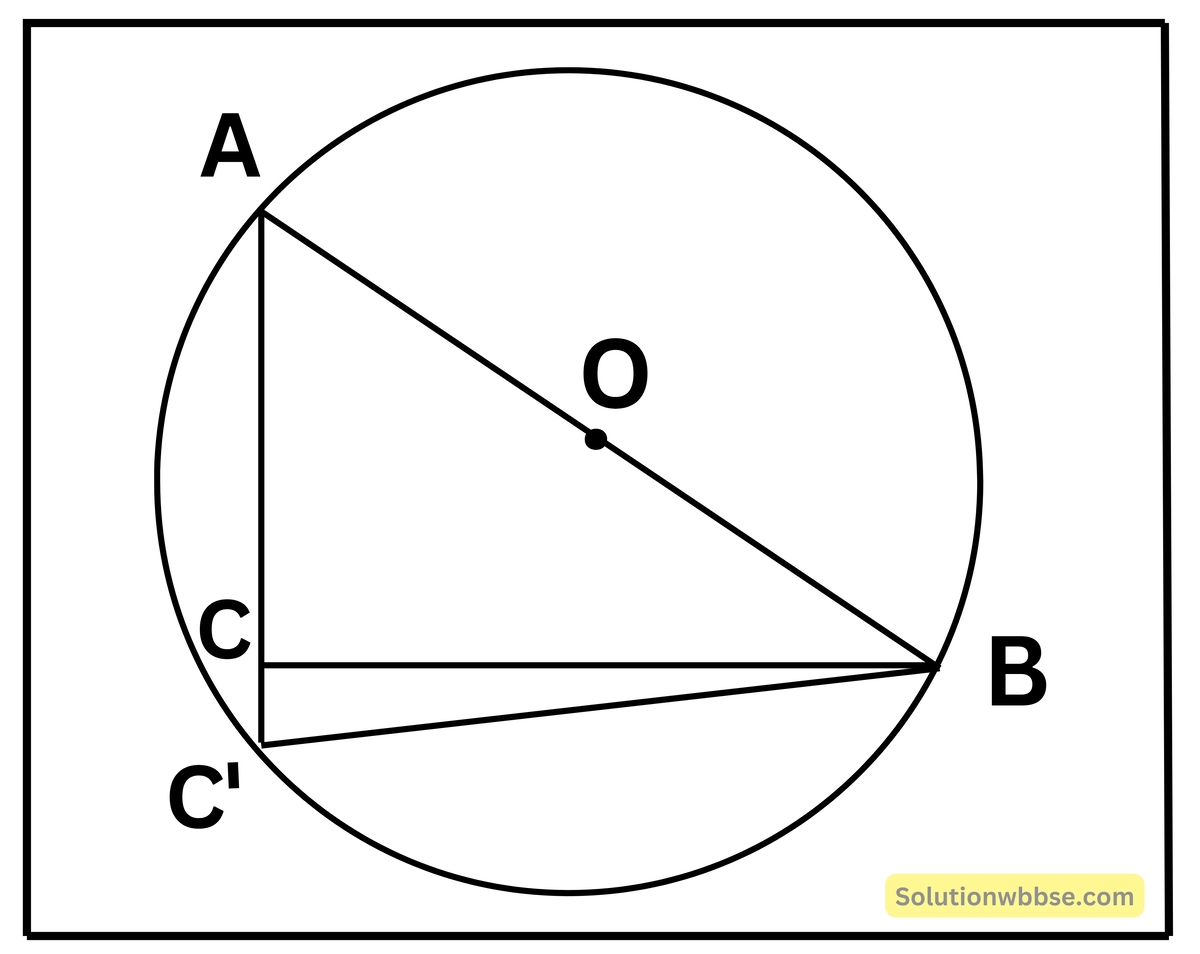
প্রদত্ত – ABC সমকোণী ত্রিভুজের ∠ACB = 90° এবং O অতিভুজ AB -এর মধ্যবিন্দু।
প্রমাণ করতে হবে যে – OA = OB = OC
আঙ্কন – O বিন্দুকে কেন্দ্র করে OB দৈর্ঘ্যের ব্যাসার্ধ নিয়ে একটি বৃত্ত অঙ্কন করলাম।
প্রমাণ – O বিন্দুকে কেন্দ্র করে OB দৈর্ঘ্যের ব্যাসার্ধ নিয়ে অঙ্কিত বৃত্তটি A ও B বিন্দুগামী। যদি বৃত্তটি C বিন্দুগামী না হয়, ধরি বৃত্তটি AC-কে বা বর্ধিত AC-কে C’ বিন্দুতে ছেদ করে। B, C’ যুক্ত করি
∴ ∠AC’B = 90° [∵ অর্ধবৃত্তস্থ কোণ সমকোণ]
আবার ∠ACB = 90°
∴ ∠ACB = ∠AC’B
এটা অসম্ভব, কারণ কোনো ত্রিভুজের বহিঃস্থ কোণ একটি অন্তঃস্থ বিপরীত কোণের সমান হতে পারে না।
এটা সম্ভব হবে যদি C ও C’ একই বিন্দু হয়।
∴ বৃত্তটি C বিন্দুগামী
∴ OA = OB = OC [প্রমাণিত]
প্রয়োগ 19. যুক্তি দিয়ে প্রমাণ করি একটি সমকোণী ত্রিভুজের অতিভুজকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি সমকৌণিক বিন্দু দিয়ে যাবে।

ABC সমকোণী ত্রিভুজের C সমকৌণিক বিন্দু অর্থাৎ, ∠ACB = 1 সমকোণ-এর O অতিভুজের (AB) -এর মধ্যবিন্দু।
প্রমাণ করতে হবে, O বিন্দুকে কেন্দ্র করে যে বৃত্ত অঙ্কন করা যাবে তা C বিন্দুগামী।
অঙ্কন – O বিন্দুকে কেন্দ্র করে OA বা OB দৈর্ঘ্যর ব্যাসার্ধ নিয়ে একটি বৃত্ত অঙ্কন করা হল।
প্রমাণ – O বিন্দুকে কেন্দ্র করে OB দৈর্ঘ্য ব্যাসার্ধ নিয়ে অঙ্কিত বৃত্তটি C বিন্দুগামী না হয়, ধরি AC -কে C’ বিন্দুতে ছেদ করে। B, C’ যোগ করা হল।
∴ ∠AC’B = 90° (অর্ধবৃত্তস্থ কোণ) আবার ∠ACB = 90°
∴∠ACB = ∠AC’B
ইহা অসম্ভব, কারণ কোনো ত্রিভুজের বহিঃকোণ একটি অস্তস্থ বিপরীত কোণের সমান হতে পারে না।
ইহা সম্ভব হবে যদি C ও C’ একই বিন্দু হয়।
∴ বৃত্তটি C বিন্দুগামী অর্থাৎ সমকোণিক বিন্দুগামী। (প্রমাণিত)
প্রয়োগ 20. যুক্তি দিয়ে প্রমাণ করি যে একটি বিষমবাহু ত্রিভুজের বৃহত্তম বাহু অপেক্ষা ক্ষুদ্রতর দুটি বাহুকে ব্যাস করে অঙ্কিত বৃত্ত দুটির ছেদবিন্দু তৃতীয় বাহুর উপর অবস্থিত হবে।
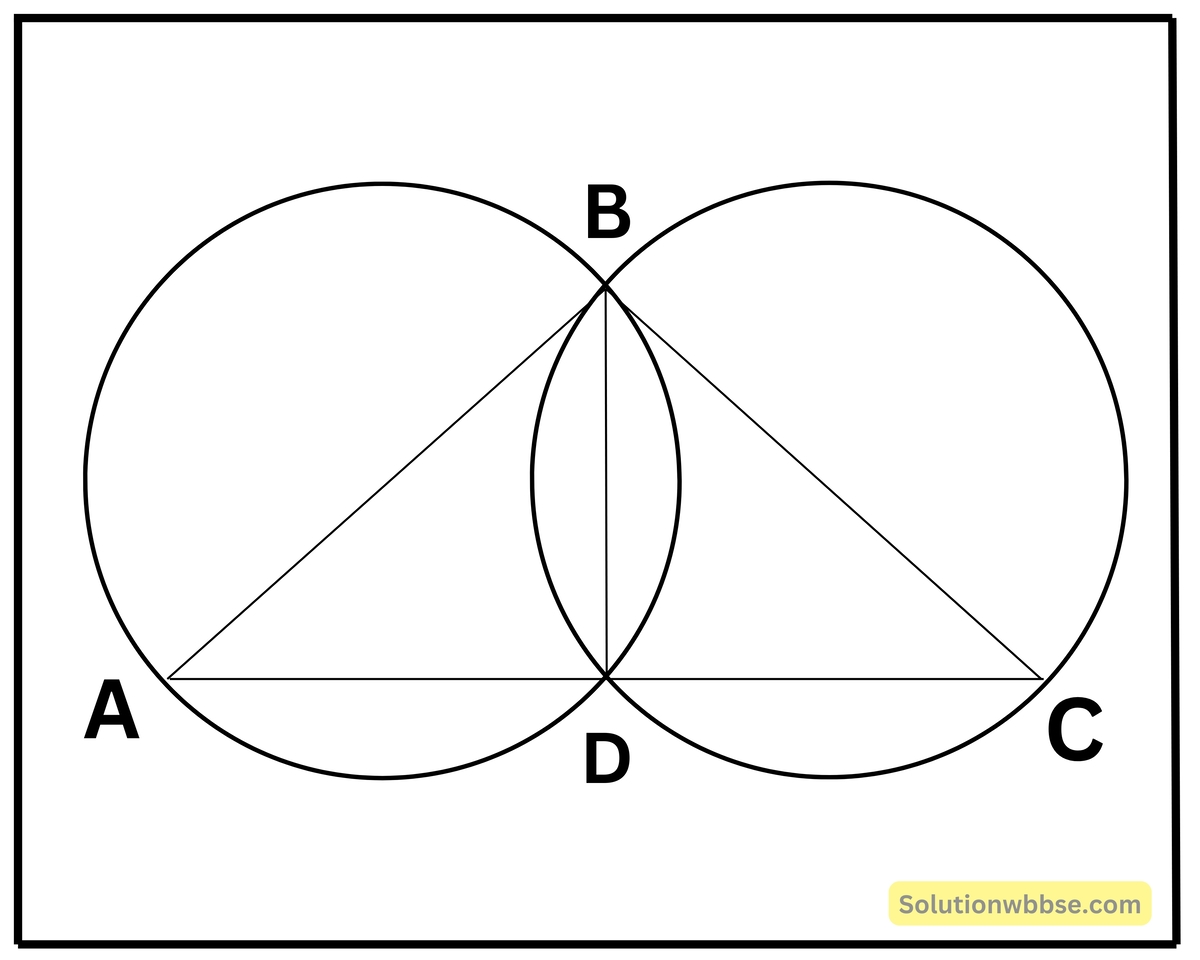
প্রদত্ত – ΔABC -এর AC বৃহত্তম বাহু।
AB বাহুকে ব্যাস করে একটি বৃত্ত অঙ্কন করলাম যা AC -কে D বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে যে – BC -কে ব্যাস করে অঙ্কিত বৃত্ত D বিন্দু দিয়ে যাবে।
অঙ্কন – B, D বিন্দুদ্বয় সরলরেখাংশ দ্বারা যুক্ত করলাম।
প্রমাণ – ∠ADB অর্ধবৃত্তস্থ কোণ।
∴ ∠ADB = 1 সমকোণ
∴ ∠CDB = 1 সমকোণ
যেহেতু, CDB সমকোণী ত্রিভুজে ∠CDB = 1 সমকোণ, সুতরাং BC বৃত্তের ব্যাস।
∴ BC -কে ব্যাস করে অঙ্কিত বৃত্ত অবশ্যই D বিন্দু দিয়ে যাবে।
প্রয়োগ 21. ABC ও ADC সমকোণী ত্রিভুজদুটির সাধারণ অতিভুজ AC; প্রমাণ করি যে ∠CAD = ∠CBD;
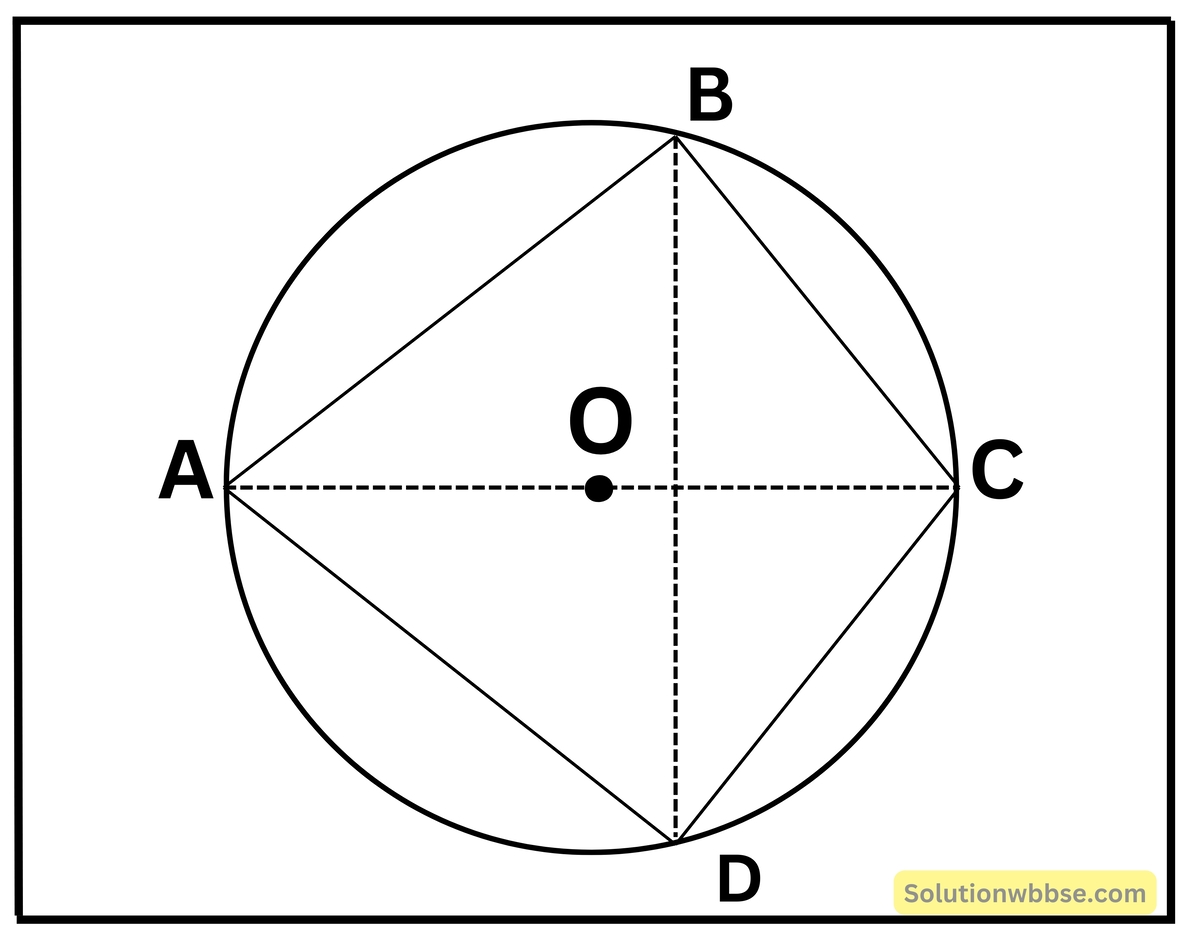
প্রদত্ত – ABC ও ADC সমকোণী ত্রিভুজের সাধারণ অতিভুজ AC।
প্রমাণ করতে হবে – ∠CAD = ∠CBD
প্রমাণ – ΔABC -এর ∠ABC = 90°
∴ AC -কে ব্যাস করে বৃত্ত অঙ্কন করলে B বিন্দুগামী হবে। অনুরূপে, AC -কে ব্যাস করে অঙ্কিত বৃত্তটি D বিন্দুগামী।
∠CAD ও ∠CBD কোণ দুটি বৃত্তের একই উপচাপ DC -এর দ্বারা গঠিত বৃত্তস্থ কোণ।
∴ ∠CAD = ∠CBD (প্রমাণিত)
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের সপ্তম অধ্যায়, ‘বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment