এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের ত্রয়োবিংশ অধ্যায়, ‘ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

প্রয়োগ 1. α ও β দুটি এমন সূক্ষ্মকোণ যে sin α = sin β; প্রমাণ করি যে, α = β
সমাধান –

ধরি, ABC এবং PQR দুটি সমকোণী ত্রিভুজ। ABC ত্রিভুজে \(\angle ABC = 90^\circ\) এবং \(\angle BCA = \alpha\); PQR ত্রিভুজে \(\angle PQR = 90^\circ\) এবং \(\angle QRP = \beta\)
সমকোণী ত্রিভুজ ABC-তে, \(\sin\alpha = \frac{AB}{AC}\)
সমকোণী ত্রিভুজ PQR-এ, \(\sin\beta = \frac{PQ}{PR}\)
যেহেতু, \(\sin\alpha = \sin\beta\), সুতরাং, \(\frac{AB}{AC} = \frac{PQ}{PR}\) বা, \(\frac{AB}{PQ} = \frac{AC}{PR} = k\) (ধরি) (\(k>0\))
\(\therefore AB = k \cdot PQ\) এবং \(AC = k \cdot PR\)
\(\therefore BC = \sqrt{AC^2 – AB^2}\) এবং \(QR = \sqrt{PR^2 – PQ^2}\)
সুতরাং, \(\frac{BC}{QR} = \frac{\sqrt{AC^2 – AB^2}}{\sqrt{PR^2 – PQ^2}}\)
= \( \frac{\sqrt{k^2PR^2 – k^2PQ^2}}{\sqrt{PR^2 – PQ^2}}\)
= \( \frac{k\sqrt{PR^2 – PQ^2}}{\sqrt{PR^2 – PQ^2}}\)
= \( k.\)
\(\therefore \frac{AB}{PQ} = \frac{AC}{PR} = \frac{BC}{QR}\)\(\therefore \triangle ABC \sim \triangle PQR\) সুতরাং, \(\angle BCA = \angle QRP\)
\(\therefore \alpha = \beta\) [প্রমাণিত]
প্রয়োগ 2. sin(90°−θ) = sin2θ হলে, θ-এর মান হিসাব করে লিখি যখন 2θ সূক্ষ্মকোণ।
সমাধান –
sin(90°−θ) = sin2θ
বা, 90°−θ = 2θ
বা, 3θ = 90°
∴ θ = 30°
প্রয়োগ 3. 5θ ধনাত্মক সূক্ষ্মকোণ এবং tan5θ = tan(60°+ θ) হলে, θ –এর মান নির্ণয় করি।
সমাধান –
tan5θ = tan(60°+ θ)
বা, 5θ = 60°+ θ
বা, 5θ – θ = 60°
বা, 4θ = 60°
বা, \(\theta = \frac{60^\circ}{4}\)
বা, θ = 15°
∴ θ = 15° (উত্তর)
প্রয়োগ 4. একটি সমকোণী ত্রিভুজে θ ধনাত্মক সূক্ষ্মকোণের পরিপ্রেক্ষিতে \(sin\theta = \frac{12}{13}\) হলে, \(tan\theta\) এবং \(cos\theta\)-এর মান হিসাব করে লিখি।
সমাধান –
ABC সমকোণী ত্রিভুজে \(\angle ABC = 90^\circ\) এবং \(\angle BCA = \theta\)
ধরি, লম্ব AB = 12k একক এবং অতিভুজ AC = 13k একক [যেখানে, k>0]
\(\therefore\) ভূমি \(BC = \sqrt{AC^2 – AB^2}\)
= \( \sqrt{(13k)^2 – (12k)^2}\) একক
= \( \sqrt{169k^2 – 144k^2}\) একক
= \( 5k\) একক
∴প্রয়োগ 5. \(\theta\) একটি ধনাত্মক সূক্ষ্মকোণ এবং \(\tan\theta = \frac{8}{15}\) হলে, \(\sin\theta\) ও \(\cos\theta\)-র মান নির্ণয় করি ও দেখাই যে \(\sin^2\theta + \cos^2\theta = 1\)
সমাধান –
ABC একটি সমকোণী ত্রিভুজ যার \(\angle ABC = 90^\circ\) এবং \(\angle ACB = \theta\)
∴ \(\tan\theta = \frac{AB}{BC} = \frac{8}{15}\)
ধরি, লম্ব \(AB = 8k\) একক এবং ভূমি \(BC = 15k\) একক [যেখানে, \(k>0\)]
∴ অতিভুজ \(AC = \sqrt{AB^2 + BC^2} = \sqrt{(8k)^2 + (15k)^2}\) একক = \( \sqrt{64k^2 + 225k^2}\) একক
= \( \sqrt{289k^2}\) একক = \( 17k\) একক
∴ \(\sin^2\theta + \cos^2\theta = \left(\frac{8}{17}\right)^2 + \left(\frac{15}{17}\right)^2 = \frac{64}{289} + \frac{225}{289} = 1\)
∴ \(\sin^2\theta + \cos^2\theta = 1\) [প্রমাণিত]
প্রয়োগ 6. যদি \( \tan\theta = \frac{4}{3} \) হয় , তাহলে দেখাই যে , \( \sin\theta + \cos\theta = \frac{7}{5} \)
সমাধান –
\( \tan\theta = \frac{4}{3} \)বা, \( \tan^2\theta = \frac{16}{9} \)
বা, \( \sec^2\theta – 1 = \frac{16}{9} \)
বা, \( \sec^2\theta = 1 + \frac{16}{9} \)
বা, \( \sec^2\theta = \frac{9+16}{9} \)
বা, \( \sec^2\theta = \frac{25}{9} \)
বা, \( \frac{1}{\sec^2\theta} = \frac{9}{25} \)
বা, \( \cos^2\theta = \frac{9}{25} \)
বা, \( \cos\theta = \frac{3}{5} \)
আবার,
\( \cos^2\theta = \frac{9}{25} \)বা, \( 1 – \sin^2\theta = \frac{9}{25} \)
বা, \( \sin^2\theta = 1 – \frac{9}{25} \)
বা, \( \sin^2\theta = \frac{25-9}{25} \)
বা, \( \sin^2\theta = \frac{16}{25} \)
বা, \( \sin\theta = \frac{4}{5} \)
\( \therefore \sin\theta + \cos\theta = \frac{4}{5} + \frac{3}{5} \)বা, \( \sin\theta + \cos\theta = \frac{7}{5} \)
\( \therefore \sin\theta + \cos\theta = \frac{7}{5} \)প্রয়োগ 7. ABC ত্রিভুজের ∠B সমকোণ এবং অতিভুজের দৈর্ঘ্য \( \sqrt{13} \) একক। ওই ত্রিভুজের অপর দুটি বাহুর দৈর্ঘ্যের সমষ্টি \( 5 \) একক হলে, \( \sin C + \sin A \)-এর মান নির্ণয় করি।
সমাধান –
ABC সমকোণী ত্রিভুজের অতিভুজ AC, ∠C-এর সাপেক্ষে লম্ব AB এবং ∠A-এর সাপেক্ষে লম্ব BC
\( \therefore \sin C + \sin A = \frac{AB}{AC} + \frac{BC}{AC} = \frac{AB+BC}{AC} = \frac{5}{\sqrt{13}} \)বিকল্প প্রমাণ –
মনে করি, \( AB = x \) একক, \( BC = (5-x) \) একক
ABC সমকোণী ত্রিভুজে পিথাগোরাসের উপপাদ্য অনুসারে,
\( x^2 + (5-x)^2 = (\sqrt{13})^2 \)বা, \( x^2 + 25 + x^2 – 10x = 13 \)
বা, \( 2x^2 – 10x + 12 = 0 \)
বা, \( x^2 – 5x + 6 = 0 \)
বা, \( x^2 – 3x – 2x + 6 = 0 \)
বা, \( x(x-3) – 2(x-3) = 0 \)
বা, \( (x-3)(x-2) = 0 \)
হয়, \( x-3 = 0 \therefore x = 3 \)
অথবা, \( x-2 = 0 \therefore x = 2 \)
যদি, \( AB = 3 \) একক হয়, তখন \( BC = (5-3) \) একক \( = 2 \) একক
সুতরাং, \( \sin C = \frac{AB}{AC} = \frac{3}{\sqrt{13}} \) এবং \( \sin A = \frac{BC}{AC} = \frac{2}{\sqrt{13}} \)
\( \therefore \sin C + \sin A = \frac{3}{\sqrt{13}} + \frac{2}{\sqrt{13}} = \frac{5}{\sqrt{13}} \)আবার, \( AB=2 \) একক হলে \( BC= 2 \) একক এবং তখন \( \sin C + \sin A = \frac{5}{\sqrt{13}}\)
প্রয়োগ 8. রীনার ঘুড়িটি যদি \(150\) মিটার লম্বা সুতো দিয়ে ওড়ানো হয় এবং ঘুড়িটি যদি অনুভূমিক রেখার সঙ্গে \(60^\circ\) কোণ করে থাকে, তবে ঘুড়িটি রীনার অবস্থান বা ভূমি থেকে কত উঁচুতে আছে হিসাব করে দেখি।
সমাধান –
নীচের ছবিতে, ABC সমকোণী ত্রিভুজ যার \(\angle ABC=90^\circ\), \(AC=150\) মিটার লম্বা সুতোসমেত ঘুড়ি এবং \(\angle BCA = 60^\circ\)
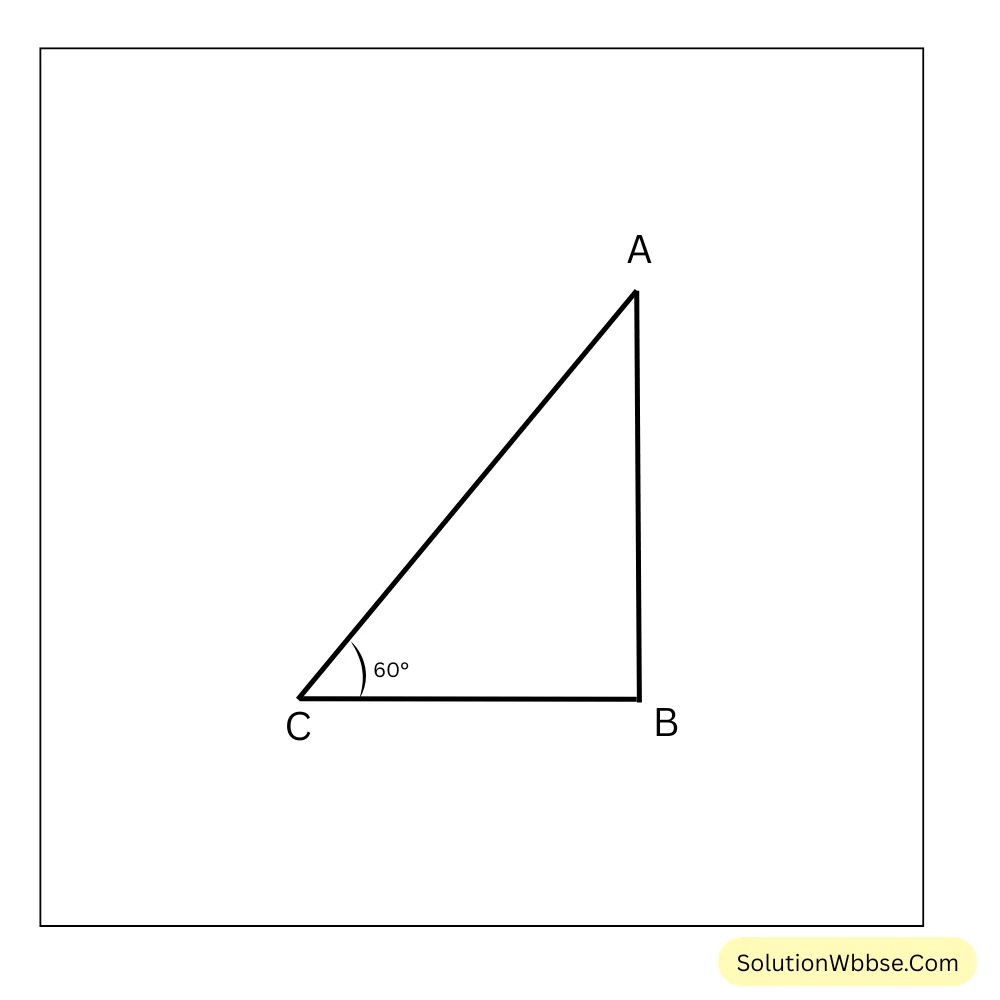
\(AB\) = রীনার অবস্থান বা ভূমি থেকে ঘুড়ির উচ্চতা
ABC সমকোণী ত্রিভুজের \(AB\) নির্ণয়ের জন্য সেই কোণানুপাতটি নেব যেখানে \(AB\) ও \(AC\) আছে। [∵ \(AC\)-এর দৈর্ঘ্য জানা]
ABC সমকোণী ত্রিভুজে, \(\sin 60^\circ = \frac{AB}{AC}\)
বা, \(\frac{\sqrt{3}}{2} = \frac{AB}{150}\) মিটার
বা, \(2AB = 150\sqrt{3}\) মিটার
বা, \(AB = \frac{150\sqrt{3}}{2}\) মিটার = \(75\sqrt{3}\) মিটার
∴ ঘুড়িটি রীনার অবস্থান বা ভূমি থেকে \(75\sqrt{3}\) মিটার উঁচুতে আছে।
প্রয়োগ 9. যদি ঘুড়িটি \(120\) মিটার লম্বা সুতো দিয়ে ওড়ানো হতো এবং ঘুড়িটি অনুভূমিক রেখার সঙ্গে \(30^\circ\) কোণ করে থাকে, তাহলে ঘুড়িটি রীনার অবস্থান বা ভূমি থেকে কত উচ্চতায় থাকবে হিসাব করে লিখি।
সমাধান –
নীচের ছবিতে, ABC সমকোণী ত্রিভুজ যার \(\angle ABC=90^\circ\), \(AC=120\) মিটার লম্বা সুতোসমেত ঘুড়ি এবং \(\angle BCA = 30^\circ\)
\(AB\) = রীনার অবস্থান বা ভূমি থেকে ঘুড়ির উচ্চতা
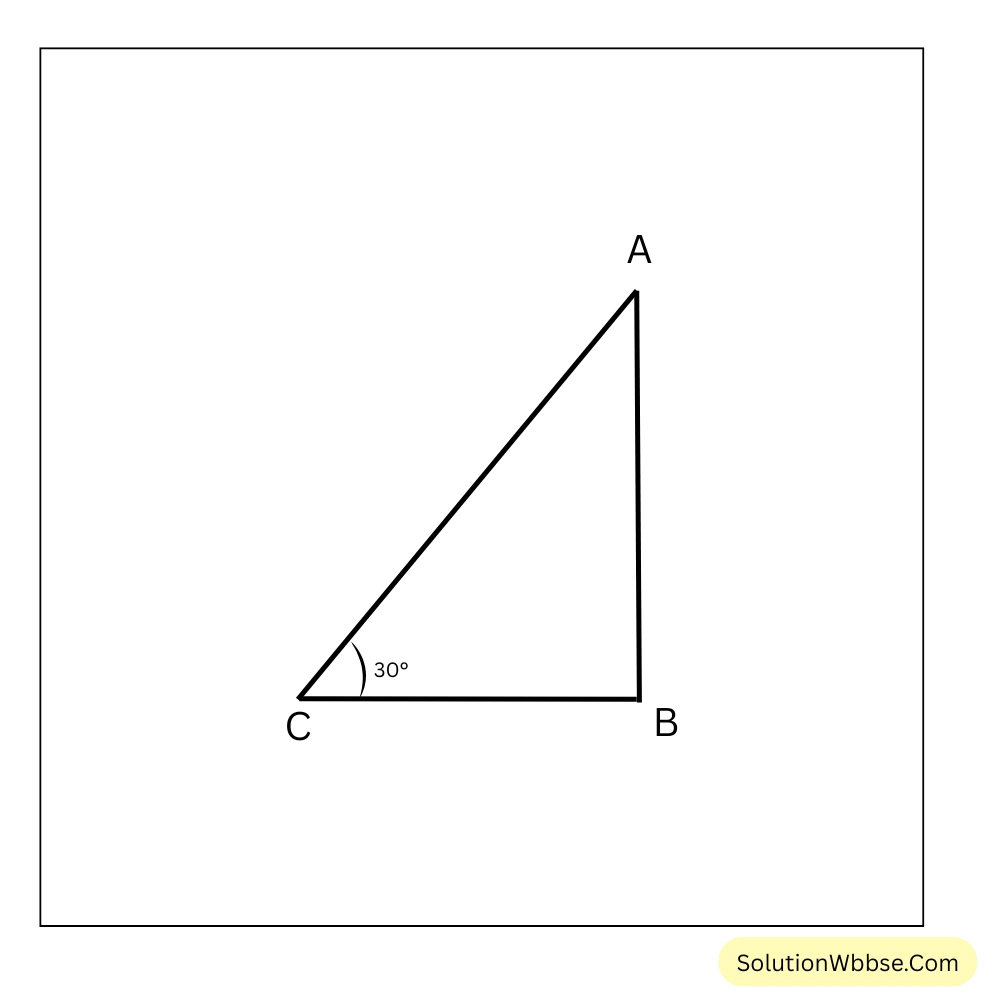
ABC সমকোণী ত্রিভুজের \(AB\) নির্ণয়ের জন্য সেই কোণানুপাতটি নেব যেখানে \(AB\) ও \(AC\) আছে। [∵ \(AC\)-এর দৈর্ঘ্য জানা]
ABC সমকোণী ত্রিভুজে, \(\sin 30^\circ = \frac{AB}{AC}\)
বা, \(\frac{1}{2} = \frac{AB}{120}\) মিটার
বা, \(2AB = 120\) মিটার
বা, \(AB = \frac{120}{2}\) মিটার = \(60\) মিটার
∴ ঘুড়িটি রীনার অবস্থান বা ভূমি থেকে \(60\) মিটার উঁচুতে আছে।
প্রয়োগ 10. PQR সমকোণী ত্রিভুজের \(\angle Q\) সমকোণ এবং \(\angle P=30^\circ\); \(RQ=6\) সেমি. হলে, \(PQ\) ও \(PR\) বাহুদ্বয়ের দৈর্ঘ্য হিসাব করে লিখি।
সমাধান –
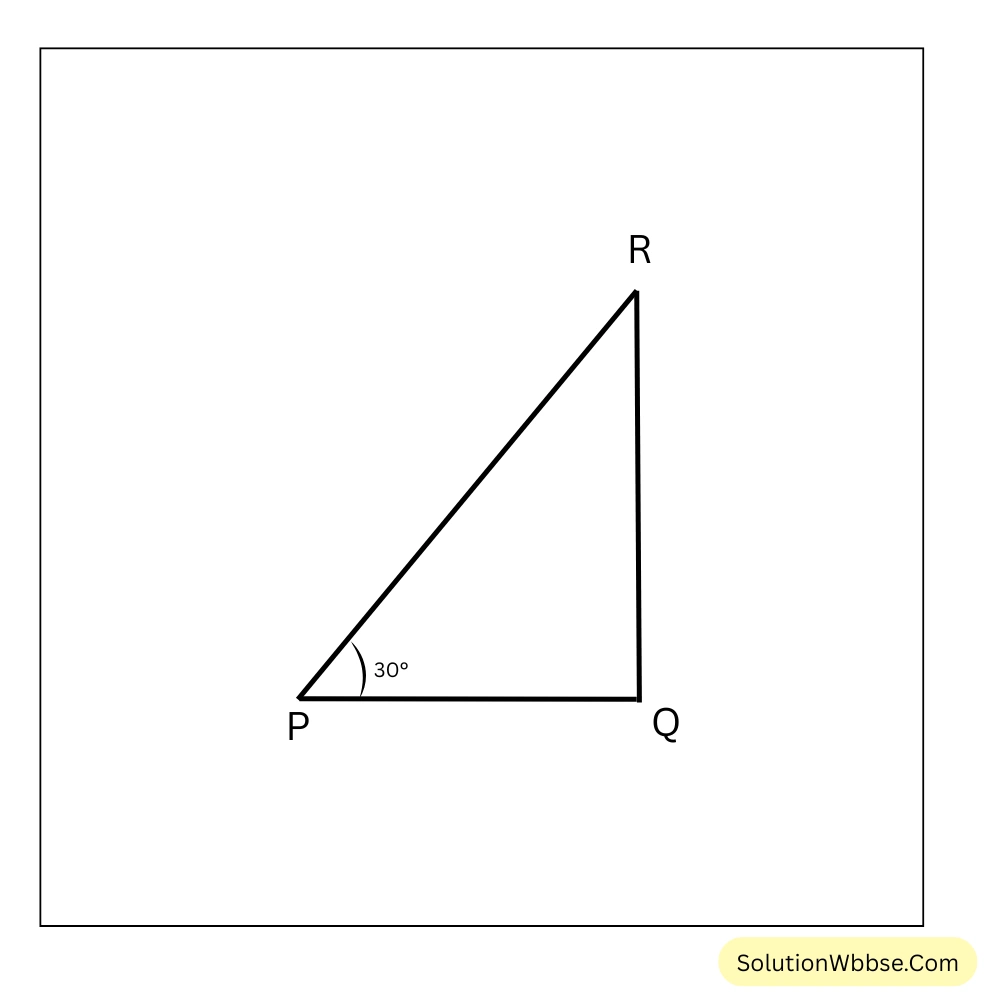
সমকোণী ত্রিভুজ PQR-এ, \(\tan 30^\circ = \frac{RQ}{PQ}\)
বা, \(\frac{1}{\sqrt{3}} = \frac{6}{PQ}\) সেমি. ∴ \(PQ = 6\sqrt{3}\) সেমি.
সমকোণী ত্রিভুজ PQR-এ, \(\sin 30^\circ = \frac{RQ}{PR}\)
বা, \(\frac{1}{2} = \frac{6}{PR}\) সেমি. ∴ \(PR = 12\) সেমি.
অন্যভাবে, পিথাগোরাসের সূত্র থেকে পাই,
\(PR^2 = PQ^2 + RQ^2\)= \( (6\sqrt{3}\) সেমি.\()^2 + (6\) সেমি.\()^2\)
= \( 108\) সেমি.\(^2 + 36\) সেমি.\(^2\)
= \( 144\) সেমি.\(^2\)
∴ \(PR = 12\) সেমি.
প্রয়োগ 11. ABC সমকোণী ত্রিভুজের \(\angle B\) সমকোণ, \(AB=5\) সেমি. এবং \(AC=10\) সেমি. হলে, \(\angle BCA\) ও \(\angle CAB\) -এর মান নির্ণয় করি।
সমাধান –
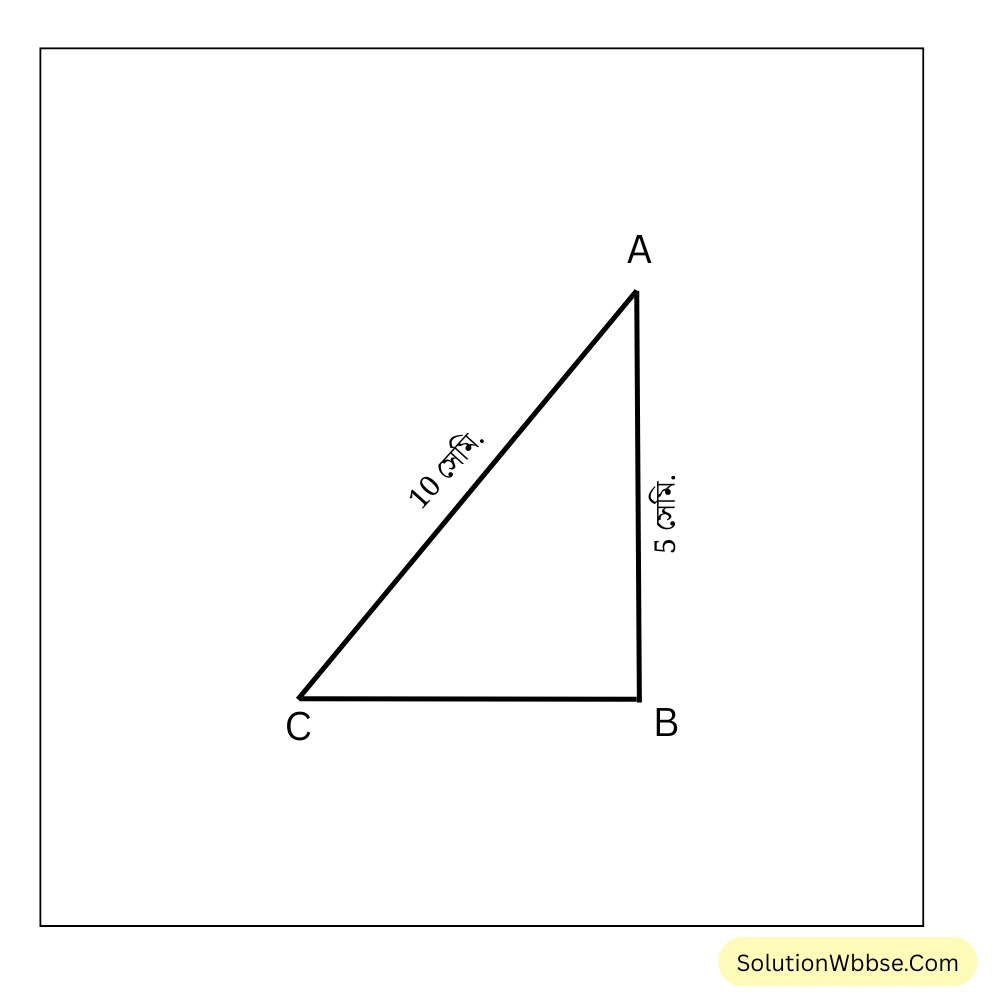
ABC সমকোণী ত্রিভুজের \(\angle B\) সমকোণ
\(AB=5\) সেমি. এবং \(AC=10\) সেমি.
সমকোণী ত্রিভুজ ABC-তে, \(\sin \angle BCA = \frac{AB}{AC} = \frac{5}{10} = \frac{1}{2} = \sin 30^\circ\)
∴ \(\angle BCA = 30^\circ\)
∴ \(\angle CAB = 90^\circ – 30^\circ = 60^\circ\)
প্রয়োগ 12. ABC সমকোণী ত্রিভুজের কোণ \(\angle B\) সমকোণ। \(AB = 7\) সেমি. এবং \(AC = 7\sqrt{2}\) সেমি. হলে, \(\angle BCA\) ও \(\angle CAB\) –এর মান হিসাব করে লিখি।
সমাধান –

\(\angle BCA\) –এর সাপেক্ষে \(AB\) লম্ব এবং \(AC\) হল অতিভুজ।
∴∴ \(\angle BCA = 45^\circ\)
আবার , \(\angle CAB\) –এর সাপেক্ষে \(AB\) হল ভূমি এবং \(AC\) হল অতিভুজ।
∴∴ \(\angle CAB = 45^\circ\)
উত্তর – \(\angle CAB = 45^\circ\) এবং \(\angle BCA = 45^\circ\)
প্রয়োগ 13. দেখাই যে, \(\sin^2 30^\circ + \cos^2 30^\circ = 1\)
সমাধান –
\(\sin^2 30^\circ + \cos^2 30^\circ = \left(\frac{1}{2}\right)^2 + \left(\frac{\sqrt{3}}{2}\right)^2 = \frac{1}{4} + \frac{3}{4} = 1\) [প্রমাণিত]
প্রয়োগ 14. দেখাই যে tan² 60° +1 =sec²60°
সমাধান –
বামপক্ষ –
tan² 60° +1
= (√3)² + 1
= 3 +1
= 4
ডানপক্ষ –
sec²60°
= (2)²
= 4
∴ বামপক্ষ = ডানপক্ষ [প্রমাণিত]
প্রয়োগ 15. ABC সমবাহু ত্রিভুজের AD মধ্যমা হলে, প্রমাণ করি যে sin∠BAD = cos∠DBA.
সমাধান –

ABC সমবাহু ত্রিভুজের AD মধ্যমা।
∴ AD ⊥ BC এবং ∠BAD = ∠DAC
ABD সমকোণী ত্রিভুজ এবং ∠DBA=60° [∵ ABC সমবাহু ত্রিভুজ]
∴ ∠BAD = 30°
∴ sin∠BAD = sin30° = 1/2 এবং cos∠DBA = cos60° = 1/2
∴ sin∠BAD = cos∠DBA [প্রমাণিত]
প্রয়োগ 16. প্রমাণ করি যে, \(\frac{1-\tan^2 30^\circ}{1+\tan^2 30^\circ} = \cos 60^\circ\)
সমাধান –
\(\frac{1-\tan^2 30^\circ}{1+\tan^2 30^\circ} = \frac{1-\left(\frac{1}{\sqrt{3}}\right)^2}{1+\left(\frac{1}{\sqrt{3}}\right)^2}\)= \( \frac{1-\frac{1}{3}}{1+\frac{1}{3}}\)
= \( \frac{\frac{2}{3}}{\frac{4}{3}}\)
= \( \frac{2}{3} \times \frac{3}{4}\)
= \( \frac{1}{2}\)
= \( \cos 60^\circ\)
প্রয়োগ 17. প্রমাণ করি যে \(\tan^2 60^\circ – 2 \sin 60^\circ = 3 – \cot 30^\circ\)
সমাধান –
বামপক্ষ –
\(\tan^2 60^\circ – 2 \sin 60^\circ\)= \( (\sqrt{3})^2 – 2 \times \frac{\sqrt{3}}{2}\)
= \( 3 – \sqrt{3}\)
ডানপক্ষ –
\(3 – \cot 30^\circ\)= \( 3 – \sqrt{3}\)
∴ বামপক্ষ = ডানপক্ষ (প্রমাণিত)
প্রয়োগ 18. মান নির্ণয় করি : \(\frac{5\cos^2\frac{\pi}{3}+4\sec^2\frac{\pi}{6}-\tan^2\frac{\pi}{4}}{\sin^2\frac{\pi}{6}+\cos^2\frac{\pi}{6}}\)
সমাধান –
\(\frac{5\cos^2\frac{\pi}{3}+4\sec^2\frac{\pi}{6}-\tan^2\frac{\pi}{4}}{\sin^2\frac{\pi}{6}+\cos^2\frac{\pi}{6}} = \frac{5\cos^2 60^\circ+4\sec^2 30^\circ-\tan^2 45^\circ}{\sin^2 30^\circ+\cos^2 30^\circ}\)= \( \frac{5\left(\frac{1}{2}\right)^2+4\left(\frac{2}{\sqrt{3}}\right)^2-(1)^2}{\left(\frac{1}{2}\right)^2+\left(\frac{\sqrt{3}}{2}\right)^2}\)
= \( \frac{\frac{5}{4}+\frac{16}{3}-1}{\frac{1}{4}+\frac{3}{4}}\)
= \( \frac{\frac{15+64-12}{12}}{\frac{4}{4}}\)
= \( \frac{67}{12}\)
= \( 5\frac{7}{12}\)
প্রয়োগ 19. sin(A+B)=1 এবং cos(A-B)=1 যেখানে, \(0^\circ \le (A+B) \le 90^\circ\) এবং A > B; A ও B কোণের মান নির্ণয় করি।
সমাধান –
\(\sin(A+B)=1 = \sin 90^\circ\)\(\therefore A+B = 90^\circ\)আবার, \(\cos(A-B)=1 = \cos 0^\circ\)
\(\therefore A-B = 0^\circ\)\(A+B = 90^\circ\)
\(A-B = 0^\circ\)
____________
\(2A = 90^\circ\)
\(\therefore A = 45^\circ\) এবং \(B = 90^\circ – 45^\circ = 45^\circ\)
প্রয়োগ 20. \(\theta\) (\(0^\circ \le \theta \le 90^\circ\)) -এর কোন মানের জন্য \(\sin^2\theta – 3\sin\theta + 2 = 0\) সত্য হবে নির্ণয় করি।
সমাধান –
\(\sin^2\theta – 3\sin\theta + 2 = 0\)বা, \(\sin^2\theta – 2\sin\theta – \sin\theta + 2 = 0\)
বা, \(\sin\theta(\sin\theta – 2) – 1(\sin\theta – 2) = 0\)
বা, \((\sin\theta – 1)(\sin\theta – 2) = 0\)
হয়, \(\sin\theta – 1 = 0 \quad \therefore \sin\theta = 1\);
অথবা, \(\sin\theta – 2 = 0 \quad \therefore \sin\theta = 2\)
যেহেতু, \(\sin\theta\)-এর মান 1-এর বেশি হতে পারে না, সুতরাং \(\sin\theta = 1 = \sin 90^\circ \quad \therefore \theta = 90^\circ\)
প্রয়োগ : 21. \(\theta\) (\(0^\circ \leq \theta \leq 90^\circ\))-এর কোন মান/মানগুলির জন্য \(2\sin\theta\cos\theta = \cos\theta\) সত্য হবে নির্ণয় করি।
সমাধান –
\(2\sin\theta\cos\theta = \cos\theta\)বা, \(2\sin\theta\cos\theta – \cos\theta = 0\)
বা, \(\cos\theta(2\sin\theta – 1) = 0\)
হয়, \(\cos\theta = 0\) অথবা, \(2\sin\theta – 1 = 0\)
\(\cos\theta = 0\) হলে, \(\cos\theta = 0 = \cos 90^\circ\) ∴ \(\theta = 90^\circ\)
আবার, \(2\sin\theta – 1 = 0\) হলে, \(\sin\theta = \frac{1}{2} = \sin 30^\circ\) ∴ \(\theta = 30^\circ\)
∴ \(\theta = 90^\circ\) বা \(\theta = 30^\circ\) মানের জন্য \(2\sin\theta\cos\theta = \cos\theta\) হবে।
প্রয়োগ 22. \(0^\circ \leq \theta \leq 90^\circ\) হলে, \(\sin\theta = 0.5\) এবং \(\cos\theta = 0.6\) হওয়া সম্ভব কিনা যুক্তিসহ লিখি।
সমাধান –
\(\sin\theta = 0.5\) ∴ \(\sin^2\theta = 0.25\)
\(\cos\theta = 0.6\) ∴ \(\cos^2\theta = 0.36\)
\(\sin^2\theta + \cos^2\theta = 0.25 + 0.36 = 0.61\)কিন্তু \(0^\circ \leq \theta \leq 90^\circ\) হলে \(\sin^2\theta + \cos^2\theta = 1\)
∴ \(\sin\theta = 0.5\) এবং \(\cos\theta = 0.6\) হওয়া সম্ভব নয়।
প্রয়োগ 23. \(0^\circ \leq \theta \leq 90^\circ\) হলে, \(\sin \theta = \frac{\sqrt{3}}{2}\) এবং \(\cos \theta = \frac{1}{3}\) হওয়া সম্ভব কিনা যুক্তিসহ লিখি।
সমাধান –
\(\sin \theta = \frac{\sqrt{3}}{2}\) ∴ \(\sin^2 \theta = \frac{3}{4}\)
\(\cos \theta = \frac{1}{3}\) ∴ \(\cos^2 \theta = \frac{1}{9}\)
এখন, \(\sin^2 \theta + \cos^2 \theta = \frac{3}{4} + \frac{1}{9} = \frac{27+4}{36} = \frac{31}{36}\)
∴ \(0^\circ \leq \theta \leq 90^\circ\) হলে \(\sin^2 \theta + \cos^2 \theta = 1\) হয় সুতরাং \(\sin \theta = \frac{\sqrt{3}}{2}\) এবং \(\cos \theta = \frac{1}{3}\) হওয়া সম্ভব নয়।
প্রয়োগ 24. \(0^\circ < \theta < 90^\circ\) হলে, দেখাই যে, \(\sin\theta + \cos\theta > 1\)
সমাধান –
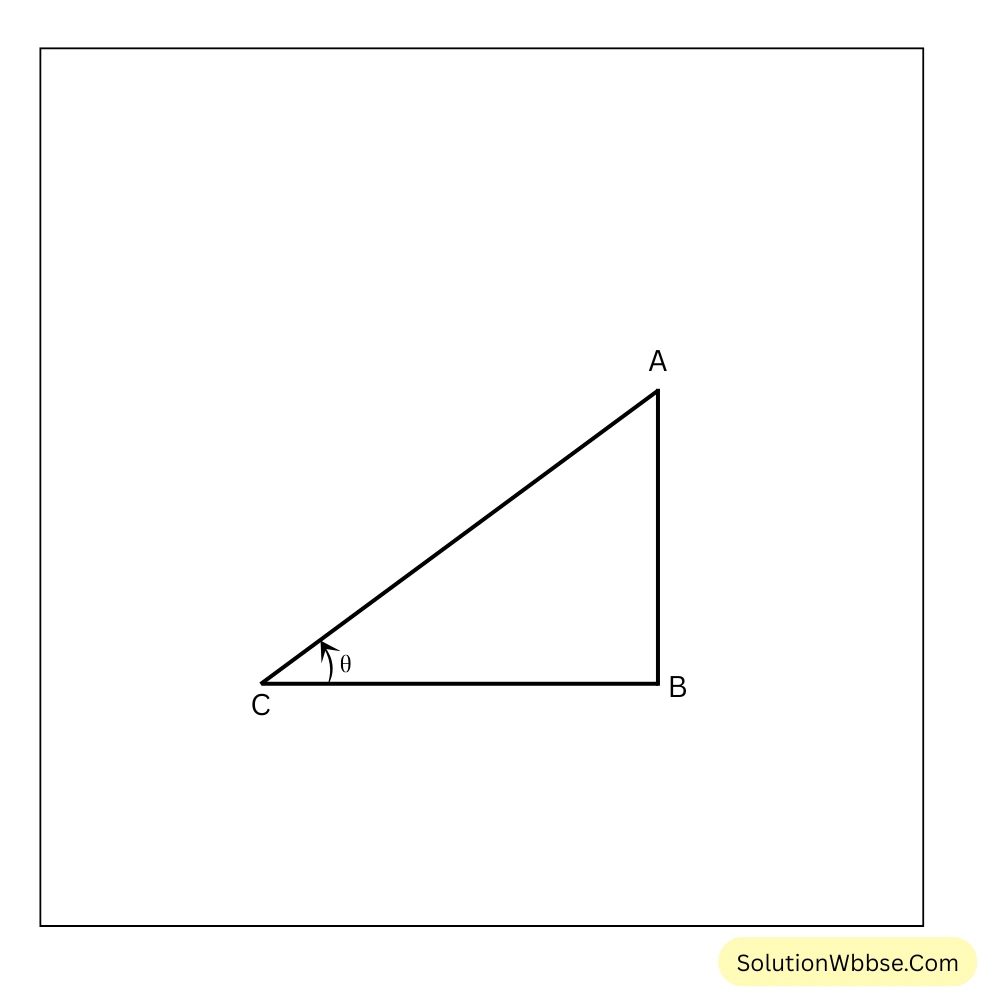
ধরি, ABC সমকোণী ত্রিভুজের \(\angle B\) সমকোণ।
ধরি, \(\angle BCA = \theta\) [যেখানে \(0^\circ < \theta < 90^\circ\)]
\(\sin\theta = \frac{AB}{AC}\) এবং \(\cos\theta = \frac{BC}{AC}\)
\(\sin\theta + \cos\theta = \frac{AB}{AC} + \frac{BC}{AC} = \frac{AB+BC}{AC}\)কিন্তু ABC ত্রিভুজে, \(AB+BC > AC\) সুতরাং, \(\frac{AB+BC}{AC} > 1\)
∴ \(\sin\theta + \cos\theta > 1\)
প্রয়োগ 25. আমি \(\cot\theta\) ও \(\sec\theta\) কে, \(\sin\theta\) -এর মাধ্যমে প্রকাশ করি।
সমাধান –
\(\sin^2\theta + \cos^2\theta = 1\)বা, \(\cos\theta = \sqrt{1-\sin^2\theta}\)
সুতরাং, \(\cot\theta = \frac{\cos\theta}{\sin\theta} = \frac{\sqrt{1-\sin^2\theta}}{\sin\theta}\)
\(\sec\theta = \frac{1}{\cos\theta} = \frac{1}{\sqrt{1-\sin^2\theta}}\)প্রয়োগ 26. আমি \(\cot \theta\) ও \(\text{cosec} \theta\) –কে \(\cos \theta\) –এর মাধ্যমে প্রকাশ করি।
সমাধান –
\(\cot \theta = \frac{\cos \theta}{\sin \theta} = \frac{\cos \theta}{\sqrt{1-\cos^2 \theta}}\)[∵ \(\sin^2 \theta + \cos^2 \theta = 1\)]
∴ \(\cot \theta = \frac{\cos \theta}{\sqrt{1-\cos^2 \theta}}\)
\(\text{cosec} \theta = \frac{1}{\sin \theta} = \frac{1}{\sqrt{1-\cos^2 \theta}}\) [∵ \(\sin^2 \theta + \cos^2 \theta = 1\)]
∴ \(\text{cosec} \theta = \frac{1}{\sqrt{1-\cos^2 \theta}}\)
প্রয়োগ 27. যদি \(tanθ = \frac{8}{15}\) হয়, তাহলে \(sinθ\) -এর মান কী হবে হিসাব করে লিখি।
সমাধান –
\(tanθ = \frac{8}{15}\)আমরা জানি, \(sec^2θ = 1+tan^2θ = 1+(\frac{8}{15})^2 = 1+\frac{64}{225} = \frac{289}{225}\)
∴ \(secθ = \frac{17}{15}\)
∴ \(cosθ = \frac{15}{17}\)
∴ \(sinθ = \sqrt{1-cos^2θ}\)
= \( \sqrt{1-(\frac{15}{17})^2}\)
= \( \sqrt{\frac{289-225}{289}}\)
= \( \sqrt{\frac{64}{289}}\)
= \( \frac{8}{17}\)
অন্যভাবে পাই, \(sinθ = \frac{tanθ}{secθ} = \frac{\frac{8}{15}}{\frac{17}{15}} = \frac{8}{17}\)
বিকল্প প্রমাণ – ABC একটি সমকোণী ত্রিভুজ যার \(\angle B\) সমকোণ। ধরি, \(\angle ACB=θ\)
∴ \(tanθ =\) লম্ব/ভূমি = \(\frac{8}{15}\)
ধরি, \(AB=8k\) একক এবং \(BC=15k\) একক (যেখানে \(k > 0\))
ABC ত্রিভুজে, \(AC^2=AB^2+BC^2 = (8k)^2+(15k)^2\)
= \(64k^2\) বর্গএকক \(+ 225k^2\) বর্গএকক = \(289k^2\) বর্গএকক
∴ \(AC=17k\) একক
\(sinθ = \frac{AB}{AC} = \frac{8k}{17k}\)∴ \(sinθ = \frac{8}{17}\)
প্রয়োগ 28. যদি \(tan\,\theta = 4/3\) হয় তাহলে \((sin\,\theta + cos\,\theta)\)-এর মান হিসাব করে লিখি।
সমাধান –
\(tan\,\theta = \frac{4}{3}\)বা, \(tan^2\,\theta = \frac{16}{9}\)
বা, \(sec^2\,\theta -1 = \frac{16}{9}\)
বা, \(sec^2\,\theta = 1 + \frac{16}{9}\)
বা, \(sec^2\,\theta = \frac{9+16}{9}\)
বা, \(sec^2\,\theta = \frac{25}{9}\)
বা, \(sec\,\theta = \sqrt{\frac{25}{9}}\)
বা, \(sec\,\theta = \frac{5}{3}\)
বা, \(cos\,\theta = \frac{1}{sec\,\theta} = \frac{3}{5}\)
বা, \(cos\,\theta = \frac{3}{5}\)
বা, \(cos^2\,\theta = (\frac{3}{5})^2\)
বা, \(cos^2\,\theta = \frac{9}{25}\)
বা, \(1-sin^2\,\theta = \frac{9}{25}\)
বা, \(1 – \frac{9}{25} = sin^2\,\theta\)
বা, \(sin^2\,\theta = \frac{25-9}{25}\)
বা, \(sin^2\,\theta = \frac{16}{25}\)
বা, \(sin\,\theta = \sqrt{\frac{16}{25}}\)
বা, \(sin\,\theta = \frac{4}{5}\)
\(\therefore (sin\,\theta + cos\,\theta ) = \frac{4}{5} + \frac{3}{5} = \frac{7}{5}\)\(\therefore (sin\,\theta + cos\,\theta ) = \frac{7}{5}\)প্রয়োগ 29. \(sinA = \frac{p}{q}\) হলে, \(tanA\), \(cotA\) ও \(secA\)-এর প্রত্যেকটি কত হবে নির্ণয় করি।
সমাধান –
\(tanA = \frac{sinA}{cosA}\)= \( \frac{sinA}{\sqrt{1-sin^2A}}\)
= \( \frac{\frac{p}{q}}{\sqrt{1-(\frac{p}{q})^2}}\)
= \( \frac{\frac{p}{q}}{\sqrt{\frac{q^2-p^2}{q^2}}}\)
= \( \frac{p}{q} \times \frac{q}{\sqrt{q^2-p^2}}\)
= \( \frac{p}{\sqrt{q^2-p^2}}\)
\(cotA = \frac{cosA}{sinA}\)= \( \frac{\sqrt{1-sin^2A}}{sinA}\)
= \( \frac{\sqrt{1-(\frac{p}{q})^2}}{\frac{p}{q}}\)
= \( \frac{\frac{\sqrt{q^2-p^2}}{q}}{\frac{p}{q}}\)
= \( \frac{\sqrt{q^2-p^2}}{q} \times \frac{q}{p}\)
= \( \frac{\sqrt{q^2-p^2}}{p}\)
\(secA = \frac{1}{cosA}\)= \( \frac{1}{\sqrt{1-sin^2A}}\)
= \( \frac{1}{\sqrt{1-(\frac{p}{q})^2}}\)
= \( \frac{1}{\frac{\sqrt{q^2-p^2}}{q}}\)
= \( \frac{q}{\sqrt{q^2-p^2}}\)
প্রয়োগ 30. যদি \( \cot\theta = \frac{x}{y} \) হয়, তবে প্রমাণ করি যে, \( \frac{x \cos\theta – y \sin\theta}{x \cos\theta + y \sin\theta} = \frac{x^2 – y^2}{x^2 + y^2} \)
সমাধান –
বামপক্ষ = \( \frac{x \cos\theta – y \sin\theta}{x \cos\theta + y \sin\theta} \)
= \( \frac{\frac{x \cos\theta}{\sin\theta} – \frac{y \sin\theta}{\sin\theta}}{\frac{x \cos\theta}{\sin\theta} + \frac{y \sin\theta}{\sin\theta}} \) [লব ও হরকে \( \sin\theta \) দিয়ে ভাগ করে পাই]
= \( \frac{x \cot\theta – y}{x \cot\theta + y} \)
= \( \frac{x \times \frac{x}{y} – y}{x \times \frac{x}{y} + y} \)
= \( \frac{\frac{x^2}{y} – y}{\frac{x^2}{y} + y} \)
= \( \frac{\frac{x^2 – y^2}{y}}{\frac{x^2 + y^2}{y}} \)
= \( \frac{x^2 – y^2}{x^2 + y^2} \) = ডানপক্ষ
বিকল্প পদ্ধতি : (I)
\( \cot\theta = \frac{x}{y} \) বা, \( \frac{\cos\theta}{\sin\theta} = \frac{x}{y} \)
∴ \( \frac{\cos\theta}{x} = \frac{\sin\theta}{y} = k \) (ধরি) যেখানে \( k > 0 \)
∴ \( \cos\theta = xk \) এবং \( \sin\theta = yk \)
∴ \( \frac{x \cos\theta – y \sin\theta}{x \cos\theta + y \sin\theta} = \frac{x \cdot xk – y \cdot yk}{x \cdot xk + y \cdot yk} = \frac{k(x^2 – y^2)}{k(x^2 + y^2)} = \frac{x^2 – y^2}{x^2 + y^2} \)
মনে রাখতে হবে : \( \cot\theta = \frac{x}{y} \) থেকে \( \frac{\cos\theta}{\sin\theta} = \frac{x}{y} \) পাই,
কিন্তু \( \cos\theta = x \) এবং \( \sin\theta = y \) লেখা ভুল। \( \cos\theta = xk \) এবং \( \sin\theta = yk \) নিতে পারি, যেখানে \( k > 0 \).
বিকল্প পদ্ধতি : (II)
\( \cot\theta = \frac{x}{y} \) বা, \( \frac{\cos\theta}{\sin\theta} = \frac{x}{y} \)
বা, \( \frac{x \cos\theta}{y \sin\theta} = \frac{x^2}{y^2} \) (উভয়পক্ষে \( \frac{x}{y} \) দ্বারা গুণ করে পাই)
বা, \( \frac{x \cos\theta + y \sin\theta}{x \cos\theta – y \sin\theta} = \frac{x^2 + y^2}{x^2 – y^2} \) (যোগ ও ভাগ প্রক্রিয়ার সাহায্যে পাই)
∴ \( \frac{x \cos\theta – y \sin\theta}{x \cos\theta + y \sin\theta} = \frac{x^2 – y^2}{x^2 + y^2} \)
প্রয়োগ 31. যদি \(\sin\theta + \cos\theta = \frac{7}{5}\) এবং \(\sin\theta\cos\theta = \frac{12}{25}\) হয়, তাহলে \(\sin\theta\) এবং \(\cos\theta\)-এর মান নির্ণয় করি।
সমাধান –
\(\sin\theta + \cos\theta = \frac{7}{5}\)\(\therefore \cos\theta = \frac{7}{5} – \sin\theta\) __________ (i)
\(\sin\theta\cos\theta = \frac{12}{25}\) সমীকরণে \(\cos\theta = \frac{7}{5} – \sin\theta\) বসিয়ে পাই,
\(\sin\theta \times (\frac{7}{5} – \sin\theta) = \frac{12}{25}\)বা, \(\frac{7\sin\theta}{5} – \sin^2\theta = \frac{12}{25}\)
বা, \(7\sin\theta – 5\sin^2\theta = \frac{12}{5}\)
বা, \(35\sin\theta – 25\sin^2\theta = 12\)
বা, \(25\sin^2\theta – 35\sin\theta + 12 = 0\)
বা, \(25\sin^2\theta – 20\sin\theta – 15\sin\theta + 12 = 0\)
বা, \(5\sin\theta(5\sin\theta – 4) – 3(5\sin\theta – 4) = 0\)
বা, \((5\sin\theta – 4)(5\sin\theta – 3) = 0\) [উৎপাদকে বিশ্লেষণ করে পেলাম]
হয়, \(5\sin\theta – 4 = 0 \quad \therefore \sin\theta = \frac{4}{5}\)
অথবা, \(5\sin\theta – 3 = 0 \quad \therefore \sin\theta = \frac{3}{5}\)
\(\sin\theta = \frac{4}{5}\) হলে, \(\cos\theta = \frac{7}{5} – \frac{4}{5} = \frac{3}{5}\)
আবার, \(\sin\theta = \frac{3}{5}\) হলে, \(\cos\theta = \frac{7}{5} – \frac{3}{5} = \frac{4}{5}\)
\(\therefore \sin\theta = \frac{4}{5}\)\(\cos\theta = \frac{3}{5}\)অথবা
\(\sin\theta = \frac{3}{5}\)\(\cos\theta = \frac{4}{5}\)প্রয়োগ 32. \(1+2\sin\theta\cos\theta\)-কে পূর্ণবর্গ রাশি হিসাবে প্রকাশ করি।
সমাধান –
\(1+2\sin\theta\cos\theta = \sin^2\theta+\cos^2\theta+2\sin\theta\cos\theta\) \([\because \sin^2\theta+\cos^2\theta=1]\)
= \((\sin\theta+\cos\theta)^2\)
প্রয়োগ 33. \(\frac{\sec\theta+\tan\theta}{\sec\theta-\tan\theta} = 2\frac{51}{79}\) হলে, \(\sin\theta\)-এর মান নির্ণয় করি।
সমাধান –
\(\frac{\sec\theta+\tan\theta}{\sec\theta-\tan\theta} = 2\frac{51}{79} = \frac{209}{79}\)বা, \(\frac{\sec\theta+\tan\theta+\sec\theta-\tan\theta}{\sec\theta+\tan\theta-\sec\theta+\tan\theta} = \frac{209+79}{209-79}\) (যোগ ও ভাগ প্রক্রিয়ার সাহায্যে পাই)
বা, \(\frac{2\sec\theta}{2\tan\theta} = \frac{288}{130}\)
বা, \(\frac{\tan\theta}{\sec\theta} = \frac{130}{288} = \frac{65}{144}\)
বা, \(\frac{\sin\theta}{\cos\theta} \times \cos\theta = \frac{65}{144}\)
\(\therefore \sin\theta = \frac{65}{144}\)প্রয়োগ 34. \(\frac{5\cot\theta+cosec\theta}{5\cot\theta-cosec\theta} = \frac{7}{3}\) হলে , \(\cos\theta\) –এর মান নির্ণয় করি।
সমাধান –
\(\frac{5\cot\theta+cosec\theta}{5\cot\theta-cosec\theta} = \frac{7}{3}\)বা, \(\frac{5\frac{\cos\theta}{\sin\theta}+\frac{1}{\sin\theta}}{5\frac{\cos\theta}{\sin\theta}-\frac{1}{\sin\theta}} = \frac{7}{3}\)
বা, \(\frac{\frac{5\cos\theta+1}{\sin\theta}}{\frac{5\cos\theta-1}{\sin\theta}} = \frac{7}{3}\)
বা, \(\frac{5\cos\theta+1}{5\cos\theta-1} = \frac{7}{3}\)
বা, \(3 (5\cos\theta+1) = 7 (5\cos\theta-1)\)
বা, \(15\cos\theta + 3 = 35\cos\theta – 7\)
বা, \(15\cos\theta – 35\cos\theta = -3 – 7\)
বা, \(-20\cos\theta = -10\)
বা, \(\cos\theta = \frac{-10}{-20}\)
বা, \(\cos\theta = \frac{1}{2}\)
\(\therefore \cos\theta\) –এর মান \(\frac{1}{2}\)।
প্রয়োগ 35. \(x=a\cos\theta\) এবং \(y=b\sin\theta\) হলে, সম্পর্ক দুটি থেকে \(\theta\) অপনয়ন করি ও কী পাই দেখি।
সমাধান –
\(x=a\cos\theta\) ∴ \(\cos\theta = \frac{x}{a}\)
আবার, \(y=b\sin\theta\) ∴ \(\sin\theta = \frac{y}{b}\)
যেহেতু, \(\sin^2\theta + \cos^2\theta = 1\)
∴ \((\frac{y}{b})^2 + (\frac{x}{a})^2 = 1\)
সুতরাং, \(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\)
প্রয়োগ 36. \(2x= 3\sin \theta\) এবং \(5y = 3\cos \theta\) সম্পর্ক দুটি থেকে \(\theta\) অপনয়ন করে \(x\) ও \(y\)-এর সম্পর্ক লিখি।
সমাধান –
\(2x= 3\sin \theta\)বা, \(\sin \theta = \frac{2x}{3}\)
আবার,
\(5y = 3\cos\theta\)বা, \(\cos \theta = \frac{5y}{3}\)
আমরা জানি,
\(\sin^2 \theta + \cos^2 \theta = 1\)বা, \((\frac{2x}{3})^2 + (\frac{5y}{3})^2 = 1\)
বা, \(\frac{4x^2}{9} + \frac{25y^2}{9} = 1\)
বা, \(4x^2 + 25y^2 = 1\)
∴ \(\theta\) বর্জিত সম্পর্কটি হল, \(4x^2 + 25y^2 = 1\)
প্রয়োগ 37. \(x \cos\theta=3\) এবং \(4\tan\theta=y\) সম্পর্ক দুটি থেকে \(\theta\) অপনয়ন করি ও \(x\) এবং \(y\) -এর সম্পর্ক লিখি।
সমাধান –
\(x \cos\theta=3\) বা, \(\cos\theta=\frac{3}{x}\) ∴ \(\sec\theta=\frac{x}{3}\)
\(4\tan\theta=y\) ∴ \(\tan\theta=\frac{y}{4}\)
যেহেতু, \(\sec^2\theta – \tan^2\theta = 1\)
সুতরাং, \((\frac{x}{3})^2 – (\frac{y}{4})^2 = 1\)
∴ \(\frac{x^2}{9} – \frac{y^2}{16} = 1\)
প্রয়োগ 38. \(x = a \sec \theta\) এবং \(y = b\tan \theta\) সম্পর্ক দুটি থেকে \(\theta\) অপনয়ন করি।
সমাধান –
\(x = a \sec \theta\)বা, \(\sec \theta = \frac{x}{a}\)
আবার,
\(y = b\tan \theta\)বা, \(\tan\theta = \frac{y}{b}\)
আমরা জানি,
\(\sec^2\theta – \tan^2\theta = 1\)∴ \((\frac{x}{a})^2 – (\frac{y}{b})^2 = 1\)
বা, \(\frac{x^2}{a^2} – \frac{y^2}{b^2} = 1\)
∴ \(\theta\) বর্জিত সম্পর্কটি হল \(\frac{x^2}{a^2} – \frac{y^2}{b^2} = 1\)
প্রয়োগ 39. \(x=a\cos\theta+b\sin\theta\), \(y=b\cos\theta−a\sin\theta\) হলে, সম্পর্ক দুটি থেকে \(\theta\) অপনয়ন করি।
সমাধান –
\(x^2+y^2 = (a\cos\theta+b\sin\theta)^2+(b\cos\theta−a\sin\theta)^2\)= a2cos2θ+b2sin2θ+2absinθcosθ+b2cos2θ+a2sin2θ−2absinθcosθ
= \( a^2(\sin^2\theta+\cos^2\theta) + b^2(\sin^2\theta+\cos^2\theta)\)
= \( a^2+b^2\) [∵ \(\sin^2\theta+\sin^2\theta=1\)]
∴ \(x^2+y^2 = a^2+b^2\)
প্রয়োগ 40. যদি \(\sin\theta + cosec\theta = 2\) হয়, তাহলে \((\sin^{10}\theta + cosec^{10}\theta)\)-এর মান নির্ণয় করি।
সমাধান –
\(\sin\theta + cosec\theta = 2\)বা, \(\sin\theta + \frac{1}{\sin\theta} = 2\)
বা, \(\frac{\sin^2\theta+1}{\sin\theta} = 2\)
বা, \(\sin^2\theta+1 = 2\sin\theta\)
বা, \(\sin^2\theta – 2\sin\theta+1 = 0\)
বা, \((\sin\theta−1)^2 = 0\)
বা, \(\sin\theta−1 = 0\)
∴ \(\sin\theta = 1\)
সুতরাং, \(cosec\theta = 1\)
\(\sin^{10}\theta + cosec^{10}\theta = (1)^{10} + (1)^{10}\)= \(1 + 1\)
= \(2\)
প্রয়োগ 41. যদি \((\cos\theta + \sec\theta) = 2\) হয় তাহলে , \((\cos^{11}\theta + \sec^{11}\theta)\) –এর মান নির্ণয় করি।
সমাধান –
\((\cos\theta + \sec\theta) = 2\)বা, \(\cos\theta + \frac{1}{\cos\theta} = 2\)
বা, \(\frac{\cos^2\theta+1}{\cos\theta} = 2\)
বা, \(\cos^2\theta + 1 = 2 \cos\theta\)
বা, \(\cos^2\theta – 2\cos\theta + 1 = 0\)
বা, \((\cos\theta-1)^2=0\)
বা, \(\cos\theta – 1 = 0\)
বা, \(\cos\theta = 1\)
বা, \(\cos\theta = \cos0°\)
বা, \(\theta = 0°\)
∴ \((\cos^{11}\theta + \sec^{11}\theta)\)
= \((1)^{11} + (1)^{11}\) [∵ \(\sec \theta = 1/\cos \theta\) ]
= \(1 + 1\)
= \(2\)
∴ \((\cos^{11}\theta + \sec^{11}\theta) = 2\) [ উত্তর ]
প্রয়োগ 42. যদি \(0° < \alpha \le 90°\) হয়, তাহলে \((4cosec^2\alpha+9\sin^2\alpha)\)-এর সর্বনিম্ন মান নির্ণয় করি।
\(4cosec^2\alpha+9\sin^2\alpha\)= \((2cosec\alpha)^2+(3\sin\alpha)^2\)
= \((2cosec\alpha-3\sin\alpha)^2+2 \times 2cosec\alpha \times 3\sin\alpha\)
= \((2cosec\alpha-3\sin\alpha)^2+12 \times \frac{1}{\sin\alpha} \times \sin\alpha\)
= \((2cosec\alpha-3\sin\alpha)^2+12\)
যে-কোনো পূর্ণবর্গ সংখ্যামালার সর্বনিম্ন মান 0 (শূন্য)। সুতরাং \((2cosec\alpha-3\sin\alpha)^2\)-এর ন্যূনতম মান শূন্য।
∴ \((4cosec^2\alpha+9\sin^2\alpha)\)-এর সর্বনিম্ন মান 12
\(4cosec^2\alpha+9\sin^2\alpha \)= \((2cosec\alpha+3\sin\alpha)^2-2 \times 2cosec\alpha \times 3\sin\alpha\)
= \((2cosec\alpha+3\sin\alpha)^2-12\)
\((2cosec\alpha+3\sin\alpha)^2\)-এর ন্যূনতম মান 0 (শূন্য)। সুতরাং \((4cosec^2\alpha+9\sin^2\alpha\)-এর ন্যূনতম মান \(-12\)
তাহলে কোনটি ন্যূনতম মান হবে?
দুটি বর্গ সংখ্যামালার সমষ্টি ঋণাত্মক হতে পারে না। তাই \((4cosec^2\alpha+9\sin^2\alpha)\)-এর মান 12।
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের ত্রয়োবিংশ অধ্যায়, ‘ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment