মাধ্যমিক গণিত – ত্রিকোণমিতিক অনুপাতের প্রয়োগ: উচ্চতা ও দূরত্ব – প্রয়োগ

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের পঞ্চবিংশ অধ্যায়, ‘ত্রিকোণমিতিক অনুপাতের প্রয়োগ: উচ্চতা ও দূরত্ব’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

প্রয়োগ 1. রীতাদের পুকুরের পাড়ে একটি নারকেল গাছ আছে। পুকুরের পাড় থেকে 12 মিটার দূরে একটি বিন্দুর সাপেক্ষে ওই গাছের শীর্ষবিন্দুর উন্নতি কোণ \(60^\circ\) হলে, রীতাদের পুকুর পাড়ের ওই নারকেল গাছটির উচ্চতা হিসাব করে লিখি। [ \(\sqrt{3} = 1.732\) (প্রায়)]

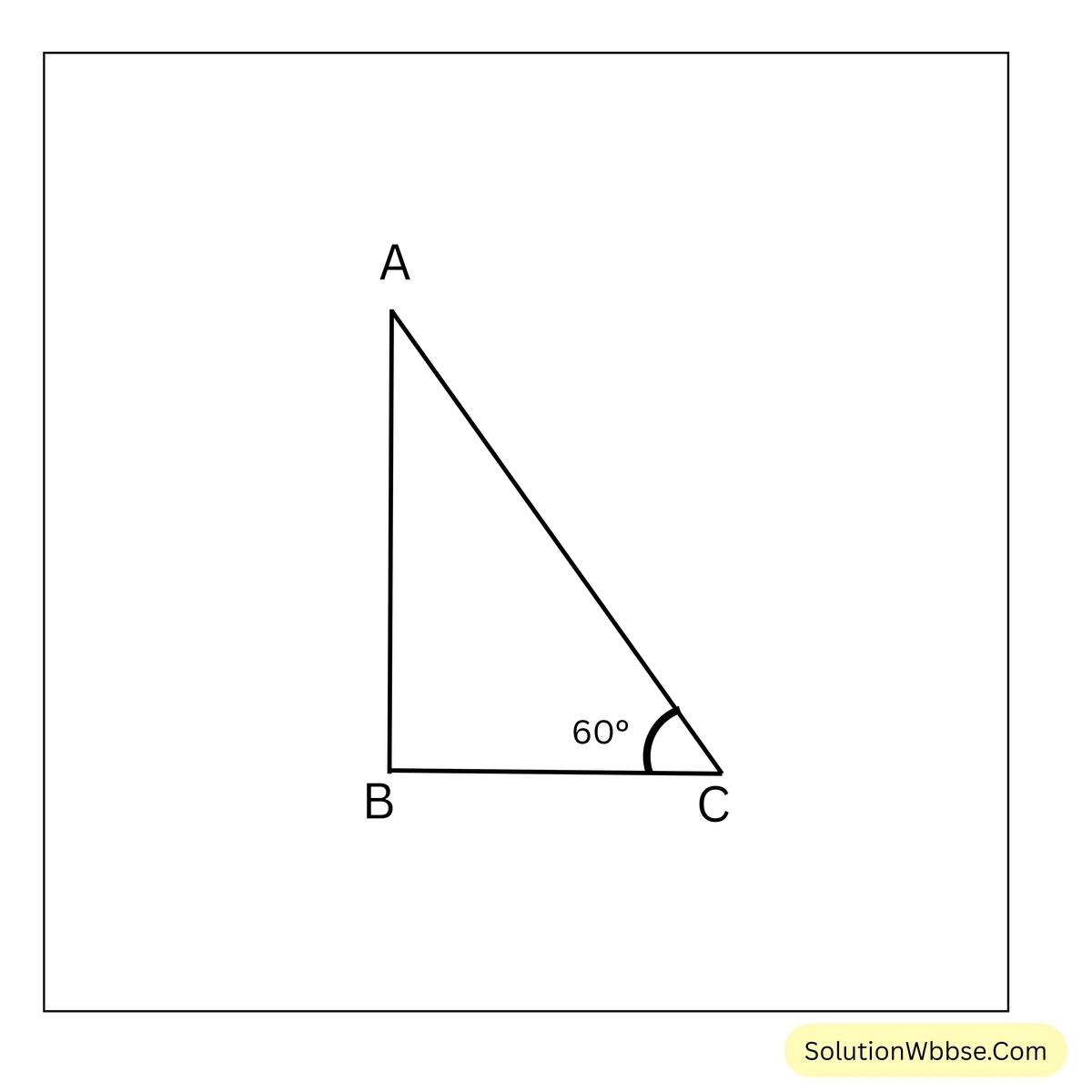
সমাধান –

ধরি, \(AB\) নারকেল গাছের উচ্চতা যা ভূমিতলের উপর লম্বভাবে আছে। B বিন্দু থেকে পুকুরের পাড় ধরে C বিন্দুতে গিয়ে C বিন্দুর সাপেক্ষে A বিন্দুর উন্নতি কোণ \(60^\circ\) হয়েছে।

A ও C বিন্দুদ্বয় যুক্ত করে \(ABC\) সমকোণী ত্রিভুজ পেয়েছি যার \(\angle B = 90^\circ\) এবং \(\angle ACB = 60^\circ\)

∴ \(\angle ACB\)-এর পরিপ্রেক্ষিতে ভূমি \(BC = 12\) মিটার। সমকোণী \(\triangle ABC\)-তে, ত্রিকোণমিতিক অনুপাতের সাহায্যে পাই,

∴ $\tan \angle \mathrm{ACB}=\tan 60°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{AB}}{12}$ মি.

বা, \(\tan 60^\circ = \frac{AB}{12}\) মি.

বা, \(\sqrt{3} = \frac{AB}{12}\) মি.

বা, \(AB = 12\sqrt{3}\) মি. = \(12 \times 1.732\) মি. (প্রায়)

= 20.784 মি. (প্রায়)

∴ নারকেল গাছটির উচ্চতা = 20.784 মিটার (প্রায়)।

প্রয়োগ 2. একটি নারকেল গাছের গোড়া থেকে অনুভূমিক তলে 20 মিটার দুরের একটি বিন্দুর সাপেক্ষে গাছটির অগ্রভাগের উন্নতি কোণ যদি \(60^\circ\) হয়, তাহলে গাছটির উচ্চতা নির্ণয় কর।

সমাধান –

ধরি, AB নারকেল গাছের গোড়া B থেকে 20 মিটার দূরে C বিন্দু থেকে গাছটির অগ্রভাগ অর্থাৎ A বিন্দুর উন্নতি কোণ \(\angle ACB = 60^\circ\)

এখন সমকোণী ত্রিভুজ ABC এর ক্ষেত্রে,

$\tan \angle \mathrm{ACB}=\tan 60°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{AB}}{20}$

বা, \(\sqrt{3} = \frac{AB}{20}\) [ যেহেতু \(tan 60^\circ = \sqrt{3}\) ]

বা, \(AB = 20\sqrt{3}\)

∴ নারকেল গাছের উচ্চতা \(20\sqrt{3}\) মিটার।

প্রয়োগ 3. গতকাল ঝড়ে একটি লাইটপোস্ট মচকে গিয়ে তার অগ্রভাগ পাদবিন্দু থেকে \(4\) মিটার দূরে ভূমি স্পর্শ করেছে এবং অনুভূমিক রেখার সঙ্গে \(45^\circ\) কোণ উৎপন্ন করেছে। লাইটপোস্টটি কত লম্বা ছিল হিসাব করে লিখি। [\(\sqrt{2}\) = 1.414 (প্রায়)]

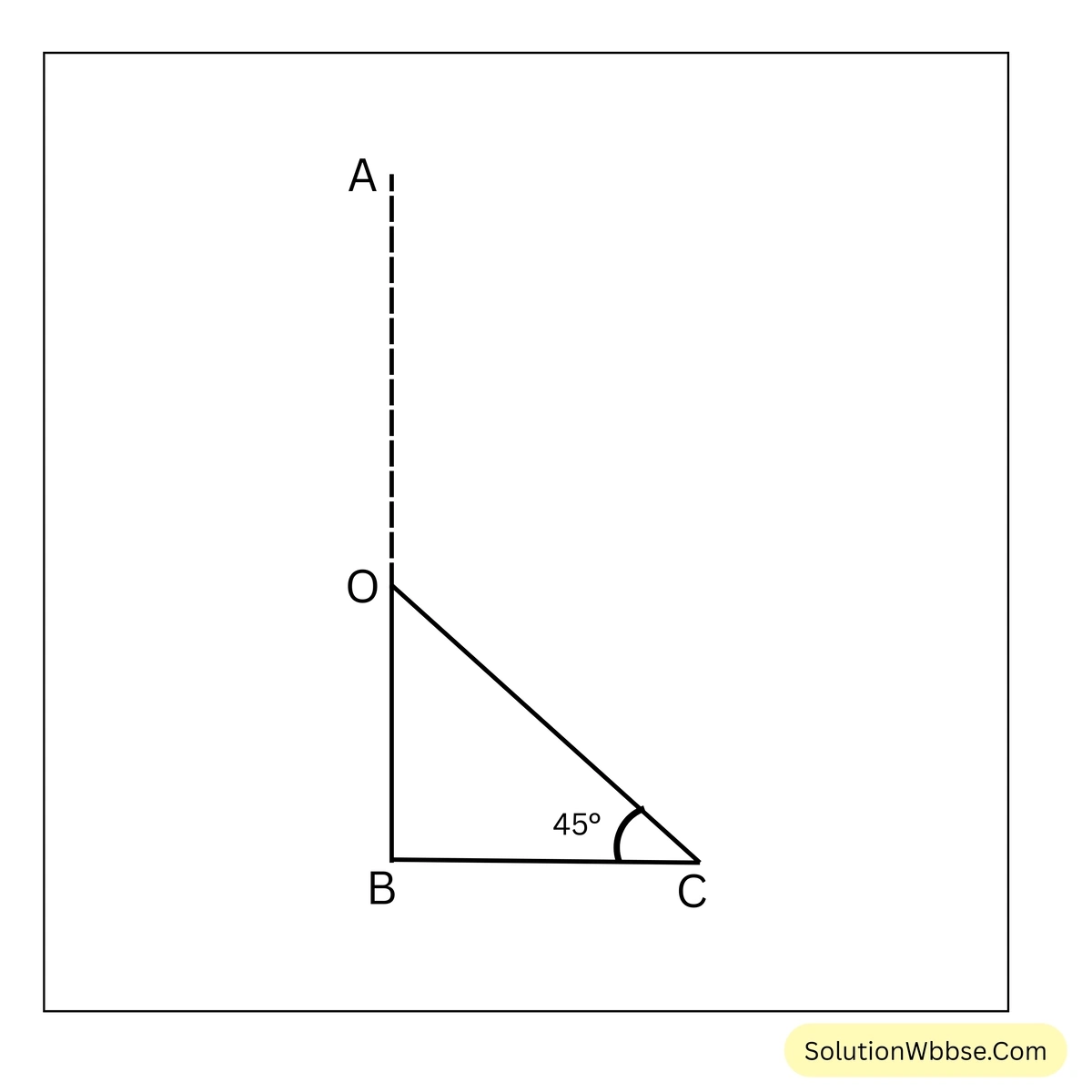
সমাধান –

ধরি, AB দৈর্ঘ্যের লাইটপোস্টটি O বিন্দুতে মচকে গিয়ে তার অগ্রভাগ C বিন্দুতে ভূমি স্পর্শ করেছে।

∴ \(AO = OC = x\) মি. (ধরি)

∴ \(AB = AO+OB = CO+OB\)

∴ OBC একটি সমকোণী ত্রিভুজ তৈরি হয়েছে যার \(\angle B=90^\circ\), \(BC=4\) মিটার ও \(OC=x\) মি.

সমকোণী \(\triangle OBC\)-তে, \(\cos45^\circ = \frac{BC}{OC} = \frac{4}{x}\)

বা, \(\frac{1}{\sqrt{2}} = \frac{4}{x} \therefore x = 4\sqrt{2}\)

∴ \(OC = 4\sqrt{2}\) মি. = \(4 \times 1.414\) মি. = 5.656 মি. (প্রায়)

\(\triangle OBC\)-এর, \(\angle OCB=45^\circ\) ∴ \(\angle BOC=90^\circ-45^\circ = 45^\circ\)

∴ \(BO = CO = 4\) মি.

∴ লাইটপোস্টের দৈর্ঘ্য = \((4+5.656)\) মিটার (প্রায়)

= 9.656 মিটার (প্রায়)

প্রয়োগ 4. সূর্যের উন্নতি কোণ \(60^\circ\) হলে একটি তালগাছের ছায়ার দৈর্ঘ্য 12 মিটার হয়। তালগাছটির উচ্চতা নির্ণয় করি।

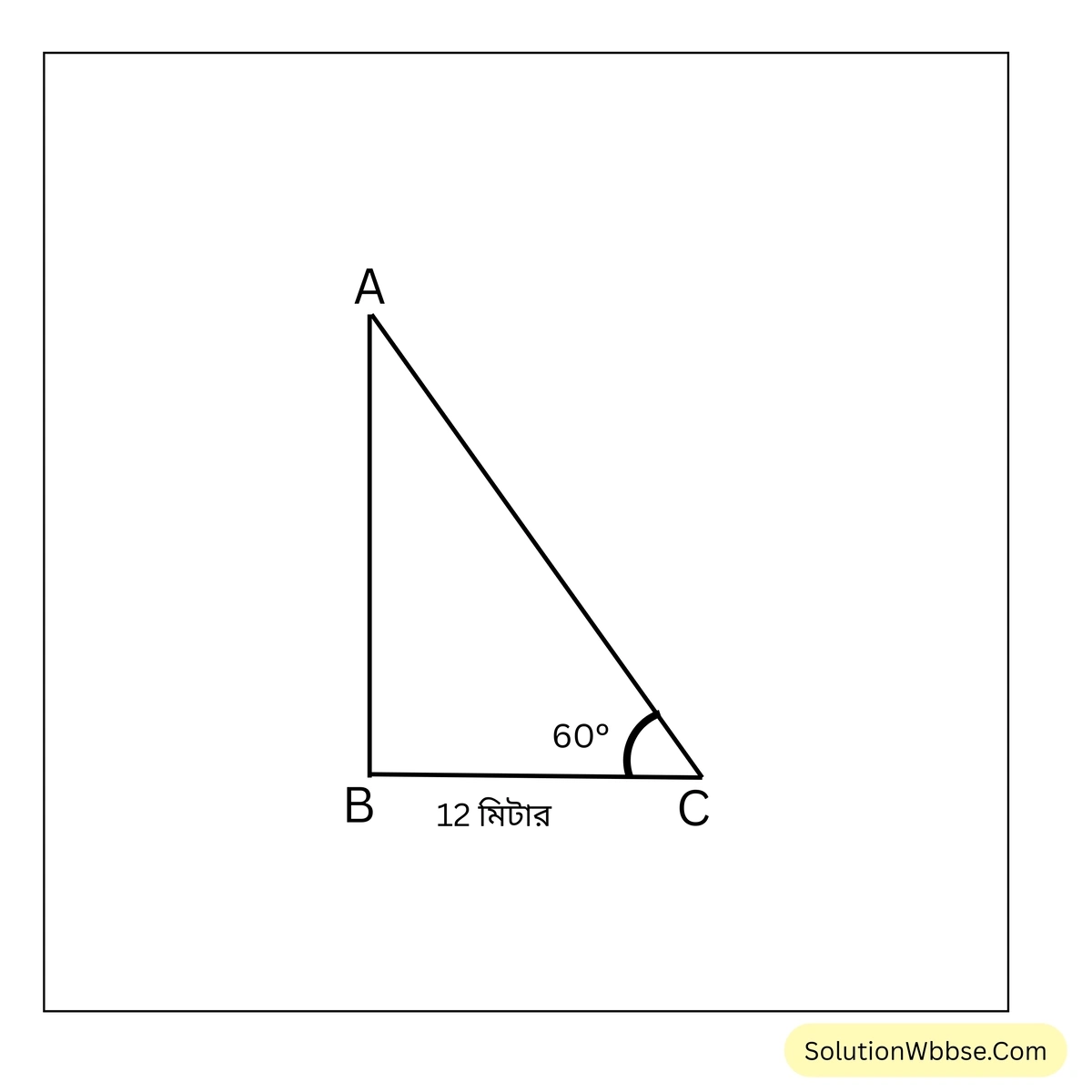
সমাধান –

পাশের চিত্রে, AB তালগাছের উচ্চতা এবং BC তালগাছের ছায়ার দৈর্ঘ্য যখন \(\angle ACB=60^\circ\)

সমকোণী \(\triangle ABC\)-তে, \(\tan 60^\circ = \frac{AB}{BC}\)

বা, \(\sqrt{3} = \frac{AB}{12 \text{ মি.}}\)

বা, \(AB = 12\sqrt{3}\) মি.

∴ তালগাছের উচ্চতা \(12\sqrt{3}\) মিটার।

কিন্তু ওই তালগাছটির (যার উচ্চতা \(12\sqrt{3}\) মিটার) ছায়ার দৈর্ঘ্য যখন 36 মিটার হবে তখন সূর্যের উন্নতি কোণ কী হবে হিসাব করে লিখি।

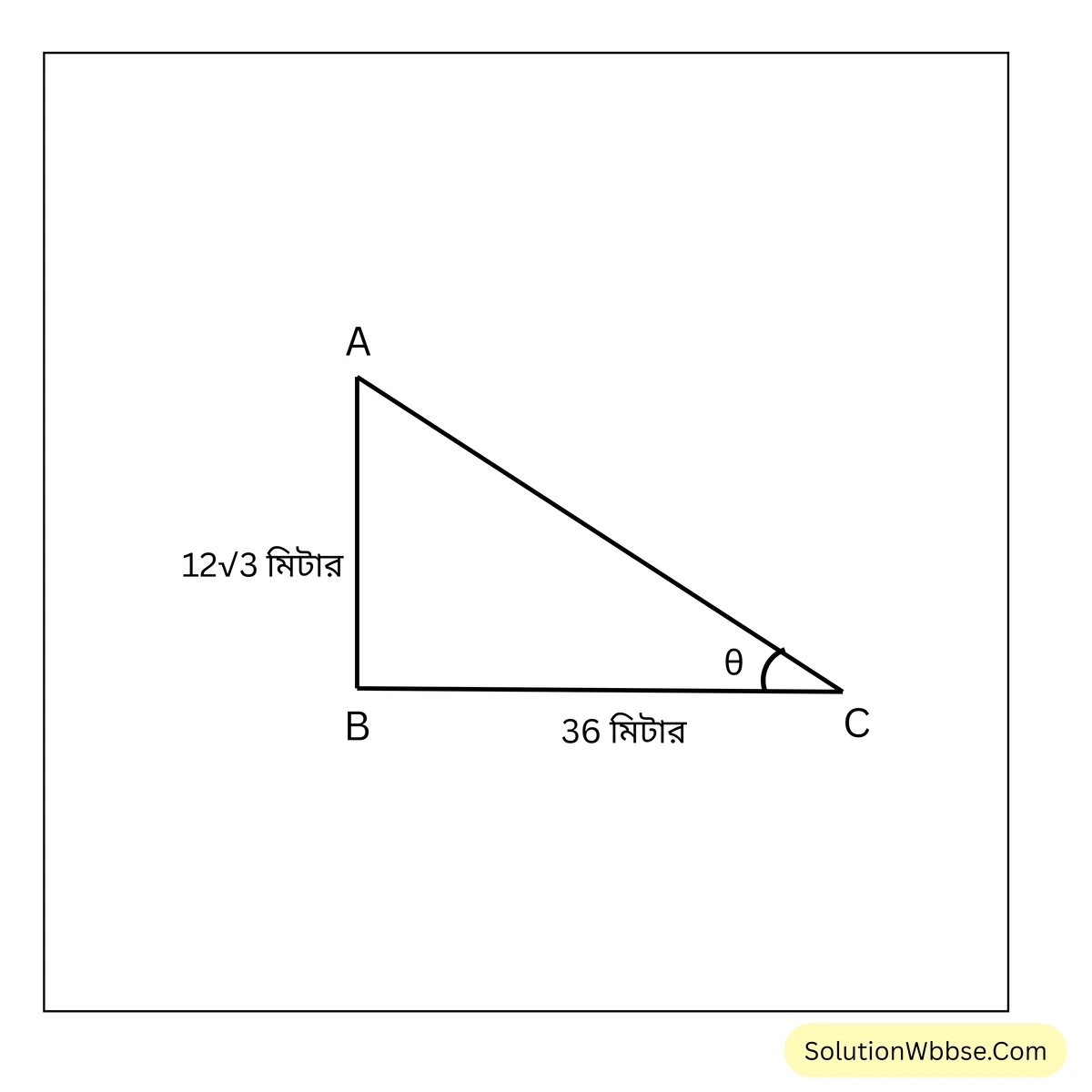
সমাধান –

ধরি, \(12\sqrt{3}\) মিটার দৈর্ঘ্যের AB তালগাছটির ছায়ার দৈর্ঘ্য BC যখন 36 মিটার তখন সূর্যের উন্নতি কোণ \(\theta\)

সমকোণী \(\triangle ABC\)-তে, \(\tan\,\theta = \frac{AB}{BC} = \frac{12\sqrt{3}}{36} = \frac{12\sqrt{3}}{12 \times 3} = \frac{1}{\sqrt{3}}\)

সুতরাং, \(\tan\,\theta = \frac{1}{\sqrt{3}} = \tan 30^\circ\) ∴ \(\theta = 30^\circ\)

∴ তখন সূর্যের উন্নতি কোণ \(30^\circ\)

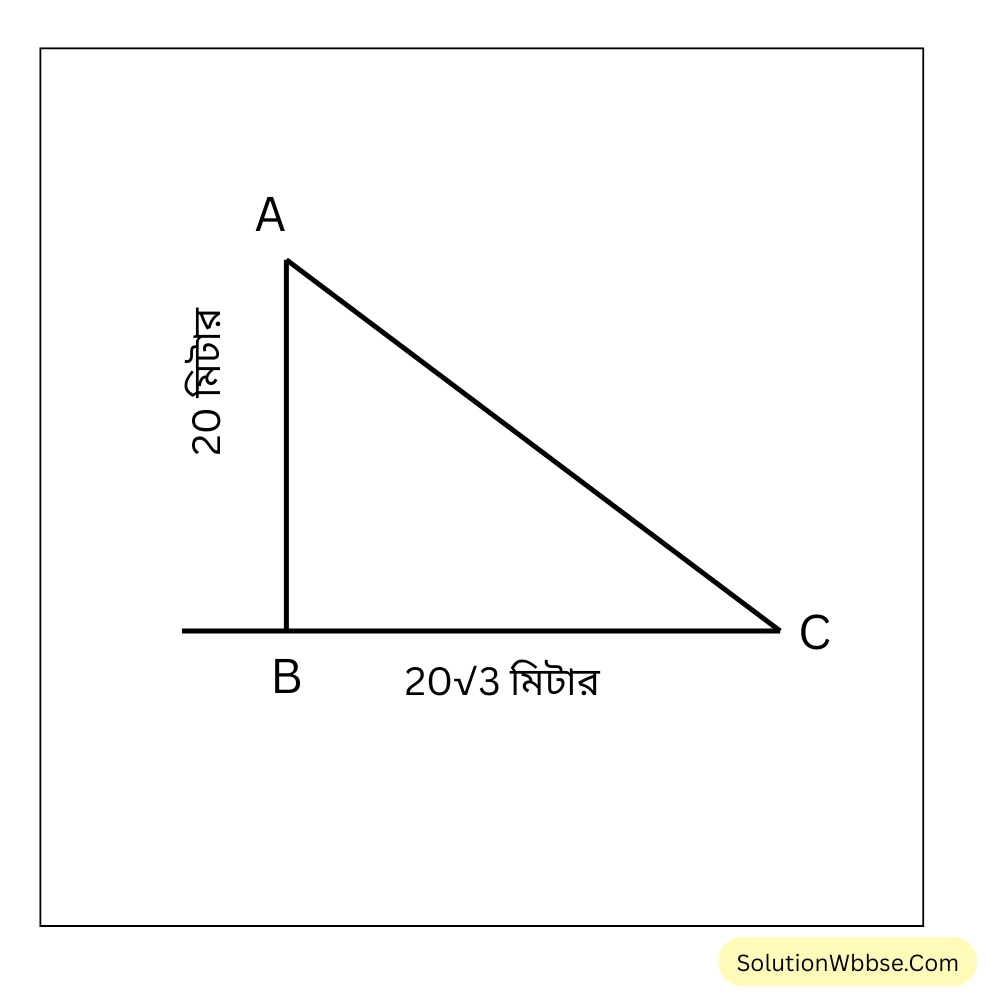
প্রয়োগ 5. সূর্যের উন্নতি কোণ কত হলে 20 মিটার লম্বা লাঠির ছায়ার দৈর্ঘ্য \(20\sqrt{3}\) মিটার হবে হিসাব করে লিখি। (নিজে করি)

সমাধান –

ধরি, AB হল 20 মি. লম্বা লাঠি এবং BC হল তার ছায়া। BC-এর দৈর্ঘ্য \(20\sqrt{3}\) মি.।

\(tan\angle ACB = \frac{AB}{BC}\)

বা, \( tan\angle ACB = \frac{20}{20\sqrt{3}}\)

বা, \( tan\angle ACB = \frac{1}{\sqrt{3}}\)

বা, \(tan\angle ACB = tan30^\circ\)

বা, \( \angle ACB = 30^\circ\)

∴ সূর্যের উন্নতি কোণ \(30^\circ\) হতে হবে।

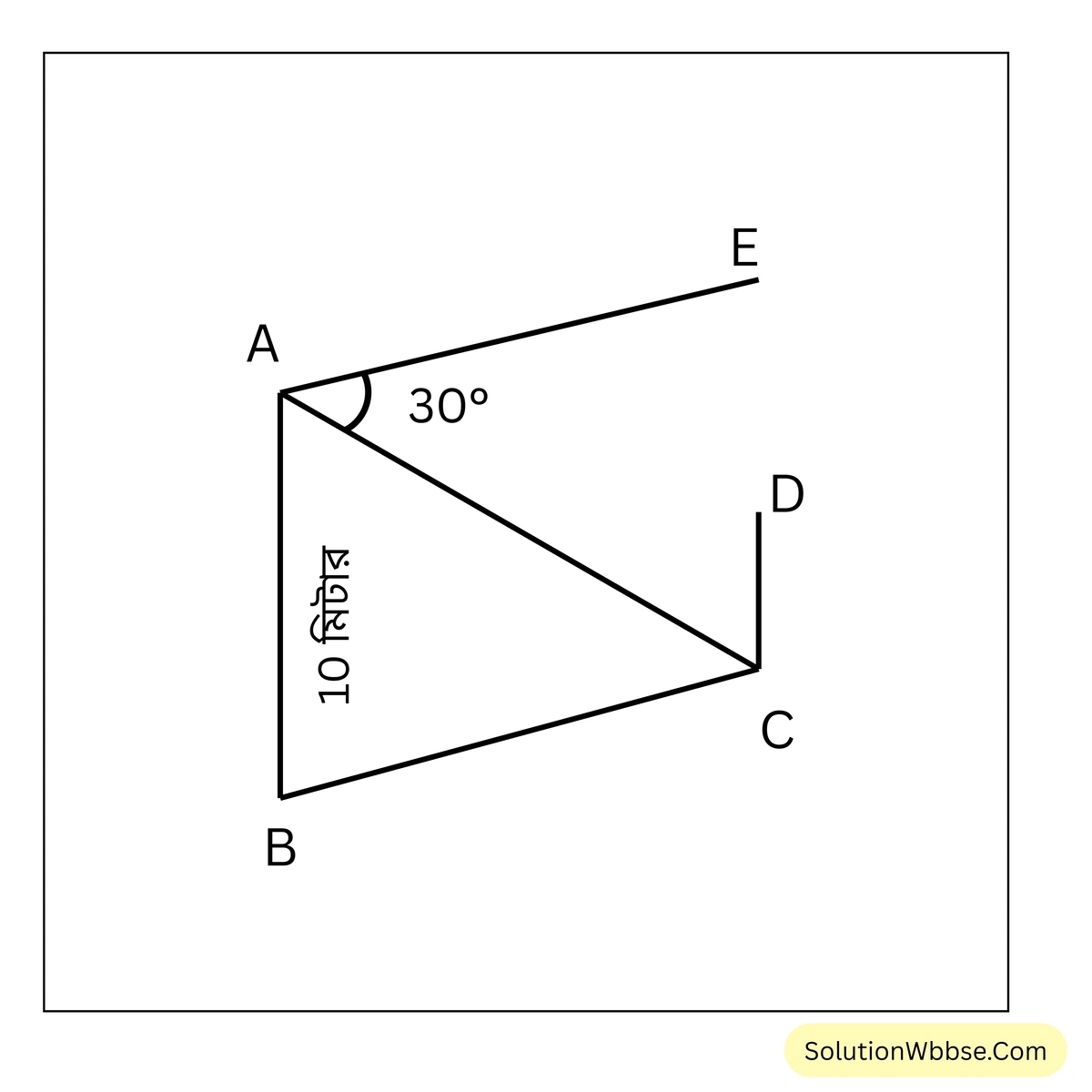
প্রয়োগ 6. হাঁসখালি পোলের বড়ো খালের ঠিক পাড়ে অবস্থিত সমীরণদের তিনতলা বাড়ির ছাদ থেকে সে সোজাসুজি খালের ঠিক অপর পারের একটি লাইটপোস্ট দেখছিল। সমীরণের চোখ থেকে সেই পোস্টের পাদবিন্দুর অবনতি কোণ যদি \(30^\circ\) হয় এবং বাড়িটির উচ্চতা যদি 10 মিটার হয়, তাহলে ছবি এঁকে ওই খালটি কত চওড়া হিসাব করি। [\(\sqrt{3} = 1.732\) (প্রায়)]

সমাধান –

ধরি, AB তিনতলা বাড়িটি এবং CD পোস্টটি BC চওড়া খালের দুই পারে এবং ঠিক বিপরীত দিকে অবস্থিত। সমীরণ A বিন্দু থেকে CD পোস্টের পাদবিন্দু C-কে \(30^\circ\) অবনতি কোণে দেখছিল।

∴ \(\angle EAC = 30^\circ\) [ধরি, AE||BC ]

∴ ABC একটি সমকোণী ত্রিভুজ পেলাম যার \(\angle B=90^\circ\), AB=10 মিটার এবং \(\angle ACB\)

= একান্তর \(\angle EAC\) [∵ AE||BC ]

∴ \(\angle ACB = 30^\circ\)

সমকোণী \(\triangle ABC\)-তে, 

$\tan 30°=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{10\text{ মি.}}{\mathrm{BC}}$

বা, $\frac{1}{\sqrt{3}}=\frac{10\text{মি.}}{\mathrm{BC}}$

∴ \(BC = 10\sqrt{3}\) মি. = \(10 \times 1.732\) মি. (প্রায়)

= 17.32 মি. (প্রায়)

∴ খালটি 17.32 মি. (প্রায়) চওড়া।

প্রয়োগ 7. কিন্তু কোনো নদীর পাড়ে যদি উঁচু অট্টালিকা থাকে তবে নদীর অপর পারে দাঁড়িয়ে ওই অট্টালিকার উচ্চতা কীভাবে মাপব দেখি।

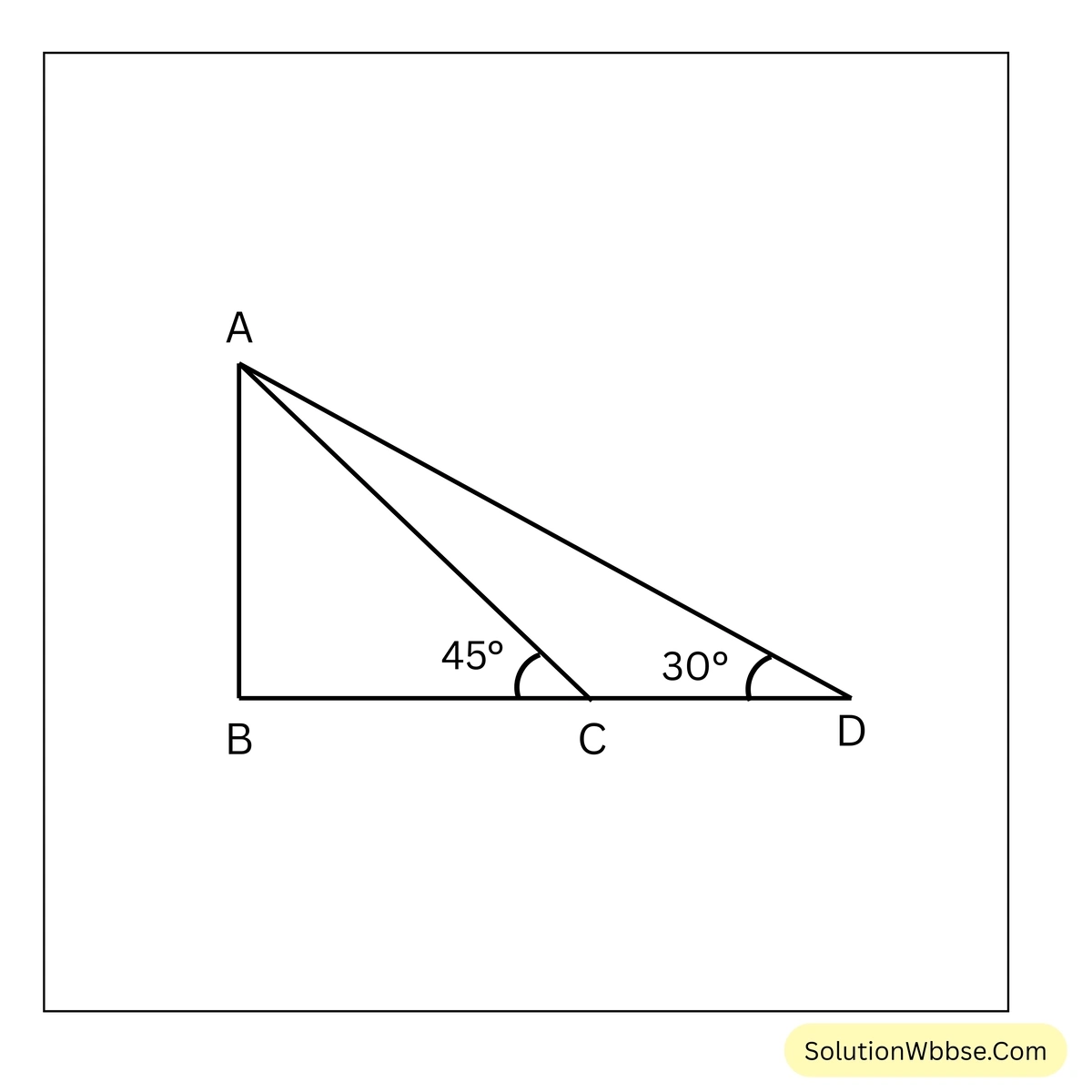
সমাধান –

ধরি, \(AB\) অট্টালিকার উচ্চতা = \( x\) মিটার

যদি নদীর অপর পারে অট্টালিকার B বিন্দুর ঠিক বিপরীত দিকে নদীর ধার বরাবর C বিন্দু থেকে অট্টালিকার চূড়ার উন্নতি কোণ \(45^\circ\) এবং C বিন্দু থেকে 14 মিটার বর্ধিত \(BC\) সরলরেখাংশ বরাবর দূরে সরে গিয়ে D বিন্দু থেকে অট্টালিকার চূড়ার উন্নতি কোণ \(30^\circ\) হয়, তবে অট্টালিকার উচ্চতা \(x\) নির্ণয় করি।

ধরি, নদীর প্রস্থ \((BC) = y\) মিটার

∴ সমকোণী ত্রিভুজ \(ABC\) থেকে পাই, \(\tan 45^\circ = \frac{AB}{BC}\)

বা, \(1 = \frac{x}{y}\)

∴ \(x = y\)

আবার সমকোণী ত্রিভুজ \(ABD\) থেকে পাই, \(\tan 30^\circ = \frac{AB}{BD} = \frac{AB}{BC+CD}\)

∴ \(\frac{1}{\sqrt{3}} = \frac{x}{y+14}\)

বা, \(y+14 = x\sqrt{3}\)

বা, \(x+14 = x\sqrt{3} \quad [\because x=y]\)

বা, \(x(\sqrt{3} – 1) = 14\)

∴ \(x = \frac{14}{\sqrt{3}-1} = \frac{14(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}\)

= \( \frac{14(1.732+1)}{3-1}\)

= \( 7 \times 2.732\) (প্রায়) = \( 19.124\) (প্রায়)

প্রয়োগ 8. যদি একটি 18 মিটার উঁচু পাঁচতলা বাড়ির ছাদ থেকে দেখলে একটি মনুমেন্টের চূড়ার উন্নতি কোণ \(45^\circ\) এবং মনুমেন্টের পাদদেশের অবনতি কোণ \(60^\circ\) হয়, তাহলে মনুমেন্টের উচ্চতা হিসাব করে লিখি। [ \(\sqrt{3} = 1.732\) (প্রায়)]

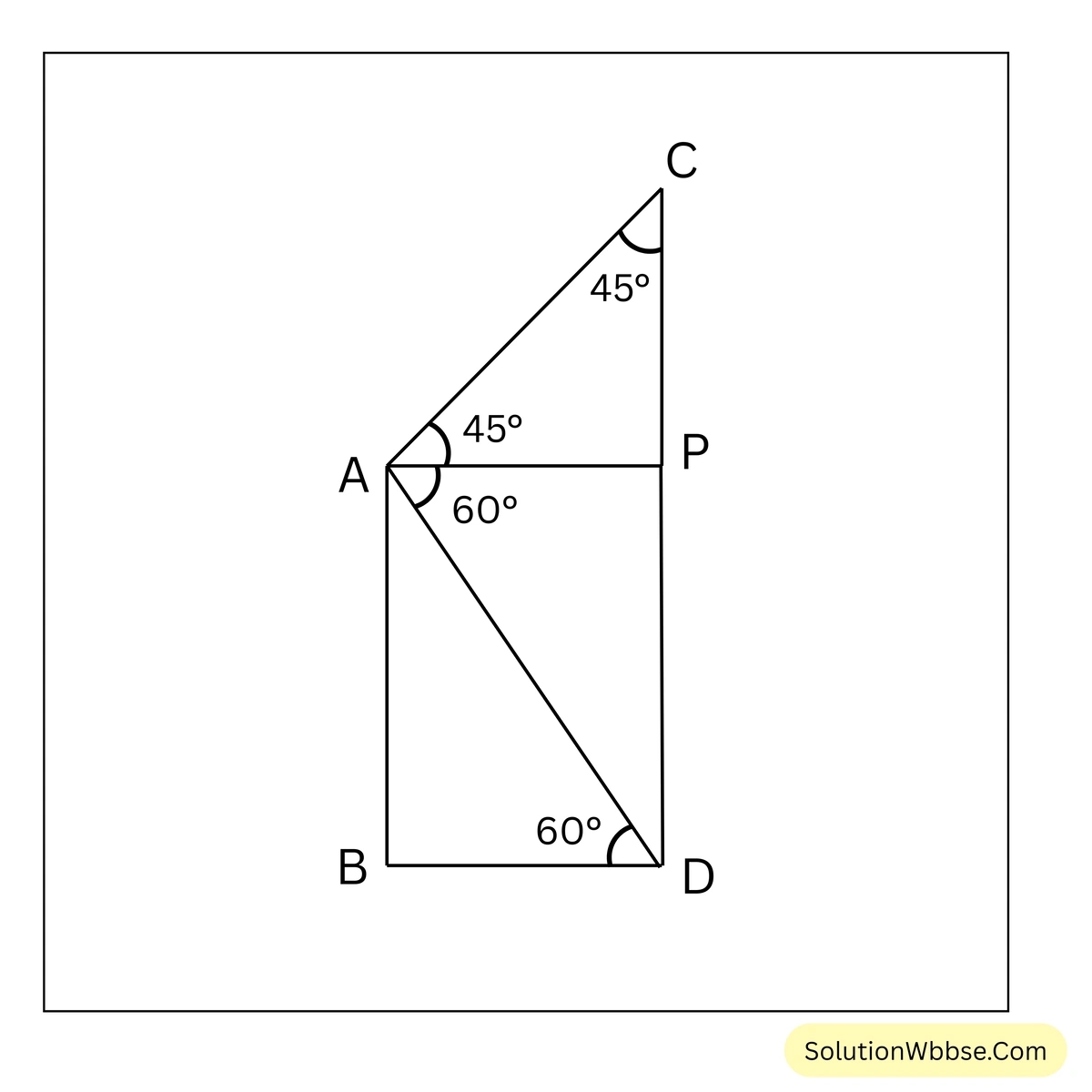
সমাধান –

ধরি, পাশের চিত্রে, \(AB\) 18 মিটার উঁচু পাঁচতলা বাড়ি এবং \(CD\) মনুমেন্টের উচ্চতা। \(AB\)-এর A বিন্দু থেকে মনুমেন্টের চূড়ার C বিন্দুর উন্নতি কোণ \(45^\circ\) ও মনুমেন্টের পাদদেশ D বিন্দুর অবনতি কোণ \(60^\circ\)।

∴ \(\angle PAC = 45^\circ\) এবং \(\angle PAD = 60^\circ\) [ধরি, \(AP \parallel BD\)]
\(\angle PAD\) = একান্তর \(\angle ADB\) [∵ \(AP \parallel BD\)] ∴ \(\angle ADB = 60^\circ\)

ধরি, মনুমেন্টের উচ্চতা \(CD=x\) মিটার এবং \(BD=y\) মিটার = \(AP\)

\(AB = 18\) মিটার। সুতরাং, \(CP = (x-18)\) মি.

সমকোণী \(\triangle ABD\) থেকে পাই, \(\tan 60^\circ = \frac{AB}{BD}\)

বা, \(\sqrt{3} = \frac{18}{y}\) ∴ \(y = \frac{18}{\sqrt{3}} = 6\sqrt{3}\)

সমকোণী \(\triangle APC\) থেকে পাই, \(\tan \angle PAC = \frac{CP}{AP}\)

বা, \(\tan 45^\circ = \frac{x-18}{y} = \frac{x-18}{6\sqrt{3}}\)

বা, \(1 = \frac{x-18}{6\sqrt{3}}\)

বা, \(x-18 = 6\sqrt{3}\)

বা, \(x = 18 + 6\sqrt{3} = 6(3+\sqrt{3})\)

বা, \(x = 6(3+1.732)\) (প্রায়)

বা, \(x = 6 \times 4.732\) (প্রায়)

∴ \(x = 28.392\) (প্রায়)

∴ মনুমেন্টের উচ্চতা \(28.392\) মি. (প্রায়)

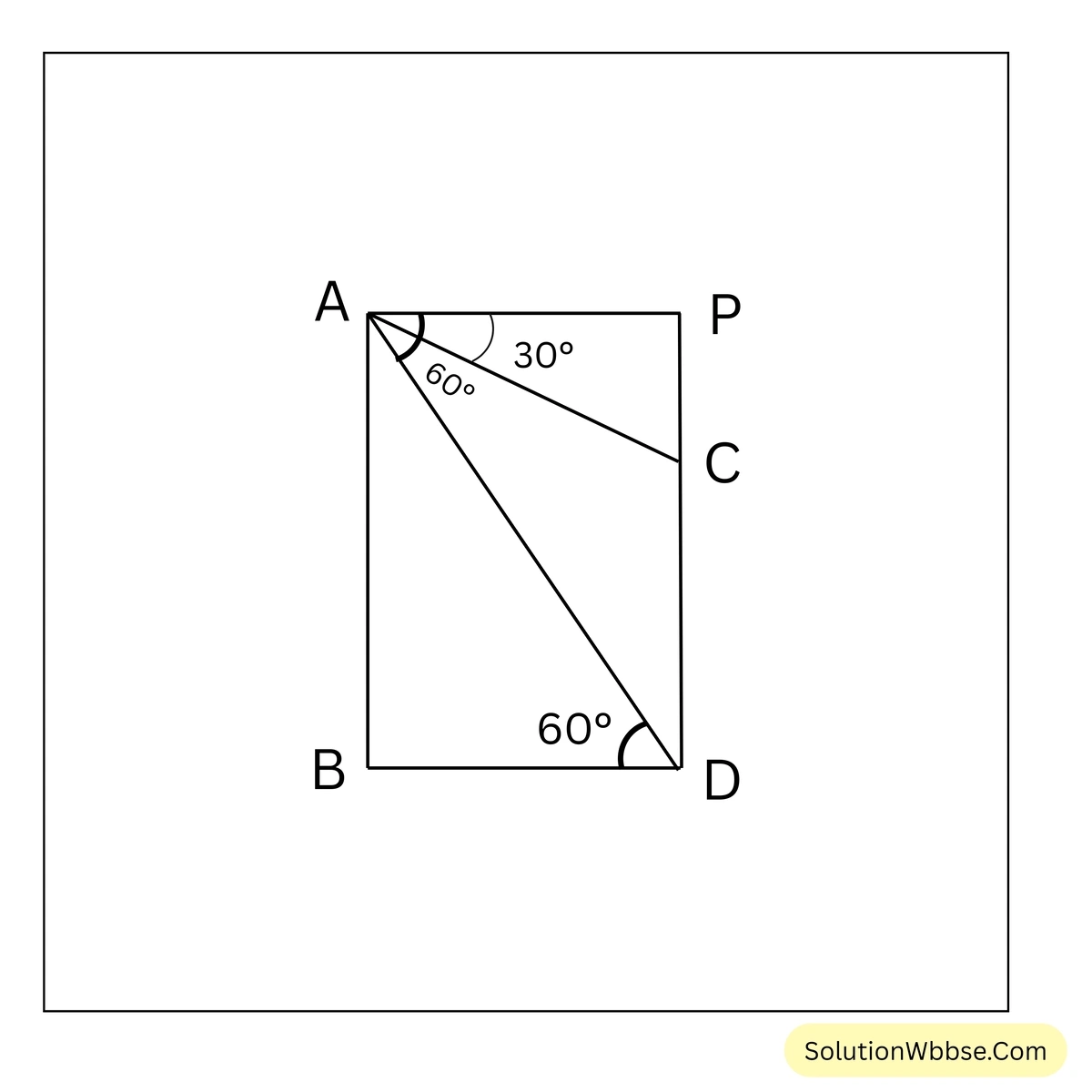
প্রয়োগ 9. 11 মিটার উঁচু একটি বাড়ির ছাদ থেকে দেখলে একটি ল্যাম্পপোস্টের চূড়া ও পাদবিন্দুর অবনতি কোণ যথাক্রমে \(30^\circ\) এবং \(60^\circ\); ল্যাম্পপোস্টটির উচ্চতা হিসাব করে লিখি।

সমাধান –

ধরি, পাশের চিত্রে, \(AB = 11\) মিটার উঁচু একটি বাড়ি

\(CD =\) ল্যাম্পপোস্টের উচ্চতা \(= x\) মিটার (ধরি)

\(AB\)-এর A বিন্দু থেকে ল্যাম্পপোস্টের চূড়া C বিন্দুর অবনতি কোণ \(30^\circ\) এবং A বিন্দু থেকে ল্যাম্পপোস্টের পাদদেশ D বিন্দুর অবনতি কোণ \(60^\circ\)

∴ \(\angle PAC=30^\circ\) এবং \(\angle PAD=60^\circ\) [ধরি, \(AP \parallel BD\) এবং \(DC\)-এর বর্ধিতাংশ \(CP\)]

\(AB=PD=11\) মি., \(CD=x\) মি. ∴ \(PC=(11-x)\) মি.

ধরি, \(BD=y\) মি. = \(AP\)

সমকোণী ত্রিভুজ \(APD\) থেকে পাই, \(\tan 60^\circ = \frac{PD}{AP} = \frac{11}{y}\)

বা, \(\sqrt{3} = \frac{11}{y}\) ∴ \(y = \frac{11}{\sqrt{3}}\) ————— (i)

আবার, সমকোণী ত্রিভুজ \(APC\) থেকে পাই, \(\tan 30^\circ = \frac{PC}{AP}\)

বা, \(\frac{1}{\sqrt{3}} = \frac{11-x}{y}\)

বা, \(y = 11\sqrt{3} – x\sqrt{3}\)

বা, \(\frac{11}{\sqrt{3}} = 11\sqrt{3} – x\sqrt{3}\) [(1) থেকে পাই]

বা, \(11 = 33 – 3x\)

বা, \(3x = 22\) ∴ \(x = \frac{22}{3} = 7\frac{1}{3}\)

∴ ল্যাম্পপোস্টটির উচ্চতা \(7\frac{1}{3}\) মিটার।

প্রয়োগ 10. 60 মিটার উঁচু একটি অট্টালিকার চূড়া থেকে কোনো টাওয়ারের চূড়া ও পাদদেশের অবনতি কোণ যথাক্রমে \(30^\circ\) ও \(60^\circ\) হলে, টাওয়ারের উচ্চতা হিসেব করে লিখি।

সমাধান –

ধরি, \(AB\) হল অট্টালিকা, \(BD\) হল অট্টালিকা ও টাওয়ারের দূরত্ব, \(\angle MAC\) হল অট্টালিকার চূড়ার অবনতি কোণ = \(30^\circ\) এবং \(\angle MAD\) হল অট্টালিকার পাদদেশের অবনতি কোণ = \(60^\circ\)

আবার \(\angle MAC\) = একান্তর \(\angle ACE\) এবং \(\angle MAD\) = একান্তর \(\angle ADB\)

এখন \(\triangle ABD\) থেকে পাই, \(\tan 60^\circ = \frac{AB}{BD}\) বা, \(\sqrt{3} = \frac{60}{BD}\)

∴ \(BD = \frac{60}{\sqrt{3}} = \frac{60\sqrt{3}}{3} = 20\sqrt{3} = CE\)

আবার, \(\triangle ACE\) থেকে পাই, \(\tan 30^\circ = \frac{AE}{CE}\), বা, \(\frac{1}{\sqrt{3}} = \frac{AE}{20\sqrt{3}}\)

∴ \(AE = 20\) মিটার।

∴ \(CD = BE = AB – AE = (60 – 20)\) মিটার = \(40\) মিটার। ∴ অট্টালিকার উচ্চতা = \(40\) মিটার।

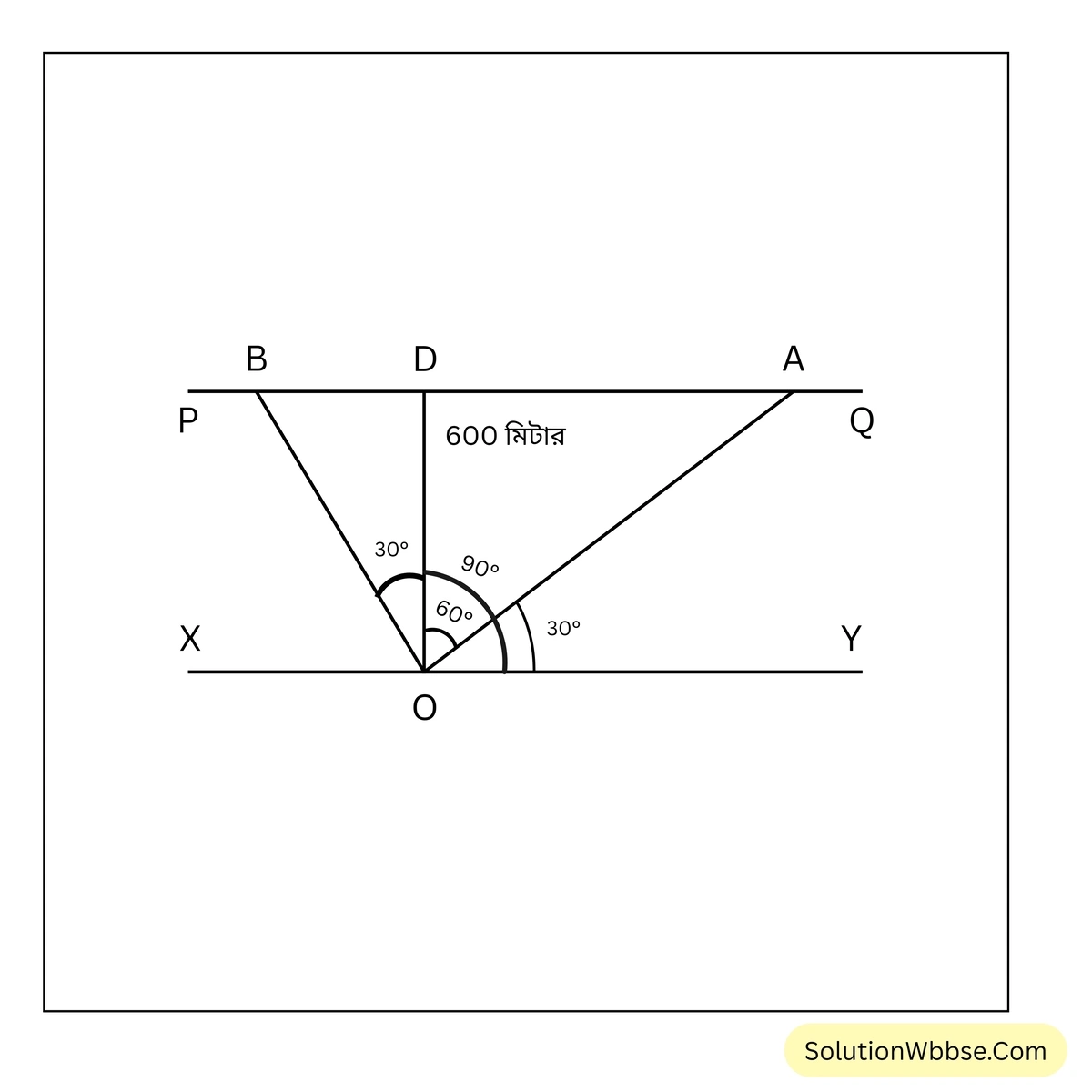
প্রয়োগ 11. 600 মিটার চওড়া কোনো নদীর একটি ঘাট থেকে দুটি নৌকা দুটি আলাদা অভিমুখে নদীর ওপারে যাওয়ার জন্য রওনা দিল। যদি প্রথম নৌকাটি নদীর এপারের সঙ্গে \(30^\circ\) কোণে এবং দ্বিতীয় নৌকাটি প্রথম নৌকার গতিপথের সঙ্গে \(90^\circ\) কোণ করে চলে ওপারে পৌঁছায়, তাহলে ওপারে পৌঁছানোর পরে নৌকাদুটির মধ্যে দূরত্ব কত হবে নির্ণয় করি। [\(\sqrt{3} = 1.732\) (প্রায়)]

সমাধান –

ধরি, পাশের ছবিতে নদীর XY পাড়ের O বিন্দুতে অবস্থিত ঘাট থেকে প্রথম নৌকা OA বরাবর গিয়ে নদীর অপর পাড় PQ-এর A বিন্দুতে এবং অপর নৌকা OB বরাবর গিয়ে B বিন্দুতে ওপারে পৌঁছায়।

∴ \(\angle YOA=30^\circ\), \(\angle AOB=90^\circ\) ; O বিন্দু থেকে AB-এর উপর OD লম্ব অঙ্কন করি।

∴ \(\angle AOD=60^\circ\) এবং \(\angle DOB=30^\circ\)

সমকোণী ত্রিভুজ AOD থেকে পাই, \(\tan 60^\circ = \frac{AD}{OD}\)

বা, \(\sqrt{3} = \frac{AD}{600}\) মি.

∴ \(AD = 600\sqrt{3}\) মি.

আবার, সমকোণী ত্রিভুজ BOD থেকে পাই, \(\tan 30^\circ = \frac{BD}{OD}\)

বা, \(\frac{1}{\sqrt{3}} = \frac{BD}{600}\) মি.

বা, \(BD = \frac{600}{\sqrt{3}}\) মি. \(= \frac{600\sqrt{3}}{3}\) মি. \(= 200\sqrt{3}\) মি.

\(AD+BD = (600\sqrt{3} + 200\sqrt{3})\) মি.

\(AB = 800\sqrt{3}\) মি. \(= 800 \times 1.732\) মি. (প্রায়) \(= 1385.6\) মি. (প্রায়)

∴ ওপারে পৌঁছালে নৌকা দুটির মধ্যে দূরত্ব হবে 1385.6 মিটার (প্রায়)

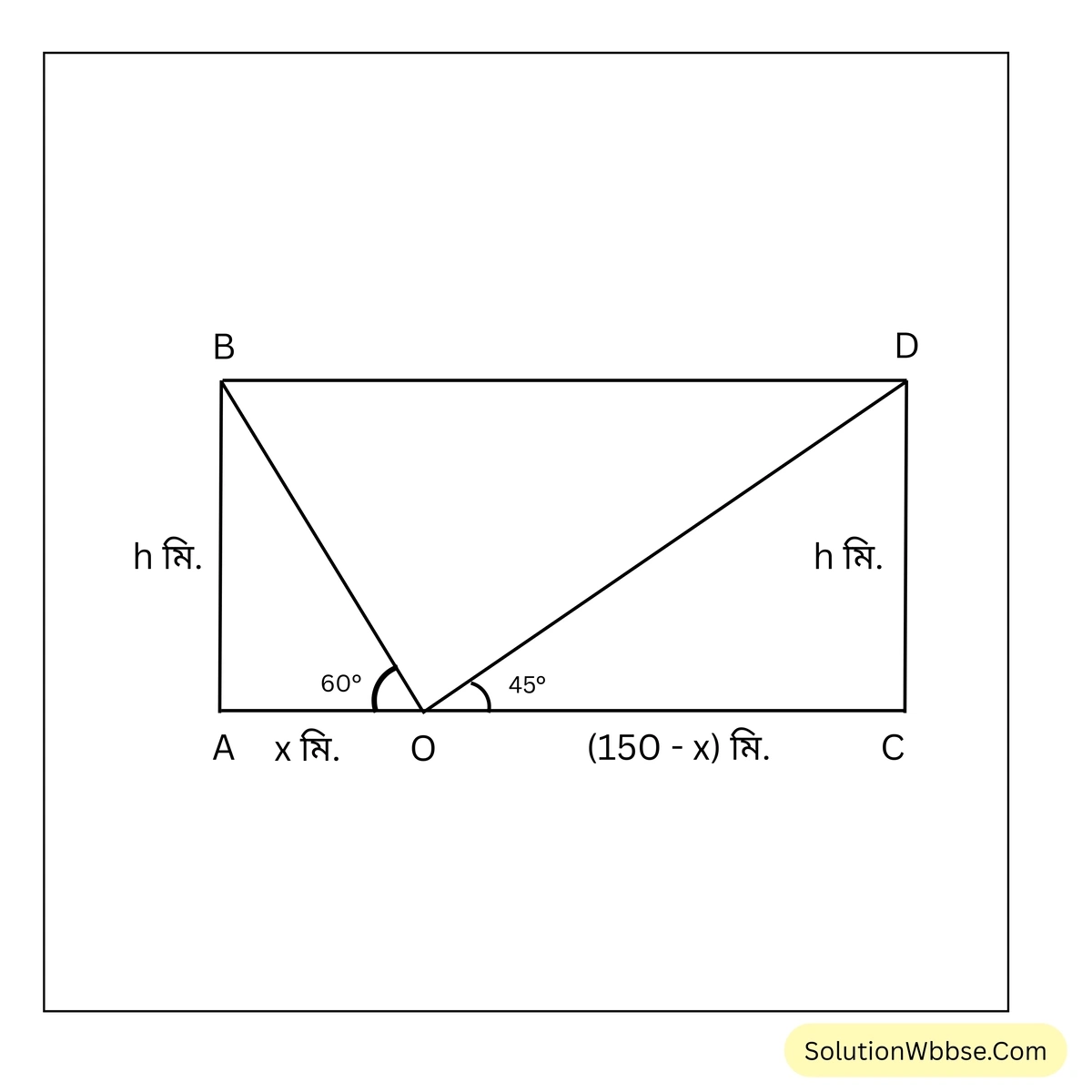
প্রয়োগ 12. একটি 150 মিটার চওড়া রাস্তার দু – পাশে ঠিক বিপরীতে দুটি সমান উচ্চতার স্তম্ভ আছে। স্তম্ভ দুটির মাঝখানে রাস্তার উপর কোনো এক নির্দিষ্ট বিন্দু থেকে স্তম্ভ দুটির চূড়ার উন্নতি কোণ যথাক্রমে \(60^\circ\) ও \(30^\circ\) হলে, প্রতিটি স্তম্ভের উচ্চতা নির্ণয় করি।

সমাধান –

ধরি, AB ও CD দুটি সমান উচ্চতার স্তম্ভ।

ধরি, \(AB = CD = h\) মিটার।

ধরি, AC রাস্তার উপর নির্দিষ্ট বিন্দু O

ধরি, \(OA=x\) মি. ∴ \(OC=(150-x)\) মি.

∴ \(\angle AOB=60^\circ\) এবং \(\angle COD=30^\circ\)

সমকোণী ত্রিভুজ AOB থেকে পাই, \(\tan 60^\circ = \frac{AB}{AO} = \frac{h}{x}\)

বা, \(\sqrt{3} = \frac{h}{x}\) ∴ \(x = \frac{h}{\sqrt{3}}\) _ (i)

আবার, সমকোণী ত্রিভুজ COD থেকে পাই,

\(\tan 30^\circ = \frac{CD}{OC} = \frac{h}{150-x}\)

বা, \(\frac{1}{\sqrt{3}} = \frac{h}{150-x}\)

বা, \(150-x = h\sqrt{3}\)

∴ \(x = 150 – h\sqrt{3}\) _ (ii)

∴ (i) ও (ii) নং তুলনা করে পাই, \(\frac{h}{\sqrt{3}} = 150 – h\sqrt{3}\)

বা, \(h = 150\sqrt{3} – 3h\)

বা, \(4h = 150\sqrt{3}\)

∴ \(h = \frac{150\sqrt{3}}{4} = \frac{75\sqrt{3}}{2}\)

∴ প্রতিটি স্তম্ভের উচ্চতা \(\frac{75\sqrt{3}}{2}\) মিটার।

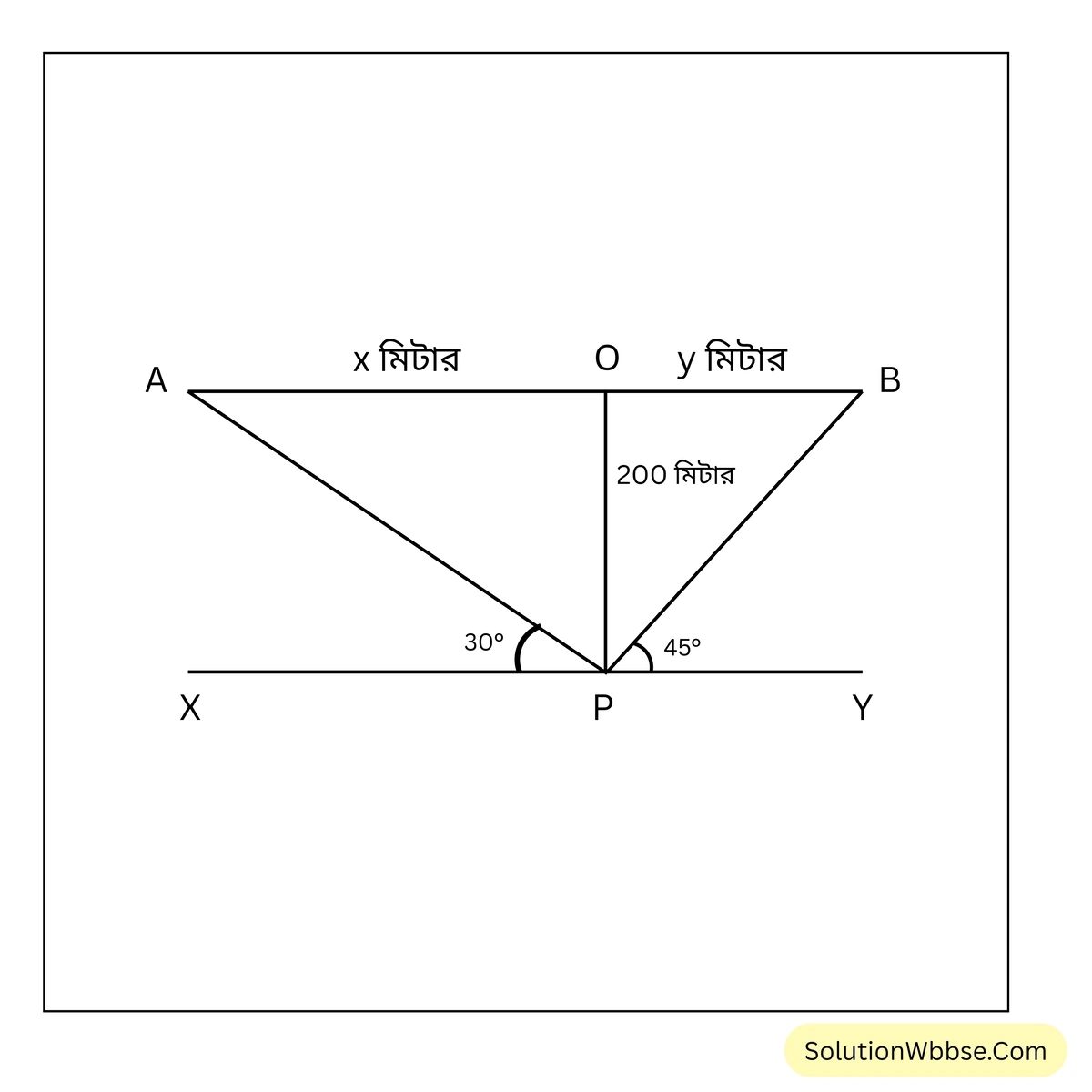
প্রয়োগ 13. একটি পাখি ভূমিরতলের সঙ্গে সমান্তরাল রেখায় 200 মিটার উঁচু দিয়ে উত্তর থেকে দক্ষিণদিকে যাচ্ছিল। মাঠের মাঝখানে দাঁড়িয়ে সুশোভন প্রথমে পাখিটিকে উত্তরদিকে \(30^\circ\) কোণে দেখতে পেল। 3 মিনিট পরে আবার দক্ষিণদিকে \(45^\circ\) কোণে দেখতে পেল। আসন্ন পূর্ণসংখ্যায় কিলোমিটারে পাখিটির গতিবেগ ঘণ্টায় কত ছিল হিসাব করে লিখি। [\(\sqrt{3} = 1.732\) (প্রায়)]

সমাধান –

মনে করি, P বিন্দু থেকে সুশোভন প্রথমে পাখিটিকে \(30^\circ\) কোণে A বিন্দুতে দেখতে পেল এবং 3 মিনিট পরে \(45^\circ\) কোণে B বিন্দুতে দেখতে পেল।

ধরি, \(AO=x\) মি. এবং \(BO=y\) মি.

P বিন্দু থেকে AB-এর উপর PO লম্ব।

∴ \(PO = 200\) মি.

∴ \(\angle XPA=30^\circ\),

∴ \(\angle APO=90^\circ-30^\circ=60^\circ\) ;

∴ \(\angle BPY=45^\circ\),

∴ \(\angle BPO=90^\circ-45^\circ=45^\circ\)

সমকোণী ত্রিভুজ APO-তে,

\(\tan \angle APO = \tan 60^\circ = \frac{x}{200}\)

বা, \(\sqrt{3} = \frac{x}{200}\) ∴ \(x = 200\sqrt{3}\)

সমকোণী ত্রিভুজ BPO-তে,

\(\tan \angle BPO = \tan 45^\circ = \frac{y}{200}\)

বা, \(1 = \frac{y}{200}\) ∴ \(y = 200\)

সুতরাং, \(x+y = 200\sqrt{3} + 200 \)

= \(200(\sqrt{3} +1) \)

= \(200 \times 2.732 \)

= \(546.4\)

3 মিনিটে পাখিটি যায় 546.4 মিটার

1 মিনিটে পাখিটি যায় \(\frac{546.4}{3}\) মি.

60 মিনিটে পাখিটি যায় \(\frac{546.4}{3} \times 60\) মিটার = 10928 মিটার = 10.928 কিমি.

∴ আসন্ন পূর্ণসংখ্যায় পাখিটির গতিবেগ ঘণ্টায় 11 কিলোমিটার।

---

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের পঞ্চবিংশ অধ্যায়, ‘ত্রিকোণমিতিক অনুপাতের প্রয়োগ: উচ্চতা ও দূরত্ব’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।

আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।