উপাক্ষীয় রশ্মির ক্ষেত্রে, প্রমাণ করো অবতল দর্পণের বক্রতা ব্যাসার্ধ ফোকাস দূরত্বের দ্বিগুণ

এই আর্টিকেলে আমরা মাধ্যমিক ভৌতবিজ্ঞানের একটি গুরুত্বপূর্ণ প্রশ্ন “উপাক্ষীয় রশ্মির ক্ষেত্রে, প্রমাণ করো অবতল দর্পণের বক্রতা ব্যাসার্ধ ফোকাস দূরত্বের দ্বিগুণ। অথবা, একটি অবতল দর্পণের বক্রতা ব্যাসার্ধ ও ফোকাস দৈর্ঘ্যের মধ্যে সম্পর্ক প্রতিষ্ঠা করো।” নিয়ে আলোচনা করব। এই প্রশ্নটি মাধ্যমিক ভৌতবিজ্ঞান পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ। এই “উপাক্ষীয় রশ্মির ক্ষেত্রে, প্রমাণ করো অবতল দর্পণের বক্রতা ব্যাসার্ধ ফোকাস দূরত্বের দ্বিগুণ। অথবা, একটি অবতল দর্পণের বক্রতা ব্যাসার্ধ ও ফোকাস দৈর্ঘ্যের মধ্যে সম্পর্ক প্রতিষ্ঠা করো।” প্রশ্নটি মাধ্যমিক ভৌতবিজ্ঞানের পঞ্চম অধ্যায় “আলো“ -এর একটি গুরুত্বপূর্ণ প্রশ্ন। এই প্রশ্নটি মাধ্যমিক পরীক্ষায় এবং চাকরির পরীক্ষায় প্রায়ই দেখা যায়।

উপাক্ষীয় রশ্মির ক্ষেত্রে, প্রমাণ করো অবতল দর্পণের বক্রতা ব্যাসার্ধ ফোকাস দূরত্বের দ্বিগুণ।

অথবা, একটি অবতল দর্পণের বক্রতা ব্যাসার্ধ ও ফোকাস দৈর্ঘ্যের মধ্যে সম্পর্ক প্রতিষ্ঠা করো।

একটি অবতল দর্পণের ওপর ওর প্রধান অক্ষের সমান্তরাল একটি উপাক্ষীয় রশ্মি \(AB\) দর্পণের উপর আপতিত হয়ে প্রতিফলনের পর মুখ্য ফোকাস \(F\) -এর মধ্য দিয়ে যাবে। দর্পণের বক্রতা কেন্দ্র \(C\) -এর সঙ্গে \(B\) -কে যুক্ত করা হলে \(BC\) হবে \(B\) বিন্দুতে দর্পণের ওপর লম্ব। এখানে, চিত্রানুযায়ী আপতন কোণ \(\angle ABC=i\) এবং প্রতিফলন কোণ \(\angle CBF=i\)।

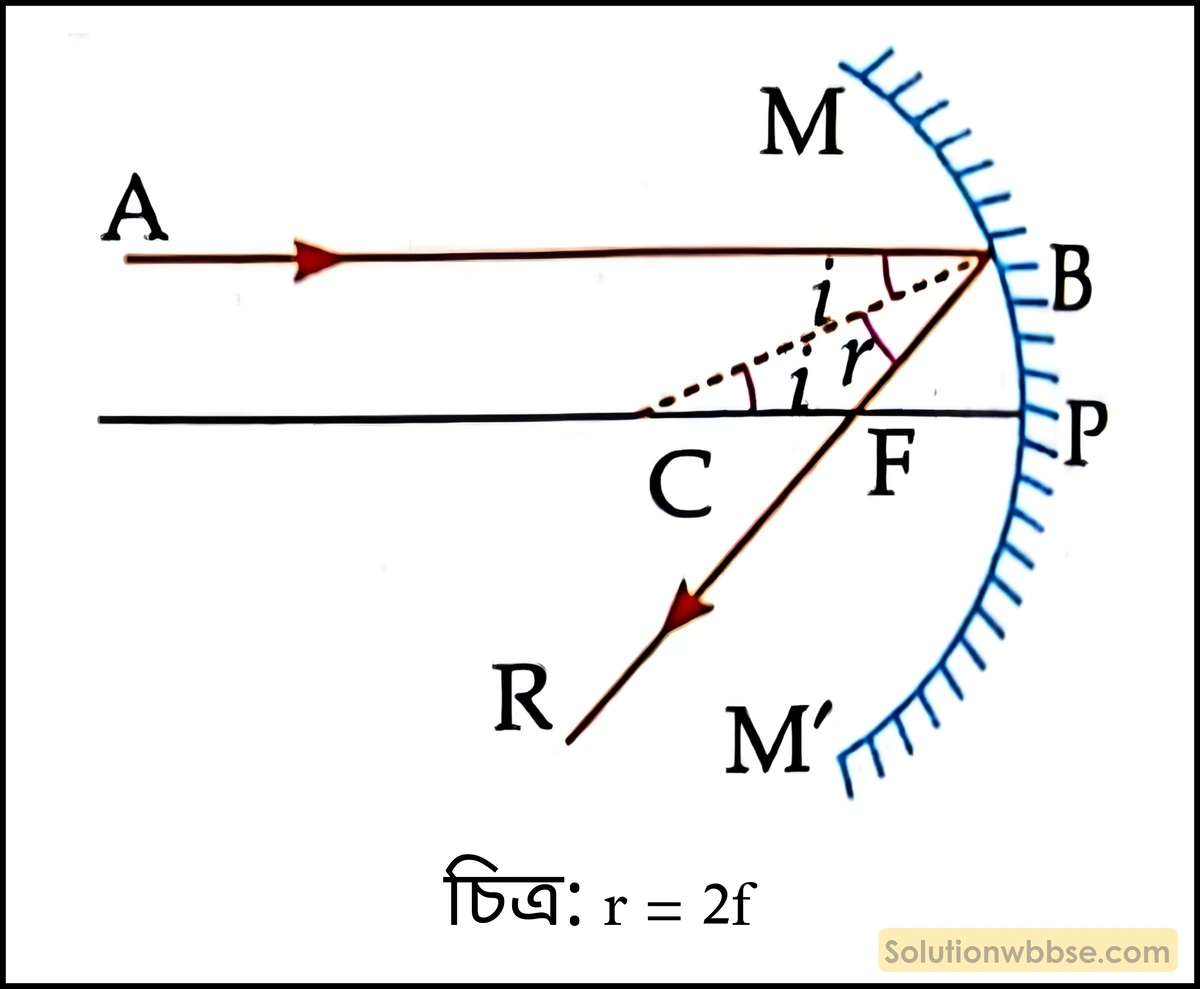
∴ \(\angle CBF=\angle ABC\) (প্রতিফলনের সূত্রানুযায়ী) এবং \(\angle ABC=\angle BCF\) (একান্তর কোণ)

∴ \(\angle CBF=\angle BCF\) অর্থাৎ \(\bigtriangleup FBC\) একটি সমদ্বিবাহু ত্রিভুজ যার \(BF=CF\)। কম উন্মেষের দর্পণে উপাক্ষীয় রশ্মির ক্ষেত্রে \(B\) ও \(P\) খুবই নিকটবর্তী হওয়ায় \(PF=BF\)।

∴ \(PF=BF=CF\) অর্থাৎ \(CF=\frac12CP\)

∴ ফোকাস দৈর্ঘ্য \(PF\left(f\right)=\frac12\) \(\times\) বক্রতা ব্যাসার্ধ \(\left(r\right)\)

∴ উপাক্ষীয় রশ্মির ক্ষেত্রে \(r=2f\)।

এই আর্টিকেলে আমরা মাধ্যমিক ভৌতবিজ্ঞানের একটি গুরুত্বপূর্ণ প্রশ্ন “উপাক্ষীয় রশ্মির ক্ষেত্রে, প্রমাণ করো অবতল দর্পণের বক্রতা ব্যাসার্ধ ফোকাস দূরত্বের দ্বিগুণ। অথবা, একটি অবতল দর্পণের বক্রতা ব্যাসার্ধ ও ফোকাস দৈর্ঘ্যের মধ্যে সম্পর্ক প্রতিষ্ঠা করো।” নিয়ে আলোচনা করব। এই প্রশ্নটি মাধ্যমিক ভৌতবিজ্ঞান পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ। এই “উপাক্ষীয় রশ্মির ক্ষেত্রে, প্রমাণ করো অবতল দর্পণের বক্রতা ব্যাসার্ধ ফোকাস দূরত্বের দ্বিগুণ। অথবা, একটি অবতল দর্পণের বক্রতা ব্যাসার্ধ ও ফোকাস দৈর্ঘ্যের মধ্যে সম্পর্ক প্রতিষ্ঠা করো।” প্রশ্নটি মাধ্যমিক ভৌতবিজ্ঞানের পঞ্চম অধ্যায় “আলো“ -এর একটি গুরুত্বপূর্ণ প্রশ্ন। এই প্রশ্নটি মাধ্যমিক পরীক্ষায় এবং চাকরির পরীক্ষায় প্রায়ই দেখা যায়। আশা করি এই আর্টিকেলটি আপনাদের জন্য উপকারী হয়েছে। আপনাদের কোনো প্রশ্ন বা অসুবিধা থাকলে, আমাদের সাথে টেলিগ্রামে যোগাযোগ করুন।