এই আর্টিকেলে আমরা মাধ্যমিক ভৌতবিজ্ঞানের একটি গুরুত্বপূর্ণ প্রশ্ন “একটি প্রিজমের \(i-\delta\) লেখচিত্র আঁকো, যেখানে \(i\) হল আপতন কোণ ও \(\delta\) হল চ্যুতিকোণ। লেখচিত্রে ন্যূনতম চ্যুতিকোণ \(\left(\delta_m\right)\) দেখাও। অথবা, আপতন কোণের সঙ্গে প্রিজমের ন্যূনতম চ্যুতির লেখচিত্র অঙ্কন করো।” নিয়ে আলোচনা করব। এই প্রশ্নটি মাধ্যমিক ভৌতবিজ্ঞান পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ। এই “একটি প্রিজমের \(i-\delta\) লেখচিত্র আঁকো, যেখানে \(i\) হল আপতন কোণ ও \(\delta\) হল চ্যুতিকোণ। লেখচিত্রে ন্যূনতম চ্যুতিকোণ \(\left(\delta_m\right)\) দেখাও। অথবা, আপতন কোণের সঙ্গে প্রিজমের ন্যূনতম চ্যুতির লেখচিত্র অঙ্কন করো।” প্রশ্নটি মাধ্যমিক ভৌতবিজ্ঞানের পঞ্চম অধ্যায় “আলো“ -এর একটি গুরুত্বপূর্ণ প্রশ্ন। এই প্রশ্নটি মাধ্যমিক পরীক্ষায় এবং চাকরির পরীক্ষায় প্রায়ই দেখা যায়।

একটি প্রিজমের \(i-\delta\) লেখচিত্র আঁকো, যেখানে \(i\) হল আপতন কোণ ও \(\delta\) হল চ্যুতিকোণ। লেখচিত্রে ন্যূনতম চ্যুতিকোণ \(\left(\delta_m\right)\) দেখাও।
অথবা, আপতন কোণের সঙ্গে প্রিজমের ন্যূনতম চ্যুতির লেখচিত্র অঙ্কন করো।
\(\delta=i_1+i_2-A\)সমীকরণে \(A\) নির্দিষ্ট হলে \(\delta\) -এর মান আপতন কোণ \(i_1\) -এর পরিবর্তনে পরিবর্তিত হয়। আপতন কোণ \(i_1\) -এর মান কমালে বা বাড়ালে \(\delta\) -এর মানের পরিবর্তন ঘটে। বর্ণালিবীক্ষণ যন্ত্রের সাহায্যে পরীক্ষা করে দেখা যায় একটি নির্দিষ্ট আপতন কোণের জন্য চ্যুতিকোণ সর্বনিম্ন \(\left(\delta_m\right)\) হয়। প্রতিটি প্রিজমের জন্য এই আপতন কোণের মান প্রিজমের প্রতিসারক কোণের ওপর নির্ভর করে। এই মানের চেয়ে কম বা বেশি হলে বিচ্যুতির মান বৃদ্ধি পায়। নির্দিষ্ট প্রতিসারক কোণ যুক্ত প্রিজমের বিভিন্ন আপতন কোণে আলোকরশ্মি প্রতিসারক তলে ফেলে প্রতিটির ক্ষেত্রে চ্যুতি পরিমাপ করা হয়। লেখচিত্রে \(X\)-অক্ষ বরাবর আপতন কোণ \(\left(i\right)\) এবং \(Y\)-অক্ষ বরাবর বিচ্যুতি \(\left(\delta\right)\) বসিয়ে একটি লেখ আঁকা হলে লেখটিকে \(\left(i-\delta\right)\) লেখ বলে।
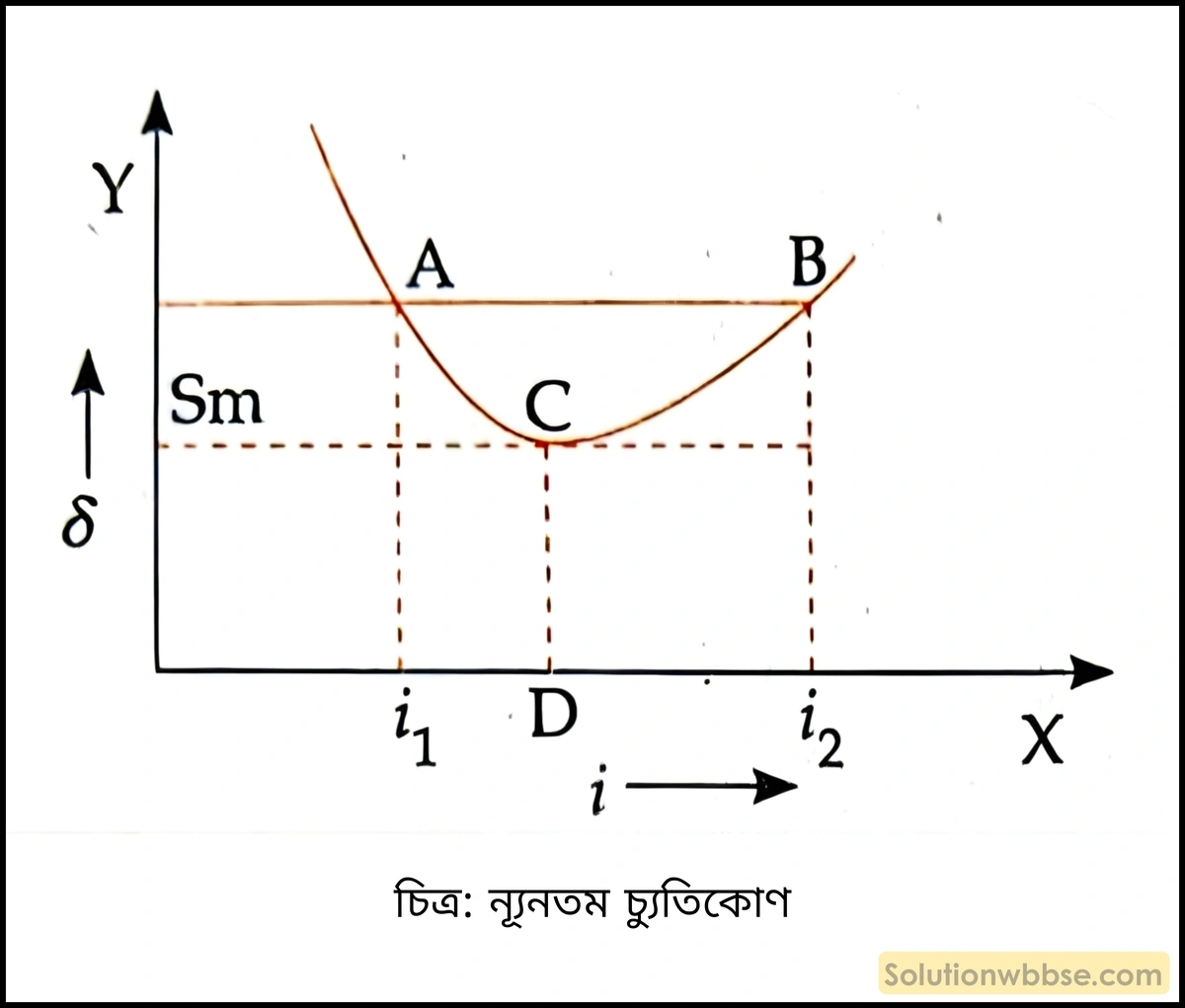
লেখচিত্র থেকে দেখা যায় যে, একটি নির্দিষ্ট আপতন কোণে \(\left(OD\right)\) আলোকরশ্মি প্রিজমের উপর আপতিত হলে বিচ্যুতি \(CD\) ন্যূনতম \(\left(\delta_m\right)\) হয়। লেখচিত্র \(X\)-অক্ষের সমান্তরালে একটি রেখা \(AB\) টানা হল। এই রেখা \(A\) এবং \(B\) বিন্দুতে লেখটিকে ছেদ করে।
\(A\) এবং \(B\) বিন্দুতে আপতন কোণ যথাক্রমে \(i_1\) এবং \(i_2\)। আলোকরশ্মির পথ প্রত্যাবর্তনশীল। তাই \(QO’\) পথে কোনো রশ্মি প্রিজমে \(i_2\) আপতন কোণে \(O’\) বিন্দুতে আপতিত হলে সেই রশ্মি \(AB\) তলের \(O\) বিন্দুতে \(i_1\) কোণে নির্গত হয়। চিত্রানুসারে এক্ষেত্রেও চ্যুতিকোণ \(\delta=i_1+i_2-A\)। সুতরাং, আপতন কোণ \(i_1\) অথবা \(i_2\) হলে চ্যুতিকোণের মান একই হবে।
লেখচিত্র থেকে দেখা যায়, \(A,\;B\) বিন্দু দুটির পার্থক্য যত কম হবে \(\)-এর মান তত কমবে। এইভাবে \(\delta=\delta_m\) হলে \(A\) এবং \(B\) বিন্দু দুটি \(C\) বিন্দুতে মিলিত হয়। এই ক্ষেত্রে অর্থাৎ \(\delta=\delta_m\) হলে, \(i_1=i_2\) হয়। এর থেকে বোঝা যায় প্রিজমে রশ্মির আপতন কোণ \(i_1=\) প্রিজম থেকে নির্গত রশ্মির নির্গমন কোণ \(i_2\) হলেই চ্যুতিকোণ \(\delta\) সর্বনিম্ন \(\left(\delta_m\right)\) হয়।
কিছু গুরুত্বপূর্ণ প্রশ্নোত্তর
i−δ লেখচিত্র কী?
i−δ লেখচিত্র হল একটি গ্রাফ যেখানে X-অক্ষ বরাবর আপতন কোণ (i) এবং Y-অক্ষ বরাবর চ্যুতিকোণ (δ) নেওয়া হয়। বিভিন্ন আপতন কোণের জন্য প্রিজম দ্বারা সৃষ্ট চ্যুতিকোণের মান পরিমাপ করে এই লেখচিত্র আঁকা হয়।
ন্যূনতম চ্যুতিকোণের শর্তটি কী?
ন্যূনতম চ্যুতিকোণের শর্ত হল, প্রিজমে রশ্মির আপতন কোণ (i₁) এবং প্রিজম থেকে নির্গমন কোণ (i₂) পরস্পর সমান হতে হবে। অর্থাৎ, i₁ = i₂ হলেই এবং কেবলমাত্র তখনই চ্যুতিকোণ সর্বনিম্ন (δm) হবে।
লেখচিত্রে ন্যূনতম চ্যুতিকোণ (δm) কীভাবে চিনতে পারি?
লেখচিত্রটি একটি U-আকৃতির (বা প্যারাবোলিক) বক্ররেখা। এই বক্ররেখার সর্বনিম্ন বিন্দুটিই ন্যূনতম চ্যুতিকোণ (δm) নির্দেশ করে। X-অক্ষের সমান্তরালে একটি রেখা টানলে এটি লেখকে যে বিন্দুতে স্পর্শ করবে, সেই বিন্দুর Y-অক্ষের মানই হল δm।
আপতন কোণ কমাতে থাকলে বা বাড়াতে থাকলে চ্যুতিকোণের মানের কী পরিবর্তন হয়?
লেখচিত্র থেকে স্পষ্ট যে, ন্যূনতম চ্যুতিকোণ (δm) এর অনুরূপ আপতন কোণ (i) থেকে আপতন কোণ কমাতে থাকলে বা বাড়াতে থাকলে উভয়ক্ষেত্রেই চ্যুতিকোণের (δ) মান বেড়ে যায়।
ন্যূনতম চ্যুতিকোণের বিশেষত্ব কী?
ন্যূনতম চ্যুতিকোণের বিশেষত্বগুলি হল –
1. এই অবস্থায় আলোর রশ্মি প্রিজমের ভিতরে প্রিজমের ভূমির সমান্তরাল হয়ে চলে।
3. এই অবস্থায় আপতন কোণ ও নির্গমন কোণ সমান (i₁ = i₂)।
3. এই অবস্থাটি একটি অনন্য অবস্থা এবং এটি ব্যবহার করে প্রিজমের উপাদানের প্রতিসরাঙ্ক সঠিকভাবে নির্ণয় করা সম্ভব।
এই আর্টিকেলে আমরা মাধ্যমিক ভৌতবিজ্ঞানের একটি গুরুত্বপূর্ণ প্রশ্ন “একটি প্রিজমের \(i-\delta\) লেখচিত্র আঁকো, যেখানে \(i\) হল আপতন কোণ ও \(\delta\) হল চ্যুতিকোণ। লেখচিত্রে ন্যূনতম চ্যুতিকোণ \(\left(\delta_m\right)\) দেখাও। অথবা, আপতন কোণের সঙ্গে প্রিজমের ন্যূনতম চ্যুতির লেখচিত্র অঙ্কন করো।” নিয়ে আলোচনা করব। এই প্রশ্নটি মাধ্যমিক ভৌতবিজ্ঞান পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ। এই “একটি প্রিজমের \(i-\delta\) লেখচিত্র আঁকো, যেখানে \(i\) হল আপতন কোণ ও \(\delta\) হল চ্যুতিকোণ। লেখচিত্রে ন্যূনতম চ্যুতিকোণ \(\left(\delta_m\right)\) দেখাও। অথবা, আপতন কোণের সঙ্গে প্রিজমের ন্যূনতম চ্যুতির লেখচিত্র অঙ্কন করো।” প্রশ্নটি মাধ্যমিক ভৌতবিজ্ঞানের পঞ্চম অধ্যায় “আলো“ -এর একটি গুরুত্বপূর্ণ প্রশ্ন। এই প্রশ্নটি মাধ্যমিক পরীক্ষায় এবং চাকরির পরীক্ষায় প্রায়ই দেখা যায়। আশা করি এই আর্টিকেলটি আপনাদের জন্য উপকারী হয়েছে। আপনাদের কোনো প্রশ্ন বা অসুবিধা থাকলে, আমাদের সাথে টেলিগ্রামে যোগাযোগ করতে পারেন, আমরা উত্তর দেওয়ার চেষ্টা করব। তাছাড়া, নিচে আমাদের এই পোস্টটি আপনার প্রিয়জনের সাথে শেয়ার করুন, যাদের এটি প্রয়োজন হতে পারে। ধন্যবাদ।






মন্তব্য করুন