পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) অষ্টম শ্রেণির গণিত পাঠ্যবইয়ের দ্বিতীয় অধ্যায় হলো ‘পাই চিত্র’। এই পোস্টে আমরা ‘কষে দেখি – 2’-এর সমস্ত প্রশ্নের সহজ ও নির্ভুল সমাধান নিয়ে আলোচনা করেছি। আশা করি, এই নোটসগুলো তোমাদের গণিত শিখতে এবং পরীক্ষার প্রস্তুতিতে দারুণভাবে সহায়তা করবে।

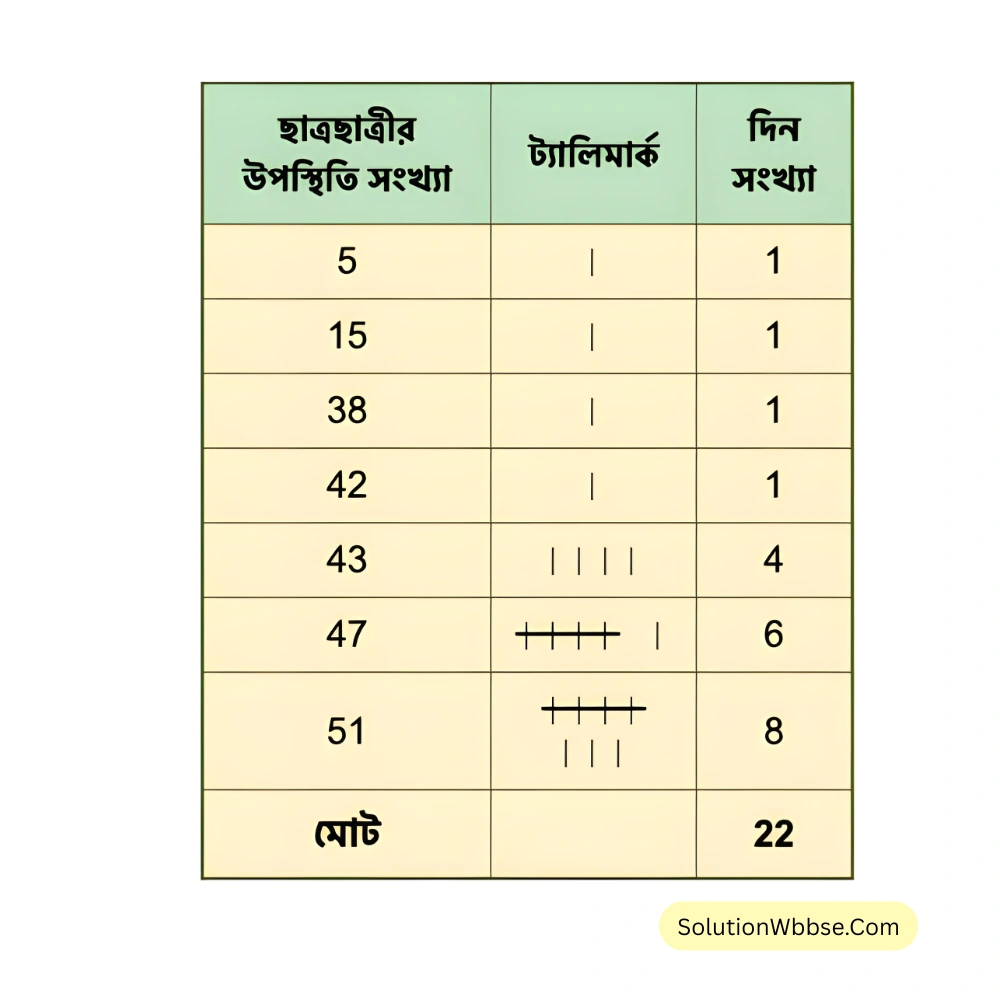
1. গতকাল এপ্রিল মাসে রোহিতদের স্কুলে 23 দিনের পঠন-পাঠন হয়েছিল। রোহিত ওই 23 দিনে তাদের শ্রেণিতে ছাত্রছাত্রীদের উপস্থিতি সংখ্যা লিখে রেখেছে। সেগুলি হল: 15, 43, 51, 47, 43, 5, 51, 47, 38, 51, 47, 51, 47, 51, 47, 51, 51, 43, 47, 43, 51, 42।
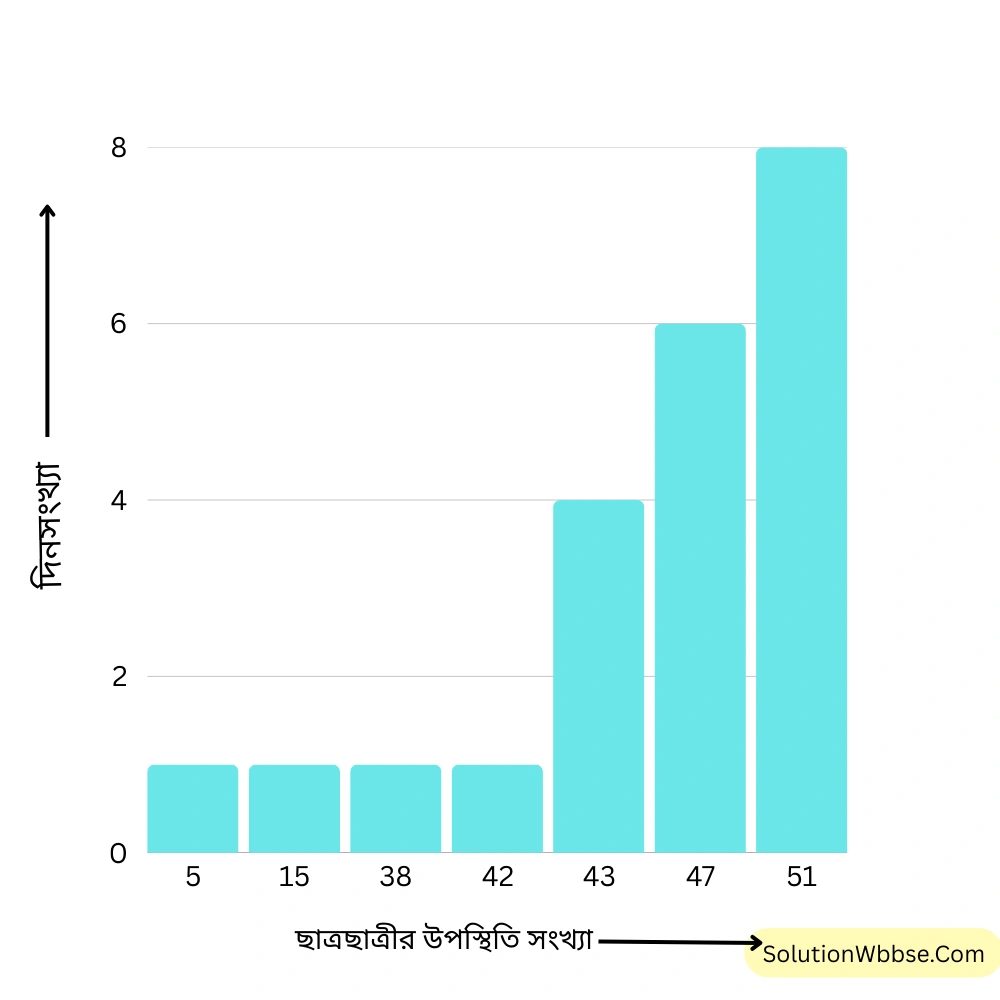
আমি ওই কাঁচা তথ্যটি ট্যালিমার্কে সাজিয়ে পরিসংখ্যা বিভাজন তালিকা তৈরি করি ও সেই তালিকা থেকে স্তম্ভচিত্র তৈরি করি।
সমাধান –
পরিসংখ্যা বিভাজন ছক –
স্তম্ভচিত্র –
2. আমাদের শ্রেণির 40 জন ছাত্রছাত্রীদের মধ্যে প্রতি ছুটির দিনে কতজন বাড়ির কাজে কত ঘন্টা সাহায্য করে তার স্তম্ভচিত্র তৈরি করলাম। এই স্তম্ভচিত্র দেখে ও নানা প্রশ্নের উত্তর খুঁজি।
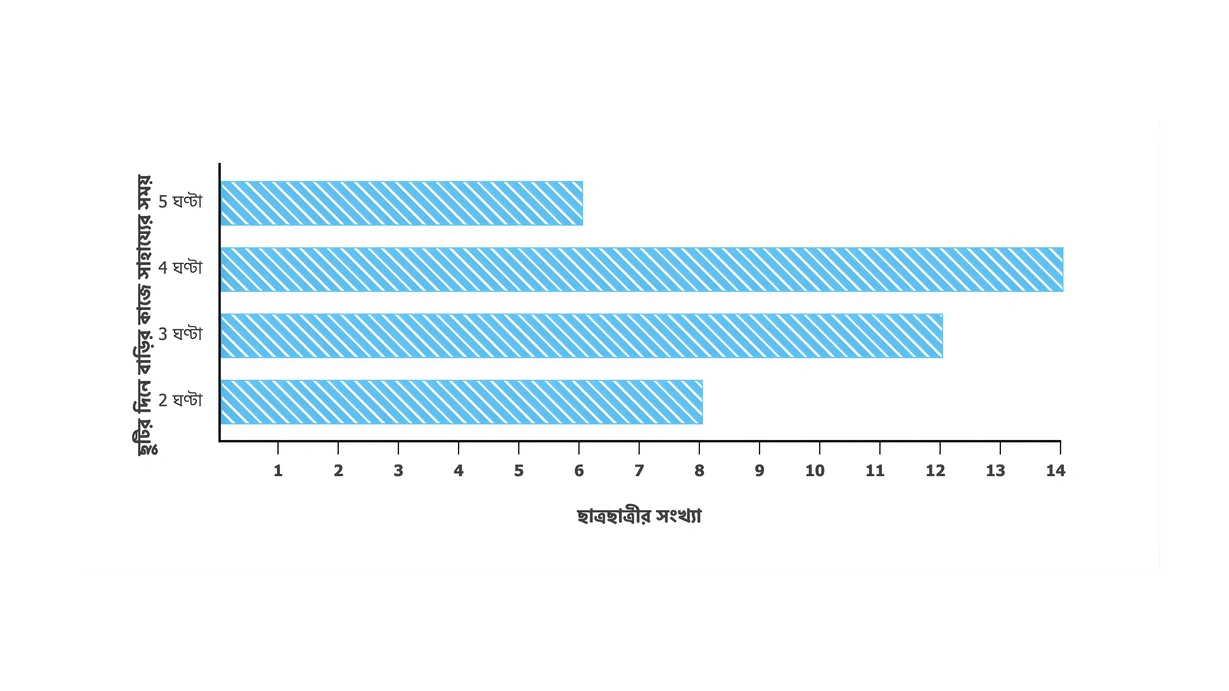
(i) স্তম্ভচিত্র থেকে আমাদের শ্রেণির কতজন করে ছাত্রছাত্রী প্রতি ছুটির দিনে কতক্ষণ বাড়ির কাজ করে তা লিখি।
(ii) কতজন ছাত্রছাত্রী ছুটির দিনে সবচেয়ে বেশি সময় বাড়ির কাজে সাহায্য করে লিখি।
(iii) প্রতি ছুটির দিনে 2 ঘন্টা করে বাড়ির কাজে কতজন ছাত্রছাত্রী সাহায্য করে লিখি।
সমাধান –
(i) স্তম্ভচিত্র থেকে পাই, 6 জন ছাত্রছাত্রী 5 ঘন্টা করে বাড়ির কাজ করে, 14 জন ছাত্রছাত্রী 4 ঘন্টা করে বাড়ির কাজ করে, 12 জন ছাত্রছাত্রী 3 ঘন্টা করে বাড়ির কাজ করে, 8 জন ছাত্রছাত্রী 2 ঘন্টা করে বাড়ির কাজ করে।
(ii) স্তম্ভচিত্র থেকে পাই, ছুটির দিনে 6 জন ছাত্রছাত্রী সবচেয়ে বেশি সময় বাড়ির কাজে সাহায্য করে।
(iii) স্তম্ভচিত্র থেকে পাই, প্রতি ছুটির দিনে 2 ঘন্টা করে বাড়ির কাজে 8 জন ছাত্রছাত্রী সাহায্য করে।
3. নিচের পাইচিত্রটি দেখি ও প্রশ্নের উত্তর খুঁজি –
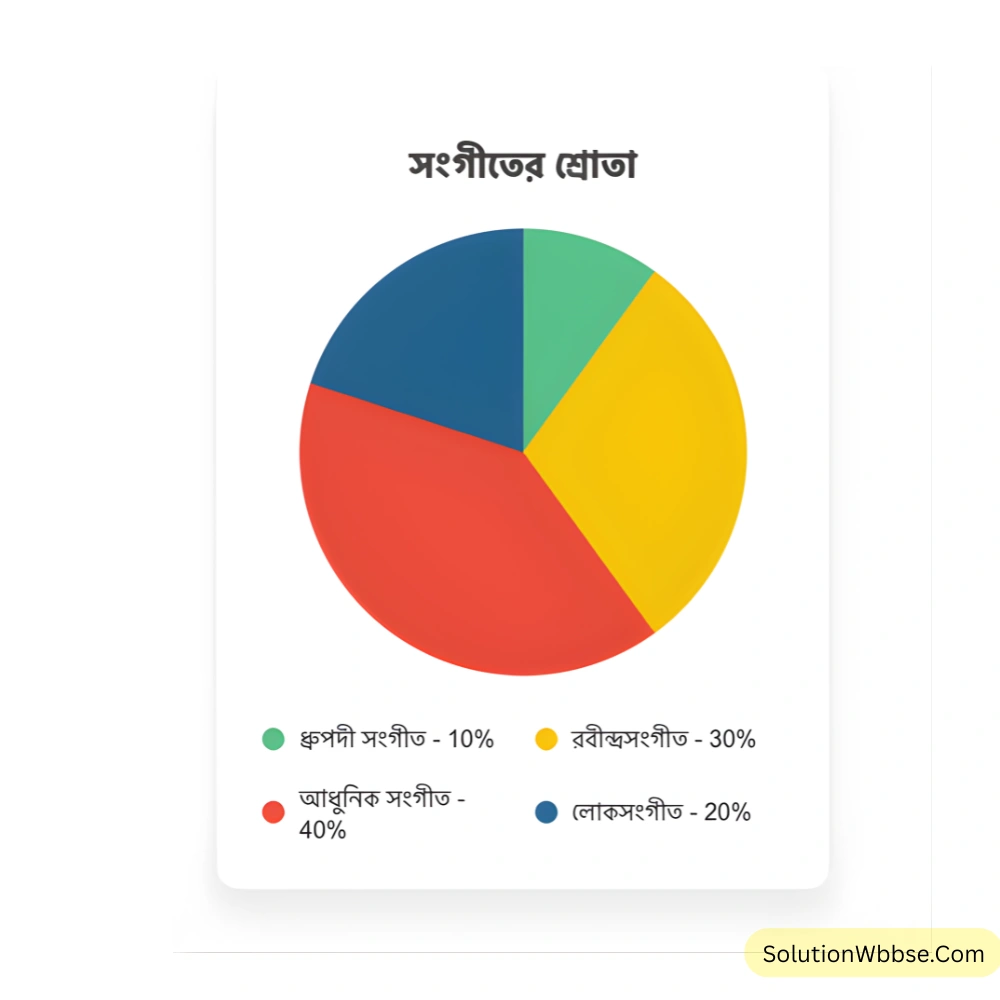
(a) শ্রোতারা কোন কোন ধরনের গান পছন্দ করেন তার পাই চিত্র –
(i) লোকসংগীতের শ্রোতার বৃত্তকলাটি সম্পূর্ণ বৃত্তাকারক্ষেত্রের কত অংশ লিখি।
(ii) পাই চিত্র থেকে কোন ধরনের গানের শ্রোতা সবচেয়ে বেশি লিখি।
(iii) কোন ধরনের গানের শ্রোতা সবচেয়ে কম লিখি।
সমাধান –
(i) লোকসংগীতের শ্রোতার বৃত্তকলাটি সম্পূর্ণ বৃত্তাকারক্ষেত্রের = \(\frac{20}{100}\) অংশ = \(\frac{1}{5}\) অংশ।
(ii) পাই চিত্র থেকে পাই, আধুনিক সংগীতের শ্রোতা সবচেয়ে বেশি।
(iii) পাই চিত্র থেকে পাই, ধ্রুপদী সংগীতের শ্রোতা সবচেয়ে কম।
(b) দর্শকরা টিভিতে কোন ধরনের অনুষ্ঠান পছন্দ করেন তার পাই চিত্র –
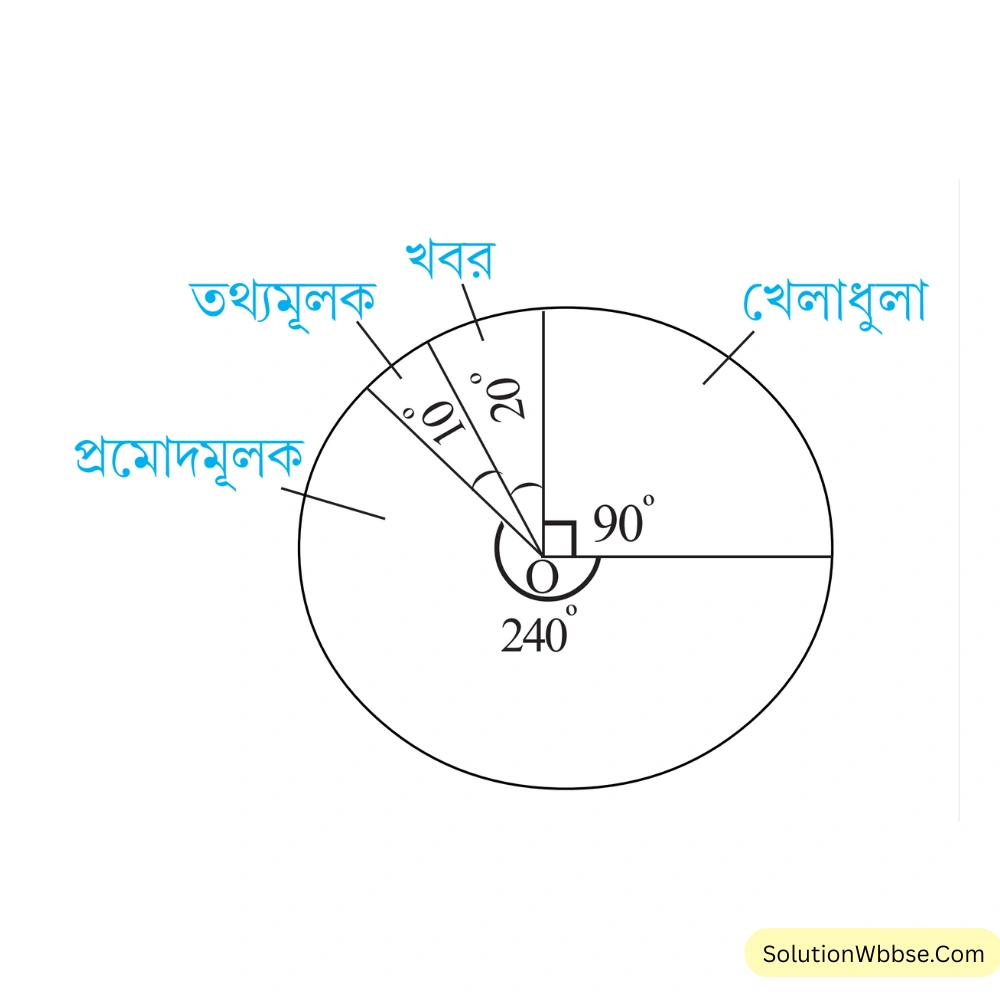
(i) পাই চিত্রে খবরের দর্শকের বৃত্তকলাটি সম্পূর্ণ বৃত্তাকার ক্ষেত্রের কত অংশ লিখি।
(ii) কোন ধরনের অনুষ্ঠানের দর্শক সবচেয়ে বেশি লিখি।
(iii) কোন্ ধরনের অনুষ্ঠানের দর্শক সবচেয়ে কম লিখি।
(iv) মোট দর্শকের কত অংশ খেলাধুলার অনুষ্ঠান দেখেন লিখি।
সমাধান –
(i) খবরের দর্শকের বৃত্তকলাটি সম্পূর্ণ বৃত্তাকার ক্ষেত্রের \(\frac{20}{360}\) অংশ = \(\frac{1}{18}\) অংশ।
(ii) প্রমোদমূলক অনুষ্ঠানের দর্শক সবচেয়ে বেশি।
(iii) তথ্যমূলক অনুষ্ঠানের দর্শক সবচেয়ে কম।
(iv) খেলাধুলার অনুষ্ঠান দেখেন \(\frac{90}{360}\) অংশ = \(\frac{1}{4}\) অংশ।
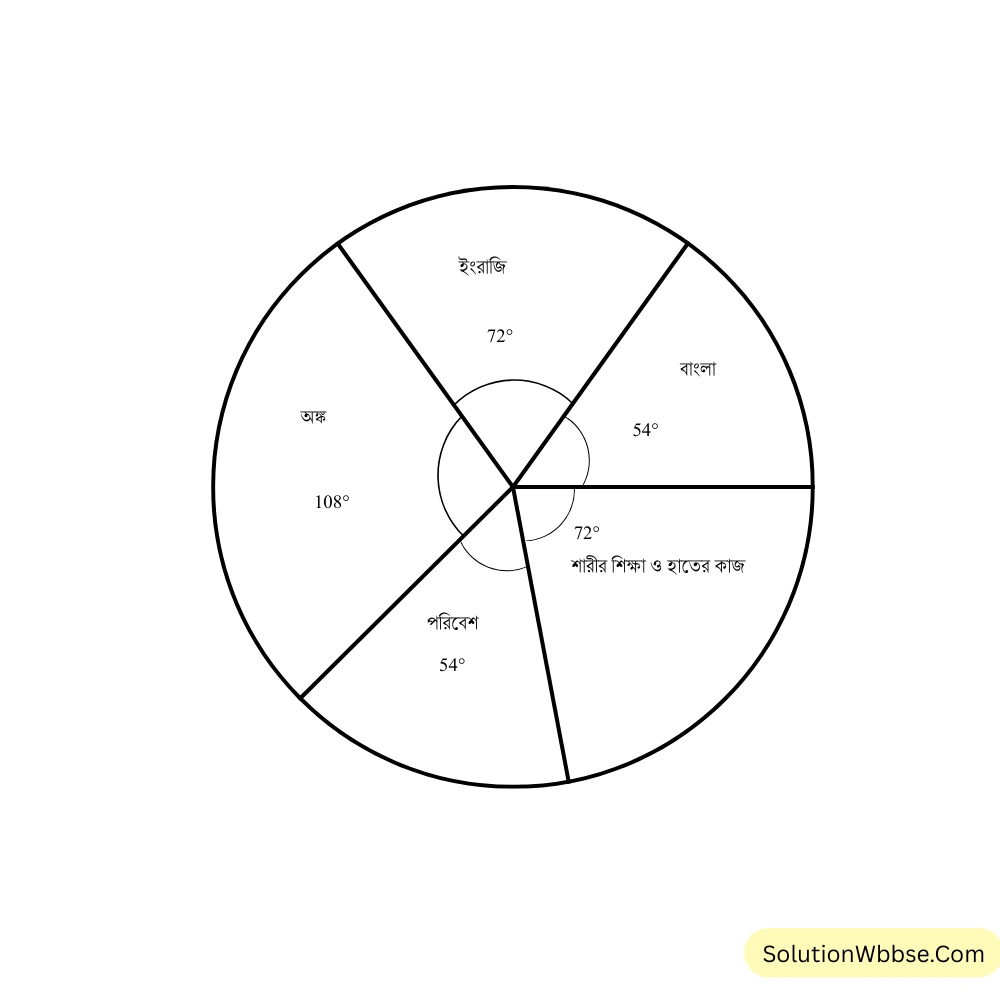
4. পঞ্চম শ্রেণির বার্ষিক মূল্যায়নে শুভম বিভিন্ন বিষয়ে যে যে নম্বর পেয়েছে তার মোট নম্বরের ওপর শতকরা হিসাব নীচের তালিকায় লিখলাম।
| বিষয় | বাংলা | ইংরেজি | অঙ্ক | পরিবেশ | শারীর শিক্ষা ও হাতের কাজ |
| প্রাপ্ত নম্বর (শতকরায়) | 15 | 20 | 30 | 15 | 20 |
সমাধান –
| বিষয় | বাংলা | ইংরাজি | অঙ্ক | পরিবেশ | শারীর শিক্ষা ও হাতের কাজ |
| প্রাপ্ত নম্বর (শতকরায়) | 15 | 20 | 30 | 15 | 20 |
| প্রাপ্ত নম্বর (ভগ্নাংশে) | \(\frac{15}{100} = \frac{3}{20}\) | \(\frac{20}{100} = \frac{1}{5}\) | \(\frac{30}{100} = \frac{3}{10}\) | \(\frac{15}{100} = \frac{3}{20}\) | \(\frac{20}{100} = \frac{1}{5}\) |
| কেন্দ্রীয় কোণ | \(360^\circ \times \frac{3}{20} = 54^\circ\) | \(360^\circ \times \frac{1}{5} = 72^\circ\) | \(360^\circ \times \frac{3}{10} = 108^\circ\) | \(360^\circ \times \frac{3}{20} = 54^\circ\) | \(360^\circ \times \frac{1}{5} = 72^\circ\) |
পাই চিত্র –
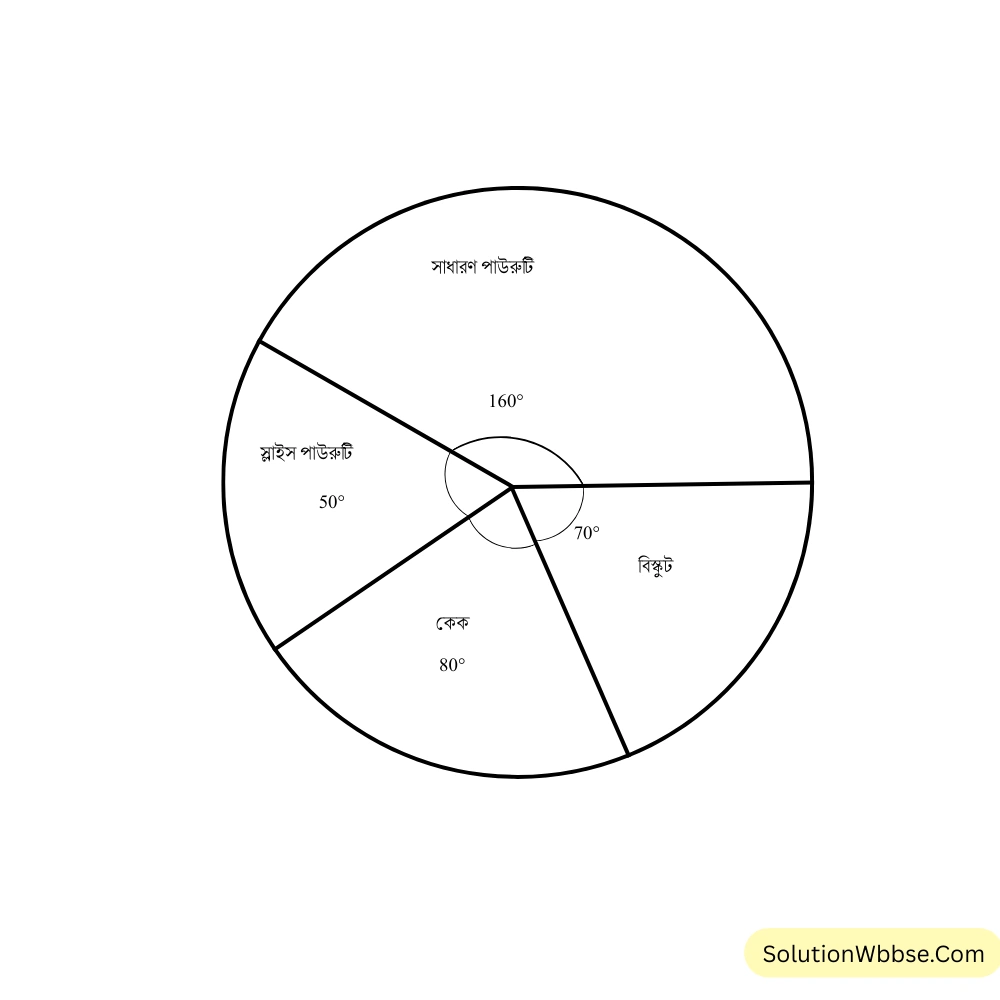
5. আমাদের পাড়ায় মধুবাবুর দোকান আছে। আমি মধুবাবুর দোকানের একদিনের বিভিন্ন ধরনের জিনিস বিক্রির তালিকা তৈরি করলাম।
| জিনিস | সাধারণ পাউরুটি | স্লাইস পাউরুটি | কেক | বিস্কুট |
| মূল্য (টাকা) | 320 | 100 | 160 | 140 |
আমি এই তথ্যটির পাই চিত্র তৈরির চেষ্টা করি।
সমাধান –
ওই একদিনে মোট \((320 + 100 + 160 + 140) = 720\) টাকার জিনিস বিক্রি হয়েছে।
সাধারণ পাউরুটি বিক্রি হয়েছে = \(\frac{320}{720}\) অংশ = \(\frac{4}{9}\) অংশ
\(\therefore\) সাধারণ পাউরুটির বিক্রির বৃত্তকলার কেন্দ্রীয় কোণ = \(360^\circ \times \frac{4}{9} = 160^\circ\)
স্লাইস পাউরুটি বিক্রি হয়েছে = \(\frac{100}{720}\) অংশ = \(\frac{5}{36}\) অংশ
\(\therefore\) স্লাইস পাউরুটি বিক্রির বৃত্তকলার কেন্দ্রীয় কোণ = \(360^\circ \times \frac{5}{36} = 50^\circ\)
কেক বিক্রি হয়েছে = \(\frac{160}{720}\) অংশ = \(\frac{2}{9}\) অংশ
\(\therefore\) কেক বিক্রির বৃত্তকলার কেন্দ্রীয় কোণ = \(360^\circ \times \frac{2}{9} = 80^\circ\)
বিস্কুট বিক্রি হয়েছে = \(\frac{140}{720}\) অংশ = \(\frac{7}{36}\) অংশ
\(\therefore\) বিস্কুট বিক্রির বৃত্তকলার কেন্দ্রীয় কোণ = \(360^\circ \times \frac{7}{36} = 70^\circ\)
পাই চিত্র –
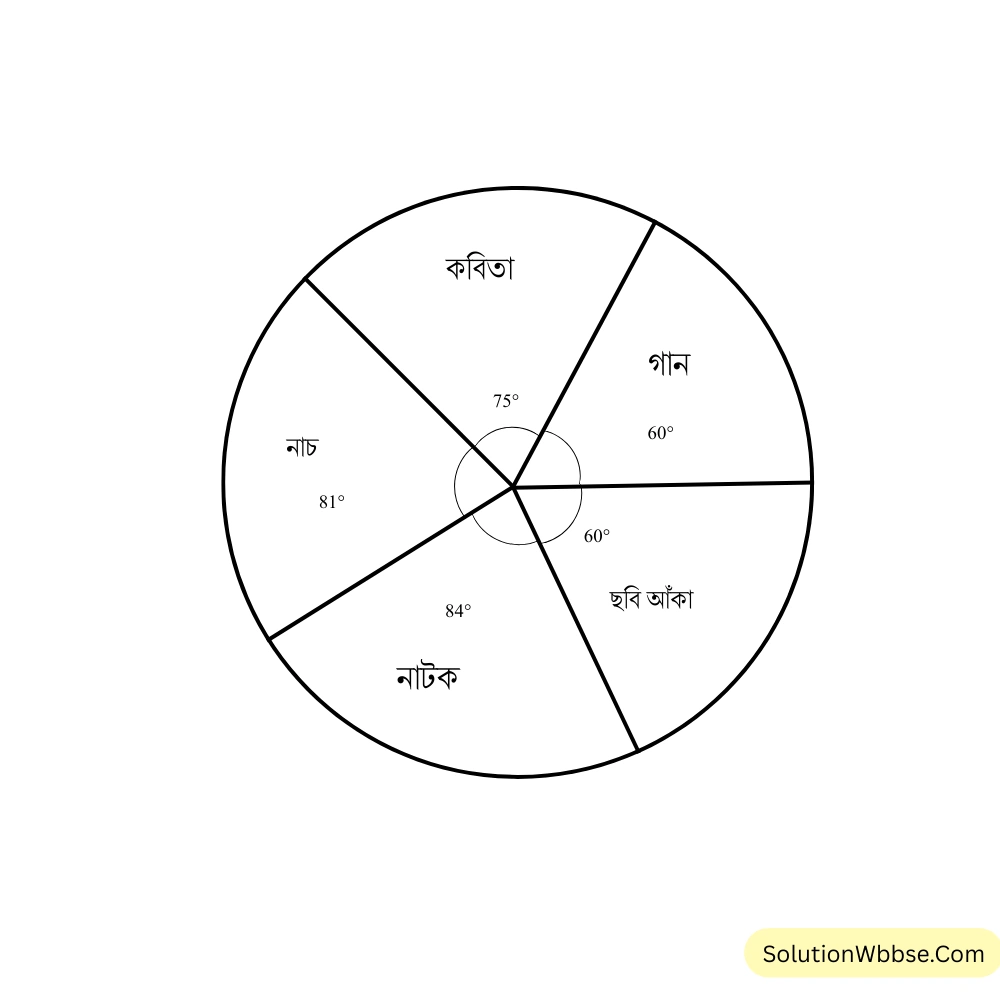
6. অষ্টম শ্রেণির দুটি বিভাগের ছাত্র ছাত্রীরা অবসর সময় কী কী বিষয় পছন্দ করেন তার একটি তালিকা তৈরি করেছি। (এক একজন একটিই বিষয় পছন্দ করবে)।
| পছন্দের বিষয় | গান | কবিতা | নাচ | নাটক | ছবি আঁকা |
| ছাত্রছাত্রীর সংখ্যা (জন) | 20 | 25 | 27 | 28 | 30 |
এই তথ্য থেকে মোট ছাত্রছাত্রীর কত অংশ কোন কোন বিষয় পছন্দ করে হিসাব করি। প্রতিটি বৃত্তকলার কেন্দ্রীয় কোণ খুঁজি ও সেই অনুযায়ী পাইচিত্র অঙ্কন করি।
সমাধান –
মোট ছাত্র ছাত্রীর সংখ্যা = \((20+25+27+28+20)\) জন = \(120\) জন।
গান পছন্দ করে মোট ছাত্র ছাত্রীর \(\frac{20}{120}\) অংশ = \(\frac{1}{6}\) অংশ
\(\therefore\) গান পছন্দ করা ছাত্রছাত্রীর কেন্দ্রীয় কোণ = \(360^{\circ} \times \frac{1}{6} = 60^{\circ}\)
কবিতা পছন্দ করে মোট ছাত্র ছাত্রীর \(\frac{25}{120}\) অংশ = \(\frac{5}{24}\) অংশ
\(\therefore\) কবিতা পছন্দ করা ছাত্রছাত্রীর কেন্দ্রীয় কোণ = \(360^{\circ} \times \frac{5}{24} = 75^{\circ}\)
নাচ পছন্দ করে মোট ছাত্র ছাত্রীর \(\frac{27}{120}\) অংশ = \(\frac{9}{40}\) অংশ
\(\therefore\) নাচ পছন্দ করা ছাত্রছাত্রীর কেন্দ্রীয় কোণ = \(360^{\circ} \times \frac{9}{40} = 81^{\circ}\)
নাটক পছন্দ করে মোট ছাত্র ছাত্রীর \(\frac{28}{120}\) অংশ = \(\frac{7}{30}\) অংশ
\(\therefore\) নাটক পছন্দ করা ছাত্রছাত্রীর কেন্দ্রীয় কোণ = \(360^{\circ} \times \frac{7}{30} = 84^{\circ}\)
ছবি আঁকা পছন্দ করে মোট ছাত্র ছাত্রীর \(\frac{20}{120}\) অংশ = \(\frac{1}{6}\) অংশ
\(\therefore\) ছবি আঁকা পছন্দ করা ছাত্রছাত্রীর কেন্দ্রীয় কোণ = \(360^{\circ} \times \frac{1}{6} = 60^{\circ}\)
পাই চিত্র –
7. আমি একটি মডেল তৈরি করেছি। উপকরণ কেনার খরচের একটি তালিকা তৈরি করলাম।
| উপকরণ | আর্ট পেপার | স্কেচ পেন | কাঁচি | রঙিন ফিতে | পিচবোর্ড |
| খরচ (টাকা) | 9 | 12 | 25 | 6 | 8 |
তথ্য গুলির পাইচিত্র তৈরি করি।
সমাধান –
মোট খরচ = \((9 + 12 + 25 + 6 + 8)\) টাকা = \(60\) টাকা।
আর্টপেপারের জন্য খরচ মোট খরচের \(\frac{9}{60}\) অংশ = \(\frac{3}{20}\) অংশ।
\(\therefore\) আর্টপেপারের জন্য বৃত্তকলার কেন্দ্রীয় কোণ = \(360^\circ \times \frac{3}{20} = 54^\circ\)
স্কেচপেনের জন্য খরচ মোট খরচের \(\frac{12}{60}\) অংশ = \(\frac{1}{5}\) অংশ।
\(\therefore\) স্কেচপেনের জন্য বৃত্তকলার কেন্দ্রীয় কোণ = \(360^\circ \times \frac{1}{5} = 72^\circ\)
কাঁচির জন্য খরচ মোট খরচের \(\frac{25}{60}\) অংশ = \(\frac{5}{12}\) অংশ।
\(\therefore\) কাঁচির জন্য বৃত্তকলার কেন্দ্রীয় কোণ = \(360^\circ \times \frac{5}{12} = 150^\circ\)
রঙিন ফিতের জন্য খরচ মোট খরচের \(\frac{6}{60}\) অংশ = \(\frac{1}{10}\) অংশ।
\(\therefore\) রঙিন ফিতের জন্য বৃত্তকলার কেন্দ্রীয় কোণ = \(360^\circ \times \frac{1}{10} = 36^\circ\)
পিচবোর্ডের জন্য খরচ মোট খরচের \(\frac{8}{60}\) অংশ = \(\frac{2}{15}\) অংশ।
\(\therefore\) পিচবোর্ডের জন্য বৃত্তকলার কেন্দ্রীয় কোণ = \(360^\circ \times \frac{2}{15} = 48^\circ\)
পাই চিত্র –
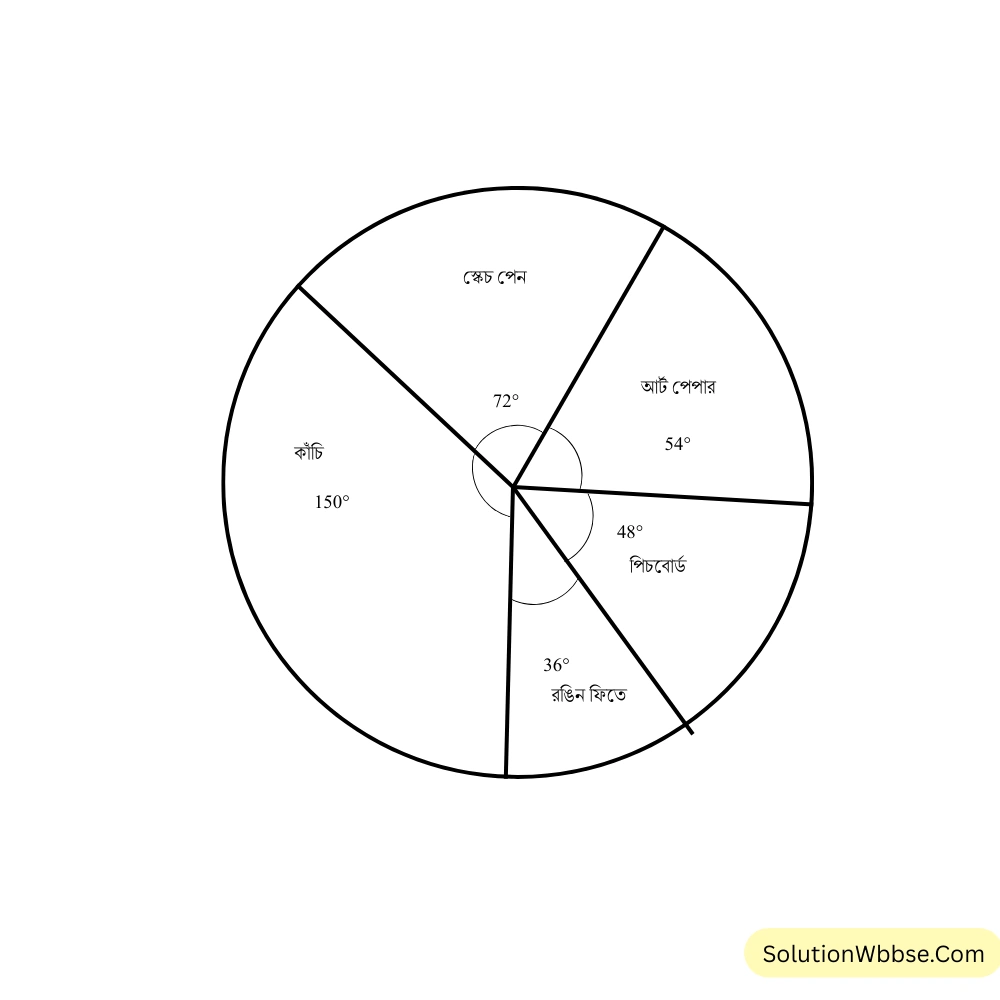
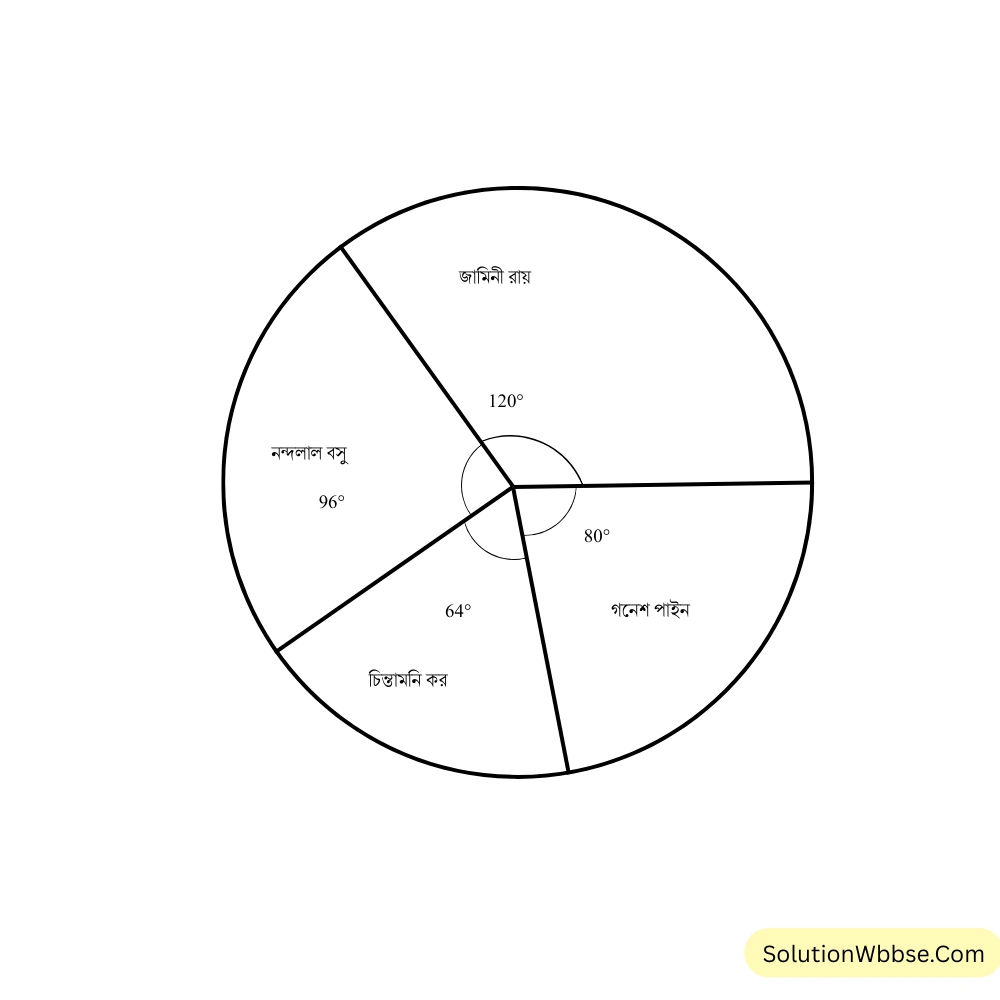
8. একদিন একটি চিত্র প্রদর্শনীতে আসা \(450\) জন দর্শকের পছন্দের চিত্রশিল্পীর তালিকা তৈরি করলাম।
| চিত্রশিল্পীর নাম | যামিনী রায় | নন্দলাল বসু | চিন্তামণি কর | গণেশ পাইন |
| পছন্দের দর্শক সংখ্যা | 150 | 120 | 80 | 100 |
এই তথ্য নিয়ে পাই চিত্র তৈরি করি ও বৃত্তকলা গুলির কেন্দ্রীয় কোণ লিখি।
সমাধান –
মোট দর্শকের সংখ্যা = \((150 + 120 + 80 + 100)\) জন = \(450\) জন
জামিনী রায়ের দর্শক সংখ্যা মোট দর্শক সংখ্যার \(\frac{150}{450}\) অংশ = \(\frac{1}{3}\) অংশ
\(\therefore\) জামিনী রায়ের দর্শক সংখ্যার কেন্দ্রীয় কোণ = \(360^\circ \times \frac{1}{3} = 120^\circ\)
নন্দলাল বসুর দর্শক সংখ্যা মোট দর্শক সংখ্যার \(\frac{120}{450}\) অংশ = \(\frac{4}{15}\) অংশ
\(\therefore\) নন্দলাল বসুর দর্শক সংখ্যার কেন্দ্রীয় কোণ = \(360^\circ \times \frac{4}{15} = 96^\circ\)
চিন্তামনি করের দর্শক সংখ্যা মোট দর্শক সংখ্যার \(\frac{80}{450}\) অংশ = \(\frac{8}{45}\) অংশ
\(\therefore\) চিন্তামনি করের দর্শক সংখ্যার কেন্দ্রীয় কোণ = \(360^\circ \times \frac{8}{45} = 64^\circ\)
গণেশ পাইনের দর্শক সংখ্যা মোট দর্শক সংখ্যার = \(\frac{100}{450}\) অংশ = \(\frac{2}{9}\) অংশ
\(\therefore\) গণেশ পাইনের দর্শক সংখ্যার কেন্দ্রীয় কোণ = \(360^\circ \times \frac{2}{9} = 80^\circ\)
পাই চিত্র –
9. 180 জনের একটি দলকে পছন্দের ঋতু জিজ্ঞাসা করে প্রাপ্ত তথ্য দিয়ে নীচের পাই চিত্র বানানো হলো –
নীচের পাই চিত্র থেকে প্রশ্নগুলির উত্তর খোঁজার চেষ্টা করি –
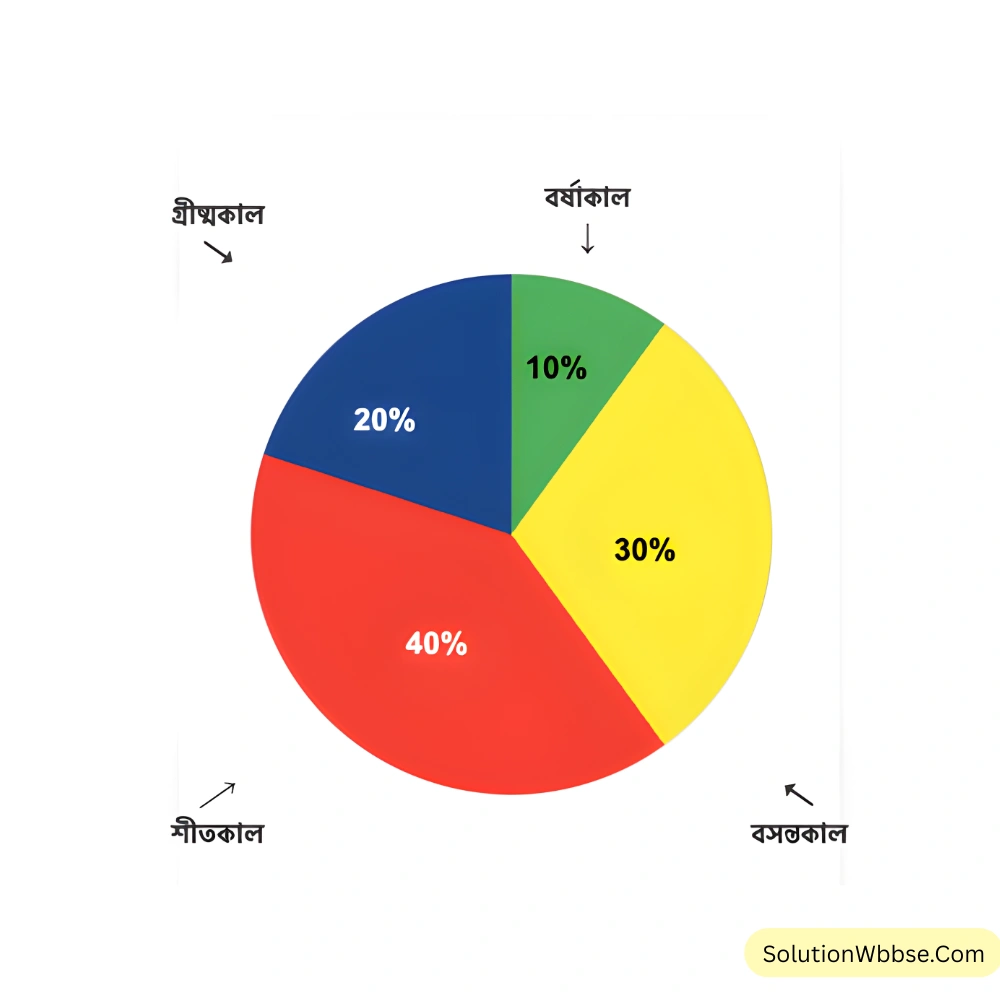
(i) সবচেয়ে বেশি জন কোন ঋতু পছন্দ করে এবং কতজন লিখি।
(ii) সবচেয়ে কমজন কোন ঋতু পছন্দ করে এবং কতজন লিখি।
(iii) কতজন গ্রীষ্মকাল পছন্দ করে লিখি।
(iv) সবচেয়ে ছোটো বৃত্তকলা দ্বারা কোন ঋতু বোঝানো হয়েছে?
(v) নিজে পাই চিত্র দেখি ও আরও দুটি নতুন প্রশ্ন তৈরি করে উত্তর খুঁজি।
সমাধান –
(i) সবচেয়ে বেশিজন শীতকাল পছন্দ করে এবং শীতকাল পছন্দ করে \(= 180 \times \frac{40}{100}\) জন \(= 72\) জন।
(ii) সবচেয়ে কম জন বর্ষাকাল পছন্দ করে এবং বর্ষাকাল পছন্দ করে \(= 180 \times \frac{10}{100}\) জন \(= 18\) জন।
(iii) গ্রীষ্মকাল পছন্দ করে \(= 180 \times \frac{20}{100}\) জন \(= 36\) জন।
(iv) সবচেয়ে ছোটো বৃত্তকলা দ্বারা বর্ষাকাল বোঝানো হয়েছে।
(v) প্রশ্ন 1 – বসন্তকাল ঋতু কতজন পছন্দ করে?
উত্তর – বসন্তকাল ঋতু পছন্দ করে \(= 180 \times \frac{30}{100}\) জন \(= 54\) জন।
প্রশ্ন 2 – সবচেয়ে বড়ো বৃত্তকলা দ্বারা কোন ঋতু বোঝানো হয়েছে?
উত্তর – সবচেয়ে বড়ো বৃত্তকলা দ্বারা শীতকাল ঋতু বোঝানো হয়েছে।
এই আর্টিকেলে অষ্টম শ্রেণির গণিতের ‘পাই চিত্র’ অধ্যায়ের ‘কষে দেখি –2’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরেছি। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে। কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment