পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) অষ্টম শ্রেণির গণিত পাঠ্যবইয়ের তৃতীয় অধ্যায় হলো ‘মূলদ সংখ্যার ধারণা’। এই পোস্টে আমরা ‘কষে দেখি – 3’-এর সমস্ত প্রশ্নের সহজ ও নির্ভুল সমাধান নিয়ে আলোচনা করেছি। আশা করি, এই নোটসগুলো তোমাদের গণিত শিখতে এবং পরীক্ষার প্রস্তুতিতে দারুণভাবে সহায়তা করবে।

1. নীচের সমীকরণগুলি সমাধান করি ও বীজগুলি \(\frac{p}{q}\) [ (\(q \neq 0\)) যেখানে \(p\) ও \(q\) পূর্ণসংখ্যা ] আকারে প্রকাশ করি।
(a) \(7x = 14\)
সমাধান –
\(7x = 14\)বা, \(x = \frac{14}{7}\)
বা, \(x = \frac{2}{1}\)
\(\therefore\) সমীকরণের বীজটি হল \(\mathbf{\frac{2}{1}}\)।
(b) \(4p + 32 = 0\)
সমাধান –
\(4p + 32 = 0\)বা, \(4p = -32\)
বা, \(p = -\frac{32}{4}\)
বা, \(p = -\frac{8}{1}\)
\(\therefore\) সমীকরণের বীজটি হল \(\mathbf{-\frac{8}{1}}\)।
(c) \(11x = 0\)
সমাধান –
\(11x = 0\)বা, \(x = \frac{0}{11}\)
\(\therefore\) সমীকরণের বীজটি হল \(\mathbf{\frac{0}{11}}\)।
(d) \(5m – 3 = 0\)
সমাধান –
\(5m – 3 = 0\)বা, \(5m = 3\)
বা, \(m = \frac{3}{5}\)
\(\therefore\) সমীকরণের বীজটি হল \(\mathbf{\frac{3}{5}}\)।
(e) \(9y + 18 = 0\)
সমাধান –
\(9y + 18 = 0\)বা, \(9y = -18\)
বা, \(y = -\frac{18}{9}\)
বা, \(y = -\frac{2}{1}\)
\(\therefore\) সমীকরণের বীজটি হল \(\mathbf{-\frac{2}{1}}\)।
(f) \(t = 8 – 12t\)
সমাধান –
\(t = 8 – 12t\)বা, \(t + 12t = 8\)
বা, \(13t = 8\)
বা, \(t = \frac{8}{13}\)
\(\therefore\) সমীকরণের বীজটি হল \(\mathbf{\frac{8}{13}}\)।
(g) \(6y = 5 + y\)
সমাধান –
\(6y = 5 + y\)বা, \(6y – y = 5\)
বা, \(5y = 5\)
বা, \(y = \frac{5}{5}\)
বা, \(y = \frac{1}{1}\)
\(\therefore\) সমীকরণের বীজটি হল \(\mathbf{\frac{1}{1}}\)।
(h) \(2x + \_\_\_\_\_ = \_\_\_\_\_\)
সমাধান –
\(2x + 4 = 6\)বা, \(2x = 6 – 4\)
বা, \(2x = 2\)
বা, \(x = \frac{2}{2}\)
বা, \(x = \frac{1}{1}\)
\(\therefore\) সমীকরণের বীজটি হল \(\mathbf{\frac{1}{1}}\)।
2. \(y = -\frac{5}{4}\) হলে, \(-(-y) = y\) যাচাই করি।
সমাধান –
\(y = -\frac{5}{4}\) হলে,
\(-(-y) = – \left\{ -\left( -\frac{5}{4} \right) \right\} = -\frac{5}{4} = y\)\(\therefore -(-y) = y\) [প্রমাণিত]
3. \(x = -\frac{3}{8}\) হলে, মান খুঁজি –
(a) \(2x + 5\)
সমাধান –
\(x = -\frac{3}{8}\) হলে,
\(2x + 5 = 2 \times \left( -\frac{3}{8} \right) + 5 = -\frac{6}{8} + 5 = \frac{-6+40}{8} = \frac{34}{8} = \frac{17}{4}\)\(\therefore 2x + 5 = \frac{17}{4}\) [উত্তর]
(b) \(x + \frac{3}{8}\)
সমাধান –
\(x = -\frac{3}{8}\) হলে,
\(x + \frac{3}{8} = -\frac{3}{8} + \frac{3}{8} = 0\)\(\therefore x + \frac{3}{8} = 0\) [উত্তর]
(c) \(5 – (-x)\)
সমাধান –
\(5 – (-x) = 5 – \left\{ -\left( -\frac{3}{8} \right) \right\} = 5 – \frac{3}{8} = \frac{40-3}{8} = \frac{37}{8}\)(d) \(\_\_\_\_\_ – (-x)\) [নিজে মূলদ সংখ্যা বসাই]
সমাধান –
শূন্যস্থানে \(\frac{3}{8}\) বসিয়ে পাই,
\(\frac{3}{8} – (-x) = \frac{3}{8} + x = \frac{3}{8} – \frac{3}{8}\) \([\because x = -\frac{3}{8}]\)
= \( 0\)
4. নীচের ফাঁকা ঘরে বুঝে সংখ্যা লিখি
(a) \(\frac{9}{11} + [ \quad ] = 0\)
সমাধান – \(\frac{9}{11} + \left[ -\frac{9}{11} \right] = 0\)
(b) \([ \quad ] + \left( -\frac{21}{29} \right) = 0\)
সমাধান –
\(\left[ \frac{21}{29} \right] + \left( -\frac{21}{29} \right) = 0\)(c) \(\frac{7}{19} \times [ \quad ] = 1\)
সমাধান –
\(\frac{7}{19} \times \left[ \frac{19}{7} \right] = 1\)(d) \(-5 \times [ \quad ] = 1\)
সমাধান –
\(-5 \times \left[ -\frac{1}{5} \right] = 1\)(e) \(-\frac{15}{23} \times [ \quad ] = 1\)
সমাধান –
\(-\frac{15}{23} \times \left[ -\frac{23}{15} \right] = 1\)(f) \(\left( -\frac{8}{3} \right) \times \left( -\frac{21}{20} \right) = [ \quad ]\)
সমাধান –
\(\left( -\frac{8}{3} \right) \times \left( -\frac{21}{20} \right) = \frac{8}{3} \times \frac{21}{20} = \frac{14}{5}\)\(\therefore \left( -\frac{8}{3} \right) \times \left( -\frac{21}{20} \right) = \left[ \frac{14}{5} \right]\)5. \(\frac{7}{18}\) কে \((-\frac{5}{6})\) – এর অনন্যক দিয়ে গুণ করে গুণফল লিখি।
সমাধান –
\((-\frac{5}{6})\) এর অনন্যক হলো \(-\frac{6}{5}\)।
\(\therefore \frac{7}{18} \times (-\frac{6}{5})\)= \( -(\frac{7}{18} \times \frac{6}{5})\)
= \( -\frac{7}{15}\) [উত্তর]
6. বিনিময় ও সংযোগ নিয়মের সাহায্যে মান খুঁজি
(i) \(\frac{5}{8} + (-\frac{7}{15}) + (\frac{3}{32}) + \frac{11}{75}\)
সমাধান –
\(\frac{5}{8} + (-\frac{7}{15}) + (\frac{3}{32}) + \frac{11}{75}\)= \( \frac{5}{8} + \{-\frac{7}{15} + \frac{3}{32}\} + \frac{11}{75}\)
= \( \frac{5}{8} + \{\frac{3}{32} + (-\frac{7}{15})\} + \frac{11}{75}\) [বিনিময় প্রক্রিয়া প্রয়োগ করে পাই]
= \( (\frac{5}{8} + \frac{3}{32}) + (-\frac{7}{15} + \frac{11}{75})\) [সংযোগ প্রক্রিয়া প্রয়োগ করে পাই]
= \( \frac{23}{32} + (-\frac{24}{75})\)
= \( \frac{23}{32} + (-\frac{8}{25})\)
= \( \frac{575-256}{800}\)
= \( \frac{319}{800}\) [উত্তর]
(ii) \(\frac{8}{121} \times \frac{35}{169} \times \frac{55}{36} \times \frac{78}{49}\)
সমাধান –
\(\frac{8}{121} \times \frac{35}{169} \times \frac{55}{36} \times \frac{78}{49}\)= \( \frac{8}{121} \times (\frac{35}{169} \times \frac{55}{36}) \times \frac{78}{49}\)
= \( \frac{8}{121} \times (\frac{55}{36} \times \frac{35}{169}) \times \frac{78}{49}\) [বিনিময় প্রক্রিয়ার সাহায্যে পাই]
= \( (\frac{8}{121} \times \frac{55}{36}) \times (\frac{35}{169} \times \frac{78}{49})\) [সংযোগ নিয়মের সাহায্যে পাই]
= \( \frac{10}{99} \times \frac{30}{91}\)
= \( \frac{100}{3003}\) [উত্তর]
7. সংখ্যারেখায় মূলদ সংখ্যাগুলি বসাই –
\(\frac{1}{4}, \frac{-3}{4}, \frac{-2}{3}, \frac{6}{5}, \frac{-8}{3}\)
সমাধান –
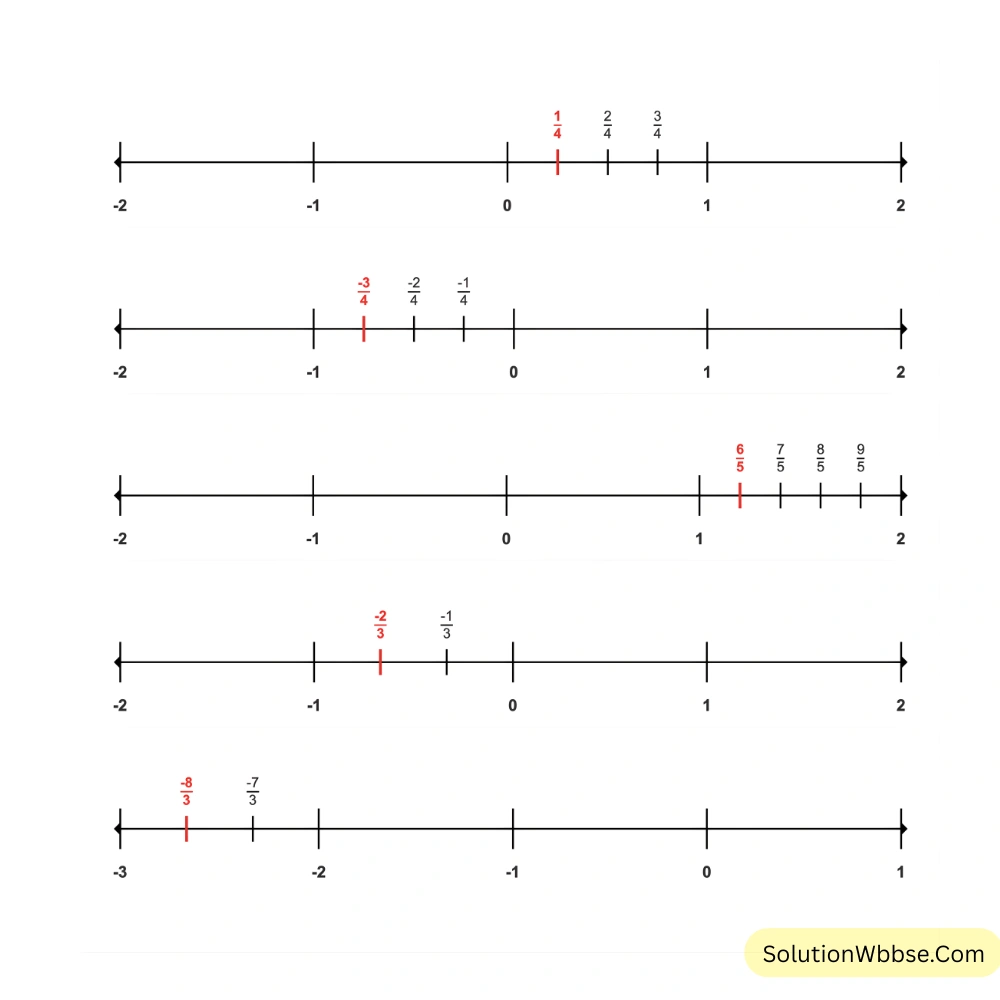
8. 4 টি মূলদ সংখ্যা লিখি যারা 1 এর থেকে বড়ো কিন্তু 2 এর থেকে ছোটো।
সমাধান –
\(1 = \frac{1 \times 5}{1 \times 5} = \frac{5}{5}\)\(2 = \frac{2 \times 5}{1 \times 5} = \frac{10}{5}\)\(\therefore\) 1 ও 2 – এর মধ্যে 4 টি মূলদ সংখ্যা হল \(\frac{6}{5}, \frac{7}{5}, \frac{8}{5}, \frac{9}{5}\)।
9. \(-\frac{3}{5}\) ও \(\frac{1}{2}\) এর মধ্যে 10 টি মূলদ সংখ্যা লিখি।
সমাধান –
\(-\frac{3}{5} = -\frac{3 \times 2}{5 \times 2} = -\frac{6}{10}\)\(\frac{1}{2} = \frac{1 \times 5}{2 \times 5} = \frac{5}{10}\)\(\therefore -\frac{3}{5}\) ও \(\frac{1}{2}\) এর মধ্যে 10 টি মূলদ সংখ্যা হল –
\(-\frac{5}{10}, -\frac{4}{10}, -\frac{3}{10}, -\frac{2}{10}, -\frac{1}{10}, 0, \frac{1}{10}, \frac{2}{10}, \frac{3}{10}, \frac{4}{10}\)10. নীচের মূলদ সংখ্যাগুলির মধ্যে পাঁচটি করে মূলদ সংখ্যা লিখি।
(a) \(\frac{1}{3}\) ও \(\frac{3}{5}\)
(b) \(\frac{1}{4}\) ও \(\frac{1}{2}\)
(c) \(-\frac{4}{3}\) ও \(\frac{3}{7}\)
সমাধান –
(a) \(\frac{1}{3}\) ও \(\frac{3}{5}\)
\(\frac{1}{3} = \frac{1 \times 5}{3 \times 5} = \frac{5}{15} = \frac{5 \times 2}{15 \times 2} = \frac{10}{30}\)\(\frac{3}{5} = \frac{3 \times 3}{5 \times 3} = \frac{9}{15} = \frac{9 \times 2}{15 \times 2} = \frac{18}{30}\)\(\therefore \frac{1}{3}\) ও \(\frac{3}{5}\) এর মধ্যে 5 টি মূলদ সংখ্যা হল –
\(\frac{11}{30}, \frac{12}{30}, \frac{13}{30}, \frac{14}{30}, \frac{15}{30}\) [উত্তর]
(b) \(\frac{1}{4}\) ও \(\frac{1}{2}\)
\(\frac{1}{4} = \frac{1 \times 6}{4 \times 6} = \frac{6}{24}\)\(\frac{1}{2} = \frac{1 \times 2}{2 \times 2} = \frac{2}{4} = \frac{2 \times 6}{4 \times 6} = \frac{12}{24}\)\(\therefore \frac{1}{4}\) ও \(\frac{1}{2}\) এর মধ্যে 5 টি মূলদ সংখ্যা হল –
\(\frac{7}{24}, \frac{8}{24}, \frac{9}{24}, \frac{10}{24}, \frac{11}{24}\) [উত্তর]
(c) \(-\frac{4}{3}\) ও \(\frac{3}{7}\)
\(-\frac{4}{3} = -\frac{4 \times 7}{3 \times 7} = -\frac{28}{21}\)\(\frac{3}{7} = \frac{3 \times 3}{7 \times 3} = \frac{9}{21}\)\(\therefore -\frac{4}{3}\) ও \(\frac{3}{7}\) এর মধ্যে 5 টি মূলদ সংখ্যা হল –
\(-\frac{27}{21}, -\frac{26}{21}, 0, \frac{5}{21}, \frac{6}{21}\) [উত্তর]
এই আর্টিকেলে অষ্টম শ্রেণির গণিতের ‘মূলদ সংখ্যার ধারণা’ অধ্যায়ের ‘কষে দেখি – 3’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরেছি। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে। কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment