পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) অষ্টম শ্রেণির গণিত পাঠ্যবইয়ের চতুর্থ অধ্যায় হলো ‘বীজগাণিতিক সংখ্যামালার গুন ও ভাগ’। এই পোস্টে আমরা ‘কষে দেখি – 4.2’-এর সমস্ত প্রশ্নের সহজ ও নির্ভুল সমাধান নিয়ে আলোচনা করেছি। আশা করি, এই নোটসগুলো তোমাদের গণিত শিখতে এবং পরীক্ষার প্রস্তুতিতে দারুণভাবে সহায়তা করবে।

1. দুটি সংখ্যার গুণফল \(3x^2 + 8x + 4\) এবং একটি সংখ্যা \(3x + 2\) হলে, অপর সংখ্যাটি হিসাব করে লিখি।
সমাধান –
অপর সংখ্যাটি হবে \((3x^2 + 8x + 4) \div (3x + 2)\)
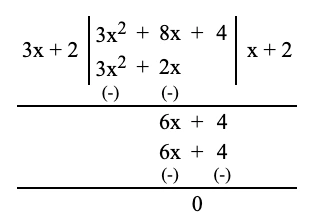
\(\therefore\) অপর সংখ্যাটি হবে \(x + 2\)।
2. একটি আয়তক্ষেত্রের ক্ষেত্রফল \((24x^2 -65xy +21y^2)\) বর্গ সেমি. এবং দৈর্ঘ্য \((8x-3y)\) সেমি. হলে প্রস্থ হিসাব করে লিখি।
সমাধান –
আয়তক্ষেত্রের প্রস্থ = ক্ষেত্রফল ÷ দৈর্ঘ্য = \((24x^2 -65xy +21y^2) \div (8x-3y)\)
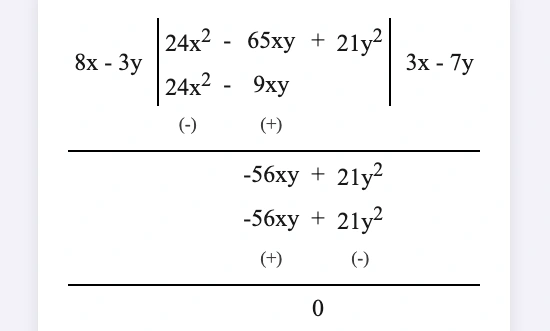
\(\therefore\) আয়তক্ষেত্রের প্রস্থ \((3x -7y)\) সেমি.।
3. একটি ভাগ অঙ্কে ভাজ্য \(x^4 + x^3y + xy^3 + y^4\) এবং ভাজক \(x^2 + xy – y^2\), ভাগফল ও ভাগশেষ হিসাব করে লিখি।
সমাধান –
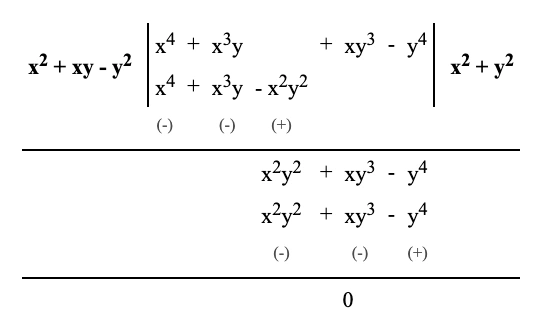
\(\therefore\) নির্ণেয় ভাগফল \((x^2 + y^2)\) এবং ভাগশেষ \(0\)।
4. ভাগ করি
(a) \((m^2 + 4m – 21)\) কে \((m – 3)\) দিয়ে
সমাধান –
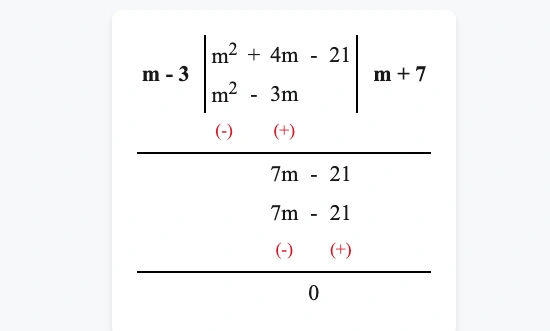
\(\therefore\) নির্ণেয় ভাগফল \((m+7)\) এবং ভাগশেষ \(0\)।
(b) \((6c^2 – 7c + 2)\) কে \((3c – 2)\) দিয়ে
সমাধান –
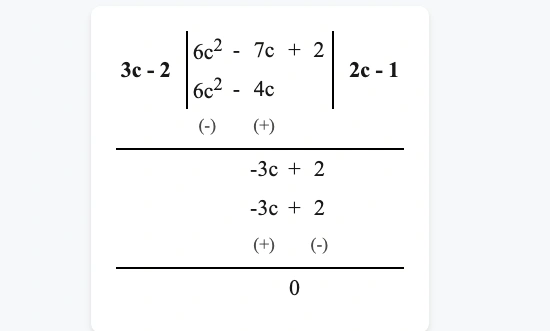
\(\therefore\) নির্ণেয় ভাগফল \((2c-1)\) এবং ভাগশেষ \(0\)।
(c) \((2a^4 – a^3 – 2a^2 + 5a – 1)\) কে \((2a^2 + a – 3)\) দিয়ে
সমাধান –

\(\therefore\) নির্ণেয় ভাগফল \((a^2 – a + 1)\) এবং ভাগশেষ \((a+2)\)।
(d) \((m^4 – 2m^3 – 7m^2 + 8m + 12)\) কে \((m^2 – m – 6)\) দিয়ে
সমাধান –

\(\therefore\) নির্ণেয় ভাগফল \((m^2 – m – 2)\) এবং ভাগশেষ \(0\)।
5. (a) \((6x^2a^3 – 4x^3a^2 + 8x^4a^2) \div 2a^2x^2\)
সমাধান –
\((6x^2a^3 – 4x^3a^2 + 8x^4a^2) \div 2a^2x^2\)= \( \frac{6x^2a^3 – 4x^3a^2 + 8x^4a^2}{2a^2x^2}\)
= \( \frac{6x^2a^3}{2a^2x^2} – \frac{4x^3a^2}{2a^2x^2} + \frac{8x^4a^2}{2a^2x^2}\)
= \( 3 \cdot a^{3-2} – 2 \cdot x^{3-2} + 4 \cdot x^{4-2}\)
= \( 3a – 2x + 4x^2\)
5. (b) \(\frac{2y^9x^5}{5x^2} \times \frac{125xy^5}{16x^4y^{10}}\)
সমাধান –
\(\frac{2y^9x^5}{5x^2} \times \frac{125xy^5}{16x^4y^{10}}\)= \( \frac{2}{5} \times \frac{125}{16} \times \frac{y^9 \cdot x^5 \cdot x \cdot y^5}{x^2 \cdot x^4 \cdot y^{10}}\)
= \( \frac{25}{8} \times \frac{y^{9+5} \cdot x^{5+1}}{x^{2+4} \cdot y^{10}}\)
= \( \frac{25}{8} \times \frac{y^{14} \cdot x^6}{x^6 \cdot y^{10}}\)
= \( \frac{25}{8} \times y^{14-10} \times x^{6-6}\)
= \( \frac{25}{8} \times y^4 \times x^0\)
= \( \frac{25y^4}{8}\)
5. (c) \(\frac{7a^4y^2}{9a^2} \times \frac{729a^6}{42y^6}\)
সমাধান –
\(\frac{7a^4y^2}{9a^2} \times \frac{729a^6}{42y^6}\)= \( \frac{7}{9} \times \frac{729}{42} \times \frac{a^4y^2}{a^2} \times \frac{a^6}{y^6}\)
= \( \frac{27}{2} \times \frac{a^{4+6}y^2}{a^2y^6}\)
= \( \frac{27}{2} \times \frac{a^{10}y^{2-6}}{a^2}\)
= \( \frac{27}{2} \times a^{10-2} y^{2-6}\)
= \( \frac{27}{2} \times a^8y^{-4}\)
= \( \frac{27a^8}{2y^4}\)
5. (d) \((p^2q^2r^5 – p^3q^5r^2 + p^5q^3r^2) \div p^2q^2r^2\)
সমাধান –
= \( \frac{p^2q^2r^5 – p^3q^5r^2 + p^5q^3r^2}{p^2q^2r^2}\)
= \( \frac{p^2q^2r^5}{p^2q^2r^2} – \frac{p^3q^5r^2}{p^2q^2r^2} + \frac{p^5q^3r^2}{p^2q^2r^2}\)
= \( p^{2-2}q^{2-2}r^{5-2} – p^{3-2}q^{5-2}r^{2-2} + p^{5-2}q^{3-2}r^{2-2}\)
= \( p^0q^0r^3 – p^1q^3r^0 + p^3q^1r^0\)
= \( r^3 – pq^3 + p^3q\)
6. কোনো ভাগ অঙ্কে ভাজক \((x-4)\), ভাগফল \((x^2+4x+4)\) ও ভাগশেষ \(3\) হলে ভাজ্য কত হিসাব করে লিখি।
সমাধান –
ভাজক = \( (x-4)\), ভাগফল = \( (x^2+4x+4)\) ও ভাগশেষ = \( 3\)
আমরা জানি, ভাজ্য = (ভাজক \(\times\) ভাগফল) \(+\) ভাগশেষ
\(\therefore\) ভাজ্য = \( (x-4) \times (x^2+4x+4) + 3\)
= \( x^3+4x^2 + 4x -4x^2 -16x -16 +3\)
= \( x^3 -12x -13\)
7. কোনো ভাগ অঙ্কে ভাজক \((a^2 +2a-1)\), ভাগফল \((5a-14)\) এবং ভাগশেষ \((35a -17)\) হলে ভাজ্য কত হবে হিসাব করে লিখি।
সমাধান –
ভাজক = \( (a^2 +2a-1)\), ভাগফল = \( (5a-14)\), ভাগশেষ = \( (35a -17)\)
আমরা জানি, ভাজ্য = (ভাজক \(\times\) ভাগফল) \(+\) ভাগশেষ
\(\therefore\) ভাজ্য = \( (a^2 +2a-1) \times (5a-14) + (35a -17)\)
= \( (5a^3+10a^2 -5a-14a^2-28a +14) +(35a -17)\)
= \( 5a^3+10a^2 -5a-14a^2-28a +14 + 35a -17\)
= \( 5a^3 -4a^2+ 2a -3\)
8. ভাগ করে ভাগফল ও ভাগশেষ লিখি
(i) \((x^2+ 11x +27) \div (x +6)\)
সমাধান –
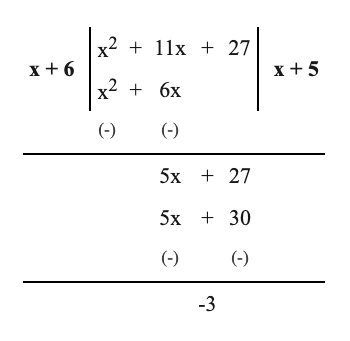
\(\therefore\) নির্ণেয় ভাগফল \((x+5)\) এবং ভাগশেষ \(-3\)।
(ii) \((81x^4+2) \div (3x-1)\)
সমাধান –

\(\therefore\) নির্ণেয় ভাগফল \((27x^3+9x^2+3x+1)\) এবং ভাগশেষ \(3\)।
(iii) \((63x^2 -19x -20) \div (9x^2+5)\)
সমাধান –
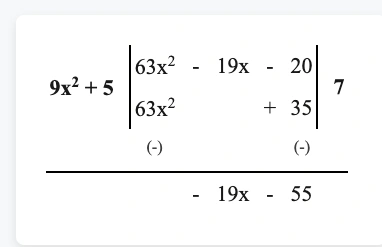
\(\therefore\) নির্ণেয় ভাগফল \(7\) এবং ভাগশেষ \((-19x-55)\)।
(iv) \((x^3 – x^2 -8x-13) \div (x^2+3x+3)\)
সমাধান –
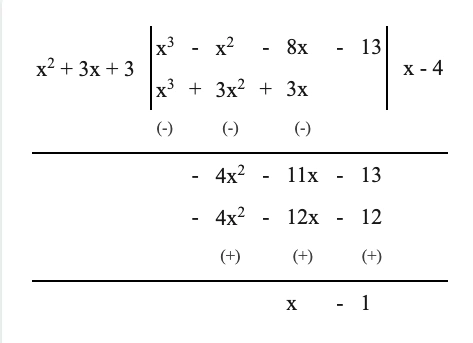
\(\therefore\) নির্ণেয় ভাগফল \((x-4)\) এবং ভাগশেষ \((x-1)\)।
এই আর্টিকেলে অষ্টম শ্রেণির গণিতের ‘বীজগাণিতিক সংখ্যামালার গুন ও ভাগ’ অধ্যায়ের ‘কষে দেখি – 4.2’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরেছি। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে। কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment