পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) অষ্টম শ্রেণির গণিত পাঠ্যবইয়ের ষষ্ঠ অধ্যায় হলো ‘পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ’। এই পোস্টে আমরা ‘কষে দেখি – 6’-এর সমস্ত প্রশ্নের সহজ ও নির্ভুল সমাধান নিয়ে আলোচনা করেছি। আশা করি, এই নোটসগুলো তোমাদের গণিত শিখতে এবং পরীক্ষার প্রস্তুতিতে দারুণভাবে সহায়তা করবে।

1. মনে মনে ভাবি ও লিখি
(a) দুটি সূক্ষ্মকোণ পরস্পর পূরক হতে পারে কিনা লিখি।
(b) দুটি সূক্ষ্মকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি।
(c) একটি সূক্ষ্মকোণ ও একটি স্থূলকোণ পরস্পর পূরক হতে পারে কিনা লিখি। দুটি সমকোণ পরস্পর পূরক হতে পারে কিনা লিখি।
(d) দুটি স্থূলকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি।
(e) দুটি সমকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি।
(f) একটি সূক্ষ্মকোণ ও একটি স্থূলকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি।
(g) দুটি সন্নিহিত কোণ পরস্পর পূরক হতে পারে কিনা লিখি।
(h) দুটি সন্নিহিত কোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি।
সমাধান –
(a) দুটি সূক্ষ্মকোণ পরস্পর পূরক হতে পারে কিনা লিখি।
দুটি সূক্ষ্মকোণ পরস্পর পূরক হতে পারে।
উদাহরণ – দুটি সূক্ষ্মকোণ \(50^{\circ}\) ও \(40^{\circ}\) এবং \(50^{\circ} + 40^{\circ} = 90^{\circ}\)
(b) দুটি সূক্ষ্মকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি।
দুটি সূক্ষ্মকোণ পরস্পর সম্পূরক হতে পারে না।
উদাহরণ – দুটি সূক্ষ্মকোণ \(80^{\circ}\) ও \(70^{\circ}\) এবং \(80^{\circ} + 70^{\circ} = 150^{\circ} \neq 180^{\circ}\)
(c) একটি সূক্ষ্মকোণ ও একটি স্থূলকোণ পরস্পর পূরক হতে পারে কিনা লিখি। দুটি সমকোণ পরস্পর পূরক হতে পারে কিনা লিখি।
একটি সূক্ষ্মকোণ ও একটি স্থূলকোণ পরস্পর পূরক হতে পারে না। দুটি সমকোণ পরস্পর পূরক হতে পারে না।
উদাহরণ – একটি সূক্ষ্মকোণ \(20^{\circ}\) ও একটি স্থূলকোণ \(150^{\circ}\) এবং \(20^{\circ} + 150^{\circ} = 170^{\circ} \neq 90^{\circ}\)
আবার, \(90^{\circ} + 90^{\circ} = 180^{\circ} \neq 90^{\circ}\)
(d) দুটি স্থূলকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি।
দুটি স্থূলকোণ পরস্পর সম্পূরক হতে পারে না।
উদাহরণঃ দুটি স্থূলকোণ যথাক্রমে \(95^{\circ}\) এবং \(105^{\circ}\) এবং \(95^{\circ} + 105^{\circ} = 200^{\circ} \neq 180^{\circ}\)
(e) দুটি সমকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি।
দুটি সমকোণ পরস্পর সম্পূরক হতে পারে।
উদাহরণ – \(90^{\circ} + 90^{\circ} = 180^{\circ}\)
(f) একটি সূক্ষ্মকোণ ও একটি স্থূলকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি।
একটি সূক্ষ্মকোণ ও একটি স্থূলকোণ পরস্পর সম্পূরক হতে পারে।
উদাহরণ – \(140^{\circ} + 40^{\circ} = 180^{\circ}\)
(g) দুটি সন্নিহিত কোণ পরস্পর পূরক হতে পারে কিনা লিখি।
দুটি সন্নিহিত কোণ পরস্পর পূরক হতে পারে।
(h) দুটি সন্নিহিত কোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি।
দুটি সন্নিহিত কোণ পরস্পর সম্পূরক হতে পারে।
2. নীচের সন্নিহিত কোণগুলি আঁকি ও কোন কোণগুলি পরস্পর পূরক অথবা সম্পূরক লিখি
\(45^{\circ}, 45^{\circ}; ; 120^{\circ}, 30^{\circ}; ; 70^{\circ}, 110^{\circ}; ; 42^{\circ}, 48^{\circ}; ; 37^{\circ}, 43^{\circ}; ; 85^{\circ}, 95^{\circ};\)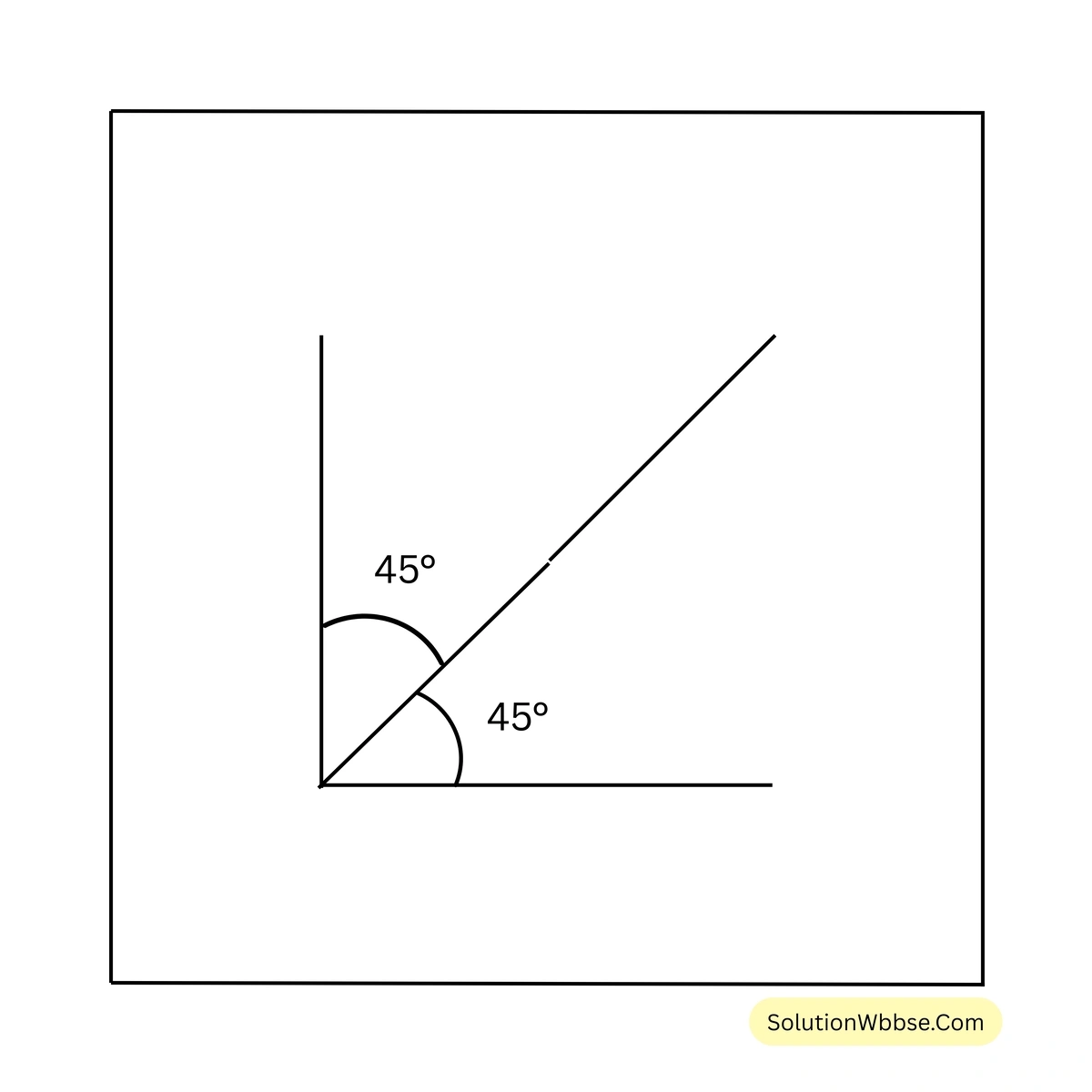
\(\therefore\) \(45^{\circ}\) এবং \(45^{\circ}\) পরস্পর পূরক কোণ।
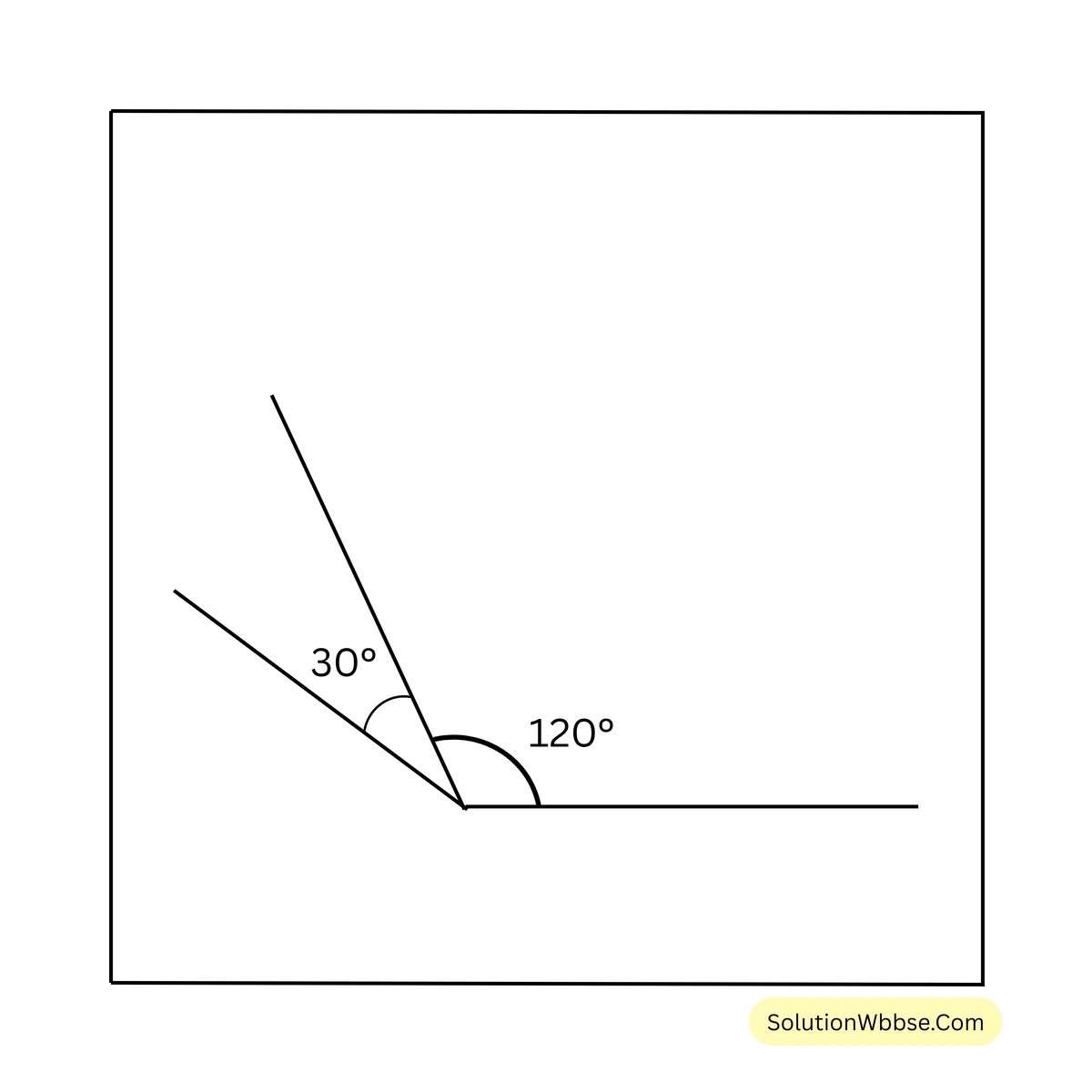
\(30^{\circ}\) ও \(120^{\circ}\) পরস্পর পূরক বা সম্পূরক কোণ নয়।
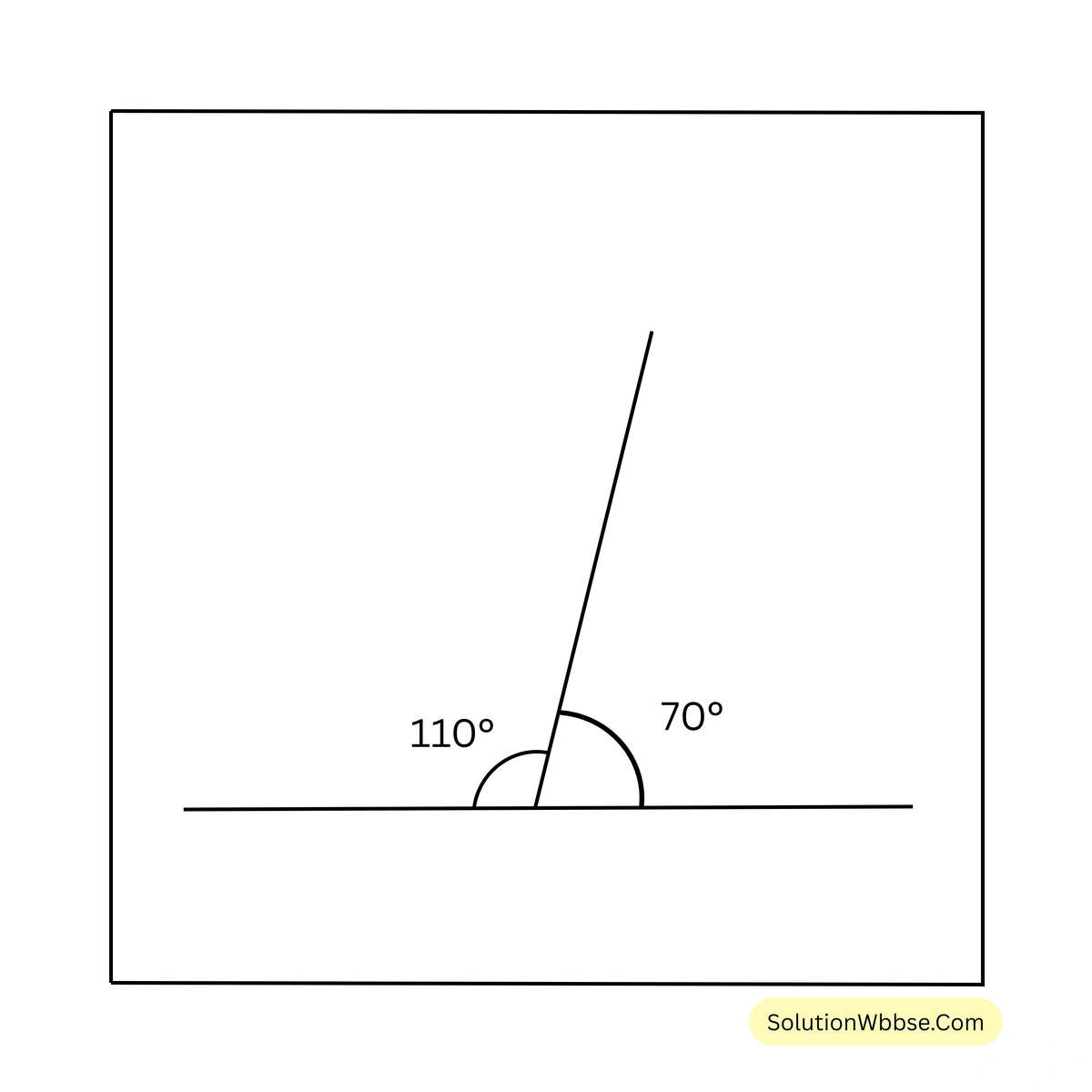
\(\therefore\) \(110^{\circ}\) ও \(70^{\circ}\) পরস্পর সম্পূরক কোণ।
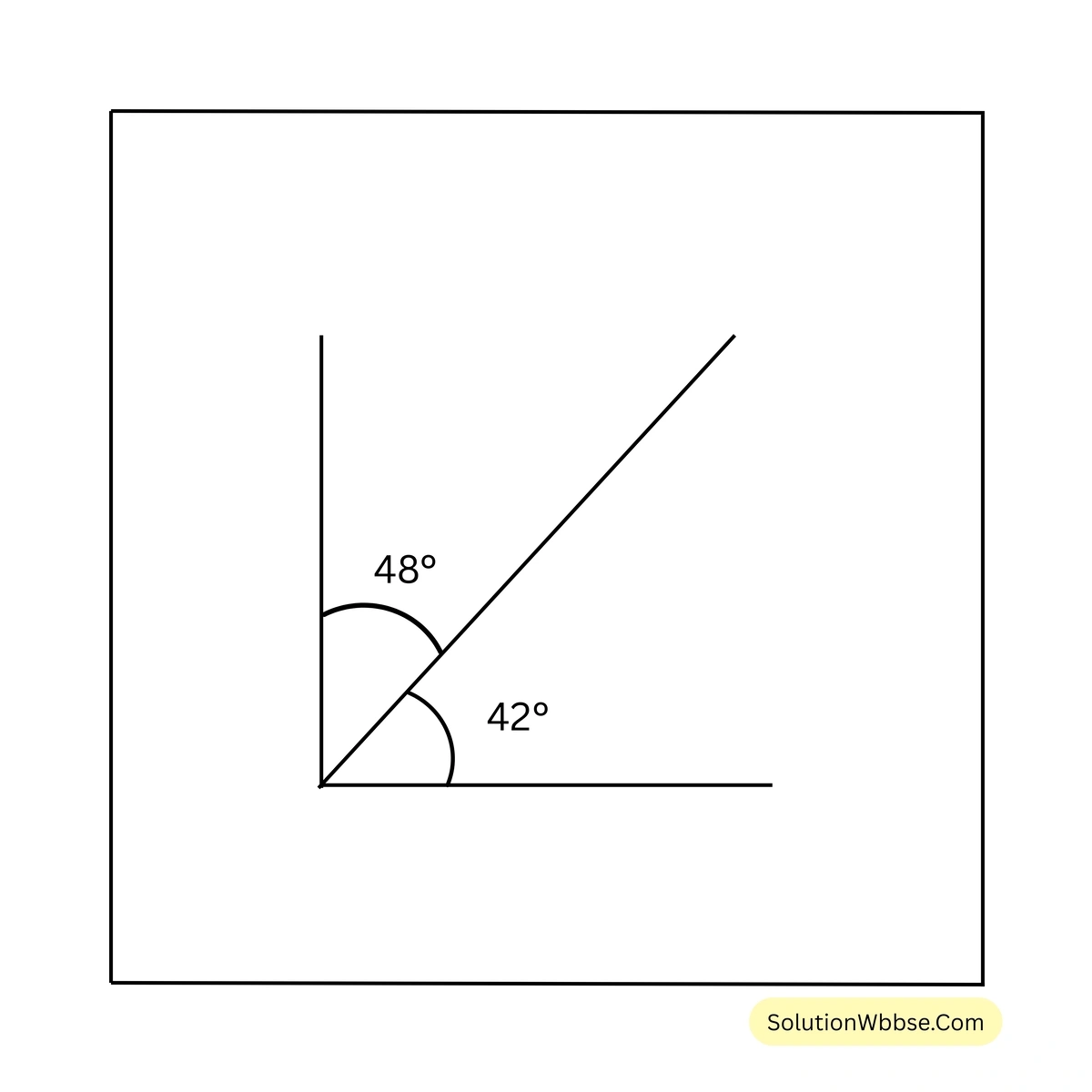
\(\therefore\) \(48^{\circ}\) এবং \(42^{\circ}\) পরস্পর পূরক কোণ।
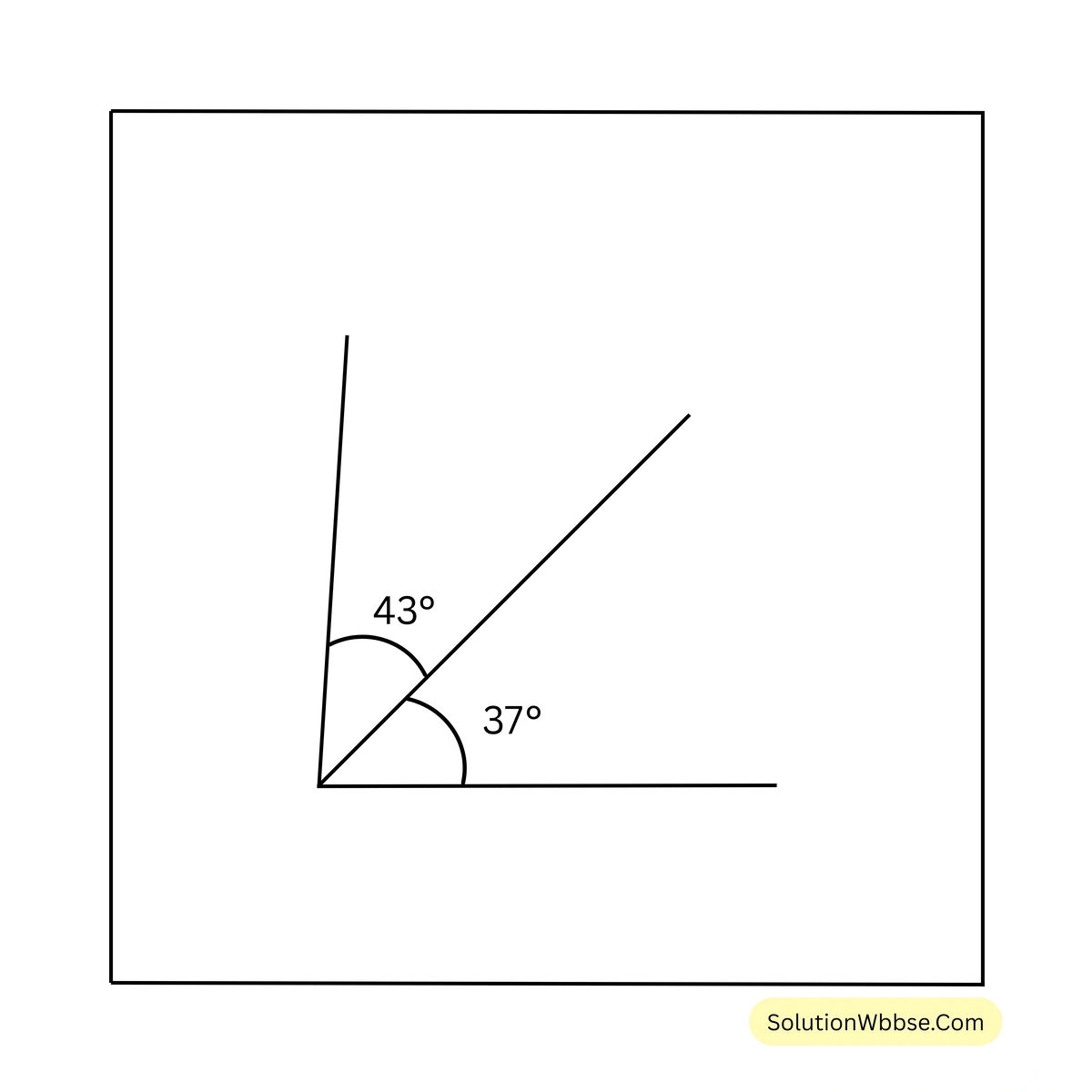
\(43^{\circ}\) ও \(37^{\circ}\) পরস্পর পূরক বা সম্পূরক কোণ নয়।
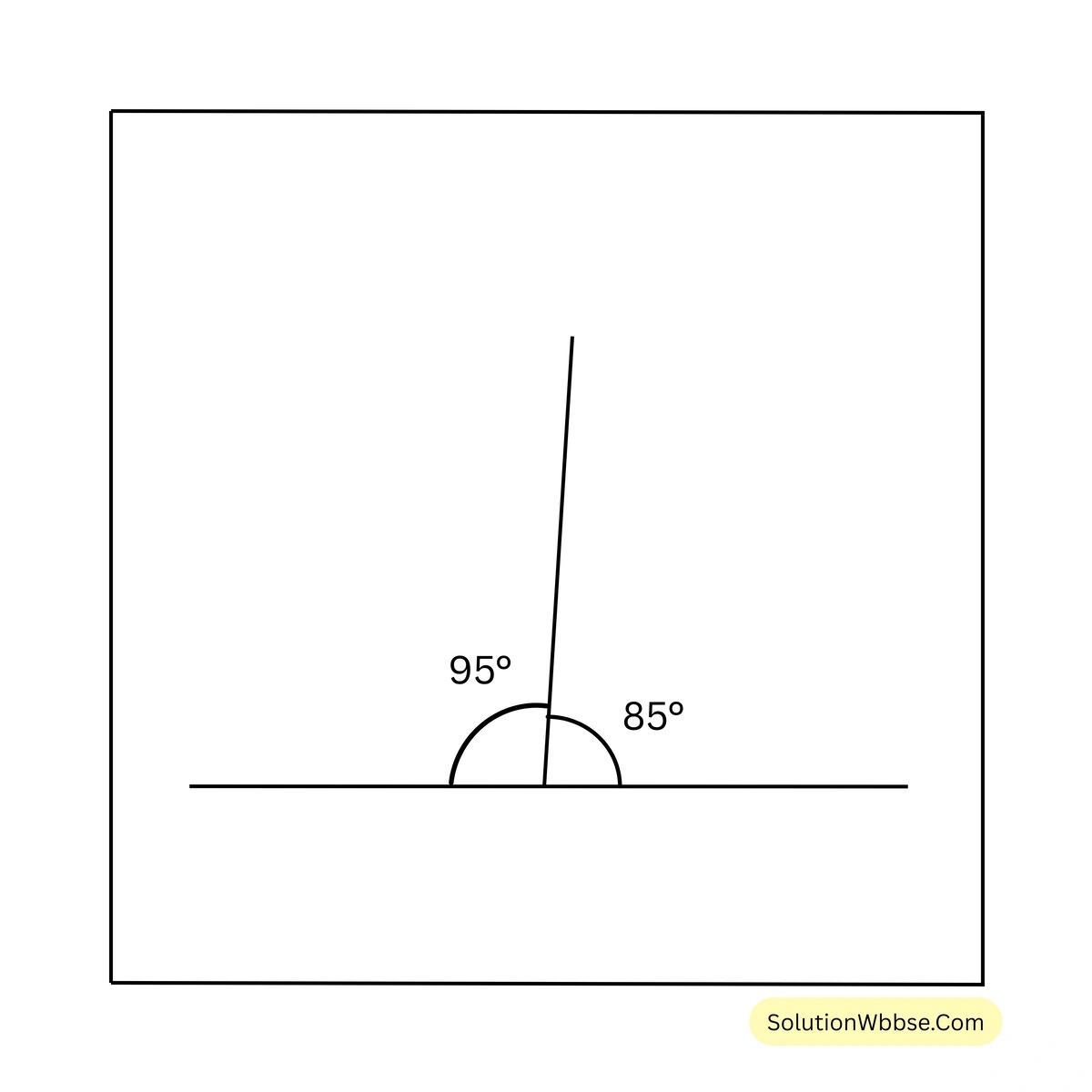
\(85^{\circ}\) ও \(95^{\circ}\) কোণদুটি পরস্পর সম্পূরক কোণ।
3. নীচের কোণগুলি দেখি ও কোন কোন কোণদুটি পরস্পর পূরক কোণ লিখি
\(31^{\circ}, 47^{\circ}, 64^{\circ}, 29^{\circ}, 43^{\circ}, 59^{\circ}, 17^{\circ}, 26^{\circ}\)উত্তর –
\(31^{\circ}\) এর পূরক কোণ = \(90^{\circ} – 31^{\circ} = 59^{\circ}\)
\(47^{\circ}\) এর পূরক কোণ = \(90^{\circ} – 47^{\circ} = 43^{\circ}\)
\(64^{\circ}\) এর পূরক কোণ = \(90^{\circ} – 64^{\circ} = 26^{\circ}\)
\(29^{\circ}\) এর পূরক কোণ = \(90^{\circ} – 29^{\circ} = 61^{\circ}\)
∴ পরস্পরের পূরক কোণগুলি – \((31^{\circ}, 59^{\circ}), (47^{\circ}, 43^{\circ}), (64^{\circ}, 26^{\circ})\)
4. নীচের কোণগুলি দেখি ও কোন কোন কোণগুলি পরস্পর সম্পূরক কোণ লিখি
\(47^{\circ}, 58^{\circ}, 69^{\circ}, 75^{\circ}, 133^{\circ}, 105^{\circ}, 122^{\circ}, 125^{\circ}\)উত্তর –
\(47^{\circ}\) এর সম্পূরক কোণ = \(180^{\circ} – 47^{\circ} = 133^{\circ}\)
\(58^{\circ}\) এর সম্পূরক কোণ = \(180^{\circ} – 58^{\circ} = 122^{\circ}\)
\(69^{\circ}\) এর সম্পূরক কোণ = \(180^{\circ} – 69^{\circ} = 111^{\circ}\)
\(75^{\circ}\) এর সম্পূরক কোণ = \(180^{\circ} – 75^{\circ} = 105^{\circ}\)
∴ পরস্পরের সম্পূরক কোণগুলি – \((47^{\circ}, 133^{\circ}), (58^{\circ}, 122^{\circ}), (75^{\circ}, 105^{\circ})\)
5. সন্নিহিত কোণ কাকে বলে লিখি ও নীচের কোন কোণগুলি সন্নিহিত কোণ বুঝে লিখি
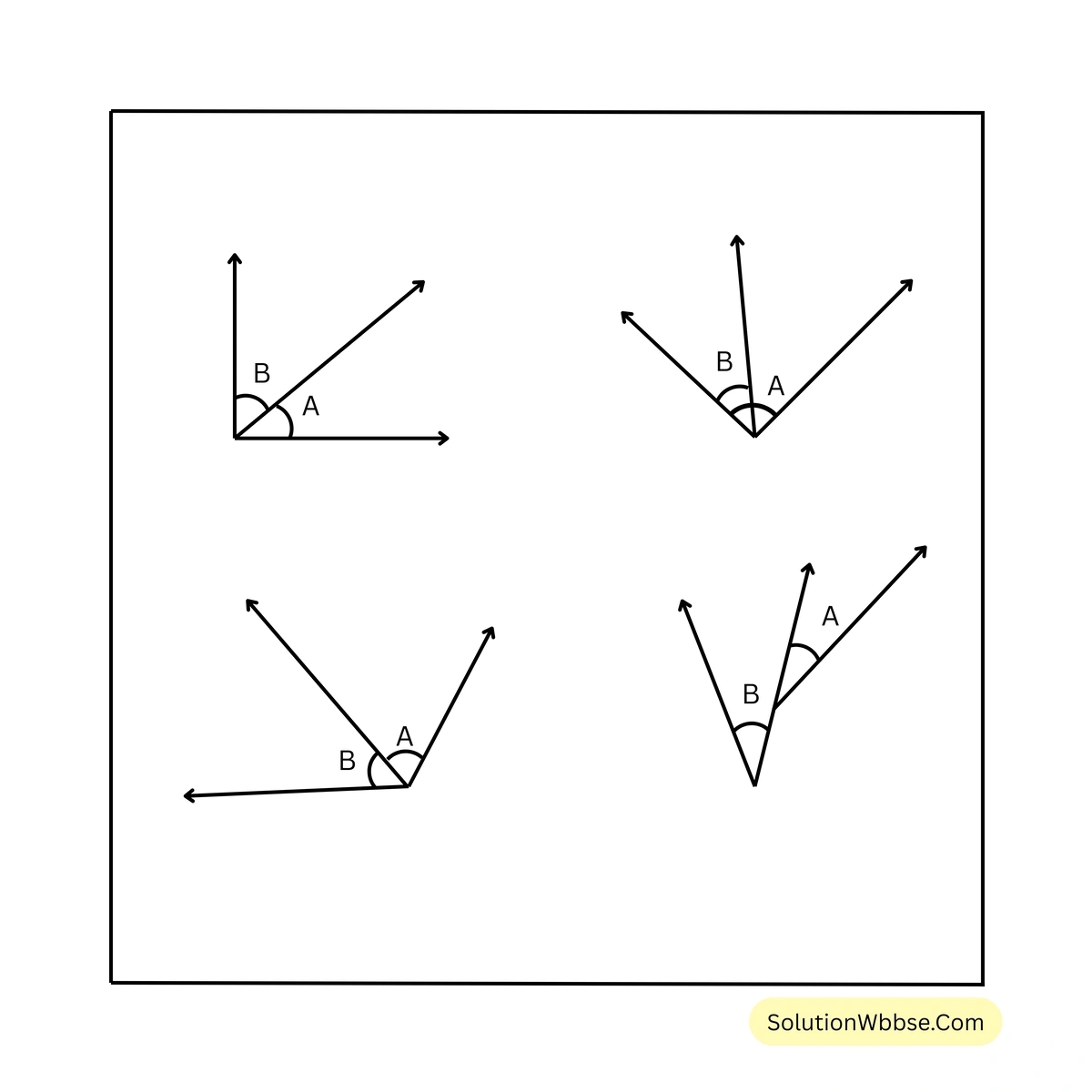
উত্তর – যখন দুটি কোণের শীর্ষবিন্দু একই ও কোণ দুটি একই সাধারণ বাহুর দুপাশে অবস্থিত হয় তখন ওই কোণ দুটিকে সন্নিহিত কোণ বলা হয়।
প্রশ্নের প্রথম, দ্বিতীয় ও তৃতীয় ছবি তিনটি সন্নিহিত কোণের ছবি। কারণ এই তিনটি ছবির প্রত্যেকটির শীর্ষবিন্দু এক এবং একই সাধারণ বাহুর দুপাশে অবস্থিত A ও B কোণ দুটি।
কিন্তু চতুর্থ ছবিটির কোণ দুটি সন্নিহিত কোণ নয়; কারণ A ও B কোণের শীর্ষবিন্দু পৃথক।
6. নিজে চাঁদার সাহায্যে সন্নিহিত কোণ আঁকি যার কোণদুটির মান হলো \(35^\circ\), \(45^\circ\); \(18^\circ\), \(42^\circ\); \(32^\circ\), \(90^\circ\); \(73^\circ\), \(63^\circ\)
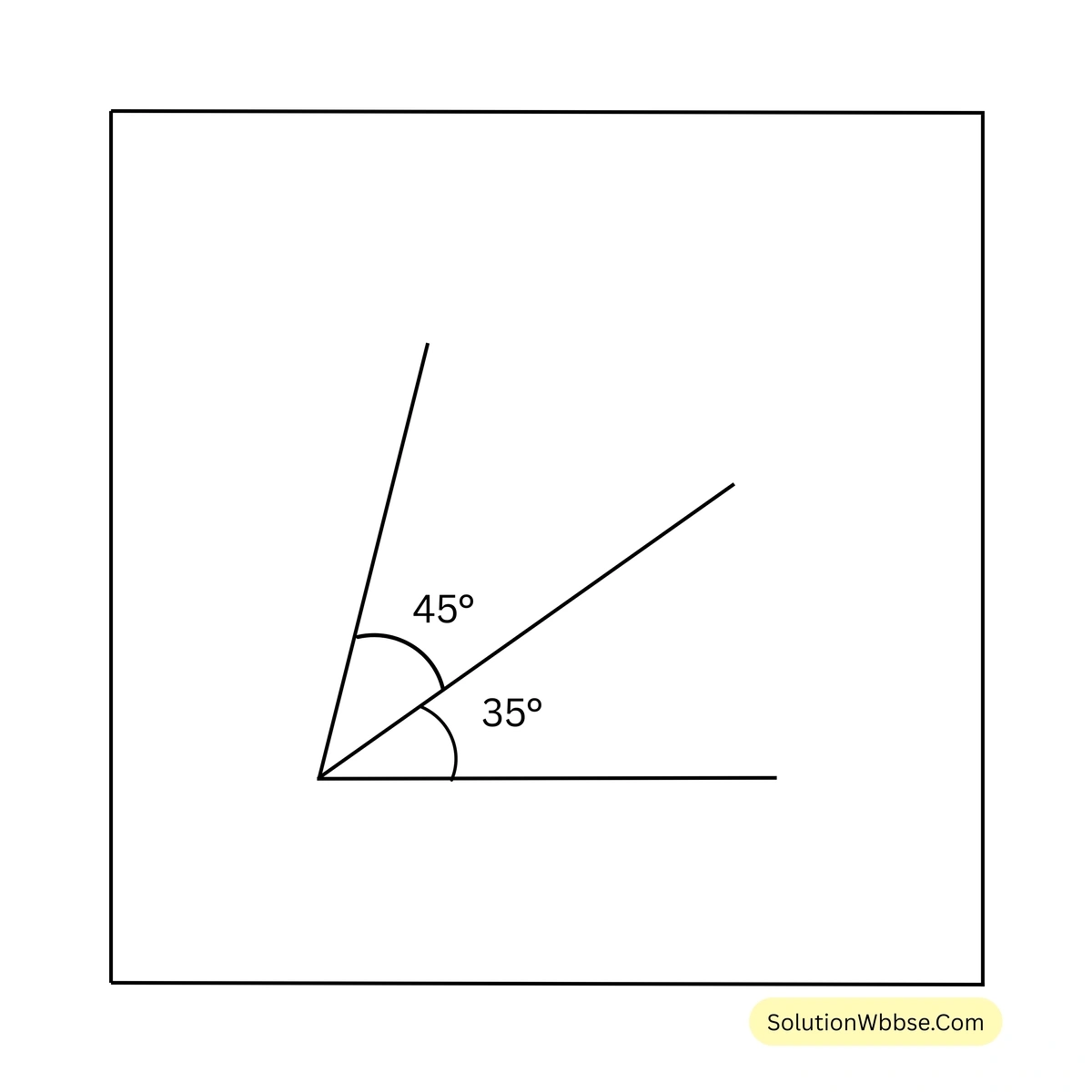
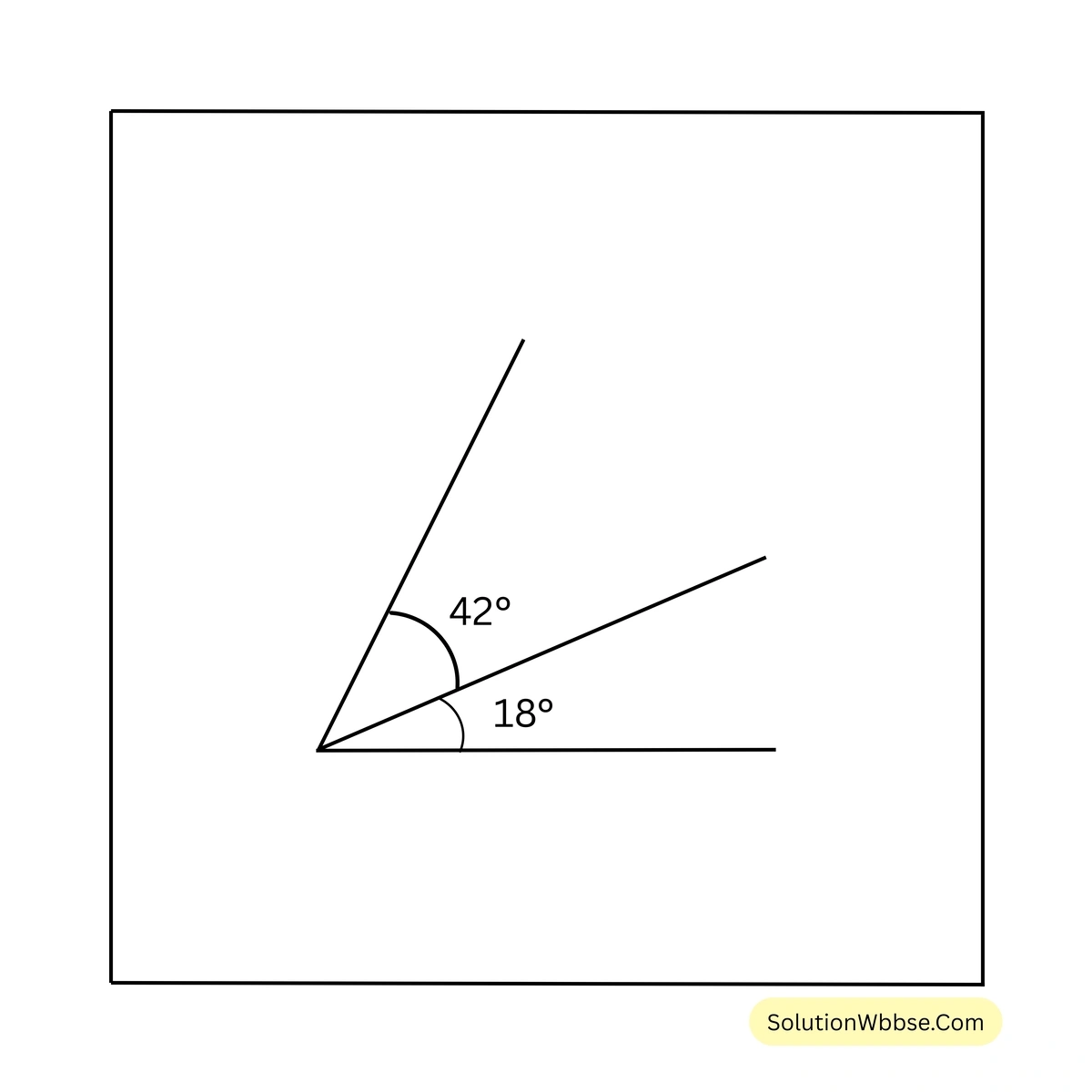
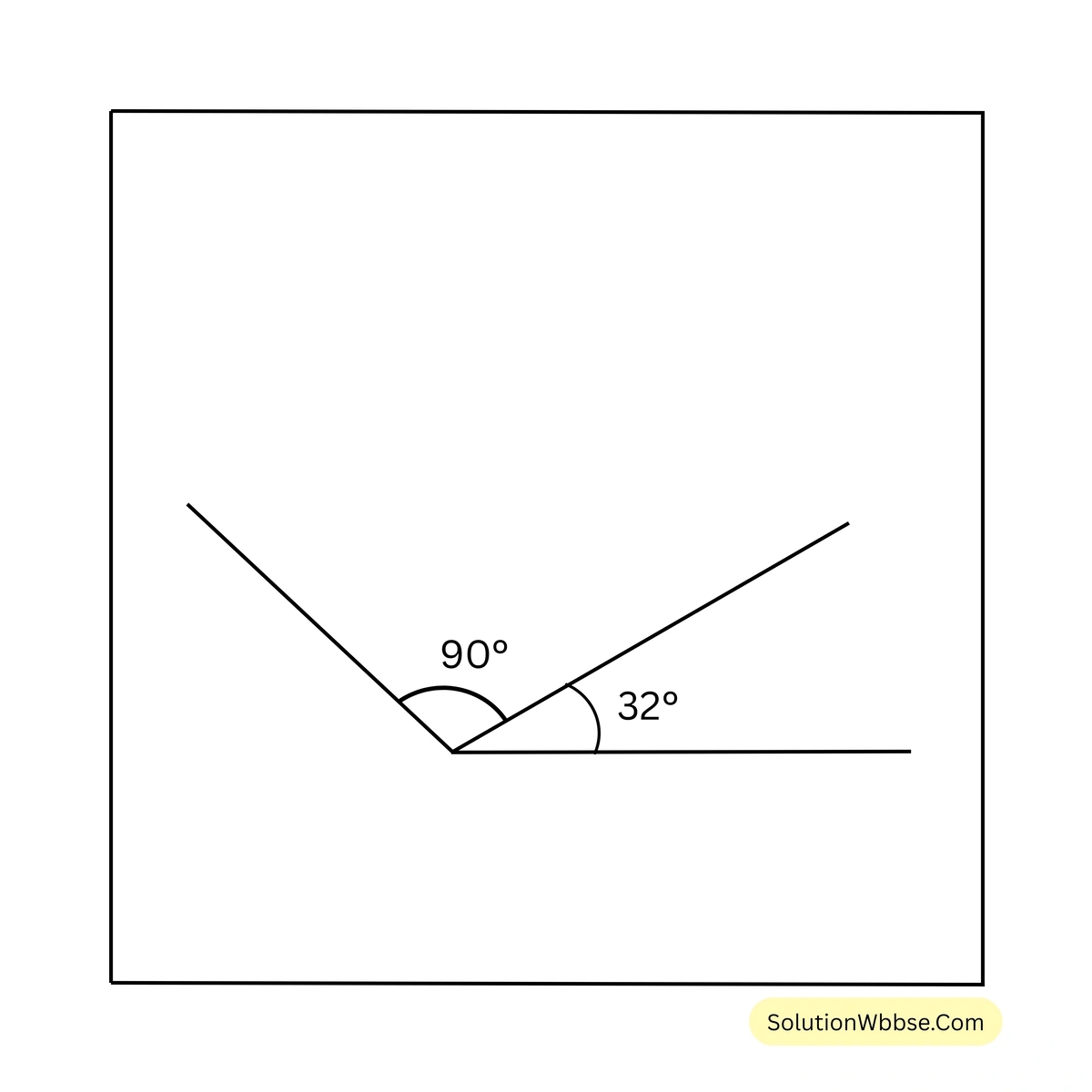
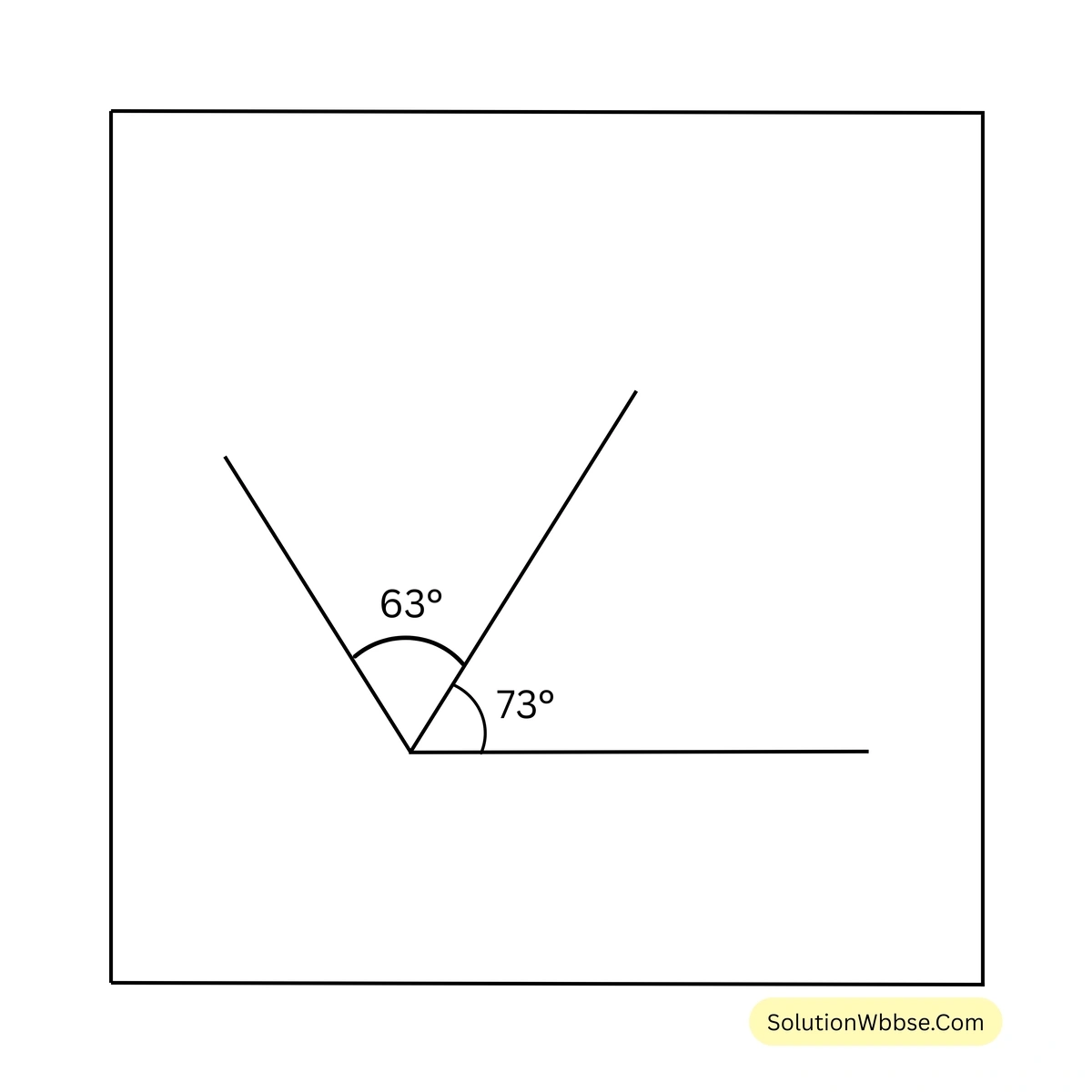
7. সায়ন্তনী একটি সরলরেখা AB আঁকল। আমি সেই সরলরেখার উপর কোনো বিন্দু P-তে অপর একটি রশ্মি PQ আঁকলাম। এর ফলে দুটি সন্নিহিত কোণ \(\angle BPQ\) ও \(\angle APQ\) তৈরি হলো। চাঁদার সাহায্যে মেপে \(\angle BPQ\) ও \(\angle APQ\)-এর পরিমাপ লিখি ও \(\angle BPQ + \angle APQ =\) কত লিখি।
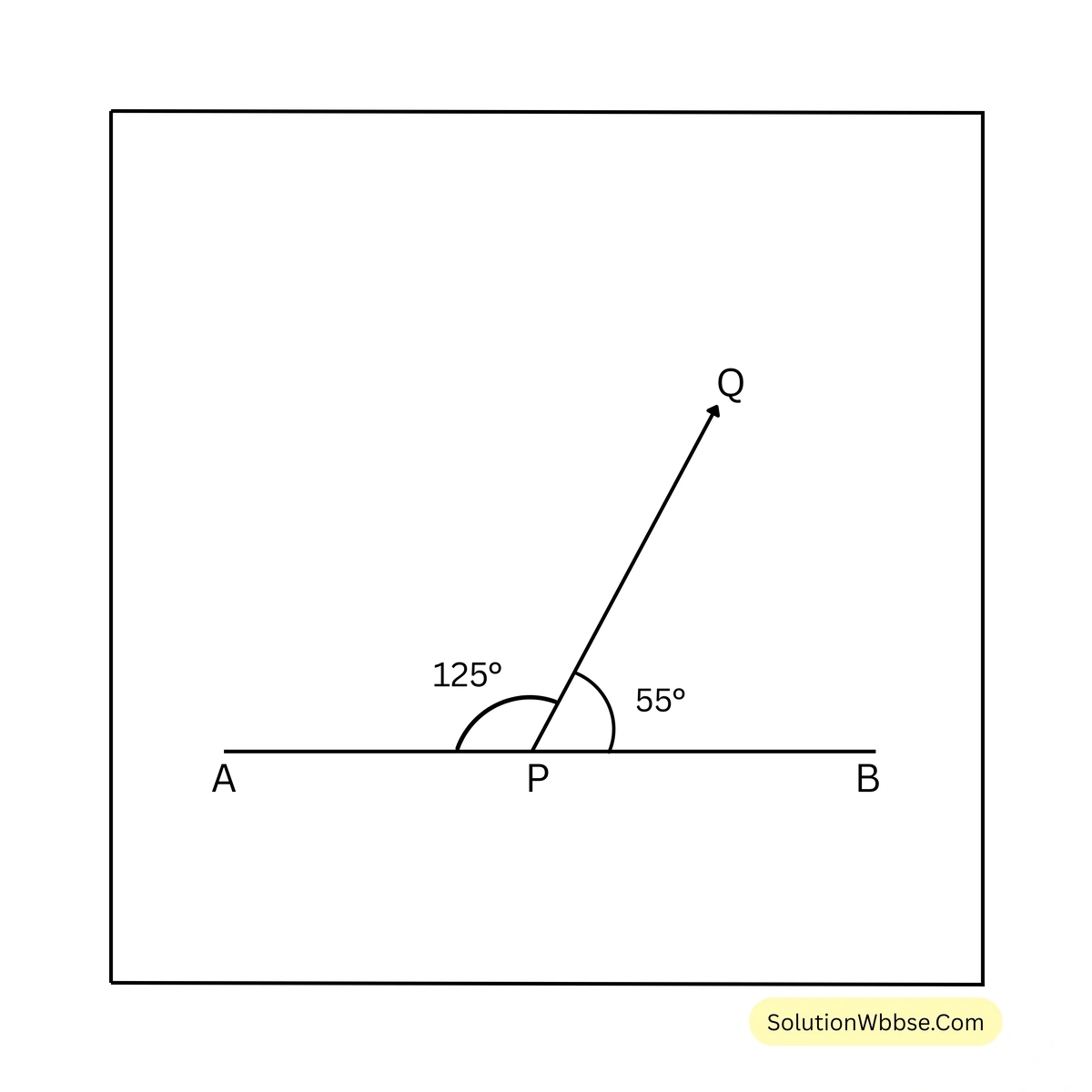
\(\angle APQ = 125^{\circ} \quad\) এবং\( \quad \angle BPQ = 55^{\circ}\)
\(\therefore \angle PBQ + \angle PQA = 55^{\circ} + 125^{\circ} = 180^{\circ}\)8. শাকিল দুটি সন্নিহিত কোণ \(\angle ABC\) ও \(\angle ABD\) আঁকল যাদের সমষ্টি \(180^\circ\); আমিও শাকিলের মত \(\angle ABC\) ও \(\angle ABD\) এঁকে দেখি D, B ও C বিন্দু তিনটি একই সরলরেখায় আছে কিনা।
উত্তর –
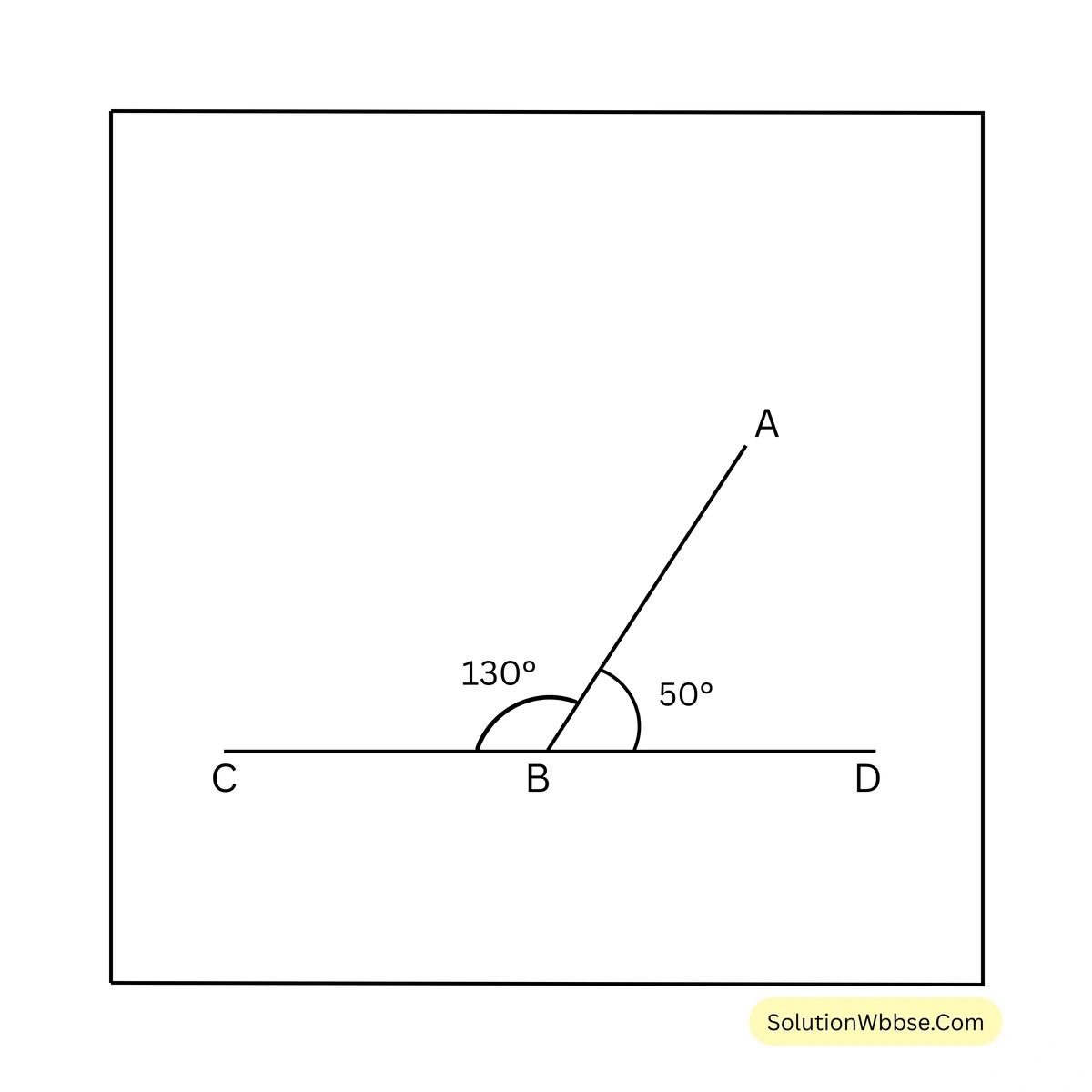
শাকিলের আঁকা দুটি সন্নিহিত কোণ \(\angle ABC\) ও \(\angle ABD\) এবং \(\angle ABC + \angle ABD = 180^\circ\)

আমিও শাকিলের মত দুটি কোণ \(\angle ABC\) এবং \(\angle ABD\) আঁকলাম এবং দেখলাম যে D, B এবং C একই সরলরেখায় অবস্থিত।
9. ছবি থেকে x -এর মান নির্ণয় করি।
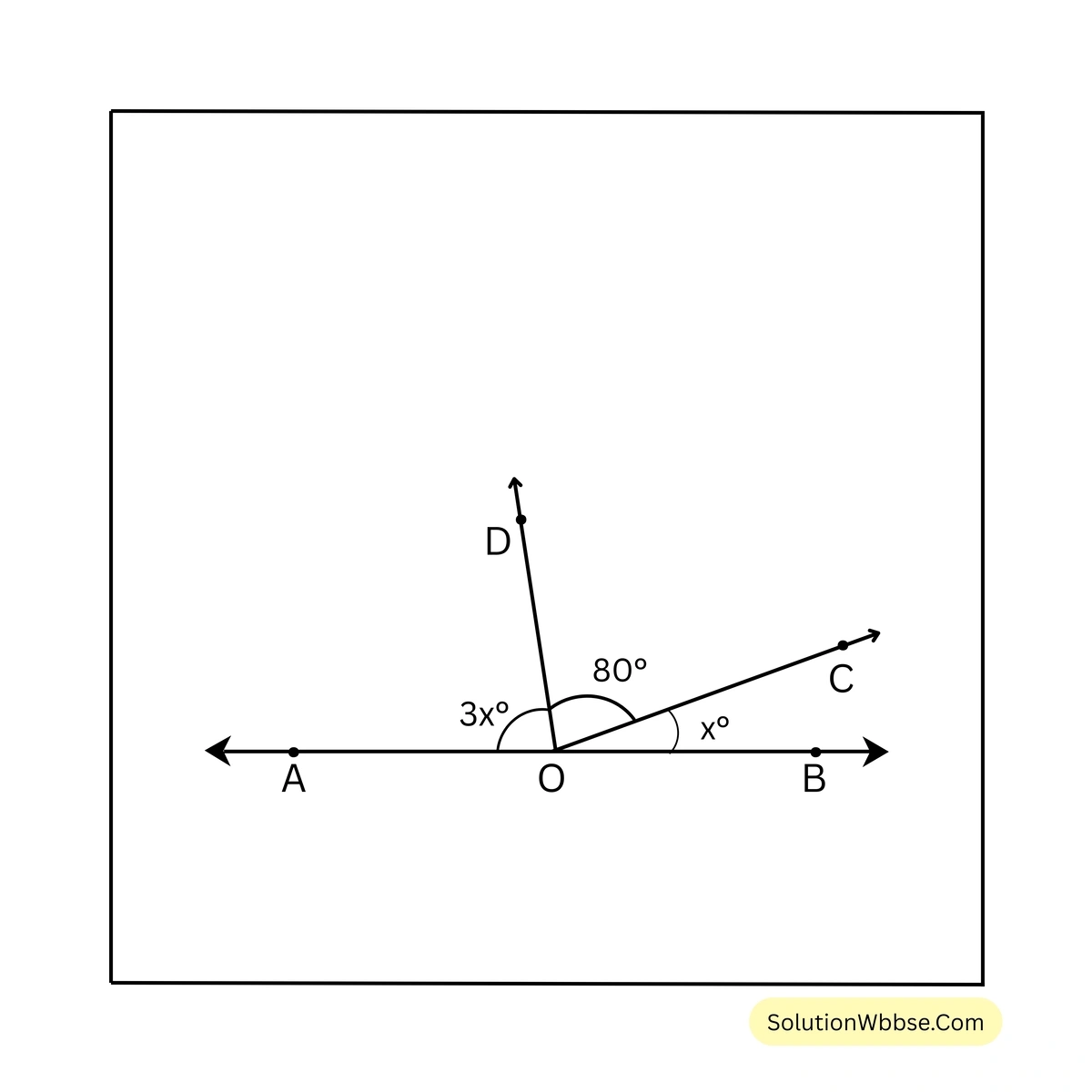
সমাধান – চিত্র থেকে পাই, \(\angle AOD = 3x\), \(\angle COD = 80^\circ\) এবং \(\angle BOC = x\)
যেহেতু, A, O এবং B বিন্দুত্রয় একই সরলরেখায় অবস্থিত
\(\therefore \angle AOD + \angle COD + \angle BOC = 180^\circ\)বা, \(3x + 80^\circ + x = 180^\circ\)
বা, \(4x + 80^\circ = 180^\circ\)
বা, \(4x = 180^\circ – 80^\circ\)
বা, \(4x = 100^\circ\)
বা, \(x = \frac{100^\circ}{4}\)
বা, \(x = 25^\circ\)
\(\therefore x = 25^\circ\)10. ছবিতে \(\angle AOP\), \(\angle BOP\) –এর চেয়ে \(140^\circ\) বেশি। \(\angle AOP\) ও \(\angle BOP\) -এর মান নির্ণয় করি।
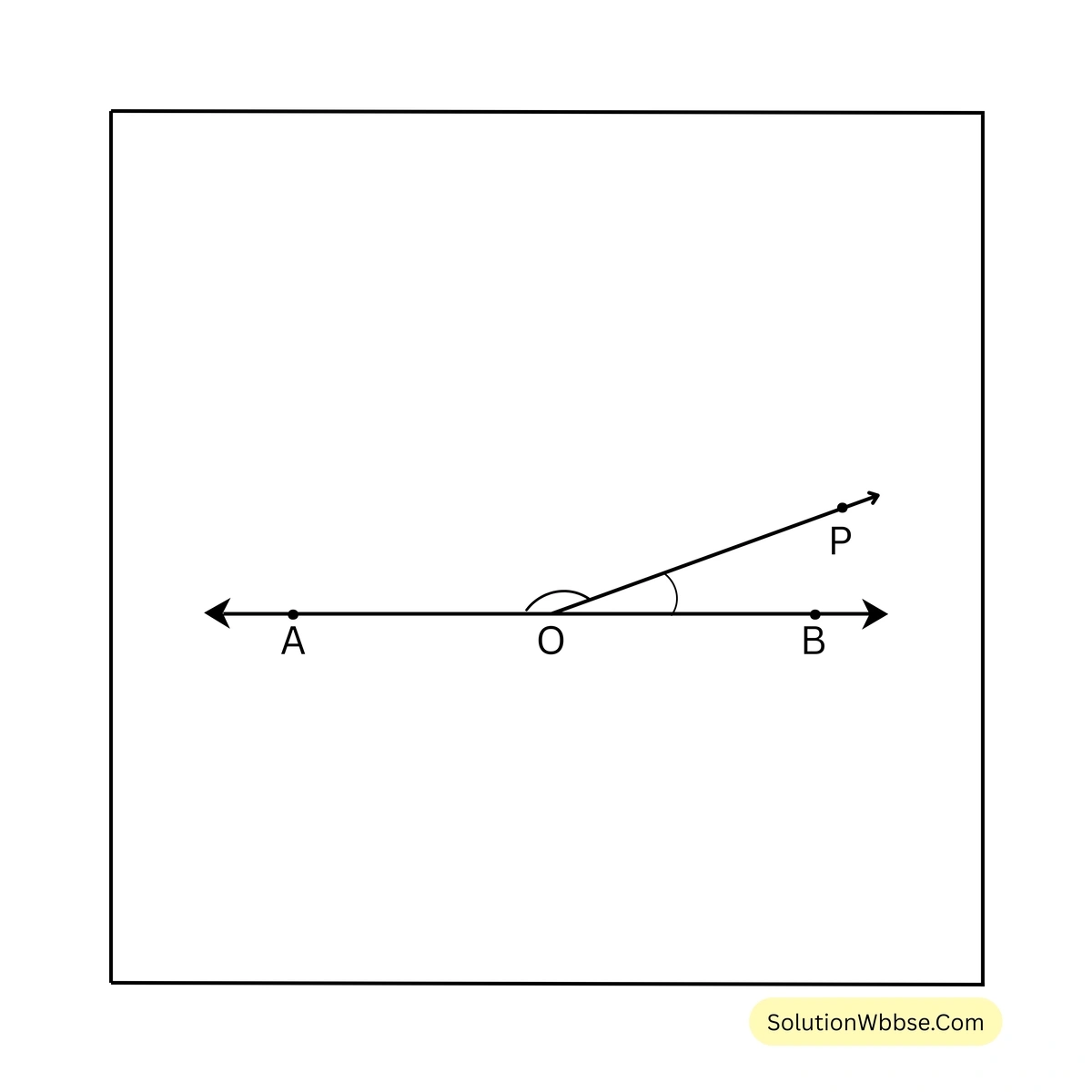
সমাধান – \(\angle AOP\), \(\angle BOP\) –এর চেয়ে \(140^\circ\) বেশি
\(\therefore \angle AOP = \angle BOP + 140^\circ\)চিত্র থেকে পাই,
\(\angle AOP + \angle BOP = 180^\circ\)বা, \(\angle BOP + 140^\circ + \angle BOP = 180^\circ\)
বা, \(2 \angle BOP = 180^\circ – 140^\circ\)
বা, \(2 \angle BOP = 40^\circ\)
বা, \(\angle BOP = \frac{40^\circ}{2}\)
বা, \(\angle BOP = 20^\circ\)
\(\therefore \angle AOP = \angle BOP + 140^\circ = 20^\circ + 140^\circ = 160^\circ\)11. দুটি সন্নিহিত কোণের মান \(35^\circ\) ও \(145^\circ\); সন্নিহিত কোণের বহিঃস্থ বাহু দুটি কীভাবে অবস্থিত লিখি।
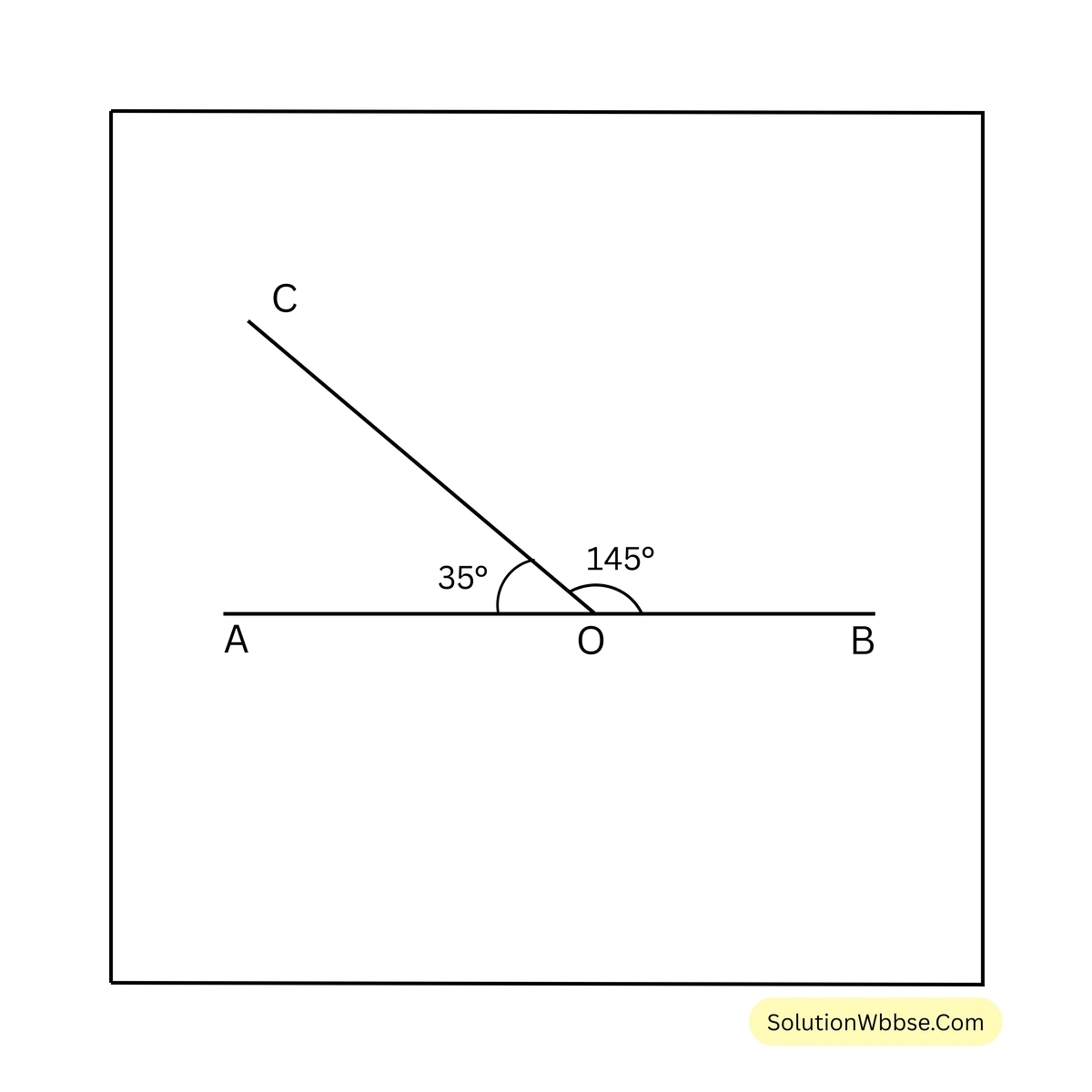
সমাধান –
সন্নিহিত কোণ দুটির সমষ্টি \(35^\circ + 145^\circ = 180^\circ\)
\(\therefore\) দুটি সন্নিহিত কোণ \(35^\circ\) ও \(145^\circ\) একই সরলরেখায় অবস্থিত।
12. ছবিতে OA ও OE কীভাবে অবস্থিত লিখি।
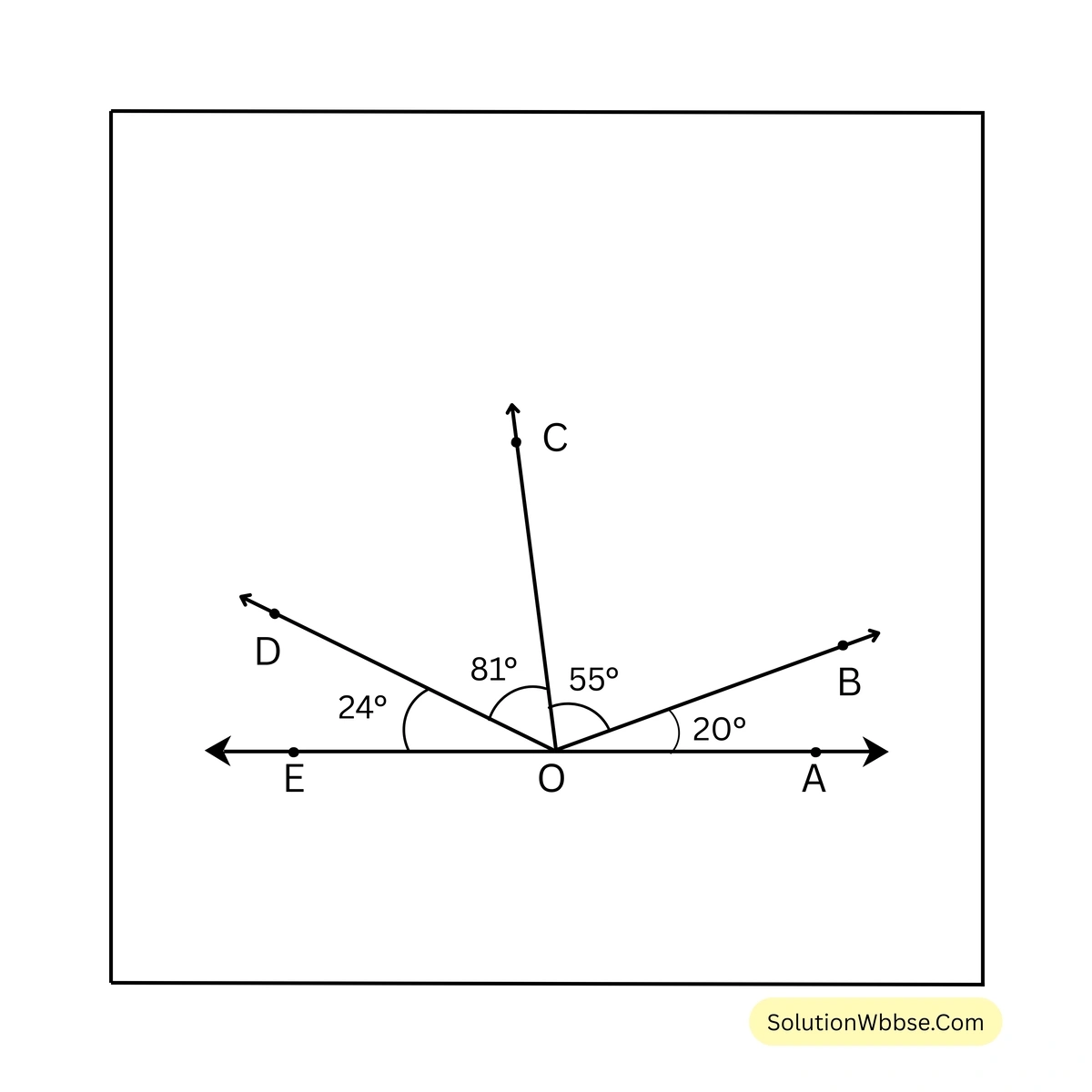
সমাধান –
চিত্রে, \(\angle COA\) এবং \(\angle COE\) পরস্পর সন্নিহিত কোণ।
\(\angle COA + \angle COE\)= \( \angle BOC + \angle AOB + \angle COD + \angle DOE\)
= \( 55^\circ + 20^\circ + 81^\circ + 24^\circ\)
= \( 180^\circ\)
\(\therefore \angle COA\) এবং \(\angle COE\) সন্নিহিত কোণ দুটির সমষ্টি \(180^\circ\)
\(\therefore\) OA এবং OE একই সরলরেখায় অবস্থিত।
এই আর্টিকেলে অষ্টম শ্রেণির গণিতের ‘পূরক কোণ, সম্পূরক কোণ ও সন্নিহিত কোণ’ অধ্যায়ের ‘কষে দেখি – 6’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরেছি। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে। কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment