পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) অষ্টম শ্রেণির গণিত পাঠ্যবইয়ের অষ্টম অধ্যায় হলো ‘সমান্তরাল সরলরেখা ও ছেদকের ধর্ম ’। এই পোস্টে আমরা ‘কষে দেখি – 8’-এর সমস্ত প্রশ্নের সহজ ও নির্ভুল সমাধান নিয়ে আলোচনা করেছি। আশা করি, এই নোটসগুলো তোমাদের গণিত শিখতে এবং পরীক্ষার প্রস্তুতিতে দারুণভাবে সহায়তা করবে।

1. চন্দ্রা লাইন টানা খাতার পাতা নিল। দুটি লাইনের মাঝে একটি ছেদক টানল। এর ফলে 4 জোড়া অনুরূপ কোণ, 2 জোড়া একান্তর কোণ ও 2 জোড়া একই পাশের অন্তঃস্থ কোণ তৈরি হলো। তাদের খুঁজে দিই ও লিখি। চাঁদার সাহায্যে মেপে যাচাই করি যে
(i) অনুরূপ কোণগুলি পরস্পর সমান,
(ii) একান্তর কোণগুলি পরস্পর সমান ও
(iii) একই পাশের অন্তঃস্থ কোণগুলি পরস্পর সম্পূরক।
সমাধান –
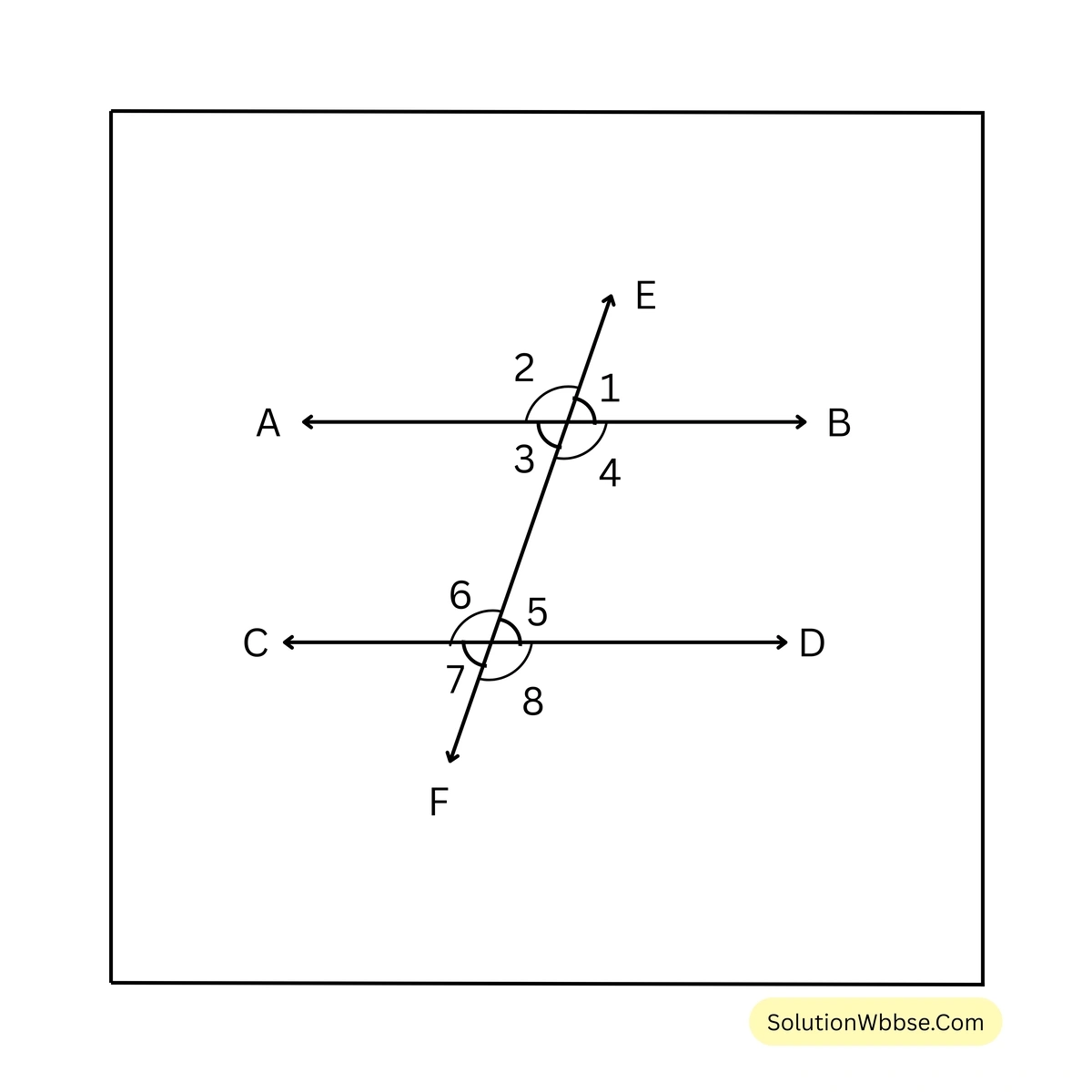
ধরি, AB ও CD হল দুটি লাইন। ছেদকটি হল EF, AB ও CD সরলরেখা দুটিকে EF ছেদ করার ফলে \(\angle 1\), \(\angle 2\), \(\angle 3\), \(\angle 4\), \(\angle 5\), \(\angle 6\), \(\angle 7\), \(\angle 8\) কোণগুলি উৎপন্ন হল।
\(\therefore\) অনুরূপ কোণগুলি হল, (\(\angle 1\), \(\angle 5\)), (\(\angle 2\), \(\angle 6\)), (\(\angle 3\), \(\angle 7\)), ও (\(\angle 4\), \(\angle 8\))
একান্তর কোণগুলি হল (\(\angle 3\), \(\angle 5\)), (\(\angle 4\), \(\angle 6\))
এবং একই দিকের অন্তঃস্থ কোণ (\(\angle 4\), \(\angle 5\)), (\(\angle 3\), \(\angle 6\))
চাঁদার সাহায্যে মেপে পেলাম,
\(\angle 1 = 45^\circ\), \(\angle 2 = 135^\circ\), \(\angle 3 = 45^\circ\), \(\angle 4 = 135^\circ\), \(\angle 5 = 45^\circ\), \(\angle 6 = 135^\circ\),
চাঁদার সাহায্যে মেপে পেলাম,
(i) অনুরূপ কোণগুলি হল –
\(\angle 1 = \angle 5 = 45^\circ\), \(\angle 2 = \angle 6 = 135^\circ\), \(\angle 3 = \angle 7 = 45^\circ\), \(\angle 4 = \angle 8 = 135^\circ\),
(ii) একান্তর কোণগুলি হল \(\angle 1 = \angle 5 = 45^\circ\), \(\angle 4 = \angle 6 = 135^\circ\)
(iii) একই পাশে অন্তঃস্থ কোণের সমষ্টি
\(\angle 4 + \angle 5 = 180^\circ\), \(\angle 3 + \angle 6 = 180^\circ\)
\(\therefore\) একই পাশের অন্তঃস্থ কোণগুলির পরস্পর সম্পূরক।
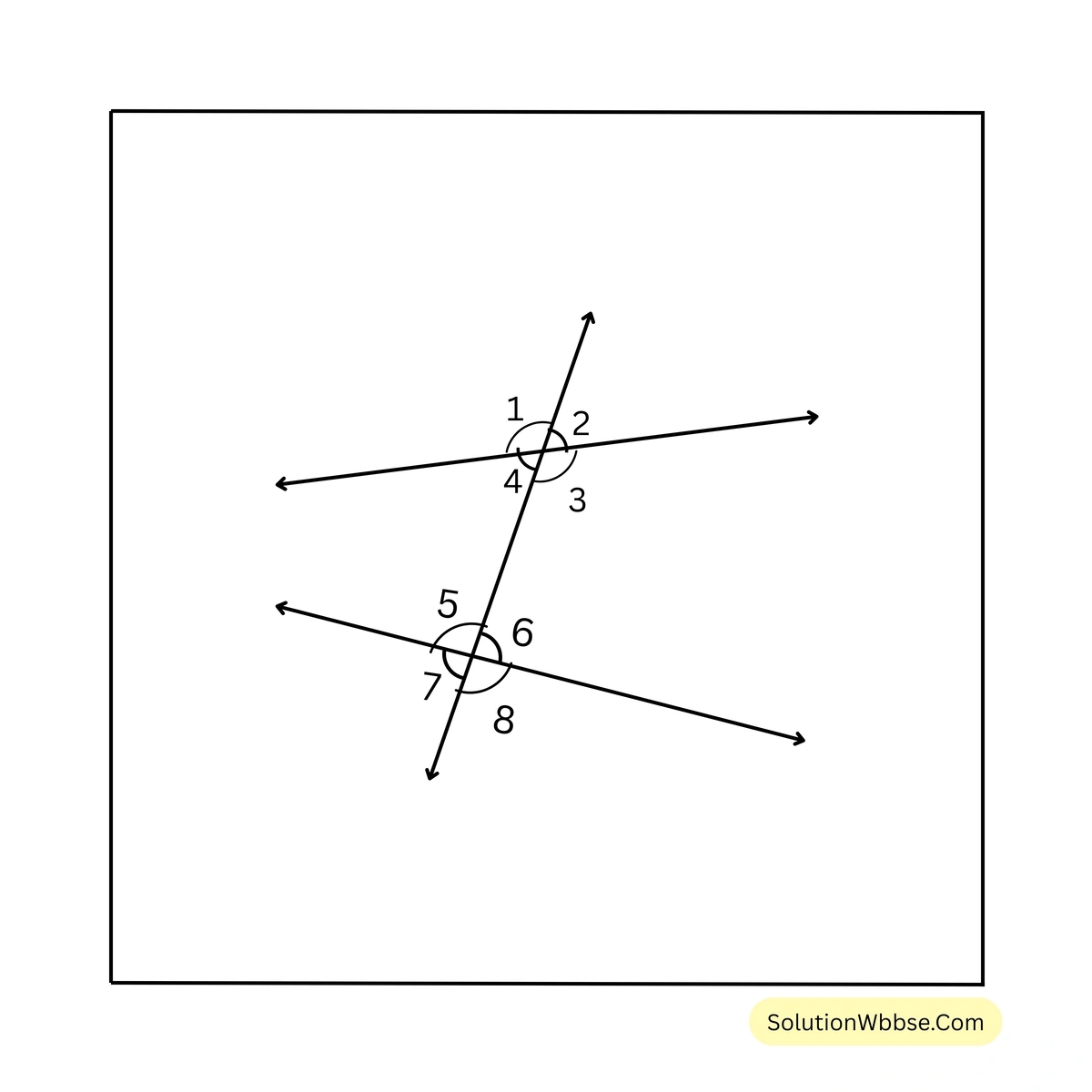
2. পাশের ছবির কোণগুলি দেখি ও কোনগুলি অনুরূপ কোণ, কোনগুলি একই পাশের অন্তঃস্থ কোণ লিখি।
সমাধান –
চিত্র থেকে পাই,
অনুরূপ কোণগুলি হল (\(\angle 1\), \(\angle 5\)), (\(\angle 2\), \(\angle 6\)), (\(\angle 3\), \(\angle 8\)), ও (\(\angle 4\), \(\angle 7\))
একই পাশের অন্তঃস্থ কোণগুলি হল (\(\angle 3\), \(\angle 6\)), (\(\angle 4\), \(\angle 5\))
3. AB \(\parallel\) CD হলে নীচের কোণগুলির মান লিখি –
(a)
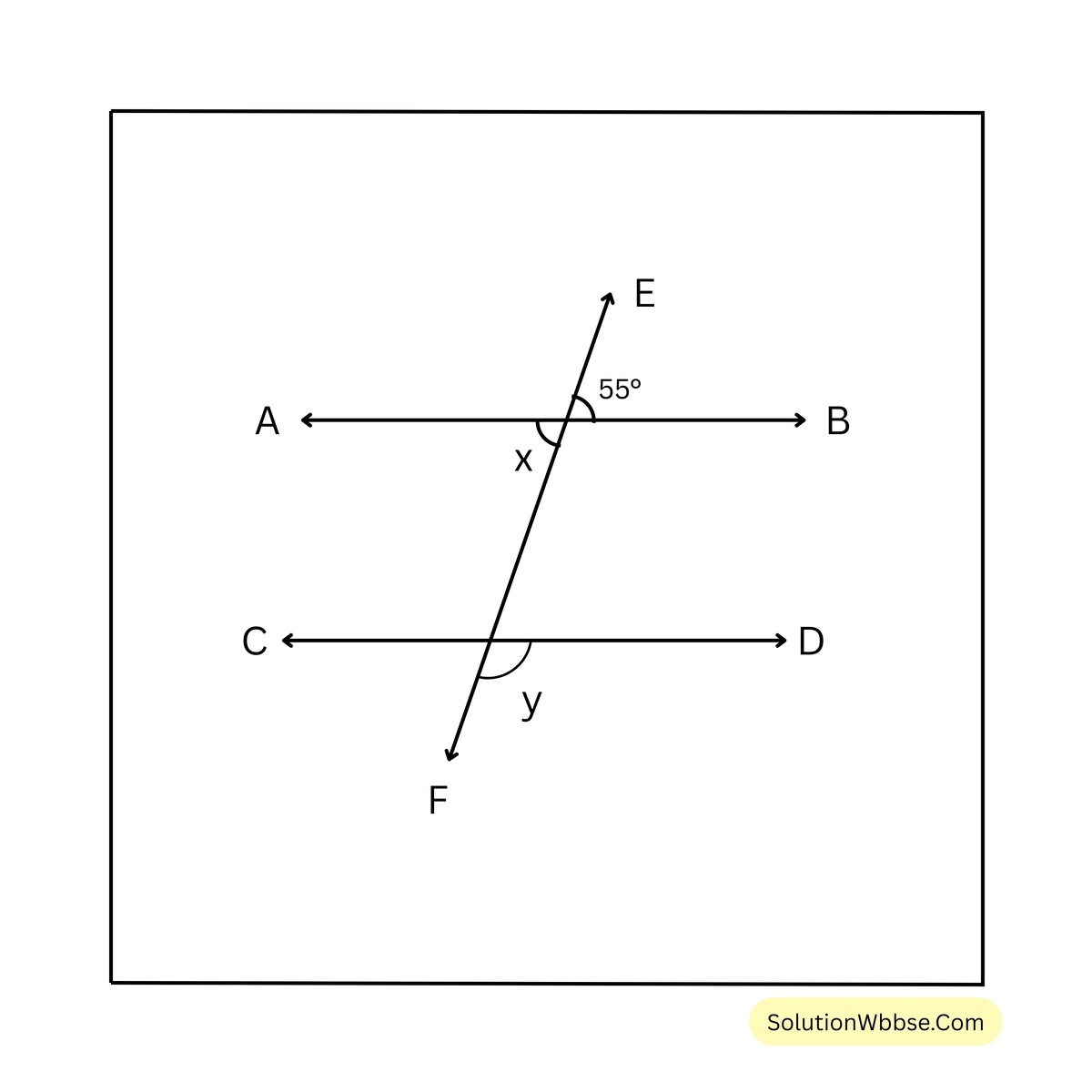
সমাধান –
ধরি, EF ছেদক AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে।
\(\therefore \angle APQ =\) বিপ্রতীপ \(\angle BPE\)
\(\therefore x = 55^\circ\)\(\angle APQ\) এবং \(\angle CQP\) একই পাশের অন্তঃস্থ কোণ
\(\therefore \angle APQ + \angle CQP = 180^\circ\)আবার, \(\angle CQP =\) বিপ্রতীপ \(\angle DQF = y\)
সুতরাং, \(y = 125^\circ\)
(b)
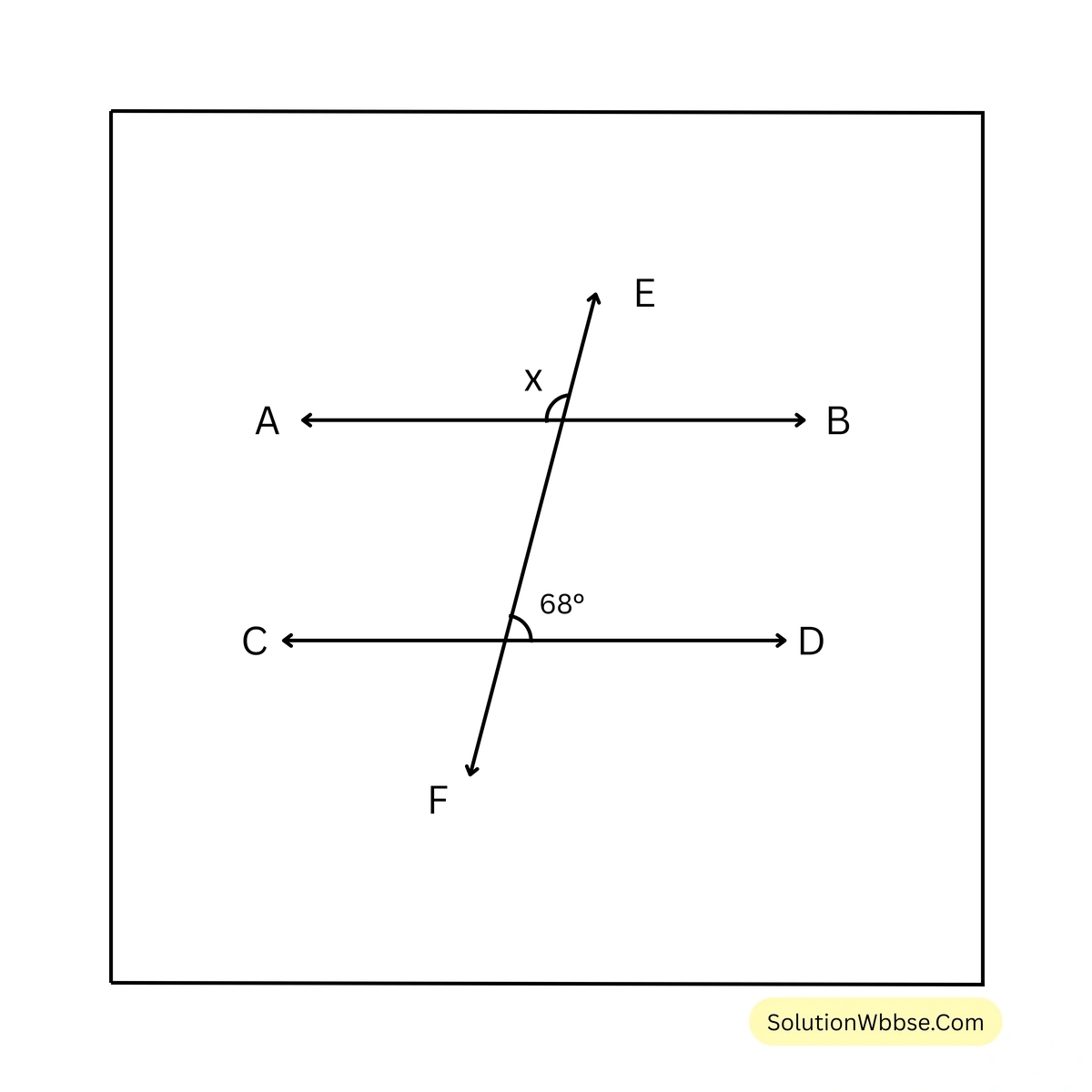
সমাধান –
ধরি, EF ছেদক, AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে।
\(\angle BPQ\) ও \(\angle DQP\) একই পাশের অন্তঃস্থ কোণ
সুতরাং, \(\angle BPQ + \angle DQP = 180^\circ\)
\(\therefore \angle BPQ = 180^\circ – \angle DQP = 180^\circ – 68^\circ = 112^\circ\)আবার, \(\angle APE =\) বিপ্রতীপ \(\angle BPQ\)
\(\angle APE = 112^\circ\)\(\therefore x = 112^\circ\)(c)
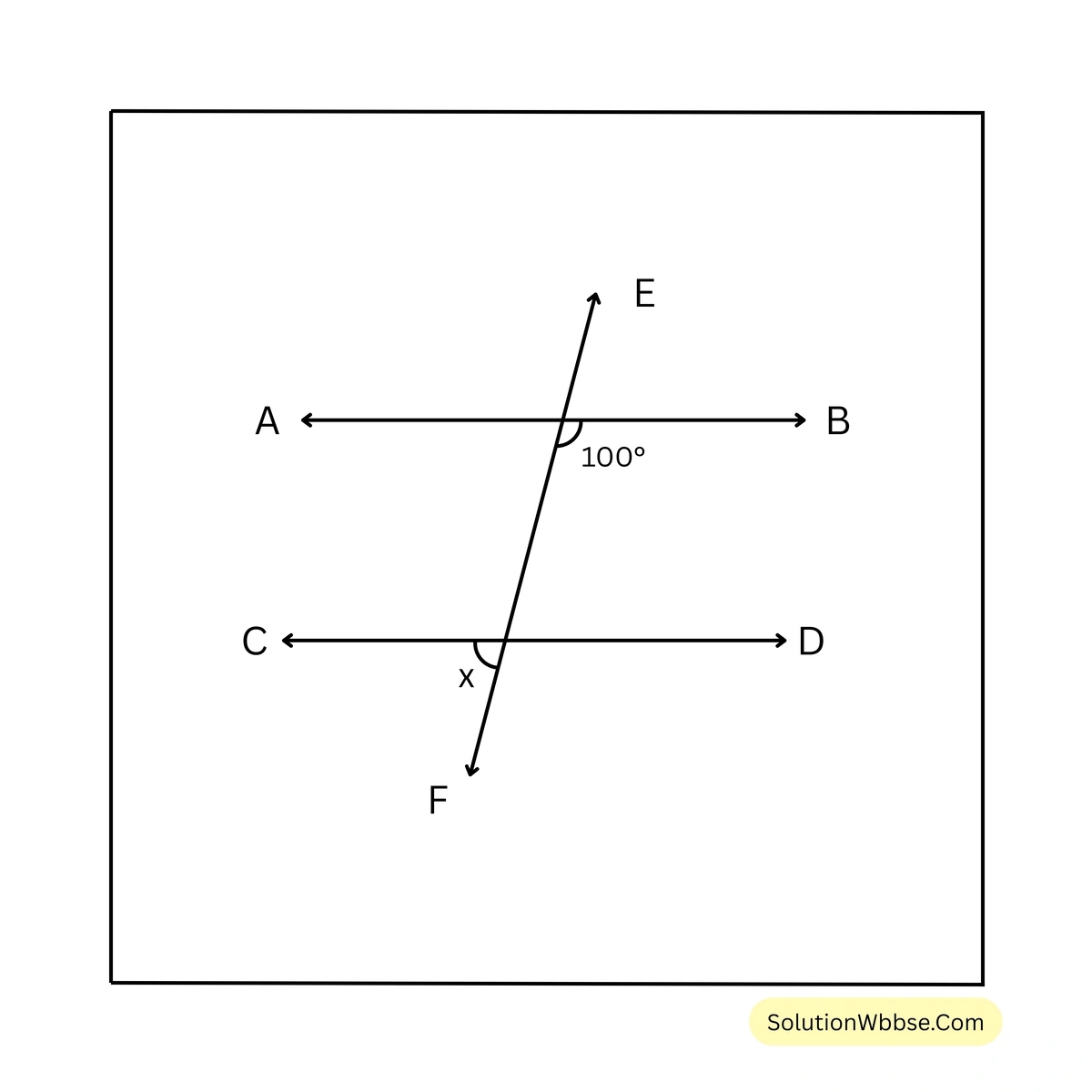
সমাধান –
ধরি, EF ছেদক AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে।
\(\angle BPQ\) ও \(\angle DQP\) একই পাশের অন্তঃস্থ কোণ
সুতরাং, \(\angle BPQ + \angle DQP = 180^\circ\)
\(\therefore \angle DQP = 180^\circ – \angle BPQ = 180^\circ – 100^\circ = 80^\circ\)আবার, \(\angle CQF =\) বিপ্রতীপ \(\angle DQP\)
4. পাশের ছবির XY \(\parallel\) PQ হলে 7টি কোণের মান লিখি।
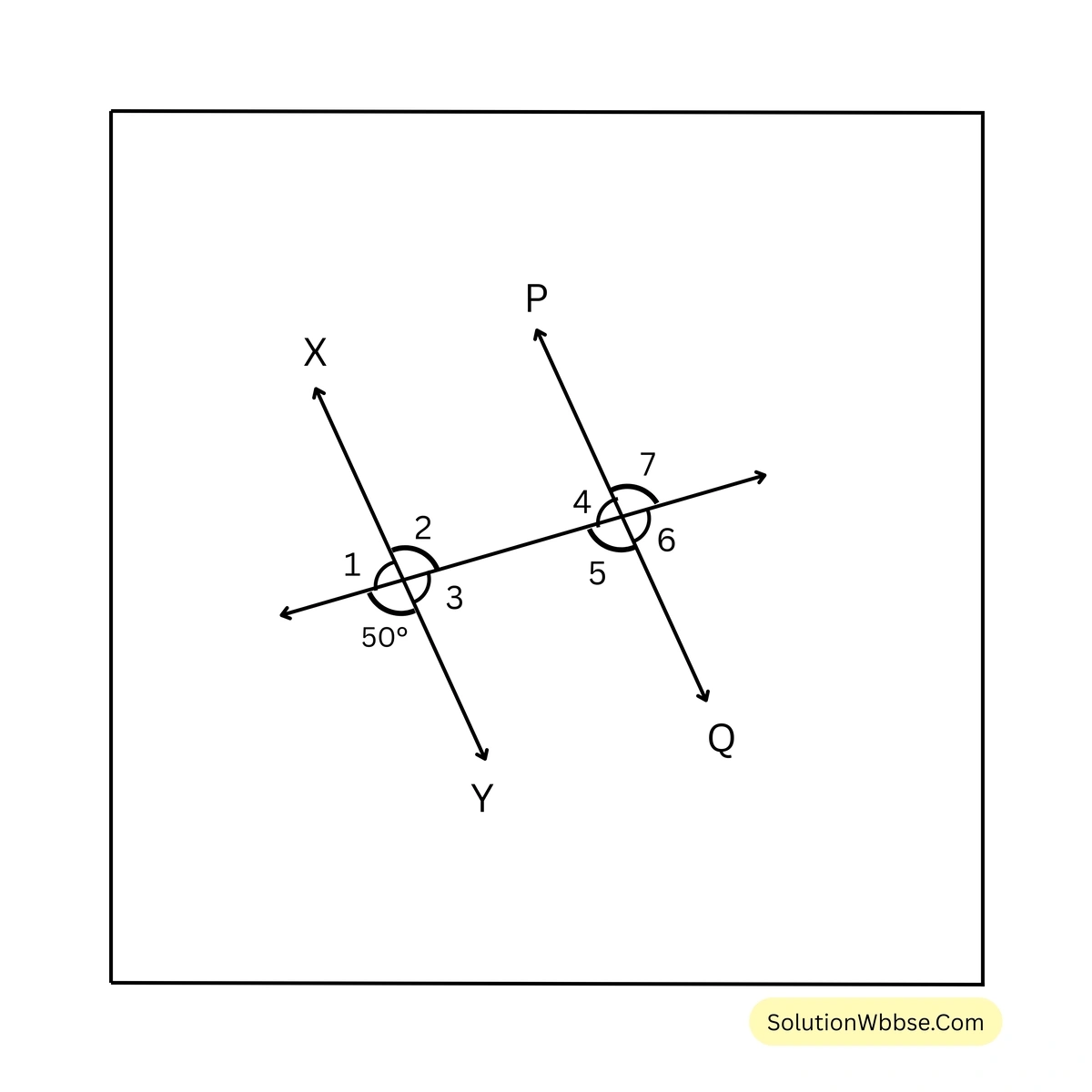
সমাধান –
\(\angle 1 + 50^\circ = 180^\circ\)\(\therefore \angle 1 = 180^\circ – 50^\circ = 130^\circ\)\(\angle 2 = 50^\circ\) [বিপ্রতীপ কোণ]
\(\angle 3 = \angle 1 = 130^\circ\) [\(\because \angle 1\), \(\angle 3\) পরস্পর বিপ্রতীপ কোণ]
\(\angle 4 = \angle 1 = 130^\circ\) [\(\because \angle 1\), \(\angle 4\) পরস্পর অনুরূপ কোণ]
\(\angle 5 = \angle 2 = 50^\circ\) [\(\because \angle 5\), \(\angle 2\) পরস্পর একান্তর কোণ]
\(\angle 6 = \angle 3 = 130^\circ\) [\(\because \angle 6\), \(\angle 3\) পরস্পর অনুরূপ কোণ]
\(\angle 7 = \angle 2 = 50^\circ\) [\(\because \angle 7\), \(\angle 2\) পরস্পর অনুরূপ কোণ]
5. নীচের AB ও CD সরলরেখা দুটি সমান্তরাল কিনা কোণের মান দেখে যুক্তি দিয়ে লিখি –
(i)
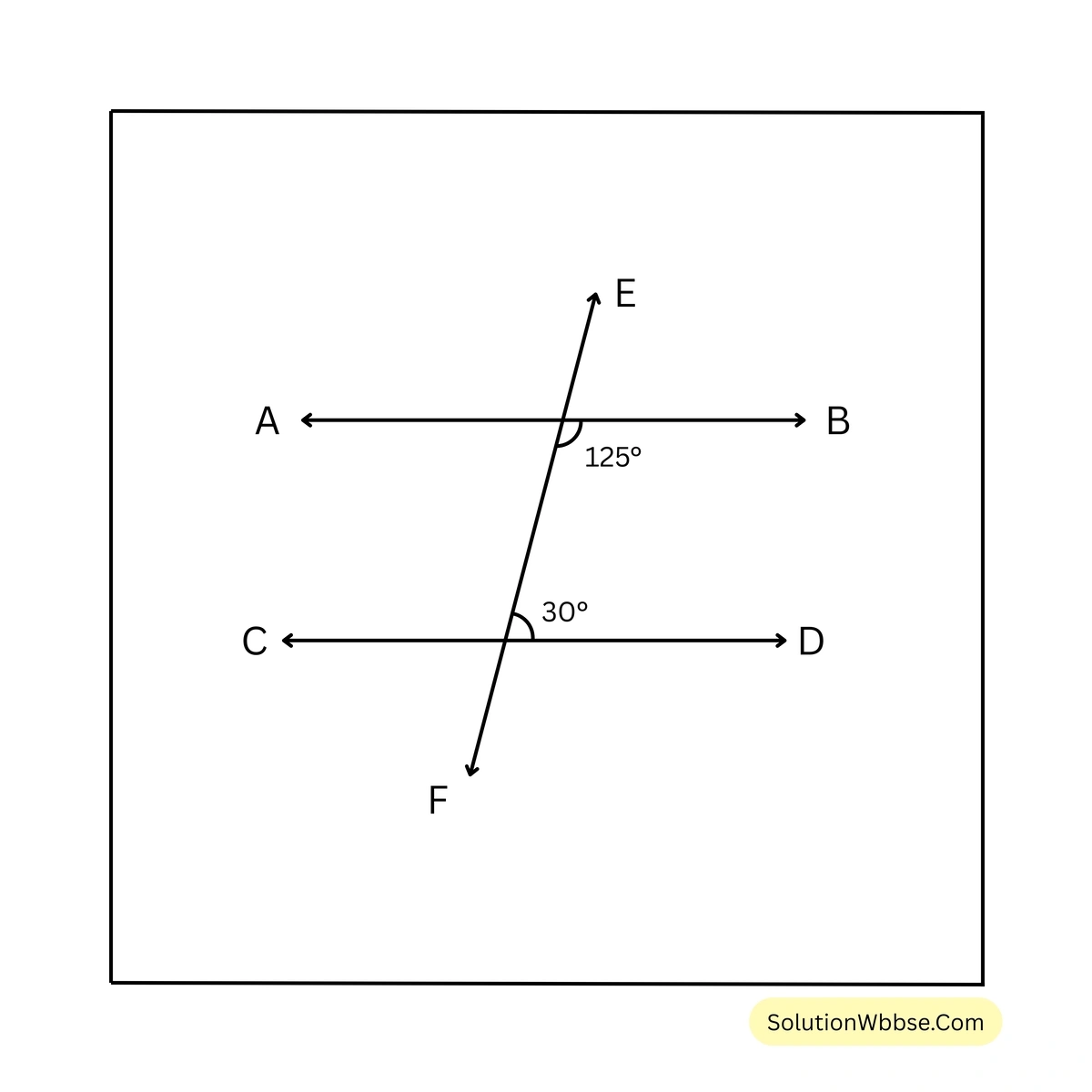
সমাধান –
ধরি, EF ছেদক AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে।
\(\angle BPQ\) ও \(\angle DQP\) একই পাশের অন্তঃস্থ কোণ।
\(\therefore \angle BPQ + \angle DQP = 125^\circ + 30^\circ = 155^\circ \neq 180^\circ\)\(\angle BPQ\) ও \(\angle DQP\) একই পাশের অন্তঃস্থ কোণ দুটি পরস্পর সম্পূরক কোণ নয়।
সুতরাং, AB ও CD সরলরেখা দুটি সমান্তরাল নয়।
(ii)
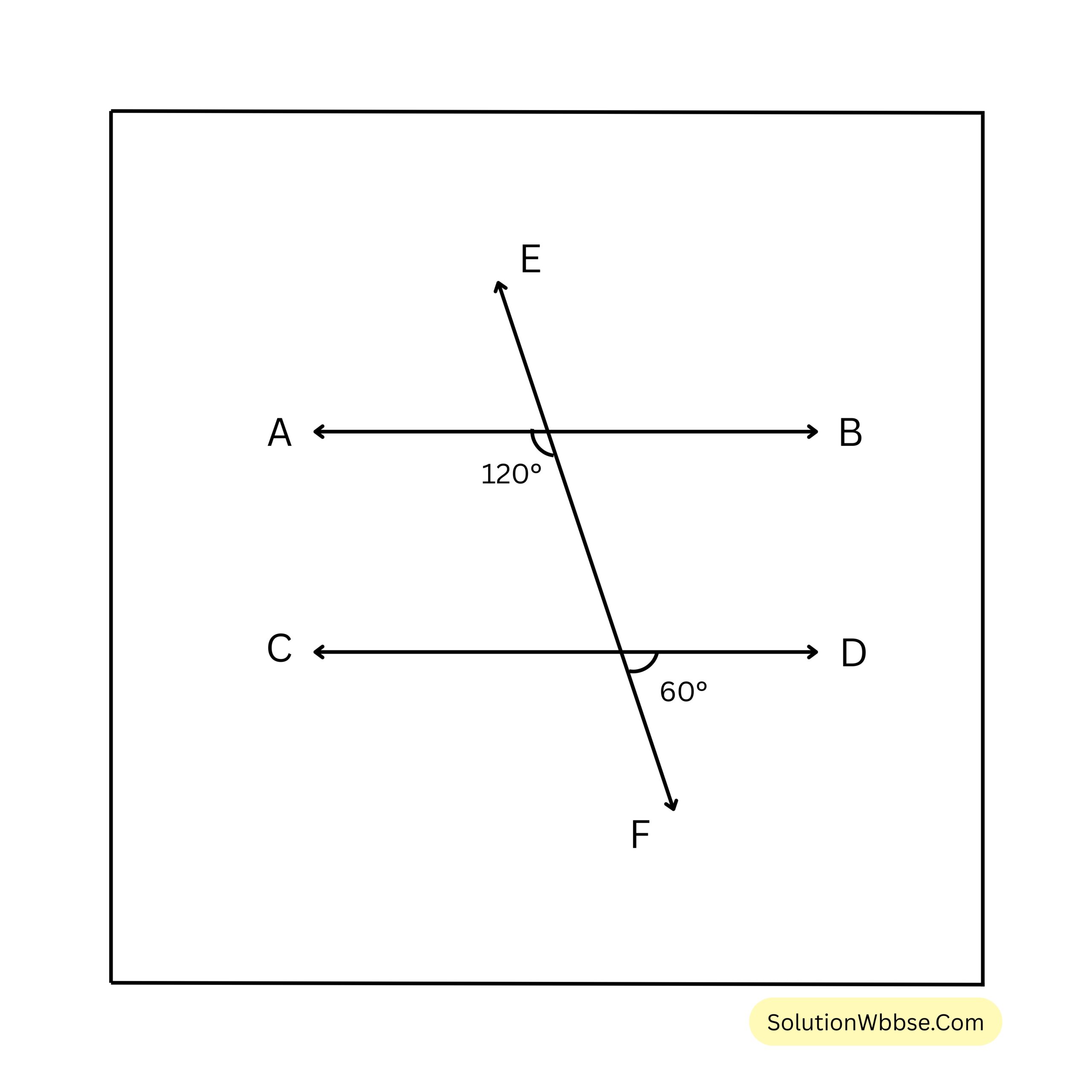
সমাধান –
ধরি, EF ছেদক AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে।
\(\angle CQP =\) বিপ্রতীপ \(\angle DQF = 60^\circ\)
\(\angle APQ\) ও \(\angle CQP\) একই পাশের অন্তঃস্থ কোণ।
\(\therefore \angle APQ + \angle CQP = 120^\circ + 60^\circ = 180^\circ\)\(\therefore \angle APQ\) ও \(\angle CQP\) একই পাশের অন্তঃস্থ কোণ দুটি পরস্পর সম্পূরক কোণ।
সুতরাং, AB ও CD সরলরেখা দুটি সমান্তরাল।
(iii)
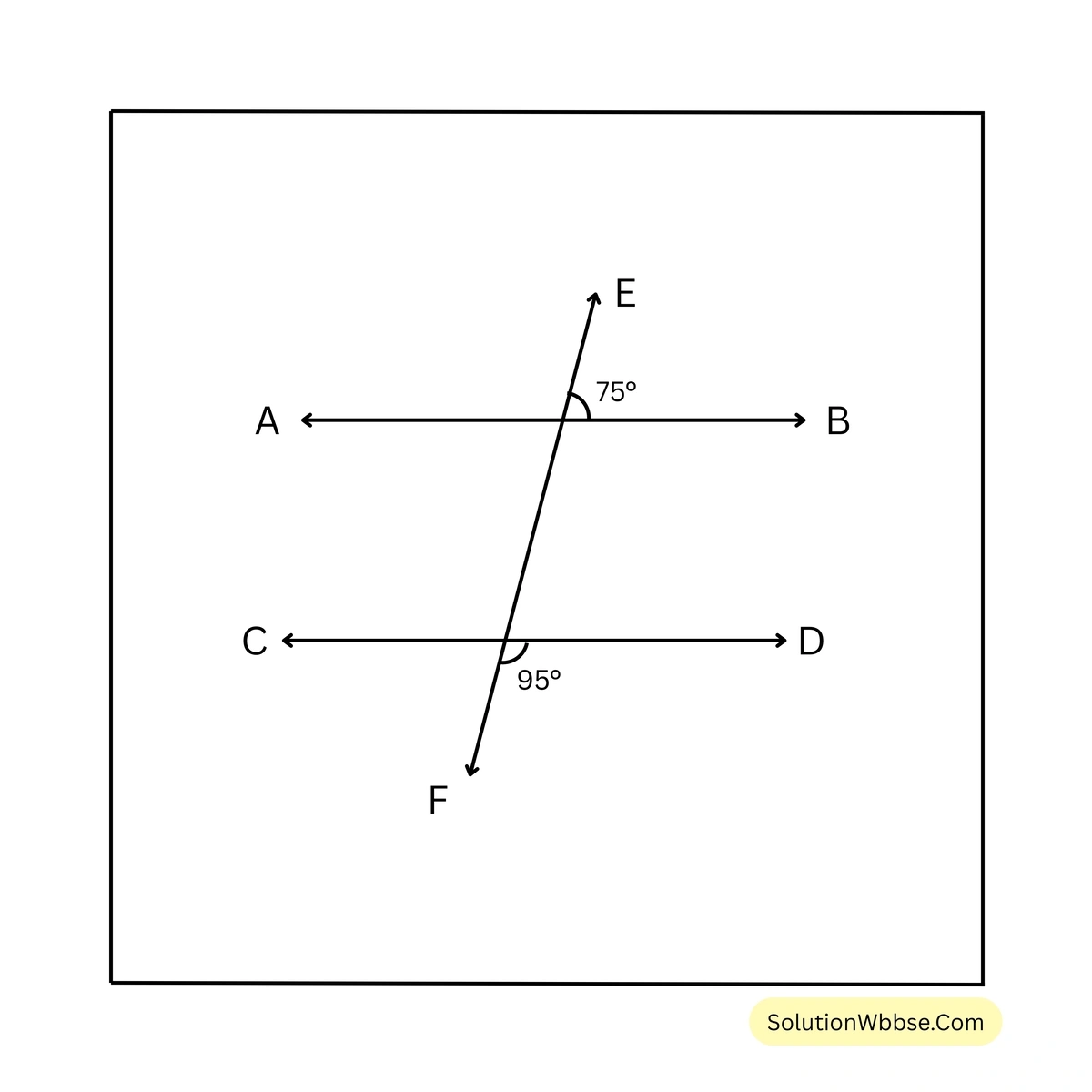
সমাধান –
ধরি, EF ছেদক AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে।
\(\angle EPB + \angle BPQ = 180^\circ\)বা, \(\angle BPQ = 180^\circ – \angle EPB\)
\(\therefore \angle BPQ = 180^\circ – 75^\circ = 105^\circ\)\(\angle BPQ\) ও \(\angle DQF\) পরস্পর অনুরূপ কোণ।
\(\angle BPQ = 105^\circ\) এবং \(\angle DQF = 95^\circ\)
\(\therefore \angle BPQ \neq \angle DQF\)সুতরাং, AB ও CD সরলরেখা দুটি সমান্তরাল নয়।
6. চিত্রে \(AB \parallel CD\) এবং \(\angle EGB = 50^\circ\); \(\angle AGE\), \(\angle AGH\), \(\angle BGH\), \(\angle GHC\), \(\angle GHD\), \(\angle CHF\) এবং \(\angle DHF\) এর পরিমাপ লিখি।
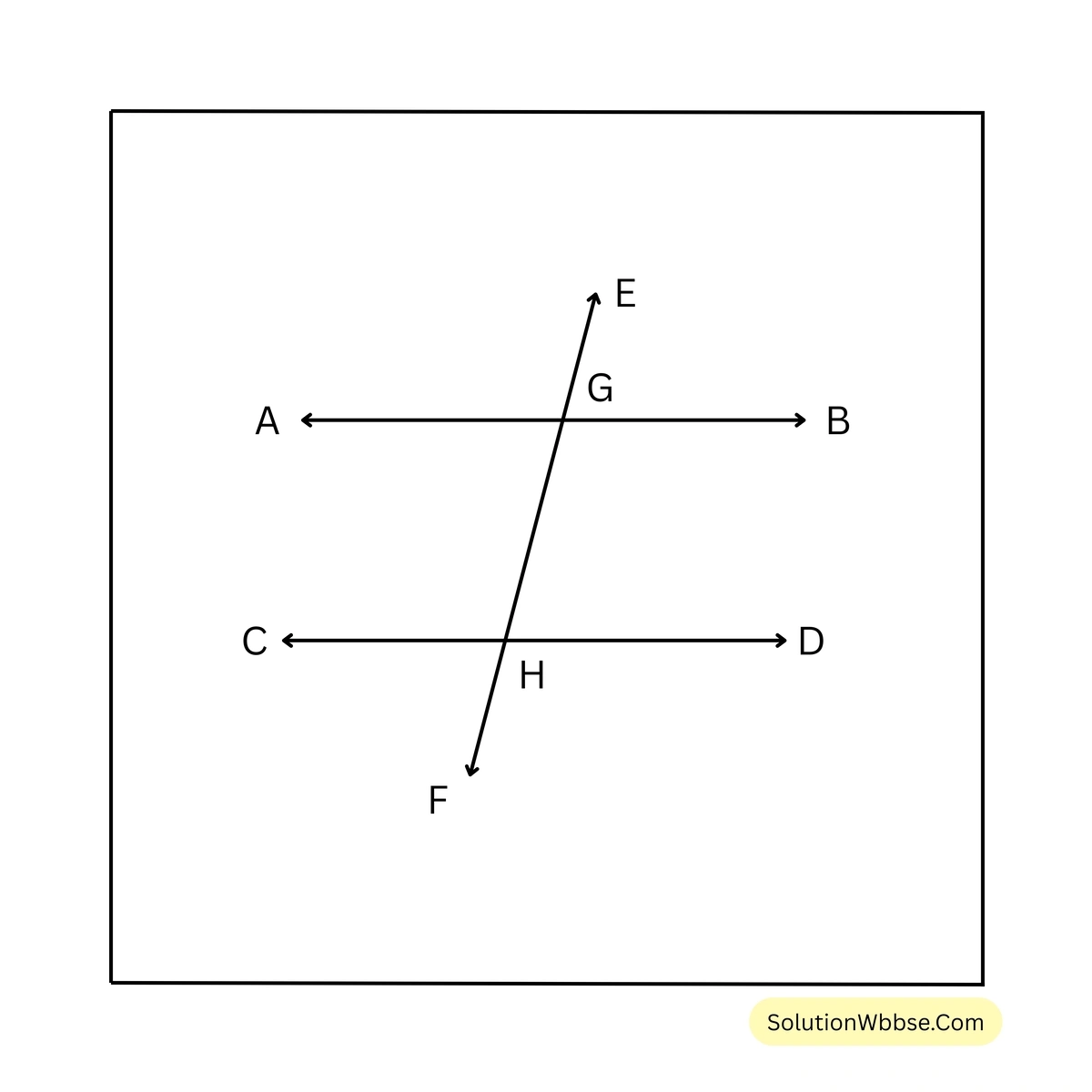
সমাধান –
\(\angle EGB + \angle AGE = 180^\circ\)বা, \(\angle AGE = 180^\circ – \angle EGB\)
\(\therefore \angle AGE = 180^\circ – 50^\circ = 130^\circ\)\(\angle AGH =\) বিপ্রতীপ \(\angle EGB = 50^\circ\)
\(\angle BGH =\) বিপ্রতীপ \(\angle AGE = 130^\circ\)
\(\angle GHC =\) অনুরূপ \(\angle AGE = 130^\circ\)
\(\angle GHD =\) অনুরূপ \(\angle EGB = 50^\circ\)
\(\angle CHF =\) বিপ্রতীপ \(\angle GHD = 50^\circ\)
\(\angle DHF =\) বিপ্রতীপ \(\angle GHC = 130^\circ\)
7. চিত্রে \(AB \parallel CD\); \(\angle PQR\) এর পরিমাপ লিখি।
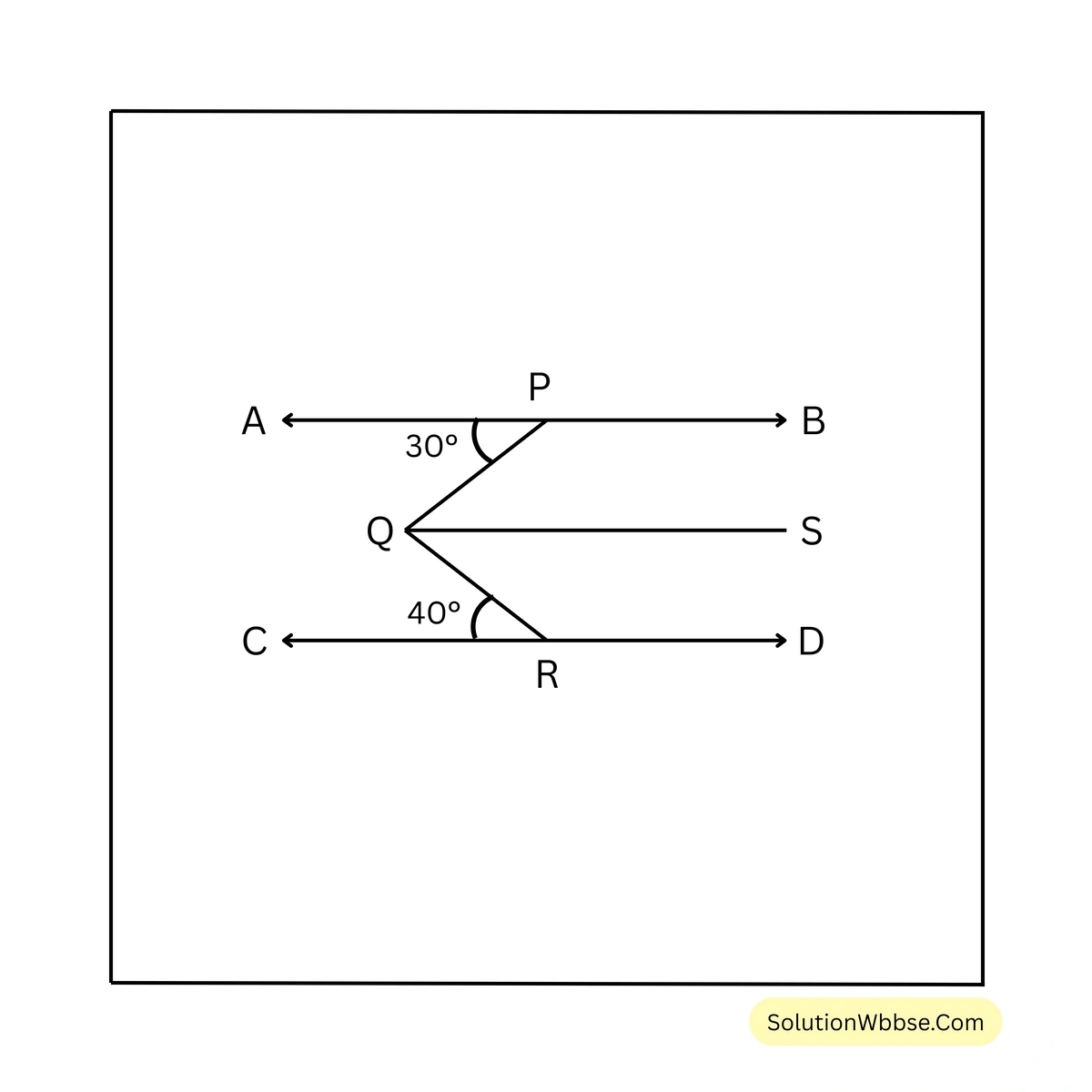
সমাধান –
Q বিন্দু থেকে AB এর সমান্তরাল সরলরেখা QS অঙ্কন করলাম।
\(\therefore AB \parallel QS \parallel CD\) [∵ \(AB \parallel CD\)]
\(\angle PQS =\) একান্তর \(\angle APQ = 30^\circ\)
এবং \(\angle RQS =\) একান্তর \(\angle CRQ = 40^\circ\)
\(\angle PQR = \angle PQS + \angle RQS = 30^\circ + 40^\circ = 70^\circ\)\(\therefore \angle PQR = 70^\circ\)8. চিত্রে \(PQ \parallel RS\), \(\angle BPQ = 40^\circ\), \(\angle BPR = 155^\circ\), এবং \(\angle CRS = 70^\circ\), \(\triangle APR\) এর কোণগুলির পরিমাপ লিখি।
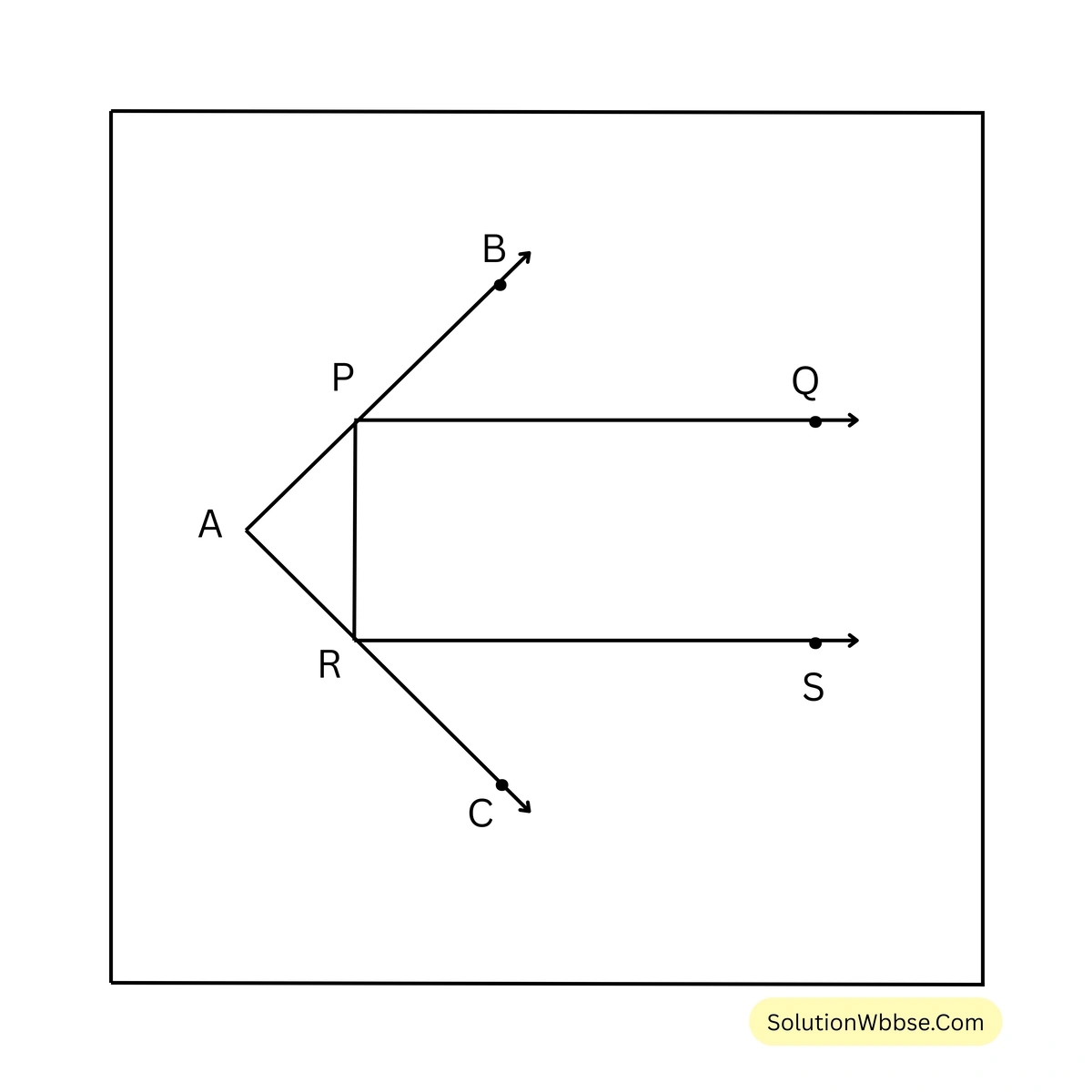
সমাধান –
AB সরলরেখার উপর PR দণ্ডায়মান।
সুতরাং, \(\angle APR + \angle BPR = 180^\circ\)
\(\therefore \angle APR = 180^\circ – \angle BPR = 180^\circ – 155^\circ = 25^\circ\)আবার, \(\angle RPQ = \angle BPR – \angle BPQ\)
\(\therefore \angle RPQ = 155^\circ – 40^\circ = 115^\circ\)\(\angle RPQ\) এবং \(\angle PRS\) একই দিকের অন্তঃস্থ কোণ [∵ \(PQ \parallel RS\) এবং \(PR\) ছেদক]
সুতরাং, \(\angle RPQ + \angle PRS = 180^\circ\) [∵ \(PQ \parallel RS\)]
\(\therefore \angle PRS = 180^\circ – \angle RPQ = 180^\circ – 115^\circ = 65^\circ\)এখন, \(\angle ARP + \angle PRS + \angle CRS = 180^\circ\)
বা, \(\angle ARP = 180^\circ – \angle PRS – \angle CRS\)
বা, \(\angle ARP = 180^\circ – 65^\circ – 70^\circ = 45^\circ\)
\(\triangle APR\) এর \(\angle APR = 25^\circ\) এবং \(\angle ARP = 45^\circ\)
\(\therefore \angle PAR = 180^\circ – 25^\circ – 45^\circ = 110^\circ\)\(\triangle APR\) এর \(\angle APR = 25^\circ\), \(\angle ARP = 45^\circ\) এবং \(\angle PAR = 110^\circ\)
9. AB এবং CD দুটি সরলরেখার ভিতর O যেকোনো একটি বিন্দু। OP ও OQ যথাক্রমে AB ও CD সরলরেখার উপর লম্ব। প্রমাণ করি যে P, O, Q বিন্দু তিনটি সমরেখ।
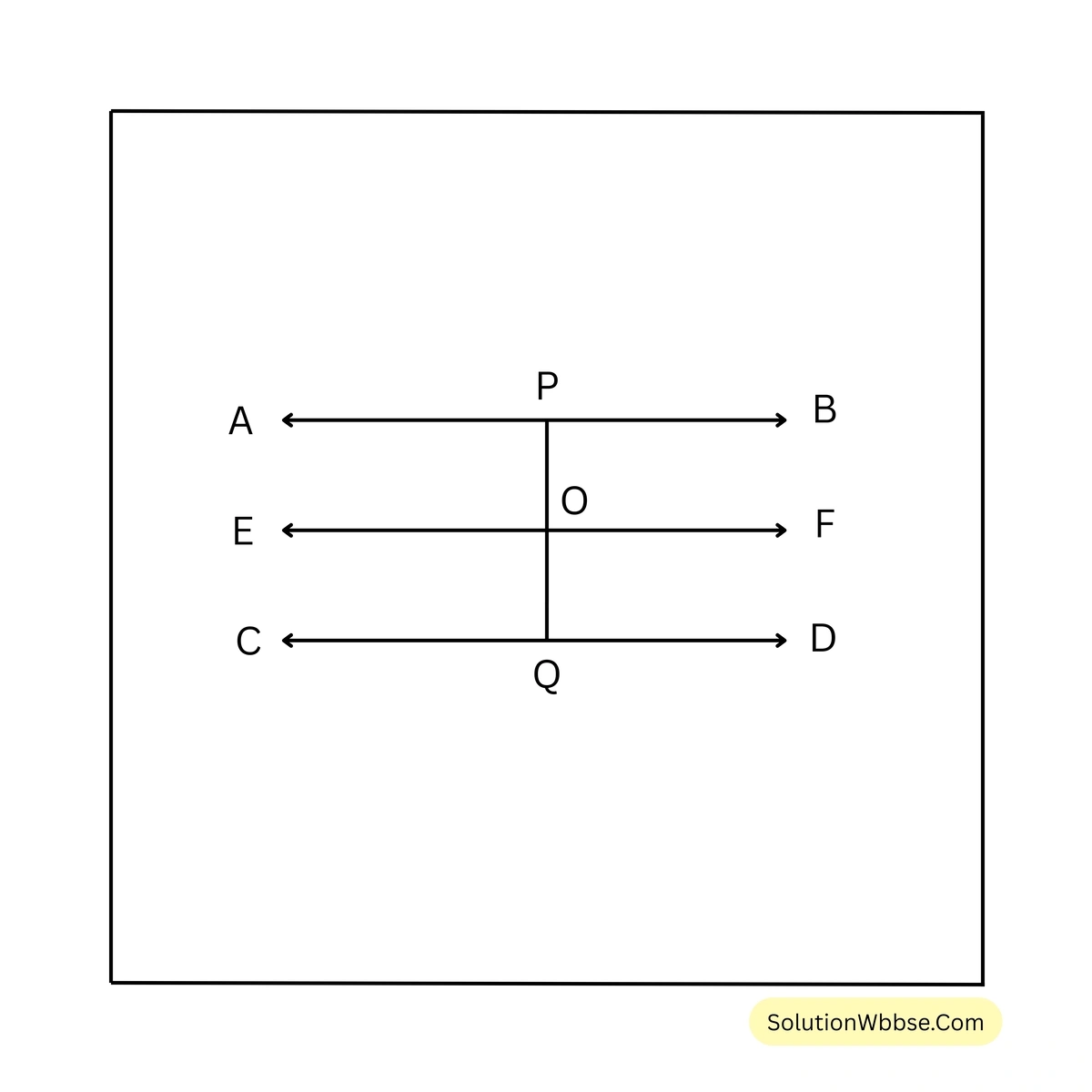
প্রদত্ত – AB এবং CD দুটি সরলরেখার ভিতর O যেকোনো একটি বিন্দু এবং \(OP \perp AB\), \(OQ \perp CD\)
প্রমাণ্য – P, O, Q বিন্দু তিনটি সমরেখ।
অঙ্কন – O বিন্দু দিয়ে AB সরলরেখার সমান্তরাল সরলরেখা EF অঙ্কন করলাম।
প্রমাণ – \(AB \parallel EF\) [অঙ্কনানুসারে]
\(\therefore \angle BPO + \angle POF = 180^\circ\) [ভেদকের একই দিকের অন্তঃস্থ কোণ]
আবার, \(\angle BPO = 90^\circ\)
\(\therefore \angle POF = 180^\circ – 90^\circ = 90^\circ\)\(CD \parallel EF\) [∵ \(AB \parallel EF\) এবং \(AB \parallel CD\)]
\(\therefore \angle DQO + \angle QOF = 180^\circ\) [ভেদকের একই দিকের অন্তঃস্থ কোণ]
আবার, \(\angle DQO = 90^\circ\)
\(\therefore \angle QOF = 180^\circ – 90^\circ = 90^\circ\)\(\angle POF\) ও \(\angle QOF\) হল পরস্পর সন্নিহিত কোণ এবং \(\angle POF + \angle QOF = 180^\circ\)
\(\therefore\) PO এবং QO একই সরলরেখায় অবস্থিত।
অর্থাৎ, P, O, Q বিন্দু তিনটি সমরেখ। [প্রমাণিত]
10. দুটি কোণের প্রতিজোড়া বাহু পরস্পর সমান্তরাল। প্রমাণ করি যে, কোণদুটি সমান অথবা পরস্পর সম্পূরক।
চিত্র 1
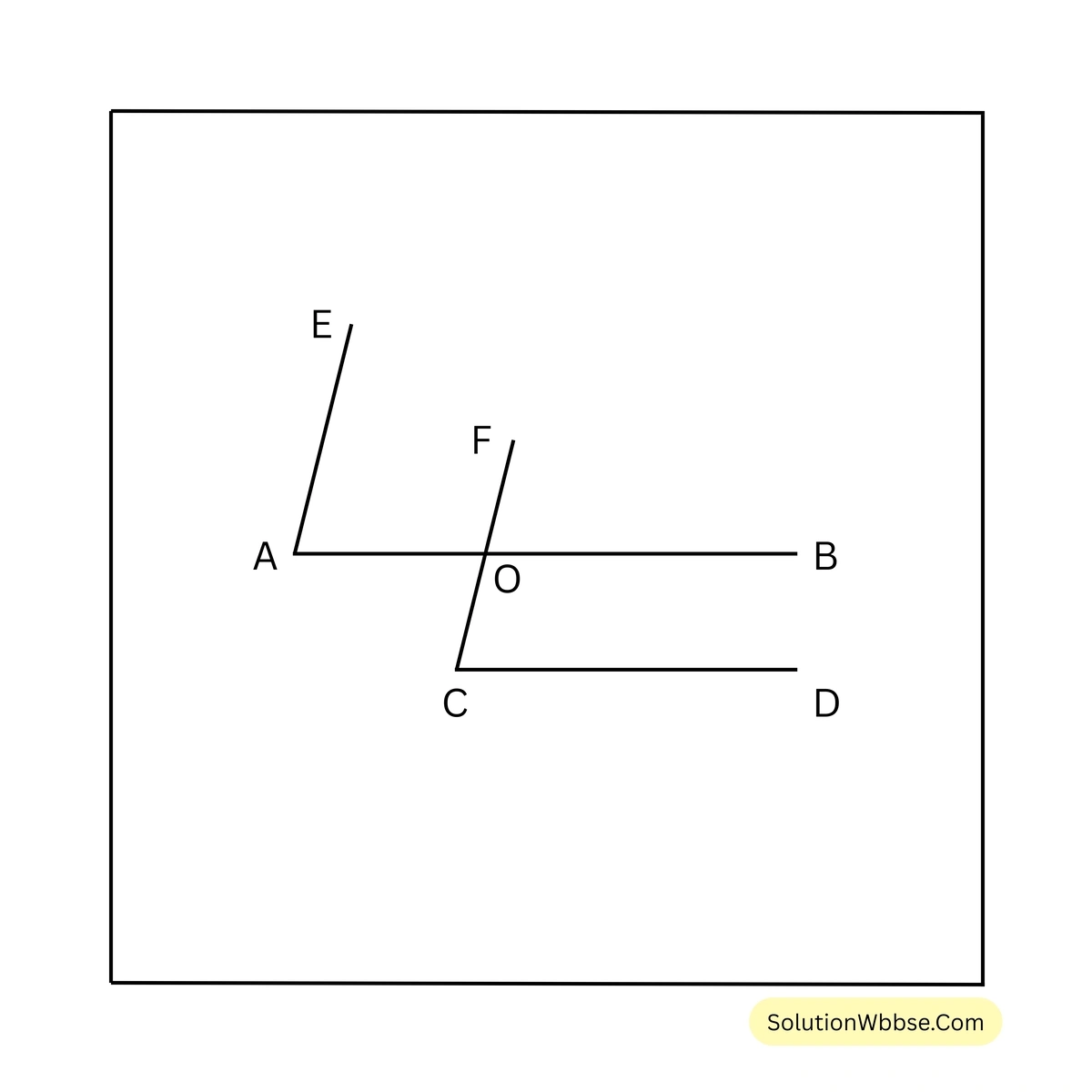
চিত্র 2
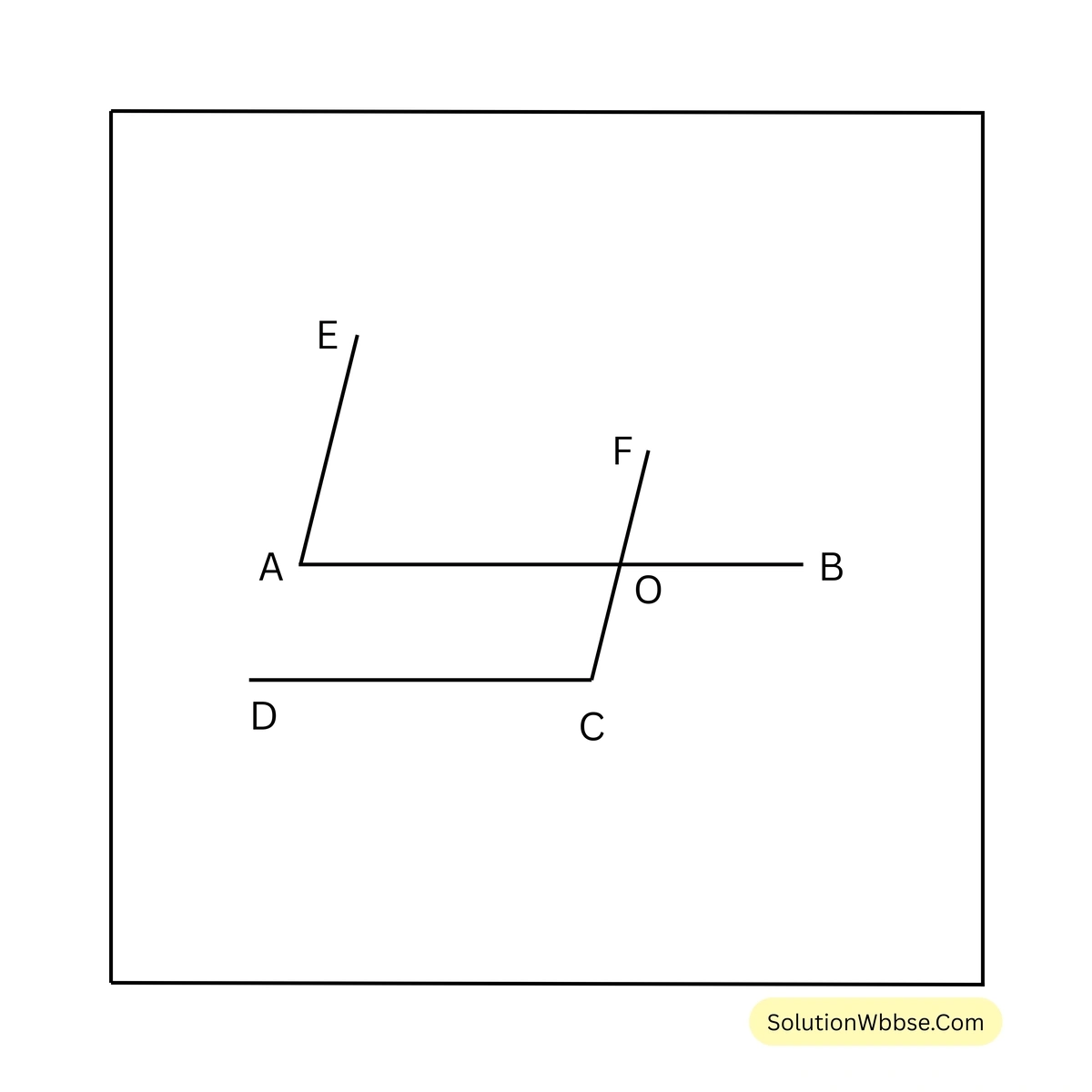
প্রদত্ত – 1 নং চিত্রে, \(\angle EAB\) এর \(AE\) ও \(AB\) বাহু যথাক্রমে \(\angle FCD\) এর \(CF\) ও \(CD\) বাহুর সঙ্গে সমান্তরাল। 2 নং চিত্রে, \(\angle EAB\) এর \(AE\) ও \(AB\) বাহু যথাক্রমে \(\angle FCD\) এর \(CF\) ও \(DC\) বাহুর সঙ্গে সমান্তরাল। উভয় চিত্রে \(AB\) ও \(CF\) সরলরেখা দুটি \(O\) বিন্দুতে ছেদ করেছে।
প্রামাণ্য – চিত্র 1-এর ক্ষেত্রে \(\angle EAB = \angle FCD\) এবং চিত্র 2-এর ক্ষেত্রে \(\angle EAB + \angle FCD = 180^\circ\)
প্রমাণ – যেহেতু, \(AE \parallel CF\) এবং \(AB\) ভেদক
\(\therefore \angle EAB =\) অনুরূপ \(\angle FOB\) —-(i)
চিত্র 1-এর ক্ষেত্রে,
\(AB \parallel CD\) এবং \(CF\) ভেদক
\(\therefore \angle FOB =\) অনুরূপ \(\angle FCD\) —-(ii)
(i) নং ও (ii) নং থেকে পাই,
\(\angle EAB = \angle FCD\) [প্রমাণিত]
চিত্র 2-এর ক্ষেত্রে,
\(AB \parallel DC\) এবং \(CF\) ভেদক
\(\therefore \angle FOA =\) অনুরূপ \(\angle FCD\) —(iii)
\(AE \parallel CF\) এবং \(AB\) ভেদক
\(\therefore \angle EAB + \angle FOA = 180^\circ\) [ভেদকের একই দিকের অন্তঃস্থ কোণ]
\(\therefore \angle EAB + \angle FCD = 180^\circ\) [(iii) নং থেকে পাই] [প্রমাণিত]
11. ABCD সামান্তরিকের AC কর্ণ \(\angle BAD\) কে সমদ্বিখণ্ডিত করে। প্রমাণ করি যে, AC কর্ণ \(\angle BCD\) কেও সমদ্বিখণ্ডিত করে।
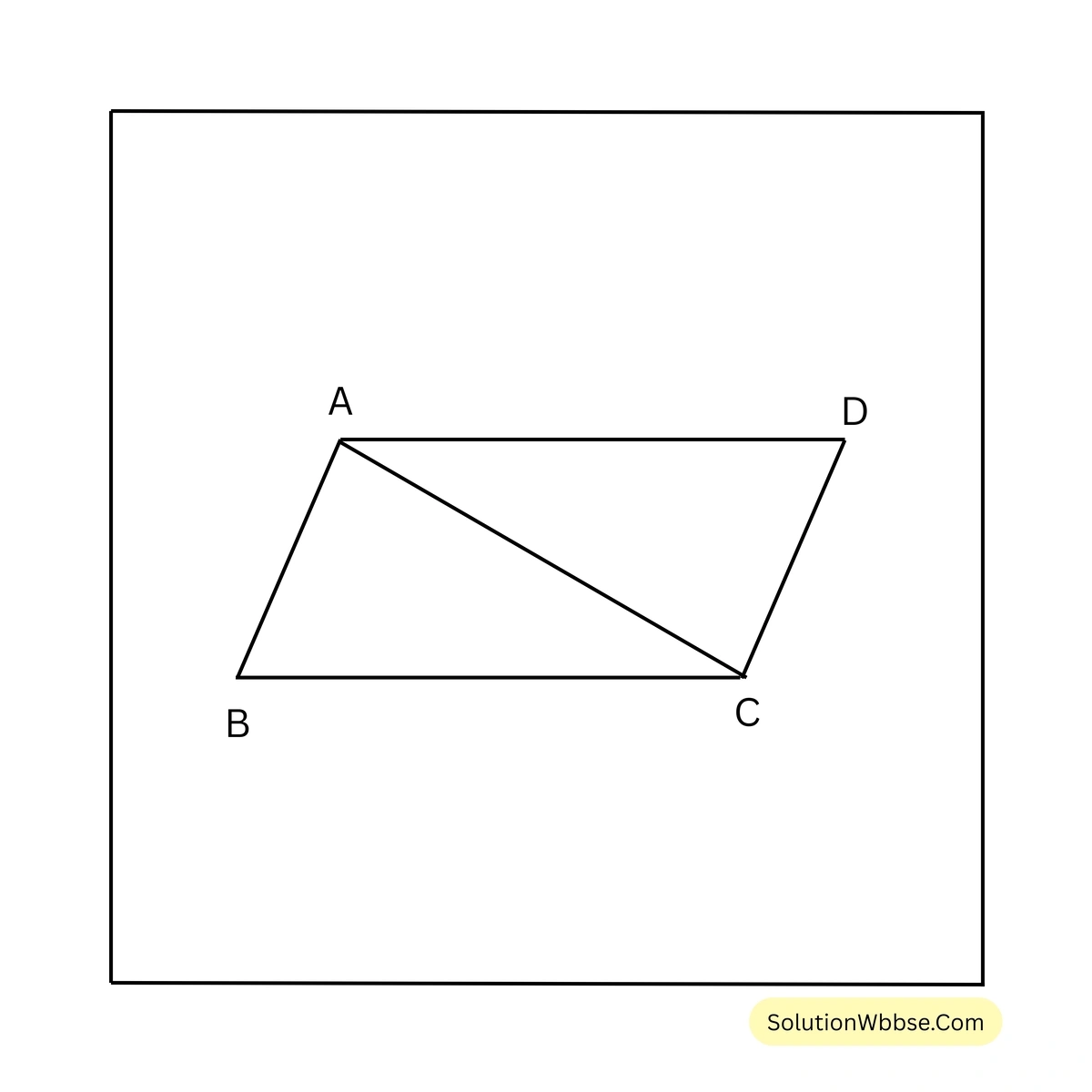
প্রদত্ত – ABCD সামান্তরিকের AC কর্ণ \(\angle BAD\) কে সমদ্বিখণ্ডিত করে অর্থাৎ
\(\angle BAC = \angle DAC\)প্রামাণ্য – AC কর্ণ \(\angle BCD\) কে সমদ্বিখণ্ডিত করে অর্থাৎ \(\angle ACB = \angle ACD\)
প্রমাণ – \(\angle BAC = \angle DAC\) [প্রদত্ত] —-(i)
সামান্তরিকের বিপরীত বাহু পরস্পর সমান্তরাল।
সুতরাং, \(AD \parallel BC\) এবং \(AB \parallel DC\)
\(AD \parallel BC\) এবং \(AC\) ছেদক
\(\therefore \angle DAC = \angle ACB\) [একান্তর কোণ] —-(ii)
আবার, \(AB \parallel DC\) এবং \(AC\) ছেদক
\(\therefore \angle BAC = \angle ACD\) [একান্তর কোণ] —-(iii)
(i) ও (ii) থেকে পাই, \(\angle BAC = \angle ACB\) —-(iv)
(iii) ও (iv) থেকে পাই, \(\angle ACB = \angle ACD\) [প্রমাণিত]
\(\therefore\) AC কর্ণ \(\angle BCD\) কে সমদ্বিখণ্ডিত করে।
12. ABCD সামান্তরিকের একটি কোণ সমকোণ হলে, প্রতিটি কোণই সমকোণ।
প্রদত্ত – ধরি, ABCD সামান্তরিকের \(\angle B = 90^\circ\)
প্রামাণ্য – সামান্তরিকের বাকি তিনটি কোণ সমকোণ। অর্থাৎ, \(\angle A = \angle C = \angle D = 90^\circ\)
প্রমাণ – সামান্তরিকের বিপরীত বাহু পরস্পর সমান্তরাল।
সুতরাং, \(AD \parallel BC\) এবং \(AB \parallel DC\)
\(AD \parallel BC\) এবং \(AB\) ছেদক
\(\therefore \angle A + \angle B = 180^\circ\) [ছেদকের একই দিকের অন্তঃস্থ কোণ]
\(\therefore \angle A = 180^\circ – \angle B = 180^\circ – 90^\circ = 90^\circ\)\(AB \parallel DC\) এবং \(BC\) ছেদক
\(\therefore \angle B + \angle C = 180^\circ\) [ছেদকের একই দিকের অন্তঃস্থ কোণ]
\(\therefore \angle C = 180^\circ – \angle B = 180^\circ – 90^\circ = 90^\circ\)\(AD \parallel BC\) এবং \(DC\) ছেদক
\(\therefore \angle C + \angle D = 180^\circ\) [ছেদকের একই দিকের অন্তঃস্থ কোণ]
\(\therefore \angle D = 180^\circ – \angle C = 180^\circ – 90^\circ = 90^\circ\)সুতরাং, \(\angle A = \angle C = \angle D = 90^\circ\) [প্রমাণিত]
এই আর্টিকেলে অষ্টম শ্রেণির গণিতের ‘সমান্তরাল সরলরেখা ও ছেদকের ধর্ম ’ অধ্যায়ের ‘কষে দেখি – 8’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরেছি। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে। কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment