পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) অষ্টম শ্রেণির গণিত পাঠ্যবইয়ের চতুর্থ অধ্যায় হলো ‘বীজগাণিতিক সংখ্যামালার গুন ও ভাগ’। এই পোস্টে আমরা ‘কষে দেখি – 4.1’-এর সমস্ত প্রশ্নের সহজ ও নির্ভুল সমাধান নিয়ে আলোচনা করেছি। আশা করি, এই নোটসগুলো তোমাদের গণিত শিখতে এবং পরীক্ষার প্রস্তুতিতে দারুণভাবে সহায়তা করবে।

1.
| প্রথম বীজগাণিতিক সংখ্যামালা | দ্বিতীয় বীজগাণিতিক সংখ্যামালা | গুণফল | গুণফলের মান |
|---|---|---|---|
| (a) x2-3x+5 | 5x+9 | (x2-3x+5)(5x+9) | X = 1 বসিয়ে পাই |
| (b) x2+12-7y | (2x-y) | (x2+12-7y)(2x-y) | X = -2, y = 2 বসিয়ে পাই |
| (c) 8p3-3p-2p2 | 4p2-5 | (8p3-3p-2p2)(4p2-5) | P = -2 বসিয়ে পাই |
| (d) (6a+5b+2) | (a-b+6) | (6a+5b+2)(a-b+6) | a = 0 এবং b = -1 বসিয়ে পাই |
| (e) (p3-p2q2+q3) | (p2+pq+q2) | (p3-p2q2+q3)(p2+pq+q2) | P = 2 এবং q = -2 বসিয়ে পাই |
| (f) (x2+y2+z2-xy-yz-zx) | (x+y+z) | (x2+y2+z2-xy-yz-zx)(x+y+z) | X = 1, y = 0 এবং z = -1 বসিয়ে পাই |
| (g) আমি নিজে একটি বীজগাণিতিক সংখ্যামালা লিখি। | আমি নিজে অন্য একটি ত্রিপদী বীজগাণিতিক সংখ্যামালা লিখি | – | চল বা চলগুলিতে যেকোনো অখণ্ড সংখ্যা বসিয়ে গুণফলের মান লিখি। |
সমাধান –
(a) x2-3x+5 ; 5x+9
প্রথম ও দ্বিতীয় সংখ্যামালার গুণফল –
= \( (x^2 – 3x + 5)(5x + 9)\)
= \( 5x^3 + 9x^2 – 15x^2 – 27x + 25x + 45\)
= \( 5x^3 – 6x^2 – 2x + 45\)
\(x = 1\) বসিয়ে পাই,
\(5x^3 – 6x^2 – 2x + 45\)= \( 5(1)^3 – 6(1)^2 – 2(1) + 45\)
= \( 5 – 6 – 2 + 45\)
= \( -3 + 45\)
= \( 42\) [উত্তর]
(b) x2+12-7y ; (2x-y)
প্রথম ও দ্বিতীয় সংখ্যামালার গুণফল
\((x^2 + 12 – 7y)(2x – y)\)= \( 2x^3 + 24x – 14xy – x^2y – 12y + 7y^2\)
= \( 2x^3 – x^2y + 24x – 12y – 14xy + 7y^2\)
\(x = -2\) এবং \(y = 2\) বসিয়ে পাই,
\(2x^3 – x^2y + 24x – 12y – 14xy + 7y^2\)= \( 2(-2)^3 – (-2)^2(2) + 24(-2) – 12(2) – 14(-2)(2) + 7(2)^2\)
= \( -16 – 8 – 48 – 24 + 56 + 28\)
= \( -12\) [উত্তর]
(c) 8p3-3p-2p2 ; 4p2-5
প্রথম ও দ্বিতীয় বীজগণিতিক সংখ্যামালার গুণফল
= \( (8p^3 – 3p – 2p^2)(4p^2 – 5)\)
= \( 32p^5 – 12p^3 – 8p^4 – 40p^3 + 15p + 10p^2\)
= \( 32p^5 – 8p^4 – 52p^3 + 10p^2 + 15p\)
\(p = -2\) বসিয়ে পাই,
\(32p^5 – 8p^4 – 52p^3 + 10p^2 + 15p\)= \( 32(-2)^5 – 8(-2)^4 – 52(-2)^3 + 10(-2)^2 + 15(-2)\)
= \( 32(-32) – 8(16) – 52(-8) + 10(4) – 30\)
= \( -1024 – 128 + 416 + 40 – 30\)
= \( -726\) [উত্তর]
(d) (6a+5b+2) ; (a-b+6)
প্রথম ও দ্বিতীয় বীজগণিতিক সংখ্যামালার গুণফল
\((6a + 5b + 2)(a – b + 6)\)= \( 6a^2 + 5ab + 2a – 6ab – 5b^2 – 2b + 36a + 30b + 12\)
= \( 6a^2 – ab + 38a + 28b – 5b^2 + 12\)
a = 0 এবং b = -1 বসিয়ে পাই
= \( 6(0)^2 – (0)(-1) + 38(0) + 28(-1) – 5(-1)^2 + 12\)
= \( -28 – 5 + 12\)
= \( -33 + 12\)
= \( -21\) [উত্তর]
(e) (p3-p2q2+q3) ; (p2+pq+q2)
প্রথম ও দ্বিতীয় বীজগণিতিক সংখ্যামালার গুণফল –
\((p^3 – p^2q^2 + q^3)(p^2 + pq + q^2)\)= \( p^5 – p^4q^2 + p^2q^3 + p^4q – p^3q^3 + pq^4 + p^3q^2 – p^2q^4 + q^5\)
\(p = 2\) এবং \(q = -2\) বসিয়ে পাই,
= \( (2)^5 – (2)^4(-2)^2 + (2)^2(-2)^3 + (2)^4(-2) – (2)^3(-2)^3 + (2)(-2)^4 + (2)^3(-2)^2 – (2)^2(-2)^4 + (-2)^5\)
= \( 32 – 64 – 32 – 32 + 64 + 32 + 32 – 64 – 32\)
= \( -64\) [উত্তর]
(f) (x2+y2+z2-xy-yz-zx) ; (x+y+z)
প্রথম ও দ্বিতীয় বীজগণিতিক সংখ্যামালার গুণফল –
\((x^2 + y^2 + z^2 – xy – yz – zx)(x + y + z)\)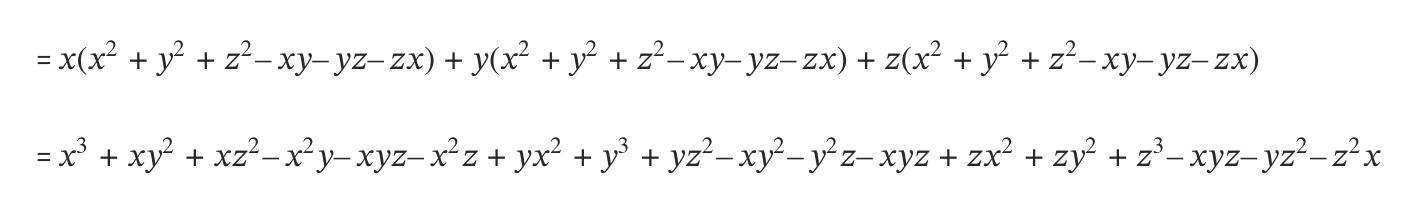
= \( x^3 + y^3 + z^3 – 3xyz\)
এখন, \(x = 1, y = 0\) ও \(z = -1\) বসিয়ে পাই,
\(x^3 + y^3 + z^3 – 3xyz\)= \( (1)^3 + (0)^3 + (-1)^3 – 3(1)(0)(-1)\)
= \( 1 – 1 + 0\)
= \( 0\) [উত্তর]
(g) ধরি, প্রথম বীজগণিতিক সংখ্যামালা হল \((x + 1)\) এবং দ্বিতীয় ত্রিপদী বীজগণিতিক সংখ্যামালা \((x^2 – x + 1)\)।
\(\therefore\) দুটি বীজগণিতিক সংখ্যামালার গুণফল –
= \( (x + 1)(x^2 – x + 1)\)
= \( x(x^2 – x + 1) + 1(x^2 – x + 1)\)
= \( x^3 – x^2 + x + x^2 – x + 1\)
= \( x^3 + 1\)
\(x = -1\) বসিয়ে পাই, [তোমরা নিজেদের পছন্দ মত অন্যান্য অখণ্ড সংখ্যা বসাতে পারো]
\(x^3 + 1\)= \( (-1)^3 + 1\)
= \( -1 + 1\)
= \( 0\) [উত্তর]
2. ধারাবাহিক গুন করে গুনফল খুঁজি (পরপর গুন করি)
(i) \((x^5+1), (3-x^4), (4+x^3+x^6)\)
সমাধান –
\((x^5+1) \times (3-x^4) \times (4+x^3+x^6)\)= \( (3x^5+3-x^9 -x^4) \times (4+x^3+x^6)\)
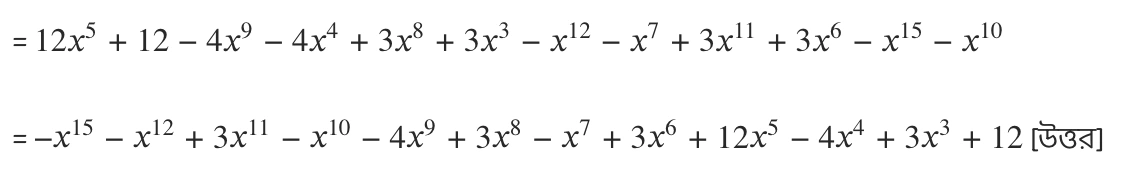
(ii) \((2a^3 -3b^5), (2a^3+3b^5), (2a^4-3a^2b^2 +b^4)\)
সমাধান –
\((2a^3 -3b^5) \times (2a^3+3b^5) \times (2a^4-3a^2b^2 +b^4)\)= \( (4a^6 -6a^3b^5 +6a^3b^5 -9 b^{10}) \times (2a^4-3a^2b^2 +b^4)\)
= \( (4a^6-9 b^{10}) \times (2a^4-3a^2b^2 +b^4)\)
= \( 8a^{10} -18 a^4b^{10} – 12a^8b^2 +27a^2b^{12} +4a^6b^4 – 9b^{14}\) [উত্তর]
(iii) \((ax+by), (ax-by), (a^4x^4 + a^2b^2x^2y^2 + b^4y^4)\)
সমাধান –
\((ax+by) \times (ax-by) \times (a^4x^4 + a^2b^2x^2y^2 + b^4y^4)\)= \( (a^2x^2 +abxy-abxy -b^2y^2) \times (a^4x^4 + a^2b^2x^2y^2 + b^4y^4)\)
= \( (a^2x^2 -b^2y^2) \times (a^4x^4 + a^2b^2x^2y^2 + b^4y^4)\)
= \( a^6x^6 + a^4 b^2x^4y^2+a^2b^4x^2y^4 -a^4b^2x^4y^2-a^2b^4x^2y^4 – b^6 y^6\)
= \( a^6x^6 – b^6y^6\) [উত্তর]
(iv) \((a+b+c), (a-b+c), (a+b-c)\)
সমাধান –
\((a+b+c) \times (a-b+c) \times (a+b-c)\)= \( \{a(a-b+c) +b(a-b+c) +c (a -b+c)\} \times (a+b-c)\)
= \( (a^2 -ab+ac +ba-b^2 +bc +ca -cb +c^2 ) \times (a+b-c)\)
= \( (a^2 +2ac -b^2+c^2) \times (a+b-c)\)
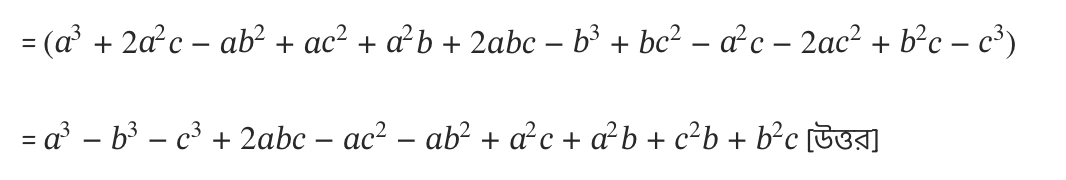
(v) \((\frac{2p^2}{q^2} + \frac{5q^2}{p^2}), (\frac{2p^2}{q^2} – \frac{5q^2}{p^2})\)
সমাধান –
\((\frac{2p^2}{q^2} + \frac{5q^2}{p^2}) \times (\frac{2p^2}{q^2} – \frac{5q^2}{p^2})\)= \( \frac{4p^4}{q^4} + \frac{10p^2q^2}{p^2q^2} – \frac{10p^2q^2}{p^2q^2} – \frac{25q^4}{p^4}\)
= \( \frac{4p^4}{q^4} – \frac{25q^4}{p^4}\)
(vi) \((\frac{x^2}{y^2} + \frac{y^2}{z^2}), (\frac{y^2}{z^2} + \frac{z^2}{x^2}), (\frac{z^2}{x^2} + \frac{x^2}{y^2})\)
সমাধান –
\((\frac{x^2}{y^2} + \frac{y^2}{z^2}) \times (\frac{y^2}{z^2} + \frac{z^2}{x^2}) \times (\frac{z^2}{x^2} + \frac{x^2}{y^2})\)= \( (\frac{x^2y^2}{y^2z^2} + \frac{y^4}{z^4} + \frac{x^2z^2}{x^2y^2} + \frac{y^2z^2}{z^2x^2}) \times (\frac{z^2}{x^2} + \frac{x^2}{y^2})\)
= \( (\frac{x^2}{z^2} + \frac{y^4}{z^4} + \frac{z^2}{y^2} + \frac{y^2}{x^2}) \times (\frac{z^2}{x^2} + \frac{x^2}{y^2})\)
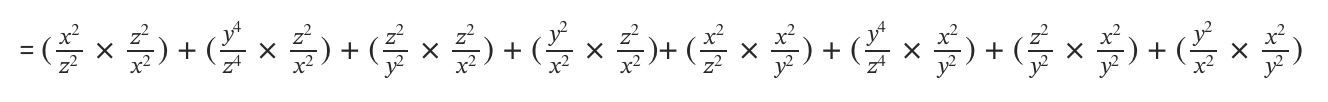
= \( 1 + \frac{y^4}{z^2x^2} + \frac{z^4}{x^2y^2} + \frac{y^2z^2}{x^4} + \frac{x^4}{z^2y^2} + \frac{x^2y^2}{z^4} + \frac{x^2z^2}{y^4} + 1\)
= \( 2 + \frac{y^4}{z^2x^2} + \frac{z^4}{x^2y^2} + \frac{y^2z^2}{x^4} + \frac{x^4}{z^2y^2} + \frac{x^2y^2}{z^4} + \frac{x^2z^2}{y^4}\)
3. সরল করি
(i) \((x+y) (x^2-xy +y^2) + (x-y) (x^2 +xy+y^2)\)
সমাধান –
\((x+y) (x^2-xy +y^2) + (x-y) (x^2 +xy+y^2)\)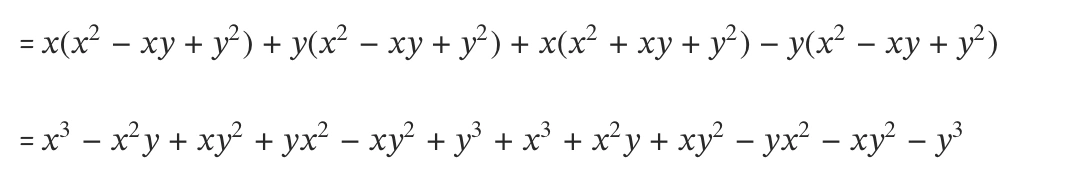
= \( (x^3 +y^3 +x^3 -y^3)\)
= \( 2x^3\) [উত্তর]
(ii) \(a^2(b^2-c^2) + b^2(c^2-a^2) +c^2(a^2 -b^2)\)
সমাধান –
\(a^2(b^2-c^2) + b^2(c^2-a^2) +c^2(a^2 -b^2)\)= \( a^2b^2 -a^2c^2 +b^2c^2 -b^2a^2 +c^2a^2 -c^2b^2\)
= \( 0\) [উত্তর]
4. (i) \(a = x^2+xy+y^2\) , \(b = y^2+yz+z^2\) , \(c = z^2+zx +x^2\) হলে , \((x-y)a +(y-z)b +(z-x)c\) – এর মান নির্ণয় করো।
সমাধান –
\((x-y)a +(y-z)b +(z-x)c\)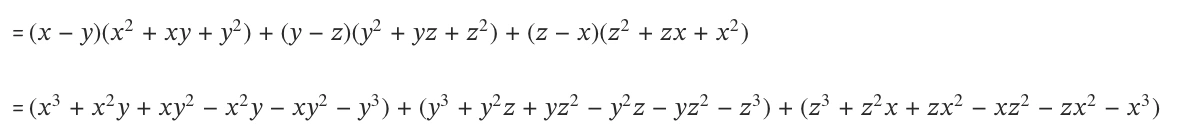
= \( (x^3 -y^3) +(y^3-z^3) +(z^3-x^3)\)
= \( x^3 -y^3 + y^3 -z^3 +z^3-x^3\)
= \( 0\) [উত্তর]
4 (ii) \(a = lx + my + n, b = mx + ny + l, c = nx + ly + m\) হলে, \(a(m+n) + b(n+l) + c(l+m)\) -এর মান কী হয় দেখি।
সমাধান –
\(a = lx + my + n, b = mx + ny + l, c = nx + ly + m\)\(\therefore a(m + n) + b(n + l) + c(l + m)\)= \( (lx + my + n)(m + n) + (mx + ny + l)(n + l) + (nx + ly + m)(l + m)\)
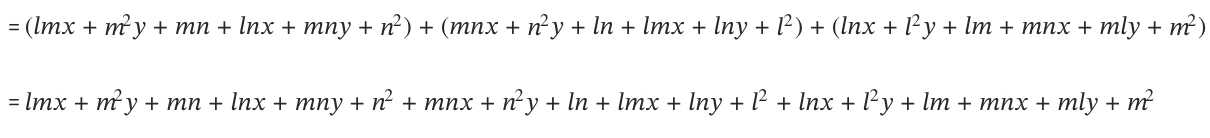
= \( m^2y + mny + n^2y + nly + l^2y + mly + 2mlx + 2mnx + 2nlx + m^2 + n^2 + l^2 + lm + mn + nl\)
= \( y(m^2 + n^2 + l^2 + mn + nl + ml) + 2x(ml + mn + nl) + m^2 + n^2 + l^2 + lm + mn + nl\) [উত্তর]
এই আর্টিকেলে অষ্টম শ্রেণির গণিতের ‘বীজগাণিতিক সংখ্যামালার গুন ও ভাগ’ অধ্যায়ের ‘কষে দেখি – 4.1’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরেছি। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে। কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment