পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) অষ্টম শ্রেণির গণিত পাঠ্যবইয়ের সপ্তম অধ্যায় হলো ‘বিপ্রতীপ কোণের ধারণা’। এই পোস্টে আমরা ‘কষে দেখি – 7’-এর সমস্ত প্রশ্নের সহজ ও নির্ভুল সমাধান নিয়ে আলোচনা করেছি। আশা করি, এই নোটসগুলো তোমাদের গণিত শিখতে এবং পরীক্ষার প্রস্তুতিতে দারুণভাবে সহায়তা করবে।

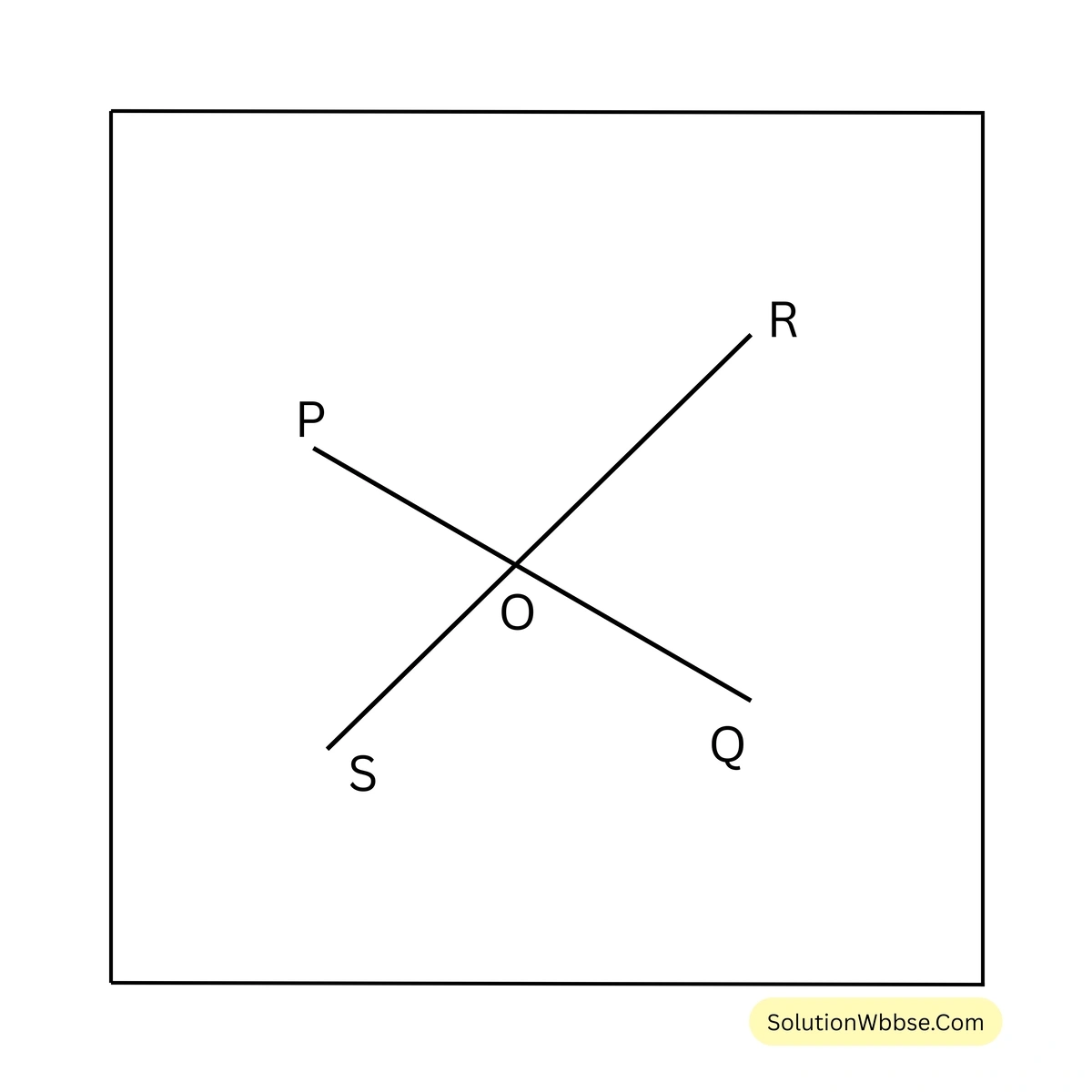
1. দুটি সরলরেখা PQ ও RS পরস্পরকে O বিন্দুতে ছেদ করলে বিপ্রতীপ কোণগুলি তৈরি হয় তাদের আঁকি ও নাম লিখি।
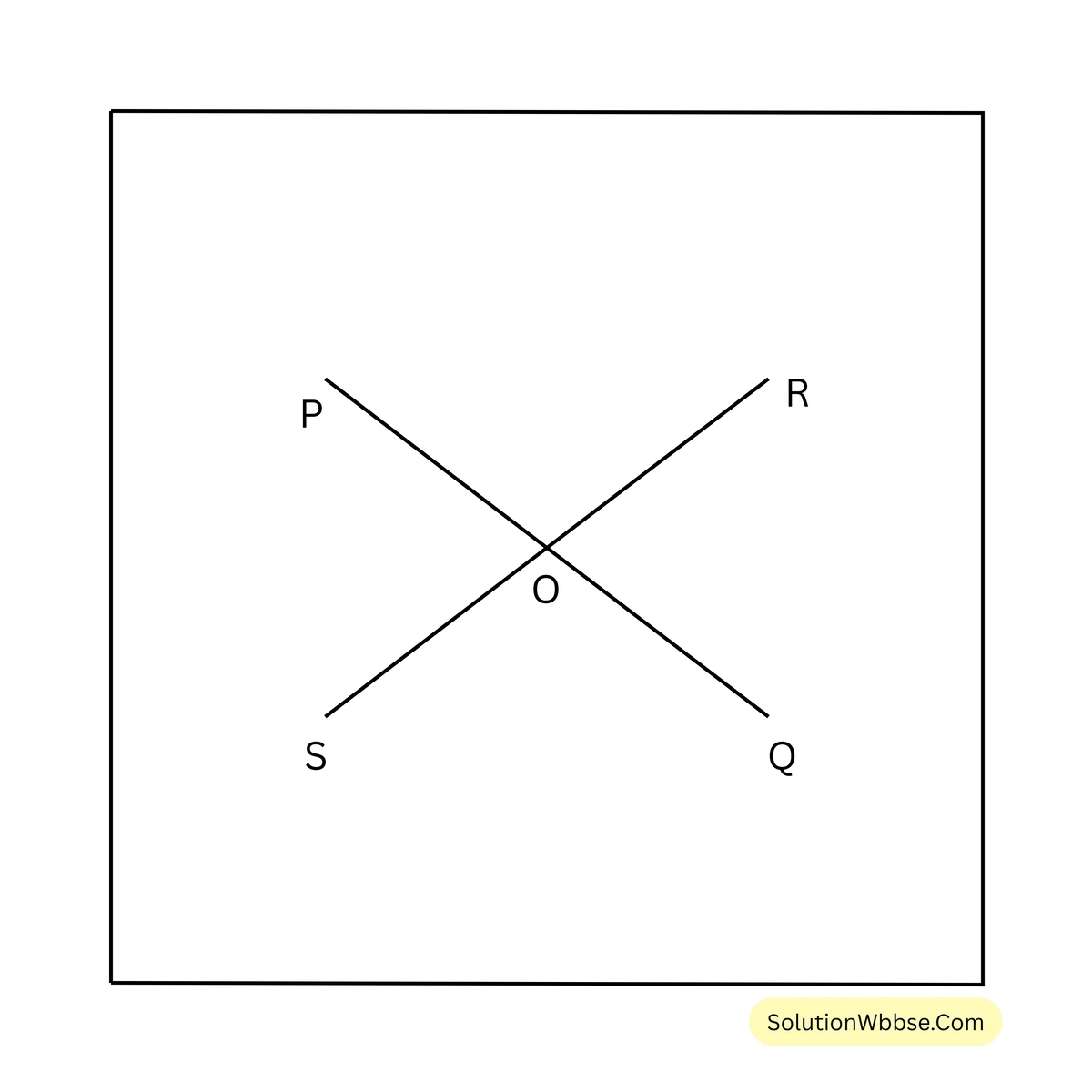
সমাধান – দুটি সরলরেখা PQ ও RS পরস্পরকে O বিন্দুতে ছেদ করলে যে বিপ্রতীপ কোণগুলি তৈরি হয় সেগুলি হল \(\angle POS\) ও \(\angle ROQ\) এবং \(\angle POR\) ও \(\angle SOQ\)।
2. ছবি দেখি ও কোণগুলির মান লেখার চেষ্টা করি
(a) \(\angle 1 = 35^\circ\), \(\angle 2 = ?\), \(\angle 3 = ?\), \(\angle 4 = ?\)
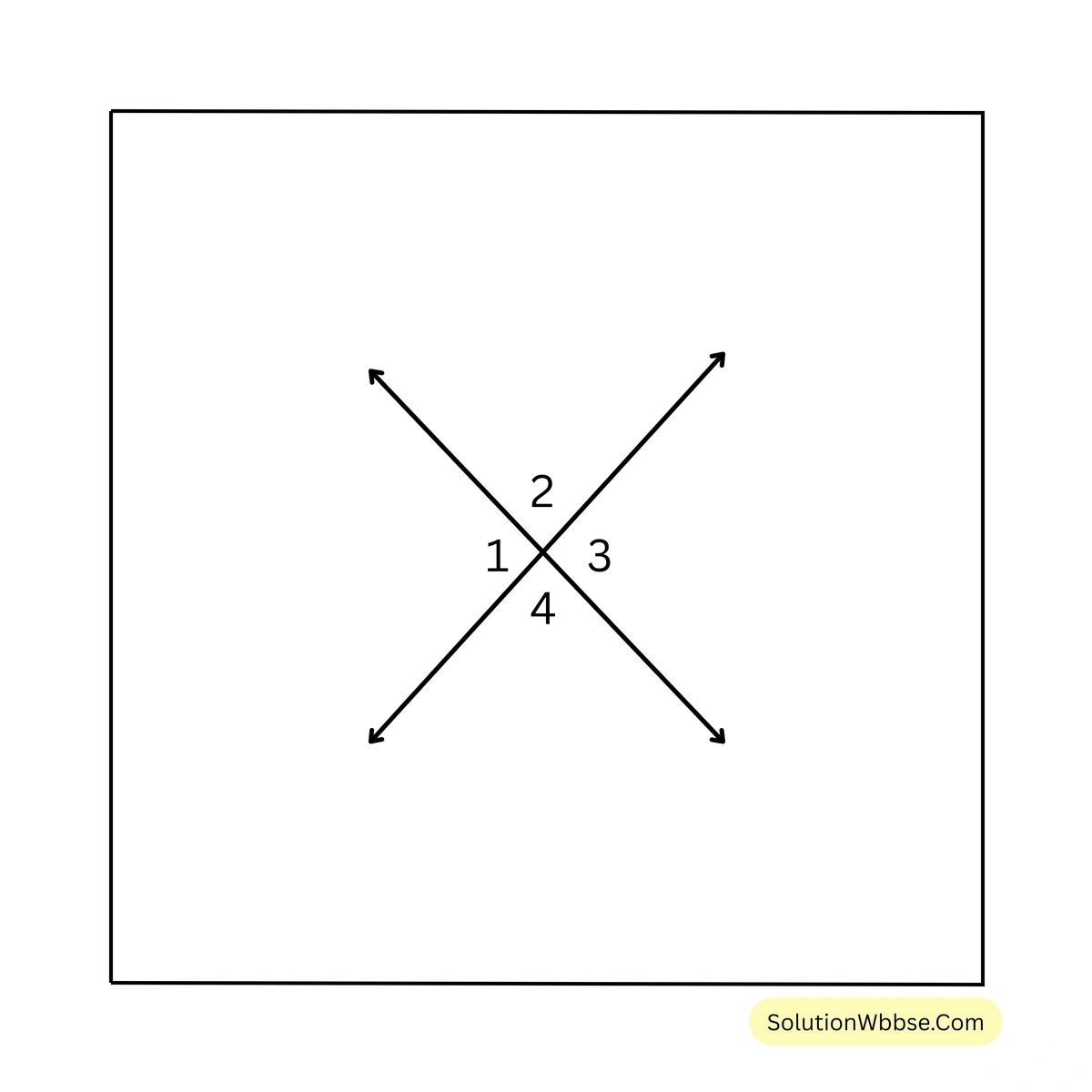
সমাধান –
\(\angle 1\) = বিপ্রতীপ \(\angle 3\) এবং \(\angle 2\) = বিপ্রতীপ \(\angle 4\)
\(\because \angle 1 = 35^\circ\), \(\therefore \angle 3 = 35^\circ\)
আবার, \(\angle 1 + \angle 2 = 180^\circ\)
\(\therefore \angle 2 = 180^\circ – \angle 1\)বা, \(\angle 2 = 180^\circ – 35^\circ\)
বা, \(\angle 2 = 145^\circ\)
\(\therefore \angle 4 = 145^\circ\)(b) \(\angle TOS = 20^\circ\), \(\angle ROQ = 60^\circ\), \(\angle POT = ?\), \(\angle ROP = ?\), \(\angle QOS = ?\)
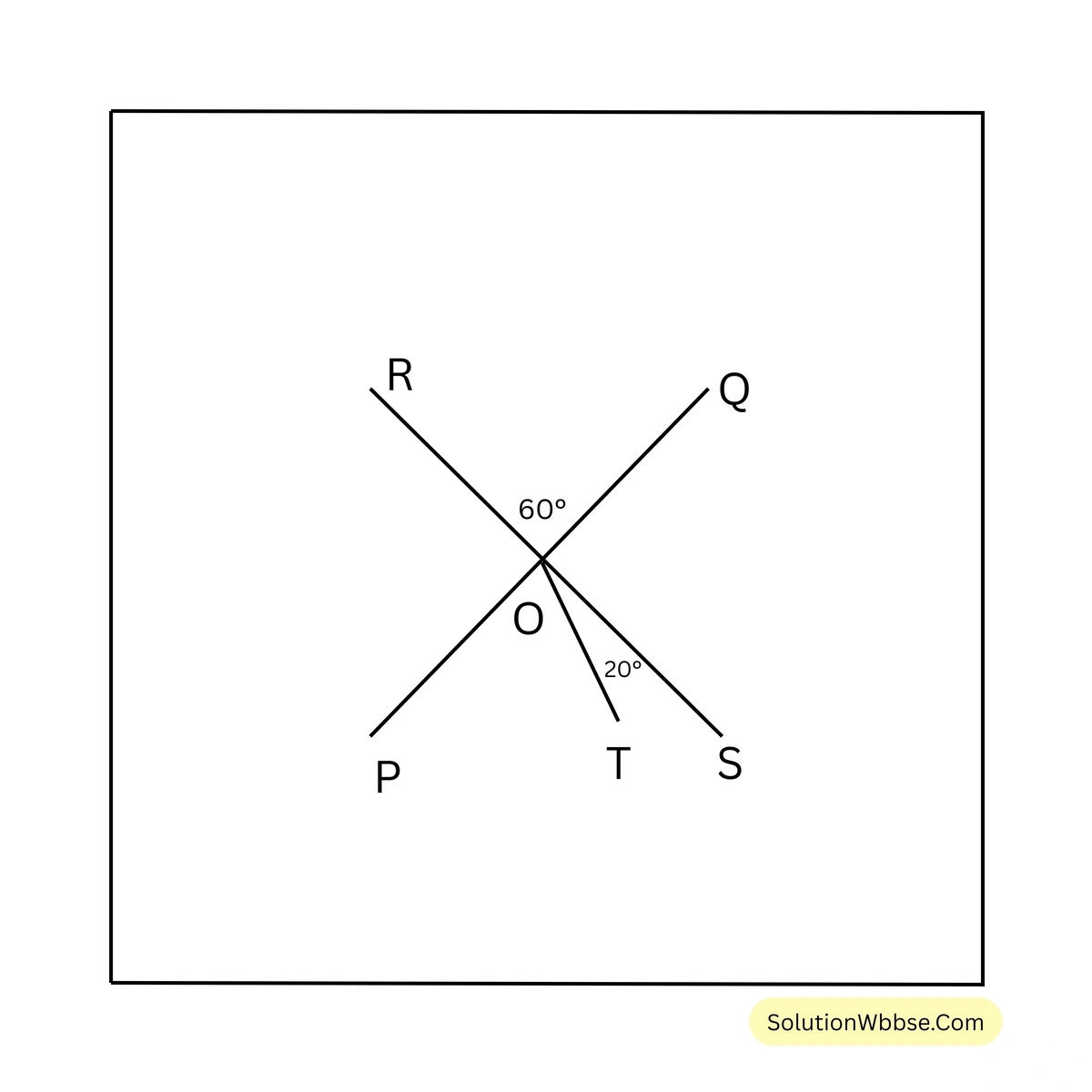
সমাধান –
\(\angle ROQ\) = বিপ্রতীপ \(\angle POS\) এবং \(\angle ROP\) = বিপ্রতীপ \(\angle QOS\)
\(\angle ROQ = 60^\circ\)সুতরাং, \(\angle POS = 60^\circ\)
বা, \(\angle POT + \angle TOS = 60^\circ\)
বা, \(\angle POT = 60^\circ – \angle TOS\)
বা, \(\angle POT = 60^\circ – 20^\circ\)
\(\therefore \angle POT = 40^\circ\)\(\angle ROP + \angle ROQ = 180^\circ\)বা, \(\angle ROP = 180^\circ – \angle ROQ\)
বা, \(\angle ROP = 180^\circ – 60^\circ\)
\(\therefore \angle QOS = 120^\circ\) [\(\because \angle ROP\) = বিপ্রতীপ \(\angle QOS\)]
3. তীর্থ PQ ও XY দুটি সরলরেখা আঁকল যারা পরস্পরকে O বিন্দু ছেদ করেছে। আমি চাঁদার সাহায্যে বিপ্রতীপ কোনগুলি মেপে দেখি।
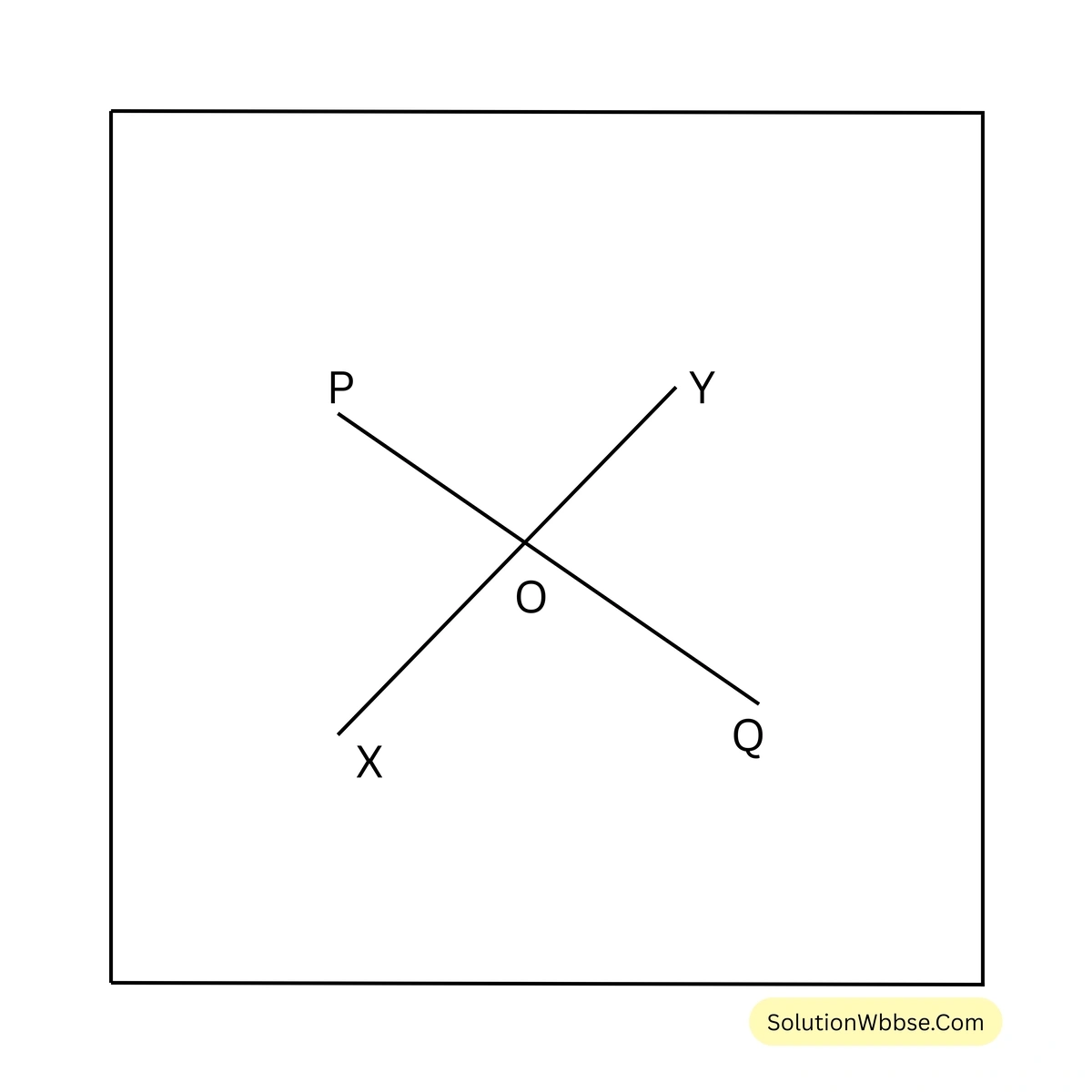
সমাধান –
PQ ও XY দুটি সরলরেখা পরস্পরকে O বিন্দুতে ছেদ করার ফলে যে দুই জোড়া বিপ্রতীপ কোণ উৎপন্ন হয় সেগুলি হল \(\angle POX\) ও \(\angle YOQ\) এবং \(\angle POY\) ও \(\angle XOQ\)
চাঁদার সাহায্যে মেপে দেখলাম, \(\angle POX\) = বিপ্রতীপ \(\angle YOQ = 30^\circ\) এবং \(\angle XOQ\) = বিপ্রতীপ \(\angle POY = 120^\circ\)
4. পাশের ছবি দেখি ও নীচের প্রশ্নের উত্তর খোঁজার চেষ্টা করি।
(i) দুটি কোণের নাম লিখি যারা পরস্পর পূরক কোণ।
(ii) দুটি কোণের নাম লিখি যারা পরস্পর সম্পূরক কোণ।
(iii) দুটি কোণের নাম লিখি যারা পরস্পর বিপ্রতীপ কোণ।
সমাধান –
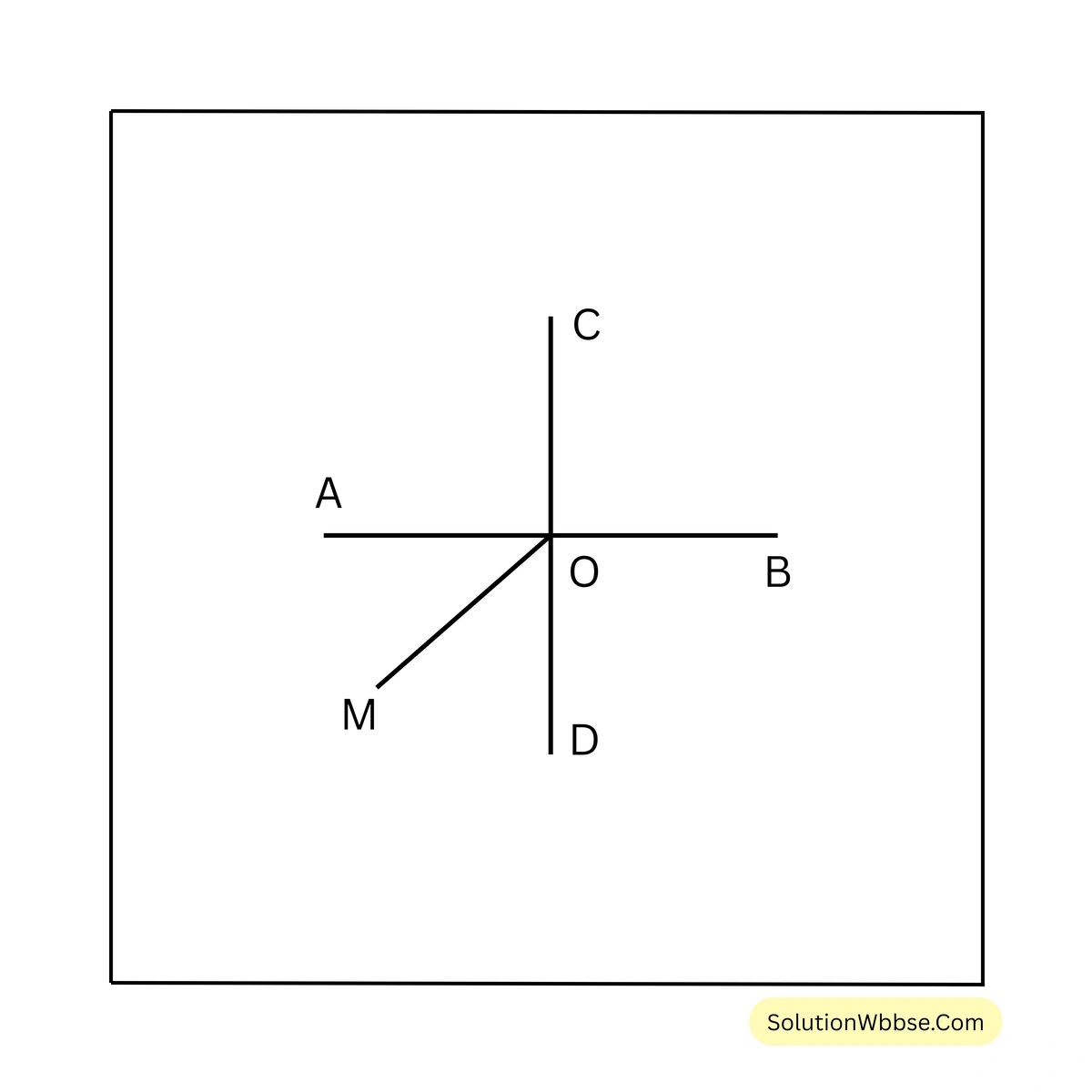
(i) \(\angle AOM\) ও \(\angle DOM\) কোণ দুটি পরস্পর পূরক কোণ।
(ii) \(\angle AOC\) ও \(\angle BOC\) কোণ দুটি পরস্পর সম্পূরক কোণ।
[এছাড়াও, \(\angle BOC\) ও \(\angle DOB\) কোণ দুটি পরস্পর সম্পূরক কোণ]
(iii) \(\angle AOD\) ও \(\angle COB\) কোণ দুটি পরস্পর বিপ্রতীপ কোণ।
[এছাড়াও, \(\angle AOC\) ও \(\angle DOB\) কোণ দুটি পরস্পর সম্পূরক কোণ]
5. দুটি সরলরেখা কোনো বিন্দুতে ছেদ করলে বিপ্রতীপ কোণগুলির পরিমাপ সমান হবে—যুক্তি দিয়ে প্রমাণ করি।
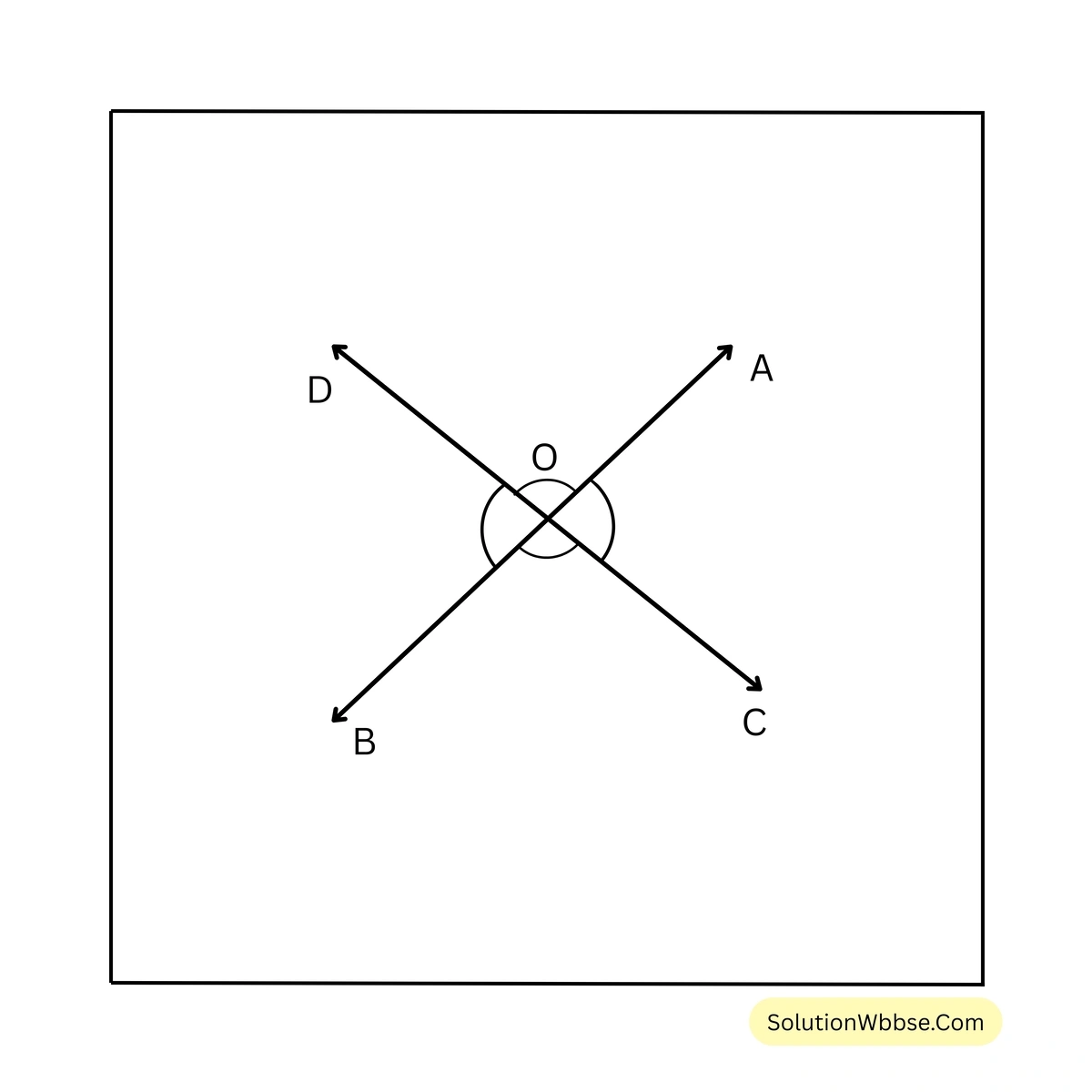
AB ও CD সরলরেখা দুটি পরস্পরকে O বিন্দুতে ছেদ করে। এর ফলে দুজোড়া বিপ্রতীপ কোণ \(\angle AOD\), \(\angle BOC\) ও \(\angle AOC\), \(\angle BOD\) তৈরি হয়েছে।
প্রমাণ করতে হবে যে, বিপ্রতীপ কোণ জোড়া দুটি সমান, অর্থাৎ \(\angle AOD = \angle BOC\) ও \(\angle AOC = \angle BOD\)।
প্রমাণ –
\(\angle AOC + \angle AOD = 180^\circ\) [∵ CD সরলরেখার উপর OA দণ্ডায়মান]
\(\angle AOC + \angle BOC = 180^\circ\) [∵ AB সরলরেখার উপর OC দণ্ডায়মান]
\(\angle AOC + \angle AOD = \angle AOC + \angle BOC\)\(\therefore \angle AOD = \angle BOC\)আবার,
\(\angle BOC + \angle BOD = 180^\circ\) [∵ CD সরলরেখার উপর OB দণ্ডায়মান]
\(\angle AOC + \angle BOC = 180^\circ\) [∵ AB সরলরেখার উপর OC দণ্ডায়মান]
\(\angle BOC + \angle BOD = \angle AOC + \angle BOC\)\(\therefore \angle BOD = \angle AOC\)সুতরাং, \(\angle AOD = \angle BOC\) এবং \(\angle BOD = \angle AOC\) [প্রমাণিত]
6. \(\angle BOD\), \(\angle BOC\) এবং \(\angle AOC\)-এর পরিমাপ লিখি।
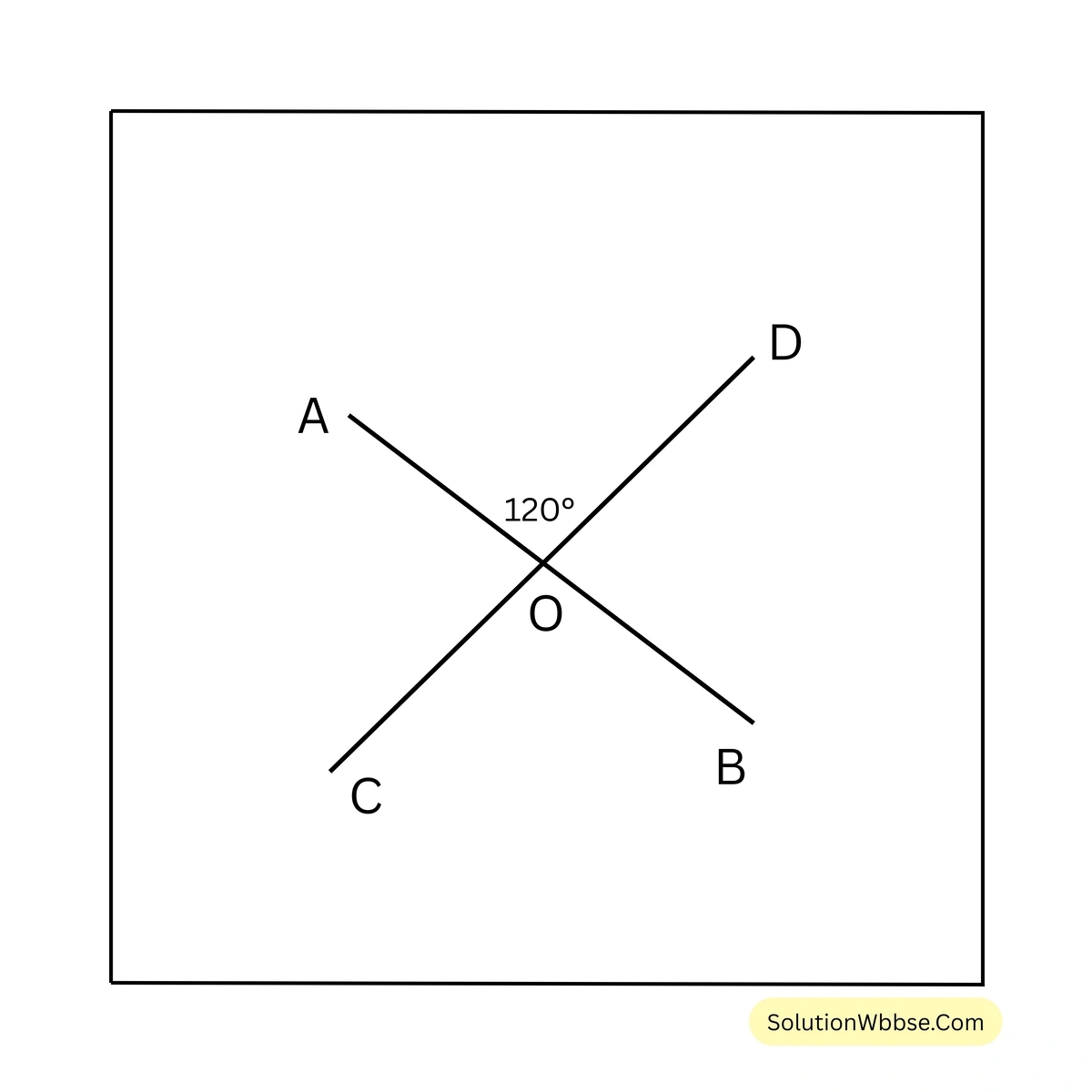
সমাধান –
\(\angle BOC\) = বিপ্রতীপ \(\angle AOD = 120^\circ\)
\(\angle AOC + \angle BOC = 180^\circ\) [∵ AB সরলরেখার উপর OC দণ্ডায়মান]
\(\therefore \angle AOC = 180^\circ – 120^\circ = 60^\circ\)সুতরাং, \(\angle BOD = 60^\circ\), \(\angle BOC = 120^\circ\) এবং \(\angle AOC = 60^\circ\)
7. \(\angle POR\) ও \(\angle QOS\)-এর সমষ্টি \(110^\circ\); \(\angle POS\), \(\angle QOS\), \(\angle QOR\) ও \(\angle POR\)-এর পরিমাপ লিখি।
সমাধান –
\(\angle POR\) = বিপ্রতীপ \(\angle QOS\)
আবার, \(\angle POR + \angle QOS = 110^\circ\)
বা, \(\angle POR + \angle POR = 110^\circ\)
বা, \(2 \angle POR = 110^\circ\)
বা, \(\angle POR = \frac{110^\circ}{2}\)
\(\therefore \angle POR = 55^\circ\)\(\angle POR + \angle POS = 180^\circ\) [∵ RS সরলরেখার উপর OP দণ্ডায়মান]
\(\therefore \angle POS = 180^\circ – 55^\circ = 125^\circ\)\(\angle QOR\) = বিপ্রতীপ \(\angle POS = 125^\circ\)
সুতরাং, \(\angle POS = 125^\circ\), \(\angle QOS = 55^\circ\), \(\angle QOR = 125^\circ\) ও \(\angle POR = 55^\circ\)
8. OP, OQ, OR এবং OS সমবিন্দু। OP এবং OR একই সরলরেখায় অবস্থিত। P ও R বিন্দু O বিন্দুর বিপরীত পাশে অবস্থিত। \(\angle POQ = \angle ROS\) এবং \(\angle POS = \angle QOR\)। যদি \(\angle POQ = 50^\circ\) হয়, তবে \(\angle QOR\), \(\angle ROS\) এবং \(\angle POS\)-এর পরিমাপ লিখি।
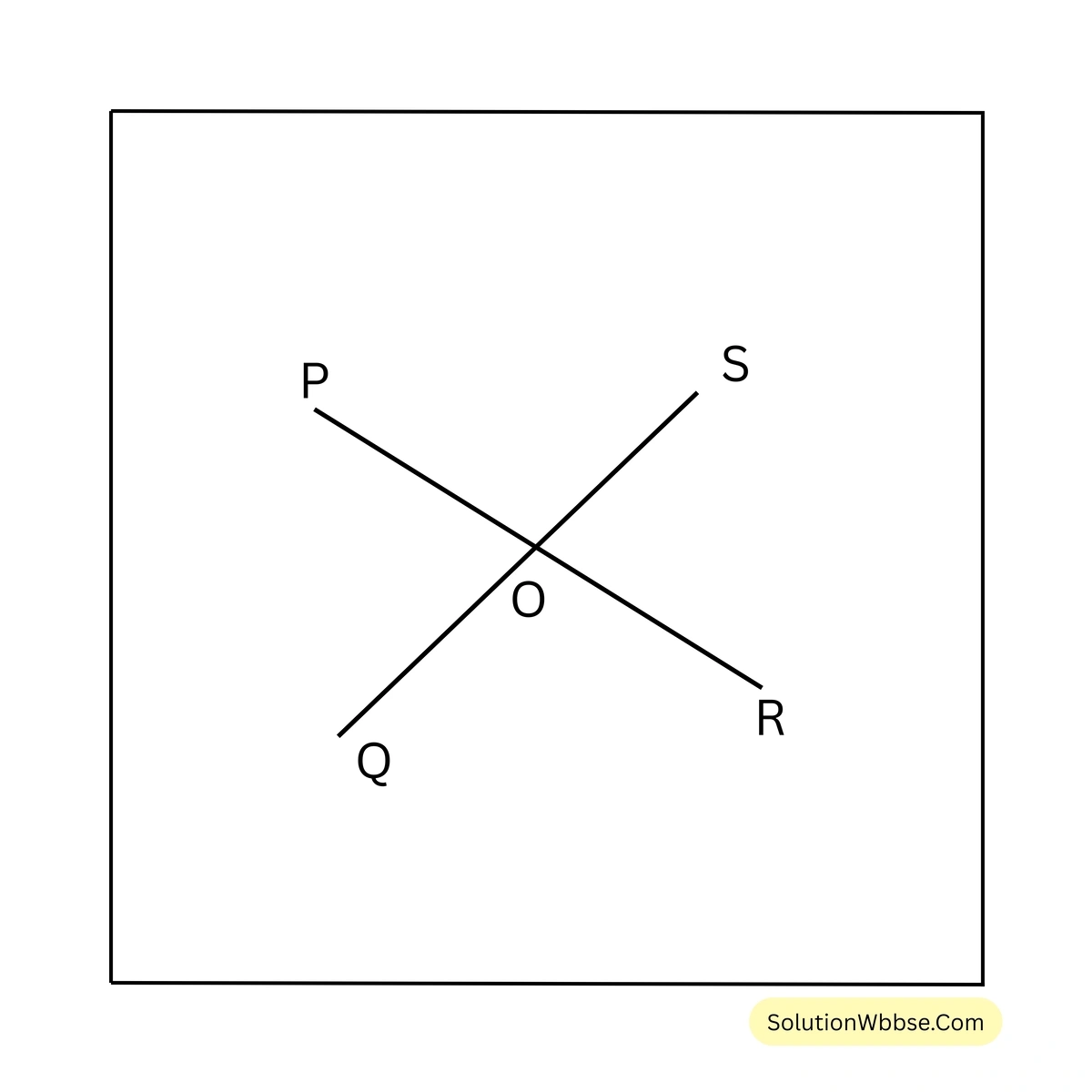
সমাধান –
\(\angle POQ = \angle ROS\) এবং \(\angle POQ = 50^\circ\)
\(\therefore \angle ROS = 50^\circ\)OP এবং OR একই সরলরেখায় অবস্থিত।
\(\therefore \angle POS + \angle ROS = 180^\circ\)বা, \(\angle POS + 50^\circ = 180^\circ\)
বা, \(\angle POS = 180^\circ – 50^\circ\)
\(\therefore \angle POS = 130^\circ\)আবার, \(\angle POS = \angle QOR\)
\(\therefore \angle QOR = 130^\circ\)সুতরাং, \(\angle QOR = 130^\circ\), \(\angle ROS = 50^\circ\), এবং \(\angle POS = 130^\circ\)
9. চারটি রশ্মি একটি বিন্দুতে এমনভাবে মিলিত হয় যে বিপরীত দিকের কোণগুলি সমান। প্রমাণ করি যে ওই চারটি রশ্মি দ্বারা দুটি সরলরেখা তৈরি হয়।
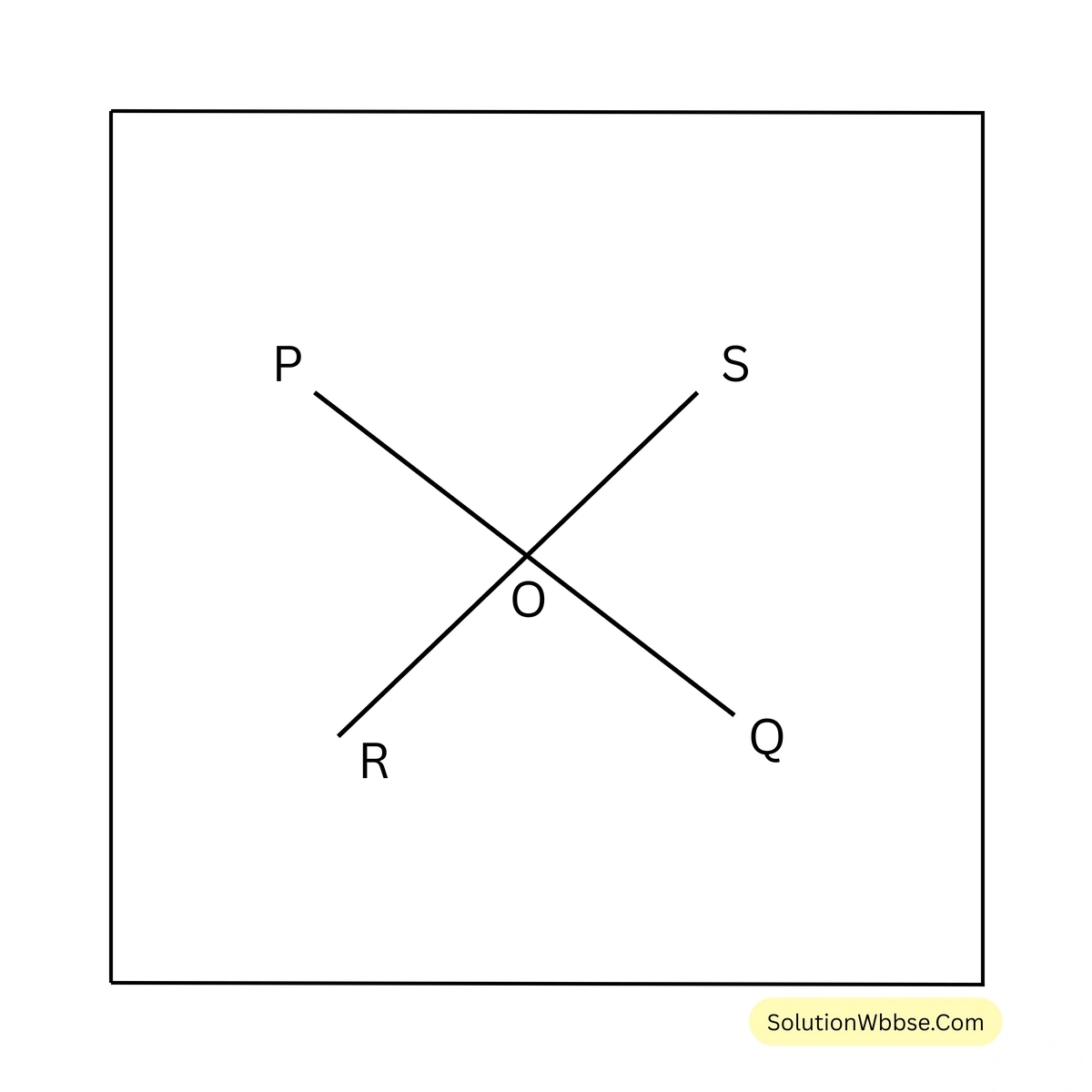
চারটি রশ্মি PO, RO, QO এবং SO, O বিন্দুতে এমনভাবে মিলিত হয়েছে যে বিপরীত দিকের কোণগুলি সমান অর্থাৎ \(\angle POS = \angle ROQ\) এবং \(\angle POR = \angle SOQ\)।
প্রমাণ করতে হবে যে, PO, RO, QO এবং SO দিয়ে দুটি সরলরেখা তৈরি হয়।
প্রমাণ – চারটি রশ্মি PO, RO, QO এবং SO, O বিন্দুতে মিলিত হয়েছে।
\(\therefore \angle POS + \angle POR + \angle ROQ + \angle SOQ = 360^\circ\)বা, \(\angle ROQ + \angle SOQ + \angle ROQ + \angle SOQ = 360^\circ\) [∵ \(\angle POS = \angle ROQ\) এবং \(\angle POR = \angle SOQ\)]
বা, \(2(\angle ROQ + \angle SOQ) = 360^\circ\)
\(\therefore \angle ROQ + \angle SOQ = 180^\circ\)\(\therefore \angle ROQ\) ও \(\angle SOQ\) সন্নিহিত কোণ দুটির সমষ্টি \(180^\circ\)
সুতরাং, R, S বিন্দুদ্বয় একই সরলরেখায় অবস্থিত।
এখন, \(\angle POS + \angle SOQ\)
= \( \angle ROQ + \angle SOQ\) [∵ \(\angle POS = \angle ROQ\)]
= \( 180^\circ\)
\(\therefore \angle POS\) ও \(\angle SOQ\) সন্নিহিত কোণ দুটির সমষ্টি \(180^\circ\)
সুতরাং, P, Q বিন্দুদ্বয় একই সরলরেখায় অবস্থিত।
\(\therefore\) PO, RO, QO এবং SO, O বিন্দুতে মিলিত হওয়ার ফলে PQ ও RS দুটি সরলরেখা তৈরি হল।
সুতরাং, PO, RO, QO এবং SO দিয়ে দুটি সরলরেখা তৈরি হয়। [প্রমাণিত]
10. একটি কোণের অন্তঃসমদ্বিখণ্ডক ও বহিঃসমদ্বিখণ্ডক পরস্পর লম্বভাবে অবস্থিত প্রমাণ করি।
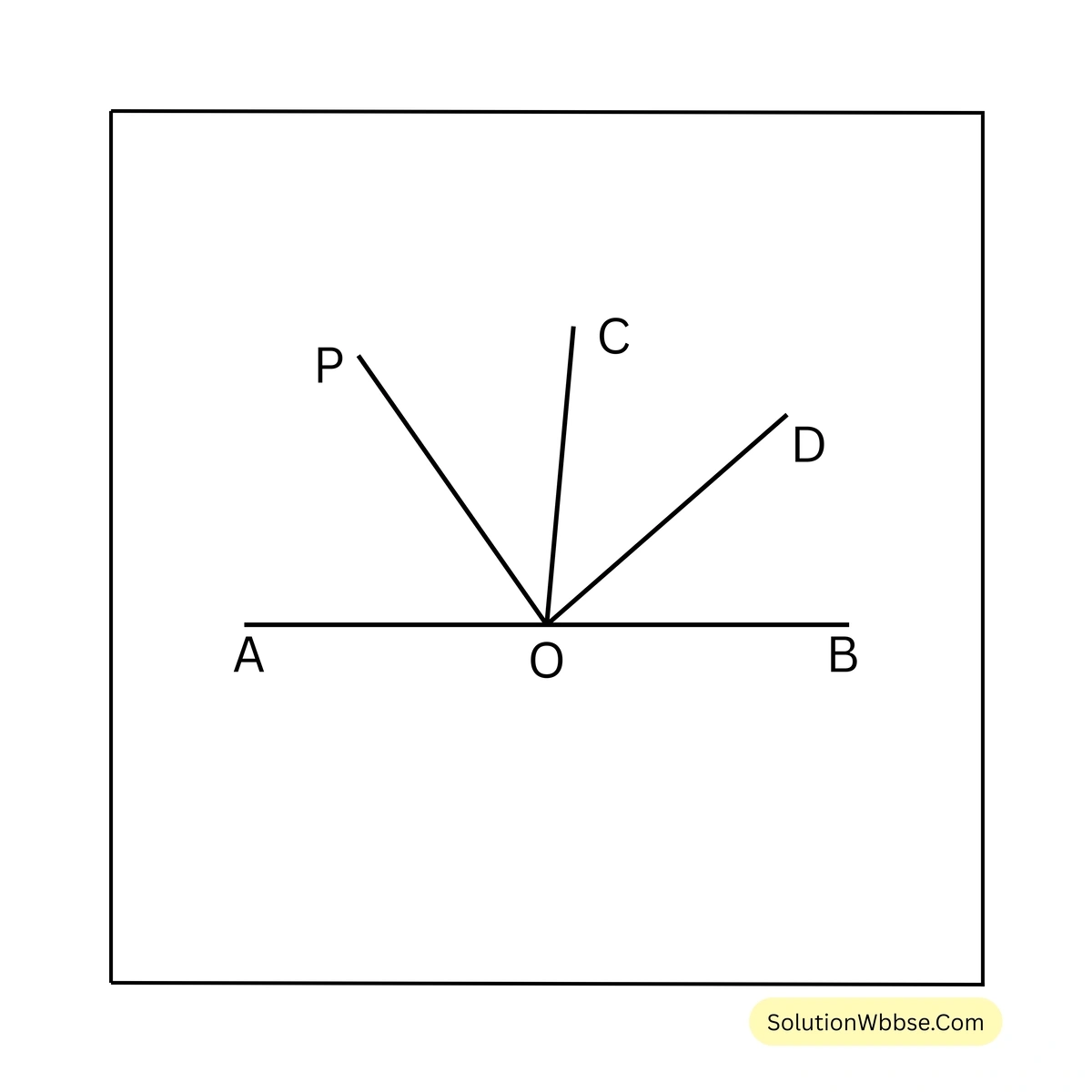
একটি কোণ \(\angle BOC\)-এর অন্তঃসমদ্বিখণ্ডক OD এবং বহিঃসমদ্বিখণ্ডক OP।
প্রমাণ করতে হবে যে, OD ও OP পরস্পর লম্বভাবে অবস্থিত।
প্রমাণ – \(\angle BOC\)-এর বহিকোণ \(\angle AOC\)
সুতরাং, \(\angle BOC + \angle AOC = 180^\circ\) —(i)
\(\angle BOC\)-এর অন্তঃসমদ্বিখণ্ডক OD
\(\therefore \angle BOC = 2 \angle COD\) —(ii)
আবার, \(\angle BOC\)-এর বহিঃকোণ, \(\angle AOC\)-এর অন্তঃসমদ্বিখণ্ডক OP
\(\therefore \angle AOC = 2 \angle COP\) —(iii)
(i) নং থেকে পাই,
\(\angle BOC + \angle AOC = 180^\circ\)বা, \(2 \angle COD + 2 \angle COP = 180^\circ\)
বা, \(2(\angle COD + \angle COP) = 180^\circ\)
\(\therefore \angle COD + \angle COP = 90^\circ\)সুতরাং, OD ও OP পরস্পর লম্ব।
11. দুটি সরলরেখা পরস্পর ছেদ করলে যে চারটি কোণ উৎপন্ন হয় তাদের সমষ্টি চার সমকোণের সমান —প্রমাণ করি।
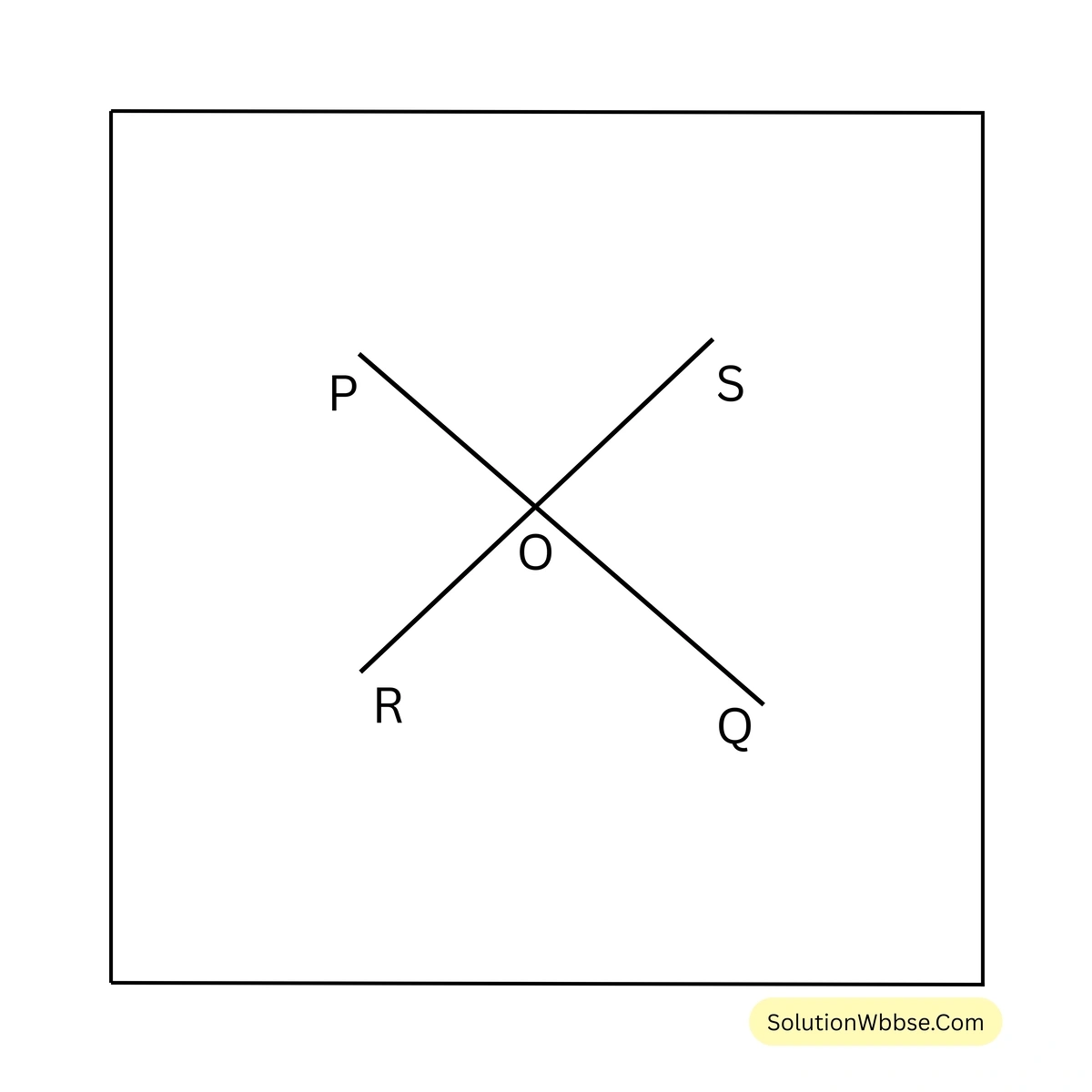
PQ ও RS সরলরেখা দুটি পরস্পরকে O বিন্দুতে ছেদ করেছে। এর ফলে \(\angle POR\), \(\angle ROQ\), \(\angle SOQ\) ও \(\angle POS\) চারটি কোণ তৈরি হয়েছে।
প্রমাণ করতে হবে যে, \(\angle POR + \angle ROQ + \angle SOQ + \angle POS = 4\) সমকোণ।
প্রমাণ –
PQ সরলরেখার উপর OR রশ্মি দণ্ডায়মান
\(\therefore \angle POR + \angle ROQ = 180^\circ\) —(i)
আবার, PQ সরলরেখার উপর OS রশ্মি দণ্ডায়মান
\(\therefore \angle POS + \angle SOQ = 180^\circ\) —(ii)
(i) নং ও (ii) নং সমীকরণ যোগ করে পাই,
\(\angle POR + \angle ROQ + \angle POS + \angle SOQ = 180^\circ + 180^\circ\)বা, \(\angle POR + \angle ROQ + \angle POS + \angle SOQ = 360^\circ\)
\(\therefore \angle POR + \angle ROQ + \angle POS + \angle SOQ = 4\) সমকোণ। [প্রমাণিত]
12. PQR ত্রিভুজের \(\angle PQR = \angle PRQ\); QR বাহুকে উভয়দিকে বর্ধিত করলে যে দুটি বহিঃকোণ উৎপন্ন হয় তাদের মান সমান—প্রমাণ করি।
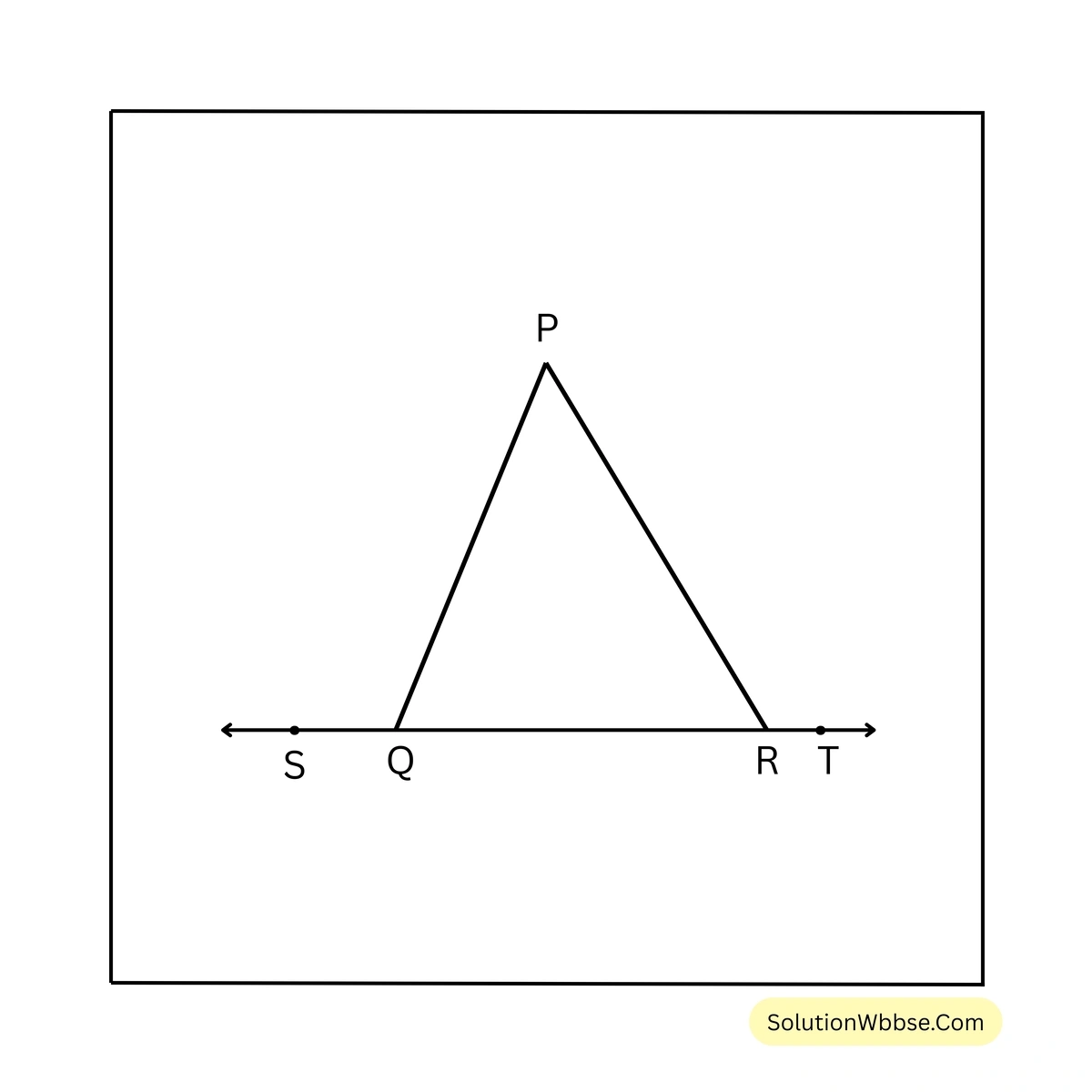
PQR ত্রিভুজের \(\angle PQR = \angle PRQ\), QR বাহুকে উভয়দিকে যথাক্রমে S ও T পর্যন্ত বর্ধিত করার ফলে যথাক্রমে দুটি বহিঃকোণ \(\angle PQS\) এবং \(\angle PRT\) তৈরি হল।
প্রমাণ করতে হবে যে, \(\angle PQS = \angle PRT\)।
প্রমাণ – SR সরলরেখার উপর QP রশ্মি দণ্ডায়মান
\(\therefore \angle PQS + \angle PQR = 180^\circ\) —(i)
আবার, QT সরলরেখার উপর RP রশ্মি দণ্ডায়মান
\(\therefore \angle PRT + \angle PRQ = 180^\circ\) —(ii)
(i) নং ও (ii) নং সমীকরণ থেকে পাই,
\(\angle PQS + \angle PQR = \angle PRT + \angle PRQ\)বা, \(\angle PQS + \angle PRQ = \angle PRT + \angle PRQ\) [∵ \(\angle PQR = \angle PRQ\)]
\(\therefore \angle PQS = \angle PRT\) [প্রমাণিত]
13. দুটি সরলরেখা পরস্পরকে একটি বিন্দুতে ছেদ করায় যে চারটি কোণ উৎপন্ন হয় তাদের সমদ্বিখণ্ডকগুলি পরস্পর দুটি লম্ব সরলরেখা—প্রমাণ করি।
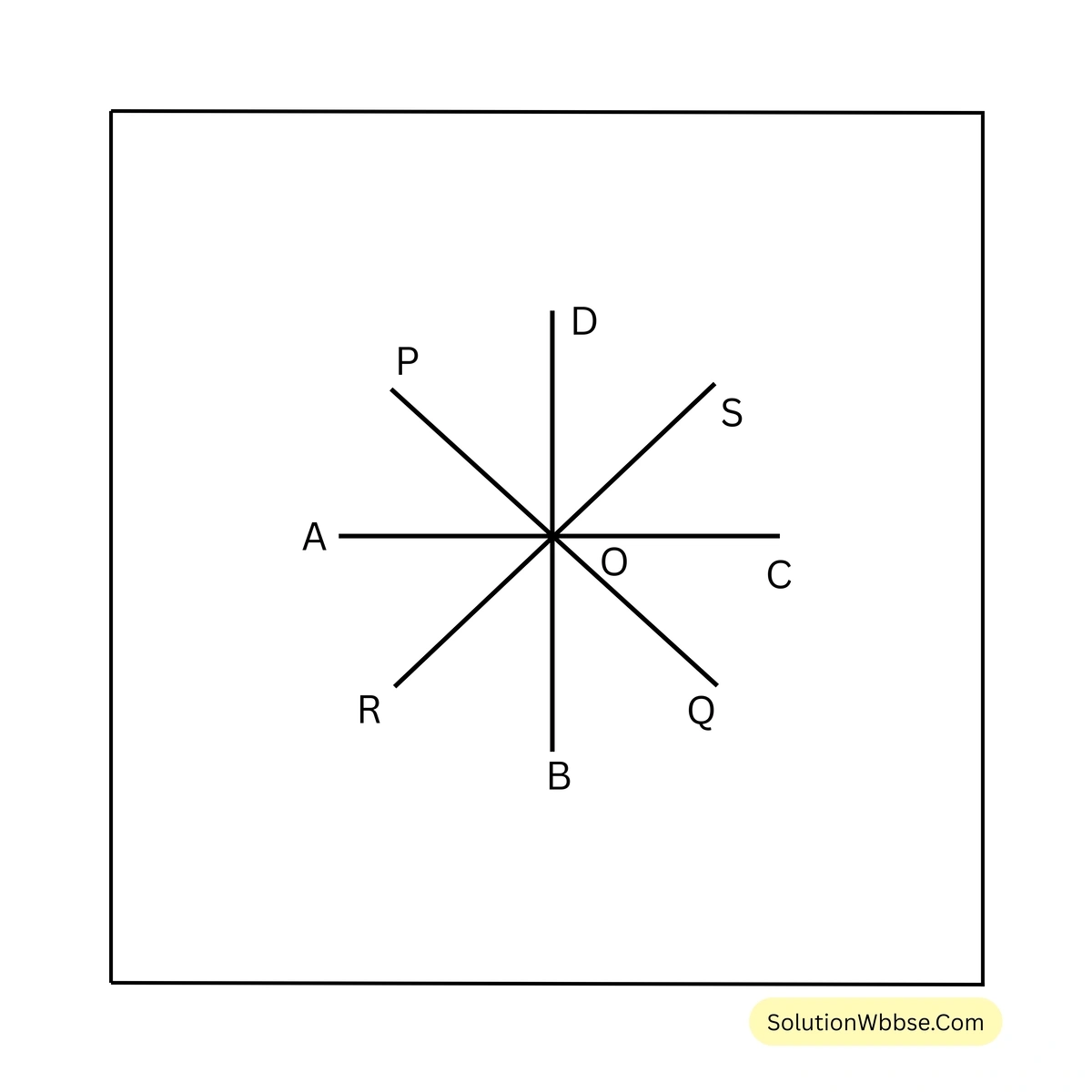
PQ ও RS সরলরেখা পরস্পরকে O বিন্দুতে ছেদ করে চারটি কোণ \(\angle POR\), \(\angle ROQ\), \(\angle SOQ\) ও \(\angle POS\) উৎপন্ন হয়েছে। AO, BO, CO ও DO যথাক্রমে চারটি কোণগুলির সমদ্বিখণ্ডক।
প্রমাণ করতে হবে যে, সমদ্বিখণ্ডকগুলি পরস্পর দুটি লম্ব সরলরেখা অর্থাৎ, AO, OC এবং BO, OD একই সরলরেখায় আছে এবং \(AC \perp BD\)।
প্রমাণ –
\(\angle POS =\) বিপ্রতীপ \(\angle ROQ\) [প্রদত্ত]
এবং \(\angle POR =\) বিপ্রতীপ \(\angle SOQ\) [প্রদত্ত]
AO, \(\angle POR\)-এর সমদ্বিখণ্ডক, \(\therefore \angle AOP = \angle AOR = \frac{1}{2} \angle POR\)
BO, \(\angle QOR\)-এর সমদ্বিখণ্ডক, \(\therefore \angle BOR = \angle BOQ = \frac{1}{2} \angle ROQ\)
CO, \(\angle SOQ\)-এর সমদ্বিখণ্ডক, \(\therefore \angle COS = \angle COQ = \frac{1}{2} \angle SOQ\)
DO, \(\angle POS\)-এর সমদ্বিখণ্ডক, \(\therefore \angle DOP = \angle DOS = \frac{1}{2} \angle POS\)
এখন, \(\angle AOD + \angle AOB\)
= \( \angle DOP + \angle AOP + \angle AOR + \angle ROB\)
= \( \frac{1}{2} \angle POS + \angle POR + \frac{1}{2} \angle ROQ\) [∵ \(\angle POS =\) বিপ্রতীপ \(\angle ROQ\)]
= \( \frac{1}{2} \angle ROQ + \angle POR + \frac{1}{2} \angle ROQ\)
= \( \angle ROQ + \angle POR\)
= \( 180^\circ\) [∵ PQ সরলরেখার উপর OR দণ্ডায়মান]
\(\angle AOD\) ও \(\angle AOB\) সন্নিহিত কোণ দুটির সমষ্টি \(180^\circ\)
\(\therefore\) OB ও OD একই সরলরেখায় অবস্থিত।
অনুরূপভাবে প্রমাণ করা যায় যে,
AO ও OC একই সরলরেখায় অবস্থিত।
\(\angle AOD = \angle AOP + \angle POD\)= \( \frac{1}{2} \angle ROP + \frac{1}{2} \angle POS\)
= \( \frac{1}{2} (\angle ROP + \angle POS)\)
= \( \frac{1}{2} \times 180^\circ\) [∵ RS সরলরেখার উপর OP দণ্ডায়মান]
= \( 90^\circ\)
\(\therefore\) AC ও BD সরলরেখা দুটি পরস্পর লম্ব।
\(\therefore AC \perp BD\) [প্রমাণিত]
এই আর্টিকেলে অষ্টম শ্রেণির গণিতের ‘বিপ্রতীপ কোণের ধারণা’ অধ্যায়ের ‘কষে দেখি – 7’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরেছি। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে। কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment