পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) অষ্টম শ্রেণির গণিত পাঠ্যবইয়ের নবম অধ্যায় হলো ‘ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক’। এই পোস্টে আমরা ‘কষে দেখি – 9’-এর সমস্ত প্রশ্নের সহজ ও নির্ভুল সমাধান নিয়ে আলোচনা করেছি। আশা করি, এই নোটসগুলো তোমাদের গণিত শিখতে এবং পরীক্ষার প্রস্তুতিতে দারুণভাবে সহায়তা করবে।

1. নীচের সমদ্বিবাহু ত্রিভুজগুলি দেখি ও না মেপে প্রতিটি ত্রিভুজের কোন দুটি বাহু সমান হবে লিখি
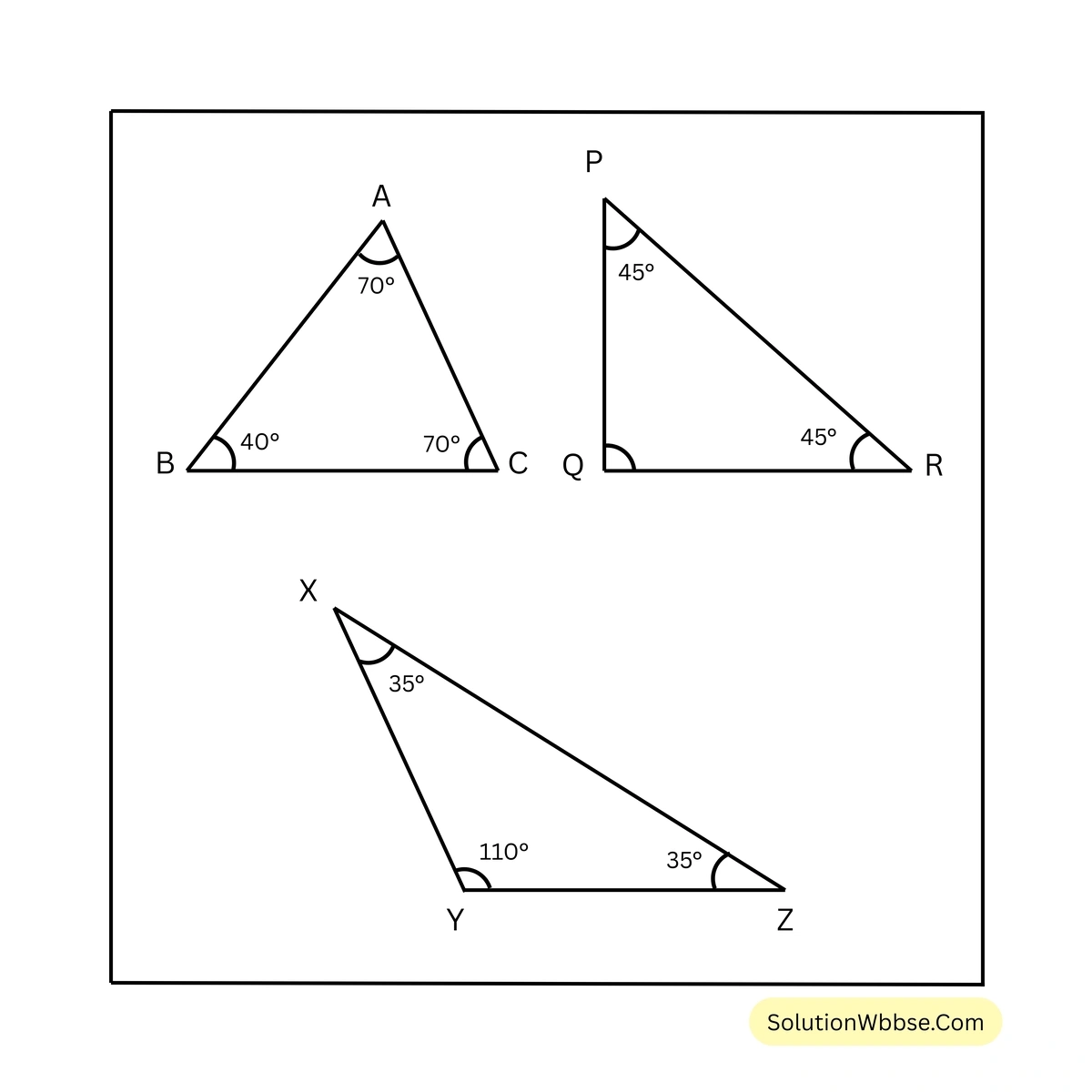
সমাধান –
প্রথম চিত্রে, ABC ত্রিভুজের \(\angle BAC = \angle ACB = 70^\circ\)
\(\therefore AB = BC\)দ্বিতীয় চিত্রে, PQR ত্রিভুজের \(\angle RPQ = \angle PRQ = 45^\circ\)
তৃতীয় চিত্রে, XYZ ত্রিভুজের \(\angle YXZ = \angle XZY = 35^\circ\)
\(\therefore XY = YZ\)2. নীচের সমদ্বিবাহু ত্রিভুজগুলি দেখি ও না মেপে প্রতিটি ত্রিভুজের কোন কোণগুলি সমান হবে লিখি
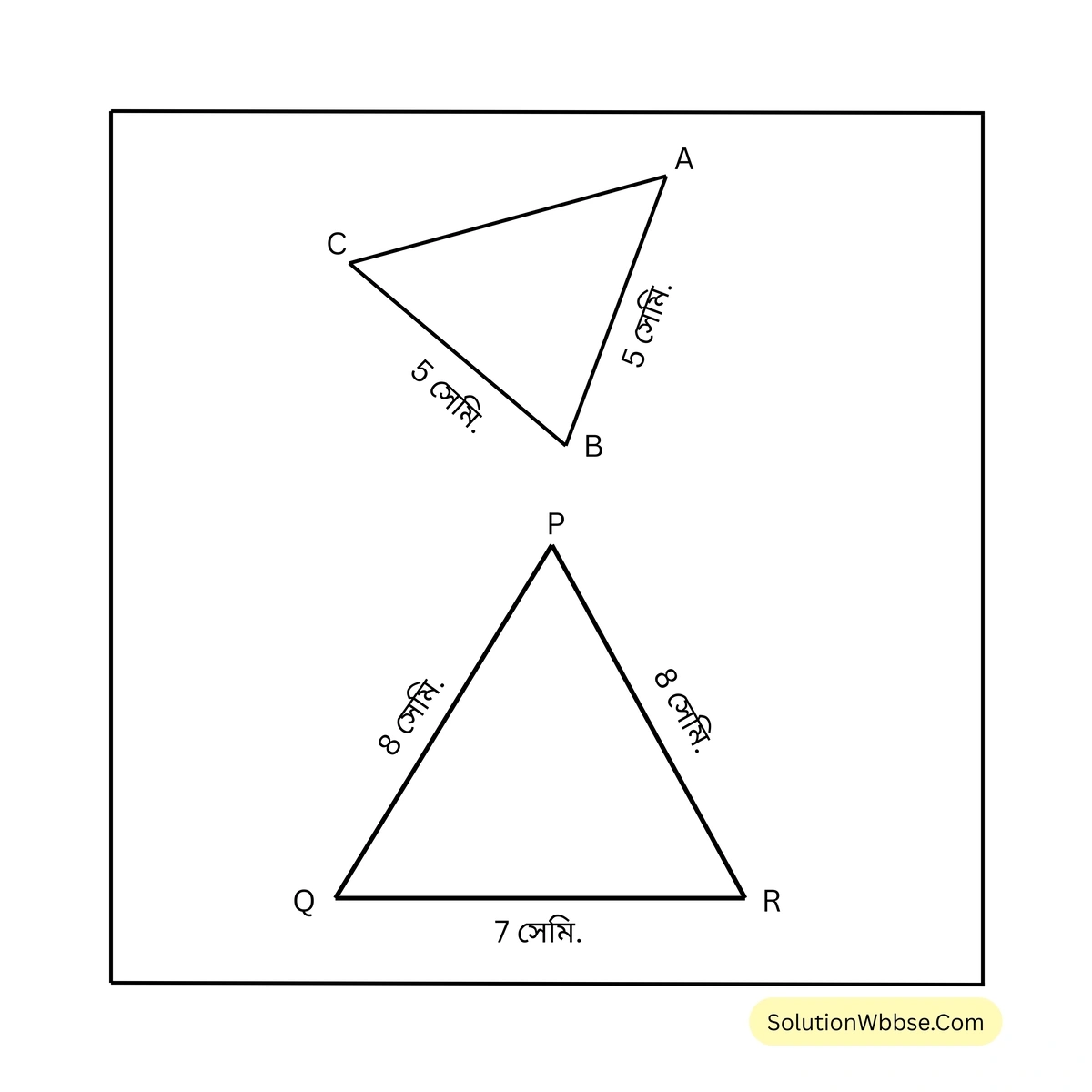
সমাধান –
প্রথম চিত্রে, ABC ত্রিভুজের \(AB = BC = 5\) সেমি
\(\therefore \angle BCA = \angle BAC\)দ্বিতীয় চিত্রে, PQR ত্রিভুজের \(PQ = PR = 8\) সেমি
\(\therefore \angle PQR = \angle PRQ\)3. AB ও CD সরলরেখাংশ দুটি পরস্পরকে O বিন্দুতে সমদ্বিখণ্ডিত করে। প্রমাণ করি যে AC ও BD সরলরেখাংশ দুটি পরস্পর সমান্তরাল। ABCD চতুর্ভুজটি কী ধরনের চতুর্ভুজ তা লিখি।
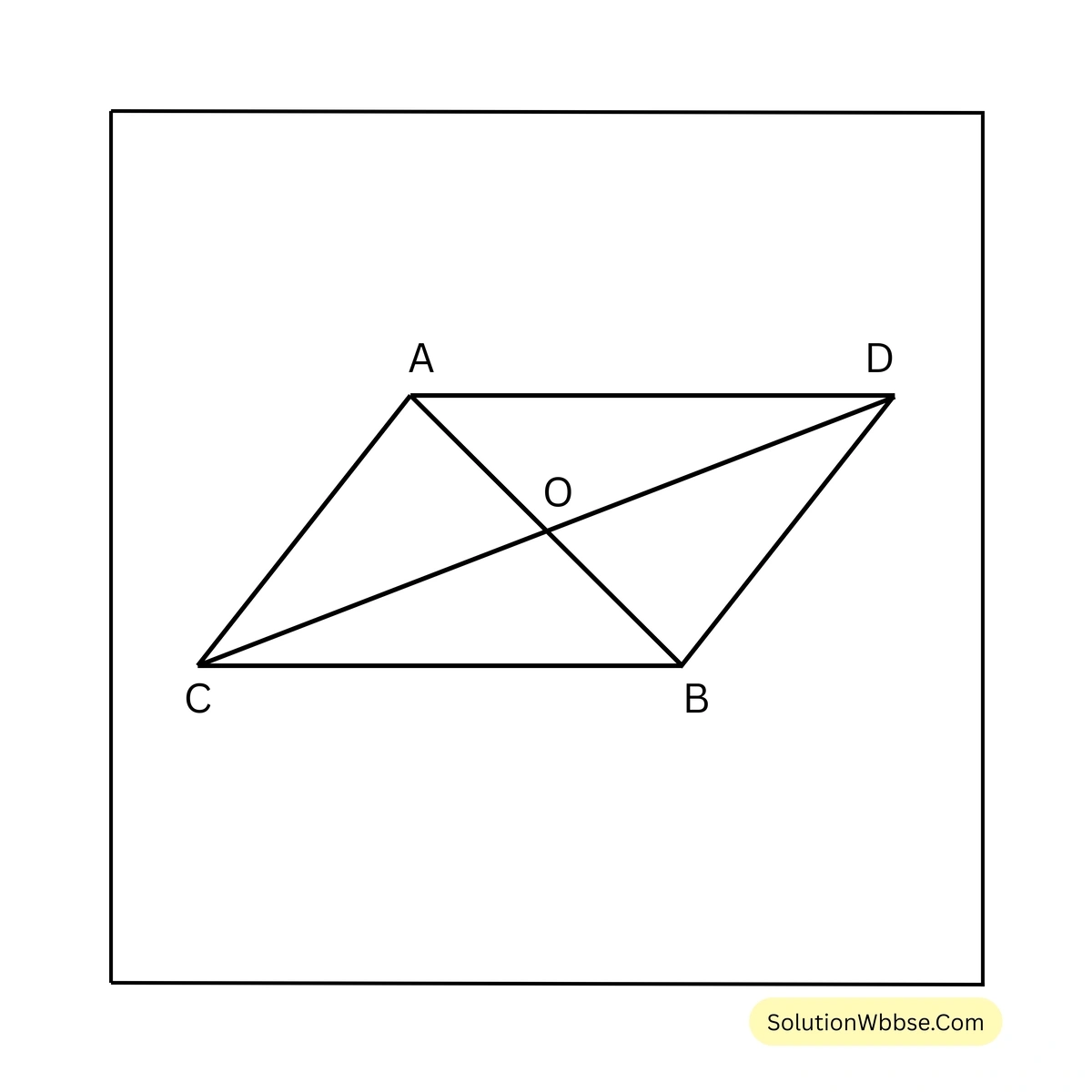
প্রদত্ত –
AB ও CD সরলরেখাংশ দুটি পরস্পরকে O বিন্দুতে সমদ্বিখণ্ডিত করেছে।
অর্থাৎ \(AO = OB\) এবং \(CO = OD\)
প্রামাণ্য –
\(AC \parallel BD\)প্রমাণ –
\(\triangle AOC\) এবং \(\triangle BOD\) এর মধ্যে,
\(AO = OB\) [প্রদত্ত]
\(\angle AOC = \angle BOD\) [বিপ্রতীপ কোণ]
\(CO = OD\) [প্রদত্ত]
\(\therefore \triangle AOC \cong \triangle BOD\) [S-A-S সর্বসমতার শর্তানুসারে]
\(\therefore \angle CAO = \angle OBD\) [সর্বসম ত্রিভুজের অনুরূপ কোণ]
\(\therefore \angle CAB = \angle ABD\)কিন্তু এরা একান্তর কোণ, \(\therefore AC \parallel BD\) [প্রমাণিত]
একইরকমভাবে \(\triangle AOD\) ও \(\triangle BOC\) সর্বসম ত্রিভুজের ক্ষেত্রে প্রমাণ করতে পারি যে,
\(AD \parallel BC\)ABCD চতুর্ভুজের \(AC \parallel BD\) এবং \(AD \parallel BC\)
\(\therefore\) ABCD চতুর্ভুজটি একটি সামান্তরিক।
4. AB এবং CD দুটি সমান্তরাল সরলরেখার উপর E ও F দুটি বিন্দু। EF সরলরেখাংশের মধ্যবিন্দু O; O বিন্দু দিয়ে যেকোনো সরলরেখাংশ টানা হল যা AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে। প্রমাণ করি যে, PQ সরলরেখাংশ O বিন্দুতে সমদ্বিখণ্ডিত হয়।
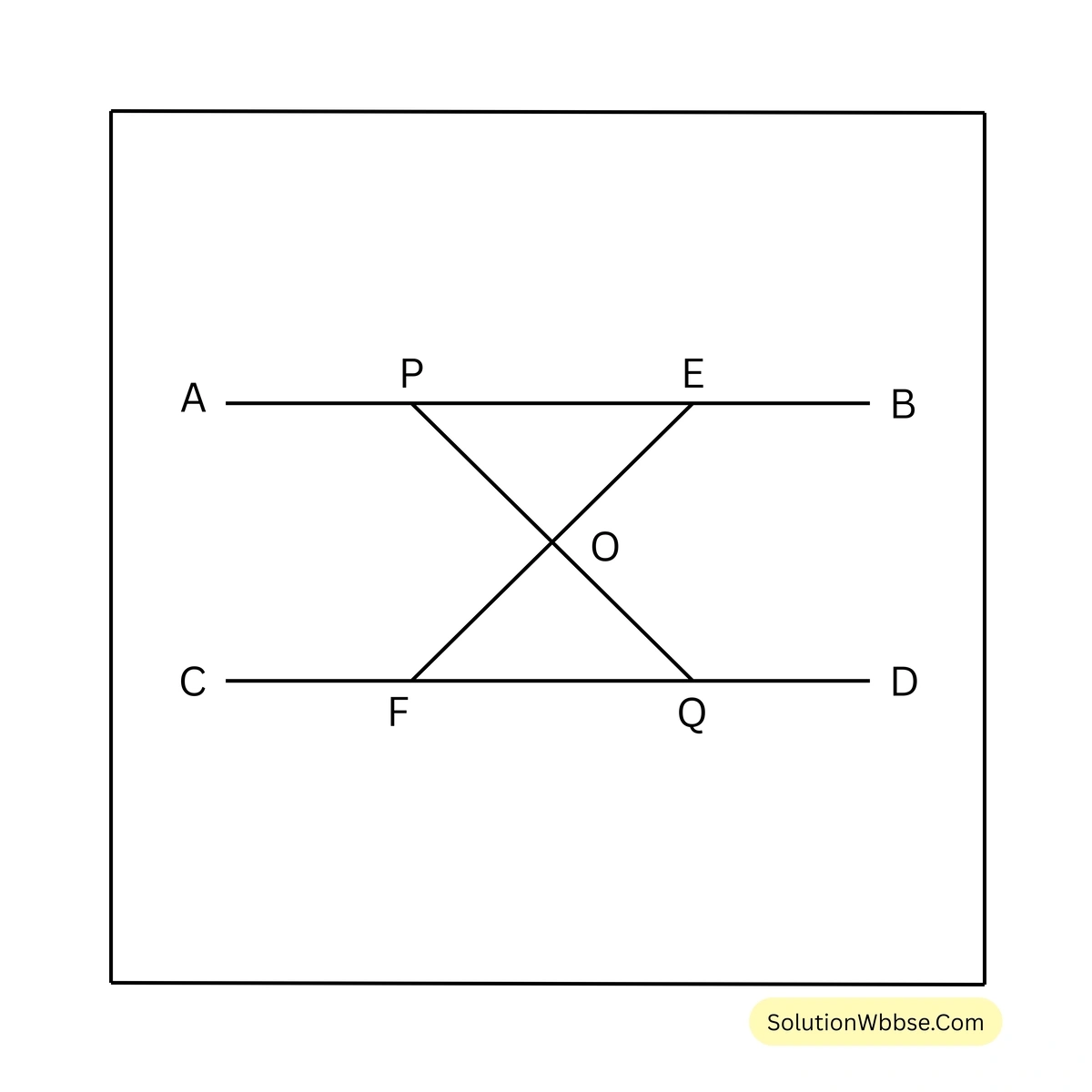
প্রদত্ত – AB এবং CD দুটি সমান্তরাল সরলরেখার উপর E ও F দুটি বিন্দু। EF সরলরেখাংশের মধ্যবিন্দু O অর্থাৎ, \(EO = OF\), O বিন্দু দিয়ে PQ সরলরেখা টানা হল যা AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে।
প্রমাণ্য – \(PO = OQ\)
প্রমাণ – \(\triangle EOP\) এবং \(\triangle FOQ\) এর মধ্যে
\(\angle EOP = \angle FOQ\) [বিপ্রতীপ কোণ]
\(\angle OEP = \angle OFQ\) [∵ \(\angle FEP\) = একান্তর \(\angle EFQ\)]
\(EO = OF\) [প্রদত্ত]
\(\therefore \triangle EOP \cong \triangle FOQ\) [সর্বসমতার A-A-S শর্তানুসারে]
\(\therefore PO = OQ\) [সর্বসম ত্রিভুজের অনুরূপ বাহু] [প্রমাণিত]
5. প্রমাণ করি যে, একটি সমদ্বিবাহু ত্রিভুজের ভূমিকে উভয়দিকে বর্ধিত করলে যে দুটি বহিঃকোণ উৎপন্ন হয় তাদের পরিমাপ সমান।
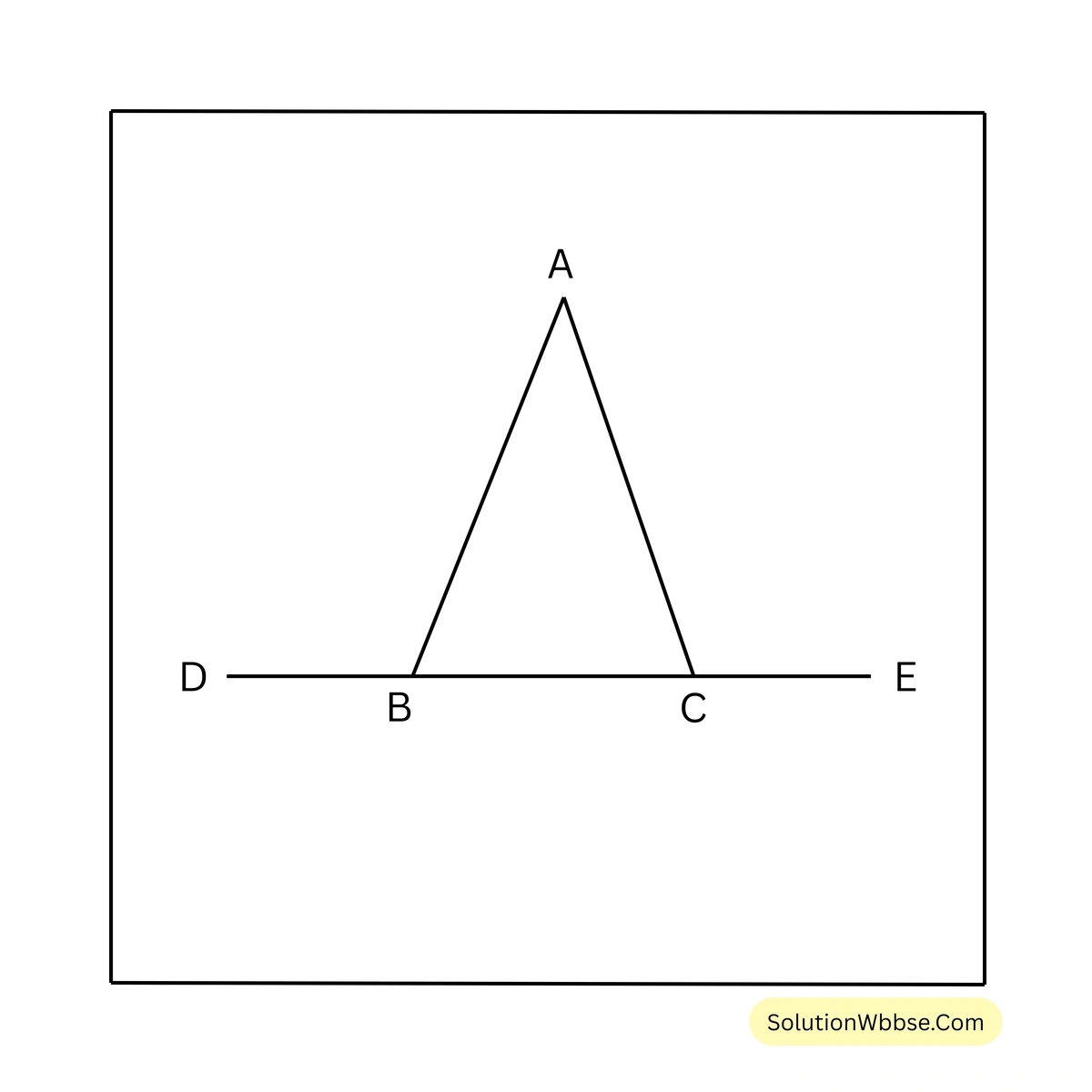
প্রদত্ত – ধরি, ABC সমদ্বিবাহু ত্রিভুজের \(AB = AC\) এবং BC বাহুকে উভয়দিকে বর্ধিত করায় দুটি বহিঃকোণ \(\angle ABD\) ও \(\angle ACE\) উৎপন্ন হল।
প্রমাণ্য – \(\angle ABD = \angle ACE\)
প্রমাণ – ABC সমদ্বিবাহু ত্রিভুজের \(AB = AC\)
DC বাহুর উপর BA দণ্ডায়মান
\(\therefore \angle ABC + \angle ABD = 180^\circ\) —–(i)
BE বাহুর উপর CA দণ্ডায়মান
\(\therefore \angle ACB + \angle ACE = 180^\circ\) —–(ii)
(i) নং ও (ii) নং থেকে পাই,
\(\angle ABC + \angle ABD = \angle ACB + \angle ACE\)বা, \(\angle ACB + \angle ABD = \angle ACB + \angle ACE\) [∵ \(\angle ABC = \angle ACB\)]
\(\therefore \angle ABD = \angle ACE\) [প্রমাণিত]
6. প্রমাণ করি যে, সমবাহু ত্রিভুজের মধ্যমা তিনটির দৈর্ঘ্য সমান।
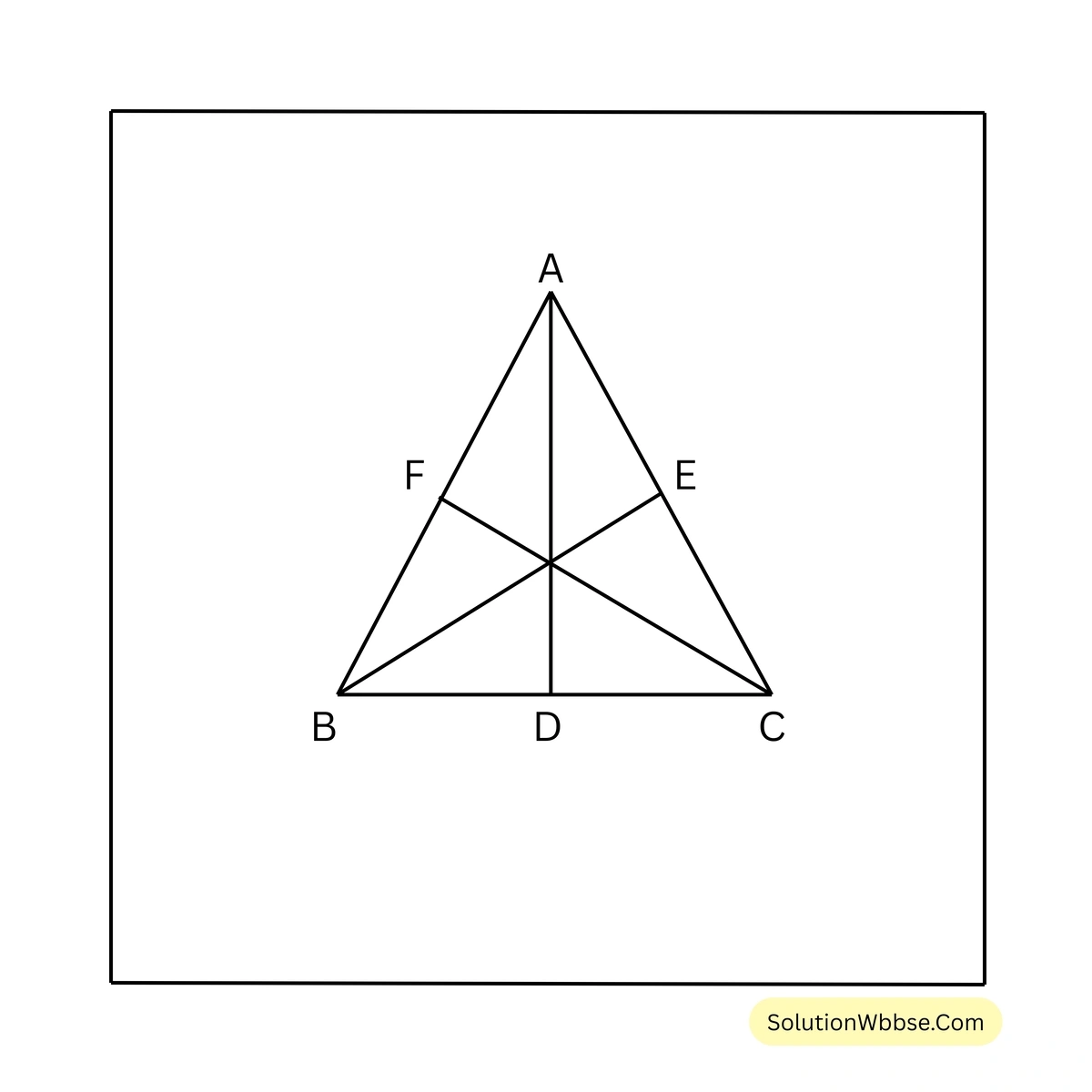
প্রদত্ত – ABC সমবাহু ত্রিভুজের AD, BE ও CF হল তিনটি মধ্যমা।
প্রমাণ্য – \(AD = BE = CF\)
প্রমাণ – \(\triangle FBC\) এবং \(\triangle ECB\) এর মধ্যে
\(\angle FBC = \angle ECB\) [∵ সমবাহু ত্রিভুজের প্রতিটি কোণ \(60^\circ\)]
\(BF = CE\) [∵ D, BC বাহুর মধ্যবিন্দু, E, AC বাহুর মধ্যবিন্দু আবার, \(AB = AC\) \(\therefore BF = CE\)]
BC সাধারণ বাহু
\(\therefore \triangle FBC \cong \triangle ECB\) [সর্বসমতার S-A-S শর্তানুসারে]
\(\therefore BE = CF\) [সর্বসম ত্রিভুজের অনুরূপ বাহু] —-(i)
একইরকমভাবে \(\triangle AFC\) ও \(\triangle CDA\) ত্রিভুজদুটি সর্বসম প্রমাণ করে দেখাতে পারি যে,
\(AD = CF\) —-(ii)
(i) নং ও (ii) নং থেকে পাই
\(AD = BE = CF\) [প্রমাণিত]
7. ABCD ট্রাপিজিয়ামের \(AD \parallel BC\) এবং \(\angle ABC = \angle BCD\); প্রমাণ করি যে, ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম।
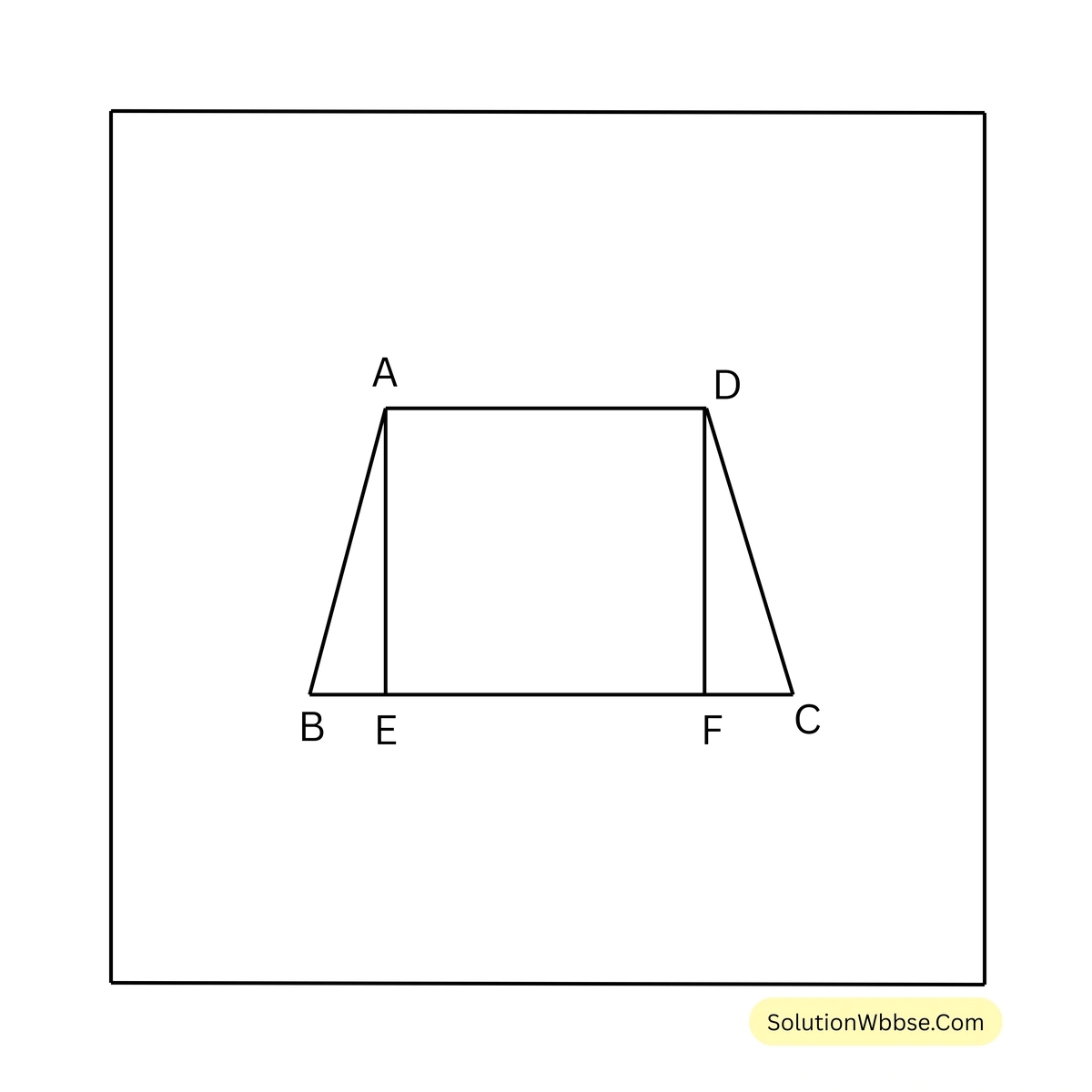
প্রদত্ত – ABCD ট্রাপিজিয়ামের \(AD \parallel BC\) এবং \(\angle ABC = \angle BCD\)
প্রমাণ্য – ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম। অর্থাৎ, \(AB = DC\)
অঙ্কন – A ও D বিন্দু থেকে BC বাহুর উপর যথাক্রমে AE ও DF লম্ব অঙ্কন করলাম।
প্রমাণ – \(\triangle AEB\) ও \(\triangle DFC\) এর মধ্যে
\(\angle ABE = \angle DCF\) [প্রদত্ত]
\(\angle AEB = \angle DFC\) [∵ AE ও DF, BC বাহুর উপর লম্ব]
\(AE = DF\) [∵ \(AD \parallel BC\) ∴ AD ও BC বাহুর মধ্যে লম্ব দূরত্ব সমান]
\(\therefore \triangle AEB \cong \triangle DFC\) [সর্বসমতার A-A-S শর্তানুসারে]
\(\therefore AB = DC\) [সর্বসম ত্রিভুজের অনুরূপ বাহু] [প্রমাণিত]
8. ABC সমকোণী সমদ্বিবাহু ত্রিভুজের AB অতিভুজ। \(\angle BAC\) এর সমদ্বিখণ্ডক AD, BC বাহুকে D বিন্দুতে ছেদ করে। প্রমাণ করি যে, \(AC + CD = AB\)
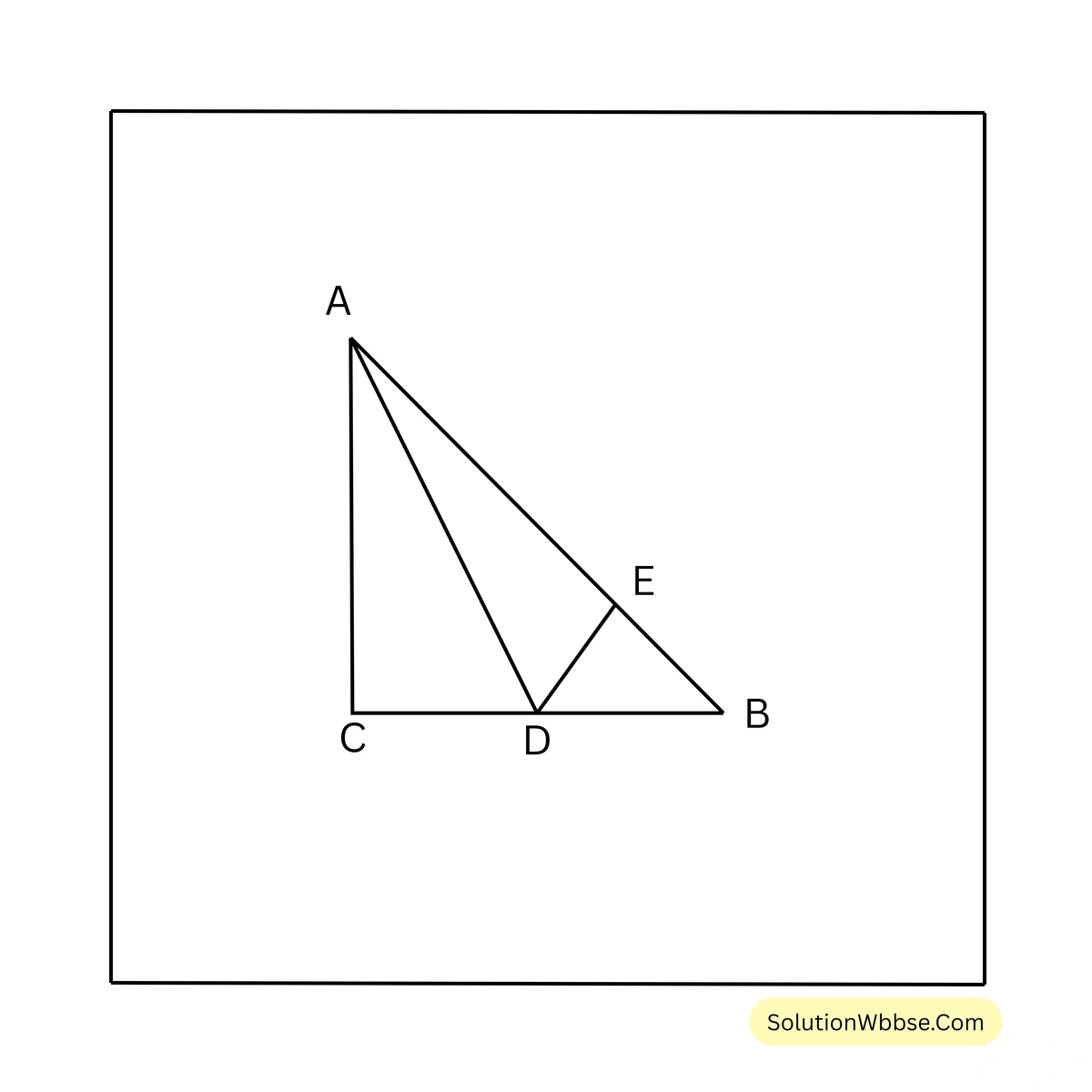
প্রদত্ত – ABC সমকোণী সমদ্বিবাহু ত্রিভুজের AB অতিভুজ। \(\angle BAC\) এর সমদ্বিখণ্ডক AD, BC বাহুকে D বিন্দুতে ছেদ করে।
প্রমাণ্য – \(AC + CD = AB\)
অঙ্কন – D বিন্দু থেকে AB বাহুর উপর DE লম্ব অঙ্কন করলাম।
প্রমাণ – যেহেতু, ABC সমকোণী সমদ্বিবাহু ত্রিভুজের AB অতিভুজ। সুতরাং, \(\angle ACB = 90^\circ\)
\(\triangle ACD\) ও \(\triangle AED\) এর মধ্যে
\(\angle ACD = \angle AED = 90^\circ\) [∵ \(DE \perp AB\)]
\(\angle CAD = \angle EAD\) [∵ \(\angle BAC\) এর সমদ্বিখণ্ডক AD]
AD সাধারণ বাহু
\(\therefore \triangle ACD \cong \triangle AED\) [সর্বসমতার A-A-S শর্তানুসারে]
\(\therefore AC = AE\) এবং \(CD = DE\) —-(i)
ABC একটি সমকোণী সমদ্বিবাহু ত্রিভুজ \(\therefore AC = BC\)
সুতরাং, \(\angle CAB = \angle ABC = \frac{90^\circ}{2} = 45^\circ\)
\(\therefore\) BDE সমকোণী ত্রিভুজের \(\angle EBD = 45^\circ\) [∵ \(\angle ABC = 45^\circ\)]
\(\angle EBD = 90^\circ – 45^\circ = 45^\circ\)\(\therefore\) BDE সমকোণী সমদ্বিবাহু ত্রিভুজ
যার \(\angle EBD = \angle EDB\) \(\therefore DE = EB\) —- (ii)
(i) ও (ii) থেকে পাই \(DE = EB\) —–(iii)
\(AC + CD = AE + DE\) [(i) নং থেকে পাই]
\(= AE + EB\) [(iii) নং থেকে পাই]
\(= AB\)\(\therefore AC + CD = AB\) [প্রমাণিত]
9. ABC এবং DBC দুটি সমদ্বিবাহু ত্রিভুজ যাদের \(AB = AC\) ও \(DB = DC\) এবং তারা BC বাহুর বিপরীত পাশে অবস্থিত। প্রমাণ করি যে, AD, BC বাহুকে সমকোণে সমদ্বিখণ্ডিত করে।
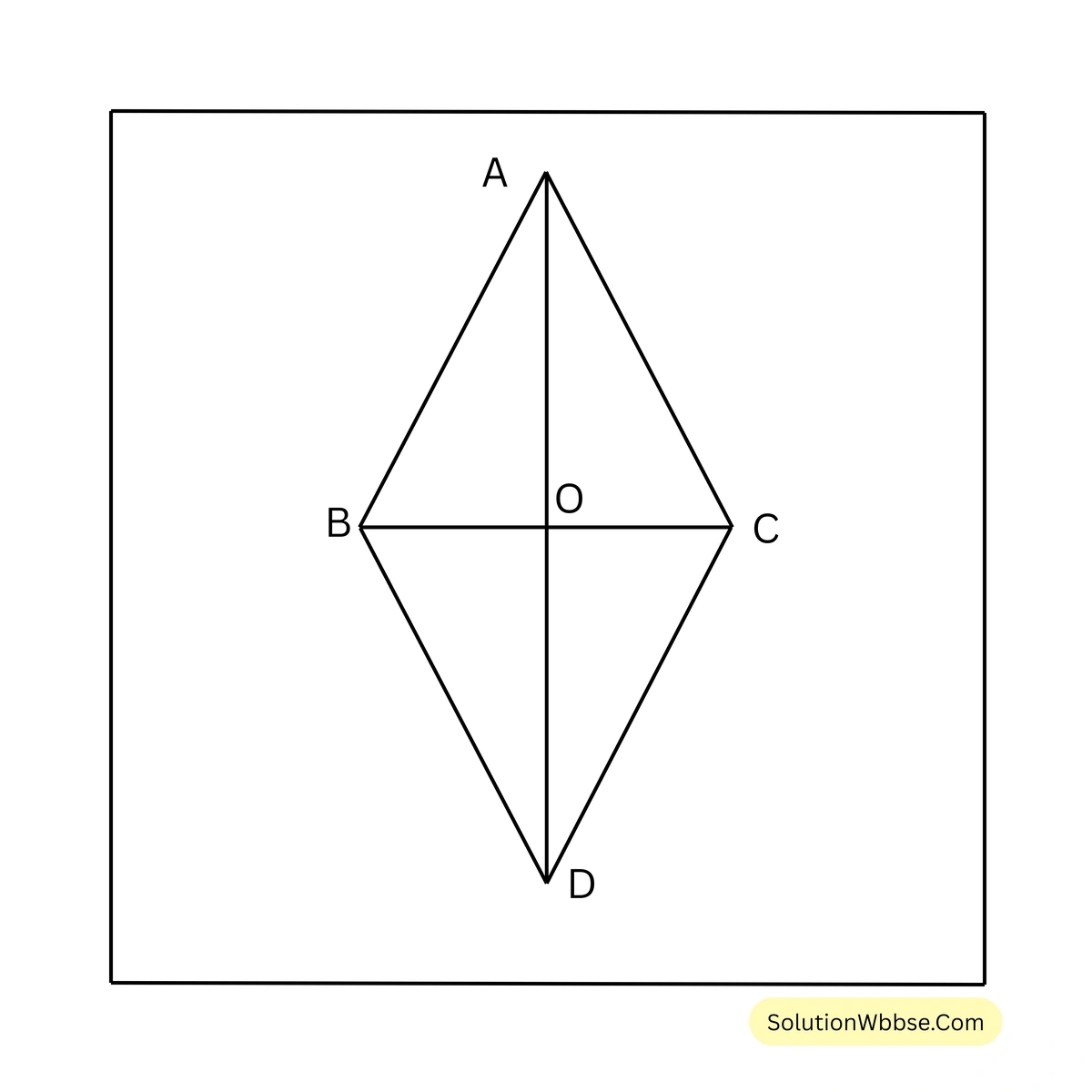
প্রদত্ত – ABC এবং DBC দুটি সমদ্বিবাহু ত্রিভুজ যাদের \(AB = AC\) ও \(DB = DC\)।
ধরি, AD, BC কে O বিন্দুতে ছেদ করেছে।
প্রামাণ্য – AD, BC বাহুকে সমকোণে সমদ্বিখণ্ডিত করে। অর্থাৎ \(BO = OC\) এবং \(AD \perp BC\)
প্রমাণ – \(\triangle ABD\) ও \(\triangle ACD\) এর মধ্যে
\(AB = AC\) [প্রদত্ত]
\(BD = DC\) [প্রদত্ত]
AD সাধারণ বাহু
\(\therefore \triangle ABD \cong \triangle ACD\) [সর্বসমতার S-S-S শর্তানুসারে]
\(\therefore \angle BAD = \angle CAD\) [সর্বসম ত্রিভুজের অনুরূপ কোণ]
\(\therefore \triangle ABO\) ও \(\triangle ACO\) এর মধ্যে
\(AB = AC\) [প্রদত্ত]
\(\angle BAO = \angle CAO\) [∵ \(\angle BAD = \angle CAD\)]
AO সাধারণ বাহু
\(\therefore \triangle ABO \cong \triangle ACO\) [সর্বসমতার S-A-S শর্তানুসারে]
\(\therefore BO = OC\) [সর্বসম ত্রিভুজের অনুরূপ বাহু]
এবং \(\angle AOB = \angle AOC\) [সর্বসম ত্রিভুজের অনুরূপ কোণ]
আবার, BC বাহুর উপর OA দণ্ডায়মান
\(\therefore \angle AOB + \angle AOC = 180^\circ\)বা, \(\angle AOB + \angle AOB = 180^\circ\)
বা, \(2 \angle AOB = 180^\circ\)
\(\therefore \angle AOB = 90^\circ\)\(\therefore AD \perp BC\)সুতরাং, \(BO = OC\) এবং \(AD \perp BC\) [প্রমাণিত]
10. দুটি সরলরেখাংশ PQ ও RS পরস্পরকে X বিন্দুতে এমনভাবে ছেদ করে যাতে \(XP = XR\) এবং \(\angle PSX = \angle RQX\) হয়। প্রমাণ করি যে, \(\triangle PXS \cong \triangle RQX\)
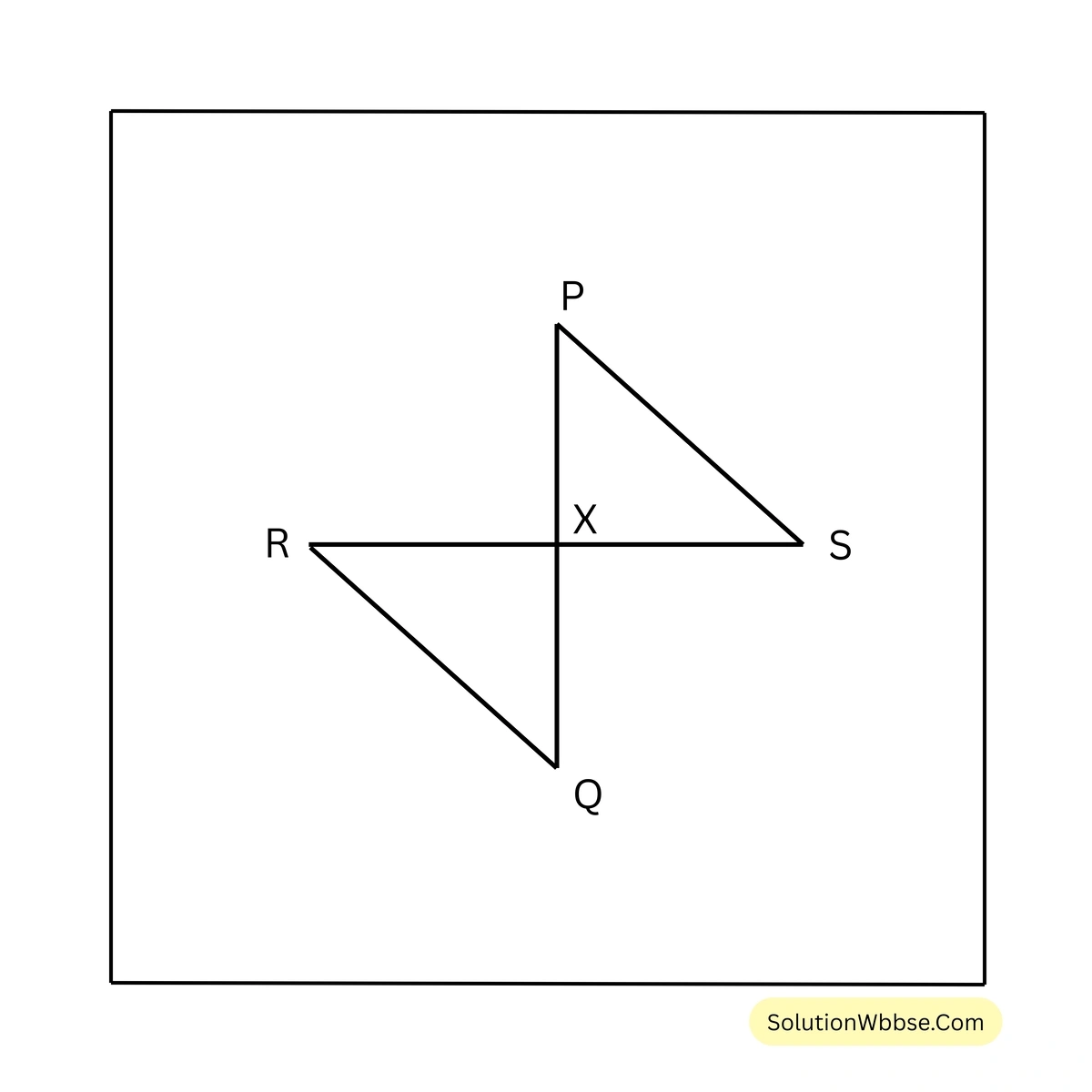
প্রদত্ত – PQ ও RS সরলরেখা দুটি পরস্পরকে X বিন্দুতে ছেদ করে এবং \(XP = XR\) এবং \(\angle PSX = \angle RQX\)
প্রামাণ্য – \(\triangle PXS \cong \triangle RQX\)
প্রমাণ – \(\triangle PXS\) ও \(\triangle RQX\) এর মধ্যে
\(\angle PSX = \angle RQX\) [প্রদত্ত]
\(\angle PXS = \angle RXQ\) [বিপ্রতীপ কোণ]
\(XP = XR\) [প্রদত্ত]
\(\therefore \triangle PXS \cong \triangle RQX\) [সর্বসমতার A-A-S শর্তানুসারে] [প্রমাণিত]
এই আর্টিকেলে অষ্টম শ্রেণির গণিতের ‘ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক’ অধ্যায়ের ‘কষে দেখি – 9’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরেছি। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে। কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment