পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) অষ্টম শ্রেণির গণিত পাঠ্যবইয়ের পঞ্চম অধ্যায় হলো ‘ঘনফল নির্ণয়’। এই পোস্টে আমরা ‘কষে দেখি – 5.1’-এর সমস্ত প্রশ্নের সহজ ও নির্ভুল সমাধান নিয়ে আলোচনা করেছি। আশা করি, এই নোটসগুলো তোমাদের গণিত শিখতে এবং পরীক্ষার প্রস্তুতিতে দারুণভাবে সহায়তা করবে।

1. দুটি ঘনক তৈরি করি যার একটি বাহুর দৈর্ঘ্য যথাক্রমে 5 সেমি. ও 1 সেমি.। কতগুলি 1 সেমি. দৈর্ঘ্যের বাহু বিশিষ্ট ঘনক জুড়ে এই বড় ঘনক পাব হিসাব করে লিখি।
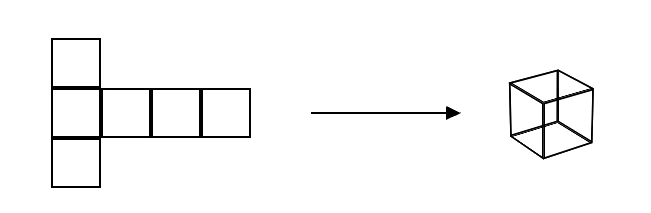
সমাধান –
যে ঘনকের বাহুর দৈর্ঘ্য 5 সেমি. তার ঘনফল:
= \( (5 \times 5 \times 5)\) ঘন সেমি.
= \( 5^{3}\) ঘন সেমি.
= \( 125\) ঘন সেমি.
যে ঘনকের বাহুর দৈর্ঘ্য 1 সেমি. তার ঘনফল:
= \( (1 \times 1 \times 1)\) ঘন সেমি.
= \( (1)^{3}\) ঘন সেমি.
= \( 1\) ঘন সেমি.
বড় ঘনক তৈরি করতে 1 সেমি. দৈর্ঘ্যের ঘনক লাগবে:
= \( \frac{125}{1}\) টি
= \( 125\) টি
2. সুমন্ত অনেকগুলি 1 সেমি. দৈর্ঘ্যের বাহুবিশিষ্ট ঘনক তৈরি করেছে। মনামী সেই ঘনকগুলি জোড়া লাগিয়ে বড় ঘনক তৈরির চেষ্টা করেছে। হিসাব করে দেখি নীচের কোন সংখ্যক ঘনকের ক্ষেত্রে মনামী বড় ঘনক তৈরি করতে পারবে?
(i) 100 (ii) 1000 (iii) 1331 (iv) 1210 (v) 3375 (vi) 2700
সমাধান –
যে সংখ্যাগুলিকে পূর্ণঘন আকারে প্রকাশ করা যাবে সেগুলির ক্ষেত্রে 1 সেমি. দৈর্ঘ্যের বাহু বিশিষ্ট ঘনককে কাজে লাগিয়ে বড় ঘনক তৈরি করা যাবে।
(i) 100
\(100 = 10^2\), কিন্তু \(100\) একটি পূর্ণঘন সংখ্যা নয় কারণ \(4^3 = 64\) এবং \(5^3 = 125\)।
সুতরাং, এইক্ষেত্রে বড় ঘনক তৈরি করা সম্ভব নয়।
(ii) 1000
\(1000 = 10^3\), যা একটি পূর্ণঘন সংখ্যা।
সুতরাং, এইক্ষেত্রে বড় ঘনক তৈরি করা সম্ভব।
(iii) 1331
\(1331 = 11 \times 11 \times 11 = 11^3\), যা একটি পূর্ণঘন সংখ্যা।
সুতরাং, এইক্ষেত্রে বড় ঘনক তৈরি করা সম্ভব।
(iv) 1210
\(1210 = 121 \times 10 = 11^2 \times 10\), এটি কোন পূর্ণঘন সংখ্যা নয় কারণ \(11^3 = 1331\) এবং \(10^3 = 1000\)।
সুতরাং, এইক্ষেত্রে বড় ঘনক তৈরি করা সম্ভব নয়।
(v) 3375
\(3375 = 15 \times 15 \times 15 = 15^3\), যা একটি পূর্ণঘন সংখ্যা।
সুতরাং, এইক্ষেত্রে বড় ঘনক তৈরি করা যাবে।
(vi) 2700
\(2700 = 27 \times 100 = 3^3 \times 10^2\), এটি পূর্ণঘন নয় কারণ \(10^2\) পূর্ণঘন নয়।
অথবা, \(14^3 = 2744\) এবং \(13^3 = 2197\), তাই 2700 পূর্ণঘন নয়।
সুতরাং, এইক্ষেত্রে বড় ঘনক তৈরি করা সম্ভব নয়।
3. নীচের সংখ্যাগুলির মধ্যে কোনটি পূর্ণঘন সংখ্যা নয় লিখি।
(i) 216 (ii) 343 (iii) 1024 (iv) 324 (v) 1744 (vi) 1372
সমাধান –
(i) 216
\(216 = 2 \times 2 \times 2 \times 3 \times 3 \times 3\)= \( (2 \times 3) \times (2 \times 3) \times (2 \times 3)\)
= \( 6 \times 6 \times 6\)
= \( (6)^3\)
\(\therefore\) 216 একটি পূর্ণঘন সংখ্যা।
(ii) 343
\(343 = 7 \times 7 \times 7\)= \( 7^3\)
\(\therefore\) 343 একটি পূর্ণঘন সংখ্যা।
(iii) 1024
\(1024 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2\)= \( 2^3 \times 2^3 \times 2^3 \times 2\)
= \( 8^3 \times 2\)
\(\therefore\) 1024 কে কোনো পূর্ণসংখ্যার ঘনফল হিসাবে প্রকাশ করা যায় না।
\(\therefore\) 1024 একটি পূর্ণঘন সংখ্যা নয়।
(iv) 324
\(324 = 2 \times 2 \times 3 \times 3 \times 3 \times 3\)= \( 2^2 \times 3^4\)
\(\therefore\) 324 কে কোনো পূর্ণসংখ্যার ঘনফল রূপে প্রকাশ করা যায় না।
\(\therefore\) 324 একটি পূর্ণঘন সংখ্যা নয়।
(v) 3375
\(1744 = 2 \times 2 \times 2 \times 2 \times 109\)= \( 2^4 \times 109\)
\(\therefore\) 1744 কে কোনো পূর্ণসংখ্যার ঘনফল রূপে প্রকাশ করা যায় না।
\(\therefore\) 1744 একটি পূর্ণঘন সংখ্যা নয়।
(vi) 1372
\(1372 = 7 \times 7 \times 7 \times 2 \times 2\)= \( 7^3 \times 2^2\)
\(\therefore\) 1372 কে কোনো পূর্ণসংখ্যার ঘনফল রূপে লেখা যায় না।
\(\therefore\) 1372 একটি পূর্ণঘন সংখ্যা নয়।
4. দেবনাথ একটি আয়তঘন তৈরি করেছে যার দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 4 সেমি., 3 সেমি. ও 3 সেমি.। হিসাব করে দেখি এইরকম কতগুলি আয়তঘন জুড়ে দেবনাথ ঘনক তৈরি করতে পারবে?
সমাধান –
আয়তঘনকটির আয়তন = \((4 \times 3 \times 3)\) ঘন সেমি. = \(36\) ঘন সেমি.
4, 3 ও 2 এর লসাগু = \(12\)
\(\therefore\) দেবনাথ যে নতুন ঘনক তৈরি করবে তার বাহুর দৈর্ঘ্য হবে \(12\) সেমি.।
নতুন ঘনকের আয়তন = \((12 \times 12 \times 12)\) ঘন সেমি. = \(1728\) ঘন সেমি.
\(\therefore\) নির্ণেয় আয়তঘনকের সংখ্যা = \(1728 / 36\) টি = \(48\) টি
5. নীচের সংখ্যাগুলিকে ক্ষুদ্রতম কোন ধনাত্মক সংখ্যা দিয়ে গুণ করলে গুণফল পূর্ণঘন সংখ্যা হবে হিসাব করে লিখি।
(i) 675 (ii) 200 (iii) 108 (iv) 121 (v) 1225
সমাধান –
(i) 675
\(675 = 5 \times 5 \times 3 \times 3 \times 3 = 5^2 \times 3^3\)\(\therefore\) 675 কে \(5\) দ্বারা গুণ করলে গুণফল একটি পূর্ণঘন সংখ্যা হবে।
(ii) 200
\(200 = 2 \times 10 \times 10 = 2 \times 2 \times 2 \times 5 \times 5 = 2^3 \times 5^2\)\(\therefore\) 200 কে \(5\) দ্বারা গুণ করলে গুণফল একটি পূর্ণঘন সংখ্যা হবে।
(iii) 108
\(108 = 2 \times 2 \times 3 \times 3 \times 3 = 2^2 \times 3^3\)\(\therefore\) 108 কে \(2\) দ্বারা গুণ করলে গুণফল একটি পূর্ণঘন সংখ্যা হবে।
(iv) 121
\(121 = 11 \times 11 = 11^2\)\(\therefore\) 121 কে \(11\) দ্বারা গুণ করলে গুণফল পূর্ণঘন সংখ্যা হবে।
(v) 1225
\(1225 = 5 \times 5 \times 7 \times 7 = 5^2 \times 7^2 = 35^2\)\(\therefore\) 1225 কে \(35\) দ্বারা গুণ করলে গুণফল পূর্ণ ঘন সংখ্যা হবে।
6. নীচের সংখ্যাগুলিকে ক্ষুদ্রতম কোন ধনাত্মক সংখ্যা দিয়ে ভাগ করলে ভাগফল পূর্ণঘন সংখ্যা হবে হিসাব করে লিখি।
(i) 7000 (ii) 2662 (iii) 4394 (iv) 6750 (v) 675
সমাধান –
(i) \(7000 = 7 \times 1000 = 7 \times 10^3\)
\(\therefore\) 7000 কে \(7\) দ্বারা ভাগ করলে ভাগফল পূর্ণঘন সংখ্যা হবে।
(ii) \(2662 = 2 \times 11 \times 11 \times 11 = 2 \times 11^3\)
\(\therefore\) 2662 কে \(2\) দ্বারা ভাগ করলে ভাগফল পূর্ণঘন সংখ্যা হবে।
(iii) \(4394 = 2 \times 13 \times 13 \times 13 = 2 \times 13^3\)
\(\therefore\) 4394 কে \(2\) দ্বারা ভাগ করলে ভাগফল পূর্ণঘন সংখ্যা হবে।
(iv) \(6750 = 5 \times 5 \times 5 \times 3 \times 3 \times 3 \times 2 = 5^3 \times 3^3 \times 2\)
\(\therefore\) 6750 কে \(2\) দ্বারা ভাগ করলে ভাগফল পূর্ণঘন সংখ্যা হবে।
(v) \(675 = 5 \times 5 \times 3 \times 3 \times 3 = 5^2 \times 3^3\)
\(\therefore\) 675 কে \(25\) (অর্থাৎ \(5^2\)) দ্বারা ভাগ করলে ভাগফল পূর্ণঘন সংখ্যা হবে।
7. নীচের পূর্ণঘন সংখ্যাগুলি মৌলিক উৎপাদকে বিশ্লেষণ করি ও ঘনমূল লিখি।
(i) 512 (ii) 1728 (iii) 5832 (iv) 15625 (v) 10648
সমাধান –
(i) 512

\(\therefore 512\) এর ঘনমূল হল \(8\)
(ii) 1728

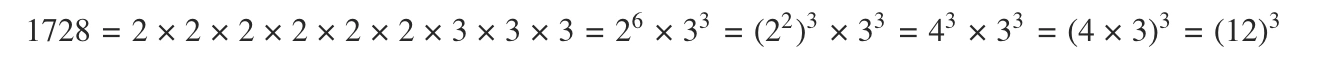
\(\therefore 1728\) এর ঘনমূল হল \(12\)
(iii) 5832

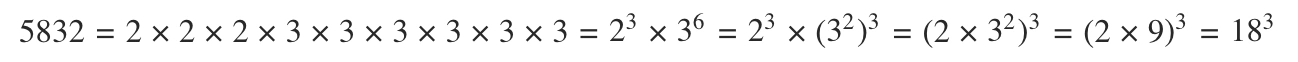
\(\therefore 5832\) এর ঘনমূল হল \(18\)
(iv) 15625
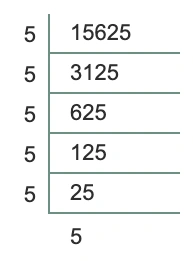
\(\therefore 15625\) এর ঘনমূল হল \(25\)
(v) 10648

\(\therefore 10648\) এর ঘনমূল হল \(22\)
এই আর্টিকেলে অষ্টম শ্রেণির গণিতের ‘ঘনফল নির্ণয়’ অধ্যায়ের ‘কষে দেখি – 5.1’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরেছি। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে। কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment