পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) অষ্টম শ্রেণির গণিত পাঠ্যবইয়ের পঞ্চম অধ্যায় হলো ‘ঘনফল নির্ণয়’। এই পোস্টে আমরা ‘কষে দেখি – 5.2’-এর সমস্ত প্রশ্নের সহজ ও নির্ভুল সমাধান নিয়ে আলোচনা করেছি। আশা করি, এই নোটসগুলো তোমাদের গণিত শিখতে এবং পরীক্ষার প্রস্তুতিতে দারুণভাবে সহায়তা করবে।

1.
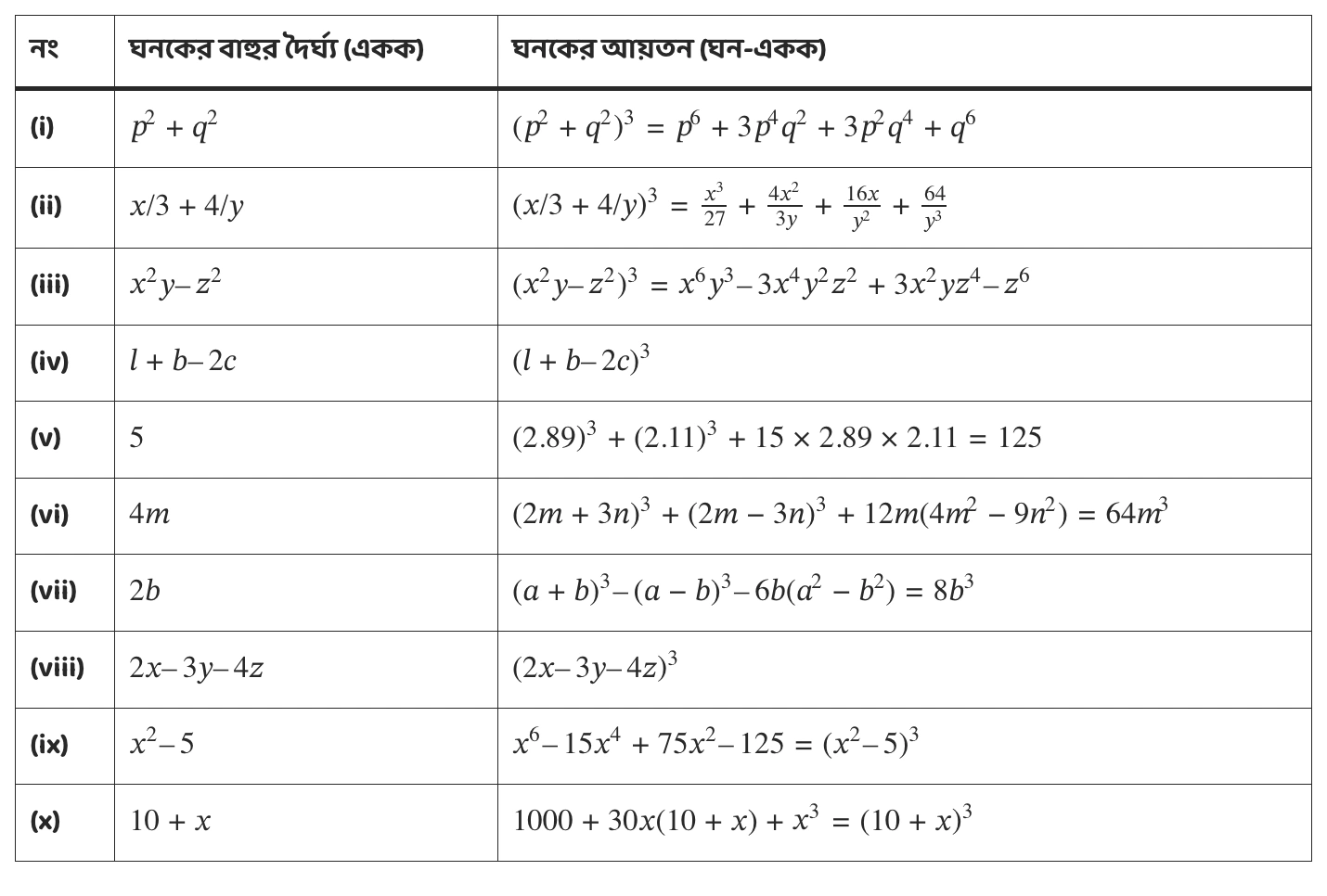
সমাধান –
(i) ঘনকের বাহুর দৈর্ঘ্য \((p^2 + q^2)\) একক
\(\therefore\) ঘনকের আয়তন
= \( (p^2 + q^2)^3\) ঘন একক
= \( \{(p^2)^3 + 3 \cdot (p^2)^2(q^2) + 3 \cdot (p^2)(q^2)^2 + (q^2)^3\}\) ঘন একক
= \( (p^6 + 3p^4q^2 + 3p^2q^4 + q^6)\) ঘন একক
(ii) ঘনকের বাহুর দৈর্ঘ্য \((\frac{x}{3} + \frac{4}{y})\) একক
\(\therefore\) ঘনকের আয়তন
= \( (\frac{x}{3} + \frac{4}{y})^3\) ঘন একক
= \( (\frac{x}{3})^3 + 3 \times (\frac{x}{3})^2 \times \frac{4}{y} + 3 \times \frac{x}{3} \times (\frac{4}{y})^2 + (\frac{4}{y})^3\) ঘন একক
= \( \frac{x^3}{27} + 3 \times \frac{x^2}{9} \times \frac{4}{y} + 3 \times \frac{x}{3} \times \frac{16}{y^2} + \frac{64}{y^3}\) ঘন একক
= \( \frac{x^3}{27} + \frac{4x^2}{3y} + \frac{16x}{y^2} + \frac{64}{y^3}\) ঘন একক
(iii) ঘনকের বাহুর দৈর্ঘ্য \((x^2y – z^2)\) একক
\(\therefore\) ঘনকের আয়তন
= \( (x^2y – z^2)^3\) ঘন একক
= \( \{(x^2y)^3 – 3(x^2y)^2(z^2) + 3(x^2y)(z^2)^2 – (z^2)^3\}\) ঘন একক
= \( (x^6y^3 – 3x^4y^2z^2 + 3x^2yz^4 – z^6)\) ঘন একক
(iv) ঘনকের বাহুর দৈর্ঘ্য \((l + b – 2c)\) একক
\(\therefore\) ঘনকের আয়তন
= \( (l + b – 2c)^3\) ঘন একক
= \( \{(l + b) – 2c\}^3\) ঘন একক
= \( \{(l + b)^3 – 3(l + b)^2(2c) + 3(l + b)(2c)^2 – (2c)^3\}\) ঘন একক
= \( \{l^3 + 3l^2b + 3lb^2 + b^3 – 3(l^2 + 2lb + b^2)(2c) + 3(l + b)(4c^2) – 8c^3\}\) ঘন একক
= \( \{l^3 + 3l^2b + 3lb^2 + b^3 – 6l^2c – 12lbc – 6b^2c + 12lc^2 + 12bc^2 – 8c^3\}\) ঘন একক
= \( (l^3 + b^3 – 8c^3 + 3l^2b + 3lb^2 – 6cl^2 – 12lcb – 6b^2c + 12lc^2 + 12bc^2)\) ঘন একক
(v) ঘনকের আয়তন
= \( \{(2.89)^3 + (2.11)^3 + 15 \times 2.89 \times 2.11\}\) ঘন একক
= \( \{(2.89)^3 + (2.11)^3 + 3 \times 5 \times 2.89 \times 2.11\}\) ঘন একক
= \( \{(2.89)^3 + (2.11)^3 + 3 \times 2.89 \times 2.11 \times (2.89 + 2.11)\}\) ঘন একক
= \( (2.89 + 2.11)^3\) ঘন একক
= \( (5)^3\) ঘন একক
\(\therefore\) ঘনকটির বাহুর দৈর্ঘ্য \(5\) একক।
(vi) ঘনকের আয়তন
= \( (2m + 3n)^3 + (2m – 3n)^3 + 12m(4m^2 – 9n^2)\) ঘন একক
= \( \{(2m + 3n)^3 + (2m – 3n)^3 + 3 \cdot 4m \cdot \{(2m)^2 – (3n)^2\}\}\) ঘন একক
= \( [(2m + 3n)^3 + (2m – 3n)^3 + 3 \cdot (2m + 3n)(2m – 3n) \{(2m + 3n) + (2m – 3n)\}]\) ঘন একক
= \( \{(2m + 3n) + (2m – 3n)\}^3\) ঘন একক
= \( (2m + 3n + 2m – 3n)^3\) ঘন একক
= \( (4m)^3\) ঘন একক
\(\therefore\) ঘনকের বাহুর দৈর্ঘ্য \(4m\) একক।
(vii) ঘনকের আয়তন
= \( \{(a + b)^3 – (a – b)^3 – 6b(a^2 – b^2)\}\) ঘন একক
= \( \{(a + b)^3 – (a – b)^3 – 3 \cdot 2b \cdot (a + b)(a – b)\}\) ঘন একক
= \( [(a + b)^3 – (a – b)^3 – 3 \cdot \{(a + b) – (a – b)\} \cdot (a + b)(a – b)]\) ঘন একক
= \( [(a + b)^3 – (a – b)^3 – 3(a + b)(a – b) \{(a + b) – (a – b)\}]\) ঘন একক
= \( \{(a + b) – (a – b)\}^3\) ঘন একক
= \( (a + b – a + b)^3\) ঘন একক
= \( (2b)^3\) ঘন একক
\(\therefore\) ঘনকের বাহুর দৈর্ঘ্য \(2b\) একক।
(viii) ঘনকের বাহুর দৈর্ঘ্য \((2x – 3y – 4z)\) একক
\(\therefore\) ঘনকের আয়তন
= \( (2x – 3y – 4z)^3\) ঘন একক
= \( \{(2x – 3y) – 4z\}^3\) ঘন একক
= \( \{(2x – 3y)^3 – 3(2x – 3y)^2(4z) + 3(2x – 3y)(4z)^2 – (4z)^3\}\) ঘন একক
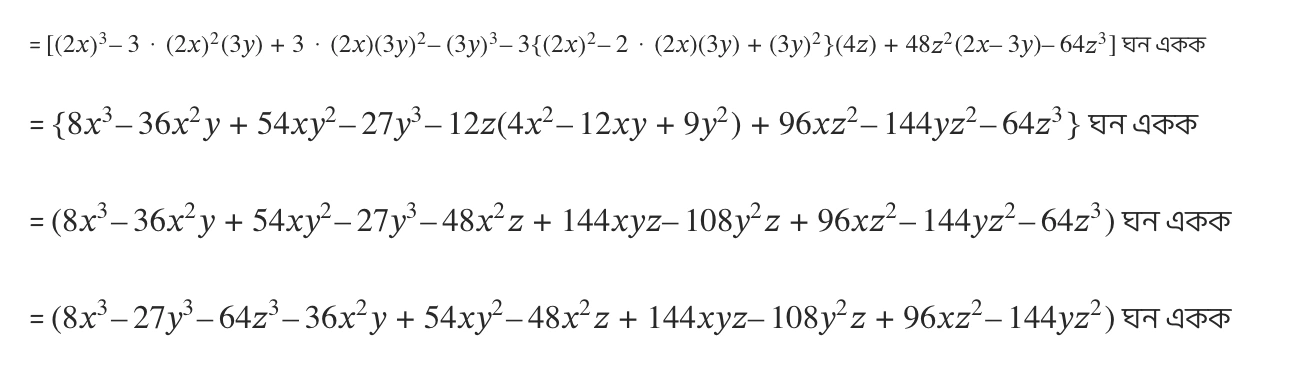
(ix) ঘনকের আয়তন
= \( (x^6 – 15x^4 + 75x^2 – 125)\) ঘন একক
= \( \{(x^2)^3 – 3 \cdot (x^2)^2 \cdot 5 + 3 \cdot (x^2)(5)^2 – (5)^3\}\) ঘন একক
= \( (x^2 – 5)^3\) ঘন একক
\(\therefore\) ঘনকের বাহুর দৈর্ঘ্য \((x^2 – 5)\) একক।
(x) ঘনকের আয়তন
= \( 1000 + 30x(10 + x) + x^3\) ঘন একক
= \( (10)^3 + x^3 + 3 \cdot 10 \cdot x \cdot (10 + x)\) ঘন একক
= \( (10 + x)^3\) ঘন একক
\(\therefore\) ঘনকের বাহুর দৈর্ঘ্য \((10 + x)\) একক।
2. I থেকে IV নং অভেদের সাহায্যে নীচের প্রশ্নগুলি সমাধান করিঃ
(a) \(x – y = 2\) হলে \(x^3 – y^3 – 6xy\) -এর মান হিসাব করে লিখি।
সমাধান –
\((x – y) = 2\)বা, \((x – y)^3 = (2)^3\) [উভয়পক্ষে ঘন করে পাই]
বা, \(x^3 – y^3 – 3 \cdot x \cdot y (x – y) = 8\) [(IV) নং অভেদ থেকে পাই]
বা, \(x^3 – y^3 – 3xy(x – y) = 8\)
বা, \(x^3 – y^3 – 3xy(2) = 8\) \([\because x – y = 2]\)
বা, \(x^3 – y^3 – 6xy = 8\) [উত্তর]
(b) \(a + b = -\frac{1}{3}\) হলে প্রমাণ করো যে, \(a^3 + b^3 – ab = -\frac{1}{27}\)
সমাধান –
\(a + b = -\frac{1}{3}\)বা, \((a + b)^3 = \left(-\frac{1}{3}\right)^3\)
বা, \(a^3 + b^3 + 3ab(a + b) = -\frac{1}{27}\) [(II) নং অভেদের সাহায্যে পাই]
বা, \(a^3 + b^3 + 3ab\left(-\frac{1}{3}\right) = -\frac{1}{27}\) \([\because a + b = -\frac{1}{3}]\)
বা, \(a^3 + b^3 – ab = -\frac{1}{27}\) [প্রমাণিত]
(c) \(x + y = 2\) এবং \(\frac{1}{x} + \frac{1}{y} = 2\) হলে \(x^3 + y^3\) -এর মান হিসাব করে লিখি।
সমাধান –
\(x + y = 2\) —(i)
\(\frac{1}{x} + \frac{1}{y} = 2\) —(ii)
(ii) নং সমীকরণ থেকে পাই,
\(\frac{1}{x} + \frac{1}{y} = 2\)বা, \(\frac{y + x}{xy} = 2\)
বা, \(\frac{2}{xy} = 2\)
বা, \(xy = \frac{2}{2}\)
বা, \(xy = 1\)
\(\therefore x^3 + y^3\)= \( (x + y)^3 – 3xy(x + y)\) [(II) নং অভেদের সাহায্যে পাই]
= \( (2)^3 – 3(1)(2)\) \([\because x + y = 2\) এবং \(xy = 1]\)
= \( 8 – 6 = 2\)
\(\therefore x^3 + y^3 = 2\) [উত্তর]
(d) \(\frac{x^2 – 1}{x} = 2\) হলে \(\frac{x^6 – 1}{x^3}\) -এর মান হিসাব করে লেখার চেষ্টা করি।
সমাধান –
\(\frac{x^2 – 1}{x} = 2\)বা, \(\left(\frac{x^2 – 1}{x}\right)^3 = (2)^3\) [উভয়পক্ষে ঘন করে পাই]
বা, \(\frac{(x^2)^3 – 3 \cdot (x^2)^2 \cdot 1 + 3 \cdot x^2 \cdot 1^2 – 1^3}{x^3} = 8\) [(IV) নং অভেদের সাহায্যে পাই]
বা, \(\frac{x^6 – 1 – 3x^2(x^2 – 1)}{x^3} = 8\)
বা, \(\frac{x^6 – 1}{x^3} – \frac{3x^2(x^2 – 1)}{x^3} = 8\)
বা, \(\frac{x^6 – 1}{x^3} – 3 \cdot \frac{x^2 – 1}{x} = 8\)
বা, \(\frac{x^6 – 1}{x^3} – 3 \cdot 2 = 8\)
বা, \(\frac{x^6 – 1}{x^3} = 8 + 6 = 14\)
\(\therefore \frac{x^6 – 1}{x^3} = 14\) [উত্তর]
(e) \(x + \frac{1}{x} = 5\) হলে, \(x^3 + \frac{1}{x^3}\) -এর মান হিসাব করে লিখি।
সমাধান –
\(x + \frac{1}{x} = 5\)বা, \(\left(x + \frac{1}{x}\right)^3 = 5^3\) [উভয়পক্ষে ঘন করে পাই]
বা, \(x^3 + \frac{1}{x^3} + 3 \cdot x \cdot \frac{1}{x} \left(x + \frac{1}{x}\right) = 125\) [(II) নং অভেদ থেকে পাই]
বা, \(x^3 + \frac{1}{x^3} + 3(5) = 125\) \([\because x + \frac{1}{x} = 5]\)
বা, \(x^3 + \frac{1}{x^3} = 125 – 15 = 110\)
\(\therefore x^3 + \frac{1}{x^3} = 110\)(f) \(x = y + z\) হলে, \(x^3 – y^3 – z^3 – 3xyz\) -এর মান হিসাব করে লিখি।
সমাধান –
\(x = y + z\)\(x^3 = (y + z)^3\) [উভয়পক্ষে ঘন করে পাই]
বা, \(x^3 = y^3 + z^3 + 3yz(y + z)\) [(II) নং অভেদের সাহায্যে পাই]
বা, \(x^3 = y^3 + z^3 + 3yz(x)\) \([\because (y + z) = x]\)
বা, \(x^3 – y^3 – z^3 – 3xyz = 0\)
\(\therefore x^3 – y^3 – z^3 – 3xyz = 0\)(g) \(xy(x + y) = m\) হলে \(x^3 + y^3 + 3m = \frac{m^3}{x^3y^3}\)
সমাধান –
\(xy(x + y) = m\)বা, \(x + y = \frac{m}{xy}\)
বা, \((x + y)^3 = \left(\frac{m}{xy}\right)^3\)
বা, \(x^3 + y^3 + 3xy(x + y) = \frac{m^3}{x^3y^3}\) [(II) নং অভেদ থেকে পাই]
বা, \(x^3 + y^3 + 3m = \frac{m^3}{x^3y^3}\) \([\because xy(x + y) = m]\)
\(\therefore x^3 + y^3 + 3m = \frac{m^3}{x^3y^3}\)(h) \(2x + \frac{1}{3x} = 4\) হলে, প্রমাণ করার চেষ্টা করি যে \(27x^3 + \frac{1}{8x^3} = 189\)
সমাধান –
\(2x + \frac{1}{3x} = 4\)\(\frac{3}{2} \left(2x + \frac{1}{3x}\right) = \frac{3}{2} \times 4\) [উভয়পক্ষে \(\frac{3}{2}\) দ্বারা গুণ করে পাই]
বা, \(3x + \frac{1}{2x} = 6\)
বা, \(\left(3x + \frac{1}{2x}\right)^3 = (6)^3\)
বা, \((3x)^3 + \frac{1}{(2x)^3} + 3 \cdot (3x) \cdot \frac{1}{2x} \left(3x + \frac{1}{2x}\right) = 216\) [(II) নং অভেদ থেকে পাই]
বা, \(27x^3 + \frac{1}{8x^3} + \frac{9}{2} \times 6 = 216\) \([\because \left(3x + \frac{1}{2x}\right) = 6]\)
বা, \(27x^3 + \frac{1}{8x^3} + 27 = 216\)
বা, \(27x^3 + \frac{1}{8x^3} = 216 – 27 = 189\) [প্রমাণিত]
(i) \(2a – \frac{2}{a} + 1 = 0\) হলে, \(a^3 – \frac{1}{a^3} + 2\) এর মান নির্ণয় করি।
সমাধান –
\(2a – \frac{2}{a} + 1 = 0\)বা, \(2 \left(a – \frac{1}{a}\right) = -1\)
বা, \(\left(a – \frac{1}{a}\right) = -\frac{1}{2}\)
বা, \(\left(a – \frac{1}{a}\right)^3 = \left(-\frac{1}{2}\right)^3\) [উভয়পক্ষে ঘন করে পাই]
বা, \(a^3 – \frac{1}{a^3} – 3 \cdot a \cdot \frac{1}{a} \left(a – \frac{1}{a}\right) = -\frac{1}{8}\) [(IV) নং অভেদ থেকে পাই]
বা, \(a^3 – \frac{1}{a^3} – 3 \left(-\frac{1}{2}\right) = -\frac{1}{8}\)
বা, \(a^3 – \frac{1}{a^3} + \frac{3}{2} = -\frac{1}{8}\)
বা, \(a^3 – \frac{1}{a^3} = -\frac{3}{2} – \frac{1}{8} = \frac{-12-1}{8} = \frac{-13}{8}\)
বা, \(a^3 – \frac{1}{a^3} + 2 = \frac{-13}{8} + 2 = \frac{-13+16}{8} = \frac{3}{8}\)
\(\therefore a^3 – \frac{1}{a^3} + 2 = \frac{3}{8}\)(j) \(a^3 + b^3 + c^3 = 3abc\) হলে \((a + b + c)\) -এর মান হিসাব করে লিখি (\(a \neq b \neq c\))
সমাধান –
\(a^3 + b^3 + c^3 = 3abc\)বা, \(a^3 + b^3 + c^3 – 3abc = 0\)
বা, \((a+b+c)(a^2 + b^2 + c^2 – ab – bc – ca) = 0\)
\(\therefore (a+b+c) = 0\) অথবা, \((a^2 + b^2 + c^2 – ab – bc – ca) = 0\)
এখন, \((a^2 + b^2 + c^2 – ab – bc – ca) = 0\) হলে আমরা পাই:
\(\frac{1}{2} \{ (a-b)^2 + (b-c)^2 + (c-a)^2 \} = 0\)যেহেতু বর্গের যোগফল শূন্য, তাই \(a = b = c\) হয়। কিন্তু প্রশ্নে বলা আছে \(a \neq b \neq c\)।
\(\therefore (a + b + c) = 0\)(k) যদি, \(m + n = 5\) এবং \(mn = 6\) হয় তবে \((m^2 + n^2)(m^3 + n^3)\) -এর মান হিসাব করে লিখি।
সমাধান –
\(m + n = 5\) এবং \(mn = 6\)
\((m^2 + n^2)(m^3 + n^3)\)= \( \{ (m+n)^2 – 2mn \} \{ (m+n)^3 – 3mn(m+n) \}\)
= \( \{ (5)^2 – 2(6) \} \{ (5)^3 – 3(6)(5) \}\)
= \( (25 – 12) (125 – 90)\)
= \( 13 \times 35 = 455\)
\(\therefore (m^2 + n^2)(m^3 + n^3) = 455\)এই আর্টিকেলে অষ্টম শ্রেণির গণিতের ‘ঘনফল নির্ণয়’ অধ্যায়ের ‘কষে দেখি – 5.2’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরেছি। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে। কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment