পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) অষ্টম শ্রেণির গণিত পাঠ্যবইয়ের প্রথম অধ্যায় হলো ‘পূর্বপাঠের পুনরালোচনা’। এই পোস্টে আমরা ‘কষে দেখি – 1.1’-এর সমস্ত প্রশ্নের সহজ ও নির্ভুল সমাধান নিয়ে আলোচনা করেছি। আশা করি, এই নোটসগুলো তোমাদের গণিত শিখতে এবং পরীক্ষার প্রস্তুতিতে দারুণভাবে সহায়তা করবে।

1. নিচের ছক কাগজে ছবি দেখি ও ছবিগুলি কতটা জায়গা জুড়ে আছে লিখি
2.আমিনাদের বাড়ির আয়তক্ষেত্রাকার উঠানের দৈর্ঘ্য \(6\) মিটার এবং প্রস্থ \(4.2\) মিটার। ওই উঠানের মাঝখানে \(3.5 \times 2.5\) মিটার মাপের একটি আয়তকার শতরঞ্জি পাতলাম। শতরঞ্জি বাদে বাকি উঠানের ক্ষেত্রফল হিসাব করে লিখি।
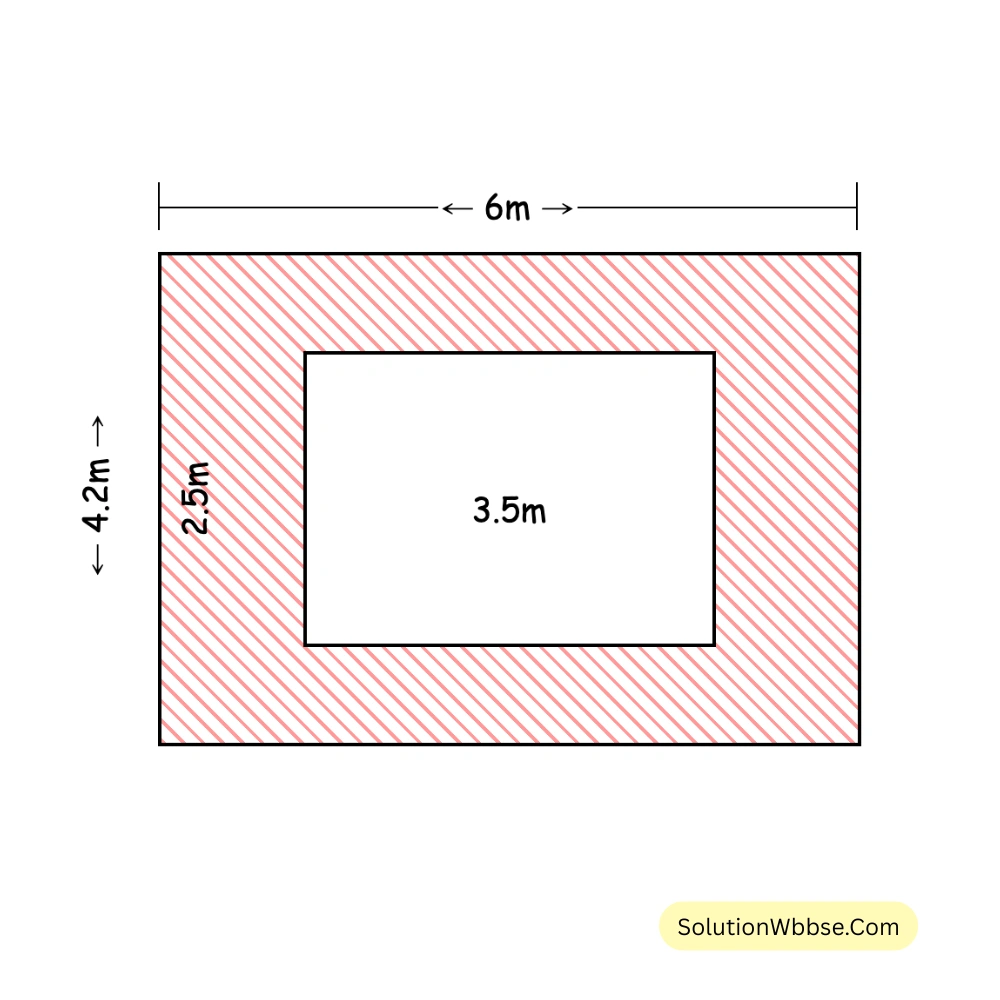
সমাধান –
আমিনাদের বাড়ির আয়তক্ষেত্রাকার উঠানের দৈর্ঘ্য \(6\) মিটার এবং প্রস্থ \(4.2\) মিটার।
\(\therefore\) আয়তকার উঠানের ক্ষেত্রফল \(= (6 \times 4.2)\) বর্গ মিটার \(= 25.2\) বর্গ মিটার।
শতরঞ্জির দৈর্ঘ্য \(3.5\) মিটার এবং প্রস্থ \(2.5\) মিটার।
\(\therefore\) শতরঞ্জির ক্ষেত্রফল \(= (3.5 \times 2.5)\) বর্গমিটার \(= 8.75\) বর্গমিটার।
\(\therefore\) শতরঞ্জি বাদে আয়তকার উঠানের ক্ষেত্রফল \(= (25.2 – 8.75)\) বর্গ মিটার \(= 16.45\) বর্গমিটার [উত্তর]।
3. অজন্তা হাউসিং কমপ্লেক্সের বর্গক্ষেত্রের পার্কের বাইরের চারিদিকে \(3\) মিটার চওড়া একটি রাস্তা আছে। রাস্তা সমেত পার্কের পরিসীমা \(484\) মিটার হলে রাস্তাটির ক্ষেত্রফল হিসাব করি।
সমাধান –
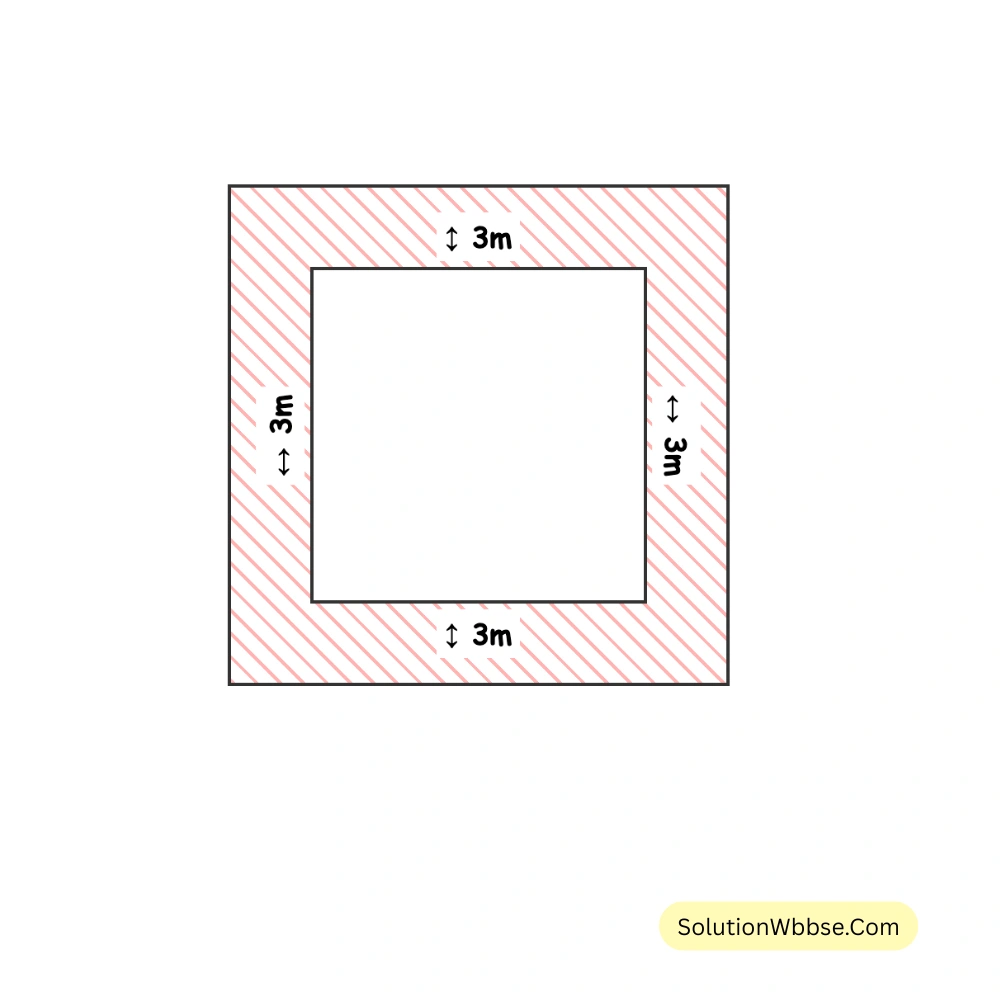
রাস্তা সহ বর্গাকার পার্কের পরিসীমা \(484\) মিটার।
\(\therefore\) রাস্তা সহ বর্গাকার পার্কের বাহুর দৈর্ঘ্য \(= 484 \div 4\) মিটার \(= 121\) মিটার।
\(\therefore\) রাস্তাসহ বর্গাকার পার্কের ক্ষেত্রফল \(= (121)^2\) বর্গমিটার \(= 14641\) বর্গমিটার।
রাস্তাটি \(3\) মিটার চওড়া।
\(\therefore\) রাস্তা বাদে বর্গাকার পার্কের বাহুর দৈর্ঘ্য \(= {121 – (3 + 3)}\) মিটার \(= (121 – 6)\) মিটার \(= 115\) মিটার।
\(\therefore\) রাস্তা বাদে বর্গাকার পার্কের ক্ষেত্রফল \(= (115)^2\) বর্গমিটার \(= 13225\) বর্গমিটার।
\(\therefore\) রাস্তার ক্ষেত্রফল \(= (14641 – 13225)\) বর্গমিটার \(= 1416\) বর্গমিটার [উত্তর]।
4. মিহিরদের আয়তক্ষেত্রাকার বাগানের দৈর্ঘ্য 50 মিটার এবং প্রস্থ 30 মিটার। ওই বাগানের মাঝবরাবর, দৈর্ঘ্যের সমান্তরালে 4 মিটার চওড়া একটি রাস্তা বাগানটিকে দুটি সমান ক্ষেত্রফলবিশিষ্ট আয়তক্ষেত্রাকার খণ্ডে ভাগ করেছে। রাস্তাটির ক্ষেত্রফল নিজে এঁকে হিসাব করে লিখি।
(a) যদি 4 মিটার চওড়া রাস্তাটি বাগানের মাঝবরাবর প্রস্থের সমান্তরালে হতো এবং বাগানটিকে দুটি সমান খণ্ডে ভাগ করত, তবে রাস্তাটির ক্ষেত্রফল কী হতো তা নিজে এঁকে হিসাব করে লিখি।
(b) যদি মিহিরদের বাগানের মাঝবরাবর দৈর্ঘ্য ও প্রস্থের সমান্তরাল দুটি রাস্তা থাকত এবং মিহিরদের বাগানকে 4 টি সমান খণ্ডে ভাগ করত, তখন রাস্তার ক্ষেত্রফল কী হতো নিজে এঁকে হিসাব করে লিখি।
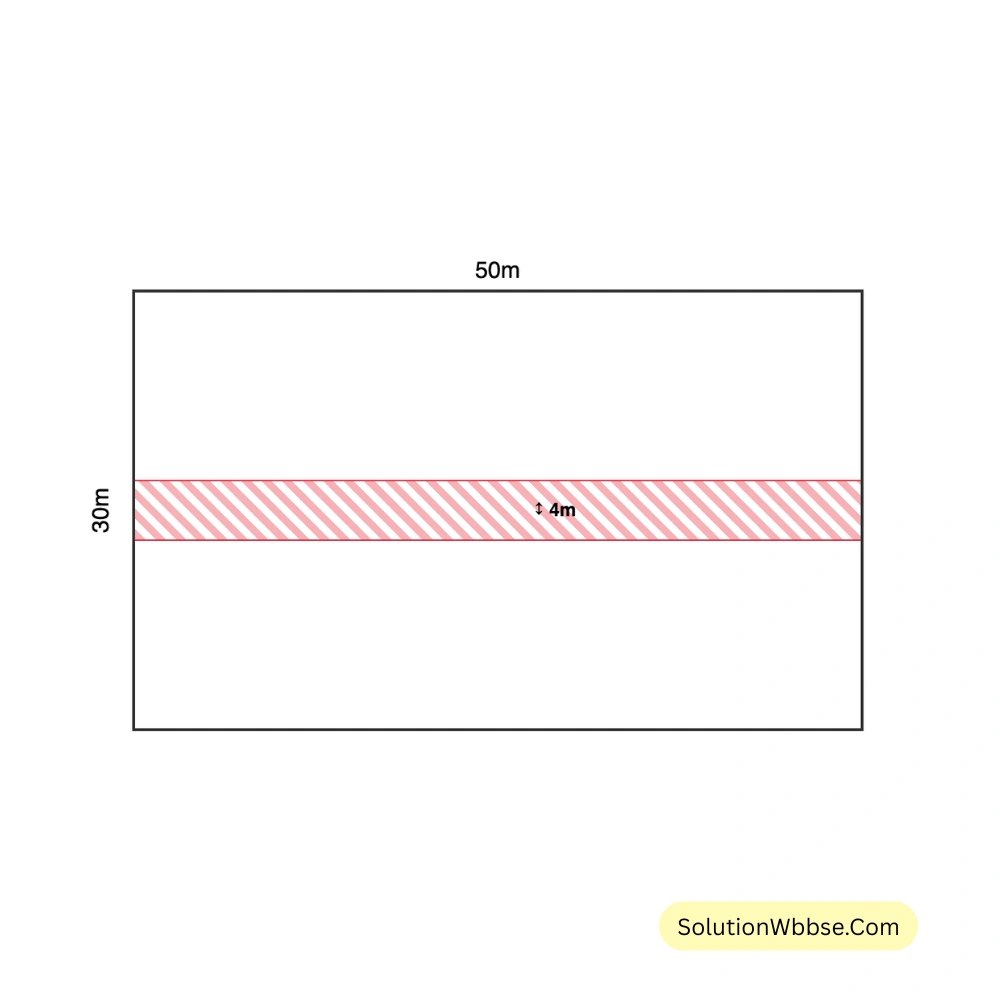
মিহিরদের আয়তক্ষেত্রাকার বাগানের দৈর্ঘ্য 50 মিটার এবং প্রস্থ 30 মিটার। ওই বাগানের মাঝবরাবর, দৈর্ঘ্যের সমান্তরালে 4 মিটার চওড়া একটি রাস্তা বাগানটিকে দুটি সমান ক্ষেত্রফলবিশিষ্ট আয়তক্ষেত্রাকার খণ্ডে ভাগ করেছে।
এক্ষেত্রে রাস্তাটিও আয়তক্ষেত্রাকার, যার দৈর্ঘ্য 50 মিটার এবং প্রস্থ 4 মিটার।
\(\therefore\) দৈর্ঘ্যের সমান্তরালে আয়তক্ষেত্রাকার রাস্তার ক্ষেত্রফল \(= (50 \times 4)\) বর্গমিটার \(= 200\) বর্গমিটার। [উত্তর]
(a) এর সমাধান –
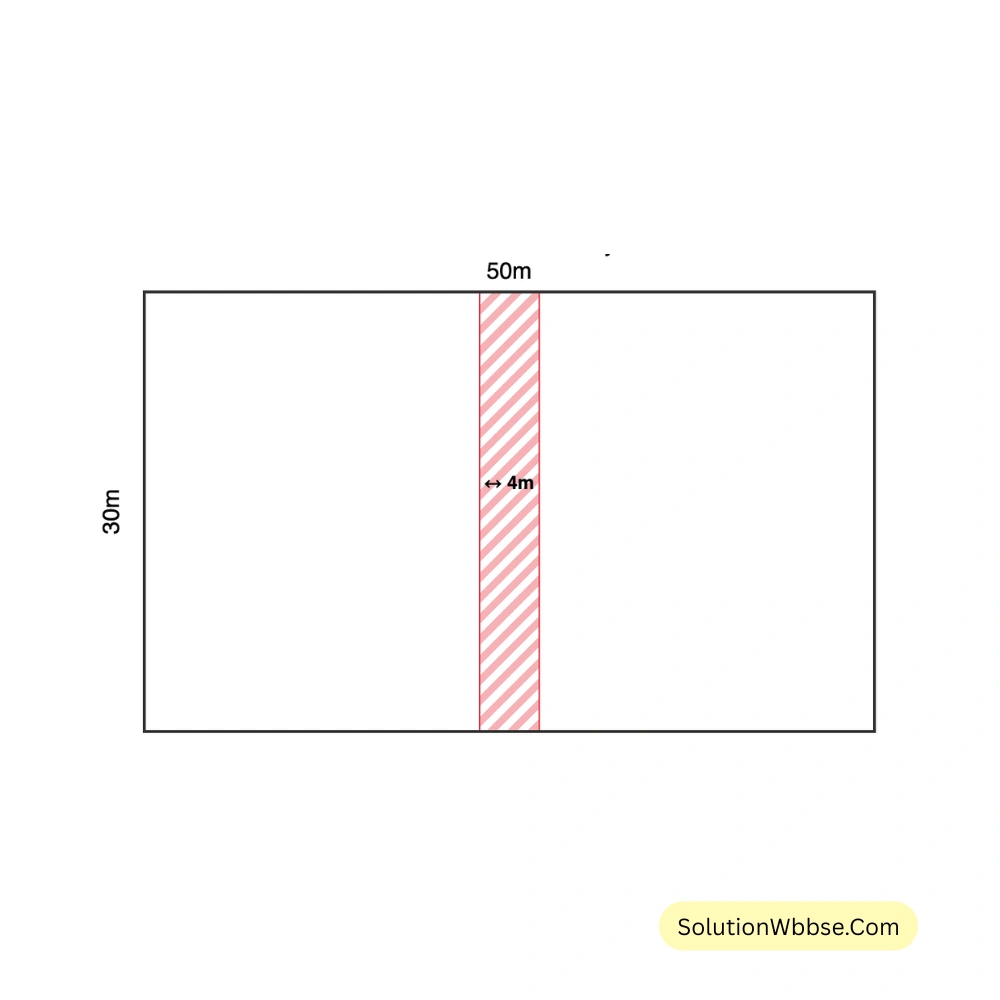
যদি 4 মিটার চওড়া রাস্তাটি বাগানের মাঝবরাবর প্রস্থের সমান্তরালে থাকত, তবে রাস্তাটিও একটি আয়তক্ষেত্র হতো যার দৈর্ঘ্য 30 মিটার এবং প্রস্থ 4 মিটার।\(\therefore\) প্রস্থের সমান্তরালে আয়তক্ষেত্রাকার রাস্তার ক্ষেত্রফল \(= (30 \times 4)\) বর্গমিটার \(= 120\) বর্গমিটার। [উত্তর]
(b) এর সমাধান –
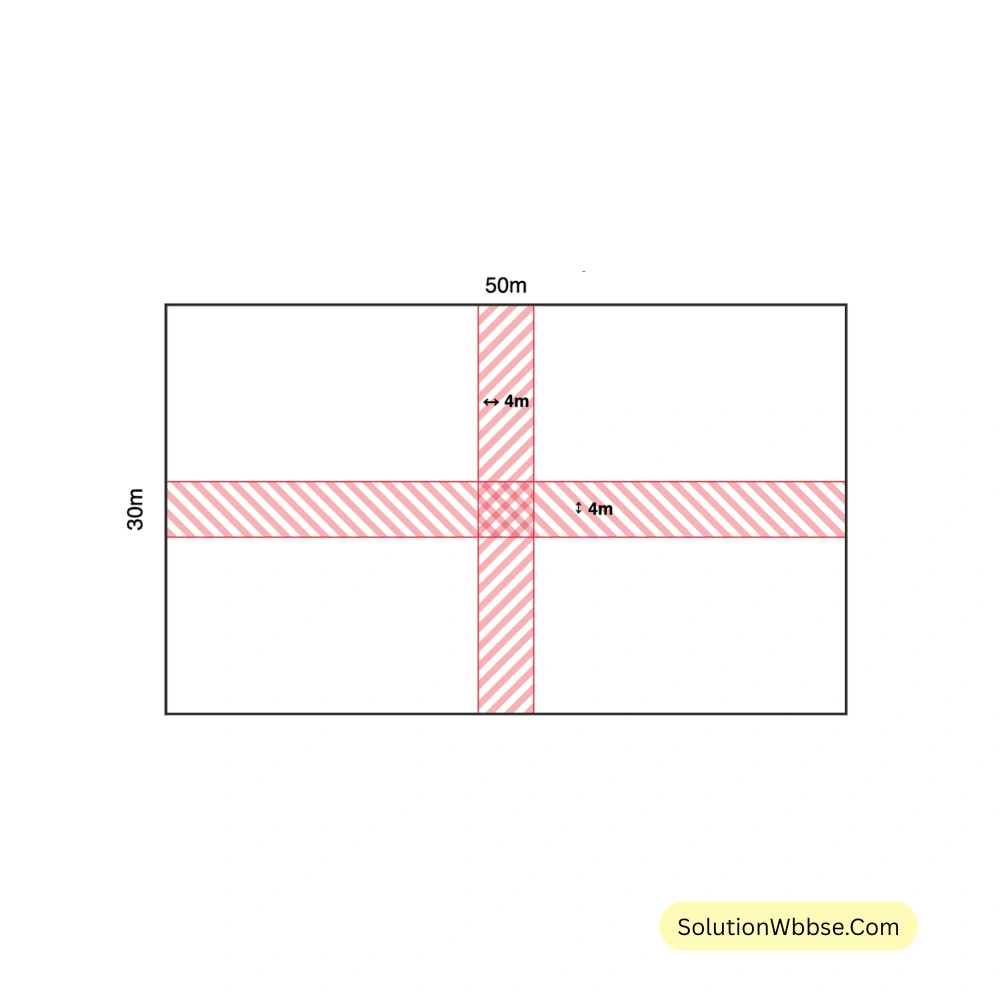
দৈর্ঘ্যের সমান্তরালে রাস্তার ক্ষেত্রফল \(= 200\) বর্গমিটার।
প্রস্থের সমান্তরালে রাস্তার ক্ষেত্রফল \(= 120\) বর্গমিটার।
যেহেতু রাস্তা দুটি পরস্পরকে বাগানের মাঝখানে ছেদ করে, তাই মাঝখানের বর্গাকার অংশটি (\(4 \times 4\) বর্গমিটার) উভয় রাস্তার মধ্যেই ধরা হয়েছে। তাই মোট ক্ষেত্রফল থেকে একবার ওই বর্গাকার অংশের ক্ষেত্রফল বিয়োগ করতে হবে।
\(\therefore\) দৈর্ঘ্য ও প্রস্থের সমান্তরালে রাস্তার মোট ক্ষেত্রফল \(= \{ (200 + 120) – (4 \times 4) \}\) বর্গমিটার
\(= (320 – 16)\) বর্গমিটার
\(= 304\) বর্গমিটার। [উত্তর]
5. আমাদের বাড়ির পাশে পাপিয়াদের আয়তক্ষেত্রাকার জমি আছে। এই আয়তক্ষেত্রাকার জমির দৈর্ঘ্য \(48\) মিটার এবং প্রস্থ \(26\) মিটার। পাপিয়াররা তাদের জমির চারিদিকে \(4\) মিটার ছেড়ে বাড়ি তৈরি করবে। হিসাব করে দেখি পাপিয়াররা কত বর্গমিটারে তাদের বাড়ি তৈরি করবে?
সমাধান –
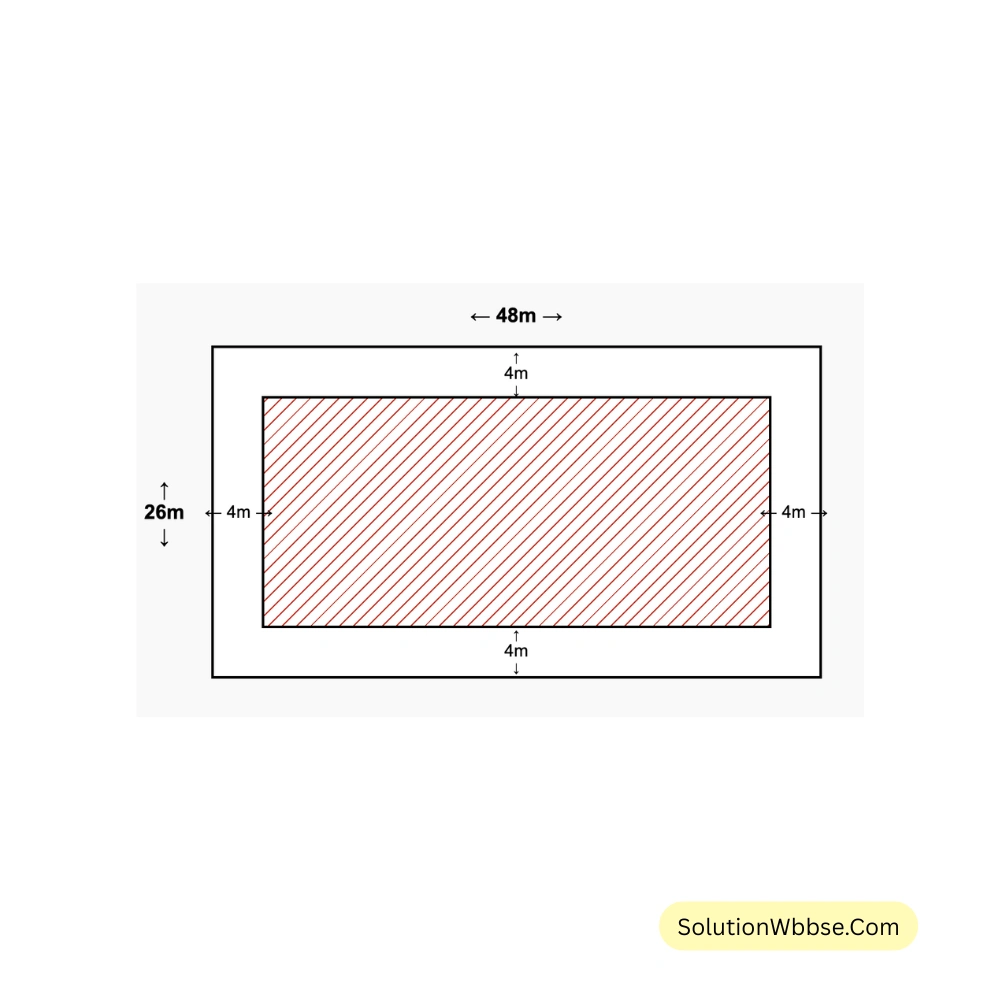
পাপিয়ারা যে আয়তকার জমিতে বাড়ি করবে তার দৈর্ঘ্য \(48\) মিটার এবং প্রস্থ \(26\) মিটার। পাপিয়াররা তাদের জমির চারিদিকে \(4\) মিটার ছেড়ে বাড়ি তৈরি করবে।
পাপিয়ারা যে জমিতে বাড়ি তৈরি করবে তার দৈর্ঘ্য \(= (48-4-4)\) মিটার \(= 40\) মিটার এবং প্রস্থ \(= (26-4-4)\) মিটার \(= 18\) মিটার
\(\therefore\) পাপিয়ারা যে আয়তকার জমিতে বাড়ি তৈরি করবে তার ক্ষেত্রফল \(= (40 \times 18)\) বর্গমিটার \(= 720\) বর্গমিটার [উত্তর]
6. আমার ভাই দীপু একটি আয়তক্ষেত্রাকার কাগজের পুরোটায় ছবি এঁকেছে, যার দৈর্ঘ্য \(15\) সেমি. এবং প্রস্থ \(8\) সেমি.।
(a) যদি দীপু আয়তক্ষেত্রাকার কাগজের প্রস্থ একই রেখে দৈর্ঘ্য দ্বিগুণ করত, তবে তার ছবির কাগজের ক্ষেত্রফল কিরূপ পরিবর্তন হতো, হিসাব করে লিখি।
(b) যদি দীপু আয়তক্ষেত্রাকার কাগজের দৈর্ঘ্য একই রেখে প্রস্থ দ্বিগুণ করত, তবে তার ছবির কাগজের ক্ষেত্রফলের কিরূপ পরিবর্তন হতো, হিসাব করে লিখি।
(c) যদি দীপু তার ছবির কাগজের দৈর্ঘ্য ও প্রস্থ উভয়কেই দ্বিগুণ করত, তখন তার ছবির কাগজের ক্ষেত্রফল (a) নং ছবির কাগজের ক্ষেত্রফলের কতগুণ হতে পারে, হিসাব করে লিখি।
(d) কিন্তু দীপু যদি তার ছবির কাগজের দৈর্ঘ্য ও প্রস্থ উভয়কেই অর্ধেক করত, তখন তার ছবির কাগজের ক্ষেত্রফলের কীরূপ পরিবর্তন হতো, হিসাব করে লিখি।
সমাধান –
দীপুরের আঁকা আয়তক্ষেত্রাকার ছবির ক্ষেত্রফল = \(15 \times 8\) বর্গ সেমি. = \(120\) বর্গ সেমি.।
(a) যদি দীপু আয়তক্ষেত্রাকার কাগজের প্রস্থ একই রেখে দৈর্ঘ্য দ্বিগুণ করত, তবে তার ছবির কাগজের ক্ষেত্রফল কিরূপ পরিবর্তন হতো, হিসাব করে লিখি।
আয়তক্ষেত্রাকার কাগজের দৈর্ঘ্য দ্বিগুণ করলে পরিবর্তিত দৈর্ঘ্য = \(15 \times 2\) সেমি. = \(30\) সেমি. এবং আয়তক্ষেত্রাকার কাগজের প্রস্থ \(8\) সেমি.।
আয়তক্ষেত্রাকার কাগজের ক্ষেত্রফল = \(30 \times 8\) বর্গ সেমি. = \(240\) বর্গ সেমি. = \(2 \times 120\) বর্গ সেমি.।
আয়তক্ষেত্রাকার কাগজের দৈর্ঘ্য দ্বিগুণ করলে পরিবর্তিত আয়তাকার কাগজের ক্ষেত্রফল পূর্বের আয়তাকার কাগজের ক্ষেত্রফলের দ্বিগুণ হবে [উত্তর]।
(b) যদি দীপু আয়তক্ষেত্রাকার কাগজের দৈর্ঘ্য একই রেখে প্রস্থ দ্বিগুণ করত, তবে তার ছবির কাগজের ক্ষেত্রফলের কিরূপ পরিবর্তন হতো, হিসাব করে লিখি।
আয়তক্ষেত্রাকার কাগজের প্রস্থ দ্বিগুণ করলে পরিবর্তিত প্রস্থ হবে \(8 \times 2\) সেমি. = \(16\) সেমি., আয়তক্ষেত্রাকার জমির দৈর্ঘ্য \(15\) সেমি.।
আয়তক্ষেত্রাকার কাগজের ক্ষেত্রফল = \(15 \times 16\) বর্গ সেমি. = \(240\) বর্গ সেমি. = \(2 \times 120\) বর্গ সেমি.।
আয়তক্ষেত্রাকার কাগজের প্রস্থ দ্বিগুণ করলে পরিবর্তিত আয়তাকার কাগজের ক্ষেত্রফল পূর্বের আয়তাকার কাগজের ক্ষেত্রফলের দ্বিগুণ হবে [উত্তর]।
(c) যদি দীপু তার ছবির কাগজের দৈর্ঘ্য ও প্রস্থ উভয়কেই দ্বিগুণ করত, তখন তার ছবির কাগজের ক্ষেত্রফল (a) নং ছবির কাগজের ক্ষেত্রফলের কতগুণ হতে পারে, হিসাব করে লিখি।
আয়তক্ষেত্রাকার কাগজের দৈর্ঘ্য দ্বিগুণ করলে পরিবর্তিত দৈর্ঘ্য = \(15 \times 2\) সেমি. = \(30\) সেমি. এবং আয়তক্ষেত্রাকার কাগজের প্রস্থ দ্বিগুণ করলে পরিবর্তিত প্রস্থ হবে \(8 \times 2\) সেমি. = \(16\) সেমি.।
আয়তক্ষেত্রাকার কাগজের ক্ষেত্রফল হবে = \(30 \times 16\) বর্গ সেমি. = \(480\) বর্গ সেমি. = \(4 \times 120\) বর্গ সেমি.।
আয়তক্ষেত্রাকার কাগজের দৈর্ঘ্য ও প্রস্থ উভয়কেই দ্বিগুণ করলে পরিবর্তিত আয়তক্ষেত্রাকার কাগজের ক্ষেত্রফল (a) নং চিত্রের ক্ষেত্রফলের **\(2\) গুণ হবে** [উত্তর]।
(d) কিন্তু দীপু যদি তার ছবির কাগজের দৈর্ঘ্য ও প্রস্থ উভয়কেই অর্ধেক করত, তখন তার ছবির কাগজের ক্ষেত্রফলের কীরূপ পরিবর্তন হতো, হিসাব করে লিখি।
আয়তক্ষেত্রাকার কাগজের দৈর্ঘ্য ও প্রস্থ উভয়কেই অর্ধেক করলে পরিবর্তিত দৈর্ঘ্য \(15 \div 2\) সেমি. = \(7.5\) সেমি. এবং পরিবর্তিত প্রস্থ = \(8 \div 2\) সেমি. = \(4\) সেমি.।
আয়তক্ষেত্রাকার কাগজের ক্ষেত্রফল = \(7.5 \times 4\) বর্গ সেমি. = \(30\) বর্গ সেমি. = \(\frac{1}{4} \times 120\) বর্গ সেমি.।
আয়তক্ষেত্রাকার কাগজের দৈর্ঘ্য ও প্রস্থ উভয়কেই অর্ধেক করলে পরিবর্তিত আয়তক্ষেত্রাকার কাগজের ক্ষেত্রফল পূর্বের আয়তক্ষেত্রাকার কাগজের ক্ষেত্রফলের এক-চতুর্থাংশ হবে [উত্তর]।
7. আমি তিনটি বর্গক্ষেত্রাকার কাগজ কাটি এবং ক্ষেত্রফলের কীরূপ পরিবর্তন হবে দেখি।
যদি, (a) দৈর্ঘ্য দ্বিগুণ করা হয় (b) দৈর্ঘ্য অর্ধেক করা হয়।
সমাধান – ধরি, প্রথম বর্গক্ষেত্রাকার কাগজের বাহুর দৈর্ঘ্য \(a\) একক, দ্বিতীয় বর্গক্ষেত্রাকার কাগজের বাহুর দৈর্ঘ্য \(b\) একক এবং তৃতীয় বর্গক্ষেত্রাকার কাগজের বাহুর দৈর্ঘ্য \(c\) একক।
বর্গক্ষেত্রাকার কাগজগুলির ক্ষেত্রফল যথাক্রমে \(a^2\) বর্গএকক, \(b^2\) বর্গএকক এবং \(c^2\) বর্গএকক।
(a) দৈর্ঘ্য দ্বিগুণ করা হয়
দৈর্ঘ্য দ্বিগুণ করা হলে প্রথম বর্গক্ষেত্রাকার কাগজের বাহুর দৈর্ঘ্য \(2a\) একক, দ্বিতীয় বর্গক্ষেত্রাকার কাগজের বাহুর দৈর্ঘ্য \(2b\) একক এবং তৃতীয় বর্গক্ষেত্রাকার কাগজের বাহুর দৈর্ঘ্য \(2c\) একক হবে।
বর্গক্ষেত্রাকার কাগজগুলির ক্ষেত্রফল যথাক্রমে \((2a)^2\) বর্গএকক = \(4a^2\) বর্গএকক, \((2b)^2\) বর্গএকক = \(4b^2\) বর্গএকক এবং \((2c)^2\) বর্গএকক = \(4c^2\) বর্গএকক।
বর্গাকার কাগজগুলির বাহুর দৈর্ঘ্য দ্বিগুণ করা হলে পরিবর্তিত বর্গাকার কাগজগুলির ক্ষেত্রফল পূর্বের বর্গাকার কাগজগুলির ক্ষেত্রফলের \(4\) গুণ হবে [উত্তর]।
(b) দৈর্ঘ্য অর্ধেক করা হয়।
দৈর্ঘ্য অর্ধেক করা হলে প্রথম বর্গক্ষেত্রাকার কাগজের বাহুর দৈর্ঘ্য \(\frac{a}{2}\) একক, দ্বিতীয় বর্গক্ষেত্রাকার কাগজের বাহুর দৈর্ঘ্য \(\frac{b}{2}\) একক এবং তৃতীয় বর্গক্ষেত্রাকার কাগজের বাহুর দৈর্ঘ্য \(\frac{c}{2}\) একক হবে।
বর্গক্ষেত্রাকার কাগজগুলির ক্ষেত্রফল যথাক্রমে –
\(\left(\frac{a}{2}\right)^2\) বর্গএকক = \(\frac{a^2}{4}\) বর্গএকক,
\(\left(\frac{b}{2}\right)^2\) বর্গএকক = \(\frac{b^2}{4}\) বর্গএকক
এবং \(\left(\frac{c}{2}\right)^2\) বর্গএকক = \(\frac{c^2}{4}\) বর্গএকক।
বর্গাকার কাগজগুলির বাহুর দৈর্ঘ্য অর্ধেক করা হলে পরিবর্তিত বর্গাকার কাগজগুলির ক্ষেত্রফল পূর্বের বর্গাকার কাগজগুলির ক্ষেত্রফলের এক-চতুর্থাংশ হবে [উত্তর]।
8. আমাদের পাড়ার ক্লাবঘরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে \(7.2\) মিটার, \(5.5\) মিটার, \(4.2\) মিটার। ঘরে \(3\) মিটার লম্বা এবং \(1.8\) মিটার চওড়া \(1\) টি দরজা এবং \(2.25\) মিটার লম্বা এবং \(1.8\) মিটার চওড়া মাপের \(2\) টি জানালা আছে।
(a) ক্লাবঘরের মেঝের ক্ষেত্রফল কত হিসাব করি। মেঝে সিমেন্ট করতে প্রতি বর্গমিটারে \(62\) টাকা হিসাবে কত খরচ পড়বে, তা হিসাব করে দেখি।
(b) দরজা ও জানালা বাদে চার দেওয়ালের ক্ষেত্রফল হিসাব করে দেখি।
(c) ঘরের ভিতরের ছাদের ক্ষেত্রফল হিসাব করে দেখি।
(d) প্রতি বর্গমিটারে \(12\) টাকা হিসাবে দরজা ও জানালা বাদে ঘরের ভিতরের দিকের চার দেওয়াল ও ছাদ চুনকাম করতে কত খরচ পড়বে, হিসাব করে লিখি।
সমাধান –
(a) ক্লাবঘরের মেঝের ক্ষেত্রফল কত হিসাব করি। মেঝে সিমেন্ট করতে প্রতি বর্গমিটারে \(62\) টাকা হিসাবে কত খরচ পড়বে, তা হিসাব করে দেখি।
ক্লাব ঘরের মেঝের দৈর্ঘ্য \(7.2\) মিটার, প্রস্থ \(5.5\) মিটার।
\(\therefore\) ক্লাবঘরের মেঝের ক্ষেত্রফল \(= (7.2 \times 5.5)\) বর্গমিটার \(= 39.60\) বর্গমিটার [উত্তর]।
\(\therefore\) মেঝে সিমেন্ট করতে প্রতি বর্গমিটারে \(62\) টাকা হিসাবে মোট খরচ পড়বে \(= (62 \times 39.60)\) টাকা \(= 2455.20\) টাকা [উত্তর]।
(b) দরজা ও জানালা বাদে চার দেওয়ালের ক্ষেত্রফল হিসাব করে দেখি।
দরজা ও জানালা সমেত চার দেওয়ালের ক্ষেত্রফল –
\(= 2 \times ( \text{দৈর্ঘ্য} + \text{প্রস্থ} ) \times \text{উচ্চতা}\)\(= \{ 2 \times (7.2 + 5.5) \times 4.2 \}\) বর্গমিটার
\(= (2 \times 12.7 \times 4.2)\) বর্গমিটার
\(= 106.68\) বর্গমিটার।
\(1\) টি দরজার ক্ষেত্রফল \(= (3 \times 1.8)\) বর্গমিটার \(= 5.4\) বর্গমিটার।
\(1\) টি জানালার ক্ষেত্রফল \(= (2.25 \times 1.8)\) বর্গমিটার \(= 4.05\) বর্গমিটার।
\(2\) টি জানালার ক্ষেত্রফল \(= (2 \times 4.05)\) বর্গমিটার \(= 8.10\) বর্গমিটার।
\(\therefore\) দরজা ও জানালা বাদে চার দেওয়ালের মোট ক্ষেত্রফল \(= (106.68 – 5.4 – 8.10)\) বর্গমিটার \(= 93.18\) বর্গমিটার [উত্তর]।
(c) ঘরের ভিতরের ছাদের ক্ষেত্রফল হিসাব করে দেখি।
ঘরের ভিতরের ছাদের ক্ষেত্রফল \(=\) ঘরের মেঝের ক্ষেত্রফল \(= 39.60\) বর্গমিটার [উত্তর]।
(d) প্রতি বর্গমিটারে \(12\) টাকা হিসাবে দরজা ও জানালা বাদে ঘরের ভিতরের দিকের চার দেওয়াল ও ছাদ চুনকাম করতে কত খরচ পড়বে, হিসাব করে লিখি।
দরজা ও জানালা বাদে ঘরের ভিতরের চার দেওয়াল ও ছাদের ক্ষেত্রফল \(= (93.18 + 39.60)\) বর্গমিটার \(= 132.78\) বর্গমিটার।
\(\therefore\) প্রতি বর্গমিটারে \(12\) টাকা হিসাবে দরজা ও জানালা বাদে ঘরের ভিতরের দিকের চার দেওয়াল ও ছাদ চুনকাম করতে খরচ পড়বে \(= (12 \times 132.78)\) টাকা \(= 1593.36\) টাকা [উত্তর]।
এই আর্টিকেলে অষ্টম শ্রেণির গণিতের ‘পূর্বপাঠের পুনরালোচনা’ অধ্যায়ের ‘কষে দেখি – 1.1’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরেছি। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে। কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment