পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) অষ্টম শ্রেণির গণিত পাঠ্যবইয়ের প্রথম অধ্যায় হলো ‘পূর্বপাঠের পুনরালোচনা’। এই পোস্টে আমরা ‘কষে দেখি – 1.2’-এর সমস্ত প্রশ্নের সহজ ও নির্ভুল সমাধান নিয়ে আলোচনা করেছি। আশা করি, এই নোটসগুলো তোমাদের গণিত শিখতে এবং পরীক্ষার প্রস্তুতিতে দারুণভাবে সহায়তা করবে।

1. নীচের প্রত্যেকটির n –তম (n –ধনাত্মক পূর্ন সংখ্যা ) সজ্জায় প্রয়োজনীয় কাঠির সংখ্যা লিখি।
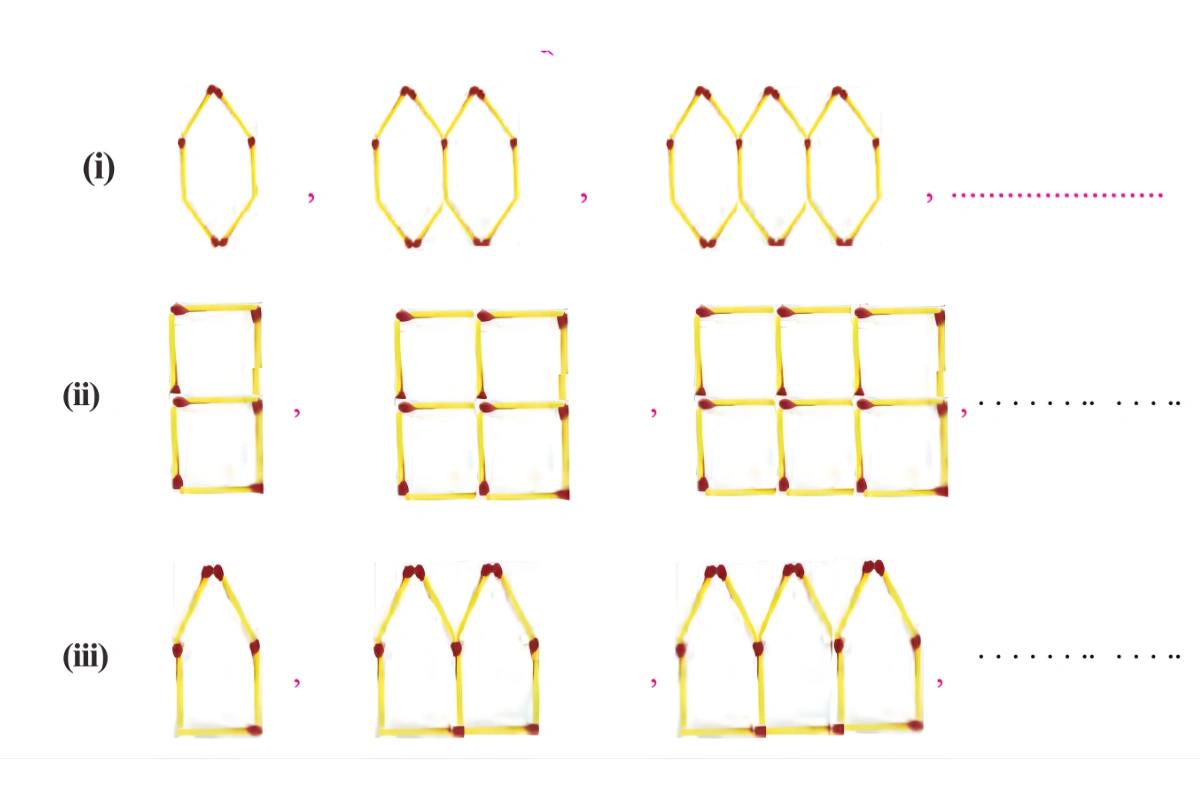
সমাধান –
(i) প্রথম সজ্জায় কাঠির সংখ্যা = \( 6 = 6 \times 1 -(1-1)\)
দ্বিতীয় সজ্জায় কাঠির সংখ্যা = \( 11 = 6 \times 2 – (2-1)\)
তৃতীয় সজ্জায় কাঠির সংখ্যা = \( 16 = 6 \times 3 -(3-1)\)
\(\therefore\) n-তম সজ্জায় কাঠির সংখ্যা = \( 6 \times n -(n-1) = 6n -n+1 = 5n+1\)
(ii) প্রথম সজ্জায় কাঠির সংখ্যা = \( 7 = 5 \times 1+2\)
দ্বিতীয় সজ্জায় কাঠির সংখ্যা = \( 12 = 5 \times 2+2\)
তৃতীয় সজ্জায় কাঠির সংখ্যা = \( 17 = 5 \times 3 +2\)
\(\therefore\) n-তম সজ্জায় কাঠির সংখ্যা = \( 5 \times n +2 = 5n+2\)
(iii) প্রথম সজ্জায় কাঠির সংখ্যা = \( 5 = 1+4 \times 1\)
দ্বিতীয় সজ্জায় কাঠির সংখ্যা = \( 9 = 1+4 \times 2\)
তৃতীয় সজ্জায় কাঠির সংখ্যা = \( 13 = 1+4 \times 3\)
\(\therefore\) n-তম সজ্জায় কাঠির সংখ্যা = \( 1+ 4 \times n = 1+4n\)
2. একটি সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য \((4y+2)\) সেমি. হলে ত্রিভুজটির পরিসীমা লিখি।
সমাধান –
সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য \((4y+2)\) সেমি. হলে ত্রিভুজটির পরিসীমা = \( \{3\times(4y+2)\}\) সেমি. = \( (12y+6)\) সেমি.।
3. একটি আয়তক্ষেত্রের দৈর্ঘ্য \((8x+3y)\) সেমি. এবং প্রস্থ \((8x-3y)\) সেমি.। ওই আয়তক্ষেত্রের ক্ষেত্রফল লিখি।
সমাধান –
একটি আয়তক্ষেত্রের দৈর্ঘ্য \((8x+3y)\) সেমি. এবং প্রস্থ \((8x-3y)\) সেমি.।
\(\therefore\) আয়তক্ষেত্রের ক্ষেত্রফল = \( \{(8x+3y) \times (8x-3y)\}\) বর্গসেমি. = \( (8x)^2 – (3y)^2\) বর্গসেমি. = \( (64x^2 – 9y^2)\) বর্গসেমি.।
4. বর্গাকার ক্ষেত্রের একটি বাহুর দৈর্ঘ্য \((3m-4)\) মিটার হলে ক্ষেত্রফল কত হবে m এর মাধ্যমে লিখি। m এর মান কত হলে বর্গাকার ক্ষেত্রের পরিসীমা \(8\) মিটার হবে, হিসাব করে লিখি।
সমাধান –
বর্গাকার ক্ষেত্রের একটি বাহুর দৈর্ঘ্য \((3m-4)\) মিটার।
\(\therefore\) বর্গাকার ক্ষেত্রের ক্ষেত্রফল = (বাহুর দৈর্ঘ্য)\(^2 = (3m-4)^2\) বর্গমিটার।
বর্গাকার ক্ষেত্রের একটি বাহুর দৈর্ঘ্য \((3m-4)\) মিটার।
\(\therefore\) পরিসীমা = 4 × বাহুর দৈর্ঘ্য = \( \{4 \times (3m-4)\}\) মিটার = \( (12m-16)\) মিটার।
শর্তানুসারে,
বা, \(12m = 16 + 8\)
বা, \(12m = 24\)
বা, \(m = 24 / 12\)
বা, \(m = 2\)
\(\therefore\) m এর মান \(2\) হলে বর্গাকার ক্ষেত্রের পরিসীমা \(8\) মিটার হবে।
5. নিচের ছক পূরণ করি (বীজগাণিতিক সংখ্যামালার যোগ ও বিয়োগ)
| বীজগাণিতিক সংখ্যামালা | যোগ করি | বিয়োগ করি |
|---|---|---|
| (a) (i) \(x^2 + 2y^2\) (ii) \(-8y^2 + 6x^2 + z^2\) | (i) + (ii) = \(7x^2 – 6y^2 + z^2\) | (i) – (ii) = \(10y^2 – 5x^2 – z^2\) |
| (b) (i) \(6a^2 + 2\) (ii) \(-3a^2 + 3a\) (iii) \(-2a + 3\) | (i)+(ii)+(iii) = \(3a^2 + a + 5\) | (ii)-(i) = \(-9a^2+3a-2\) (iii)-(i) = \(-6a^2-2a+1\) |
| (c) (i) \(9m^2 – 2mn + n^2\) (ii) \(m^2 + n^2\) (iii) \(m^2 – 3mn – 2n^2\) | (i)+(ii)+(iii) = \(11m^2 – 5mn\) | (i)-(ii) = \(8m^2-2mn\) (ii)-(iii) = \(3n^2+3mn\) |
6. নিচের ছক দেখি ও লিখি (বীজগাণিতিক সংখ্যামালার গুণ ও ভাগ)
| বীজগাণিতিক সংখ্যামালা | গুণ করি | ভাগ করি |
|---|---|---|
| (a) (i) \(9a^3b^2 – 15a^2b^3\) (ii) \(3ab\) | \(27a^4b^3 – 45a^3b^4\) | \(3a^2b – 5ab^2\) |
| (b) (i) \(x^4 – 4x^3 + 6x^2\) (ii) \(x^2\) | \(x^6 – 4x^5 + 6x^4\) | \(x^2 – 4x + 6\) |
| (i) \(3m^2n^3 + 40m^3n^4 – 5m^4n^5\) (ii) \(10m^2n^2\) | \(30m^4n^5 + 400m^5n^6 – 50m^6n^7\) | \(\frac{3}{10}n + 4mn^2 – \frac{1}{2}m^2n^3\) |
| (c) (i) \((49l^2 – 100m^2)\) (ii) \((7l + 10m)\) | \(343l^3 – 700lm^2 + 490l^2m – 1000m^3\) | \((7l – 10m)\) |
| (d) (i) \(625a^4 – 81b^4\) (ii) \(5a + 3b\) | \(3125a^5 – 405b^4a + 1875a^4b – 243b^5\) | \((25a^2 + 9b^2)(5a – 3b)\) |
7. সরল করি
(i) (a-b) + (b-c) + (c-a)
সমাধান –
\((a-b) + (b-c) + (c-a)\)= \( a – b + b – c + c – a\)
= \( 0\)
(ii) (a+b)(a-b) + (b+c)(b-c) + (c+a)(c-a)
সমাধান –
\((a+b)(a-b) + (b+c)(b-c) + (c+a)(c-a)\)= \( a^2 – b^2 + b^2 – c^2 + c^2 – a^2\)
= \( 0\)
(iii) \(x^2 \times (\frac{y}{x} – \frac{x}{y}) \times (\frac{y}{x} + \frac{x}{y}) \times y^2\)
সমাধান –
\(x^2 \times (\frac{y}{x} – \frac{x}{y}) \times (\frac{y}{x} + \frac{x}{y}) \times y^2\)= \( x^2 \times \frac{y^2-x^2}{xy} \times \frac{y^2+x^2}{xy} \times y^2\)
= \( \frac{x^2 y^2 (y^2-x^2)(y^2+x^2)}{x^2 y^2}\)
= \( (y^2-x^2)(y^2+x^2)\)
= \( y^4 – x^4\)
(iv) a(b-c) + b(c-a) + c(a-b)
সমাধান –
= \( ab – ac + bc – ab + ac – bc\)
= \( 0\)
(v) \(x^2(y^2-z^2) + y^2(z^2-x^2) + z^2(x^2-y^2)\)
সমাধান –
\(x^2(y^2-z^2) + y^2(z^2-x^2) + z^2(x^2-y^2)\)= \( x^2 y^2 – x^2 z^2 + y^2 z^2 – x^2 y^2 + z^2 x^2 – z^2 y^2\)
= \( 0\)
(vi) \((x^3+y^3)(x^3-y^3) + (y^3+z^3)(y^3-z^3) + (z^3+x^3)(z^3-x^3)\)
সমাধান –
\((x^3+y^3)(x^3-y^3) + (y^3+z^3)(y^3-z^3) + (z^3+x^3)(z^3-x^3)\)= \( (x^6 – y^6) + (y^6 – z^6) + (z^6 – x^6)\)
= \( x^6 – y^6 + y^6 – z^6 + z^6 – x^6\)
= \( 0\)
8. \((a+b)^2 = a^2+2ab+b^2\) এবং \((a-b)^2 = a^2-2ab+b^2\) — এই অভেদগুলি ব্যবহার করে নীচের সংখ্যামালাগুলির বর্গ করি।
(i) \(5x – 2y\)
(ii) \(7 + 2m\)
(iii) \(x + y + z\)
(iv) \(a + b – c – d\)
সমাধান –
(i) \(5x – 2y\)
\((5x – 2y)\) এর বর্গ
= \( (5x – 2y)^2\)
= \( (5x)^2 – 2 \cdot 5x \cdot 2y + (2y)^2\)
= \( 25x^2 – 20xy + 4y^2\)
(ii) \(7 + 2m\)
\((7 + 2m)\) এর বর্গ
= \( (7 + 2m)^2\)
= \( (7)^2 + 2 \cdot 7 \cdot 2m + (2m)^2\)
= \( 49 + 28m + 4m^2\)
(iii) \(x + y + z\)
\((x + y + z)\) এর বর্গ
= \( (x + y + z)^2\)
= \( \{(x + y) + z\}^2\)
= \( (x + y)^2 + 2 \cdot (x + y) \cdot z + z^2\)
= \( (x^2 + 2xy + y^2) + 2xz + 2yz + z^2\)
= \( x^2 + y^2 + z^2 + 2xy + 2yz + 2zx\)
(iv) \(a + b – c – d\)
\((a + b – c – d)\) এর বর্গ
= \( (a + b – c – d)^2\)
= \( \{(a + b) – (c + d)\}^2\)
= \( (a + b)^2 – 2(a + b)(c + d) + (c + d)^2\)
= \( a^2 + 2ab + b^2 – 2ac – 2bc – 2ad – 2bd + c^2 + 2cd + d^2\)
= \( a^2 + b^2 + c^2 + d^2 + 2ab + 2cd – 2ac – 2bc – 2ad – 2bd\)
9. \((a+b)^2 = a^2+2ab+b^2\) এবং \((a-b)^2 = a^2-2ab+b^2\) — এই অভেদগুলি ব্যবহার করে নীচের সংখ্যামালাগুলি পূর্ণবর্গাকারে প্রকাশ করি
(i) \(9x^2 + \frac{9}{25y^2} – \frac{18x}{5y}\)
(ii) \(25m^2 – 70mn + 49n^2\)
(iii) \((2a – b)^2 + (4a – 2b)(a + b) + (a + b)^2\)
(iv) \(\frac{p^2}{q^2} + \frac{q^2}{p^2} – 2\)
সমাধান –
(i) \(9x^2 + \frac{9}{25y^2} – \frac{18x}{5y}\)
= \( 9x^2 – \frac{18x}{5y} + \frac{9}{25y^2}\)
= \( (3x)^2 – 2 \cdot 3x \cdot \frac{3}{5y} + \left(\frac{3}{5y}\right)^2\)
= \( \left(3x – \frac{3}{5y}\right)^2\)
(ii) \(25m^2 – 70mn + 49n^2\)
= \( (5m)^2 – 2 \cdot 5m \cdot 7n + (7n)^2\)
= \( (5m – 7n)^2\)
(iii) \((2a – b)^2 + (4a – 2b)(a + b) + (a + b)^2\)
= \( (2a – b)^2 + 2(2a – b)(a + b) + (a + b)^2\)
= \( \{(2a – b) + (a + b)\}^2\)
= \( (2a – b + a + b)^2\)
= \( (3a)^2\)
(iv) \(\frac{p^2}{q^2} + \frac{q^2}{p^2} – 2\)
= \( \left(\frac{p}{q}\right)^2 – 2 \times \frac{p}{q} \times \frac{q}{p} + \left(\frac{q}{p}\right)^2\)
= \( \left(\frac{p}{q} – \frac{q}{p}\right)^2\)
10. নীচের সংখ্যামালাকে দুটি বর্গের অন্তর রূপে প্রকাশ করি
(i) \(391 \times 409\)
(ii) \((4x + 3y)(2x – 3y)\)
(iii) \(x\)
সমাধান –
(i) \(391 \times 409\)
= \( (400 – 9)(400 + 9)\)
= \( (400)^2 – (9)^2\)
(ii) \((4x + 3y)(2x – 3y)\)
= \( \left(\frac{4x + 3y + 2x – 3y}{2}\right)^2 – \left(\frac{4x + 3y – 2x + 3y}{2}\right)^2\)
= \( \left(\frac{6x}{2}\right)^2 – \left(\frac{2x + 6y}{2}\right)^2\)
= \( (3x)^2 – (x + 3y)^2\)
(iii) \(x\)
= \( x \cdot 1\)
= \( \left(\frac{x+1}{2}\right)^2 – \left(\frac{x-1}{2}\right)^2\)
11. উৎপাদকে বিশ্লেষণ করি
(i) \(225m^2 – 100n^2\)
সমাধান –
\(225m^2 – 100n^2\)= \( (15m)^2 – (10n)^2\)
= \( (15m + 10n)(15m – 10n)\)
= \( 25(3m + 2n)(3m – 2n)\)
(ii) \(25x^2 – \frac{1}{9}y^2z^2\)
সমাধান –
\(25x^2 – \frac{1}{9}y^2z^2\)= \( (5x)^2 – \left(\frac{1}{3}yz\right)^2\)
= \( \left(5x + \frac{1}{3}yz\right)\left(5x – \frac{1}{3}yz\right)\)
(iii) \(7ax^2 + 14ax + 7a\)
সমাধান –
\(7ax^2 + 14ax + 7a\)= \( 7a(x^2 + 2x + 1)\)
= \( 7a(x + 1)^2\)
= \( 7a(x + 1)(x + 1)\)
(iv) \(3x^4 – 6x^2a^2 + 3a^4\)
সমাধান –
\(3x^4 – 6x^2a^2 + 3a^4\)= \( 3(x^4 – 2x^2a^2 + a^4)\)
= \( 3\{(x^2)^2 – 2\cdot x^2\cdot a^2 + (a^2)^2\}\)
= \( 3(x^2 – a^2)^2\)
= \( 3\{(x+a)(x-a)\}^2\)
= \( 3(x+a)^2(x-a)^2\)
= \( 3(x+a)(x+a)(x-a)(x-a)\)
(v) \(4b^2c^2 – (b^2+c^2-a^2)^2\)
সমাধান –
\(4b^2c^2 – (b^2+c^2-a^2)^2\)= \( (2bc)^2 – (b^2+c^2-a^2)^2\)
= \( (2bc + b^2+c^2-a^2)(2bc – b^2 – c^2 + a^2)\)
= \( \{(b+c)^2 – a^2\}\{a^2 – (b^2 – 2bc + c^2)\}\)
= \( \{(b+c)^2 – a^2\}\{a^2 – (b-c)^2\}\)
= \( (b+c+a)(b+c-a)(a+b-c)(a-b+c)\)
(vi) \(64ax^2 – 49a(x-2y)^2\)
সমাধান –
\(64ax^2 – 49a(x-2y)^2\)= \( a[(8x)^2 – \{7(x-2y)\}^2]\)
= \( a\{8x + 7(x-2y)\}\{8x – 7(x-2y)\}\)
= \( a(8x + 7x – 14y)(8x – 7x + 14y)\)
= \( a(15x – 14y)(x + 14y)\)
(vii) \(x^2 – 9 – 4xy + 4y^2\)
সমাধান –
\(x^2 – 9 – 4xy + 4y^2\)= \( (x^2 – 4xy + 4y^2) – 9\)
= \( \{(x)^2 – 2\cdot x\cdot (2y) + (2y)^2\} – (3)^2\)
= \( (x – 2y)^2 – (3)^2\)
= \( (x – 2y + 3)(x – 2y – 3)\)
(viii) \(x^2 – 2x – y^2 + 2y\)
সমাধান –
\(x^2 – 2x – y^2 + 2y\)= \( x^2 – 2x + 1 – y^2 + 2y – 1\)
= \( (x^2 – 2x + 1) – (y^2 – 2y + 1)\)
= \( (x – 1)^2 – (y – 1)^2\)
= \( \{(x – 1) + (y – 1)\}\{(x – 1) – (y – 1)\}\)
= \( (x – 1 + y – 1)(x – 1 – y + 1)\)
= \( (x + y – 2)(x – y)\)
(ix) \(3 + 2a – a^2\)
সমাধান –
\(3 + 2a – a^2\)= \( 3 + (3 – 1)a – a^2\)
= \( 3 + 3a – a – a^2\)
= \( 3(1 + a) – a(1 + a)\)
= \( (1 + a)(3 – a)\)
(x) \(x^4 – 1\)
সমাধান –
\(x^4 – 1\)= \( (x^2)^2 – 1\)
= \( (x^2 + 1)(x^2 – 1)\)
= \( (x^2 + 1)(x + 1)(x – 1)\)
(xi) \(a^2 – b^2 – c^2 + 2bc\)
সমাধান –
\(a^2 – b^2 – c^2 + 2bc\)= \( a^2 – (b^2 – 2bc + c^2)\)
= \( a^2 – (b – c)^2\)
= \( (a + b – c)(a – b + c)\)
(xii) \(ac + bc + a + b\)
সমাধান –
\(ac + bc + a + b\)= \( c(a + b) + 1(a + b)\)
= \( (a + b)(c + 1)\)
(xiii) \(x^4 + x^2y^2 + y^4\)
সমাধান –
\(x^4 + x^2y^2 + y^4\)= \( \{(x^2)^2 + 2x^2y^2 + (y^2)^2\} – x^2y^2\)
= \( (x^2 + y^2)^2 – (xy)^2\)
= \( (x^2 + xy + y^2)(x^2 – xy + y^2)\)
12. সূত্রের সাহায্যে গুণ করি –
(i) \((xy+pq)(xy-pq)\)
সমাধান –
\((xy+pq)(xy-pq)\)= \( \{(xy)^2 – (pq)^2\}\)
= \( (x^2y^2 – p^2q^2)\)
(ii) \(49 \times 51\)
সমাধান –
\(49 \times 51\)= \( (50 – 1)(50 + 1)\)
= \( (50)^2 – (1)^2\)
= \( 2500 – 1\)
= \( 2499\)
(iii) \((2x-y+3z)(2x+y+3z)\)
সমাধান –
\((2x-y+3z)(2x+y+3z)\)= \( \{(2x+3z) – y\}\{(2x+3z) + y\}\)
= \( \{(2x+3z)^2 – (y)^2\}\)
= \( \{(2x)^2 + 2 \cdot 2x \cdot 3z + (3z)^2\} – y^2\)
= \( (4x^2 + 12xz + 9z^2 – y^2)\)
(iv) \(1511 \times 1489\)
সমাধান –
\(1511 \times 1489\)= \( (1500 + 11)(1500 – 11)\)
= \( (1500)^2 – (11)^2\)
= \( 2250000 – 121\)
= \( 2249879\)
(v) \((a-2)(a+2)(a^2+4)\)
সমাধান –
\((a-2)(a+2)(a^2+4)\)= \( (a^2 – 2^2)(a^2 + 4)\)
= \( (a^2 – 4)(a^2 + 4)\)
= \( (a^2)^2 – (4)^2\)
= \( (a^4 – 16)\)
(vi) \((a+b-c)(b+c-a)\)
সমাধান –
\((a+b-c)(b+c-a)\)= \( \{b + (a-c)\}\{b – (a-c)\}\)
= \( (b)^2 – (a-c)^2\)
= \( b^2 – (a^2 – 2ac + c^2)\)
= \( b^2 – a^2 + 2ac – c^2\)
13. (a) \(x + \frac{1}{x} = 4\) হলে দেখাই যে, \(x^2 + \frac{1}{x^2} = 14\) এবং \(x^4 + \frac{1}{x^4} = 194\)
সমাধান –
\(x + \frac{1}{x} = 4\)উভয়পক্ষকে বর্গ করে পাই,
\((x + \frac{1}{x})^2 = (4)^2\)বা, \( x^2 + 2 \cdot x \cdot \frac{1}{x} + (\frac{1}{x})^2 = 16\)
বা, \( x^2 + \frac{1}{x^2} + 2 = 16\)
বা, \( x^2 + \frac{1}{x^2} = 16 – 2\)
বা, \( x^2 + \frac{1}{x^2} = 14\) [উত্তর]
আবার, উভয়পক্ষকে বর্গ করে পাই,
\(\therefore (x^2 + \frac{1}{x^2})^2 = (14)^2\)বা, \( (x^2)^2 + 2 \cdot x^2 \cdot \frac{1}{x^2} + (\frac{1}{x^2})^2 = 196\)
বা, \( x^4 + 2 + \frac{1}{x^4} = 196\)
বা, \( x^4 + \frac{1}{x^4} = 196 – 2\)
বা, \( x^4 + \frac{1}{x^4} = 194\) [উত্তর]
13. (b) \(m + \frac{1}{m} = -5\) হলে দেখাই যে, \(m^2 + \frac{1}{m^2} = 23\)
সমাধান –
\(m + \frac{1}{m} = -5\)উভয়পক্ষকে বর্গ করে পাই,
\((m + \frac{1}{m})^2 = (-5)^2\)বা, \(m^2 + 2 \cdot m \cdot \frac{1}{m} + (\frac{1}{m})^2 = 25\)
বা, \(m^2 + 2 + \frac{1}{m^2} = 25\)
বা, \(m^2 + \frac{1}{m^2} = 25 – 2\)
বা, \(m^2 + \frac{1}{m^2} = 23\) [প্রমাণিত]
13. (c) \(p – \frac{1}{p} = m\) হলে দেখাই যে,
(i) \(p^2 + \frac{1}{p^2} = m^2 + 2\)
(ii) \((p + \frac{1}{p})^2 = m^2 + 4\)
সমাধান –
(i) \(p – \frac{1}{p} = m\)
উভয়পক্ষকে বর্গ করে পাই,
\(\therefore (p – \frac{1}{p})^2 = (m)^2\)বা, \(p^2 – 2 \cdot p \cdot \frac{1}{p} + (\frac{1}{p})^2 = m^2\)
বা, \(p^2 – 2 + \frac{1}{p^2} = m^2\)
বা, \(p^2 + \frac{1}{p^2} = m^2 + 2\) [প্রমাণিত]
(ii) \(p – \frac{1}{p} = m\)
উভয়পক্ষকে বর্গ করে পাই,
\(\therefore (p – \frac{1}{p})^2 = (m)^2\)বা, \( (p + \frac{1}{p})^2 – 4 \cdot p \cdot \frac{1}{p} = m^2\)
বা, \( (p + \frac{1}{p})^2 – 4 = m^2\)
বা, \( (p + \frac{1}{p})^2 = m^2 + 4\) [প্রমাণিত]
13. (d) \((a+b) = 5, (a-b) = 1\) হলে সূত্রের সাহায্যে দেখাই যে, \(8ab(a^2 + b^2) = 624\)
সমাধান –
\(8ab(a^2 + b^2)\)= \( 4ab \cdot 2(a^2 + b^2)\)
= \( \{(a+b)^2 – (a-b)^2\} \{(a+b)^2 + (a-b)^2\}\)
= \( \{(5)^2 – (1)^2\} \{(5)^2 + (1)^2\}\) [যেহেতু, \(a+b=5\) এবং \(a-b=1\)]
= \( (25 – 1)(25 + 1)\)
= \( 24 \times 26\)
= \( 624\) [প্রমাণিত]
13. (e) \(x – y = 3\), \(xy = 28\) হলে, \((x^2 + y^2)\) এর মান হিসাব করে লিখি।
সমাধান –
\(x – y = 3\), \(xy = 28\)
\((x^2 + y^2)\)= \( (x^2 – 2xy + y^2 + 2xy)\)
= \( (x – y)^2 + 2xy\)
= \( (3)^2 + 2(28)\) [যেহেতু, \(x – y = 3\) এবং \(xy = 28\)]
= \( 9 + 56\)
= \( 65\)
14. দুটি বর্গের সমষ্টি রূপে প্রকাশ করি –
(a) \(2(a^2+b^2)\)
সমাধান –
\(2(a^2+b^2)\)= \( (a+b)^2 + (a-b)^2\)
(b) \(50x^2+18y^2\)
সমাধান –
\(50x^2+18y^2\)= \( 2(25x^2+9y^2)\)
= \( 2\{(5x)^2 + (3y)^2\}\)
= \( (5x+3y)^2 + (5x-3y)^2\)
(c) \(a^2+b^2+c^2+d^2+2(ac-bd)\)
সমাধান –
\(a^2+b^2+c^2+d^2+2(ac-bd)\)= \( a^2+b^2+c^2+d^2+2ac-2bd\)
= \( a^2+2ac+c^2+b^2-2bd+d^2\)
= \( (a+c)^2 + (b-d)^2\)
15. (i) \(t\) এর কোন মানের জন্য \(x^2 – tx + \frac{1}{4}\) একটি পূর্ণবর্গ সংখ্যামালা হবে তা লিখি।
সমাধান –
\(x^2 – tx + \frac{1}{4}\)= \( x^2 – 2 \cdot x \cdot \frac{t}{2} + \left(\frac{t}{2}\right)^2 + \frac{1}{4} – \left(\frac{t}{2}\right)^2\)
= \( \left(x – \frac{t}{2}\right)^2 + \frac{1}{4} – \frac{t^2}{4}\)
= \( \left(x – \frac{t}{2}\right)^2 + \frac{1-t^2}{4}\)
এই সংখ্যামালাটিকে পূর্ণবর্গ হতে গেলে, \(\frac{1-t^2}{4} = 0\) হতে হবে।
\(\therefore \frac{1-t^2}{4} = 0 \implies 1-t^2 = 0 \implies t^2 = 1 \implies t = \pm 1\)\(\therefore t\) এর মান \(\pm 1\) হলে \(x^2 – tx + \frac{1}{4}\) সংখ্যামালাটি পূর্ণবর্গ হবে।
(ii) \(a^2+4\) এর সঙ্গে কত যোগ করলে তা একটি পূর্ণবর্গ সংখ্যামালা হবে লিখি।
সমাধান –
\(a^2+4 = (a)^2 + (2)^2 = (a+2)^2 – 2 \cdot a \cdot 2 = (a+2)^2 – 4a\)আবার, \(a^2+4 = (a)^2 + (2)^2 = (a-2)^2 + 2 \cdot a \cdot 2 = (a-2)^2 + 4a\)
\(\therefore a^2+4\) এর সঙ্গে \(\pm 4a\) যোগ করলে যোগফল পূর্ণবর্গ হবে।
(iii) \(a\) ও \(b\) ধনাত্মক পূর্ণসংখ্যা এবং \(a^2-b^2 = 9 \times 11\) হলে \(a\) ও \(b\) এর মান লিখি।
সমাধান –
\(a^2-b^2 = 9 \times 11\)\(\implies a^2-b^2 = (10-1)(10+1)\)\(\implies a^2-b^2 = (10)^2 – (1)^2\)\(\therefore a = 10\) এবং \(b = 1\) [যেহেতু \(a\) এবং \(b\) উভয়ই ধনাত্মক পূর্ণসংখ্যা]
(iv) \((x+y)^2 – (x-y)^2 = 4xy\) অভেদটি কি সমীকরণ? যুক্তিসহ লিখি।
সমাধান –
\((x+y)^2 – (x-y)^2 = (x^2+2xy+y^2) – (x^2-2xy+y^2) = x^2+2xy+y^2-x^2+2xy-y^2 = 4xy\)এক্ষেত্রে \(x\) ও \(y\) এর যেকোনো মানের জন্য \((x+y)^2 – (x-y)^2 = 4xy\) সম্পর্কটি সিদ্ধ হচ্ছে। সুতরাং এটি একটি অভেদ। সমীকরণ হলে \(x\) এবং \(y\) এর বিশেষ কিছু মানের জন্য সম্পর্কটি সিদ্ধ হতো।
(v) শূন্য ছাড়া \(x\) ও \(y\) এর যেকোনো ধনাত্মক মানের জন্য \((x^2+y^2)\) এর মান সর্বদাই হবে [ধনাত্মক / ঋণাত্মক]
সমাধান –
শূন্য ছাড়া \(x\) ও \(y\) এর যেকোনো ধনাত্মক মানের জন্য \((x^2+y^2)\) এর মান সর্বদাই ধনাত্মক হবে।
যেহেতু, \(x\) ধনাত্মক \(\therefore x^2\) ধনাত্মক
যেহেতু, \(y\) ধনাত্মক \(\therefore y^2\) ধনাত্মক
\(\therefore x^2+y^2\) ধনাত্মক
16. সমাধান করি
(i) \(6x = 72\)
সমাধান –
\(6x = 72\)বা, \(x = 72 / 6\)
বা, \(x = 12\)
\(\therefore\) নির্ণেয় সমাধান \(x = 12\)।
(ii) \(9x + 2 = 20\)
সমাধান –
\(9x + 2 = 20\)বা, \(9x = 20 – 2\)
বা, \(9x = 18\)
বা, \(x = 18 / 9\)
বা, \(x = 2\)
\(\therefore\) নির্ণেয় সমাধান \(x = 2\)।
(iii) \(4x – 2x + 3 = 9 – 4x\)
সমাধান –
\(4x – 2x + 3 = 9 – 4x\)বা, \(2x + 3 = 9 – 4x\)
বা, \(2x + 4x = 9 – 3\)
বা, \(6x = 6\)
বা, \(x = 6 / 6\)
বা, \(x = 1\)
\(\therefore\) নির্ণেয় সমাধান \(x = 1\)।
(iv) \(\frac{x}{4} – \frac{x}{2} = 3\frac{1}{2} – \frac{x}{3}\)
সমাধান –
\(\frac{x}{4} – \frac{x}{2} = 3\frac{1}{2} – \frac{x}{3}\)বা, \(\frac{x}{4} – \frac{x}{2} + \frac{x}{3} = 3\frac{1}{2}\)
বা, \(\frac{3x – 6x + 4x}{12} = \frac{7}{2}\)
বা, \(\frac{x}{12} = \frac{7}{2}\)
বা, \(x = \frac{7 \times 12}{2}\)
বা, \(x = 42\)
\(\therefore\) নির্ণেয় সমাধান \(x = 42\)।
(v) \(2x – 5\{7 – (x – 6) + 3x\} – 28 = 39\)
সমাধান –
\(2x – 5\{7 – (x – 6) + 3x\} – 28 = 39\)বা, \(2x – 35 + 5(x – 6) – 15x – 28 = 39\)
বা, \(2x – 35 + 5x – 30 – 15x – 28 = 39\)
বা, \(7x – 15x = 39 + 28 + 30 + 35\)
বা, \(-8x = 132\)
বা, \(x = \frac{132}{-8}\)
বা, \(x = -16\frac{1}{2}\)
\(\therefore\) নির্ণেয় সমাধান \(x = -16\frac{1}{2}\)।
(vi) \(\frac{(x-2)}{3} + \frac{(x+3)}{4} = \frac{(x+4)}{5} + 15\)
সমাধান –
\(\frac{(x-2)}{3} + \frac{(x+3)}{4} = \frac{(x+4)}{5} + 15\)বা, \(\frac{(x-2)}{3} + \frac{(x+3)}{4} – \frac{(x+4)}{5} = 15\)
বা, \(\frac{20(x-2)+15(x+3)-12(x+4)}{60} = 15\)
বা, \(\frac{20x-40+15x+45-12x-48}{60} = 15\)
বা, \(23x – 43 = 900\)
বা, \(23x = 900 + 43\)
বা, \(23x = 943\)
বা, \(x = \frac{943}{23}\)
বা, \(x = 41\)
\(\therefore\) নির্ণেয় সমাধান \(x = 41\)।
এই আর্টিকেলে অষ্টম শ্রেণির গণিতের ‘পূর্বপাঠের পুনরালোচনা’ অধ্যায়ের ‘কষে দেখি – 1.2’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরেছি। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে। কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment