পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) অষ্টম শ্রেণির গণিত পাঠ্যবইয়ের একাদশ অধ্যায় হলো ‘শতকরা’। এই পোস্টে আমরা ‘কষে দেখি –11’-এর সমস্ত প্রশ্নের সহজ ও নির্ভুল সমাধান নিয়ে আলোচনা করেছি। আশা করি, এই নোটসগুলো তোমাদের গণিত শিখতে এবং পরীক্ষার প্রস্তুতিতে দারুণভাবে সহায়তা করবে।

1. আমার কাছে 50 টাকা আছে। 50 টাকার 12% আমি স্কুলে পেন কিনতে খরচ করলাম। আমি কত টাকার পেন কিনলাম হিসাব করে লিখি।
সমাধান – 50 টাকার 12% = \(50 \times \frac{12}{100}\) টাকা = 6 টাকা
\(\therefore\) আমি 6 টাকার পেন কিনলাম।
2. বিদেশ থেকে একই মেশিনে এখানে আনতে 120% কর দিতে হয়। যদি মেশিনটির দাম বিদেশে 300000 টাকা হয় তবে কর দেওয়ার পর এখানে দাম কত হবে হিসাব করে লিখি।
সমাধান – বিদেশে মেশিনটির দাম 300000 টাকা।
300000 টাকার 120% = \(300000 \times \frac{120}{100}\) টাকা = 360000 টাকা
\(\therefore\) কর দেওয়ার পর মেশিনটির দাম হবে = \((300000 + 360000)\) টাকা = 660000 টাকা
3. হিসাব করে মান লিখি
(i) 80 টাকার 15%
সমাধান – 80 টাকার 15% = \(80 \times \frac{15}{100}\) টাকা = 12 টাকা
(ii) 215 টাকার 12%
সমাধান – 215 টাকার 12% = \(215 \times \frac{12}{100}\) টাকা = 25.8 টাকা
(iii) 37.8 মিটারের 110%
সমাধান – 37.8 মিটারের 110% = \(37.8 \times \frac{110}{100}\) মিটার = \((\frac{378}{10} \times \frac{110}{100})\) মিটার = \(\frac{4158}{100}\) মিটার = 41.58 মিটার
(iv) 480 গ্রামের 200%
সমাধান – 480 গ্রামের 200% = \(480 \times \frac{200}{100}\) গ্রাম = 960 গ্রাম
4. (i) 2.25 টাকা 5 টাকার শতকরা কত লিখি।
সমাধান –
2.25 টাকা 5 টাকার শতকরা \((\frac{2.25}{5} \times 100)\)
\(= (\frac{225}{5 \times 100} \times 100)\)\(= 45\)4. (ii) 85 গ্রাম, 17 কিলোগ্রামের শতকরা কত লিখি।
সমাধান –
17 কিলোগ্রাম = 17000 গ্রাম
\(\therefore\) 85 গ্রাম, 17 কিলোগ্রামের শতকরা \((\frac{85}{17000} \times 100) = 0.5\)
4. (iii) 2 কিগ্রা 250 গ্রাম, 0.72 কুইন্টালের শতকরা কত লিখি।
সমাধান –
2 কিগ্রা 250 গ্রাম = 2250 গ্রাম
0.72 কুইন্টাল = 72 কিলোগ্রাম = 72000 গ্রাম
\(\therefore\) 2 কিগ্রা 250 গ্রাম, 0.72 কুইন্টালের শতকরা \((\frac{2250}{72000} \times 100) = 3.125\)
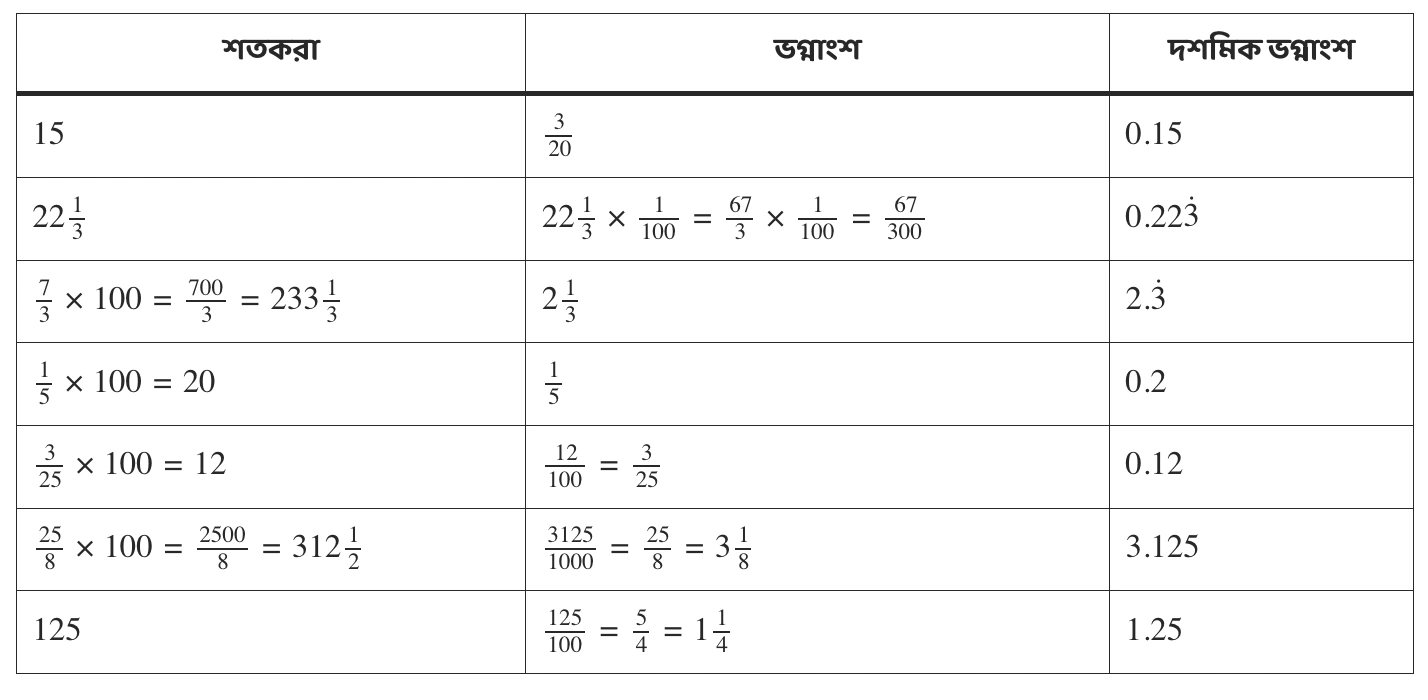
5. শূন্যস্থান পূরণ করি
6. জলে হাইড্রোজেন ও অক্সিজেন \(2:1\) অনুপাতে আছে। জলের মোট পরিমাণে হাইড্রোজেন ও অক্সিজেন শতকরা কত আছে লিখি।
সমাধান –
জলে হাইড্রোজেন ও অক্সিজেনের অনুপাত \(2:1\)।
হাইড্রোজেনের শতকরা পরিমাণ = \((\frac{2}{2+1} \times 100)\% = (\frac{2}{3} \times 100)\% = \frac{200}{3}\% = 66 \frac{2}{3}\%\)
জলে অক্সিজেনের শতকরা পরিমাণ = \((\frac{1}{2+1} \times 100)\% = (\frac{1}{3} \times 100)\% = \frac{100}{3}\% = 33 \frac{1}{3}\%\)
7. হৃদয়পুরের একটি কারখানায় আগে দৈনিক \(1500\) টি বোতল তৈরি হত। এখন তৈরি হয় \(1695\) টি বোতল। ওই কাঁচের কারখানায় উৎপাদন শতকরা কত বৃদ্ধি পেয়েছে হিসাব করে লিখি।
সমাধান –
গণিতের ভাষায় সমস্যাটি হল —
| পূর্বে বোতল তৈরির সময় | বর্তমানে বোতল তৈরির সংখ্যা |
| 1500 | 1695 |
| 100 | ? |
পূর্বে বোতল তৈরির সংখ্যা ও বর্তমানে বোতল তৈরির সংখ্যার পরস্পর সরল সম্পর্ক।
\(\therefore\) বর্তমানে বোতল তৈরির সংখ্যা পূর্বের তুলনায় শতকরা = \(\frac{100}{1500} \times 1695 = \frac{339}{3} = 113\%\)
বর্তমানে বোতল তৈরির সংখ্যা বৃদ্ধি পেয়েছে = \((113 – 100)\% = 13\%\)
\(\therefore\) ওই কারখানায় উৎপাদন \(13\%\) বৃদ্ধি পেয়েছে।
8. সাধারণ বায়ুতে নাইট্রোজেন, অক্সিজেন ও কার্বন ডাই অক্সাইডের পরিমাণ যথাক্রমে \(75.6\%\), \(23.04\%\) ও \(1.36\%\)। \(25\) লিটার বায়ুতে কোন গ্যাস কতটুকু আছে হিসাব করে লিখি।
সমাধান –
\(25\) লিটার বায়ুতে নাইট্রোজেনের পরিমাণ = \(25 \times \frac{75.6}{100}\) লিটার = \(18.9\) লিটার
\(25\) লিটার বায়ুতে অক্সিজেনের পরিমাণ = \(25 \times \frac{23.04}{100}\) লিটার = \(5.76\) লিটার
\(25\) লিটার বায়ুতে কার্বন ডাই অক্সাইডের পরিমাণ = \(25 \times \frac{1.36}{100}\) লিটার = \(0.34\) লিটার
\(\therefore\) \(25\) লিটার বায়ুতে নাইট্রোজেনের পরিমাণ \(18.9\) লিটার, অক্সিজেনের পরিমাণ \(5.76\) লিটার এবং কার্বন ডাই অক্সাইডের পরিমাণ \(0.34\) লিটার।
9. তৃষা মিলনদার বইয়ের দোকান থেকে একটি বই কিনল। মিলনদাদা বইয়ের লেখা দামের ওপর যথাক্রমে \(10\%\) ও \(5\%\) ছাড় দিলেন। বইটির ওপর লেখা দাম \(200\) টাকা হলে তৃষা মিলনদাকে কত টাকা দিল হিসাব করে লিখি।
সমাধান –
বইটির ওপর লেখা দাম \(200\) টাকা। মিলনদাদা বইটির লেখা দামের ওপর যথাক্রমে \(10\%\) ও \(5\%\) ছাড় দিলেন।
\(\therefore\) বইটির জন্য তৃষা মিলনদাদাকে দেবে = \(200 \times (1 – \frac{10}{100})(1 – \frac{5}{100})\) টাকা
= \(200 \times \frac{90}{100} \times \frac{95}{100}\) টাকা = \(171\) টাকা
\(\therefore\) তৃষা মিলনদাকে \(171\) টাকা দিল।
10. একটি বর্গক্ষেত্রের প্রতিটি বাহুর দৈর্ঘ্য \(10\%\) বাড়ালাম। ওই বর্গক্ষেত্রের ক্ষেত্রফল শতকরা কত বাড়ল হিসাব করে লিখি।
সমাধান –
ধরি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য \(100\) একক।
\(\therefore\) বর্গক্ষেত্রের ক্ষেত্রফল = \((100 \times 100)\) বর্গ একক = \(10000\) বর্গ একক।
বর্গক্ষেত্রের বাহুর দৈর্ঘ্য \(10\%\) বৃদ্ধি পেলে এখন বর্গক্ষেত্রের বাহুর দৈর্ঘ্য হয় \(110\) একক।
\(\therefore\) এখন বর্গক্ষেত্রের ক্ষেত্রফল = \((110 \times 110)\) বর্গ একক = \(12100\) বর্গ একক।
\(\therefore\) বর্গক্ষেত্রের ক্ষেত্রফল বৃদ্ধি পেল = \((12100 – 10000)\) বর্গ একক = \(2100\) বর্গ একক।
\(\therefore\) বর্গক্ষেত্রের ক্ষেত্রফল শতকরা বৃদ্ধি পেল = \((\frac{2100}{10000} \times 100)\% = 21\%\)
\(\therefore\) বর্গক্ষেত্রের ক্ষেত্রফল শতকরা বৃদ্ধি পেল \(21\%\)।
11. সময় মত বিদ্যুতের বিল জমা দিলে \(15\%\) ছাড় পাওয়া যায়। সময় মত বিল দিয়ে আমার কাকিমা \(54\) টাকা ছাড় পেলেন। বিদ্যুৎ বিলের পরিমাণ কত ছিল হিসাব করে লিখি।
সমাধান –
সময় মত বিদ্যুতের বিল জমা দিলে \(15\%\) ছাড় পাওয়া যায়। অর্থাৎ \(100\) টাকা বিদ্যুতের বিল হলে ছাড় পাওয়া যায় \(15\) টাকা।
সুতরাং, \(15\) টাকা ছাড় হয় যখন বিদ্যুতের বিল \(100\) টাকা।
\(1\) টাকা ছাড় হয় যখন বিদ্যুতের বিল \(\frac{100}{15}\) টাকা।
\(54\) টাকা ছাড় হয় যখন বিদ্যুতের বিল \(\frac{100 \times 54}{15}\) টাকা = \(360\) টাকা।
\(\therefore\) \(54\) টাকা ছাড় পেলে বিদ্যুতের বিলের পরিমাণ ছিল \(360\) টাকা।
12. চিনির মূল্য \(20\%\) বেড়ে গেছে। তাই চিনির মাসিক খরচ অপরিবর্তিত রাখতে চিনির মাসিক ব্যবহার শতকরা কত কম করতে হবে হিসাব করে লিখি।
সমাধান –
ধরি, পূর্বে \(100\) টাকায় \(100\) একক চিনি পাওয়া যেত।
চিনির মূল্য \(20\%\) বেড়ে যাওয়ায় এখন \(120\) টাকায় \(100\) একক চিনি পাওয়া যায়।
অর্থাৎ, \(120\) টাকায় পাওয়া যায় \(100\) একক চিনি
\(1\) টাকায় পাওয়া যায় \(\frac{100}{120}\) একক চিনি
\(100\) টাকায় পাওয়া যায় \(\frac{100 \times 100}{120}\) একক চিনি
\(= \frac{250}{3}\) একক চিনি
চিনির মাসিক ব্যবহার কমাতে হবে \(= (100 – \frac{250}{3})\) একক
\(= (\frac{300 – 250}{3})\) একক চিনি
\(= \frac{50}{3}\) একক চিনি
\(= 16\frac{2}{3}\) একক
\(\therefore\) চিনির মাসিক ব্যবহার \(16\frac{2}{3}\%\) কমাতে হবে।
13. জল জমে বরফ হলে আয়তন \(10\%\) বৃদ্ধি পায়। এই বরফ গলে জল হলে আয়তনে শতকরা কত হ্রাস পাবে হিসাব করে লিখি।
সমাধান –
ধরি, জলের আয়তন \(100\) ঘন একক।
জল জমে বৃদ্ধি পেলে বরফের আয়তন \(10\%\) বৃদ্ধি পায়।
সুতরাং, \(100\) ঘন একক জল জমে বরফ হলে আয়তন হবে \((100 + 10)\) ঘন একক = \(110\) ঘন একক।
\(\therefore\) \(110\) ঘন একক বরফের আয়তন হলে জলের আয়তন হয় \(100\) ঘন একক।
\(1\) ঘন একক বরফের আয়তন হলে জলের আয়তন হয় \(\frac{100}{110}\) ঘন একক।
\(100\) ঘন একক বরফের আয়তন হলে জলের আয়তন হয় \(\frac{100 \times 100}{110}\) ঘন একক।
\(= \frac{1000}{11}\) ঘন একক।
\(\therefore\) বরফ গলে জল হলে আয়তন হ্রাস পাবে \(= (100 – \frac{1000}{11})\) ঘন একক
\(= (\frac{1100 – 1000}{11})\) ঘন একক
\(= \frac{100}{11}\) ঘন একক
\(= 9\frac{1}{11}\) ঘন একক
\(\therefore\) বরফ গলে জলের আয়তন শতকরা \(9\frac{1}{11}\%\) হ্রাস পায়।
14. উৎপলবাবু অধিক ফলনশীল ধানবীজ ব্যবহার করায় ধানের ফলন \(55\%\) বৃদ্ধি পেয়েছে। কিন্তু তার জন্য চাষের খরচ \(40\%\) বেড়েছে। আগে উৎপল বাবু তার জমিতে \(1200\) টাকা খরচ করে \(3000\) টাকার ফলন পেতেন। এখন জমিতে অধিক ফলনশীল ধানবীজ ব্যবহার করায় তার আয় কত পরিমাণ বাড়বে বা কমবে হিসাব করে লিখি।
সমাধান –
উৎপলবাবু অধিক ফলনশীল ধানবীজ ব্যবহার করায় চাষের খরচ \(40\%\) বেড়েছে।
পূর্বে চাষের খরচ ছিল \(1200\) টাকা।
\(\therefore\) এখন চাষের জন্য খরচ \(= (1200 + 1200 \times \frac{40}{100})\) টাকা = \((1200+480)\) টাকা = \(1680\) টাকা
উৎপলবাবু অধিক ফলনশীল ধানবীজ ব্যবহার করায় ধানের ফলন \(55\%\) বৃদ্ধি পেয়েছে।
পূর্বে ধানের ফলন ছিল \(3000\) টাকা
\(\therefore\) এখন ধানের ফলন \(= (3000 + 3000 \times \frac{55}{100})\) টাকা = \((3000+1650)\) টাকা = \(4650\) টাকা
পূর্বে উৎপল বাবুর আয় ছিল = \((3000 -1200)\) টাকা = \(1800\) টাকা
\(\therefore\) অধিক ফলনশীল ধান ব্যবহার করায় উৎপল বাবুর আয় = \((4650 – 1680)\) টাকা = \(2970\) টাকা
15. একটি বিধানসভা কেন্দ্রের ভোটারদের \(80\%\) ভোট দিয়েছেন। এবং বিজয়ী প্রার্থী প্রদত্ত ভোটের \(65\%\) ভোট পেয়ে নির্বাচিত হয়েছেন। তিনি মোট ভোটের শতকরা কত ভোট পেয়েছেন হিসাব করে লিখি।
সমাধান –
ধরি, মোট ভোটার \(100\) জন।
\(\therefore\) ভোট দিয়েছেন = \(80\) জন
বিজয়ী প্রার্থী প্রদত্ত ভোটের \(65\%\) পেয়েছেন
\(\therefore\) বিজয়ী প্রার্থী ভোট পেয়েছেন = \(( 80 \times \frac{65}{100} )\) জন = \(52\) জন
\(\therefore\) তিনি \(100\) জন ভোটারদের মধ্যে \(52\) জনের ভোট পেয়েছেন
\(\therefore\) তিনি \(52\%\) ভোট পেয়েছেন।
16. এই বছর নন্দলাল উচ্চমাধ্যমিক বিদ্যালয়ের পরীক্ষার্থীদের \(85\%\) বাংলায়, \(70\%\) অঙ্কে এবং \(65\%\) উভয় বিষয়ে A+ পেয়েছে। পরীক্ষার্থীদের সংখ্যা যদি \(120\) জন হয়, তবে হিসাব করে দেখি কতজন পরীক্ষার্থী—
(i) উভয় বিষয়ে A+ পেয়েছে
(ii) শুধু বাংলায় A+ পেয়েছে
(iii) শুধু অঙ্কে A+ পেয়েছে
(iv) উভয় বিষয়ে A+ পায়নি
সমাধান –
(i) উভয় বিষয়ে A+ পেয়েছে
মোট পরীক্ষার্থী \(120\) জন
উভয় বিষয়ে A+ পেয়েছে মোট পরীক্ষার্থীর \(65\%\)
\(\therefore\) উভয় বিষয়ে A+ পেয়েছে = \((120 \times \frac{65}{100})\) জন = \(78\) জন
(ii) শুধু বাংলায় A+ পেয়েছে
মোট পরীক্ষার্থী \(120\) জন।
শুধু বাংলায় A+ পেয়েছে = \((85 – 65)\% = 20\%\)
\(\therefore\) শুধু বাংলায় A+ পেয়েছে = \((120 \times \frac{20}{100})\) জন = \(24\) জন।
(iii) শুধু অঙ্কে A+ পেয়েছে
মোট পরীক্ষার্থী \(120\) জন।
শুধু অঙ্কে A+ পেয়েছে = \((70 – 65)\% = 5\%\)
\(\therefore\) শুধু অঙ্কে A+ পেয়েছে = \((120 \times \frac{5}{100})\) জন = \(6\) জন
(iv) উভয় বিষয়ে A+ পায়নি
মোট পরীক্ষার্থী \(120\) জন।
উভয় বিষয়ে A+ পায়নি এমন পরীক্ষার্থী সংখ্যা = \((100 – 65 – 20 – 5)\% = 10\%\)
\(\therefore\) উভয় বিষয়ে A+ পায়নি = \((120 \times \frac{10}{100})\) জন = \(12\) জন
17. আমিনা বিবির বেতন প্রথমে \(20\%\) বৃদ্ধি পেয়ে পরে \(20\%\) হ্রাস পেল। আমিনা বিবির বেতন শতকরা কত পরিবর্তন হলো হিসাব করে লিখি।
সমাধান –
ধরি, আমিনা বিবির বেতন \(100\) টাকা।
আমিনা বিবির বেতন প্রথমে \(20\%\) বৃদ্ধি পায়।
∴ আমিনা বিবির বর্তমান বেতন = \((100+20)\) টাকা = \(120\) টাকা।
আবার আমিনা বিবির বেতন \(20\%\) হ্রাস পায়।
∴ হ্রাস পাওয়ার পর আমিনা বিবির বেতন = \((120-120\times\frac{20}{100})\) টাকা = \((120-24)\) টাকা = \(96\) টাকা।
∴ আমিনা বিবির বেতন শতকরা হ্রাস পেল \((100-96)\%=4\%\)।
18. একটি আয়তক্ষেত্রের দৈর্ঘ্য \(15\%\) বৃদ্ধি করা হল এবং প্রস্থ \(15\%\) হ্রাস করা হল। আয়তক্ষেত্রের ক্ষেত্রফল শতকরা কত বৃদ্ধি বা হ্রাস পেল হিসাব করে লিখি।
সমাধান –
ধরি, আয়তক্ষেত্রের দৈর্ঘ্য \(x\) একক এবং আয়তক্ষেত্রের প্রস্থ \(y\) একক।
সুতরাং, আয়তক্ষেত্রের ক্ষেত্রফল \(xy\) বর্গ একক।
এখন, আয়তক্ষেত্রের দৈর্ঘ্য \(15\%\) বৃদ্ধি করা হলে, পরিবর্তিত দৈর্ঘ্য =
\(\left(x + \frac{15}{100} \times x\right)\) একক \(= \left(x + \frac{15x}{100}\right)\) একক \(= \frac{115x}{100}\) একক
আবার, আয়তক্ষেত্রের প্রস্থ \(15\%\) হ্রাস করা হলে, পরিবর্তিত প্রস্থ =
\(\left(y – \frac{15}{100} \times y\right)\) একক \(= \left(y – \frac{15y}{100}\right)\) একক \(= \frac{85y}{100}\) একক
\(\therefore\) নতুন আয়তক্ষেত্রের ক্ষেত্রফল = \(\left(\frac{115x}{100} \times \frac{85y}{100}\right)\) বর্গ একক = \(\left(\frac{23x}{20} \times \frac{17y}{20}\right)\) বর্গ একক = \(\frac{391xy}{400}\) বর্গ একক
\(\therefore\) আয়তক্ষেত্রের ক্ষেত্রফল হ্রাস পেয়েছে = \(\left(xy – \frac{391xy}{400}\right)\) বর্গ একক = \(\left(\frac{400xy-391xy}{400}\right)\) বর্গ একক = \(\frac{9xy}{400}\) বর্গ একক
\(\therefore\) আয়তক্ষেত্রের ক্ষেত্রফল শতকরা হ্রাস পেয়েছে = \(\left(\frac{\frac{9xy}{400}}{xy} \times 100\right)\% = \left(\frac{9xy}{400xy} \times 100\right)\% = 2\frac{1}{4}\%\)
\(\therefore\) আয়তক্ষেত্রের ক্ষেত্রফল শতকরা হ্রাস পেয়েছে \(2\frac{1}{4}\%\)
19. একটি ঘরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে \(15\) মিটার, \(10\) মিটার ও \(5\) মিটার। যদি দৈর্ঘ্য, প্রস্থ ও উচ্চতার প্রত্যেকটি \(10\%\) বৃদ্ধি করা হয় তবে চার দেওয়ালের ক্ষেত্রফল শতকরা কত বৃদ্ধি পাবে হিসাব করে লিখি।
সমাধান –
একটি ঘরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে \(15\) মিটার, \(10\) মিটার ও \(5\) মিটার।
\(\therefore\) ঘরটির চার দেওয়ালের ক্ষেত্রফল = 2(দৈর্ঘ্য + প্রস্থ) \(\times\) উচ্চতা = \(\{2 \times (15+10)\times5\}\) বর্গমিটার = \(250\) বর্গ মিটার
দৈর্ঘ্য \(10\%\) বৃদ্ধি করলে, পরিবর্তিত দৈর্ঘ্য = \(\left(15 + \frac{10}{100} \times 15\right)\) মিটার = \((15 + 1.5)\) মিটার = \(16.5\) মিটার
প্রস্থ \(10\%\) বৃদ্ধি করলে, পরিবর্তিত প্রস্থ = \(\left(10 + \frac{10}{100} \times 10\right)\) মিটার = \((10+1)\) মিটার = \(11\) মিটার।
উচ্চতা \(10\%\) বৃদ্ধি করলে, পরিবর্তিত উচ্চতা = \(\left(5 + \frac{10}{100} \times 5\right)\) মিটার = \((5 + 0.5)\) মিটার = \(5.5\) মিটার।
দৈর্ঘ্য, প্রস্থ ও উচ্চতা বৃদ্ধি পাওয়ার পরে ঘরটির চার দেওয়ালের ক্ষেত্রফল =
\(2 \times (16.5+ 11) \times 5.5\) বর্গ মিটার \(= 11 \times 27.5\) বর্গ মিটার \(= 302.5\) বর্গ মিটার
\(\therefore\) চার দেওয়ালের ক্ষেত্রফল বৃদ্ধি পেল = \((302.5 – 250)\) বর্গ মিটার = \(52.5\) বর্গ মিটার
চার দেওয়ালের ক্ষেত্রফল শতকরা বৃদ্ধি পেল = \(\left(\frac{52.5}{250} \times 100\right)\% = \left(\frac{525}{2500} \times 100\right)\% = 21\%\)
\(\therefore\) ক্ষেত্রফল শতকরা বৃদ্ধি পেল \(21\%\)।
20. বার্ষিক ক্রীড়া প্রতিযোগিতায় \(20\%\) শিক্ষার্থী \(100\) মিটার দৌড়ে, \(15\%\) শিক্ষার্থী \(200\) মিটার দৌড়ে এবং \(10\%\) শিক্ষার্থী লংজাম্প প্রতিযোগিতায় নাম দেয়। \(5\%\) শিক্ষার্থী তিনটেতেই নাম দেয়। বিদ্যালয়ে শিক্ষার্থীর সংখ্যা \(780\) জন হলে কতজন শিক্ষার্থী ওই প্রতিযোগিতায় নাম দেয় হিসাব করে লিখি। (কোনো প্রতিযোগী একসাথে দুটিতে নাম দেয়নি)
সমাধান –
তিনটি প্রতিযোগিতায় নাম দিয়েছে \(5\%\) শিক্ষার্থী
শুধু \(100\) মিটার দৌড়ে নাম দিয়েছে = \((20-5)\%\) শিক্ষার্থী = \(15\%\) শিক্ষার্থী
শুধু \(200\) মিটার দৌড়ে নাম দিয়েছে = \((15 -5)\%\) শিক্ষার্থী = \(10\%\) শিক্ষার্থী
শুধু লংজাম্প দিয়েছে = \((10-5)\%\) শিক্ষার্থী = \(5\%\) শিক্ষার্থী
\(\therefore\) প্রতিযোগিতায় নাম দেওয়া শিক্ষার্থীর মোট শতকরা = \((15+10+5+5)\% = 35\%\)
বিদ্যালয়ে শিক্ষার্থীর সংখ্যা = \(780\) জন
\(\therefore\) প্রতিযোগিতায় নাম দেওয়া শিক্ষার্থীর সংখ্যা = \(780 \times \frac{35}{100} = 273\) জন
\(\therefore\) \(273\) জন শিক্ষার্থী ওই প্রতিযোগিতায় নাম দিয়েছে।
এই আর্টিকেলে অষ্টম শ্রেণির গণিতের ‘শতকরা’ অধ্যায়ের ‘কষে দেখি – 11’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরেছি। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে। কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment