এই আর্টিকেলে আমরা মাধ্যমিক ভৌতবিজ্ঞানের একটি গুরুত্বপূর্ণ অংশ “কুলম্বের সূত্র, তড়িৎ বিভব ও তড়িৎ কোশ” নিয়ে আলোচনা করব। এই অংশটি মাধ্যমিক ভৌতবিজ্ঞান পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ। এই “কুলম্বের সূত্র, তড়িৎ বিভব ও তড়িৎ কোশ” অংশটি মাধ্যমিক ভৌতবিজ্ঞানের ষষ্ঠ অধ্যায় “চলতড়িৎ” -এর একটি গুরুত্বপূর্ণ অংশ। এই “কুলম্বের সূত্র, তড়িৎ বিভব ও তড়িৎ কোশ” থেকে গুরুত্বপূর্ণ প্রশ্ন মাধ্যমিক পরীক্ষায় এবং চাকরির পরীক্ষায় প্রায়ই দেখা যায়।

মাধ্যমিক ভৌতবিজ্ঞান – চলতড়িৎ – কুলম্বের সূত্র, তড়িৎ বিভব ও তড়িৎ কোশ
তড়িদাধান –
- তড়িদাধান হল বস্তুর এমন একটি বৈশিষ্ট্য যার কারণে সেটি অন্য তড়িৎগ্রস্ত বা নিস্তড়িৎ বস্তুকে আকর্ষণ বা বিকর্ষণ করতে পারে।
- তড়িদাধান মূলত দুই প্রকার। যথা – ধনাত্মক ও ঋণাত্মক।
- তড়িদাধান সৃষ্টি হয় মূলত ইলেকট্রন কণার আদানপ্রদানের মাধ্যমে।
- ইলেকট্রনের আধান হল \(e = -1.6 \times 10^{-19}\) কুলম্ব বা \(-4.8 \times 10^{-10}\) স্ট্যাটকুলম্ব।
- তড়িদাধানের একক হল SI -তে কুলম্ব ও CGS -এ স্ট্যাটকুলম্ব। \(1 \ C = 3 \times 10^9\) statcoulomb
- তড়িদাধানের মাত্রা হল [IT]।
- দুটি বিপরীতধর্মী আধান পরস্পরকে আকর্ষণ করে কিন্তু সমজাতীয় আধান পরস্পরকে বিকর্ষণ করে। এই আকর্ষণ বা বিকর্ষণ বল কুলম্বের সূত্রের সাহায্যে মাপা যায়।
কুলম্বের সূত্র –
দুটি তড়িদাধানকে নির্দিষ্ট দূরত্বে থাকলে তাদের মধ্যে আকর্ষণ বা বিকর্ষণ বল আধান দুটির গুণফলের সমানুপাতিক ও দূরত্বের বর্গের ব্যস্তানুপাতিক।
\(q_1\) ও \(q_2\) আধান দুটিকে r দূরত্বে রাখলে তাদের মধ্যে আকর্ষণ বল SI -তে হবে \(F = \frac{9 \times 10^9 . q_1q_2}{r^2}\) [SI পদ্ধতিতে]
বা, \(F = \frac{1}{k} \cdot \frac{q_1q_2}{r^2}\) [CGS পদ্ধতিতে]
এটি হল কুলম্বের সূত্রের গাণিতিক রূপ। এখানে k রাশিটি আধানগুলি যে মাধ্যমে রাখা থাকে তার বৈশিষ্ট্যের ওপর নির্ভর করে। বায়ুতে রাখা হলে তখন k = 1 বসাতে হয়। এই k -রাশিটির কোনো একক বা মাত্রা নেই।

তড়িৎক্ষেত্র –
কোনো তড়িদাধানের চারপাশে যে অঞ্চলে দ্বিতীয় কোনো তড়িৎগ্রস্ত বস্তুকে নিয়ে আসলে সেটি প্রথমটির জন্য বল অনুভব করে তাকে তড়িৎক্ষেত্র বলে।
- তড়িৎক্ষেত্রের মধ্যে কোনো বিন্দুতে যদি একটি একক ধনাত্মক আধানকে রাখা হয় তাহলে সেটি যে পরিমাণ বল অনুভব করে তাকে ওই বিন্দুর তড়িৎক্ষেত্র প্রাবল্য বলে।
- তড়িৎক্ষেত্র প্রাবল্য রাশিটির একক নিউটন.কুলম্ব⁻¹।
তড়িৎবিভব –
অসীম থেকে কোনো একক ধনাত্মক আধানকে তড়িৎক্ষেত্রের মধ্যে কোনো বিন্দুতে আনতে কৃতকার্য হল তড়িৎ বিভব।
- q আধানকে V বিভব পার্থক্যের মধ্যে দিয়ে নিয়ে যেতে কৃতকার্য W = q⋅V
- তড়িৎ বিভব হল স্কেলার রাশি।
- বিভবের একক হল –
- SI -তে জুল-কুলম্ব⁻¹ বা volt
- CGS -এ আর্গ-স্ট্যাটকুলম্ব⁻¹ বা statvolt
- \(1\) volt = \(\frac{1}{300}\) statvolt
- বিভবের মাত্রা হল \(ML^2T^{-3}A^{-1}\)।
- তড়িৎক্ষেত্রের মধ্যে একটি বিন্দু থেকে অন্য বিন্দুতে একক ধনাত্মক আধানকে স্থানান্তরিত করতে কৃতকার্যকে বিন্দু দুটির বিভবপ্রভেদ বলে।
- দুটি বিন্দুর মধ্যে বিভবপার্থক্য 1 volt বলতে বোঝায় যে তড়িৎক্ষেত্রের বিপরীতের একটি বিন্দু থেকে অন্য বিন্দুতে 1 C আধানকে নিয়ে যেতে কৃতকার্য হল 1 joule। 1 J = 1 C × 1 V
- ধনাত্মক তড়িৎগ্রস্ত বস্তু হল উচ্চ বিভবগ্রস্ত বস্তু এবং ঋণাত্মক তড়িৎগ্রস্ত বস্তু হল নিম্ন বিভবযুক্ত বস্তু।
তড়িৎ কোশ –
তড়িৎ কোশ হল এমন একটি ব্যবস্থা যার দুটি প্রান্তের মধ্যে রাসায়নিক বিক্রিয়ার মাধ্যমে বিভবের পার্থক্য বজায় রাখা হয়। এর একটি প্রান্ত ঋণাত্মক ও অন্য প্রান্ত ধনাত্মক হয়।
- বিভিন্ন ধরনের তড়িৎ কোশ হল প্রাথমিক কোশ (যেমন – সরল ভোল্টীয় কোশ, ড্যানিয়েল কোশ), গৌণ কোশ।
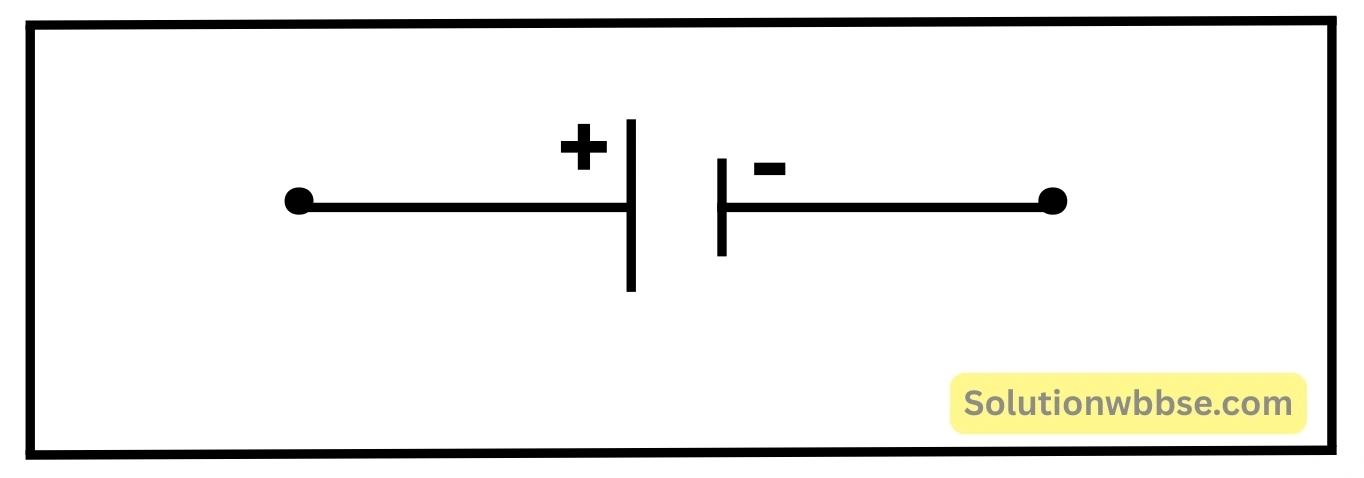
- তড়িৎ কোশের চিহ্ন হল –

- তড়িৎচালক বল – একক ধনাত্মক আধানকে কোশের ঋণাত্মক প্রান্ত থেকে ধনাত্মক প্রান্তে স্থানান্তরিত করতে যে পরিমাণ কার্য করতে হবে তাকে কোশের তড়িৎচালক বল বলা হয়। এর একক ভোল্ট।
- কোশের দুই প্রান্তে যদি মুক্ত অবস্থায় থাকে বা মুক্ত বর্তনীতে কোশের দুই প্রান্তের বিভব পার্থক্যকেও তড়িৎচালক বল বলে।
- কোশের তড়িৎচালক বল মাপা হয় পোটেনশিওমিটার যন্ত্রের সাহায্যে।
- কোনো কোশের তড়িৎচালক বল 1.5 volt বলতে বোঝায় যে কোশটির ঋণাত্মক প্রান্ত থেকে 1 C আধানকে ধনাত্মক প্রান্তে পাঠাতে কৃতকার্য হল 1.5 জুল।
তড়িৎচালক বল ও বিভবপ্রভেদের মধ্যে তুলনামূলক আলোচনা –
| তড়িৎচালক বল | বিভবপ্রভেদ |
| বৈসাদৃশ্য – রাসায়নিক শক্তি বা অন্য কোনো প্রকার শক্তি তড়িৎ শক্তিতে রূপান্তরিত হলে তড়িৎচালক বলের সৃষ্টি হয়। | বৈসাদৃশ্য – বর্তনীর কোনো অংশে তড়িৎশক্তি অন্য কোনো শক্তিতে রূপান্তরিত হলে ওই অংশে বিভবপ্রভেদ সৃষ্টি হয়েছে বলা হয়। |
| তড়িৎচালক বল হল বিভবপ্রভেদের কারণ। | বিভবপ্রভেদ হল তড়িৎচালক বলের ফল। |
| কোশের তড়িৎচালক বলের মান বিভবপ্রভেদের তুলনায় বেশি হয়। | কোশের বিভবপ্রভেদের মান তড়িৎচালক বলের তুলনায় কম হয়। |
| কোশের তড়িৎচালক বলের মান বর্তনীর রোধের ওপর নির্ভর করে না। | বর্তনীর কোনো দুটি বিন্দুর মধ্যে বিভবপ্রভেদ ওই অংশের রোধের ওপর নির্ভর করে। |
| কোশের তড়িৎচালক বল পরিমাপ করা হয় পোটেনশিওমিটার যন্ত্রের সাহায্যে। | বর্তনীর দুটি বিন্দুর বিভবপ্রভেদ পরিমাপ করা হয় ভোল্টমিটার যন্ত্রের সাহায্যে। |
| সাদৃশ্য – SI একক ভোল্ট। | সাদৃশ্য – SI একক ভোল্ট। |
এই আর্টিকেলে আমরা মাধ্যমিক ভৌতবিজ্ঞানের একটি গুরুত্বপূর্ণ অংশ “কুলম্বের সূত্র, তড়িৎ বিভব ও তড়িৎ কোশ” নিয়ে আলোচনা করেছি। এই অংশটি মাধ্যমিক ভৌতবিজ্ঞান পরীক্ষার জন্য অত্যন্ত গুরুত্বপূর্ণ। এই “কুলম্বের সূত্র, তড়িৎ বিভব ও তড়িৎ কোশ” অংশটি মাধ্যমিক ভৌতবিজ্ঞানের ষষ্ঠ অধ্যায় “চলতড়িৎ“ -এর একটি গুরুত্বপূর্ণ অংশ। এই “কুলম্বের সূত্র, তড়িৎ বিভব ও তড়িৎ কোশ” অংশটি মাধ্যমিক পরীক্ষায় এবং চাকরির পরীক্ষায় প্রায়ই দেখা যায়। আশা করি এই আর্টিকেলটি আপনাদের জন্য উপকারী হয়েছে। আপনাদের কোনো প্রশ্ন বা অসুবিধা থাকলে, আমাদের সাথে টেলিগ্রামে যোগাযোগ করুন।






Leave a Comment