মাধ্যমিক গণিত – আয়তঘন – প্রয়োগ

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের চতুর্থ অধ্যায়, ‘আয়তঘন’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

প্রয়োগ 1. আয়তঘনাকার বাক্সের দৈর্ঘ্য 40 সেমি., প্রস্থ 25 সেমি. এবং উচ্চতা 15 সেমি.। আয়তঘনাকার বাক্সের সমগ্রতলের ক্ষেত্রফল নির্ণয় করো।

আয়তঘনাকার বাক্সের সমগ্রতলের ক্ষেত্রফল = 2 × (দৈর্ঘ্য × প্রস্থ + প্রস্থ × উচ্চতা + উচ্চতা × দৈর্ঘ্য)

∴ এই আয়তঘনাকার বাক্সের সমগ্রতলের ক্ষেত্রফল = 2(40 × 25 + 40 × 15 + 25 × 15) বর্গ সেমি.

= 2(1000 + 600 + 375) বর্গ সেমি.

= 3950 বর্গ সেমি.

প্রয়োগ 2. যে আয়তঘনাকার বাক্সের দৈর্ঘ্য 15 সেমি., প্রস্থ 12 সেমি. এবং উচ্চতা 20 সেমি. তার সমগ্রতলের ক্ষেত্রফল হিসাব করে লিখি।

আয়তঘনাকার বাক্সের সমগ্রতলের ক্ষেত্রফল = 2 × (দৈর্ঘ্য × প্রস্থ + প্রস্থ × উচ্চতা + উচ্চতা × দৈর্ঘ্য)

∴ এই আয়তঘনাকার বাক্সের সমগ্রতলের ক্ষেত্রফল = 2(15 × 12 + 15 × 20 + 12 × 20) বর্গ সেমি.

= 2(180 + 300 + 240) বর্গ সেমি.

= 1440 বর্গ সেমি.

প্রয়োগ 3. রাজিয়ার আনা ঘনকের একটি বাহুর দৈর্ঘ্য 27 সেমি। ঘনকটির সমগ্রতলের ক্ষেত্রফল কত?

ঘনকের সমগ্রতলের ক্ষেত্রফলের = 6 × (বাহু)²

ওই ঘনকটির সমগ্রতলের ক্ষেত্রফল = 6 × (27)² বর্গ সেমি. = 4374 বর্গ সেমি.।

প্রয়োগ 4. যে ঘনকের একটি বাহুর দৈর্ঘ্য 12 সেমি. সেই ঘনকটির চারপাশ রঙিন কাগজ দিয়ে মুড়তে কত বর্গ সেমি. রঙিন কাগজ লাগবে হিসাব করে লিখি।

ঘনকের সমগ্রতলের ক্ষেত্রফলের = 6 × (বাহু)²

ঘনকের সমগ্রতলের ক্ষেত্রফল = 6 × (12)² বর্গ সেমি

= 6 × 144 বর্গ সেমি

= 864 বর্গ সেমি

প্রয়োগ 5. আমরা যে ঘরে বসে কাজ করছি সেই ঘরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 7মি., 5 মি. ও 4 মি.। ঘরের চার দেওয়ালের ক্ষেত্রফল হিসাব করি।

ঘরটির চার দেওয়াল রং করতে মোট কতটা ক্ষেত্রফল রং করতে হবে হিসাব করি।

ঘরের চার দেওয়াল রং করব অর্থাৎ ঘরের মেঝে ও ছাদ রং করব না।

∴ রং করতে হবে = 2 (দৈর্ঘ্য × উচ্চতা) +2(প্রস্থ × উচ্চতা)

= 2(7×4) বর্গ মিটার +2(5×4) বর্গ মিটার

=​ 56 বর্গ মিটার + 40 বর্গ মিটার

= 96 বর্গ মিটার

[ঘরের চার দেওয়ালের ক্ষেত্রফল = 2 × (দৈর্ঘ্য + প্রস্থ) × উচ্চতা = ভূমির পরিসীমা × উচ্চতা।]

প্রয়োগ 6. যদি একটি ঘনকের সমগ্রতলের ক্ষেত্রফল 150 বর্গ মিটার হয়, তবে ওই ঘনকের একটি বাহুর দৈর্ঘ্য কত হবে হিসাব করে লিখি।

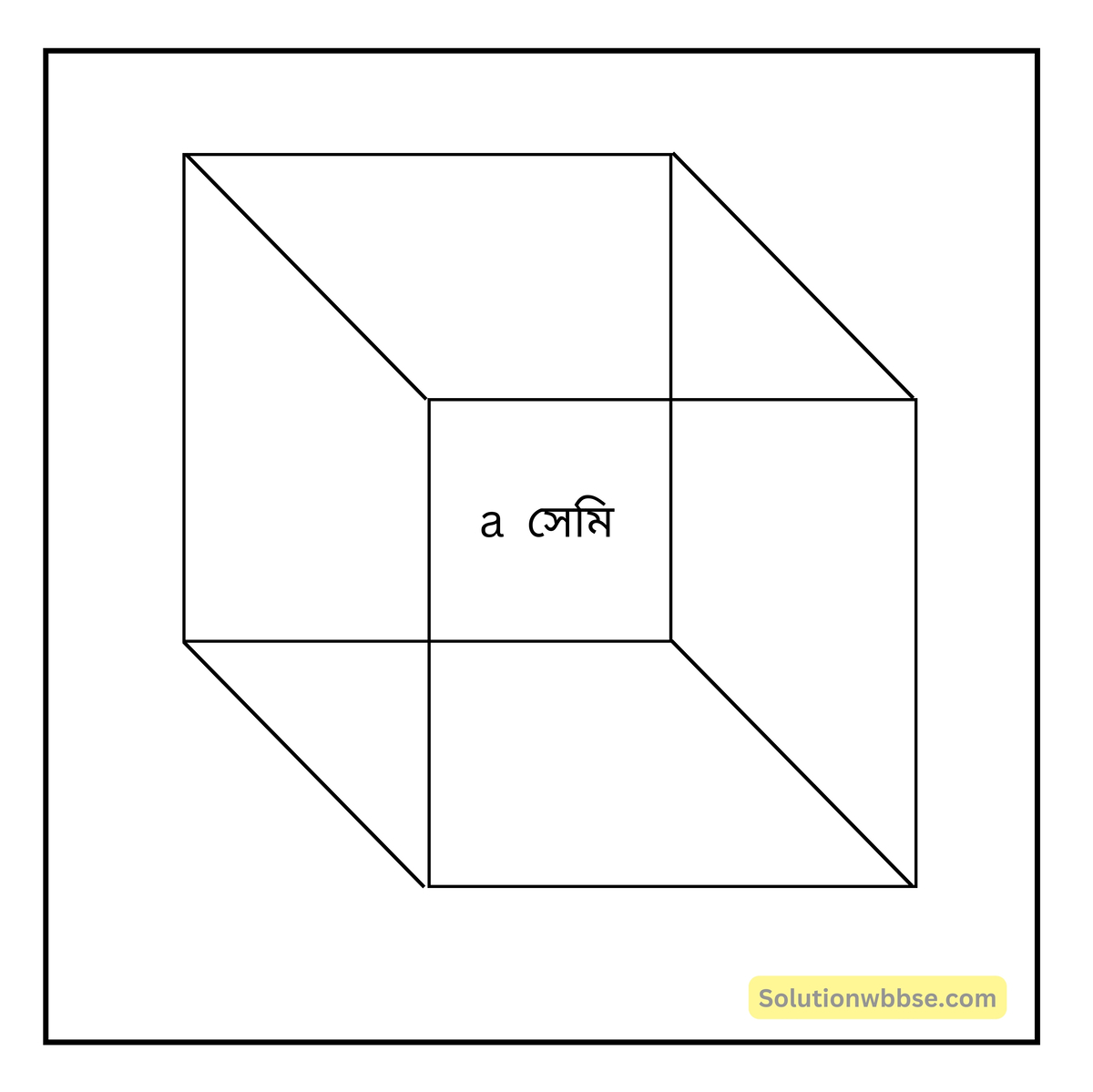
ধরি, ঘনকের একটি বাহুর দৈর্ঘ্য a সেমি.

∴ ঘনকের সমগ্রতলের ক্ষেত্রফল 6a² বর্গ সেমি. [ঘনকের সমগ্রতলের ক্ষেত্রফলের = 6 × (বাহু)²]

শর্তানুসারে, 6a² = 150

বা, \(\require{cancel}a^2=\frac{\displaystyle\overset{25}{\cancel{150}}}{\cancel6}=25\)

∴ a = ±5

কিন্তু a ≠ – 5, যেহেতু দৈর্ঘ্য সর্বদা ধনাত্মক হয়। ∴ a = 5; সুতরাং ঘনকের একটি বাহুর দৈর্ঘ্য 5 সেমি.।

প্রয়োগ 7. যদি একটি ঘনকের সমগ্রতলের ক্ষেত্রফল 486 বর্গ মিটার হয়, তবে ওই ঘনকের একটি বাহুর দৈর্ঘ্য কত হবে হিসাব করি।

ধরি ঘনকের একটি বাহুর = a দৈর্ঘ্য

ঘনকের সমগ্রতলের ক্ষেত্রফলের = 6 × (বাহু)²

প্রশ্নানুসারে, 6a² = 486

বা, \(a^2 = \frac{486}{6}\)

বা, a² = 81

বা, a = \(\sqrt{81}=9\)

∴ ঘনকের বাহুর দৈর্ঘ্য = 9 মিটার।

প্রয়োগ 8. আয়তঘনাকার বাক্সের দৈর্ঘ্য 20 সেমি., প্রস্থ 15 সেমি. এবং উচ্চতা 10 সেমি. হলে তার কর্ণের দৈর্ঘ্য কত হবে?

আয়তঘনাকার বাক্সের কর্ণের দৈর্ঘ্য = √(দৈর্ঘ্য² + প্রস্থ² + উচ্চতা²)।

কর্ণের দৈর্ঘ্য হবে = √(20² + 15² + 10²)।

 = 5√29 সেমি.।

প্রয়োগ 9. একটি আয়তঘনাকৃতি ঘরের দৈর্ঘ্য, প্রস্থ এবং উচ্চতা যথাক্রমে a, b এবং c একক এবং a + b + c = 25, ab + bc + ca = 240.5 হলে, ঘরের মধ্যে যে বৃহত্তম দৈর্ঘ্যের দণ্ডটি রাখা যাবে তার দৈর্ঘ্য কত হবে হিসাব করে লিখি।

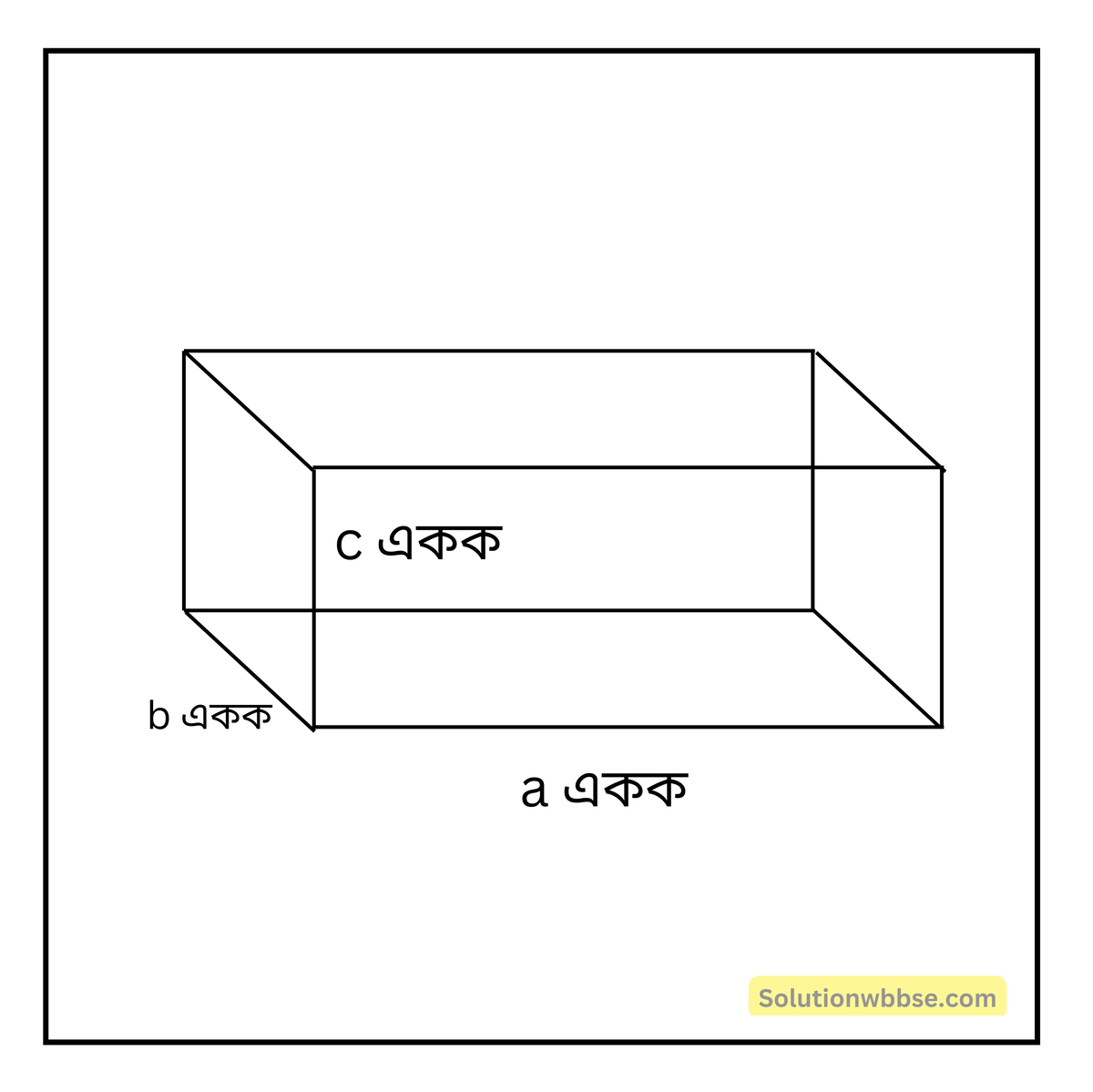
ঘরের দৈর্ঘ্য = a একক, প্রস্থ = b একক, উচ্চতা = c একক হলে, ঘরের মধ্যে যে বৃহত্তম দৈর্ঘ্যের দণ্ডটি রাখা যাবে তার দৈর্ঘ্য = ঘরটির কর্ণের দৈর্ঘ্য = \(\sqrt{a^2 + b^2 + c^2}\) একক

এখন,

\((a + b + c)^2 = a^2 + b^2 + c^2 + 2(ab + bc + ca)\)

বা, \(25^2 = a^2 + b^2 + c^2 + 2 \times 240.5\)

∴ \(a^2 + b^2 + c^2 = 625 – 481 = 144\)

∴ ঘরটির কর্ণের দৈর্ঘ্য = \(\sqrt{a^2 + b^2 + c^2}\) = \(\sqrt{144} = 12\) একক।

প্রয়োগ 10. মিতার তৈরি দুটি ঘনক, যাদের প্রত্যেকটির ধার 8 সেমি. দৈর্ঘ্যের, পাশাপাশি যুক্ত করে একটি আয়তঘন তৈরি করো। এইভাবে তৈরি আয়তঘনের সমগ্রতলের ক্ষেত্রফল ও কর্ণের দৈর্ঘ্য হিসাব করো।

উত্তর সংকেত – দুটি ঘনক পাশাপাশি যুক্ত করে তৈরি করা আয়তঘনের দৈর্ঘ্য = (8 + 8 ) সেমি. = 16 সেমি., প্রস্থ = 8 সেমি., উচ্চতা = 8 সেমি.

দুটি ঘনক পাশাপাশি যুক্ত করে তৈরি করা আয়তঘনের দৈর্ঘ্য (8 + 8) = 16 সেমি, প্রস্থ 8 সেমি ও উচ্চতা = 8 সেমি

∴ আয়তঘনের সমগ্রতলের ক্ষেত্রফল 2(16 × 8 + 8 × 16 + 8 × 8) বর্গ সেমি

= 2(128 + 128 + 64) বর্গ সেমি

= 2 × 320 = 640 বর্গ সেমি

আয়তঘনের কর্ণের দৈর্ঘ্য \(\sqrt{\left(16\right)^2+\left(8\right)^2+\left(8\right)^2}\) সেমি

= \(\sqrt{256+64+64}=\sqrt{384}=8\sqrt6\) সেমি

আয়তঘনের উচ্চতা বাড়লে আয়তন বাড়ছে।

প্রয়োগ 11. আয়তঘনাকার কৌটোর দৈর্ঘ্য 32 সেমি., প্রস্থ 21 সেমি. এবং উচ্চতা 15 সেমি.। আয়তঘনাকার কৌটোর আয়তন হিসাব করে করো।

∴ ওই টিনে বালি ধরব (দৈর্ঘ্য × প্রস্থ × উচ্চতা) ঘন সেমি.

= (32 × 2 1× 15) ঘন সেমি. 

= 10080 ঘন সেমি.

প্রয়োগ 12. প্রয়োগ : 12. যে ঘনকের একটি বাহুর দৈর্ঘ্য 5 সেমি., তার আয়তন ​5³ ঘন সেমি. =​ 125 ঘন সেমি.

প্রয়োগ 13. যদি টিনের কৌটোর প্রতিটি ধার সমান দৈর্ঘ্যের হলে ঘনকের আয়তন কীভাবে পাব হিসাব করে দেখি।

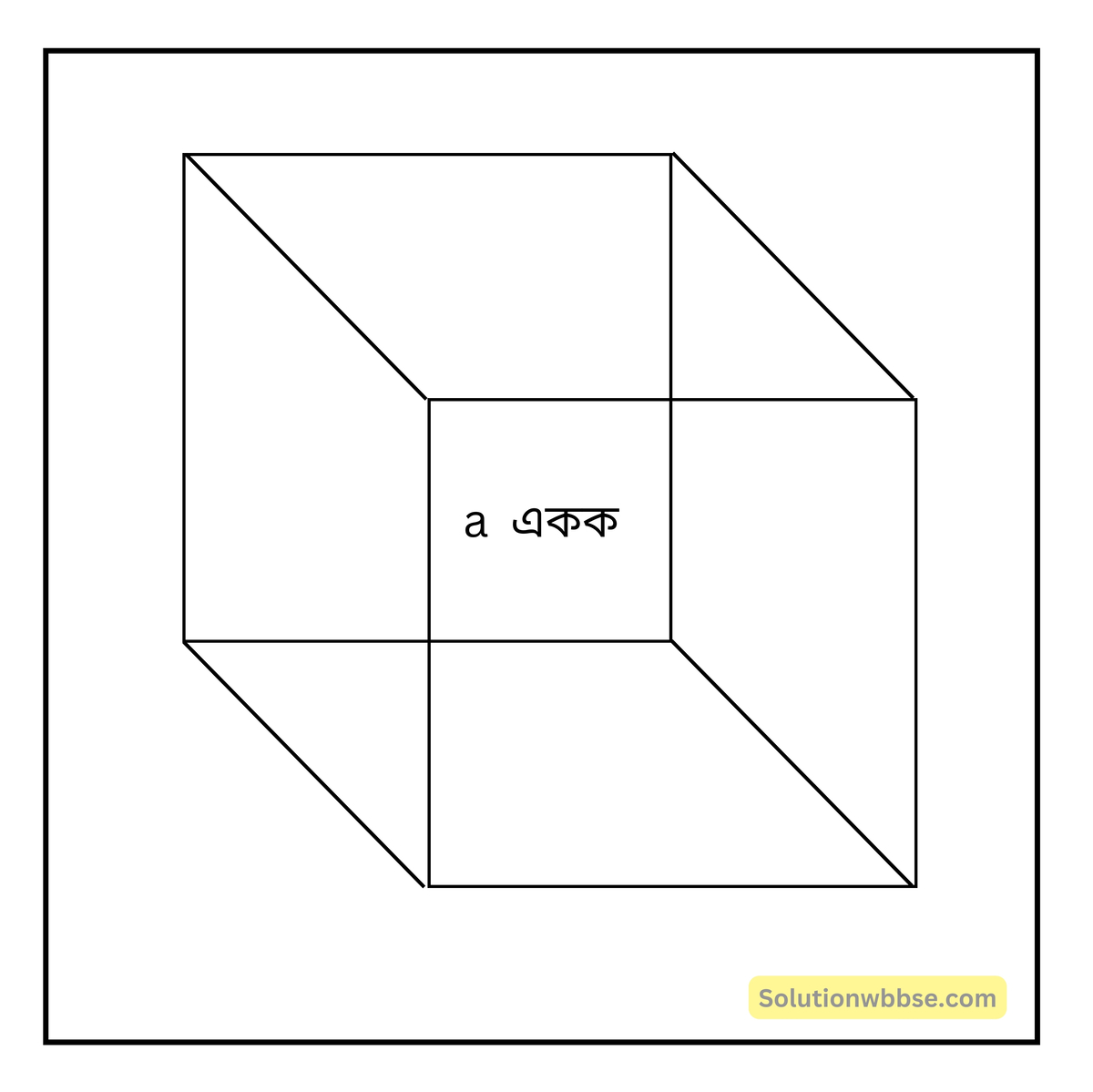
ধরি, ঘনকের একটি ধারের দৈর্ঘ্য a একক।

∴ ঘনকের আয়তন (a × a × a) ঘন একক = a³ ঘন একক।

∴ ঘনকের আয়তন = (একটি বাহুর দৈর্ঘ্য)³

প্রয়োগ 14. একটি আয়তঘনের মাত্রাগুলি যথাক্রমে 12 সেমি., 6 সেমি. ও 3 সেমি.। ওই আয়তঘনের সমান আয়তনের একটি ঘনকের প্রতিটি ধারের দৈর্ঘ্য কত হবে হিসাব করে লিখি।

আয়তঘনের আয়তন = (12 × 6 × 3) ঘন সেমি. = (6 × 2 × 6 × 3) ঘন সেমি. = 216 ঘন সেমি.

ধরি, ঘনকের একটি ধারের দৈর্ঘ্য a সেমি.।

\( ∴ a^3 = 216 \)

\( ∴ a = 6 \)

∴ ঘনকের প্রতিটি ধারের দৈর্ঘ্য 6 সেমি.

প্রয়োগ 15. যদি একটি সমকোণী চৌপল আকারের ঘরের দৈর্ঘ্য, প্রস্থ ও আয়তন যথাক্রমে 8 মি., 6 মি. এবং 192 ঘন মিটার হয়, তবে ঘরের উচ্চতা এবং চার দেয়ালের ক্ষেত্রফল হিসাব করে লিখি।

ধরি, ঘরের উচ্চতা = \(h \)মিটার

∴ ঘরের আয়তন = \((8\times6\times h)\) ঘন মি.

শর্তানুসারে, \((8\times6\times h) = 192\)

∴\( h = \frac{192}{8\times6}\) = 4

∴ ঘরের উচ্চতা 4 মিটার।

∴ ঘরের চার দেয়ালের ক্ষেত্রফল = 2 × (দৈর্ঘ্য + প্রস্থ) × উচ্চতা

= 2 × (8 + 6) × 4 = 112 বর্গমিটার।

প্রয়োগ 16. যদি কোনো ঘনকের একটি তলের ক্ষেত্রফল, অপর একটি ঘনকের একটি তলের ক্ষেত্রফলের 4 গুণ হয়, তবে প্রথম ঘনকটির ঘনফল দ্বিতীয় ঘনকটির ঘনফলের কতগুণ হবে হিসাব করে লিখি।

মনে করি, প্রথম ঘনকের একটি ধারের দৈর্ঘ্য = x একক এবং দ্বিতীয় ঘনকের একটি ধারের দৈর্ঘ্য = y একক।

∴ প্রথম ঘনকের 1 টি তলের ক্ষেত্রফল x² বর্গ একক এবং দ্বিতীয় ঘনকের 1টি তলের ক্ষেত্রফল y² বর্গ একক।

শর্তানুসারে, x² = 4y²

∴ x = 2y [∵ x ≠ – 2y]

সুতরাং, $\frac{\mathrm{প্রথম\; ঘনকের\; ঘনফল}}{\mathrm{দ্বিতীয়\; ঘনকের\; ঘনফল}}$

= \(\frac{x^3}{y^3}=\frac{\left(2y\right)^3}{y^3}=\frac{8y^3}{y^3}=8\) [∵ y ≠ 0]

∴ প্রথম ঘনকের ঘনফল = 8 × দ্বিতীয় ঘনকের ঘনফল।

সুতরাং, প্রথম ঘনকের ঘনফল দ্বিতীয় ঘনকের ঘনফলের 8 গুণ।

প্রয়োগ 17. পাশের গ্রামের একটি আয়তাকার জলাধারের জমির দৈর্ঘ্য ও প্রস্থ যথাক্রমে 18 মিটার ও 11 মিটার। সেই জলাধারে পাশের পুকুর থেকে একটি পাম্প দিয়ে জলসেচ করা হচ্ছে। পাম্পটি যদি ঘণ্টায় 39600 লিটার জলসেচ করতে পারে, তবে পাম্পটি কতক্ষণ চললে জলাধারটিতে 3.5 ডেসিমিটার উচ্চতার জল জমা হবে তা হিসাব করে লিখি। [1 লিটার = 1 ঘন ডেসিমিটার]

আয়তাকার জলাধারে 3.5 ডেসিমিটার গভীর জল জমা হলে সেই জলের আয়তন হবে (180 × 110 × 3.5) ঘন ডেসিমিটার [∵ 18 মিটার = 180 ডেসিমি., 11 মিটার = 110 ডেসিমি.]

= (180 × 110 × 3.5) লিটার [যেহেতু 1 লিটার = 1 ঘন ডেসিমি.]

পাম্পটি ঘণ্টায় 39600 লিটার জল ভর্তি করে।

∴ পাম্পটি চালাতে হবে = \(\frac{180\times110\times3.5}{39600}\) ঘণ্টা

= \(\frac74\) = 1 ঘণ্টা 45 মিনিট।

প্রয়োগ 18. যদি পাম্পটি ঘণ্টায় 37400 লিটার জলভর্তি করতে পারত, তাহলে 18 মিটার দীর্ঘ ও 11 মিটার প্রস্থবিশিষ্ট আয়তাকার জলাধারে 17 ডেসিমিটার উচ্চতার জল ভরার জন্য পাম্পটিকে কতক্ষণ চালাতে হতো হিসাব করে লিখি।

আয়তাকার জলাধারের দৈর্ঘ্য = 18 মি. =180 ডেসিমি

আয়তাকার জলাধারের প্রস্থ = 11 মি. = 110 ডেসিমি

আয়তাকার জলাধারের উচ্চতা = 17 ডেসিমি

আয়তাকার জলাধারের আয়তন = (180 × 110 × 17) ঘন ডেসিমি

= 180 × 110 × 17 লিটার

∴ [1 ঘনডেসিমি আয়তনের জল = 1 লিটার জল]

∴ পাম্পটি চালাতে হবে = \( \frac{180\times110\times3.5}{39600}\) ঘণ্টা = 9 ঘণ্টা।

প্রয়োগ 19. 4 মিটার লম্বা, 5 ডেসিমি. চওড়া এবং 3 ডেসিমি. পুরু একটি কাঠের লগ থেকে 2 মিটার লম্বা, 2 ডেসিমি. চওড়া, 40টি তক্তা চেরাই করা হলো। চেরাই-এর ফলে 2% কাঠ নষ্ট হয়েছে। কিন্তু এখনও লগটিতে 108 ঘন ডেসিমি. কাঠ রয়ে গেছে। প্রতিটি তক্তা কতটা পুরু করে চেরাই করা হয়েছিল তা হিসাব করে লিখি।

লগটিতে কাঠ ছিল = (40 × 5 × 3) ঘন ডেসিমি. = 600 ঘন ডেসিমি.

কাঠ নষ্ট হয়েছে = 600 × \(\frac2{100}\) ঘন ডেসিমি. = 12 ঘন ডেসিমি.

ধরি প্রতিটি তক্তা x ডেসিমি. পুরু।

∴ 1টি তক্তায় কাঠ আছে \(20\times2\times x\) ঘন ডেসিমি.

∴ 40টি তক্তায় কাঠ আছে \(40(20\times2\times x)\) ঘন ডেসিমি. = \(1600x\) ঘন ডেসিমি.।

চেরাই করার পরে লগটিতে কাঠ পড়ে রয়েছে 108 ঘন ডেসিমি.।

শর্তানুসারে, \(1600x+108+12=600\)

বা, \(1600x = 480\)

∴ \( x = \frac{480}{1600}\) = 0.3 ডেসিমি.।

প্রতিটি তক্তা 0.3 ডেসিমি. বা 3 সেমি. পুরু করে চেরাই করা হয়েছিল।

---

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের চতুর্থ অধ্যায়, ‘আয়তঘন’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।

আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।