মাধ্যমিক গণিত – ত্রিকোণমিতিক অনুপাতের প্রয়োগ : উচ্চতা ও দূরত্ব – কষে দেখি 25

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের পঞ্চবিংশ অধ্যায়, ‘ত্রিকোণমিতিক অনুপাতের প্রয়োগ: উচ্চতা ও দূরত্ব’ -এর ‘কষে দেখি – 25’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

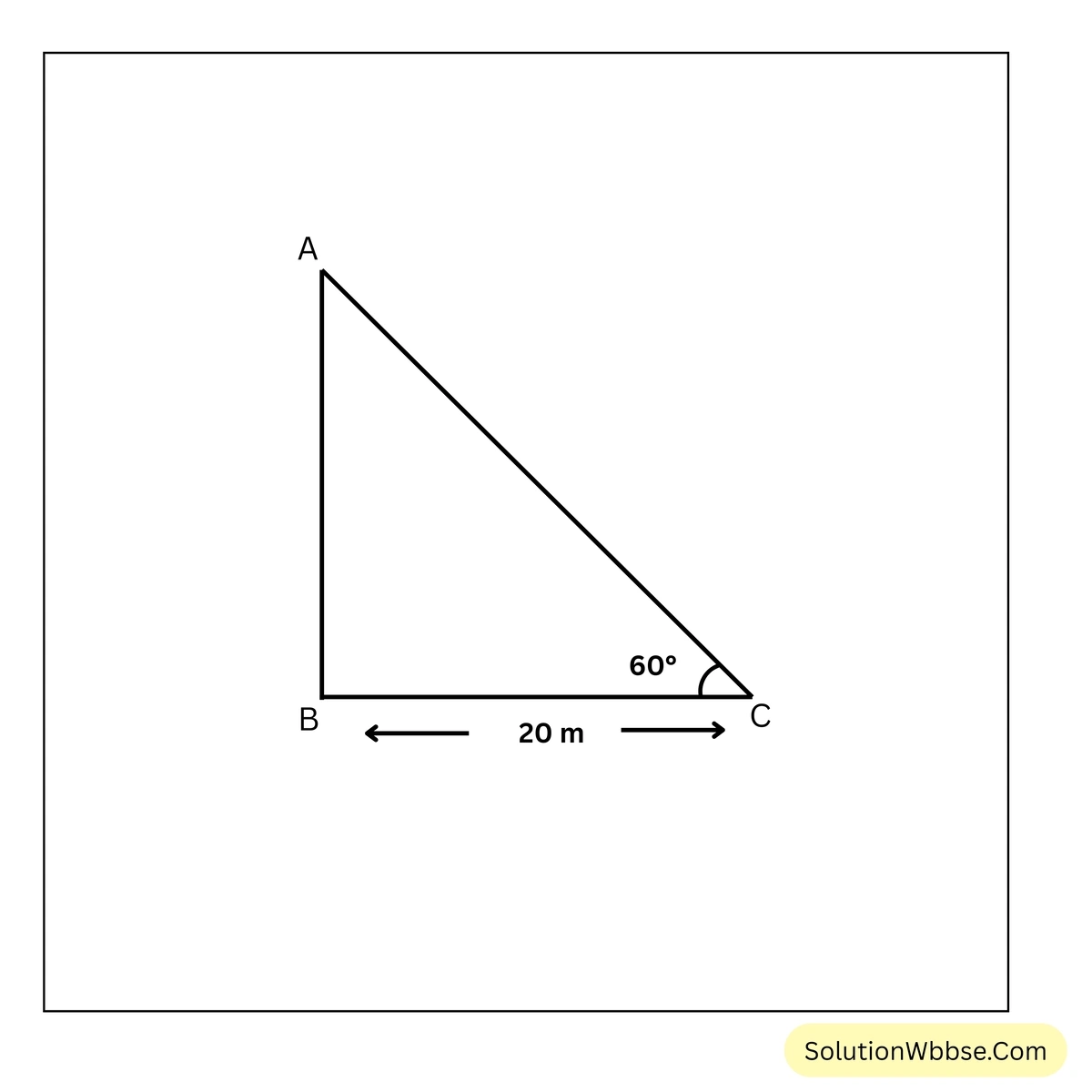
1. একটি নারকেল গাছের গোড়া থেকে অনুভূমিক তলে 20 মিটার দূরের একটি বিন্দুর সাপেক্ষে গাছটির অগ্রভাগের উন্নতি কোণ যদি \(60^\circ\) হয়, তাহলে গাছটির উচ্চতা নির্ণয় কর।

সমাধান –

ধরি, \(AB\) নারকেল গাছের গোড়া \(B\) থেকে 20 মিটার দূরে \(C\) বিন্দু থেকে গাছটির অগ্রভাগ অর্থাৎ \(A\) বিন্দুর উন্নতি কোণ \(\angle ACB = 60^\circ\)

এখন সমকোণী ত্রিভুজ \(ABC\) এর ক্ষেত্রে,

$\tan \angle \mathrm{ACB}=\tan 60°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{AB}}{20}$

বা, \(\sqrt{3} = \frac{AB}{20}\) [ যেহেতু \(\tan 60^\circ = \sqrt{3}\) ]

বা, \(AB = 20\sqrt{3}\)

∴ নারকেল গাছের উচ্চতা \(20\sqrt{3}\) মিটার।

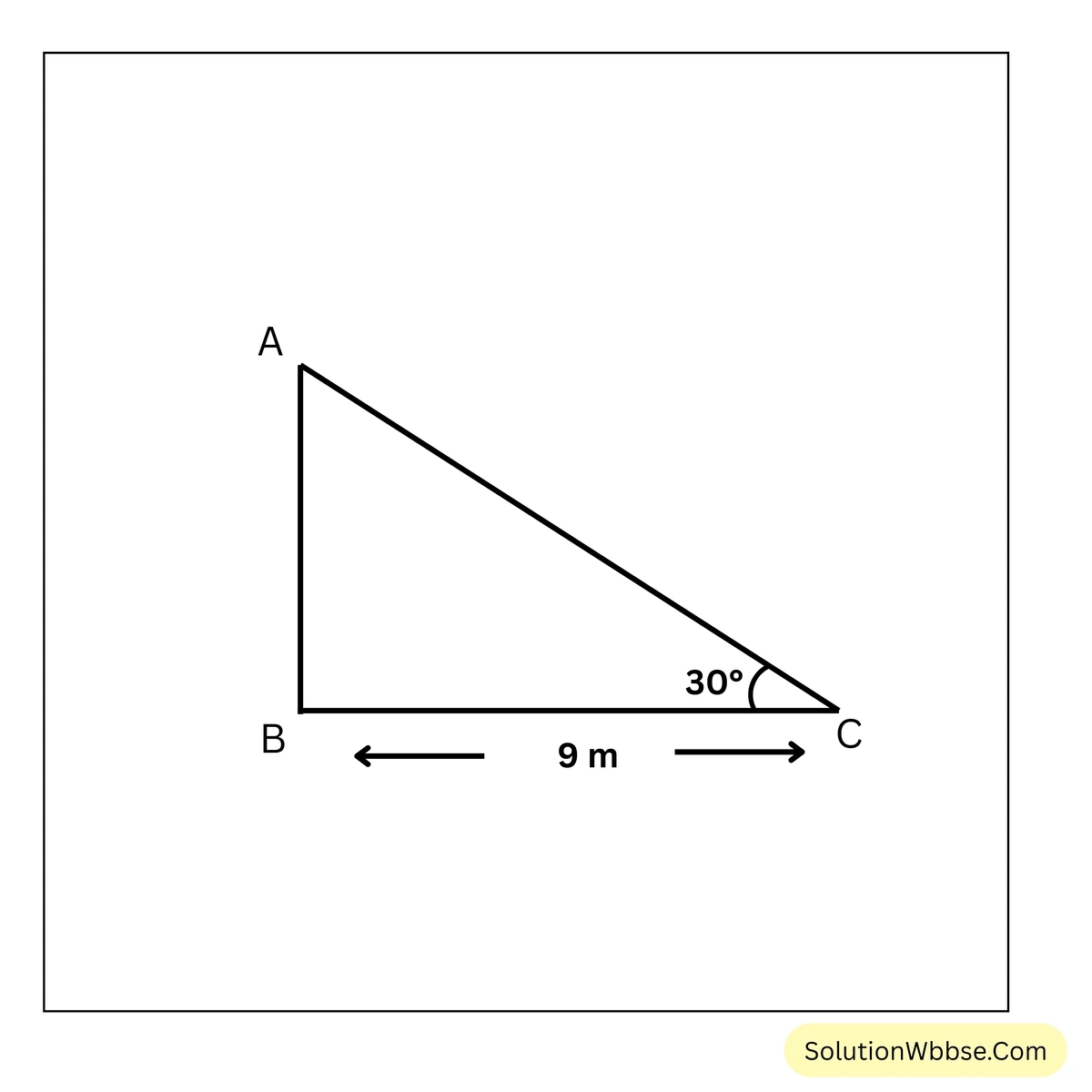
2. সূর্যের উন্নতি কোণ যখন \(30^\circ\) তখন স্তম্ভের ছায়ার দৈর্ঘ্য \(9\) মিটার হয়। স্তম্ভটির উচ্চতা হিসাব করে লিখি।

সমাধান –

ধরাযাক, \(AB\) হল স্তম্ভটির দৈর্ঘ্য। সূর্যের উন্নতি কোণ যখন \(30^\circ\) তখন স্তম্ভের ছায়ার দৈর্ঘ্য \(BC=9\) মিটার।

এখন \(ABC\) ত্রিভুজের \(\angle ABC = 90^\circ\) এবং \(\angle ACB = 30^\circ\)

∴ $\tan \angle \mathrm{ACB}=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BC}}$

বা, \(\tan 30^\circ = \frac{AB}{9}\) [যেহেতু, \(\tan 30^\circ = \frac{1}{\sqrt{3}}\) ]

বা, \(\frac{1}{\sqrt{3}} = \frac{AB}{9}\)

বা, \(AB = \frac{9}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)

বা, \(AB = \frac{9\sqrt{3}}{3}\)

বা, \(AB = 3\sqrt{3}\)

∴ স্তম্ভটির উচ্চতা \(3\sqrt{3}\) মিটার।

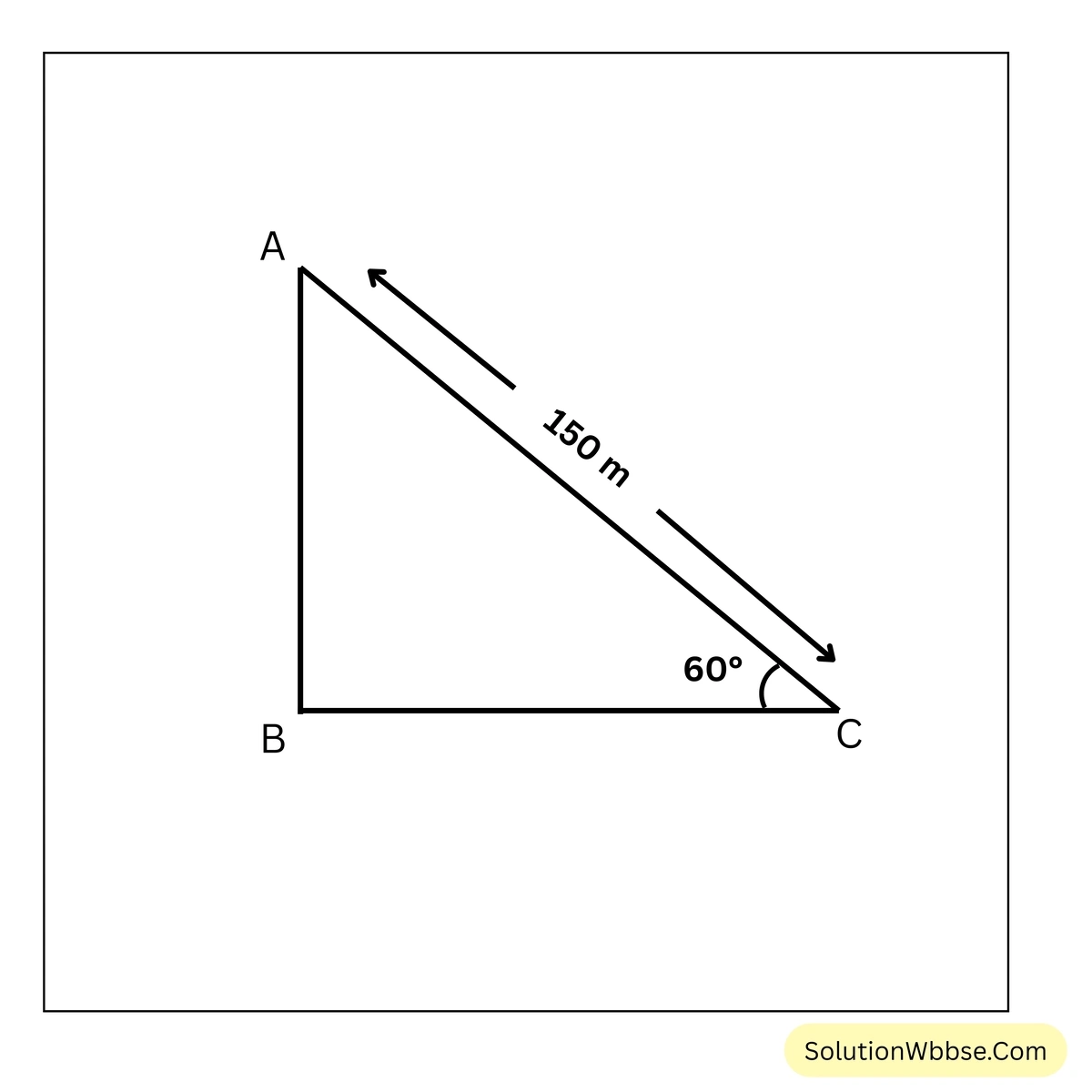
3. 150মি. লম্বা সুতো দিয়ে একটি মাঠ থেকে ঘুড়ি ওড়ানো হয়েছে। ঘুড়িটি যদি অনুভূমিক রেখার সঙ্গে 60° কোণ করে উড়তে থাকে, তাহলে ঘুড়িটি মাঠ থেকে কত উঁচুতে রয়েছে হিসাব করে লিখি।

সমাধান –

ধরাযাক, \(AB\) হল মাঠ থেকে ঘুড়িটির উচ্চতা। \(AC\) হল সুতোর দৈর্ঘ্য।

∴ \(AC=150\) মিটার। \(\angle ACB = 60^\circ\)

এখন \(ABC\) ত্রিভুজে \(\angle ABC =90^\circ\) এবং \(\angle ACB = 60^\circ\)

∴ $\sin \angle ACB=\frac{\mathrm{লম্ব}}{\mathrm{অতিভুজ}}=\frac{AB}{AC}$

বা, \( \sin 60^\circ = \frac{AB}{150} \)

বা, \( \frac{\sqrt{3}}{2} = \frac{AB}{150} \) [যেহেতু, \( \sin 60^\circ = \frac{\sqrt{3}}{2} \)]

বা, \( AB = \frac{150\sqrt{3}}{2} \)

বা, \( AB = 75\sqrt{3} \)

∴ মাঠ থেকে ঘুড়িটির উচ্চতা \( 75\sqrt{3} \) মিটার।

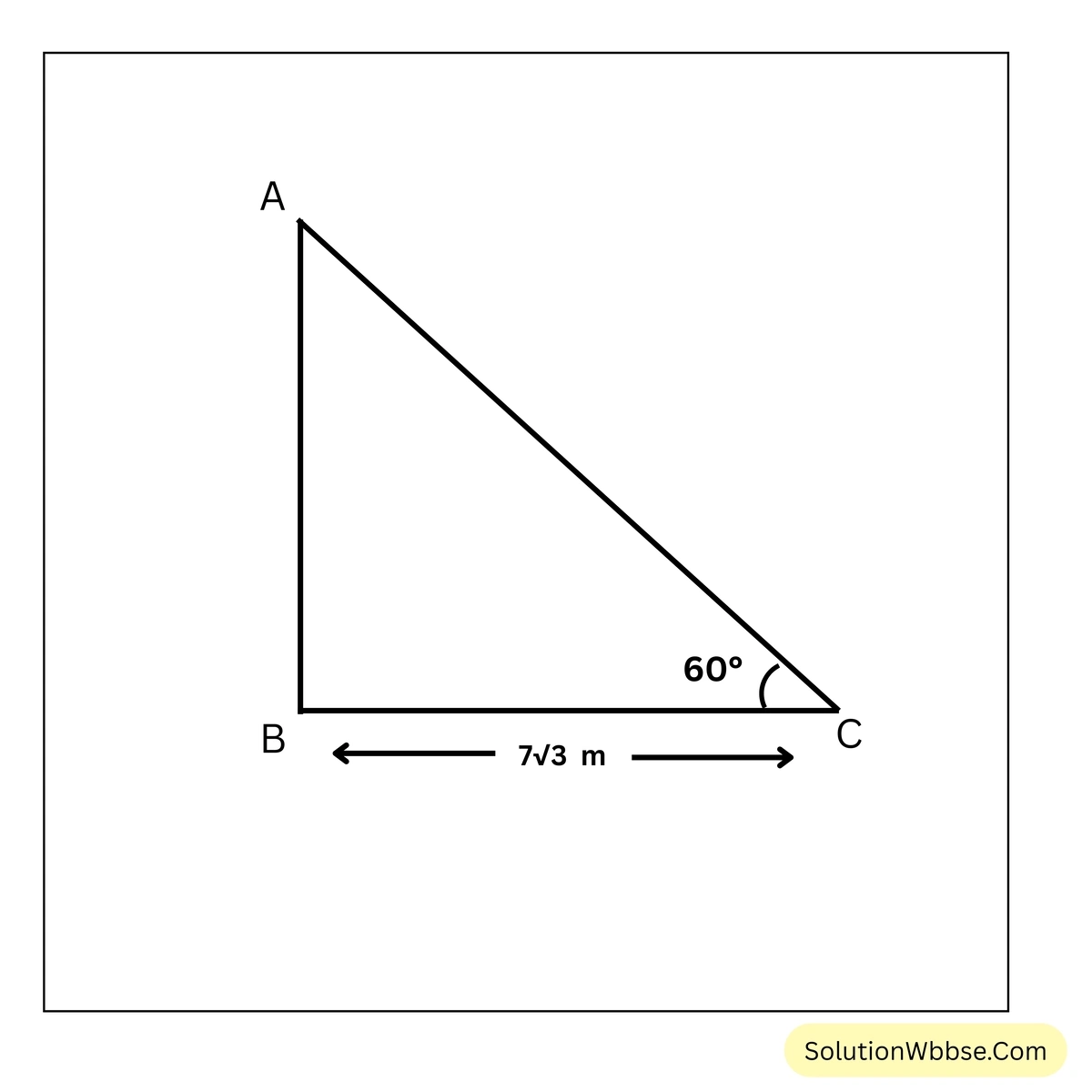
4. একটি নদীর একটি পাড়ের একটি তালগাছের সোজাসুজি অপর পাড়ে একটি খুঁটি পুঁতলাম। এবার নদীর পাড় ধরে ওই খুঁটি থেকে \(7\sqrt{3}\) মিটার সরে গিয়ে দেখছি নদীর পাড়ের পরিপ্রেক্ষিতে গাছটির পাদদেশ \(60^\circ\) কোণে রয়েছে। নদীটি কত মিটার চওড়া হিসাব করে লিখি।

সমাধান –

ধরাযাক, A বিন্দুতে গাছটির অবস্থান এবং B বিন্দুতে খুঁটি পোঁতা হয়েছে। এখন B বিন্দু থেকে \(7\sqrt{3}\) মিটার দূরে C বিন্দু থেকে গাছটির পাদদেশ অর্থাৎ A বিন্দু, \(60^\circ\) কোণে রয়েছে।

∴ \(\triangle ABC\) ত্রিভুজে \(\angle ABC = 90^\circ\) এবং \(BC = 7\sqrt{3}\) মিটার এবং \(\angle ACB=60^\circ\)

∴ $\tan \angle ACB=\tan 60°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{AB}}{7\sqrt{3}}$

বা, \(\sqrt{3} = \frac{AB}{7\sqrt{3}}\) [যেহেতু, \(\tan 60^\circ = \sqrt{3}\) ]

বা, \(AB = 7\sqrt{3} \times \sqrt{3}\)

বা, \(AB = 21\)

∴ নদীটি 21 মিটার চওড়া।

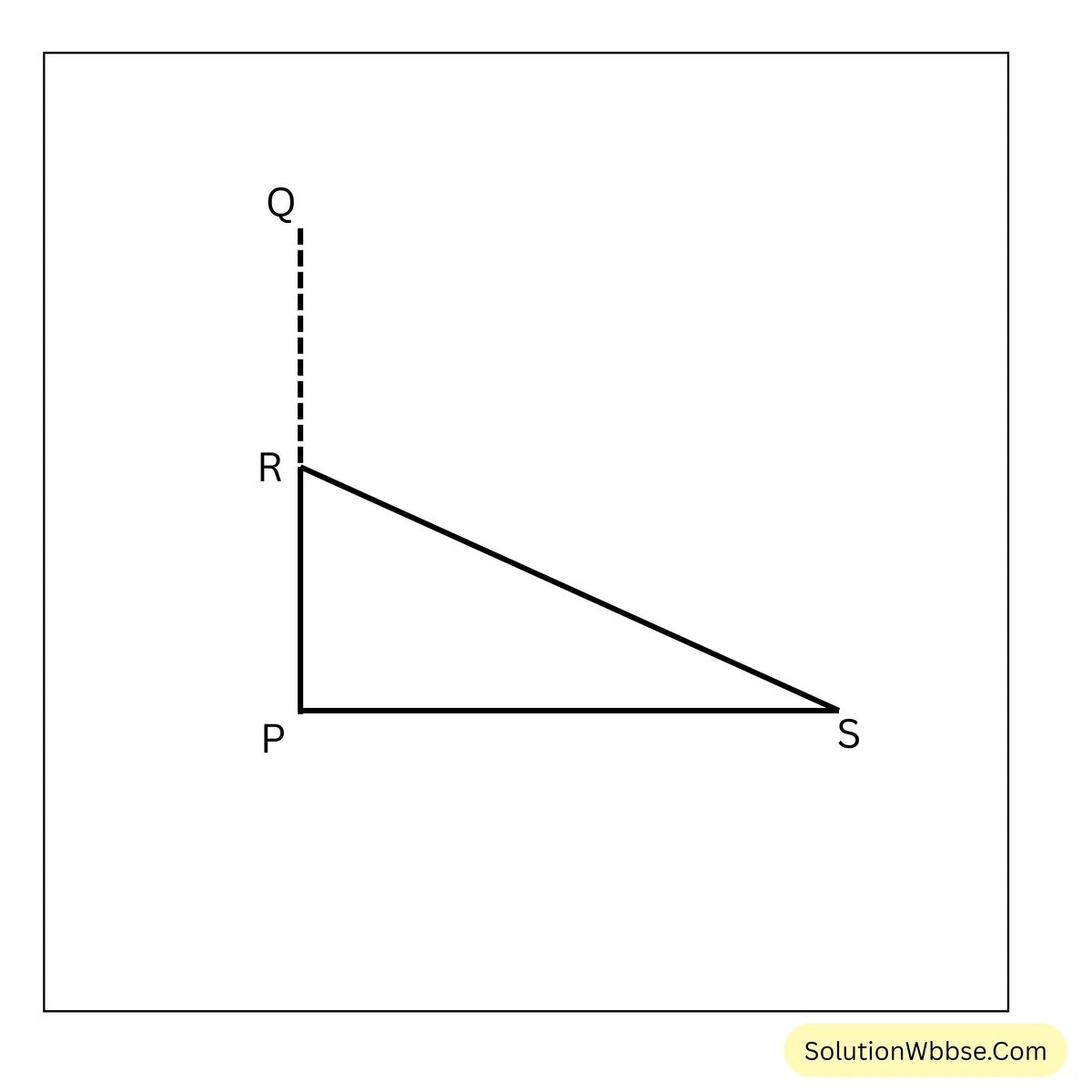
5.ঝড়ে একটি টেলিগ্রাফপোস্ট মাটি থেকে কিছু উপরে মচকে যাওয়ায় তার অগ্রভাগ গোড়া থেকে \(8\sqrt{3}\) মিটার দূরে মাটি স্পর্শ করেছে এবং অনুভূমিকরেখার সঙ্গে \(30^\circ\) কোণ উৎপন্ন করেছে। পোস্টটি মাটি থেকে কত উপরে মচকে ছিল এবং পোস্টটির উচ্চতা কত ছিল হিসাব করে লিখি।

সমাধান –

ধরাযাক, PQ টেলিগ্রাফ পোস্টটি R বিন্দুতে মচকে ছিল এবং মচকে যাওয়ার ফলে পোস্টটি \(8\sqrt{3}\) মিটার দূরে S বিন্দুতে মাটি স্পর্শ করেছে এবং অনুভূমিক রেখার সঙ্গে \(30^\circ\) কোণ উৎপন্ন করেছে।

∴ \(PS = 8\sqrt{3}\) মিটার এবং \(\angle PSR =30^\circ\)

ধরি, পোস্টটি মাটি থেকে \(x\) মিটার উপরে ভেঙ্গেছিল। ∴ \(PR = x\) মিটার

এখন, \(\triangle PSR\) ত্রিভুজে \(\angle RPS =90^\circ\) এবং \(\angle RSP =30^\circ\)

∴ $\tan 30°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{PR}}{\mathrm{PS}}$

বা, \(\frac{1}{\sqrt{3}} = \frac{PR}{PS}\)

বা, \(\frac{1}{\sqrt{3}} = \frac{x}{8\sqrt{3}}\)

বা, \(x = \frac{8\sqrt{3}}{\sqrt{3}}\)

বা, \(x = 8\)

∴ টেলিগ্রাফ পোস্টটি মাটি থেকে \(8\) মিটার উঁচুতে ভেঙ্গেছিল।

আবার ত্রিভুজ \(PRS\) এর ক্ষেত্রে

\(\sin \angle PSR = \frac{PR}{RS}\)

বা, \(\sin 30^\circ = \frac{8}{RS}\)

বা, \(\frac{1}{2} = \frac{8}{RS}\)

বা, \(RS = 16\)

যেহেতু, \(RS = RQ\)

∴ \(RQ = 16\) মিটার

∴ \(PQ = PR+RQ =(8+16)\) মিটার \(= 24\) মিটার

∴ টেলিগ্রাফ পোস্টটির উচ্চতা \(24\) মিটার।

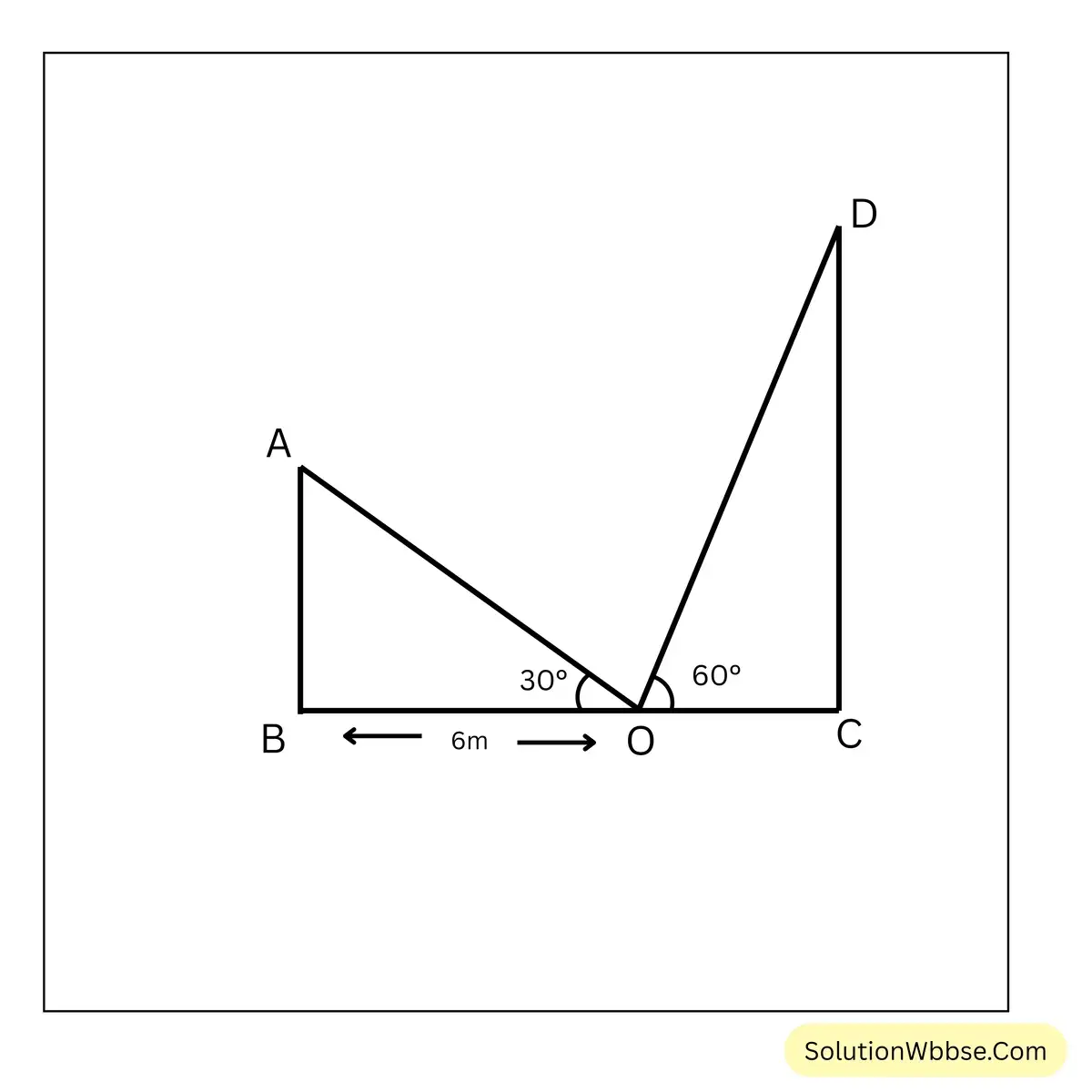
6. আমাদের পাড়ায় রাস্তার দুপাশে পরস্পর বিপরীত দিকে দুটি বাড়ি আছে। প্রথম বাড়ির দেওয়ালের গোড়া থেকে 6 মিটার দূরে একটি মইয়ের গোড়া রেখে যদি মইটিকে দেওয়ালে ঠেকানো যায়, তবে তা অনুভূমিক রেখার সঙ্গে 30° কোণ উৎপন্ন করে। কিন্তু মইটিকে যদি একই জায়গায় রেখে দ্বিতীয় বাড়ির দেওয়ালে লাগানো যায়, তাহলে অনুভূমিক রেখার সঙ্গে 60° কোণ উৎপন্ন করে।

সমাধান –

ধরাযাক, AB ও CD হল BC রাস্তার দুপাশে পরস্পর বিপরীত দিকে দুটি বাড়ি। B বিন্দু থেকে 6 মিটার দূরে O বিন্দু থেকে মইটিকে একটি বাড়ির দেওয়ালে ঠেকাল হলে তা অনুভূমিক রেখার সঙ্গে \(30^\circ\) কোণ উৎপন্ন করে।

∴ \(\angle AOB =30^\circ\).

আবার ওই একই বিন্দু O থেকে মইটিকে অপর বাড়ির দেওয়ালে ঠেকালে তা অনুভূমিক রেখার সঙ্গে \(60^\circ\) কোণ উৎপন্ন করে।

∴ \(\angle COD= 60^\circ\)

(i) ধরাযাক, মইটির দৈর্ঘ্য x মিটার। ∴ \(OA =OD=x\) মিটার

এখন, ABO ত্রিভুজে \(\angle ABO =90^\circ\) এবং \(\angle AOB =30^\circ\)

∴ $\cos \angle AOB=\cos 30°=\frac{\mathrm{ভূমি}}{\mathrm{অতিভুজ}}=\frac{\mathrm{OB}}{\mathrm{OA}}$

বা, \(\frac{\sqrt{3}}{2} = \frac{OB}{OA}\) [যেহেতু, \(\cos 30^\circ = \frac{\sqrt{3}}{2}\)]

বা, \(\frac{\sqrt{3}}{2} = \frac{6}{x}\)

বা, \(x = \frac{12}{\sqrt{3}}\)

বা, \(x = \frac{12}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)

বা, \(x = \frac{12\sqrt{3}}{3}\)

বা, \(x = 4\sqrt{3}\)

∴ মইটির দৈর্ঘ্য \(4\sqrt{3}\) মিটার।

(ii) OCD ত্রিভুজে ∠OCD=90° এবং ∠COD = 60°

∴ \(\cos \angle COD = \frac{OC}{OD}\)

বা, $\cos 60°=\frac{\mathrm{ভূমি}}{\mathrm{অতিভুজ}}=\frac{\mathrm{OC}}{4\sqrt{3}}$ [যেহেতু, OD হল মইয়ের দৈর্ঘ্য]

বা, \(\frac{1}{2} = \frac{OC}{4\sqrt{3}}\) [যেহেতু, \(\cos 60^\circ = \frac{1}{2}\)]

বা, \(OC = 2\sqrt{3}\)

∴ দ্বিতীয় বাড়ির দেওয়ালের গোড়া থেকে মইয়ের গোড়া \(2\sqrt{3}\) মিটার দূরে রয়েছে।

(iii) \(BC=OB+OC=6+2\sqrt{3} = 2(3+\sqrt{3})\)

∴ রাস্তাটি \(2(3+\sqrt{3})\) মিটার চওড়া।

(iv) ∠OCD ত্রিভুজে ∠OCD=90° এবং ∠COD = 60°

∴ $\tan \angle \mathrm{COD}=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{CD}}{\mathrm{OC}}$

বা, \(\tan 60^\circ = \frac{CD}{2\sqrt{3}}\)

বা, \(\sqrt{3} = \frac{CD}{2\sqrt{3}}\) [যেহেতু, \(\tan 60^\circ = \sqrt{3}\)]

বা, \(CD = \sqrt{3} \times 2\sqrt{3}\)

বা, \(CD=6\)

∴ দ্বিতীয় বাড়ির 6 মিটার উঁচুতে মইটির অগ্রভাগ স্পর্শ করবে।

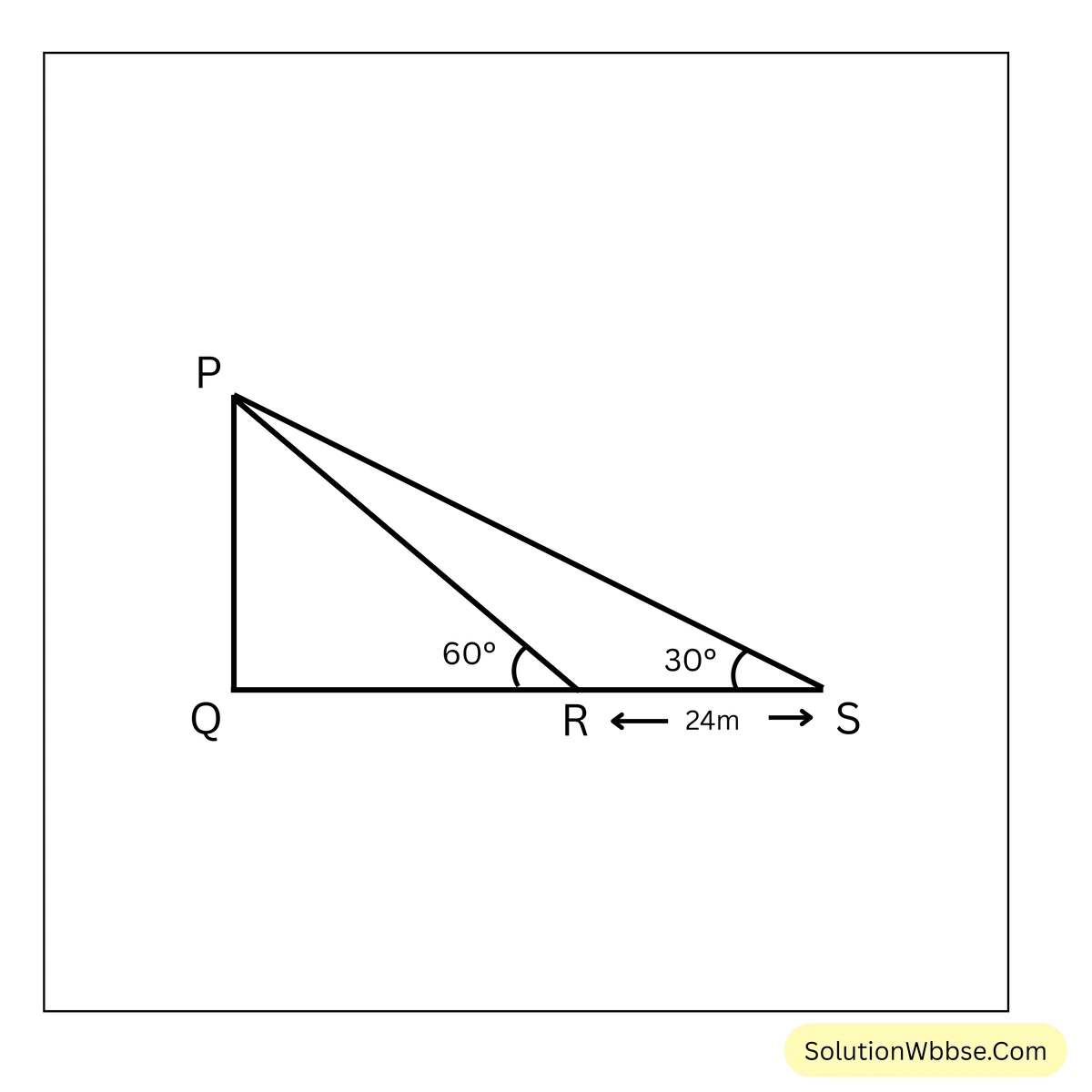
7. যদি একটি চিমনির গোড়ার সঙ্গে একই সমতলে অবস্থিত একটি বিন্দুর সাপেক্ষে চিমনির চূড়ার উন্নতি কোণ \(60^\circ\) হয় এবং সেই বিন্দু ও চিমনির গোড়ার সঙ্গে একই সরলরেখায় অবস্থিত ওই বিন্দু থেকে আরও \(24\) মিটার দুরের অপর একটি বিন্দুর সাপেক্ষে চিমনির চূড়ার উন্নতি কোণ \(30^\circ\) হয়, তাহলে চিমনির উচ্চতা হিসাব করে লিখি। [\(\sqrt{3}\)-এর আসন্ন মান \(1.732\) ধরে তিন দশমিক স্থান পর্যন্ত আসন্ন মান নির্ণয় করি।]

সমাধান –

ধরাযাক, \(PQ\) চিমনির গোড়া অর্থাৎ \(Q\) বিন্দুর সঙ্গে একই সমতলে অবস্থিত \(R\) বিন্দুর সাপেক্ষে চিমনির চূড়ার উন্নতি কোণ \(60^\circ\)

∴ \(\angle QRP = 60^\circ\)

আবার \(Q\) বিন্দুর সঙ্গে একই সমতলে অবস্থিত \(R\) বিন্দু থেকে \(24\) মিটার দূরে \(S\) বিন্দুর সাপেক্ষে চিমনির চূড়া অর্থাৎ \(P\) বিন্দুর উন্নতি কোণ \(30^\circ\)।

∴ \(\angle QSP=30^\circ\) এবং \(RS=24\) মিটার

এখন \(\triangle PQR\) ত্রিভুজে \(\angle PQR=90^\circ\) এবং \(\angle PRQ = 60^\circ\)

∴ $\tan \angle PRQ=\tan 60°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{PQ}}{\mathrm{QR}}$

বা, \(\sqrt{3} = \frac{PQ}{QR}\) [ যেহেতু, \(\tan 60^\circ = \sqrt{3}\) ]

বা, \(QR = \frac{PQ}{\sqrt{3}}\) —-(i)

আবার, \(\triangle PQS\) ত্রিভুজে \(\angle PQS=90^\circ\) এবং \(\angle PSQ=30^\circ\)

∴ $\tan \angle PSQ=\tan 30°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{PQ}}{\mathrm{QS}}=\frac{\mathrm{PQ}}{\mathrm{QR}+\mathrm{RS}}=\frac{\mathrm{PQ}}{\mathrm{RQ}+24}$

বা, \(\tan 30^\circ = \frac{PQ}{RQ+24}\)

বা, \(\frac{1}{\sqrt{3}} = \frac{PQ}{RQ+24}\) [যেহেতু, \(\tan 30^\circ = \frac{1}{\sqrt{3}}\) ]

বা, \(RQ+24 = \sqrt{3} PQ\)

বা, \(\frac{PQ}{\sqrt{3}} + 24 = \sqrt{3}PQ\) [(i) নং সমীকরন থেকে RQ এর মান বসিয়ে পাই]

বা, \(\sqrt{3} PQ – \frac{PQ}{\sqrt{3}} = 24\)

বা, \(\frac{3PQ-PQ}{\sqrt{3}} = 24\)

বা, \(\frac{2PQ}{\sqrt{3}} = 24\)

বা, \(2PQ=24\sqrt{3}\)

বা, \(PQ = \frac{24\sqrt{3}}{2}\)

বা, \(PQ = 12\sqrt{3}\)

বা, \(PQ = 12 \times 1.732\)

বা, \(PQ = 20.784\)

∴ চিমনির উচ্চতা \(20.784\) মিটার।

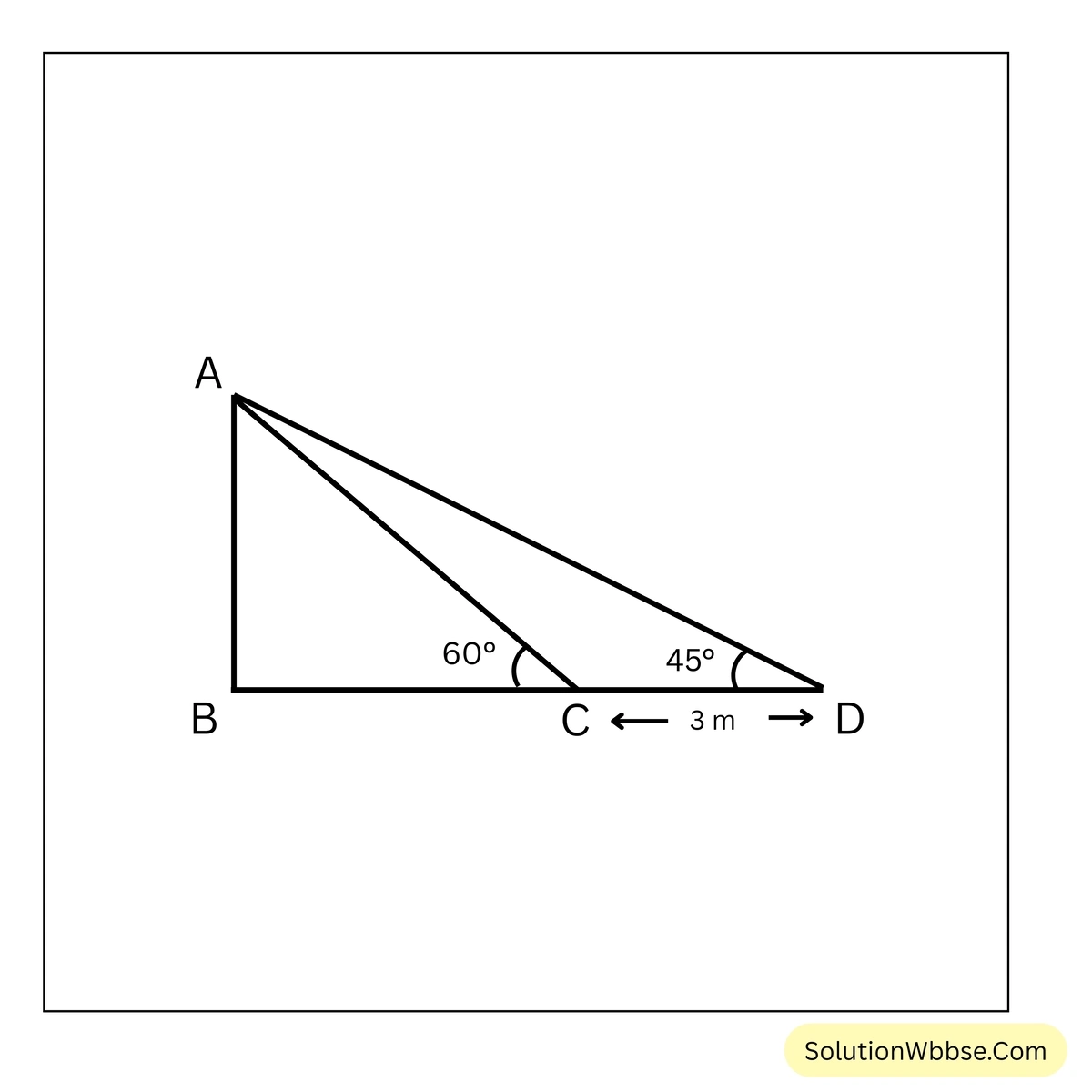
8. সূর্যের উন্নতি কোণ 45° থেকে বৃদ্ধি পেয়ে 60° হলে, একটি খুঁটির ছায়ার দৈর্ঘ্য 3 মিটার কমে যায়। খুঁটিটির উচ্চতা নির্ণয় করি। [√3-এর আসন্ন মান 1.732 ধরে তিন দশমিক স্থান পর্যন্ত আসন্ন মান নির্ণয় করি।]

সমাধান –

ধরাযাক, \(AB\) হল খুঁটির দৈর্ঘ্য। যখন সূর্যের উন্নতি কোণ \(45^\circ\) হলে খুঁটির ছায়ার দৈর্ঘ্য হয় \(BD\) এবং সূর্যের উন্নতি কোণ \(60^\circ\) হলে খুঁটির ছায়ার দৈর্ঘ্য হয় \(BC\), অর্থাৎ খুঁটির ছায়ার দৈর্ঘ্য \(CD\) একক কমে যায়।

∴ \(CD = 3\) মিটার

\(\triangle ABC\) ত্রিভুজে, \(\angle ABC=90^\circ\) এবং \(\angle ACB =60^\circ\)
এখন \(\triangle ABC\) সমকোণী ত্রিভুজ থেকে পাই,

∴ $\tan \angle ACB=\tan 60°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BC}}$

বা, \(\sqrt{3} = \frac{AB}{BC}\) [ যেহেতু, \(\tan 60^\circ = \sqrt{3}\) ]

বা, \(BC = \frac{AB}{\sqrt{3}}\) —-(i)

আবার \(\triangle ABD\) ত্রিভুজে, \(\angle ABD=90^\circ\) এবং \(\angle ADB =45^\circ\)

\(\triangle ABD\) সমকোণী ত্রিভুজ থেকে পাই,

∴ $\tan \angle ADB=\tan 45°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BD}}$

বা, \(1 = \frac{AB}{BD}\) [ যেহেতু, \(\tan 45^\circ = 1\) ]

বা, \(AB = BD\)

বা, \(AB = BC+CD\)

বা, \(AB = \frac{AB}{\sqrt{3}} + 3\) [ যেহেতু, \(BC = \frac{AB}{\sqrt{3}}\) এবং \(CD=3\) মিটার ]

বা, \(AB\sqrt{3} = AB+3\sqrt{3}\)

বা, \(AB\sqrt{3} – AB=3\sqrt{3}\)

বা, \(AB(\sqrt{3}-1) = 3\sqrt{3}\)

বা, \(AB = \frac{3\sqrt{3}}{(\sqrt{3}-1)}\)

বা, \(AB = \frac{3\sqrt{3}}{(\sqrt{3}-1)} \times \frac{(\sqrt{3}+1)}{(\sqrt{3}+1)}\)

বা, \(AB = \frac{3\sqrt{3}(\sqrt{3}+1)}{(\sqrt{3})^2-1}\)

বা, \(AB = \frac{9+3\sqrt{3}}{3-1}\)

বা, \(AB = \frac{9+3(1.732)}{2}\)

বা, \(AB = \frac{14.196}{2}\)

বা, \(AB = 7.098\)

∴ খুঁটির উচ্চতা \(7.098\) মিটার।

9. \(9\sqrt{3}\) মিটার উঁচু তিনতলা বাড়ির ছাদ থেকে দেখলে 30মিটার দূরে অবস্থিত একটি কারখানার চিমনির উন্নতি কোণ \(30^\circ\) হয়। চিমনির উচ্চতা হিসাব করে লিখি।

সমাধান –

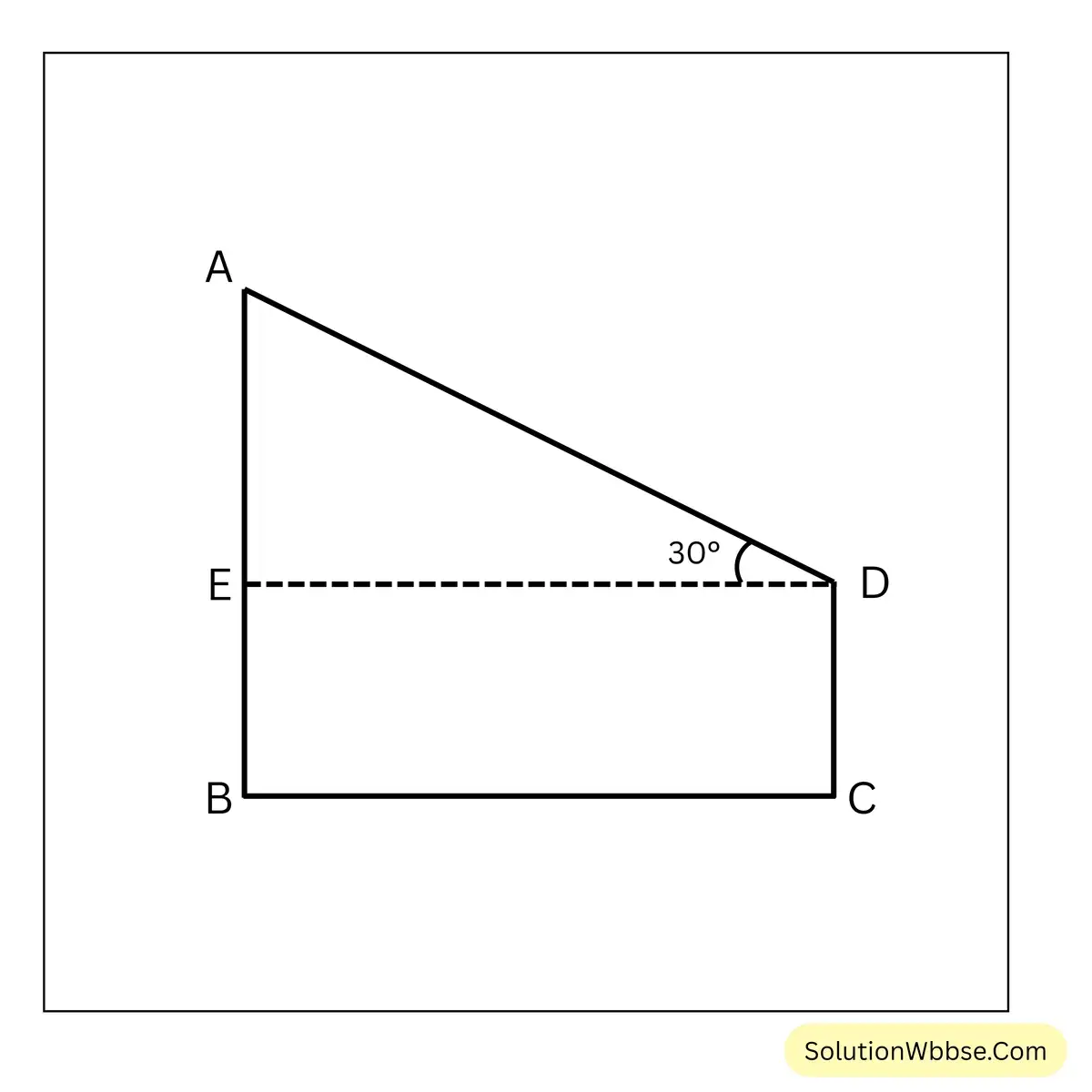
ধরাযাক, চিমনির উচ্চতা \(AB\) এবং তিনতলা বাড়ির উচ্চতা \(CD\)। তিনতলা বাড়ির ছাদ অর্থাৎ D বিন্দু থেকে চিমনির চূড়া অর্থাৎ A বিন্দুর উন্নতি কোণ \(30^\circ\)। তিনতলা বাড়ির উচ্চতা \(9\sqrt{3}\) মিটার

∴ \(CD =9\sqrt{3}\) মিটার

চিমনি ও তিনতলা বাড়ির দুরত্ব 30মিটার

∴ \(BC = 30\) মিটার।

এখন \(DE \perp AB\) অঙ্কন করা হল।

∴ \(\angle ADE=30^\circ\) এবং \(CD= BE=9\sqrt{3}\) মিটার এবং \(BC=ED=30\) মিটার

এখন, AED সমকোণী ত্রিভুজ থেকে পাই,

$\tan \angle \mathrm{ADE}=\tan 30°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AE}}{\mathrm{ED}}$

বা, \(\frac{1}{\sqrt{3}} = \frac{AE}{30}\) [ যেহেতু, \(\tan 30^\circ =1/\sqrt{3}\) ]

বা, \(AE = \frac{30}{\sqrt{3}}\)

বা, \(AE = \frac{30}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)

বা, \(AE = \frac{30\sqrt{3}}{3}\)

বা, \(AE = 10\sqrt{3}\)

∴ চিমনির উচ্চতা \(AB =AE+EB = (10\sqrt{3}+9\sqrt{3})\) মিটার \(= 19\sqrt{3}\) মিটার।

10. একটি লাইট হাউস থেকে তার সঙ্গে একই সরলরেখায় অবস্থিত দুটি জাহাজের মাস্তুলের গোড়ার অবনতি কোণ যথাক্রমে \(60^\circ\) ও \(30^\circ\) হয় এবং কাছের জাহাজের মাস্তুল যদি লাইট হাউস থেকে 150 মিটার দূরত্বে থাকে, তাহলে দুরের জাহাজের মাস্তুল লাইট হাউস থেকে কত দূরত্বে রয়েছে এবং লাইট হাউসটির উচ্চতা হিসাব করে লিখি।

সমাধান –

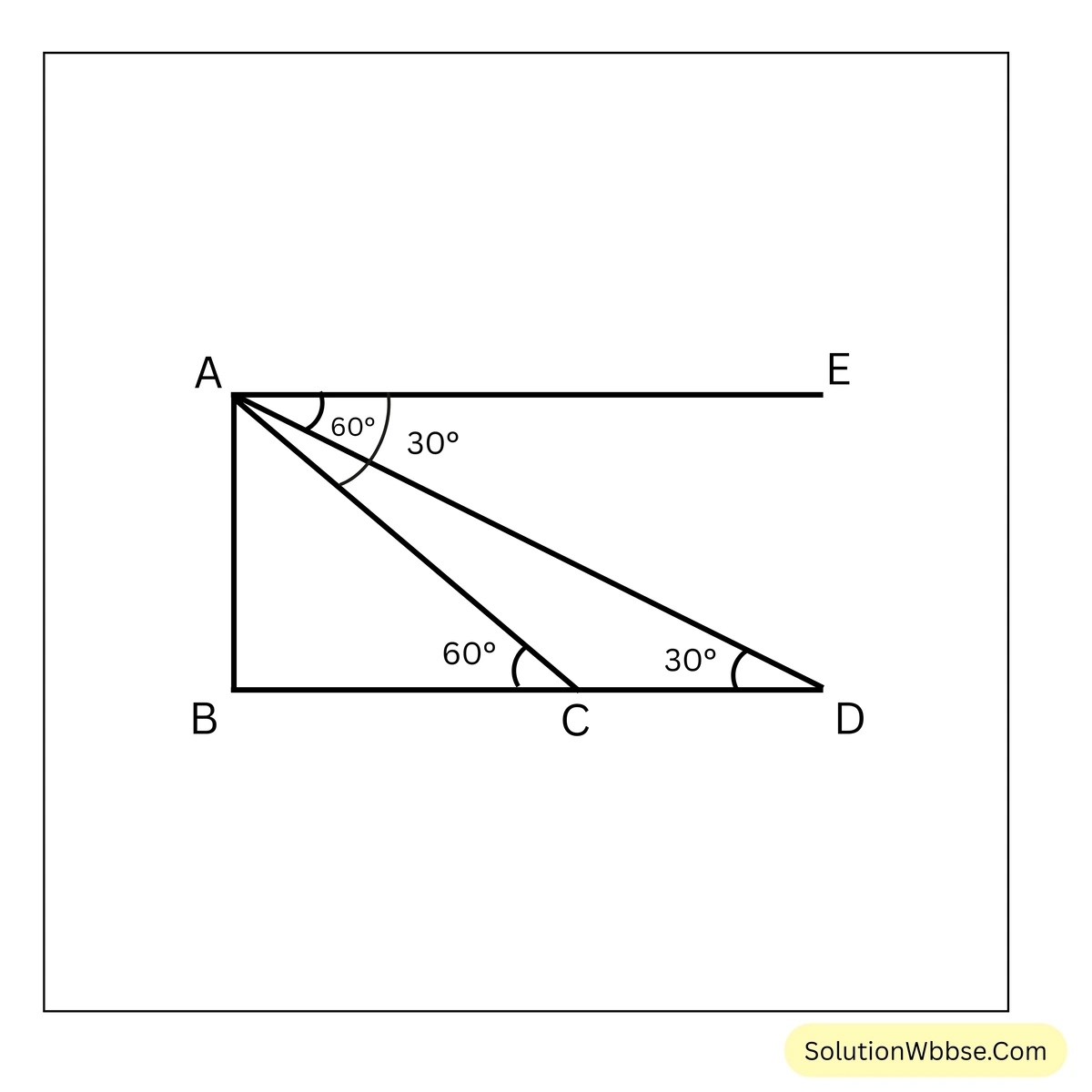
ধরাযাক, \(AB\) হল লাইট হাউসের উচ্চতা। \(A\) বিন্দু থেকে \(C\) বিন্দুতে এবং \(D\) বিন্দুতে অবস্থিত জাহাজের মাস্তুলের অবনতি কোণ যথাক্রমে \(60^\circ\) ও \(30^\circ\)। আবার লাইট হাউস থেকে কাছের জাহাজের দুরত্ব 150 মিটার।

∴ \(BC =150\) মিটার।

\(AE \parallel BD\) অঙ্কন করা হল

∴ \(\angle EAC = 60^\circ\) এবং \(\angle EAD = 30^\circ\)

আবার, \(\angle ACB = \angle EAC\) [একান্তর কোণ] এবং \(\angle EAD = \angle ADB\) [একান্তর কোণ]

∴ \(\angle ACB =60^\circ\) এবং \(\angle ADB = 30^\circ\)

\(\triangle ABC\) ত্রিভুজে \(\angle ACB = 60^\circ\) এবং \(\angle ABC = 90^\circ\)

∴ $\tan \angle ACB=\tan 60°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BC}}$

বা, \(\sqrt{3} = \frac{AB}{BC}\) [যেহেতু, \(\tan 60^\circ =\sqrt{3}\) ]

বা, \(\sqrt{3} = \frac{AB}{150}\)

বা, \(AB = 150\sqrt{3}\) —-(i)

আবার, \(\triangle ABD\) ত্রিভুজে \(\angle ABD =90^\circ\) এবং \(\angle ADB = 30^\circ\)

∴ $\tan \angle ADB=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BD}}$

বা, \(\tan 30^\circ = \frac{AB}{BC+CD}\)

বা, \(\frac{1}{\sqrt{3}} = \frac{150\sqrt{3}}{150+CD}\) [যেহেতু, \(AB=150\sqrt{3}\) এবং \(\tan 30^\circ =1/\sqrt{3}\)]

বা, \(150+CD = 450\)

বা, \(CD = 300\)

∴ \(BD = BC+CD = 150+300=450\) মিটার

∴ লাইট হাউস থেকে দুরের জাহাজের দুরত্ব 450 মিটার এবং লাইট হাউসের উচ্চতা \(150\sqrt{3}\) মিটার।

11. একটি পাঁচতলা বাড়ির ছাদের কোনো বিন্দু থেকে দেখলে মনুমেন্টের চূড়ার উন্নতি কোণ ও গোড়ার অবনতি কোণ যথাক্রমে \(60^\circ\) এবং \(30^\circ\) ; বাড়িটির উচ্চতা \(16\) মিটার হলে, মনুমেন্টের উচ্চতা এবং বাড়িটি মনুমেন্ট থেকে কত দূরে অবস্থিত হিসাব করে লিখি।

সমাধান –

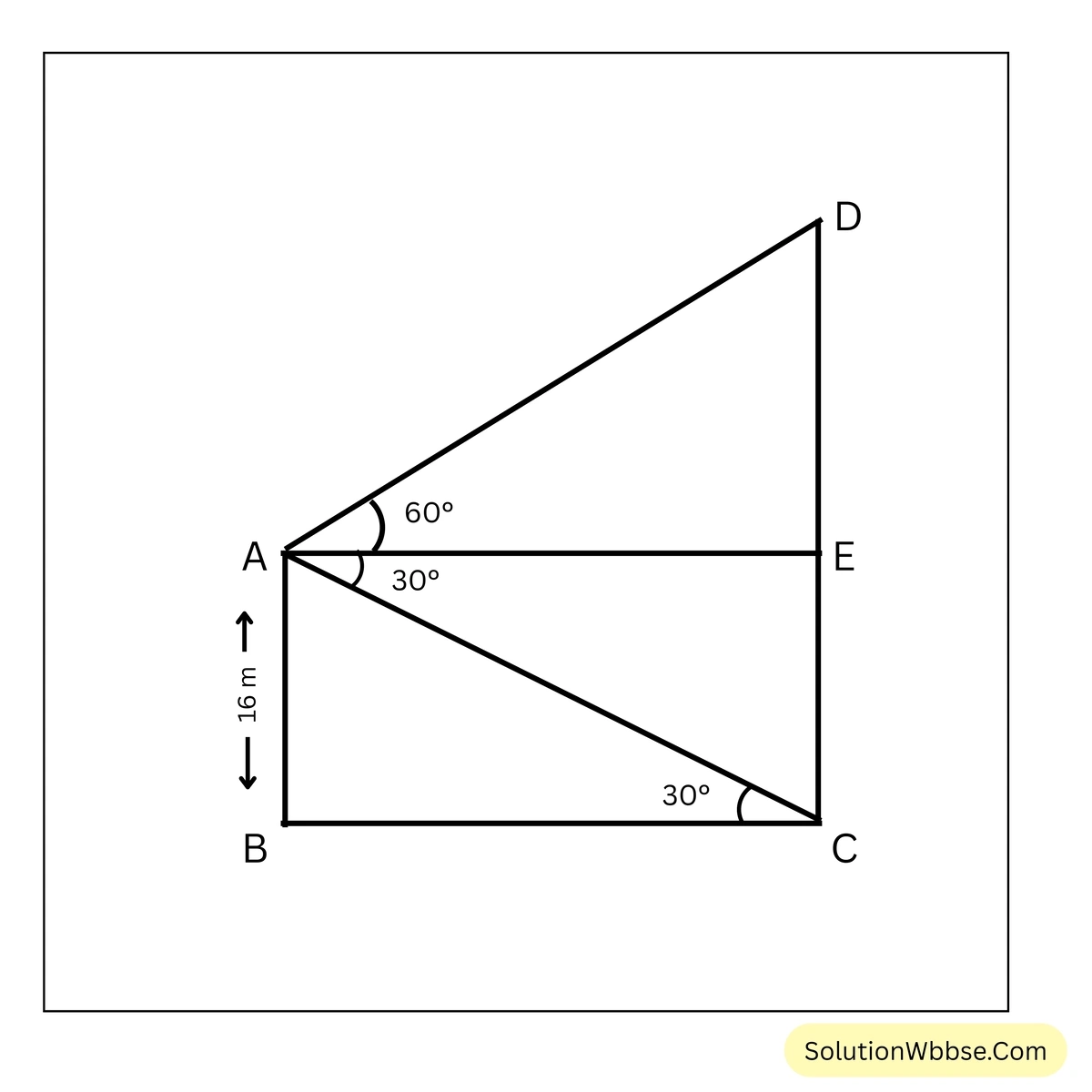
ধরাযাক , \(AB\) হল বাড়িটির উচ্চতা এবং \(CD\) হল মনুমেন্টের উচ্চতা।

∴ \(AB= 16\) মিটার।

বাড়ির ছাদ অর্থাৎ \(A\) বিন্দু থেকে মনুমেন্টের চূড়া অর্থাৎ \(D\) বিন্দুর উন্নতি কোণ \(60^\circ\) এবং মনুমেন্টের গোড়ার অর্থাৎ \(C\) বিন্দুর অবনতি কোণ \(30^\circ\)।

∴ \(\angle DAE = 60^\circ\)

এখন \(AE \perp CD\) অঙ্কন করা হল।

∴ \(AE \parallel BC\)

∴ \(\angle EAC =\) একান্তর কোণ \(\angle ACB = 30^\circ\)

যেহেতু , \(AE \parallel BC\) এবং \(AB \parallel EC\) এবং \(\angle ABC=\angle BCE= 90^\circ\)

∴ \(ABCE\) একটি আয়তক্ষেত্র।

∴ \(AB =CE =16\) মিটার এবং \(BC=AE\)

এখন , \(\triangle ABC\) ত্রিভুজে , \(\angle ABC = 90^\circ\) এবং \(\angle ACB = 30^\circ\)

∴ $\tan \angle ACB=\tan 30°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BC}}$

বা, \(\frac{1}{\sqrt{3}} = \frac{AB}{BC}\) [ যেহেতু , \(\tan 30^\circ = \frac{1}{\sqrt{3}}\) ]

বা, \(\frac{1}{\sqrt{3}} = \frac{16}{BC}\)

বা, \(BC = 16\sqrt{3}\)
∴ বাড়ি থেকে মনুমেন্টের দূরত্ব \(16\sqrt{3}\) মিটার।

এখন , \(\triangle AED\) ত্রিভুজে , \(\angle AED = 90^\circ\) এবং \(\angle DAE =60^\circ\)

∴ $\tan \angle DAE=\tan 60°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{DE}}{\mathrm{AE}}$

বা, \(\sqrt{3} = \frac{DE}{AE}\) [ যেহেতু , \(\tan 60^\circ = \sqrt{3}\) ]

বা, \(DE = AE\sqrt{3}\)

বা, \(DE = 16\sqrt{3} \times \sqrt{3}\) [ যেহেতু , \(AE=BC\) ]

বা, \(DE = 48\)

∴ মনুমেন্টের উচ্চতা = \((DE+EC) = (48+16)\) মিটার = \(64\) মিটার।

12. 250 মিটার লম্বা সুতো দিয়ে একটি ঘুড়ি ওড়াচ্ছি। সুতোটি যখন অনুভূমিক রেখার সঙ্গে 60° কোণ করে থাকে এবং সুতোটি যখন অনুভূমিক রেখার সঙ্গে 45° কোণ করে থাকে তখন ঘুড়িটি আমার থেকে কত উপরে থাকবে হিসাব করে লিখি। এদের মধ্যে কোন ক্ষেত্রে ঘুড়িটি বেশি উঁচুতে থাকবে নির্ণয় করি।

সমাধান –

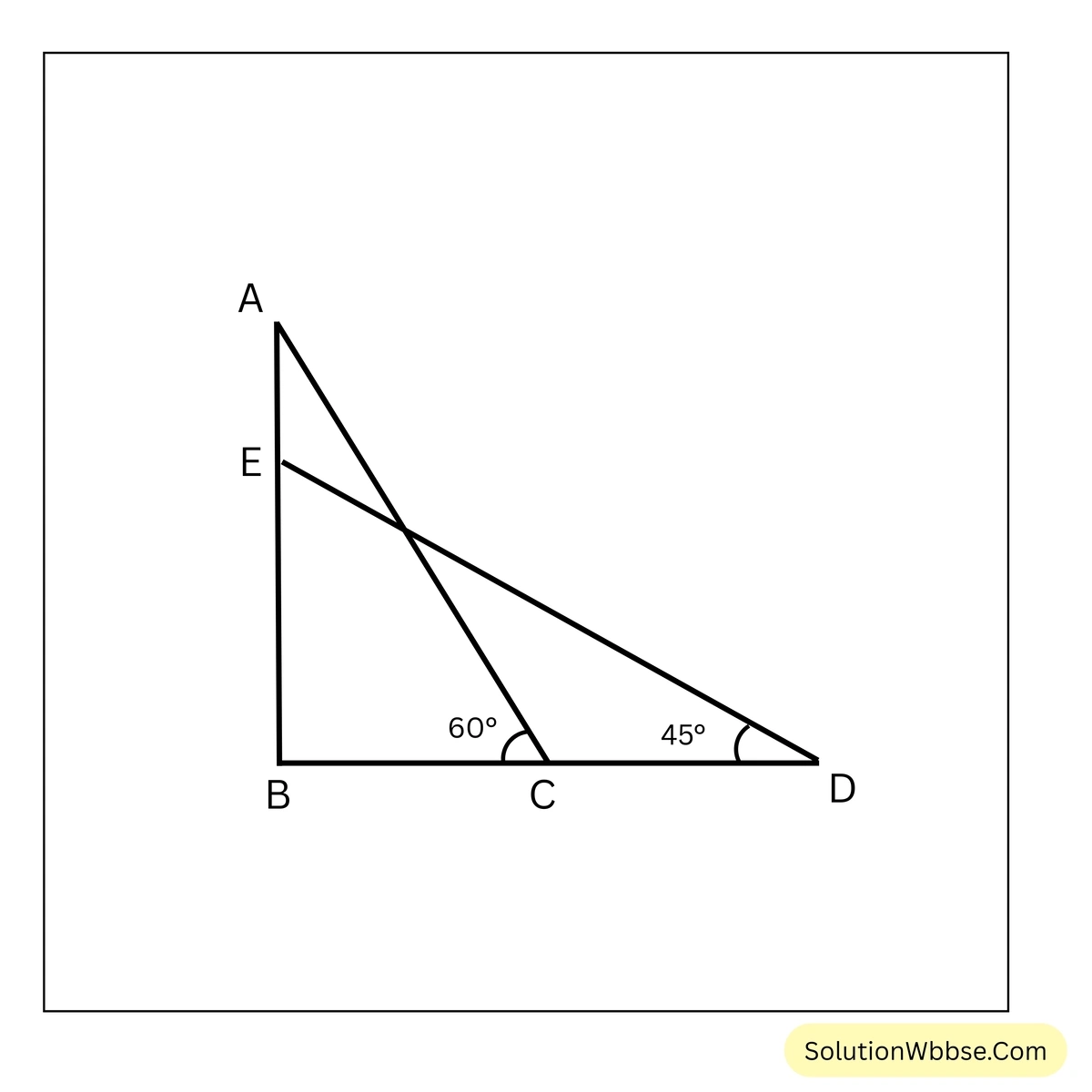
ধরাযাক, যখন ঘুড়ির সুতো অনুভূমিক রেখার সঙ্গে \(60^\circ\) কোণ করে তখন ঘুড়ির উচ্চতা \(AB\), আবার যখন ঘুড়ির সুতো অনুভূমিক রেখার সঙ্গে \(45^\circ\) কোণ করে তখন ঘুড়ির উচ্চতা \(EB\)। প্রতিক্ষেত্রে সুতোর দৈর্ঘ্য \(250\) মিটার। ∴ \(DE = AC = 250\) মিটার।

এখন, \(\triangle ABC\) ত্রিভুজে \(\angle ABC = 90^\circ\) এবং \(\angle ACB = 60^\circ\)

∴ $\sin \angle ACB=\sin 60°=\frac{\mathrm{লম্ব}}{\mathrm{অতিভুজ}}=\frac{\mathrm{AB}}{\mathrm{AC}}$

বা, \(\frac{\sqrt{3}}{2} = \frac{AB}{AC}\) [ যেহেতু, \(\sin 60^\circ = \frac{\sqrt{3}}{2}\) ]

বা, \(\frac{\sqrt{3}}{2} = \frac{AB}{250}\)

বা, \(AB = 250 \times \frac{\sqrt{3}}{2}\)

বা, \(AB = 125\sqrt{3}\)

আবার, \(\triangle BDE\) ত্রিভুজে \(\angle DBE = 90^\circ\) এবং \(\angle BDE = 45^\circ\)

∴ $\sin \angle BDE=\sin 45°=\frac{\mathrm{লম্ব}}{\mathrm{অতিভুজ}}=\frac{\mathrm{BE}}{\mathrm{DE}}$

বা, \(\frac{1}{\sqrt{2}} = \frac{BE}{DE}\) [ যেহেতু, \(\sin 45^\circ = \frac{1}{\sqrt{2}}\) ]

বা, \(\frac{1}{\sqrt{2}} = \frac{BE}{250}\)

বা, \(BE = \frac{250}{\sqrt{2}}\)

বা, \(BE = \frac{250 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}\)

বা, \(BE = \frac{250\sqrt{2}}{2}\)

বা, \(BE = 125\sqrt{2}\)

∴ যখন ঘুড়ির সুতো অনুভূমিক রেখার সঙ্গে \(60^\circ\) কোণ করে তখন ঘুড়ির উচ্চতা হবে \(125\sqrt{3}\) মিটার।

আবার যখন ঘুড়ির সুতো অনুভূমিক রেখার সঙ্গে \(45^\circ\) কোণ করে তখন ঘুড়ির উচ্চতা হবে \(125\sqrt{2}\) মিটার।

অর্থাৎ, এদের মধ্যে যেহেতু \(125\sqrt{3}\) মিটার দৈর্ঘ্যটি বড়, ∴ যখন ঘুড়ির সুতো অনুভূমিক রেখার সঙ্গে \(60^\circ\) কোণ করে তখন ঘুড়ির উচ্চতা বেশি হবে।

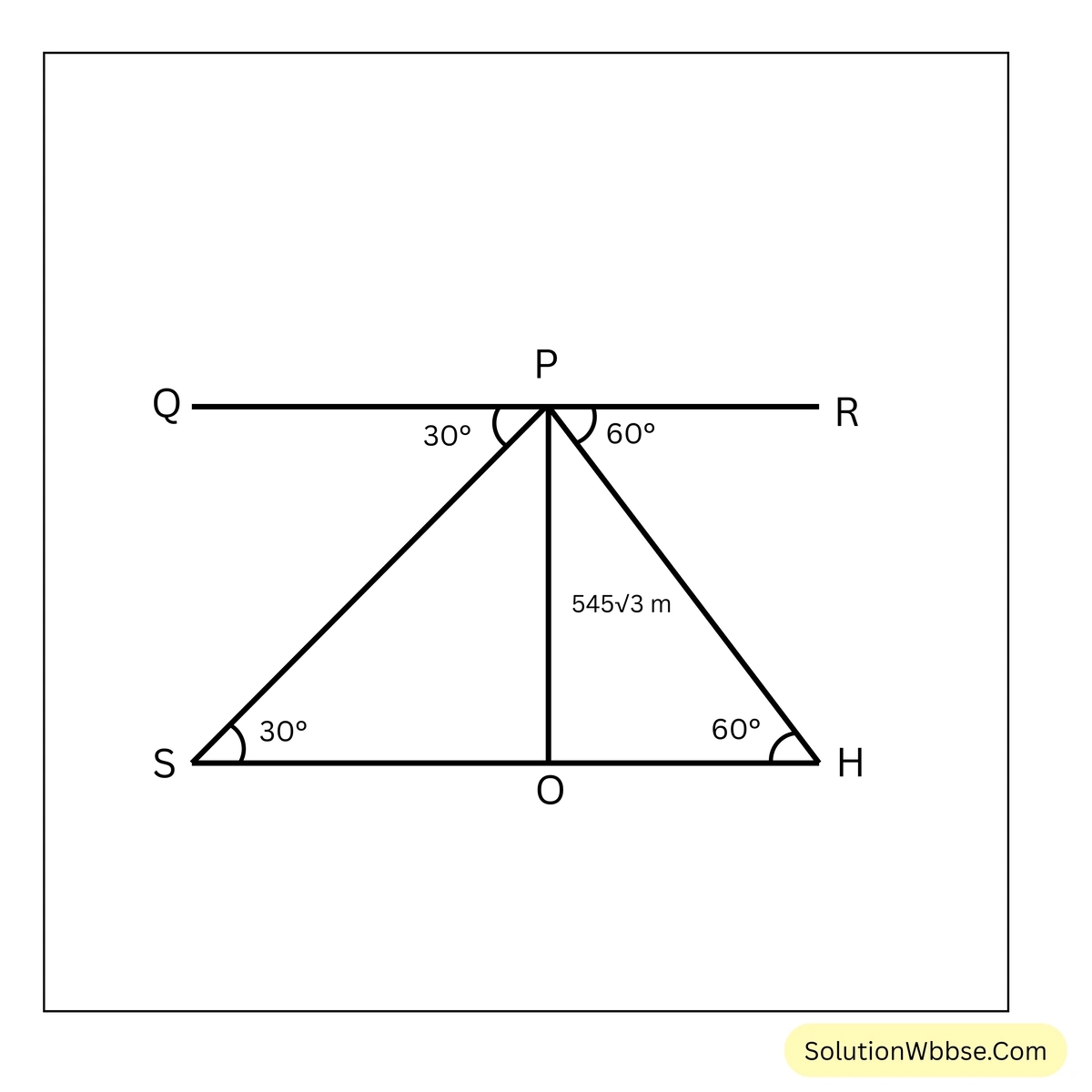
13. উড়োজাহাজের একজন যাত্রী কোনো এক সময় তাঁর এক পাশে হাওড়া স্টেশনটি এবং ঠিক তাঁর বিপরীত পাশে শহিদ মিনারটি যথাক্রমে \(60^\circ\) ও \(30^\circ\) অবনতি কোণে দেখতে পান। ওই সময় উড়োজাহাজটি যদি ঠিক \(545\sqrt{3}\) মিটার উঁচুতে থাকে, তাহলে হাওড়া স্টেশন ও শহিদ মিনারের দূরত্ব নির্ণয় করি।

সমাধান –

ধরাযাক, H, S এবং P যথাক্রমে হাওড়া স্টেশন, শহিদ মিনার এবং উড়োজাহাজের অবস্থান।

∴ P বিন্দু থেকে H বিন্দুর অবনতি কোণ \(60^\circ\) এবং P বিন্দু থেকে S বিন্দুর অবনতি কোণ \(30^\circ\) এবং মাটি থেকে উড়োজাহাজটির উচ্চতা \(OP = 545\sqrt{3}\) মিটার।

এখন, P বিন্দু দিয়ে SH সরলরেখার সমান্তরাল সরলরেখা QR টানা হল।

∴ \(\angle QPS = 30^\circ\) এবং \(\angle RPH = 60^\circ\)

∴ \(\angle QPS =\) একান্তর কোণ \(\angle PSO = 30^\circ\)

এবং \(\angle RPH =\) একান্তর কোণ \(\angle PHO = 60^\circ\)

এখন, \(\triangle PSO\) ত্রিভুজে \(\angle POS = 90^\circ\) এবং \(\angle PSO = 30^\circ\)

∴ $\tan \angle PSO=\tan 30°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{PO}}{\mathrm{OS}}$

বা, \(\frac{1}{\sqrt{3}} = \frac{PO}{OS}\)

বা, \(\frac{1}{\sqrt{3}} = \frac{545\sqrt{3}}{OS}\)

বা, \(OS = 545\sqrt{3} \times \sqrt{3}\)

বা, \(OS = 545 \times 3\)

বা, \(OS = 1635\)

আবার, \(\triangle POH\) ত্রিভুজের ক্ষেত্রে,

$\tan \angle PHO=\tan 60°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{PO}}{\mathrm{OH}}$

বা, \(\sqrt{3} = \frac{PO}{OH}\)

বা, \(\sqrt{3} = \frac{545\sqrt{3}}{OH}\)

বা, \(OH = 545\)

∴ \(SH = SO + OH = (1635 + 545)\) মিটার = \(2180\) মিটার

∴ হাওড়া স্টেশন থেকে শহিদ মিনারের দূরত্ব \(2180\) মিটার।

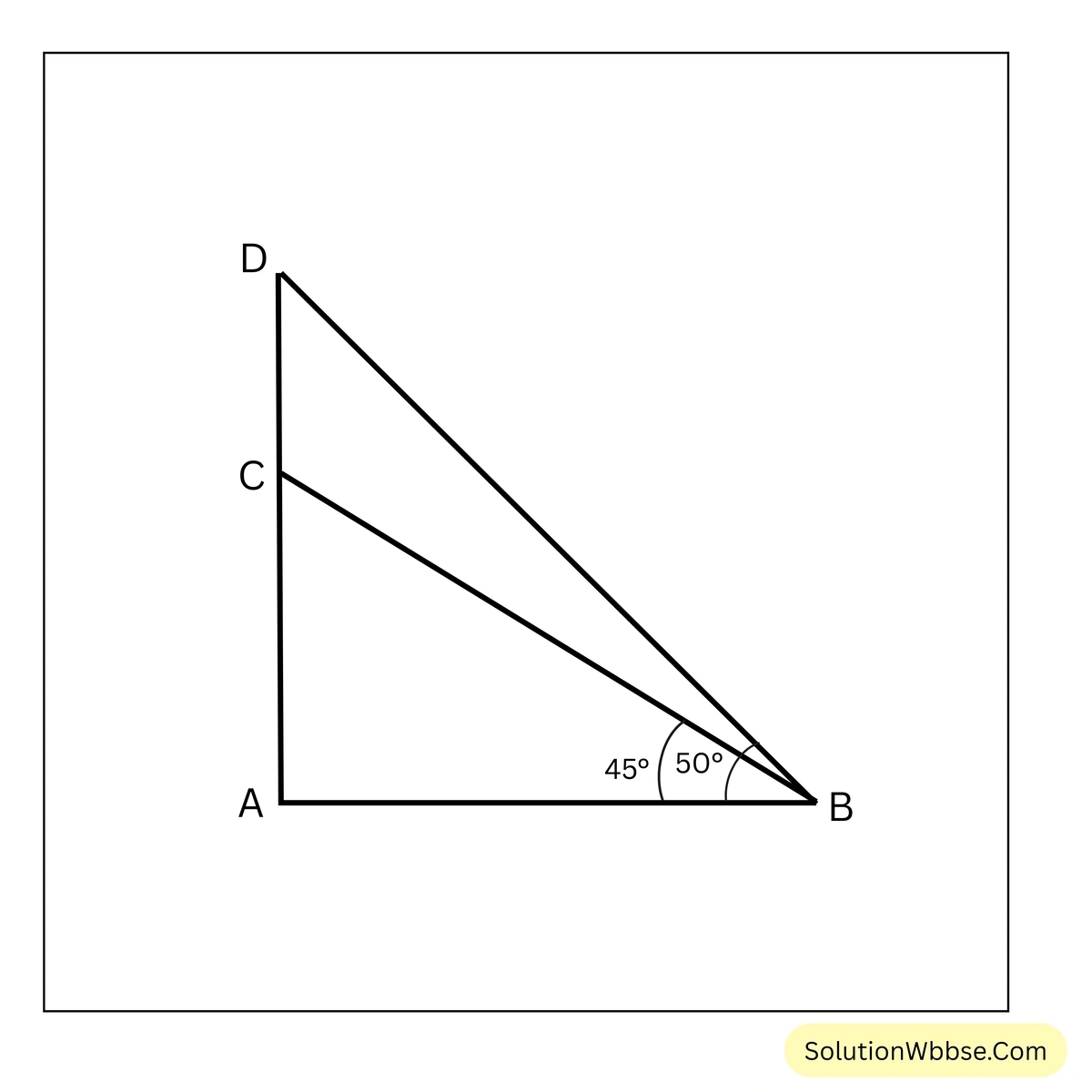
14. একটি তিনতলা বাড়ির ছাদে \(3.3\) মিটার দৈর্ঘ্যের একটি পতাকা আছে। রাস্তার কোনো এক স্থান থেকে দেখলে পতাকা দণ্ডটির চূড়া ও পাদদেশের উন্নতি কোণ যথাক্রমে \(50^\circ\) ও \(45^\circ\) হয়। তিনতলা বাড়িটির উচ্চতা হিসাব করে লিখি।

সমাধান –

\(AC\) হল তিনতলা বাড়িটির উচ্চতা এবং \(CD\) হল পতাকার দৈর্ঘ্য। রাস্তার উপর একটি বিন্দু \(B\) থেকে পতাকার পাদদেশের অর্থাৎ \(C\) বিন্দুর উন্নতি কোণ \(45^\circ\) এবং \(B\) বিন্দু থেকে পতাকার চূড়া অর্থাৎ \(D\) বিন্দুর উন্নতি কোণ \(50^\circ\)।

∴ \(CD = 3.3\) এবং \(\angle ABC = 45^\circ\) এবং \(\angle ABD = 50^\circ\)

এখন, \(\triangle ABC\) ত্রিভুজে \(\angle BAC = 90^\circ\) এবং \(\angle ABC = 45^\circ\)

∴ <math xmlns=”http://www.w3.org/1998/Math/MathML”><mi>tan</mi><mi>∠</mi><mi>A</mi><mi>B</mi><mi>C</mi><mo>=</mo><mi>tan</mi><mn>45</mn><mo>°</mo><mo>=</mo><mfrac><mi>লম্ব</mi><mi>ভূমি</mi></mfrac><mo>=</mo><mfrac><mi>AC</mi><mi>AB</mi></mfrac></math>

বা, \(1 = \frac{AC}{AB}\)

বা, \(AB = AC\) –(i)

আবার, \(\triangle ABD\) ত্রিভুজে \(\angle BAD = 90^\circ\) এবং \(\angle ABD = 50^\circ\)

∴ <math xmlns=”http://www.w3.org/1998/Math/MathML”><mi>tan</mi><mi>∠</mi><mi>A</mi><mi>B</mi><mi>D</mi><mo>=</mo><mfrac><mi>লম্ব</mi><mi>ভূমি</mi></mfrac><mo>=</mo><mfrac><mi>AD</mi><mi>AB</mi></mfrac></math>

বা, \(\tan 50^\circ = \frac{AD}{AB}\)

বা, \(1.192 = \frac{AD}{AB}\)

বা, \(1.192 = \frac{AC+CD}{AC}\) [ যেহেতু, \(AB = AC\) ]

বা, \(1.192 = \frac{AC+3.3}{AC}\)

বা, \(1.192AC = AC+3.3\)

বা, \(1.192AC – AC = 3.3\)

বা, \(0.192AC = 3.3\)

বা, \(AC = \frac{3.3}{0.192}\)

বা, \(AC = 17.188\)

বা, \(AC = 17.19\) (প্রায়)

∴ তিনতলা বাড়িটির উচ্চতা \(17.19\) মিটার প্রায়।

15. দুটি স্তম্ভের উচ্চতা যথাক্রমে 180 মিটার ও 60 মিটার। দ্বিতীয় স্তম্ভটির গোড়া থেকে প্রথমটির চূড়ার উন্নতি কোণ 60° হলে, প্রথমটির গোড়া থেকে দ্বিতীয়টির চূড়ার উন্নতি কোণ হিসাব করে লিখি।

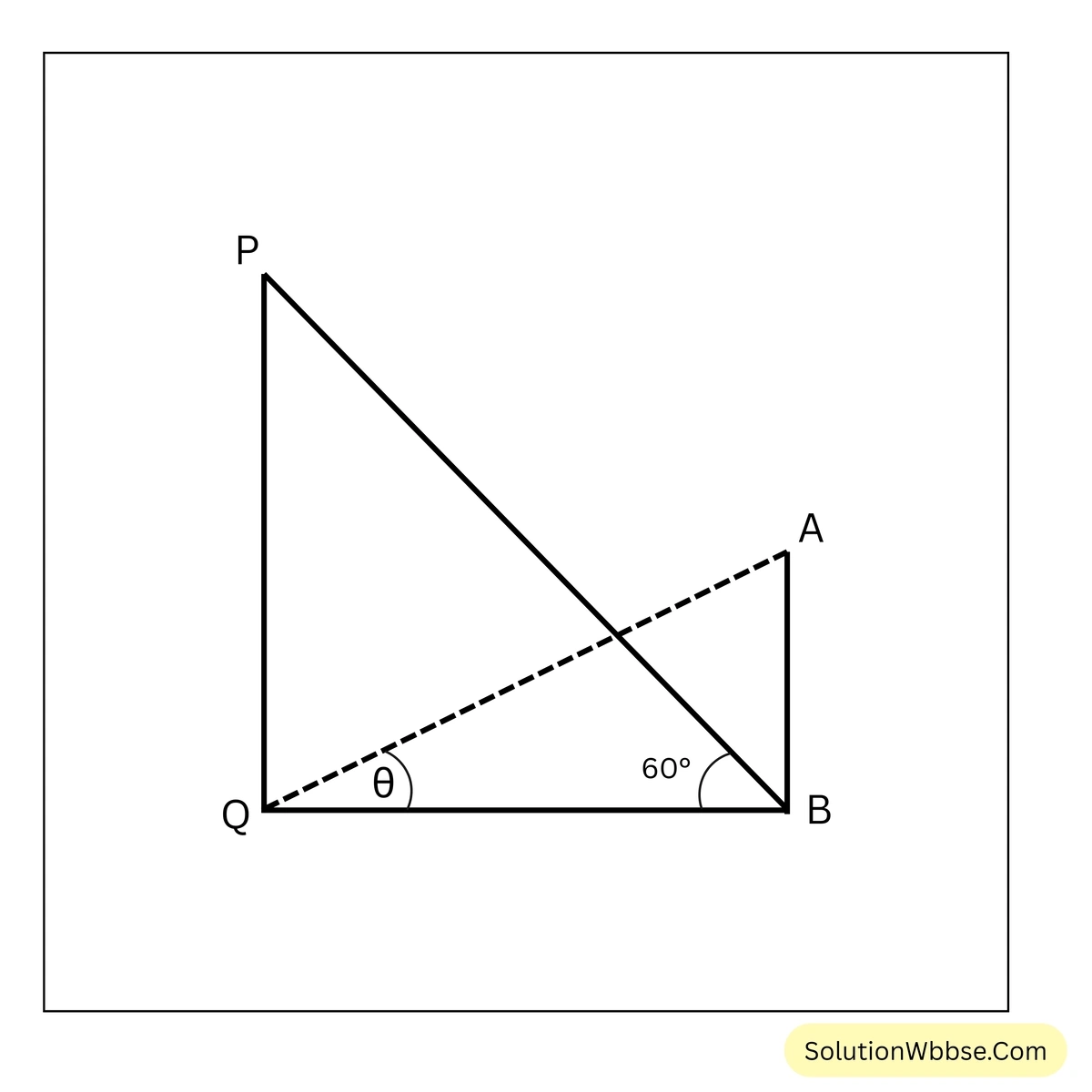
মনেকর, স্তম্ভ দুটি যথাক্রমে \(PQ\) এবং \(AB\)।

এখানে \(PQ=180\) মিটার এবং \(AB=60\) মিটার।

প্রশ্নানুসারে, \(\angle PBQ=60^\circ\)।

এখন \(\triangle PBQ\)-এর \(\angle PQB=90^\circ\)

এবং \(\angle PBQ=60^\circ\)।

∴ \(\tan 60^\circ = \frac{PQ}{BQ}\)

বা, \(\sqrt{3} = \frac{180}{BQ}\)

বা, \(BQ = \frac{180}{\sqrt{3}}\)

বা, \(BQ = \frac{180 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}\)

বা, \(BQ = \frac{180\sqrt{3}}{3}\)

∴ \(BQ = 60\sqrt{3}\) মিটার।

মনেকর, \(PQ\) স্তম্ভের গোড়া থেকে \(AB\) স্তম্ভের চূড়ার উন্নতি কোণ \(\theta\)।

∴ \(\triangle ABQ\)-এর \(\angle ABQ=90^\circ\) এবং \(\angle AQB=\theta\)।

∴ \(\tan \theta = \frac{AB}{BQ}\)

বা, \(\tan \theta = \frac{60}{60\sqrt{3}}\)

বা, \(\tan \theta = \frac{1}{\sqrt{3}}\)

বা, \(\tan \theta = \tan 30^\circ\)

∴ \(\theta = 30^\circ\)।

∴ উন্নতি কোণটির নির্ণেয় মান = \(30^\circ\)।

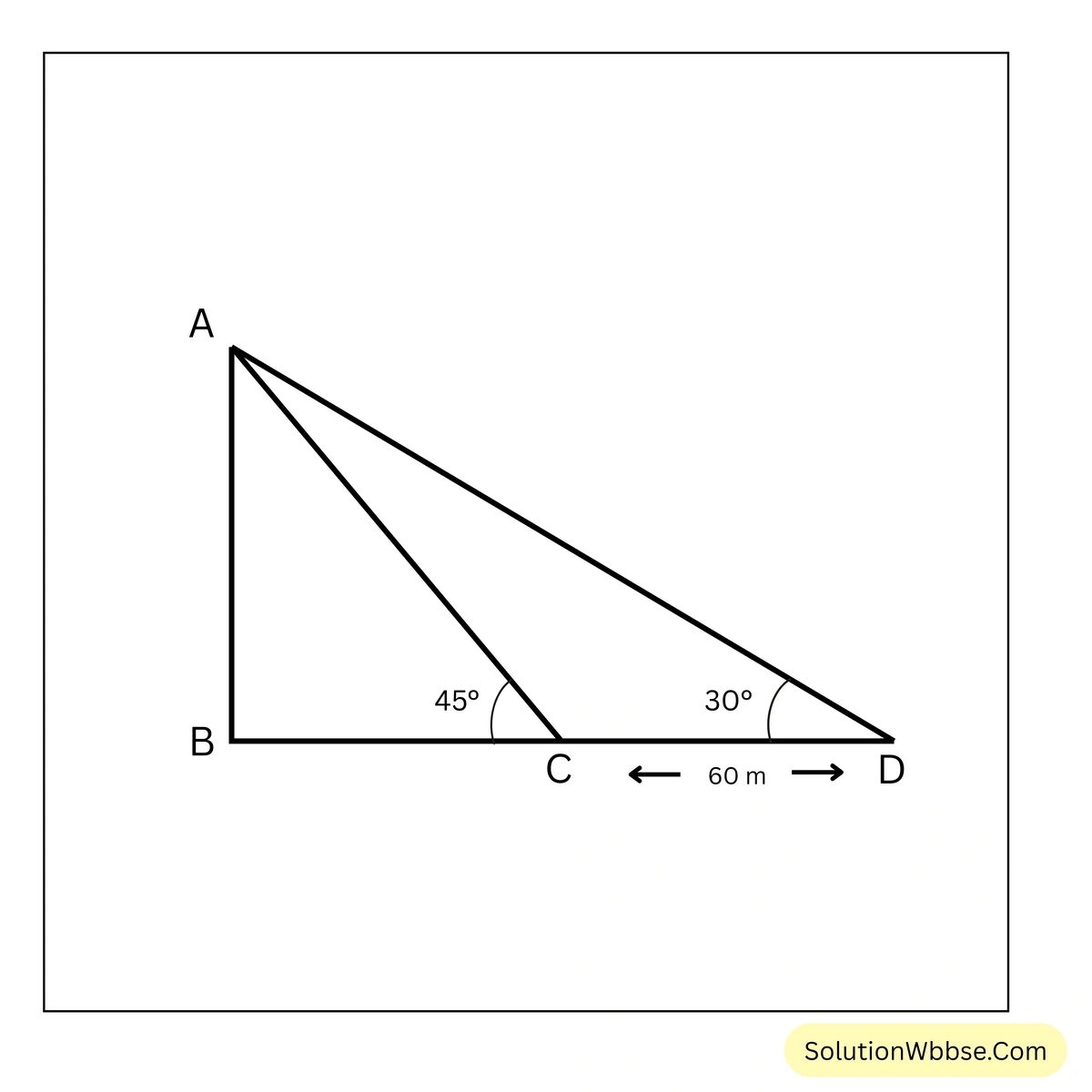
16. সূর্যের উন্নতি কোণ 45° হলে কোনো সমতলে অবস্থিত একটি স্তম্ভের ছায়ার দৈর্ঘ্য যা হয়, উন্নতি কোণ 30° হলে ছায়ার দৈর্ঘ্য তার চেয়ে 60 মিটার বেশি হয়। স্তম্ভটির উচ্চতা নির্ণয় করি।

সমাধান –

ধরাযাক, AB হল স্তম্ভের দৈর্ঘ্য। যখন সূর্যের উন্নতি কোণ 45° তখন AB স্তম্ভের ছায়ার দৈর্ঘ্য হয় BC এবং সূর্যের উন্নতি কোণ যখন 30° তখন ছায়ার দৈর্ঘ্য CD=60 মিটার বৃদ্ধি পায় এবং ছায়ার দৈর্ঘ্য হয় BD

∴ \(BD = BC+CD = (BC+60)\) মিটার

ABC ত্রিভুজের ∠ABC =90° এবং ∠ACB = 45°

∴ $\tan \angle ACB=\tan 45°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BC}}$

বা, \(1 = \frac{AB}{BC}\)

বা, \(AB = BC\) –(i)

ABD ত্রিভুজের ∠ABD =90° এবং ∠ADB = 30°

∴ $\tan \angle ADB=\tan 30°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BD}}$

বা, \(\frac{1}{\sqrt{3}} = \frac{AB}{BD}\)

বা, \(\frac{1}{\sqrt{3}} = \frac{AB}{BC+60}\) [যেহেতু, \(BD = BC+CD = (BC+60)\)]

বা, \(\frac{1}{\sqrt{3}} = \frac{AB}{AB+60}\) [ যেহেতু, \(BC=AB\)]

বা, \(AB+60 = \sqrt{3} AB\)

বা, \(\sqrt{3} AB – AB = 60\)

বা, \(AB(\sqrt{3} – 1) = 60\)

বা, \(AB = \frac{60}{\sqrt{3}-1}\)

বা, \(AB = \frac{60}{\sqrt{3}-1} \times \frac{\sqrt{3}+1}{\sqrt{3}+1}\)

বা, \(AB = \frac{60(\sqrt{3}+1)}{3-1}\)

বা, \(AB = 30(\sqrt{3}+1) = 30(1.732+1) = 30 \times 2.732 = 81.96\)

∴ \(AB=81.96\) মিটার (প্রায়)

∴ স্তম্ভের দৈর্ঘ্য 81.96 মিটার (প্রায়)।

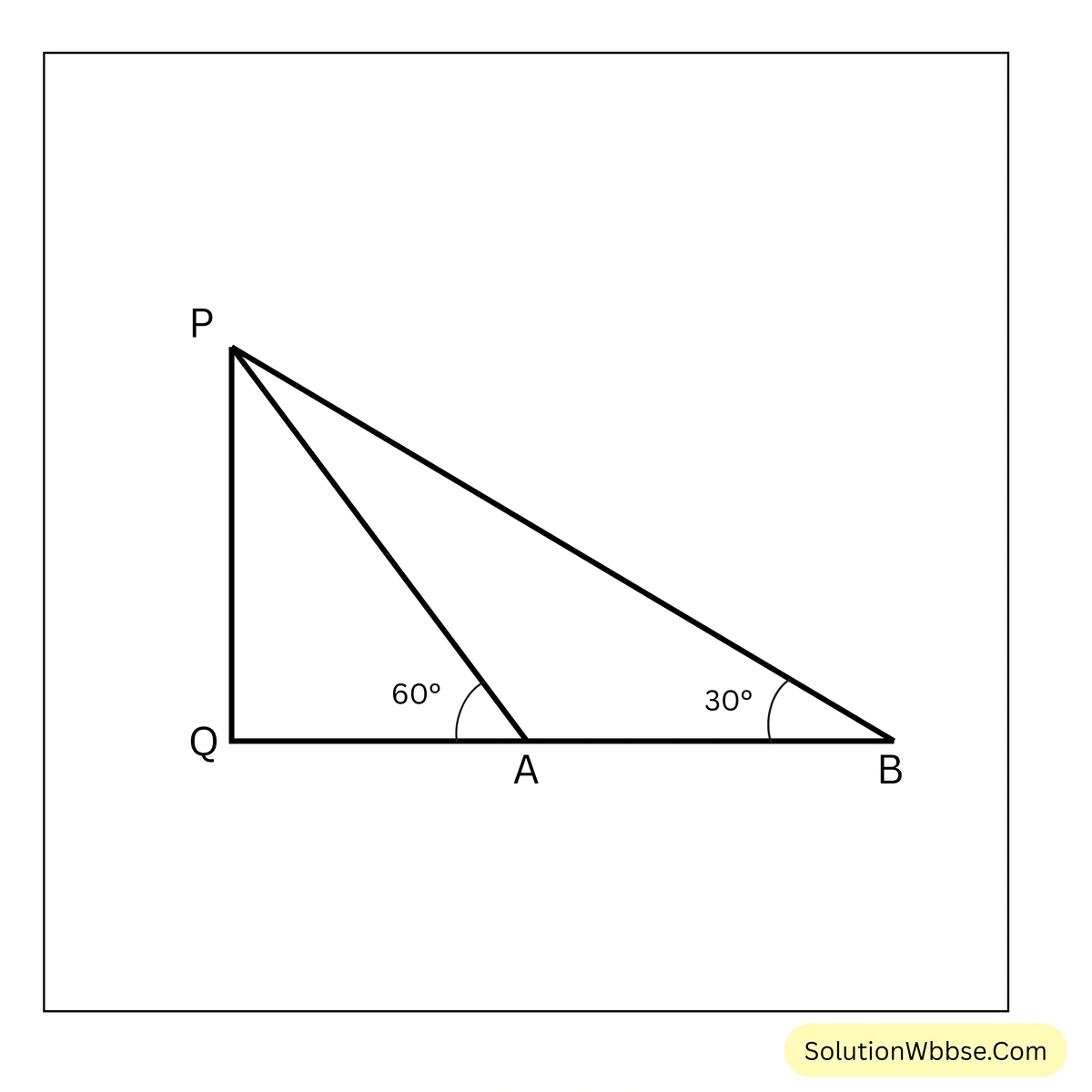
17. একটি চিমনির সঙ্গে একই সমতলে অবস্থিত অনুভূমিক সরলরেখায় কোনো বিন্দু থেকে চিমনির দিকে 50 মিটার এগিয়ে যাওয়ায় তার চূড়ার উন্নতি কোণ 30° থেকে 60° হল। চিমনির উচ্চতা হিসাব করে লিখি।

সমাধান –

ধরাযাক, PQ চিমনির পাদদেশের সঙ্গে একই সমতলে অবস্থিত অনুভূমিক সরলরেখার B এবং A বিন্দু থেকে চিমনির চূড়ার উন্নতি কোণ যথাক্রমে 30° এবং 60°; অর্থাৎ \(AB = 50\) মিটার।

এখন PAQ ত্রিভুজের \(\angle PQA = 90^\circ\) এবং \(\angle PAQ = 60^\circ\)

∴ \(\tan 60^\circ = \frac{PQ}{QA}\)

বা, \(\sqrt{3} = \frac{PQ}{QA}\)

বা, \(QA = \frac{PQ}{\sqrt{3}}\) —-(i)

আবার PBQ ত্রিভুজের \(\angle PQB = 90^\circ\) এবং \(\angle PBQ = 30^\circ\)

∴ \(\tan 30^\circ = \frac{PQ}{QB}\)

বা, \(\frac{1}{\sqrt{3}} = \frac{PQ}{QB}\)

বা, \(QB = \sqrt{3} PQ\)

বা, \(QA + AB = \sqrt{3} PQ\)

বা, \(\frac{PQ}{\sqrt{3}} + 50 = \sqrt{3} PQ\) [ যেহেতু, \(QA = \frac{PQ}{\sqrt{3}}\) এবং \(AB = 50\) ]

বা, \(\sqrt{3} PQ – \frac{PQ}{\sqrt{3}} = 50\)

বা, \(\frac{3PQ – PQ}{\sqrt{3}} = 50\)

বা, \(\frac{2PQ}{\sqrt{3}} = 50\)

বা, \(PQ = \frac{50\sqrt{3}}{2}\)

বা, \(PQ = 25\sqrt{3}\)

∴ চিমনির উচ্চতা \(25\sqrt{3}\) মিটার।

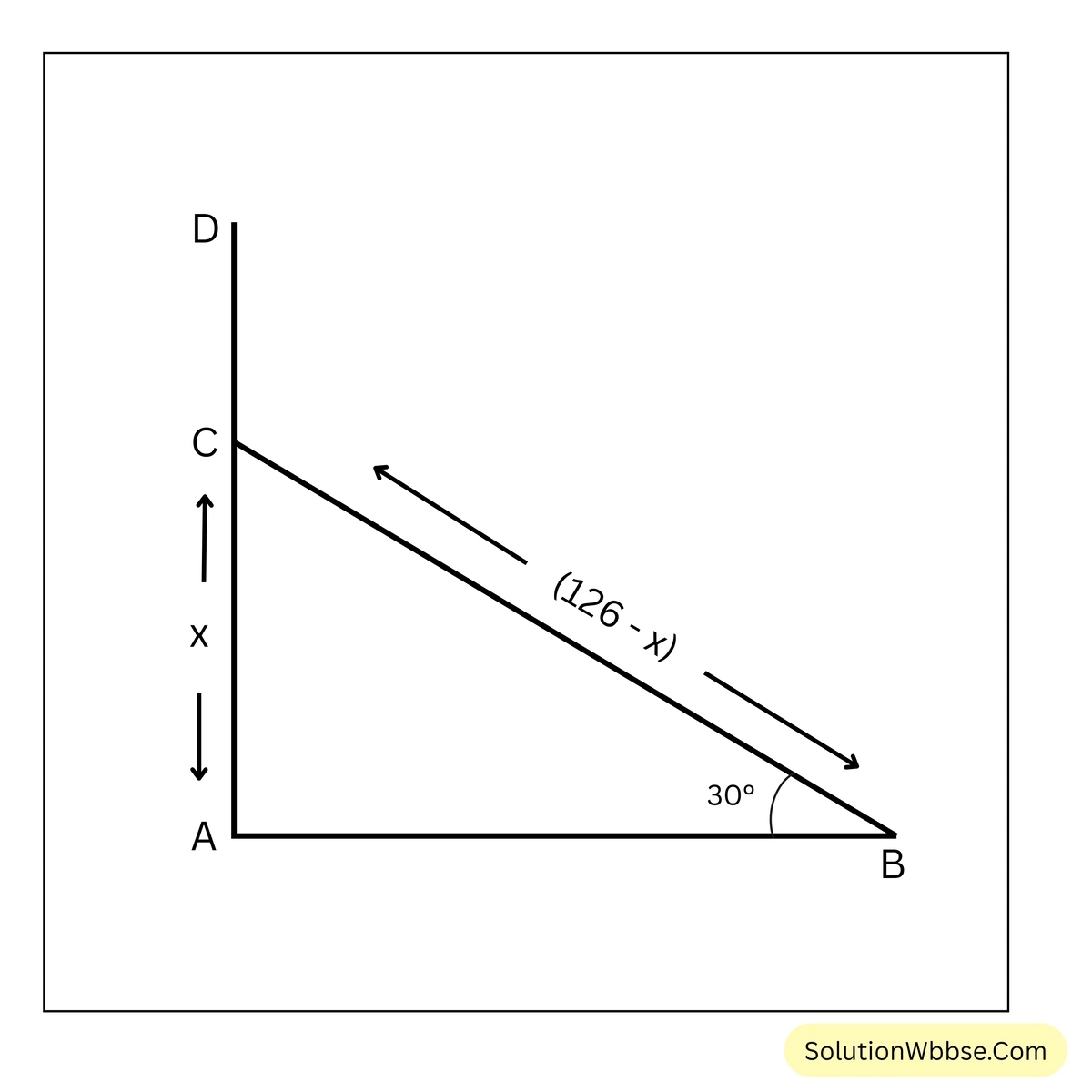
18. 126 ডেসিমি. উঁচু একটি উলম্ব খুঁটি মাটি থেকে কিছু উপরে দুমড়ে গিয়ে উপরের অংশ কাত হয়ে পড়ায় তার অগ্রভাগ মাটি স্পর্শ করে ভূমির সঙ্গে 30° কোণ উৎপন্ন করেছে। খুঁটিটি কত উপরে দুমড়ে গিয়েছিল এবং তার অগ্রভাগ গোড়া থেকে কত দূরে মাটি স্পর্শ করেছিল হিসাব করে লিখি।

সমাধান –

ধরাযাক, AD খুঁটি x ডেসিমি. উচ্চতায় C বিন্দুতে মচকে গিয়েছিল। ∴ \(AD=126\) ডেসিমি. এবং \(AC=x\) ডেসিমি.
∴ \(CD=BC=(126-x)\) ডেসিমি.

এখন ABC ত্রিভুজে \(\angle BAC =90^\circ\) এবং \(\angle ABC =30^\circ\)

∴ $\sin \angle ABC=\sin 30°=\frac{\mathrm{লম্ব}}{\mathrm{অতিভুজ}}=\frac{\mathrm{AC}}{\mathrm{BC}}$

বা, \(\frac{1}{2} = \frac{x}{BC}\)

বা, \(\frac{1}{2} = \frac{x}{126-x}\)

বা, \(126-x = 2x\)

বা, \(3x = 126\)

বা, \(x = \frac{126}{3}\)

বা, \(x = 42\)

∴ খুঁটিটি মাটি থেকে 42 ডেসিমি. উঁচুতে ভেঙেছিল।

আবার ABC সমকোণী ত্রিভুজ থেকে পাই,

$\tan \angle ABC=\tan 30°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AC}}{\mathrm{AB}}$

বা, \(\frac{1}{\sqrt{3}} = \frac{AC}{AB}\)

বা, \(\frac{1}{\sqrt{3}} = \frac{42}{AB}\)

বা, \(AB = 42\sqrt{3}\)

∴ খুঁটিটির অগ্রভাগ \(42\sqrt{3}\) ডেসিমিটার দূরে মাটি স্পর্শ করেছিল।

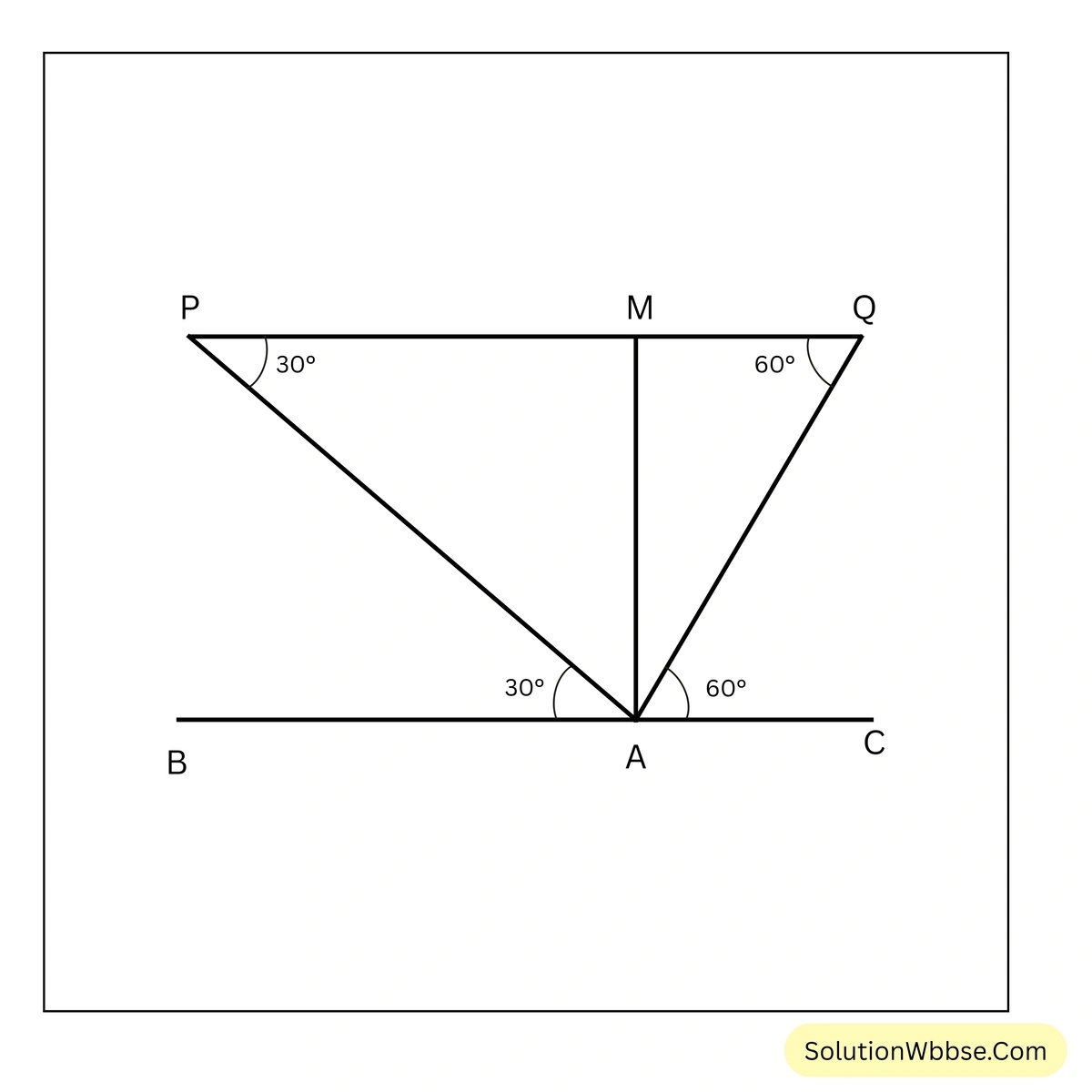
19. মাঠের মাঝখানে দাঁড়িয়ে মোহিত একটি উড়ন্ত পাখিকে প্রথমে উত্তরদিকে 30° উন্নতি কোণে এবং 2 মিনিট পর দক্ষিণ দিকে 60° উন্নতি কোণে দেখতে পেল। পাখিটি যদি একই সরলরেখা বরাবর \(50\sqrt{3}\) মিটার উঁচুতে উড়ে থাকে, তবে তার গতিবেগ কিলোমিটার প্রতি ঘণ্টায় নির্ণয় করি।

সমাধান –

ধরি, মাটিতে BC মাঠের A বিন্দুতে দাঁড়িয়ে পাখিটিকে প্রথমে P বিন্দুতে 30° উন্নতি কোণে এবং 2 মিনিট পরে Q বিন্দুতে 60° উন্নতি কোণে দেখে। যেহেতু পাখিটি একই সরলরেখায় উড়ছিল, তাই PQ || BC ও A বিন্দু থেকে পাখিটির উচ্চতা AM = \(50\sqrt{3}\) মিটার

এখন, \(\angle APM =\) একান্তর \(\angle BAP = 30^\circ\) [যেহেতু, PQ||BC]

এবং, \(\angle AQM =\) একান্তর \(\angle QAC = 60^\circ\) [যেহেতু, PQ||BC]

সমকোণী ত্রিভুজ APM থেকে পাই,

$\tan 30°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AM}}{\mathrm{PM}}$

বা, \(\frac{1}{\sqrt{3}} = \frac{50\sqrt{3}}{PM}\)

বা, \(PM = 150\)

সমকোণী ত্রিভুজ AMQ থেকে পাই,

$\tan 60°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AM}}{\mathrm{MQ}}$

বা, \(\sqrt{3} = \frac{50\sqrt{3}}{MQ}\)

বা, \(MQ = \frac{50\sqrt{3}}{\sqrt{3}}\)

বা, \(MQ = 50\)

∴ \(PQ = PM+MQ = (150+50)\) মিটার \(= 200\) মিটার

$\therefore \mathrm{পাখিটির\; গতিবেগ}=\frac{\mathrm{মোট\; দূরত্ব}}{\mathrm{সময়}}=\frac{200}{2}\mathrm{মিটার/মিনিট}=100\mathrm{মিটার/মিনিট}$

$=\frac{100}{1000}\mathrm{কিমি}/\frac{1}{60}\mathrm{ঘন্টা}=\frac{1}{10}\times 60=6\mathrm{কিমি/ঘন্টা}$

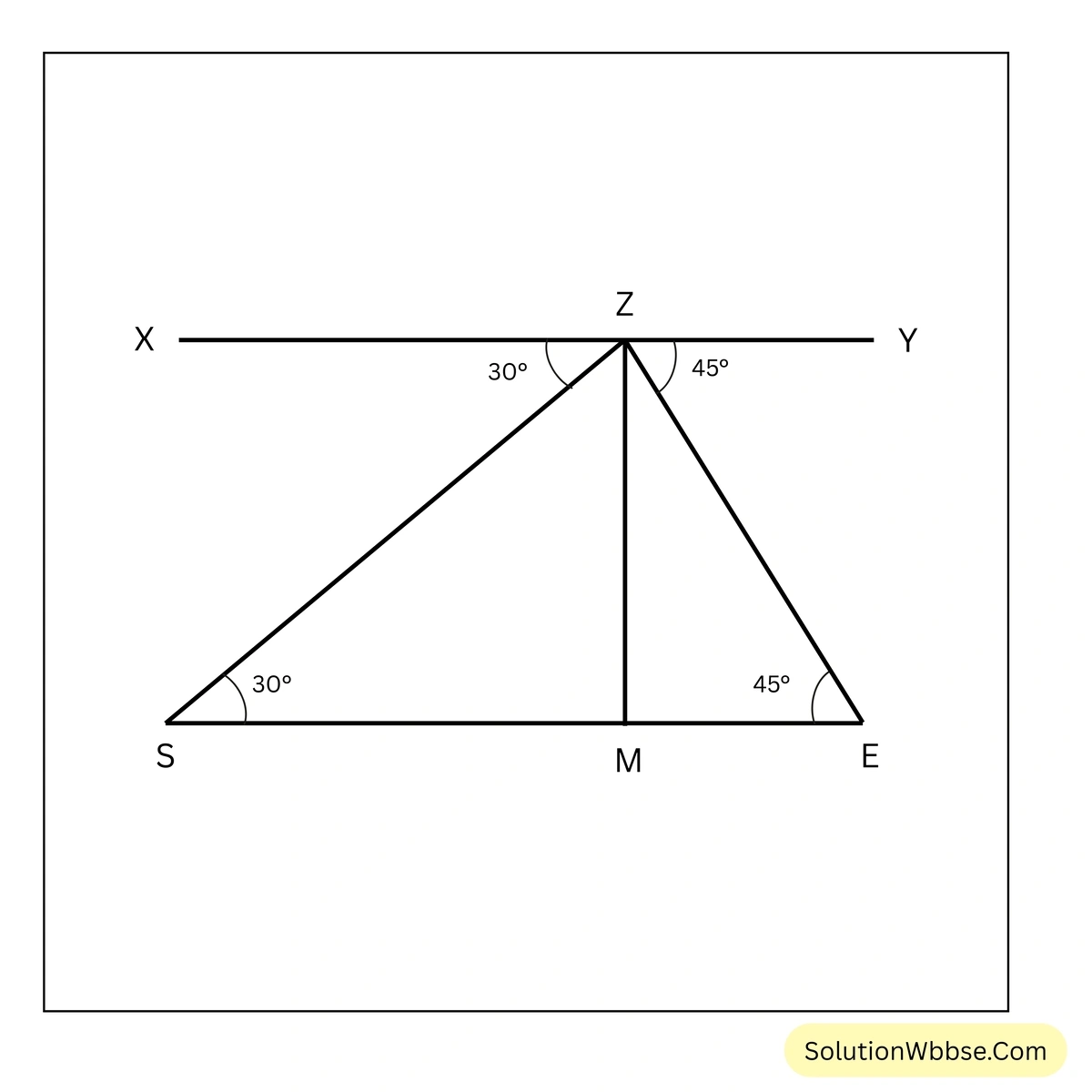
2. \(5\sqrt{3}\) মিটার উঁচু রেলওয়ে ব্রিজে দাঁড়িয়ে অমিলাদিদি প্রথমে একটি ট্রেনের ইঞ্জিনকে ব্রিজের এপারে \(30^\circ\) অবনতি কোণে দেখলেন। কিন্তু 2 সেকেন্ড পরেই ওই ইঞ্জিনকে ব্রিজের ওপারে \(45^\circ\) অবনতি কোণে দেখলেন। ট্রেনটির গতিবেগ মিটার প্রতি সেকেন্ডে হিসাব করে লিখি।

সমাধান –

ধরি, অমিলাদিদি XY রেলওয়ে ওভারব্রিজের Z বিন্দুতে দাঁড়িয়ে ট্রেনের ইঞ্জিনকে প্রথমে S বিন্দুতে এবং 2 সেকেন্ড পরে E বিন্দুতে দেখলেন। অবনতি কোণ \(\angle XZS = 30^\circ\) এবং \(\angle YZE = 45^\circ\)

ZM = রেলওয়ে ওভারব্রিজের উচ্চতা = \(5\sqrt{3}\) মিটার

আবার যেহেতু XY || SE

∴ \(\angle ZSM =\) একান্তর \(\angle XZS = 30^\circ\)

এবং \(\angle ZEM =\) একান্তর \(\angle YZE = 45^\circ\)

সমকোণী ত্রিভুজ ZSM থেকে পাই

$\tan 30°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{ZM}}{\mathrm{SM}}=\frac{5\sqrt{3}}{\mathrm{SM}}$

বা, \(\frac{1}{\sqrt{3}} = \frac{5\sqrt{3}}{SM}\)

বা, \(SM = 15\)

সমকোণী ত্রিভুজ ZEM থেকে পাই

$\tan 45°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{ZM}}{\mathrm{ME}}=\frac{5\sqrt{3}}{\mathrm{ME}}$

বা, \(1 = \frac{5\sqrt{3}}{ME}\)

বা, \(ME = 5\sqrt{3}\)

∴ \(SE = SM + ME = (15 + 5\sqrt{3}) = 15 + 5 \times 1.732 = 15 + 8.660 = 23.660\)

∴ ট্রেনটির গতিবেগ = \(\frac{23.660}{2}\) মিটার/সেকেন্ড = \(11.83\) মিটার/সেকেন্ড (প্রায়)

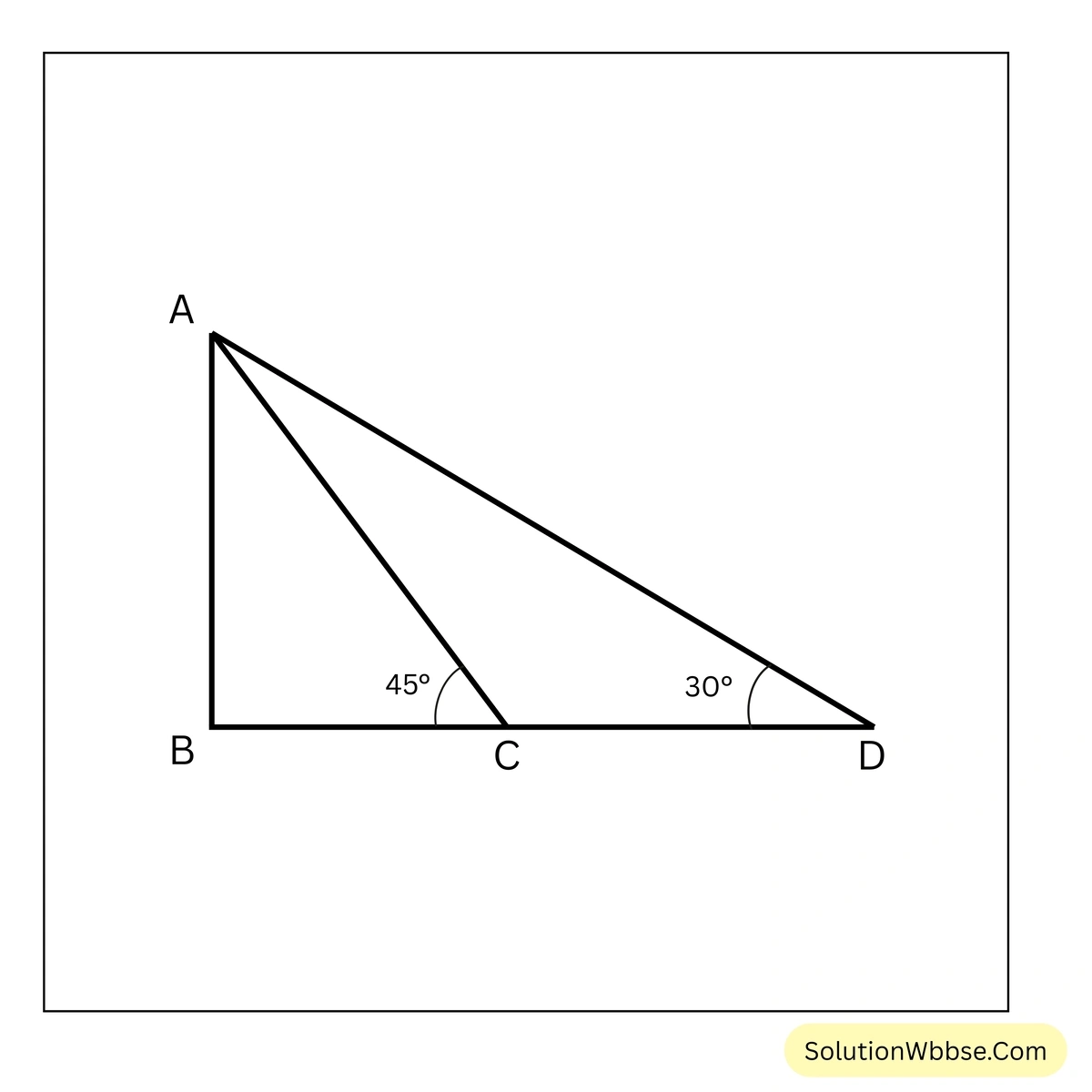
21. একটি নদীর পাড়ের সঙ্গে লম্বভাবে একটি সেতু আছে। সেতুটির একটি পাড়ের প্রান্ত থেকে নদীর পাড় ধরে কিছু দূর গেলে সেতুর অপর প্রান্তটি 45° কোণে এবং পাড় ধরে আরও 400 মিটার দূরে সরে গেলে সেই প্রান্তটি 30° কোণে দেখা যায়। সেতুটির দৈর্ঘ্য নির্ণয় করি।

সমাধান –

ধরি, নদীর পাড়ের সঙ্গে লম্ব ভাবে অবস্থিত একটি সেতু হল \(AB\) এবং তার \(B\) প্রান্ত থেকে কিছু দূরে \(C\) বিন্দু থেকে সেতুর অপর প্রান্ত \(A\) বিন্দুর সাপেক্ষে উৎপন্ন কোণ \(\angle BCA = 45^\circ\) এবং \(C\) বিন্দু থেকে আরও 400 মিটার দূরে \(D\) বিন্দু থেকে \(A\) বিন্দুর সাপেক্ষে উৎপন্ন কোণ \(\angle BDA = 30^\circ\) এবং \(CD = 400\) মিটার।

সমকোণী ত্রিভুজ \(ABC\) থেকে পাই,

$\tan 45°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BC}}$

বা, \(1 = \frac{AB}{BC}\)

বা, \(AB = BC\) —(i)

সমকোণী ত্রিভুজ \(ABD\) থেকে পাই,

$\tan 30°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BD}}$

বা, \(\frac{1}{\sqrt{3}} = \frac{AB}{BD}\)

বা, \(\frac{1}{\sqrt{3}} = \frac{AB}{BC+CD}\)

বা, \(\frac{1}{\sqrt{3}} = \frac{AB}{BC+400}\)

বা, \(\frac{1}{\sqrt{3}} = \frac{AB}{AB+400}\) [ যেহেতু, \(BC = AB\) ]

বা, \(AB+400 = \sqrt{3} AB\)

বা, \(\sqrt{3} AB – AB = 400\)

বা, \(AB(\sqrt{3}-1) = 400\)

বা, \(AB = \frac{400}{(\sqrt{3}-1)}\)

বা, \(AB = \frac{400}{(\sqrt{3}-1)} \times \frac{(\sqrt{3}+1)}{(\sqrt{3}+1)}\)

বা, \(AB = \frac{400(\sqrt{3}+1)}{(\sqrt{3})^2 – 1^2}\)

বা, \(AB = \frac{400(\sqrt{3}+1)}{3-1}\)

বা, \(AB = \frac{400(\sqrt{3}+1)}{2}\)

বা, \(AB = 200(\sqrt{3}+1)\)

∴ সেতুটি \(200(\sqrt{3}+1)\) মিটার লম্বা।

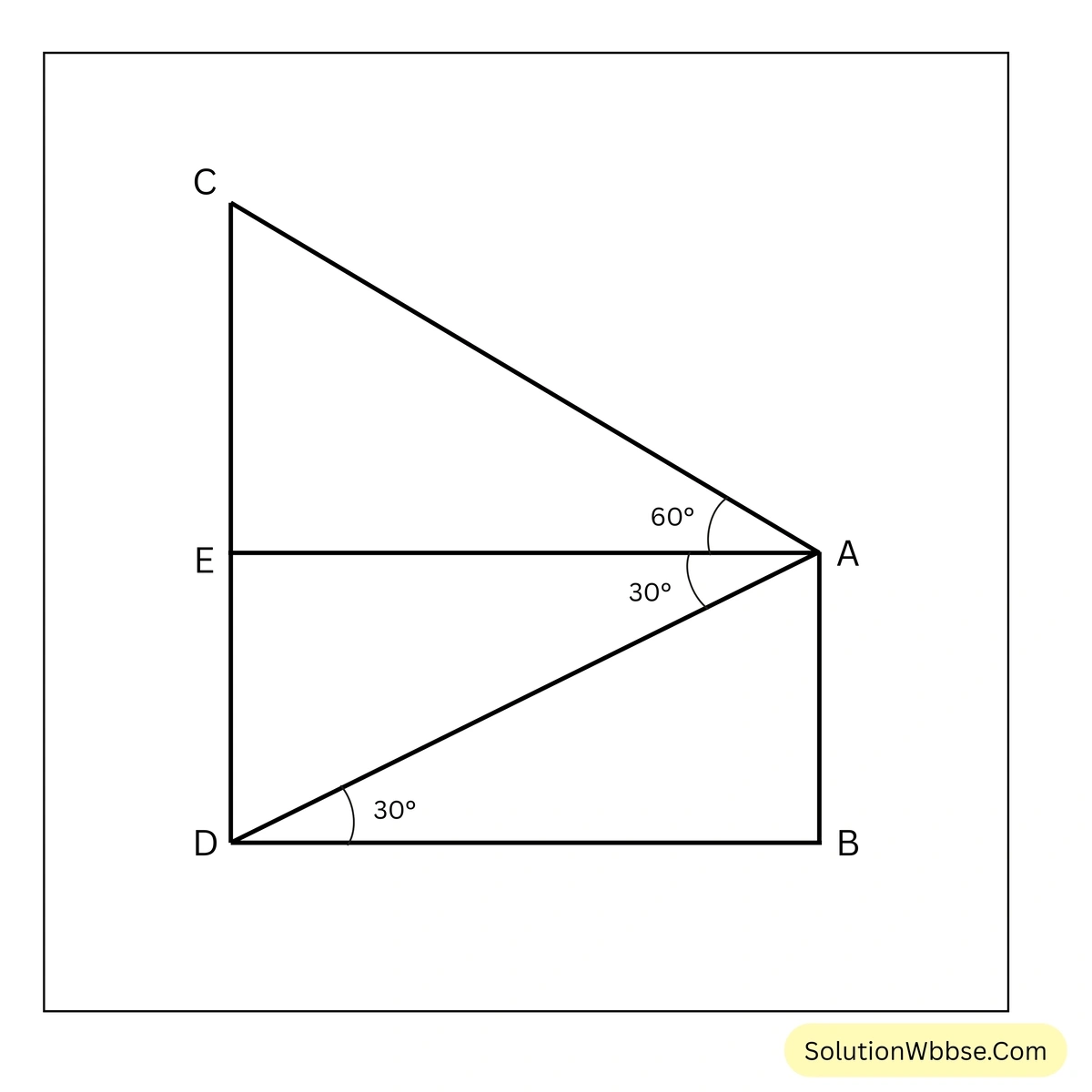
22. একটি পার্কের একপ্রান্তে অবস্থিত 15 মিটার উঁচু একটি বাড়ির ছাদ থেকে পার্কের অপর পারে অবস্থিত একটি ইটভাটার চিমনির পাদদেশ ও অগ্রভাগ যথাক্রমে \(30^\circ\) অবনতি কোণে এবং \(60^\circ\) উন্নতি কোণে দেখা যায়। ইটভাটার চিমনির উচ্চতা এবং ইটভাটা ও বাড়ির মধ্যে দূরত্ব নির্ণয় করি।

সমাধান –

ধরি, \(AB\) একটি 15 মিটার উঁচু বাড়ি এবং \(CD\) ইটভাটার চিমনি। বাড়ির ছাদ \(A\) থেকে চিমনির পাদদেশ \(D\) এর অবনতি কোণ এবং অগ্রভাগ \(C\) এর উন্নতি কোণ যথাক্রমে \(30^\circ\) এবং \(60^\circ\)

\(A\) বিন্দু থেকে \(BD\) এর সমান্তরাল সরলরেখা \(CD\) কে \(E\) বিন্দুতে ছেদ করে। যেহেতু \(AE \parallel BD\)

∴ \(\angle ADB =\) একান্তর \(\angle EAD = 30^\circ\)

সমকোণী ত্রিভুজ \(ABD\) থেকে পাই,

$\tan 30°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BD}}$

বা, \(\frac{1}{\sqrt{3}} = \frac{15}{BD}\)

বা, \(BD = 15\sqrt{3}\)

∴ ইট ভাটা ও বাড়ির মধ্যে দূরত্ব \(15\sqrt{3}\) মিটার।

আবার, \(AE=BD = 15\sqrt{3}\)

সমকোণী ত্রিভুজ \(AEC\) থেকে পাই,

$\tan 60°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{CE}}{\mathrm{AE}}$

বা, \(\sqrt{3} = \frac{CE}{15\sqrt{3}}\)

বা, \(CE = 45\)

∴ \(CD = CE+ED = CE+AB = 45+15=60\)

∴ চিমনির উচ্চতা \(60\) মিটার।

23. একটি উড়োজাহাজ থেকে রাস্তায় পরপর দুটি কিলোমিটার ফলকের অবনতি কোণ যথাক্রমে \(60^\circ\) ও \(30^\circ\) হলে, উড়োজাহাজটির উচ্চতা নির্ণয় করি, (i) যখন ফলক দুটি উড়োজাহাজের বিপরীত পাশে অবস্থিত (ii) যখন ফলক দুটি উড়োজাহাজের একই পাশে আছে।

(i) যখন ফলক দুটি উড়োজাহাজের বিপরীত পাশে অবস্থিত

সমাধান –

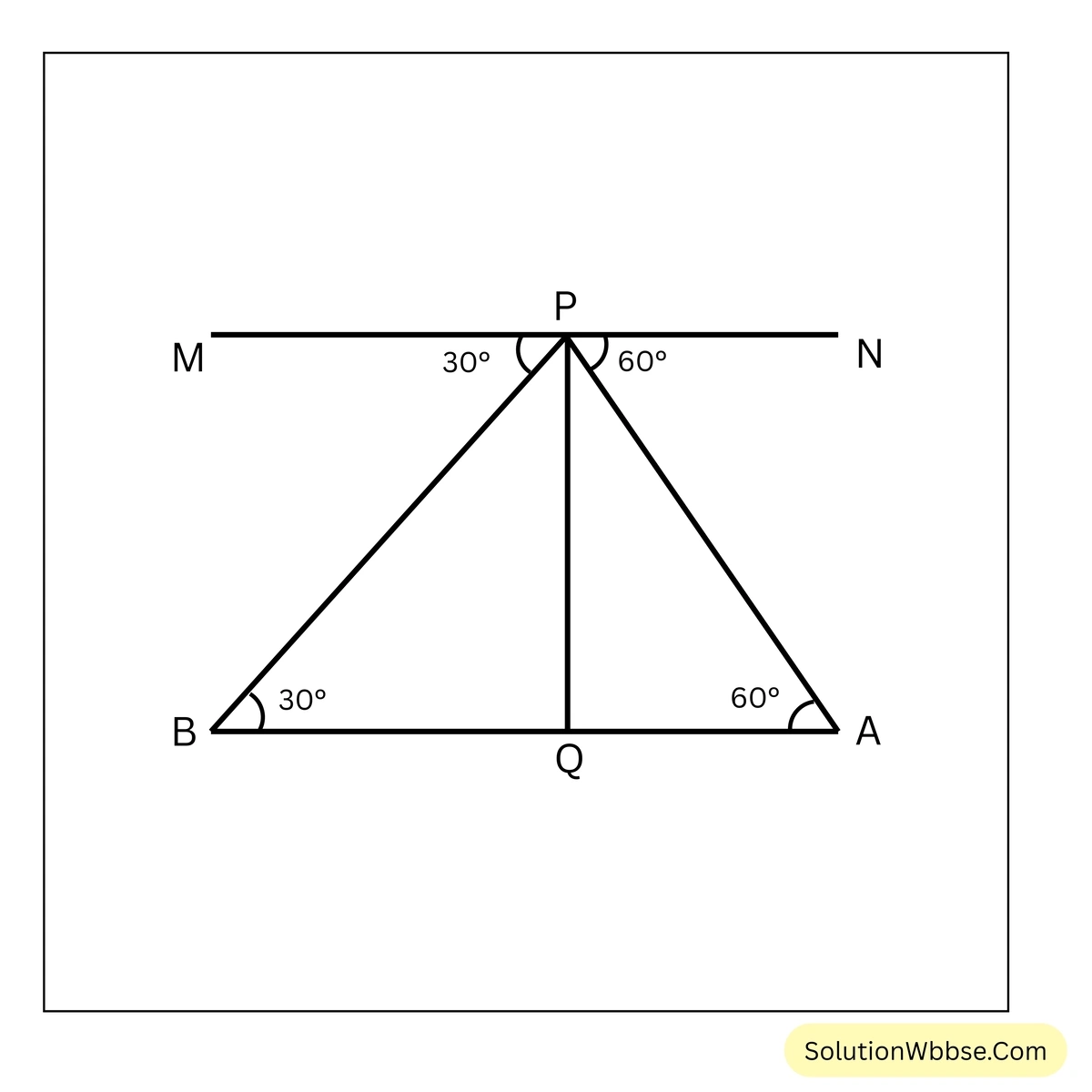
ধরাযাক, P উড়োজাহাজটির অবস্থান এবং A ও B যথাক্রমে সোজা রাস্তার উপর P –এর বিপরীত দিকে পরপর দুটি কিলোমিটার ফলক। অর্থাৎ \(AB = 1\) কিলোমিটার।

আবার, P থেকে কিলোমিটার ফলক দুটির অবনতি কোণ যথাক্রমে \(60^\circ\) ও \(30^\circ\)।

∴ \(\angle APN = 60^\circ\) এবং \(\angle BPM = 30^\circ\)

PQ ⊥ AB অঙ্কন করা হল।

এখন MN || AB, ∴ \(\angle PAQ =\) একান্তর \(\angle APN = 60^\circ\) এবং \(\angle PBQ =\) একান্তর \(\angle BPM = 30^\circ\)

∴ △APQ এর \(\angle AQP = 90^\circ\) এবং \(\angle PAQ = 60^\circ\)

∴ $\tan 60°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{PQ}}{\mathrm{QA}}$

বা, \(\sqrt{3} = \frac{PQ}{QA}\)

বা, \(\sqrt{3} QA = PQ\)

বা, \(QA = \frac{PQ}{\sqrt{3}}\) —(i)

আবার, PBQ এর \(\angle PQB = 90^\circ\) এবং \(\angle PBQ = 30^\circ\)

∴ $\tan 30°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{PQ}}{\mathrm{QB}}$

বা, \(\frac{1}{\sqrt{3}} = \frac{PQ}{QB}\)

বা, \(QB = \sqrt{3} PQ\)

বা, \(AB – QA = \sqrt{3} PQ\)

বা, \(1 – \frac{PQ}{\sqrt{3}} = \sqrt{3} PQ\) [ যেহেতু, \(AB = 1\) কিমি, এবং \(QA = \frac{PQ}{\sqrt{3}}\) ]

বা, \(\sqrt{3} PQ + \frac{PQ}{\sqrt{3}} = 1\)

বা, \(\frac{3PQ + PQ}{\sqrt{3}} = 1\)

বা, \(4PQ = \sqrt{3}\)

বা, \(PQ = \frac{\sqrt{3}}{4}\)

∴ \(PQ = \frac{\sqrt{3}}{4}\) কিমি.

∴ \(PQ = \frac{\sqrt{3}}{4} \times 1000 = 250\sqrt{3}\) মিটার

∴ উড়োজাহাজের উচ্চতা \(250\sqrt{3}\) মিটার।

(ii) যখন ফলক দুটি উড়োজাহাজের একই পাশে আছে।

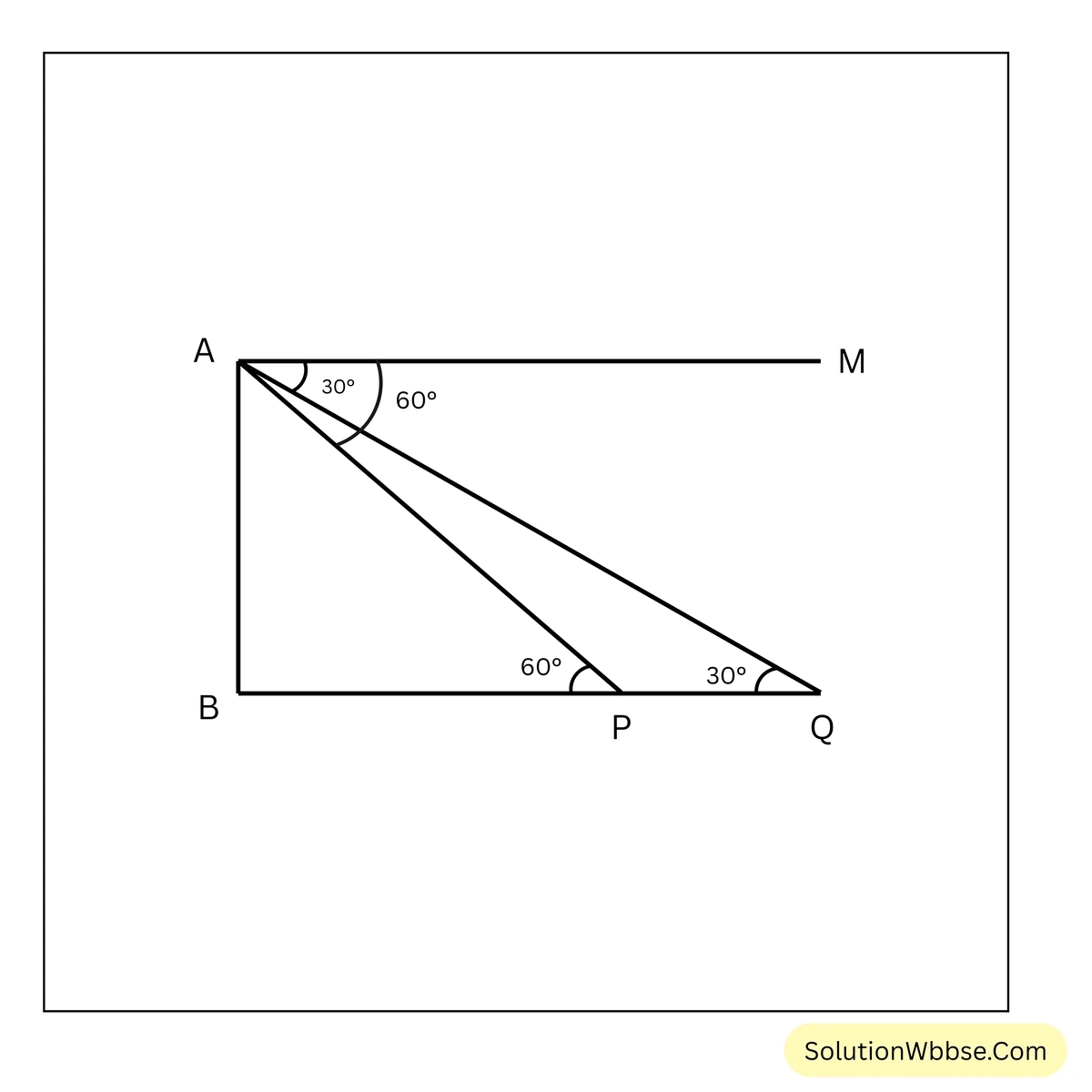
ধরি, যখন উড়োজাহাজটির অবস্থান A বিন্দুতে ছিল তখন পরস্পর দুটি কিলোমিটার ফলক P এবং Q এর অবনতি কোণ যথাক্রমে \(60^\circ\) ও \(30^\circ\) ছিল এবং উড়োজাহাজটি AB উচ্চতায় উড়ছিল।

ধরি, AM || BQ

∴ \(\angle MAP = 60^\circ\) এবং \(\angle MAQ = 30^\circ\)

\(\angle APB =\) একান্তর কোণ \(\angle MAP = 60^\circ\)

এবং \(\angle AQB =\) একান্তর কোণ \(\angle MAQ = 30^\circ\)

একইসঙ্গে \(PQ = 1\) কিমি.

সমকোণী ত্রিভুজ APB থেকে পাই

$\tan 60°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{PB}}$

বা, \(\sqrt{3} = \frac{AB}{PB}\)

বা, \(PB = \frac{AB}{\sqrt{3}}\) —(i)

সমকোণী ত্রিভুজ ABQ থেকে পাই

$\tan 30°=\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BQ}}$

বা, \(\frac{1}{\sqrt{3}} = \frac{AB}{BQ}\)

বা, \(\frac{1}{\sqrt{3}} = \frac{AB}{PB + PQ}\)

বা, \(\frac{1}{\sqrt{3}} = \frac{AB}{PB + 1}\)

বা, \(PB + 1 = \sqrt{3} AB\)

বা, \(\frac{AB}{\sqrt{3}} + 1 = \sqrt{3} AB\)

বা, \(\sqrt{3} AB – \frac{AB}{\sqrt{3}} = 1\)

বা, \(\frac{3AB – AB}{\sqrt{3}} = 1\)

বা, \(2AB = \sqrt{3}\)

বা, \(AB = \frac{\sqrt{3}}{2}\)

∴ \(AB = \frac{\sqrt{3}}{2}\) কিমি. = \(\left( \frac{\sqrt{3}}{2} \times 1000 \right)\) মিটার \(= 500\sqrt{3}\) মিটার।

সুতরাং রাস্তা থেকে উড়োজাহাজের উচ্চতা \(500\sqrt{3}\) মিটার।

24. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (M.C.Q.)

(i) মাঠের উপর একটি বিন্দু থেকে মোবাইল টাওয়ারের চূড়ার উন্নতি কোণ \(60^\circ\) এবং টাওয়ারের গোড়া থেকে ওই বিন্দুর দূরত্ব 10 মিটার। টাওয়ারের উচ্চতা

(a) 10 মিটার
(b) \(10\sqrt{3}\) মিটার
(c) \(\frac{10}{\sqrt{3}}\) মিটার
(d) 100 মিটার

উত্তর – (b) \(10\sqrt{3}\) মিটার

সমাধান –

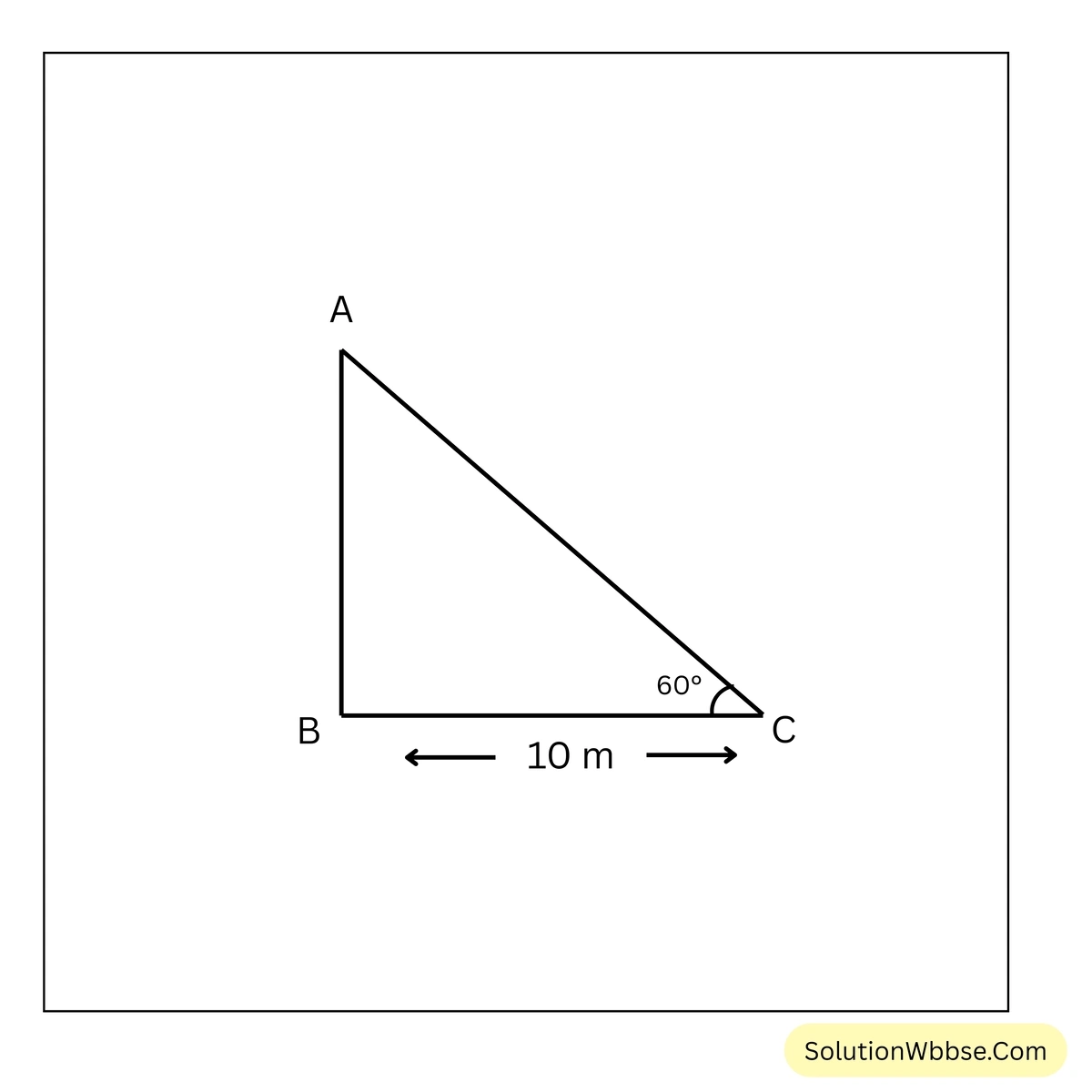
ধরি, \(AB\) হল টাওয়ারের উচ্চতা এবং মাঠের উপর \(C\) বিন্দু থেকে টাওয়ারের চূড়ার উন্নতি কোণ \(60^\circ\)

∴ \(\angle ACB = 60^\circ\)

এবং \(BC = 10\) মিটার

\(\triangle ABC\) ত্রিভুজের \(\angle ABC = 90^\circ\) এবং \(\angle ACB = 60^\circ\)

∴ $\tan 60°=\frac{\mathrm{AB}}{\mathrm{BC}}$

বা, \(\sqrt{3} = \frac{AB}{10}\)

বা, \(AB = 10\sqrt{3}\)

∴ টাওয়ারের উচ্চতা \(10\sqrt{3}\) মিটার।

(ii) θ এর মান

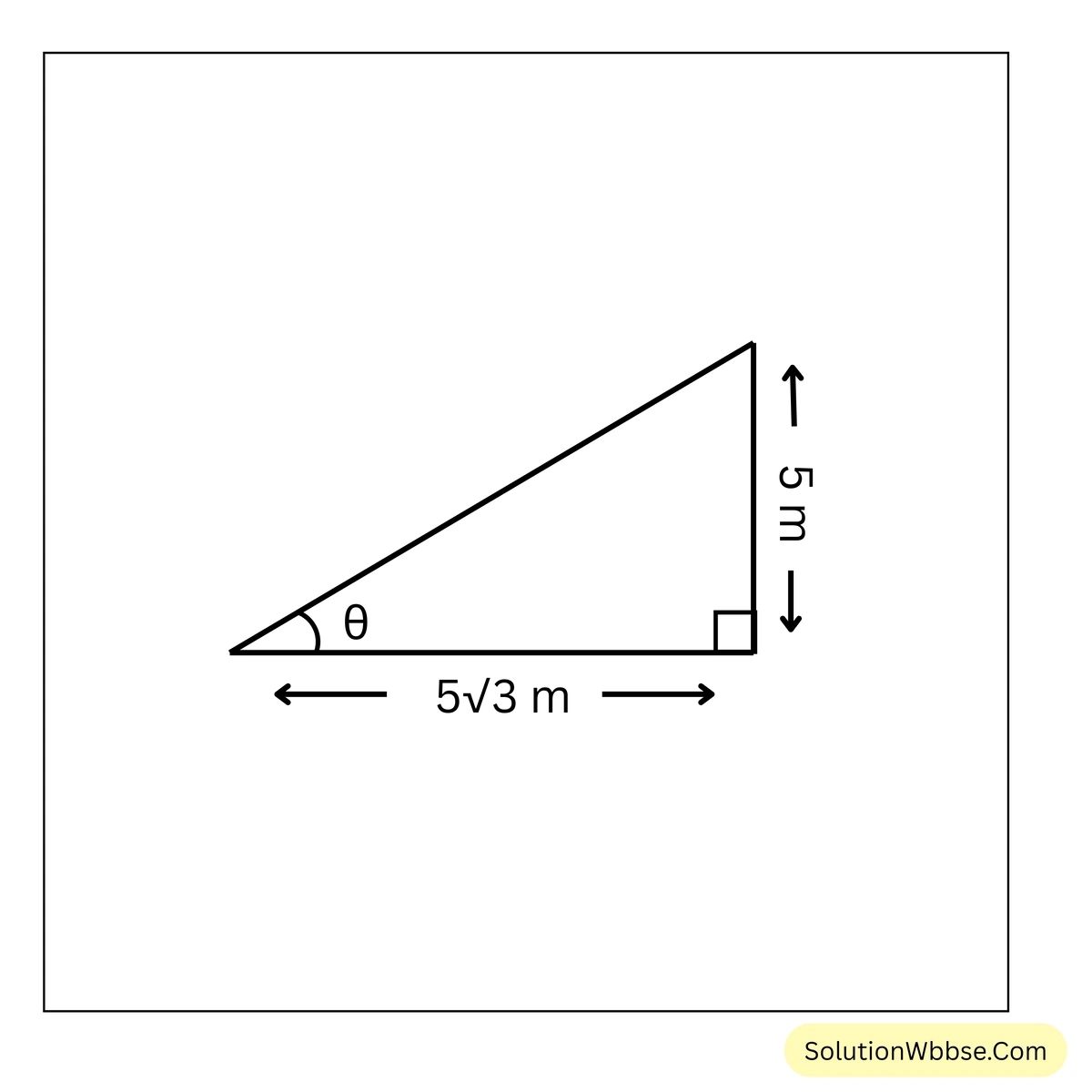
(a) 30°
(b) 45°
(c) 60°
(d) 75°

উত্তর – (a) 30°

সমাধান –

$\tan \theta =\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{5}{5\sqrt{3}}=\frac{1}{\sqrt{3}}=\tan 30°$

∴ \(\theta = 30^\circ\)

(iii) তিনতলা বাড়ির ছাদ থেকে মাটিতে পড়ে থাকা একটি বস্তুকে যত কোণে দেখলে বাড়ির উচ্চতা ও বাড়ি থেকে বস্তুটির দূরত্ব সমান হয় তা হল

(a) 15°
(b) 30°
(c) 45°
(d) 60°

উত্তর – (c) 45°

সমাধান –

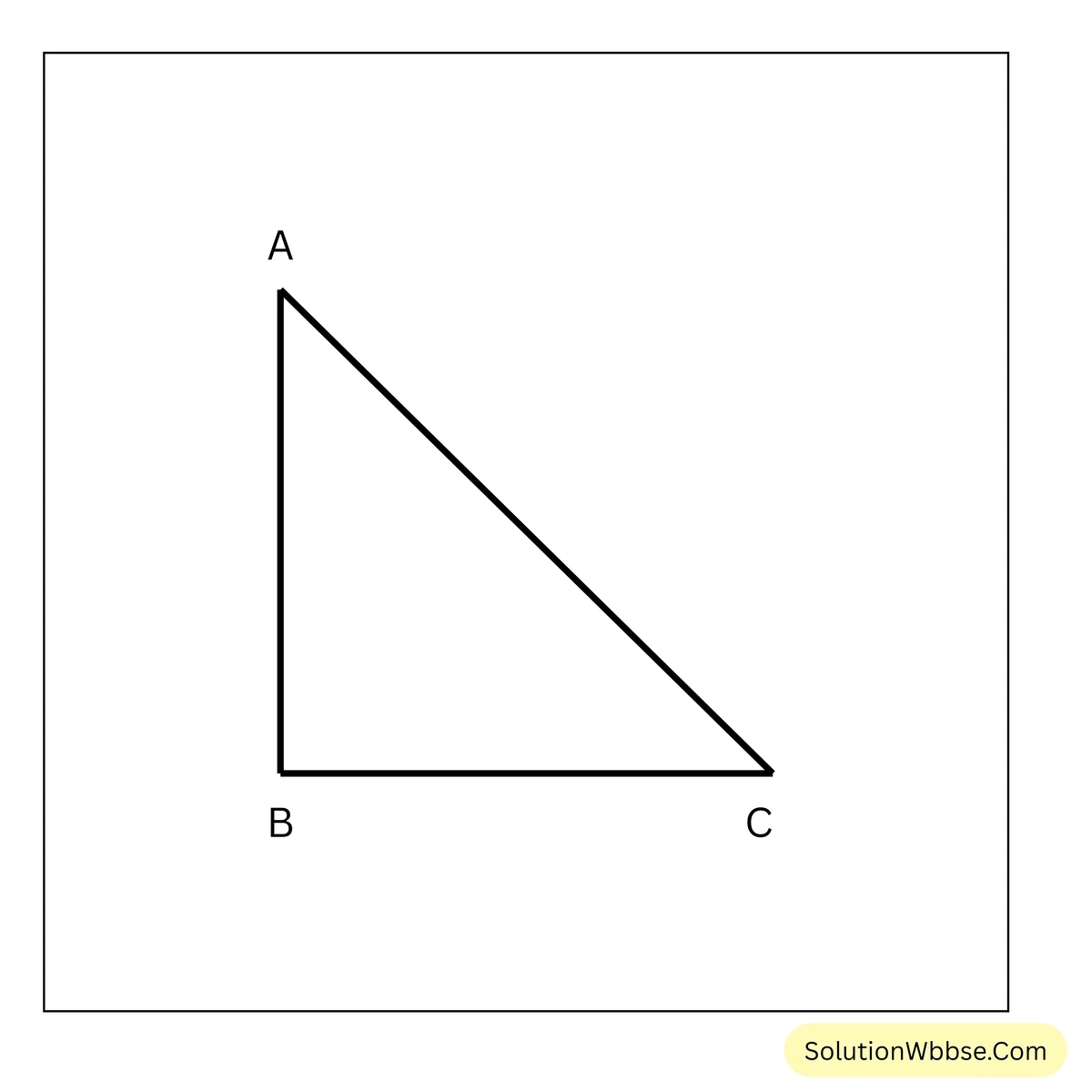
ধরাযাক, AB হল তিনতলা বাড়ি। C হল বস্তুর অবস্থান।

ধরি, ছাদ A থেকে বস্তুকে θ কোণে দেখলে বাড়ির উচ্চতা এবং বাড়ি থেকে বস্তুর দূরত্ব সমান হয়।

∴ \(AB = BC\)

∴ \(\tan \theta = \frac{AB}{BC}\)

বা, \(\tan \theta = \frac{AB}{AB}\)

বা, \(\tan \theta = 1 = \tan 45^\circ\)

বা, \(\theta = 45^\circ\)

(iv) একটি টাওয়ারের উচ্চতা \(100\sqrt{3}\) মিটার। টাওয়ারের পাদবিন্দু থেকে 100 মিটার দূরে একটি বিন্দু থেকে টাওয়ারের চূড়ার উন্নতি কোণ

(a) 30°
(b) 45°
(c) 60°
(d) কোনোটিই নয়

উত্তর – (c) 60°

সমাধান –

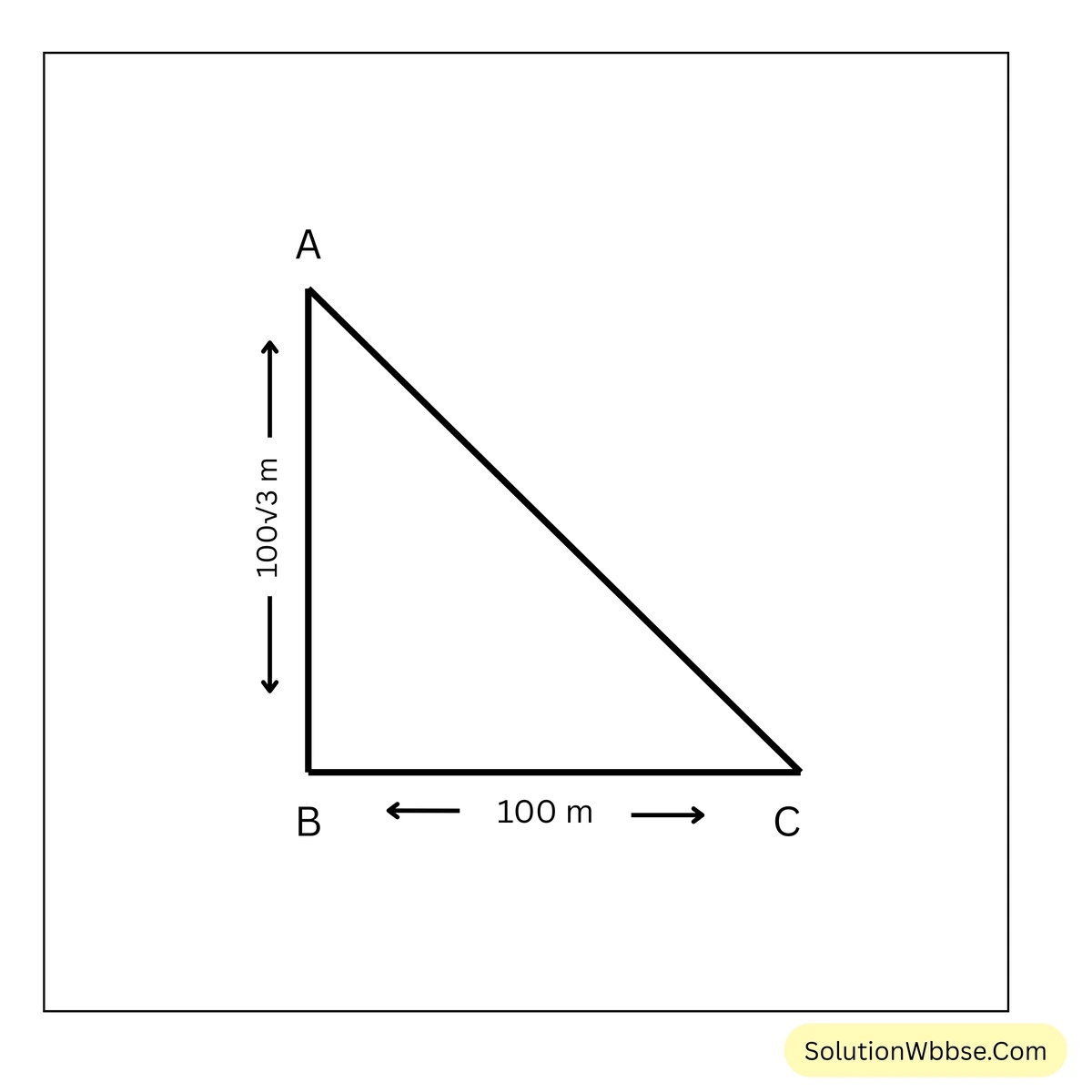
ধরাযাক, AB হল টাওয়ারের উচ্চতা। ∴ \(AB = 100\sqrt{3}\)

ধরি, AB টাওয়ারের পাদবিন্দু থেকে 100 মিটার দূরের একটি বিন্দু C থেকে টাওয়ারের চূড়ার উন্নতি কোণ \(\theta\)

∴ \(\angle ACB = \theta\) এবং \(BC = 100\) মিটার

∴ \(\tan \theta = \frac{AB}{BC}\)

বা, \(\tan \theta = \frac{100\sqrt{3}}{100}\)

বা, \(\tan \theta = \sqrt{3} = \tan 60^\circ\)

বা, \(\theta = 60^\circ\)

∴ টাওয়ারের চূড়ার উন্নতি কোণ \(60^\circ\)

(v) একটি পোস্টের ভূমিতলের ছায়ার দৈর্ঘ্য পোস্টের উচ্চতার \(\sqrt{3}\) গুণ হলে, সূর্যের উন্নতি কোণ

(a) \(30^\circ\)
(b) \(45^\circ\)
(c) \(60^\circ\)
(d) কোনোটিই নয়

উত্তর – (a) \(30^\circ\)

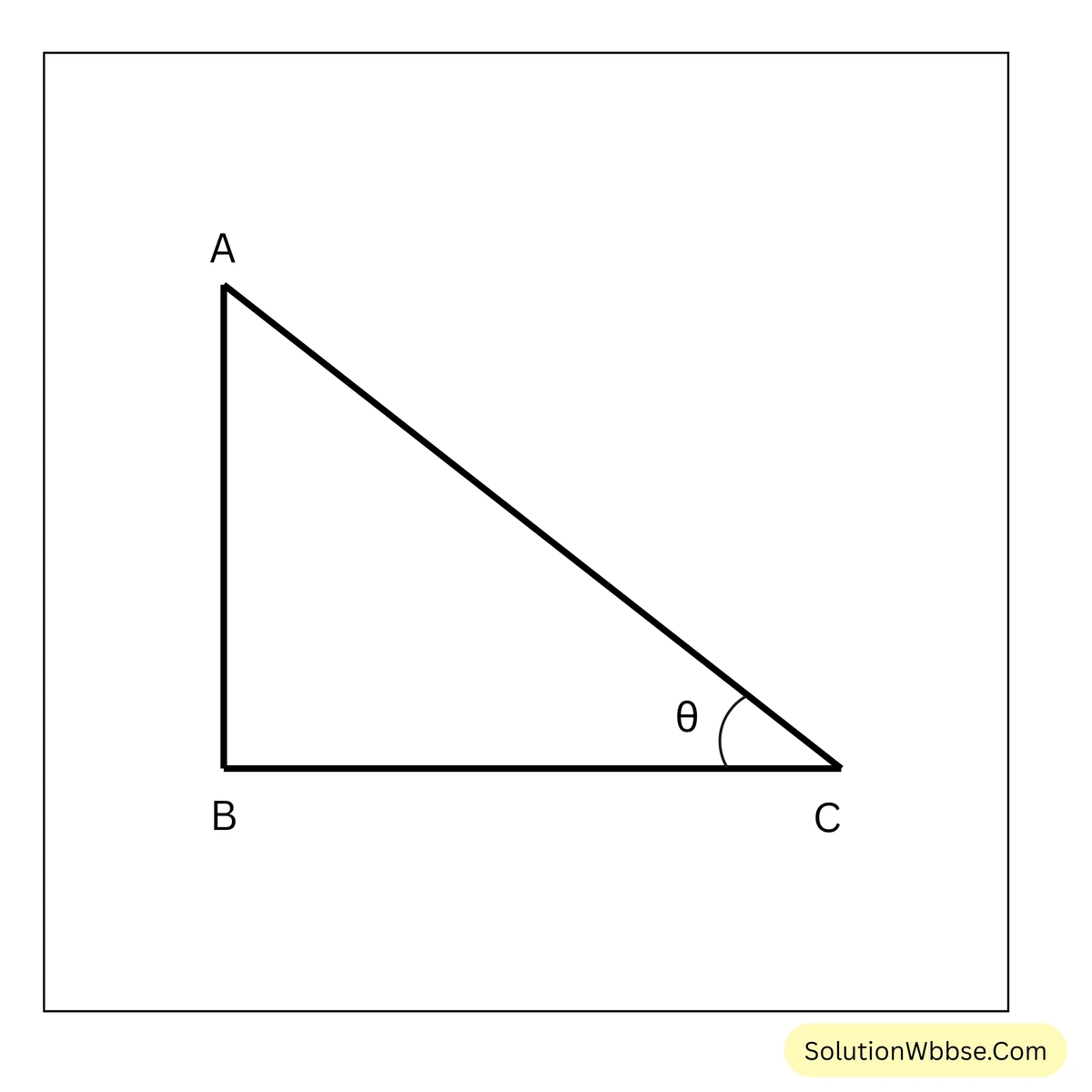
সমাধান –

ধরাযাক, পোস্টটার উচ্চতা \(AB\) এবং পোস্টের ছায়ার দৈর্ঘ্য \(BC\) এবং সূর্যের উন্নতি কোণ \(\theta\)

\(\therefore BC = \sqrt{3} AB\)

বা, \(\frac{AB}{BC} = \frac{1}{\sqrt{3}}\)

বা, \(\tan \theta = \tan 30^\circ\)

বা, \(\theta = 30^\circ\)

B. নীচের বিবৃতি গুলি সত্যি না মিথ্যা লিখি

(i) ABC এর \(\angle B=90^\circ\), AB=BC হলে \(\angle C=60^\circ\)

উত্তর – মিথ্যা

(ii) PQ একটি বাড়ির উচ্চতা, QR ভূমি। P থেকে R বিন্দুর অবনতি কোণ \(\angle SPR\); সুতরাং \(\angle SPR = \angle PRQ\)

উত্তর – সত্য

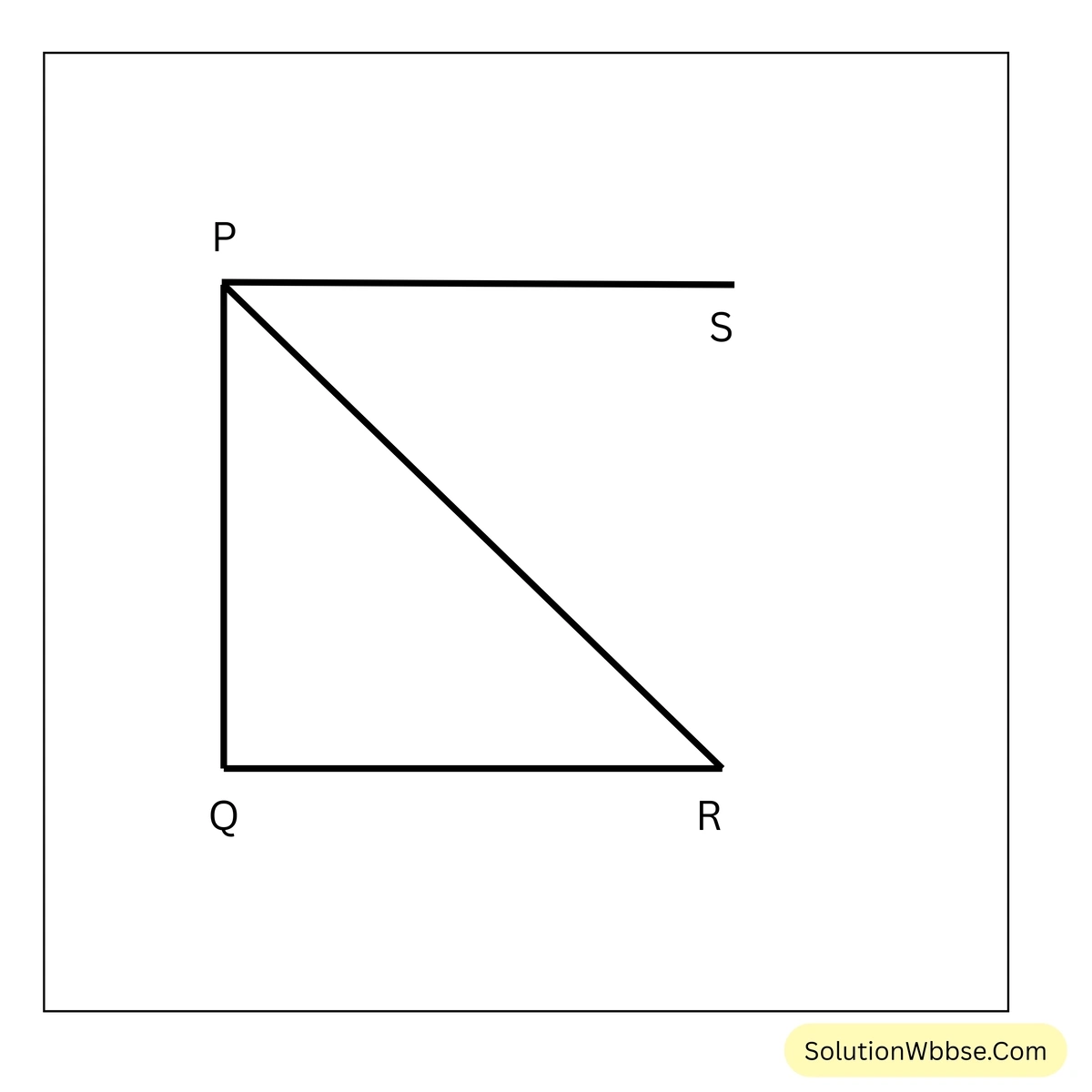
যেহেতু, PS || QR এবং PR ভেদক

\(\therefore \angle SPR = \angle PRQ\) [একান্তর কোণ]

(C) শূন্যস্থান পূরণ করি

(i) সূর্যের উন্নতি কোণ থেকে বৃদ্ধি পেয়ে হলে, একটি পোস্টের ছায়ার দৈর্ঘ্য ___________ পায়। (বৃদ্ধি/হ্রাস )

উত্তর – হ্রাস পাবে।

(ii) সূর্যের উন্নতি কোণ হলে , একটি পোস্টের দৈর্ঘ্য ও তার ছায়ার দৈর্ঘ্য ___________ হবে।

উত্তর – সমান হবে।

(iii) যখন সূর্যের উন্নতি কোণ -এর ___________ তখন একটি স্তম্ভের ছায়ার দৈর্ঘ্য স্তম্ভের উচ্চতা থেকে কম।

উত্তর – বেশি

25. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

(i) একটি ঘুড়ির উন্নতি কোণ \(60^\circ\) এবং সুতোর দৈর্ঘ্য \(20\sqrt{3}\) মিটার হলে, ঘুড়িটি মাটি থেকে কত উচ্চতায় আছে হিসাব করে লিখি।

সমাধান –

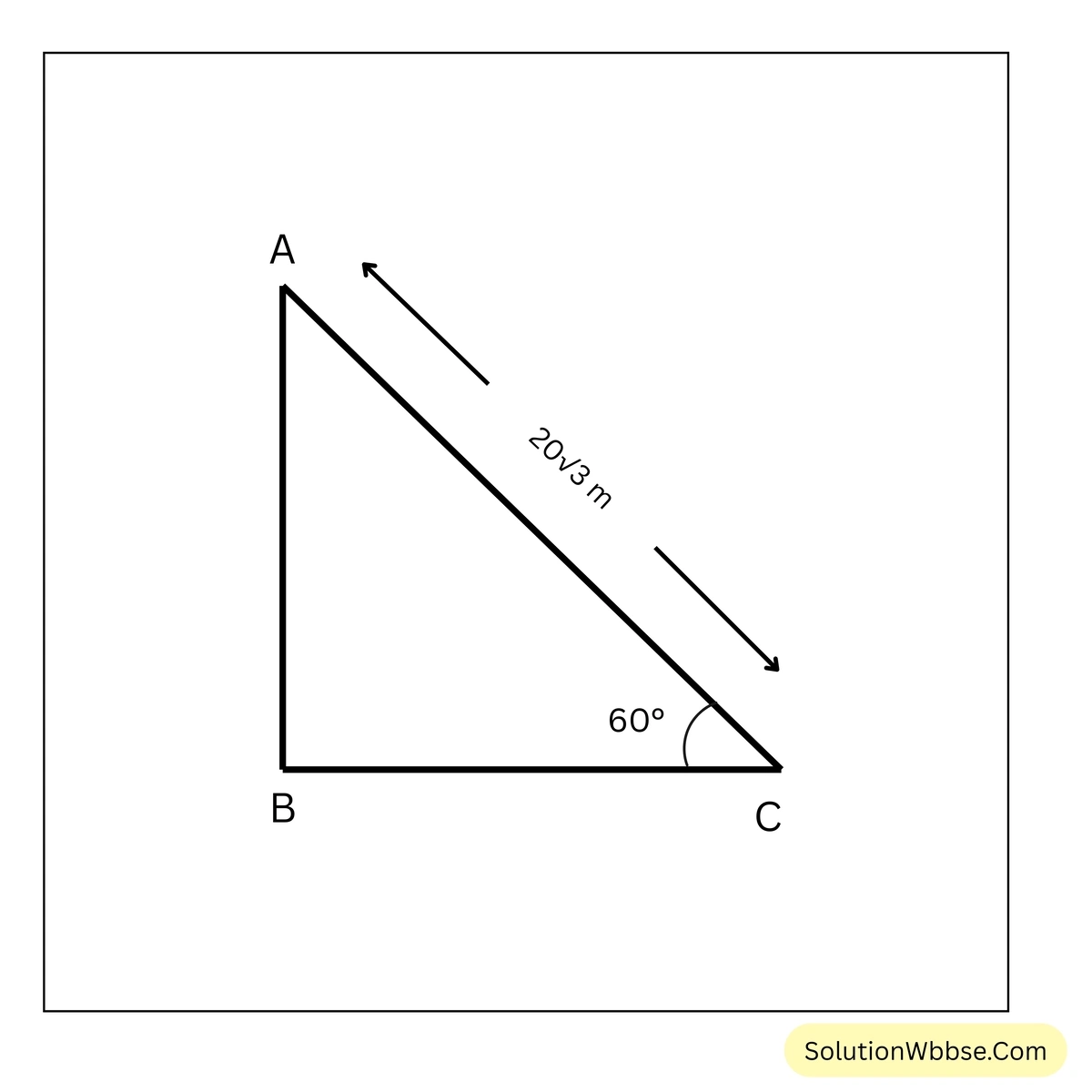
ধরাযাক, AB হল মাটি থেকে ঘুড়ির উচ্চতা। C বিন্দু থেকে A বিন্দুতে ঘুড়ির উন্নতি কোণ \(60^\circ\) এবং AC সুতোর দৈর্ঘ্য \(20\sqrt{3}\) মিটার।

ABC ত্রিভুজের \(\angle ABC=90^\circ\) এবং \(\angle ACB=60^\circ\)

\(\therefore \sin \angle ACB = \frac{AB}{AC}\)

বা, \(\sin 60^\circ = \frac{AB}{20\sqrt{3}}\)

বা, \(\frac{\sqrt{3}}{2} = \frac{AB}{20\sqrt{3}}\)

বা, \(2AB = 60\)

বা, \(AB = 60/2\)

বা, \(AB = 30\)

\(\therefore\) মাটি থেকে ঘুড়িটির উচ্চতা 30 মিটার।

(ii) একটি সমকোণী ত্রিভুজাকারক্ষেত্র ABC –এর অতিভুজ AC এর দৈর্ঘ্য \(100\) মিটার এবং \(AB =50\sqrt{3}\) মিটার হলে, \(\angle C\) এর মান নির্ণয় করি।

সমাধান –

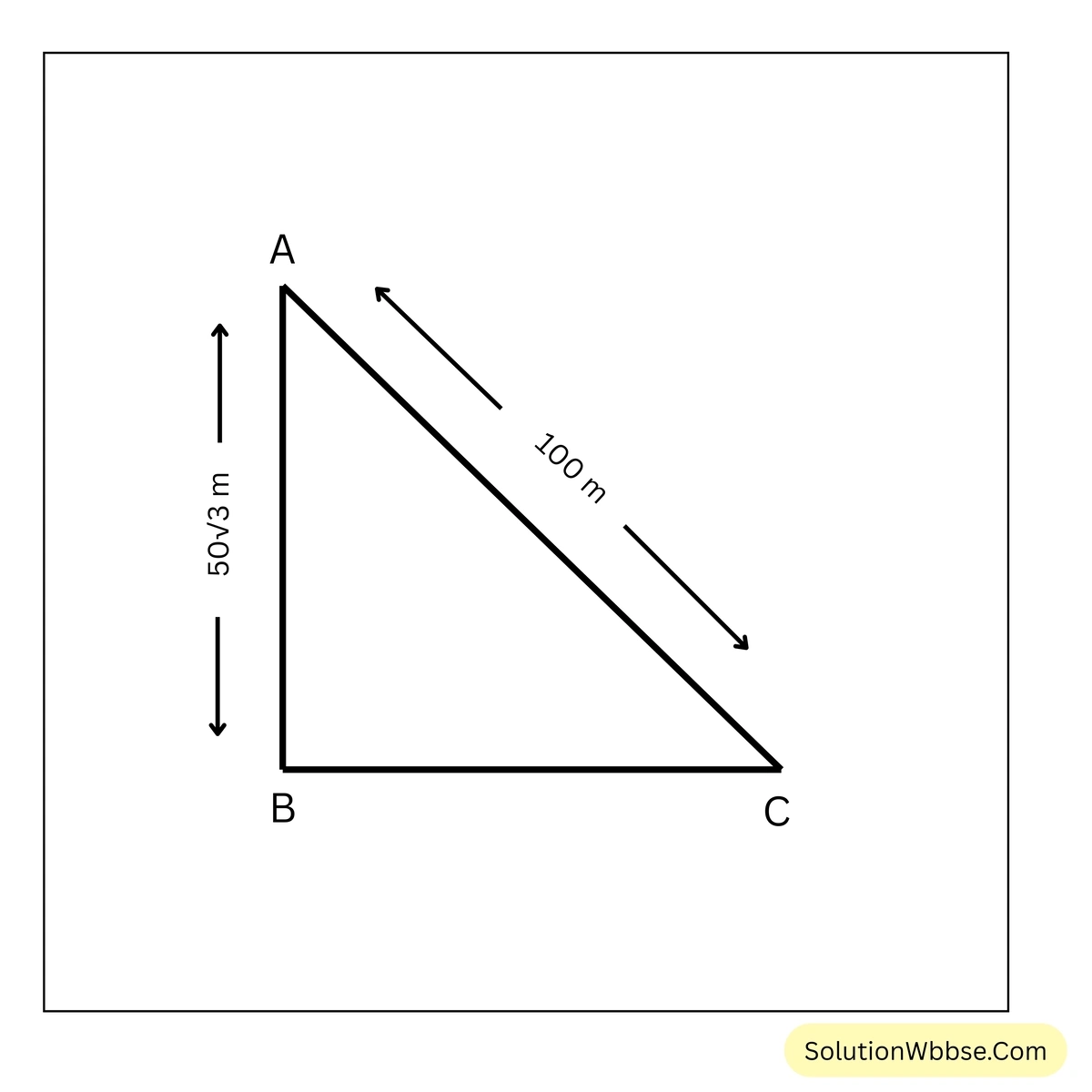
ABC সমকোণী ত্রিভুজ, C কোণের সাপেক্ষে AB হল লম্ব এবং AC হল অতিভুজ।

∴ $\sin C=\frac{\mathrm{লম্ব}}{\mathrm{অতিভুজ}}=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{50\sqrt{3}}{100}=\frac{\sqrt{3}}{2}=\sin 60°$

বা, \(\sin C = \sin 60^\circ\)

বা, \(\angle C = 60^\circ\)

(iii) ঝড়ে একটি গাছ মচকে গিয়ে তার অগ্রভাগ এমনভাবে ভূমি স্পর্শ করেছে যে গাছটির অগ্রভাগ থেকে গোড়ার দূরত্ব এবং বর্তমান উচ্চতা সমান। গাছটির অগ্রভাগ ভূমির সাথে কত কোণ করেছে হিসাব করে লিখি।

সমাধান –

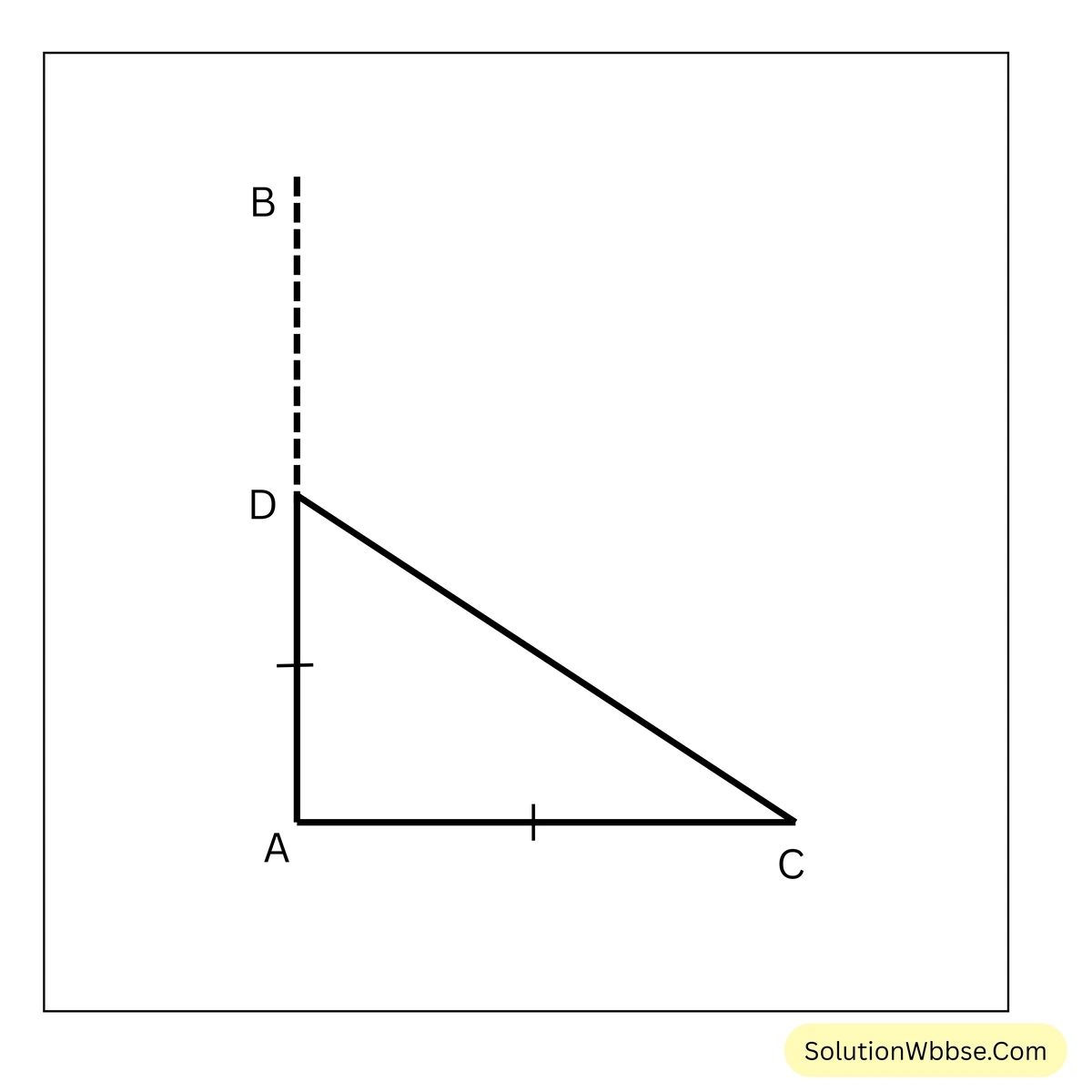
ধরাযাক, AB গাছটি ঝড়ে D বিন্দুতে মচকে গিয়ে গাছটির অগ্রভাগ C বিন্দুতে ভূমি স্পর্শ করেছে।
প্রশ্নানুসারে, \(AD = AC\)

বা, \(\frac{AD}{AC}=1\)

বা, \(\frac{DB}{BC}=1\)

বা, \(\tan \angle C =1 = \tan 45^\circ\)

বা, \(\angle C = 45^\circ\)

∴ গাছটির অগ্রভাগ ভূমির সাথে \(45^\circ\) কোণ করেছে।

(iv) ABC সমকোণী ত্রিভুজের \(\angle B = 90^\circ\), AB –এর উপর D এমন বিন্দু যে AB:BC:BD = \(\sqrt{3}:1:1\), \(\angle ACD\) –এর মান কত হিসাব করে লিখি।

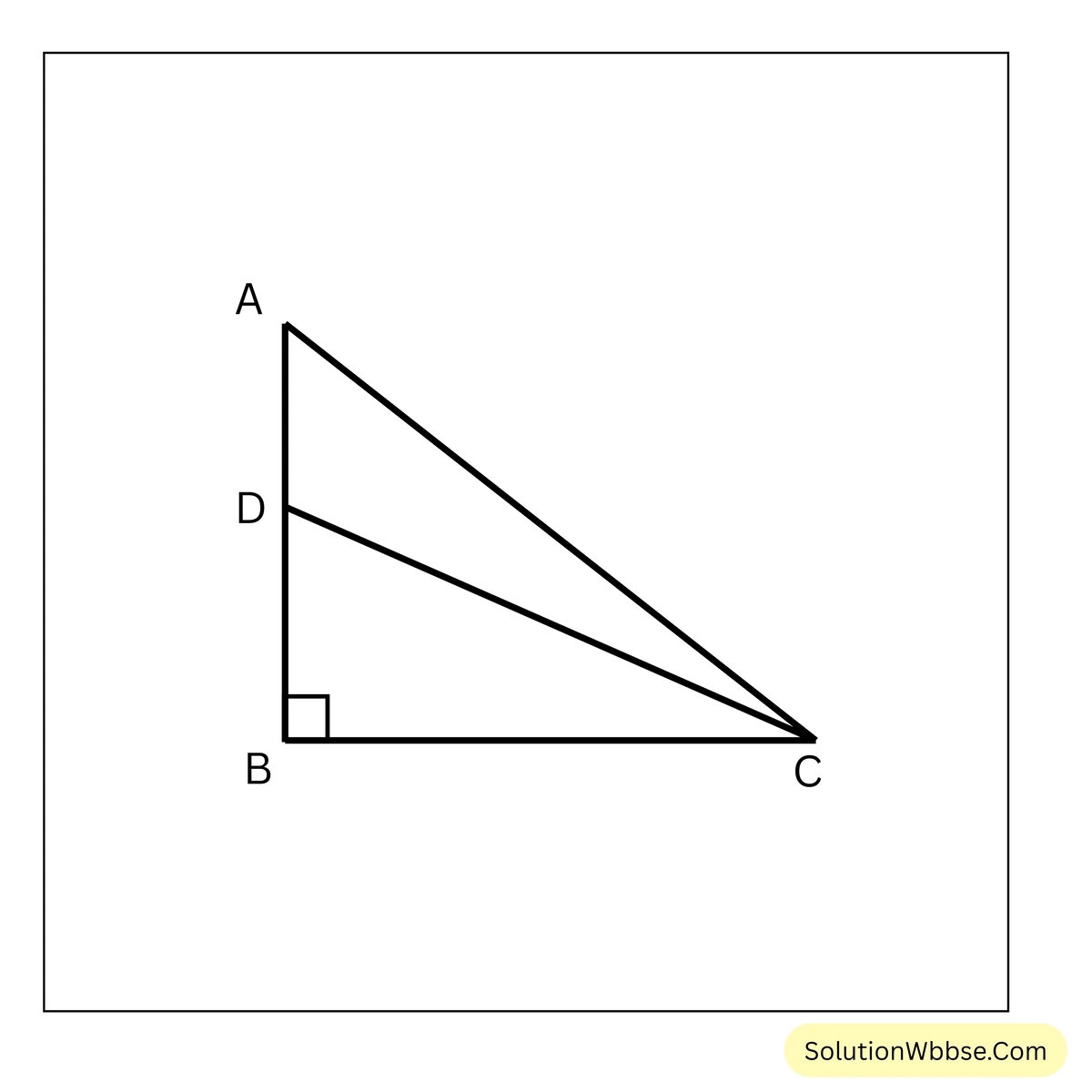
সমাধান –

ধরি, AB, BC এবং BD –এর দৈর্ঘ্য যথাক্রমে \(\sqrt{3}x\) একক, \(x\) একক এবং \(x\) একক।
ত্রিভুজ ABC এর, \(\angle ABC = 90^\circ\)

∴ \(\tan \angle ACB = \frac{AB}{BC} = \frac{\sqrt{3}x}{x} = \sqrt{3} = \tan 60^\circ\)

বা, \(\angle ACB = 60^\circ\)

আবার, ত্রিভুজ DBC এর ক্ষেত্রে \(\angle DBC = 90^\circ\)

∴ \(\tan \angle DCB = \frac{DB}{BC} = \frac{x}{x} = 1 = \tan 45^\circ\)

বা, \(\angle DCB = 45^\circ\)

∴ \(\angle ACD = \angle ACB – \angle DCB = 60^\circ – 45^\circ = 15^\circ\)

(v) একটি স্তম্ভের ছায়ার দৈর্ঘ্য এবং স্তম্ভের উচ্চতার অনুপাত \(\sqrt{3}:1\) হলে, সূর্যের উন্নতি কোণ নির্ণয় করি।

সমাধান –

ধরি, AB স্তম্ভের ছায়ার দৈর্ঘ্য BC যখন সূর্যের উন্নতি কোণ \(\theta\)।

এখন ABC ত্রিভুজের, \(\angle ABC = 90^\circ\)

∴ $\tan \theta =\frac{\mathrm{লম্ব}}{\mathrm{ভূমি}}=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{1}{\sqrt{3}}=\tan 30°$

বা, \(\theta = 30^\circ\), সূর্যের উন্নতি কোণ \(30^\circ\)

---

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের পঞ্চবিংশ অধ্যায়, ‘ত্রিকোণমিতিক অনুপাতের প্রয়োগ: উচ্চতা ও দূরত্ব’ -এর ‘কষে দেখি – 25’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।

আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।