এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের ষোড়শ অধ্যায়, ‘লম্ব বৃত্তাকার শঙ্কু’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

প্রয়োগ 1. আমি যে মুখখোলা লম্ব বৃত্তাকার শঙ্কু তৈরি করেছি তার ভূমির ব্যাসের দৈর্ঘ্য 14 সেমি এবং তির্যক উচ্চতা 12 সেমি হলে, ওই শঙ্কু তৈরি করতে কী পরিমাণ কাগজ লেগেছে হিসাব করে লিখি।
সমাধান –
লম্ব বৃত্তাকার শঙ্কুর ভূমির ব্যাসার্ধ (r) = 14/2 = 7 সেমি এবং তির্যক উচ্চতা (l) = 12 সেমি।
∴ লম্ব বৃত্তাকার শঙ্কুর পার্শ্বতলের ক্ষেত্রফল = \(\pi r l\) বর্গ সেমি
= \(\frac{22}{7} \times 7 \times 12\) বর্গ সেমি
= \(264\) বর্গ সেমি
উত্তর – শঙ্কুটি তৈরি করতে 264 বর্গ সেমি কাগজ লেগেছে।
প্রয়োগ 2. যে লম্ব বৃত্তাকার শঙ্কুর ভূমির ব্যাসার্ধ 1.5 মিটার এবং তির্যক উচ্চতা 2 মিটার তার পার্শ্বতলের ক্ষেত্রফল হিসাব করে লিখি।
সমাধান –
লম্ব বৃত্তাকার শঙ্কুর ভূমির ব্যাসার্ধ (r) = 1.5 মিটার এবং তির্যক উচ্চতা (I) = 2 মিটার।
∴ লম্ব বৃত্তাকার শঙ্কুর পার্শ্বতলের ক্ষেত্রফল = \(\pi r l\) বর্গ মিটার
= \(\frac{22}{7}\) × 1.5 × 2 বর্গ মিটার
= \(\frac{66}{7}\) বর্গ মিটার
= 9\(\frac{3}{7}\) বর্গ মিটার
উত্তর – শঙ্কুটির পার্শ্বতলের ক্ষেত্রফল 9\(\frac{3}{7}\) বর্গ মিটার।
প্রয়োগ 3. কোনো শঙ্কুর ভূমির ক্ষেত্রফল \(78 \frac{4}{7}\) বর্গ সেমি. এবং তির্যক উচ্চতা \(13\) সেমি. হলে, শঙ্কুর পার্শ্বতলের ক্ষেত্রফল হিসাব করে লিখি।
সমাধান –
ধরি, শঙ্কুর ভূমির ব্যাসার্ধের দৈর্ঘ্য \(r\) সেমি।
শর্তানুসারে, \(\frac{22}{7} r^2 = 78 \frac{4}{7}\)
বা, \(\frac{22}{7} r^2 = \frac{550}{7}\)
বা, \(22 r^2 = 550\)
বা, \(r^2 = \frac{550}{22} = 25\)
বা, \(r = 5\) সেমি।
∴ শঙ্কুর পার্শ্বতলের ক্ষেত্রফল = \(\pi r l\) বর্গ সেমি
= \(\frac{22}{7} \times 5 \times 13\) বর্গ সেমি
= \(\frac{1430}{7}\) বর্গ সেমি
= \(204 \frac{2}{7}\) বর্গ সেমি।
উত্তর – শঙ্কুর পার্শ্বতলের ক্ষেত্রফল \(204 \frac{2}{7}\) বর্গ সেমি।
প্রয়োগ 4. কোনো শঙ্কুর ভূমির পরিধি \(\frac{660}{7}\) সেমি. এবং তির্যক উচ্চতা 25 সেমি. হলে, শঙ্কুর পার্শ্বতলের ক্ষেত্রফল কত?
সমাধান –
ধরি, শঙ্কুর ব্যাসার্ধ \(r\) সেমি.
শর্তানুসারে,
\(2\pi r = \frac{660}{7}\)বা, \(2 \times \frac{22}{7} \times r = \frac{660}{7}\)
বা, \(44r = 660\)
বা, \(r = \frac{660}{44}\)
বা, \(r = 15\)
∴ শঙ্কুর ব্যাসার্ধ \(r = 15\) সেমি.
আবার শঙ্কুর তির্যক উচ্চতা (\(l\)) = 25 সেমি.
∴ শঙ্কুর পার্শ্বতলের ক্ষেত্রফল = \(\pi r l\) বর্গ সেমি.
= \(\frac{22}{7} \times 15 \times 25\) বর্গ সেমি.
= \(\frac{8250}{7}\) বর্গ সেমি.
= \(1178 \frac{4}{7}\) বর্গ সেমি.
উত্তর – শঙ্কুর পার্শ্বতলের ক্ষেত্রফল \(1178 \frac{4}{7}\) বর্গ সেমি.
প্রয়োগ 5. যে শঙ্কুর ভূমির ব্যাসার্ধের দৈর্ঘ্য 1.5 সেমি. এবং তির্যক উচ্চতা 2.5 সেমি., তার সমগ্রতলের ক্ষেত্রফল হিসাব করে লিখি।
সমাধান –
শঙ্কুর ভূমির ব্যাসার্ধ \(r = 1.5\) সেমি. এবং তির্যক উচ্চতা \(l = 2.5\) সেমি.
∴ শঙ্কুর সমগ্রতলের ক্ষেত্রফল = \(\pi r (l + r)\) বর্গ সেমি.
= \(\frac{22}{7} \times 1.5 \times (2.5 + 1.5)\) বর্গ সেমি.
= \(\frac{22}{7} \times 1.5 \times 4\) বর্গ সেমি.
= \(\frac{22}{7} \times 6\) বর্গ সেমি.
= \(\frac{132}{7}\) বর্গ সেমি.
= \(18 \frac{6}{7}\) বর্গ সেমি.
উত্তর – শঙ্কুটির সমগ্রতলের ক্ষেত্রফল \(18 \frac{6}{7}\) বর্গ সেমি।
প্রয়োগ 6. যে শঙ্কুর ভূমির ব্যাসের দৈর্ঘ্য \(20\) সেমি. এবং তির্যক উচ্চতা \(25\) সেমি.। তার সমগ্রতলের ক্ষেত্রফল কত হবে হিসাব করে লিখি।
সমাধান –
শঙ্কুটির ব্যাসের দৈর্ঘ্য \(20\) সেমি.
∴ ব্যাসার্ধ (r) = \(20/2\) সেমি. = \(10\) সেমি.
তির্যক উচ্চতা (I) = \(25\) সেমি.
শঙ্কুটির সমগ্রতলের ক্ষেত্রফল = \(\pi r l + \pi r^2\) বর্গ সেমি.
= \(\pi r (l + r)\) বর্গ সেমি.
= \(\frac{22}{7} \times 10 \times (25 + 10)\) বর্গ সেমি.
= \(\frac{22}{7} \times 10 \times 35\) বর্গ সেমি.
= \((22 \times 50)\) বর্গ সেমি.
= \(1100\) বর্গ সেমি.
উত্তর – শঙ্কুটির সমগ্রতলের ক্ষেত্রফল \(1100\) বর্গ সেমি.
প্রয়োগ 7. একটি লম্ব বৃত্তাকার শঙ্কু তৈরি করেছি যার ভূমির ব্যাসের দৈর্ঘ্য \(12\) সেমি. এবং তির্যক উচ্চতা \(10\) সেমি.। ওই শঙ্কুটির উচ্চতা কত হবে হিসাব করে লিখি।
সমাধান –
লম্ব বৃত্তাকার শঙ্কুর ভূমির ব্যাসার্ধের দৈর্ঘ্য = \(\frac{1}{2}\) \(\times\) \(12\) সেমি. = \(6\) সেমি.
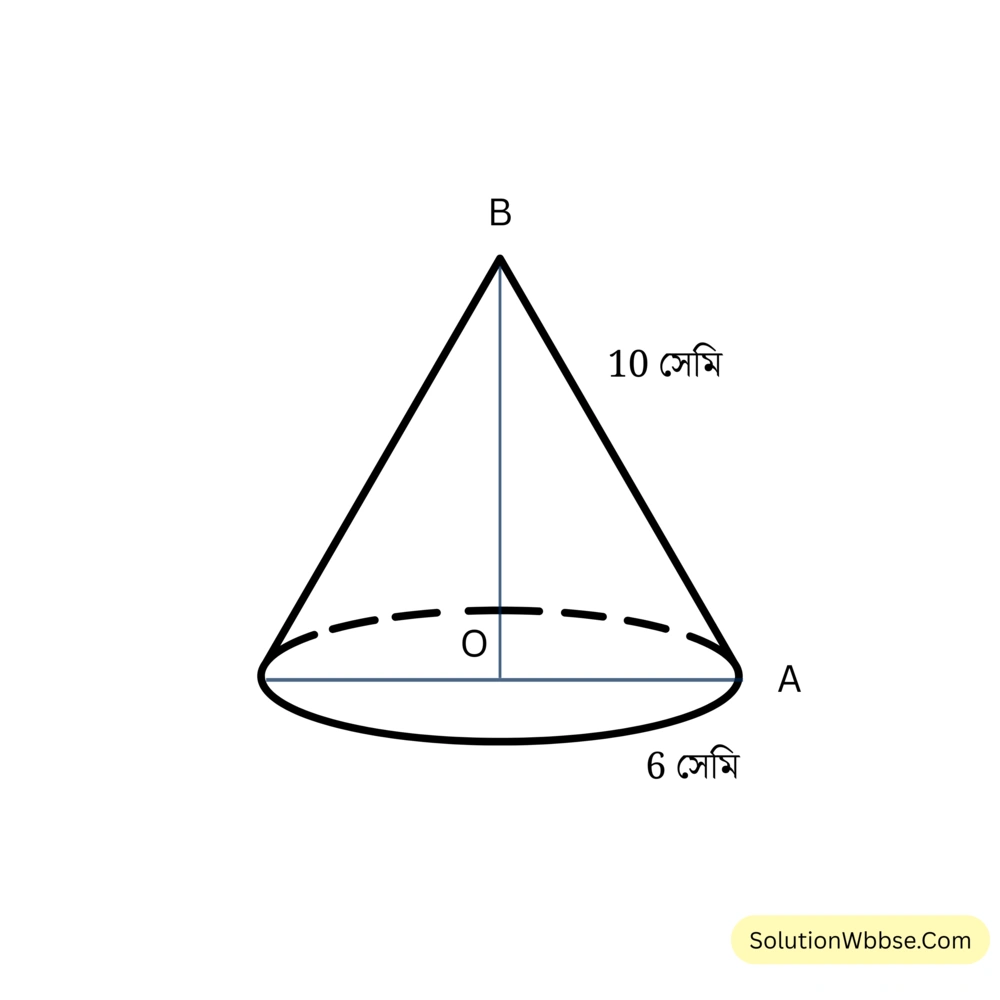
চিত্রে শঙ্কুর ভূমির ব্যাসার্ধ OA, তির্যক উচ্চতা AB এবং উচ্চতা OB
OA = \(6\) সেমি., AB = \(10\) সেমি. শঙ্কুর উচ্চতা = OB
∴ সমকোণী ত্রিভুজ OAB-তে, \(AB^2 = OB^2 + OA^2\) (পিথাগোরাসের উপপাদ্য থেকে পেলাম)
বা, \(OB^2 = AB^2 – OA^2\)
বা, OB = \(\sqrt{AB^2 – OA^2}\) [ ∵ উচ্চতা ঋণাত্মক হতে পারে না]
== \(\sqrt{(10)^2 – 6^2}\) সেমি.
= \(\sqrt{64}\) সেমি.
= \(8\) সেমি.
উত্তর – শঙ্কুর উচ্চতা \(8\) সেমি.
প্রয়োগ 8. যে লম্ব বৃত্তাকার শঙ্কুর পরিধি \(\frac{660}{7}\) সেমি এবং উচ্চতা 20 সেমি, তার তির্যক উচ্চতা হিসাব করে লিখি।
সমাধান –
ধরি, লম্ব বৃত্তাকার শঙ্কুটির ব্যাসার্ধ r সেমি এবং শঙ্কুটির তির্যক উচ্চতা l সেমি।
\(2\pi r = \frac{660}{7}\)বা, \(2 \times \frac{22}{7} \times r = \frac{660}{7}\)
বা, \(44r = 660\)
বা, \(r = \frac{660}{44}\)
বা, \(r = \frac{60}{4}\)
বা, \(r = 15\)
\(\therefore\) শঙ্কুটির ব্যাসার্ধ 15 সেমি।
শঙ্কুটির উচ্চতা (h) = 20 সেমি। (প্রদত্ত)
আমরা জানি,
\(l^2 = h^2 + r^2\)বা, \(l^2 = (20)^2 + (15)^2\)
বা, \(l^2 = 400 + 225\)
বা, \(l^2 = 625\)
বা, \(l^2 = (25)^2\)
বা, \(l = 25\)
উত্তর – শঙ্কুটির তির্যক উচ্চতা 25 সেমি।
প্রয়োগ 9. স্কুলের বিজ্ঞানের ল্যাবরেটরির শঙ্কু আকৃতির ফ্লাক্সের উচ্চতা \(4\) ডেসিমি. এবং তির্যক উচ্চতা \(5\) ডেসিমি. হলে, ওই ফ্লাক্সে কী পরিমাণ জল ধরবে তা হিসাব করে লিখি।
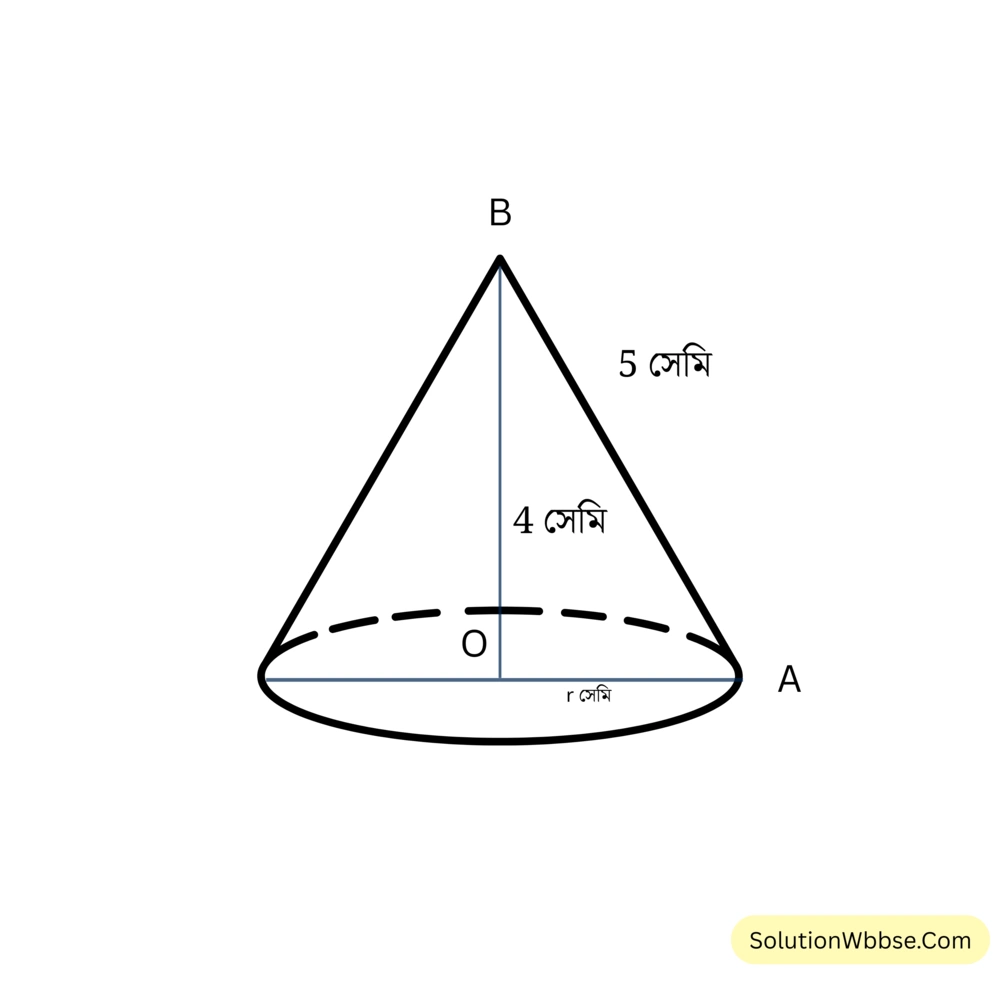
সমাধান –
ধরি, শঙ্কু আকৃতির ফ্লাক্সের ভূমির ব্যাসার্ধের দৈর্ঘ্য = \(r\) ডেসিমি.
সুতরাং \((5)^2 = r^2 + (4)^2\)
বা, \(r^2 = 5^2 – 4^2 = 9\)
∴ \(r = \pm 3\)
কিন্তু ব্যাসার্ধের দৈর্ঘ্য ঋণাত্মক হতে পারে না।
∴ \(r \neq -3\)
∴ \(r = 3\)
∴ ওই ফ্লাক্সে জল ধরবে = \(\frac{1}{3} \times \frac{22}{7} \times 3 \times 3 \times 4\) ঘন ডেসিমি. = \(\frac{264}{7}\) ঘন ডেসিমি.
উত্তর – ওই ফ্লাক্সে জল ধরবে \(\frac{264}{7}\) ঘন ডেসিমি.
প্রয়োগ 10. যদি কোনো লম্ব বৃত্তাকার শঙ্কুর ভূমির পরিধি \(2.2\) মিটার এবং উচ্চতা \(45\) ডেসিমি. হয়, তবে ওই লম্ব বৃত্তাকার শঙ্কুর আয়তন হিসাব করে লিখি।
সমাধান –
ধরি, লম্ব বৃত্তাকার শঙ্কুর ব্যাসার্ধ \(r\) ডেসিমি.
ভূমির পরিধি = \(2.2\) মিটার = \(22\) ডেসিমি.
শঙ্কুটির উচ্চতা (\(h\)) = \(45\) ডেসিমি.
\(\therefore 2\pi r = 22\)বা, \(2 \times \frac{22}{7} \times r = 22\)
বা, \(r = \frac{22 \times 7}{22 \times 2}\)
বা, \(r = \frac{7}{2}\)
বা, \(r = 3.5\)
শঙ্কুটির আয়তন = \(\frac{1}{3} \pi r^2 h\)
= \(\frac{1}{3} \times \frac{22}{7} \times (3.5)^2 \times 45\) ঘনডেসিমি.
= \(\frac{1}{3} \times \frac{22}{7} \times 12.25 \times 45\) ঘনডেসিমি.
= \(1.75 \times 15 \times 22\) ঘনডেসিমি.
= \(577.5\) ঘনডেসিমি.
উত্তর – শঙ্কুটির আয়তন \(577.5\) ঘন ডেসিমি.
প্রয়োগ 11. একটি সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহু দুটির দৈর্ঘ্য 4 সেমি. ও 3 সেমি.। সমকোণ সংলগ্ন বাহু দুটির দীর্ঘ বাহুটিকে অক্ষ ধরে ত্রিভুজটিকে একবার পূর্ণ আবর্তন করলে যে ঘনবস্তু তৈরি হয়, তার পার্শ্বতলের ক্ষেত্রফল, সমগ্রতলের ক্ষেত্রফল এবং আয়তন হিসাব করে লিখি।
সমাধান –
লম্ব বৃত্তাকার শঙ্কুর তির্যক উচ্চতা \(l = \sqrt{(4)^2 + (3)^2}\)
= \( \sqrt{16+9}\)
= \( \sqrt{25}\)
= \( 5\) সেমি.
∴ পার্শ্বতলের ক্ষেত্রফল = \(\pi r l\)
= \( \pi \times 3 \times 5\)
= \( 15\pi\) বর্গ সেমি.
সমগ্রতলের ক্ষেত্রফল = \(\pi r (r+l)\)
= \( \pi \times 3 \times (3+5)\)
= \( \pi \times 3 \times 8\)
= \( 24\pi\) বর্গ সেমি.
আয়তন = \(\frac{1}{3} \pi r^2 h\)
= \( \frac{1}{3} \pi \times 9 \times 4\)
= \( 12\pi\) ঘন সেমি.
প্রয়োগ 12. একটি লম্ব বৃত্তাকার শঙ্কুর তির্যক উচ্চতা \(7\) সেমি. এবং সমগ্রতলের ক্ষেত্রফল \(147.84\) বর্গ সেমি.। শঙ্কুটির ভূমির ব্যাসার্ধের দৈর্ঘ্য নির্ণয় করি।
সমাধান –
ধরি, শঙ্কুটির ভূমির ব্যাসার্ধের দৈর্ঘ্য = \(r\) সেমি.
∴ শঙ্কুর সমগ্রতলের ক্ষেত্রফল = \(\frac{22}{7} r (r+7)\) বর্গ সেমি.
শর্তানুসারে, \(\frac{22}{7} r (r+7) = 147.84\)
বা, \(r (r+7) = \frac{14784}{100} \times \frac{7}{22} = \frac{1176}{25}\)
বা, \(25r^2 + 175r – 1176 = 0\)
বা, \(25r^2 + 280r – 105r – 1176 = 0\)
বা, \(5r (5r + 56) – 21 (5r + 56) = 0\)
বা, \((5r + 56) (5r – 21) = 0\)
হয়, \(5r – 21 = 0\) বা, \(5r = 21\) বা, \(r = \frac{21}{5}\)
∴ \(r = 4.2\)
অথবা, \(5r + 56 = 0\) বা, \(5r = -56\)
∴ \(r = -\frac{56}{5}\)
কিন্তু ব্যাসার্ধের দৈর্ঘ্য ঋণাত্মক হতে পারে না।
∴ \(r \neq -\frac{56}{5}\)
সুতরাং \(r = 4.2\)
উত্তর – শঙ্কুটির ভূমির ব্যাসার্ধের দৈর্ঘ্য \(4.2\) সেমি.
প্রয়োগ 13. যদি দুটি লম্ব বৃত্তাকার শঙ্কুর উচ্চতার অনুপাত 1 : 3 এবং তাদের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত যথাক্রমে 3 : 1 হয়, তবে হিসাব করে দেখাই যে শঙ্কুদ্বয়ের আয়তনের অনুপাত 3 : 1 হবে।
সমাধান –
ধরি, প্রথম শঙ্কুর উচ্চতা \(x\) একক এবং দ্বিতীয় শঙ্কুর উচ্চতা \(3x\) একক, যেখানে \(x > 0\);
আবার, প্রথম শঙ্কুর ব্যাসার্ধের দৈর্ঘ্য \(3y\) একক এবং দ্বিতীয় শঙ্কুর ব্যাসার্ধের দৈর্ঘ্য \(y\) একক, যেখানে \(y > 0\)
সুতরাং,
প্রথম শঙ্কুর আয়তন / দ্বিতীয় শঙ্কুর আয়তন
= \(\frac{\frac{1}{3} \times \pi \times (3y)^2 \times x}{\frac{1}{3} \times \pi \times (y)^2 \times 3x}\)
= \(\frac{9}{3}\)
= \(\frac{3}{1}\)
উত্তর – শঙ্কু দুটির আয়তনের অনুপাত \(3 : 1\)
প্রয়োগ 14. যদি দুটি লম্ব বৃত্তাকার শঙ্কুর উচ্চতার অনুপাত \(2 : 3\) এবং তাদের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত \(3 : 5\) হয়, তবে শঙ্কুদ্বয়ের আয়তনের অনুপাত হিসাব করে লিখি।
সমাধান –
ধরি, শঙ্কুদ্বয়ের ব্যাসার্ধ যথাক্রমে \(r_1\) একক ও \(r_2\) একক এবং শঙ্কুদ্বয়ের উচ্চতা যথাক্রমে \(h_1\) একক এবং \(h_2\) একক।
∴ \(r_1 : r_2 = 3 : 5\) এবং \(h_1 : h_2 = 2 : 3\)
শঙ্কুদ্বয়ের আয়তনের অনুপাত = \( \left(\frac{1}{3} \pi r_1^2 h_1\right) : \left(\frac{1}{3} \pi r_2^2 h_2\right)\)
= \( \frac{\frac{1}{3} \pi r_1^2 h_1}{\frac{1}{3} \pi r_2^2 h_2}\)
= \( \left(\frac{r_1}{r_2}\right)^2 \times \left(\frac{h_1}{h_2}\right)\)
= \( \left(\frac{3}{5}\right)^2 \times \left(\frac{2}{3}\right)\)
= \( \frac{9}{25} \times \frac{2}{3}\)
= \( \frac{6}{25}\)
= \( 6 : 25\)
উত্তর – শঙ্কুদ্বয়ের আয়তনের অনুপাত \(6 : 25\)।
প্রয়োগ 15. লম্ব বৃত্তাকার শঙ্কু আকৃতির একটি তাঁবুর ভূমির ক্ষেত্রফল 13.86 বর্গ মিটার। তাঁবুটি তৈরি করতে 5775 টাকা মূল্যের একটি ত্রিপল লাগে এবং এক বর্গমিটার ত্রিপলের মূল্য 150 টাকা হলে, তাঁবুর উচ্চতা নির্ণয় করি। তাঁবুটিতে কত লিটার বায়ু আছে হিসাব করে লিখি।
সমাধান –
ধরি, তাঁবুর ভূমির ব্যাসার্ধের দৈর্ঘ্য \(r\) মিটার, উচ্চতা \(h\) মিটার এবং তির্যক উচ্চতা \(l\) মিটার।
ভূমির ক্ষেত্রফল = \( 13.86\) বর্গ মিটার।
শর্তানুসারে, \(\frac{22}{7} \times r^2 = 13.86\)
\(\therefore r^2 = \frac{13.86 \times 7}{22}\)= \( \frac{97.02}{22}\)
= \( 4.41\)
\(\therefore r = \sqrt{4.41}\)= \( 2.1\) মিটার।
প্রতি বর্গ মিটার \(150\) টাকা হিসাবে \(5775\) টাকায় ত্রিপলের পরিমাণ = \( \frac{5775}{150}\)
= \( 23.1\) বর্গ মিটার [নিজে হিসাব করি]
∴ পার্শ্বতলের ক্ষেত্রফল = \( \pi r l\)
= \( 23.1\) বর্গ মিটার
\(\frac{22}{7} \times 2.1 \times l = 23.1\)\(\therefore l = \frac{23.1 \times 7}{22 \times 2.1}\)= \( \frac{161.7}{46.2}\)
= \( 3.5\) মিটার
∴ তির্যক উচ্চতা = \( 3.5\) মিটার
∴ \(h = +\sqrt{l^2 – r^2}\)
= \( \sqrt{(3.5)^2 – (2.1)^2}\)
= \( \sqrt{12.25 – 4.41}\)
= \( \sqrt{7.84}\)
= \( 2.8\) মিটার
∴ তাঁবুটিতে বায়ু আছে = \( \frac{1}{3} \times \frac{22}{7} \times 2.1 \times 2.1 \times 2.8\)
= \( \frac{1}{3} \times \frac{22}{7} \times 4.41 \times 2.8\)
= \( \frac{1}{3} \times \frac{22}{7} \times 12.348\)
= \( \frac{1}{3} \times 38.808\)
= \( 12.936\) ঘন মিটার
= \( 12936\) ঘন ডেসিমি.
= \( 12936\) লিটার
উত্তর – তাঁবুটিতে 12936 লিটার বায়ু আছে।
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের ষোড়শ অধ্যায়, ‘লম্ব বৃত্তাকার শঙ্কু’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






Leave a Comment