মাধ্যমিক গণিত – বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য – উপপাদ্য

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের পঞ্চদশ অধ্যায়, ‘বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য’ -এর উপপাদ্যমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

উপপাদ্য 40. বৃত্তের কোনো বিন্দুতে স্পর্শক ও ওই স্পর্শবিন্দুগামী ব্যাসার্ধ পরস্পর লম্বভাবে অবস্থিত।

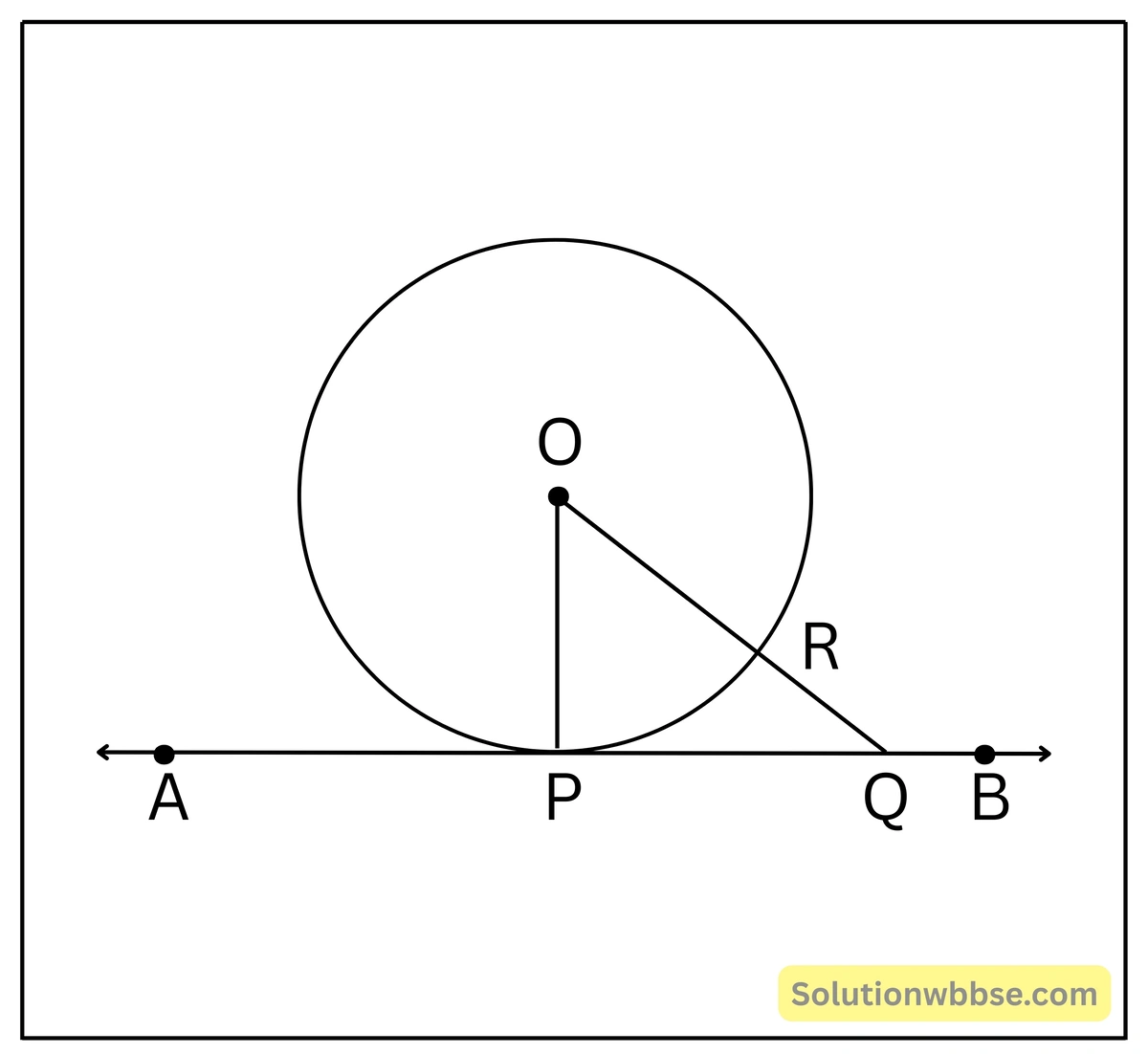
প্রদত্ত – O কেন্দ্রীয় বৃত্তের P বিন্দুতে AB স্পর্শক এবং OP, P বিন্দুগামী ব্যাসার্ধ।

প্রমাণ করতে হবে – OP ও AB স্পর্শক পরস্পর লম্ব। অর্থাৎ, OP ⊥ AB

অঙ্কন – AB স্পর্শকের ওপর যে-কোনো একটি বিন্দু Q নিলাম। O, Q বিন্দুদ্বয় যোগ করলাম।

প্রমাণ – স্পর্শক AB-এর উপর স্পর্শবিন্দু P ছাড়া অন্য যে-কোনো বিন্দু বৃত্তের বাইরে অবস্থিত।

সুতরাং, OQ বৃত্তটিকে একটি বিন্দুতে ছেদ করবে।

মনে করি, ছেদবিন্দু R।

∴ OR < OQ [R বিন্দু O, Q-এর মধ্যবর্তী]

আবার, OR = OP [একই বৃত্তের ব্যাসার্ধ]

∴ OP < OQ

∴ Q বিন্দু AB স্পর্শকের উপর যে-কোনো বিন্দু, সুতরাং বৃত্তের কেন্দ্র O থেকে AB স্পর্শক পর্যন্ত যত সরলরেখাংশ অঙ্কন করা যায় তাদের মধ্যে ক্ষুদ্রতম। আবার ক্ষুদ্রতম দূরত্ব লম্ব দূরত্ব।

সুতরাং, OP ⊥ AB (প্রমাণিত)

উপপাদ্য 41. বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে যে দুটি স্পর্শক অঙ্কন করা যায় তাদের স্পর্শবিন্দু দুটির সঙ্গে বহিঃস্থ বিন্দুর সংযোজক সরলরেখাংশ দুটির দৈর্ঘ্য সমান এবং তারা কেন্দ্রে সমান কোণ উৎপন্ন করে।

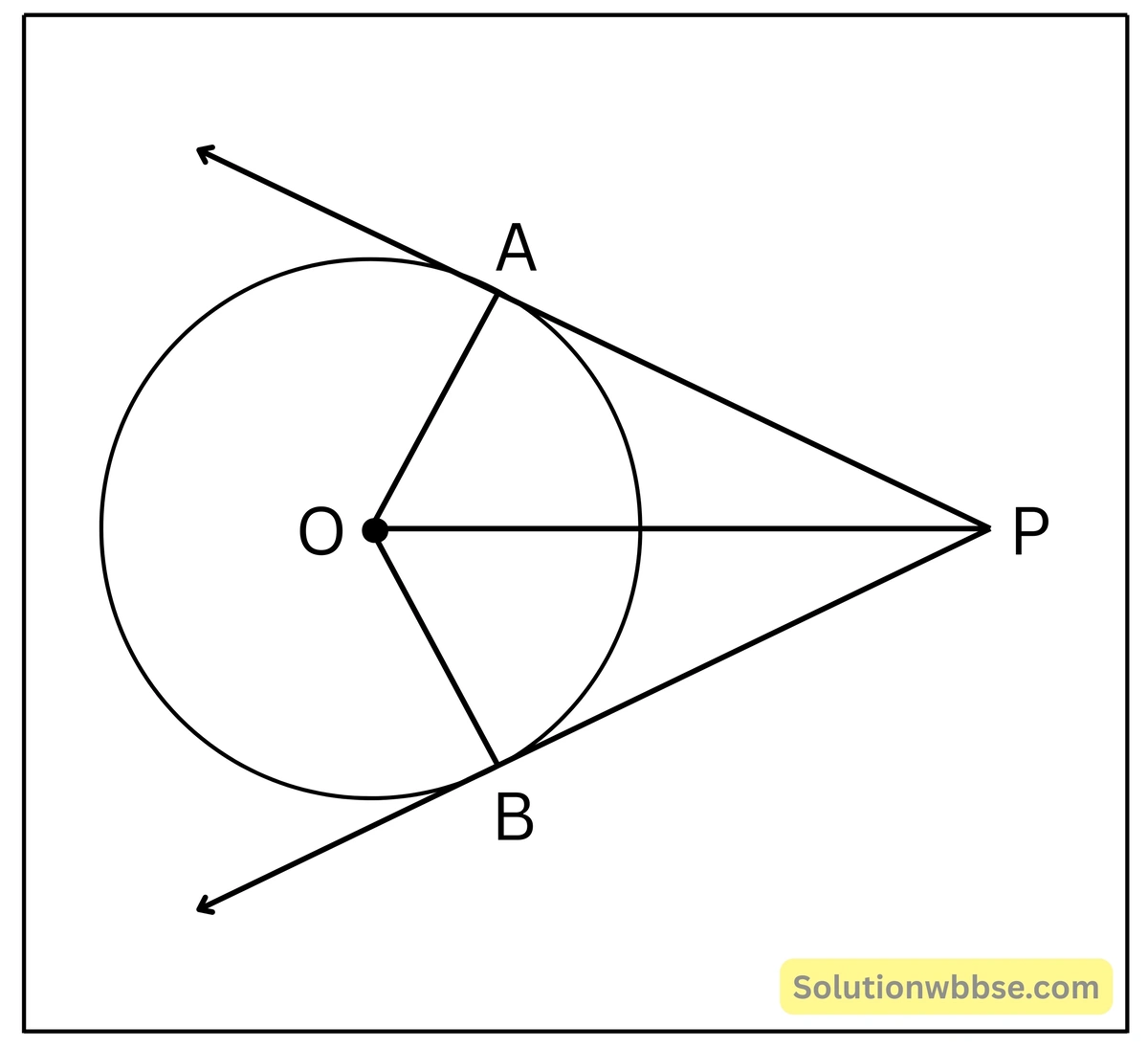
প্রদত্ত – O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু P থেকে PA ও PB দুটি স্পর্শক যাদের স্পর্শবিন্দু যথাক্রমে A ও B, OA, OB, O; P, B যুক্ত করায় PA ও PB সরলরেখাংশ দুটি কেন্দ্রে যথাক্রমে ∠POA ও ∠POB দুটি কোণ উৎপন্ন করেছে।

প্রমাণ করতে হবে – (i) PA = PB (ii) ∠POA = ∠POB

প্রমাণ – PA ও PB স্পর্শক এবং OA ও OB স্পর্শবিন্দুগামী ব্যাসার্ধ।

∴ OA ⊥ PA এবং OB ⊥ PB

△POA ও △POB সমকোণী ত্রিভুজদ্বয়ের মধ্যে, ∠OAP = ∠OBP (প্রত্যেকে 1 সমকোণ)

অতিভুজ OP সাধারণ বাহু এবং OA = OB (একই বৃত্তের ব্যাসার্ধ)

∴△PAO ≅ △PBO [সর্বসমতার R-H-S শর্তানুসারে]

∴ PA = PB (সর্বসম ত্রিভুজের অনুরূপ বাহু) ……… (i) প্রমাণিত

এবং ∠POA = ∠POB (সর্বসম ত্রিভুজের অনুরূপ কোণ) ……… (ii) প্রমাণিত

উপপাদ্য 42. যদি দুটি বৃত্ত পরস্পরকে স্পর্শ করে, তাহলে স্পর্শবিন্দু কেন্দ্র দুটির সংযোজক সরলরেখাংশের উপর অবস্থিত হবে।

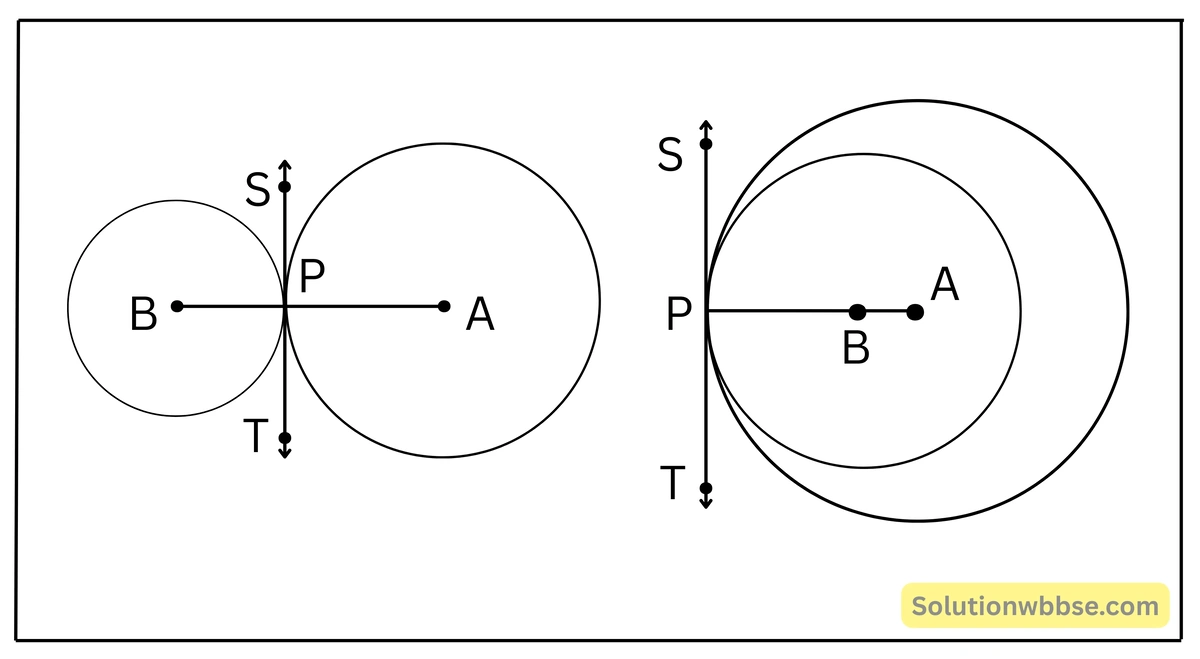
প্রদত্ত – A ও B কেন্দ্রীয় দুটি বৃত্ত পরস্পরকে P বিন্দুতে স্পর্শ করেছে।

প্রমাণ করতে হবে – A, P ও B সমরেখ।

অঙ্কন – A, P ও B, P যোগ করলাম।

প্রমাণ – A কেন্দ্রীয় ও B কেন্দ্রীয় বৃত্তদুটি পরস্পরকে P বিন্দুতে স্পর্শ করেছে।

∴ P বিন্দুতে বৃত্তদুটির একটি সাধারণ স্পর্শক আছে।

ধরি, ST হলো সাধারণ স্পর্শক যা দুটি বৃত্তকেই P বিন্দুতে স্পর্শ করেছে।

∴ A কেন্দ্রীয় বৃত্তের ST স্পর্শক এবং AP স্পর্শবিন্দুগামী ব্যাসার্ধ,

∴ AP ⊥ ST

আবার, যেহেতু B কেন্দ্রীয় বৃত্তের ST স্পর্শক এবং BP স্পর্শবিন্দুগামী ব্যাসার্ধ,

∴ BP ⊥ ST

∴ AP ও BP একই P বিন্দুতে ST সরলরেখার উপর লম্ব।

∴ AP ও BP একই সরলরেখায় অবস্থিত অর্থাৎ A, P ও B সমরেখ। (প্রমাণিত)

এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের পঞ্চদশ অধ্যায়, ‘বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য’ -এর উপপাদ্যমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।

আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করুন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।