এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের অষ্টদশ অধ্যায়, ‘সদৃশতা’ -এর ‘কষে দেখি – 18.2’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

1. ΔABC এর BC বাহুর সমান্তরাল সরলরেখা AB ও AC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে।
(i) PB =AQ, AP=9 একক, QC = 4 একক হলে, PB এর দৈর্ঘ্য হিসাব করে লিখি।
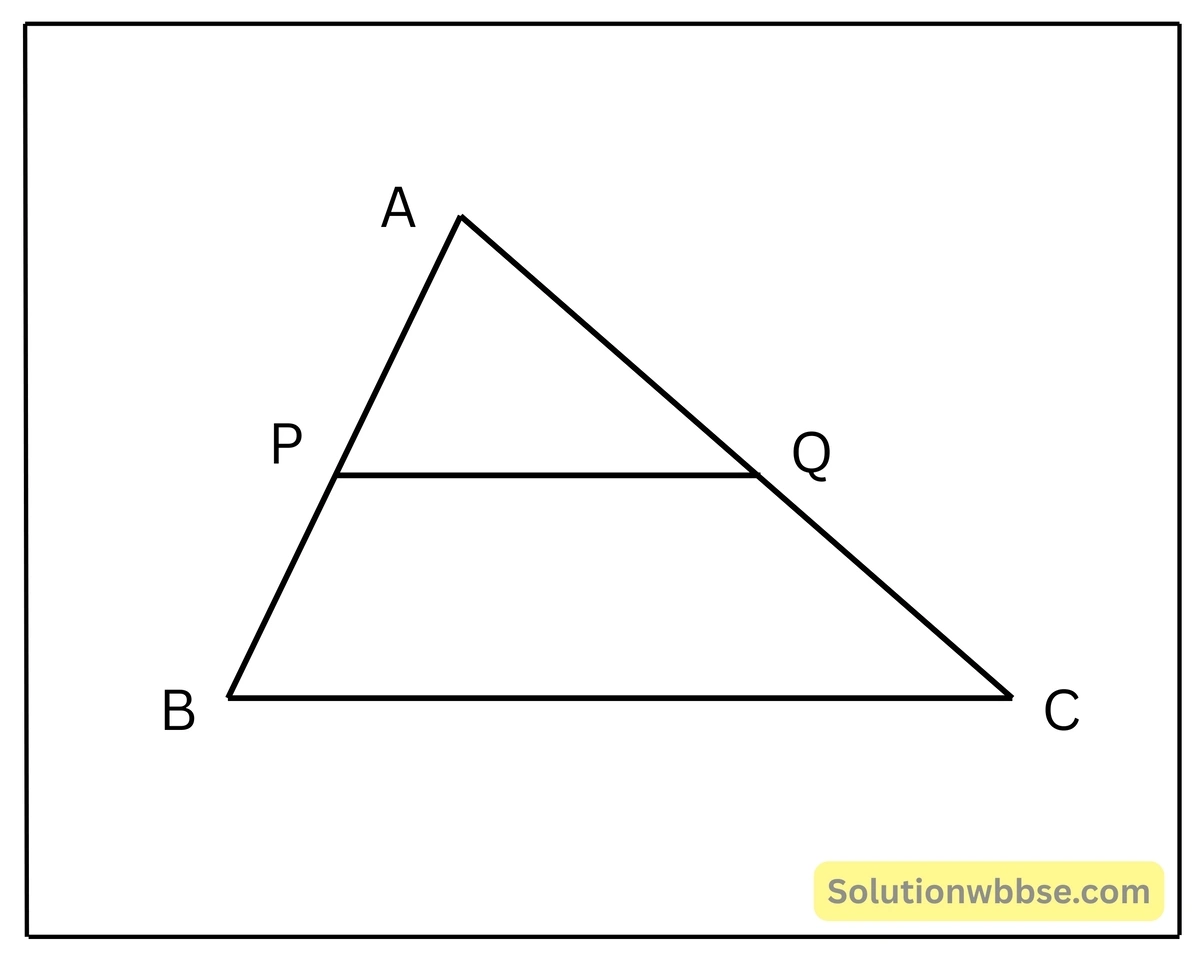
সমাধান –
যেহেতু, PQ || BC
∴ থ্যালেসের উপপাদ্য অনুসারে, \(\frac{AP}{PB} = \frac{AQ}{QC}\)
বা, \(\frac{9}{PB} = \frac{PB}{4}\)
বা, PB² = 36 বা,
PB = √36 বা,
PB = 6
∴ PB এর দৈর্ঘ্য 6 একক।
(ii) PB এর দৈর্ঘ্য AP এর দৈর্ঘ্যের দ্বিগুণ এবং QC এর দৈর্ঘ্য AQ এর দৈর্ঘ্যের চেয়ে 3 একক বেশি হলে, AC এর দৈর্ঘ্য কত হবে হিসাব করে লিখি।

সমাধান –
যেহেতু, \(PQ \parallel BC\)
∴ থ্যালেসের উপপাদ্য অনুসারে,
\(\frac{AP}{PB} = \frac{AQ}{QC}\) —(i)
ধরি, \(AP=x\) একক এবং \(AQ=y\) একক
∴ \(PB=2x\) একক এবং \(QC=(y+3)\) একক
∴ (i) নং সমীকরণ থেকে পাই,
\(\frac{x}{2x} = \frac{y}{y+3}\)বা, \(\frac{1}{2} = \frac{y}{y+3}\)
বা, \(y+3 = 2y\)
বা, \(y=3\)
∴ \(AC = AQ + QC\)
\(= (y+y+3)\) একক
\(= (2y+3)\) একক
\(= (2(3)+3)\) একক
\(= 9\) একক
(iii) যদি AP = QC হয়, AB এর দৈর্ঘ্য 12 একক এবং AQ এর দৈর্ঘ্য 2 একক হয়, তবে CQ এর দৈর্ঘ্য কত হবে, হিসাব করে লিখি।

সমাধান –
যেহেতু, \(PQ \parallel BC\)
∴ থ্যালেসের উপপাদ্য অনুসারে,
\(\frac{AP}{PB} = \frac{AQ}{QC}\)বা, \(\frac{AP}{AB-AP} = \frac{AQ}{QC}\) [যেহেতু, \(PB=AB-AP\)]
বা, \(\frac{QC}{12-QC} = \frac{2}{QC}\) [যেহেতু \(AP=QC\), \(AB=12\) একক এবং \(QC=2\) একক]
বা, \(QC^2 = 2(12-QC)\)
বা, \(QC^2 = 24-2QC\)
বা, \(QC^2+2QC-24=0\)
বা, \(QC^2+6QC-4QC-24=0\)
বা, \(QC(QC+6)-4(QC+6)=0\)
বা, \((QC+6)(QC-4)=0\)
দুটি রাশির গুণফল শূন্য
হয়, \((QC+6)=0\)
বা, \(QC = -6\)
অথবা, \((QC-4)=0\)
বা, \(QC=4\)
কিন্তু QC বাহুর দৈর্ঘ্য ঋণাত্মক হতে পারে না।
∴ \(QC = 4\) একক।
2. ΔPQR এর PQ ও PR বাহুর উপর যথাক্রমে X ও Y দুটি বিন্দু নিলাম।
(i) PX = 2 একক, XQ = 3.5 একক, YR = 7 একক এবং PY = 4.25 একক হলে, XY ও QR পরস্পর সমান্তরাল হবে কিনা যুক্তিসহ লিখি।
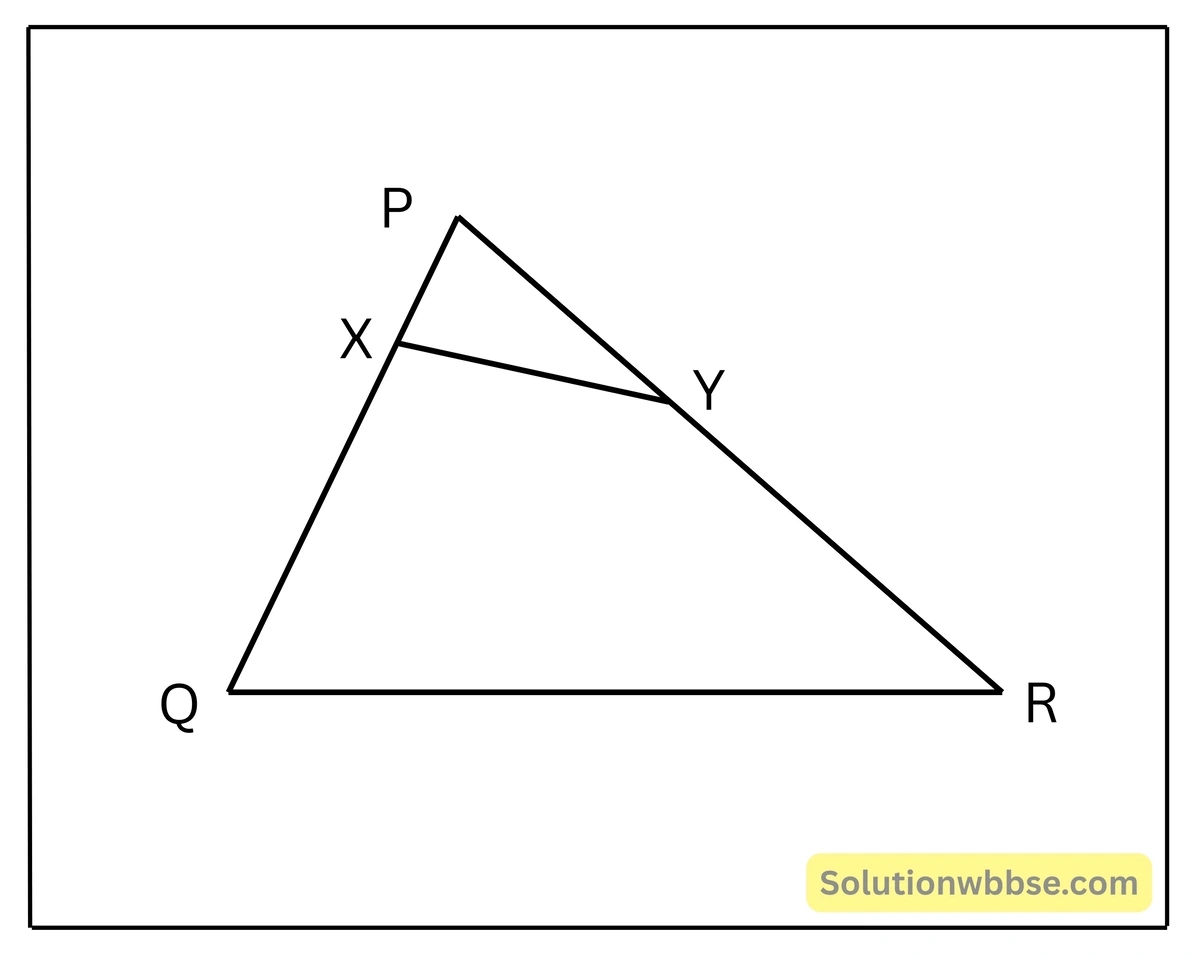
সমাধান –
XY ও QR পরস্পর সমান্তরাল হতে গেলে,
\(\frac{PX}{XQ} = \frac{PY}{YR}\) হতে হবে।
এখন, \(\frac{PX}{XQ} = \frac{2}{3.5} = \frac{20}{35} = \frac{4}{7}\)
আবার, \(\frac{PY}{YR} = \frac{4.25}{7} = \frac{425}{700} = \frac{17}{28}\)
∴ \(\frac{PX}{XQ} \neq \frac{PY}{YR}\)
∴ XY ও QR পরস্পর সমান্তরাল নয়।
(ii) PQ = 8 একক, YR = 12 একক, PY = 4 একক এবং PY এর দৈর্ঘ্য XQ এর দৈর্ঘ্যের চেয়ে 2 একক কম হলে, XY ও QR সমান্তরাল হবে কি না যুক্তিসহ লিখি।
সমাধান –
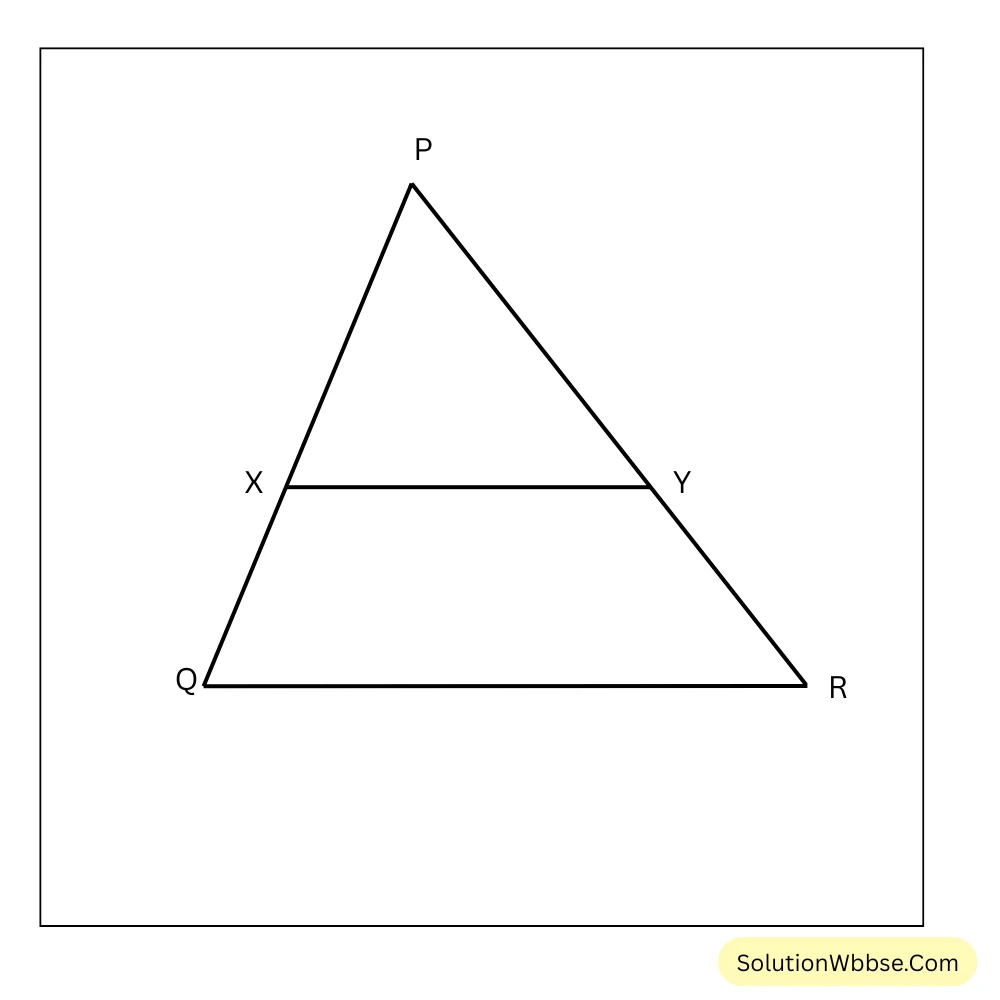
XY ও QR পরস্পর সমান্তরাল হতে গেলে,
\(\frac{PX}{XQ} = \frac{PY}{YR}\) হতে হবে।
এখন,\(\frac{PX}{XQ} = \frac{PQ-XQ}{XQ} = \frac{8-6}{6} = \frac{2}{6} = \frac{1}{3}\)
আবার,\(\frac{PY}{YR} = \frac{4}{12} = \frac{1}{3}\)
\(\therefore \frac{PX}{XQ} = \frac{PY}{YR}\)\(\therefore XY || QR\)\(\therefore\) XY ও QR পরস্পর সমান্তরাল।
3. প্রমাণ করি যে, কোনো ত্রিভুজের একটি বাহুর মধ্যবিন্দু দিয়ে অঙ্কিত দ্বিতীয় বাহুর সমান্তরাল সরলরেখা তৃতীয় বাহুকে সমদ্বিখণ্ডিত করে। [ থ্যালেসের উপপাদ্যের সাহায্যে প্রমাণ করি]

ধরাযাক, ABC ত্রিভুজের AB বাহুর মধ্যবিন্দু P, P বিন্দু দিয়ে অঙ্কিত BC বাহুর সমান্তরাল সরলরেখা PQ, AC বাহুকে Q বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে Q, AC এর মধ্যবিন্দু।
প্রমাণ – যেহেতু, \(PQ \parallel BC\),
∴থ্যালেসের উপপাদ্য অনুসারে,
\(\frac{AP}{PB} = \frac{AQ}{QC}\)যেহেতু P, AB এর মধ্যবিন্দু
∴AP = PB
\(\therefore \frac{AP}{PB} = 1\)\(\therefore \frac{AQ}{QC} = 1\)\(\therefore AQ = QC\)সুতরাং, Q, AC এর মধ্যবিন্দু [প্রমাণিত]
4. ΔABC এর AD মধ্যমার উপর P যেকোনোএকটিবিন্দু। বর্ধিত BP ও CP যথাক্রমে AC ও AB কে Q ও R বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, RQ || BC.
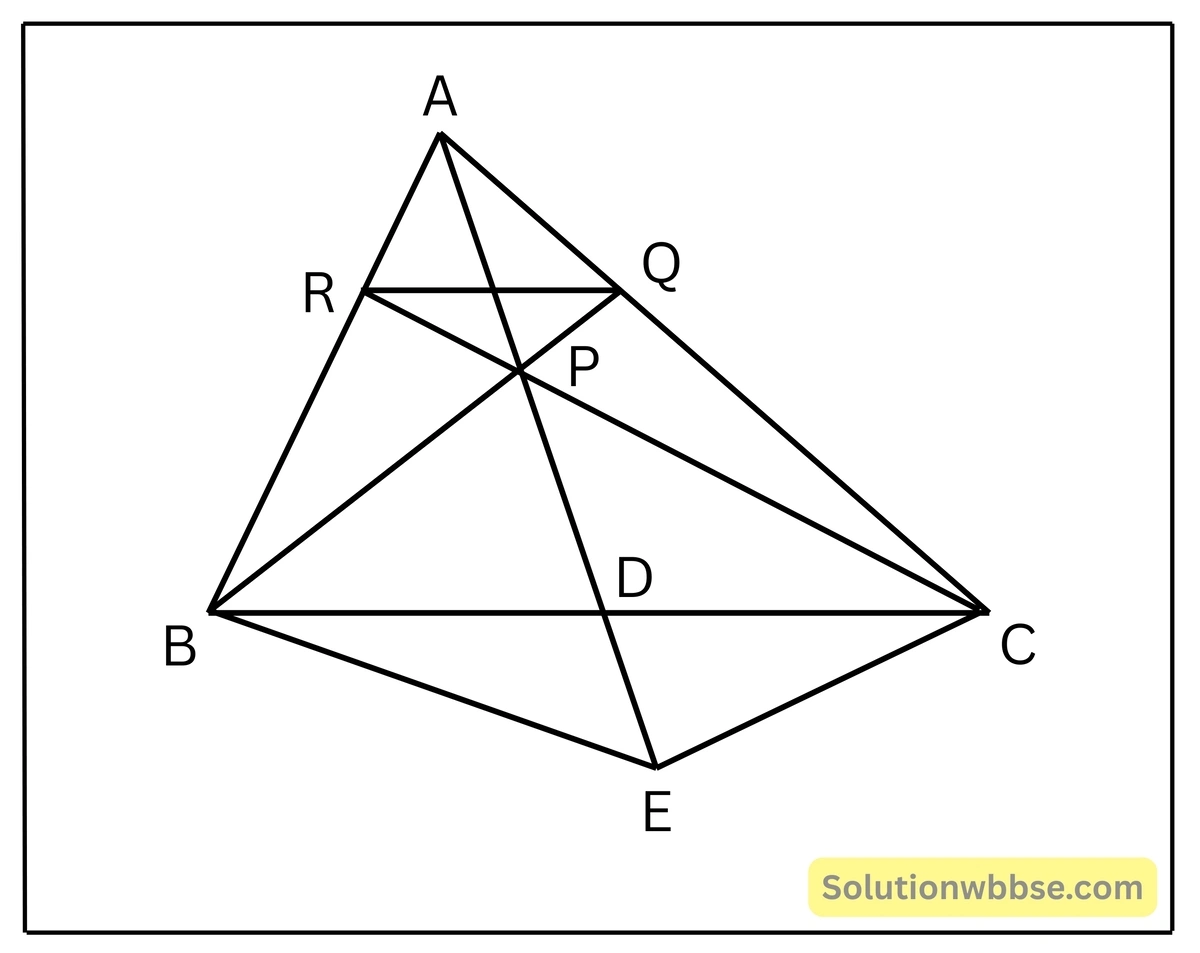
ABC এর AD মধ্যমার উপর P যেকোনো একটি বিন্দু, বর্ধিত BP ও CP যথাক্রমে AC ও AB কে Q ও R বিন্দুতে ছেদ করে, প্রমাণ করতে হবে যে, RQ||BC
অঙ্কন – AD- কে Eপর্যন্ত এমনভাবে বর্ধিত করা হল যেন PD = DE হয়। B,E ; C,E যুক্ত করা হল।
প্রমাণ – PBEC চতুর্ভুজের PD = DE [ অঙ্কনানুসারে] এবং BD = DC [ যেহেতু, AD মধ্যমা]
∴ PBEC একটি সামান্তরিক [ যেহেতু, সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে]
∴PC || BE
∴ RP || BE
∴ \(\frac{AR}{RB} = \frac{AP}{PE}\) [থ্যালেসের উপপাদ্য অনুসারে]
আবার যেহেতু, PBEC একটি সামান্তরিক
∴ BP || EC
∴ PQ || EC
∴ \(\frac{AP}{PE} = \frac{AQ}{QC}\) [থ্যালেসের উপপাদ্য অনুসারে]
(i) ও (ii) থেকে পাই,
\(\frac{AR}{RB} = \frac{AQ}{QC}\)∴ RQ || BC [ থ্যালেসের বিপরীত উপপাদ্য অনুসারে] [ প্রমাণিত]
5. ΔABC এর BE ও CF মধ্যমা দুটি পরস্পরকে G বিন্দুতে ছেদ করেছে এবং FE সরলরেখাংশ AG সরল রেখাংশকে O বিন্দুতে ছেদ করলে, প্রমাণ কর যে, AO = 3OG.
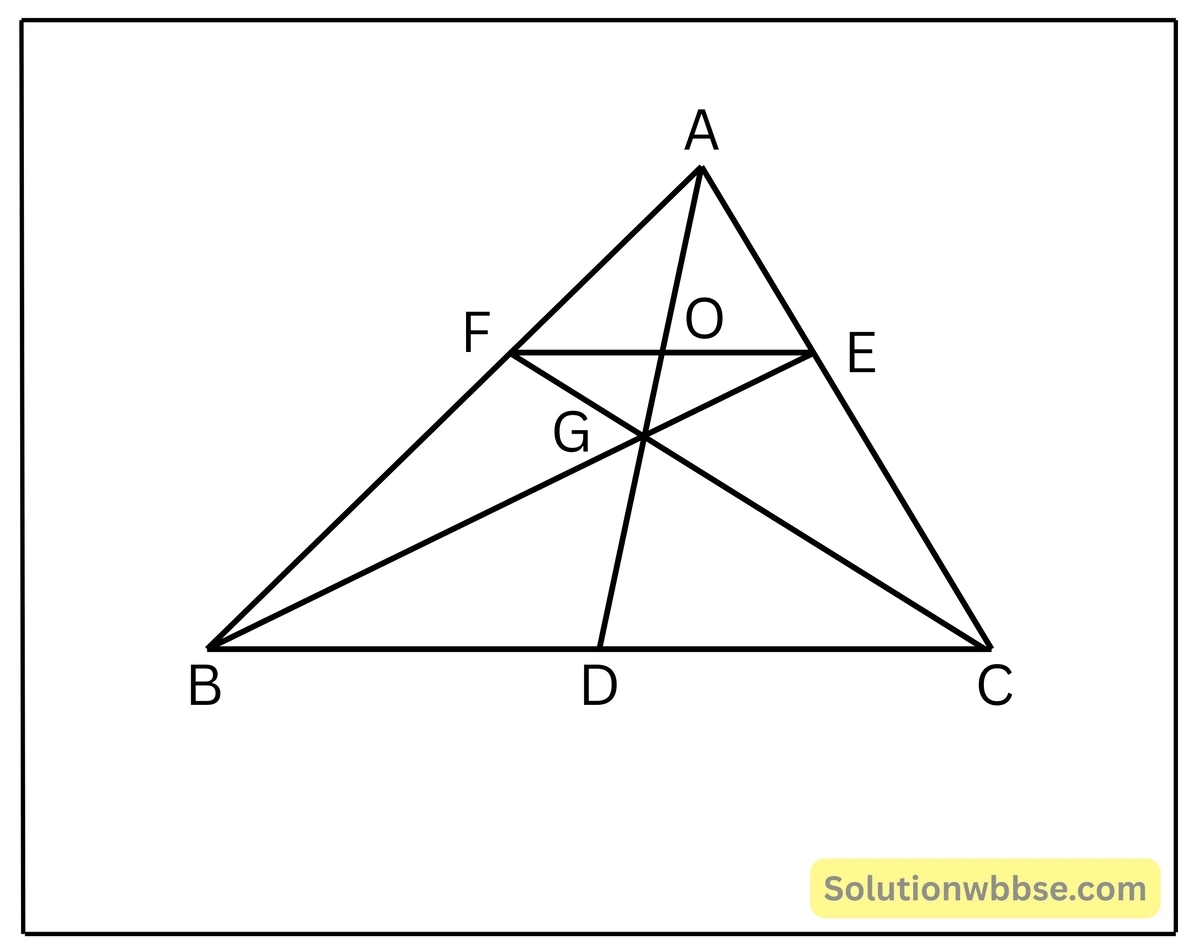
সমাধান –
মনে করো, ΔABC-এর BE ও CF মধ্যমা দুটির ছেদবিন্দু G, AG, EF কে O বিন্দুতে ছেদ করে।
প্রমাণ করতে হবে যে, AO = 3OG
অঙ্কন AG কে বর্ধিত করায় উহা BC বাহুকে D বিন্দুতে ছেদ করে।
প্রমাণ এখানে AB ও AC বাহুর মধ্যবিন্দু যথাক্রমে F ও E।
∴ EF || BC
∴ OE || CD
এখন ΔADC এর OE || CD
∴ \(\frac{AO}{OD}=\frac{AE}{CE}\)
যেহেতু, AE = CE অতএব AO = OD
আবার G বিন্দু ΔABC এর ভরকেন্দ্র।
∴ AG = 2GD
∴ AO + OG = 2(OD – OG)
∴ AO + OG = 2(AO – OG)
∴ 2AO – 2OG = AO+OG
∴ AO = 3OG [প্রমাণিত]
6. প্রমাণ করি যে, ট্রাপিজিয়াম এর তির্যক বাহুগুলির মধ্যবিন্দু দুটির সংযোজক সরলরেখাংশ সমান্তরাল বাহুগুলির সমান্তরাল।
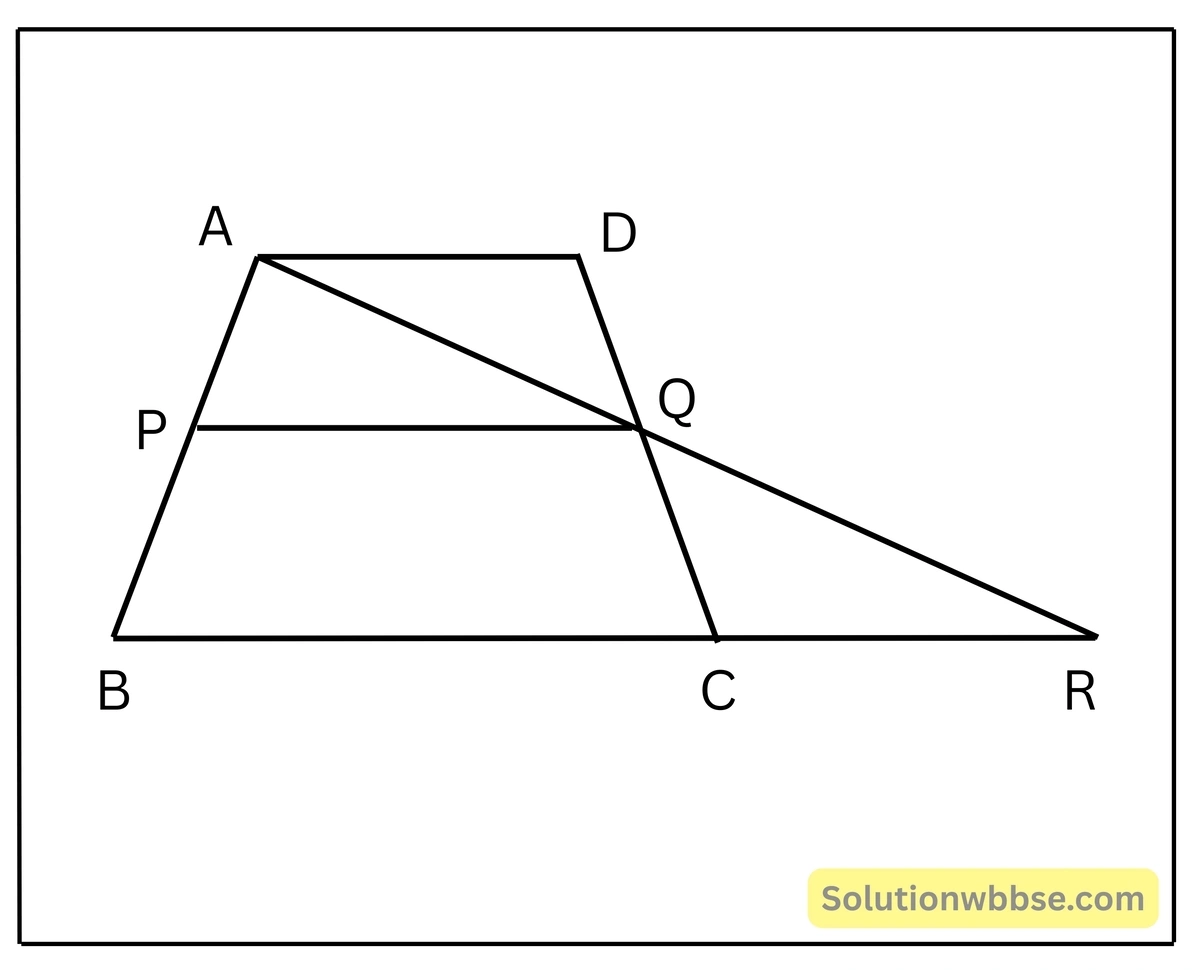
ধরাযাক, ABCD একটি ট্রাপিজিয়াম যার তির্যক বাহুগুলি হল AB এবং CD। AB ও CD বাহুগুলির মধ্যবিন্দুদ্বয় যথাক্রমে P এবং Q, প্রমাণ করতে হবে যে, PQ || BC|| AD।
অঙ্কন – A,Q যুক্ত করে বর্ধিত করা হল, যা বর্ধিত BC-কে, R বিন্দুতে ছেদ করে।
প্রমাণ – এখন, ABCD ট্রিপিজিয়াম এর AD || BC,
∴ AD || BR
আবার, ΔCQR এবং ΔAQD এর,
∠CQR = ∠AQD [বিপ্রতীপ কোণ]
এবং ∠QRC = ∠QAD [একান্তর কোণ কারণ AD||BR এবং AR ভেদক]
এবং DQ = QC [যেহেতু, Q, DC এর মধ্যবিন্দু]
∴ ΔCQR ≅ ΔAQD [AAS সর্বসমসারে]
∴ AQ = QR
∴ Q, AC এর মধ্যবিন্দু।
∴ΔABR এর AB বাহুর মধ্যবিন্দু P এবং AR বাহুর মধ্যবিন্দু Q
∴ AP =PB এবং AQ=QR
∴ [/latex]\frac{AP}{PB} = \frac{AQ}{QR}[/latex]
∴ PQ || BR [থ্যালেসের বিপরীত উপপাদ্য অনুসারে]
∴ PQ || BC [যেহেতু, B,C,R সমরেখ]
আবার, AD || BC
∴ PQ || AD—(ii)
(i) ও (ii) থেকে পাই, PQ || BC || AD [প্রমাণিত]
7. ΔABC এর BC বাহুর উপর D যেকোনো একটি বিন্দু। P, Q যথাক্রমে ABD ও ADC -এর ভরকেন্দ্র। প্রমাণ করি যে, PQ || BC.
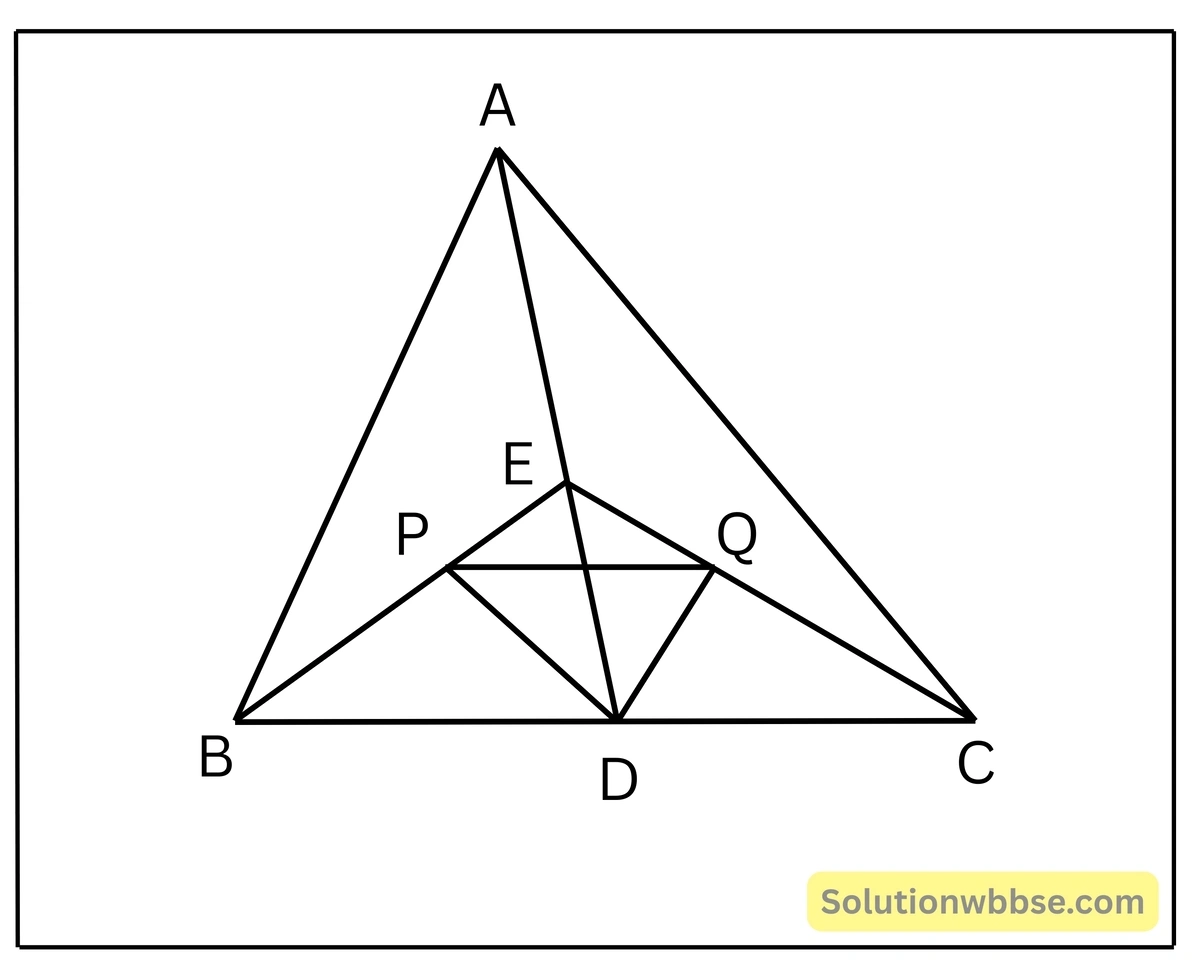
সমাধান –
মনে করো, ΔABC -এর BC বাহুর উপর D একটি বিন্দু। AD অঙ্কন করা হল।
মনে করো, AD -এর মধ্যবিন্দু E; BE ও CE অঙ্কন করা হল। তাহলে, ΔABD ও ΔACD -এর মধ্যমা যথাক্রমে BE ও CE. আবার P ও Q বিন্দু যথাক্রমে ΔABD ও ΔACD -এর ভরকেন্দ্র। PQ অঙ্কন করা হল। প্রমাণ করতে হবে যে, PQ || BC.
প্রমাণ – এখানে ΔABD -এর ভরকেন্দ্র P ; অতএব, \(\frac{PE}{BP} = \frac{1}{2}\)
আবার, ΔACD -এর ভরকেন্দ্র Q;
\(\frac{CE}{CQ} = \frac{1}{2}\)∴ \(\frac{PE}{BP} = \frac{CE}{CQ}\)
∴ PQ || BC
8. একই ভূমি QR এর উপর এবং একই পার্শ্বে দুটি ত্রিভুজ ΔPQR ও ΔSQR অঙ্কন করেছি যাদের ক্ষেত্রফল সমান। F ও G যথাক্রমে ত্রিভুজদুটির ভরকেন্দ্র হলে প্রমাণ করি যে, FG || QR.
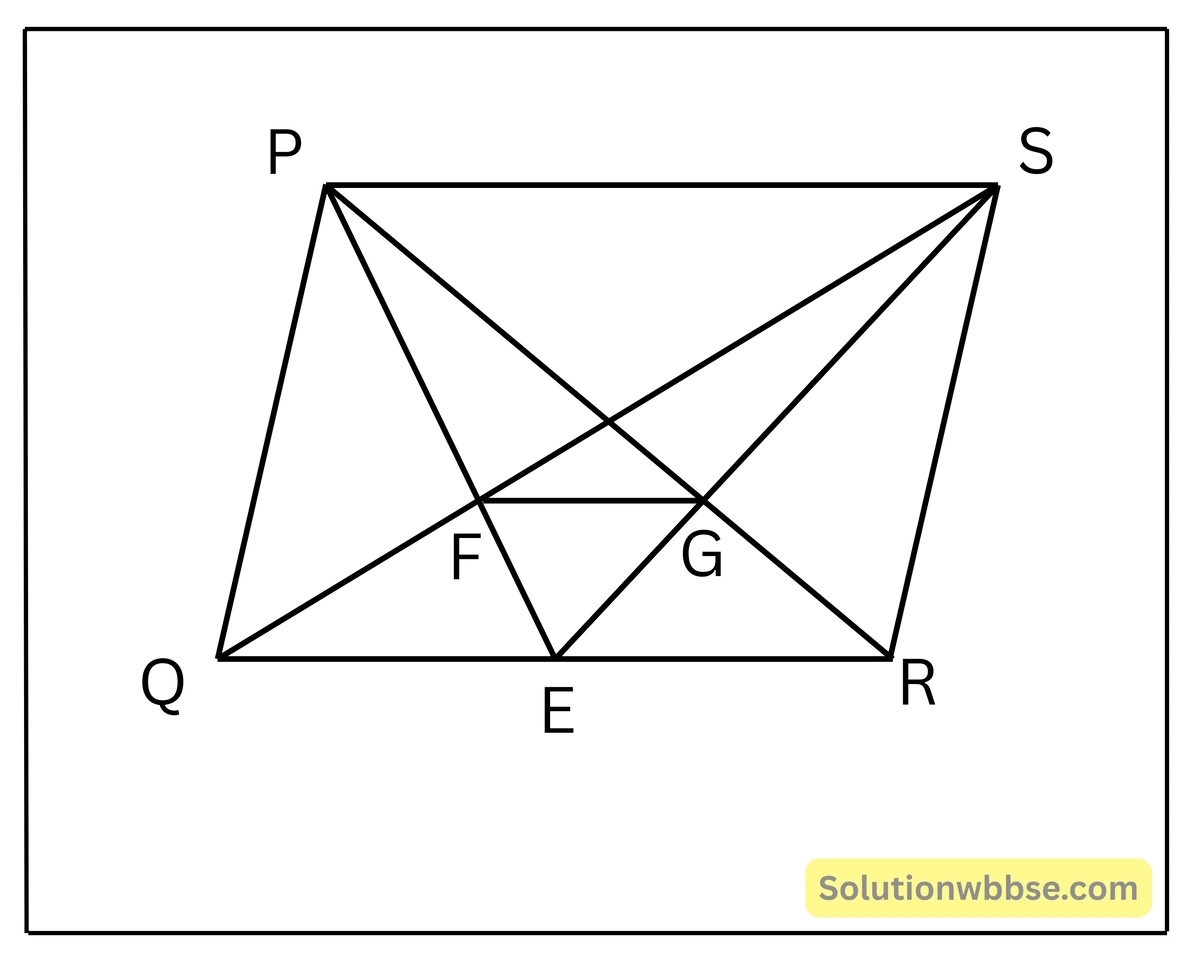
ΔPQR ও ΔSQR দুটি সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজ, QR ভূমির একই পার্শ্বে অবস্থিত। F ও G ত্রিভুজ দুটির ভরকেন্দ্র হলে প্রমাণ করতে হবে যে, FG || QR.
অঙ্কন – P,S যুক্ত করা হল। P,F এবং S,G যুক্ত করে বর্ধিত করলে তা QR কে E বিন্দুতে ছেদ করে।
প্রমাণ – যেহেতু, ΔPQR এবং ΔSQR এর ক্ষেত্রফল সমান এবং তারা একই ভূমি QR এর উপর এবং QR এর একই পার্শ্বে অবস্থিত সুতরাং তারা একই সমান্তরাল যুগলের মধ্যে অবস্থিত হবে।
∴ PS || QR —(i)
আবার, F, ΔPQR এর মধ্যমা এবং PE মধ্যমার উপর অবস্থিত
∴ PF : FE = 2:1—(ii)
আবার যেহেতু, G, ΔSQR এর মধ্যমা এবং SE মধ্যমার উপর অবস্থিত
∴ SG : GE = 2:1—(iii)
(ii) ও (iii) থেকে পাই,
PF : FE = SG:GE
এখন, ΔPES ত্রিভুজের
\(\frac{PE}{FE} = \frac{SG}{GE}\)∴ PS || FG —(iv)[থ্যালেসের বিপরীত উপপাদ্য অনুসারে]
(i) ও (iv) থেকে পাই,
FG || QR [ প্রমাণিত ]
9. প্রমাণ করি যে, কোনো সমদ্বিবাহু ট্রাপিজিয়ামের সমান্তরাল বাহুদুটির যেকোনো একটির সংলগ্ন কোণ দুটি সমান।
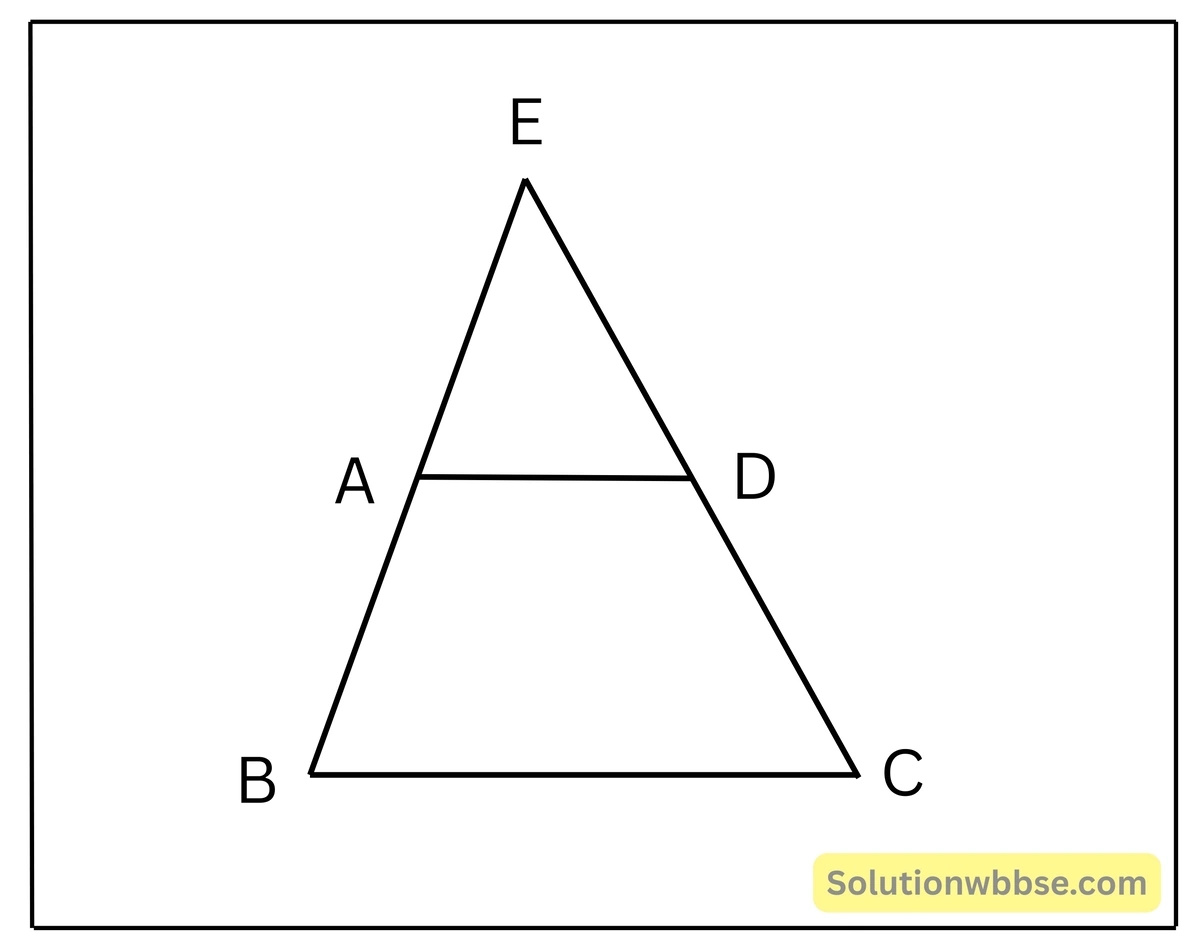
ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম যার AB = DC, প্রমাণ করতে হবে যে, ট্রাপিজিয়ামটির সমান্তরাল বাহুদুটির যেকোনো একটির সংলগ্ন কোণ দুটি সমান অর্থাৎ প্রমাণ করতে হবে যে, ∠DAB = ∠ADC.
অঙ্কন – BA এবং CD বাহুকে বর্ধিত করা হল যারা পরস্পরকে E বিন্দুতে ছেদ করে।
প্রমাণ – ΔEBC এর AD || BC
∴ \(\frac{EA}{AB} = \frac{ED}{DC}\) [থ্যালেসের বিপরীত উপপাদ্য অনুসারে]
আবার, AB = DC [ যেহেতু, সমদ্বিবাহু ট্রাপিজিয়ামের তির্যক বাহুদুটি সমান ]
∴ EA = ED [(i) থেকে পাই ]
∴ ∠EAD = ∠EDA
∴ 180 – ∠EAD = 180 – ∠EDA
∴ ∠DAB = ∠ADC [ প্রমাণিত ]
10. ΔABC এবং ΔDBC একই ভূমি BC – এর উপর এবং BC এর একই পার্শ্বে অবস্থিত। BC বাহুর উপর E যেকোনো একটি বিন্দু। E বিন্দু দিয়ে AB এবং BD –এর সমান্তরাল সরলরেখা AC এবং DC বাহুকে যথাক্রমে F ও G বিন্দুতে ছেদ করে। প্রমাণ করি যে, AD || FG.
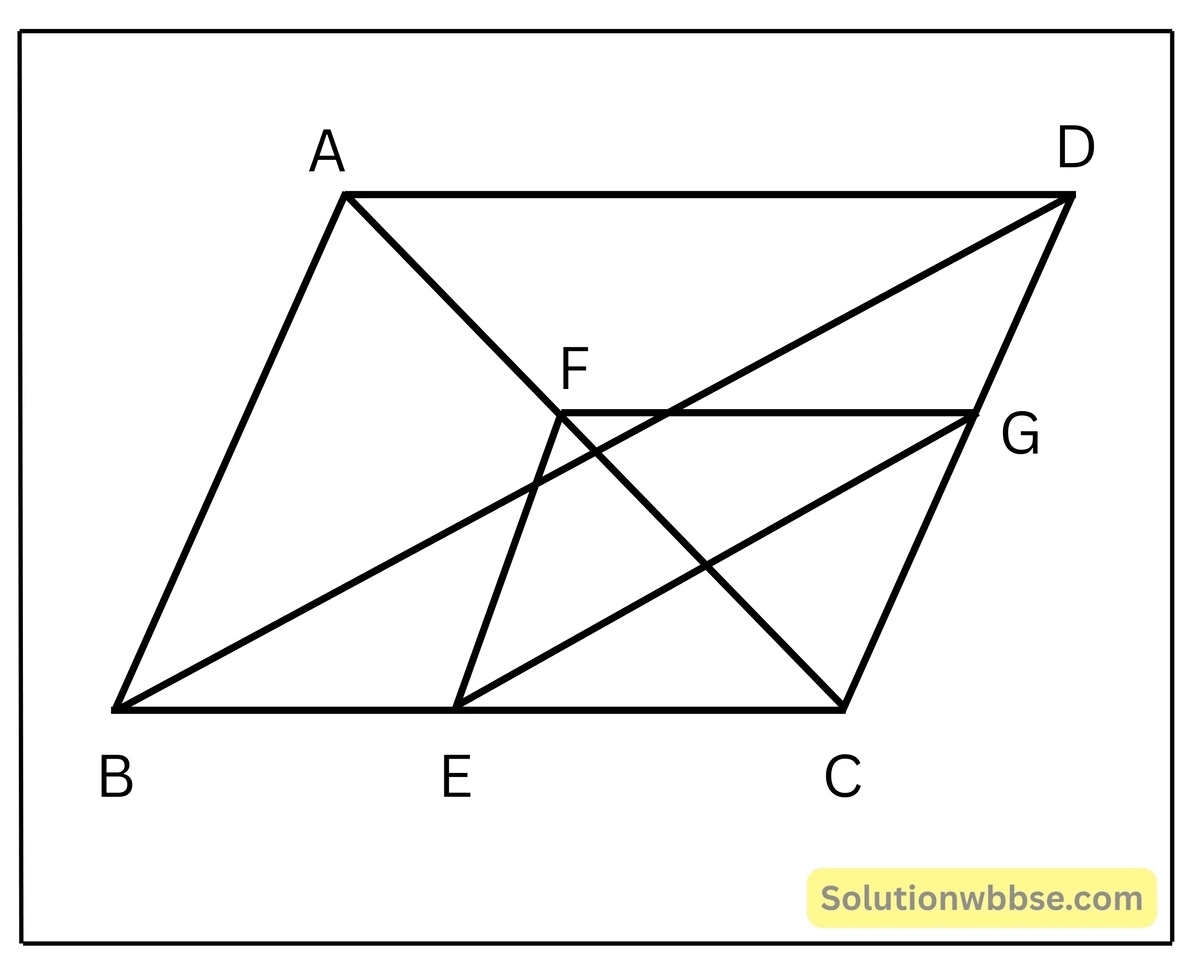
অঙ্কন – AD ও FG অঙ্কন করা হল।
প্রমাণ – এখন, ABC এর AB || EF.
∴ \(\frac{CF}{AF} = \frac{CE}{BE}\) [থ্যালেসের উপপাদ্য অনুসারে]
∴ CF:AF = CE:BE
আবার, ΔBCD ত্রিভুজের BD || EG.
∴ \(\frac{CG}{GD} = \frac{CE}{BE}\)
∴ CG : GD = CE : BE [ থ্যালেসের উপপাদ্য অনুসারে]—(ii)
(i) ও (ii)থেকে পাই,
\(\frac{CF}{AF} = \frac{CG}{GD}\)∴ ΔACD এর, \(\frac{CF}{AF} = \frac{CG}{GD}\)
∴ থ্যালেসের বিপরীত উপপাদ্য অনুসারে, AD || FG [ প্রমাণিত]
11.অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A)
(i) ΔABC এর BC বাহুর সমান্তরাল সরলরেখা AB ও AC কে যথাক্রমে X ও Y বিন্দুতে ছেদ করে। AX = 2.4 সেমি., AY = 3.2 সেমি. এবং YC= 4.8 সেমি., হলে, AB এর দৈর্ঘ্য
(a) 3.6 সেমি.
(b) 6 সেমি.
(c) 6.4 সেমি.
(d) 7.2 সেমি.
উত্তর – (b) 6 সেমি.
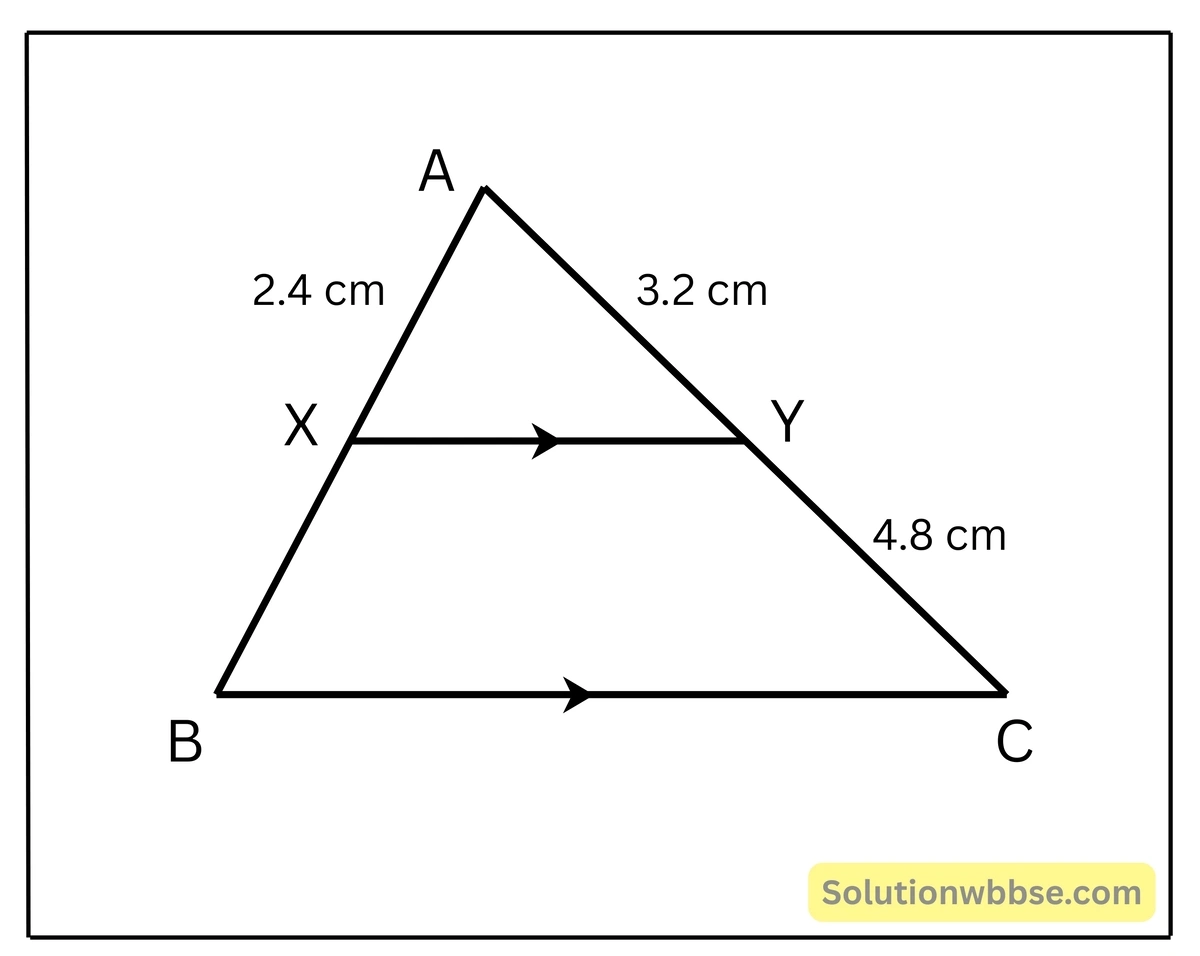
সমাধান –
যেহেতু, \(XY || BC\)
∴ থ্যালেসের বিপরীত উপপাদ্য থেকে পাই,
\(\frac{AX}{XB} = \frac{AY}{YC}\)বা, \(\frac{2.4}{XB} = \frac{3.2}{4.8}\)
বা, \(\frac{2.4}{XB} = \frac{32}{48}\)
বা, \(\frac{2.4}{XB} = \frac{2}{3}\)
বা, \(2XB = 3 \times 2.4\)
বা, \(2XB = 7.2\)
বা, \(XB = \frac{7.2}{2}\)
বা, \(XB = 3.6\)
(ii) ΔABC ত্রিভুজের AB এবং AC বাহুর উপর D ও E বিন্দু এমন ভাবে অবস্থিত যে DE || BC এবং AD : DB = 3 : 1; যদি EA = 3.3 সেমি. হয়, তাহলে AC এর দৈর্ঘ্য
(a) 1.1 সেমি.
(b) 4 সেমি.
(c) 4.4 সেমি.
(d) 5.5 সেমি.
উত্তর – (c) 4.4 সেমি.
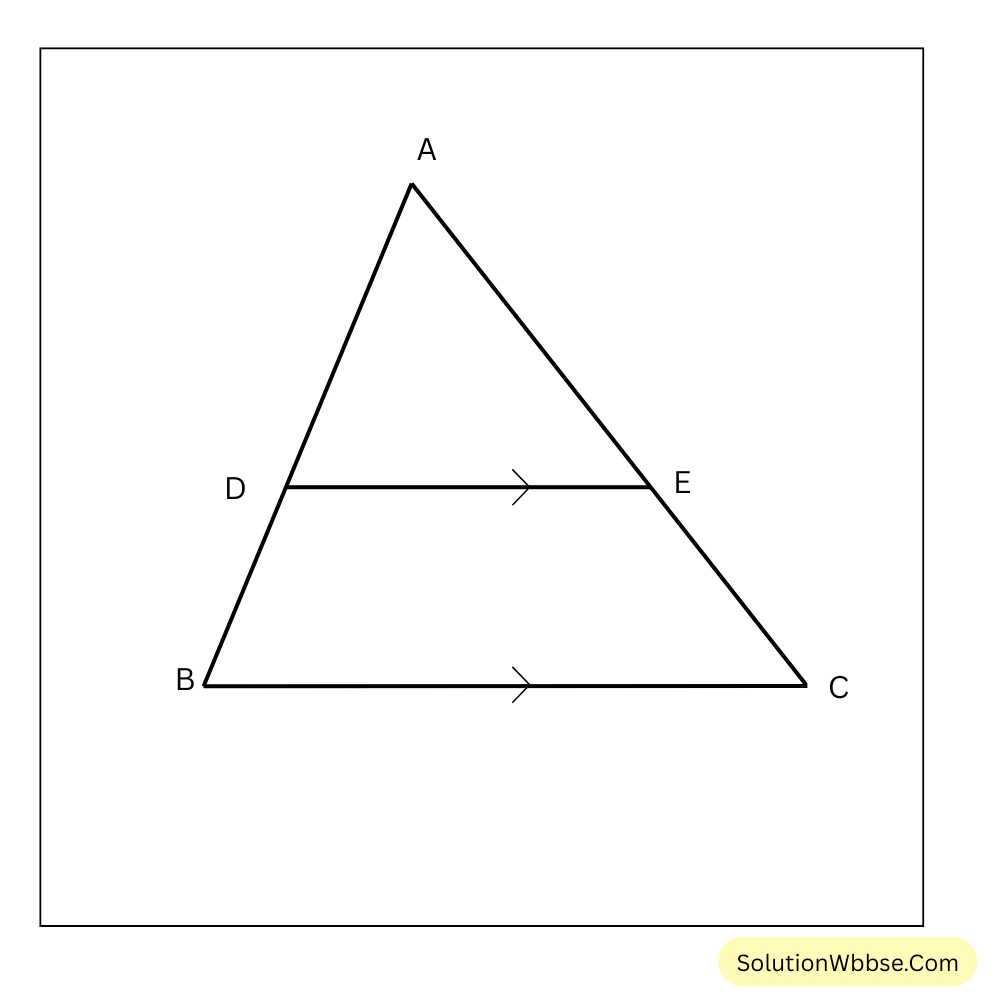
সমাধান –
\(DE || BC\)∴ থ্যালেসের উপপাদ্য থেকে পাই, \(\frac{AD}{DB} = \frac{AE}{EC}\)
বা, \(\frac{3}{1} = \frac{3.3}{EC}\)
বা, \(3EC = 3.3\)
বা, \(EC = \frac{3.3}{3}\)
বা, \(EC = 1.1\)
∴ \(AC = AE+EC = (3.3+1.1)\) সেমি. \(= 4.4\) সেমি.
(iii) পাশের চিত্রে DE||BC হলে, x এর মান
(a) 4
(b) 1
(c) 3
(d) 2
উত্তর – (d) 2
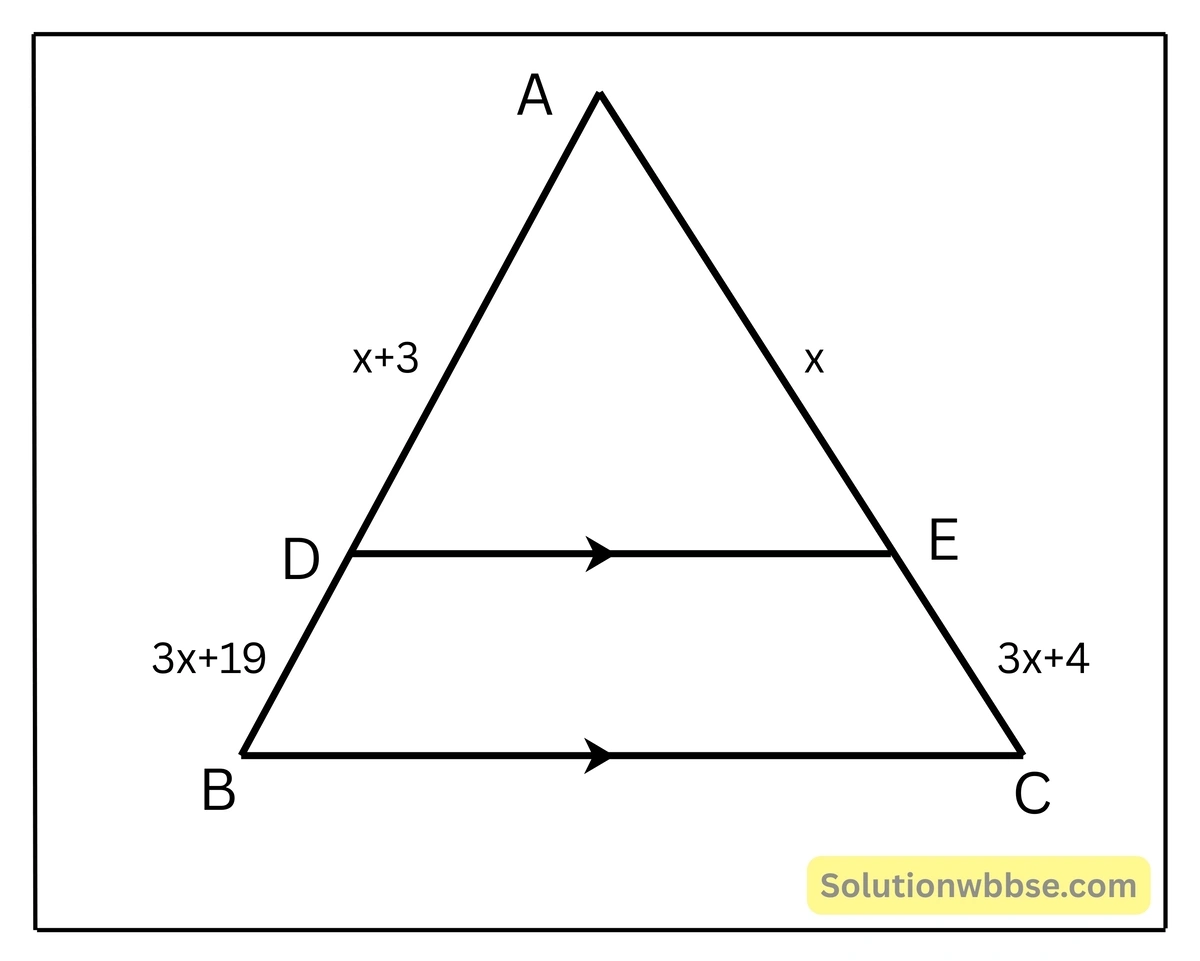
সমাধান –
যেহেতু , \(DE || BC\)
∴ থ্যালেসের বিপরীত উপপাদ্য থেকে পাই,
\(\frac{AD}{DB} = \frac{AE}{EC}\)বা, \(\frac{x+3}{3x+19} = \frac{x}{3x+4}\)
বা, \((x + 3)(3x + 4) = x(3x + 19)\)
বা, \(3x^2 + 9x + 4x + 12 = 3x^2 + 19x\)
বা, \(3x^2 + 13x + 12 = 3x^2 + 19x\)
বা, \(3x^2 + 13x + 12 – 3x^2 – 19x = 0\)
বা, \(– 6x + 12 = 0\)
বা, \(6x = 12\)
বা, \(x = \frac{12}{6}\)
বা, \(x = 2\)
(iv) ABCD ট্রাপিজিয়ামের AB||DC এবং AD ও BC বাহুর উপর যথাক্রমে P ও Q দুটি বিন্দু এমন ভাবে অবস্থিত যে PQ || DC ; যদি PD=18 সেমি., BQ=35 সেমি., QC=15 সেমি. হয়, তাহলে AD এর দৈর্ঘ্য
(a) 60 সেমি.
(b) 30 সেমি.
(c) 12 সেমি.
(d) 15 সেমি.
উত্তর – (a) 60 সেমি.
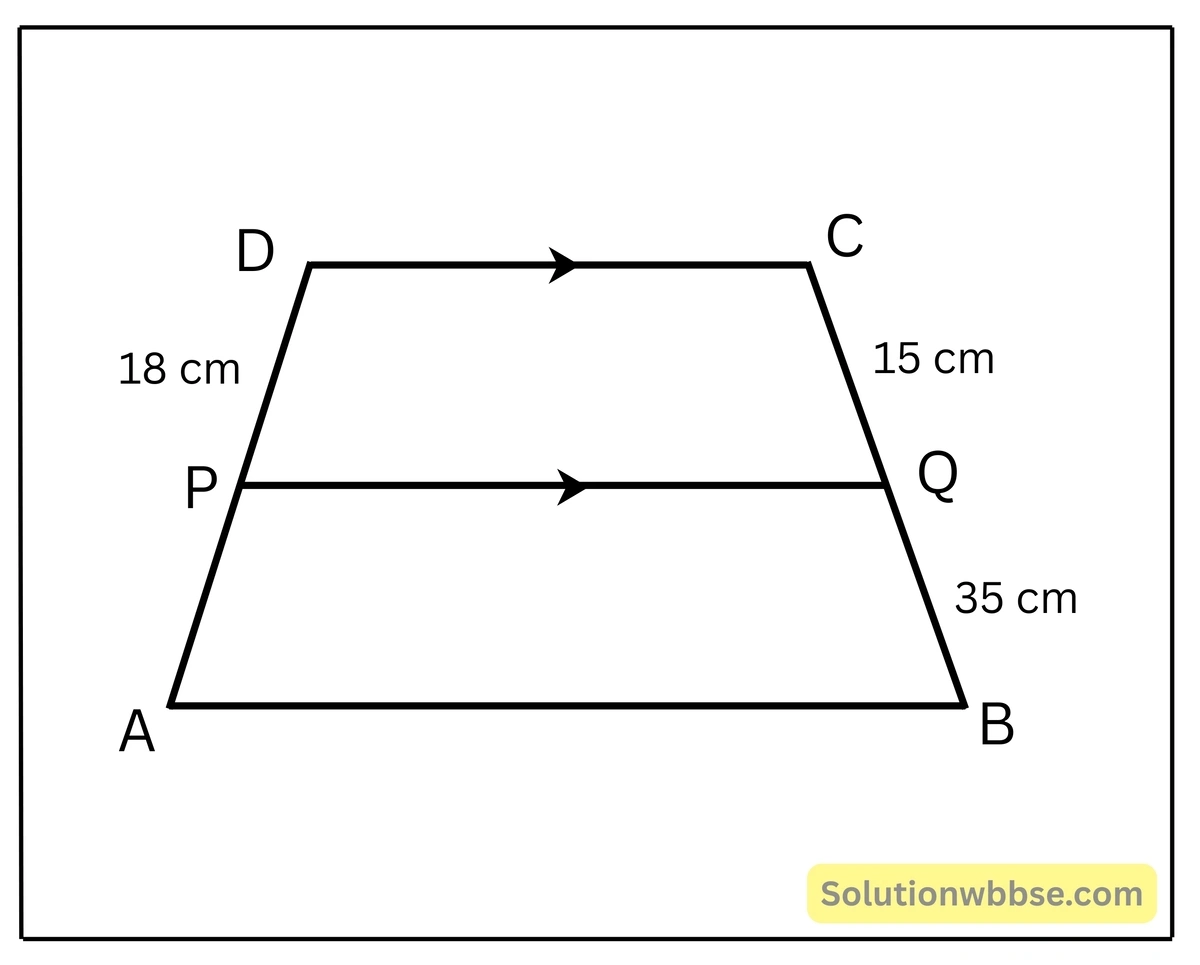
সমাধান –
\(\frac{AP}{PD} = \frac{BQ}{QC}\)বা, \(\frac{AP}{18} = \frac{35}{15}\)
বা, \(\frac{AP}{18} = \frac{7}{3}\)
বা, \(AP = \frac{7}{3} \times 18\)
বা, \(AP = 42\)
∴ \(AD=AP+PD=(42+18)\) সেমি. \(= 60\) সেমি.
(v) পাশের চিত্রে, DP=5 সেমি., DE=15 সেমি., DQ= 6 সেমি. এবং QF=18 সেমি. হলে,
(a) PQ=EF
(b) PQ||EF
(c) PQ ≠ EF
(d) PQ ∦ EF
উত্তর – (d) PQ ∦ EF
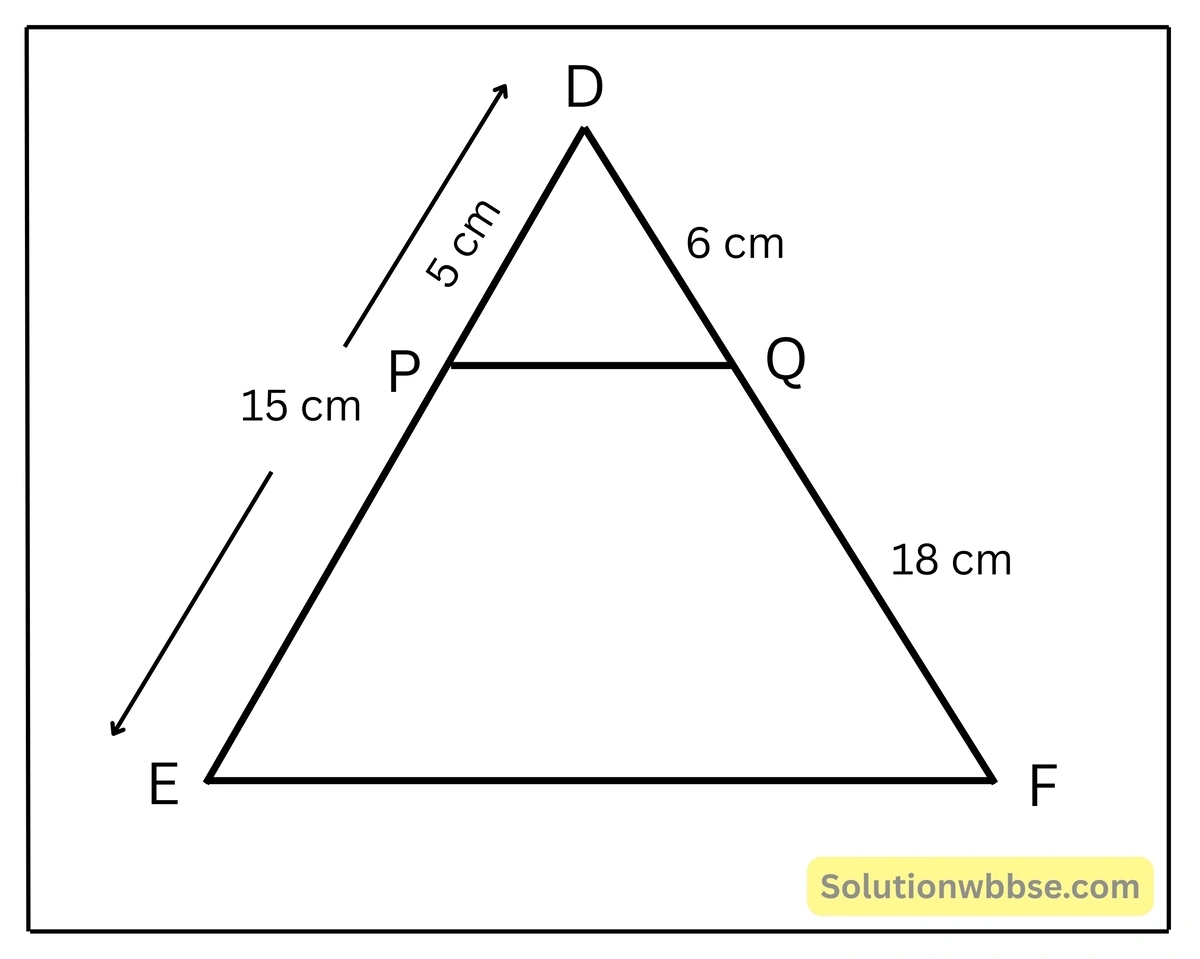
সমাধান –
\(DP=5\)সেমি. ∴ \(PE=(15-5)\)সেমি.\(=10\)সেমি.
আবার , \(DQ=6\)সেমি. এবং \(QF=18\) সেমি.
এখন , \(\frac{DP}{PE} = \frac{5}{10} = \frac{1}{2}\)
আবার, \(\frac{DQ}{QF} = \frac{6}{18} = \frac{1}{3}\)
∴ \(\frac{DP}{PE} \neq \frac{DQ}{QF}\)
∴ \(PQ ∦ EF\)
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি
(i) দুটি সদৃশ চিত্র সর্বদা সর্বসম।
উত্তর – মিথ্যা
(ii) পাশের চিত্রে DE ||BC হলে, \(\frac{AB}{BD} = \frac{AC}{CE}\) হবে।
উত্তর – সত্য
(C) শূন্যস্থান পূরণ করি
(i) একটি ত্রিভুজের যেকোনো বাহুর সমান্তরাল সরলরেখা অপর দুটি বাহুকে বা তাদের বর্ধিতাংশকে ___________ বিভক্ত করে।
উত্তর – সমানুপাতে
(ii) দুটি ত্রিভুজের ভূমি একই সরলরেখায় অবস্থিত এবং ত্রিভুজ দুটির অপর শীর্ষবিন্দুটি সাধারণ হলে ত্রিভুজ দুটির ক্ষেত্রফলের অনুপাত ভূমির দৈর্ঘ্যের অনুপাতের ___________।
উত্তর – সমান
(iii) একটি ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের সমান্তরাল সরলরেখা অপর বাহুদ্বয়কে ___________ বিভক্ত করে।
উত্তর – সমানুপাতে
12. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
(i) পাশের চিত্রে ABC ত্রিভুজে \(\frac{AD}{DB} = \frac{AE}{EC} \) এবং ∠ADE = ∠ACB হলে , বাহুভেদে ABC ত্রিভুজটি কী ধরনের নির্ণয় লিখি।
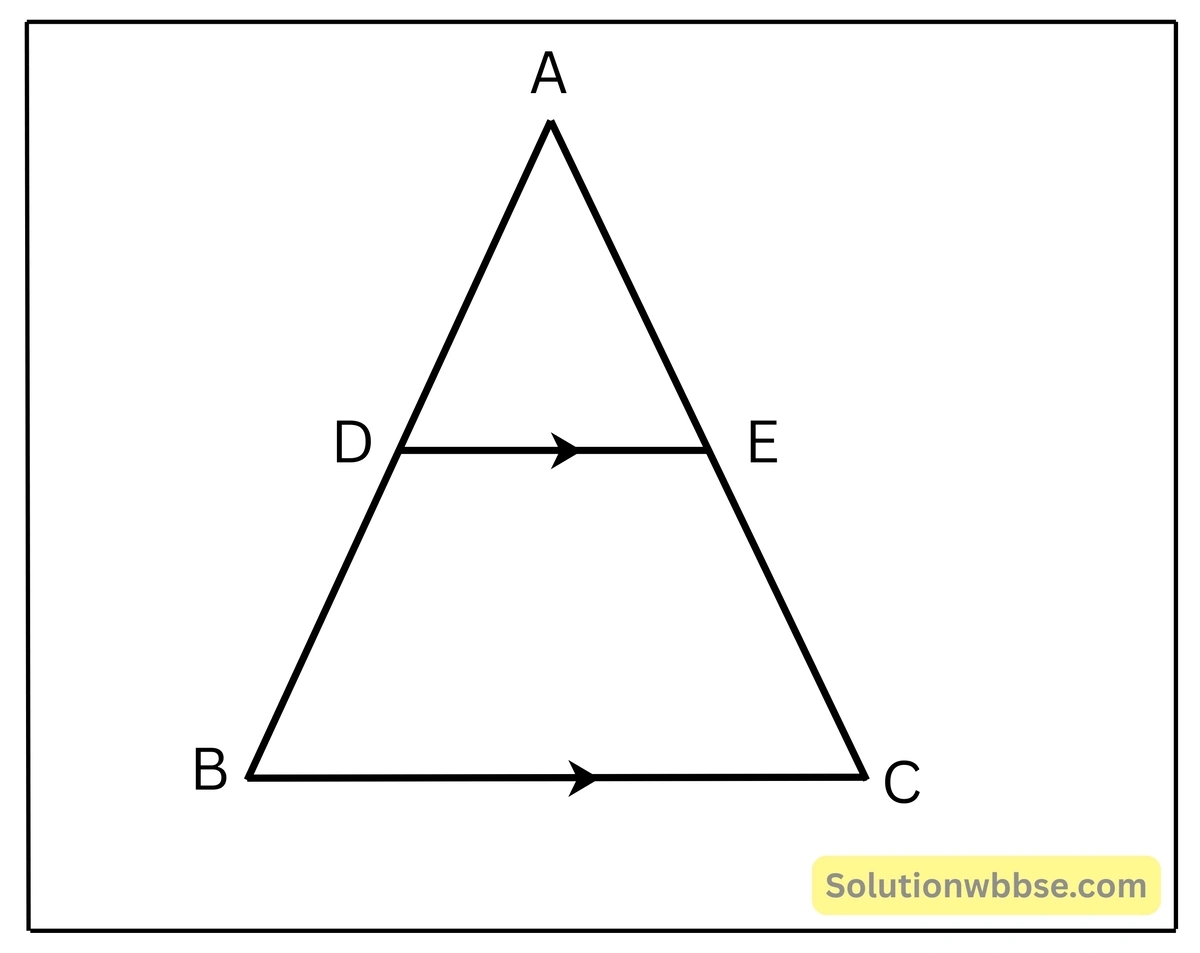
সমাধান –
ΔABC এর \(\frac{AD}{DB} = \frac{AE}{EC} \)
∴ DE||BC
∠ADE = ∠ABC [ অনুরূপ কোণ ] আবার ∠ADE = ∠ACB [ প্রদত্ত ]
∴ ∠ABC = ∠ACB
∴ AB =AC
∴ বাহুভেদে ABC ত্রিভুজটি সমদ্বিবাহু ত্রিভুজ।
(ii) পাশের চিত্রে DE||BC এবং AD:BD = 3:5 হলে, ΔADE এর ক্ষেত্রফল, ΔCDE এর ক্ষেত্রফল কত তা লিখি।
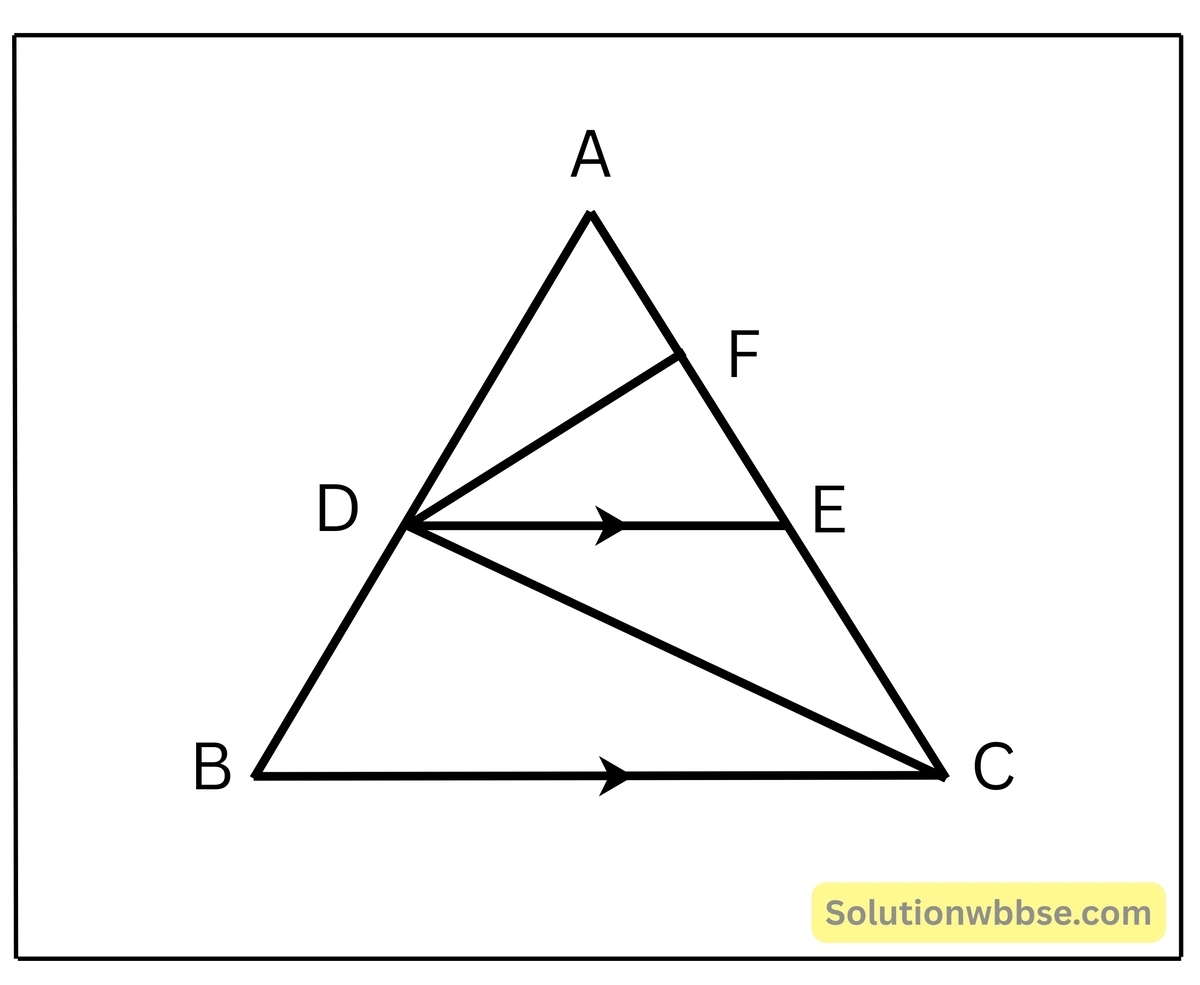
সমাধান
∴ DE ||BC
∴ \(\frac{AD}{BD} = \frac{AE}{CE} \) [থ্যালেসের উপপাদ্য থেকে]
∴ \(\frac{AE}{CE} = \frac{3}{5} \) [ ∴ AD:BD =3:5 ]
D বিন্দু থেকে AC বাহুর উপরে DF লম্ব টানা হল।
∴ DF হল ΔADE ও ΔCDE উভয় ত্রিভুজের উচ্চতা।
ধরি, DF = h একক
∴ ΔADE এর ক্ষেত্রফলঃ ΔCDE এর ক্ষেত্রফল
\(= \frac{1}{2} \times AE \times h : \frac{1}{2} \times CE \times h \)= AE:CE
= 3:5
(iii) পাশের চিত্রে, LM || AB এবং AL=(x-3) একক, AC=2x একক , BM=(x-2) একক এবং BC=(2x+3) একক হলে, x এর মান নির্ণয় করি।
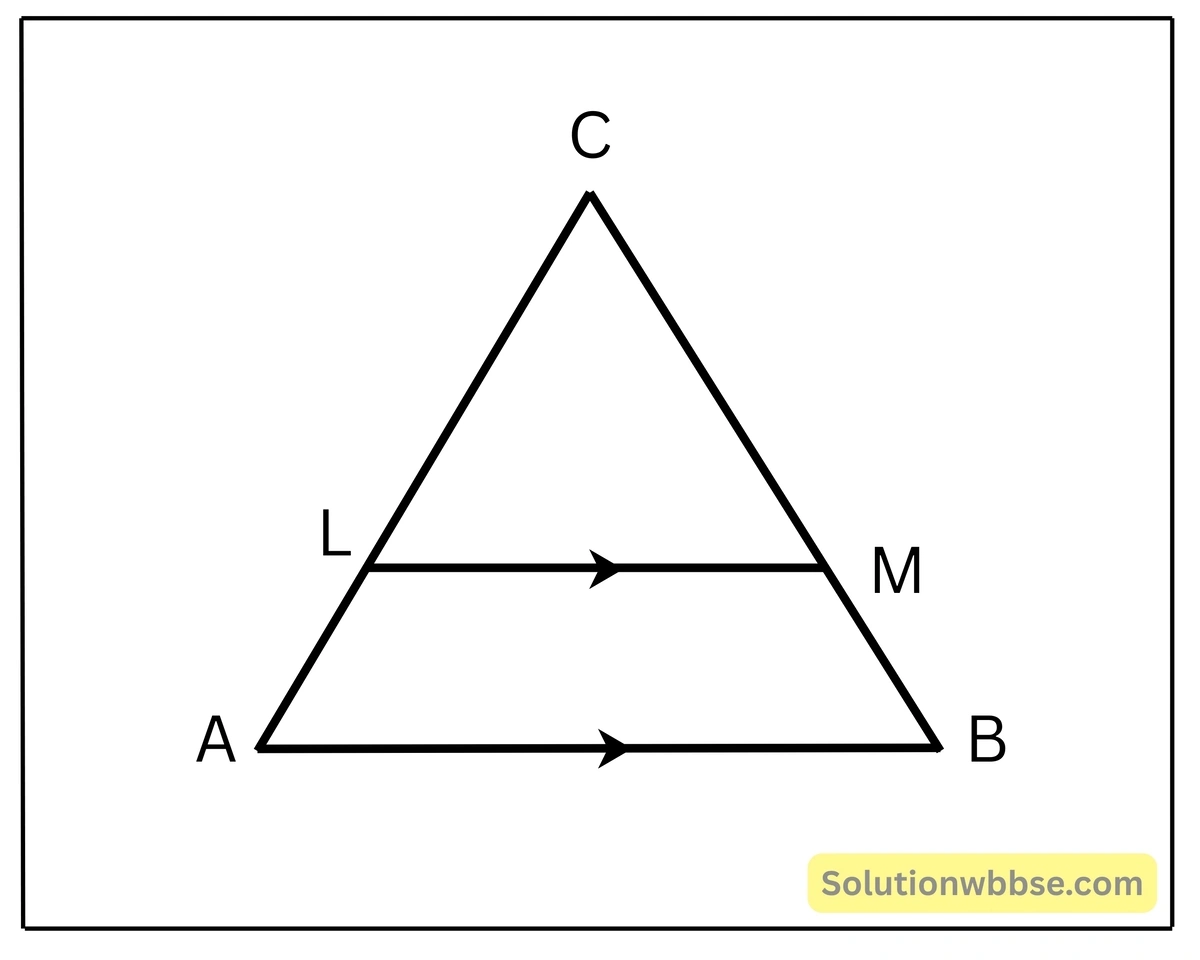
সমাধান –
\(LM || AB\)∴ \(\frac{CL}{AL} = \frac{CM}{BM}\) [থ্যালেসের উপপাদ্য অনুসারে]
বা, \(\frac{CL}{AL} + 1 = \frac{CM}{BM} + 1\)
বা, \(\frac{CL+AL}{AL} = \frac{CM+BM}{BM}\)
বা, \(\frac{AC}{AL} = \frac{BC}{BM}\)
বা, \(\frac{2x}{x-3} = \frac{2x+3}{x-2}\)
বা, \(2x(x-2) = (2x+3)(x-3)\)
বা, \(2x^2 – 4x = 2x^2 + 3x – 6x – 9\)
বা, \(2x^2 – 4x – 2x^2 – 3x + 6x + 9 = 0\)
বা, \(– 4x – 3x + 6x + 9 = 0\)
বা, \(– 7x + 6x + 9 = 0\)
বা, \(– x + 9 = 0\)
বা, \(x = 9\)
(iv) পাশের চিত্রে , ABC ত্রিভুজে DE||PQ||BC এবং AD = 3 সেমি., DP=x সেমি., PB=4 সেমি., AE=4 সেমি., EQ=5সেমি., QC=y সেমি.হলে, x ও y এর মান নির্ণয় করি।
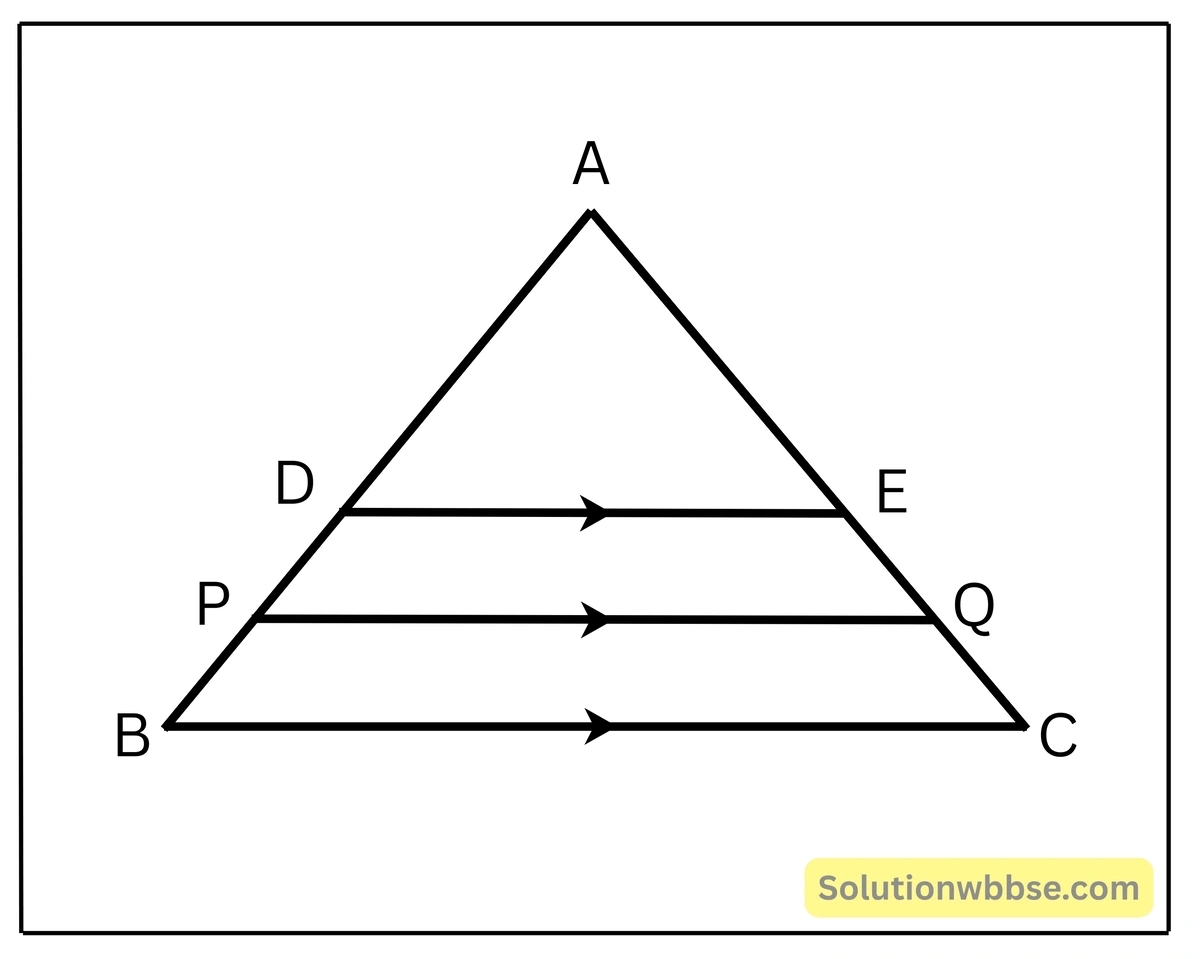
সমাধান –
\(ΔAPQ\) -এর \(DE || PQ\)
∴ \(\frac{AD}{DP} = \frac{AE}{EQ}\) [থ্যালেসের উপপাদ্য অনুসারে]
বা, \(\frac{3}{x} = \frac{4}{5}\)
বা, \(4x = 15\)
বা, \(x = \frac{15}{4}\)
আবার \(ΔABC\) -এর \(PQ || BC\)
∴ \(\frac{AP}{PB} = \frac{AQ}{QC}\) [থ্যালেসের উপপাদ্য অনুসারে]
বা, \(\frac{3+x}{4} = \frac{4+5}{y}\)
বা, \(\frac{3+x}{4} = \frac{9}{y}\)
বা, \(3y + xy = 36\)
বা, \(3y + \frac{15y}{4} = 36\)
বা, \(\frac{12y+15y}{4} = 36\)
বা, \(27y = 144\)
বা, \(y = \frac{144}{27}\)
বা, \(y = \frac{16}{3}\) [উত্তর]
(v) পাশের চিত্রে, DE||BC, BE||XC এবং AD/DB=2/1 হলে, AX/XB এর মান নির্ণয় করি।
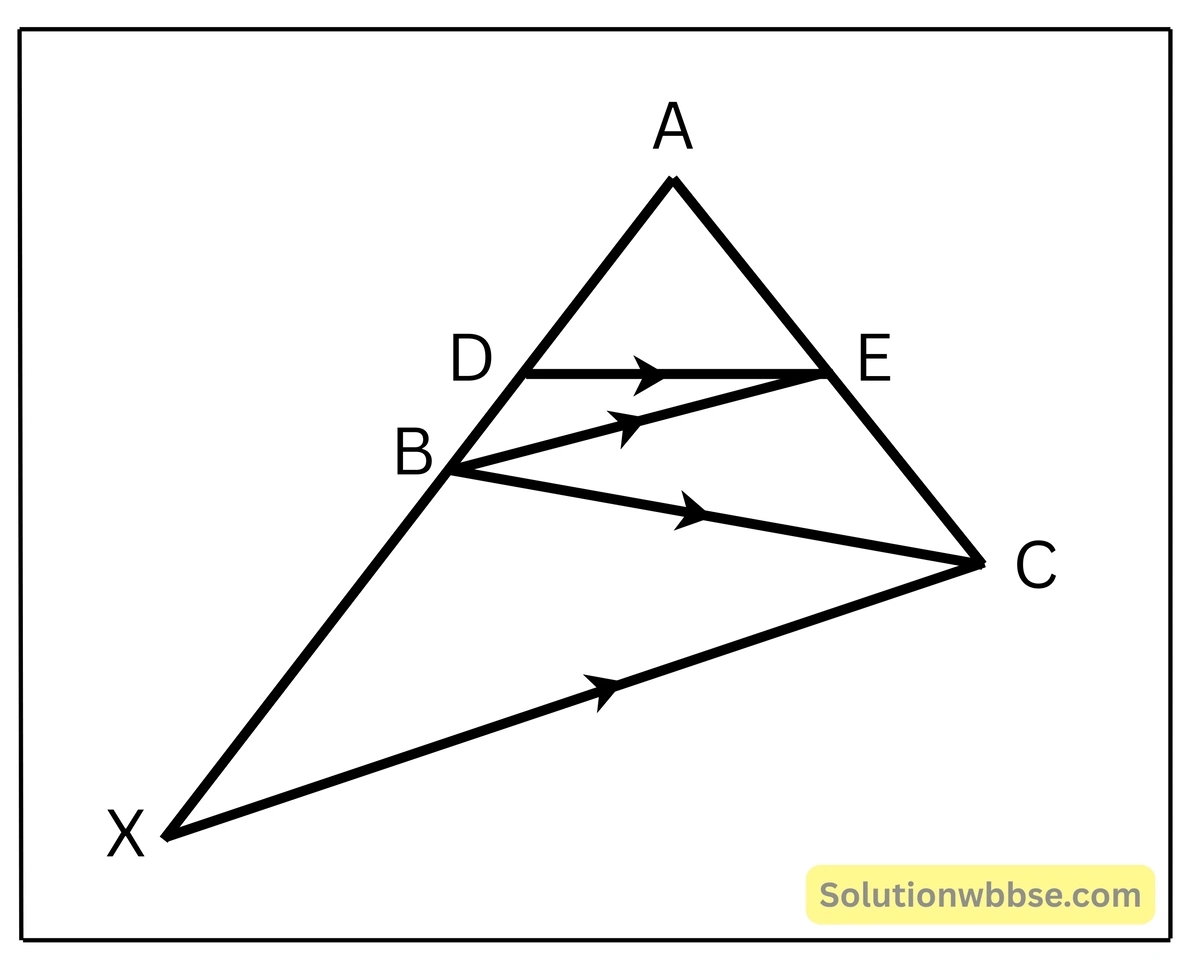
সমাধান –
\(DE || BC\)∴ \(\frac{AD}{DB} = \frac{AE}{EC}\)
বা, \(\frac{2}{1} = \frac{AE}{EC}\)
বা, \(\frac{AE}{EC} = 2\)
আবার , \(BE || XC\)
∴ \(\frac{AB}{BX} = \frac{AE}{EC}\)
বা, \(\frac{AB}{BX} = 2\) [∵ \(\frac{AE}{EC} = 2\)]
বা, \(\frac{AB}{BX} + 1 = 2 + 1\)
বা, \(\frac{AB+BX}{BX} = 3\)
বা, \(\frac{AX}{BX} = 3\)
∴ \(\frac{AX}{XB} = 3\) [উত্তর]
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের অষ্টদশ অধ্যায়, ‘সদৃশতা’ -এর ‘কষে দেখি – 18.2’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন