এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের অষ্টদশ অধ্যায়, ‘সদৃশতা’ -এর ‘কষে দেখি – 18.3’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

1. নীচের কোন ত্রিভুজ জোড়া সদৃশ হিসাব করে লিখি।
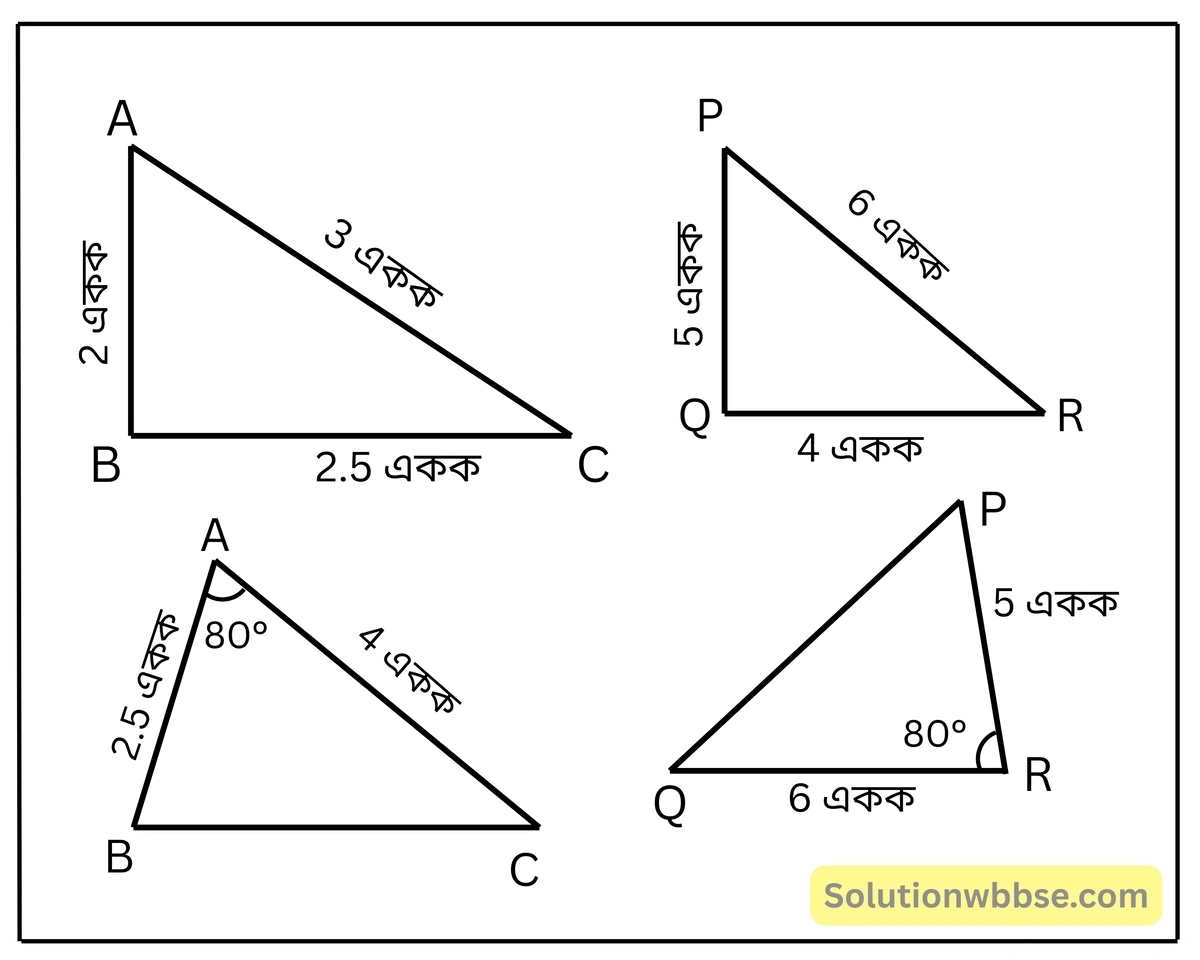
সমাধান –
প্রথম ত্রিভুজদ্বয়ের ক্ষেত্রে,
স্পষ্টতই, \(\frac{AB}{QR} = \frac{BC}{PR} = \frac{AC}{PQ} = \frac{1}{2} \)
∴ \(\triangle ABC \) এবং \(\triangle RQP \) এর অনুরূপ বাহুগুলি পরস্পর সমানুপাতিক।
সুতরাং \(\triangle ABC \) এবং \(\triangle RQP \) ত্রিভুজদ্বয় পরস্পর সদৃশ।
দ্বিতীয় ত্রিভুজদ্বয়ের ক্ষেত্রে,
\(\frac{AB}{QR} \neq \frac{AC}{PR} \)আবার, \(\frac{AB}{PR} \neq \frac{AC}{QR} \)
সুতরাং ত্রিভুজদ্বয়ের অনুরূপ বাহুগুলি সমানুপাতি নয় সুতরাং ত্রিভুজদ্বয় সদৃশ নয়।
2. নীচের ত্রিভুজ জোড়া দেখি ও ∠A এর মান হিসাব করে লিখি।
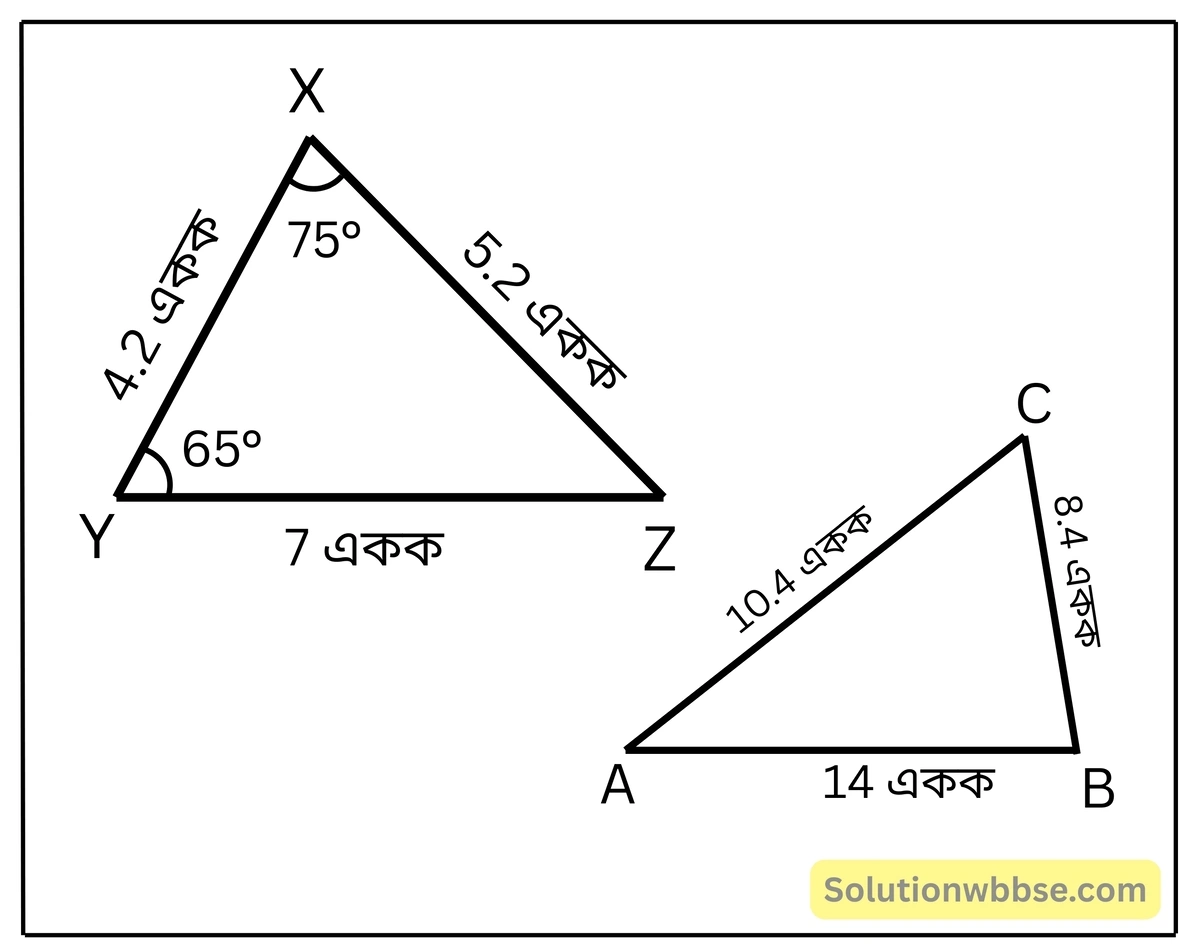
সমাধান –
এক্ষেত্রে, \(\frac{XY}{BC} = \frac{4.2}{8.4} = \frac{1}{2} \)
আবার, \(\frac{XZ}{AC} = \frac{5.2}{10.4} = \frac{1}{2} \)
এবং \(\frac{YZ}{AB} = \frac{7}{14} = \frac{1}{2} \)
∴ \(\frac{XY}{BC} = \frac{XZ}{AC} = \frac{YZ}{AB} \)
সুতরাং \(\triangle XYZ \) এবং \(\triangle CAB \) এর অনুরূপ বাহুগুলি সমানুপাতি।
∴ \(\triangle XYZ \) এবং \(\triangle CAB \) সদৃশকোণী
∴ \(\angle A = \angle Y = 65^\circ \)
3. আমাদের মাঠে 6 সেমি. দৈর্ঘ্যের একটি কাঠির 4 সেমি. দৈর্ঘ্যের ছায়া মাটিতে পড়েছে। ওই একই সময়ে যদি একটি উঁচু টাওয়ারের ছায়ার দৈর্ঘ্য 28 মিটার হয়, তবে টাওয়ারের উচ্চতা কত হবে হিসাব করে দেখি।
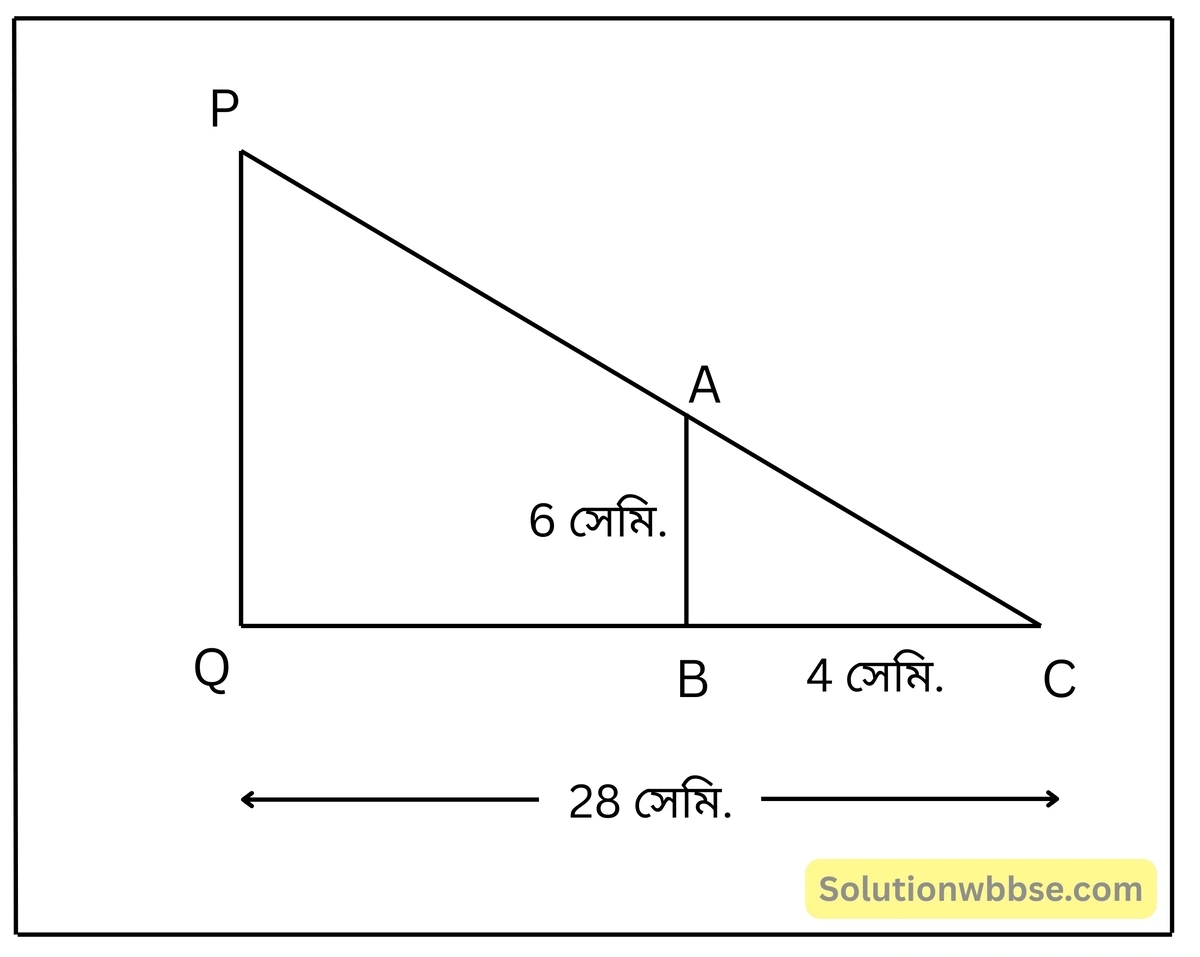
সমাধান –
AB এবং PQ খুঁটি দুটি QC ভূমির উপর লম্বভাবে দণ্ডায়মান।
এক্ষেত্রে AB= 6 মিটার, BC= 4 মিটার, QC =28 মিটার
∴ ∠PQC = ∠ABC = 90°
∴ △CPQ এবং △CAB এর,
∠CBA = ∠CQP = 90°
এবং ∠C, দুটি ত্রিভুজেরই সাধারণ কোণ
এবং ∠CPQ=∠CAB [অনুরূপ কোণ, যেহেতু, PQ||AB এবং PC ভেদক]
∴ △CPQ এবং △CAB সদৃশকোণী
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি পরস্পর সমানুপাতিক
∴ \(\frac{CB}{CQ} = \frac{AB}{PQ} = \frac{CA}{CP} \)
বা, \(\frac{4}{28} = \frac{6}{PQ} \)
বা, 4PQ = 6×28
বা, PQ = 6×7
বা, PQ = 42
∴ টাওয়ারের উচ্চতা 42 মিটার।
4. প্রমাণ করি যে, কোনো ত্রিভুজের দুটি বাহুর মধ্যবিন্দুর সংযোজক সরলরেখাংশ তৃতীয় বাহুর সমান্তরাল ও অর্ধেক।
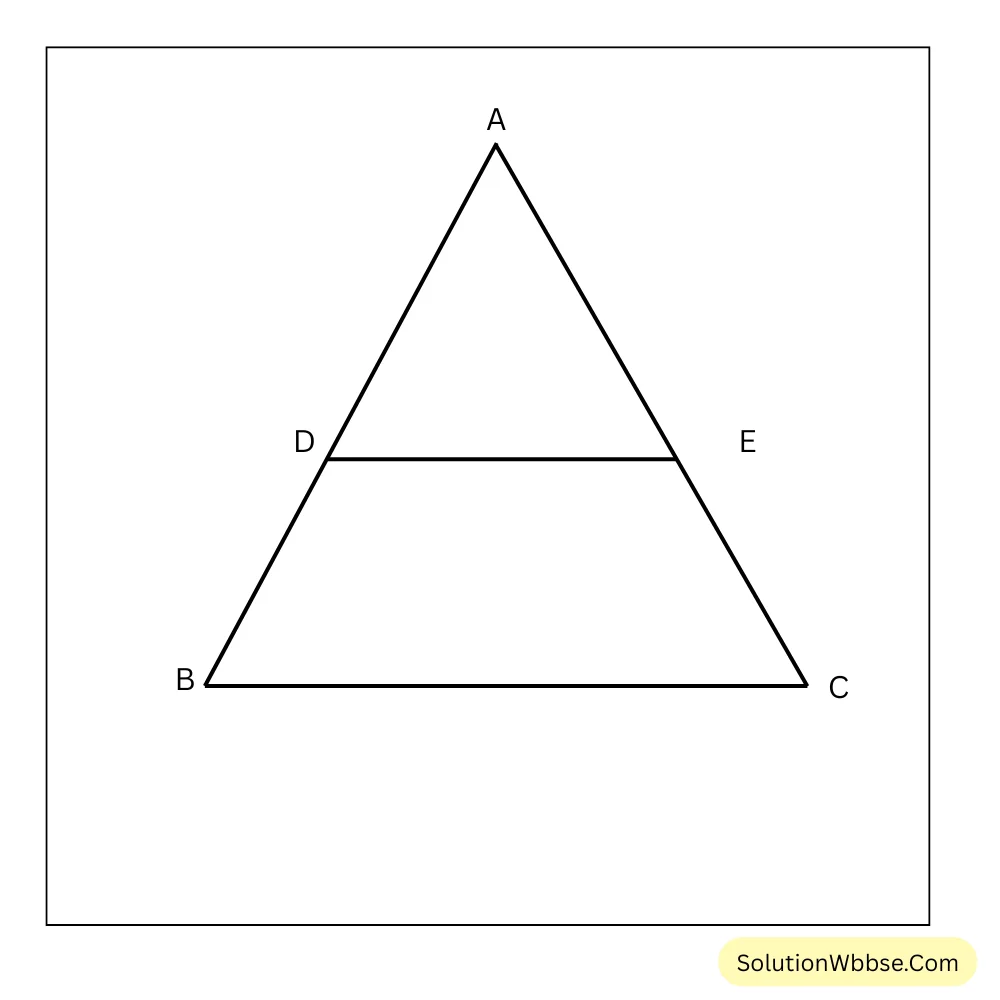
ধরাযাক, \(\triangle ABC\) এর \(AB\) এবং \(BC\) বাহুর মধ্যবিন্দু যথাক্রমে \(D\) ও \(E\) ; প্রমাণ করতে হবে যে, \(DE \parallel BC\) এবং \(DE = \frac{1}{2} BC\).
প্রমাণ – \(\triangle ABC\) এর \(AB\) ও \(AC\) বাহুর মধ্যবিন্দুদ্বয় যথাক্রমে \(D\) ও \(E\) .
\(\therefore AD=DB\)এবং \(AE=EC\)
\(\therefore \frac{AD}{DB} = \frac{AE}{EC}\)\(\therefore DE \parallel BC\) [থ্যালেসের বিপরীত উপপাদ্য থেকে পাই]
এখন, \(\triangle ADE\) ও \(\triangle ABC\) এর
\(\angle ADE = \angle ABC\) [অনুরূপ কোণ, কারণ \(DE \parallel BC\) এবং \(AB\) ভেদক]
আবার, \(\angle AED = \angle ACE\) [অনুরূপ কোণ, কারণ \(DE \parallel BC\) এবং \(AC\) ভেদক]
এবং \(\angle A\) দুটি ত্রিভুজেরই সাধারণ কোণ
\(\therefore \triangle ADE\) এবং \(\triangle ABC\) সদৃশকোণী
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক
\(D\) এবং \(E\) যথাক্রমে \(AB\) ও \(AC\) এর মধ্যবিন্দু।
\(\therefore AB = 2AD\) এবং \(AC = 2AE\)
\(\therefore \frac{AD}{AB} = \frac{AE}{AC} = \frac{1}{2}\)\(\therefore \frac{DE}{BC} = \frac{1}{2}\)বা, \(DE = \frac{1}{2} BC\) [প্রমাণিত]
5. তিনটি সমবিন্দু সরলরেখাಕ್ಕೆ দুটি সমান্তরাল সরলরেখা যথাক্রমে A,B,C ও X,Y,Z বিন্দুতে ছেদ করেছে, প্রমাণ করি যে, AB : BC = XY : YZ.
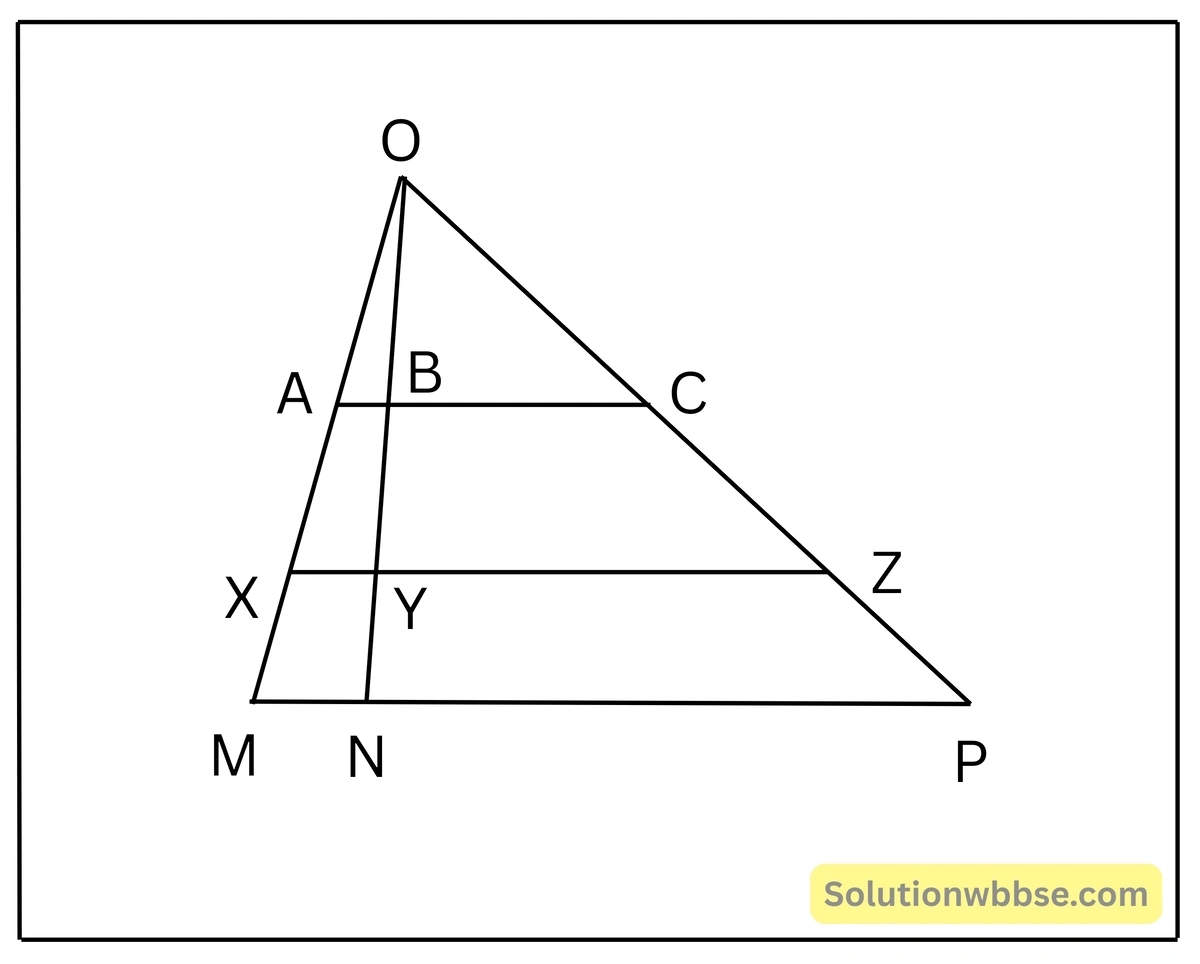
তিনটি সমবিন্দু সরলরেখা হল OM,ON এবং OP, OM,ON এবং OP তিনটি সমবিন্দু সরলরেখাকে দুটি সমান্তরাল সরলরেখা যথাক্রমে A,B,C ও X,Y,Z বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে, AB : BC = XY : YZ.
প্রমাণ – এখন, \(\triangle OAB \) এবং \(\triangle OXY \) এর,
∴ ∠OAB = ∠OXY [অনুরূপ কোণ, কারণ AC||XZ এবং OX ভেদক]
∠OBA = ∠OYX [অনুরূপ কোণ, কারণ AC || XZ এবং OY ভেদক]
∠AOB = ∠XOY [একই কোণ]
∴ \(\triangle OAB \) এবং \(\triangle OXY \) সদৃশকোণী
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
∴ \(\frac{OA}{OX} = \frac{OB}{OY} = \frac{AB}{XY} \)—-(i)
একই ভাবে প্রমাণ করা যায়, \(\triangle OBC \) এবং \(\triangle OYZ \) সদৃশকোণী,
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
∴ \(\frac{OB}{OY} = \frac{OC}{OZ} = \frac{BC}{YZ} \)—-(ii)
(i) ও (ii) থেকে পাই,
\(\frac{AB}{XY} = \frac{BC}{YZ} \)∴ \(\frac{AB}{BC} = \frac{XY}{YZ} \)
বা, AB:BC = XY:YZ
∴ AB:BC = XY:YZ [প্রমাণিত]
6. PQRS একটি ট্রাপিজিয়াম অঙ্কন করেছি যার PQ || SR; PR ও QS কর্ণদুটি O বিন্দুতে পরস্পরকে ছেদ করলে, প্রমাণ করি যে, OP:OR=OQ:OS ; যদি SR=2PQ হয়, তাহলে প্রমাণ করি যে, O বিন্দু কর্ণ দুটির প্রত্যেকটির সমত্রিখন্ডক বিন্দুর একটি বিন্দু হবে।
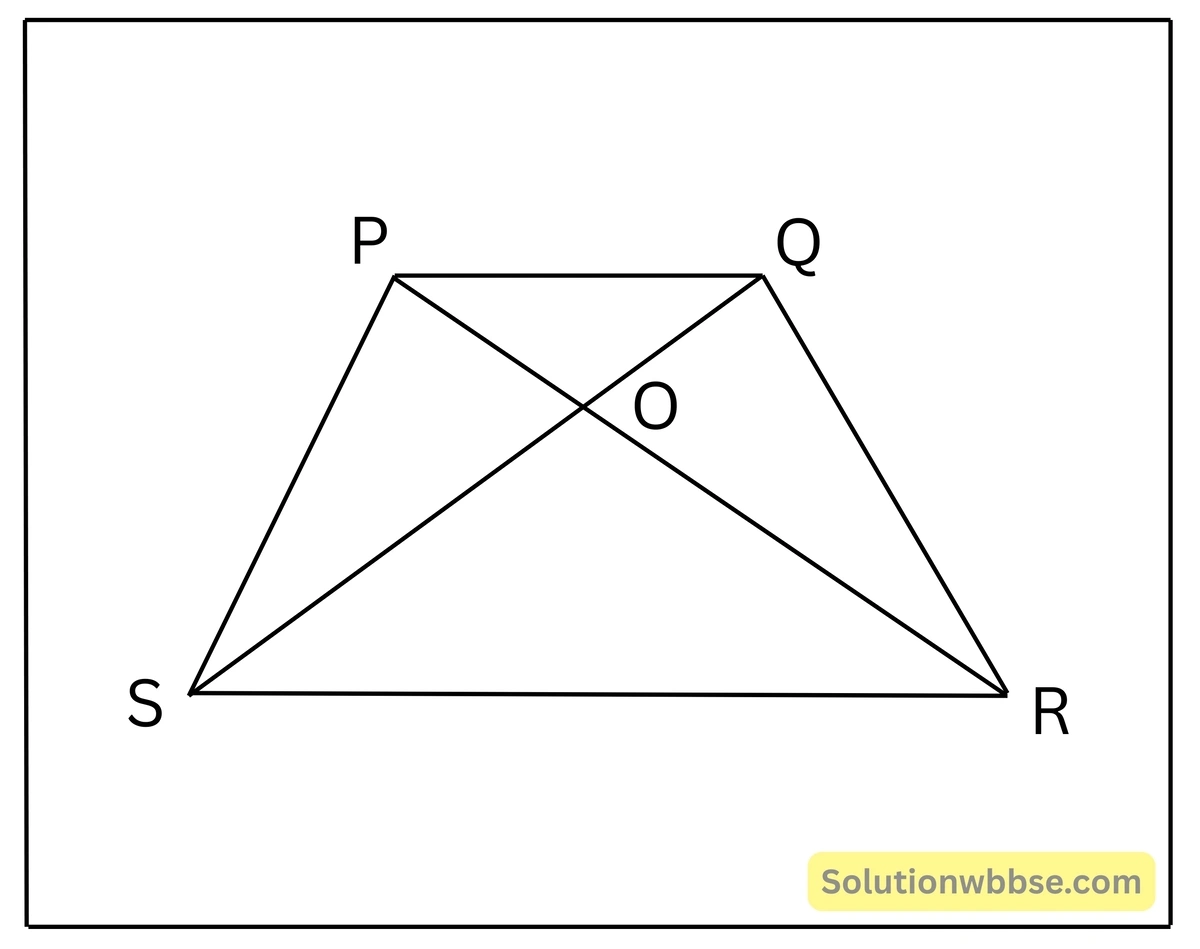
PQRS একটি ট্রাপিজিয়াম, যার PQ || SR; PR ও QS কর্ণদুটি O বিন্দুতে পরস্পরকে ছেদ করেছে। প্রমাণ করতে হবে যে, OP : OR = OQ : OS ; যদি SR = 2PQ হয়, তাহলে প্রমাণ করতে হবে যে, O বিন্দু কর্ণ দুটির প্রত্যেকটির সমত্রিখন্ডক বিন্দুর একটি বিন্দু হবে। অর্থাৎ প্রমাণ করতে হবে যে, OP : OR = OQ : OS = 1 : 2
প্রমাণ – ΔOPQ এবং ΔORS এর,
∠OPQ = ∠ORS [একান্তর কোণ, কারণ PQ||SR এবং PR ভেদক]
∠OQP = ∠OSR [একান্তর কোণ, কারণ PQ||SR এবং QS ভেদক]
এবং ∠POQ = ∠ROS [বিপ্রতীপ কোণ]
∴ ΔOPQ এবং ΔORS সদৃশকোণী
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
∴ \(\frac{OP}{OR} = \frac{PQ}{RS} = \frac{OQ}{OS}\) —(i)
বা, \(\frac{OP}{OR} = \frac{OQ}{OS}\)
∴ \(OP:OR=OQ:OS\) [প্রমাণিত]
\(\frac{PQ}{RS} = \frac{1}{2}\) [প্রদত্ত]
∴ (i) নং সমীকরণ থেকে পাই,
\(\frac{OP}{OR} = \frac{OQ}{OS} = \frac{1}{2}\)∴ \(OP:OR=OQ:OS=1:2\) [প্রমাণিত]
7. PQRS একটি সামান্তরিক। S বিন্দুগামী একটি সরলরেখা PQ ও বর্ধিত RQ –কে যথাক্রমে X ও Y বিন্দুতে ছেদ করলে, প্রমাণ কর যে PS:PX=QY:QX=RY:RS.
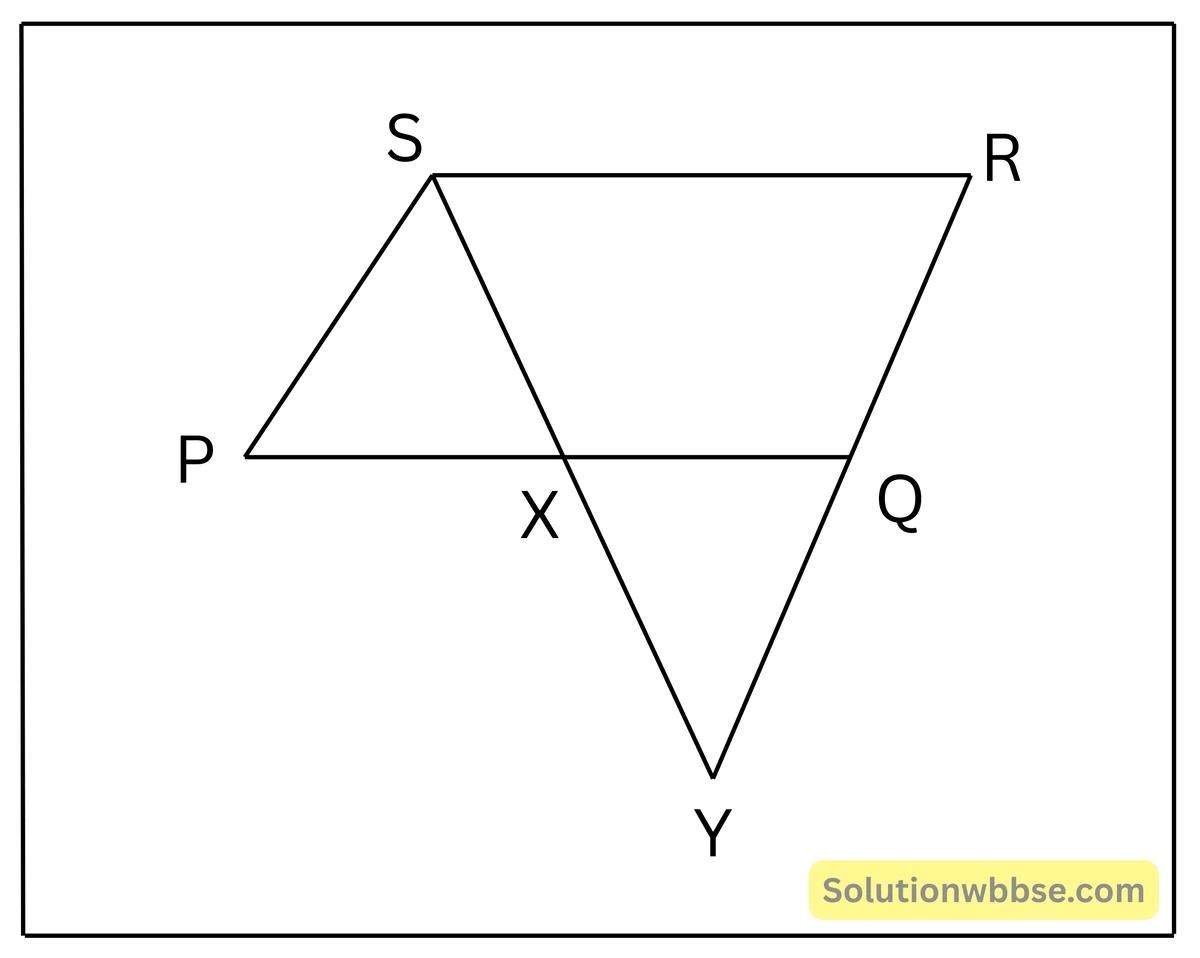
PQRS একটি সামান্তরিক, S বিন্দুগামী একটি সরলরেখা PQ ও বর্ধিত PQ কে X ও Y বিন্দুতে ছেদ করেছে, প্রমাণ করতে হবে যে, PS : PX = QY : YZ = RY : RS.
প্রমাণ –
ΔXSP এবং ΔXYQ এর,
∠XSP = ∠XYQ [একান্তর কোণ, কারণ SP||QY এবং SY ভেদক]
∠SXP = ∠YXQ [বিপ্রতীপ কোণ]
এবং ∠SPX = ∠YQX [একান্তর কোণ, কারণ SP||QY এবং PQ ভেদক]
∴ ΔXSP এবং ΔXYQ সদৃশকোণী
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
∴ \(\frac{XS}{XY} = \frac{SP}{YQ} = \frac{XP}{XQ}\)
বা, \(\frac{SP}{XP} = \frac{YQ}{XQ}\) –(i)
আবার, ΔYQX এবং ΔYRS এর,
∠YXQ = ∠YSR [অনুরূপ কোণ, কারণ PQ||SR এবং YS ভেদক]
∠YQX = ∠YRS [অনুরূপ কোণ, কারণ PQ||SR এবং YR ভেদক]
∠Y দুটি ত্রিভুজেরই সাধারণ কোণ
∴ ΔYQX এবং ΔYRS সদৃশকোণী।
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
∴ \(\frac{YQ}{YR} = \frac{YX}{YS} = \frac{XQ}{SR}\)
বা, \(\frac{SR}{YR} = \frac{XQ}{YQ}\)
বা, \(\frac{YR}{SR} = \frac{YQ}{XQ}\) –(ii)
(i) ও (ii) থেকে পাই,
\(\frac{SP}{XP} = \frac{YQ}{XQ} = \frac{YR}{SR}\)∴ \(SP:XP=YQ:XQ=YR:SR\)
বা, \(PS:PX = QY:QX = RY:RS\) [প্রমাণিত]
8. দুটি সদৃশকোণী ত্রিভুজ ΔABC ও ΔPQR সদৃশকোণী। তাদের পরিবৃত্ত যথাক্রমে X এবং Y; BC ও QR অনুরূপ বাহু হলে, প্রমাণ করি যে, BX:QY=BC:QR.
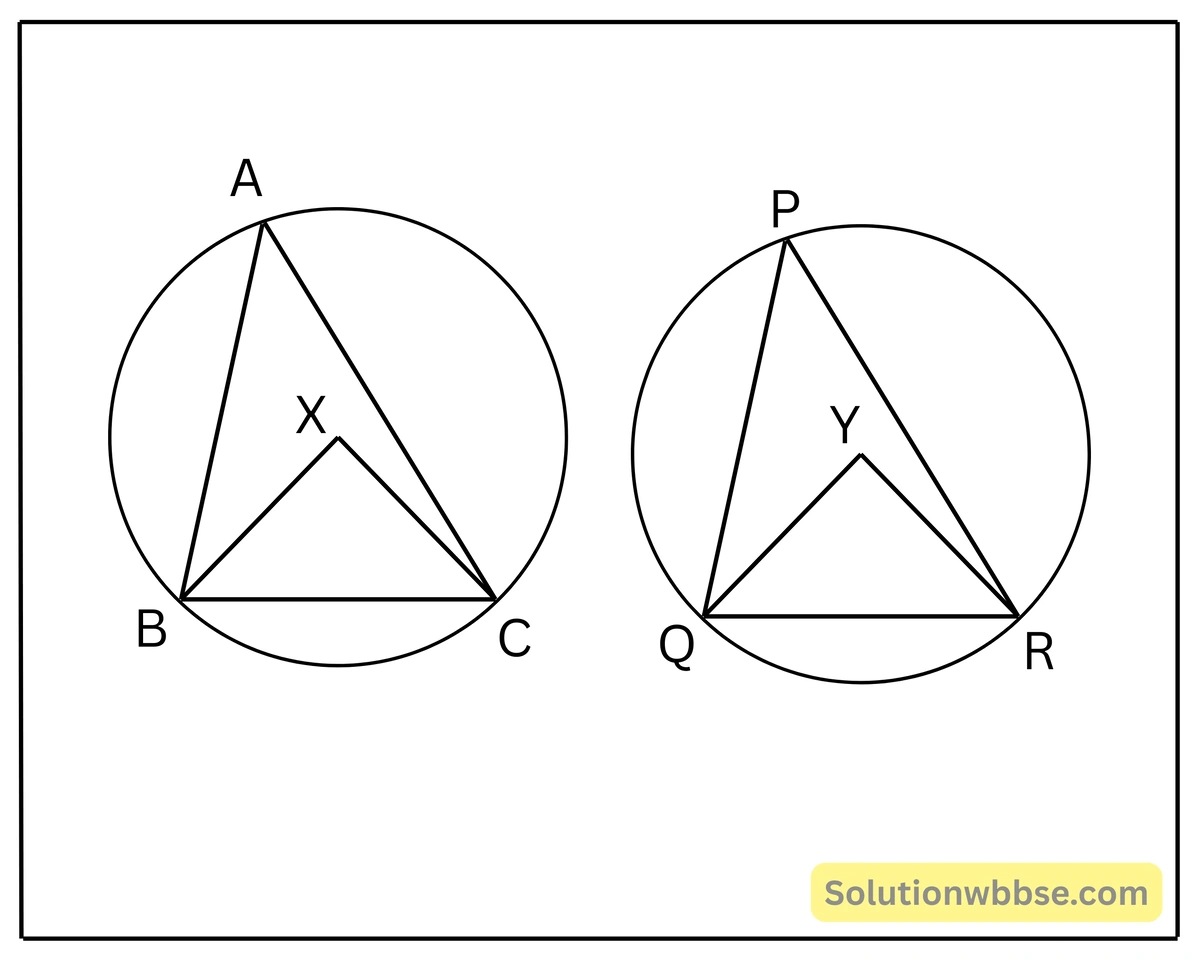
সমাধান –
দুটি সদৃশকোণী ত্রিভুজ ΔABC ও ΔPQR সদৃশকোণী।
∴ ∠A=∠P, ∠B=∠Q এবং ∠C=∠R.
X ও Y যথাক্রমে ΔABC এবং ΔPQR এর পরিকেন্দ্র।
BC বৃত্তচাপের উপর ∠BXC কেন্দ্রস্থ কোণ এবং ∠BAC পরিধিস্থ কোণ।
∴ ∠BXC=2∠BAC
আবার, QR বৃত্তচাপের উপর ∠QYR কেন্দ্রস্থ কোণ এবং ∠QPR পরিধিস্থ কোণ
∴ ∠QYR=2∠QPR
আবার, ∠BAC=∠QPR, ∴ ∠BXC=∠QYR
এখন, BX =XC [একই বৃত্তের ব্যাসার্ধ]
∴ ∠XBC = ∠XCB
ধরি, ∠XBC = ∠XCB =a
ত্রিভুজ ΔBXC থেকে পাই,
∠XBC + ∠XCB+∠BXC = 180
বা, a+a = 180°-∠BXC
বা, 2a = 180°-∠BXC
বা, \(a = \frac{180^\circ – \angle BXC}{2}\)
আবার, YQ = YR [একই বৃত্তের ব্যাসার্ধ]
∴ ∠YQR=∠YRQ
ধরি, ∠YQR = ∠YRQ = b
এখন ΔQYR থেকে পাই,
∠YQR+∠YRQ+∠QYR=180°
বা, b+b= 180°-∠QYR
বা, 2b= 180°-∠QYR
বা, \(b = \frac{180^\circ – \angle QYR}{2}\)
এখন, \(\frac{180^\circ – \angle BXC}{2} = \frac{180^\circ – \angle QYR}{2}\) [যেহেতু, ∠BXC = ∠QYR]
∴ a=b
∴ ΔBXC এবং ΔQYR এর ∠XBC = ∠YQR, ∠XCB = ∠YRQ এবং ∠BXC = ∠QYR.
সুতরাং ΔBXC এবং ΔQYR সদৃশকোণী
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
∴ BX:QY = BC:QR = XC:YR
∴ BX:QY = BC:QR [প্রমাণিত]
9. কোনো বৃত্তের PQ ও RS দুটি জ্যা বৃত্তের অভ্যন্তরে X বিন্দুতে পরস্পরকে ছেদ করলে P,S ও R,Q যুক্ত করে, প্রমাণ করি যে, ΔPXS ও ΔRSQ সদৃশকোণী। এর থেকে প্রমাণ করি যে, PX.XQ = RX.XS.
অথবা, একটি বৃত্তে দুটি জ্যা পরস্পরকে অন্তঃস্থ ভাবে ছেদ করলে একটির অংশদ্বয়ের আয়তক্ষেত্র অপরটির অংশদ্বয়ের আয়তক্ষেত্রের সমান হবে।
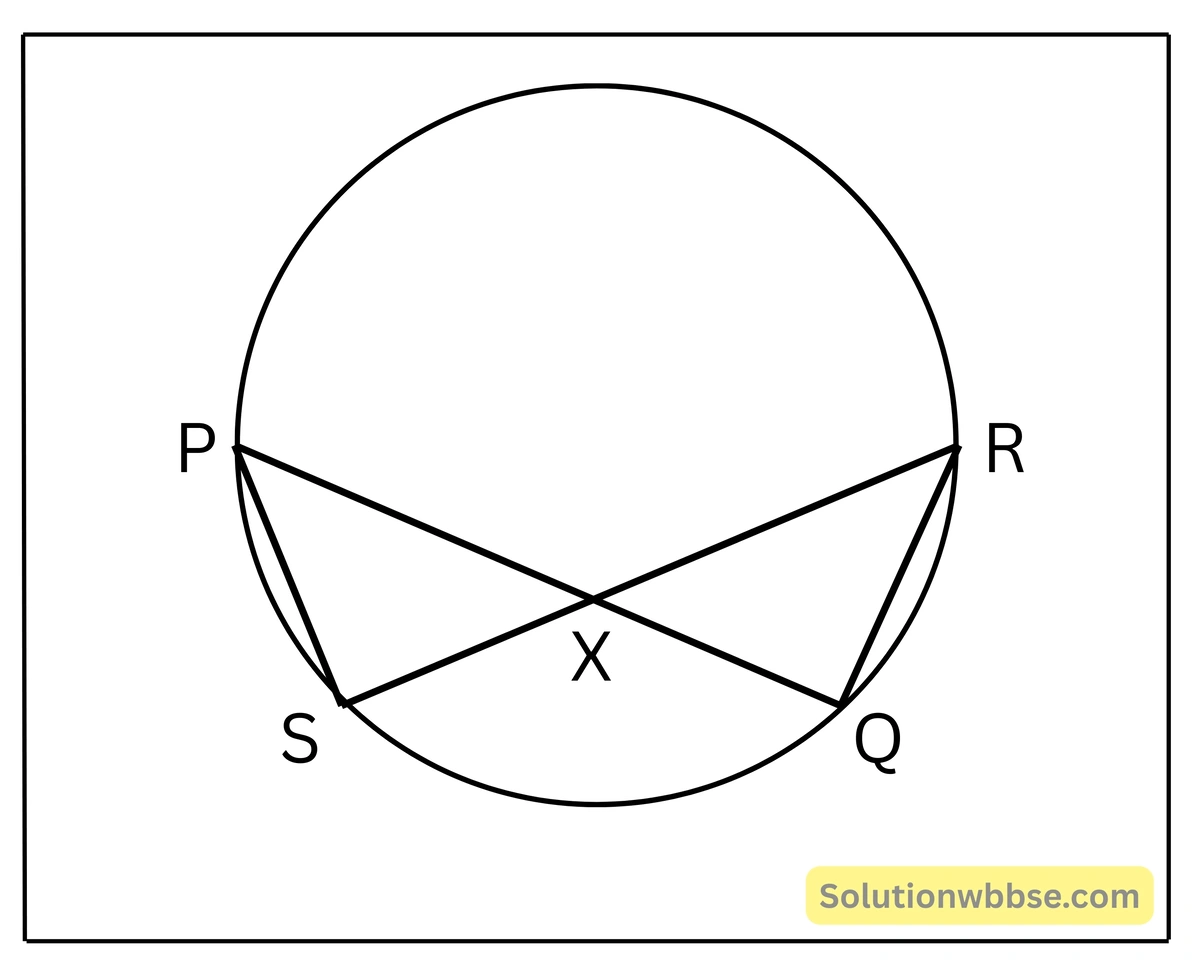
PQ ও RS দুটি জ্যা বৃত্তের অভ্যন্তরে X বিন্দুতে পরস্পরকে ছেদ করেছে, PS ও RQ যুক্ত করা হল, প্রমাণ করতে হবে যে ΔPXS এবং ΔRSQ সদৃশকোণী। আরও প্রমাণ করতে হবে যে, PX.XQ = RX.XS
প্রমাণঃ ΔPXS এবং ΔRXQ ত্রিভুজের ক্ষেত্রে,
∠XPS=∠XRQ [যেহেতু একই বৃত্তাংশস্থ সকল কোণের মান সমান]
∠XSP=∠XQX [যেহেতু একই বৃত্তাংশস্থ সকল কোণের মান সমান]
∠PXS =∠RXQ [বিপ্রতীপ কোণ]
∴ ΔPXS এবং ΔRXQ সদৃশকোণী [প্রমাণিত]
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
∴ \(\frac{PX}{RX} = \frac{XS}{XQ} = \frac{PS}{RQ}\)
∴ \(\frac{PX}{RX} = \frac{XS}{XQ}\)
বা, PX.XQ = RX.XS [প্রমাণিত]
10. একটি সরলরেখার উপর P ও Q দুটি বিন্দু। P এবং Q বিন্দুতে সরলরেখাটির উপর যথাক্রমে PR এবং QS লম্ব। PS এবং QR পরস্পরকে O বিন্দুতে ছেদ করে। OT, PQ –এর উপর লম্ব। প্রমাণ করি যে, \(\frac{1}{OT} = \frac{1}{PR} + \frac{1}{QS}\)
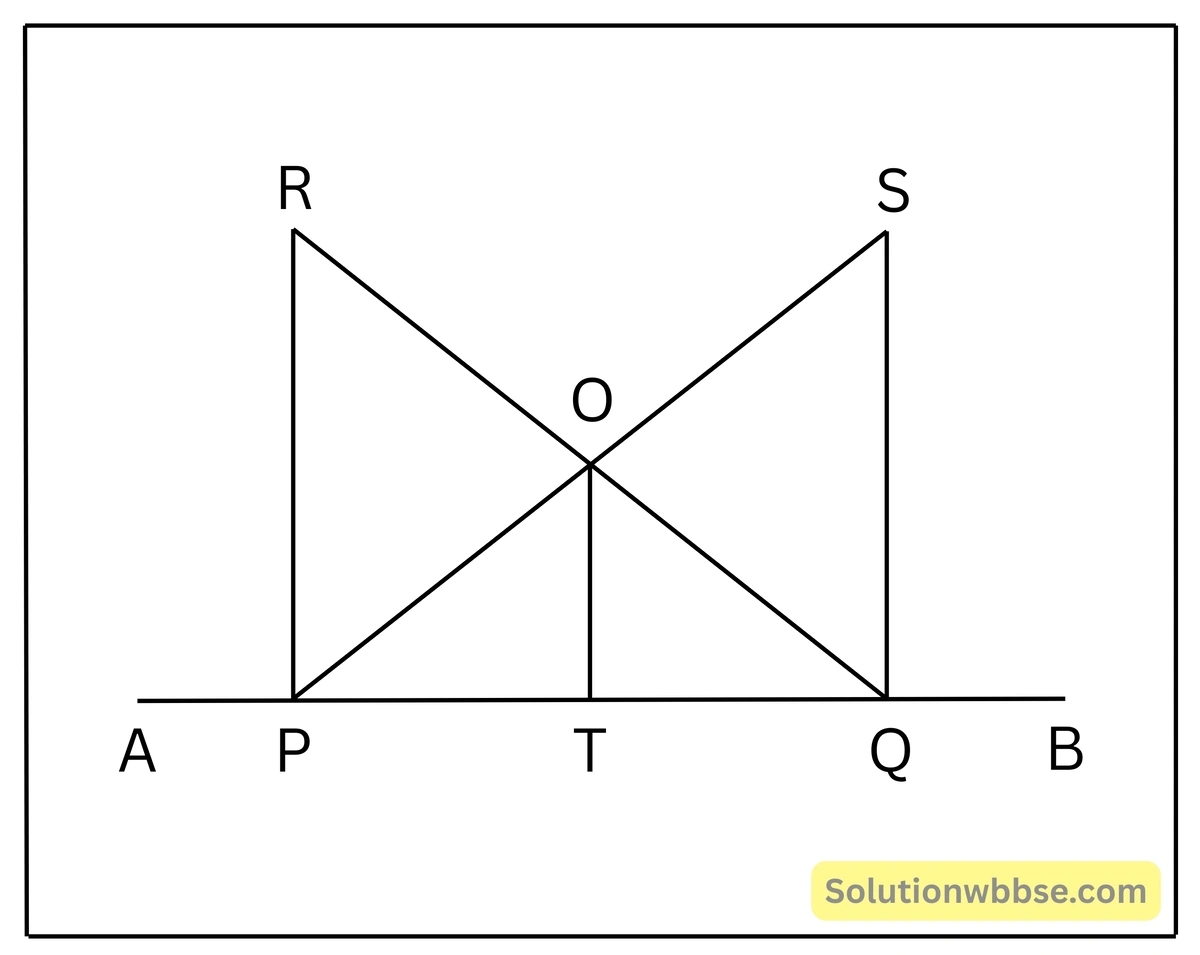
প্রমাণ –
ΔRPQ এবং ΔOTQ এর মধ্যে,
∠RPQ = ∠OTQ [উভয়ই 1 সমকোণ]
∠RQP = ∠OQT [একই কোণ]
∠PRQ = ∠TOQ [অনুরূপ কোণ, যেহেতু, PR || TO এবং RQ ভেদক]
∴ ΔOTQ এবং ΔRPQ সদৃশকোণী
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
∴ \(\frac{OT}{PR} = \frac{TQ}{PQ} = \frac{OQ}{RQ}\)
∴ \(\frac{OT}{PR} = \frac{TQ}{PQ}\) —- (i)
আবার,ΔSPQ এবং ΔOPT এর মধ্যে
∠SQP = ∠OTP [উভয়ই 1 সমকোণ]
∠SPQ = ∠OPT [একই কোণ]
∠PSQ =∠POT [অনুরূপ কোণ, যেহেতু, OT || SQ এবং PS ভেদক]
∴ ΔOPT এবং ΔSPQ সদৃশকোণী
এবং সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
∴ \(\frac{OP}{SP} = \frac{PT}{PQ} = \frac{OT}{SQ}\)
∴ \(\frac{OT}{SQ} = \frac{PT}{PQ}\) —- (ii)
(i) ও (ii) যোগ করে পাই,
\(\frac{OT}{PR} + \frac{OT}{SQ} = \frac{PT}{PQ} + \frac{TQ}{PQ}\)বা, \(OT\left(\frac{1}{PR} + \frac{1}{SQ}\right) = \frac{PT+TQ}{PQ}\)
বা, \(OT\left(\frac{1}{PR} + \frac{1}{SQ}\right) = \frac{PQ}{PQ}\)
বা, \(OT\left(\frac{1}{PR} + \frac{1}{SQ}\right) = 1\)
বা, \(\left(\frac{1}{PR} + \frac{1}{SQ}\right) = \frac{1}{OT}\)
বা, \(\frac{1}{OT} = \left(\frac{1}{PR} + \frac{1}{SQ}\right)\) [প্রমাণিত]
11. একটি বৃত্তে অন্তর্লিখিত ত্রিভুজ ΔABC ; বৃত্তের ব্যাস AD এবং AE, BC বাহুর উপর লম্ব যা BC বাহুকে E বিন্দুতে ছেদ করে। প্রমাণ করি যে, ΔAEB এবং ΔACD সদৃশকোণী। এর থেকে প্রমাণ করি যে, AB.AC = AE.AD.
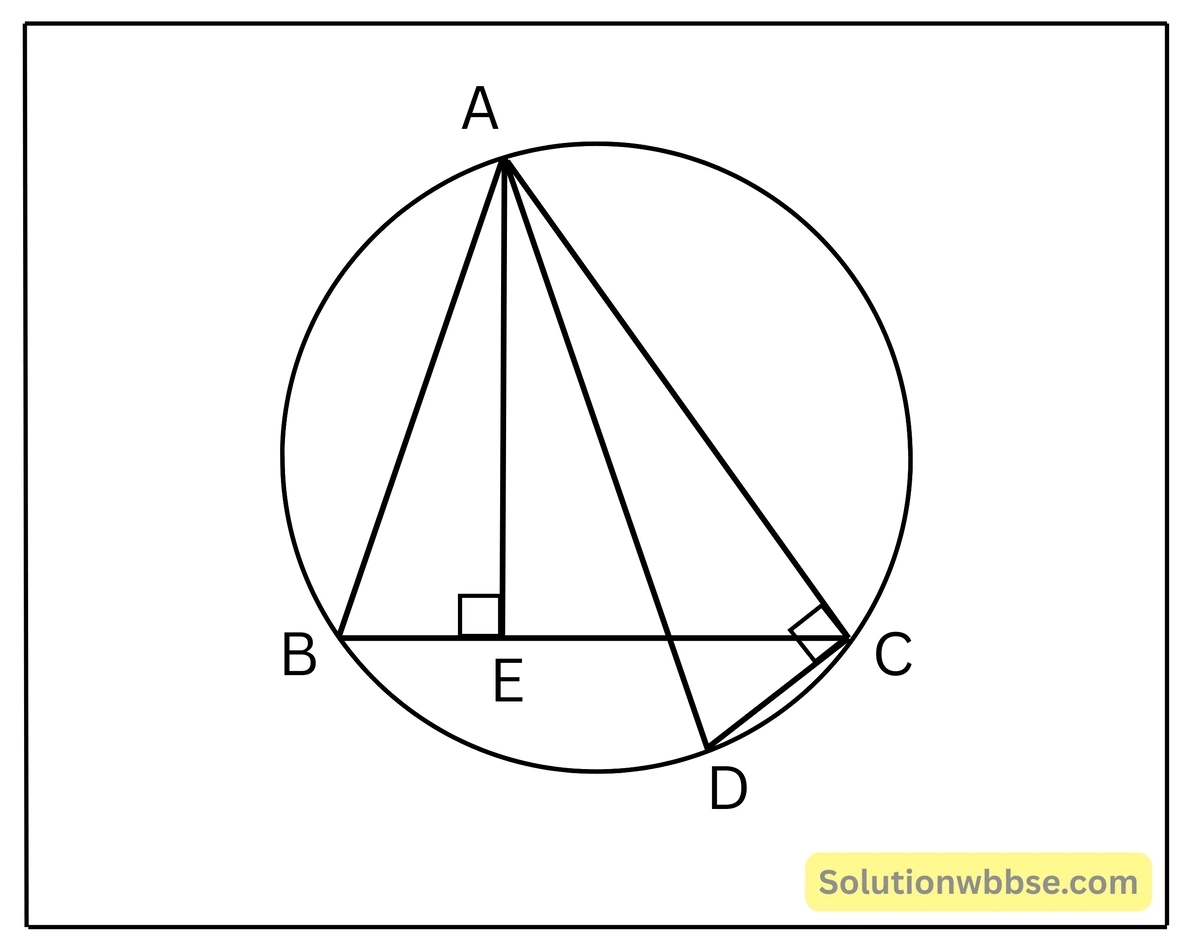
- একটি বৃত্তে অন্তর্লিখিত ত্রিভুজ ΔABC ; বৃত্তের ব্যাস AD এবং AE, BC বাহুর উপর লম্ব যা BC বাহুকে E বিন্দুতে ছেদ করে। প্রমাণ করি যে, ΔAEB এবং ΔACD সদৃশকোণী। এর থেকে প্রমাণ করি যে, AB.AC = AE.AD.
ABC ত্রিভুজটি বৃত্তে অন্তর্লিখিত, যার ব্যাস AD,AE, BC বাহুর উপর লম্ব যা BC বাহুকে E বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে,ΔAEB এবং ΔACD সদৃশকোণী,আরও প্রমাণ করতে হবে যে, AB.AC = AE.AD.
প্রমাণঃ ΔAEB এবং ΔACD ত্রিভুজের ক্ষেত্রে,
∠AEB = ∠ACD = 90°
∠ABE = ∠ADC [যেহেতু,একই বৃত্তাংশস্থ সকল কোণের মান সমান]
∠BAE = ∠DAC [অবশিষ্ট কোণ]
∴ ΔAEB এবং ΔACD সদৃশকোণী
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
∴ \(\frac{AE}{AC} = \frac{EB}{CD} = \frac{AB}{AD}\)
∴ \(\frac{AE}{AC} = \frac{AB}{AD}\)
∴ AB.AC = AE.AD [প্রমাণিত]
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের অষ্টদশ অধ্যায়, ‘সদৃশতা’ -এর ‘কষে দেখি – 18.3’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন