এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের অষ্টদশ অধ্যায়, ‘সদৃশতা’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

প্ৰয়োগ 1. পাশের চিত্রে \(\triangle\)ABC-এর DE \(|\) BC; যদি AD = 5 সেমি., DB = 6 সেমি. এবং AE = 7.5 সেমি. হয়, তবে AC-এর দৈর্ঘ্য হিসাব করে লিখি।
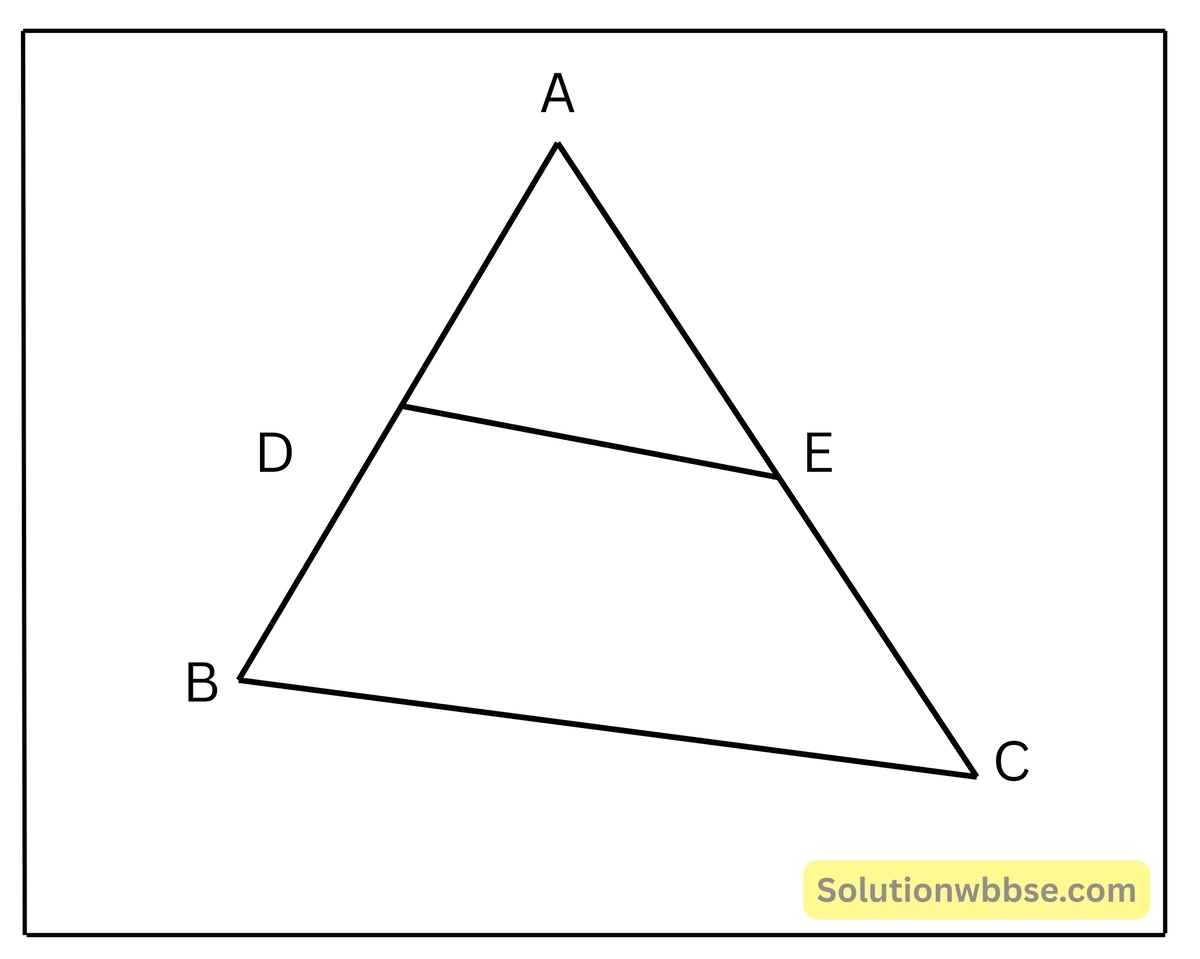
\(\triangle\)ABC-এর DE || BC,
∴ \(\frac{AD}{DB}\) = \(\frac{AE}{EC}\) [থ্যালেসের উপপাদ্য থেকে পেলাম]
∴ \(\frac{5}{6}\) = \(\frac{7.5}{EC}\)
∴ EC = 7.5 \(\times\) \(\frac{6}{5}\) সেমি. = 9 সেমি.
∴ AC = AE + EC = \(7.5\) + \(9\) = \(16.5\) সেমি।
প্রয়োগ 2. যদি \(\triangle\)ABC-এর BC || DE, \(\frac{AD}{DB}\) = \(\frac{2}{5}\) এবং AC = 21 সেমি. হয়, তবে AE-এর মান হিসাব করে লিখি।
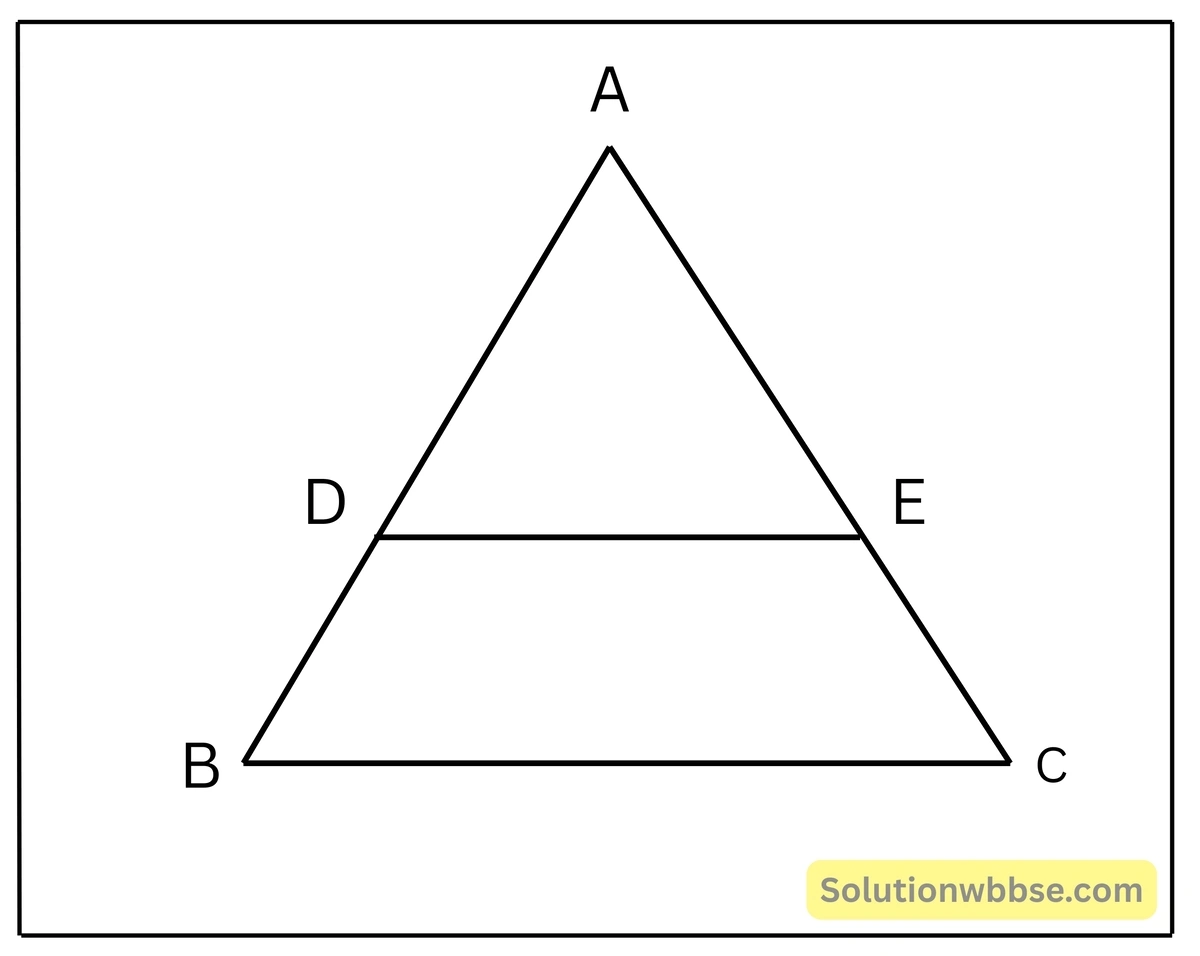
\(\triangle\)ABC-এর BC \(|\) DE, ∴ \(\frac{AD}{DB}\) = \(\frac{AE}{EC}\) [থ্যালেসের উপপাদ্য থেকে পেলাম]
∴ \(\frac{2}{5}\) = \(\frac{AE}{EC}\)
ধরি, AE = x সেমি. ∴ EC = (21 – x) সেমি.
∴ \(\frac{2}{5}\) = \(\frac{x}{21-x}\)
∴ 2(21 – x) = 5x
42 – 2x = 5x
42 = 7x
x = 6
∴ AE = \(6\) সেমি.
প্রয়োগ 3. \(ABC\) ত্রিভুজের \(BC\) বাহুর সমান্তরাল সরলরেখা \(AB\) ও \(AC\)-কে যথাক্রমে \(D\) ও \(E\) বিন্দুতে ছেদ করেছে। যদি \(AE = 2AD\) হয়, তবে \(DB : EC\)-এর মান হিসাব করে লিখি।
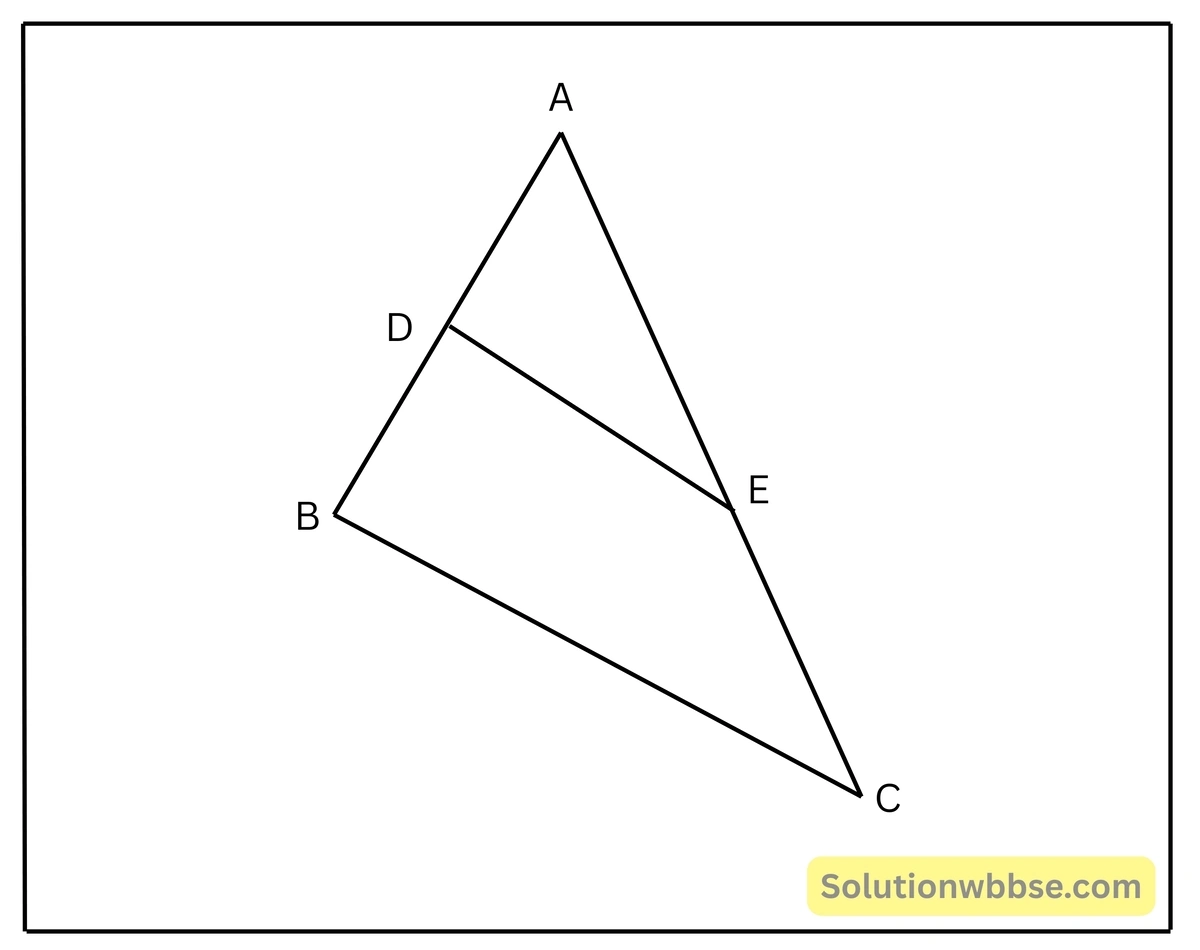
\(\triangle ABC\)-এর \(DE || BC\),
∴ \(\frac{AD}{DB} = \frac{AE}{EC}\)
∴ \(\frac{DB}{EC} = \frac{AD}{AE} = \frac{1}{2}\) [ ∵ \(AE = 2AD\) ∴ \(\frac{AD}{AE} = \frac{1}{2}\)]
∴ \(DB : EC = 1 : 2\)
প্রয়োগ 4. পাশের চিত্রে PQ || AB এবং PR || AC হলে, প্রমাণ করি যে QR || BC
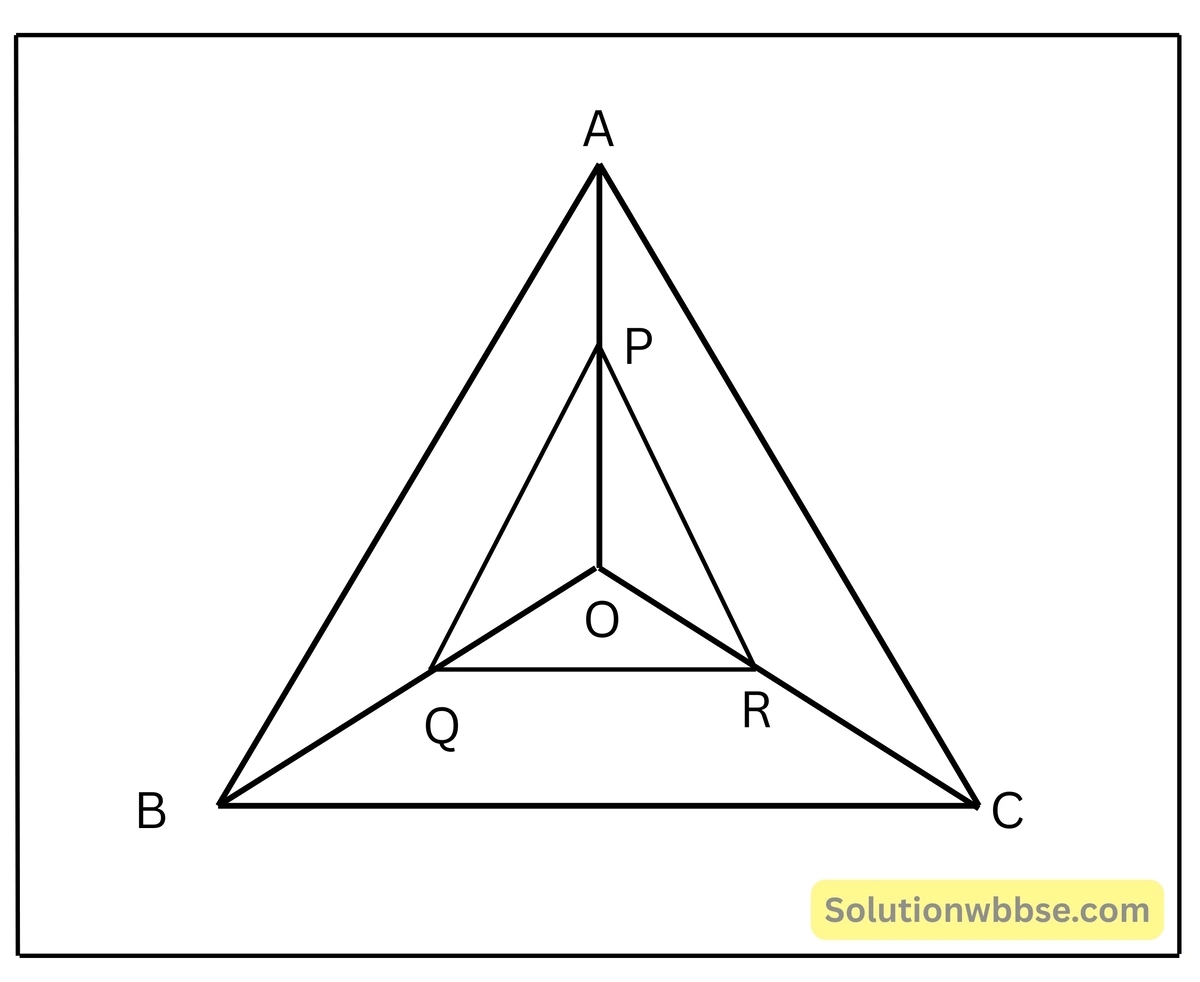
△OAB-এর PQ || AB,
∴ \(\frac{OP}{PA} = \frac{OQ}{QB}\) [থ্যালেসের উপপাদ্য থেকে পাই] __ (i)
আবার, △AOC-এর PR || AC,
∴ \(\frac{OP}{PA} = \frac{OR}{RC}\) [থ্যালেসের উপপাদ্য থেকে পাই] __ (ii)
(i) ও (ii) থেকে পাই,
∴ △OBC-এর OB ও OC-এর ওপর যথাক্রমে দুটি এমন বিন্দু Q ও R পেলাম যাতে \(\frac{OQ}{QB} = \frac{OR}{RC}\)
∴ থ্যালেসের বিপরীত উপপাদ্য থেকে পেলাম, QR || BC.
প্রয়োগ 5. একটি সরলরেখা △ABC-এর AB ও AC -কে যথাক্রমে D ও E বিন্দুতে এমনভাবে ছেদ করল যে \(\frac{AD}{DB} = \frac{AE}{EC}\) হলো। যদি ∠ADE = ∠ACB হয়, প্রমাণ করি যে, △ABC সমদ্বিবাহু ত্রিভুজ।

প্রদত্ত – △ABC-এর DE সরলরেখাংশ AB ও AC বাহুকে যথাক্রমে D ও E বিন্দুতে এমনভাবে ছেদ করেছে যে \(\frac{AD}{DB} = \frac{AE}{EC}\)
প্রমাণ করতে হবে – △ABC সমদ্বিবাহু ত্রিভুজ।
প্রমাণ –
যেহেতু, \(\frac{AD}{DB} = \frac{AE}{EC}\)
সুতরাং, থ্যালেসের বিপরীত উপপাদ্য থেকে পাই, DE || BC
∴ অনুরূপ ∠ADE = ∠ABC (i)
আবার, ∠ADE = ∠ACB [প্রদত্ত] (ii)
∴ (i) ও (ii) থেকে পাই, ∠ABC = ∠ACB
∴ AB = AC ∴ ABC একটি সমদ্বিবাহু ত্রিভুজ।
প্রয়োগ 6. ABCD একটি ট্র্যাপিজিয়াম অঙ্কন করেছি যার AB || DC; AB-এর সমান্তরাল একটি সরলরেখা অঙ্কন করেছি যা AD ও BC-কে যথাক্রমে E ও F বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, AE : ED = BF : FC
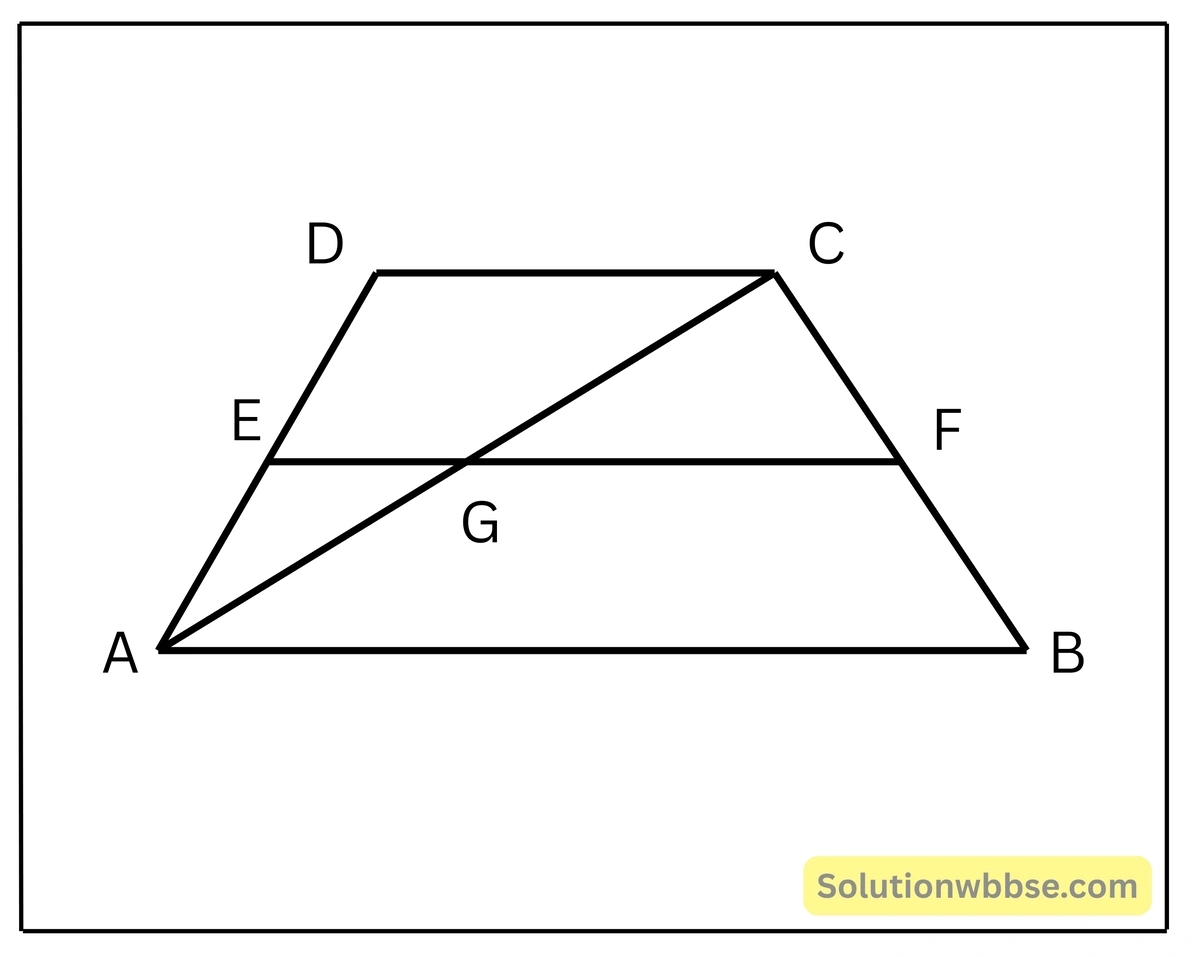
প্রদত্ত – ABCD ট্র্যাপিজিয়ামের AB || DC; AB-এর সমান্তরাল সরলরেখা AD ও BC-কে যথাক্রমে E ও F বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে – AE : ED = BF : FC
অঙ্কন – A, C যোগ করলাম যা EF-কে G বিন্দুতে ছেদ করল।
প্রমাণ – △ADC -এর DC || EG
সুতরাং, থ্যালেসের উপপাদ্য থেকে পাই \(\frac{AE}{ED} = \frac{AG}{GC}\) __ (i)
আবার, △ACB -এর AB || GF
∴ থ্যালেসের উপপাদ্য থেকে পাই, \(\frac{AG}{GC} = \frac{BF}{FC}\) __ (ii)
সুতরাং, (i) ও (ii) থেকে পাই, \(\frac{AE}{ED} = \frac{BF}{FC}\)
∴ AE : ED = BF : FC
প্রয়োগ 7. থ্যালেসের বিপরীত উপপাদ্যের সাহায্যে প্রমাণ করো যে, ত্রিভুজের যেকোনো দুটি বাহুর মধ্যবিন্দুদ্বয়ের সংযোজক সরলরেখাংশ তৃতীয় বাহুর সমান্তরাল হবে।
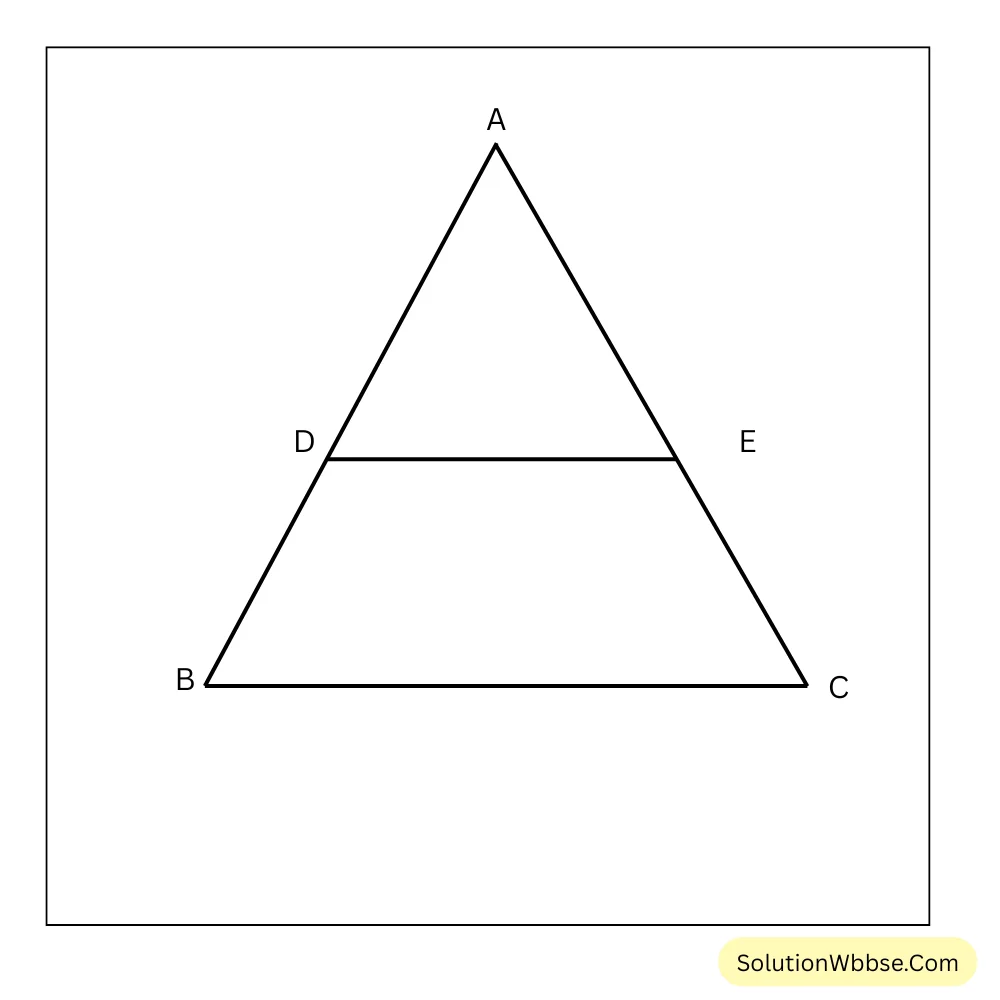
প্রদত্ত – মনে করি, △ABC একটি ত্রিভুজ। D এবং E যথাক্রমে AB এবং AC বাহুর মধ্যবিন্দু। D ও E বিন্দু দুটি যোগ করা হলো।=
প্রমাণ করতে হবে – \(DE \parallel BC\)
প্রমাণ –
যেহেতু D, AB বাহুর মধ্যবিন্দু,
সেহেতু, \(AD = DB\)
বা, \(\frac{AD}{DB} = 1\) —- (i)
আবার, যেহেতু E, AC বাহুর মধ্যবিন্দু,
সেহেতু, \(AE = EC\)
বা, \(\frac{AE}{EC} = 1\) —- (ii)
এখন, সমীকরণ (i) এবং (ii) থেকে আমরা পাই,
\(\frac{AD}{DB} = \frac{AE}{EC}\)থ্যালেসের বিপরীত উপপাদ্য অনুযায়ী, যদি কোনো সরলরেখা একটি ত্রিভুজের যেকোনো দুটি বাহুকে সমান অনুপাতে বিভক্ত করে, তবে ওই সরলরেখাটি ত্রিভুজের তৃতীয় বাহুর সমান্তরাল হয়।
যেহেতু DE সরলরেখাংশ △ABC-এর AB ও AC বাহুকে সমান অনুপাতে বিভক্ত করেছে, তাই আমরা থ্যালেসের বিপরীত উপপাদ্য থেকে বলতে পারি যে,
\(DE \parallel BC\) (প্রমাণিত)
প্রয়োগ 8. ABCD একটি ট্র্যাপিজিয়াম অঙ্কন করেছি যার AB || DC; AD ও BC-এর উপর যথাক্রমে P ও Q এমন দুটি বিন্দু নিলাম যাতে AP : PD = BQ : QC হয়। প্রমাণ করি যে, PQ || DC.
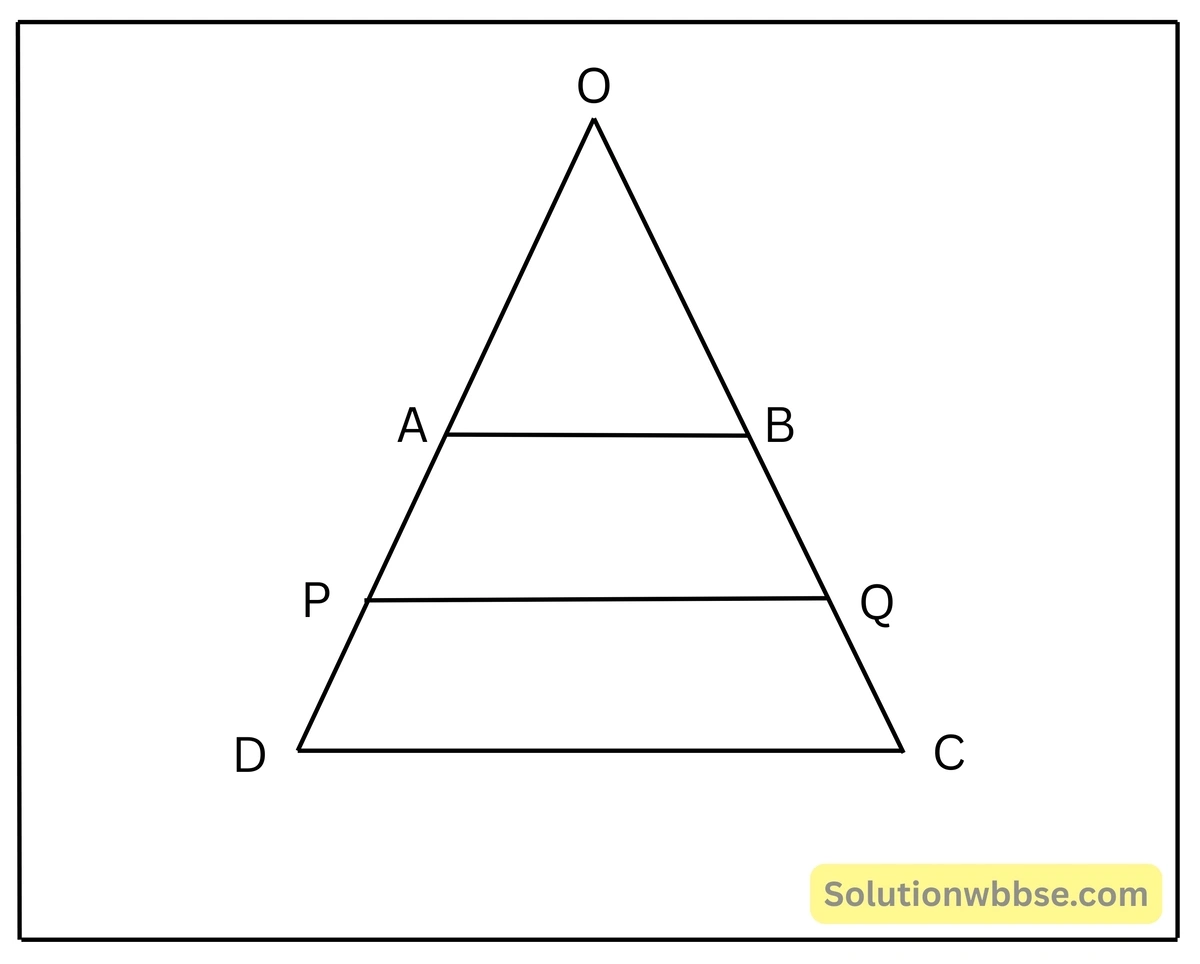
প্রদত্ত – ABCD ট্র্যাপিজিয়ামের AB || DC; P ও Q বিন্দু দুটি যথাক্রমে AD ও BC বাহুর উপর এমনভাবে অবস্থিত যাতে AP : PD = BQ : QC হয়।
প্রমাণ করতে হবে – PQ || DC
অঙ্কন – ধরি AB < DC; DA এবং CB বাহুকে বর্ধিত করা হলো। বর্ধিত DA ও CB বাহু পরস্পরকে O বিন্দুতে ছেদ করল। PQ যোগ করলাম।
প্রমাণ – △ODC-এর AB || DC
∴ \(\frac{OA}{AD} = \frac{OB}{BC}\) [থ্যালেসের উপপাদ্য থেকে পেলাম] —- (i)
আবার \(\frac{AP}{PD} = \frac{BQ}{QC}\) [প্রদত্ত]
অর্থাৎ, \(\frac{PD}{AP} = \frac{QC}{BQ}\)
বা, \(1 + \frac{PD}{AP} = 1 + \frac{QC}{BQ}\)
বা, \(\frac{AP+PD}{AP} = \frac{BQ+QC}{BQ}\)
∴ \(\frac{AD}{AP} = \frac{BC}{BQ}\) —- (ii)
(i) ও (ii) থেকে পাই, \(\frac{OA}{AD} \times \frac{AD}{AP} = \frac{OB}{BC} \times \frac{BC}{BQ}\)
∴ \(\frac{OA}{AP} = \frac{OB}{BQ}\)
∴ পেলাম, △OPQ-এর \(\frac{OA}{AP} = \frac{OB}{BQ}\)
∴ থ্যালেসের বিপরীত উপপাদ্য থেকে পাই, AB || PQ আবার, AB || DC. ∴ PQ || DC [প্রমাণিত]
প্রয়োগ 9. যুক্তি দিয়ে প্রমাণ করি যে একটি ত্রিভুজের কোনো কোণের অন্তঃসমদ্বিখণ্ডক বা বহিঃসমদ্বিখণ্ডক কোণটির বিপরীত বাহুকে অন্তঃস্থভাবে বা বহিঃস্থভাবে কোণসংলগ্ন বাহু দুটির দৈর্ঘ্যের অনুপাতে বিভক্ত করে। (প্রমাণ মূল্যায়নের অন্তর্ভুক্ত নয়)
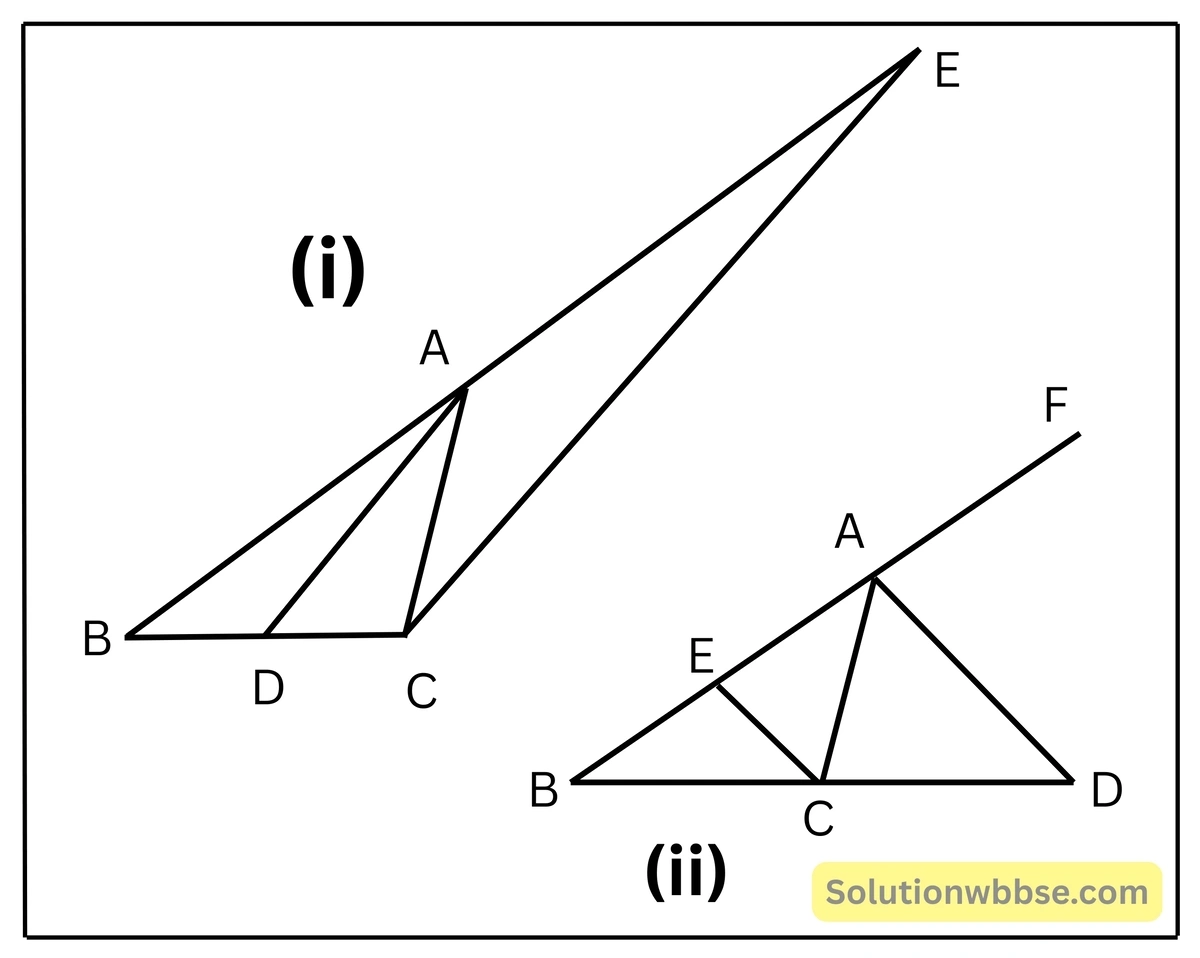
প্রদত্ত – ABC ত্রিভুজের ∠BAC-এর AD অন্তঃসমদ্বিখণ্ডক (চিত্র-i) বা বহিঃসমদ্বিখণ্ডক (চিত্র-ii) BC বাহুকে বা BC-এর বর্ধিতাংশকে D বিন্দুতে ছেদ করে।
প্রমাণ করতে হবে – BD : DC = AB : AC
অঙ্কন – C বিন্দু দিয়ে DA বাহুর সমান্তরাল সরলরেখা অঙ্কন করি যা বর্ধিত BA বাহুকে (চিত্র-i) বা BA বাহুকে (চিত্র-ii) E বিন্দুতে ছেদ করে।
প্রমাণ – DA || CE ∴ ∠DAC = একান্তর ∠ACE
DA || CE,
∴ ∠BAD (বা ∠FAD চিত্র নং (ii)) = অনুরূপ ∠AEC
কিন্তু ∠BAD (বা ∠FAD চিত্র নং (ii)) = ∠DAC
∴ ∠ACE = ∠AEC
সুতরাং, AC = AE
△BEC (চিত্র i) বা △BDA (চিত্র ii)-তে DA || CE;
সুতরাং, \(\frac{BD}{DC} = \frac{BA}{AE}\) (থ্যালেসের উপপাদ্য অনুযায়ী)
অর্থাৎ BD : DC = AB : AE
সুতরাং, BD : DC = AB : AC (∵ AE = AC) [প্রমাণিত]
প্রয়োগ 10. যুক্তি দিয়ে প্রমাণ করি যে, একটি ত্রিভুজের কোনো কোণ থেকে অঙ্কিত কোনো সরলরেখা যদি ওই কোণের বিপরীত বাহুকে অন্তঃস্থভাবে বা বহিঃস্থভাবে ত্রিভুজের কোণ সংলগ্ন বাহু দুটির দৈর্ঘ্যের অনুপাতে বিভক্ত করে তাহলে সরলরেখাটি কোণটির অন্তঃসমদ্বিখণ্ডক বা বহিঃসমদ্বিখণ্ডক হবে। (প্রমাণ মূল্যায়নের অন্তর্ভুক্ত নয়)

প্রদত্ত – ABC ত্রিভুজে A বিন্দু দিয়ে অঙ্কিত একটি সরলরেখা BC (চিত্র-i) বা বর্ধিত BC (চিত্র-ii) বাহুকে D বিন্দুতে এমনভাবে ছেদ করে যে, BD : DC = AB : AC হয়।
প্রমাণ করতে হবে – AD, ∠BAC-এর অন্তঃসমদ্বিখণ্ডক (চিত্র-i) বা বহিঃসমদ্বিখণ্ডক (চিত্র-ii)
অঙ্কন – C বিন্দু দিয়ে DA বাহুর সমান্তরাল সরলরেখা অঙ্কিত করি যা বর্ধিত BA বাহুকে (চিত্র-i) বা BA বাহুকে (চিত্র-ii) E বিন্দুতে ছেদ করে।
প্রমাণ – △BCE (চিত্র-i) বা △ABD (চিত্র-ii)-তে, DA || CE
∴ \(\frac{BD}{DC} = \frac{AB}{AE}\) (থ্যালেসের উপপাদ্য অনুযায়ী)
কিন্তু, \(\frac{BD}{DC} = \frac{AB}{AC}\) (প্রদত্ত)
সুতরাং, \(\frac{AB}{AE} = \frac{AB}{AC}\)
∴ AE = AC
সুতরাং, ∠AEC = ∠ACE
আবার, DA || CE ;
∴ ∠DAC = একান্তর ∠ACE এবং ∠BAD (চিত্র-i) বা ∠FAD (চিত্র-ii) = অনুরূপ ∠AEC.
যেহেতু, ∠AEC = ∠ACE,
সুতরাং ∠BAD (চিত্র-i) বা ∠FAD (চিত্র-ii) = ∠DAC.
সুতরাং AD, ∠BAC এর অন্তঃসমদ্বিখণ্ডক (চিত্র-i) বা বহিঃসমদ্বিখণ্ডক (চিত্র-ii) [প্রমাণিত]
প্রয়োগ 11. নীচের কোন ত্রিভুজ জোড়া সদৃশ হিসাব করে লিখি।
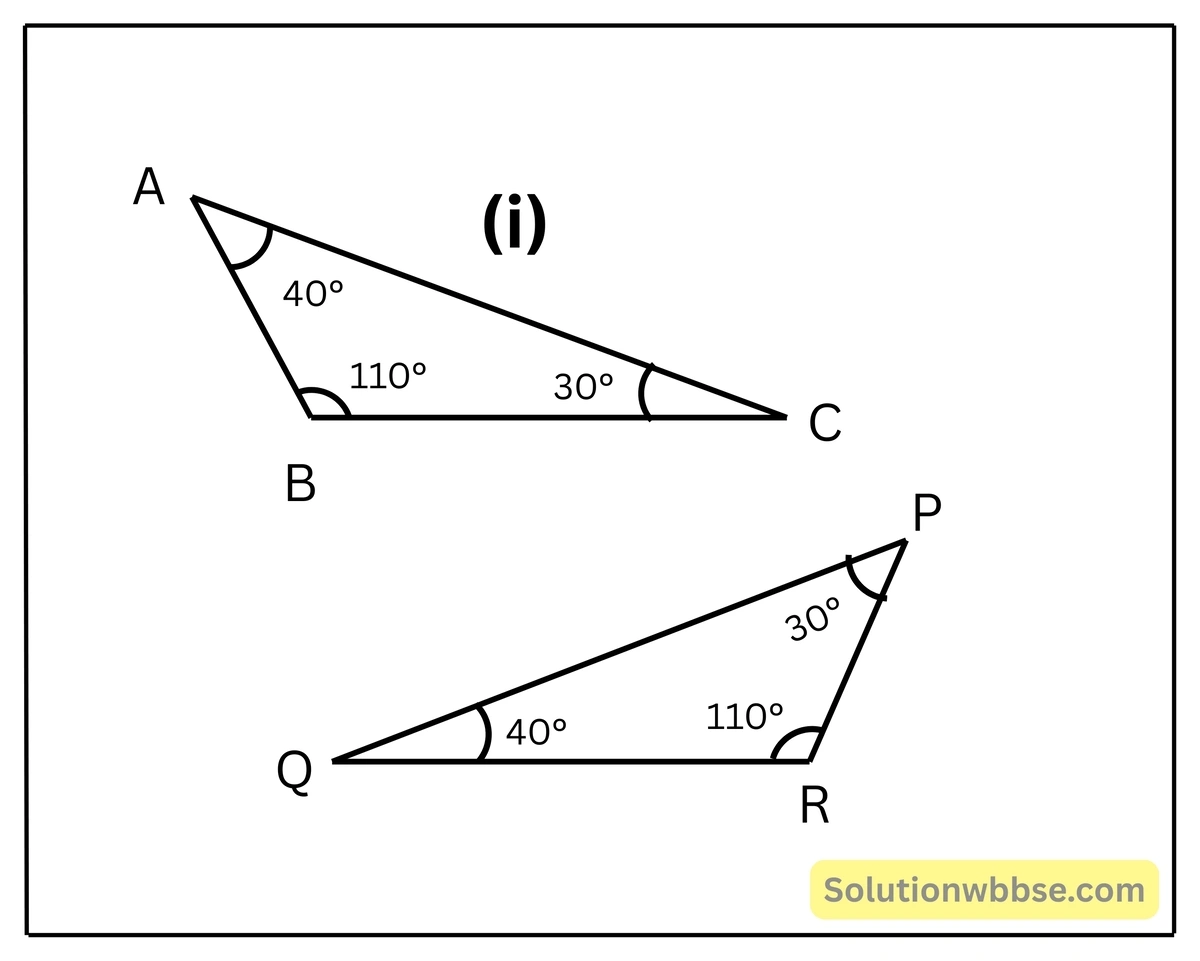
(i) ∠A = ∠Q, ∠B = ∠R এবং ∠C = ∠P
∴ △ABC ও △QRP সদৃশকোণী
∴ △ABC ও △QRP সদৃশ বা △ABC ~ △QRP
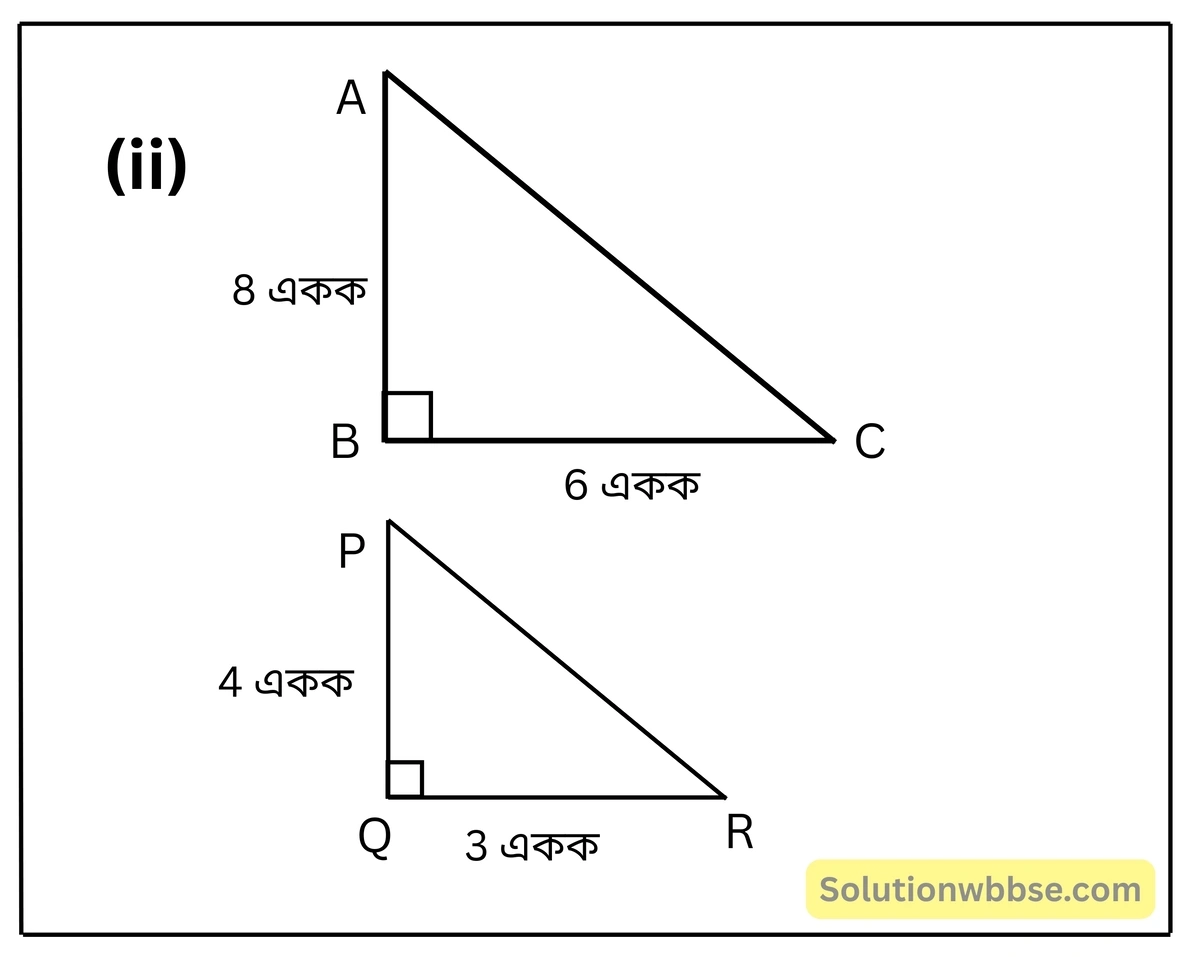
(ii) \(\frac{AB}{RQ} = \frac{BC}{QP} = \frac{CA}{PR}\)
∴ △ABC ও △RQP-এর বাহুগুলি সমানুপাতী।
∴ △ABC ও △RQP সদৃশ বা △ABC ~ △RQP
প্রয়োগ 12. পাশের ছবি দেখি ও ∠P-এর মান হিসাব করে লিখি।
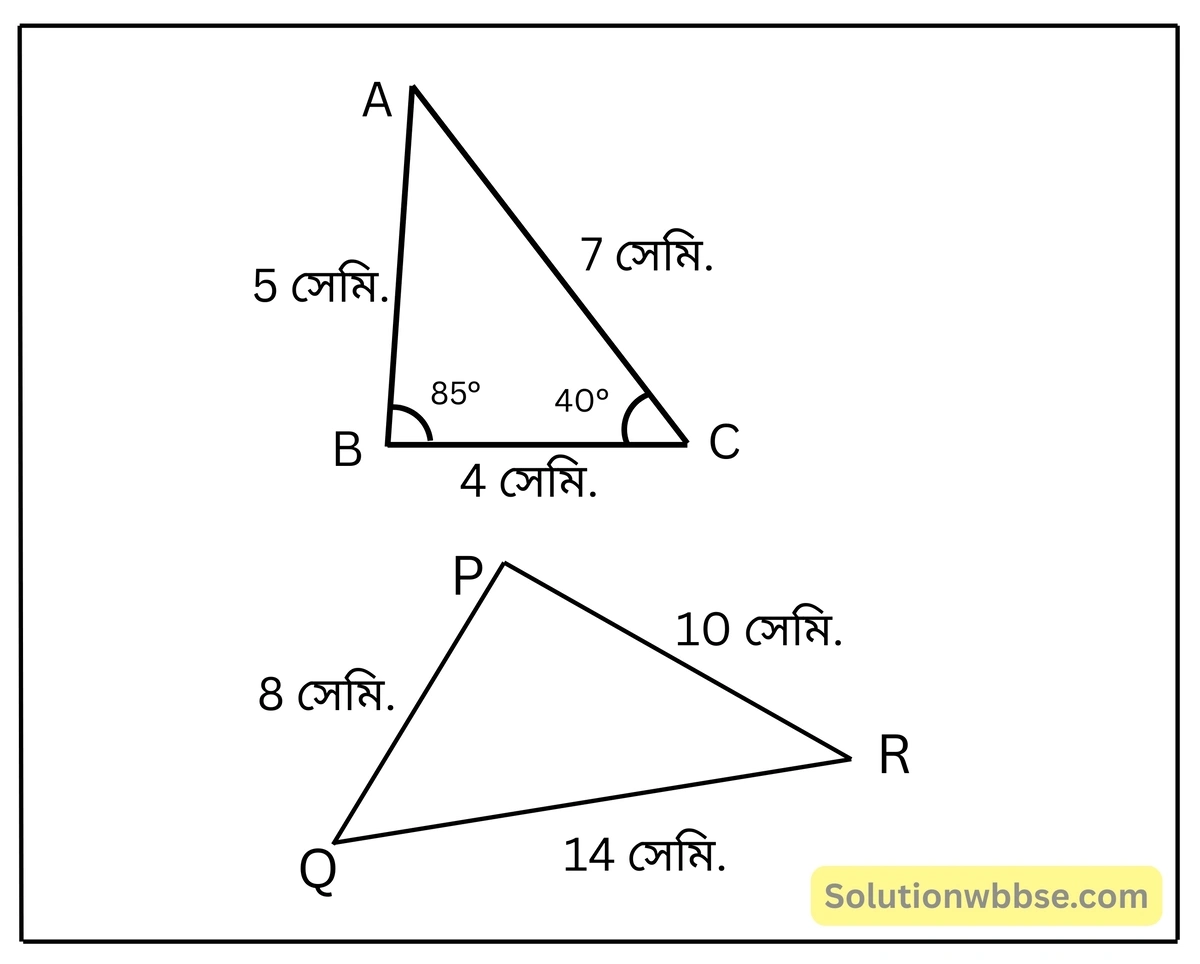
সমাধান – △ABC ও △PQR -এর,
\(\frac{AB}{PR} = \frac{5}{10} = \frac{1}{2}\), \(\frac{BC}{PQ} = \frac{4}{8} = \frac{1}{2}\) এবং \(\frac{AC}{QR} = \frac{7}{14} = \frac{1}{2}\)
∴ \(\frac{AB}{RP} = \frac{BC}{PQ} = \frac{CA}{QR} = \frac{1}{2}\)
∴ △ABC ও △RPQ সদৃশকোণী
∴ \(\angle A = \angle R\), \(\angle B = \angle P\) এবং \(\angle C = \angle Q\)
∴ \(\angle P = \angle B = 85^\circ\)
প্রয়োগ 13. প্রমাণ করি যে, দুটি সদৃশ ত্রিভুজের পরিসীমা ত্রিভুজ দুটির অনুরূপ বাহুগুলির সঙ্গে সমানুপাতী।
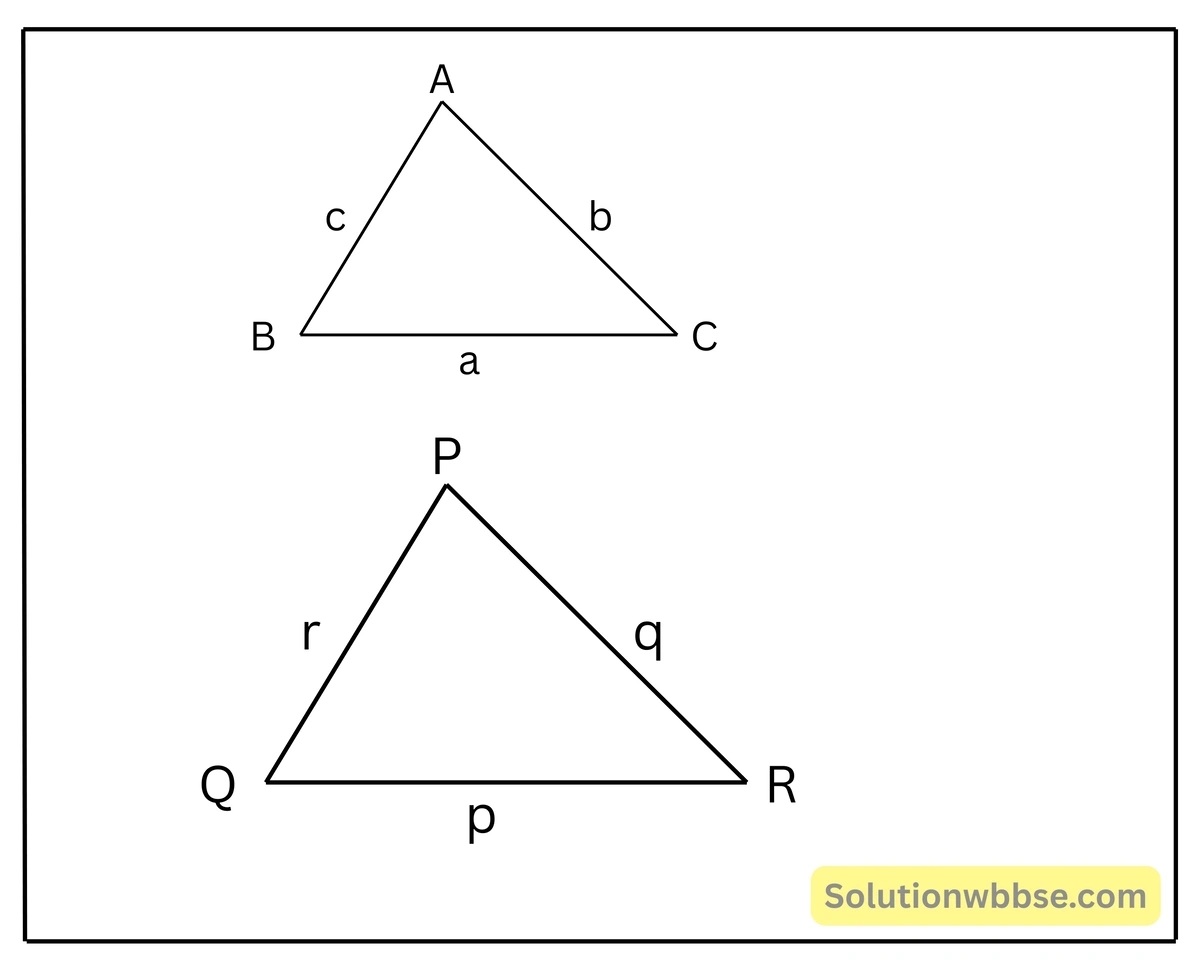
প্রদত্ত – ABC ও PQR দুটি সদৃশ ত্রিভুজ।
প্রমাণ করতে হবে –
\( = \frac{AB}{PQ} = \frac{BC}{QR} = \frac{CA}{RP}\)প্রমাণ – \(\triangle ABC\) ও \(\triangle PQR\) সদৃশ।
\(\therefore \frac{AB}{PQ} = \frac{BC}{QR} = \frac{CA}{RP}\)সুতরাং, \(\frac{AB}{PQ} = \frac{BC}{QR} = \frac{CA}{RP} = \frac{AB+BC+CA}{PQ+QR+PR}\)
(সংযোজন প্রক্রিয়া করে পাই)
প্রয়োগ 14.দুটি সদৃশ ত্রিভুজের পরিসীমা যথাক্রমে 20 সেমি ও 16 সেমি। প্রথম ত্রিভুজের একটি বাহুর দৈর্ঘ্য 9 সেমি হলে, দ্বিতীয় ত্রিভুজের অনুরূপ বাহুর দৈর্ঘ্য কত?
আমরা জানি,
ধরি, দ্বিতীয় ত্রিভুজের অনুরূপ বাহুর দৈর্ঘ্য \(x\) সেমি।
∴ \(\frac{9}{x} = \frac{20}{16}\)
বা, \(20x = 9 \times 16\)
বা, \(x = 7.2\)
∴ দ্বিতীয় ত্রিভুজের অনুরূপ বাহুর দৈর্ঘ্য \(7.2\) সেমি।
প্রয়োগ 15. প্রমাণ কর যে, যে-কোনো ত্রিভুজের কোনো একটি বাহুর মধ্যবিন্দু দিয়ে অপর একটি বাহুর সমান্তরাল সরলরেখা তৃতীয় বাহুকে সমদ্বিখণ্ডিত করবে এবং দুটি বাহু দ্বারা সমান্তরাল সরলরেখার খণ্ডিতাংশ দ্বিতীয় বাহুর অর্ধেক হবে।
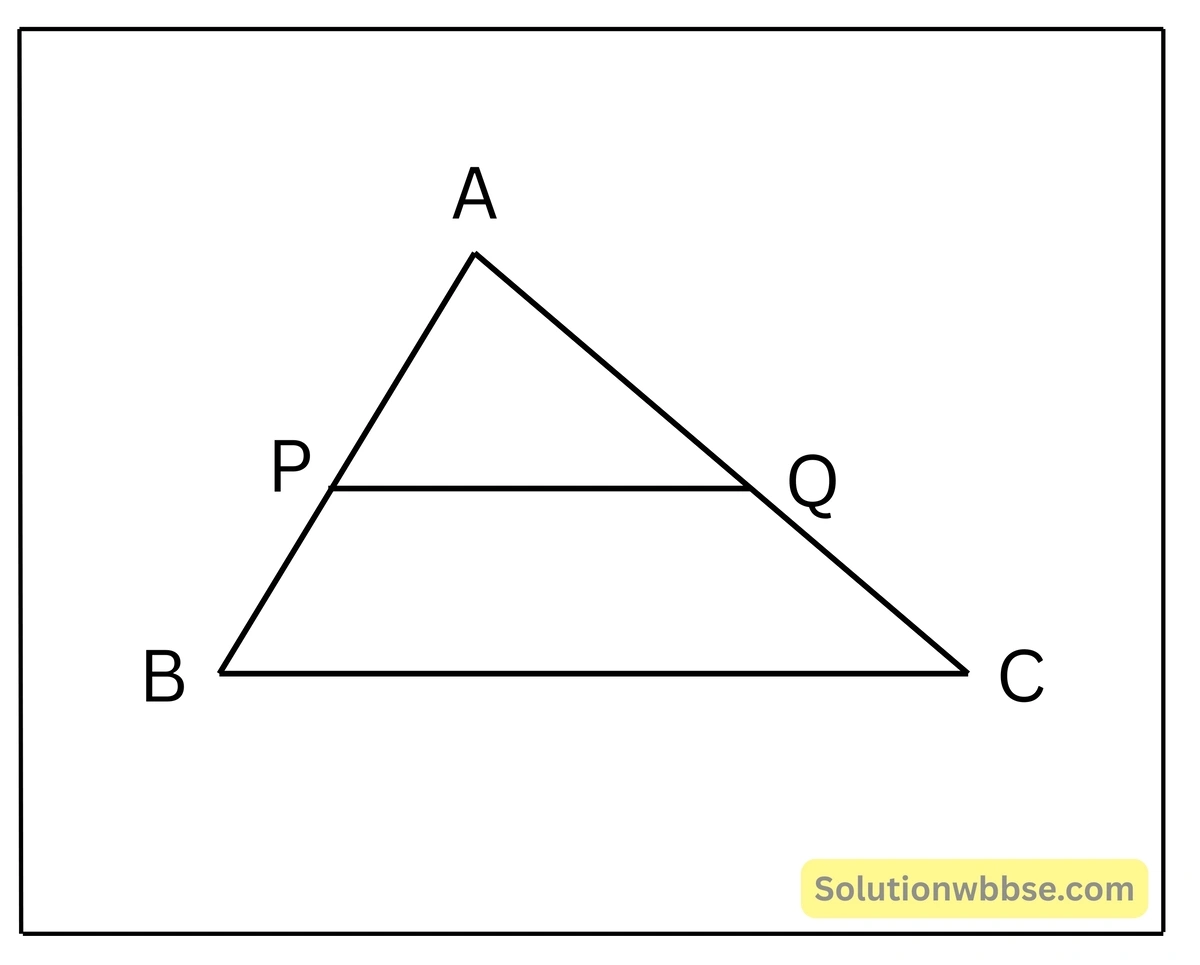
প্রদত্ত – ΔABC-এর AB বাহুর মধ্যবিন্দু P দিয়ে BC-এর সমান্তরাল সরলরেখা AC-কে Q বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে – (i) Q, AC-এর মধ্যবিন্দু (ii) PQ = \(\frac12\) BC
প্রমাণ – ΔAPQ ও ΔABC-এর
∠PAQ = ∠BAC [সাধারণ কোণ]
∠APQ = ∠ABC [∵ PQ || BC এবং AB ভেদক]
∴ ΔAPQ ও ΔABC সদৃশকোণী।
সুতরাং, ΔAPQ ও ΔABC সদৃশ।
∴ \(\frac{AP}{AB}=\frac{AQ}{AC}=\frac{PQ}{BC}\)
কিন্তু, \(\frac{AP}{AB}\) = \(\frac12\) [∵ P, AB-এর মধ্যবিন্দু]
∴ \(\frac{AQ}{AC}\) = \(\frac12\)
বা, AQ = \(\frac12\) AC
∴ Q, AC-র মধ্যবিন্দু [(i) প্রমাণিত]
আবার, \(\frac{PQ}{BC}\) = \(\frac12\)
∴ PQ = \(\frac12\) BC [(ii) প্রমাণিত]
প্রয়োগ 16. ΔABC-এর ∠B = ∠C, D ও E বিন্দু BA ও CA-এর উপর এমনভাবে অবস্থিত যে, BD = CE; প্রমাণ করি যে, DE || BC [নিজে করি]

প্রদত্ত – DE || BC
ΔABC-এর ∠B = ∠C BD = CE
প্রমাণ –
∠B = ∠C
∴ AB = AC.
আবার, \(\frac{AB}{BD} = \frac{AC}{EC}\) [কারণ PB = EC]
∴ DE || BC. (প্রমাণিত)
প্রয়োগ 17. ΔABC-এর একটি মধ্যমা AD অঙ্কন করেছি। যদি BC-এর সমান্তরাল কোনো সরলরেখা AB ও AC বাহুদ্বয়কে যথাক্রমে P ও Q বিন্দুতে ছেদ করে, তবে প্রমাণ করি যে AD দ্বারা PQ সরলরেখাংশ সমদ্বিখণ্ডিত হবে।
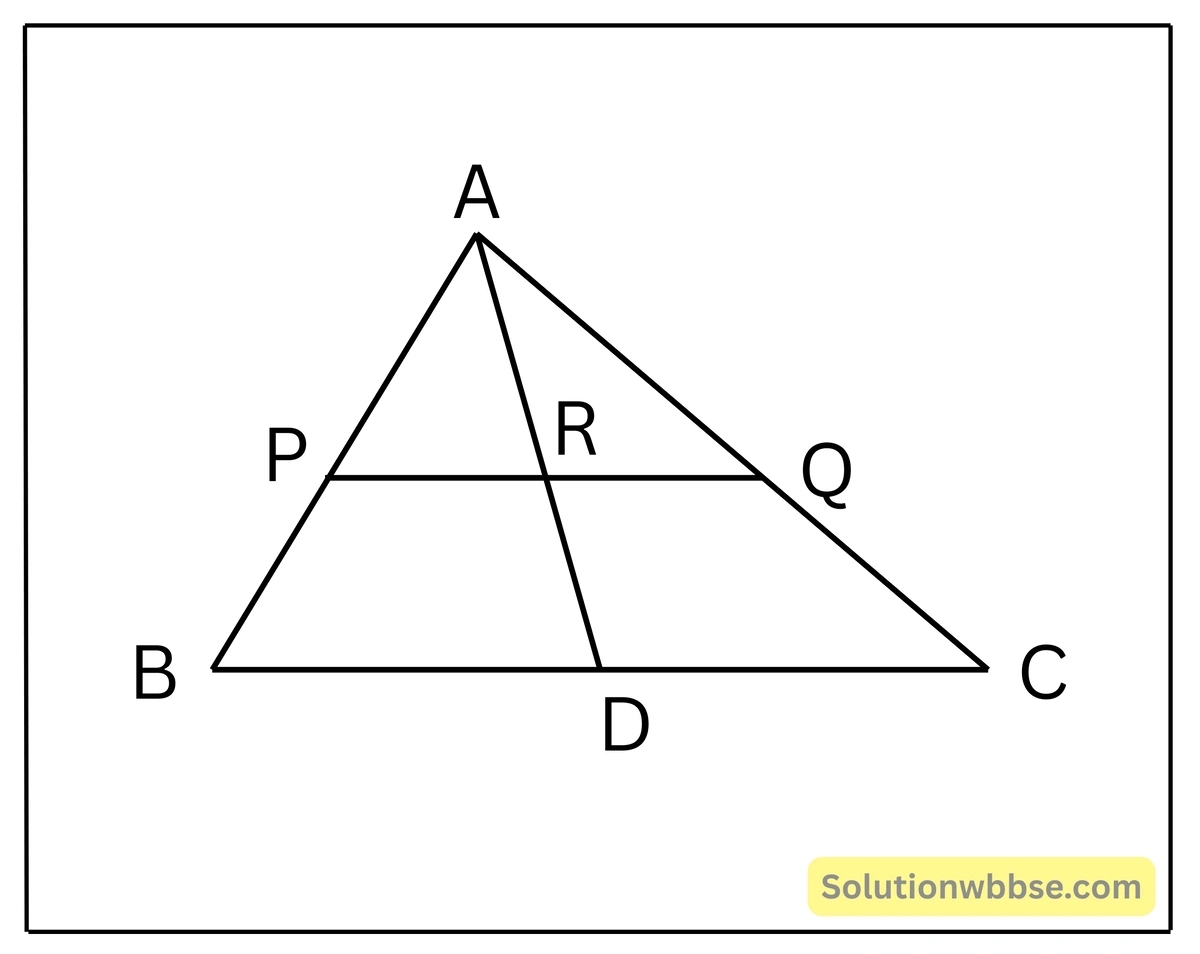
প্রদত্ত – ABC-এর AD মধ্যমা। BC বাহুর সমান্তরাল সরলরেখা AB, AD ও AC-কে যথাক্রমে P, R ও Q বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে – PR = RQ
প্রমাণ –
ΔAPR ও ΔABD-এর ∠PAR = ∠BAD [একই কোণ]
এবং ∠APR = অনুরূপ ∠ABD [∵ PR || BD এবং AB ভেদক]
∴ ΔAPR ও ΔABD সদৃশকোণী।
সুতরাং, ΔAPR ও ΔABD সদৃশ।
∴ \(\frac{PR}{BD} = \frac{AR}{AD}\) ______ (i)
ΔARQ ও ΔADC থেকে অনুরূপ প্রমাণ করা যায়, \(\frac{RQ}{DC} = \frac{AR}{AD}\) ______ (ii)
(i) ও (ii) থেকে পাই, \(\frac{PR}{BD} = \frac{RQ}{DC}\)
কিন্তু, BD = DC [∵ AD মধ্যমা]
∴ PR = RQ [প্রমাণিত]
প্রয়োগ 18. একটি বৃত্তস্থ চতুর্ভুজ ABCD অঙ্কন করেছি। বর্ধিত AB ও DC বাহুদ্বয় পরস্পরকে P বিন্দুতে ছেদ করলে, প্রমাণ করি যে, PA.PB = PC.PD
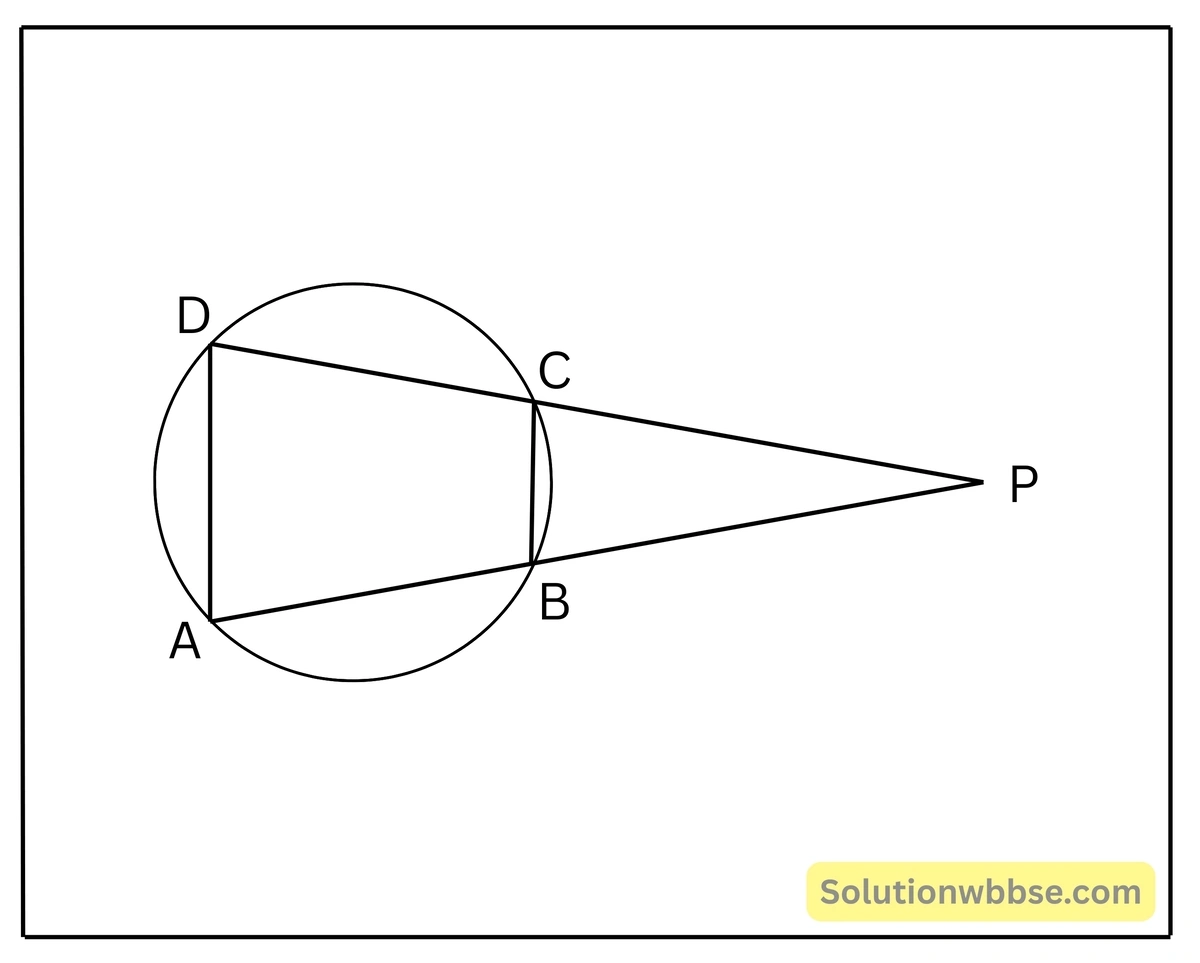
প্রদত্ত – ABCD বৃত্তস্থ চতুর্ভুজের বর্ধিত AB ও DC বাহুদ্বয় পরস্পরকে P বিন্দুতে ছেদ করে।
প্রমাণ করতে হবে – PA.PB = PC.PD
প্রমাণ – ABCD বৃত্তস্থ চতুর্ভুজ।
∴ ∠DAB + ∠DCB = 180°
আবার, ∠DCB + ∠BCP = 180°
∴ ∠DAB + ∠DCB = ∠DCB + ∠BCP
∴ ∠DAB = ∠BCP ______ (i)
ΔAPD ও ΔCPB-এর, ∠APD = ∠CPB [একই কোণ]
এবং ∠PAD = ∠BCP [(i) থেকে পেলাম]
∴ ΔAPD ও ΔCPB সদৃশকোণী।
সুতরাং, ΔAPD ও ΔCPB সদৃশ।
∴ \(\frac{PA}{PC} = \frac{PD}{PB}\)
সুতরাং, PA.PB = PC.PD (প্রমাণিত)
উপরের প্রমাণে দেখছি, ΔAPD ও ΔCPB-এর PA ও PC অনুরূপ বাহু এবং PD ও PB অনুরূপ বাহু।
প্রয়োগ 19. ABC সমকোণী ত্রিভুজের ∠A সমকোণ। সমকৌণিক বিন্দু A থেকে অতিভুজ BC-এর উপর AD লম্ব অঙ্কন করলাম। প্রমাণ করি (i) AB² = BC.BD, (ii) AD² = BD.CD এবং (iii) AC² = BC.CD
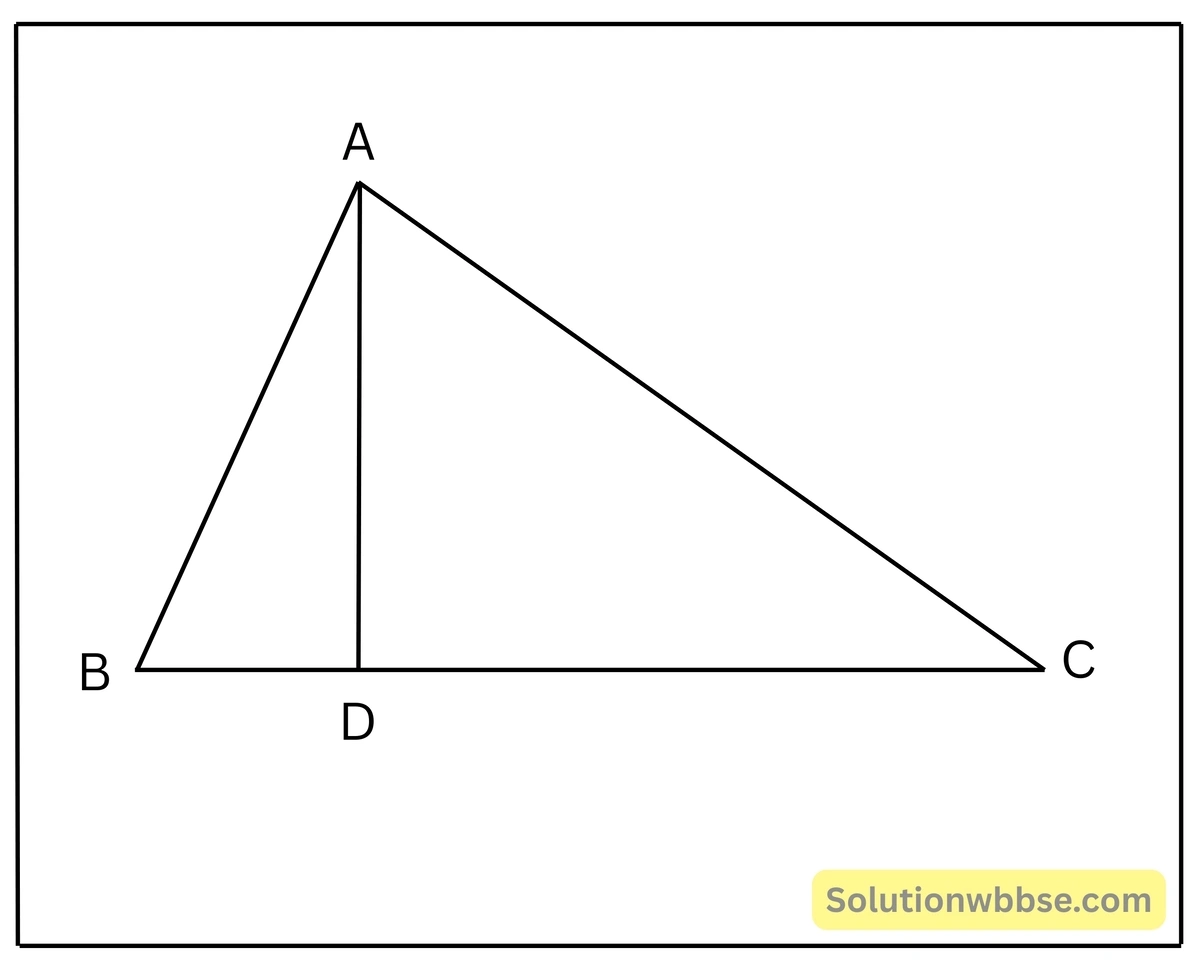
প্রদত্ত – ABC ত্রিভুজের ∠BAC = 90°; AD ⊥ BC.
প্রমাণ করতে হবে – (i) AB² = BC·BD, (ii) AD² = BD·CD এবং (iii) AC² = BC·CD
প্রমাণ – (i) ΔDBA ও ΔABC সদৃশ। (∵ ABC ত্রিভুজের সমকৌণিক বিন্দু A থেকে অতিভুজ BC-এর উপর AD লম্ব)
∴ \(\frac{AB}{BC} = \frac{BD}{AB}\)
সুতরাং, AB² = BC.BD[(i) প্রমাণিত]
(ii) ΔDBA ও ΔDAC সদৃশ।
∴ \(\frac{AD}{CD} = \frac{BD}{AD}\)
সুতরাং, AD² = BD.CD[(ii) প্রমাণিত]
(iii) ΔDAC ও ΔABC সদৃশ।
∴ \(\frac{AC}{BC} = \frac{CD}{AC}\)
সুতরাং, AC² = BC.CD[(iii) প্রমাণিত]
প্রয়োগ 20. ΔABC-এর ∠ABC = 90° এবং BD ⊥ AC, যদি BD = 6 সেমি. এবং AD = 4 সেমি. হয়, তবে CD-এর দৈর্ঘ্য হিসাব করে লিখি।
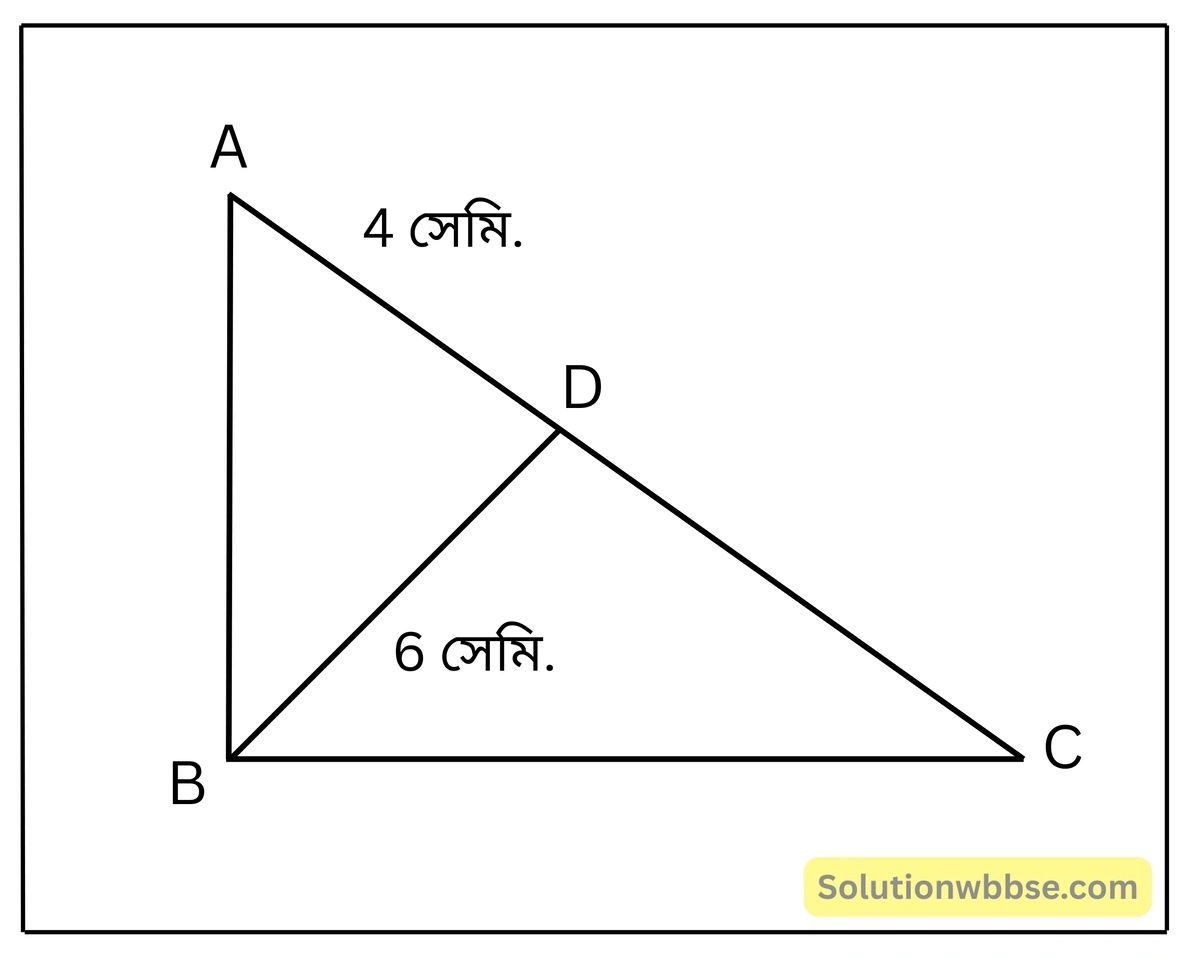
ΔDAB ও ΔDBC সদৃশ।
∴ BD² = AD·CD
বা, 6² = 4×CD
∴ CD = 12 সেমি.।
প্রয়োগ 21. ΔABC-এর ∠ABC = 90° এবং BD ⊥ AC; যদি AB = 6 সেমি এবং BD = 3 সেমি এবং CD = 5.4 সেমি হয়, তবে BC বাহুর দৈর্ঘ্য হিসাব করে লিখি। [নিজে লিখি]
প্রদত্ত, AB = 6 সেমি BD = 3 সেমি CD = 5.4 সেমি BC = ?
∴ ∠B = 90°, ∠CBD + ∠DBA = 90° ………………(i)
আবার, ΔDBA ত্রিভুজের ∠D = 90°
∴ ∠DBA + ∠BAD = 90°………………(ii)
সুতরাং (i) ও (ii)নং থেকে, ∠BAD = ∠CBD
আবার ∠DCB + ∠CBD = ∠DBA + ∠BAD (= 90°)
বা, ∠DCB = ∠DBA
সুতরাং ΔABD ও ΔCBD-এর ক্ষেত্রে, ∠BAD = ∠CBD ও ∠DCB = ∠DBA, ∠BDA = 90° = ∠CDB
অতএব, ΔABD ও ΔCBD সদৃশকোণী, সুতরাং ইহাদের অনুরূপ বাহুগুলি সমানুপাতী
অর্থাৎ \(\frac{AD}{BD} = \frac{BD}{CD} = \frac{AB}{BC}\)
∴ \(AD = \frac{BD \times BD}{CD} = \frac{3 \times 3 \times 10}{54} = \frac{5}{3}\)
∴ \(BC = \frac{AB \times BD}{AD} = \frac{6 \times 3}{\frac{5}{3}} = \frac{54}{5} = 10\frac{4}{5}\) সেমি
সুতরাং, BC বাহুর দৈর্ঘ্য \(10\frac{4}{5}\) সেমি।
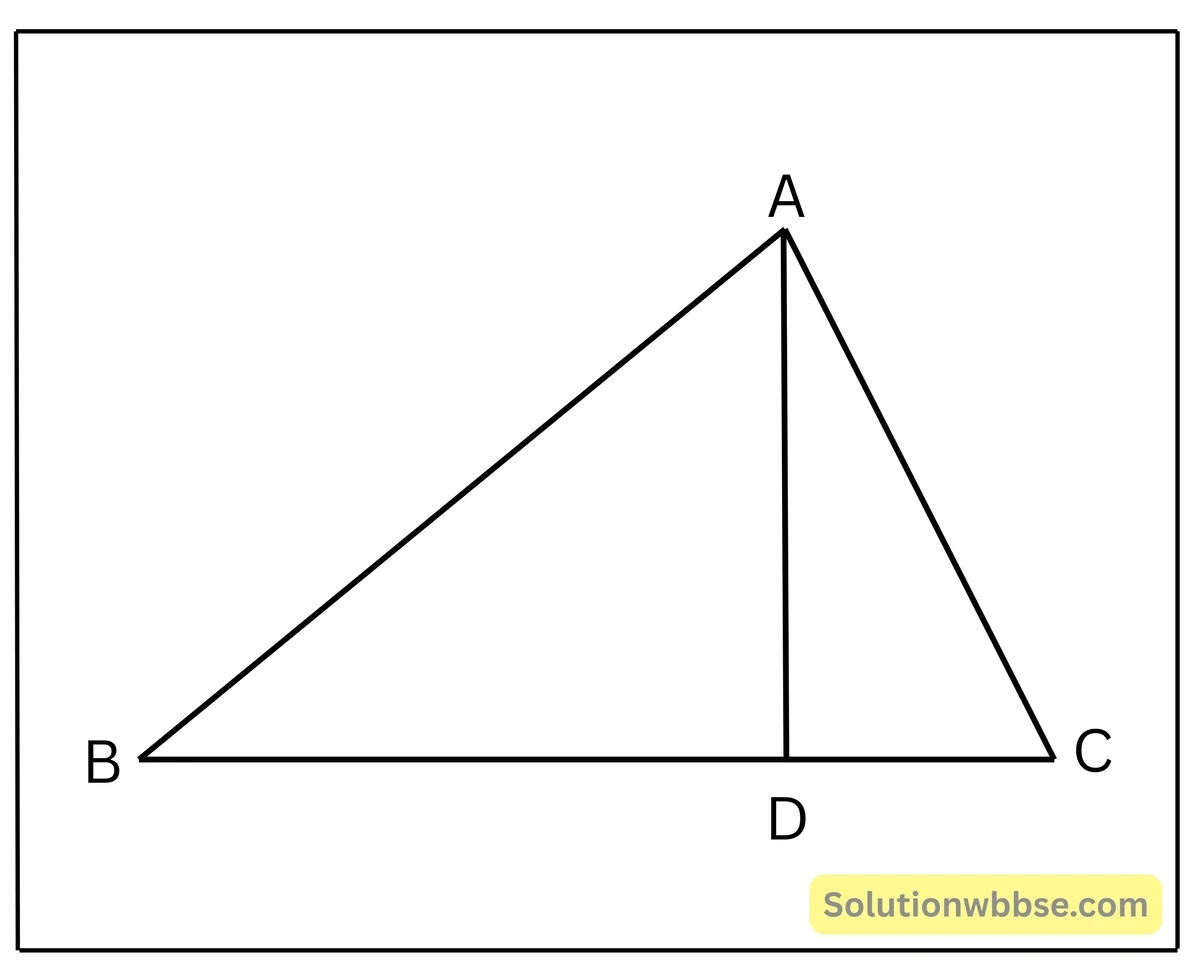
প্রয়োগ 22. ΔABC-এর শীর্ষবিন্দু A থেকে BC বাহুর উপর AD লম্ব অঙ্কন করলাম। যদি \(\frac{BD}{DA} = \frac{DA}{DC}\) হয়, তবে প্রমাণ করি যে, ABC একটি সমকোণী ত্রিভুজ।

প্রমাণ – ΔBDA ও ΔADC-এর ∠BDA = ∠ADC = 90° [∵ AD ⊥ BC] এবং \(\frac{BD}{DA} = \frac{DA}{DC}\)
∴ ΔBDA ও ΔADC সদৃশ। [যেহেতু দুটি ত্রিভুজের একটির একটি কোণ অপরটির একটি কোণের সমান হলে এবং কোণগুলির ধারক বাহুগুলি সমানুপাতী হলে, ত্রিভুজদ্বয় সদৃশ হয়]
সুতরাং, ∠ABD = ∠CAD এবং ∠BAD = ∠ACD
∴ ∠ABD + ∠ACD = ∠CAD + ∠BAD
বা, ∠B + ∠C = ∠A
বা, ∠A + ∠B + ∠C = 2∠A
বা, 2∠A = 180°
∴ ∠A = 90°
∴ ABC একটি সমকোণী ত্রিভুজ।
প্রয়োগ 23. যদি কোনো সমকোণী ত্রিভুজ ABC-এর সমকৌণিক বিন্দু A থেকে অতিভুজের উপর লম্ব অঙ্কন করি এবং যদি AC, AB ও BC ক্রমিক সমানুপাতী হয়, তবে প্রমাণ করি যে, অতিভুজটির বৃহত্তম অংশ ত্রিভুজটির ক্ষুদ্রতম বাহুর সমান হবে।
প্রদত্ত – সমকোণী ত্রিভুজ ABC-এর ∠A সমকোণ; A থেকে অতিভুজ BC-এর উপর AD লম্ব অঙ্কন করলাম। ধরি, AC ক্ষুদ্রতম বাহু। AC : AB = AB : BC
প্রমাণ করতে হবে – অতিভুজ BC-এর বৃহত্তম অংশ AC বাহুর সমান। যেহেতু ADC সমকোণী ত্রিভুজের DC, অতিভুজ AC-এর সমান হতে পারে না, সুতরাং, প্রমাণ করতে হবে BD = AC
প্রমাণ – সমকৌণিক বিন্দু A থেকে BC-এর উপর AD লম্ব।
∴ ΔABD ও ΔABC সদৃশ।
∴ \(\frac{BD}{AB} = \frac{AB}{BC}\) কিন্তু \(\frac{AC}{AB} = \frac{AB}{BC}\) [প্রদত্ত]
সুতরাং, \(\frac{BD}{AB} = \frac{AC}{AB}\)
∴ BD = AC [প্রমাণিত]
প্রয়োগ 24. একটি বৃত্ত অঙ্কন করেছি যার ব্যাস AB এবং কেন্দ্র O; বৃত্তের উপরিস্থিত কোনো বিন্দু P থেকে AB ব্যাসের উপর একটি লম্ব অঙ্কন করলাম যা AB কে N বিন্দুতে ছেদ করল। প্রমাণ করি যে, PB² = AB.BN
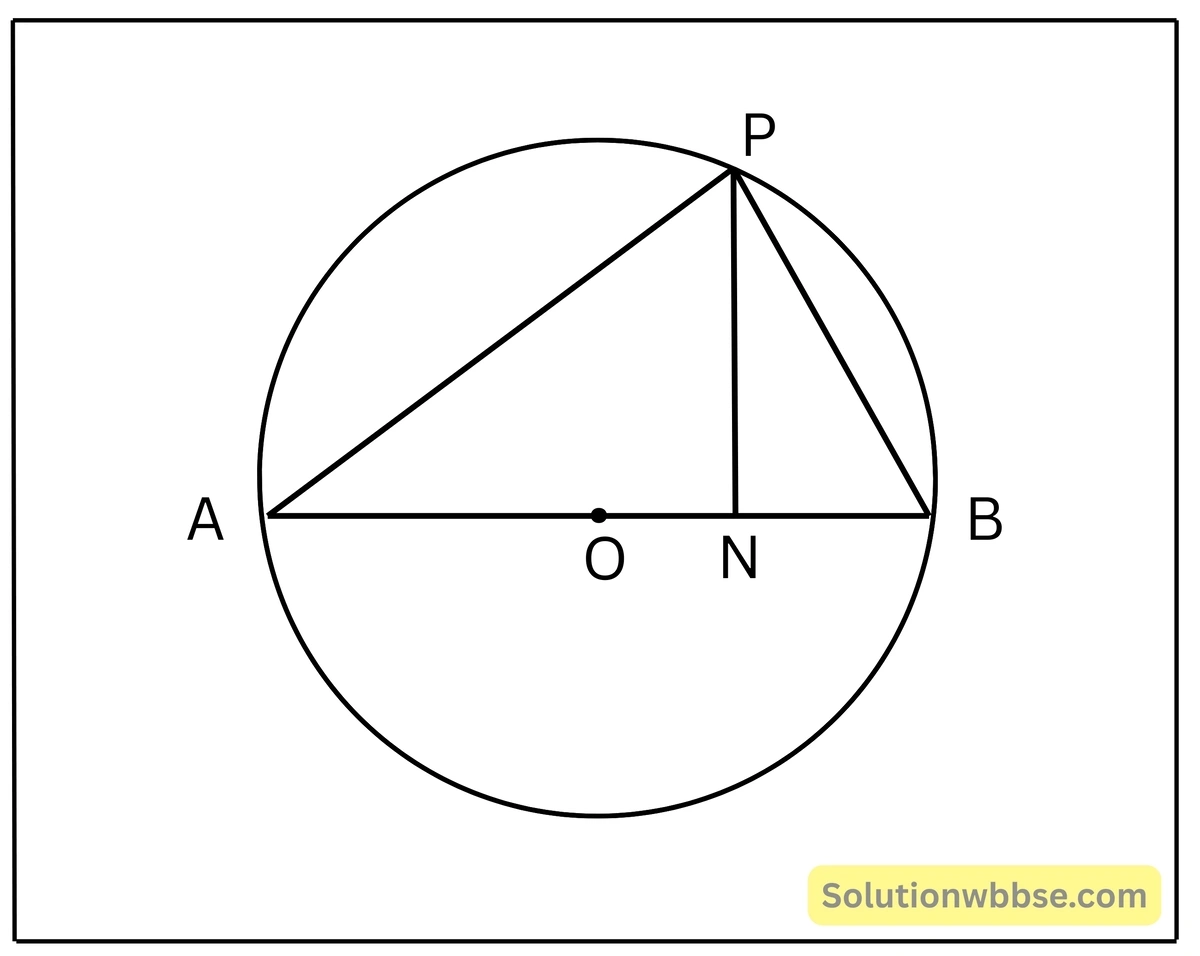
প্রদত্ত – O কেন্দ্রীয় বৃত্তের AB ব্যাস। P বৃত্তের উপরিস্হ যেকোনো একটি বিন্দু এবং PN ⊥ AB
প্রমাণ করতে হবে – PB² = AB.BN
প্রমাণ – AB বৃত্তের ব্যাস। সুতরাং ∠APB অর্ধবৃত্তস্থ কোণ।
∴ ∠APB = 1 সমকোণ।
সমকোণী ত্রিভুজ APB-এর সমকৌণিক বিন্দু P থেকে অতিভুজ AB-এর উপর PN লম্ব।
∴ ΔABP ও ΔPBN পরস্পর সদৃশ।
সুতরাং, \(\frac{PB}{BN} = \frac{AB}{PB}\)
∴ PB² = AB.BN [প্রমাণিত]
প্রয়োগ 25. দুটি বৃত্ত পরস্পরকে A বিন্দুতে বহিস্পর্শ করেছে। PQ ওই দুটি বৃত্তের একটি সরল সাধারণ স্পর্শক। যদি বৃত্ত দুটির ব্যাসার্ধের দৈর্ঘ্য যথাক্রমে r ও r’ হয়, তাহলে প্রমাণ করি যে, PQ² = 4rr’
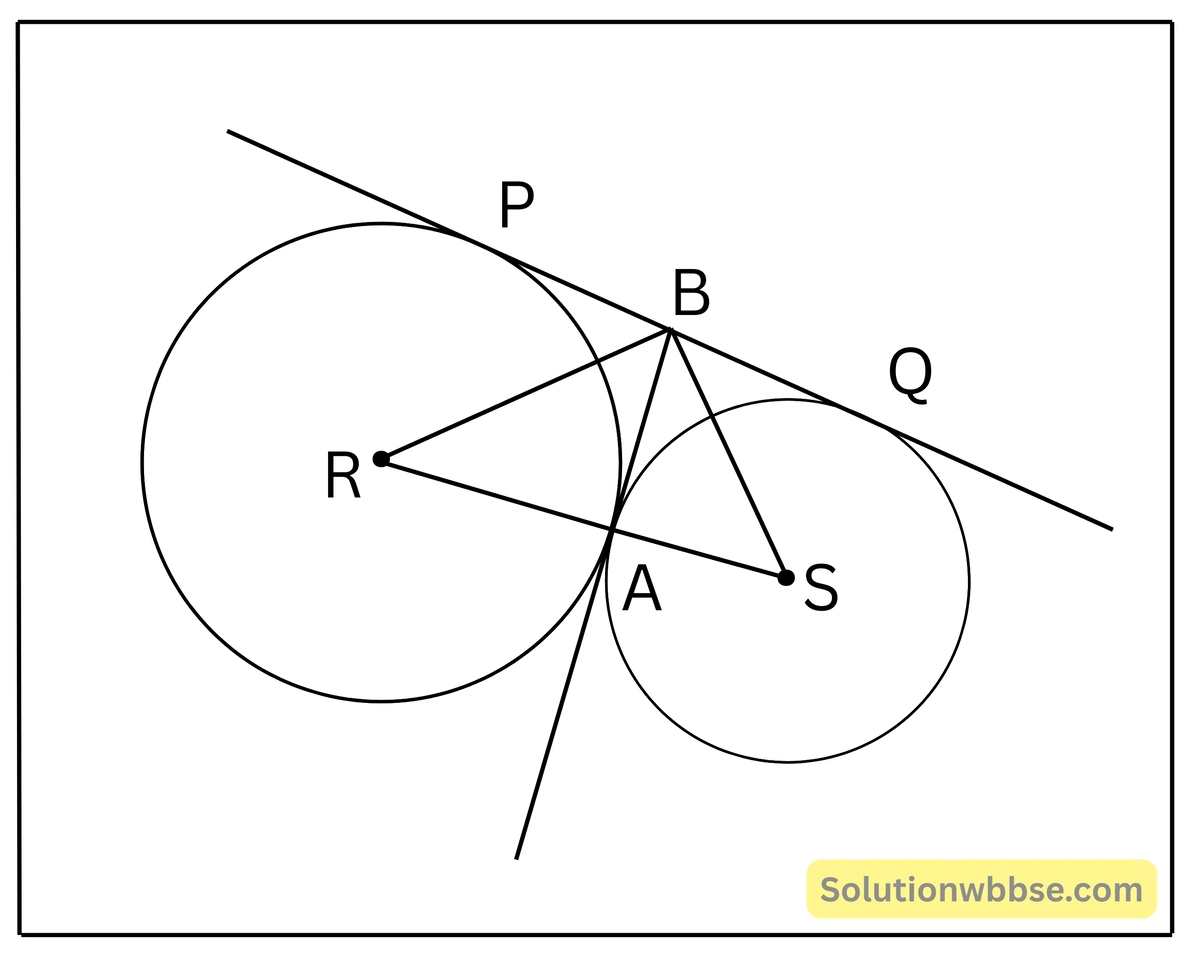
প্রদত্ত – R ও S কেন্দ্রীয় দুটি বৃত্ত যাদের ব্যাসার্ধের দৈর্ঘ্য যথাক্রমে r ও r’, পরস্পরকে A বিন্দুতে বহিস্পর্শ করেছে। PQ ওই দুটি বৃত্তের একটি সরল সাধারণ স্পর্শক এবং বৃত্ত দুটিকে P ও Q বিন্দুতে স্পর্শ করেছে।
প্রমাণ করতে হবে – PQ² = 4rr’
অঙ্কন – R, A ও A, S যোগ করলাম, A বিন্দুতে বৃত্ত দুটির সাধারণ স্পর্শক অঙ্কন করলাম যা PQ-কে B বিন্দুতে ছেদ করল। R, B ও S, B যোগ করলাম।
প্রমাণ – B বিন্দু থেকে R কেন্দ্রীয় বৃত্তের দুটি স্পর্শক BP ও BA.
∴ BP = BA এবং RB, ∠ABP-এর সমদ্বিখণ্ডক।
সুতরাং, ∠RBA = \(\frac12\) ∠PBA
আবার, B বিন্দু থেকে S কেন্দ্রীয় বৃত্তের দুটি স্পর্শক BQ ও BA
∴ BQ = BA এবং BS, ∠ABQ-এর সমদ্বিখণ্ডক।
∴ ∠SBA = \(\frac12\) ∠QBA
∠RBA + ∠SBA = \(\frac12\)(∠PBA + ∠QBA)
বা, ∠RBS = \(\frac12\) ∠PBQ = \(\frac12\) × 180° = 90°
∴ ∠RBS = 1 সমকোণ
R, S দুটি বৃত্তের কেন্দ্র এবং A স্পর্শবিন্দু।
∴ R, A, S বিন্দু তিনটি সমরেখ এবং AB ⊥ RS [∵ বৃত্তের স্পর্শক এবং স্পর্শবিন্দুগামী ব্যাসার্ধ পরস্পর লম্ব]
সমকোণী ত্রিভুজ RBS-এর সমকৌণিক বিন্দু B থেকে অতিভুজ RS-এর উপর BA লম্ব।
ΔABR ও ΔASB পরস্পর সদৃশ।
সুতরাং, \(\frac{AB}{AS} = \frac{AR}{AB}\)
বা, AB² = AR.AS
= r.r’ [∵ AR = r এবং AS = r’]
∴ 4AB² = 4r.r’
বা, (2AB)² = 4rr’
∴ PQ² = 4r.r’
∵ PQ = PB + BQ = 2AB;
∴ PB = BA এবং QB = BA
প্রয়োগ 26. যুক্তি দিয়ে প্রমাণ করি যে, দুটি সদৃশ ত্রিভুজের ক্ষেত্রফলের অনুপাত অনুরূপ বাহুর বর্গের অনুপাতের সঙ্গে সমান [সদৃশ সমান প্রমাণ মূল্যায়নের অন্তর্ভুক্ত নয়]
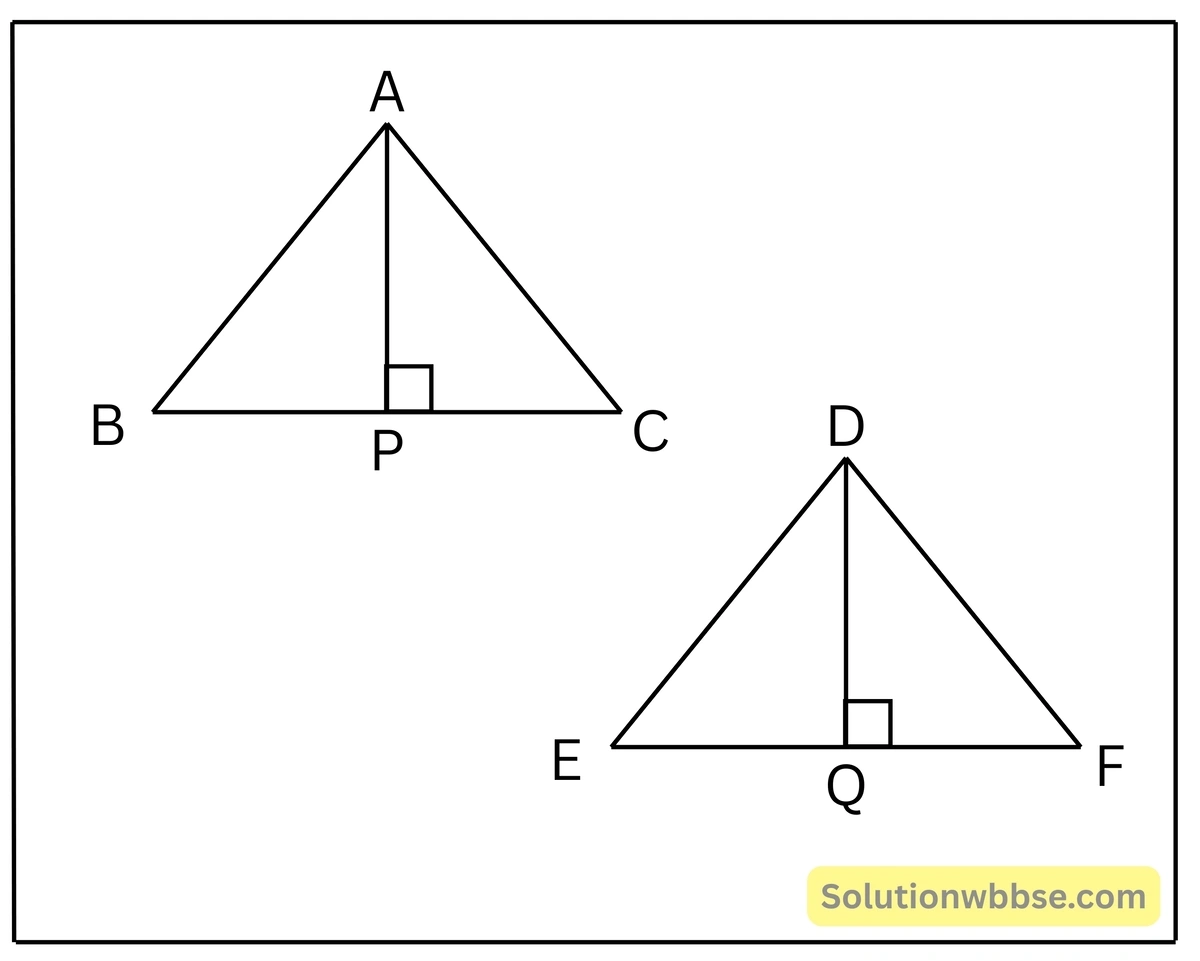
প্রদত্ত – \(\triangle ABC \sim \triangle DEF\);
সুতরাং, ত্রিভুজ দুটি সদৃশকোণী।
∴ \(\angle A = \angle D\), \(\angle B = \angle E\) এবং \(\angle C = \angle F\)
প্রমাণ করতে হবে – \(\frac{\triangle ABC}{\triangle DEF} = \frac{AB^2}{DE^2} = \frac{AC^2}{DF^2} = \frac{BC^2}{EF^2}\)
অঙ্কন – ABC ত্রিভুজে \(AP \perp BC\) এবং DEF ত্রিভুজে \(DQ \perp EF\) অঙ্কন করি।
প্রমাণ – \(\triangle ABC = \frac{1}{2} \cdot BC \cdot AP\) এবং \(\triangle DEF = \frac{1}{2} \cdot EF \cdot DQ\)
\(\frac{\triangle ABC}{\triangle DEF} = \frac{\frac{1}{2} \cdot BC \cdot AP}{\frac{1}{2} \cdot EF \cdot DQ} = \frac{BC \cdot AP}{EF \cdot DQ}\)\(\triangle ABP\) ও \(\triangle DEQ\)-তে, \(\angle ABP = \angle DEQ\)
(\(\because \angle B = \angle E\))
\(\angle APB = \angle DQE\) (প্রত্যেকটি সমকোণ)
সুতরাং, অবশিষ্ট \(\angle PAB = \angle QDE\).
∴ \(\triangle ABP\) ও \(\triangle DEQ\) সদৃশকোণী। সুতরাং সদৃশ।
∴ \(\frac{AB}{DE} = \frac{AP}{DQ}\)
আবার, \(\triangle ABC\) ও \(\triangle DEF\) সদৃশ।
সুতরাং \(\frac{AB}{DE} = \frac{AC}{DF} = \frac{BC}{EF}\)
∴ \(\frac{AP}{DQ} = \frac{BC}{EF}\)
\(∴\frac{\triangle ABC}{\triangle DEC} = \left( \frac{BC}{EF} \right) \cdot \left( \frac{AP}{DQ} \right) = \left( \frac{BC}{EF} \right) \cdot \left( \frac{BC}{EF} \right) = \frac{BC^2}{EF^2}\)যেহেতু, \(\frac{AB}{DE} = \frac{AC}{DF} = \frac{BC}{EF}\)
সুতরাং, \(\frac{AB^2}{DE^2} = \frac{AC^2}{DF^2} = \frac{BC^2}{EF^2}\)
∴ \(\frac{\triangle ABC}{\triangle DEF} = \frac{AB^2}{DE^2} = \frac{AC^2}{DF^2} = \frac{BC^2}{EF^2}\) [প্রমাণিত]
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের অষ্টদশ অধ্যায়, ‘সদৃশতা’ -এর প্রয়োগমূলক বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন