এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের চতুর্বিংশ অধ্যায়, ‘পূরক কোণের ত্রিকোণমিতিক অনুপাত’ -এর ‘কষে দেখি – 24’ বিভাগের সমস্ত সমস্যার সমাধান করে দেওয়া হয়েছে। এই আর্টিকেলটি তোমাদের মাধ্যমিক পরীক্ষার প্রস্তুতিতে বিশেষভাবে সাহায্য করবে।

1. মান নির্ণয় করি –
(i) \(\frac{\sin 38^{\circ}}{\cos 52^{\circ}}\)
(ii) \(\frac{\csc 79^{\circ}}{\sec 11^{\circ}}\)
(iii) \(\frac{\tan 27^{\circ}}{\cot 63^{\circ}}\)
(i) \(\frac{\sin 38^{\circ}}{\cos 52^{\circ}}\)
সমাধান –
\(\frac{\sin 38^{\circ}}{\cos 52^{\circ}}\)= \( \frac{\sin 38^{\circ}}{\cos (90^{\circ}-38^{\circ})}\)
= \( \frac{\sin 38^{\circ}}{\sin 38^{\circ}}\) [যেহেতু, \(\cos(90^{\circ}-\theta)=\sin\theta\)]
= \( 1\)
(ii) \(\frac{\csc 79^{\circ}}{\sec 11^{\circ}}\)
সমাধান –
\(\frac{\csc 79^{\circ}}{\sec 11^{\circ}}\)= \( \frac{\csc 79^{\circ}}{\sec (90^{\circ}-79^{\circ})}\)
= \( \frac{\csc 79^{\circ}}{\csc 79^{\circ}}\) [যেহেতু \(\sec(90^{\circ}-\theta) = \csc\theta\)]
= \( 1\)
(iii) \(\frac{\tan 27^{\circ}}{\cot 63^{\circ}}\)
সমাধান –
\(\frac{\tan 27^{\circ}}{\cot 63^{\circ}}\)= \( \frac{\tan 27^{\circ}}{\cot (90^{\circ}-27^{\circ})}\)
= \( \frac{\tan 27^{\circ}}{\tan 27^{\circ}}\) [যেহেতু \(\cot(90^{\circ}-\theta)=\tan\theta\)]
= \( 1\)
2. দেখাই যে
(i) \(\sin 66^{\circ} – \cos 24^{\circ} = 0\)
(ii) \(\cos^2 57^{\circ} + \cos^2 33^{\circ} = 1\)
(iii) \(\cos^2 75^{\circ} – \sin^2 15^{\circ} = 0\)
(iv) \(\csc^2 48^{\circ} – \tan^2 42^{\circ} = 1\)
(v) \(\sec 70^{\circ} \sin 20^{\circ} + \cos 20^{\circ} \csc 70^{\circ} = 2\)
(i) \(\sin 66^{\circ} – \cos 24^{\circ} = 0\)
\(\sin 66^{\circ} – \cos 24^{\circ}\)= \( \sin 66^{\circ} – \cos(90^{\circ}-66^{\circ})\)
= \( \sin 66^{\circ} – \sin 66^{\circ}\) [যেহেতু \(\cos(90^{\circ}-\theta)=\sin\theta\)]
= \( 0\) [প্রমাণিত]
(ii) \(\cos^2 57^{\circ} + \cos^2 33^{\circ} = 1\)
\(\cos^2 57^{\circ} + \cos^2 33^{\circ}\)= \( \cos^2 57^{\circ} + \cos^2(90^{\circ}-57^{\circ})\)
= \( \cos^2 57^{\circ} + \sin^2 57^{\circ}\) [যেহেতু, \(\cos(90^{\circ}-\theta)=\sin\theta\)]
= \( 1\) [যেহেতু , \(\sin^2\theta+\cos^2\theta=1\)]
\(\therefore \cos^2 57^{\circ} + \cos^2 33^{\circ} = 1\) [প্রমাণিত]
(iii) \(\cos^2 75^{\circ} – \sin^2 15^{\circ} = 0\)
\(\cos^2 75^{\circ} – \sin^2 15^{\circ}\)= \( \cos^2 75^{\circ} – \sin^2(90^{\circ}-75^{\circ})\)
= \( \cos^2 75^{\circ} – \cos^2 75^{\circ}\) [যেহেতু , \(\sin(90^{\circ}-\theta)=\cos\theta\)]
= \( 0\) [প্রমাণিত]
(iv) \(\csc^2 48^{\circ} – \tan^2 42^{\circ} = 1\)
\(\csc^2 48^{\circ} – \tan^2 42^{\circ}\)= \( \csc^2 48^{\circ} – \tan^2(90^{\circ}-48^{\circ})\)
= \( \csc^2 48^{\circ} – \cot^2 48^{\circ}\) [যেহেতু \(\tan(90^{\circ}-\theta) = \cot\theta\)]
= \( 1\) [প্রমাণিত ] [যেহেতু \(\csc^2\theta-\cot^2\theta=1\)]
(v) \(\sec 70^{\circ} \sin 20^{\circ} + \cos 20^{\circ} \csc 70^{\circ} = 2\)
\(\sec 70^{\circ} \sin 20^{\circ} + \cos 20^{\circ} \csc 70^{\circ}\)= \( \sec(90^{\circ}-20^{\circ}) \sin 20^{\circ} + \cos(90^{\circ}-70^{\circ}) \csc 70^{\circ}\)
= \( \csc 20^{\circ} \sin 20^{\circ} + \sin 70^{\circ} \csc 70^{\circ}\)
[যেহেতু, \(\sec(90^{\circ} \theta)=\csc\theta\) এবং \(\cos(90^{\circ}-\theta)=\sin\theta\)]
= \( \frac{1}{\sin 20^{\circ}} \sin 20^{\circ} + \sin 70^{\circ} \frac{1}{\sin 70^{\circ}}\)
= \( 1+1\)
= \( 2\) [প্রমাণিত]
3. যদি \(\alpha\) ও \(\beta\) কোণ দুটি পরস্পর পূরক কোণ হয়, তাহলে দেখাই যে,
(i) \(\sin^2\alpha + \sin^2\beta = 1\)
সমাধান –
যেহেতু \(\alpha\) ও \(\beta\) কোণ দুটি পরস্পর পূরক কোণ
\(\therefore \alpha+\beta = 90^{\circ}\)বা, \(\beta = 90^{\circ}-\alpha\)
\(\therefore \sin^2\alpha + \sin^2\beta\)= \( \sin^2\alpha + \sin^2(90^{\circ}-\alpha)\)
= \( \sin^2\alpha + \cos^2\alpha\) [যেহেতু \(\sin(90^{\circ}-\theta)=\cos\theta\)]
= \( 1\)
\(\therefore \sin^2\alpha + \sin^2\beta = 1\) [প্রমাণিত]
(ii) \(\cot\beta + \cos\beta = \frac{\cos\beta}{\cos\alpha}(1+\sin\beta)\)
সমাধান –
যেহেতু \(\alpha\) ও \(\beta\) কোণ দুটি পরস্পর পূরক কোণ
\(\therefore \alpha+\beta = 90^{\circ}\)বা, \(\beta = 90^{\circ}-\alpha\)
বা, \(\alpha = 90^{\circ}-\beta\)
\(\therefore \cot\beta + \cos\beta\)= \( \frac{\cos\beta}{\sin\beta} + \cos\beta\)
= \( \frac{\cos\beta}{\sin(90^{\circ}-\alpha)} + \cos\beta\)
= \( \frac{\cos\beta}{\cos\alpha} + \cos\beta\) [যেহেতু \(\sin(90^{\circ}-\theta)=\cos\theta\)]
= \( \frac{\cos\beta(1+\cos\alpha)}{\cos\alpha}\)
= \( \frac{\cos\beta\{1+\cos(90^{\circ}-\beta)\}}{\cos\alpha}\)
= \( \frac{\cos\beta(1+\sin\beta)}{\cos\alpha}\) [যেহেতু \(\cos(90^{\circ}-\theta)=\sin\theta\)]
\(\therefore \cot\beta + \cos\beta = \frac{\cos\beta}{\cos\alpha}(1+\sin\beta)\) [প্রমাণিত]
(iii) \(\frac{\sec\alpha}{\cos\alpha} – \cot^2\beta = 1\)
সমাধান –
যেহেতু \(\alpha\) ও \(\beta\) কোণ দুটি পরস্পর পূরক কোণ
\(\therefore \alpha+\beta = 90^{\circ}\)বা, \(\beta = 90^{\circ}-\alpha\)
\(\therefore \frac{\sec\alpha}{\cos\alpha} – \cot^2\beta\)= \( \frac{1}{\cos^2\alpha} – \cot^2\beta\)
= \( \sec^2\alpha – \cot^2(90^{\circ}-\alpha)\)
= \( \sec^2\alpha – \tan^2\alpha\) [যেহেতু \(\cot(90^{\circ}-\theta)=\tan\theta\)]
= \( 1\)
\(\therefore \frac{\sec\alpha}{\cos\alpha} – \cot^2\beta = 1\) [প্রমাণিত]
4. যদি \(\sin 17^{\circ} = \frac{x}{y}\) হয়, তাহলে দেখাই যে, \(\sec 17^{\circ} – \sin 73^{\circ} = \frac{x^2}{y\sqrt{y^2-x^2}}\)
সমাধান –
\(\sin 17^{\circ} = \frac{x}{y}\)= \( \sqrt{1-\sin^2 17^{\circ}}\)
= \( \sqrt{1-(\frac{x}{y})^2}\)
= \( \sqrt{1-\frac{x^2}{y^2}}\)
= \( \sqrt{\frac{y^2-x^2}{y^2}}\)
= \( \frac{\sqrt{y^2-x^2}}{y}\)
\(\therefore \sec 17^{\circ} – \sin 73^{\circ}\)= \( \frac{1}{\cos 17^{\circ}} – \sin(90^{\circ}-17^{\circ})\)
= \( \frac{1}{\cos 17^{\circ}} – \cos 17^{\circ}\) [যেহেতু \(\sin(90^{\circ}-\theta)=\cos\theta\)]
= \( \frac{1-\cos^2 17^{\circ}}{\cos 17^{\circ}}\)
= \( \frac{\sin^2 17^{\circ}}{\cos 17^{\circ}}\)
= \( \frac{(\frac{x}{y})^2}{\frac{\sqrt{y^2-x^2}}{y}}\)
= \( \frac{\frac{x^2}{y^2}}{\frac{\sqrt{y^2-x^2}}{y}}\)
= \( \frac{x^2}{y^2} \times \frac{y}{\sqrt{y^2-x^2}}\)
= \( \frac{x^2}{y\sqrt{y^2-x^2}}\)
\(\therefore \sec 17^{\circ} – \sin 73^{\circ} = \frac{x^2}{y\sqrt{y^2-x^2}}\) [প্রমাণিত]
5. দেখাই যে, \(\sec^2 12^{\circ} – \frac{1}{\tan^2 78^{\circ}} = 1\)
সমাধান –
\(\sec^2 12^{\circ} – \frac{1}{\tan^2 78^{\circ}}\)= \( \sec^2 12^{\circ} – \cot^2 78^{\circ}\)
= \( \sec^2 12^{\circ} – \cot^2(90^{\circ}-12^{\circ})\)
= \( \sec^2 12^{\circ} – \tan^2 12^{\circ}\) [যেহেতু \(\cot(90^{\circ}-\theta)=\tan\theta\)]
= \( 1\)
\(\therefore \sec^2 12^{\circ} – \frac{1}{\tan^2 78^{\circ}} = 1\) [প্রমাণিত]
6. A+B=90° হলে, দেখাই যে, \(1 + \frac{\tan A}{\tan B} = \sec^2 A\)
সমাধান –
A+B = 90°
\(\therefore\) B = 90°-A
\(1 + \frac{\tan A}{\tan B}\)= \( 1 + \frac{\tan A}{\tan(90^{\circ}-A)}\)
= \( 1 + \frac{\tan A}{\cot A}\) [যেহেতু \(\tan(90^{\circ}-A)=\cot A\)]
= \( 1 + \frac{\tan A}{\frac{1}{\tan A}}\)
= \( 1 + \tan^2 A\)
= \( \sec^2 A\)
\(\therefore 1 + \frac{\tan A}{\tan B} = \sec^2 A\) [প্রমাণিত]
7. দেখাই যে , \(\csc^2 22^{\circ} \cot^2 68^{\circ} = \sin^2 22^{\circ} + \sin^2 68^{\circ} + \cot^2 68^{\circ}\)
সমাধান –
বামপক্ষ –
\(\csc^2 22^{\circ} \cot^2 68^{\circ}\)= \( \csc^2 22^{\circ} \cot^2(90^{\circ}-22^{\circ})\)
= \( \csc^2 22^{\circ} \tan^2 22^{\circ}\)
= \( \frac{1}{\sin^2 22^{\circ}} \times \frac{\sin^2 22^{\circ}}{\cos^2 22^{\circ}}\)
= \( \frac{1}{\cos^2 22^{\circ}}\)
= \( \sec^2 22^{\circ}\)
= \( \sec^2(90^{\circ}-68^{\circ})\)
= \( \csc^2 68^{\circ}\)
ডানপক্ষ –
\(\sin^2 22^{\circ} + \sin^2 68^{\circ} + \cot^2 68^{\circ}\)= \( \sin^2 22^{\circ} + \sin^2(90^{\circ}-22^{\circ}) + \cot^2 68^{\circ}\)
= \( \sin^2 22^{\circ} + \cos^2 22^{\circ} + \cot^2 68^{\circ}\)
= \( 1 + \cot^2 68^{\circ}\)
= \( \csc^2 68^{\circ}\)
\(\therefore\) বামপক্ষ = ডানপক্ষ [ প্রমাণিত ]
8. যদি P + Q = 90° হয়, তবে দেখাই যে, \(\sqrt{\frac{\sin P}{\cos Q} – \sin P \cos Q} = \cos P\)
সমাধান –
P+Q=90°
বা, Q = 90°-P
বামপক্ষ –
\(\sqrt{\frac{\sin P}{\cos Q} – \sin P \cos Q}\)= \( \sqrt{\frac{\sin P}{\cos(90^{\circ}-P)} – \sin P \cos(90^{\circ}-P)}\)
= \( \sqrt{\frac{\sin P}{\sin P} – \sin P \sin P}\) [যেহেতু \(\cos(90^{\circ}-\theta)=\sin\theta\)]
= \( \sqrt{1 – \sin^2 P}\)
= \( \cos P\) = ডানপক্ষ
\(\therefore\) বামপক্ষ = ডানপক্ষ [ প্রমাণিত ]
9. প্রমাণ করি যে, \(\cot 12^{\circ} \cot 38^{\circ} \cot 52^{\circ} \cot 78^{\circ} \cot 60^{\circ} = \frac{1}{\sqrt{3}}\)
সমাধান –
\(\cot 12^{\circ} \cot 38^{\circ} \cot 52^{\circ} \cot 78^{\circ} \cot 60^{\circ}\)= \( \cot 12^{\circ} \cot 38^{\circ} \cot(90^{\circ}-38^{\circ}) \cot(90^{\circ}-12^{\circ}) \cot 60^{\circ}\)
= \( \cot 12^{\circ} \cot 38^{\circ} \tan 38^{\circ} \tan 12^{\circ} \cot 60^{\circ}\)
= \( \cot 12^{\circ} \times \cot 38^{\circ} \times \frac{1}{\cot 38^{\circ}} \times \frac{1}{\cot 12^{\circ}} \times \frac{1}{\sqrt{3}}\)
= \( \frac{1}{\sqrt{3}}\)
\(\therefore \cot 12^{\circ} \cot 38^{\circ} \cot 52^{\circ} \cot 78^{\circ} \cot 60^{\circ} = \frac{1}{\sqrt3}\)10. O কেন্দ্রীয় বৃত্তের AOB একটি ব্যাস। A,C,B এবং O,C যুক্ত করে দেখাই যে,
(i) \(\tan \angle ABC = \cot \angle ACO\)
(ii) \(\sin^2 \angle BCO + \sin^2 \angle ACO = 1\)
(iii) \(\csc^2 \angle CAB – 1 = \tan^2 \angle ABC\)
সমাধান –
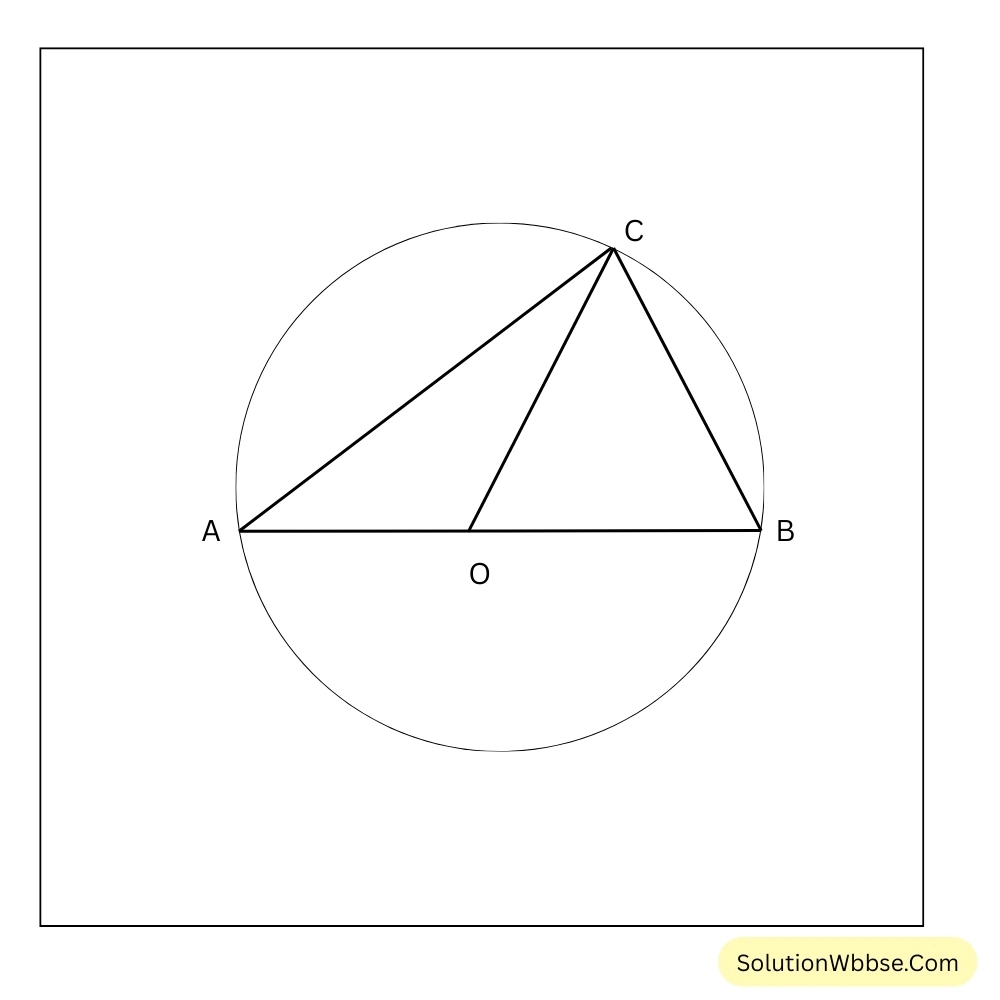
O কেন্দ্রীয় বৃত্তের AOB একটি ব্যাস। A,C,B এবং O,C যুক্ত করা হল।
স্পষ্টতই \(\angle ACB = 90^{\circ}\) [ যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]
\(\therefore \angle ACO + \angle BCO = 90^{\circ}\)বা, \(\angle ACO = 90^{\circ} – \angle BCO\)
এবং ABC ত্রিভুজে \(\angle CAB + \angle ABC = 90^{\circ}\)
বা, \(\angle ABC = 90^{\circ} – \angle CAB\)
বা, \(\angle CAB = 90^{\circ} – \angle ABC\)
(i) \(\tan \angle ABC\)
= \( \tan(90^{\circ} – \angle CAB)\) [যেহেতু \(\angle ABC = 90^{\circ} – \angle CAB\)]
= \( \cot \angle CAB\) [যেহেতু \(\tan(90^{\circ}-\theta)=\cot\theta\)]
= \( \cot \angle ACO\) [যেহেতু \(\triangle ACO\) কারণ OC=OA(একই বৃত্তের ব্যাসার্ধ)]
\(\therefore \tan \angle ABC = \cot \angle ACO\) [প্রমাণিত]
(ii) \(\sin^2 \angle BCO + \sin^2 \angle ACO\)
= \( \sin^2 \angle BCO + \sin^2(90^{\circ} – \angle BCO)\) [যেহেতু \(\angle ACO = 90^{\circ} – \angle BCO\)]
= \( \sin^2 \angle BCO + \cos^2 \angle BCO\) [যেহেতু \(\sin(90^{\circ}-\theta)=\cos\theta\)]
= \( 1\)
\(\therefore \sin^2 \angle BCO + \sin^2 \angle ACO = 1\) [প্রমাণিত]
(iii) \(\csc^2 \angle CAB – 1\)
= \( \csc^2(90^{\circ} – \angle ABC) – 1\) [যেহেতু \(\angle CAB = 90^{\circ} – \angle ABC\)]
= \( \sec^2 \angle ABC – 1\) [যেহেতু \(\csc(90^{\circ}-\theta)=\sec\theta\)]
= \( \tan^2 \angle ABC\)
\(\therefore \csc^2 \angle CAB – 1 = \tan^2 \angle ABC\) [প্রমাণিত]
11. ABCD একটি আয়তকার চিত্র। A,C যুক্ত করে প্রমাণ করি যে,
(i) \(\tan\angle ACD = \cot\angle ACB\)
(ii) \(\tan^2\angle CAD + 1 = \frac{1}{\sin^2\angle BAC}\)
সমাধান –
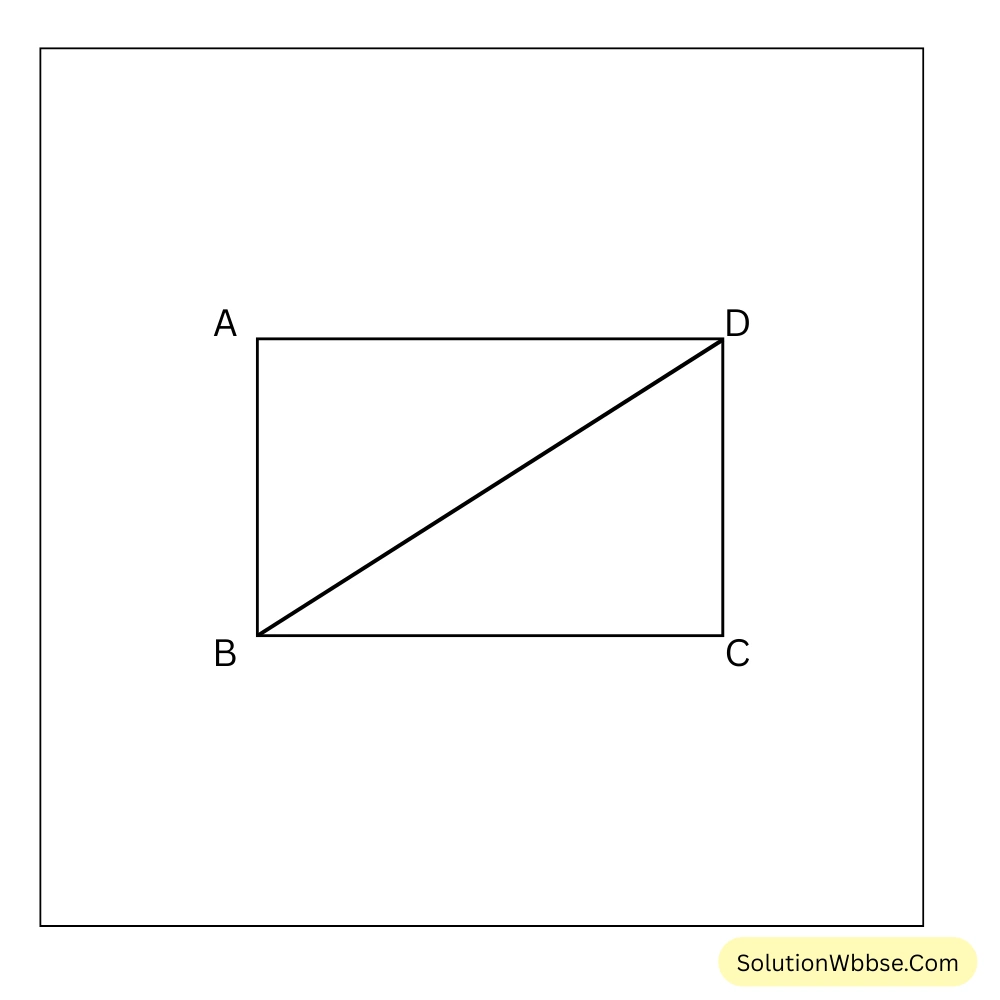
যেহেতু ABCD একটি আয়তক্ষেত্র
\(\therefore \angle BCD = 90^{\circ}\)বা, \(\angle ACB + \angle ACD = 90^{\circ}\)
বা, \(\angle ACD = 90^{\circ} – \angle ACB\)
এবং \(\angle BAD = 90^{\circ}\)
বা, \(\angle BAC + \angle CAD = 90^{\circ}\)
বা, \(\angle CAD = 90^{\circ} – \angle BAC\)
(i) \(\tan \angle ACD\)
= \( \tan(90^{\circ} – \angle ACB)\) [যেহেতু, \(\angle ACD=(90^{\circ}-\angle ACB)\)]
= \( \cot \angle ACB\) [যেহেতু, \(\tan(90^{\circ}-\theta)=\cot\theta\)]
\(\therefore \tan \angle ACD = \cot \angle ACB\) [প্রমাণিত]
(ii) \(\tan^2 \angle CAD + 1\)
= \( \tan^2(90^{\circ} – \angle BAC) + 1\) [যেহেতু, \(\angle CAD=(90^{\circ}-\angle BAC)\)]
= \( \cot^2 \angle BAC + 1\) [যেহেতু \(\tan(90^{\circ}-\theta)=\cot\theta\)]
= \( \csc^2 \angle BAC\)
= \( \frac{1}{\sin^2 \angle BAC}\)
\(\therefore \tan^2 \angle CAD + 1 = \frac{1}{\sin^2 \angle BAC}\) [প্রমাণিত]
12. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.)
(i) \((\sin 43^{\circ} \cos 47^{\circ} + \cos 43^{\circ} \sin 47^{\circ})\) -এর মান
(a) 0
(b) 1
(c) \(\sin 4^{\circ}\)
(d) \(\cos 4^{\circ}\)
উত্তর – (b) 1
সমাধান –
\((\sin 43^{\circ} \cos 47^{\circ} + \cos 43^{\circ} \sin 47^{\circ})\)= \( \sin 43^{\circ} \cos(90^{\circ}-43^{\circ}) + \cos 43^{\circ} \sin(90^{\circ}-43^{\circ})\)
= \( \sin 43^{\circ} \times \sin 43^{\circ} + \cos 43^{\circ} \times \cos 43^{\circ}\)
= \( \sin^2 43^{\circ} + \cos^2 43^{\circ}\)
= \( 1\)
(ii) \((\frac{\tan 35^{\circ}}{\cot 55^{\circ}} + \frac{\cot 78^{\circ}}{\tan 12^{\circ}})\) -এর মান
(a) 0
(b) 1
(c) 2
(d) কোনোটিই নয়
উত্তর – (c) 2
সমাধান –
\((\frac{\tan 35^{\circ}}{\cot 55^{\circ}} + \frac{\cot 78^{\circ}}{\tan 12^{\circ}})\)= \( (\frac{\tan 35^{\circ}}{\cot(90^{\circ}-35^{\circ})} + \frac{\cot 78^{\circ}}{\tan(90^{\circ}-78^{\circ})}\)
= \( \frac{\tan 35^{\circ}}{\tan 35^{\circ}} + \frac{\cot 78^{\circ}}{\cot 78^{\circ}}\)
= \( 1+1\)
= \( 2\)
(iii) \(\cos(40^{\circ}+\theta) – \sin(50^{\circ}-\theta)\)-এর মান
(a) \(2\cos\theta\)
(b) \(7\sin\theta\)
(c) \(0\)
(d) \(1\)
উত্তর – (c) \(0\)
সমাধান –
\(\cos(40^{\circ}+\theta) – \sin(50^{\circ}-\theta)\)= \(\cos(40^{\circ}+\theta) – \sin(90^{\circ} – (40^{\circ}+\theta))\)
= \(\cos(40^{\circ}+\theta) – \cos(40^{\circ}+\theta)\)
= \(0\)
(iv) ABC একটি ত্রিভুজ। \(\sin\left(\frac{B+C}{2}\right)\) =
(a) \(\sin \frac{A}{2}\)
(b) \(\cos \frac{A}{2}\)
(c) \(\sin A\)
(d) \(\cos A\)
উত্তর – (b) \(\cos \frac{A}{2}\)
সমাধান –
\(\sin\left(\frac{B+C}{2}\right)\)= \(\sin\left(\frac{180^{\circ}-A}{2}\right)\) [যেহেতু \(\angle A+\angle B+\angle C=180^{\circ}\)]
= \(\sin\left(\frac{180^{\circ}}{2} – \frac{A}{2}\right)\)
= \(\sin\left(90^{\circ} – \frac{A}{2}\right)\)
= \(\cos \frac{A}{2}\)
(v) \(A+B=90^{\circ}\) এবং \(\tan A = \frac{3}{4}\) হলে \(\cot B\) –এর মান
(a) \(\frac{3}{4}\)
(b) \(\frac{4}{3}\)
(c) \(\frac{3}{5}\)
(d) \(\frac{4}{5}\)
উত্তর – (a) \(\frac{3}{4}\)
সমাধান –
\(A+B =90^{\circ}\)বা, \(B = 90^{\circ}-A\)
\(\therefore \cot B\) = \( \cot(90^{\circ}-A)\)
= \( \tan A\)
= \( \frac{3}{4}\)
(B) নীচের বিবৃতি গুলি সত্য না মিথ্যা লিখ
(i) \(\cos 54^{\circ}\) এবং \(\sin 36^{\circ}\) এর সরলতম মান সমান।
উত্তর – সত্য
সমাধান –
\(\cos 54^{\circ} = \cos(90^{\circ}-36^{\circ}) = \sin 36^{\circ}\)(ii) \((\sin 12^{\circ} – \cos 78^{\circ})\)-এর সরলতম মান 1.
উত্তর – মিথ্যা
সমাধান –
\((\sin 12^{\circ} – \cos 78^{\circ})\)= \( \sin 12^{\circ} – \cos(90^{\circ}-12^{\circ})\)
= \( \sin 12^{\circ} – \sin 12^{\circ}\)
= \( 0\)
(C) শূন্যস্থান পূরণ করি
(i) \((\tan 15^{\circ} \times \tan 45^{\circ} \times \tan 60^{\circ} \times \tan 75^{\circ})\)-এর মান ______
উত্তর – \(\sqrt{3}\)
সমাধান –
\((\tan 15^{\circ} \times \tan 45^{\circ} \times \tan 60^{\circ} \times \tan 75^{\circ})\)= \( \tan 15^{\circ} \times 1 \times \sqrt{3} \times \tan(90^{\circ}-15^{\circ})\)
= \( \tan 15^{\circ} \times \sqrt{3} \times \cot 15^{\circ}\)
= \( \tan 15^{\circ} \times \sqrt{3} \times \frac{1}{\tan 15^{\circ}}\)
= \( \sqrt{3}\)
(ii) \((\sin 12^{\circ} \times \cos 18^{\circ} \times \sec 78^{\circ} \times \csc 72^{\circ})\)-এর মান ______
উত্তর – \(1\)
সমাধান – \((\sin 12^{\circ} \times \cos 18^{\circ} \times \sec 78^{\circ} \times \csc 72^{\circ})\)
= \( \sin 12^{\circ} \times \cos 18^{\circ} \times \sec(90^{\circ}-12^{\circ}) \times \csc(90^{\circ}-18^{\circ} \)
= \( \sin 12^{\circ} \times \cos 18^{\circ} \times \csc 12^{\circ} \times \sec 18^{\circ}\)
= \( \sin 12^{\circ} \times \cos 18^{\circ} \times \frac{1}{\sin 12^{\circ}} \times \frac{1}{\cos 18^{\circ}}\)
= \( 1\)
(iii) A এবং B পরস্পর পূরক কোণ হলে, \(\sin A =\) ______
উত্তর – \(\cos B\)
সমাধান –
যেহেতু A এবং B পরস্পর পূরক
\(\therefore A+B =90^{\circ}\)বা, \(A = 90^{\circ}-B\)
\(\sin A = \sin(90^{\circ}-B) = \cos B\)13. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
(i) \(\sin 10\theta = \cos 8\theta\) এবং \(10\theta\) ধনাত্মক সূক্ষ্মকোণ হলে , \(\tan 9\theta\) এর মান নির্ণয় করি।
সমাধান –
\(\sin 10\theta = \cos 8\theta\)বা, \(\sin 10\theta = \sin(90^{\circ}-8\theta)\)
বা, \(10\theta=90^{\circ}-8\theta\)
বা, \(18\theta =90^{\circ}\)
বা, \(\theta= \frac{90^{\circ}}{18}\)
বা, \(\theta=5^{\circ}\)
\(\therefore \tan 9\theta\)= \( \tan (9\times 5^{\circ})\)
= \( \tan 45^{\circ}\)
= \(1\)
\(\therefore \tan 9\theta=1\)(ii) \(\tan 4\theta \times \tan 6\theta=1\) এবং \(6\theta\) ধনাত্মক সূক্ষ্মকোণ হলে , \(\theta\) এর মান নির্ণয় করি।
সমাধান – \(\tan 4\theta \times \tan 6\theta=1\)
বা, \(\tan 6\theta= \frac{1}{\tan 4\theta}\)
বা, \(\tan 6\theta = \cot 4\theta\)
বা, \(\tan 6\theta = \tan(90^{\circ}-4\theta)\)
বা, \(6\theta=90^{\circ}-4\theta\)
বা, \(10\theta = 90^{\circ}\)
বা, \(\theta = \frac{90^{\circ}}{10}\)
বা, \(\theta = 9^{\circ}\)
(iii) \(\frac{2\sin^2 63^{\circ}+1+2\sin^2 27^{\circ}}{3\cos^2 17^{\circ}-2+3\cos^2 73^{\circ}}\)-এর মান নির্ণয় করি।
সমাধান –
\(\frac{2\sin^2 63^{\circ}+1+2\sin^2 27^{\circ}}{3\cos^2 17^{\circ}-2+3\cos^2 73^{\circ}}\)= \( \frac{2\sin^2 63^{\circ}+1+2\sin^2(90^{\circ}-63^{\circ})}{3\cos^2 17^{\circ}-2+3\cos^2(90^{\circ}-17^{\circ})}\)
= \( \frac{2\sin^2 63^{\circ}+1+2\cos^2 63^{\circ}}{3\cos^2 17^{\circ}-2+3\sin^2 17^{\circ}}\)
= \( \frac{2(\sin^2 63^{\circ}+\cos^2 63^{\circ})+1}{3(\cos^2 17^{\circ}+\sin^2 17^{\circ})-2}\)
= \( \frac{2(1)+1}{3(1)-2}\) [যেহেতু \(\sin^2\theta+\cos^2\theta=1\)]
= \( \frac{3}{1}\)
= \( 3\)
(iv) \((\tan 1^{\circ} \times \tan 2^{\circ} \times \tan 3^{\circ} \cdots \tan 89^{\circ})\)
সমাধান –
\((\tan 1^{\circ} \times \tan 2^{\circ} \times \tan 3^{\circ} \cdots \tan 89^{\circ})\)
= \( 1 \times 1 \times 1 \cdots 1\) [যেহেতু \(\tan\theta \times \cot\theta = 1\)]
= \( 1\)
(v) \(\sec 5A = \csc(A+36^{\circ})\) এবং \(5A\) ধনাত্মক সূক্ষ্মকোণ হলে, \(A\) এর মান নির্ণয় করি।
সমাধান –
\(\sec 5A = \csc(A+36^{\circ})\)বা, \(\sec 5A = \sec\{90^{\circ}-(A+36^{\circ})\}\) [যেহেতু \(\sec(90^{\circ}-\theta)=\csc\theta\)]
বা, \(5A = 90^{\circ}-(A+36^{\circ})\)
বা, \(5A = 90^{\circ}-A-36^{\circ}\)
বা, \(5A+A = 90^{\circ}-36^{\circ}\)
বা, \(6A = 54^{\circ}\)
বা, \(A = \frac{54^{\circ}}{6}\)
বা, \(A = 9^{\circ}\)
এই আর্টিকেলে মাধ্যমিক (দশম শ্রেণী) গণিতের চতুর্বিংশ অধ্যায়, ‘পূরক কোণের ত্রিকোণমিতিক অনুপাত’ -এর ‘কষে দেখি – 24’ বিভাগের সমস্ত সমস্যার সমাধান করা হয়েছে।
আশা করি, এই আর্টিকেলটি আপনাদের পরীক্ষার প্রস্তুতিতে কিছুটা হলেও সহায়ক হয়েছে। যদি কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হয়, নিচে কমেন্ট করে জানাতে পারেন অথবা টেলিগ্রামের মাধ্যমে যোগাযোগ করতে পারেন—আমরা আপনাদের সকল প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন