পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) নবম শ্রেণির গণিত পাঠ্যবইয়ের পঞ্চম অধ্যায় হলো ‘রৈখিক সহসমীকরণ (দুই চল বিশিষ্ট)’। এই পোস্টে ‘কষে দেখি – 5.3‘-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. নীচের দুইচল বিশিষ্ট একঘাত সহসমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি ও লেখচিত্রের সাহায্যে সমাধান করে যাচাই করি
(a) \(8x+5y-11=0\) , \(3x-4y-10 = 0\)
সমাধান –
প্রদত্ত সহসমীকরণ দুটি হল –
\(8x+5y-11=0\) —(i) এবং \(3x-4y-10 = 0\) —(ii)
এখন, (i) নং সমীকরণকে 4 দ্বারা এবং (ii) নং সমীকরণকে 5 দ্বারা গুণ করে পাই,
\(32x+20y-44 = 0\) —(iii)
\(15x -20y -50 = 0\) —(iv)
(iii) নং ও (iv) নং সমীকরণ যোগ করে পাই,
\(32x+20y-44+15x -20y -50 = 0\)বা, \(47x – 94 =0\)
বা, \(47x = 94\)
বা, \(x = \frac{94}{47}\)
বা, \(x = 2\)
\(x\)–এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই,
\(8(2)+5y-11 = 0\)বা, \(16+5y-11= 0\)
বা, \(5y + 5 = 0\)
বা, \(5y = -5\)
বা, \(y = \frac{-5}{5}\)
বা, \(y = -1\)
∴ নির্ণেয় সমাধান \(x = 2\) এবং \(y = -1\)
লেখচিত্রের সাহায্যে সমাধান –
\(8x+5y-11 = 0\)বা, \(x = \frac{11-5y}{8}\)
| X | -3 | 2 | 7 |
| y | 7 | -1 | -9 |
বা, \(x = \frac{10+4y}{3}\)
| X | 6 | 10 | 2 |
| y | 2 | 5 | -1 |
ছক কাগজে \(XOX\) এবং \(YOY\) দুটি পরপর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের একটি বাহুকে 1 একক ধরে \((-3,7)\), \((2,-1)\) এবং \((7,-9)\) বিন্দুগুলি স্থাপন করে ও যোগ করে \(AB\) সরলরেখা এবং \((6,2)\), \((10,5)\), \((2,-1)\) বিন্দুগুলি যোগ করে \(CD\) সরলরেখা অঙ্কন করলাম। \(AB\) ও \(CD\) সরলরেখা পরস্পর \(P\) বিন্দুতে ছেদ করে। \(P\) বিন্দুর স্থানাঙ্ক \((2,-1)\)। সুতরাং নির্ণেয় সমাধান \(x=2\), \(y=-1\)
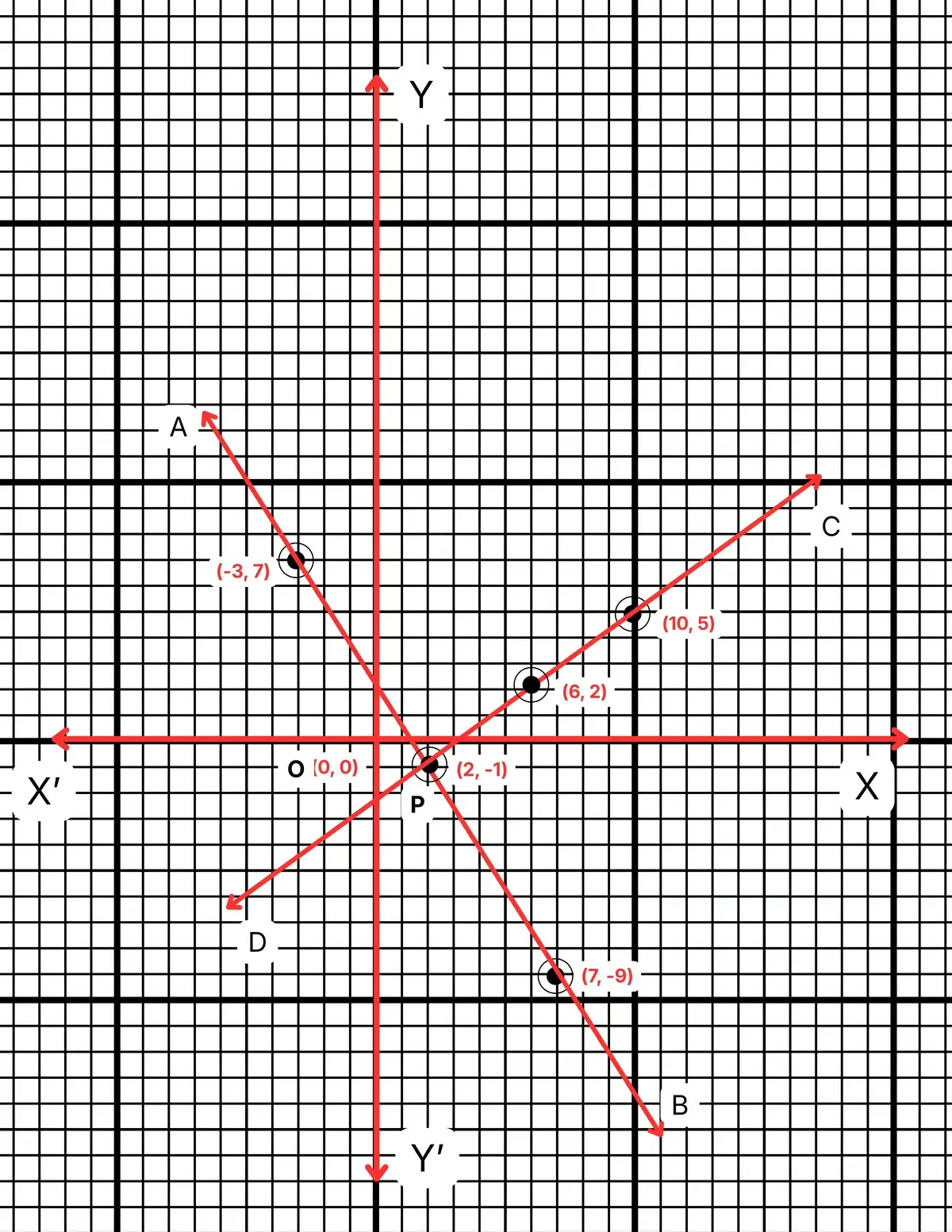
অর্থাৎ অপনয়ন পদ্ধতিতে সহসমীকরণ দুটির সমাধান এবং লেখচিত্রের মাধ্যমে নির্ণেয় সমাধান সমান।
(b) \(2x+3y-7=0\) , \(3x+2y -8 = 0\)
সমাধান –
প্রদত্ত সহ-সমীকরণ দুটি হল –
\(2x+3y-7=0\) — (i)
\(3x+2y -8 = 0\) — (ii)
(i) নং সমীকরণকে 2 দ্বারা এবং (ii) নং সমীকরণকে 3 দ্বারা গুণ করে পাই,
\(4x + 6y -14 = 0\) — (iii)
\(9x +6y – 24 = 0\) — (iv)
এখন, (iii) নং ও (iv) নং সমীকরণকে বিয়োগ করে পাই,
\((4x+6y-14) – (9x+6y-24) = 0\)বা, \(4x + 6y -14 – 9x -6y +24 = 0\)
বা, \(-5x +10 = 0\)
বা, \(5x = 10\)
বা, \(x = \frac{10}{5}\)
বা, \(x = 2\)
\(x\)-এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই,
\(2(2) +3y -7 = 0\)বা, \(4 + 3y -7 = 0\)
বা, \(3y -3 = 0\)
বা, \(3y = 3\)
বা, \(y = \frac{3}{3}\)
বা, \(y = 1\)
∴ নির্ণেয় সমাধান \(x = 2\) এবং \(y = 1\)
লেখচিত্রের সাহায্যে সমাধান –
\(2x+3y-7=0\)বা, \(2x = 7-3y\)
বা, \(x = \frac{7-3y}{2}\)
| X | 2 | -1 | 5 |
| y | 1 | 3 | -1 |
বা, \(x = \frac{8-2y}{3}\)
| x | 0 | -2 | -4 |
| y | 4 | 7 | 10 |
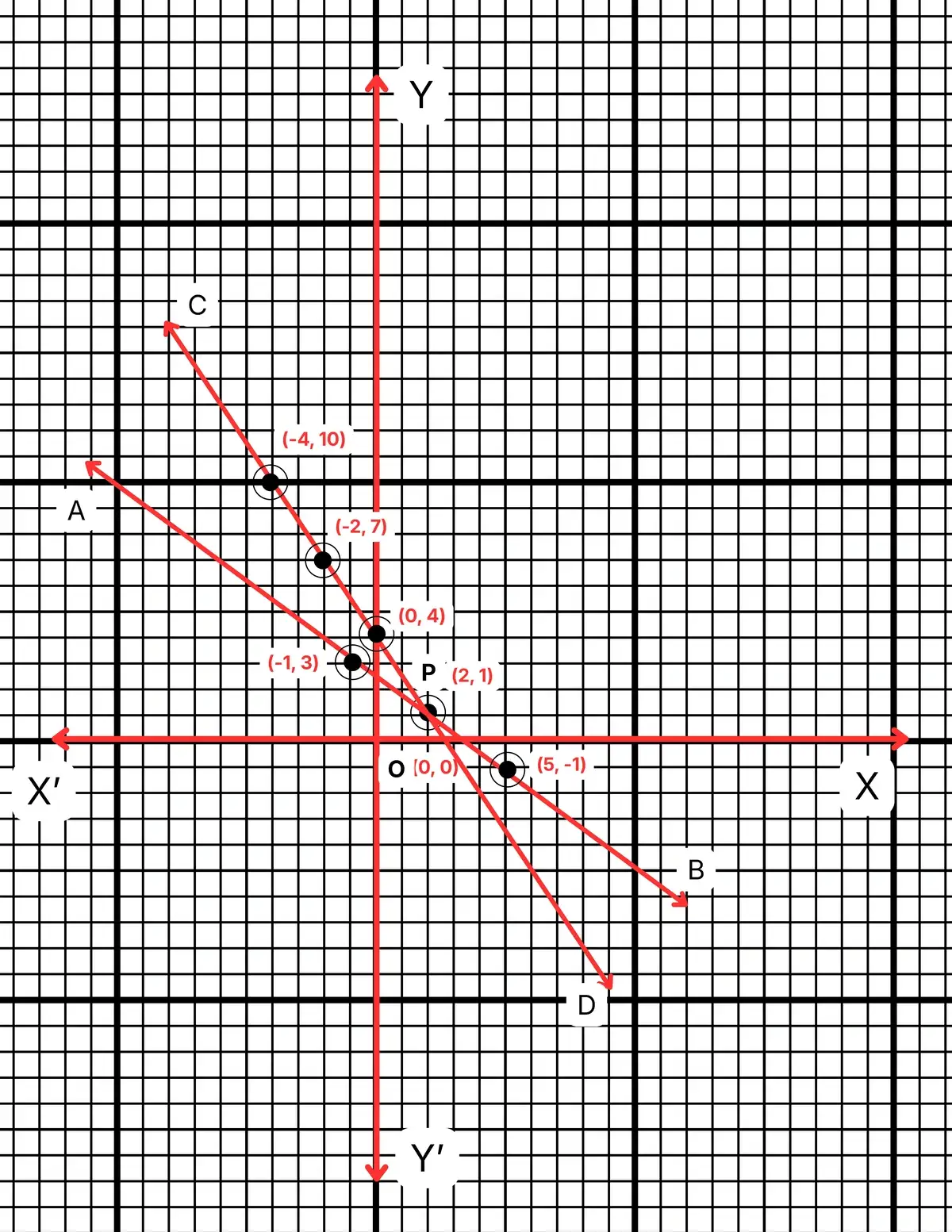
ছক কাগজে \(XOX\) এবং \(YOY\) দুটি পরপর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের একটি বাহুকে 1 একক ধরে \((2,1)\), \((-1,3)\) এবং \((5,-1)\) বিন্দুগুলি স্থাপন করে ও যোগ করে \(AB\) সরলরেখা এবং \((0,4)\), \((-2,7)\), \((-4,10)\) বিন্দুগুলি যোগ করে \(CD\) সরলরেখা অঙ্কন করলাম। \(AB\) ও \(CD\) সরলরেখা পরস্পর \(P\) বিন্দুতে ছেদ করে। \(P\) বিন্দুর স্থানাঙ্ক \((2,1)\)। সুতরাং নির্ণেয় সমাধান \(x=2\), \(y=1\)।
অর্থাৎ অপনয়ন পদ্ধতিতে সহ-সমীকরণ দুটির সমাধান এবং লেখচিত্রের মাধ্যমে নির্ণেয় সমাধান সমান।
2. \(7x-5y+2 = 0\) সমীকরণকে কত দিয়ে গুণ করে \(2x+15y+3 = 0\) সমীকরণের সঙ্গে যোগ করব যাতে \(y\) চলটিকে অপনীত করতে পারি।
সমাধান –
\(7x-5y+2 = 0\) — (i)
\(2x+15y+3 = 0\) — (ii)
\(5\) এবং \(15\)-এর লসাগু \(15\)। অর্থাৎ \(y\)–কে অপনীত করতে গেলে (i) নং সমীকরণকে \(3\) দ্বারা গুণ করতে হবে।
3. \(4x-3y = 16\) ও \(6x+5y = 62\) উভয় সমীকরণকে সবচেয়ে ছোট কোন স্বাভাবিক সংখ্যা দিয়ে গুণ করলে দুটি সমীকরণের \(x\)–এর সহগ সমান হবে তা লিখি।
সমাধান –
\(4x-3y = 16\) — (i)
\(6x+5y = 62\) — (ii)
(i) নং ও (ii) নং সমীকরণে \(x\)-এর সহগ যথাক্রমে \(4\) ও \(6\)।
\(4\) ও \(6\)-এর লসাগু \(12\)।
∴ (i) নং সমীকরণকে \(3\) দ্বারা ও (ii) নং সমীকরণকে \(2\) দ্বারা গুণ করলে সমীকরণদ্বয়ের \(x\)–এর সহগ সমান হবে।
4. নীচের দুইচল বিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।
(i) \(3x+2y = 6\) , \(2x -3y = 17\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(3x+2y = 6\) — (i)
\(2x -3y = 17\) — (ii)
(i) নং সমীকরণকে 3 দ্বারা এবং (ii) নং সমীকরণকে 2 দ্বারা গুণ করে পাই,
\(9x + 6y = 18\) — (iii)
এবং \(4x – 6y = 34\) — (iv)
এখন (iii) ও (iv) নং সমীকরণ যোগ করে পাই,
\(9x + 6y +4x – 6y = 18+34\)বা, \(13x = 52\)
বা, \(x = \frac{52}{13}\)
বা, \(x = 4\)
\(x\)-এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই,
\(3x+2y = 6\)বা, \(3(4) +2y = 6\)
বা, \(12 + 2y = 6\)
বা, \(2y = 6 -12\)
বা, \(2y = -6\)
বা, \(y = \frac{-6}{2}\)
বা, \(y = -3\)
∴ নির্ণেয় সমাধান \(x = 4\) এবং \(y = -3\)।
(ii) \(2x+3y = 32\) , \(11y-9x = 3\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(2x+3y = 32\) — (i)
\(11y-9x = 3\) — (ii)
(i) নং সমীকরণকে 9 দ্বারা এবং (ii) নং সমীকরণকে 2 দ্বারা গুণ করে পাই,
\(18x + 27y = 288\) — (iii)
\(22y – 18x = 6\) — (iv)
(iii) নং ও (iv) নং সমীকরণ যোগ করে পাই,
\(18x +27y + 22y -18x = 288 +6\)বা, \(49y = 294\)
বা, \(y = \frac{294}{49}\)
বা, \(y = 6\)
\(y\)-এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই,
\(2x+3(6) = 32\)বা, \(2x + 18 = 32\)
বা, \(2x = 32-18\)
বা, \(2x = 14\)
বা, \(x = \frac{14}{2}\)
বা, \(x = 7\)
∴ নির্ণেয় সমাধান \(x = 7\) এবং \(y = 6\)।
(iii) \(x+y = 48\) , \(x+4 = \frac{5}{2} (y+4)\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(x+y = 48\) — (i)
\(x+4 = \frac{5}{2} (y+4)\) — (ii)
(ii) নং সমীকরণ থেকে পাই,
\(2(x+4) = 5(y+4)\)বা, \(2x+8 = 5y+20\)
বা, \(2x-5y = 20-8\)
বা, \(2x-5y = 12\) — (iii)
(i) নং সমীকরণকে 5 দ্বারা এবং (iii) নং সমীকরণকে 1 দ্বারা গুণ করে পাই,
\(5x+5y = 240\) — (iv)
\(2x-5y = 12\) — (v)
এখন, (iv) নং ও (v) নং সমীকরণ যোগ করে পাই,
\(5x+5y+2x-5y =240+12\)বা, \(7x = 252\)
বা, \(x = \frac{252}{7}\)
বা, \(x = 36\)
\(x\)-এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই,
\(36 + y = 48\)বা, \(y = 48-36\)
বা, \(y = 12\)
∴ নির্ণেয় সমাধান \(x = 36\) এবং \(y = 12\)।
(iv) \(\frac{x}{2} + \frac{y}{3} = 8\), \(\frac{5x}{4} – 3y = -3\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(\frac{x}{2} + \frac{y}{3} = 8\) — (i)
\(\frac{5x}{4} – 3y = -3\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(\frac{x}{2} + \frac{y}{3} = 8\)বা, \(\frac{3x+2y}{6} = 8\)
বা, \(3x + 2y = 48\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(\frac{5x}{4} – 3y = -3\)বা, \(\frac{5x-12y}{4} = -3\)
বা, \(5x – 12y = -12\) — (iv)
(iii) নং সমীকরণকে 6 দ্বারা এবং (iv) নং সমীকরণকে 1 দ্বারা গুণ করে পাই,
\(18x + 12y = 288\) — (v)
এবং, \(5x – 12y = -12\) — (vi)
(v) ও (vi) নং সমীকরণকে যোগ করে পাই,
\(18x + 12y + 5x – 12y = 288 – 12\)বা, \(23x = 276\)
বা, \(x = \frac{276}{23}\)
বা, \(x = 12\)
\(x\)-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(3x + 2y = 48\)বা, \(3(12) + 2y = 48\)
বা, \(36 + 2y = 48\)
বা, \(2y = 48 – 36\)
বা, \(2y = 12\)
বা, \(y = \frac{12}{2}\)
বা, \(y = 6\)
∴ নির্ণেয় সমাধান \(x = 12\) এবং \(y = 6\)।
(v) \(3x – \frac{2}{y} = 5\), \(x + \frac{4}{y} = 4\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(3x – \frac{2}{y} = 5\) — (i)
\(x + \frac{4}{y} = 4\) — (ii)
(i) নং সমীকরণকে 2 দ্বারা গুণ করে পাই,
\(6x – \frac{4}{y} = 10\) — (iii)
(ii) নং ও (iii) নং সমীকরণ যোগ করে পাই,
\(x + \frac{4}{y} + 6x – \frac{4}{y} = 4 + 10\)বা, \(7x = 14\)
বা, \(x = \frac{14}{7}\)
বা, \(x = 2\)
\(x\)–এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই,
\(3(2) – \frac{2}{y} = 5\)বা, \(6 – \frac{2}{y} = 5\)
বা, \(\frac{2}{y} = 6-5\)
বা, \(\frac{2}{y} = 1\)
বা, \(y = 2\)
∴ নির্ণেয় সমাধান \(x = 2\) এবং \(y = 2\)।
(vi) \(\frac{x}{2} + \frac{y}{3} = 1\), \(\frac{x}{3} + \frac{y}{2} = 1\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(\frac{x}{2} + \frac{y}{3} = 1\) — (i)
\(\frac{x}{3} + \frac{y}{2} = 1\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(\frac{x}{2} + \frac{y}{3} = 1\)বা, \(\frac{3x+2y}{6} = 1\)
বা, \(3x+2y = 6\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(\frac{x}{3} + \frac{y}{2} = 1\)বা, \(\frac{2x+3y}{6} = 1\)
বা, \(2x+3y = 6\) — (iv)
(iii) নং সমীকরণকে 3 দ্বারা এবং (iv) নং সমীকরণকে 2 দ্বারা গুণ করে পাই,
\(9x+6y = 18\) — (v)
এবং \(4x+6y = 12\) — (vi)
(v) ও (vi) নং সমীকরণকে বিয়োগ করে পাই,
\((9x+6y) – (4x+6y) = 18-12\)বা, \(9x+6y -4x-6y = 6\)
বা, \(5x = 6\)
বা, \(x = \frac{6}{5}\)
বা, \(x = 1\frac{1}{5}\)
\(x\)-এর মান (v) নং সমীকরণে বসিয়ে পাই,
\(9x+6y = 18\)বা, \(9(1\frac{1}{5}) +6y = 18\)
বা, \(9(\frac{6}{5}) +6y = 18\)
বা, \(\frac{54}{5} + 6y = 18\)
বা, \(6y = 18 – \frac{54}{5}\)
বা, \(6y = \frac{90-54}{5}\)
বা, \(6y = \frac{36}{5}\)
বা, \(y = \frac{36}{5 \times 6}\)
বা, \(y = \frac{6}{5}\)
বা, \(y = 1\frac{1}{5}\)
∴ নির্ণেয় সমাধান \(x=1\frac{1}{5}\), \(y = 1\frac{1}{5}\)
(vii) \(\frac{x+y}{2} + \frac{3x-5y}{4} = 2\), \(\frac{x}{14} + \frac{y}{18} = 1\)
সমাধান –
প্রদত্ত সমীকরণদ্বয় হল –
\(\frac{x+y}{2} + \frac{3x-5y}{4} = 2\) — (i)
এবং \(\frac{x}{14} + \frac{y}{18} = 1\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(\frac{x+y}{2} + \frac{3x-5y}{4} = 2\)বা, \(\frac{2(x+y)+3x-5y}{4} = 2\)
বা, \(2x+2y+3x-5y = 8\)
বা, \(5x -3y = 8\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(\frac{x}{14} + \frac{y}{18} = 1\)বা, \(\frac{9x+7y}{126} = 1\)
বা, \(9x+7y = 126\) — (iv)
(iii) নং সমীকরণকে 7 দ্বারা ও (iv) নং সমীকরণকে 3 দ্বারা গুণ করে পাই,
\(35x-21y = 56\) — (v)
\(27x + 21y = 378\) — (vi)
(v) নং ও (vi) নং সমীকরণ যোগ করে পাই,
\(35x-21y + 27x + 21y = 56+378\)বা, \(62x = 434\)
বা, \(x = \frac{434}{62}\)
বা, \(x = 7\)
\(x\) এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(5(7) -3y = 8\)বা, \(35 -3y = 8\)
বা, \(35 – 8 =3y\)
বা, \(3y = 27\)
বা, \(y = \frac{27}{3}\)
বা, \(y = 9\)
∴ নির্ণেয় সমাধান \(x = 7\) এবং \(y = 9\)
(viii) \(\frac{xy}{x+y} = \frac{1}{5}\), \(\frac{xy}{x-y} = \frac{1}{9}\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(\frac{xy}{x+y} = \frac{1}{5}\) — (i)
\(\frac{xy}{x-y} = \frac{1}{9}\) — (ii)
(i) নং সমীকরণের বিপরীত (অনোন্যক) নিয়ে পাই,
\(\frac{x+y}{xy} = 5\)বা, \(\frac{x}{xy} + \frac{y}{xy} = 5\)
বা, \(\frac{1}{y} + \frac{1}{x} = 5\) — (iii)
(ii) নং সমীকরণের বিপরীত (অনোন্যক) নিয়ে পাই,
\(\frac{x-y}{xy} = 9\)বা, \(\frac{x}{xy} – \frac{y}{xy} = 9\)
বা, \(\frac{1}{y} – \frac{1}{x} = 9\) — (iv)
(iii) নং ও (iv) নং সমীকরণ যোগ করে পাই,
\(\frac{1}{y} + \frac{1}{x} + \frac{1}{y} – \frac{1}{x} = 9 + 5\)বা, \(\frac{2}{y} = 14\)
বা, \(y = \frac{2}{14}\)
বা, \(y = \frac{1}{7}\)
\(y\)-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(\frac{1}{y} + \frac{1}{x} = 5\)বা, \(\frac{1}{\frac{1}{7}} + \frac{1}{x} = 5\)
বা, \(7 + \frac{1}{x} = 5\)
বা, \(\frac{1}{x} = 5 – 7\)
বা, \(\frac{1}{x} = -2\)
বা, \(x = -\frac{1}{2}\)
∴ নির্ণেয় সমাধান \(x = -\frac{1}{2}\) এবং \(y = \frac{1}{7}\)
(ix) \(\frac{1}{x-1} + \frac{1}{y-2} = 3\), \(\frac{2}{x-1} + \frac{3}{y-2} = 5\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(\frac{1}{x-1} + \frac{1}{y-2} = 3\) — (i)
\(\frac{2}{x-1} + \frac{3}{y-2} = 5\) — (ii)
(i) নং সমীকরণকে 3 দ্বারা গুণ করে পাই,
\(\frac{3}{x-1} + \frac{3}{y-2} = 9\) — (iii)
(ii) নং ও (iii) নং সমীকরণ বিয়োগ করে পাই,
\(\frac{2}{x-1} + \frac{3}{y-2} – \frac{3}{x-1} – \frac{3}{y-2} = 5 – 9\)বা, \(-\frac{1}{x-1} = -4\)
বা, \(\frac{1}{x-1} = 4\)
বা, \(x-1 = \frac{1}{4}\)
বা, \(x = 1+\frac{1}{4}\)
বা, \(x = \frac{5}{4}\)
বা, \(x = 1\frac{1}{4}\)
\(x-1\)–এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই,
\(\frac{1}{x-1} + \frac{1}{y-2} = 3\)বা, \(\frac{1}{\frac{1}{4}} + \frac{1}{y-2} = 3\)
বা, \(4 + \frac{1}{y-2} = 3\)
বা, \(\frac{1}{y-2} = 3-4\)
বা, \(\frac{1}{y-2} = -1\)
বা, \(y-2 = -1\)
বা, \(y = 2-1\)
বা, \(y = 1\)
∴ নির্ণেয় সমাধান \(x = 1\frac{1}{4}\) এবং \(y = 1\)
(x) \(\frac{14}{x+y} + \frac{3}{x-y} = 5\), \(\frac{21}{x+y} – \frac{1}{x-y} = 2\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(\frac{14}{x+y} + \frac{3}{x-y} = 5\) — (i)
\(\frac{21}{x+y} – \frac{1}{x-y} = 2\) — (ii)
(ii) নং সমীকরণকে 3 দ্বারা গুণ করে পাই,
\(\frac{63}{x+y} – \frac{3}{x-y} = 6\) — (iii)
(i) নং ও (iii) নং সমীকরণ যোগ করে পাই,
\(\frac{14}{x+y} + \frac{3}{x-y} + \frac{63}{x+y} – \frac{3}{x-y} = 5+6\)বা, \(\frac{77}{x+y} = 11\)
বা, \(x+y = \frac{77}{11}\)
বা, \(x+y = 7\) — (iv)
\((x+y)\)–এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই,
\(\frac{14}{x+y} + \frac{3}{x-y} = 5\)বা, \(\frac{14}{7} + \frac{3}{x-y} = 5\)
বা, \(2 + \frac{3}{x-y} = 5\)
বা, \(\frac{3}{x-y} = 5-2\)
বা, \(\frac{3}{x-y} = 3\)
বা, \(x-y = \frac{3}{3}\)
বা, \(x-y = 1\) — (v)
(iv) নং ও (v) নং সমীকরণ যোগ করে পাই,
\(x+y + x-y = 7+1\)বা, \(2x = 8\)
বা, \(x = \frac{8}{2}\)
বা, \(x = 4\)
\(x\)–এর প্রাপ্ত মান (iv) নং সমীকরণে বসিয়ে পাই,
\(4+y = 7\)বা, \(y = 7-4\)
বা, \(y = 3\)
∴ নির্ণেয় সমাধান \(x = 4\) এবং \(y = 3\)
(xi) \(\frac{x+y}{5} – \frac{x-y}{4} = \frac{7}{20}\), \(\frac{x+y}{3} – \frac{x-y}{2} + \frac{5}{6} = 0\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(\frac{x+y}{5} – \frac{x-y}{4} = \frac{7}{20}\) — (i)
\(\frac{x+y}{3} – \frac{x-y}{2} + \frac{5}{6} = 0\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(\frac{x+y}{5} – \frac{x-y}{4} = \frac{7}{20}\)বা, \(\frac{4(x+y)-5(x-y)}{20} = \frac{7}{20}\)
বা, \(4x+4y-5x+5y = 7\)
বা, \(9y – x = 7\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(\frac{x+y}{3} – \frac{x-y}{2} + \frac{5}{6} = 0\)বা, \(\frac{2(x+y)-3(x-y)+5}{6} = 0\)
বা, \(2x+2y-3x+3y +5=0\)
বা, \(5y – x = -5\) — (iv)
(iii) নং ও (iv) নং সমীকরণ বিয়োগ করে পাই,
\((9y-x)- (5y-x) = 7-(-5)\)বা, \(9y – x – 5y + x = 7+5\)
বা, \(4y = 12\)
বা, \(y = \frac{12}{4}\)
বা, \(y = 3\)
\(y\)–এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(9y-x =7\)বা, \(9(3) – x =7\)
বা, \(27 – x = 7\)
বা, \(x = 27-7\)
বা, \(x = 20\)
∴ নির্ণেয় সমাধান \(x = 20\) এবং \(y = 3\)
(xii) \(x+y = a+b\), \(ax-by = a^2-b^2\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(x+y = a+b\) — (i)
\(ax-by = a^2-b^2\) — (ii)
(i) নং সমীকরণকে \(b\) দ্বারা গুণ করে পাই,
\(bx + by = ab+b^2\) — (iii)
(ii) ও (iii) নং সমীকরণ যোগ করে পাই,
\(ax-by + bx + by = a^2-b^2 + ab+b^2\)বা, \(ax+bx = a^2+ab\)
বা, \(x(a+b) = a(a+b)\)
বা, \(x = a\) [ উভয়পক্ষে \((a+b)\) দ্বারা ভাগ করে পাই ]
\(x\)-এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই,
\(x+y = a+b\)বা, \(a+y = a+b\)
বা, \(y = a+b-a\)
বা, \(y = b\)
∴ নির্ণেয় সমাধান \(x = a\) এবং \(y = b\)
(xiii) \(\frac{x+a}{a} = \frac{y+b}{b}\), \(ax – by = a^2-b^2\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(\frac{x+a}{a} = \frac{y+b}{b}\) — (i)
\(ax – by = a^2-b^2\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(\frac{x+a}{a} = \frac{y+b}{b}\)বা, \(b(x+a) = a(y+b)\)
বা, \(bx + ab = ay + ab\)
বা, \(bx – ay = 0\) — (iii)
(ii) নং সমীকরণকে \(a\) দ্বারা এবং (iii) নং সমীকরণকে \(b\) দ্বারা গুণ করে পাই,
\(a^2x – aby = a^3 – ab^2\) — (iv)
\(b^2x – aby = 0\) — (v)
(iv) ও (v) নং সমীকরণ বিয়োগ করে পাই,
\((a^2x – aby) – (b^2x – aby) = a^3 – ab^2\)বা, \(a^2x – aby – b^2x + aby = a^3 – ab^2\)
বা, \(a^2x – b^2x = a(a^2 – b^2)\)
বা, \(x(a^2 – b^2) = a(a^2 – b^2)\)
বা, \(x = a\) [ উভয়পক্ষে \((a^2 – b^2)\) দ্বারা ভাগ করে পাই ]
\(x\)-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(b(a) – ay = 0\)বা, \(ab = ay\)
বা, \(y = b\)
∴ নির্ণেয় সমাধান \(x = a\) এবং \(y = b\)
(xiv) \(ax+by =c\), \(a^2x+b^2y =c^2\)
সমাধানঃ প্রদত্ত সহ-সমীকরণদ্বয় হল–
\(ax+by =c\) — (i)
\(a^2x+b^2y =c^2\) — (ii)
(i) নং সমীকরণকে \(b\) দ্বারা গুণ করে পাই,
\(abx +b^2y = bc\) — (iii)
(ii) নং ও (iii) নং সমীকরণ বিয়োগ করে পাই,
\((a^2x+b^2y)-( abx +b^2y ) = c^2 -bc\)বা, \(a^2x +b^2y -abx-b^2y = c^2-bc\)
বা, \(a^2x -abx = c^2-bc\)
বা, \(ax (a-b) = c(c-b)\)
বা, \(x = \frac{c(c-b)}{a(a-b)}\)
\(x\) –এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই,
\(ax+by =c\)বা, \(a \cdot \frac{c(c-b)}{a(a-b)} + by = c\)
বা, \(\frac{c(c-b)}{(a-b)} + by = c\)
বা, \(by = c – \frac{c(c-b)}{(a-b)}\)
বা, \(by = \frac{c(a-b) – c(c-b)}{(a-b)}\)
বা, \(by = \frac{c(a-b-c+b)}{(a-b)}\)
বা, \(by = \frac{c(a-c)}{(a-b)}\)
বা, \(y = \frac{c(a-c)}{b(a-b)}\)
∴ নির্ণেয় সমাধান \(x = \frac{c(c-b)}{a(a-b)}\) এবং \(y = \frac{c(a-c)}{b(a-b)}\)
(xv) \(ax+by = 1\), \(bx+ay = \frac{(a+b)^2}{a^2+b^2} – 1\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল–
\(ax+by = 1\) — (i)
\(bx+ay = \frac{(a+b)^2}{a^2+b^2} – 1\) — (ii)
(i) নং সমীকরণকে \(a\) দ্বারা গুণ করে পাই,
\(a^2x + aby = a\) — (iii)
(ii) নং সমীকরণকে \(b\) দ্বারা গুণ করে পাই,
\(b^2x + aby = \frac{b(a+b)^2}{a^2+b^2} – b\) — (iv)
(iii) নং ও (iv) নং সমীকরণ বিয়োগ করে পাই,
\((a^2x + aby) – (b^2x + aby) = a – \frac{b(a+b)^2}{a^2+b^2} + b\)বা, \(a^2x – b^2x = a + b – \frac{b(a+b)^2}{a^2+b^2}\)
বা, \(x(a^2 – b^2) = \frac{(a+b)(a^2+b^2) – b(a+b)^2}{a^2+b^2}\)
বা, \(x(a^2 – b^2) = \frac{(a+b)\left[ (a^2+b^2) – b(a+b) \right]}{a^2+b^2}\)
বা, \(x(a^2 – b^2) = \frac{(a+b)(a^2+b^2 – ab – b^2)}{a^2+b^2}\)
বা, \(x(a^2 – b^2) = \frac{(a+b)(a^2 – ab)}{a^2+b^2}\)
বা, \(x(a^2 – b^2) = \frac{a(a+b)(a-b)}{a^2+b^2}\)
বা, \(x = \frac{a(a+b)(a-b)}{(a^2+b^2)(a^2-b^2)}\)
বা, \(x = \frac{a(a+b)(a-b)}{(a^2+b^2)(a-b)(a+b)}\)
বা, \(x = \frac{a}{a^2+b^2}\)
\(x\) এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই,
\(ax+by = 1\)বা, \(a \cdot \frac{a}{a^2+b^2} + by = 1\)
বা, \(\frac{a^2}{a^2+b^2} + by = 1\)
বা, \(by = 1 – \frac{a^2}{a^2+b^2}\)
বা, \(by = \frac{a^2+b^2 – a^2}{a^2+b^2}\)
বা, \(by = \frac{b^2}{a^2+b^2}\)
বা, \(y = \frac{b}{a^2+b^2}\)
∴ নির্ণেয় সমাধান \(x = \frac{a}{a^2+b^2}\), \(y = \frac{b}{a^2+b^2}\)
(xvi) \((7x-y-6)^2+(14x+2y-16)^2 =0\)
সমাধান –
প্রদত্ত সমীকরণটি হল – \((7x-y-6)^2+(14x+2y-16)^2 =0\)
দুটি বর্গ রাশির সমষ্টি শূন্য।
∴ তারা আলাদা আলাদাভাবে শূন্য।
∴ \(7x-y-6 = 0\) — (i)
এবং \(14x+2y-16 = 0\) — (ii)
(i) নং সমীকরণকে 2 দ্বারা গুণ করে পাই,
\(14x -2y -12 = 0\) — (iii)
(ii) নং ও (iii) নং সমীকরণ যোগ করে পাই,
\(14x+2y-16 + 14x-2y-12 = 0\)বা, \(28x -28 = 0\)
বা, \(28x = 28\)
বা, \(x = \frac{28}{28}\)
বা, \(x = 1\)
\(x\) এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই,
\(7(1) – y – 6 = 0\)বা, \(7 – 6 – y = 0\)
বা, \(1 – y = 0\)
বা, \(y = 1\)
∴ নির্ণেয় সমাধান \(x = 1\) এবং \(y = 1\)
এই আর্টিকেলে নবম শ্রেণির গণিতের ‘রৈখিক সহসমীকরণ (দুই চল বিশিষ্ট)’ অধ্যায়ের ‘কষে দেখি – 5.3’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন