পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) নবম শ্রেণির গণিত পাঠ্যবইয়ের পঞ্চম অধ্যায় হলো ‘রৈখিক সহসমীকরণ (দুই চল বিশিষ্ট)’। এই পোস্টে ‘কষে দেখি – 5.4‘-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. \(\frac{x}{3} + \frac{y}{2} = 8\) সমীকরণের \(x\)-কে \(y\) চলের মাধ্যমে প্রকাশ করি।
সমাধান –
\(\frac{x}{3} + \frac{y}{2} = 8\)বা, \(\frac{x}{3} = 8 – \frac{y}{2}\)
বা, \(x = 3\left(8 – \frac{y}{2}\right)\)
বা, \(x = 24 – \frac{3y}{2}\)
2. \(\frac{2}{x} + \frac{7}{y} = 1\) সমীকরণের \(y\)-কে \(x\) চলের মাধ্যমে প্রকাশ করি।
সমাধান –
\(\frac{2}{x} + \frac{7}{y} = 1\)বা, \(\frac{7}{y} = 1 – \frac{2}{x}\)
বা, \(\frac{7}{y} = \frac{x-2}{x}\)
বা, \(\frac{y}{7} = \frac{x}{x-2}\)
বা, \(y = \frac{7x}{x-2}\)
3. নীচের সমীকরণগুলি তুলনামূলক পদ্ধতিতে সমাধান করি এবং সমাধানের মানগুলি সমীকরণকে সিদ্ধ করে কিনা যাচাই করি।
(a) \(2(x-y) = 3\), \(5x+8y = 14\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(2(x-y) = 3\) — (i)
\(5x+8y = 14\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(2(x-y) = 3\)বা, \(2x – 2y = 3\)
বা, \(2x = 3 + 2y\)
বা, \(x = \frac{3+2y}{2}\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(5x+8y = 14\)বা, \(5x = 14 – 8y\)
বা, \(x = \frac{14-8y}{5}\) — (iv)
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত \(x\)-এর মান তুলনা করে পাই,
\(\frac{3+2y}{2} = \frac{14-8y}{5}\)বা, \(5(3+2y) = 2(14-8y)\)
বা, \(15 + 10y = 28 – 16y\)
বা, \(10y + 16y = 28 – 15\)
বা, \(26y = 13\)
বা, \(y = \frac{13}{26}\)
বা, \(y = \frac{1}{2}\)
\(y\)-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(x = \frac{3+2 \times \frac{1}{2}}{2}\)বা, \(x = \frac{4}{2}\)
বা, \(x = 2\)
∴ নির্ণেয় সমাধান \(x = 2\) এবং \(y = \frac{1}{2}\)
\(x\) ও \(y\)-এর প্রাপ্ত মান প্রদত্ত সমীকরণে বসিয়ে পাই,
∴ নির্ণেয় সমাধানগুলি প্রদত্ত সমীকরণগুলোকে সিদ্ধ করছে।
(b) \(2x + \frac{3}{y} = 5\), \(5x – \frac{2}{y} = 3\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(2x + \frac{3}{y} = 5\) — (i)
\(5x – \frac{2}{y} = 3\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(2x + \frac{3}{y} = 5\)বা, \(2x = 5 – \frac{3}{y}\)
বা, \(2x = \frac{5y – 3}{y}\)
বা, \(x = \frac{5y – 3}{2y}\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(5x – \frac{2}{y} = 3\)বা, \(5x = 3 + \frac{2}{y}\)
বা, \(x = \frac{3y + 2}{5y}\) — (iv)
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত \(x\)-এর মান তুলনা করে পাই,
\(\frac{5y – 3}{2y} = \frac{3y + 2}{5y}\)বা, \(5y(5y – 3) = 2y(3y + 2)\)
বা, \(25y – 15 = 6y + 4\)
বা, \(25y – 6y = 15 + 4\)
বা, \(19y = 19\)
বা, \(y = \frac{19}{19}\)
বা, \(y = 1\)
\(y\)-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(x = \frac{5(1) – 3}{2(1)}\)বা, \(x = \frac{5 – 3}{2}\)
বা, \(x = \frac{2}{2}\)
বা, \(x = 1\)
∴ নির্ণেয় সমাধান \(x = 1\) এবং \(y = 1\)
এখন, \(2x + \frac{3}{y} = 2(1) + \frac{3}{1} = 2 + 3 = 5\)
আবার, \(5x – \frac{2}{y} = 5(1) – \frac{2}{1} = 5 – 2 = 3\)
∴ \(x\) ও \(y\)-এর প্রাপ্ত মান প্রদত্ত সহ-সমীকরণদ্বয়কে সিদ্ধ করে।
(c) \(\frac{x}{2} + \frac{y}{3} = 1\), \(\frac{x}{3} + \frac{y}{2} = 1\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(\frac{x}{2} + \frac{y}{3} = 1\) — (i)
এবং \(\frac{x}{3} + \frac{y}{2} = 1\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(\frac{x}{2} + \frac{y}{3} = 1\)বা, \(\frac{x}{2} = 1 – \frac{y}{3}\)
বা, \(\frac{x}{2} = \frac{3-y}{3}\)
বা, \(x = \frac{6-2y}{3}\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(\frac{x}{3} + \frac{y}{2} = 1\)বা, \(\frac{x}{3} = 1 – \frac{y}{2}\)
বা, \(x = \frac{3(2-y)}{2}\)
বা, \(x = \frac{6-3y}{2}\) — (iv)
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত \(x\)-এর মান তুলনা করে পাই,
\(\frac{6-2y}{3} = \frac{6-3y}{2}\)বা, \(2(6-2y) = 3(6-3y)\)
বা, \(12 – 4y = 18 – 9y\)
বা, \(9y – 4y = 18 – 12\)
বা, \(5y = 6\)
বা, \(y = \frac{6}{5}\)
বা, \(y = 1\frac{1}{5}\)
\(y\)-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(x = \frac{6-2y}{3}\)বা, \(x = \frac{6 – 2 \times \frac{6}{5}}{3}\)
বা, \(x = \frac{6 – \frac{12}{5}}{3}\)
বা, \(x = \frac{\frac{30-12}{5}}{3}\)
বা, \(x = \frac{18}{15}\)
বা, \(x = \frac{6}{5}\)
বা, \(x = 1\frac{1}{5}\)
∴ নির্ণেয় সমাধান \(x = 1\frac{1}{5}\) এবং \(y = 1\frac{1}{5}\)
এখন, \(\frac{x}{2} + \frac{y}{3}\)
= \( \frac{1\frac{1}{5}}{2} + \frac{1\frac{1}{5}}{3}\)
= \( \frac{6}{10} + \frac{6}{15}\)
= \( \frac{18+12}{30}\)
= \( \frac{30}{30}\)
= \( 1\)
এবং \(\frac{x}{3} + \frac{y}{2}\)
= \( \frac{1\frac{1}{5}}{3} + \frac{1\frac{1}{5}}{2}\)
= \( \frac{6}{15} + \frac{6}{10}\)
= \( \frac{12+18}{30}\)
= \( \frac{30}{30}\)
= \( 1\)
∴ \(x\) ও \(y\)-এর প্রাপ্ত মান প্রদত্ত সহ-সমীকরণদ্বয়কে সিদ্ধ করে।
(d) \(4x -3y = 18\), \(4y -5x = -7\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(4x -3y = 18\) — (i)
\(4y -5x = -7\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(4x -3y = 18\)বা, \(4x = 18+3y\)
বা, \(x = \frac{18+3y}{4}\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(4y -5x = -7\)বা, \(4y +7 = 5x\)
বা, \(x = \frac{4y+7}{5}\) — (iv)
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত \(x\)-এর মান তুলনা করে পাই,
\(\frac{18+3y}{4} = \frac{4y+7}{5}\)বা, \(5(18+3y) = 4(4y+7)\)
বা, \(90 + 15y = 16y +28\)
বা, \(15y-16y = 28 -90\)
বা, \(-y = -62\)
বা, \(y = 62\)
\(y\)-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(x = \frac{18+3(62)}{4}\)বা, \(x = \frac{18+186}{4}\)
বা, \(x = \frac{204}{4}\)
বা, \(x = 51\)
∴ নির্ণেয় সমাধান \(x = 51\) এবং \(y = 62\)
এখন, \(4x -3y = 4(51) -3(62) = 204 – 186 = 18\)
আবার, \(4y -5x = 4(62) – 5(51) = 248 – 255 = -7\)
∴ \(x\) ও \(y\)-এর প্রাপ্ত মান প্রদত্ত সহ-সমীকরণদ্বয়কে সিদ্ধ করে।
4. \(2x+y = 8\) ও \(2y -3x = -5\) সমীকরণগুলি তুলনামূলক পদ্ধতিতে সমাধান করি ও লেখচিত্রের সাহায্যে সমাধান করে যাচাই করি।
সমাধানঃ প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(2x+y = 8\) — (i)
\(2y -3x = -5\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(2x = 8-y\)বা, \(x = \frac{8-y}{2}\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(2y -3x = -5\)বা, \(2y +5 = 3x\)
বা, \(x = \frac{2y+5}{3}\) — (iv)
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত \(x\)-এর মান তুলনা করে পাই,
\(\frac{8-y}{2} = \frac{2y+5}{3}\)বা, \(3(8-y) = 2(2y+5)\)
বা, \(24 – 3y = 4y +10\)
বা, \(-3y -4y = 10-24\)
বা, \(-7y = -14\)
বা, \(y = \frac{-14}{-7}\)
বা, \(y = 2\)
\(y\)–এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(x = \frac{8-2}{2}\)বা, \(x = \frac{6}{2}\)
বা, \(x = 3\)
∴ নির্ণেয় সমাধান \(x = 3\) এবং \(y = 2\)
লেখচিত্রের মাধ্যমে সমাধান –
\(2x+y = 8\)বা, \(2x = 8-y\)
বা, \(x = \frac{8-y}{2}\)
| x | 0 | 2 | 1 |
| y | 8 | 4 | 6 |
বা, \(2y +5 = 3x\)
বা, \(x = \frac{2y+5}{3}\)
| x | 5 | 7 | 9 |
| y | 5 | 8 | 11 |
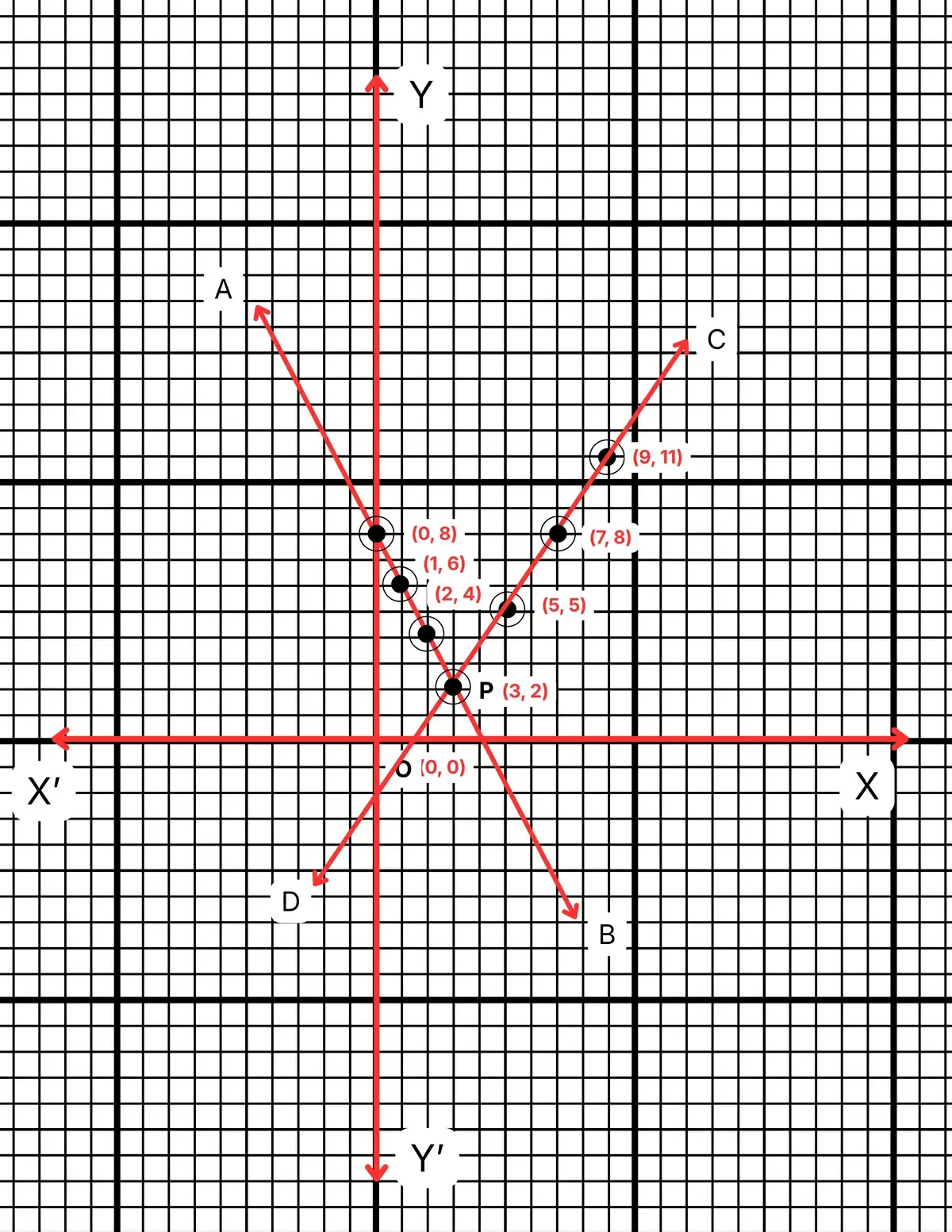
ছক কাগজে \(XOX’\) এবং \(YOY’\) যথাক্রমে পরস্পর লম্ব দুটি অক্ষ। ছক কাগজের প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের প্রতিটি বাহুকে 1 একক ধরে \((0,8)\), \((2,4)\) এবং \((1,6)\) বিন্দুগুলি স্থাপন করে এবং যুক্ত করে \(AB\) সরলরেখা এবং \((5,5)\), \((7,8)\) ও \((9,11)\) বিন্দুগুলি স্থাপন করে এবং যুক্ত করে \(CD\) সরলরেখা অঙ্কন করা হল। \(AB\) ও \(CD\) সরলরেখা পরস্পরকে \(P\) বিন্দুতে ছেদ করে। \(P\) বিন্দুর স্থানাঙ্ক \((3,2)\)। সুতরাং নির্ণেয় সমাধান \(x = 3\) এবং \(y = 2\)।
সুতরাং তুলনামূলক পদ্ধতিতে নির্ণেয় সমাধান এবং লেখচিত্রের মাধ্যমে নির্ণেয় সমাধান সমান। [প্রমাণিত]
5. নীচের দুইচল বিশিষ্ট সমীকরণগুলি তুলনামূলক পদ্ধতিতে সমাধান করিঃ
(i) \(3x -2y = 2\), \(7x+3y = 43\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(3x -2y = 2\) — (i)
\(7x+3y = 43\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(3x – 2y = 2\)বা, \(3x = 2y +2\)
বা, \(x = \frac{2y+2}{3}\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(7x+3y = 43\)বা, \(7x = 43 -3y\)
বা, \(x = \frac{43-3y}{7}\) — (iv)
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত \(x\)-এর মান তুলনা করে পাই,
\(\frac{2y+2}{3} = \frac{43-3y}{7}\)বা, \(7(2y+2) = 3(43-3y)\)
বা, \(14y +14 = 129 -9y\)
বা, \(14y+9y = 129-14\)
বা, \(23y = 115\)
বা, \(y = \frac{115}{23}\)
বা, \(y = 5\)
\(y\)-এর মান (iii) নং সমীকরণে বসিয়ে পাই,
\(x = \frac{2y+2}{3}\)বা, \(x = \frac{2(5)+2}{3}\)
বা, \(x = \frac{12}{3}\)
বা, \(x = 4\)
∴ নির্ণেয় সমাধান \(x = 4\) এবং \(y = 5\)
(ii) \(2x-3y = 8\), \(\frac{x+y}{x-y} = \frac{7}{3}\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(2x-3y = 8\) — (i)
\(\frac{x+y}{x-y} = \frac{7}{3}\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(2x-3y = 8\)বা, \(2x = 8+3y\)
বা, \(x = \frac{8+3y}{2}\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(\frac{x+y}{x-y} = \frac{7}{3}\)বা, \(3(x+y) = 7(x-y)\)
বা, \(3x+3y = 7x-7y\)
বা, \(3x-7x = -3y-7y\)
বা, \(-4x = -10y\)
বা, \(x = \frac{5y}{2}\) — (iv)
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত \(x\)-এর মান তুলনা করে পাই,
\(\frac{8+3y}{2} = \frac{5y}{2}\)বা, \(8+3y = 5y\)
বা, \(8 = 5y-3y\)
বা, \(8 = 2y\)
বা, \(y = \frac{8}{2}\)
বা, \(y = 4\)
\(y\)-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(x = \frac{8+3y}{2}\)বা, \(x = \frac{8+3(4)}{2}\)
বা, \(x = \frac{20}{2}\)
বা, \(x = 10\)
∴ নির্ণেয় সমাধান \(x = 10\) এবং \(y = 4\)
(iii) \(\frac{1}{3}(x-y) = \frac{1}{4}(y-1)\), \(\frac{1}{7}(4x-5y) = x-7\)
সমাধান –
প্রদত্ত সমীকরণদ্বয় হল –
\(\frac{1}{3}(x-y) = \frac{1}{4}(y-1)\) — (i)
\(\frac{1}{7}(4x-5y) = x-7\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(\frac{1}{3}(x-y) = \frac{1}{4}(y-1)\)বা, \(4(x-y) = 3(y-1)\)
বা, \(4x-4y = 3y-3\)
বা, \(4x = 4y+3y-3\)
বা, \(4x = 7y -3\)
বা, \(x = \frac{7y-3}{4}\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(\frac{1}{7}(4x-5y) = x-7\)বা, \(4x-5y = 7(x-7)\)
বা, \(4x-5y = 7x-49\)
বা, \(4x-7x = 5y-49\)
বা, \(-3x = 5y-49\)
বা, \(3x = 49-5y\)
বা, \(x = \frac{49-5y}{3}\) — (iv)
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত \(x\)-এর মান তুলনা করে পাই,
\(\frac{7y-3}{4} = \frac{49-5y}{3}\)বা, \(3(7y-3) = 4(49-5y)\)
বা, \(21y -9 = 196 -20y\)
বা, \(21y +20y = 196 +9\)
বা, \(41y = 205\)
বা, \(y = \frac{205}{41}\)
বা, \(y = 5\)
\(y\)-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(x = \frac{7y-3}{4}\)বা, \(x = \frac{7(5)-3}{4}\)
বা, \(x = \frac{35-3}{4}\)
বা, \(x = \frac{32}{4}\)
বা, \(x = 8\)
∴ নির্ণেয় সমাধান \(x = 8\) এবং \(y = 5\)
(iv) \(\frac{x+1}{y+1} = \frac{4}{5}\), \(\frac{x-5}{y-5} = \frac{1}{2}\)
সমাধান –
প্রদত্ত সমীকরণদ্বয় হল –
\(\frac{x+1}{y+1} = \frac{4}{5}\) — (i)
\(\frac{x-5}{y-5} = \frac{1}{2}\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(\frac{x+1}{y+1} = \frac{4}{5}\)বা, \(5(x+1) = 4(y+1)\)
বা, \(5x+5 = 4y+4\)
বা, \(5x = 4y+4-5\)
বা, \(5x = 4y-1\)
বা, \(x = \frac{4y-1}{5}\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(\frac{x-5}{y-5} = \frac{1}{2}\)বা, \(2(x-5) = y-5\)
বা, \(2x-10 = y-5\)
বা, \(2x = 10+y-5\)
বা, \(2x = 5+y\)
বা, \(x = \frac{5+y}{2}\) — (iv)
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত \(x\)-এর মান তুলনা করে পাই,
\(\frac{4y-1}{5} = \frac{5+y}{2}\)বা, \(2(4y-1) = 5(5+y)\)
বা, \(8y-2 = 25+5y\)
বা, \(8y-5y = 25+2\)
বা, \(3y = 27\)
বা, \(y = \frac{27}{3}\)
বা, \(y = 9\)
\(y\)-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(x = \frac{4y-1}{5}\)বা, \(x = \frac{4(9)-1}{5}\)
বা, \(x = \frac{35}{5}\)
বা, \(x = 7\)
∴ নির্ণেয় সমাধান \(x = 7\) এবং \(y = 9\)
(v) \(x+y = 11\), \(y+2 = \frac{1}{8}(10y+x)\)
সমাধান –
প্রদত্ত সমীকরণদ্বয় হল –
\(x+y = 11\) — (i)
\(y+2 = \frac{1}{8}(10y+x)\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(x = 11-y\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(y+2 = \frac{1}{8}(10y+x)\)বা, \(8(y+2) = 10y + x\)
বা, \(8y + 16 = 10y+x\)
বা, \(16 -2y = x\)
বা, \(x = 16-2y\) — (iv)
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত \(x\)-এর মান তুলনা করে পাই,
\(11-y = 16-2y\)বা, \(2y-y = 16-11\)
বা, \(y = 5\)
\(y\)-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(x = 11-5\)বা, \(x = 6\)
∴ নির্ণেয় সমাধান \(x = 6\) এবং \(y = 5\)
(vi) \(\frac{x}{3} + \frac{y}{4} = 1\), \(2x+4y=11\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(\frac{x}{3} + \frac{y}{4} = 1\) — (i)
\(2x+4y = 11\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(\frac{x}{3} + \frac{y}{4} = 1\)বা, \(\frac{x}{3} = 1 – \frac{y}{4}\)
বা, \(\frac{x}{3} = \frac{4-y}{4}\)
বা, \(x = \frac{3(4-y)}{4}\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(2x+4y = 11\)বা, \(2x = 11-4y\)
বা, \(x = \frac{11-4y}{2}\) — (iv)
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত \(x\)-এর মান তুলনা করে পাই,
\(\frac{3(4-y)}{4} = \frac{11-4y}{2}\)বা, \(6(4-y) = 4(11-4y)\)
বা, \(24-6y = 44 -16y\)
বা, \(24-44 = 6y-16y\)
বা, \(-20 = -10y\)
বা, \(y = \frac{-20}{-10}\)
বা, \(y = 2\)
\(y\)-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(x = \frac{3(4-y)}{4}\)বা, \(x = \frac{3(4-2)}{4}\)
বা, \(x = \frac{6}{4}\)
বা, \(x = \frac{3}{2}\)
∴ নির্ণেয় সমাধান \(x = \frac{3}{2}\) এবং \(y = 2\)
(vii) \(x + \frac{2}{y} = 7\), \(2x – \frac{6}{y} = 9\)
সমাধান – প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(x + \frac{2}{y} = 7\) — (i)
\(2x – \frac{6}{y} = 9\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(x + \frac{2}{y} = 7\)বা, \(x = 7 – \frac{2}{y}\)
বা, \(x = \frac{7y-2}{y}\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(2x – \frac{6}{y} = 9\)বা, \(2x = 9 + \frac{6}{y}\)
বা, \(x = \frac{9y+6}{2y}\) — (iv)
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত \(x\)-এর মান তুলনা করে পাই,
\(\frac{7y-2}{y} = \frac{9y+6}{2y}\)বা, \(\frac{7y-2}{1} = \frac{9y+6}{2}\)
বা, \(2(7y-2) = 9y+6\)
বা, \(14y – 4 = 9y+6\)
বা, \(14y – 9y = 4+6\)
বা, \(5y = 10\)
বা, \(y = \frac{10}{5}\)
বা, \(y = 2\)
\(y\)-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(x = \frac{7y-2}{y}\)বা, \(x = \frac{7(2)-2}{2}\)
বা, \(x = \frac{14-2}{2}\)
বা, \(x = \frac{12}{2}\)
বা, \(x = 6\)
∴ নির্ণেয় সমাধান \(x = 6\) এবং \(y = 2\)
(viii) \(\frac{1}{x} + \frac{1}{y} = \frac{5}{6}\), \(\frac{1}{x} – \frac{1}{y} = \frac{1}{6}\)
সমাধান – প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(\frac{1}{x} + \frac{1}{y} = \frac{5}{6}\) — (i)
\(\frac{1}{x} – \frac{1}{y} = \frac{1}{6}\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(\frac{1}{x} + \frac{1}{y} = \frac{5}{6}\)বা, \(\frac{1}{x} = \frac{5}{6} – \frac{1}{y}\)
বা, \(\frac{1}{x} = \frac{5y-6}{6y}\)
বা, \(x = \frac{6y}{5y-6}\) [উভয়পক্ষে অনোন্যক নিয়ে পাই] — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(\frac{1}{x} – \frac{1}{y} = \frac{1}{6}\)বা, \(\frac{1}{x} = \frac{1}{6} + \frac{1}{y}\)
বা, \(\frac{1}{x} = \frac{y+6}{6y}\)
বা, \(x = \frac{6y}{y+6}\) [উভয়পক্ষে অনোন্যক নিয়ে পাই] — (iv)
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত \(x\)-এর মান তুলনা করে পাই,
\(\frac{6y}{5y-6} = \frac{6y}{y+6}\)বা, \(\frac{1}{5y-6} = \frac{1}{y+6}\)
বা, \(y+6 = 5y-6\)
বা, \(y-5y = -6-6\)
বা, \(-4y = -12\)
বা, \(y = \frac{-12}{-4}\)
বা, \(y = 3\)
\(y\)-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(x = \frac{6y}{y+6}\)বা, \(x = \frac{6(3)}{3+6}\)
বা, \(x = \frac{18}{9}\)
বা, \(x = 2\)
∴ নির্ণেয় সমাধান \(x = 2\) এবং \(y = 3\)
(ix) \(\frac{x+y}{xy}=2\), \(\frac{x-y}{xy}=1\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(\frac{x+y}{xy}=2\) — (i)
\(\frac{x-y}{xy}=1\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(\frac{x+y}{xy}=2\)বা, \(\frac{x}{xy} + \frac{y}{xy} = 2\)
বা, \(\frac{1}{y} + \frac{1}{x} = 2\)
বা, \(\frac{1}{x} = 2 – \frac{1}{y}\)
বা, \(\frac{1}{x} = \frac{2y-1}{y}\)
বা, \(x = \frac{y}{2y-1}\) [উভয়পক্ষে অনোন্যক নিয়ে পাই] — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(\frac{x-y}{xy}=1\)বা, \(\frac{x}{xy} – \frac{y}{xy} = 1\)
বা, \(\frac{1}{y} – \frac{1}{x} = 1\)
বা, \(\frac{1}{x} = \frac{1}{y} – 1\)
বা, \(\frac{1}{x} = \frac{1-y}{y}\)
বা, \(x = \frac{y}{1-y}\) [উভয়পক্ষে অনোন্যক নিয়ে পাই] — (iv)
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত \(x\)-এর মান তুলনা করে পাই,
\(\frac{y}{2y-1} = \frac{y}{1-y}\)বা, \(\frac{1}{2y-1} = \frac{1}{1-y}\)
বা, \(1-y = 2y-1\)
বা, \(-y-2y = -1-1\)
বা, \(-3y = -2\)
বা, \(y = \frac{2}{3}\)
\(y\)-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(x = \frac{y}{2y-1}\)বা, \(x = \frac{\frac{2}{3}}{2 \times \frac{2}{3} – 1}\)
বা, \(x = \frac{\frac{2}{3}}{\frac{4}{3} – 1}\)
বা, \(x = \frac{\frac{2}{3}}{\frac{1}{3}}\)
বা, \(x = \frac{2}{3} \div \frac{1}{3}\)
বা, \(x = \frac{2}{3} \times 3\)
বা, \(x = 2\)
∴ নির্ণেয় সমাধান \(x = 2\) এবং \(y = \frac{2}{3}\)
(x) \(\frac{x+y}{5} + \frac{x-y}{4} = 5\), \(\frac{x+y}{4} + \frac{x-y}{5} = 5\frac{4}{5}\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(\frac{x+y}{5} + \frac{x-y}{4} = 5\) — (i)
\(\frac{x+y}{4} + \frac{x-y}{5} = 5\frac{4}{5}\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(\frac{x+y}{5} + \frac{x-y}{4} = 5\)বা, \(\frac{4(x+y)+5(x-y)}{20} = 5\)
বা, \(4x+4y+5x-5y = 100\)
বা, \(9x – y = 100\)
বা, \(9x = 100+y\)
বা, \(x = \frac{100+y}{9}\) — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(\frac{x+y}{4} + \frac{x-y}{5} = 5\frac{4}{5}\)বা, \(\frac{5(x+y)+4(x-y)}{20} = \frac{29}{5}\)
বা, \(\frac{5x+5y+4x-4y}{20} = \frac{29}{5}\)
বা, \(\frac{9x+y}{20} = \frac{29}{5}\)
বা, \(5(9x+y) = 580\)
বা, \(9x+y = 116\)
বা, \(9x = 116 – y\)
বা, \(x = \frac{116-y}{9}\) — (iv)
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত \(x\) এর মান তুলনা করে পাই,
\(\frac{100+y}{9} = \frac{116-y}{9}\)বা, \(100+y = 116-y\)
বা, \(100 – 116 = -y-y\)
বা, \(-16 = -2y\)
বা, \(y = \frac{16}{2}\)
বা, \(y = 8\)
\(y\) এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(x = \frac{100+y}{9}\)বা, \(x = \frac{100+8}{9}\)
বা, \(x = \frac{108}{9}\)
বা, \(x = 12\)
∴ নির্ণেয় সমাধান \(x = 12\) এবং \(y = 8\)
(xi) \(\frac{4}{x} – \frac{y}{2} = -1\), \(\frac{8}{x} + 2y = 10\)
সমাধান –
প্রদত্ত সহ-সমীকরণদ্বয় হল –
\(\frac{4}{x} – \frac{y}{2} = -1\) — (i)
\(\frac{8}{x} + 2y = 10\) — (ii)
(i) নং সমীকরণ থেকে পাই,
\(\frac{4}{x} = \frac{y}{2} – 1\)বা, \(\frac{4}{x} = \frac{y-2}{2}\)
বা, \(\frac{x}{4} = \frac{2}{y-2}\)
বা, \(x = \frac{8}{y-2}\) [উভয়পক্ষে অনোন্যক নিয়ে পাই] — (iii)
(ii) নং সমীকরণ থেকে পাই,
\(\frac{8}{x} + 2y = 10\)বা, \(\frac{8}{x} = 10 – 2y\)
বা, \(\frac{x}{8} = \frac{1}{10-2y}\)
বা, \(x = \frac{8}{10-2y}\) [উভয়পক্ষে অনোন্যক নিয়ে পাই] — (iv)
(iii) নং ও (iv) নং সমীকরণ তুলনা করে পাই,
\(\frac{8}{y-2} = \frac{8}{10-2y}\)বা, \(10-2y = y-2\)
বা, \(10+2 = 2y+y\)
বা, \(3y = 12\)
বা, \(y = \frac{12}{3}\)
বা, \(y = 4\)
\(y\) এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(x = \frac{8}{y-2}\)বা, \(x = \frac{8}{4-2}\)
বা, \(x = \frac{8}{2}\)
বা, \(x = 4\)
∴ নির্ণেয় সমাধান \(x = 4\) এবং \(y = 4\)
(xii) \(2 – 2(3x-y) = 10(4-y) – 5x = 4(y-x)\)
সমাধান –
প্রদত্ত সমীকরণটি হল –
প্রথমত, \(2 – 2(3x-y) = 10(4-y) – 5x\)
দ্বিতীয়ত, \(10(4-y) – 5x = 4(y-x)\)
প্রথম সমীকরণ থেকে পাই,
\(2 – 2(3x-y) = 10(4-y) – 5x\)বা, \(2 – 6x + 2y = 40 – 10y – 5x\)
বা, \(10y+2y = 6x-5x+40-2\)
বা, \(12y = x + 38\)
বা, \(y = \frac{x+38}{12}\) — (iii)
দ্বিতীয় সমীকরণ থেকে পাই,
\(10(4-y) – 5x = 4(y-x)\)বা, \(40 – 10y – 5x = 4y – 4x\)
বা, \(-10y – 4y = 5x – 4x – 40\)
বা, \(-14y = x – 40\)
বা, \(y = \frac{x-40}{-14}\) — (iv)
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত \(y\) এর মান তুলনা করে পাই,
\(\frac{x+38}{12} = \frac{x-40}{-14}\)বা, \(\frac{x+38}{6} = \frac{x-40}{-7}\)
বা, \(7(x+38) = 6(40-x)\)
বা, \(7x + 266 = 240 – 6x\)
বা, \(7x + 6x = 240 – 266\)
বা, \(13x = -26\)
বা, \(x = \frac{-26}{13}\)
বা, \(x = -2\)
\(x\)-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই,
\(y = \frac{x+38}{12}\)বা, \(y = \frac{-2+38}{12}\)
বা, \(y = \frac{36}{12}\)
বা, \(y = 3\)
∴ নির্ণেয় সমাধান \(x = -2\) এবং \(y = 3\)
এই আর্টিকেলে নবম শ্রেণির গণিতের ‘রৈখিক সহসমীকরণ (দুই চল বিশিষ্ট)’ অধ্যায়ের ‘কষে দেখি – 5.4’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন