পশ্চিমবঙ্গ মধ্যশিক্ষা পর্ষদের (WBBSE) নবম শ্রেণির গণিত পাঠ্যবইয়ের পঞ্চম অধ্যায় হলো ‘রৈখিক সহসমীকরণ (দুই চল বিশিষ্ট)’। এই পোস্টে ‘কষে দেখি – 5.6‘-এর সমস্ত প্রশ্নের সমাধান দেওয়া হয়েছে। আশাকরি, এই নোটসগুলো তোমাদের গণিত পরীক্ষার প্রস্তুতিতে সহায়তা করবে।

1. \(8x+5y = 11\), \(3x-4y = 10\)
সমাধান –
প্রদত্ত সমীকরণদ্বয় হল –
\(8x+5y = 11\)বা, \(8x+5y-11=0 \quad -(i)\)
এবং, \(3x-4y = 10\)
বা, \(3x-4y-10=0 \quad -(ii)\)
(i) নং ও (ii) নং সমীকরণদ্বয়কে বজ্রগুণন করে পাই,
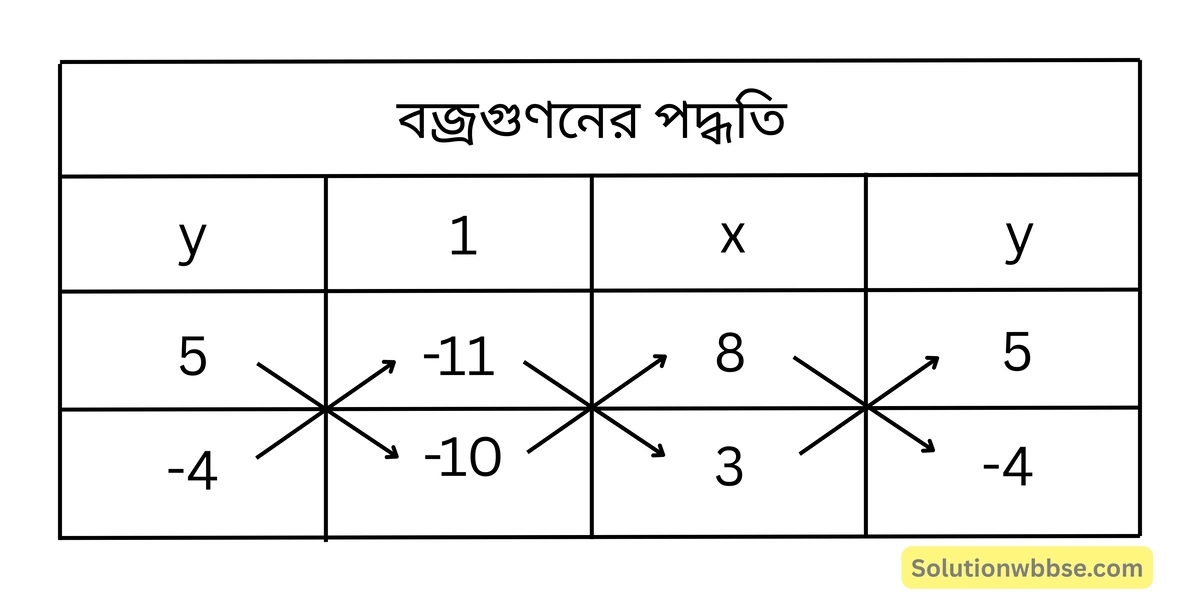
বা, \(\frac{x}{-50-44} = \frac{y}{-33+80} = \frac{1}{-32-15}\)
বা, \(\frac{x}{-94} = \frac{y}{47} = \frac{1}{-47}\)
সুতরাং, \(\frac{x}{-94} = \frac{1}{-47}\)
বা, \(x = \frac{-94}{-47}\)
বা, \(x = 2\)
এবং, \(\frac{y}{47} = \frac{1}{-47}\)
বা, \(y = \frac{-47}{47}\)
বা, \(y = -1\)
\(\therefore\) নির্ণেয় সমাধান \(x = 2\) এবং \(y = -1\)।
2. \(3x -4y = 1\), \(4x = 3y +6\)
সমাধান –
প্রদত্ত সমীকরণদ্বয় হল –
\(3x -4y = 1\)বা, \(3x -4y – 1 = 0 \quad -(i)\)
এবং, \(4x = 3y +6\)
বা, \(4x – 3y – 6 = 0 \quad -(ii)\)
(i) নং ও (ii) নং সমীকরণদ্বয়কে বজ্রগুণন করে পাই,
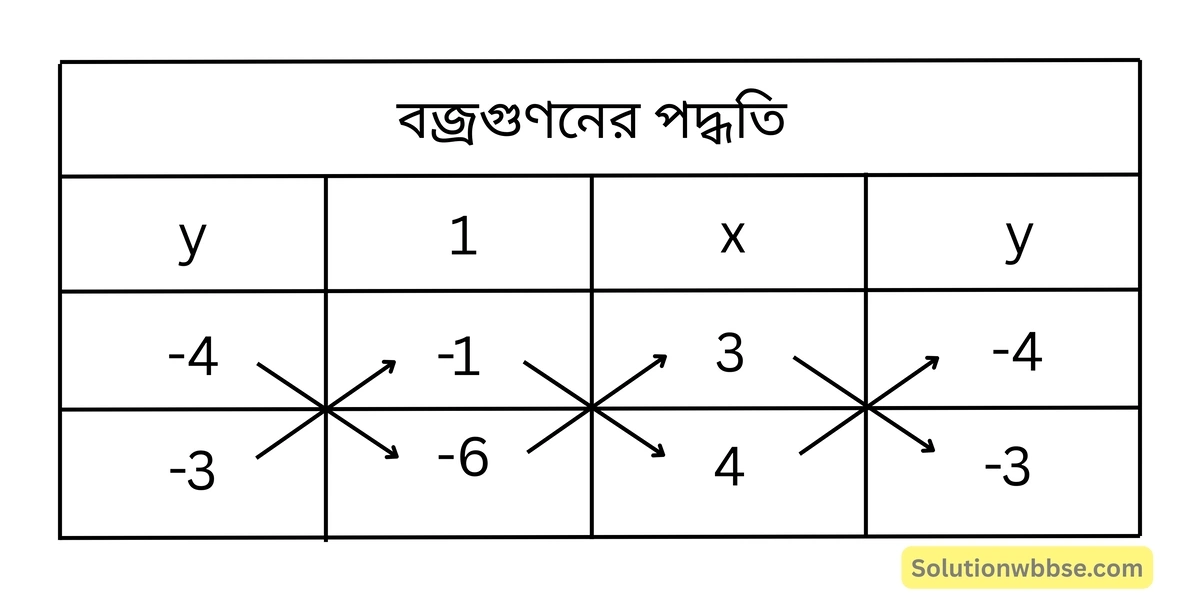
বা, \(\frac{x}{24-3} = \frac{y}{-4-(-18)} = \frac{1}{-9+16}\)
বা, \(\frac{x}{21} = \frac{y}{14} = \frac{1}{7}\)
সুতরাং, \(\frac{x}{21} = \frac{1}{7}\)
বা, \(x = \frac{21}{7}\)
বা, \(x = 3\)
এবং, \(\frac{y}{14} = \frac{1}{7}\)
বা, \(y = \frac{14}{7}\)
বা, \(y = 2\)
\(\therefore\) নির্ণেয় সমাধান \(x = 3\), \(y = 2\)।
3. \(5x+3y = 11\), \(2x-7y = -12\)
সমাধান –
\(5x+3y = 11\)বা, \(5x+3y-11 = 0 \quad -(i)\)
\(2x-7y = -12\)বা, \(2x-7y+12 = 0 \quad -(ii)\)
(i) নং ও (ii) নং সমীকরণদ্বয়কে বজ্রগুণন করে পাই,
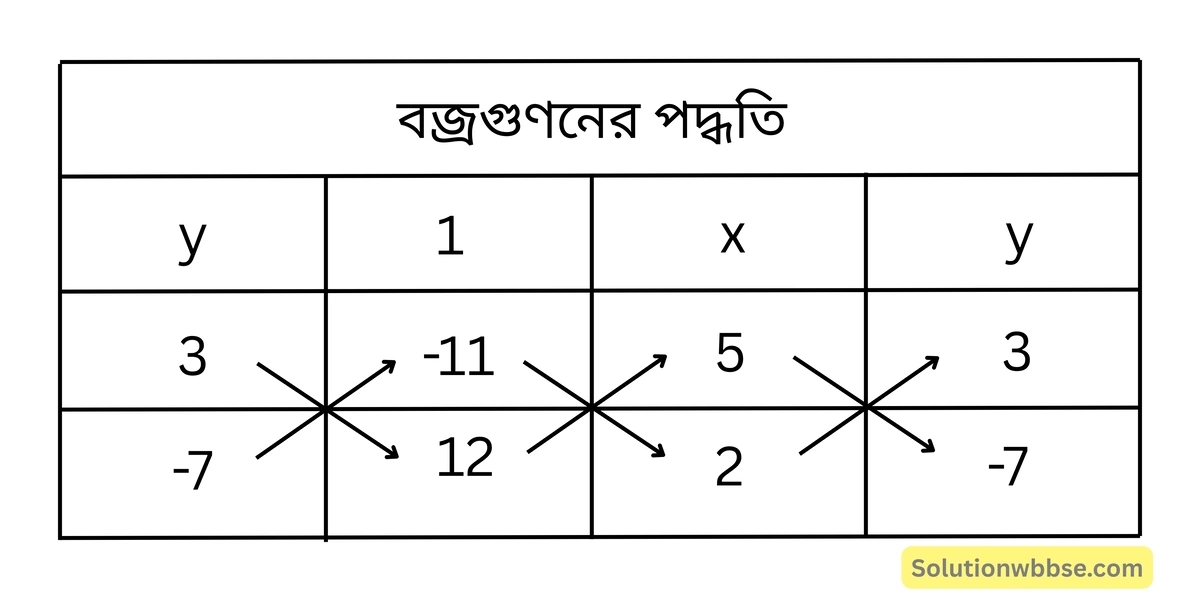
বা, \(\frac{x}{36-77} = \frac{y}{-22-60} = \frac{1}{-35-6}\)
বা, \(\frac{x}{-41} = \frac{y}{-82} = \frac{1}{-41}\)
সুতরাং, \(\frac{x}{-41} = \frac{1}{-41}\)
বা, \(x = \frac{-41}{-41}\)
বা, \(x = 1\)
এবং, \(\frac{y}{-82} = \frac{1}{-41}\)
বা, \(y = \frac{-82}{-41}\)
বা, \(y = 2\)
\(\therefore\) নির্ণেয় সমাধান \(x = 1\), \(y = 2\)
4. \(7x-3y-31 = 0\), \(9x-5y-41 = 0\)
সমাধান –
প্রদত্ত সমীকরণদ্বয় হল –
\(7x-3y-31 = 0\)\(9x-5y-41 = 0\)বজ্রগুণন করে পাই,
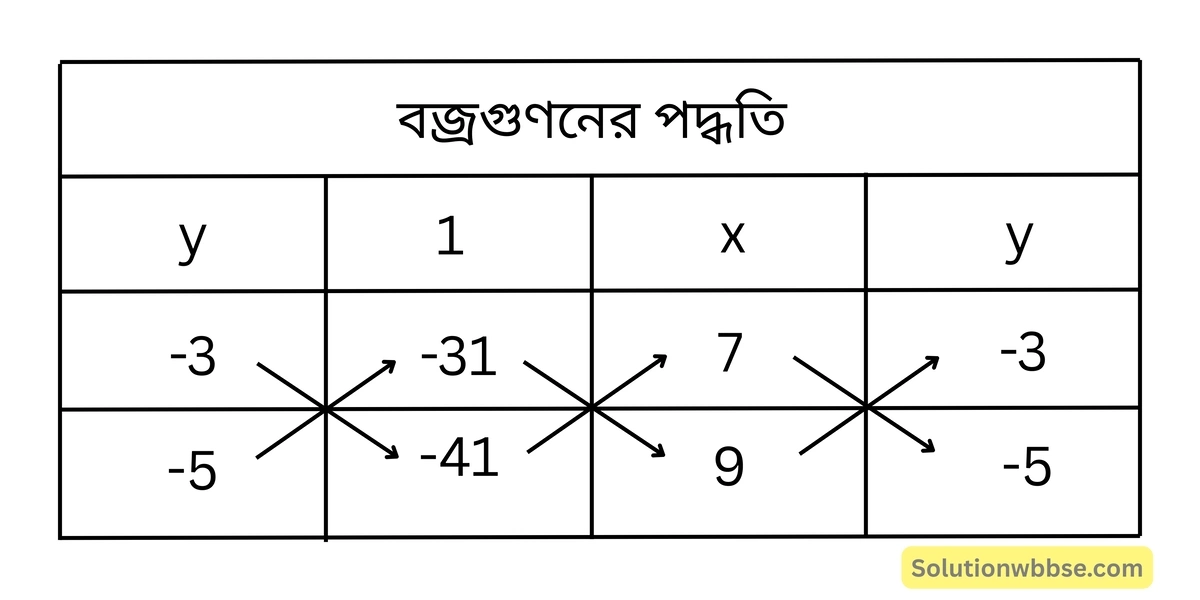
বা, \(\frac{x}{123-155} = \frac{y}{-279+287} = \frac{1}{-35+27}\)
বা, \(\frac{x}{-32} = \frac{y}{8} = \frac{1}{-8}\)
সুতরাং, \(\frac{x}{-32} = \frac{1}{-8}\)
বা, \(x = \frac{-32}{-8}\)
বা, \(x = 4\)
এবং, \(\frac{y}{8} = \frac{1}{-8}\)
বা, \(y = \frac{8}{-8}\)
বা, \(y = -1\)
\(\therefore\) নির্ণেয় সমাধান \(x = 4\), \(y = -1\)।
5. \(\frac{x}{6} – \frac{y}{3} = \frac{x}{12} – \frac{2y}{3} = 4\)
সমাধান –
প্রদত্ত সমীকরণদ্বয় হল –
\(\frac{x}{6} – \frac{y}{3} = 4 \quad -(i)\)\(\frac{x}{12} – \frac{2y}{3} = 4 \quad -(ii)\)(i) নং সমীকরণ থেকে পাই,
\(\frac{x}{6} – \frac{y}{3} = 4\)বা, \(\frac{x-2y}{6} = 4\)
বা, \(x-2y = 24\)
বা, \(x -2y -24 = 0 \quad -(iii)\)
(ii) নং সমীকরণ থেকে পাই,
\(\frac{x}{12} – \frac{2y}{3} = 4\)বা, \(\frac{x-8y}{12} = 4\)
বা, \(x- 8y = 48\)
বা, \(x -8y -48 = 0 \quad -(iv)\)
(iii) নং ও (iv) নং সমীকরণকে বজ্রগুণন করে পাই,
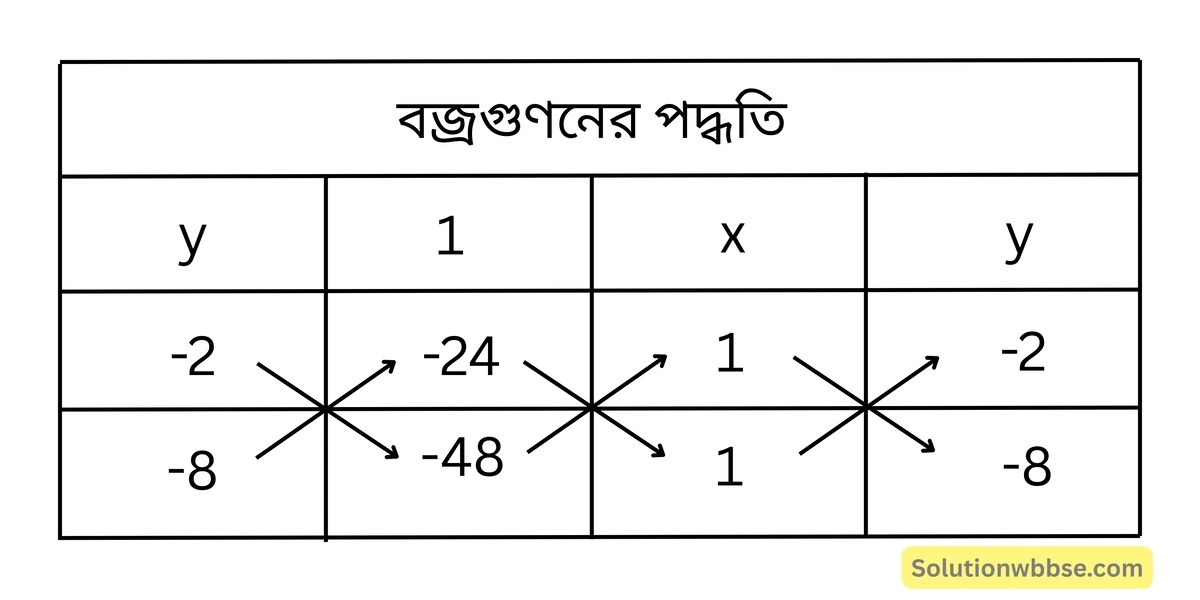
বা, \(\frac{x}{96-192} = \frac{y}{-24+48} = \frac{1}{-8+2}\)
বা, \(\frac{x}{-96} = \frac{y}{24} = \frac{1}{-6}\)
সুতরাং, \(\frac{x}{-96} = \frac{1}{-6}\)
বা, \(x = \frac{-96}{-6}\)
বা, \(x = 16\)
এবং, \(\frac{y}{24} = \frac{1}{-6}\)
বা, \(y = \frac{24}{-6}\)
বা, \(y = -4\)
\(\therefore\) নির্ণেয় সমাধান \(x = 16\), \(y = -4\)।
6. \(\frac{x}{5} + \frac{y}{3} = \frac{x}{4} – \frac{y}{3} – \frac{3}{20} = 0\)
সমাধান –
প্রদত্ত সমীকরণদ্বয় হল –
\(\frac{x}{5} + \frac{y}{3} = \frac{x}{4} – \frac{y}{3} – \frac{3}{20} = 0\)\(\therefore \frac{x}{5} + \frac{y}{3} = 0\)বা, \(\frac{3x+5y}{15} = 0\)
বা, \(3x+5y = 0 \quad -(i)\)
এবং, \(\frac{x}{4} – \frac{y}{3} – \frac{3}{20} = 0\)
বা, \(\frac{15x-20y-9}{60} = 0\)
বা, \(15x -20y – 9 = 0 \quad -(ii)\)
(i) নং ও (ii) নং সমীকরণ দ্বয়কে বজ্রগুণন করে পাই,
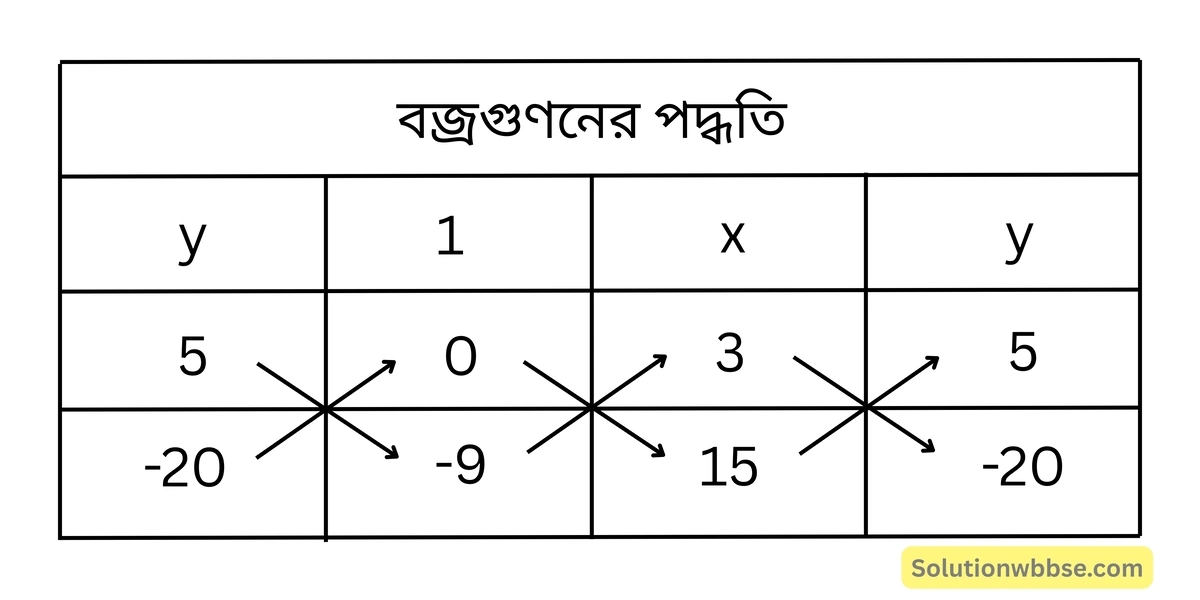
বা, \(\frac{x}{-45} = \frac{y}{27} = \frac{1}{-60-75}\)
বা, \(\frac{x}{-45} = \frac{y}{27} = \frac{1}{-135}\)
সুতরাং, \(\frac{x}{-45} = \frac{1}{-135}\)
বা, \(x = \frac{-45}{-135}\)
বা, \(x = \frac{1}{3}\)
এবং, \(\frac{y}{27} = \frac{1}{-135}\)
বা, \(y = \frac{27}{-135}\)
বা, \(y = -\frac{1}{5}\)
\(\therefore\) নির্ণেয় সমাধান \(x = \frac{1}{3}\), \(y = -\frac{1}{5}\)।
7. \(\frac{x+2}{7} + \frac{y-x}{4} = 2x – 8\), \(\frac{2y-3x}{3} + 2y = 3x + 4\)
সমাধান –
প্রদত্ত সমীকরণদ্বয় হল –
\(\frac{x+2}{7} + \frac{y-x}{4} = 2x – 8 \quad -(i)\)\(\frac{2y-3x}{3} + 2y = 3x + 4 \quad -(ii)\)(i) নং সমীকরণ থেকে পাই,
\(\frac{x+2}{7} + \frac{y-x}{4} = 2x – 8\)বা, \(\frac{4(x+2)+7(y-x)}{28} = 2x-8\)
বা, \(\frac{4x+8+7y-7x}{28} = 2x -8\)
বা, \(7y -3x +8 = 28(2x-8)\)
বা, \(7y -3x +8 = 56x – 224\)
বা, \(-3x -56x +7y = -8 -224\)
বা, \(-59x +7y = -232\)
বা, \(59x -7y – 232 = 0 \quad -(iii)\)
(ii) নং সমীকরণ থেকে পাই,
\(\frac{2y-3x}{3} + 2y = 3x + 4\)বা, \(\frac{2y-3x+6y}{3} = 3x +4\)
বা, \(8y -3x = 9x +12\)
বা, \(8y -3x -9x = 12\)
বা, \(8y – 12x = 12\)
বা, \(2y -3x = 3\)
বা, \(3x -2y +3 = 0 \quad -(iv)\)
(iii) নং ও (iv) নং সমীকরণ দ্বয়কে বজ্রগুণন পদ্ধতি প্রয়োগ করে পাই,
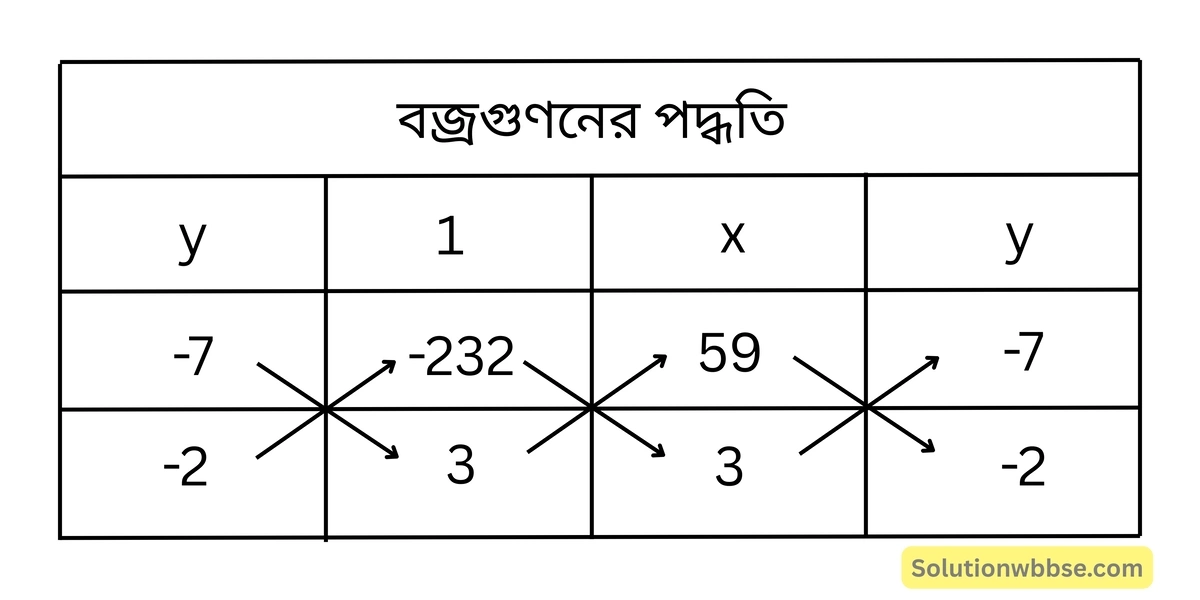
বা, \(\frac{x}{-21-464} = \frac{y}{-696-177} = \frac{1}{-118+21}\)
বা, \(\frac{x}{-485} = \frac{y}{-873} = \frac{1}{-97}\)
সুতরাং, \(\frac{x}{-485} = \frac{1}{-97}\)
বা, \(x = \frac{-485}{-97}\)
বা, \(x = 5\)
এবং, \(\frac{y}{-873} = \frac{1}{-97}\)
বা, \(y = \frac{-873}{-97}\)
বা, \(y = 9\)
\(\therefore\) নির্ণেয় সমাধান \(x = 5\), \(y = 9\)।
8. \(x+5y = 36\), \(\frac{x+y}{x-y} = \frac{5}{3}\)
সমাধান –
প্রদত্ত সমীকরণদ্বয় হল –
\(x+5y = 36\)বা, \(x+5y -36 = 0 \quad -(i)\)
এবং, \(\frac{x+y}{x-y} = \frac{5}{3}\)
বা, \(3(x+y) = 5(x-y)\)
বা, \(3x+3y = 5x -5y\)
বা, \(3x -5x = -5y-3y\)
বা, \(-2x = -8y\)
বা, \(x = 4y\)
বা, \(x-4y = 0 \quad -(ii)\)
(i) নং ও (ii) নং সমীকরণদ্বয়কে বজ্রগুণন করে পাই,
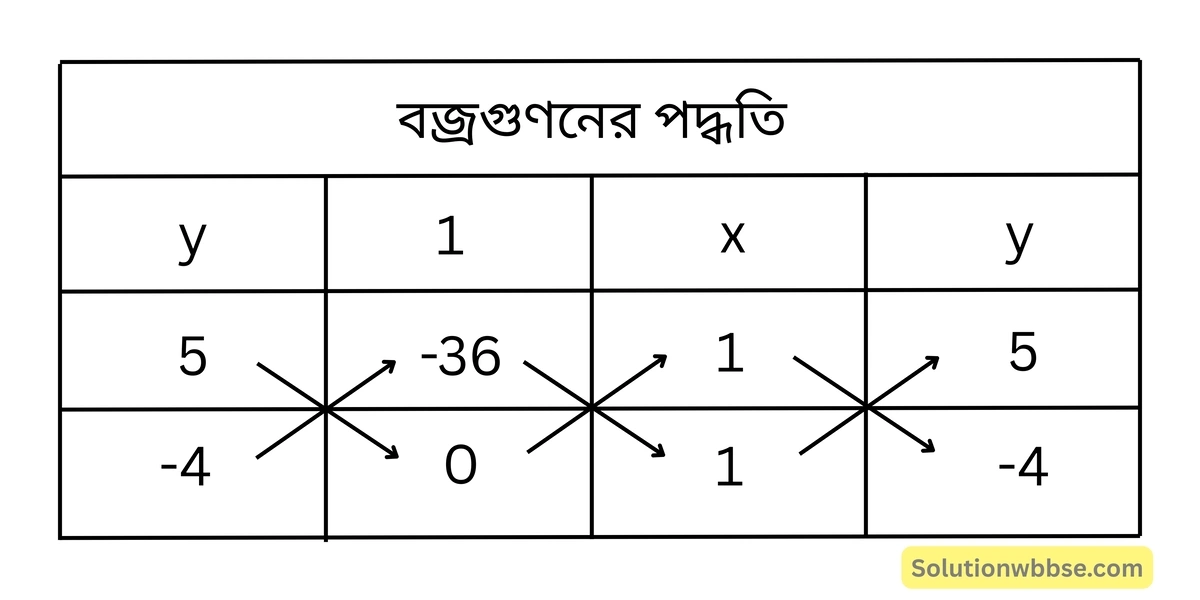
বা, \(\frac{x}{-144} = \frac{y}{-36} = \frac{1}{-9}\)
সুতরাং, \(\frac{x}{-144} = \frac{1}{-9}\)
বা, \(x = \frac{-144}{-9}\)
বা, \(x = 16\)
এবং, \(\frac{y}{-36} = \frac{1}{-9}\)
বা, \(y = \frac{-36}{-9}\)
বা, \(y = 4\)
\(\therefore\) নির্ণেয় সমাধান \(x = 16\), \(y = 4\)।
9. \(13x -12y +15 = 0\), \(8x -7y = 0\)
সমাধান –
\(13x -12y +15 = 0\)\(8x -7y = 0\)বজ্রগুণন করে পাই,
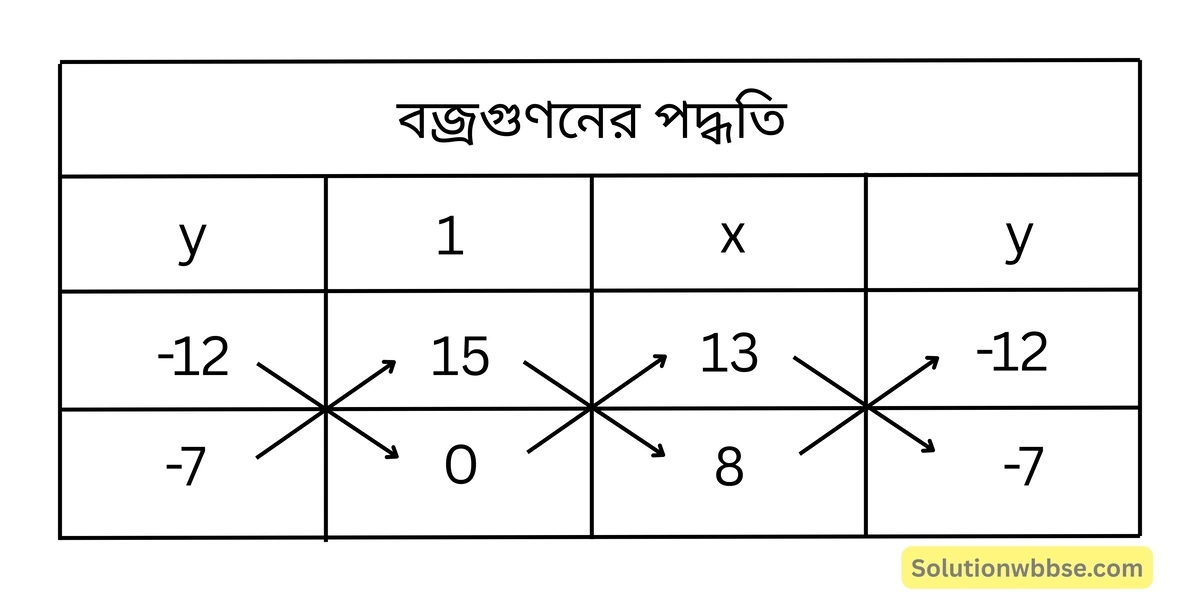
বা, \(\frac{x}{105} = \frac{y}{120} = \frac{1}{5}\)
সুতরাং, \(\frac{x}{105} = \frac{1}{5}\)
বা, \(x = \frac{105}{5}\)
বা, \(x = 21\)
এবং, \(\frac{y}{120} = \frac{1}{5}\)
বা, \(y = \frac{120}{5}\)
বা, \(y = 24\)
\(\therefore\) নির্ণেয় সমাধান \(x = 21\), \(y = 24\)।
10. \(x+y = 2b\), \(x-y = 2a\)
সমাধান –
\(x+y = 2b\)বা, \(x +y -2b = 0 \quad -(i)\)
\(x-y=2a\)বা, \(x -y-2a = 0 \quad -(ii)\)
(i) নং ও (ii) নং সমীকরণদ্বয়কে বজ্রগুণন করে পাই,
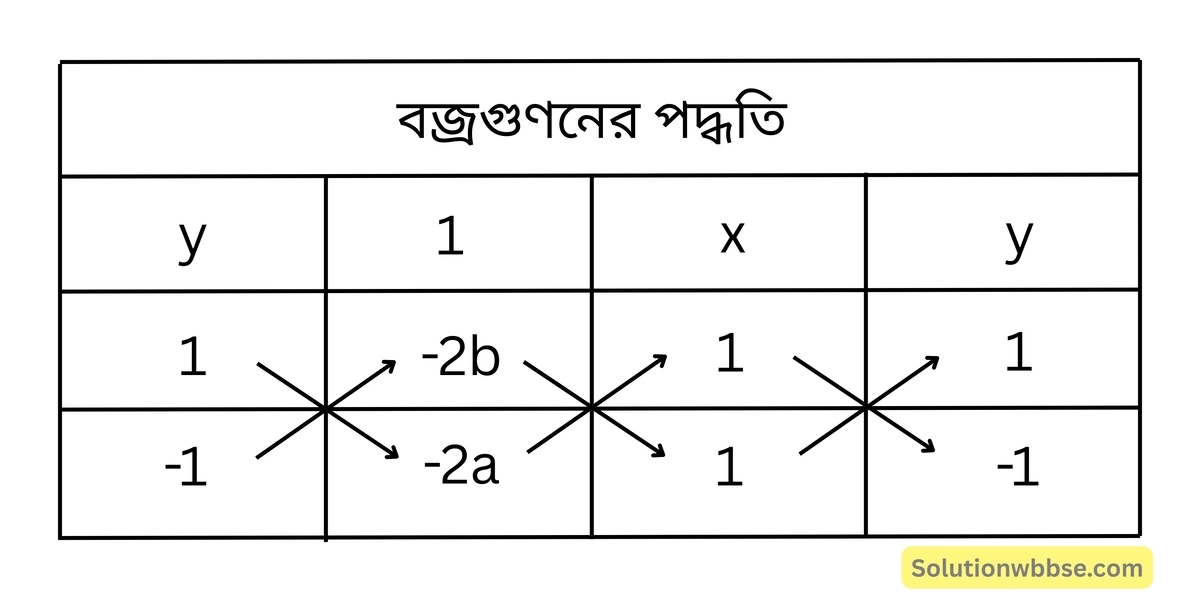
বা, \(\frac{x}{-2a-2b} = \frac{y}{-2b+2a} = \frac{1}{-1-1}\)
বা, \(\frac{x}{-2(a+b)} = \frac{y}{-2(b-a)} = \frac{1}{-2}\)
সুতরাং, \(\frac{x}{-2(a+b)} = \frac{1}{-2}\)
বা, \(x = \frac{-2(a+b)}{-2}\)
বা, \(x = (a+b)\)
এবং, \(\frac{y}{-2(b-a)} = \frac{1}{-2}\)
বা, \(y = \frac{-2(b-a)}{-2}\)
বা, \(y = (b-a)\)
\(\therefore\) নির্ণেয় সমাধান \(x = (a+b)\), \(y = (b-a)\)।
11. \(x -y = 2a\), \(ax+by = a^2+b^2\)
সমাধান –
প্রদত্ত সমীকরণদ্বয় হল –
\(x -y = 2a\)বা, \(x -y -2a = 0 \quad -(i)\)
এবং, \(ax+by =a^2+b^2\)
বা, \(ax+by -(a^2+b^2) = 0 \quad -(ii)\)
এখন, (i) ও (ii) নং সমীকরণ দুটিকে বজ্রগুণন করে পাই,
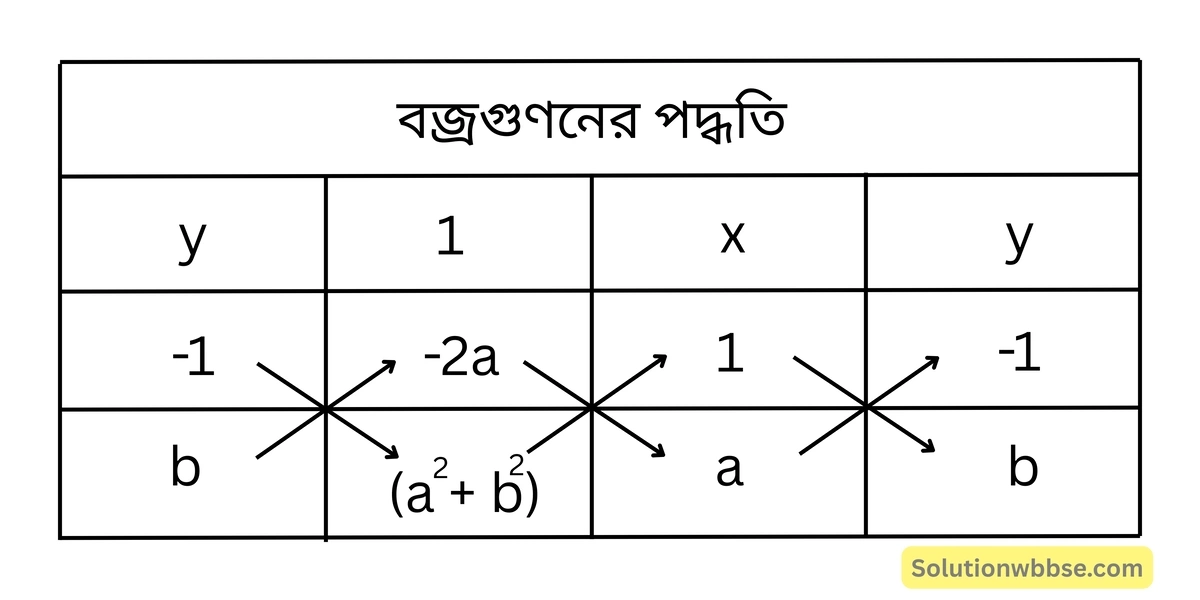
বা, \(\frac{x}{(a^2+b^2)+2ab} = \frac{y}{-2a^2+a^2+b^2} = \frac{1}{b+a}\)
বা, \(\frac{x}{(a+b)^2} = \frac{y}{b^2-a^2} = \frac{1}{b+a}\)
বা, \(\frac{x}{(a+b)^2} = \frac{y}{(b+a)(b-a)} = \frac{1}{b+a}\)
সুতরাং, \(\frac{x}{(a+b)^2} = \frac{1}{b+a}\)
বা, \(x = \frac{(a+b)^2}{(a+b)}\)
বা, \(x = (a+b)\)
এবং, \(\frac{y}{b^2-a^2} = \frac{1}{b+a}\)
বা, \(y = \frac{b^2-a^2}{(b+a)}\)
বা, \(y = \frac{(b+a)(b-a)}{(b+a)}\)
বা, \(y = (b-a)\)
\(\therefore\) নির্ণেয় সমাধান \(x = (a+b)\), \(y = (b-a)\)।
12. \(\frac{x}{a} + \frac{y}{b} = 2\), \(ax – by = a^2 – b^2\)
সমাধান –
প্রদত্ত সমীকরণদ্বয় হল –
\(\frac{x}{a} + \frac{y}{b} = 2\)বা, \(\frac{bx+ay}{ab} = 2\)
বা, \(bx + ay – 2ab = 0 \quad -(i)\)
এবং, \(ax – by = a^2 – b^2\)
বা, \(ax – by – (a^2 – b^2) = 0 \quad -(ii)\)
(i) নং ও (ii) নং সমীকরণদ্বয়কে বজ্রগুণন করে পাই,
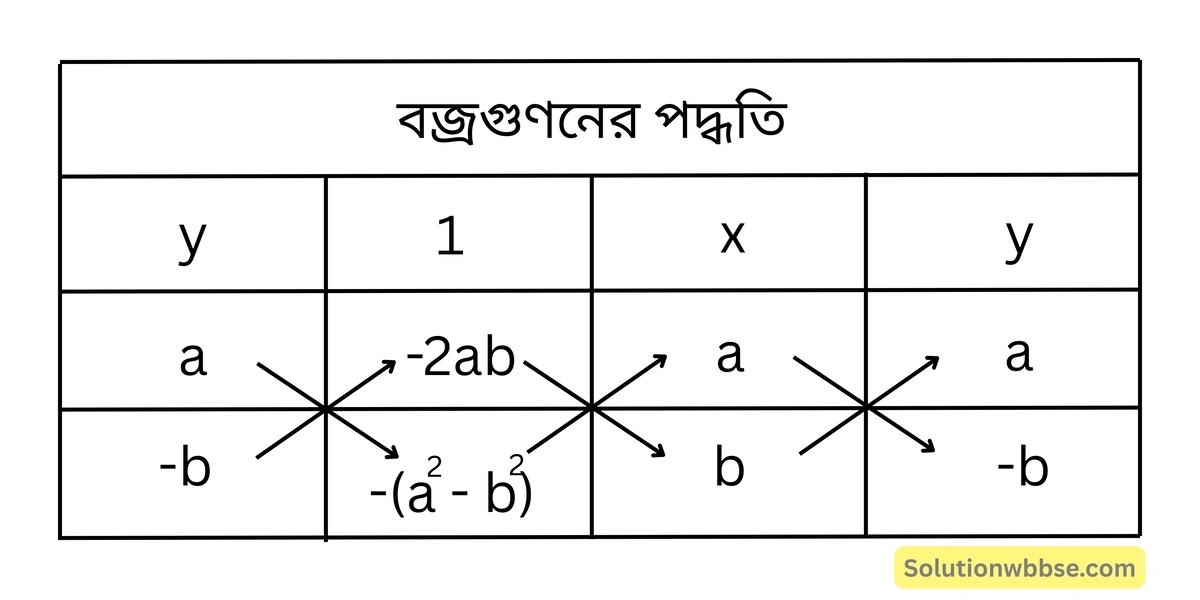
বা, \(\frac{x}{-a^3+ab^2-2ab^2} = \frac{y}{-2a^2b+a^2b-b^3} = \frac{1}{-b^2-a^2}\)
বা, \(\frac{x}{-a^3-ab^2} = \frac{y}{-a^2b-b^3} = \frac{1}{-(b^2+a^2)}\)
বা, \(\frac{x}{-a(a^2+b^2)} = \frac{y}{-b(a^2+b^2)} = \frac{1}{-(b^2+a^2)}\)
সুতরাং, \(\frac{x}{-a(a^2+b^2)} = \frac{1}{-(b^2+a^2)}\)
বা, \(x = \frac{-a(a^2+b^2)}{-(b^2+a^2)}\)
বা, \(x = a\)
এবং, \(\frac{y}{-b(a^2+b^2)} = \frac{1}{-(b^2+a^2)}\)
বা, \(y = \frac{-b(a^2+b^2)}{-(b^2+a^2)}\)
বা, \(y = b\)
\(\therefore\) নির্ণেয় সমাধান \(x = a\), \(y = b\)।
13. \(ax + by = 1\), \(bx + ay = \frac{2ab}{a^2+b^2}\)
সমাধান –
প্রদত্ত সমীকরণদ্বয় হল –
\(ax + by = 1\)বা, \(ax + by – 1 = 0 \quad -(i)\)
এবং, \(bx + ay = \frac{2ab}{a^2+b^2}\)
বা, \(b(a^2+b^2)x + a(a^2+b^2)y = 2ab\)
বা, \(b(a^2+b^2)x + a(a^2+b^2)y – 2ab = 0 \quad -(ii)\)
(i) নং ও (ii) নং সমীকরণদ্বয়কে বজ্রগুণন করে পাই,
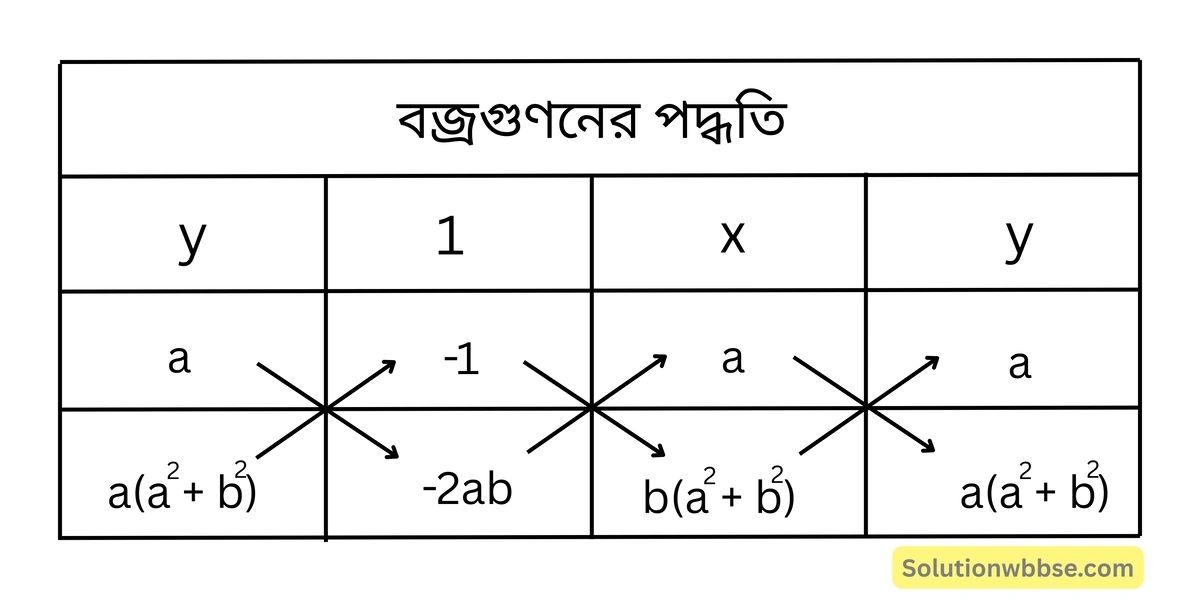
বা, \(\frac{x}{-2ab^2 + a^3 + ab^2} = \frac{y}{-ba^2 – b^3 + 2a^2b} = \frac{1}{a^4 + a^2b^2 – b^2a^2 – b^4}\)
বা, \(\frac{x}{a^3 – ab^2} = \frac{y}{-b^3 + a^2b} = \frac{1}{a^4 – b^4}\)
বা, \(\frac{x}{a(a^2-b^2)} = \frac{y}{b(a^2-b^2)} = \frac{1}{(a^2-b^2)(a^2+b^2)}\)
সুতরাং, \(\frac{x}{a(a^2-b^2)} = \frac{1}{(a^2-b^2)(a^2+b^2)}\)
বা, \(x = \frac{a(a^2-b^2)}{(a^2-b^2)(a^2+b^2)}\)
বা, \(x = \frac{a}{a^2+b^2}\)
এবং, \(\frac{y}{b(a^2-b^2)} = \frac{1}{(a^2-b^2)(a^2+b^2)}\)
বা, \(y = \frac{b(a^2-b^2)}{(a^2-b^2)(a^2+b^2)}\)
বা, \(y = \frac{b}{a^2+b^2}\)
\(\therefore\) নির্ণেয় সমাধান \(x = \frac{a}{a^2+b^2}\), \(y = \frac{b}{a^2+b^2}\)।
এই আর্টিকেলে নবম শ্রেণির গণিতের ‘রৈখিক সহসমীকরণ (দুই চল বিশিষ্ট)’ অধ্যায়ের ‘কষে দেখি – 5.6’-এর সমস্ত গাণিতিক সমস্যার সমাধান তুলে ধরা হয়েছে। আশা করি, এই পোস্টটি আপনাদের বা শিক্ষার্থীদের পরীক্ষার প্রস্তুতিতে সহায়ক হবে।
কোনো প্রশ্ন, মতামত বা সাহায্যের প্রয়োজন হলে নিচে কমেন্ট করতে পারেন অথবা সরাসরি আমাদের টেলিগ্রাম চ্যানেলে যোগাযোগ করুন। আমরা আপনাদের সব প্রশ্নের উত্তর দেওয়ার জন্য সর্বদা প্রস্তুত।






মন্তব্য করুন